Reconsidering “The inappropriateness of conventional cephalometrics”

Abstract

Of all the articles on cephalometrics published in the AJO-DO during the last half-century, the one most cited in the scientific literature is the 1979 article, “The inappropriateness of conventional cephalometrics,” by Robert Moyers and me. The durable salience of this article is perplexing; its critique was misdirected (it should have been aimed at the craniometrics of the early twentieth century, not merely the roentgenographic extension used in the orthodontic clinic), and its proposed remedies have all failed to establish themselves as methods of any broad utility. When the problems we highlighted have been resolved at all, the innovations that resolved them owe to tools very different from those we suggested and were imported from fields quite a bit farther from biometrics than we expected back in 1979. One of these tools was the creation de novo of a new abstract mathematical construction, statistical shape space, in the 1980s and 1990s; another was a flexible and intuitive new graphic, the thin-plate spline, for meaningfully and suggestively visualizing a wide variety of biological findings in these spaces. On the other hand, many of the complaints Moyers and I enunciated back in 1979, especially those stemming from the disarticulation of morphometrics from the explanatory styles and purposes of clinical medicine, remain unanswered even today. The present essay, a retrospective historical meditation, reviews the context of the 1979 publication, its major themes, and its relevance today. This essay is dedicated to the memory of Robert E. Moyers on the 100th anniversary of the American Journal of Orthodontics and Dentofacial Orthopedics.

Introduction

“The inappropriateness of conventional cephalometrics,” is the title of a lecture, originally delivered by Robert E. Moyers (1919–1996) and me on May 17, 1978 in London (Cordwainers Lecture, Institute of Dental Surgery, University of London). A subsequent article bearing the same name was published in this journal in 1979,¹ and today is the most-cited article on cephalometrics of the last 50 years. Its title, though intentionally provocative, was not an exaggeration, and its argument, viewed from 37 years on, can still be viewed as a daring piece of intellectual criticism. From Moyers’ point of view it must have felt like a pitiless intellectual self-portrait, an explicit and mostly destructive critique of the biostatistical methodology embraced by the clinical profession (orthodontics) that he had served, as an academic chairman for 15 years and then as the director of an even more interdisciplinary research center (craniofacial growth and development) for 15 years more.²

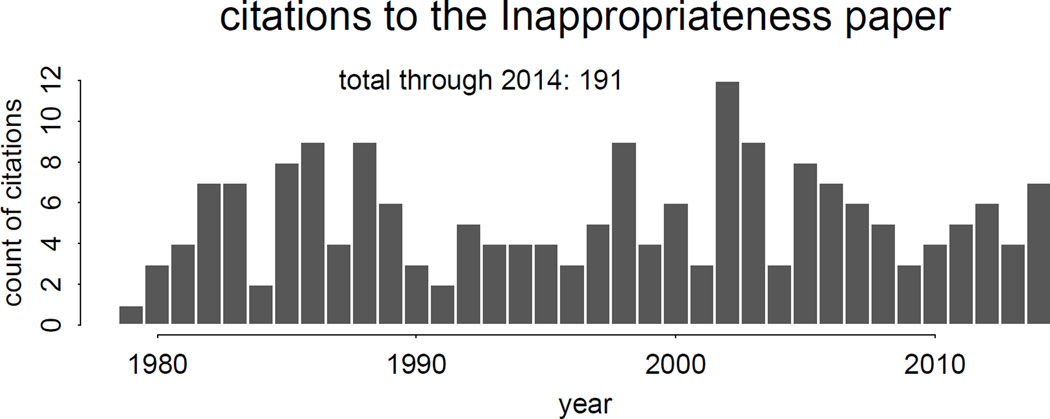
The citation history of the article differs strikingly from the early-peaking, long-tailing shape that constitutes the commonest form of citation history for peer-reviewed biomedical articles in primary research journals. As Figure 1 shows, “Inappropriateness” (as I will be referring to the article in these pages, for brevity) has been cited steadily, though irregularly, throughout the whole time span since its appearance. The year of peak citation count, in fact, was 2002, nearly a quarter of a century after its publication and 6 years after the death of its senior author, and it was cited as many times in 2014 as it was in 1982 or 1983. The article is actually the senior author’s most cited journal article (although of course there are far more citations to his celebrated textbook of orthodontics), and it also serves as my own most-cited article on any aspect of skeletal or craniofacial biology. Those who were present at its original presentation surely numbered dozens more.

Figure 1.

Citation history of Inappropriateness1. Data from the Thomson-Reuters Web of ScienceTM, retrieved June 19, 2015.

In addition to this odd stability of citation frequency, or perhaps in spite of it, Inappropriateness is unusual for 2 other reasons. As I already hinted, it objects to the methodology of nearly everything else that its senior author had recently published, including the long-awaited and widely distributed Atlas of Craniofacial Growth³ that had appeared just a few years earlier; and every methodological resolution that it prophesied for the problems and infelicities it diagnosed proved just about as inappropriate as the conventional methods that were pilloried in its own pages.

Whereas I was the brash young applied mathematician (less than 2 years past my own Ph.D.) slashing through the lore of an established field (clinical orthodontics) in which I had neither training nor professional stake, Moyers had committed decades of his career to publications based in just the quantitative language regarding which he had already turned skeptical, a language I seemed to be trying to demolish. But the proposed upgrades of method I offered Moyers’ readers in 1979 did not last even 5 years. Already by 1984, for instance, biorthogonal grids, the core technique of my doctoral dissertation,⁴ had been replaced by the shape coordinates (see below) that proved far more suitable for statistical summaries such as variance and covariance. So my co-author had far more status at risk than I had, and yet his contributions to the radical part of the argument proved far more cogent than mine. Of the systematic charges that Inappropriateness laid against conventional cephalometrics— I will review them below under the rubrics of “fabrication,” “camouflage,” “confusion,” and “subtraction” — some remain unresolved to this day, while those that have been resolved owe their resolution not to the techniques we identified as promising— representations of curvature, medial axes, and biorthogonal grids — but to innovations arising from other branches of biometrics and medical image analysis entirely: the class of methods that are nowadays generally referred to as geometric morphometrics (GMM).

That was not what I expected the fate of Inappropriateness to be. Nor did I properly understand its own academic context, which was not the setting of craniofacial biology into which Moyers had inducted me when he appointed me assistant research scientist in his Center for Human Growth and Development at the University of Michigan in 1977, but the much older context of anthropometry and in particular craniometry^* that had been under relatively unsupervised development since at least the turn of the twentieth century. That “there is no theory of cephalometrics,” as Inappropriateness cogently argued, is because there was not and never had been any proper methodology of craniometrics either. The channels of “misinformation” that Inappropriateness unearthed were entirely exogenous in their origin: the combination of problems pervading all of twentieth-century craniometry with the newer ambiguities of a purportedly standardized medical imaging modality, to wit, cephalography. The solution to the problems highlighted by Moyers and me awaited a proper biometrical theory of the way that patterns of geometry in medical images could be turned into valid inferences about the underlying biological processes; but this theory did not exist until very recently, when Inappropriateness was already more than a third of a century old.

A brief iconoclastic history

A substantial minority of the problems that Moyers and I complained about were an intrinsic component of the classical stance in anthropometrics that had been in place since before he was born. I knew none of this back in 1979; it has come to my attention only since I’ve been professor of anthropology at the University of Vienna. As I have already noted in 2 recent books,^7,8 the incoherence of craniometry as a scientific methodology was already clear in Rudolf Martin’s great textbook Lehrbuch der Anthropologie (first edition, one volume, 1914; second edition, three volumes, 1928, posthumous).⁶ Martin seems to have been concerned that an earlier generation of anthropometrists tabulated averages or ranges of physical measurements such as lengths, ratios, and angles without any principled basis for the list of measures thus presented. For instance, the Croatian anthropologist Karl (Dragutin) Gorjanovi´c -Kramberger, in his great treatise of 1906 on the newly identified Krapina Neanderthals,⁹ couched his rhetoric of group comparisons as “tabular overviews” (tabellarische Übersichte) of seemingly arbitrary lists (cf. page 119 or page 167) each of which “instructs us” (belehrt uns) about what group a particular reconstructed skull “doubtless belongs to” (zweifellos angehört).

Martin’s solution was a clever one: to focus on the actual formulas for the entries in these tables. (Our current approach emphasizes rather the information in the locations of the points that drive those formulas, but information in this narrowly statistical sense would not be invented for another 30 years.) As those formulas all involved measurements keyed to the locations of specific points, he called them Meßpunkte, “measuring points”; today, in English and in most other European languages, we call them “landmarks.” Martin systematized the images of these points in multiple views and wrote out all of their operational definitions at length. By the time of the 1928 edition there were 68 of these points. What remained was to list all the distances that anybody had ever reported among pairs of these points, all the lines set by pairs of points or tangents to curves, and all the ratios of 2 distances, heights of triangles, and 3-point or 4-point angles that any of his colleagues had ever used. The list of these indices ran to dozens of pages, many augmented by little tables of cutpoints for words like “brachycephalic” or averages by racial/ethnic group.

The missing “theory” of cephalometrics (or craniometrics) that Inappropriateness was referring to was reified in the chaos of Martin’s lists. Such a disorder persevered right into Moyers’ own work: the roster of measurements entailed in the Riolo et al. Atlas of 1974³ was the exact equivalent of Martin’s approach when the points were restricted to the 45 highlighted there — the measurements tabulated were an equally arbitrary selection of all the possible choices (990 distinct distances among pairs of the 45 points, 42570 distances from points to lines, 85140 angles) potentially pertinent to analysis of the same data resource of point locations. The development of morphometrics from the late 1970s on can be summarized as a technology for literally reversing the logic Martin was instantiating: not guessing first at distances or ratios, then tabulating them for purposes of group comparison, but instead letting the group comparisons themselves (or the multivariate equivalents, such as shape regressions or principal components) drive the specification of variables or composites. The biorthogonal method highlighted in Inappropriateness’ constructive comments was a first attempt at this reversal, but it did not support any parallel statistical method, and so was quickly replaced by the shape space methods that my colleagues and I would develop a few years later.

At just about the same time as Martin’s first edition, D’Arcy Thompson¹⁰ was announcing his “method of Cartesian transformations.” (My biorthogonal method actually incorporated a variant of this.) In this approach, which can be traced back centuries, any single shape comparison could be plausibly rendered as the deformation of a piece of graph paper. (Around 1960, by relaxing the constraint of continuity, Coenraad Moorrees would convert this into an explicit diagnostic technique, his “mesh method.”¹¹) But in the absence of appropriate statistical tools for samples of these grids, the visualization served mainly as a charming diversion, always “promising” but ultimately no help for any form of quantitative persuasion, calibration, or theory-testing. (I reviewed the general history of Thompson’s suggestion in 1978.⁴)

I noted above that Inappropriateness was this journal’s most-cited discussion of cephalometrics of the last half-century. If the date filter is disabled, however, a new winner emerges: Cecil Steiner’s “Cephalometrics for you and me,” published in 1953.¹² “The cephalometer is here to stay,” he opined, but is not yet in general use by clinical orthodontists, who must steel themselves to “master its mysteries.” He continued: “Hundreds of measurements and combinations of measurements [ratios] can be made from cephalometric x-rays. Many of these have value…. In our office, the following measurements and assessments are made. I now shall attempt to justify them.” In other words, Steiner conceded the main point Inappropriateness would make 26 years later: there would be no intersubjective basis for the quantifications that underlie cephalometric clinical judgments in any of the conventional systems — no logical basis for the proferred number of different features of form worth measuring, nor for the specific formulations of the distances, angles, or ratios that are put forward in order to measure them.

Steiner began with the problem of telling left-side landmarks from right, a point we overlooked, because the Atlas used averaged bilateral landmarks only. After that, he was particularly concerned to locate Porion; we shall see presently that the team assembled by Horst Seidler in Vienna in 1998 ended up instead abandoning the very idea of landmark-based registration (whether via the Frankfort Horizontal, which required Porion for its alignment, or any other rule). The justification of the Frankfort, though, is because it was traditional for anthropologists in that its reference points were on the outer surface of the skull, where they were visually accessible. This is an unconvincing basis for a methodology like the Broadbent-Bolton that is intended for x-ray images instead. While the internal midsagittal points could not be located by the conventional anthropologist without hemisecting an actual skull, some bilateral landmarks could be located from the lateral cephalogram with great precision indeed. Steiner highlighted particular angles that he measured, among them the angle ANB, without ever admitting the possibility that what he was actually recommending was a scientific method — that its ambit might go beyond the task of clinical description so as to also embrace the assignment of making and verifying truth claims that could then be brought to bear upon clinical observations of the single case.

Where Steiner was interested in representing the motion of the mandible over the opening-closing cycle, including a representation of a condylar “axis” that was explicitly criticized in Inappropriateness, Moyers and his colleagues in the Atlas work were more concerned with changes over time. For this they exploited a statistical method quite a bit older than Martin’s work: the method of growth charts that Edith Boyd¹³ reviewed from its origins in the 1700s. The tradition of referring growth to such charts, one distance or other extensive measure per page, was well-established by midcentury (see, for example, the systematic survey of California schoolchildren’s growth by Tuddenham and Snyder¹⁴). But, in what is an irony for our present purposes, the statistics for a proper analysis of groups of such curves did not mature until well into the 1990s (cf. Ramsay and Silverman¹⁵) and remains a topic of active research even today.¹⁶

Similarly, the methods for combination of multiple measurements (what is now called “multivariate analysis”) that were in the hands of the anthropologists by the 1950s (see Srivastava¹⁷ for a bit of history) did not acknowledge the possibility that measurements of landmark configurations would have to be treated differently. The problem was well-known since the work of Beni Solow in the 1960s¹⁸ — correlations of measurements overlapping in their lists of reference points were not distributed around zero the way textbook Fisherian theory presumed they should be — but no solution would be at hand until the mid-1990s (the principal components of shape with respect to Procrustes distance; see below).

If craniometrics can be blamed for about half the dilemmas that Inappropriateness was pinpointing, the other half can be attributed to the particular geometric problems of getting to measurements from roentgenography, the projection imagery that likewise predated my own life by at least half a century. Martin⁶ could describe his canonical views (norma lateralis, norma frontalis, etc. — what Melvin Moss somewhere sardonically referred to as “the six ladies of the cephalometric laboratory”) by direct inspection of the solid objects being measured. But the orthodontist could not see these objects, and every rule for their standardization came up against the same repeated objection — that the form-variations one was interested in discussing were entangled with the very conventions according to which those skulls were being reduced to flat images and then discrete points in the course of measurement.

The basic intuition driving the cephalostat — that general variations of a form as complicated as the human skull, even a nominally symmetric skull, can be captured by a set of just a few views at fixed angles to one another — is mathematically unfounded and geometrically unsound. The best critical language had not yet been developed (this theme will recur many times in my pages today); it was first crystallized in accessible textbook form at the surprisingly late date of 1990 by the Dutch physicist Jan Koenderink.¹⁹ Koenderink’s book, as its title (Solid Shape) implies, deals with a variety of formalisms for comprehending and apprehending shape features of smoothly curving surfaces in 3 dimensions by looking at them from various directions carefully calculated so as to highlight a range of explicit features of those same surfaces. A surprising number of these features — call them “silhouettes,” the name they are assigned in the portrait literature— are manifest in the edges of these surfaces as they appear in projected images. (Please do not confuse these images with sections of the original solid; they are representations of surface geometry only.) The apparent edges of these projected images can have a variety of features, such as extremes of curvature (e.g., Gonion) or self-intersections (e.g., Articulare, Pterygomaxillary Fissure). Usually these and their analogues over the whole form are explicit functions of the coordinate system used for projecting the surface down onto a plane. Because they are coordinate-dependent, in turn, their locations are not functions of the biological form per se, but also depend on the choice of coordinate system, which is, of course, a human artifact.

A prime example is Orbitale, “the lowest point of the orbital rim.” Martin⁶ said of this point, “Es dient nicht als Meßpunkt” (p. 556) — it does not serve as a landmark; its sole function is to help align what he called the Ohraugen-Ebene, the ear-eye plane (nowadays the Frankfort plane). Orbitale is not a landmark because it is not actually on a curve; “the orbital rim” is not a well-defined curve on the actual cranial form, nor does it lie on any silhouette of the projected surface. Its location on the lateral cephalogram is entirely an aesthetic judgment corresponding to the schema of Koenderink’s¹⁹ Figure 418 when the book is viewed upside-down.

Such points are never among the Meßpunkte accepted by Martin in his craniometric discussions of a century ago. Rather, nearly all of Martin’s landmarks are intersections of curves, sometimes on the external surface of the skull and otherwise on the intersection of the solid form with its (nominal) midsagittal plane. This applies even when the curve in question is not itself explicit on the skull. Thus Porion (Martin⁶, page 512) is defined as a point on the upper margin of the porus acusticus externus, but that opening does not actually have an “upper border,” any more than the bell of a tuba does (if you ignore the actual edge where the metal stops).

Inasmuch as neither Orbitale nor Porion is a valid craniometric point, then the “line” they delineate, the Frankfort horizontal, cannot be a component of any biologically valid quantification. The problem is not their ambiguity as points sampled upon curves, but rather the nonexistence of the curves on which they purportedly lie: these are, in truth, curves neither on the solid skull nor on its radiographic image. Findings dependent on the Frankfort horizontal, therefore, cannot even be considered to be multilocal, analogous to angles among three or four points. Rather, the dependence of any measure on the Frankfort is entirely an artifact of where the observer chooses to place the nonphysical points Porion and Orbitale that purport to summarize small regions of the projected image.

Interestingly, it was precisely this incoherence of the classical notion of the Frankfort plane that induced Horst Seidler, Professor of Anthropology at the University of Vienna, to assemble the conference in 1998 at which contemporary geometric morphometric ideas were first introduced to the European craniometric community. The conference instigated the 1999 article by Bookstein et al²⁰ and so was responsible for the entire “Vienna school of morphometrics,” emphasizing not landmark points but semilandmarks upon curves and surfaces. (Ironically, the impossibility of validly operationalizing the Frankfort horizontal makes hardly any difference for the analysis of the lateral cephalogram, the main concern of Inappropriateness as it is of orthodontists today. It is the anteroposterior image that demands standardization in this or some other completely arbitrary way.)

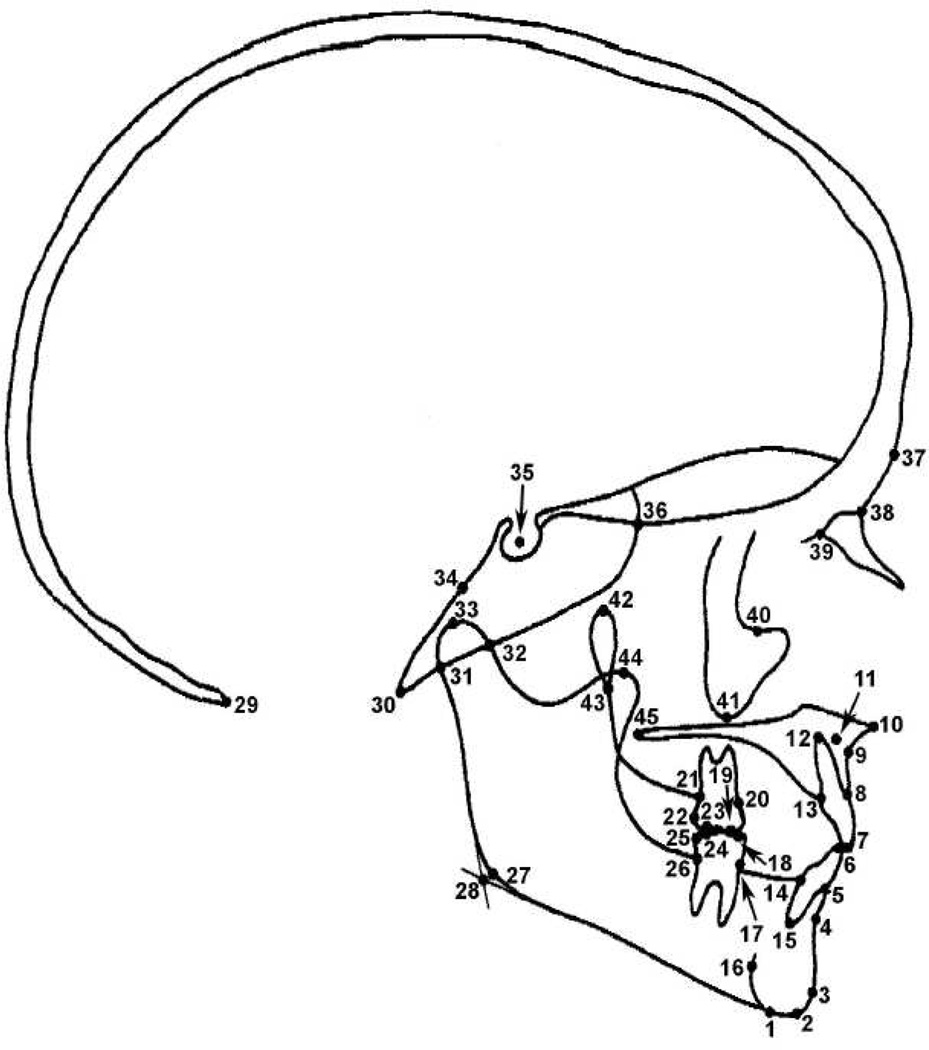
The tension between geometric reality and cephalometric convention was already clear in the Riolo-Moyers Atlas of 1974.³ Figure 2 is a template of the 45 purported landmark points entailed in their study. But some points (#35, #28, #11) lie on no image structures at all, while others (e.g., #40, Orbitale; also #42, #43) lie on purported curves that do not actually exist on the solid skull. (The curving arc through #40 and #41, for instance, is actually the nonplanar curving locus in space where the surface tangent plane to a sheet of cortical bone passes through the origin of the x-ray beam, a location that has no meaning whatever as far as the biomechanics, growth, and physiology of the head are concerned.) Several points, including #36, #31, and #32, represent overlays of curves on the cephalogram that do not actually correspond to loci in space, but rather lines tangent to the solid skull at two separate locations whose join happens to lie perpendicular to the nominal midsagittal plane. (In other words, the “landmark” as located combines the anteroposterior coordinate of one surface patch with the craniocaudal coordinate of another at some distance — quite a perplexing biological construction, to say the least.) Many points lie on single curves in ambiguous positions lacking robust operational definitions (examples include #37 Glabella, #9 A point, #4 B point, #33 Condylion, and all four of the points on the mandibular symphysis). Omitting the teeth, the number of points that could conceivably qualify as craniometrically valid is at most six (#29, #30, #38, #39, #10, #45). So Moyers’ own reference publication is fully vulnerable to the sharp criticisms he would be publishing less than five years later. Finally, notice that Porion does not appear in this figure at all — indeed, there is no curve for the auditory meatus, as whatever position its “border” might actually be imagined to occupy is obliterated in the image by the steel rods used to restrict the subject’s head position. “Fabrication, camouflage, confusion, and subtraction.”¹ These are Moyers’ terms for 4 of the systematic ways in which the conventional cephalometrics of his day would “misinform,” would mismanage the data even after the images had been (inappropriately) reduced to landmark point locations already. Most of these problems are familiar to today’s student from later critiques of diverse morphometric methods. For example, “fabrication” was Moyers’ term for the generation of “growth curves” as series of positions of a landmark point within a coordinate system registered on others in some fashion. The critique boils down to the observation that such traces are not susceptible to proper biometrical analysis, as they confound changes in the region of the landmark with changes and frank registration artifacts at a distance. The fallacy is declared to be a troublesome consequence of the fact that divergences between neighboring landmarks are “much less than their common translation.” The formal resolution of this problem was not published until just this year,²¹ but the 1979 critique was certainly valid as far as it went.

Figure 2.

The 45-landmark scheme of the Riolo-Moyers Atlas of Craniofacial Growth3. See text. Permission to be requested.

By “camouflage” the 1979 authors meant the concealment of this registration dependence among the superpositions that would generally convey the findings of a conventional cephalometric analysis. Those superpositions would typically fix a landmark point (Sella, perhaps) and some line through it in the direction of a second landmark point — Nasion, perhaps. Figure 7 of Inappropriateness already announced the principle of “tensor biometrics” that would be the core of my lengthy innovation of 1984,²² the role of weighted averages of landmarks in breaking through the obvious asymmetries of this formulation to unearth simple summaries of change whenever such summaries were in fact available.

Inappropriateness already acknowledged that for the proper description of a uniform transformation (a simple shear or directional stretch), a registration needed to be along principal strains of the landmark change, not interlandmark segments. In other words, the appropriate registration was a function of the change to be described, not vice versa.

The Moyers rubric of “confusion” covered 3 major rhetorical difficulties besetting the conventional methodologies: description of rotations, “controlling for size” (the quotation marks are in the original article), and reporting changes in angle. As for the preceding 2 categories, while these criticisms were all correct, the corresponding resolutions were widely scattered in time and in discipline of application.

Reporting changes in angle turned out to be the formal dual of the problem of optimal reporting of a uniform transformation already noted under the heading of “camouflage.” This pairing, the explicit topic of a table on pages 220–221 of my treatise of 1991,²³ originally appeared in this Journal as one component of a growth analysis.²⁴

The issue of “controlling for size” was resolved in several distinct steps. First²⁵ came the introduction of a standardized size scalar, Centroid Size (square root of the sum of the principal moments of the suite of landmarks around their centroid). The extension of this concept to drive regressions of shape on size (the implementation of allometry in the context of landmark data) was the essence of the notion of shape regressions that was introduced at the NATO conference on morphometrics run by Les Marcus in 1993.²⁶

Finally, the idea of form space, the extension of shape space to incorporate size explicitly, in the form of the natural logarithm of Centroid Size, was the subject of the theorems presented²⁷ and exemplified by one classic application (allometric shape trajectories of humans and great apes).

Rotations of small features of form were dealt with by the method of edgels published for a mathematical audience²⁸ and implemented in the two-dimensional module ew2 of W. D. K. Green’s program package Edgewarp. In contrast, issues of rotation in the large remain a site of active innovation as of this writing. The regionalized rotation associated with the bending of a rigid body is dealt with,²⁹ while the general case remains unformalized as yet.

Finally, Moyers’ fourth category of misinformation, “subtraction,” would today be regarded as a misnomer. The crux of the critique as published had nothing much to do with the arithmetical operation of that name. Its concern would better be described as the relation of any scheme of landmarks or curves to the actual osteology of bone, depending as it does on coordinated processes of deposition and resorption all over multiple surfaces.

In other words, the objection was to the conceit that comparison of measurements on static structures could lead to biologically appropriate insights into actual processes of regulated biological change over time in osteal tissue. Already by 1979 we knew that analyses of growth as quantified via locations of metal implants were incommensurate with cephalometric analyses of the same growing animals. During growth, “form moves through bone”: Moyers himself had made this point in his Handbook of Facial Growth,³⁰ appearing just a few years before Inappropriateness. Recently a seminal article by Oxnard and O’Higgins³¹ has broadened the concern here from bone per se to the soft tissues adjacent, particularly the muscle insertions that we often rely on to infer selective effects of function on dried skeletal material. Other applications, such as the way the dental enamel comes to ride on top of the dentin, are even more recent.³²

In summary, Moyers’ pessimism about the state of cephalometrics circa 1979 — its “inappropriateness” for most scientific purposes — was a natural outgrowth of methodological stasis across the fields for which he had been responsible at the University of Michigan: first orthodontics, then craniofacial growth and development more generally. By the 1970s, it was clear to many of us, not just Moyers and me, that something was deeply wrong with the way that sets of points, either on a skull or on an x-ray of a skull, were converted into lists of decimal numbers and then into pattern statements referring to those lists. There seemed to be no way that those numbers or pattern claims could be used either for consilient scientific research or for objectively rational clinical decision-making.

In other words, cephalometrics was not yet a numerical method, but only a sort of subjective guide to form, along the lines of the guides to artistic anatomy that had concerned analogous representations of the face by portraitists for hundreds of years. This failure, which characterized Moyers’ own Atlas as much as it did anybody else’s work, was one of the main drivers of the Inappropriateness critique. When I joined his research group in 1977, as a freshly minted Ph.D. in the measurement of biological shape, it was reasonable to hope that developments would come quickly. Some did — shape coordinates were published by 1986,²⁵ thin-plate splines by 1989,³³ analysis of asymmetry and analysis of semilandmarks on curves by 1991.²³ The issues of “fabrication, camouflage, and confusion” in particular that concerned the 1979 authors were, for the most part, resolved by the mid-1990s, and the new methods had been published widely in the literatures of applied statistics and image-processing, with specific reference to some pioneering medical (but noncephalometric) applications such as the shape features of the human brain. But reversion of the new methods back into craniometrics and particularly into orthodontics was considerably delayed past that date, partially owing to lack of clinical demand but more, in my view, to our failure to deal with the more fundamental set of problems, the problems of the cephalogram as a source of data in the first place. As a result, from the date of Inappropriateness’ publication (1979) to the date of that Vienna conference 19 years later, there seems to have been no obvious progress within the literature of cephalometrics itself: no resolution of any of the issues focused on by Moyers and me. Yet by the time of that Vienna meeting, the adaptive radiation that became modern geometric morphometrics was about to become explosive. What a shame that Moyers did not live to see any of this.

The emergence of geometric morphometrics

In the last five pages of Inappropriateness, Moyers and I turned to 3 suggested resolutions for some of these issues: the analysis of outline curves by tangent angle and curvature, the analysis of the interiors of such curves by the medial axis, and “the reduction of change in shape to differential changes in size,” which was my method of biorthogonal grids of the preceding year.⁴ It is fair to say that over the intervening decades of morphometric improvisation, all of these methods have proven wholly recalcitrant in application to the archive of representations of the solid skull by either surface representations or volume representations.

Such a denouement was probably predictable. The paper gives credit for its recommendations to “our collaborations these past two years” (page 613) — what hubris! The work has taken nearly 20 times that long, so far; the collaborations involved range very far from orthodontics; and the task — the building of a flexible geometric morphometrics for contemporary medical images — is far from finished. Specifically:

Biorthogonal grids ceased to be of interest at almost the same time this article recommending them was published. In retrospect they involved not only an inappropriate graphic but inappropriate mathematics: these grids can have multiple singularities, “stars,” “monstars,” and “lemons,” that are biologically meaningless and also graphically incomprehensible. More generally, tensors were almost but not quite the right answer. They apply to one subspace of shape space (the uniform transformations), but a formalism like bending energy was needed to organize them appropriately across the figure or space of the organism. We are only now, in 2015, beginning to figure out how to do this.²¹ The medial axis, another of Inappropriateness’ recommended approaches, has proved helpful to some extent for shape recognition in other medical imaging applications quite distant from studies of the bones of the head. It is now mainly regarded as a technique of cognitive psychology (which was its originator’s original thrust³⁴) rather than a system for arriving at meaningful parameterizations of morphological differences. (But a generalization of the medial-axis statistics of the 1970s, the method of “centers and spokes,” is proving quite promising at present in applications to soft-tissue volumes: see 35.) And tangent angles and curvatures proved intractable for reasons of numerical instability. Indeed, Koenderink’s book of 1990¹⁹ was intended to replace this local point of view by a global perspective based on integrals of some of the same geometrical descriptors.

One might have inferred this collective failure from the welter of dates involved in the citation pattern of my last few paragraphs here. Some of Inappropriateness’ criticisms were answered by articles or worked examples in the 1980s, others in the 1990s, still others in the present century and some as recently as this year. This is not the timecourse of a coherent methodological breakthrough. That is because, at root, Moyers and I had not correctly guessed the level of sophistication that would be required if these diverse paradoxes were to be usefully resolved. It took mathematical work, work at the foundations of applied statistics of manifolds, the foundations of interpolation theory, the foundations of multivariate statistical analysis, and the foundations of a biomathematical grammar of form. None of those requisites are even hinted at in Inappropriateness’ text; contributions from a much broader community, extending well past the boundaries of medical image analysis, turned out to be needed first.

The present essay is not the place for a conventional review of this collective response. I have written out overviews of these developments in a range of recent monographs (Chapter 4,⁷, Chapter 7,⁸ and Chapter 5,³⁶ for example), and their relation to some of these historical antecedents is the subject of discussions in many of my most recent papers.^17,21,29,37 In the next few paragraphs I would like instead to sketch some of the central advances, nearly all wholly unanticipated in the arguments of Inappropriateness, that were key to this development; then the most important components of today’s morphometric toolkit; and finally, in imitation of the stance of the 1979 authors, offer a critical review of that current state, with an emphasis on the new assortment of unwarranted assumptions and infelicities and new speculations about possible future resolutions in turn.

“No theory of cephalometrics”

“There is no theory of cephalometrics.” True enough in 1979; but where was such a theory to come from? Not the biological sciences, nor the clinical sciences of image-driven diagnosis, but from statistics and the sciences of information in complex data structures in general.

Shape space

Moyers and I took note of the biorthogonal method, an explicit (but badly flawed) graphic for the comparison of forms in pairs. We failed to notice the possibility of a formal statistical space for the individual configurations being thus compared — a statistical space for arbitrarily many configurations of arbitrarily many landmarks per se. Such a space was to emerge very shortly afterward in the effectively simultaneous work of David Kendall, a mathematician specializing in probability, and myself.^38,25 We were saying the same thing in 2 different mathematical notations, a coincidence apparently first noticed by Kanti Mardia. He and his students announced the first effective null distributions for this space shortly afterward (see the review in Dryden and Mardia³⁹). I had published only approximations, but Mardia had exact methods, which would be far more highly prized by statistical professionals.

The points of shape space are shape coordinate vectors, which are, roughly speaking, lists of landmark coordinates, x, y, x, y, …, or x, y, z, x, y, z, …, such that each specimen lies as if digitized in a different coordinate system that has been custom-sized, custom-centered, and custom-rotated to optimize exactly the statistical comparisons that are to come. For one specific version of those implicit digitizing rules, the shape space of vectors that results is a so-called Riemannian manifold, that is to say, a mathematical structure with a built-in measure of interpoint “distance” (Procrustes distance, for those who have seen this term before). The space is curving, a little like the surface of the Earth, but there are a variety of approaches (Bookstein coordinates, Kent coordinates, Kendall coordinates) that represent empirical data sets by “flattened” structures (points projected onto hyperplanes the way cities are projected onto paper maps). Once the landmark data had been represented on those hyperplanes, owing to the presence of that Procrustes distance formula in the background, principal components and other standard multivariate maneuvers could easily be formalized, both in the approximate setting²³ and exactly.³⁹ I noticed, too,⁴⁰ that the statistical method of Partial Least Squares, which had recently coalesced in the applied sciences from such diverse fields as chemometrics, econometrics, and psychometrics, was perfect for the task of correlating these patterns with their causes, concomitants, or effects when the latter were measured with equivalent redundancy as other blocks of endogenous (cephalometric) or exogenous variables. Taken all together, these tools amounted to an enormously important alternative approach that Martin never anticipated: the provenance of protocols for producing appropriate variables a posteriori from analyses of the shape contrasts, differences, or correlations themselves.

A new visualization

This underlying shape space is a curving Riemannian manifold, and thus rather difficult to draw. It is little help to have extracted a feature of optimal shape signal (say, a principal component) if the scientist or her readers cannot actually see how the signal lies upon a typical or averaged landmark form. The biorthogonal grid never came close to getting this right even in two dimensions, owing to some stubbornly fundamental facts about orthogonal coordinate systems. (That was just as well, as there was no proper mathematical extension to three-dimensional data anyway.) Instead, it turned out to be the explicit imagery of warping that, as already suspected by Albrecht Dürer, D’Arcy Thompson, and Coenraad Moorrees, bridged the novel statistical technology to the ordinary scientist’s ordinary retina.

The specific warping function on which we are most dependent nowadays, the thinplate spline, came not from any prior biological context but from the distant world of mathematical interpolation theory as modified for remote sensing and computer animation. The article that announced this advance³³ noted the unexpected mathematical alignment of a new mathematical formalism^41,42 (for the applied-mathematical context of these, see Wahba⁴³) with the needs of the landmark-dependent morphologist: namely, a function that can be computed by simple matrix operations in closed form, no iterations required, that nevertheless proves uncannily intuitive as a display of both local and global features of shape comparison. A thin-plate spline is indeed a sort of mathematical miracle: parseable by nearly everyone with normal binocular vision, it almost automatically directs the viewing eye to features that lead, in turn, to effective qualitative summaries. Both the two-dimensional and the three-dimensional implementations (they differ a bit in details of the formulas) have been in widespread use for many years, either as visualizations on their own or (in other branches of medical image analysis) as the starting values for computed maps that optimize more delicate quantitative summaries.

Semilandmarks

The thin-plate spline is not just any old interpolation function, but has a very specific mathematical formulation. It minimizes the bending energy of the resulting grid, and this energy is a quadratic form in the landmark coordinates of the average form. This formalism makes possible⁴⁴ the extension of all of the landmark-based statistical methods to “semilandmarks” (this clever bit of jargon is John Kent’s), combinations of landmarks with points on curves or surfaces colocated, all at once, so as to minimize their net bending energy around an average. Analysis of data sets of semilandmarks accounts for the vast majority of computer cycles absorbed by the toolkit of geometric morphometrics as applied today in craniometrics and in anthropometrics generally, both in Europe and in the Americas.

Today’s best software environments for GMM analysis usually combine these 3 themes with the core thrust of statistical data analysis in one variant or another of the following series of 3 basic maneuvers:

• raw data in the form of landmark and semilandmark locations in 4-dimensional space are derived manually or semiautomatically from surfaces or CT imagery, and converted to shape coordinate vectors by the Procrustes method (about which I will have more to say below);

• statistical questions are asked in terms of the landmark configurations as a whole via these vectors — questions about dimensions of greatest shape variability per se or of dependence of shape on group, age, or other causes or consequences of form; and

• the answers to those statistical questions are interpreted as contrasts of form along the dimension(s) in question, each one drawn out in turn as a thin-plate spline deformation of an average or typical form. To date many thousands of these elegant graphical objects have been published or presented at scientific meetings as powerpoint frames or posters, including hundreds, I would guess, in the course of clinical craniofacial studies.

Open issues

This, then, is the response that the relevant community of 2015 would report back to the authors of the critique of 1979. Today we have a method that deals with most of the infelicities of the cephalogram by replacing it as data source by a different data stream, the direct input of Cartesian coordinates in three dimensions; that deals with those coordinates all at once using a statistical strategy for comparisons of interest that eschews all specification of relevant variables a priori; and that visualizes the resulting findings in a way that ends up suggesting “the variables that should have been measured” for the specific comparison(s) at hand.

Clearly this method is driven by the second step, the computation of those “comparisons of interest.” But that would seem to leave it less than fully qualified as a diagnostic method, one aimed at finding the abnormalities that might be treatable in the single case. That is to say, the morphometric toolkit of 2016 embodies a method relatively more adapted to issues of the scientific study of form than its assessment in the clinical setting. (This is not for lack of trying: see, for instance, the application of all these methods to the diagnosis of fetal alcohol damage from the shape of the midcurve of the corpus callosum.^8,45,46 Someone who was going to repeat Moyers’ highwire act today (a public lecture, followed by a high-profile professional sermon) would nevertheless find a great deal to talk about, more, perhaps, than enspirited our Inappropriateness lecture itself.

So it is an irony, and not necessarily a gentle one, that this toolkit has been relatively rarely applied back in the orthodontic or craniofacial clinic that generated the original 1979 critique Inappropriateness conveyed. Rarely but not never: among this group of indigenous adopters must be numbered Demetrios Halazonetis, Tiziano Bacchetti, Lorenzo Franchi, David Singh, Erwin Jonke, Markus Bastir, Tomislav Lauc, Hans Wellens, James McNamara, and Lucia Cevidanes. (Forgive me if I have overlooked your name; in my own defense I would note only that you are not actually sending me your papers to archive — I must find them by tracking forward their citations to my own publications, like any other author must do.)

Of course a great many other methodological schools use information from 3-dimensional surface representations. Their techniques include the exploitation of surface geodesic distances such as Leslie Farkas’s analyses of soft-tissue facial form⁴⁷ or Project CAESAR’s diameters and circumferences of whole scanned bodies,⁴⁸ analyses of curving facial form for purposes ranging from face recognition to dysmorphology (eg⁴⁹), more general forms of surface-to-surface correspondence for the purposes of “applied anthropometrics” as in the garment industries, and customized representations for specific practical problem settings, such as the morphometric work of Dennis Slice and colleagues on the sizing of gas masks.⁵⁰ The critique here, like Inappropriateness’ own, is not claimed to extend to these richer data resources, but only to the versions that rely on discrete configurations of points as the crux of their data representations.

What, precisely, is the biological relevance of the cephalogram?

In contrast to the enforcement of statistical themes, implying the privileging of explanation over diagnosis, many technical issues have been left unresolved over the course of erecting the morphometric synthesis I just reviewed. It will doubtless not have escaped your notice that the original stimulus, the projection cephalogram itself, is not among the data types that these tools find acceptable. The problems of radiographic superposition and the ensuing emergence of false geometric pattern information remain as troublesome here in 2016 as they were in 1979.

I do not mean that every clinic should immediately switch to solid imaging, such as computed tomography; the radiation load is simply indefensible for the ordinary range of clinical encounters. Rather, what is lacking is a formal theory of what information has actually been preserved in the Broadbent-Bolton cephalogram by comparison with the 3-dimensional structure that that cephalogram is meant to represent. Such a formal theory is not yet available, as far as I know; it might be accessible by modifying Koenderink’s glossary so as to apply to projection imagery instead of surface representations per se. For instance, what is the meaning of the curves we trace on the cephalogram? — what sort(s) of curves on realistically convoluted surfaces are actually traced by the touching points of tangent lines that go through a fixed point at a considerable distance outside? Points #40 and #41 of Figure 2 lie on one such curve, but there is a different curve for every outside point, and this dependence needs to be conscientiously explored. Such a concern could have been raised in 1979, but it was not, and so we still cannot formalize just what it is that the lines of the cephalometric tracing (and thus all the named points on them that are not actual landmarks upon the solid skull) are supposed to be telling us.

Analogously, it is well-known that the “gonion” of the lateral film and the “gonion” of the anteroposterior film are not the same point — the vertices of the mandibular edge as traced in projection are different between the two projections. How do these 2 points relate to one another, and how does the combination of the two relate to the corresponding unitary vertex on the ridge curve of the mandible when considered in its proper 3-dimenstional setting (if they relate at all)? The resolution of this and a multitude of similar paradoxes can emerge only from a careful geometric study of the typical features of surface form in the vicinity of such vertices in the full range of projections, not just the canonical two.

And there still remains the problem posed by the “landmark” numbered #36 in the Atlas: the meaning of loci at which spatially unrelated curves intersect on the projected cephalogram. To a locus like this evidently corresponds a real line in the space of the laboratory that is doubly tangent upon the skull, once on each surface, and that also passes through the origin of the x-ray beam. The treatment of such “intercepts” is necessarily different from that of points like #38 or #10 that actually exist on the solid skull in some plane (here, the midsagittal) the location of which can be estimated from evidence outside the cephalogram. A biomathematical theory of the diversity of classes like these would be very useful indeed.

Limitations of the model of smooth deformation

Continuing with the list of omissions, there is the problem of nonsmooth comparisons. This includes many subproblems: morphogenesis (structures growing from size zero to some finite size); the problem of structures like third molars that are simply not present in one form but present in another; and the problem of features that reside within the same manifold but correspond across instances in discontinuous ways, such as individual differences in the sequence of eruption of the permanent dentition and the consequent difficulties of statistical analysis in the mixed dentition. For an approach to the first of these problems, morphogenesis, see Bookstein and Smith⁵¹; for analysis of fields superimposed discontinuously over a smooth bony surface, see, in general, Oxnard and O’Higgins,³¹ the intended application of which was to the muscle sheets that drive the jaw motions of chewing, breathing, and speech that are of particular evolutionary as well as orthodontic interest. Regarding the analysis of structures that are just plain missing (as distinct from being present but invisible), I am not aware of any tenable morphometric suggestions at this time. Other methodological challenges arise when one tries to extend these tools of geometric location so as to deal with other sorts of geometric representations, such as texture, branching, or (of particular interest to orthodontics) intermaxillary biomechanics. These are just examples of kinds of comparisons that do not particularly suit the underlying metaphor of deformation that is embodied in the current geometric morphometric toolkit. Teeth move rigidly but, once erupted, they also wear down — how, then, do we represent their relationship to the growing or aging jawbone? Textures either do or do not deform along with the tissue patches that bear them; branching structures, whether cerebral (white-matter tracts) or visceral (arteries, bronchi, nerves and their foramina), just don’t suit these models of form-comparison at all. There is also the problem of explicitly interwoven structures, like the “normal variants” of joint tendon positions set out in the pages of Barry Anson’s great human anatomy atlas⁵²; variations in the fasciculation patterns of the muscles of mastication; and the representation of freely remodeled surfaces like the normal nasal septum. The inevitability of a discrete spectrum of normal variants is the curse of many otherwise fine landmark schemes.

How to get from shape spaces to biological explanations?

This collection of problems has caused me particular discomfort ever since Inappropriateness first appeared. As regards localization, one of the central problems that Moyers and I claimed was mishandled by the methods of 1979 (that charge of “fabrication”), we are still stumbling toward an effective general vocabulary of local versus global phenomena to match the clinician’s intuitive (but perhaps inaccurate) assessments of the same. I have recently put forward a candidate methodology for this purpose.²¹ Ties to biomechanics, which is after all the underlying constitutive theory of all the changes we seek to impose clinically, are resisting us. There is a recent suggestion¹⁷ of how to integrate global measures of function with Procrustes shape spaces, but much more work is to be done if we are to quantify aspects of the forces that accompany mastication (Bookstein²⁹).

Perhaps the ultimate difficulty is a fundamental “inappropriateness” of the Procrustes formulation itself. (This is a worry I have raised in several earlier essays.) Although this method is usually understood as an algorithm for producing “superpositions,” that is, revised landmark coordinates, what it actually represents is an investigator’s tacit commitment to the Procrustes distance formula that stands for “dissimilarity” among the original configurations (Sections 7.2–7.3⁸). It is this formula, square root of the minimum sum of squared distances between corresponding landmarks of 2 different forms, that causes all the trouble.⁵³ The formula for Procrustes distance is an overly symmetric construal that does not have and never can have a principled biological basis. A Procrustes analysis is an essentially cognitive analytic strategy — an approach based on the psychology of the scientist, not the biology of his subject-matter. While this might suit some of the aesthetic aspects of the orthodontic clinic very well (as it does the occupants of the neighboring office suite concerned with reconstructive or cosmetic plastic surgery) it is not particularly well-aligned with the aspects of biological function that account for our explanations of how we accomplish what we actually accomplish by our treatments. More fundamentally, the most often encountered statistical tool of the current toolkit, principal component analysis (PCA), not only depends crucially on Procrustes distance for its gauge metric but is itself under siege as a biomathematical technique sensu stricto.^21,53 The people who developed PCA (for anthropometrics, the list starts with P. C. Mahalanobis and continues with W. W. Howells and C. E. Oxnard) never intended it to apply to the task of explaining (as distinct from classifying) the multiscale phenomena whose effects are so very well captured by the (semi-)landmark methods based in actual xyz coordinates (not projections).

Some concluding observations

We have seen that the discipline of orthodontics is as responsible as any other current health sciences unit for the existence of GMM, yet these same departments do not have much use for the current toolkit, because the questions it answers are still not the questions of greatest importance to clinical practitioners: the questions of diagnosis, treatment planning, and treatment assessment. We have, in other words, solved Rudolf Martin’s problems to a far greater extent than we have solved Robert Moyers’.

I imagine that Moyers might have approved this narrative and might even, in his role as critic of the scientific establishment, relish the irony. Another essay of ours,⁵⁴ composed as a companion piece to Inappropriateness at about the same time, argued that bits of anatomical jargon used in clinical applications of cephalometrics, such as “vertical growers,” need to have a meaning different from just the craft knowledge shared among clinicians; they have to be able to persuade colleagues in the other biomedical sciences as well. To be real, in other words, clinically specified “types” of form or form-change must share information with other channels of observation, such as forecasts of change or responses to interventions. In other exact sciences, there is a substitute for typology that is currently of some interest: the idea of the Kalman filter that continually updates a dynamical system by alternating prediction and correction steps, each of which is by formula common across the whole sample. If there is ever to be a predictive science of orthodontic interventions, the mathematics of prediction and correction is likely to prove much more powerful than anything available in Moyers’ own time, no matter the length to which the Riolo-Moyers Atlas³ might have been extended. This is because the dynamics that need modeling were always the mechanics-specific dynamics of intervention per se, different in its geometry for every appliance. The methodology of group averages, of principal components and regressions, does not naturally suit the methodology of clinical assessments and interventions, any more than basal physiology predicts the response of a cardiac patient to an intervention in that rather more serious domain. (For instance, how is the “dose” of an orthodontic treatment to be measured?)

The statistical shape space in which GMM is couched solves most of the problems Moyers and I identified in 1979 that so far have any solutions at all. But these are at root the craniofacial scientist’s problems, not the orthodontic clinician’s problems. The driving concern of our 1979 lecture remains unresolved: the translation of our knowledge of craniofacial growth patterns for the benefit of the individual orthodontic patient. Statistical spaces may be the wrong formalism entirely for this purpose, just as they fail to handle most of the questions of bioinformatics more broadly. Diagnosis, treatment planning, treatment assessment: these are still arts, not crafts. Today’s geometric morphometrics supports these activities only a little less badly than the cephalometric methods that Moyers and I so sharply critiqued back in 1979.

In short, an appropriate pattern language for translating images of the single patient’s skull, jaws, teeth, airway, and soft tissues into proper clinical decision tools still does not exist. When such a tool is invented, if ever it is invented, it may resemble GMM no more than today’s industrial biometrics resembles, say, the art of portraiture, or pharmacogenomics resembles physiology: which is to say, hardly at all. Moyers’ challenge of 1979 is still patent, and with an appropriate updating, a change in statistical language from Martin’s tables to the grids and scatterplots of geometric morphometrics, it could be published with equal pessimism today.

Moyers and I concluded the published Inappropriateness text with an explicit prod to our colleagues:

Our ambition is the rectification of imbalance between computerized biomedical shape data and the archaic tools of morphometrics — ruler and protractor —bequeathed us by the Greeks. We hope that the new cephalometrics will spur craniofacial science to a much-needed sophistication of measurement for the most stubborn outstanding problems.¹

With the substitution of “principal components and regression coefficients” for “ruler and protractor,” and “professors” for “Greeks,” that peroration might apply as well to the present essay as it did to the 1979 original. The imbalance between our computerized data resources and our analytic toolkit is, if anything, even more out of balance than it was³⁶ years ago, and likewise the need for explicit methodologies that bridge these resources to the actual questions clinicians ask of their data. The response to the Inappropriateness challenge seems to have met the needs of biomedical scientists more than those of the craniofacial clinicians at whom it was actually addressed. Here in 2016, with bioinformatic face recognition operating via digital cameras all around (see, for example, Taigman⁵⁵), it is high time we renewed our attention to this imbalance. If clinical orthodontics needs new tools of high-dimensional pattern recognition (for assessments like “mandibular prognathism” or “balanced occlusion”), now, in this new era when machine intelligence is often comparable to our own in some ways, is an excellent time to construct the new data structures and analytic approaches that would move us closer to that end. Even the lateral cephalogram, for all its obvious imperfections, might yield up a useful subset of the information we seek— if only we could model that information better, and if only we had the right set of tools.

“The inappropriateness of conventional cephalometrics” was published in 1979

The article, by Moyers and Bookstein, remains widely cited today.

This essay reviews the context of the 1979 article, its themes, and its relevance.

It is dedixcated to the late Robert E. Moyers on the 100th anniversary of the AJO-DO.

Biography