Phase-corrected Bipolar Gradients in Multiecho Gradient-echo Sequences for Quantitative Susceptibility Mapping

Abstract

Object

The large echo spacing of unipolar readout gradients in current multiecho gradient-echo sequences for mapping fields in quantitative susceptibility mapping (QSM) can be reduced using bipolar readout gradients to improve acquisition efficiency.

Materials and Methods

Phase discrepancies between odd and even echoes in the bipolar readout gradients caused by non-ideal gradient behaviors were measured, modeled as polynomials in space and corrected for accordingly in field mapping. The bipolar approach for multiecho gradient-echo field mapping was compared with the unipolar approach for QSM.

Results

The odd-even-echo phase discrepancies were approximately constant along the phase encoding direction and linear along the readout and slice-selection directions. A simple linear phase correction in all three spatial directions was shown to enable accurate QSM in the human brain using a bipolar multiecho GRE sequence. Bipolar multiecho acquisition provides QSM in good quantitative agreement with unipolar acquisition while also reducing noise.

Conclusion

With a linear phase correction between odd-even echoes, bipolar readout gradients can be used in multiecho gradient-echo sequences for QSM.

Introduction

Magnetic susceptibility is an intrinsic physical property of a material corresponding to the amount of magnetization induced by an external magnetic field. Susceptibility is relevant to the main magnetic field, B₀, of a magnetic resonance imaging (MRI) system. The field of the induced magnetization can be measured using MRI signal phases and can be deconvolved to yield quantitative susceptibility maps (QSMs) [1-9]. QSMs provide a noninvasive means of assessing iron deposition [5,8,10-17], blood oxygen saturation [6,10,18,19], the myelin in white matter tracts [7,20,21], cortical and deep gray matter structures and substructures [17,22-25], and the biodistribution of contrast agents for clinical and preclinical investigations [26,27]. Because of its promising potential, QSM has recently received increased scientific and clinical attention [28-30].

Single-echo and multiecho gradient echo (GRE) can be used to obtain the field map for QSM. The multiecho gradient-echo sequence offers the benefit of simultaneous acquisition of all echo times in one excitation with improved phase unwrapping, signal-to-noise ratio (SNR), and better sensitivity to susceptibility than the single-echo approach [14,31,32]. To ensure phase consistency among the echoes, multiecho acquisitions typically use unipolar gradients that acquire all echoes with the same gradient polarity by inserting ‘fly-back’ gradients between echo readouts [33]. However, these fly-back gradients in unipolar multiecho sequences reduce acquisition efficiency and increase echo spacing.

The bipolar gradients that cut the fly-back gradients can be used to improve the acquisition efficiency and reduce echo spacing. Opposite polarities of the readout gradients with different non-ideal behaviors (the waveform delays and eddy currents) can cause phase discrepancies between the odd and even echoes. These phase discrepancies can be modeled and compensated [34-38]. Accordingly,in this paper we present a bipolar gradient multiecho GRE sequence with a linear phase correction along all three spatial directions to improve QSM SNR over the established unipolar technique.

Materials and methods

Algorithm

For data acquired using a three-dimensional (3D) bipolar multiecho gradient-echo sequence with short interecho spacing, ignoring flow-induced components, the phase at voxel location r at time TE_i for a right-handed system can be written as [34]:

$$\phi (\mathit{r},T{E}_i)=\{\begin{array}{cc}{\phi }_0\left(\mathit{r}\right)-\gamma \Delta B\left(\mathit{r}\right)T{E}_i\hfill & \forall \mathrm{i}\text{is odd}\hfill \\ {\phi }_0\left(\mathit{r}\right)-\gamma \Delta B\left(\mathit{r}\right)T{E}_i+\Delta \theta \left(\mathit{r}\right)\hfill & \forall \mathrm{i}\text{is even}\hfill \end{array}\phantom{\}}$$ (1)

where φ₀ is a constant phase offset, γ is the gyromagnetic ratio, r is the spatial coordinate of the voxel, ΔB(r) is the local field variation, and Δθ(r) is the gradient delay and eddy-current induced phase offset along all three spatial directions. Taking into account identical echo spacing, the echo time can be written as TE_i = TE₁ + (i – 1)ΔTE. Then, Δθ(r) can be obtained from the phases of the first three echoes[34]::

$$\Delta \theta \left(\mathit{r}\right)=\phi (\mathit{r},T{E}_2)-\frac{1}{2}(\phi (\mathit{r},T{E}_1)+\phi (\mathit{r},T{E}_3)).$$ (2)

Assuming that the eddy-current behavior reaches a steady state, the gradient delay and eddy-current terms can be described by a polynomial, the simplest being a linear phase shift along all three spatial directions [34,36,38]:

$$\Delta \theta \left(\mathit{r}\right)=\mathit{g}\cdot \mathit{r}+{\theta }_0.$$ (3)

Where g is the first order phase shift coefficients along the three spatial directions and θ₀ is the zero order phase shift. One way to estimate g and θ₀ is to fit linearly a relatively homogeneous phase discrepancy map along all three spatial directions [34,36,38].. In this study, all the pixels excluding the unreliable pixels in a cubic 3D volume (128×116×64 pixels for the readout, phase encoding, and slice-selection directions, respectively) were used for linear fitting. The unreliable pixels were determined based on spatial smoothness[10] of phase discrepancy map. The difference between value of the pixel and mean value of the neighboring pixels was used in this study. Pixels with an empirically established absolute difference greater than 0.2 radian were difined as unreliable. Then the phase shift of even echoes can be removed by:

$${\phi }^{corr}(\mathit{r},T{E}_i)=\{\begin{array}{cc}\phi (\mathit{r},T{E}_i)\hfill & \forall i\text{is odd}\hfill \\ \phi (\mathit{r},T{E}_i)-(\mathit{g}\cdot \mathit{r}+{\theta }_0)\hfill & \forall i\text{is even}.\hfill \end{array}\phantom{\}}$$ (4)

Incorporating this phase correction into Eq. 1, we obtain:

$${\phi }^{corr}(\mathit{r},T{E}_i)={\phi }_0-\gamma \Delta B\left(\mathit{r}\right)T{E}_i$$ (5)

which is ready for input into the QSM algorithm, as in the case of unipolar acquisition.

Data Acquisition

The study was approved by internal institutional review board that oversees compliance with the Declaration of Helsinki. Written informed consent was obtained from all subjects prior to imaging. Six healthy volunteers ranging in age from 22–26 years participated in this study. All imaging experiments were performed on a clinical 3T MRI system (Magnetom Trio Tim; Siemens Medical Solutions, Erlangen, Germany) using a 12-channel head coil for signal reception whose images were combined using sum-of-squares by scanner software. 3D axial multiecho gradient-echo data were acquired using a unipolar sequence (as the reference standard) and a bipolar sequence with the following imaging parameters for both sequences: repetition time (TR)=43 ms, the first echo time (TE₁) = 5.19 ms, bandwidth=360 Hz/pixel, flip angle=15°, field of view=240 mm × 217 mm × 128 mm, acquisition matrix=256×232×64, and spatial resolution=0.93 mm × 0.93 mm × 2.0 mm. Additionally, a GRAPPA parallel imaging acceleration factor of 2 in the right-left direction and elliptical sampling were used to reduce acquisition time. The acquisition time for each sequence was 5 min 18 s. The number of echoes was maximized and the echo spacing ΔTE was minimized separately for the unipolar and bipolar gradients: eight echoes with ΔTE=4.40 ms for unipolar and 12 echoes with ΔTE=3.01 ms were used for bipolar. Both sequences were repeated twice, allowing for evaluation of the local noise standard deviation from the subtraction of the two acquisitions [32,39].

MRI Data Processing

The processing of the data is schematically depicted in Fig. 1. The phase images (Fig. 1a and c) were first extracted from the complex MRI data. Then, for the bipolar sequence, the phase shift of even echoes induced by gradient delay and eddy current was estimated and corrected (Fig. 1b). To estimate the field map (Fig. 1d), a one-dimensional temporal unwrapping of the phase was performed in each voxel followed by a weighted least squares fit of the temporally unwrapped phases in each voxel over TE [1,40]. To account for the frequency aliasing on the field map, a magnitude map guided spatial unwrapping algorithm was subsequently applied [41]. An automatic brain extraction algorithm[42] was used to mask out the nonbrain region. A method based on projection onto dipole fields was used to remove the background field [1,43]. The local field map (Fig. 1e) was next input into a solver with the following cost function for the field-to-source inverse problem [1,44]:

$${\chi }^{\ast }=argmi{n}_{\chi }{\Vert M\nabla \chi \Vert }_1+\lambda {\Vert W(\delta -d\ast \chi )\Vert }_2^2.$$ (6)

Here, ∇ is a 3D gradient operator, M is a binary mask with a value of 0 for voxels of non-trivial gradients in the magnitude image (defined as five times greater than the background noise standard deviation in the magnitude image) and 1 otherwise [33,44,45], W is a weighting set to the SNR of the magnitude image, and λ is the regularization parameter. λ was determined by the discrepancy principle and was chosen such that the data term ∥W(δ – d * χ)∥₂ approximately equaled the norm of the noise in Wδ, the weighted relative difference field. The convergence criterion and the choice of regularization parameters were determined empirically from previous studies[33,44,45]. The same strength of regularization were applied to both bipolar and monopolar reconstructions.

Fig. 1.

Schematic view of the QSM process for bipolar GRE images in a healthy volunteer.

Quantitative Data Analysis

Ten regions of interest (ROIs) – the caudate nucleus, globus pallidus, putamen, red nucleus, and the substantia nigra from both hemispheres – were manually segmented on QSM images using ITK-SNAP (PennImage Computing and Science Laboratory, Philadelphia, PA, USA). ROIs were drawn on central slices depicting these structures unambiguously. The spatial mismatch between the repeated acquisitions was evaluated with SPM8 (Statistical Parametric Mapping, Wellcome Department of Imaging Neuroscience, London, UK) implemented in MATLAB. The average susceptibility value for each ROI was defined as the mean value of two repeated acquisitions. The noise of the QSM for each ROI was locally defined as the standard deviation of the difference between the repeated acquisitions calculated over all voxels in the ROI [39].

Results

The odd-even-echo phase discrepancies were approximately constant along the phase encoding direction and linear along the readout and slice-selection directions, as illustrated in Fig. 2. Figure 2d–f show the phase discrepancy profiles of narrow strips along the three directions in the brain of a single scan of one subject. The linear model for phase offset of even echoes calculated from the first three echoes (Eq. 3) was good in all spatial directions: the correlation coefficients were 0.98 for the readout direction (Fig. 2d), −0.65 for the phase encoding direction (Fig. 2e), and 0.94 for the slice-selection direction (Fig. 2f). The result of 3D linear fitting for this scan was:

$$\Delta \theta (\mathit{x},\mathit{y},\mathit{z})=0.0022\mathit{y}-0.0002\mathit{x}+0.0015\mathit{z}+0.4561$$ (7)

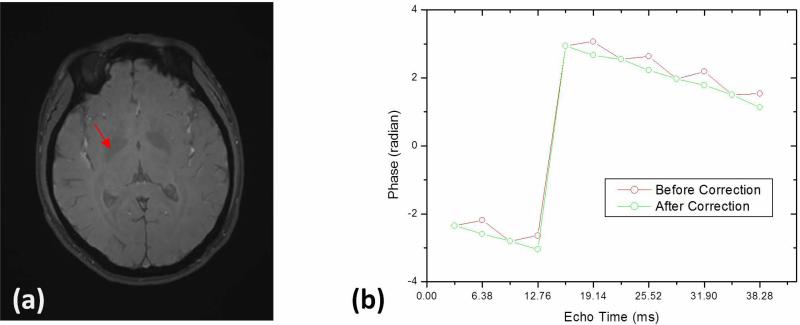
Here, Δθ is phase offset in radian and y, x, and z are spatial coordinates of the voxel in millimeters, which correspond to the readout, phase encoding, and slice-selection directions, respectively. The linear fitting coefficients depended on different scans and the values for all scans were 0.0023±0.0002, −0.0002±0.0001, and 0.0009±0.0006 radian/mm for the readout, phase encoding, and slice-selection directions, respectively, and 0.2269±0.1702 radians for the zero-order term. Figure 3 shows the phase at a voxel located in the right globus pallidus changing with echo time in the bipolar GRE sequence. The phase was directly proportional to the echo time after correcting for the phase offset of even echoes (Fig. 3b).

Fig. 2.

The phase offset of even echoes calculated from the first three echoes in the bipolar sequence for one scan of a single subject. The red rectangular section in the axial (a), coronal (b), and sagittal (c) views has a width of 10 pixels. The pixels along the width of the rectangular section are averaged to produce the phase offset profile (black line) along the readout direction (d), the phase encoding direction (e), and the slice-selection direction (f). The blue line in d, e, and f is the linear fitting of the profile.

Fig. 3.

Phase at a voxel located in the right globus pallidus changing with echo time in the bipolar GRE sequence before corrections (red circle) and after corrections (green circle).

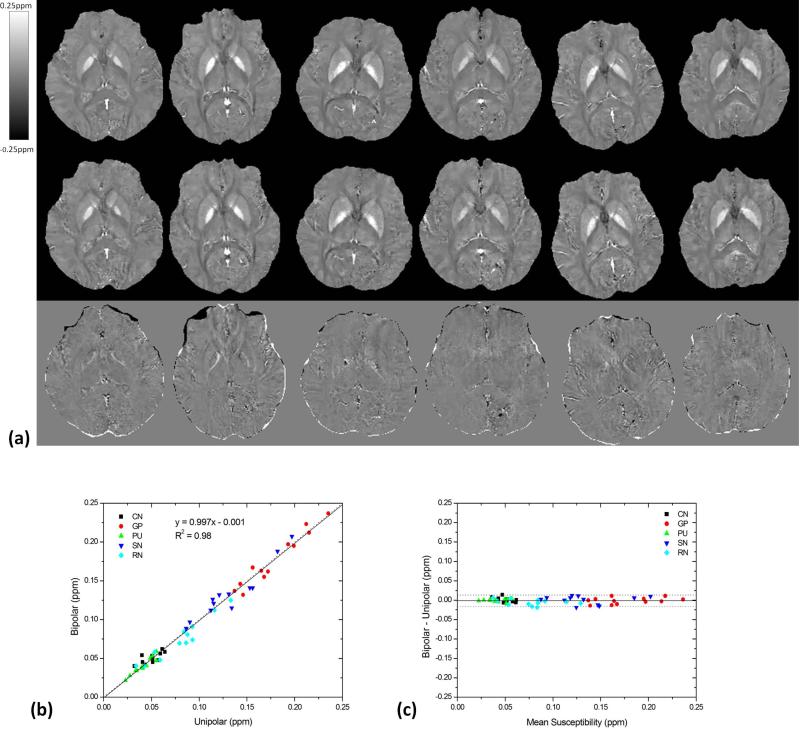
The image quality using bipolar and unipolar techniques was similar, as observed in Fig. 4a. The average susceptibility values in different brain regions across all volunteers are summarized in Table 1. No group statistically significant difference was found in the average susceptibility values for all these structures (P=0.18). In the ROI-based quantitative comparison, the slope of the linear regression (k=0.997) between the bipolar and unipolar methods was close to unity and the intercept (y₀=−0.001) was close to zero. The correlation coefficient (R²=0.98) was also close to 1, indicating a good agreement between the bipolar and unipolar susceptibility measurements (Fig. 4b). The Bland-Altman plot exhibited no significant bias or trend between the bipolar and unipolar methods. The 95% limit of agreement between the bipolar and unipolar methods ranged from −0.016–0.014 ppm over the range of approximately 0.022–0.236 ppm (Fig. 4c) for the six subjects.

Fig. 4.

Qualitative and quantitative comparison between bipolar and unipolar acquisitions. (a) Bipolar (top row) and unipolar (middle row) acquired QSM at an axial section through the globus pallidus are, displayed for the six volunteers (one subject per column) at the same window/level. The bottom row were the difference images between bipolar and unipolar QSM. (b) Linear regression and (c) Bland-Altman analysis demonstrate excellent agreement between bipolar and unipolar QSM on regional susceptibility measurements. The solid and dotted lines in b are the trend line of the linear regression and the line of equality, respectively. The solid and dotted lines in c indicate the mean difference ± 1.96×the standard deviation of the difference, respectively. CN: caudate nucleus, GP: globus pallidus, PU: putamen, SN: substantia nigra, RN: the red nucleus.

Table 1.

Susceptibilities (mean±standard deviation) in different brain regions (ppb)

Region		Bipolar	Unipolar
caudate nucleus	Right	49±6	51±9
	Left	52±8	49±11
globus pallidus	Right	168±30	171±29
	Left	186±39	186±35
putamen	Right	40±9	42±10
	Left	40±13	41±11
substantia nigra	Right	137±36	138±33
	Left	130±36	128±37
red nucleus	Right	73±30	81±31
	Left	76±25	79±30

Means and standard deviations were calculated from the average values in the ROI across subjects.

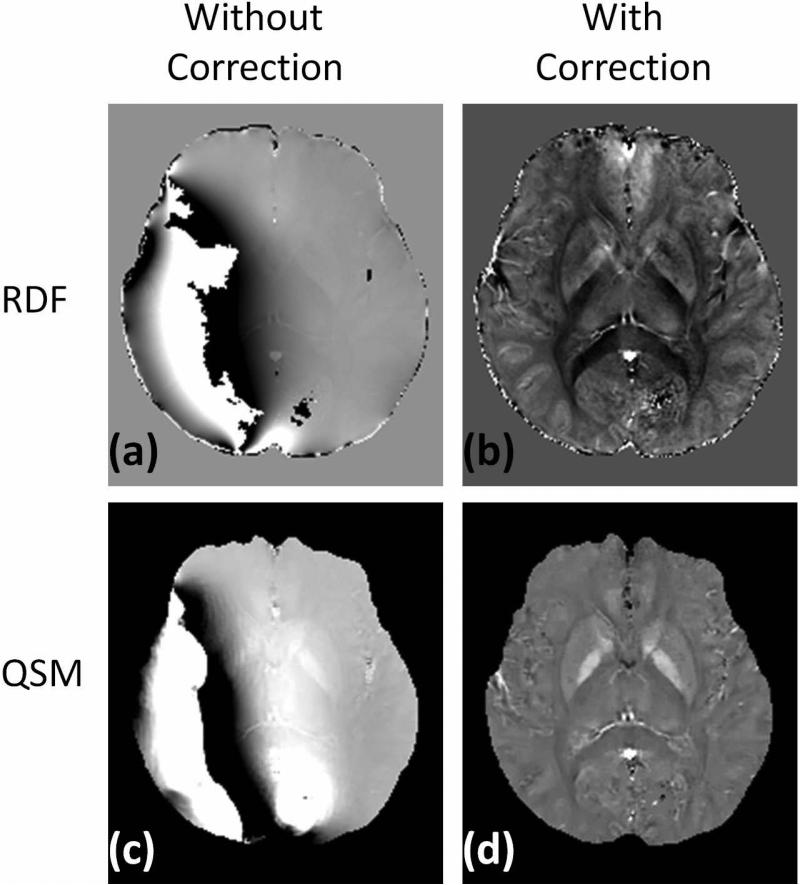
All the spatial positions between the repeated acquisitions matched remarkably well (mean translations: 0.16±0.10 mm; mean rotations: 0.20±0.19 degrees), so registration was not performed before calculating the noise. The noise measurements are summarized in Fig. 5. The use of bipolar multiecho acquisition leads to a statistically significant noise reduction for all subjects and all ROIs (P<0.0001). On average, this noise reduction ranges from 18.0% for the caudate nucleus to 31.2% for substantia nigra. Figure 6 shows the local field map and quantitative susceptibility map of one case acquired with bipolar 12 echoes and reconstructed without or with correction of the phase shift of even echoes. The reconstruction failed to obtain correct local field map and consequent quantitative susceptibility map in this case if the echoes were combined naively, i.e. without accounting for the phase shifts (Fig.6a&c).

Fig. 5.

A bar chart showing that the QSM noise decreases in different brain regions with the 12 bipolar echoes. CN: caudate nucleus, GP: globus pallidus, PU: putamen, SN: substantia nigra, RN: red nucleus, -R: right, -L: left.

Fig. 6.

The local field maps (top row) and quantitative susceptibility maps (bottom row) of one case acquired with bipolar 12 echoes and reconstructed without (left column) or with (right column) correction of the phase shift of even echoes.

Discussion

Multiecho sequences using bipolar readout gradients are attractive because of their efficient data acquisition scheme. However, this bipolar method requires corrections for phase errors. Our results demonstrate that the phase discrepancies between odd and even echoes in human brain imaging are approximately constant along the phase encoding direction and linear along the readout and slice-selection directions. QSM from bipolar multiecho GRE sequences with a linear phase correction in the readout direction agrees with QSM from unipolar acquisition and provides the benefit of reduced noise for the same scan time.

Gradient delays and eddy currents caused by the rapidly changing gradient field may induce phase changes in all spatial directions [38]. The odd-even-echo phase discrepancies are fairly constant along the phase (ky) encoding directions and can be explained by the gradient waveforms changing very little among different k_y encodings. The linear phase error in the readout and slice-selection directions is the dominant component seen in the bipolar multiecho acquisitions, which can be explained as the effects of both gradient delays and stronger eddy currents in the readout and slice-selection directions. The linearity offers a simple and robust correction for phase discrepancies. It is possible to fail to obtain correct local field maps and quantitative susceptibility maps if the echoes were combined naively, i.e. without accounting for the phase shifts.

Multiecho acquisitions offer several advantages for field mapping, including improved SNR, sensitivity, and image quality. For a given echo time, a low receiver bandwidth may be used to acquire a single echo with a high SNR. However, a single echo with a desired echo time may not make use of the entire available sampling time in a repetition time, leading to a lower SNR than that of the sum of all echo times in the multiecho approach. Multiple echo times (TEs) can optimally sensitize a range of susceptibilities with short TEs for high susceptibility and long TEs for low susceptibility. The increased bandwidth in the multiecho method results in a reduction of geometric distortions and reduced blurring along the readout direction [31]. Furthermore, the temporal evolution information in the multiecho approach enhances the robustness of the unwrapping algorithm on the estimated field map [14,34].

The bipolar multiecho gradient-echo sequence yields more efficient acquisition than the unipolar sequence. For the same acquisition time, the improved efficiency translates into reduced noise in QSM. In our study, 12 echoes were acquired for the bipolar sequence and only eight echoes were obtained for the unipolar sequence. The measured average noise reduction ranges from 18.0% for the caudate nucleus to 31.2% for substantia nigra over six subjects. The improved scan efficiency of the bipolar sequence can also translate into a reduction in the scanning time and an improvement in the imaging resolution. Furthermore, the bipolar multiecho gradient-echo sequence yields a reduction in ΔTE, which may enhance the robustness of the unwrapping algorithm on the estimated field map [34]. Instead of using a bipolar acquisition scheme, a reduction of ΔTE may be obtained using multishot techniques, where echoes are acquired during multiple TRs with slightly shifted TEs [23,46]. However, the TR must be shortened to maintain a short scan time, which requires the lowering of the flip angle and thus a reduced SNR. Furthermore, the image data must be coregistered to correct for the image displacement due to head motion or system stability; phases offset among the scans must be corrected as well.

Only the linear phase correction in all three spatial directions was applied to the bipolar data in this study. Phase corrections with higher-order errors may further improve the accuracy of the field map estimation, which has been demonstrated to be important to fat quantification using multiecho sequences with bipolar gradients [36,38,47]. The application of the presented technique may be extended from brain tissue to include venous blood by including flow compensation gradients and additional phase modeling [19],, and may be further extended to imaging organs outside the brain by including the fat component in the signal model[48,49].

Conclusion

In this study, a simple linear phase correction in all three spatial directions was shown to enable accurate QSM in the human brain using a bipolar multiecho GRE sequence. Bipolar multiecho acquisition provides good quantitative agreement with unipolar acquisition while also reducing noise. With a linear phase correction between odd-even echoes, bipolar readout gradients can be used in multiecho gradient-echo sequences for QSM. The improved scan efficiency of the bipolar sequence can translate into a reduction in the scanning time and improvement in the imaging resolution. Furthermore, the bipolar multiecho gradient-echo sequence yields a reduction in ΔTE, which may enhance the robustness of the unwrapping algorithm on the estimated field map.