Keratin network modifications lead to the mechanical stiffening of the hair follicle fiber

Significance

Mechanical properties of tissues often emerge from fibrous protein networks spanning multiple cell lengths. For the first time, to our knowledge, atomic force microscopy was used to measure the mechanical properties of the human hair follicle. We find a considerable stiffening along the first millimeter that we link to changes in the keratin network architecture and composition. In early keratinization stages, the thickening, densification, and increasing orientation of fibers are responsible for the mechanical stiffening, whereas in later stages, intermolecular cross-linking becomes predominant. Our results corroborate the known biological and structural events during hair keratinization and underline the link between the mechanical properties of the hair follicle and its multiscale tridimensional organization.

Abstract

The complex mechanical properties of biomaterials such as hair, horn, skin, or bone are determined by the architecture of the underlying fibrous bionetworks. Although much is known about the influence of the cytoskeleton on the mechanics of isolated cells, this has been less studied in tridimensional tissues. We used the hair follicle as a model to link changes in the keratin network composition and architecture to the mechanical properties of the nascent hair. We show using atomic force microscopy that the soft keratinocyte matrix at the base of the follicle stiffens by a factor of ∼360, from 30 kPa to 11 MPa along the first millimeter of the follicle. The early mechanical stiffening is concomitant to an increase in diameter of the keratin macrofibrils, their continuous compaction, and increasingly parallel orientation. The related stiffening of the material follows a power law, typical of the mechanics of nonthermal bending-dominated fiber networks. In addition, we used X-ray diffraction to monitor changes in the (supra)molecular organization within the keratin fibers. At later keratinization stages, the inner mechanical properties of the macrofibrils dominate the stiffening due to the progressive setting up of the cystine network. Our findings corroborate existing models on the sequence of biological and structural events during hair keratinization.

Biological tissues are structurally complex materials with remarkable mechanics and elastic moduli that can range from a few pascals to several gigapascals (1–3). An active field aims at understanding how the local structural and mechanical properties of bionetworks define its macroscopic mechanics from a molecular scale toward a cellular and tissue scale (4–6). One challenge is that the properties of these networks have to be considered over multiple length and force scales with macroscopic mechanical forces being transduced from the whole tissue scale down to the cellular and molecular level and vice versa.

At the cellular level, the last decades witnessed for a considerable advancement toward a better understanding of how the cytoskeleton composed of actin, microtubules, and intermediate filaments (IFs) determines cellular mechanics (1, 6–8). In vitro studies on isolated cells (6) and reconstituted in vitro bionetworks with controllable architecture and composition (9–12) considerably advanced our knowledge of cytoskeletal mechanics. However, these models are only approximations of the complex tridimensional architecture of most tissues. At the tissue level, the mechanical anisotropy together with the variety of mechanically different constituents usually hamper direct correlations between network architecture and mechanical properties (3, 13). Analytical models and computer modeling allow to theoretically link the macroscopic mechanical properties of the network with parameters of the local network architecture (5, 14, 15).

The human hair follicle was used here as a model system to show how the local, microscopic network architecture is connected to local mechanical properties in a tridimensional tissue. The stiffness of the hair follicle is expected to extend over several orders of magnitude, due to the differentiation of its soft keratinocytes into a hair fiber with Young moduli in the gigapascal range (16, 17). Between these two extremes, the keratinization process of the IF network transforms a living isotropic cell matrix into an inert and anisotropic material (18), bridging length and force scales from the subcellular level to the tissue level. This transition shares similarities with the formation of other keratinized structures such as nails and horn and with the formation of the stratum corneum, the outermost layer of the skin. It is accompanied by multiple biological processes such as a specific expression of different keratins and keratin-associated proteins (KAPs) (19) that lead, together with the reorganization of the keratin network and the loss of water, to a compaction and hardening of the fiber. However, although several complementary studies analyzed the changes in the network architecture accompanying the keratinization process (20–22), little is known about the consequence, its mechanical hardening.

To address this, we used atomic force microscopy (AFM) to measure the hardening of the keratin structure along the follicle axis while simultaneously quantifying the local keratin network architecture, as well as the keratin supramolecular organization.

Results

Follicle Mechanics.

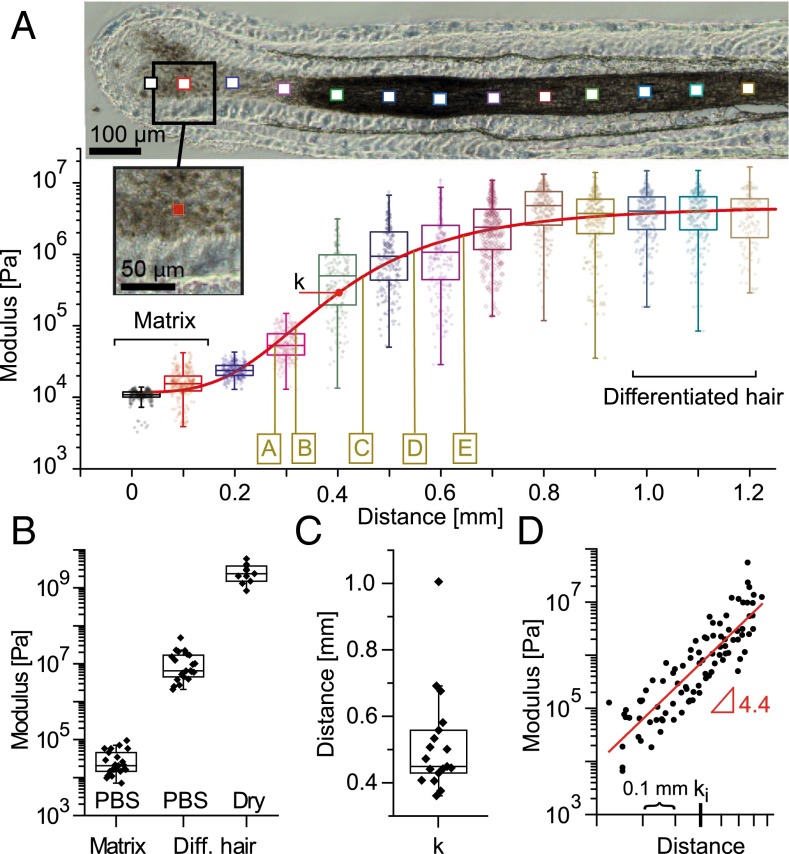
In a first step, the stiffening of the keratin network was quantified throughout human hair follicles dissected from healthy white individuals. Longitudinal 10-µm-thick sections were obtained by cryotomy and adsorbed onto glass slides. To mimic in vivo conditions, the water content had to be kept high to prevent tissue drying and collapse. Thus, after cutting, we immediately immersed the sections in PBS solution (Fig. 1A and Fig. S1A). AFM examination of the immersed sections allows a local probing of mechanical properties due to a sharp tip with a radius in the nanometer range (r = 20–60 nm). We used the force-volume mode in which force and indentation depth were recorded for 256 equidistant approach curves within regions of 10 × 10 µm² (Fig. S1 A and B). The related elastic moduli are calculated using the Hertz model (SI Text) (23, 24). Note that the determined absolute moduli values depend on the tip shape and the used fitting model; sharp tips are expected to rather probe the local mechanics of the underlying fibrous network (SI Text) (25–27). The deduced elastic moduli recorded along the follicle axis are shown as boxplots in Fig. 1A. The large dispersion of moduli within one 10 × 10-µm² region arises from inhomogeneities on the nanometer scale of the sample and prompts the averaging over the recorded force indentation curves to be a representative measurement for the local follicle mechanics (Fig. S1H).

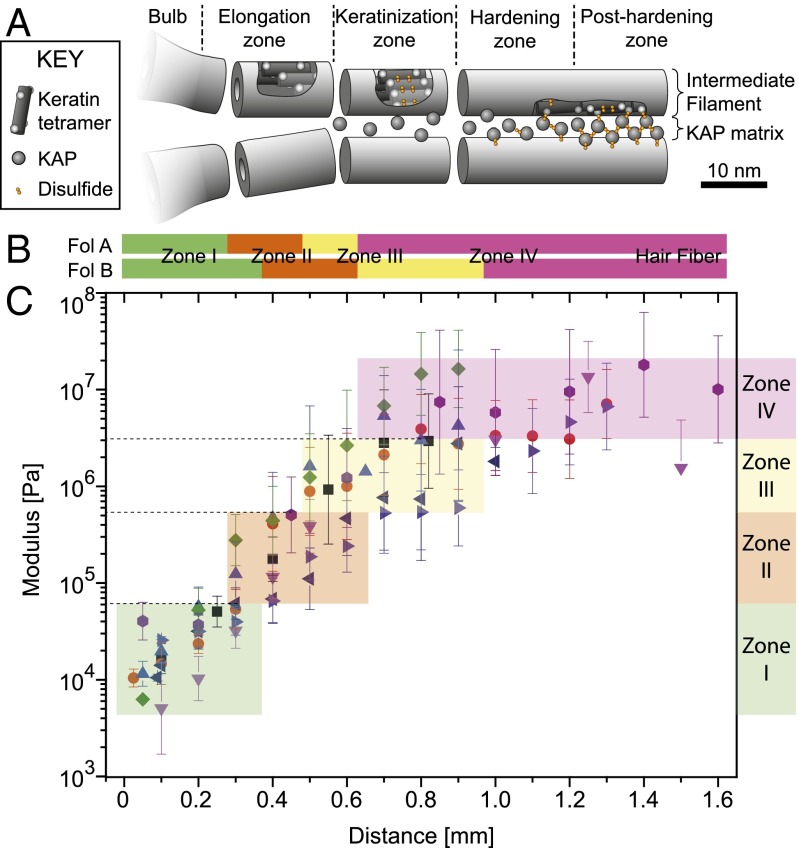
Fig. 1.

Mechanical characterization of the hair follicle. (A) Elastic modulus map for increasing distances along one follicle. Boxplots depict the moduli obtained from 256 force-indentation curves measured in equidistant positions within the corresponding 10 × 10-μm² areas represented by squares on the optical microscopy picture (actual size depicted in the higher-magnification Inset). The red curve is a sigmoidal function fitted to the logarithmic data (SI Text); k denotes the position of the inflection point. The brown letters denote approximate positions where images shown in Fig. 2 were recorded on the same follicle. (B) Boxplots of the mean moduli measured on different follicles in the keratinocyte matrix and on the plateau (distances > 800 μm) in PBS (n = 25) or after drying the sections (n = 9). (C) Position of the inflection point for different follicles, (n = 18). (D) Moduli increase between ∼200- and ∼900-μm distances from different follicles shown in a log-log plot. Every point corresponds to the mean of a probed 10 × 10-μm² zone. The traces are aligned on the x axis to their respective inflection points k_i (n = 18).

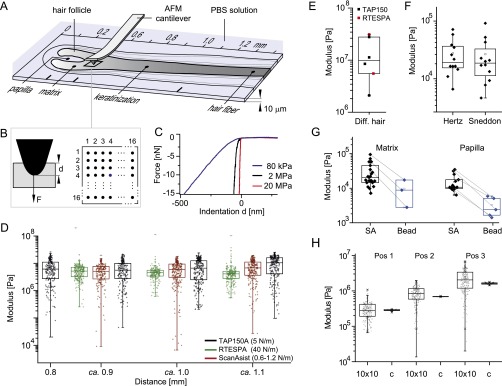
Fig. S1.

Experimental setup and controls for mechanical characterization of the follicle. (A) A 10-µm-thick longitudinal section of a human hair follicle is adsorbed on a glass slide immersed in PBS solution. An AFM is used to locally determine the elasticity of the substrate within 10 × 10-μm² zones. (B) Scheme for the used force-volume mode to determine the substrates modulus. On 16 × 16 equidistant positions, the AFM tip is indented into the substrate up to a depth d until a defined peak-force F (15–20 nN) is reached. (C) Three representative single force-indentation traces measured on the follicle. To calculate the elastic modulus the traces are fitted using the Hertz model. (D) Calculated moduli measured within the differentiated region of one follicle (distances >0.8 mm) immersed in PBS using three different cantilevers. The boxplots correspond to one 10 × 10-μm² zone, where every point corresponds to the fitted value of one single force-indentation trace. The three levers with different force constants lead to the same mean modulus, showing that the substrates modulus is within the detection range of the different levers. (E) Plateau value of four different follicle cuts measured with the TAP150 and the RTESPA lever. Every point in the boxplot corresponds to the mean of multiple 10 × 10-μm² boxplots measured at distances >0.8 mm of one follicle cut. (F) Comparison of the same experimental data measured on the same donor (n = 12) and fitted either with the Hertz or the Sneddon model. Every point corresponds to the mean of 256 force-indentation curves recorded in a 10 × 10-μm² zone within the matrix (distance of ∼0.1 mm). (G) Comparison of Young’s moduli determined with sharp (ScanAsyst-Fluid, SA) levers or with levers with a mounted bead (Bead), measured either in the matrix (distances of ∼0.1 mm) or in the papilla. (H) Distribution of moduli measured at different positions of the follicle either at 256 equidistant positions within a rectangular 10-µm² zone (10 × 10) or at a constant position (c) within the zone.

Fig. 1A shows an increase of the elastic modulus by almost three orders of magnitude along the first millimeter of a representative hair follicle. This observation was validated on 25 sections, of 12 follicles obtained from three different donors, and is summarized in Fig. 1B. The mean stiffness of 30 ± 23 kPa obtained in the keratinocyte matrix of the bulb increases to 11 ± 10 MPa measured on the plateau (distances > 800 μm) of the differentiated hair immersed in PBS. In vivo, the hair would in addition dry at the latest when protruding from the scalp. The related stiffening leads to 2.7 ± 1.4 GPa (Fig. 1B), measured at distances above 800 μm after drying of the follicles (SI Text). Note that the modulus of the developing, dried hair measured from 800 µm on is similar to moduli determined on mature hair (16, 28).

To quantify the stiffness increase throughout the follicle and to compare different samples, we fitted a sigmoid Hill function to the logarithmic data of individual follicle cuts (SI Text; red line in Fig. 1A). The low variability of the position of the inflection point of the sigmoidal function (k = 512 ± 150 µm; Fig. 1C) shows that the mechanical hardening of the hair fiber reproducibly takes place in the first millimeter of the follicle and suggests that it follows the same general mechanism even for different donors. To quantify the functional form of the moduli increase in the keratinization zone, we plotted for all measured follicles the mean moduli at a specific distance relative to their individual inflection point k_i (black dots in Fig. 1D). On average, the moduli show a linear dependence with a slope of 4.4 ± 1.3 in a log-log plot, arguing for a power law behavior E ∼ x^4.4 for the mechanical hardening of the fiber.

Changes in Network Architecture During Keratinization.

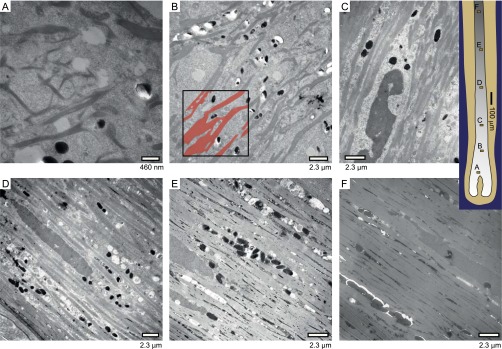
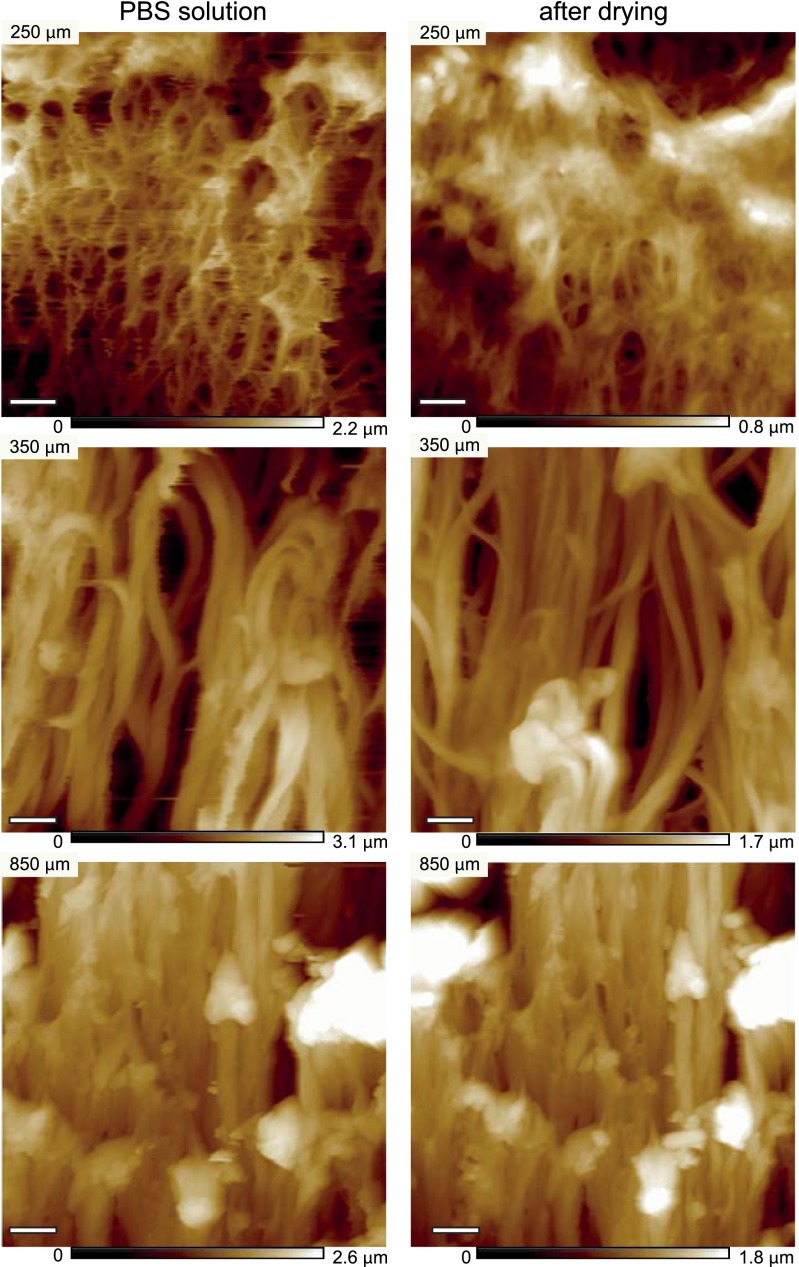
To understand how the observed macroscopic hardening of the hair follicle corresponds to microscopic changes in the keratin network architecture, topographic images of longitudinal sections of hair follicles were recorded along their axis. AFM enables high-resolution images to be recorded without the ultrathin sectioning or staining required for transmission electron microscopy (TEM) (Figs. S2 and S3), which already revealed profound changes in the IF network (29, 30). The topographic images were obtained using the peak force quantitative nanomechanical mapping (QNM) mode of the AFM on dried follicles that retain the fiber-network architecture (Fig. S4). Fig. 2 shows representative topographic images at increasing distances from the follicle bulb. The network appears above ∼170 µm (Fig. 2A), with an architecture that changes along the keratinization process: fibers become thicker, more aligned, and more densely packed. A TEM study revealed consistent changes (Fig. S2).

Fig. S2.

TEMs of longitudinal sections of a human hair follicle at various distances from the base of the follicle. Briefly, hair follicles obtained as described in Materials and Methods are fixed with 2.5% glutaraldehyde in cacodylate buffer, postfixed in OsO₄, thoroughly dehydrated in successive ethanol baths, submitted to diluted epoxy resin and finally embedded in epoxy (EPON 812) resin, and polymerized 2 d at 37 °C and overnight at 60 °C; 80-nm-thick longitudinal sections are then ultramicrotomed and poststaining using lead citrate/uranium acetate is carried out before TEM observation. A grayscale thresholding of the images allows locating the macrofibrils, as depicted in red on the Inset in position B. It also allows determining the area occupied by macrofibrils in all micrographs and measuring their diameter reported in Fig. S3.

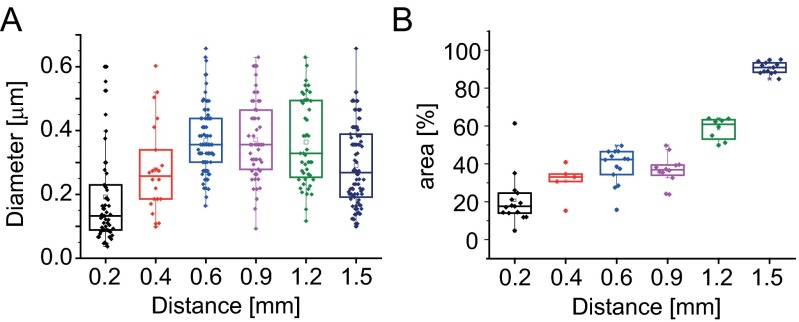
Fig. S3.

Image analysis of TEM micrographs. (A) Changes in MF diameter as determined on TEM micrographs. (B) Approximate section occupied by the MFs at various distances from the base of the follicle, representative of the macrofibril volume fraction.

Fig. S4.

Changes in MF topography during drying and reduction. Comparison between several zones of the follicles (zone I, early zone II, end of zone III), before and after drying, to illustrate the maintained network topography. Note the similarity of the overall morphology. (Scale bar, 1 μm.)

Fig. 2.

Structural changes in the macrofibril network along the hair follicle. AFM topographic images taken along the follicle axis at increasing distances from the bulb. The Inset positions the recorded locations along the follicle axis, which are also shown in Fig. 1A. Note the evolution of macrofibril diameters and alignment.

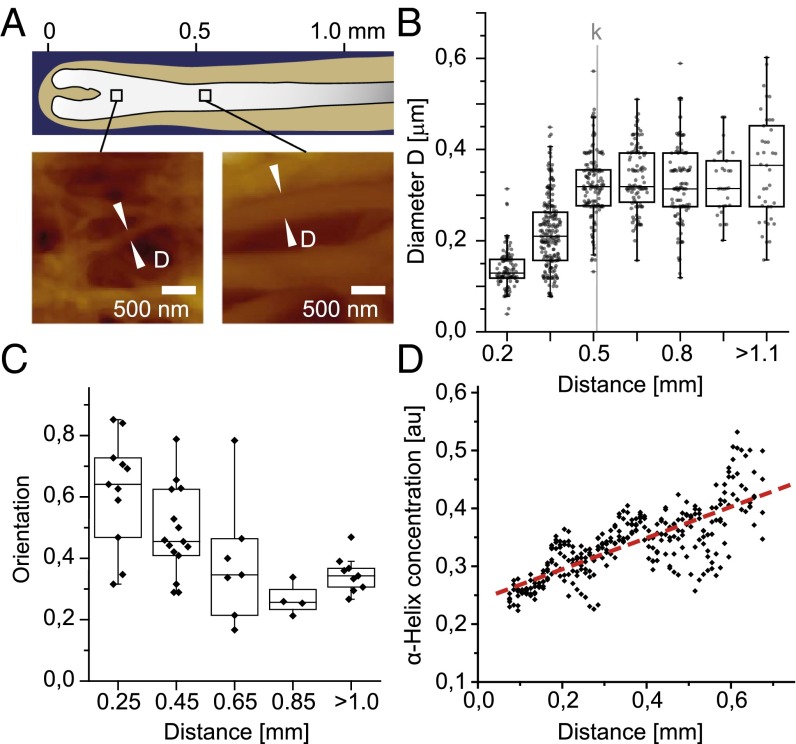
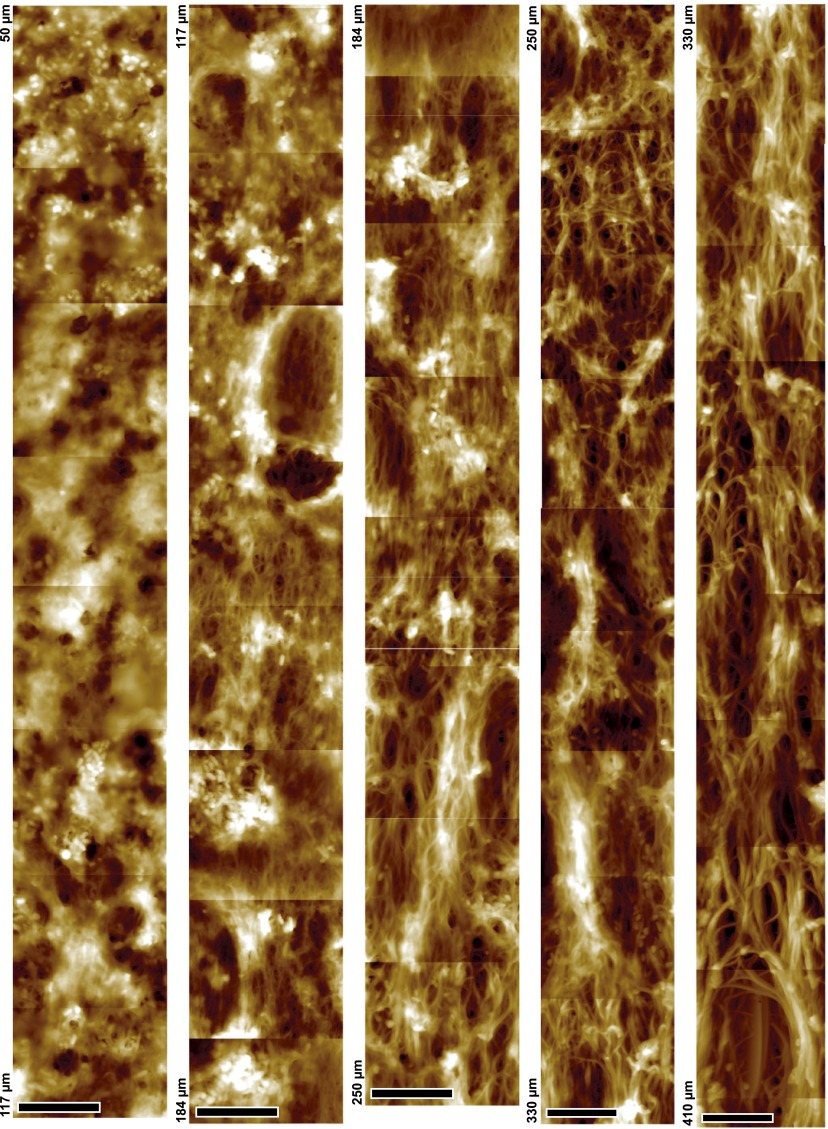
To quantify these observations, the diameter of macrofibrils and their orientation were measured from height profiles of randomly chosen filaments in sections of seven different follicles (Fig. 3A). The mean macrofibril diameter increases from 137 ± 42 nm (distance 200 µm) to a plateau value of 333 ± 84 nm above 500 µm (Fig. 3B). Analysis of TEM data revealed a similar evolution (Fig. S3A). Imaging of a 10-μm-wide stripe along 760 μm of a single follicle section shows that the macrofibril diameter increases continuously below a distance of 500 µm (Figs. S5 and S6). The preferential orientation of the fibers was analyzed by calculating the decay length of the autocorrelation function along different angles. The ratio of the shortest to the longest autocorrelation decay for two specific angles (Fig. 3C) is related to the preferential orientation of fibers relative to the follicle axis. Consistently with Fig. 2, the keratin network below 500 µm shows some degree of anisotropy, whereas the fibers become predominantly aligned in parallel above 500 µm. In addition, a compaction of the network can be observed along the follicle axis (Fig. 2 and Fig. S3B), indicating an increasing volume fraction of macrofibrils. To quantify the volume fraction of keratin-containing macrofibrils, we used synchrotron FTIR microspectroscopy as a direct local measurement of keratin concentration along the follicle. Spectra were recorded in dried sections of six different follicles, and the baseline-corrected absorbance of the amide I band in the α-helical region (1,652 cm⁻¹) was plotted (a representative dataset is shown in Fig. 3D). A linear increase in the keratin filament volume concentration is observed along the follicle axis for the first 700 µm, after which a saturation of the FTIR signal is reached due to the linearly increasing thickness of the section.

Fig. 3.

Quantification of changes in the network architecture. (A) Quantification of macrofibril diameters D on randomly chosen and zoomed positions along the follicle using the AFM height profiles. (B) Boxplots of macrofibril diameters in dependency on their distance along the follicle axis. The average inflection point k for the mechanical stiffening is shown as gray line. (C) Preferential network orientation given by the ratio of the shortest to the longest decay of the autocorrelation function calculated for different angles. Values close to 1 indicate an isotropic picture, whereas values close to 0 indicate a preferred direction. (D) α-Helical protein concentration (1,652-cm⁻¹ band) measured by synchrotron FT-IR microspectroscopy along the follicle.

Fig. S5.

Changes in MF network along the hair follicle. Stitching of ∼100 AFM topography mappings conducted on the same hair follicle section, to give a 10 × 760-µm stripe. Shown are the images recorded between 50 and 410 μm. Note the continuity of the gradual increase of microfibril diameter along with network orientation and connections between fibrils. (Scale bar, 5 µm.)

Fig. S6.

Changes in MF network along the hair follicle Stitching of ∼100 AFM topography mappings conducted on the same hair follicle section, to give a 10 × 760-µm stripe. Shown are images that were recorded between distances of 410 and 810 μm along the follicle. Note the continuity of the gradual increase of microfibril diameter along with network orientation and connections between fibrils. (Scale bar, 5 µm.)

Effect of Cysteine Cross-Linking and (Supra)Molecular Structure on Network Mechanics.

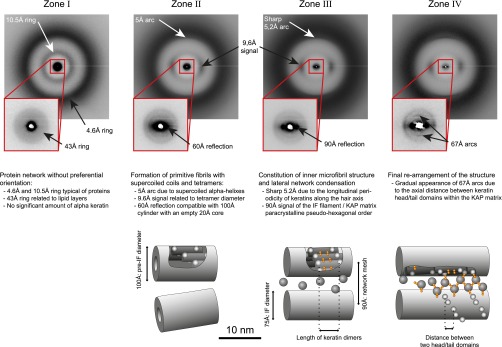
The mechanics of a bionetwork are not only determined by its geometrical factors and the fiber concentration but also by the stiffness of the individual fibers. The microscopic network alterations of the fiber diameter and orientation slow down after the inflection point k of the stiffness curve around 500 μm above the bulb (Fig. 3). To better understand the still considerable increase of the elastic modulus that occurs after the inflection point, we studied the molecular substructure of the macrofibrils using X-ray microdiffraction. The small-angle and wide-angle X-ray diffraction (SAXS/WAXS) mappings of two follicles were analyzed as previously described (21), and the approximate positions of the four distinct keratinization zones (explained in Fig. S7) are reported in Fig. 4B. A comparison with the mechanical mapping on follicles of the same donor (Fig. 4C) shows that a fivefold stiffening occurs in zone I that contains nonoriented, amorphous structures. Zone II and zone III, which show IF formation, orientation, and later condensation into a network, each correspond to a 10-fold increase in modulus. Little stiffening occurs in zone IV that corresponds to the final axial rearrangement of the IFs within the macrofibrils. The keratin fibers in differentiated wool and hair contain a high amount of cysteine residues. Together with cysteine-rich KAPs, this ensures a covalent cross-linking of the IFs (31). Evidence of a gradual constitution of this disulfide keratin-KAP network was shown by X-ray diffraction in the late hair follicle (21). These observations indicate that cysteine formation and final axial rearrangement together with drying of the structure leads to the final stiffening.

Fig. S7.

Correspondence of the four zones determined by XRD to structural features of the human hair follicle. The criteria introduced by Er Rafik et al. (21) are used to divide the keratinization process of the follicle into four distinct zones. For every zone, a representative diffractogram is shown. The observed diffraction patterns are outlined in the corresponding text and the corresponding model with the characteristic spatial periods are shown as cartoons (Fig. 4A).

Fig. 4.

Correlation between the mechanical characterization of the hair follicle and structural information given by XRD mapping. (A) Cartoon of the supramolecular organization of IFs and KAPs within the four zones defined by XRD studies (adapted from ref. 21). (B) Positions of the four zones on two dried follicles (A and B), both from the same donor determined with XRD. The experimental identification of the four zones is detailed in SI Text and Fig. S7. (C) Modulus maps for eight hydrated sections of five different follicles of the same donor used for the XRD study. Each point is the mean ± SD of 256 single force-indentation curves measured in a 10 × 10-μm² zone.

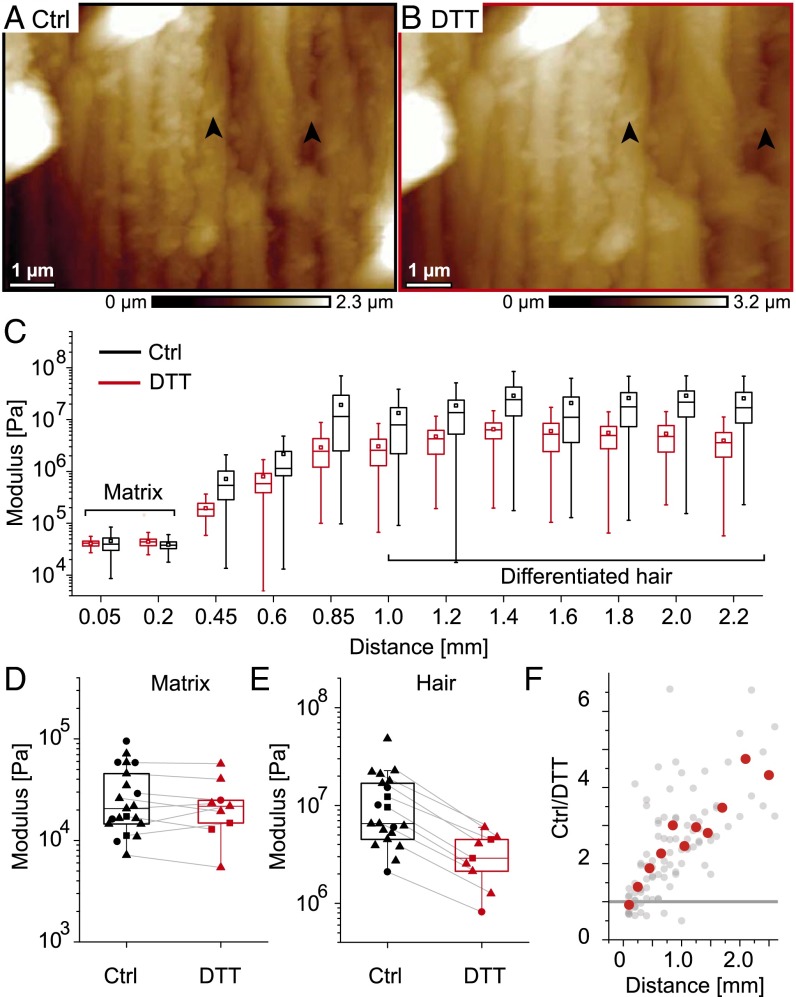
To test the influence of cysteine cross-linking on the network stability, the mechanics of the follicle was probed before and after reduction by DTT. DTT is a reducing agent breaking cysteine-disufide bonds and causes macrofibril swelling evidenced by topographic AFM images (Fig. 5 A and B). Fig. 5C shows the mechanical mapping of a representative follicle before (black) and 3 h after addition of DTT (red). The measured modulus in the bulb is not affected by the addition of DTT (Fig. 5D; n = 9; 30 ± 23 vs. 24 ± 15 kPa). In contrast, DTT softens the network in the differentiated hair (Fig. 5E, gray lines). Note that the inflection point k (570 ± 214 μm) and the parameter n (3.1 ± 0.7) obtained by fitting the Hill function to the AFM data (SI Text) of DTT-treated follicles show no significant difference compared with the untreated ones (511 ± 150 μm and 3.7 ± 1.0, respectively). A plot of the moduli ratios of individual control to DTT-treated follicles (Fig. 5F) revealed that cysteine cross-linking exerts a continuously increasing influence on the elastic moduli along the follicle axis. The first notable effects of DTT occur at around 400–500 µm, followed by a gradual increase, up to three- to fourfold due to cysteine cross-linking in the differentiated hair.

Fig. 5.

Effect of cysteine cross-linking on macrofibril morphology and follicle mechanics. AFM topographic images of the same region of a follicle section in PBS (A) and after cystine reduction by DTT (B). Arrows highlight the same distinct features before and after DTT treatment. (C) Representative mechanical mapping along one follicle before (black) and 3 h after addition of 300 mM DTT (red). (D) Boxplots of mean stiffness modulus determined in the matrix of different follicles before and after DTT reduction. The gray lines connect points obtained from the same follicle (n = 9). (E) Boxplots of mean values measured in the differentiated hair (distances > 800 μm) of different follicles before and after addition of DTT (n = 9). (F) Ratio of untreated to treated mean moduli for each individual follicle according to the distance from the bulb along the follicle axis (gray points). Red points show averages within bins of 200 μm.

Discussion

Our results represent, to our knowledge, the first measurement of the gradual stiffening of the hair fiber over the course of the entire keratinization process within the hair follicle. We will now put the mechanical measurements into perspective with concomitant changes in the microscopic network architecture, supramolecular organization of the local keratin, and biological events (Fig. 4).

Our AFM and TEM data show that an isotropic IF network appears right above the dermal papilla, within the elongation zone (zone I; Fig. 4) ∼200 µm from the base of the follicle (Fig. 2A and Fig. S2) (30). The observed appearance of the IF network is consistent with previous reports on the formation of keratins such as K35 and K85 (32, 33), together with high-glycine-tyrosine and high-sulfur KAPs in the early zone I, just above the dermal papilla (19). Our DTT reduction experiments revealed that cysteine cross-linking does not significantly contribute to mechanical properties at this stage (Fig. 5D). We hypothesize that this early network is rather stabilized by isopeptide (γ-glutamyl-ε-lysine) bonds between early KAPs and keratins, enabled by the previously established expression and activity of transglutaminase 3 at the base of the hair follicle (34).

From zone I on until the end of zone III (∼800 µm from the bulb), we observe a continuous mechanical stiffening of the network following a power law (Fig. 1D). During zones I and II, the IFs start forming a network of small macrofibrils that grow in diameter by lateral aggregation (Fig. 2 and 3B) (21, 35, 36). Also a gradual increase in volume fraction occupied by the macrofibrils occurs (Fig. S3B), along with a progressive orientation of the microscopic network as observed by AFM (Fig. 3C) and an increasing polarization of supercoiled keratin coils as determined by X-ray diffraction (XRD; Fig. 4). Together, these observations indicate that a significant portion of the proteins required to form the mature hair are assembled into macrofibrils by the end of zone II and mostly held by a transglutaminase-based network, which is consistent with the absence of further changes in the type of expressed keratins from zone III onward (37). We can theoretically model the related mechanical stiffening within the regions I and II by using an isotropic semiflexible, cross-linked 3D network model (4, 38) (SI Text) where nonaffine fiber bending is the dominant elastic mechanism. In such nonthermal networks, the network mesh size has to be smaller than the fiber persistence length, which we deduce from the macrofibril architecture within zones I and II (SI Text). These nonthermal models are common to fibrous tissues such as collagen (39) and differ from other models used, e.g., to describe actin networks (11, 12). In a bending dominated network, the Young’s modulus scales with $E\approx 3G\hspace{0.17em}\sim \hspace{0.17em}\kappa /l_0^4\sim \hspace{0.17em}{E}_f\left(r^4/l_0^4\right)$, where E_f denotes the modulus, r denotes the radius of a single macrofiber, and l₀ denotes the distance between vertices (4, 38). The linearly increasing radius of the macrofibers along the follicle axis during zones I and II (Fig. 3B) (r = const x), alone would therefore be sufficient to explain the network's increase in elastic modulus following a powerlaw with an exponent of 4, which is close to our observed value of 4.4.

However, the macrofibrils reach their maximum diameter in late zone II (∼500 µm; Fig. 3B), whereas the mechanical stiffening is still ongoing. This continued stiffening can thus not be explained by the above model and suggests additional contributions to the hardening, such as an increasing network orientation and compaction and internal mechanical reinforcement of the macrofibrils by disulfide cross-links. The internal reinforcement of the macrofibrils might be driven by a continued synthesis of KAPs (especially of the ultra-high-sulfur family) until late zone III as shown by in situ hybridization studies (19), suggesting a continued influx of KAPs into the macrofibrils. In agreement, XRD experiments revealed a gradual appearance of the KAP/IF quasi-hexagonal network and final maturation of the IF internal structure in zone III, after 500–700 µm. Our DTT reduction experiments show that a significant contribution of disulfide bonds to the overall network mechanics becomes visible already in zone II (Fig. 5F), whereas the matrix architecture there is far from being complete because most of the KAP/IF disulfide bonds are constituted much further up the follicle (in zone IV, 650 µm at earliest) (21). Those early disulfides should therefore mainly represent intra-IF disulfides (40), which contribute to the overall mechanical properties of the macrofibril. It is plausible that this intra-IF disulfide formation constitutes the driving force that leads to the maturation of the IFs in this area of the follicle (21, 41). This picture is in agreement with recent work by Fraser and Parry (42), establishing that the maturation of the IFs in zone III should be accompanied by an alignment of intra-IF cysteine moieties to enable such crosslinks.

Within zone IV (from 800 μm on), we found that the modulus of the hair fiber only slightly increased (by a factor of 2). For a follicle immersed in PBS, the mechanical maturation is therefore finished from 1,000 µm on above the bulb. The measured plateau of the mechanical modulus is consistent with the observation that the modulus of ∼11 MPa that we observed at the end of zone IV is very close to the estimated value of ∼6–9 MPa for a single IF in aqueous solution (10, 43, 44). This, together with closely packed fiber organization, suggests a transition to a stretching–dominated network, in opposition to zones I and II where the network mechanics were bending dominated. However, the effect of DTT on the follicle mechanics at 1,500 µm is twice as much as that at 800 µm (Fig. 5D), indicating further changes in the network. X-ray microdiffraction results show that the formation of the KAP/IF disulfide network evidenced by the strengthening of the 67-Å reflection is the only structural rearrangement occurring above 800 µm (Fig. 4) (20, 21). This low influence of the IF/KAP disulfide network on the follicle mechanics, despite its extremely high density, is likely a consequence of the immersion in PBS during our experiments. Due to the hygroscopic nature of the KAP matrix, it will swell in water, whereas the IFs show only little water uptake (45), causing a weakening of ionic and H-bond interactions. This swelling could minimize the mechanical contribution of the matrix in our measurements. To confirm this, AFM measurements were performed on the same follicles after drying, leading to values of moduli of 2.7 ± 1.4 GPa (Fig. 1B) at positions >800 µm. These values are comparable to those measured on mature dry hair using microindentation techniques and AFM (16, 28). This high Young's modulus indicates that the final rearrangement of the KAP/IF disulfide network together with the loss of water finalizes the keratinization process of the hair fiber.

Conclusion

Our observations link changes in the architecture and molecular structure of keratin macrofibrils to the local mechanical behavior at a tissue scale level. The complex simultaneous changes including macrofibril thickening, fiber orientation, and keratinization leads to an increase in stiffness by three orders of magnitude in just over the course of 1 mm. Our results are fully consistent with the existing structural and biological literature on the hair follicle and are also compatible with theoretical models relating structure and mechanical properties. Moreover, we further substantiate the hypothesis of an isopeptide network scaffold to stabilize the early keratin macrofibrils and propose a sequence of disulfide network formation events thereafter.

Materials and Methods

Sample Preparation.

Individual human terminal anagen hair follicles were obtained from facelift surgery, dissected, and stored at −80° in TissueTek (Sakura Finetek). Longitudinal 10-µm-thick sections were obtained using a Leica CM3050 Cryotome at −30°. For AFM studies, the slices were adsorbed on glass coverslips and immediately placed in PBS (Gibco). For FTIR microspectroscopy studies, sections were deposited on BaF₂ slides and dried. For XRD mapping, the follicles were inserted in a glass capillary and dried before analysis.

Mechanical Mapping of Follicles Using AFM.

Mechanical quantification of the hair follicle with force volume mode was either done in PBS on the DimensionIcon AFM (Bruker) using a ScanAsyst-Fluid lever (k_c ∼ 1 N/m, r = 20–60 nm) at room temperature or in dried conditions using the stiffer RTESPA (k_c ∼40 N/m, r = 8 nm) or TAP525A (k_c ∼200 N/m, r = 8 nm) levers (Bruker). In the force volume mode, 256 equidistant force-indentation traces with constant velocity are recorded with 5,000 points per trace within a 10 × 10-μm² zone. Traces are fitted with the Hertz model to obtain the mean Young’s modulus within one zone. The lever calibration and the details for the determination of macroscopic moduli within a 10 × 10-µm² zone are detailed in SI Text.

Topographic Imaging Using AFM.

Topographic imaging was performed with the Peak Force QNM mode with a scanning frequency of 0.1 Hz/line and a peak force of ∼6 nN on the DimensionIcon AFM. When measuring in PBS solution the ScanAsyst-Fluid+ lever (k_c = 0.7 N/m, r = 2 nm) was used, and the ScanAsyst-Air lever (k_c = 0.4 N/m, r = 2 nm) was used when measuring in dry conditions.

Infrared Spectroscopy.

Follicles were characterized at the SOLEIL Synchrotron on the SMIS beamline. The setup consists of a Nicolet 5700 FTIR spectrometer (Thermo Fisher) equipped with a Michelson interferometer and a KBr beam splitter, a Prior XYZ motorized stage, and a Continuum XL microscope (Thermo Fisher) used in confocal/transmission mode. The aperture was set at 10 × 10 µm². Spectra were recorded at 4-cm⁻¹ resolution and treated using Omnic (Thermo Fisher) and The Unscrambler (Camo) software. Collections of nonsaturated spectra were baseline corrected to remove artifacts within the amide 1 region (1,720–1580 cm⁻¹), and thickness corrected to offset variations in sample thickness using measurements performed with an NT9100 optical profilometer (Bruker).

X-Ray Microdiffraction Studies.

The follicles were characterized at the European Synchrotron Radiation Facility (ESRF) Synchrotron on the ID13 beamline (beam wavelength, 0.8556 Å; dimensions, 1.6 × 3 µm²). The experiments were carried out with a 117.5-mm sample–detector distance, which was calibrated using silver behenate (first order of 58.38 Å). Patterns were recorded on a CCD FRELON detector (2,048 × 2,048 pixels; pixel size of 50 × 50 µm²). Exposure time was set at 1 s, which caused no radiation damage.

About 1,800 diffractograms were collected on each follicle, by conducting a mapping with a lateral step of 5 µm and a longitudinal step of 50 µm in the first 1.5 mm from the base of the follicle and 250-µm step thereafter. The four keratinization zones were located according to the criteria described in ref. 21 that are recalled in SI Text and Fig. S7.

SI Text

Modeling of Mechanical Properties of the Follicle.

To better understand the measured mechanical stiffening of the hair follicle in terms of network structure, we first have to define the elastic regime for the theoretical model of our network, which can be either affine or nonaffine, entropic (thermal) or enthalpic (nonthermal), and stretching or bending dominated (4, 5). To this end, we make the hypothesis that the mechanical behavior is driven by the macrofiber (MF) network rather than by the unbundled and much thinner intermediate filament (IF) network (invisible in the TEM data). We assume that the regions I and II, where the network is less anisotropic, can be mechanically described as an isotropic semiflexible cross-linked biopolymer network in which nonaffine enthalpic bending is the dominant elastic mechanism. To justify this, we observe that the network mesh size L (approximate length between two fiber–fiber vertices), as estimated by TEM and AFM, is of the order of 300 nm, which is much smaller than the estimated fiber persistence length $l_p=\kappa /k_B\hspace{0.17em}T\approx$ 10 cm, over which the thermal effects would bend the MF; here $\kappa \approx E_f{r}^4$ is the fiber bending stiffness, r its radius, and $E_f\approx$ 6–9 MPa its Young’s modulus, assuming to be of the same order of magnitude than the IF’s Young modulus in aqueous solution (10, 43, 44), $k_B$ the Boltzmann constant, and T the temperature. The bending-dominated behavior, in opposition to the stretching-dominated one, can be inferred by observing that the cross-over length scale ${\lambda }_{NA}=\hspace{0.17em}{L}^2/l_b\hspace{0.17em}\approx 1\hspace{0.17em}\mu m$ between bending-dominated and stretching-dominated mechanical domains (38) is larger than the mesh size; here L is the distance between vertices and $l_b=\sqrt{\kappa /\mu }$, where $\mu =E_f{r}^2$ is the stretching modulus. This nonthermal behavior, common to fibrous tissues like collagen (39), differs from most studied isotropic networks, which are mostly described as affine entropic or enthalpic (46). These models can be used to describe controllable, reconstituted networks composed of actin (11, 12, 14), neurofilaments or vimentin (47), individual keratin polymers (48), and fibrin (9), where the values of elastic moduli are in a range of 1–100 Pa. The moduli in the follicle at the very beginning of zone I are in the range of 10 kPa and thus much higher than those of thermal networks, further arguing against an affine entropic model. In addition, up to 0.7 mm along the follicle, a linear increase in α-keratin concentration is shown by FTIR (Fig. 3D). Therefore, a thermal model would predict a power law with an exponent far from 4, in particular an exponent around 2.5 in dependency of concentration alone, or an exponent higher than 4 when a linear increase of the filament diameter as a function of the distance along the follicle axis is also taken into account (11, 12, 46). To compare the used nonthermal model with our experiments, we observe that the Young modulus of an isotropic network in the bending dominated regime is $E=3G\approx \kappa /L^4\propto r^4\propto x^4$, the last step derives from the measured linear increase of the MF radius with the distance x from the hair bulb. This theoretical power law is close to the power 4.4 that we measured by AFM. In addition, assuming a MF modulus of E_f = 6–9 MPa from measured single IF in aqueous solution (10, 43, 44), we can estimate the network elasticity in the beginning of zone I to be in the range 50–70 kPa, which is not far from the value observed experimentally (Fig. 1B).

We observe that, even neglecting the MF alignment along the hair axis, the nonthermal bending-dominated behavior assumed for the zones I and II could switch to a stretching-dominated behavior due to the higher MF compaction (and thus the smaller mesh size L) on the late zone IV, which would decrease the crossover length scale ${\lambda }_{NA}$ below the mesh size. Therefore, the network stiffness evolution within the zone IV would be primarily related to the MF stiffening due to increase of the cysteine cross-links.

Mechanical Mapping of Follicles Using AFM.

Experimental protocol.

Longitudinal sections of 10-µm thickness where cut from frozen human hair follicles, adsorbed on glass slides, immediately immersed in PBS solution (Fig. S1A), and kept at 4 °C. Within 2 d after cutting, the follicle was mechanically characterized using AFM (Dimension Icon, Bruker) in PBS buffer with a “ScanAsyst-Fluid” lever (Bruker) at room temperature. The force constant of the lever (k_c ∼ 0.4–1.2 N/m) was determined via the thermal noise power spectrum of the lever before every experiment (49, 50). For mechanical characterization, several 10 × 10-μm² zones were chosen along the follicle, and 256 independent force-indentation curves within one zone were recorded using Bruker’s force-volume mode. In this mode, 16 × 16 equally spaced, single force-indentation curves (Fig. S1B) with constant pulling speed (1–5 μm/s) were recorded with 5,000 points per curve. Fig. S1C shows three exemplary force-indentation curves. When the cantilever tip is pushed into the substrate, the force becomes nonzero, and the indentation depth is related to the local elastic modulus of the substrate: softer substrates are indented more. From each 10 × 10-μm² zone along the follicle, the elastic moduli are calculated using the Hertz model for all 256 force-indentation traces and shown in boxplots (Fig. 1A and Fig. S1D). The choice of the Hertz model and the fitting routine is explained later.

Choice of the cantilever.

Cantilevers have a specific detection range for measuring the Young’s moduli of substrates; to indent materials with higher moduli, levers with higher stiffness are needed. The ScanAsyst-Fluid’s force constant and its relatively large tip radius (k_c ∼ 1 N/m; r ∼20–60 nm) are optimized for mechanical measurements in aqueous solution on soft materials with a modulus around 1 MPa (which is close to the modulus measured at the inflection point k of the follicles; Fig. 1D). For substrates with higher rigidity, the indentation depth becomes smaller and more difficult to detect. To test whether the ScanAsyst-Fluid lever still correctly detects the observed moduli plateau around 11 MPa for the differentiated hair follicle (distances > 0.8 mm in Fig. 1A) we used two additional cantilevers with higher force constants. Fig. S1D shows boxplots on three regions within the differentiated hair of the same follicle measured in PBS with the ScanAsyst-Fluid Lever (k_c = 1.0 N/m, r = 20–60 nm), the TAP150A lever (k_c = 4 N/m, r = 8 nm), and the RTESPA lever (k_c = 40 N/m, r = 8 nm). All different levers detect a similar plateau value around 6 MPa for this specific follicle. In addition, the mean of the plateau values from different follicle cuts measured with the RTESPA and the TAP150A lever gives 12 ± 10 MPa (n = 4; Fig. S1E), which is identical to the value measured with the ScanAsyst-Fluid lever (11 ± 10 MPa; Fig. 1B). These values show that the softer ScanAsyst-Fluid lever is still within its detection range for the Young’s modulus of differentiated hair in PBS solution.

However, when the same follicles are measured after drying, the ScanAsyst-Fluid lever is above its detection range. Thus, to correctly measure the moduli of the differentiated hair (distances > 0.8 mm) after drying we used the stiffer RTESPA (k_c = 40 N/m) and TAP525A (k_c ∼ 200 N/m) levers (Fig. 1B). The obtained average values measured on dried and differentiated hair follicles are similar to the elastic moduli determined by macroscopic techniques such as microindentation (16).

Calculating the elastic modulus from indentation data.

Different theoretical models are available that allow calculating the Young’s modulus of a body based on local indentation experiments. Hertz described the local deformations of two elastic bodies in contact using infinitesimal strain theory and local parabolic shape approximations (24). He developed analytical functions describing how the indentations of simple geometries such as spheres depend on the force and the Young’s modulus of the substrate. Later, solutions for conical and flat cylindrical indenters were given by Love (51) and Sneddon (52). It is important to note that these models consider only very small indentations on homogeneous, isotropic, and elastic materials. To account for large indentations, a finite element theory was developed by Costa et al. (53). Importantly, the absolute values calculated via finite element theory can differ by a factor of 10 from values calculated using the Hertz model (54). Despite this difference in absolute values, relative changes in the substrates Young’s modulus are still detected by both theories (54). Today, a multitude of different models (23, 55, 56) are available also considering additional adhesive force contributions such as the Johnson–Kendall–Roberts (JKR) model (57) and the Derjaguin–Muller–Toporov (DMT) model (58). The Hertz model is used for hard substrates where the indentation is small compared with the cantilever radius, whereas the Sneddon model is often used for soft substrates with large indentation depths compared with the cantilever radius. Therefore, the Hertz model is well suited to calculate indentation data obtained using the ScanAsyst-Fluid lever with a tip radius of up to 60 nm on the differentiated fiber (>1 MPa; Fig. S1C). To this end, we fitted using SPIP 5.1.6 (Image Metrology) every single force-indentation curve from a 10 × 10-μm² zone via the formula

$$F=\frac{4}{3}{E}^{\#}\sqrt{r{d}^3},$$

where E^# is given by $1/E^{\#}=\left[\left(1-{\nu }_s^2\right)/E_s\right]+\left[\left(1-{\nu }_p^2\right)/E_p\right]$. Because the modulus of the substrate E_s is much smaller than the one of the AFM tip E_p, we neglect the second term and we assume the Poisson ratio to be ν_s = 0.5. The tip radius r was determined before every experiment via indentation of a substrate with known modulus of 2.5 MPa (PDMS; Bruker). Note that with this type of calibration, the Young’s moduli of different follicles are measured relative to the constant Young’s moduli of the test substrate. Occasionally, the tip radius was cross-checked via topographic imaging of a calibrated substrate composed of sharp spikes (TGT01; MikroMasch, NanoAndMore GmbH), leading to comparable results. The variability of moduli measured within one 10 × 10-μm² area that has an SD of 0.6 times the mean value (Fig. S1H) comes from the mechanical inhomogeneity of the substrate, because a repetitive indentation of only one position (position c in Fig. S1H) shows an SD that is decreased by a factor of 10.

For soft regions below a modulus of around 100 kPa, the cantilever indentation becomes larger than the tip radius, and therefore the assumptions of the Hertz model are not valid any more. To test the corresponding error, we analyzed the same data in the soft regime using the Hertz and the Sneddon model. For the Sneddon model (52), we fitted the formula

$$F=\frac{2E_s\tan \left(\alpha \right)}{\pi \left(1-{\nu }^2\right)}{d}^2,$$

to the force-indentation data analyzed before with the Hertz model, where the Poisson ratio ν is assumed to be 0.5, and the half angle of the conical indenter α is taken as 19°. Note that the used formula is an approximation because the actual form of the lever is not conical but pyramidal (59), having a front half angle of 15°, a back half angle of 25°, and a side half angle of 17.5°. Because the PDMS test substrate with 2.5 MPa is too rigid for the determination of α using the relative calibration method, we choose α = 19° as the mean value of the different tip angles. Fig. S1F shows the mean modulus of similar regions (distances of 0.1–0.2 mm) of different follicle cuts from the same donor (n = 12, one point corresponds to the mean of 256 force indentation curves within one 10 × 10-μm² zone) calculated with both the Hertz and the Sneddon model. Interestingly both models lead to comparable results showing that using the Hertz model even for the soft regime (between 10 and 100 kPa) does not introduce large systematic errors. This comparability is likely due to the fibrillary organization of the substrate, where, not the indentation of the lever into the fiber is measured, but rather the deformation of the fiber that is fixed between two neighboring vortices. It is known that when testing the cytoskeleton of cells with sharp tips, the Young’s modulus is overestimated compared with a testing with AFM probes with mounted spheres (27). This overestimation indicates that one rather probes the mechanics of the underlying fibrous network when a sharp tip is used (25, 26), as it was intended within our study. To estimate the related discrepancies between sharp and round tips in our tissue model, we used soft levers with mounted spheres (NovaScan; k_c = 0.05 N/m, r = 1.2 μm) and measured a 6.5 times smaller modulus at the base of the follicle when using the Hertz model (Fig. S1G; Bead, n = 4) compared with the sharp ScanAsyst-Fluid lever (Fig. S1G; SA). A similar decrease is observed when comparing values measured in the dermal papilla of the follicles. Note that both methods still allow resolving relative differences between the papilla and the matrix.

Quantification of the moduli increase along the follicle.

To quantify the sharpness of the stiffness increase along the follicle axis we fitted the Hill function

$$y=M+\left(H-M\right)\frac{x^n}{k^n+x^n},$$

to the logarithmized data of individual follicle cuts (see red line in Fig. 1A). The fixed parameters M and H correspond to the moduli values determined for the matrix and the differentiated hair fiber, respectively. The fitting parameter k corresponds to the distance where half of the stiffening occurred on a logarithmized axis, and the fitting parameter n is related to the steepness [the slope in Fig. 1D at k_i is equal to 0.25·(H – M)·ln(10)·n] of the logarithmized moduli rise. The inflection point k would be 0.1 mm smaller if the moduli values obtained with the NovaScan levers with a mounted sphere would be taken into account for the parameter M.

X-Ray Microdiffraction Studies.

Fig. S7 shows how the four different keratinization zones were defined based on the XRD mapping experiments. About 1,800 diffractograms were collected on each follicle, by conducting a mapping with a lateral step of 5 µm and a longitudinal step of 50 µm in the first 1.5 mm from the base of the follicle and a 250-µm step thereafter. The following criteria were used:

• • Zone I: no preferential orientation of organized structures (4.6-, 10.5-, and 43-Å rings);

• • Zone II: 5-Å reflection on the meridian (supercoiled α-keratin coils); 60-Å signal on the equator (early IF lateral order: larger diameter than final IFs);

• • Zone III: thin-5.2 Å reflection on the meridian (internal long-range order inside the IFs) and 90-Å signal on the equator (IF/KAP matrix paracrystalline order); and

• • Zone IV: progressive appearance of 67-Å signal on the meridian (formation of IF/KAP disulfide network and finalization of the longitudinal order).