Estimating option values of solar radiation management assuming that climate sensitivity is uncertain

Significance

Stratospheric sulfur injection is an unprecedented manipulation of climate systems to rapidly decrease the global mean temperature and could entail environmental risk as well as confront ethical and governance challenges. Nonetheless, most studies have only evaluated impacts of solar radiation management (SRM) on the premise of its deployment. This paper presents one possible methodology for estimating option values of SRM assuming a fairly moderate scenario on SRM’s use compared with preceding literature, which would be helpful to examine realistic values of SRM for the society where social acceptability of SRM’s actual deployment is not high. Our results emphasize the near- to mid-term role of retaining SRM as a later risk-hedging option in the face of the uncertainty about climate sensitivity.

Abstract

Although solar radiation management (SRM) might play a role as an emergency geoengineering measure, its potential risks remain uncertain, and hence there are ethical and governance issues in the face of SRM’s actual deployment. By using an integrated assessment model, we first present one possible methodology for evaluating the value arising from retaining an SRM option given the uncertainty of climate sensitivity, and also examine sensitivities of the option value to SRM’s side effects (damages). Reflecting the governance challenges on immediate SRM deployment, we assume scenarios in which SRM could only be deployed with a limited degree of cooling (0.5 °C) only after 2050, when climate sensitivity uncertainty is assumed to be resolved and only when the sensitivity is found to be high (T2x = 4 °C). We conduct a cost-effectiveness analysis with constraining temperature rise as the objective. The SRM option value is originated from its rapid cooling capability that would alleviate the mitigation requirement under climate sensitivity uncertainty and thereby reduce mitigation costs. According to our estimates, the option value during 1990–2049 for a +2.4 °C target (the lowest temperature target level for which there were feasible solutions in this model study) relative to preindustrial levels were in the range between $2.5 and $5.9 trillion, taking into account the maximum level of side effects shown in the existing literature. The result indicates that lower limits of the option values for temperature targets below +2.4 °C would be greater than $2.5 trillion.

Uncertainties surrounding equilibrium climate sensitivity (T2x) (1) pose a challenge to mitigation policymaking aimed at achieving the goal of limiting the temperature rise below certain levels (e.g., +2 °C relative to preindustrial levels). The inertia of temperature rise would demand more stringent mitigation policy over the period of climate sensitivity uncertainty in preparation for possible occurrence of high climate sensitivity, because it is difficult to reduce emissions sufficiently rapidly even with all of the currently available technologies of mitigation.

The possibility of higher climate sensitivity (2) and the inability to instantaneously control the temperature via mitigation have sparked positive debates about solar radiation management (SRM), especially about conducting research and development (R&D) on the topic (3, 4). SRM has been regarded as a rapid (5) and relatively inexpensive geoengineering measure compared with mitigation; in this study, our cost estimates are based on albedo enhancement via stratospheric sulfur injections (Materials and Methods). However, SRM’s overall costs would be higher than simply the deployment costs alone when its environmental risks (6, 7) [e.g., polar ozone depletion (4, 8), changes in precipitation patterns (9)] are factored in, although the true magnitude of all of the risks is still unknown. Moreover, SRM cannot prevent ocean acidification because it does not directly affect the carbon cycle.

Thus far, cost–benefit analyses (CBA) have attempted to answer whether and how much SRM should be deployed given its costs and negative side effects (10–13). Among the CBAs of SRM, ref. 13 highlighted the role of SRM as a climate emergency measure under the assumption that SRM would be implemented after learning the extent of climate sensitivity. With a comprehensive damage function, including the damages caused by ocean acidification, SRM deployment, and climate change, the above study found that SRM would reduce total net economic costs (comprising the above three types of damages and costs for mitigation and SRM deployment) by ∼2% of global gross domestic product (GDP) in 2100 when damages due to SRM are not included. This figure would reduce to ∼1% when SRM-related damages are raised to as high as 4.5% of GDP/Wm⁻². Furthermore, ref.13 estimated that learning on the true magnitude of damages can reduce the overall costs of climate change in the order of 10%, equivalent to 0.01% of GDP. This number can be interpreted as the value of information on the damages from SRM, or the potential benefit of R&D on the topic.

However, the results are based on a static two-stage model consisting of prelearning (uncertain) and postlearning stages regarding climate sensitivity, and therefore little is known about when such savings due to SRM and learning of its damages would generate. Due to the static nature of the model (13), it is unknown how much value would be originated by SRM, especially during the period in which climate sensitivity uncertainty remains and SRM is not allowed to be deployed, although we believe that quantifying such value of SRM before its implementation would be useful for determining the near-term strategies (e.g., whether to continue R&D for SRM and to what extent in terms of cost).

In this study, we attempt to obtain new insights mainly on two points mentioned below by conducting a cost effectiveness analysis (CEA) that drives a cost-minimizing combination of mitigation and SRM, given temperature change targets by the year 2100, using a dynamic world energy model (14) (Materials and Methods). Note that we do not conduct a CBA as in refs. 10–13 because estimation of damage caused by climatic changes does not yet have a sound empirical basis (15, 16).

First, we show how the strategy of retaining SRM as an option in preparation for possible higher climate sensitivity would alter the CO₂ emission pathways of uncertain (1990 to 2049) and post-uncertain (2050–2100) periods regarding climate sensitivity (we choose the year 2050 arbitrarily as the point at which uncertainty is resolved). Such time-dependent effect that SRM has on the CO₂ emission pathways was not explicitly analyzed in ref. 13, whereas our study can show the optimal emission pathways during the prelearning period regarding climate sensitivity for two cases with and without SRM options (see SI Appendix, Table S2 for a more detailed comparison of our study and ref. 13).

Second, and most importantly, we present one possible methodology for estimating option values of SRM for the period 1990–2049 in which it is not truly implemented (Materials and Methods). The SRM option value in this paper refers to a value arising from the policy flexibility provided by an addition of SRM option to a set of mitigation technologies. In our model calculation, the value is computed in terms of the reduction of mitigation costs thanks to retaining an SRM option (Materials and Methods). We show the relationship between option values and temperature change targets of +2.4 °C, +2.5 °C, and +3 °C relative to preindustrial levels, with plausible ranges reflecting the uncertainty about its side effects. Side effects proportional to the extent of cooling by SRM as high as $3 trillion/°C are considered, which is roughly equivalent to the highest value shown in the existing literature, i.e., around $2.3 trillion/Wm⁻², or 4.5% of GDP/Wm⁻² ($50 trillion) (13). The SRM option value estimated in our study is different from the value of information on SRM’s side effects shown in ref. 13; the former is the cost savings induced by having SRM as an option that allows higher CO₂ emissions under uncertainties in climate sensitivity for a given temperature target, whereas the latter is the benefits by learning (accumulation of knowledge) about the true magnitude of side effects, which was calculated as the expected reduction of total climate change costs assuming that it is equally possible that side effects are found to be either high or low (zero) as a result of learning. In sum, our study estimated the option values including side effects (damages) of SRM, whereas ref. 13 estimated the value of information (learning) about its side effects (for a more detailed comparison with ref. 13, see SI Appendix, Table S2).

For temperature targets below +2.3 °C, there were no feasible solutions for the model runs not including SRM options, and therefore their option values were not evaluated. Note that our estimates of the SRM option values are computed in a bottom-up model of energy systems with detailed mitigation technologies (Materials and Methods and SI Appendix), whereas the estimates of ref. 13 are derived using a top-down model, which are far simpler than ours in terms of mitigation cost estimates but consider benefits of both mitigation and SRM strategies as described above.

Before presenting assessment results, it is particularly important to be explicit about implementation scenario of SRM. Ref. 17 stressed this point, and showed a temporary and moderate scenario where SRM is implemented after 2020 and offsets only half of the growth in anthropogenic climate forcing, before SRM will be gradually terminated by 2200. This scenario on SRM implementation provides a basis to lessen governance challenges (18, 19) and ethical concerns (20); we share this viewpoint in terms of moderateness of SRM implementation, but endeavor to frame a distinct scenario on its timing where SRM is not allowed to be implemented immediately. Our “later implementation scenario” is based on our view that governance challenges related to SRM implementation are significant today because the uncertainty in the side effects of SRM is still large and hence international society is not ready for implementing it immediately as a policy choice even in a coordinated manner (19, 21). Another practical reason of assuming this scenario is to allow for the possibility that SRM might be deployed only after the resolution of climate sensitivity uncertainty, as shown in ref. 13. Furthermore, it is worth recognizing that some of public evaluations of SRM revealed that immediate implementation of SRM could gain fewer supports than conducting the study of SRM, even though the overall support for use of SRM is high (22). Other studies revealed that SRM’s social acceptability is much lower than that of carbon dioxide removal (23) and most are uncomfortable with SRM implementation, although there is some support for promoting its research and conducting a field trial (22, 24).

Taking into account the governance challenges and people’s reluctance to a rush toward SRM implementation, we will allow SRM to be implemented only in the future (after 2050) in the face of high climate sensitivity, although ref. 17 argued that time for leaning-by-doing would be necessary even if SRM is assumed to be used in a climate emergency situation (17). The reason behind our assumption of SRM implementation only in a high climate sensitivity case is to examine the role of SRM as insurance in comparison with ref. 13 (SI Appendix, Table S2). This assumption may also be supported by the finding of ref. 22 that SRM implementation in the incidence of a climate emergency situation was more supported by the public than its immediate implementation.

Based on such a backdrop, we assume that SRM could only be deployed with a limited degree of cooling (0.5 °C) by future generations (after 2050) if climate sensitivity is found to be high (T2x = 4 °C) (Table 1, scenario 3). This amount of cooling is more moderate than most CBA results [e.g., refs. 12 and 13 derived optimal cooling of no less than 1 Wm⁻² (roughly equivalent to 2/3 °C), although ref. 13 considered SRM’s side effects and ref. 12 introduced an additional constraint to soften its termination effect]. The amount of cooling of 0.5 °C is also analogous to that of ref. 17. Note that if we change the above assumptions on the amount of cooling, time at which climate sensitivity uncertainty is resolved, number for high climate sensitivity, its probability, and discount rate, then the estimates shown below would change (Discussion).

Table 1.

Scenarios after the resolution of uncertainty in climate sensitivity

Scenario no.	Equilibrium climate sensitivity (T2x)	Occurrence probability, %	SRM implementation
Scenario 1	2 °C (low)	10	No
Scenario 2	3 °C (moderate)	71	No
Scenario 3	4 °C (high)	19	Yes

SRM is deployed after 2050 only if climate sensitivity is found to be high.

Results

CO₂ Emission Pathways.

Because SRM is implemented only when scenario 3 occurs after 2050, SRM is merely retained as an option when (i) there is uncertainty regarding climate sensitivity (before 2050) and (ii) when climate sensitivity is found to be low (T2x = 2 °C) or moderate (T2x = 3 °C) (scenarios 1 and 2 in Table 1). Accordingly, we define two types of option value: option value A accumulated during 1990–2049, and option value B during 1990–2100. The SRM option value is defined as the difference between the total energy systems costs (discounted by 5% per year) without SRM and those with SRM (Materials and Methods and Eq. 1).

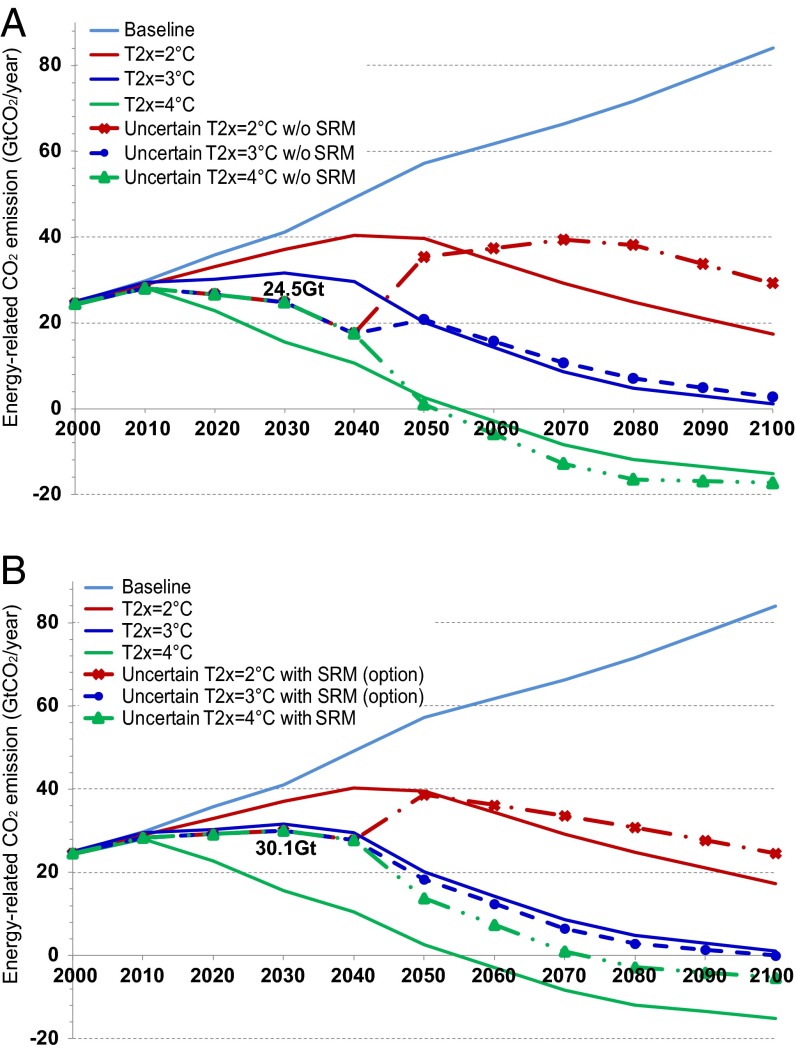
Fig. 1 A and B shows the energy-related CO₂ emission pathways for a +2.5 °C target (+2.4 °C and +3 °C targets are qualitatively the same). Emission pathways will diverge into three branches after 2050. The higher the climate sensitivities are, the more stringent the respective mitigation pathways will be. From 2000 to 2040, a period in which uncertainties remain, stringent mitigation pathways are derived (Fig. 1A), because a CEA must satisfy temperature change constraints taking into account the inertia of a temperature rise and the inability of regular mitigation technologies to cool down the temperature sufficiently rapidly (25). This model result would parallel the debate on precautionary abatement of CO₂ emissions given uncertain climate sensitivity (26, 27).

Fig. 1.

Effects of SRM options on CO₂ emission pathways for a +2.5°C target relative to preindustrial levels in 2100. Two panels show emission pathways (A) without SRM options and (B) with SRM options.

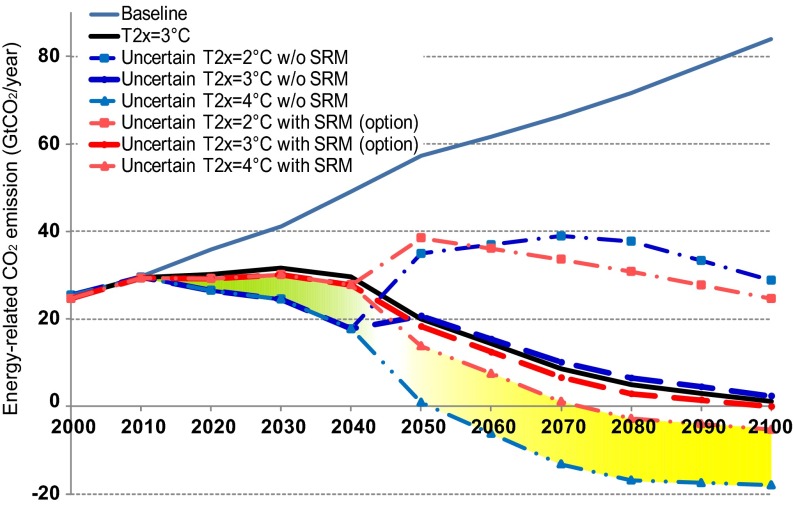
However, when SRM is incorporated (Fig. 1B), it is implemented to the allowed maximum extent (0.5 °C) by the year 2100, resulting in alleviation of the stringency of near-term mitigation pathways (moderating the reduction of, for example, 5.6 GtCO₂ in 2030) compared with pathways not including SRM. SRM’s deployment effects manifest themselves only in the long-term (2050–2100) mitigation pathway for T2x = 4 °C (Fig. 2, yellow area), but it also provides room for the near-term (2000–2040) mitigation policy (Fig. 2, green area). This upward shift of optimal emission pathways during the 2000–2040 period decreases energy systems costs and generates option values. In other words, preparing SRM options for the possible occurrence of high sensitivity would allow for emitting more CO₂ in the near term in the face of uncertainty about climate sensitivity. However, it should be noted that there is concern about the moral hazard of emitting more CO₂ thanks to future SRM implementation (7), although our assumption regarding the limited degree of cooling (0.5 °C) by SRM may reduce such concern. Looking at the two emission pathways with the moderate climate sensitivity (Fig. 2, thick blue and red lines) for the period 2010–2049, SRM causes optimal emission pathways under uncertainty to approach the pathway (solid black line) where climate sensitivity is deterministically moderate (T2x = 3 °C), implying that holding SRM as a later option might justify mitigation policymaking based on moderate sensitivity rather than high sensitivity.

Fig. 2.

Comparison of CO₂ emission pathways with and without SRM options where climate sensitivity is uncertain.

SRM Option Value.

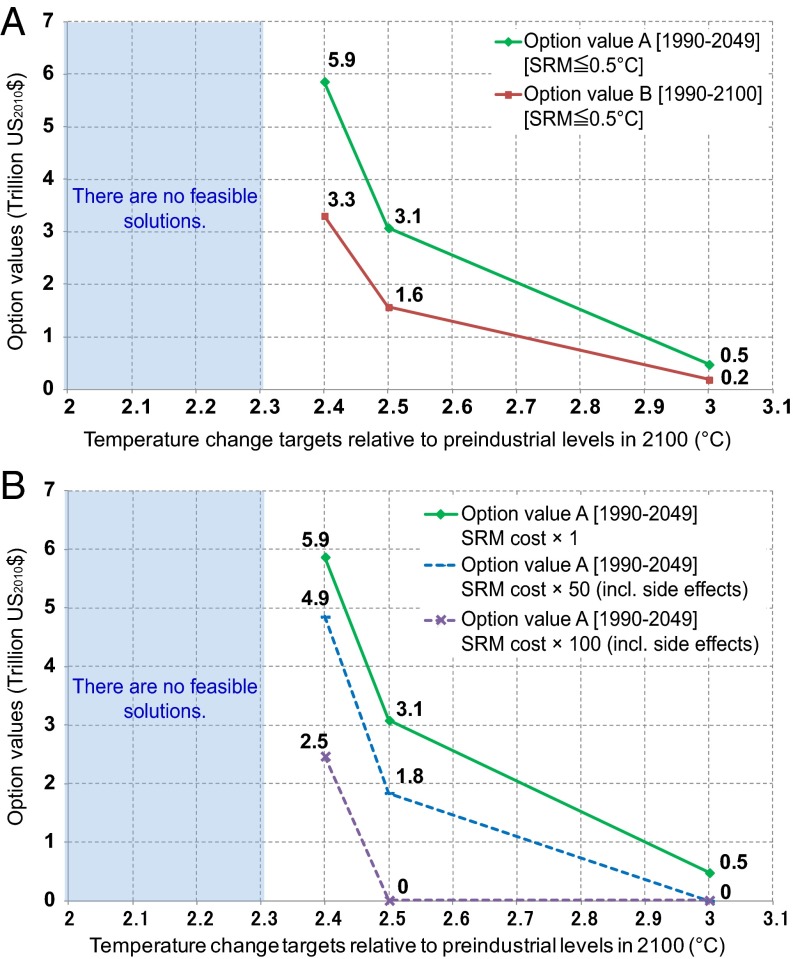
The SRM option value increases with the stringency of temperature change targets (Fig. 3A) because the absence of SRM would result in higher systems costs under more stringent temperature targets. Option value A (accumulated during 1990–2049) is estimated to be higher than option value B (1990–2100) because with SRM the mitigation after 2050 increases whereas the mitigation before 2050 decreases (Fig. 2, thick red line). According to our estimates under the assumptions described above, option value A is estimated to be $0.5 trillion for the +3 °C target relative to preindustrial levels in 2100. For +2.5 °C, the figure rises to $3.1 trillion, and for +2.4 °C it jumps to $5.9 trillion.

Fig. 3.

Relationship between SRM option values and temperature change targets. Shown are (A) SRM option values for different time periods and (B) sensitivities of SRM option values to the total cost of SRM consisting of its deployment costs and side effects.

Precisely, the sharp rise in the option value from the target of +2.5 °C to +2.4 °C is attributed to the large difference in near- to mid-term abatements of the two targets. In 2040, the +2.4 °C target requires abatement of 61% relative to 2010, whereas the +2.5 °C target requires a 41% reduction (SI Appendix, Fig. S5). This difference in abatements leads to a significant cost difference between the two targets. As noted previously, there were no feasible solutions for the model runs not including SRM options with temperature targets below the +2.3 °C target, and the sharp increase in the option value results from the fact that costs for mitigation rise dramatically as a temperature target approaches its achievable limit.

We conduct a sensitivity analysis regarding damages from SRM’s side effects because these remain deeply uncertain; it shows that the option value decreases with the magnitude of side effects and even becomes zero for the +3 °C target when side effects equivalent to 50 times the deployment costs are considered (Fig. 3B). However, for the +2.4 °C target, the option value still remains positive at $2.5 trillion even when side effects equivalent to 100 times the deployment costs (roughly equivalent to the highest value for SRM damages in CBAs (10, 12, 13): 4.5% of GDP/Wm⁻² in ref. 13 are considered; this is because SRM with a cost (including side effects) equivalent to 50 times its deployment cost would not be acceptable under a moderate temperature target such as a +3 °C target [optimal SRM implementation amount (°C) = 0], but 100 times the cost of SRM would still be acceptable under a stringent target such as +2.4 °C [optimal SRM implementation amount (°C) = 0.06 > 0] (SI Appendix, Fig. S6).

In sum, based on our estimates, the option value of SRM in 1990–2049 for a +2.4 °C target (the lowest temperature target level for which there were feasible solutions in this model study) by 2100 relative to preindustrial levels was estimated at approximately $2.5–5.9 trillion with the magnitude of side effects ranging from 0- to 100-fold SRM’s deployment costs. Accordingly, it can be reasonably inferred that, for temperature targets below +2.3 °C, the option value during 1990–2049 would be greater than $2.5 trillion even when the highest side effects due to SRM in the preceding literature are considered.

Discussion

Note that the results need to be interpreted together with the underlying assumptions. The results are dependent on assumptions about the maximum allowable amount of cooling (0.5 °C); time at which climate sensitivity uncertainty is resolved (the year 2050); probability function of climate sensitivity [combination of numbers for three discrete climate sensitivities and their probabilities: P(1) = 0.1; P(2) = 0.71; P(3) = 0.19, where 1, 2, and 3 show climate sensitivity scenarios of T2x = 2, 3, and 4 °C]; discount rate (5%/year); and baseline scenario and its relevant dataset regarding energy and climate systems (SI Appendix, SI Text, Baseline Scenario and Table S1). All these factors would change the option values of SRM estimated in this study. For example, if the maximum allowable amount of cooling is changed from 0.5 to 0.75 °C, the option value for the +2.4 °C target increases from $2.5–5.9 trillion to $2.5–6.2 trillion (the ranges depend on the assumed breadth of the SRM’s side effects). Though the upper limit of option values increases, the lower limit is unchanged because the cost-efficient amount of SRM is 0.06 °C cooling when the SRM’s side effects are their assumed upper limits, i.e., 100-fold the deployment costs (SI Appendix, Fig. S6). If we assume that the true climate sensitivity is known in, for example, 2040 and SRM is implemented from the same year, the option values of SRM would decrease because the length of the period under uncertainty in climate sensitivity is shortened. Another source of uncertainty is the model used, and hence for refinement of estimates in this regard, model intercomparison may be required with harmonized assumptions on various factors listed above.

Recognizing these multiple factors that may affect estimates, we showed a possible methodology for evaluating the option value of SRM for different temperature change targets by 2100 with plausible ranges for the side effects due to SRM, with a particular focus on the uncertainty about climate sensitivity. A CEA method based on an energy systems model enables us to maintain the robustness of estimated option values in terms of costs for mitigation given temperature change targets; in other words, we set aside the uncertainty in estimation of damages due to climate change.

It is important to recognize that there are other uncertainties that are not captured in our model framework but may influence global mean temperature rise and the magnitude of SRM option values. These uncertainties include those originated from human activity (e.g., socioeconomic development and technological progress regarding production and mitigation) and natural process affecting emissions and concentration (e.g., land/ocean carbon sinks through biomass). Under such large uncertainties, the option values of SRM could be higher or lower than those estimated in this study. There is uncertainty even in the statistics of emissions, and this uncertainty could also affect option values of SRM because it would affect temperature rise. To take another example that could directly alter the estimates of option value, the assumption about costs for mitigation technologies may well vary by a factor of 2–3 (28), and therefore the option values shown in our study can change with the same magnitude. Ethical and political concerns could also affect SRM’s option values in reality, but these issues are beyond the scope of this analysis.

Regarding the uncertainty about side effects due to SRM, our assumption on the allowed maximum cooling of 0.5 °C, which is considered to be fairly moderate compared with the existing literature, would play a role of narrowing down the variance of side effects due to SRM, thereby decreasing their magnitude in absolute terms; with this in mind, the sensitivity analysis (Fig. 3B) would illustrate plausible lower limits of the option value of SRM with regard to its side effects in the sense that the side effects are assumed to reach one of the highest values in the existing literature—namely, 4.5% of GDP/Wm⁻² (13).

The estimates of option values of SRM originated in the period 1990–2049 may have implications as to how to spend budgets for SRM-related R&D before its possible deployment in the incidence of high climate sensitivity. Suppose that international society aim to keep 2100 global mean temperature below +2.4 °C, and that true magnitude of SRM side effects fall within the range of this study. Then, an SRM option value of $2.5–5.9 trillion would be generated (Fig. 3B), which would surpass the current spending on SRM research which is less than $10 million per year (13), or $0.0003 trillion accumulated over 60 y (1990–2049) with an annual discount rate of 5%. To take another example, a first round of albedo modification-related experimental studies, which are comprised of eight field projects proposed at workshops in the United States, would cost more than $1.124 million in total (29, 30), or $0.03 trillion accumulated over 60 y (1990–2049), assuming that the total cost for the eight field projects is spent annually. This number is sufficiently smaller than the option value. The option value could be also used for a wide range of other SRM-related research topics such as legal, ethical, social, political, and economic ones as well as engineering studies about deployment technologies. As ref. 30 suggests, it may be of importance that SRM-related research would simultaneously advance basic understanding of the climate system with regard to, for example, climate sensitivity.

Our estimates are based on an optimization-type model that allows for mitigation policymaking in combination with SRM, although it only allows for a partial substitution for mitigation. Some may question this premise from ethical and moral perspectives, and may argue against the option value of SRM estimated with our approach. However, in this regard again, our fairy moderate assumption on the allowed maximum amount of SRM and time at which SRM is allowed to be deployed may be helpful to soften such concerns of moral hazard. It should be stressed that our results do not justify neglecting best efforts to cut emissions. As a final note, the model of this study is a dynamic optimization model that assumes climate sensitivity uncertainty is resolved as a single step, but it may be possible as future works to consider multistages regarding the state of knowledge about climate sensitivity, and a full stochastic dynamic programming model that allows for evolution of knowledge over time (31).

Materials and Methods

Assessment Model.

The Dynamic New Earth 21 (DNE21) model (14), composed of three fully integrated submodels of energy systems, the macroeconomy, and climate change is an intertemporal nonlinear optimization model with 10 world regions, and its energy supply system is formulated in a bottom-up fashion with ∼50 types of technology. Non-CO₂ greenhouse gas emission scenarios are exogenously assumed on the basis of ref. 32. Assumption data such as those for energy demand and supply and climate model parameters are updated to the latest version.

SRM is incorporated into the energy systems model as an independent variable that incurs costs, and it is formulated as directly decreasing global mean temperature, affecting neither CO₂ emissions nor its concentration. With SRM options added into the energy systems model, the structure of the optimization problem includes a choice problem between CO₂ abatement (mitigation) and SRM. Mitigation technologies are grouped into improving energy efficiency, fossil fuel switching, renewables, nuclear, carbon capture and storage, and others. The cost minimization problem allows for the selection of lower-cost mitigation technologies one by one to meet temperature change constraints, and if SRM is more cost-effective in meeting a temperature constraint, then SRM is selected on a priority basis. It is assumed that SRM can cancel a temperature rise of no more than 0.5 °C; in other words, the total annual sulfur mass injected into the stratosphere faces maximum constraints. This assumption is to prevent unconstrained massive injection of sulfate aerosols.

Scenarios and Definition of Option Value.

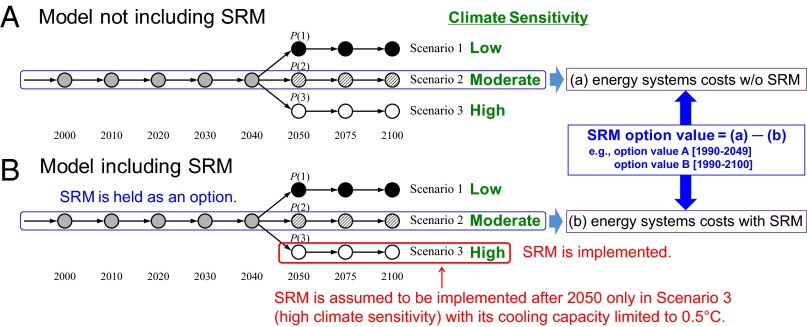
We use the decision tree analysis (33) whose assessment periods are between 1990 and 2100 with eight time points. In Fig. 4, (i) time at which uncertainty is resolved (the year 2050), (ii) scenarios regarding three-branched climate sensitivities (low, moderate, and high), (iii) probabilities of the three scenarios [P(1) = 0.1; P(2) = 0.71; P(3) = 0.19], (iv) SRM implementation (only after the year 2050, only in scenario 3, and with the cooling capacity limited to 0.5 °C), and (v) the definition of the SRM option value, which is the difference between the systems costs including SRM and those not including SRM [(a) − (b)], are represented. Formally, we define the option value of SRM as follows:

$$\text{Option\hspace{0.17em}value\hspace{0.17em}A\hspace{0.17em}}\equiv {\displaystyle \sum }_{t=1990}^{2049}{\left(\frac{1}{1+r}\right)}^{t-1990}ES{C}_t-{\displaystyle \sum }_{t=1990}^{2049}{\left(\frac{1}{1+r}\right)}^{t-1990}ES{C}_t^{SRM},$$ [1]

Fig. 4.

Framework for assessing SRM option values (decision tree analysis). Shown are model runs (A) not including SRM options and (B) including SRM options.

where t, r, ESC, and ESC^SRM represent the year, discount rate per year (%), energy systems costs without SRM, and energy systems costs with SRM, respectively. Option value B is defined for the period from the year 1990 to 2100 based on the same Eq. 1. Note that the total discounted sum of energy systems costs during 1950–2100 for option value B is calculated based on the scenario of T2x = 3 °C (SI Appendix, Fig. S4) rather than T2x = 2 °C because much higher occurrence probability (71%) is put on the scenario of T2x = 3 °C. Note that we ruled out the scenario of T2x = 4 °C for the calculation of option value B because SRM is actually deployed in the scenario.

The discrete probability function of climate sensitivity (Fig. 4) is defined using a unique probability density function (PDF) presented in ref. 34 that summarized the comprehensive knowledge of the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (likely range: 2–4.5 °C; best estimate: 3 °C). We assume three climate sensitivity scenarios, T2x = 2 °C (low), T2x = 3 °C (moderate), and T2x = 4 °C (high), and give the scenarios their respective probabilities as P(1) = 0.1, P(2) = 0.71, and P(3) = 0.19, where P(i) (i = 1, 2, 3) represents scenario i’s probability. This probability function implies that the original PDF is skewed to the right. Note that our optimization does not allow for achieving the +2.4 °C target, the most stringent temperature target of this study, if we assume that climate sensitivity turns out to be higher than T2x = 4 °C. Other combinations of climate sensitivities and their respective probabilities are of course possible, and results would change if we select other combinations.

Costs and Damages of SRM.

Annual deployment costs for cooling the global mean temperature by 1 °C [(a)$/°C] are calculated on the basis of cost estimates per year [(b)$/Mt-S] (35), the relationship between radiative forcing and the sulfur injection rate [(c)Mt-S/Wm⁻²] (36), and the relationship between temperature changes and radiative forcing in the DNE21 model [(d)Wm⁻²/°C]. The relationship (a) = (b) × (c) × (d) obviously holds. Recall that SRM is assumed to cancel at most 0.5 °C, which is roughly equivalent to 0.79 Wm⁻² in the DNE21 model (SI Appendix, Fig. S2). By selecting an average type of particle, i.e., 180 nm H₂SO₄ (2 Mt-S reduces radiative forcing by ∼1 Wm⁻²), we determined that the above cooling capacity constraint of 0.5 °C, or equivalently 0.79 Wm⁻², would be comparable to SRM of 1.58 Mt-S. Note that the ratio of temperature changes (°C) to radiative forcing (Wm⁻²) and sulfate injection rate (Mt-S) is ∼1:1.5:3 on an annual basis. Consequently, (c) × (d) = 2 × 1.5 = 3 (Mt-S/°C) holds. Regarding SRM deployment costs per year [(b)$/Mt-S] based on delivery systems with, for example, hybrid lift airships, we use $10/kg-S (= $10 billion/Mt-S), which represents the high end of estimates in the existing literature ranging between $1–10/kg-S (12, 13, 37, 38). We chose the highest cost estimate to make the SRM option values conservative, although almost no effects arise within this variation range of cost estimates. Because sulfate aerosols of 3 Mt-S are necessary to decrease the mean temperature by 1 °C, the costs amount to $30 billion/°C, which is calculated as (b) × (c) × (d) = 10 × 2 × 1.5 = 30 ($ billion/°C). Therefore, it costs $15 billion to cancel 0.5 °C on an annual basis.

To take into account uncertainty about damages from SRM, we assumed that additional costs incurred by SRM’s side effects could be as high as 100-fold the deployment costs, making the annual total cost for SRM amount to $1,500 billion/0.5 °C, nearly equal to the high end of the total cost for global mitigation (e.g., $200–2,000 billion per year) (35). Note that the side effect as high as 100-fold the deployment costs is approximately equivalent to the highest value shown in the existing literature, i.e., $2.3 trillion/Wm⁻² or 4.5% of GDP/Wm⁻² (13). Strictly speaking, we assumed that side effects of SRM increase linearly with its deployment amount, whereas ref. 13 assumed they would increase steeper than linearly (a convex function); this is because scientific knowledge for determining the strict functional form of side effects is not yet sufficient and side effects can be considered to be negligible within the range of SRM implementation between 0 and 0.5 °C.