Information capacity of specific interactions

Significance

The past 15 years have seen a proliferation of experimental techniques aimed at engineering self-assembled structures. These bottom–up techniques rely on specific interactions between components that arise from diverse physical mechanisms such as chemical affinities and shape complementarity attraction. Comparisons of specificity across such diverse systems, each with unique physics and constraints, can be difficult. Here we describe an information theoretic measure, capacity, to quantify specificity in a range of recent experimental systems. Capacity quantifies the maximal amount of information that can be encoded and then resolved by a system of specific interactions, as a function of experimentally tunable parameters. Our framework can be applied to specific interactions of diverse origins, from colloidal experiments to protein interactions.

Abstract

Specific interactions are a hallmark feature of self-assembly and signal-processing systems in both synthetic and biological settings. Specificity between components may arise from a wide variety of physical and chemical mechanisms in diverse contexts, from DNA hybridization to shape-sensitive depletion interactions. Despite this diversity, all systems that rely on interaction specificity operate under the constraint that increasing the number of distinct components inevitably increases off-target binding. Here we introduce “capacity,” the maximal information encodable using specific interactions, to compare specificity across diverse experimental systems and to compute how specificity changes with physical parameters. Using this framework, we find that “shape” coding of interactions has higher capacity than chemical (“color”) coding because the strength of off-target binding is strongly sublinear in binding-site size for shapes while being linear for colors. We also find that different specificity mechanisms, such as shape and color, can be combined in a synergistic manner, giving a capacity greater than the sum of the parts.

Specific interactions between many species of components are the bedrock of biochemical function, allowing signal transduction along complex parallel pathways and self-assembly of multicomponent molecular machines. Inspired by their role in biology, engineered specific interactions have opened up tremendous opportunities in materials synthesis, achieving new morphologies of self-assembled structures with varied and designed functionality. The two major design approaches for programming specific interactions use either chemical specificity or shape complementarity.

Chemical specificity is achieved by dividing binding sites into smaller regions, each of which can be given one of A “colors” or unique chemical identities. Sites bind to each other based on the sum of the interactions between corresponding regions. For example, a recent two-color system paints the flat surfaces of three-dimensional polyhedra with hydrophobic and hydrophilic patterns (1) or with a pattern of solder dots (2), allowing polyhedra to stick to each other based on the registry between their surface patterns. Another popular approach uses DNA hybridization, where specific matching of complementary sequences has been used to self-assemble structures purely from DNA strands (3, 4) and from nanoparticles coated with carefully chosen DNA strands (5–9).

Shape complementarity uses the shapes of the component surfaces to achieve specific binding, even though the adhesion is via a nonspecific, typically short-range potential. In the synthetic context, shape-based modulation of attractive forces over a large dynamic range was first proposed and experimentally demonstrated for colloidal particles (10, 11), using tunable depletion forces (12, 13). Recent experiments have explored the range of possibilities opened up by such ideas, from lithographically designed planar particles (14) with undulating profile patterns to “Pacman” particles with cavities that exactly match smaller complementary particles (15). The number of possible shapes that can be made using these types of methods depends on fabrication constraints but the possibilities can be quite rich (16, 17). Using only nonspecific surface attraction, experiments have achieved numerous and complex morphologies such as clusters, crystals, glasses, and superlattices (10, 18–21).

A further class of programmable specific interactions combines both chemical specificity and shape complementarity. The canonical example is protein-binding interactions (22); the binding interactions between two cognate proteins are specified by their amino acid sequence, which programs binding pockets with complex shape and chemical specificity. Recent efforts (23, 24) aim to rationally design these protein interactions for self-assembly. Because both the shape of the binding pocket and its chemical specificity are determined by the same amino acid sequence, these two features cannot be controlled independently. Other synthetic systems offer the promise of independent control of chemical and shape binding specificity, giving a larger set of possible interactions.

These diverse systems achieve specific interactions through disparate physical mechanisms, with different control parameters for tuning binding specificity. However, they must all solve a common problem (25, 26): create a family of N “lock” and “key” pairs that bind well within pairs but avoid off-target binding across pairs (“crosstalk”). Any crosstalk limits the efficacy of the locks and keys. For example, in the context of DNA-based affinities, although there are $4^L$ unique sequences of length L, the strong off-target binding severely restricts the number that can be productively used. Analogously, for colloidal systems driven by depletion interactions, there can be significant off-target binding due to partial contact. The performance of a system of specific interactions depends acutely on how the system constraints (e.g., number of available bases, fabrication length scale, etc.) limit its ability to avoid crosstalk.

In this paper, we develop a general information theory-based framework for quantitatively analyzing specificity in both natural and synthetic systems. We use a metric based on mutual information to derive a bound on the number of different interacting particles that a system can support before crosstalk overwhelms interaction specificity. Increasing the number of nominally distinct pairs beyond this limit cannot increase the effective number of distinguishable species. We compute this information-theoretic “capacity” for different experimental systems of recent interest, including DNA-based affinities and colloidal experiments in shape complementarity. We show that shape-based coding fundamentally results in lower crosstalk and higher capacity than color-based coding. We also find that shape- and color-based coding can be combined synergistically, giving a superadditive capacity that is greater than the sum of the color and shape parts.

The Capacity of Random Ensembles

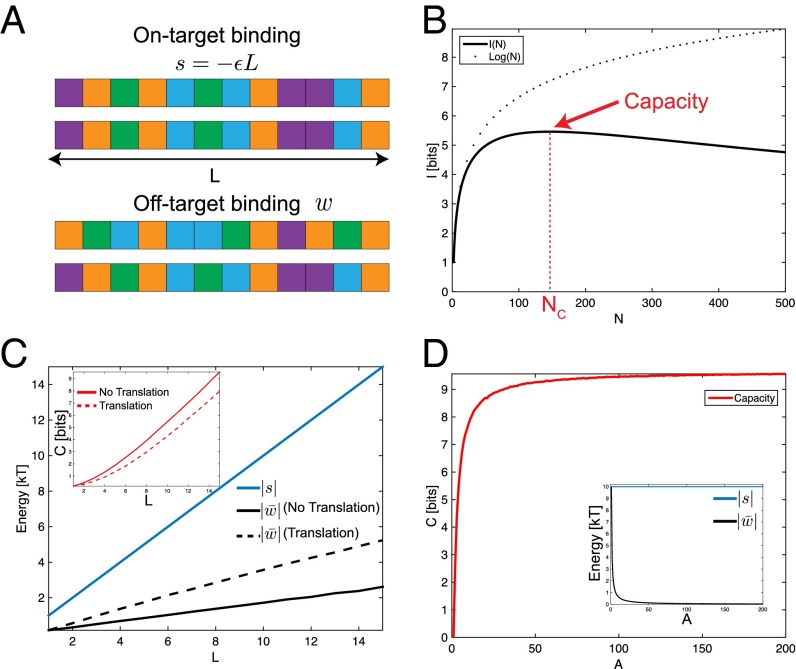
We consider systems where every component is designed to interact specifically with a single cognate partner, whereas interactions between “off-target” components are undesirable crosstalk. We assume that N distinct “locks” $x_1$, $x_2$,…, $x_N\in X$, have unique binding partners, “keys” $y_1$, $y_2$,…, $y_N\in Y$ (Fig. 1A). The physics of a particular system determines the binding energy $E_{ij}\equiv E\left(x_i,y_j\right)$ between every lock and key. Assuming equal concentrations of locks and keys in a well-mixed solution, binding between lock $x_i$ and key $y_j$ will occur with probability $p\left(x_i,y_j\right)=e^{-\beta E_{ij}}/Z$, where Z is a normalization factor such that ${\displaystyle {\sum }_{i,j}p\left(x_i,y_j\right)}=1$ (Supporting Information) and ${\beta }^{-1}=k_{B}T$ is the temperature scale. The mutual information $I\left(X;Y\right)$ transmitted through binding is defined as

$$I\left(X;Y\right)={\displaystyle \sum _{x_i\in X,y_j\in Y}p\left(x_i,y_j\right){\log }_2\frac{p\left(x_i,y_j\right)}{p\left(x_i\right)p\left(y_j\right)}},$$ [1]

where $p\left(x_i\right)$ is the marginal distribution of $x_i$, representing the total probability of seeing $x_i$ in a bound pair [and similarly $p\left(y_j\right)$]. Mutual information $I\left(X;Y\right)$ is a global measure of interaction specificity in systems with many distinct species; it quantifies how predictive the identity of a lock $x_i$ is of the identity of a key $y_j$ found bound to it.

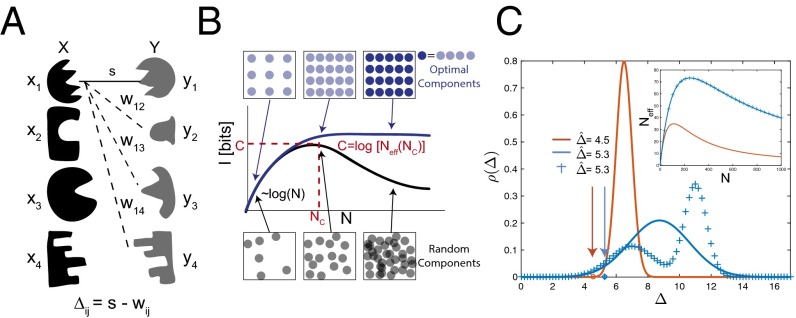
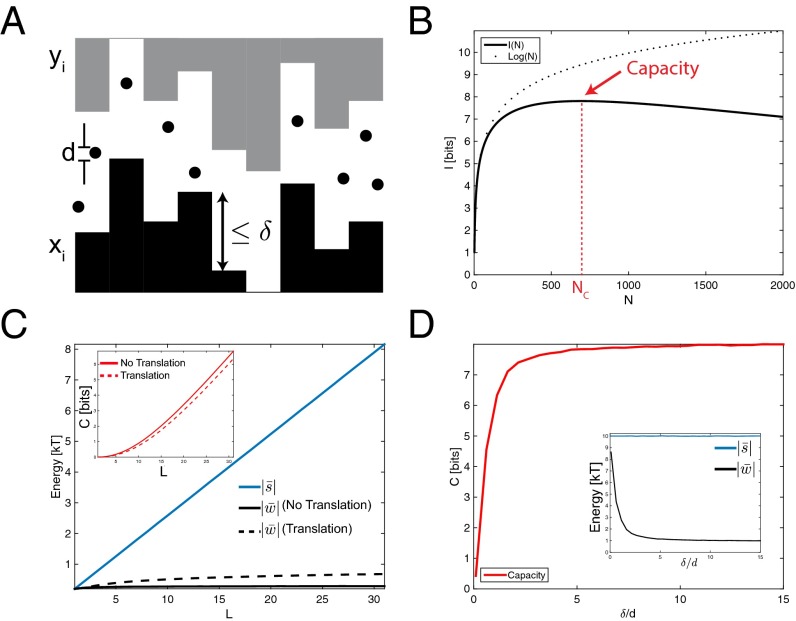
Fig. 1.

Information theory determines the capacity of systems of specific interactions. (A) A model system of locks (black) that each bind with energy s to their specific key (gray) via some specific interaction. (B) As the number N of lock–key pairs is increased, noncognate locks and keys inevitably start resembling each other as they fill up the finite space of all possible components (boxes), both with optimized or random design of lock–key pairs (circles). Consequently, mutual information I between bound locks and keys rises with N for small N but reaches a point of diminishing returns at $N=N_C$; due to the rapid rise in off-target binding energy, I can no longer increase and, for randomly chosen pairs, will typically decrease. The largest achievable value of I is the capacity C. (C) Capacity C can be estimated from the distribution $\rho \left(\mathrm{\Delta }\right)$ of the gap $\mathrm{\Delta }=w-s$ between off-target binding energy w and on-target binding energy s for randomly generated lock–key pairs. Among the three distinct $\rho \left(\mathrm{\Delta }\right)$ shown, the blue distributions have the same $\beta \widehat{\mathrm{\Delta }}=-\log {\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle }_{\rho }$. (C, Inset) $I\left(N\right)$ (compare Eq. 3) is the same for the blue distributions that, despite being markedly different in shape, have the same $\widehat{\mathrm{\Delta }}$, which captures the essential aspects of crosstalk.

Consider a set of interacting lock–key pairs for which $E_{ii}=s$ for all cognate pairs (strong binding), whereas for crosstalking interactions (weak binding) $E_{ij}=w_{ij}=s+{\mathrm{\Delta }}_{ij}$. We assume ${\mathrm{\Delta }}_{ij}$ are independent and identically distributed random numbers drawn from a distribution of gap energies $\rho \left(\mathrm{\Delta }\right)$, with $\mathrm{\Delta }>0$, where the exact form of $\rho \left(\mathrm{\Delta }\right)$ depends on the physics of the system. Denoting $\langle \rangle$ as an average with respect to $\rho \left(\mathrm{\Delta }\right)$, one can approximate Eq. 1 as

$$I={\log }_2{N}_{\text{eff}}\left(N\right),$$ [2]

$$N_{\text{eff}}\left(N\right)=\frac{N}{1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle }{e}^{-\left(\left(N-1\right)\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle /\left(1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle \right)\right)}$$ [3]

(Supporting Information). In a system with crosstalk that contains N nominally distinct lock–key pairs, $N_{\text{eff}}\left(N\right)$ is the effective number of fully distinguishable lock–key pairs. $N_{\text{eff}}$ can be much smaller than N if crosstalk is significant [e.g., if $\langle e^{-\beta \mathrm{\Delta }}\rangle \sim O\left(1\right)$].

Intuitively, information theory predicts that a system with $N_{\text{eff}}\left(N\right)$ noncrosstalking lock–key pairs can perform a task with the same effectiveness as a system with N crosstalking species. For example, in the self-assembly of a multicomponent structure, distinct but crosstalking species can take each other’s place, decreasing the effective number of species. This effect has been shown to reduce self-assembly yield (27–29). Similarly, the efficacy of N parallel signaling pathways is known to be reduced by crosstalk (30). In Fig. 1B we show a typical plot of $I={\log }_2{N}_{\text{eff}}\left(N\right)$. $N_{\text{eff}}$ grows initially with N, but stops growing at $N\sim N_C$, the point of diminishing returns; adding any further species beyond $N_C$ increases only the superficial diversity of species but cannot increase $N_{\text{eff}}$.

Paralleling Shannon’s theory of communication, we define “capacity” C as

$$C\equiv \underset{N}{\text{max}}I={\log }_2{N}_{\text{eff}}\left(N_C\right)$$ [4]

(Fig. 1B). [Capacity in information theory is often measured in bits per second, whereas here we intentionally use the same units as I. Furthermore, capacity is traditionally defined as a maximum over all possible distributions $p\left(X\right)$; here we restrict to maximizing only over one parameter, N, where all N pairs are randomly chosen from the ensemble (Supporting Information).] The capacity is the largest number of bits of information that can be encoded using a system of specific interactions and still be uniquely resolved by the physics of interactions. Determining C, or equivalently the largest value of $N_{\text{eff}}$, is of crucial importance to both synthetic and biological systems because it limits, for example, the number of independent signaling pathways or the complexity of self-assembled structures.

We can compute capacity for any crosstalk energy distribution $\rho \left(\mathrm{\Delta }\right)$ by finding the maximum of Eq. 3. A useful approximation is

$$C\approx -{\log }_2\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }+1}\rangle ,$$ [5]

giving a simple rule for the dependence of capacity on the binding energy distribution (Supporting Information). The importance of maximizing $\beta \widehat{\mathrm{\Delta }}\equiv -\log \langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle$ in Eq. 5 is intuitive: To increase the capacity of the system, the (exponential average of the) gap between on-target binding $\beta \overline{s}\equiv -\log \langle e^{-\beta s}\rangle$ and off-target binding $\beta \overline{w}\equiv -\log \langle e^{-\beta w}\rangle$ should be made as large as possible (see Supporting Information for the precise relationship between $\widehat{\mathrm{\Delta }},\overline{s}$ and $\overline{w}$). Fig. 1C shows three distinct probability distributions, two of which have identical $\widehat{\mathrm{\Delta }}$. As predicted, $N_{\text{eff}}$ reaches a higher maximum for distributions with larger $\widehat{\mathrm{\Delta }}$.

We note that our definition of capacity uses equilibrium binding probabilities and hence applies only at long times compared with unbinding times. In practice, this typically limits $\left|s\right|\le$ $10\hspace{0.17em}{k}_{B}T$, and so we use this bound on s herein. The formalism can be easily extended to include kinetic effects by computing $p\left(x_i,y_j\right)$ at a finite time t, although this is not our focus here.

In what follows, we show how capacity depends on binding interactions and fabrication constraints for several systems of recent interest. In most systems, the on-target binding energy typically strengthens with the binding surface area S of cognate pairs as $\overline{s}=-\mathit{ϵ}S$, where ε is the binding energy per unit area. However, we find that the off-target energies $\overline{w}$ can grow with S at very different rates across several systems we study. We parameterize this variation as

$$\overline{w}=-\mathit{ϵ}\alpha S^{\gamma },$$ [6]

where $\alpha ,\gamma$ depend on the details of binding interactions. We show below that if the specificity is determined purely by “colors” (i.e., chemical identities), then $\gamma =1$. In contrast, if specificity arises from shape complementarity, $\gamma \approx 0$, as long as the range of the surface attraction is small compared with the length scale of shape variation. Thus, crosstalk grows very slowly with the number of independent binding units in shape-based systems, allowing for a dramatic decrease in crosstalk and improvement of capacity relative to systems that use chemical specificity.

Mutual Information in Random Ensembles

Derivation.

Below we derive Eqs. 2 and 3 in the main text. Our model system has N distinct “locks” $x_1$, $x_2$,…, $x_N\in X$, which each have unique binding partners, “keys” $y_1$, $y_2$,…, $y_N\in Y$. We do not specify the physics of these interacting components but require that there is a well-defined binding energy $E_{ij}\equiv E\left(x_i,y_j\right)$ between every lock and key and that locks do not bind to locks (and respectively keys to keys). We assume that each lock binds with its cognate key with a strong on-target energy $E_{ii}=s$, whereas each off-target lock and key bind with a weak off-target energy $E_{i,j\ne i}=w\ge s$ that is drawn from some random distribution. We can equivalently rewrite formulas in terms of $\mathrm{\Delta }=w-s$, where $\mathrm{\Delta }\sim \rho \left(\mathrm{\Delta }\right)$.

In this model we assume that there are equal concentrations of locks and keys in a well-mixed solution, and binding probabilities are determined by the Boltzmann distribution such that lock $x_i$ and key $y_j$ bind with probability $p\left(x_i,y_j\right)=e^{-\beta E_{ij}}/Z$. Here

$$Z={\displaystyle \sum _{x_i\in X,y_j\in Y}{e}^{-\beta E_{ij}}}$$ [S1]

$$={\displaystyle \sum _{x_i}\left(e^{-\beta s}+{\displaystyle \sum _{y_j,j\ne i}{e}^{-\beta w_{ij}}}\right)}$$ [S2]

$$=e^{-\beta s}{\displaystyle \sum _{x_i}\left(1+{\displaystyle \sum _{j\ne i}{e}^{-\beta {\mathrm{\Delta }}_{ij}}}\right)}.$$ [S3]

As the N pairs of locks and keys are drawn randomly from the ensemble, we replace Z with $\langle Z\rangle$, where the angled brackets denote the average with respect to $\rho \left(\mathrm{\Delta }\right)$. This gives

$$\langle Z\rangle =e^{-\beta s}N\left[1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle \right].$$ [S4]

$p\left(x_i\right)$ is the marginal distribution of $x_i$, representing the total probability of seeing $x_i$ in a bound pair. We approximate

$$p\left(x_i\right)=\frac{e^{-\beta s}}{Z}\left(1+{\displaystyle \sum _{j\ne i}{e}^{-\beta {\mathrm{\Delta }}_{ij}}}\right)$$ [S5]

$$\approx \frac{e^{-\beta s}}{\langle Z\rangle }\left(1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle \right)$$ [S6]

$$=\frac{1}{N}.$$ [S7]

In the same manner, $p\left(y_j\right)\approx 1/N$.

Mutual information between components X and Y is defined as

$$I\left(X;Y\right)={\displaystyle \sum _{x_i\in X,y_j\in Y}p\left(x_i,y_j\right)\log \frac{p\left(x_i,y_j\right)}{p\left(x_i\right)p\left(y_j\right)}}.$$ [S8]

For a mixture of N pairs of locks and keys, we can rewrite the mutual information as a function of N and the distribution $\rho \left(\mathrm{\Delta }\right)$:

$$\begin{array}{l}I\left(N\right)={\displaystyle \sum _{x_i}(\frac{1}{N\left[1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle \right]}\log \frac{N}{1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle }}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _{y_j,j\ne i}\frac{e^{-\beta {\mathrm{\Delta }}_{ij}}}{N\left[1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle \right]}\log \frac{N{e}^{-\beta {\mathrm{\Delta }}_{ij}}}{1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle }}).\end{array}$$ [S9]

Replacing the last sum with its expected value, we get

$$I\left(N\right)=\log \frac{N}{1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle }-\frac{\left(N-1\right)\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle }{1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle }$$ [S10]

$$=\log N_{\text{eff}}$$ [S11]

$$N_{\text{eff}}\left(N\right)=\frac{N}{1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle }{e}^{-\left(\left(N-1\right)\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle /\left(1+\left(N-1\right)\langle e^{-\beta \mathrm{\Delta }}\rangle \right)\right)}.$$ [S12]

If the $\log$ in the above equation is ${\log }_2$, I will have units of bits.

Two Types of Behavior for I.

Examination of Eq. S10 reveals two distinct behaviors of the mutual information that depend on $\rho \left(\mathrm{\Delta }\right)$ and specifically on $\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle \ge 0$ and $0\le \langle e^{-\beta \mathrm{\Delta }}\rangle \le 1$. When $D\equiv \langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle -\langle e^{-\beta \mathrm{\Delta }}\rangle +{\langle e^{-\beta \mathrm{\Delta }}\rangle }^2>0$, I will have a distinct maximum.

Type I: $D>0$.

If interactions have reasonable specificity, typical values of the gap will be at least $1-2k_{B}T$. In this case, the distribution $\rho \left(\mathrm{\Delta }\right)$ will be mostly supported at $\mathrm{\Delta }>1-2k_{B}T$ and for any such reasonable distribution, $\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle >\langle e^{-\beta \mathrm{\Delta }}\rangle >{\langle e^{-\beta \mathrm{\Delta }}\rangle }^2$ and hence $D>0$.

When $D>0$, we can calculate the capacity as the maximum value of I, occurring at $N=N_C$, as

$$N_C=\frac{{\left(1+\langle e^{-\beta \mathrm{\Delta }}\rangle \right)}^2}{\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle -\langle e^{-\beta \mathrm{\Delta }}\rangle +{\langle e^{-\beta \mathrm{\Delta }}\rangle }^2}$$ [S13]

$$C_{D>0}=-\log \langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle +\frac{\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle }{1-\langle e^{-\beta \mathrm{\Delta }}\rangle }+\log \left(1-\langle e^{-\beta \mathrm{\Delta }}\rangle \right)-1$$ [S14]

$$\approx -\log \langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle -1$$ [S15]

[where for simplicity, C throughout this section is written in units of nats, although it can be converted to the equations in the main text by multiplying by ${\log }_2\left(e\right)$.]

Type II: $D<0$.

For completeness, we discuss the case of $D=\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle -\langle e^{-\beta \mathrm{\Delta }}\rangle +{\langle e^{-\beta \mathrm{\Delta }}\rangle }^2<0$ that can occur for distributions $\rho \left(\mathrm{\Delta }\right)$ whose typical values are near $\mathrm{\Delta }<1k_{B}T$; i.e., typical off-target interactions are as large as on-target binding.

When $D<0$, $I>0$ reaches its maximum either at $N=1$ or at $N=\infty$. In the latter case, we can compute $C=I(N\to \infty )$. Taking the limit of I as N goes to infinity gives

$$C_{D<0}=-\log \langle e^{-\beta \mathrm{\Delta }}\rangle -\frac{\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle }{\langle e^{-\beta \mathrm{\Delta }}\rangle }$$ [S16]

$$\approx -\log \langle e^{-\beta \mathrm{\Delta }}\rangle$$ [S17]

(where the last approximation results from $D<0\Rightarrow \langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle /\langle e^{-\beta \mathrm{\Delta }}\rangle <1$).

It is instructive to see these two behaviors for two simple distributions. If the gap distribution comes from a Dirac delta function, $\rho \left(\mathrm{\Delta }\right)=\delta \left(\mathrm{\Delta }-\mu \right)$, we find that

$$\langle e^{-\beta \mathrm{\Delta }}\rangle =e^{-\beta \mu }$$ [S18]

$$\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle =\beta \mu e^{-\beta \mu }$$ [S19]

$$D=e^{-\beta \mu }\left(\beta \mu +e^{-\beta \mu }-1\right).$$ [S20]

$$>0$$ [S21]

Thus, the mutual information behaves as type I, and

$$N_C=\frac{e^{\beta \mu }-2+e^{-\beta \mu }}{\beta \mu -1+e^{-\beta \mu }}$$ [S22]

$$\to e^{\beta \mu }\frac{1}{\beta \mu }$$ [S23]

$$C=\log \left(\frac{e^{\beta \mu }-1}{\beta \mu }\right)+\frac{\beta \mu }{e^{\beta \mu }-1}-1$$ [S24]

$$\to \beta \mu$$ [S25]

as $\beta \mu \to \mathrm{\infty }$. Gap energy distributions $\rho \left(\mathrm{\Delta }\right)$ that are tightly centered at a large mean value (Gaussian, Poisson, etc.) behave similarly.

On the other hand, if $\mathrm{\Delta }$ is drawn from an exponential distribution, $\rho \left(\mathrm{\Delta }\right)=\left(1/\mu \right)e^{-\mathrm{\Delta }/\mu }$, the behavior is different. In this case

$$\langle e^{-\beta \mathrm{\Delta }}\rangle =\frac{1}{1+\beta \mu }$$ [S26]

$$\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle =\frac{\beta \mu }{{\left(1+\beta \mu \right)}^2}$$ [S27]

$$D=0.$$ [S28]

The mutual information for a system with this gap distribution thus does not exhibit a maximum, but rather follows the equation for type II,

$$C=\log \left(1+\beta \mu \right)-\frac{\beta \mu }{1+\beta \mu }$$ [S29]

$$\to \log \left(\beta \mu \right)$$ [S30]

as $\beta \mu \to \mathrm{\infty }$. [For small $\beta \mu \ll 1$, we can expand the log to get $C\approx {\left(1-\beta \mu \right)}^2\sim {\left(\beta \mu \right)}^2$.] This is exactly what we find when we calculate the mutual information numerically (Fig. S1).

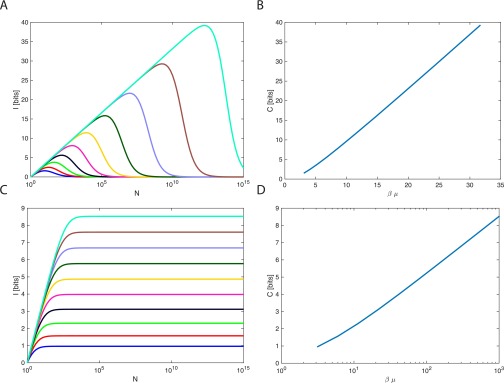
Fig. S1.

(A) Mutual information plotted for the delta distribution $\rho \left(\mathrm{\Delta }\right)=\delta \left(\mathrm{\Delta }-\mu \right)$ for various (log-spaced) $\beta \mu$. I displays a characteristic rise with $\log \left(N\right)$, maximum, and then a decay at large N. (B) The capacity is plotted for $\rho \left(\mathrm{\Delta }\right)=\delta \left(\mathrm{\Delta }-\mu \right)$. As $\beta \mu$ gets large, capacity is linear. (C) Mutual information plotted for the exponential distribution $\rho \left(\mathrm{\Delta }\right)=\left(1/\mu \right)e^{-\mathrm{\Delta }/\mu }$ for various (log-spaced) $\beta \mu$. I displays a characteristic rise with $\log \left(N\right)$ and then plateaus at its maximum. (D) The capacity as a function of $\beta \mu$ for the exponential distribution. As $\beta \mu$ gets large, the capacity goes as $\log \left(\beta \mu \right)$ (the x axis is log scale).

Normalization Choice.

To compute mutual information, one needs to first transform a matrix of binding energies between N locks and N keys into one of probabilities. Above we have chosen $p\left(x_i,y_j\right)=e^{-\beta E_{ij}}/Z$, where $Z={\displaystyle {\sum }_{x_i\in X,y_j\in Y}{e}^{-\beta E_{ij}}}$. This corresponds to a model where all of the locks and keys are placed in a well-mixed enclosure together and every key has the chance to bind to every lock.

An alternative model might choose a different normalization. For example, to encompass analyte sensing in synthetic applications and protein sensors in biological signal transduction pathways, a slightly different model, which would also more closely reflect the Shannon communication setting, is necessary. For these systems one may choose a model in which the locks (which here we think of as sensors) are held in place at a given location, while each key (the object to be detected) enters and has a chance to bind to each of the locks. In this case, the probability of encountering a key $y_j$ should sum to one over all possible locks. Thus, $p\left(x_i,y_j\right)=e^{-\beta E_{ij}}/Z_j$, and $Z_j={\displaystyle {\sum }_{x_i\in X}{e}^{-\beta E_{ij}}}$.

Although results for the two normalizations closely resemble one another, a significant difference can arise, for example, when the kth lock–key pair does not bind very well ($\left|E_{kk}\right|$ is small), but is highly specific ($\left|E_{kk}\right|\gg \left|E_{k,j\ne k}\right|$). In this case, the kth pair would not contribute to the mutual information in the well-mixed case (because it rarely binds), whereas in the communication setting, it would contribute.

Relationship Between $\widehat{\mathrm{\Delta }}$, $\overline{s}$, and $\overline{w}$.

In the text we have defined $\beta \widehat{\mathrm{\Delta }}=-\log \langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle$, where the average is taken over the probability distribution $\rho \left(\mathrm{\Delta }\right)$ and $\mathrm{\Delta }=w-s>0$. If s is the same for all lock–key pairs (as is the case, for example, with DNA binding), we may rewrite this as

$$\beta \widehat{\mathrm{\Delta }}=-\log \langle \beta \left(w-s\right)e^{-\beta \left(w-s\right)}\rangle$$ [S31]

$$=-\log \left(e^{\beta s}\right)-\log \left(-\beta s\langle e^{-\beta w}\rangle +\langle \beta w{e}^{-\beta w}\rangle \right)$$ [S32]

$$=-\beta \overline{s}-\log \left(-\beta s\langle e^{-\beta w}\rangle +\langle \beta w{e}^{-\beta w}\rangle \right)$$ [S33]

$$\approx -\beta \overline{s}-\log \langle e^{-\beta w}\rangle -\log \left(-\beta s\right)$$ [S34]

$$=\beta \overline{w}-\beta \overline{s}-\log \left(-\beta s\right),$$ [S35]

where the approximation follows for $\left|s\right|\gg \left|w\right|$.

Numerical Sampling Methods for Random Ensembles.

To numerically calculate the capacity of a random ensemble of lock–key pairs, two options are available. First, for each N, one can randomly sample many N × N matrices, drawn from the ensemble, and calculate the average $I\left(N\right)$ at that point, using Eq. S8 above. The capacity C is then given by the maximum I achieved and $N_C$ by just the N at which I reaches C.

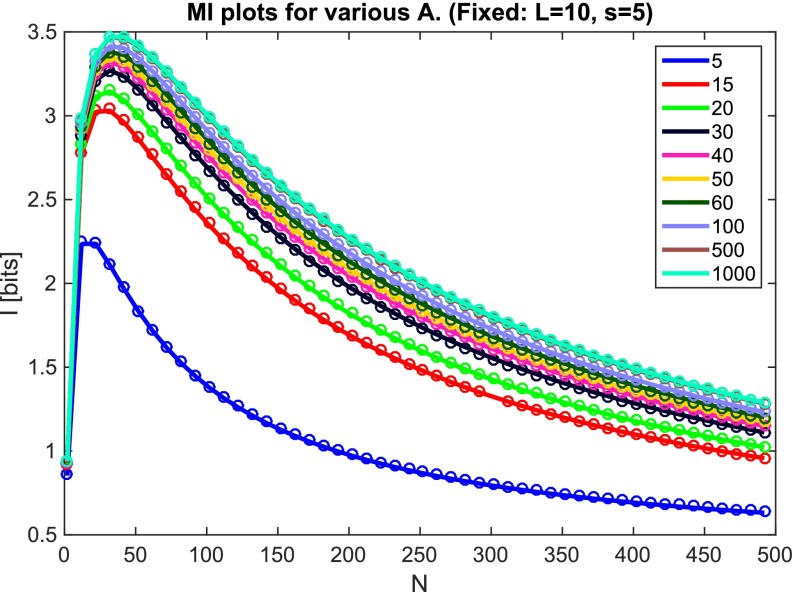
Alternatively, one can use Eq. S10 above. This requires calculating $\langle e^{-\beta \mathrm{\Delta }}\rangle$ and $\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle$. If an analytical formula for these terms is available, this may be computed directly. However, even in complex energy scenarios, as long as one can randomly sample pairs of locks and keys and measure their binding energy, one can calculate these terms numerically and then use Eq. S10. These two give the same results in most cases (Fig. S2).

Fig. S2.

Averaging over N × N matrices and 2 × 2 matrices gives the same result. We simulate our color model with $L=10$, $\beta s=-5$, $\beta =1$, for various values of A, denoted in the legend. Lines, N × N simulation; circles, 2 × 2 sampling.

Case Study: Binomial Binding

It is instructive to see how capacity scales for the case of a binomially distributed gap, which serves as a model for binding in color systems. Here we assume that each on-target pair of letters binds with energy $-\mathit{ϵ}\hspace{0.17em}{k}_{B}T$, whereas an off-target pair of letters binds with energy 0 $k_{B}T$. (One may also allow for a nonzero binding energy between off-target letters—and, in fact, we do so for Fig. 5C, for which on-target letters bind with ${\mathit{ϵ}}_{x^l=y^l}=0.5\hspace{0.17em}{k}_{B}T$ and off-target letters bind with ${\mathit{ϵ}}_{x^l\ne y^l}=0.25\hspace{0.17em}{k}_{B}T$ . However, for simplicity, the rest of this paper and the analysis below set off-target letter binding to zero.)

Fig. 5.

Color and shape can be combined synergistically. (A) Shape and color can be “linked” in an independent manner (Left, $\oplus$) or “mixed” in a dependent manner (Right, $\otimes$), where the shapes are coated with the chemical binding agent. Crosstalk in $\oplus$ results from accidental matches in either channel, whereas in the $\otimes$ model, accidental matches in color contribute to crosstalk only if shapes are also matched at the same sites. (B) As a result, the gap energy for Shape $\otimes$ Color is higher than for Shape $\oplus$ Color. Here $L=10$ for both color and shape, $d=0.05$ μm, $\delta =1$ μm, $A=4$, and ${\lambda }_{\text{color}}=0.01$ μm. (C) The capacity as a function of ${\lambda }_{\text{color}}$, the spatial range of color-based interactions. When ${\lambda }_{\text{color}}$ is smaller than δ, the typical size of shape-based features, shape helps reduce crosstalk in color. This synergy is lost when ${\lambda }_{\text{color}}\sim \delta$, and color and shape act independently (${\mathit{ϵ}}_{x^l=y^l}=0.5\hspace{0.17em}{k}_{B}T,{\mathit{ϵ}}_{x^l\ne y^l}=0.25\hspace{0.17em}{k}_{B}T$) (Supporting Information).

If crosstalk is negligible ($\beta \mathit{ϵ}=\infty$), then we can use all $A^L$ possible pairs, and $C=L{\log }_{2}A$. However, when crosstalk plays a significant role, we must use Eq. S10 above to determine the capacity and $N_C<A^L$. Plugging in $\rho \left(\mathrm{\Delta }\right)=\left(1/\mathit{ϵ}\right)f_{\text{binom}}\left(\mathrm{\Delta }/\mathit{ϵ},L,1-1/A\right)$ for the distribution, we can calculate the capacity using the approximation from Eq. 5 (main text) as

$$C\approx \beta \mathit{ϵ}L\hspace{0.17em}{\log }_2\left(e\right)-{\text{log}}_2\left(e\beta \mathit{ϵ}L\right)+L\hspace{0.17em}{\log }_2\frac{A}{A-1+e^{\beta \mathit{ϵ}}}+{\log }_2\left(1+\frac{e^{\beta \mathit{ϵ}}}{\left(A-1\right)}\right).$$ [S36]

One interesting consequence of this is that $C\left(2L\right)>2C\left(L\right)$. In other words, more information can be encoded if a single channel is composed of a longer sequence than if many channels of smaller sequences are used. However, the difference is logarithmic in L and so is negligible for large L.

We may examine how the capacity scales as A, the alphabet size, becomes large:

$$\underset{A\to \infty }{\text{lim}}C=\beta \mathit{ϵ}L{\log }_2\left(e\right)-{\log }_2\left(e\beta \mathit{ϵ}L\right)$$ [S37]

$$\underset{A\to \infty }{\text{lim}}{N}_c=\frac{{\left(e^{\beta \mathit{ϵ}L}-1\right)}^2}{1+e^{\beta \mathit{ϵ}L}\left(\beta \mathit{ϵ}L-1\right)}.$$ [S38]

From the above one can see that $\beta \mathit{ϵ}$ is what sets the upper limit of the capacity in the crosstalk-limited regime. Because on-target binding is fixed as $s=-\mathit{ϵ}L$, capacity is determined by w. In the worst-case scenario, an on-target lock looks identical to an off-target lock, which would mean every letter binds, giving $w_{ij}^{\text{worst}}=s$ and thus a gap (given by $\mathrm{\Delta }=w-s$) of ${\mathrm{\Delta }}^{\text{worst}}=0$. This would occur if $A=1$, in other words when the surfaces are just sticky. On the other hand, in the best-case scenario, none of the letters in $x_i$ bind to the letters $y_j$, giving $w_{ij}^{\text{best}}=0$ and ${\mathrm{\Delta }}^{\text{best}}=-s=\mathit{ϵ}L$. This occurs when $A\to \infty$. Thus, A is just a tuning factor that allows the system to go from $w^{\text{worst}}$ to $w^{\text{best}}$ with increasing A: As A is increased, the more likely it is that a letter in $x_i$ is mismatched to a letter in $y_j$, giving a zero contribution for that pair.

Furthermore the weak binding is given by

$$\overline{w}=-L\hspace{0.17em}\log \frac{A-1+e^{\beta \mathit{ϵ}}}{A}$$ [S39]

$$\underset{L\to \infty }{\text{lim}}\overline{w}\left(\mathit{ϵ}=s/L\right)=-\beta s/A.$$ [S40]

The mutual information in the binomial case has a maximum at $N_C<\infty$, but plateaus down to a constant for large N. We can derive that limit by taking the limit of I as $N\to \infty$ of Eq. S10. Alternatively, we can derive the limit from Eq. S8 without any averaging, by assuming that when $N\gg A^L$, the total possible unique pairs, the information content should be the same as using each of the $A^L$ pairs exactly once. In either case we find

$$I\left(N\to \infty \right)=\beta \mathit{ϵ}L\hspace{0.17em}{\log }_2\left(e\right)+L\hspace{0.17em}{\log }_2\frac{A}{A-1+e^{\beta \mathit{ϵ}}}.$$ [S41]

Fabrication Defects

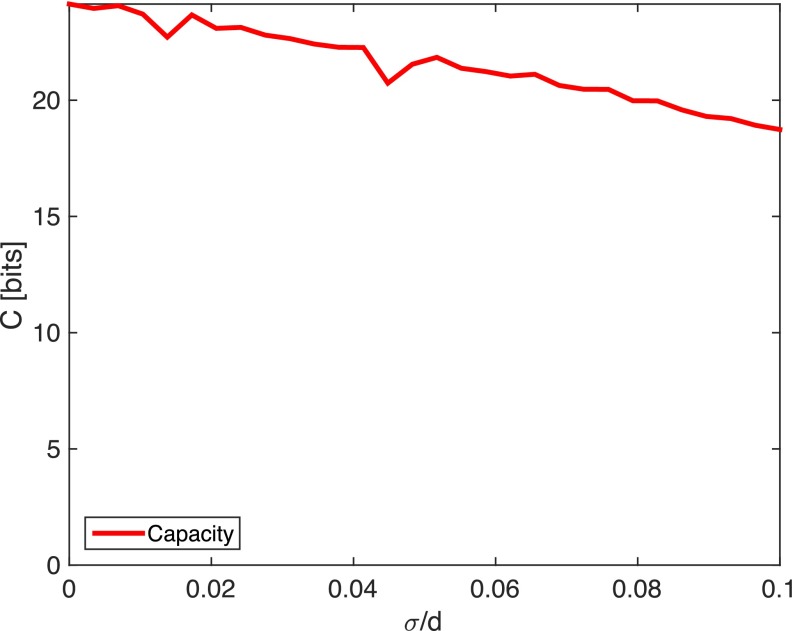
Unintended defects in synthesis can cause mismatch between cognate pairs and thus reduce on-target binding and capacity. We model such defects by adding independent (normally distributed) random undulations of order σ to keys that would otherwise be cognate to their lock, thereby reducing on-target binding. We find that the effect of such defects is small when $\sigma \ll d$, the depletion particle size, but degrades capacity significantly when $\sigma \sim d$. Such degradation originates from the same aspect of shape coding that gives it lower crosstalk than color coding; a single large mismatch can be sufficient to dramatically reduce on-target binding (Fig. S3).

Fig. S3.

Fabrication defects of order σ degrade the capacity when $\sigma \sim d$. In the main text we assume $\sigma \ll d$. Here $L=10$ and $d=0.2\hspace{0.17em}\mu \text{m}$.

Contact Between Random Surfaces

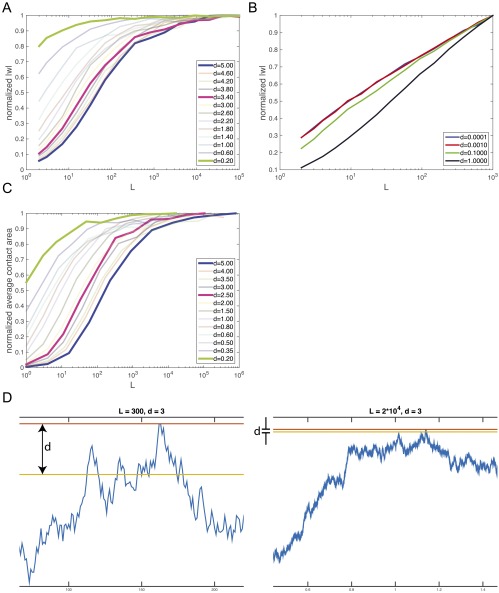
In the main text, we emphasized that shape-based coding achieves better specificity than color-based coding because the amount of crosstalk for shapes is much smaller than that for color. The intuitive idea is that when coding with shapes, off-target binding between two mismatched random shapes typically constitutes only a few points of contact and does not scale linearly with the size of the components. We verified this by simulating off-target pairs of shaped components and measuring the average $\left|w\right|$, the off-target binding energy, as a function of L and d. As shown in Fig. S4A, the binding energy first rises sublinearly with L and then saturates for large L. When we allow translations between the components (Fig. S4B), such that w is taken as the strongest possible off-target binding across all translations, the curve is still strongly sublinear in L (indeed, highly logarithmic).

Fig. S4.

(A) We measure the average off-target energy $\left|w\right|$ for shaped components (of the form shown in Fig. 3A, main text) at various d and L. No translation is allowed between components. Each curve is normalized by its maximal value. As L increases, $\left|w\right|$ first increases sublinearly with L and then saturates. (B) The normalized $\left|w\right|$ for shaped components when translation is allowed. w for each pair is taken as the strongest possible binding across all translations. Each curve is normalized by its maximal value. As L increases, $\left|w\right|$ increases logarithmically with L. There does not appear to be saturation for the range of numerically achievable L. (C) Similarly, we measure the average amount of time a random 1D walk of L time steps spends within d of its maximum. As L becomes large with respect to d, the average time saturates. Each curve is normalized by its maximal value. (D) Two typical random walks of length 300 (Left) and 20,000 (Right). The amount of time that the random walk spends between its maximum (red line) and within $d=3$ of its maximum (yellow line) is a large fraction of the length for small L, but for very long walks is independent of L.

We may further verify this by examining random 1D walks of length L and measuring how much time they typically spend within a distance d of their maximum. We simulate random walks $x\left(t\right)$, where in each “time” step, the random walk can take a step of $x\left(t+1\right)=x\left(t\right)\pm 1$. Examining a range of d from 0.5 to 5 of various lengths, we find that the average amount of time spent within d of the maximum first increases sublinearly with L and then flattens out to a constant (Fig. S4C). Two typical walks of $L=300$ and $L=\mathrm{20,000}$, at $d=3$, give intuition for why this is the case (Fig. S4D): When L is small relative to d, a good fraction of the walk is contained between d of its maximum, and so increasing L increases the amount of time spent in this area. When L is much larger than d, only a small fraction of the time is spent close to the maximum.

Pacman Particle Interactions

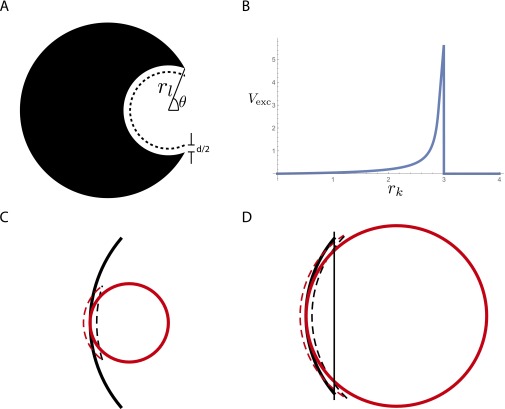
We derive the depletion-driven interactions between pairs of spherical lock–key Pacman particles of the type described in ref. 15. We describe each lock (Fig. S5A) as a sphere containing a hemispherical cavity of radius $r_l$, cut off at angle θ (although all calculations in the main text were performed for $\theta =\pi /2$). Each key is a sphere of size $r_k$, and for a cognate lock and key pair, $r_k=r_l$. Attraction is mediated by depletant particles of diameter $d\ll r_k,r_l$, and the energy of attraction between a lock and a key is $E=-\mathit{ϵ}{V}_{\text{exc}}$, where $V_{\text{exc}}$ is the change of excluded depletant particle volume (and ε mediates the strength of the attraction). We derive a formula for $V_{\text{exc}}$ that is more accurate than that used in ref. 15, particularly when the radii of the lock and key are close to each other [e.g., $r_l-r_k=O\left(d\right)$].

Fig. S5.

(A) Model lock, with a spherical cavity of radius r_l cut off at angle θ. When a key is not bound, depletant particles are excluded from the volume between the lock and the dashed line. This excluded volume, originally $d\Omega r_l^2$, can be decreased via key binding inside the cavity. (B) Full calculation for the change in excluded volume V_exc as a function of $r_k$. The maximal change, and therefore the most energetically favorable radius for binding, occurs when $r_k=r_l$. Here $r_l=3$ and $\theta =\pi /2$. (C) When $r_k\ll r_l$, the excluded volume is just given by the contact area of the two spheres. Black, lock; red, key. Dashed lines indicate the respective excluded volumes when the lock and key are separated. (D) When $r_k$ approaches $r_l$, the intersection with the plane must be taken into account. Black, lock; red, key. The vertical line indicates the plane through the opening of the lock. Dashed lines indicate the respective excluded volumes when the lock and key are separated.

We derived $V_{\text{exc}}$ (Fig. S5B) for four regimes of lock/key sizes:

When $r_k=r_l$, $V_{\text{exc}}=d{A}_{\text{contact}}$, where $A_{\text{contact}}$ is the contact area between the lock and the key. The contact area is simply the entire inner area of the lock, $A_{\text{contact}}=\mathrm{\Omega }{r}_l^2=2\pi \left(1-\cos \theta \right)r_l^2$, where θ is half the total angle subtended by the inner surface of the lock at its origin.

When $r_k>r_l$, the key does not fit into the lock and makes contact along an annulus of radius $2\pi r_l\cos \theta$. As discussed in ref. 15, the width t of this annulus is set by fabrication constraints (in particular, how sharp the edges of the locks are) and was estimated to be $t=190$ nm. Hence the effective contact area is $A_{\text{contact}}=t\left(2\pi r_l\cos \theta \right)$ and $V_{\text{exc}}=d{A}_{\text{contact}}$. We assume that the contact area drops to this value at $r_k=r_l+2d$ from the value of $\mathrm{\Omega }{r}_l^2$ at $r_k=r_l$ and linearly interpolate between the two.

When $r_k<r_l$, we consider two regimes:

• i)If $r_k\ll r_l$: In this case, we wish to compute the excluded volume shown as the area between dashed lines in Fig. S5C. The excluded volume is entirely contained within the lock; in particular, the edges of the lock play no role. Hence, the excluded volume is easily computed as the intersection of two overlapping spheres. We find

$$V_{\text{exc}}=\pi d^2\left(\frac{d}{6}-\frac{r_k{r}_l}{r_k-r_l}\right).$$ [S42]

• ii)When $r_k$ approaches $r_l$ from below, at a particular radius $r_{\text{thresh}}<r_l$, the excluded volume reaches the edges of the lock. See Fig. S5D; using the formula for intersecting spheres would give an overestimate of the binding energy. Instead, we draw a plane through the opening of the lock (line in Fig. S5D) and count only the excluded volume contained between the plane and the lock. The radius $r_{\text{thresh}}$ at which such edge effects become important is given by

$$r_{\text{thresh}}=\frac{r_l\left(d/2-r_l\right)\left(\cos \theta -1\right)}{d/2+r_l+\left(d/2-r_l\right)\cos \theta }.$$ [S43]

The formula for a triple intersection for $r_{\text{thresh}}<r_k<r_l$ gives

$$x=r_l\cos \theta +d^2/\left(12r_l\right)$$ [S44]

$$h_k=r_l+d/2-x$$ [S45]

$$v_k=h_k^2\pi \left(\left(r_k+d/2\right)-h_k/3\right)$$ [S46]

$$h_l=r_l-d/2-x$$ [S47]

$$v_l=h_l^2\pi \left(\left(rl-d/2\right)-h_l/3\right)$$ [S48]

$$V_{\text{exc}}=vk-vl.$$ [S49]

The full curve for $V_{\text{exc}}$ is shown in Fig. S5B.

The Capacity of Color

We first consider the capacity of interactions mediated through binding sites that are subdivided into multiple regions, each of which can be assigned any one of A chemical identities or colors. We take inspiration from DNA coding that acts via complementary hybridization between single-stranded DNA. Previous work (31) developed engineering principles for determining the optimal length and nucleotide composition of these DNA strands based on detailed models of the binding energy. Information theoretic measures have also been used to understand binding of transcription factors to DNA and other sequence-based molecular recognition problems (32–36). Although the theory of DNA coding has a long history (37), our contribution here formulates the problem in a mutual information framework that relates the capacity to a physical quantity and hence allows for direct comparison of varied chemical (color) and shape systems.

In our simplified color model, a lock is composed of L units, each of which is painted with one of A chemical colors (Fig. 2A). Each color binds to itself with energy $-\mathit{ϵ}$ and binds to other colors with energy 0, such that locks and their cognate keys have the same sequence. The binding energy of any two strands $x_i$ and $y_j$ is given by $E_{ij}={\displaystyle {\sum }_{l=1}^L-\mathit{ϵ}{\delta }_{x_i^l,y_j^l}}$ (where $x_i^l$ is the color of the lth site of $x_i$, and δ is the Kronecker delta). We analyze this system with translations, where $E_{ij}$ is given by the strongest binding across all possible translations of the two strands relative to each other, as well as without translations.

Fig. 2.

Complementary color components demonstrate the capacity of programmable interactions. (A) Each lock $x_i$ has L distinct units, each of which can be one of $A=4$ colors or chemical identities. Each color has a strong affinity ε for itself. Cognate locks and keys have the same sequence of colors and bind with energy $s=-\mathit{ϵ}L$. Off-target binding energy w is given by the number of accidental color matches; $w=-5\mathit{ϵ}$ in the example shown. (B) Mutual information as a function of N, the number of lock–key pairs. I increases initially as $\log \left(N\right)$, but then reaches a maximum value, the capacity, and then decreases ($L=10$, $\mathit{ϵ}=1\hspace{0.17em}{k}_{B}T$, $A=4$). (C) Increasing L increases both the on-target strength $\left|s\right|$ and the off-target strength $\left|\overline{w}\right|$. (C, Inset) Capacity scales linearly with L. If translation is allowed, $\left|s\right|$ is unaffected, but $\left|\overline{w}\right|$ is higher (black, dashed line), and therefore the capacity is lower (red, dashed line) ($L=10$, $\mathit{ϵ}=1\hspace{0.17em}{k}_{B}T$, $A=4$). (D) Increasing the alphabet size A does not affect on-target binding s, but does decrease $\left|\overline{w}\right|$, thereby increasing $\widehat{\mathrm{\Delta }}$ ($L=10$, $\mathit{ϵ}=1\hspace{0.17em}{k}_{B}T$).

We calculate $I\left(N\right)$ by sampling N randomly selected pairs of locks and keys, constructing the interaction matrix E, and computing $I\left(N\right)$ using Eq. 1. We average $I\left(N\right)$ over many repetitions. An approximate but faster method to compute $I\left(N\right)$ (necessary for large $L,N$) uses Eq. 3, sampling random pairs of off-target locks and keys to estimate $\langle e^{-\beta \mathrm{\Delta }}\rangle$ and $\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle$. The two methods give nearly identical results (Supporting Information and Fig. S2), and the calculations in this paper henceforth are carried out with the second method.

Fig. 2B examines $I\left(N\right)$ when $L=10$, $A=4$, and $\mathit{ϵ}=1\hspace{0.17em}{k}_{B}T$ so that a lock and its key bind together with on-target energy $\beta s=-10$. The mutual information has a maximum of 5.5 bits near $N_C=146$, far less than the total number of unique sequences ($4^{10}=\mathrm{1,048,576}$). Due to crosstalk, even though there are nominally 146 pairs at capacity, the system behaves as if there are only $N_{\text{eff}}=44$ independent pairs.

An obvious way of increasing capacity is to boost $\widehat{\mathrm{\Delta }}$ by increasing L. This strengthens both on-target binding and off-target binding, because both s and w scale with L $\left(\beta \overline{w}=-L\log \left(\left(A-1+e^{\beta \mathit{ϵ}}\right)/A\right)\right)$. However, the gap between them widens (Fig. 2C, solid lines), and the capacity scales linearly with L (Fig. 2C, Inset) (Supporting Information). As a comparison, we also show the capacity when translation is allowed between any two strands. Off-target strands can now translate until they find the strongest binding, increasing crosstalk and thus lowering capacity.

In practice, on-target binding $\left|s\right|$ must be limited to below ∼10 $k_{B}T$ for the binding to be reversible; hence L cannot be increased arbitrarily without also decreasing ε. An alternate way to increase capacity at fixed s is to increase the number of colors A. As $A\to \infty$, accidental mismatches in off-target binding are rare; $\left|w\right|\to 0$, and the capacity is limited only by s. In Fig. 2D, capacity in the large A limit can be approximated by setting $\beta \mathrm{\Delta }=-s=10$ in Eq. 5, giving $C=9.6$ bits. However, in practice, alphabet size A cannot be easily increased in experiments, and other techniques must be used to decrease the off-target binding strength, such as the use of shape complementarity.

The Capacity of Shape

Systems of interacting, complementary shapes are characterized by the nonspecific binding of surfaces mediated by a short-range force of characteristic length ${\lambda }_{\text{shape}}$. The components’ shapes sterically allow or inhibit two surfaces from coming into contact, dictating specificity. We find that crosstalk is qualitatively weaker in such shape-based systems, resulting in higher capacity than in color-based models.

We examine the capacity of a model inspired by a recent experimental system consisting of lithographically sculpted micron-sized particles with complementary shapes (14) whose attractive interactions are mediated by the depletion force. The constraints on the shapes of these components (size $< 10$ μm, line width $> 400$ nm, radius of curvature $> 200$ nm) still leave a large variety of shapes that can interact in a lock and key fashion, yet crosstalk between similarly shaped components reduces the number of effectively unique pairs. We model this system by defining each solo component as a series of L adjoining bars of various heights, whose profile is similar to a Tetris piece. For each lock $x_i$, the shape of the cognate key $y_i$ is exactly complementary, as in Fig. 3A. We account for fabrication constraints by setting the width of each bar to 1 μm and restricting the change of one bar height relative to its neighboring bars to be less than $\delta =1$ μm. Depletant particles of diameter d (typically $100 - 200$ nm) create an attractive energy of $-\mathit{ϵ}\left(d-h\right)$ for two surfaces separated by $h<d$. Thus, ${\lambda }_{\text{shape}}\sim d$. In experiments, ε is set by the depletant particle volume fraction and the temperature. In principle, the fabrication fidelity must also be accounted for, as local defects in the shape will disrupt cognate binding. The effect of such defects is shown in Fig. S3; we find that defects of size much less than d, the depletant particle size, have minimal impact on capacity. We assume such a limit in the remainder of the text.

Fig. 3.

Complementary shapes demonstrate the capacity of programmable interactions. (A) Each shape $x_i$ is made of L vertical bars of different heights and has a corresponding binding partner $y_i$ shaped exactly as its complement; interactions are mediated via depletant particles of diameter d, and each adjoining bar can change by a maximum amount of δ. (B) Mutual information as a function of N, the number of lock–key pairs, showing a capacity of 7.8 bits ($L=10$, $d=0.2\hspace{0.5em}\mu \text{m}$, $\delta =1\hspace{0.5em}\mu \text{m}$, $\overline{s}=-10\hspace{0.17em}{k}_{B}T$). (C) Increasing L increases the on-target binding strength $\left|s\right|$ (blue), but has little effect on off-target binding strength $\left|\overline{w}\right|$ (black), unlike with colors (Fig. 2C). (C, Inset) Capacity scales linearly with L. Allowing translations has no effect on $\left|\overline{s}\right|$, but increases $\left|\overline{w}\right|$ (black, dashed line) and therefore decreases C (red, dashed line). ($d=0.07\hspace{0.5em}\mu \text{m}$, $\delta =1\hspace{0.5em}\mu \text{m}$, $\mathit{ϵ}=1\hspace{0.17em}{k}_{B}T$). (D) Fixing $\overline{s}=-10\hspace{0.17em}{k}_{B}T$, the capacity can be increased by increasing δ: When $\delta /d$ is small, on-target keys are indistinguishable from off-target keys, and so capacity is small. Increasing δ decreases the crosstalk, and capacity increases accordingly.

We find that crosstalk with shapes differs fundamentally from the color models discussed earlier. Whereas on-target binding strength still increases linearly with L, off-target binding is almost independent of L (Fig. 3C). In fact, we find that for large enough L, off-target binding $\overline{w}\sim -L^0$; for larger $\delta /d$ (or smaller L), $\overline{w}$ is still strongly sublinear in L (Supporting Information and Fig. S4). The weak dependence of $\overline{w}$ on L can be understood intuitively, as a lock pressed to a random mismatched key will typically come into contact at a single location. In contrast, in color-based systems, off-target locks and keys are in full contact and hence $\overline{w}\sim -L$. Thus, $\widehat{\mathrm{\Delta }}$ and hence capacity C for shape systems can be significantly higher than for color-based systems with the same strong binding energy $\overline{s}$. In Fig. 3B, $C_{\text{shape}}=7.8$ bits whereas $C_{\text{color}}=5.5$ bits with similar parameters ($\overline{s}=-10\hspace{0.17em}{k}_{B}T$, $L=10$). Finally, in Fig. 3D, for fixed L, we find that capacity falls rapidly and all specificity is lost when the spatial range of depletion interactions ${\lambda }_{\text{shape}}\sim d$ exceeds the scale of spatial features δ, as expected. These results are consistent with earlier experiments (12) and computational models (13) that established a high dynamic range in the strength of depletion interactions between surfaces roughened by asperities and in particular found that the attraction between surfaces was diminished when the asperity height was below the depletion particle size.

Our results, although intuitive in retrospect, point to a qualitative advantage for coding through shapes; random mismatched shapes have a crosstalk that is, at worst, sublinear in binding-site size whereas crosstalk is linear in site size for color-based systems. Our work suggests that such increased specificity is very robust as it is derived from basic properties of shape itself. Knowing the precise benefits of shape-based coding is important in deciding to incorporate it in engineering efforts going forward.

We may further apply this framework to the recent experimental system of Pacman-like lock–key colloids. In this system (15), a key is a sphere of radius r (typically 1–3 μm), whereas its cognate lock is a larger sphere with a hemispherical cavity of radius r, complementary to its key (Supporting Information and Fig. S5). The attraction is mediated by depletant particles of diameter $d\approx 50-100$ nm. Multiple pairs of locks and keys may be used concurrently, with the ith pair having a key radius of $r_i$, with the risk of keys binding to incorrect locks.

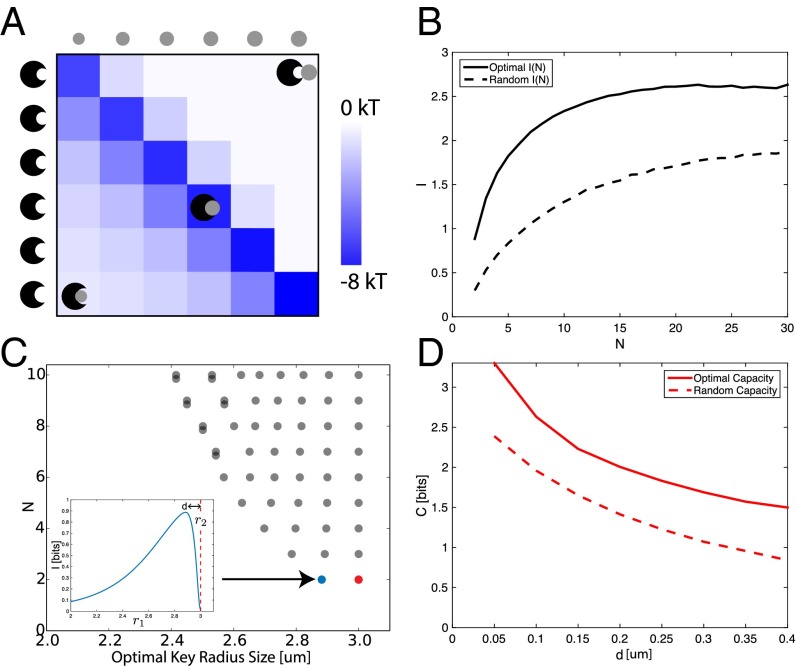
How should one choose N lock–key radii $r_i$ to minimize crosstalk and maximize capacity? We may gain some intuition by considering a system containing only two lock–key pairs of radii $r_1$ and $r_2$, respectively. The on-target binding energies of the two pairs are proportional to the area of contact: $E_{11}\sim r_1^2$, $E_{22}\sim r_2^2$ because each key makes perfect contact with its own lock. Assuming $r_1<r_2$, crosstalk energy $E_{12}\sim r_1$, corresponding to the larger key of size $r_2$ contacting an annulus around the smaller lock of size $r_1$. The other crosstalk energy $E_{21}\sim r_2^2-\left(r_2-r_1\right)f\left(r_2,d\right)$ is typically much larger, corresponding to the smaller key fitting into the larger lock of size $r_2$ (see Supporting Information for complete derivation). Thus, there are two competing pressures on the radii $r_1,r_2$: Increasing the overall size of both pairs $r_1,r_2$ improves specificity because the on-target energies $r_1^2,r_2^2$ grow faster than the crosstalk terms. However, $E_{21}$ grows rapidly if the radii are too similar to each other. Hence the optimal solution for $N=2$ requires setting $r_2=R_{\text{max}}$ (the largest allowed radius) and $r_2-r_1\approx d$. The binding energy of six particles (in this case optimally chosen to maximize I) is shown in Fig. 4A, with on-target binding and the two types of off-target binding shown.

Fig. 4.

Pacman lock–key pairs demonstrate the capacity of shape space. (A) Interaction energies of six optimally selected lock–key pairs. Cognate locks and keys fit snugly, whereas crosstalk is most severe between small keys and larger locks. (B) Mutual information plotted as a function of the number of pairs N shows that both optimal (solid) and random (dashed) sets of ${\left\{r_i\right\}}_N$ display a maximum in mutual information. [The radius for random lock–key pairs is drawn uniformly from (1, 3) μm.] (C) Each row, plotted at $y=N$, shows the optimal ${\left\{r_i\right\}}_N$ for N lock–key pairs. After saturation ($N>6$), particles are duplicated (overlapping circles). (C, Inset) Mutual information with $r_2$ held fixed at 3 μm varies as $r_1$ changes and has a maximum at $r_1\approx r_2-d$ ($d=100$ nm, $s_{\text{max}}=-8\hspace{0.17em}{k}_{B}T$). (D) The capacity decreases with larger depletant particle size. (On-target binding at $r=R_{\text{max}}$ is fixed to $-8\hspace{0.17em}{k}_{B}T$.)

This intuitive argument does not capture many-body effects that determine capacity for larger N. We find the optimal ${\left\{r_i\right\}}_N$ at fixed N by maximizing the mutual information I in Eq. 1 numerically through gradient descent; note that Eq. 3 cannot be used because the on-target binding energy s varies across pairs. Fig. 4B (solid line) shows the mutual information of optimally chosen radii as a function of N, an improvement over randomly chosen radii (dashed line). Fig. 4C shows the optimal set of radii for various N, with $d=100$ nm and $R_{\text{max}}=3\hspace{0.5em}\mu \text{m}$; the optimal spacing of the radii is $O\left(d\right)$.

Interestingly, when $N>6$, the system has saturated. I does not increase any further (Fig. 4B) and the optimal set involves repeating locks and keys of the smallest radii. Intuitively, the smallest lock–key pairs have become so small that making an additional lock–key pair of an even smaller radius would yield very low self-binding energy relative to the incurred crosstalk. Hence the only way to increase N without decreasing I is to create new nominal pairs at the smallest radius; such pairs are obviously indistinguishable through physical interactions and hence do not increase mutual information any further. We find that the capacity decreases with increasing size of depletant particles and that by $d=400$ nm the system is saturated (reuses radii) when N > 2. Similarly, increasing $R_{\text{max}}$ (with fixed largest cognate binding energy $s=-8\hspace{0.17em}{k}_{B}T$) increases capacity.

Thus, we find that this colloidal particle system can support about $N\sim 6 - 8$ lock–key pairs without much crosstalk, with depletion particles of diameter 100 nm and restricting the largest binding energy to $s_{\text{max}}=-10\hspace{0.17em}{k}_{B}T$. This is far smaller than the capacity of the previously described DNA sequences or general shape-based strategies. However, these lock–key colloidal pairs are characterized by only one parameter (the radius), so the space of available pairs is significantly smaller than DNA or shape systems with L parameters. In particular, in the current system, additional lock–key pairs are forced to be of smaller radii and hence of lower and lower cognate binding energies. Such considerations emphasize the importance of quantitative information-theoretic optimization in systems with such a limited shape space.

Combining Channels

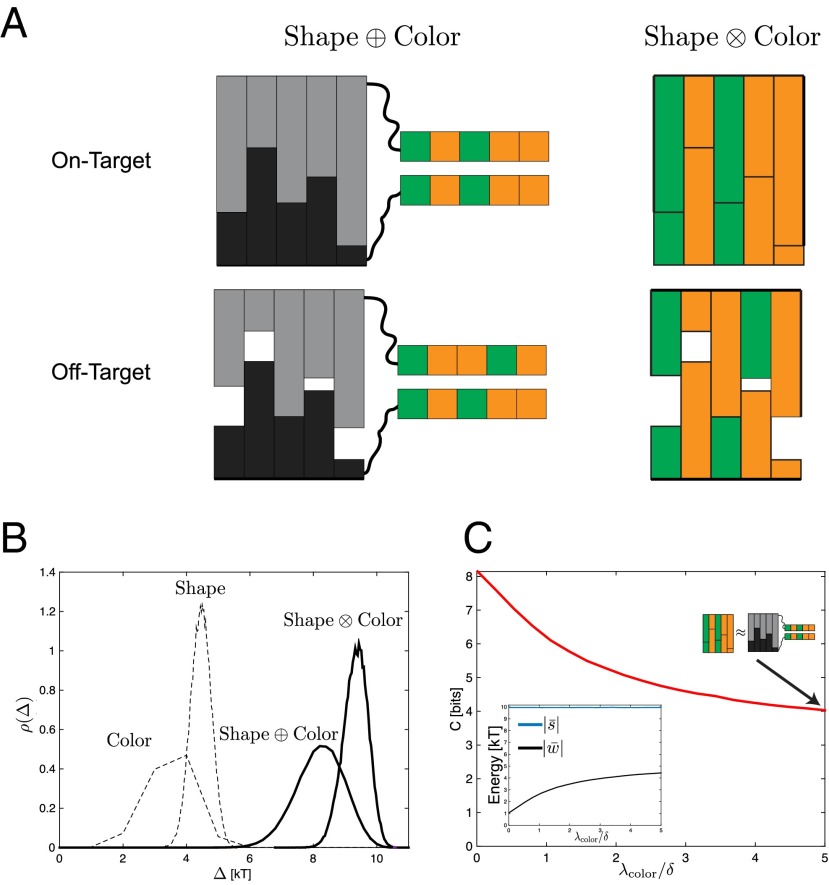
Thus far we have focused on locks and keys interacting exclusively through a single kind of physical interaction. Using our quantitative framework, we may now ask how capacity increases when multiple sources of specificity, such as shape and color, are combined in a single set of locks and keys. As is known in information theory (38, 39), the combined capacity of two interacting channels can be significantly higher than the sum of the individual capacities.

Linking Two Systems.

The simplest model for combining two channels is to physically link a lock of system 1 to a lock of system 2. We assume that there is no interaction between the two parts of the lock or between the key from one system and the lock of the other system. (We do not take into account entropic effects due to avidity.) Thus, for a linked system (which we denote as ${\text{System}}_1\oplus {\text{System}}_2$), the two independent systems with gaps of ${\mathrm{\Delta }}_1$ and ${\mathrm{\Delta }}_2$ are combined such that ${\mathrm{\Delta }}_{\text{Tot}}={\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2$. Hence the gap distribution of the linked system is the convolution of the independent systems: ${\rho }_{\text{Tot}}\left(\mathrm{\Delta }\right)={\rho }_1\left(\mathrm{\Delta }\right)*{\rho }_2\left(\mathrm{\Delta }\right)$, and the capacity can be computed using Eq. 3 in terms of the gap distributions of the individual systems.

When two channels are linked in this form without any interaction, we expect the total capacity of the system to be $C_{\text{Tot}}=C_1+C_2$ (39). We explicitly compute this linked capacity for the physical system shown in Fig. 5A, Left, in which a color system of length L is linked to a shape system of length L (Shape $\oplus$ Color). The distribution ${\rho }_{\text{Tot}}\left(\mathrm{\Delta }\right)$, obtained by convolving ${\rho }_{\text{color}}\left(\mathrm{\Delta }\right)$ and ${\rho }_{\text{shape}}\left(\mathrm{\Delta }\right)$, is shown in Fig. 5B. The resulting capacity $C_{\text{Tot}}\approx C_1+C_2$ is additive up to $\log L$ corrections that are small when L is large (Supporting Information).

Mixing Two Systems.

In a mixed system, the physics of the individual systems are combined, and there is no general formula for the resulting gap distribution because ${\mathrm{\Delta }}_{\text{Tot}}\ne {\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2$. We study a model in which the surfaces of shapes are coated with chemical colors, and we denote mixed systems by ${\text{System}}_1\otimes {\text{System}}_2$ (Fig. 5A, Right). The energy is the sum of the shape and color interactions, but the color interaction energy implicitly depends on the shape; only when the surfaces are near each other can the color-dependent interaction matter. We assume a distance dependence of the color interaction, with length scale ${\lambda }_{\text{color}}$, such that the energy of interaction decays as $e^{-h/{\lambda }_{\text{color}}}$ for two surfaces separated at a distance h.

We can intuitively understand how the mixed model differs from the linked model by examining random off-target pairs, as shown in Fig. 5A. In the $\oplus$ model, crosstalk arises from accidental matches in either independent channel; hence the crosstalk is simply the sum of the number of matching sites in the two channels. However, in the $\otimes$ model, crosstalk in the color channel can arise at a site only when there is an accidental match in both color and shape channels at that site. For example, in Fig. 5A, all three matching color sites contribute to crosstalk in the $\oplus$ model. However, in the $\otimes$ model, these three sites are not accidentally matched in the shape channel; because the three color sites are not in contact, they do not contribute to crosstalk. As a result, off-target binding is generally weaker and the typical gap $\mathrm{\Delta }$ higher in the $\otimes$ model, as we find in Fig. 5B. Thus, the mixing of shape and color in this interactive manner increases the capacity.

We may further examine how the capacity changes as a function of ${\lambda }_{\text{color}}$, the interaction range of the color system. When ${\lambda }_{\text{color}}$ is small compared with δ, the maximum height of local shape features, shape features can be easily distinguished by the color force and so the color and shape work in concert to increase capacity. Increasing ${\lambda }_{\text{color}}$ blurs the shape contours and the color interactions no longer distinguish shapes, thereby becoming less specific. Indeed, Fig. 5C shows that when ${\lambda }_{\text{color}}/\delta$ becomes large, the color system and the shape system act independently, and the capacity relaxes to the capacity of the linked system Shape $\oplus$ Color.

In summary, laying out color-based codes on undulating surfaces significantly reduces the total crosstalk because color-matched sites must also be matched in shape to contribute to crosstalk. Such color–shape synergy persists as long as the spatial range of color interactions is shorter than the length scale of shape variation.

Discussion

Here we have shown that mutual information provides a general metric for specificity, bounding the number of distinct lock–key pairs that can be supported by systems of programmable specific affinities. Mutual information is well suited as a measure of specificity for many reasons. First, mutual information is a global measure of specificity, accounting for all possible interactions between N species of locks and keys. Second, as a result, it provides a precise answer as to how many particle pairs can be productively used in a given system. As N is increased, crosstalk necessarily increases as we crowd the space of possible components (Fig. 1B) (25), with more and more lock–key pairs. Capacity is determined by the point $N=N_C$ at which the information gain due to larger N is negated by the increase in crosstalk.

Third, we can use mutual information to quantitatively compare disparate types of programmable interactions, from DNA hybridization to depletion-driven interactions. Our framework can also quantitatively predict how varying physical parameters (e.g., depletion particle size, range of interactions, elastic modulus of shapes) raises or lowers specificity. The models we discuss can be further refined in various ways, for example by allowing DNA strands to fold, examining shapes in three dimensions, or taking into account the entropic effects of multivalency and avidity (40).

Using such an approach, we found that (i) shape complementarity intrinsically suffers less crosstalk than color (i.e., chemical specificity)-based interactions and (ii) multiple physical interactions, such as color-based and shape-based interactions, can be combined in a synergistic manner, giving a capacity that is greater than the sum of the parts. Such predictions are especially valuable, given the proliferation of different mechanisms for creating and combining distinct mechanisms of specificity: Mutual information provides an unbiased way of comparing their efficacy to each other. As programmable specificity continues to drive technological developments in self-assembly (41), understanding how the mutual information of paired components can be built up toward creating larger, multicomponent objects is a critical future direction of this work.

Although we focus on applications to colloidal systems, we note that the framework developed here can be used to study biological systems as well. In 1894, Emil Fischer proposed the “lock and key” model as an analogy for understanding enzyme–substrate specificity (42), focusing on the physical shapes of paired interacting components; mutual information encompasses this idea and can be applicable to a large number of biological systems. In particular, our model is useful for predicting the differences between interacting proteins that use shape complementarity alone and those that combine both shape and electrostatic complementarity (e.g., Dpr-DIP vs. Dscam proteins) (43) and may also be applied to a host of other biological interaction networks (22) where information transmission and pair specificity play critical roles in biological function [e.g., histidine kinase/response regulator proteins (44) and the immune system (25)]. Crucially, the mutual information model provided above is flexible enough to be extended to some of the challenging physics encountered in biology. Nonequilibrium systems can be accounted for by computing time-dependent probabilities of interactions instead of the equilibrium probabilities, whereas hypotheses for increased specificity like “induced fit” and recent variants (35) can be tested directly for their impact on capacity.

In this work, we have shown that mutual information is a powerful tool to describe diverse specificity models. The strength of our framework is that it is broadly applicable—it may immediately be applied to any system for which the pairwise energies of interactions are known, both in biology and in synthetic experiments. We believe that using the capacity as a measure of system specificity will provide a simple metric for analyzing, comparing, and optimizing systems of programmable interactions.