A standardized approach to estimating survival statistics for population based cystic fibrosis registry cohorts

Abstract

Objective

Our objective was to quantify the effect of different statistical techniques, inclusion/exclusion criteria and missing data on the predicted median survival age.

Study Design and Setting

Using the Canadian CF registry (CCFR), the median age of survival was calculated using both the Cox Proportional Hazards (PH) and the life-table methods. Through simulations, we examined how the median age of survival would change when: 1) patients were excluded, 2) death dates were inaccurate, 3) patients were lost to follow-up, 4) entire years with no clinic visits were excluded even if the patient had a visit in subsequent years, and 5) censoring patients at their date of transplant. Simulations were run assuming 5% to 35% of data were affected by each scenario.

Results

Over the period 2009 to 2013, there were 4,666 individuals in the CCFR with 240 deaths. The observed median age of survival calculated by the Cox PH method was 50.9 (95% CI: 47.4–54.3) and 50.5 from the life-table method (95% CI: 47.5–53.5). Censoring patients at their transplant date overestimated the median age of survival by 7.2 years (58.1, 95% CI: 53.3–64.7). Simulations determined that by missing just 15% of deaths, the median age of survival can be overestimated by 3.5 years (54.4, 95% CI: 54.2, 56.1), and having 25% of patients lost to follow-up can underestimate the median age of survival by 3.3 years (47.6, 95% CI: 46.8–47.7).

Conclusions

We present several recommendations to assist national CF registries in calculating and reporting the median age of survival in a standardized fashion. It is imperative to state the statistical method used as well as the proportion lost to follow-up and the treatment of missing data and transplanted patients. Registries must be diligent in their data collection as incomplete data can lead to over and underestimation of survival.

1. Introduction

National cystic fibrosis (CF) data registries are powerful resources for describing patient characteristics, understanding epidemiologic trends, and predicting life expectancy in the CF population. By analyzing these registry data, several countries are able to calculate the median age of survival, the age past which 50% of the population is expected to live assuming the mortality rate and age distribution are held constant. In 2012, the median age of survival varied between countries: 49.7 years in Canada (95% CI: 46.1–52.2) [1], 43.5 years in the United Kingdom (UK) (95% CI: 37.6 – 49.9) [2] and 41.1 years in the United States (USA) (95% CI: 37.4–43.1) [3]. Understanding the reasons behind these international differences in survival may provide valuable information for the CF community; however the lack of a standardized approach for calculating and reporting median survival makes direct comparison between countries challenging.

The statistical technique for calculating the median age of survival differs between countries with the USA and UK applying the period life-table method and Canada adopting the period Cox proportional hazards (PH) method [4]. International comparisons may still be limited even when the same statistical approach is used. Jackson et al (2011) analyzed data from the USA and Republic of Ireland (RoI) CF registries using the same statistical method and found that the estimates of median predicted survival varied considerably from year-to-year, particularly in the RoI where the number of annual deaths is small [5]. In order to reduce year-to-year variability in survival, a longer time window can be utilized to smooth out estimates, particularly when death numbers are few. For this reason, a five-year time window is employed by Canada, the USA and the UK when calculating the median age of survival [4]. Despite best efforts, registries often suffer from missing data. Variables essential for survival calculations (e.g. date of diagnosis, date of death) may be difficult to accurately obtain, and patients may become lost to follow-up. Healthier and non-adherent patients may defer regular clinic appointments, creating missing intervening years in the registry, which would affect estimates when the median age of survival is calculated using the life-table method. The distance of CF centres may also influence the degree of follow-up. Furthermore, a recent study by Nick et al showed that although approximately 10% of deaths occur over the age of 45 years, the US CF registry only captured 45.9% of deaths in this age group when compared to Centre for Disease Control Mortality statistics [6], indicating that registries may be underestimating the number of deaths among older patients. Inaccurate data within the registry will impact survival estimates for any population, however, there is no literature to date which quantifies the impact of these biases on survival statistics in CF.

A standardized approach to calculating and reporting median age of survival for CF Registries is needed for comparisons across countries. In this study, we aim to (1) compare the impact of different statistical methodologies, specifically, the life-table and the Cox proportional hazard methods, on survival estimates in the CF population; and (2) investigate the impact of different methodological and data processing approaches on median age of survival when a) patients were excluded, b) death dates were inaccurate, c) patients were lost to follow-up, d) entire years with no clinic visits were excluded even if the patient had a visit in subsequent years, and e) censoring patients at their date of transplant; and (3) develop a unified standardized approach for calculating the median age of survival that can be used in all CF registries.

2. Methods

2.1 Data Source

We utilized the Canadian CF Registry (CCFR). Individuals followed in the registry between January 1, 2009 and December 31, 2013 were included in these analyses. The CCFR was first developed in 1970 and incorporates patients from 42 accredited centres across the country. CF Canada provides funding to centres contingent upon submitting data to the registry. In addition, there are incentives for CF patients to attend CF centres as many medications are covered by provincial drug plans if dispensed from a CF pharmacy. It is estimated that less than 1% of the Canadian CF population have declined consent to have their data captured in the registry. For these reasons, it is felt that the CCFR captures essentially all CF patients in Canada. The CCFR collects demographic and clinical information annually and these data undergo routine validation checks to minimize errors. Any discrepancies are resolved by contacting the reporting CF centre to cross-reference with original data. As transplanted CF patients are followed closely by their transplant team in lieu of their original CF team in the post-transplant period, each CF clinic was contacted to confirm follow-up status of these post-transplant patients. All individuals within the registry have provided informed consent to have their data collected and used for research purposes. This study was approved by the Research Ethics Board at St. Michael’s Hospital, Toronto, Ontario (REB # 14-148c).

2.2 Statistical Methods

We briefly summarize here the life-table and Cox PH methods and how they were used to calculate the median age of survival.

2.2.1 The Lifetable Method

In the cohort lifetable method, the data are grouped into equally spaced time intervals, typically one-year age intervals. For each age interval, the age-specific mortality rate is calculated and then applied to a hypothetical population to determine the median age of survival. Therefore, an individual can be counted multiple times to account for each age interval they contribute during the analysis window. For each age interval i ∈ (0,1,2,…,100), the probability of an individual dying at age i is calculated as the proportion of deaths D occurring at that age over the population N at risk assuming the deaths occur halfway through the age interval, i.e.

$$p_i=\frac{M_i}{1+\frac{1}{2}(M_i)},$$ (1)

where M_i is the mortality rate at age i and is calculated as

$$M_i=\frac{D_i}{(N_i-D_i)+0.5D_i}$$ (2)

The proportion surviving at age a is then $S_i(a)={\prod }_{i=0}^a(1-p_i)$. The median age of survival is calculated as the largest age a such that ${\prod }_{i=0}^a(1-p_i)\le 0.5$. Further details may be found in Chiang CL (1967) [7].

2.2.2 Cox Proportional Hazards

Conversely, in the Cox PH model, an individual only contributes a unique summary time period estimate that summarizes their length of contribution time. That is,

$$S_i(a)=exp(-{\int }_0^{a}h(u)du)$$ (3)

where h(u) is the rate of death at age u, and is calculated as the number of deaths d occurring at age u, over the number at risk of dying, n:

$$h(u)=\frac{d_u}{n_u}$$ (4)

The median age of survival is the maximum age a for which S_i(a)≤0.5.

2.2.3 Simulations

The life-table and Cox PH methods outlined above are sensitive to both data processing and missing data. It may be noted from (2) that as the population at risk N_i-D_i increases, the mortality rate decreases. A decreased mortality rate corresponds to a decreased probability of death p_i and smaller increments in the proportion surviving at age a, leading to a longer overall median survival age. The population at risk could increase if the number of deaths D_i is underestimated, and it could decrease if individuals were excluded from that age interval – for example, due to exclusions, loss to follow-up or missing clinic visits during that year. From (4), we see the Cox proportional hazards model will behave similarly – a smaller h(u) would increase the incremental proportion surviving, S_i(a), lengthening the median survival age. Furthermore, in the life-table method, an individual would contribute to multiple age intervals over their life course. Therefore, if a patient is missing all clinic visits within a one-year period, one of their exposure years will be excluded, causing the population at risk for that age interval to be underestimated - in turn overestimating the mortality rate and underestimating the median survival age. Contrary to the life-table method, the Cox PH method would not be affected by an individual missing all clinic visits in a given year since this method considers only a final unique survival time per patient. That is, the number of years of exposure in Cox PH is calculated from birth to their death or last known follow-up date.

To assess the impact the aforementioned registry limitations may have on the median age of survival, we conducted a simulation study wherein we recalculated the median age of survival under each of the following scenarios: a) exclusion of patients such as removing those with an unknown date of diagnosis, b) censoring deceased patients at their last follow-up date due to inadequate death data, c) losing patients to follow-up, d) exclusion of intervening years for which patients did not have a clinic visit, and e) censoring patients at transplant. We randomly assigned a fixed proportion of patients (5%, 10%, 15%, 20%, 25%, 30%, and 35%) to be affected by each scenario. These increments were chosen so that we could showcase the pattern of the impact and assess linearity. For scenarios 3 and 4, the number of years missing was randomly assigned assuming a uniform distribution. Each simulation was repeated 100 times. The median age of survival from each of the 100 simulations was averaged and a violin plot was used to graphically visualize the mean and variability of the replicates. The 95th percentile interval (PI) for each simulation was calculated by determining the 2.5^th and 97.5^th percentiles of the 100 simulations.

The gold standard median age of survival to which all simulated results were compared was calculated by imputing any missing dates of diagnosis to 30 days after birth and including all intervening years. The median age of survival and corresponding 95% confidence interval (CI) were calculated using the Cox PH model with age as the time scale. The SAS and R code used to calculate the median age of survival is provided in the Supplemental Materials. To show the effect of excluding the intervening years (scenario d) above) we utilized the life-table method as this is the only method that considers each individual year. Follow-up and death data were assumed to be accurate as collected. For scenario c), patients with no known date of death were assumed to be alive up until December 31, 2013. Data were assumed to be left-truncated at January 01, 2009; survival contribution from each patient was measured from this start date or their age of diagnosis if the patient was born during the study period until their date of death or December 31^st of their last known reporting year.

3. Results

There were 4,666 patients followed in the registry during this time period and 240 deaths. Patient demographics are presented in Table 1. 115 (2.5%) patients were missing date of diagnosis and 185 (4.0%) had a transplant during the study period. Of the 4,426 patients alive at last follow-up, 57 (1.2%) had their last reporting year in 2010 or earlier, 57 (1.2%) were last seen in 2011 and 221 (4.7%) were last seen in 2012. If we define lost to follow-up as any patients that have not been seen for at least two years, then 114 (2.4%) of patients in the CCFR were lost to follow-up over this time period. An additional 390 patients were excluded from the analysis as their last known follow-up date was 2008 and earlier. Of the 4,426 patients censored at last known follow-up, 3,433 (77.6%) had clinic visits in every year until their last known clinic date. The remaining 22.4% had between 1 and 4 missing years. For deceased patients, 187/240 (or 77.9%) had complete follow-up in intervening years with 22.1% missing at least one intervening year.

Table 1.

Patient clinical and demographic summary

Patient Characteristic	Frequency	Proportion
N	4,666	100.0%
Age at diagnosis
Median (range)	0.5	(0 – 71.7)
0–2 years	3,095	66.3%
2–18 years	1,234	26.5%
≥18 years	337	7.2%
Sex
Male	2,497	53.5%
Female	2,169	46.5%
Ethnicity
Caucasian	4,308	92.3%
Other	348	7.5%
Unknown	10	0.2%
Genotype
Homozygous ΔF508	2,237	47.9%
Heterozygous ΔF508	1,816	38.9%
Other	478	10.2%
Unknown	135	2.9%
Pancreatic Status
Insufficient	3,978	85.3%
Sufficient	688	14.7%
CF-Related Diabetes
Yes	1,170	25.1%
No	3,496	74.9%
FEV1 % predicted at last visit
Not Available	866	18.6%
Median (range)	74.3	(10.9 – 138.7)
BMI at last visit
Unknown	83	1.8%
Underweight	881	18.9%
Normal	3,046	65.3%
Overweight	741	15.9%
Microbiology (ever)
Unknown	58	1.2%
BCC	489	10.5%
Pseudomonas	3,609	77.4%
Staph	4,128	88.5%
Steno	1,877	40.2%
MRSA	480	10.3%
Transplants
Yes	474	10.2%
No	4,192	89.8%
Missing Intervening Years
0 years	3,620	77.6%
1 year	374	8.0%
2 years	249	5.3%
3 years	243	5.2%
4 years	180	3.9%
Deaths
Overall	240	5.1%
Males	114	47.5%
Females	126	52.5%

3.1 Comparison of the lifetable and the Cox PH method

Using the Cox PH method, the median age of survival was estimated as 50.9 years (95% CI: 47.4 – 54.3) compared to 50.5 years (95% CI: 47.5 – 53.5) calculated by the life-table method. The small difference in median survival stems from the innate rounding procedure of the life-table method (the age is calculated to the nearest half-interval), while the Cox model calculates an exact age. Small rounding differences aside, the two methods yielded nearly identical results when the intervening years were included in the life-table method. As the results proved to be similar, the simulations were all performed using the Cox PH model, with the exception of Scenario d), which used the life-table method.

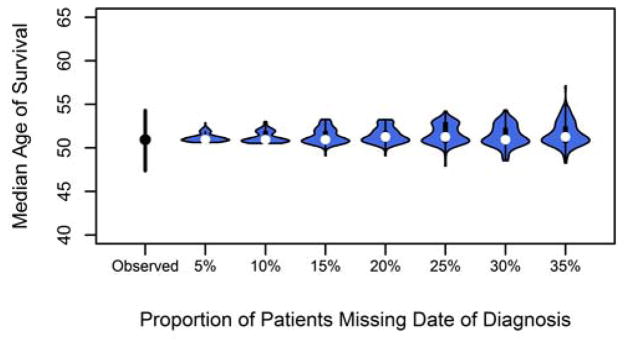
3.2 Excluding patients with missing date of diagnosis

In Figure 1, it is shown that excluding random patients with their date of diagnosis set to missing did not greatly affect the estimated median age of survival as the average remained the same at 50.9 years over the simulations. Regardless of the proportion of patients excluded, the median calculated age of survival remained steady at 50.9 years using the Cox PH method. However, as the proportion of patients excluded increased, the width of the 95% PI greatly increased. If 35% of patients were excluded, the 95% PI ranged from 49.2 to 54.4 years. This increase in variability suggests that, depending on the patient group excluded, the median age of survival could be overestimated by 3 years or underestimated by almost 2 years. The PI range is just inside the observed 95% CI, indicating that caution must be used if excluding a larger proportion of the population than 35% as the survival age will be overestimated.

Figure 1.

Median age of survival after randomly excluding 5–35% of cases for missing a date of diagnosis.

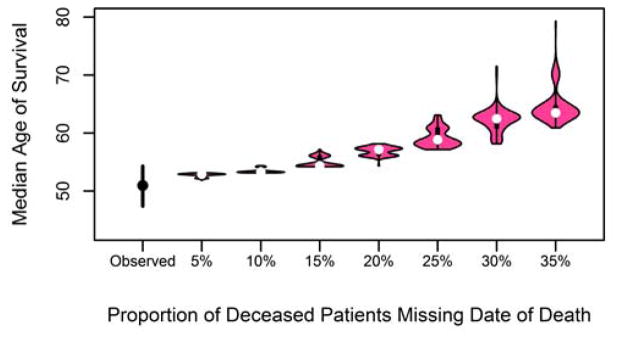
3.3 Incomplete death data

In this scenario, we randomly assigned from 5% to 35% of confirmed deaths in the CCFR to be censored at last known follow-up date to simulate missing death dates. The results in Figure 2, calculated using the Cox PH method, show that when 5% of deaths are underreported, the median age of survival is overestimated at 52.9 years (95% PI 52.2–53.0). This overestimation increases with the number of deaths missed, with the median age of survival estimated to be 63.5 years (95% PI: 62.5 – 71.5) when 35% of deaths were excluded. When 15% (36/240) of the deaths were excluded, the 95% PI (54.2 – 56.1) exceeded the upper limit of the observed CI (54.3 years), indicating that misreporting of 15% or more will overestimate the median age of survival.

Figure 2.

Median age of survival after randomly censoring 5–35% of deceased cases at date of death.

The above simulations randomly selected deceased patients. As the Nick et al. paper discovered, incomplete death data steadily increases after the age of 15 [6]. We ran a separate simulation assigning 0.5*proportion to those under age 35, with the remaining higher proportion assigned to those over 35. The results show that the overestimation in median survival gets exaggerated even further with the median age of survival estimated at 71.5 (95% PI: 69.9–79.3) when 35% of deaths are excluded (Supplemental Figure 1).

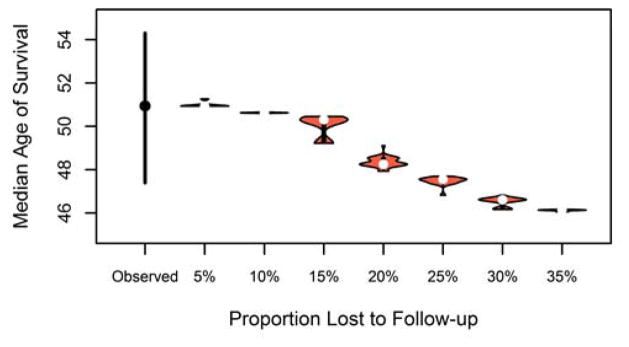
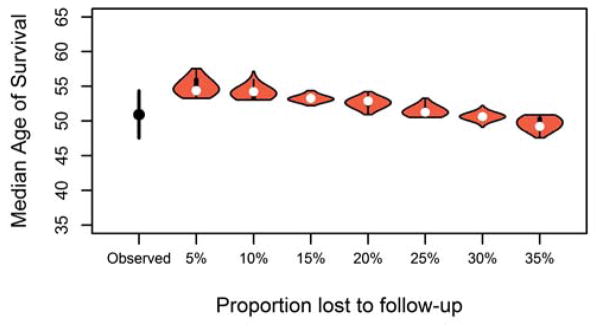
3.4 Impact of loss to follow-up

Some patients move to another country or do not return to clinic for several years while they are feeling well, and therefore are lost to follow-up for a period of time. The results of the simulation, calculated using the Cox PH method, are shown in Figure 3 and demonstrate that as the proportion of randomly selected patients with loss to follow-up increases, the median age of survival is underestimated. When only 10% of patients are lost to follow-up, the median age of survival would be underestimated by only a few months at 50.6 years (95% PI: 50.5–50.7), but when 35% of the population are lost to follow-up, the median age of survival was underestimated by 4.8 years (46.1, 95% PI: 46.0 – 46.1). When the proportion of patients lost to follow-up reaches 25% (47.6, 95% PI: 46.8–47.7), we start to see the median age of survival be underestimated outside of the observed lower CI of 47.6.

Figure 3.

Median age of survival after randomly assigning 5–35% of patients to be lost to follow-up.

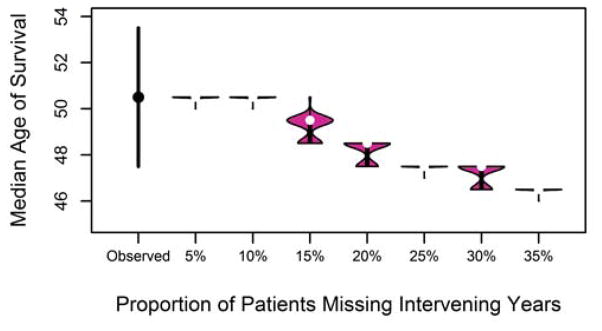
3.5 Impact of excluding intervening years

Using the life-table method, when 15% of patients were missing some of their intervening years, the median predicted survival age was underestimated by one year at 49.5 years, but this underestimation grew as the proportion of patients with intervening years missing grew (3 years with 25% missing, 4 years underestimated with 35% patients missing, Figure 4). Similar to the results found when patients were lost to follow-up, caution should be exercised if the proportion of patients missing intervening years exceeds 25%.

Figure 4.

Median age of survival after randomly excluding between 1 to 5 intervening years for 5–35% of patients.

3.6 Censoring patients at transplant date

When we censored patients at transplant, the median age of survival calculated via the Cox PH method increased to 58.1 years (95% CI: 53.3 – 64.7). The increase in median survival is caused by the fact that the analysis ignores the number of years of exposure that transplant patients contribute but more importantly, the deaths post-transplant are not taken into consideration in the analysis.

3.7 Scenarios working in concert

The simulations thus far have analyzed each scenario independently of one another. In reality, however, some patients will have incomplete death data while others will be lost to follow-up in the same cohort. To determine what effect two scenarios working together would have on median survival, we fixed the proportion of censored deaths to 15% and varied the loss to follow-up from 5 to 35%. The results, shown in Figure 5, show that if 15% of deaths are incomplete and only 5% of patients are lost to follow-up, the median age of survival will be overestimated at 54.4 (95% CI: 54.2 – 57.1). However, as the proportion of patients lost to follow-up increases, the median age of survival begins to fall within the observed CI bounds at 15% lost to follow-up (53.3, 95% PI: 52.9 – 54.3). When the proportion of lost to follow-up hits 30%, the median age of survival is estimated to be on par with the observed median survival at 50.6 (95% PI: 50.3–50.9). Therefore, it appears that if the proportion of lost to follow-up exceeds the proportion of inaccurate deaths, the overestimation in median survival caused by inaccurate death data will be balanced out.

Figure 5.

Median age of survival after randomly censoring 15% of deaths at their date of death and randomly assigning 5–35% of patients to be lost to follow-up.

4. Discussion

National CF registries produce survival statistics in order to better understand epidemiologic trends and the needs of the patient population although the statistical approach used may vary. Our results show that the particular statistical method used does not affect the median age of survival as long as the intervening years are considered in the life-table method, but survival estimates may be over- or underestimated based on the statistical approach used as well as how data are captured and processed, and the missingness of key data. These results confirm the importance of maintaining complete follow-up within registries and emphasize the need to obtain accurate patient records and vital statistics. Furthermore, this study highlights the fact that in order to compare survival statistics between countries, information on methodological and data processing approaches as well as the proportion of missing data is required in order to make accurate and appropriate comparisons.

Limitations of our study should be acknowledged. The two statistical methods described in this paper are not exhaustive and both methods come with their own inherent limitations. The semi-parametric Cox PH model lacks flexibility in assuming proportionality of hazards, and cannot be used to predict survival into the future [10], while the life-table method requires more diligence on the part of the programmer to ensure that intervening years are accounted for and can only estimate age of survival to the nearest half-year. Other statistical methods (such as parametric survival models) may be more appropriate and warrant further study.

We chose to use the CCFR data for this analysis instead of simulated data so that the underlying data structure and relationships between measured and latent variables could be preserved. We feel that by using real data for these simulations, we ensure the results are realistic and can be generalized to other CF registries. In using real data, however, we assume that the data are accurate as collected. Inaccuracies in the data should not affect the results obtained as the inaccuracies in the dataset would remain consistent throughout the simulations and the impact of key factors used in the calculation of survival statistics would be maintained. Although real data were utilized, the proportions of missing patients were randomly assigned. In reality, patients lost to follow-up or missing intervening years are likely to be either healthier patients or conversely non-adherent patients with poor lung health, and patients with inaccurate death data are likely older patients. A sensitivity analysis that placed a larger bias on patients who died over age 35 showed that the magnitude of overestimation of survival only increased when non-random assignment was taken into account. Finally, we ran each scenario separately from one another as a proof of concept to demonstrate the impact each one has on the median age of survival. In reality, however, these scenarios are working in tandem and more work needs to be done to assess if this would exacerbate the over-estimation even more or actually cancel each other out.

Based on these analyses, we recommend that when reporting population survival estimates, the statistical methodology used, data processing techniques, whether missing data were imputed, and the treatment of transplanted patients should be explicitly stated. Although the life-table method and Cox PH method produced nearly identical results, the potential for errors increases with the use of the life-table method as the programmer must be diligent to ensure that intervening years are included. In addition, there is some loss of accuracy due to rounding to the nearest 0.5 years when using the life-table method. Use of the Cox PH method has the added flexibility of covariate adjustment in order to investigate the survival of different subgroups. For these reasons, we recommend using the Cox PH method. Special attention should be made to the proportion of patients lost to follow-up and the technique used to calculate median survival age must incorporate the intervening years in order to produce accurate estimates. Providing this information in national annual reports will help to acknowledge possible over- or underestimation of the median survival. A complete summary of our recommendations for estimating survival from CF registries can be found in Table 2.

Table 2.

Recommendations when Reporting Survival Statistics using CF Registry Data

Key General Points: Registries must diligently capture deaths within the registry in order to avoid biased survival statistics. If available, comparing the number of deaths within the CF registry to national death statistics where the cause of death is CF is a way to estimate the impact of missing deaths. In order to stabilize survival estimates and minimize year-to-year variability, it is recommended that a five-year window be used. Registries with few deaths per year may require a longer time window to produce stable results, while larger registries may find a time period shorter than five years will suffice. Stability of the results can be judged by examining the width of the 95% confidence interval and the consistency between period estimates. In particular circumstances, if the CF population is very small and there are few deaths, it may not be possible to accurately estimate the median age of survival despite maximizing the time window. Registries should minimize the number of patients who are lost-to-follow up when calculating survival statistics. Efforts should be made, where possible, to confirm the vital statistics of patients within the registry prior to survival calculations. Assuming that post-transplant patients are not lost-to-follow-up following transplantation, transplanted patients should be included in the survival analysis rather than being censored at the time of transplant because censoring results in an over- estimation of survival. If the life-table method is used to calculate survival, intervening years must be accounted for in the analysis in order to produce unbiased results.

Registries should consider including the following parameters in their survival reports: The length of the time window under consideration (for example, 2009 to 2013). The number of patients in the time window. The number of deaths in the time window. The statistical methodology used (i.e. life-table method, Cox PH method). How missing data were treated (i.e. listwise deletion, simple imputation, multiple imputation). Whether or not transplanted patients are included in the analysis or whether they are censored at transplant. Proportion of patients lost-to-follow-up, where lost-to-follow-up is defined as those patients alive with their last verified year of contact occurring more than two years before the end of the five-year window (for example, 2011 if the window in question is 2009 to 2013).

As the median age of survival should reflect the outcome of all CF patients regardless of treatment, the Canadian survival calculation includes transplanted patients. Including transplanted patients causes some controversy as some may argue that CF post-transplantation should be considered as a completely different disease than CF pre-transplantation. Therefore, some registries may choose to censor patients at the date of transplant. Censoring patients at transplant will overestimate the median age of survival. Registries should take care to explicitly outline whether or not patients were censored at transplant.

Having a uniform, standardized approach to survival calculations will allow for international comparisons. Without this, any differences noted between countries could be explained by differences in data processing or analytic techniques, rather than actual differences in the health outcomes of the populations studied. A uniform approach to cohort development and statistical analyses would provide greater confidence in comparing outcomes across registries and more meaningful conclusions regarding factors that have contributed to observed differences. To this end, we have provided our SAS and R code for calculating the median age of survival that can be adapted to each CF registry to facilitate a uniform approach.

Identifying factors that contribute to increased survival has the potential to impact all individuals living with CF. For example, Corey et al used a unified statistical approach to compare health outcomes at two adult CF clinics in Boston and Toronto from 1972–1981 and found that the median age of survival differed by 9 years [8]. More recently, McCormick et al (2005) compared demographic and clinical differences between countries and found that patient age and infection rates were significantly different among the UK, US, France and Australia [9]. These studies confirm that some differences in survival may be attributed to country-wide differences in clinical and demographic factors but we must first ensure that the differences are not simply due to methodological differences in statistical analyses. Despite using similar methodologies, international differences do exist and may contribute to the differences in median age of survival and future studies are needed to understand what is driving these discrepancies.

Supplementary Material

1. Supplemental Figure 1.

Median age of survival after randomly censoring 5–35% of deceased cases at date of death. Deaths over the age of 35 were oversampled to illustrate the impact as death dates for older patients are more likely to be missed than younger deaths.

What is new?

Key findings

• The Cox proportional hazards and life-table method yield nearly identical results when data processing techniques are the same.

• Losing patients to follow-up has the potential to under-estimate the median survival age while missing death dates will over-estimate the median survival age.

• Censoring patients at transplant results in an over-estimation of the median survival age.

What this adds to what is known

• The magnitude of the bias on predicting CF survival when data are missing or patients were lost to follow-up is now quantified.

• Recommendations are provided to help reduce bias in calculating the median age of survival and to improve transparency in reporting survival estimates.

Implication

• Researchers should report the sample size, the statistical method used, the proportion lost to follow-up, treatment of missing data, and whether transplanted patients were censored or not when reporting the median age of survival from data registries to acknowledge the magnitude of under/overestimation in survival.

• National CF registries should standardize the reporting of median survival to aid in international comparison.