Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Jun 1.
Published in final edited form as: Neuroimage. 2016 Mar 5;133:88–97. doi: 10.1016/j.neuroimage.2016.03.002

Subject-level Measurement of Local Cortical Coupling

Simon N Vandekar a,b,*, Russell T Shinohara b, Armin Raznahan c, Ryan D Hopson a, David R Roalf a, Kosha Ruparel a, Ruben C Gur a,d,e, Raquel E Gur a,d, Theodore D Satterthwaite a
PMCID: PMC4889557  NIHMSID: NIHMS776386  PMID: 26956908

Abstract

The human cortex is highly folded to allow for a massive expansion of surface area. Notably, the thickness of the cortex strongly depends on cortical topology, with gyral cortex sometimes twice as thick as sulcal cortex. We recently demonstrated that global differences in thickness between gyral and sulcal cortex continue to evolve throughout adolescence. However, human cortical development is spatially heterogeneous, and global comparisons lack power to detect localized differences in development or psychopathology. Here we extend previous work by proposing a new measure – local cortical coupling – that is sensitive to differences in the localized topological relationship between cortical thickness and sulcal depth. After estimation, subject-level coupling maps can be analyzed using standard neuroimaging analysis tools. Capitalizing on a large cross-sectional sample (n=932) of youth imaged as part of the Philadelphia Neurodevelopmental Cohort, we demonstrate that local coupling is spatially heterogeneous and exhibits nonlinear development-related trajectories. Moreover, we uncover sex differences in coupling that indicate divergent patterns of cortical topology. Developmental changes and sex differences in coupling support its potential as a neuroimaging phenotype for investigating neuropsychiatric disorders that are increasingly conceptualized as disorders of brain development. R code to estimate subject-level coupling maps from any two cortical surfaces generated by FreeSurfer is made publicly available along with this manuscript.

Keywords: MRI, development, adolescence, gyrification, cortex, folding, cortical thickness

INTRODUCTION

To accommodate a marked expansion of surface area, the cortical sheet of the human brain is highly folded (Van Essen, 1997; Zilles et al., 2013). Such folding has important functional implications and may increase computational efficiency due to reduced axonal distance within a gyrus (Van Essen, 1997). Moreover, folding patterns and local cortical thickness are closely inter-related (Fischl, 2013; von Economo, 1925). von Economo (1925) described that the thickness of the cortex is significantly reduced in passing from the crown of a gyrus to the floor of a sulcus. This striking relationship was subsequently verified in vivo using structural neuroimaging techniques (Fischl and Dale, 2000).

It was long posited that this relationship between sulcal depth (SD) and cortical thickness (CT) is established in utero or in the perinatal period simultaneously with the development of cortical convolution (Toro and Burnod, 2005; von Economo, 1925; Zilles et al., 1997). However, we recently demonstrated that the relationship between CT and SD evolves dynamically throughout youth (Vandekar et al., 2015). Notably, topological position influences cortical maturation throughout this critical period. We found that linear thinning is widespread across the cortex but is maximal in the depths of the sulcus, whereas circumscribed areas of gyral cortex demonstrate marked nonlinear thickening between the ages of 8 and 14 years (Vandekar et al., 2015).

This work established that understanding relationships between cortical measures (e.g., thickness and depth) is critical for an accurate characterization of the plastic remodeling that occurs during youth. Furthermore, it suggests that such brain phenotypes may be important to understanding neuropsychiatric disorders (schizophrenia, autism, ADHD) that are increasingly conceptualized as disorders of brain development (Insel, 2010; Krain and Castellanos, 2006; Rapoport et al., 2012; Shaw et al., 2012; Steen et al., 2006; White et al., 2003) and may occur on a localized scale (Ronan et al., 2012; Wagstyl, 2015).

There are important methodological considerations in trying to relate the properties of two cortical surfaces or volumetric brain images: cortical surfaces and brain images are highly autocorrelated, non-independent measures that can be re-sampled to an arbitrary number of observations. Thus, standard parametric statistics are not applicable. Prior work used canonical correlation analysis (Avants et al., 2010; Ouyang et al., 2015) to describe the relationship between two measures in volumetric space. In order to assess the significance of the observed correlation, Avants et al. (2010) relied on permutation tests that relabeled subjects. This approach seeks to understand the relationship between the two measures across subjects. In our recent work (Vandekar et al. 2015), we introduced a novel spatial permutation testing procedure, adapted from the field of microscopy research, that evaluates the relationship between cortical measures in a statistically rigorous framework. Our approach differed from Avants et al. in that the interest was in assessing the spatial relationship between two variables within two averaged cortical surfaces. While this approach successfully delineated robust spatial effects associated with development in youth, it was limited in that analyses studied only global effects across subjects. For studies of more subtle individual and group differences in spatial relationships such an approach is not ideal, as it does not allow exploration of local regional effects. A within-subject map describing the spatial relationship among cortical measures would be a substantial advance and allow the application of standard tools for group-level analysis (e.g., GLM, MVPA, etc.) across subjects.

Here we introduce a method for describing local cortical coupling on a within-subject basis using a surface-based, locally-weighted regression procedure. Although this procedure could be used for any two surface maps, we apply it to extend our prior work describing how changes in CT are coupled to SD in development. We capitalize on the Philadelphia Neurodevelopmental Cohort (PNC), a large-scale, single-site study of brain development (Calkins et al., 2015; Satterthwaite et al., 2015, 2014a). Results demonstrate that local coupling is developmentally relevant and specific to regions where the relationship between CT and SD is evolving. We further illustrate the measure’s applicability to studies of individual and group differences by demonstrating the presence of substantial sex differences in cortical coupling. Finally, we provide publically available R code (https://bitbucket.org/simonvandekar/coupling) for the estimation of coupling of Freesurfer surfaces as a resource for the neuroimaging community.

METHODS

Subjects

Subjects included 932 youths (504 females) aged 8–22 (mean=14.8; sd=3.6) who completed neuroimaging as part of the PNC. The Institutional Review Boards of Penn and the Children’s Hospital of Philadelphia approved all study procedures. All study participants provided informed consent; minors under age 18 provided assent and the parent or guardian provided consent. The sample, screening, and quality assurance procedures were previously detailed (Satterthwaite et al., 2014a; Vandekar et al., 2015).

Briefly, this study considered 1,445 subjects imaged as part of the PNC. Of this sample, 332 subjects met exclusionary criteria due to a history of potential abnormalities in brain development: medical problems that may affect the brain (n=166), inpatient psychiatric hospitalization (n=51), or current use of psychotropic medication (n=165). Two hundred thirty-nine subjects met image quality assurance exclusionary criteria that included an automated and manual screening. Many subjects were excluded due to multiple of the listed criteria, yielding the 932 subjects included in the present analysis and also used in our prior report (Vandekar et al., 2015). Quality assurance screening was based only on the standard Freesurfer output; no additional screening was made on the estimated cortical coupling maps. That is, if the data quality is suitable for the analysis of standard cortical measures (e.g. thickness and sulcal depth), then it should be suitable for analyses of coupling estimated from these measures.

Image acquisition and preprocessing

Image acquisition, preprocessing, and cortical reconstruction steps are as described in Vandekar et al. (2015). A magnetization-prepared, rapid acquisition gradient-echo (MPRAGE) T1-weighted structural image was acquired, using the following parameters: TR, 1810 ms; TE, 3.51 ms; FOV, 180×240 mm; matrix, 192×256; 160 slices; TI, 1100 ms; flip angle, 9°; effective voxel resolution, 0.9375×0.9375×1mm; axial acquisition plane (Satterthwaite et al., 2014a).

Cortical reconstruction was performed using Freesurfer 5.3.0. Freesurfer processing includes intensity normalization, gray and white matter segmentation, tessellation of the pial and gray/white matter boundaries, and spherical registration to a template (Dale et al., 1999), ultimately producing CT and SD surface maps (Dale et al., 1999; Fischl et al., 1999) which were used to estimate coupling for each subject. Cortical thickness is estimated in Freesurfer as the shortest distance between the estimated gray/white and pial surfaces. SD is estimated by the formula

∫n(k)T∂J∂xktdt,

where n(k)T is the surface normal vector at vertex k, ∂J∂xkt is the gradient of J with respect to xk at time t, and J is a cost function for the inflation of the cortical surface that is based on the distance of each vertex from its neighbors. SD measures the distance a given vertex moves outward during the inflation process. Prior to Freesurfer 6 the units of sulcal depth are in arbitrary units. Other proposed methods for investigating SD use different geometry for estimating SD (Yun et al., 2013), or allow for comparison of SD in subject space using automatically labeled neuroanatomical regions of interest (Mangin et al., 2004). The pointwise calculation of SD in Freesurfer allows for estimation of coupling in template space.

After estimation of CT and SD, surface maps were registered to the fsaverage5 template using the standard spherical registration procedure in Freesurfer (Fischl et al., 1999). The fsaverage5 template was used to decrease the time to estimate coupling and reduce the number of comparisons conducted.

Estimation of coupling maps

Local CT-SD coupling is a subject specific measure that is estimated at each vertex on the cortical surface in template space. The measure is intended to capture one aspect of the multivariate nature of cortical measurements; specifically, coupling describes the localized relationship between CT and SD in a neighborhood of a given vertex.

For CT and SD, the coupling measure at a given vertex, ν0, is defined as the slope parameter estimate of a weighted regression of CT onto SD in a neighborhood, Nν0, of ν0 (Figure 1). The weights in the regression are related to the neighboring vertices’ distance from the central vertex.

Figure 1.

Figure 1

Open in a new tab

Estimation of local coupling using cortical thickness and sulcal depth for FWHM=15. (A) For each subject a neighborhood for each vertex is used to estimate the slope of a weighted regression of thickness onto sulcal depth. (B) Weights in the regression are inversely related to the distance from the central vertex. The central vertex is indicated with a white point. (C) The estimated slope parameter from the regression is assigned to the central vertex. The white point indicates the central vertex, which is shown in black on the surface.

Distance is defined as the Euclidean distance between points on the surface. We allow neighbors up to 15 degrees of separation. Weights are all less than or equal to one and rounded to three decimal places. To minimize interpolation through the surface, weights for neighbors of the same order as a neighbor with a weight of zero are all set to zero. The weights, wj, used in the regression are proportional to the standard normal probability density function,

wj=e(−12σ2d(ν0,νj)2)

where σ is a parameter that can be changed to modify the smoothness of the surface by adjusting the weights in the regression. A larger value of σ gives a smoother coupling surface. The units specified by σ are millimeters, measured from the center vertex. The R code provided with the manuscript gives the smoothness parameter in FWHM for consistency with Freesurfer’s convention. After estimating weights, a regression in the local neighborhood for each vertex is performed and the estimated slope parameter is the measure of coupling for that vertex.

The units of coupling are in (mm thickness)/(1 unit sulcal depth) where negative values indicate thinner cortex within a sulcus and positive values indicate thicker cortex within a sulcus. For the current analyses coupling was estimated for each subject within a FWHM kernel of 5, 10, and 15mm in fsaverage5 space. After estimation, mean maps were created to summarize the measure. After review of summary statistics, coupling maps with FWHM=15 were analyzed using the group-level statistical analyses discussed below. Linear analyses with FWHM=10 are included as supplementary analyses (Figure S1). In order to assess the fit of the coupling maps, weighted correlation coupling (WC-coupling) maps were estimated for each subject. By squaring these maps, a vertexwise R2 map can be estimated that allows for a visual assessment of the quality of coupling estimation. The correlation maps can also be used as an outcome in analyses.

Notably, use of coupling is not restricted to relating CT and SD, or even to analyses on the cortical surface. Coupling could be estimated from registered volumetric brain images of different modalities. At present, the R code provided allows for estimation of coupling between any two FreeSurfer surfaces in template space.

Mean coupling surface maps

Mean coupling surface maps were created by averaging the surfaces of all 932 subjects. Local plots of CT and SD were created by averaging across all subjects and then plotting the local neighborhood of each vertex. To assess the fit of the coupling estimates, R2 maps were created by squaring the WC-coupling maps. Though R2 does not explain whether the linear assumption of the coupling model is correct, it does serve as a useful scalar assessment of model fit. Local coupling relationships were investigated visually, (as in Figure 3C & D) using the Desikan-Killiany and Destrieux atlases (Desikan et al., 2006; Destrieux et al., 2010).

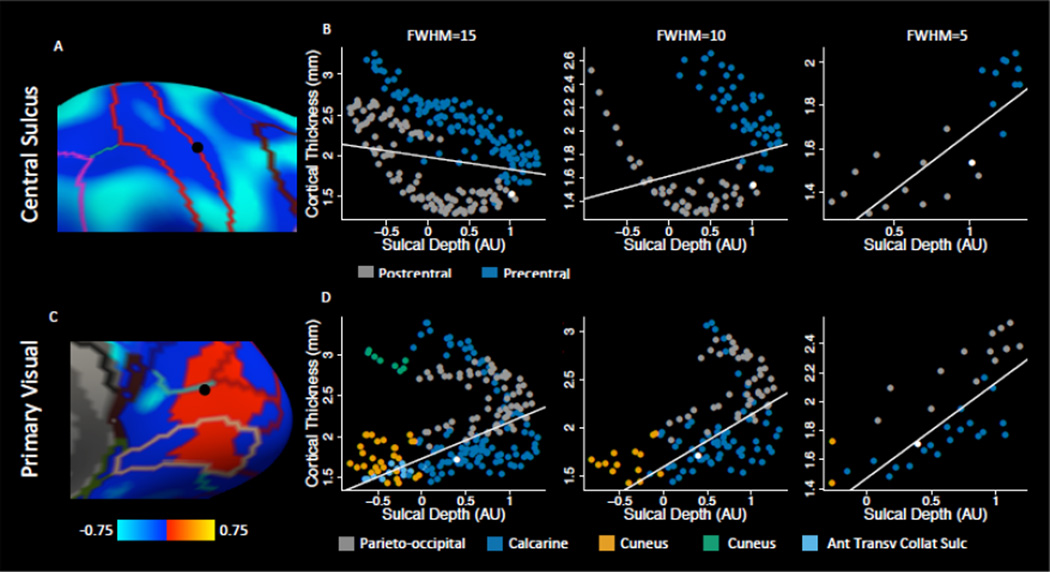
Figure 3.

Figure 3

Open in a new tab

An illustration of coupling over kernels of FWHM=15, 10, and 5mm in (A) the central sulcus, where coupling changes between kernels and (C) primary visual cortex, where coupling is positive. Vertices plotted were selected based on their location in a junction of anatomical regions. Plotting the local neighborhood for a vertex in the central sulcus shows the juxtaposition of cortex with very different characteristics: the postcentral gyrus is much thinner than the precentral gyrus. (B) The larger kernels capture the more general trend, however within a small neighborhood within the sulcus coupling is positive. (D) The local neighborhood of a vertex in primary visual cortex shows that positive coupling is the result of the vertex lying on the border of three anatomically distinct regions. Colors in the scatter plots indicate regions from the (A) Desikan-Killiany and (B) Destrieux atlases. White lines are the fit of a weighted regression on average cortical thickness and sulcal depth maps. The white point indicates the central vertex in the scatterplots, which is shown in black on the surfaces in (A) and (C).

Mass-univariate statistical analyses

To demonstrate the biological importance of coupling we investigated linear and nonlinear age effects, as well as sex differences on the coupling at each vertex. Race and intracranial volume (ICV) were included as covariates in all analyses. Additionally, we assess the effect of ICV as a covariate with respect to sex differences. No smoothing was applied to the surfaces as the local weighting in the estimation of coupling maps acts as a smoothing kernel. Separate analyses of CT and SD are presented in the supplement. These maps were smoothed with a kernel of 10mm instead of the 15mm used for coupling. The smaller kernel was used to preserve localized differences in CT in order to demonstrate that the results are sensitive to gyral and sulcal regions. We use a larger kernel for coupling in order to characterize differences across sulcal and gyral boundaries. All statistical maps were false discovery rate thresholded at q=0.01.

Linear models were fit within Freesurfer. Shapiro-Wilk maps were created to assess the normality of the residuals from the linear models for coupling as well as thickness. If the Shapiro-Wilk test is significant it indicates deviance from normality. Flexible nonlinear functions were estimated with thin plate splines using Generalize Additive Models (GAMs) with the mgcv package in R (R Core Team, 2012; Satterthwaite et al., 2014b; Wood, 2011). The penalty parameters for the nonlinear spline terms were fit as random effects and tested using restricted likelihood ratio tests with RLRsim (Scheipl et al., 2008). Note that these tests of nonlinearity are for nonlinear effects over and above any linear effects that may be present. In addition to a nonlinear main effect of age we also tested for nonlinear and linear age by sex interactions. This is a single test at each vertex for linear or nonlinear differences in the age trajectory between sexes.

Significant differences in coupling indicate regions where the independent variable (e.g. age) affects the topological relationship between CT and SD. Thus, analyses of coupling allow direct assessment and hypothesis testing of the spatial relationship between the two variables that is not possible by analyzing the two measures separately. However, to understand if variation in one variable is driving the coupling results, it is necessary to investigate the relationship between CT and SD. This can be done by investigating CT and SD surface maps separately to identify which variable has significant associations in the region where coupling results are observed.

Alternatively, we can understand the relationship between the two measures better by stratifying each cluster of significant coupling with respect to one of the imaging measures and plotting the relationship of the other with the independent variable. We do this for the nonlinear age results and the sex differences: to explore nonlinear age results, in each cluster we averaged CT over regions where SD was less than and greater than the median SD separately. We then fit age trajectories to the mean CT values to demonstrate how CT trajectories differ in regions of high and low SD (Figure 5). To understand the sex differences we also averaged CT over regions where SD was less than and greater than the median of SD. Then we create scatterplots of CT for these subregions of each cluster (Figure 7).

Figure 5.

Figure 5

Open in a new tab

Nonlinear age-related differences in coupling are driven by nonlinear differences in cortical thickness that are spatially related to sulcal depth. Nonlinear development-related effects were observed bilaterally in temporal and parietal lobes and left frontal pole. (A, B, C) Mean trajectories of coupling (blue curve) in significant regions were characterized by a smooth decline until age 14, when coupling stabilized. In the same regions, age-related increases in thickness occur in regions of gyral cortex until age 14 (gray curve), when thinning begins to occur at a rate similar to surrounding sulcal regions (white curve). Trajectories are fit using generalized additive models. Gyral and sulcal cortex are defined as above and below the median in each region. Statistical maps are FDR thresholded at q=0.01. Color bars show uncorrected p-values.

Figure 7.

Figure 7

Open in a new tab

Sex differences in coupling are driven by thicker gyral cortex in females. Mean cortical thickness data is plotted for gyral and sulcal cortex separately in clusters of significant sex differences in coupling. (A) Females show lower coupling in left frontal lobe. (B) Within this cluster gyral cortex is thicker for females than males, while sulcal cortex is similar between the two sexes. (C) Similarly, in right parieto-occipital junction females have stronger negative coupling due to (D) thicker gyral cortex than males in this region. Gyral and sulcal cortex are defined as above and below the median in each region. Color bars show signed p-values where blue represents more negative coupling in females than males.

RESULTS

Cortical coupling mean characteristics

Mean maps were created to summarize the spatial distribution of local coupling between CT and SD. Coupling maps showed the expected global negative relationship between CT and SD, indicating that over most of the cortex the cortical sheet is thinner in sulcal compared to gyral locations (Figure 2A, B, & C). However, there was also marked spatial heterogeneity, suggesting that the method detects effects that are localized to specific regions compared to the whole brain spatial correlations we previously documented (Vandekar et al., 2015). The strongest negative coupling was observed on gyral locations throughout parietal, temporal, and frontal cortex.

Figure 2.

Figure 2

Open in a new tab

Mean maps of coupling for healthy adolescents show substantial spatial heterogeneity with FWHM of 5, 10, and 15.

Notably, in contrast to the negative coupling seen in most regions, clusters within inferior temporal, primary visual, and somatomotor cortex (Figure 2A) show positive correlations between CT and SD for some kernels. Detailed examination of primary visual and somatomotor clusters revealed that this is due to complex nonlinear relationships in local neighborhoods that have unique topological characteristics, where regions of different thickness coalesce (Figure 3). This effect is clearly seen in the central sulcus, where precentral cortex is substantially thicker than postcentral cortex at a similar SD (Figure 3B). The sign of the relationship changes in the central sulcus based on the size of the kernel used because in a localized neighborhood in the sulcus (FWHM=5) there is a positive association, however at a broader scale (FWHM=15) there is a negative association. Similarly, for visual cortex there is a gradient in thickness in the regions around the calcarine fissure, with parieto-occipital cortex being thicker than calcarine cortex, which in turn is thicker than cuneal cortex. The nonlinear relationship in these regions represents a violation in the linearity assumption of coupling. This is indicated by a relative reduction in R2 in this region (Figure S2). Significant results in regions with a low R2 must be interpreted carefully with scatterplots of the data. Though the larger kernels lose some information about the complexity of the relationship, they provide information about the general trend that occurs in larger neighborhoods that encompass gyral and sulcal regions. Because differences across gyral/sulcal boundaries are of interest, we selected a kernel of 15mm for analyses.

Shapiro-Wilk tests of the residuals from the group level linear models indicated significant deviation from normality in much of the cortex for coupling and thickness (Figure S3). These results suggest the assumptions of the regression model used are violated. However, linear regression estimators are known to be asymptotically normal by the central limit theorem (Boos and Stefanski, 2013). This justifies the use of the normal distribution for inference in large samples. The default in Freesurfer is to use the t-distribution, which is asymptotically equivalent to the normal distribution as the degrees of freedom go to infinity, so inference in large samples using this distribution will be approximately equivalent to inference using the normal distribution.

Local cortical coupling evolves markedly with age in youth

Having established that local cortical coupling is spatially heterogeneous, we next examined how coupling evolves in development. Robust linear declines in coupling with age were observed in bilateral middle and superior temporal gyrus, parietal cortex, occipital cortex, and frontopolar cortex (Figure 4). The changes in coupling are due primarily to thinning in the surrounding sulcal regions (Figure S4A) rather than changes in SD itself (Figure S4B). While there is significant linear thinning throughout the cortex, coupling is sensitive to regions where thinning occurs differentially between gyral and sulcal regions, highlighting bivariate patterns of change. In addition to age-related declines, we observed age-related increases in the coupling coefficient (a negative slope becoming more positive) in the left precuneus. This region also exhibited decreasing thickness overall, but the positive change in coupling reflects relatively greater age associated thinning in gyral cortex.

Figure 4.

Figure 4

Open in a new tab

Coupling shows linear age-related decreases in occipital, parietal, temporal, and anterior frontal lobes. Increases are observed in left cuneus and bilateral anterior parietal cortex. Statistical maps are FDR thresholded at q=0.01. Color bars show signed p-values where blue indicates decreases with age and red indicates increases with age.

Nonlinear developmental effects in local cortical coupling

In order to assess whether regions exhibited nonlinear developmental differences over and above linear effects, cortical coupling was evaluated using penalized splines with generalized additive models (GAMs). Results demonstrated significant nonlinearities in the temporal lobe where linear age related differences were also observed (Figure 5A). Plotted mean trajectories within significant clusters indicate that nonlinear effects are characterized by a decline in coupling (becoming more negative) until age 14, at which point coupling stabilizes (Figure 5B, C, & D). To investigate the effects driving coupling differences we created mean gyral and sulcal CT trajectories by stratifying CT by the median SD in each cluster. Examination of gyral and sulcal CT changes in these regions revealed that this effect is driven principally by nonlinear age related differences in CT, with effects in CT following an inverse trajectory to coupling in gyral regions until age 14 (Figure 5B, C, & D). After age 14 coupling is stable because cortical thinning in gyral regions occurs in tandem with the surrounding sulcal regions (Figure 5B, C, & D). These results suggest that nonlinear age related differences in coupling are principally driven by nonlinear thickening in gyral cortex prior to age 14. These results again indicate that the effects in CT occur differentially in sulcal and gyral locations, and demonstrate coupling’s sensitivity to nonlinear, bivariate patterns of age related effects. Plots of SD by stratified by CT were stable with respect to age and are not shown. The test for a nonlinear age by sex interaction in coupling yielded no significant results.

Evidence for greater coupling in females than males

As a final step, in order to further examine local coupling’s sensitivity to studies of group and individual differences, a linear model was used to assess sex differences while controlling for age, ICV, and race. Sex differences were found in bilateral inferior parietal cortex and frontal lobe. Females have stronger negative CT-SD coupling than males in this region (Figure 6). By stratifying CT by the median SD within significant clusters we see that these coupling results are driven by thicker cortex in females than males in gyral locations (Figure 7). Vertexwise CT and SD analyses corroborate this finding (Figure S5).

Figure 6.

Figure 6

Open in a new tab

Females show stronger coupling between cortical thickness and sulcal depth. This effect is present in bilateral occipital and parietal cortex, and indicates a stronger negative correlation between thickness and sulcal depth in this region. Statistical maps are FDR thresholded at q=0.01. Color bars show signed p-values where blue represents regions that are greater in males.

Because sex is associated with ICV we investigated the effect of ICV and the results after removing it from the model. With sex and age included in the model, the effect of ICV on coupling was spatially conservative with significant associations in the frontal pole, precuneus, and anterior cingulate (Figure S6A). However, sex differences were more robust in the frontal and temporal lobes when ICV was not included as a covariate (Figure S6B), suggesting it may be an important covariate to include in analyses of coupling.

DISCUSSION

Neuroanatomists discovered almost 100 years ago that CT varies substantially with cortical topology (von Economo, 1925), wherein gyral cortex is thicker than sulcal cortex. While it was previously thought that this relationship was fully established in the pre- or perinatal period, we recently demonstrated that coupling continues to evolve during adolescence (Vandekar et al., 2015). Because many major neuropsychiatric disorders are linked to abnormalities of cortical development and folding (Insel, 2010; Krain and Castellanos, 2006; Rapoport et al., 2012; Shaw et al., 2012; Steen et al., 2006; White et al., 2003), quantitative measurement of this relationship between CT and SD may be useful for studies of developmental psychopathology.

Here we introduced a new measure of local cortical coupling to describe the relationship between CT and SD, which was historically examined manually in post-mortem brains by early investigators. Local cortical coupling is a subject-level, surface-based measure that can be calculated using the R code made publically available (https://bitbucket.org/simonvandekar/coupling), and can be readily applied to studies of development or individual difference using standard analysis tools. We demonstrate that local cortical coupling is spatially heterogeneous and evolves with age. Importantly, age-related differences in coupling demonstrate that local cortical topology is not fixed, but continues to develop in specific regions through adolescence. Moreover, significant sex differences in coupling are present, with females exhibiting more robust coupling than males in inferior parietal and posterior temporal cortex.

Local regression provides subject-level estimate of cortical coupling

Given the highly complex nature of the human cortex, there is increasing interest in describing how different cortical measures inter-relate. Local cortical coupling is an approach that can be used to investigate the localized bivariate relationship between two cortical measures. Previously, using PCA and spatial permutation tests, we showed that age-related thinning was concentrated primarily in sulcal cortex and that age-related thickening occurred in surrounding gyral cortex (Vandekar et al., 2015). Similar analyses have considered the topological relationship between measures on a regional basis (Alemán-Gómez et al., 2013; Klein et al., 2014). However, in all previous studies, these associations were identified across the entire cortex or averaged across large regions. We developed coupling as a vertexwise measure that describes localized relationships between cortical measures. Notably, CT-SD coupling is spatially heterogeneous, providing a fine level of resolution that could not be captured in prior studies.

Calculation of local cortical coupling produces a subject-level measure that allows it to be easily integrated into standard analysis tools as an outcome variable or high dimensional predictor. Here, coupling was used to describe the relationship between CT and SD. However, it should be noted that any surface based map in Freesurfer could be used; indeed, coupling could also be estimated in registered volumetric images. Coupling therefore may represent a valuable new subject-level imaging phenotype for studies of development that is sensitive to individual differences, and potentially to the presence of neuropsychiatric disorders.

Coupling identifies topologically heterogeneous regions

As documented by early anatomists, CT-SD coupling is negative across most of the cortical surface. However, our local coupling measure provides novel evidence of spatial heterogeneity in this relationship. Notably, coupling is most robust in gyral heteromodal association cortex and large sulci such as the insula. Local variations in coupling delineate developmentally relevant regions that are not well differentiated by cortical measures evaluated on their own.

In contrast to the negative coupling seen throughout the cortex, clusters of positive coupling for larger kernels are quite sparse. Positive coupling is not driven by an inversion of the normal relationship between CT and SD, but rather is seen at junctions of anatomic regions where there are systematic differences in thickness between gyri on opposite sides of a sulcus (Fischl and Dale, 2000; von Economo, 1925). Larger kernels detect more general changes in the CT-SD relationship at the expense of having complex nonlinear relationships go undetected. Low R2 in these regions is indicative of a failure of coupling to capture these complex relationships. This relationship is particularly evident in visual cortex and central sulcus. Significant coupling results in these regions should be interpreted carefully.

Age and sex differences in coupling

Human adolescent development is characterized by a decrease in gray matter volume and an increase in white matter volume (Huttenlocher and Dabholkar, 1997; Levitt, 2003; Matsuzawa et al., 2001). However, such remodeling has substantial local variation that occurs at multiple spatial scales. The results shown here and in our prior report (Vandekar et al., 2015) indicate that cortical remodeling occurs at a fine scale that is strongly related to cortical topology. Within-subject measurement of local cortical coupling allows us to evaluate such developmental effects in much greater detail. Coupling changes robustly during youth, and follows both linear and non-linear developmental patterns. Such age related differences in coupling are driven by cortical thinning that occurs more robustly in sulci, as well as in gyral cortex that shows nonlinear increases in CT. Our findings therefore emphasize that changes in gray matter development are topologically sensitive to SD and also that continued development of CT-SD coupling occurs in specific regions during youth, contributing to the well-established relationship between CT and SD observed in adults.

In addition to such developmental changes, we found evidence for sex differences in cortical coupling. Specifically, females had stronger negative coupling in the temporal and parietal lobes, which was driven by greater gyral CT in females. As substantial developmental strengthening in coupling occurs in these regions, sex differences suggest that coupling may advance more rapidly in females from an early age. Greater CT in females in parietal and posterior temporal lobes has been reported across various age ranges (Im et al., 2006; Luders et al., 2006; Sowell et al., 2007). The results reported here thus accord with prior literature, and also demonstrate that sex differences in CT are topologically related to SD, producing stronger coupling in females. These results further underline the utility of local cortical coupling as a useful subject-level measure for studies of individual differences and, potentially, developmental psychopathology.

Limitations

As noted above, nonlinear spatial relationships of CT and SD are not detected with this methodology. Instead coupling will take a positive or negative value based on the general direction of the relationship between the two variables. This has the advantage of being easily interpretable at the cost of missing complex nonlinear patterns that may be of interest.

Because coupling maps are slope estimates they represent the anatomical strength of the relationship, but do not capture the statistical strength or give any representation of how much noise is in the estimate of the slope. Two vertices with similar values of coupling can have different correlations. If the statistical strength of the relationship is of interest then WC-coupling maps can be analyzed instead.

Due to the computational burden of estimating geodesic distance across the folded pial surface, Euclidean distance on the inflated surface was used to estimate neighborhoods and weights in the regression. Using Euclidean distance on the inflated cortical sheet serves only as an approximation to the true anatomical distances measured across the surface. Because of this approximation the number of points used in each local regression is variable depending on the folding of the cortex at that location. Euclidean distances on the inflated surface are shorter than the geodesic distances in places where the cortex is highly folded, so estimates of coupling in these regions are likely smoother than in other regions that are less folded.

Future Directions

Examining the bivariate relationship of brain phenotypes through local cortical coupling may have several potentially fruitful applications moving forward. First, several studies have reported correlations of MRI derived measures, including folding and thickness, with cytoarchitecture (Fischl, 2013; Fischl et al., 2008; Wagstyl et al., 2015). These prior reports suggest coupling may be a valuable tool to combine measures to predict cytoarchitecture using MRI. Second, developmental and neuropsychiatric differences in thickness (Raznahan et al., 2011; Shaw et al., 2008; Sowell et al., 2007) and gyrification (Cachia et al., 2008; Csernansky et al., 2008; Klein et al., 2014; Shaw et al., 2012) suggest the promising potential of coupling to identify regions where these measures interact. For example, thickness differences that are spatially related to SD have been reported in development and neuropsychiatric disorders (Goghari et al., 2007; Selemon et al., 1998; Vandekar et al., 2015). Goghari et al. identified regions of sulcal cortex in the temporal lobe where patients with schizophrenia showed significant reductions in thickness compared to controls. Their findings suggest that coupling should be more negative in the temporal lobe in schizophrenia. Reductions in the CT of sulci in schizophrenia have been attributed to thinning of Layer 2, which is relatively thicker in sulci than gyri (Selemon et al., 1998; Wagstyl, 2015). Coupling may be a useful tool to easily identify regions where such complex relationships occur. Third and finally, spatial relationships with other cortical characteristics, such as underlying white matter (Vandekar et al., 2015), can also be investigated using the coupling approach. More generally, coupling is not restricted to surface based analyses and can be used to describe the relationship of volumetric images of different modalities.

Conclusions

We introduced a novel method for measurement of local cortical coupling, which captures the bivariate relationship between CT and SD. This measure is spatially heterogeneous, evolves conspicuously in youth, and is different between males and females. Coupling is not restricted to surface based analyses and can be used to describe the relationship of volumetric images of different modalities. Such measures can facilitate investigation of local individual differences in cortical topology, and may offer a valuable brain phenotype for identification of abnormal brain development related to neuropsychiatric illness.

Supplementary Material

1
2
3
4
5
6
7
8

Acknowledgments

Thanks for assistance with data processing (Madhura Ingalhalikar, Alex Smith, Nicholas DeLeo, and Ragini Verma); the PNC acquisition and recruitment team (Monica Calkins, Jeff Valdez, Ryan Hopson, Raphael Gerraty, Marisa Riley, Jack Keefe, Elliott Yodh, and Rosetta Chiavacci); data management (Chad Jackson); help with hypothesis testing in general additive models (Fabian Scheipl); advice on implementation of the general additive model (Aaron Alexander-Bloch and Phil Reiss). REG served on the Advisory Board Member for Otsuka Pharmaceuticals. Supported by RC2 grants from the National Institute of Mental Health MH089983 and MH089924. Support for developing statistical analyses (SNV, RTS, TDS) was provided by a seed grant by the Center for Biomedical Computing and Image Analysis (CBICA) at Penn. TDS was supported by K23MH098130 and R01MH107703; RTS was supported by R01NS085211; DRR was supported by K01MH10260; SNV was supported by T32MH065218-11. Additional support was provided by the Dowshen Program for Neuroscience.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

The authors declare no competing financial interests.

REFERENCES

  1. Alemán-Gómez Y, Janssen J, Schnack H, Balaban E, Pina-Camacho L, Alfaro-Almagro F, Castro-Fornieles J, Otero S, Baeza I, Moreno D, Bargalló N, Parellada M, Arango C, Desco M. The Human Cerebral Cortex Flattens during Adolescence. J. Neurosci. 2013;33:15004–15010. doi: 10.1523/JNEUROSCI.1459-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Avants BB, Cook PA, Ungar L, Gee JC, Grossman M. Dementia induces correlated reductions in white matter integrity and cortical thickness: A multivariate neuroimaging study with sparse canonical correlation analysis. NeuroImage. 2010;50:1004–1016. doi: 10.1016/j.neuroimage.2010.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Boos DD, Stefanski LA. Essential Statistical Inference, Springer Texts in Statistics. New York, NY, USA: Springer New York; 2013. Large Sample Results for Likelihood-Based Methods; pp. 275–293. [Google Scholar]
  4. Cachia A, Paillère-Martinot M-L, Galinowski A, Januel D, de Beaurepaire R, Bellivier F, Artiges E, Andoh J, Bartrés-Faz D, Duchesnay E, Rivière D, Plaze M, Mangin J-F, Martinot J-L. Cortical folding abnormalities in schizophrenia patients with resistant auditory hallucinations. NeuroImage. 2008;39:927–935. doi: 10.1016/j.neuroimage.2007.08.049. [DOI] [PubMed] [Google Scholar]
  5. Calkins ME, Merikangas KR, Moore TM, Burstein M, Behr MA, Satterthwaite TD, Ruparel K, Wolf DH, Roalf DR, Mentch FD, Qiu H, Chiavacci R, Connolly JJ, Sleiman PMA, Gur RC, Hakonarson H, Gur RE. The Philadelphia Neurodevelopmental Cohort: constructing a deep phenotyping collaborative. J. Child Psychol. Psychiatry. 2015:n/a–n/a. doi: 10.1111/jcpp.12416. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Csernansky JG, Gillespie SK, Dierker DL, Anticevic A, Wang L, Barch DM, Van Essen DC. Symmetric abnormalities in sulcal patterning in schizophrenia. NeuroImage. 2008;43:440–446. doi: 10.1016/j.neuroimage.2008.07.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
  8. Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
  9. Destrieux C, Fischl B, Dale A, Halgren E. Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. NeuroImage. 2010;53:1–15. doi: 10.1016/j.neuroimage.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fischl B. Estimating the Location of Brodmann Areas from Cortical Folding Patterns Using Histology and Ex Vivo MRI. In: Geyer S, Turner R, editors. Microstructural Parcellation of the Human Cerebral Cortex. Berlin Heidelberg: Springer; 2013. pp. 129–156. [Google Scholar]
  11. Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc. Natl. Acad. Sci. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fischl B, Rajendran N, Busa E, Augustinack J, Hinds O, Yeo BTT, Mohlberg H, Amunts K, Zilles K. Cortical Folding Patterns and Predicting Cytoarchitecture. Cereb. Cortex. 2008;18:1973–1980. doi: 10.1093/cercor/bhm225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis: II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
  14. Goghari VM, Rehm K, Carter CS, Macdonald AW. Sulcal thickness as a vulnerability indicator for schizophrenia. Br. J. Psychiatry. 2007;191:229–233. doi: 10.1192/bjp.bp.106.034595. [DOI] [PubMed] [Google Scholar]
  15. Huttenlocher PR, Dabholkar AS. Regional differences in synaptogenesis in human cerebral cortex. J. Comp. Neurol. 1997;387:167–178. doi: 10.1002/(sici)1096-9861(19971020)387:2<167::aid-cne1>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
  16. Im K, Lee J-M, Lee J, Shin Y-W, Kim IY, Kwon JS, Kim SI. Gender difference analysis of cortical thickness in healthy young adults with surfacebased methods. Neuroimage. 2006;31:31–38. doi: 10.1016/j.neuroimage.2005.11.042. [DOI] [PubMed] [Google Scholar]
  17. Insel TR. Rethinking schizophrenia. Nature. 2010;468:187–193. doi: 10.1038/nature09552. [DOI] [PubMed] [Google Scholar]
  18. Klein D, Rotarska-Jagiela A, Genc E, Sritharan S, Mohr H, Roux F, Han CE, Kaiser M, Singer W, Uhlhaas PJ. Adolescent Brain Maturation and Cortical Folding: Evidence for Reductions in Gyrification. PLoS ONE. 2014;9:e84914. doi: 10.1371/journal.pone.0084914. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Krain AL, Castellanos FX. Brain development and ADHD. Clin. Psychol. Rev., Attention Deficit Hyperactivity Disorder From A Neurosciences And Behavioral Approach. 2006;26:433–444. [Google Scholar]
  20. Levitt P. Structural and functional maturation of the developing primate brain. J. Pediatr., Mechanisms of Action of LCPUFA Effects on Infant Growth and Neurodevelopment. 2003;143:35–45. doi: 10.1067/s0022-3476(03)00400-1. [DOI] [PubMed] [Google Scholar]
  21. Luders E, Narr Kl, Thompson Pm, Rex De, Woods Rp, DeLuca H, Jancke L, Toga Aw. Gender effects on cortical thickness and the influence of scaling. Hum. Brain Mapp. 2006;27:314–324. doi: 10.1002/hbm.20187. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Mangin J-F, Riviere D, Cachia A, Duchesnay E, Cointepas Y, Papadopoulos-Orfanos D, Collins DL, Evans AC, Regis J. Object-Based Morphometry of the Cerebral Cortex. IEEE Trans. Med. Imaging. 2004;23:968–982. doi: 10.1109/TMI.2004.831204. [DOI] [PubMed] [Google Scholar]
  23. Matsuzawa J, Matsui M, Konishi T, Noguchi K, Gur RC, Bilker W, Miyawaki T. Age-related Volumetric Changes of Brain Gray and White Matter in Healthy Infants and Children. Cereb. Cortex. 2001;11:335–342. doi: 10.1093/cercor/11.4.335. [DOI] [PubMed] [Google Scholar]
  24. Ouyang X, Chen K, Yao L, Hu B, Wu X, Ye Q, Guo X. Simultaneous changes in gray matter volume and white matter fractional anisotropy in Alzheimer’s disease revealed by multimodal CCA and joint ICA. Neuroscience. 2015;301:553–562. doi: 10.1016/j.neuroscience.2015.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Rapoport JL, Giedd JN, Gogtay N. Neurodevelopmental model of schizophrenia: update 2012. Mol. Psychiatry. 2012;17:1228–1238. doi: 10.1038/mp.2012.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Raznahan A, Shaw P, Lalonde F, Stockman M, Wallace GL, Greenstein D, Clasen L, Gogtay N, Giedd JN. How Does Your Cortex Grow? J. Neurosci. 2011;31:7174–7177. doi: 10.1523/JNEUROSCI.0054-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. R Core Team. R Foundation for Statistical Computing. Vienna, Austria: 2012. R: A language and environment for statistical computing. [Google Scholar]
  28. Ronan L, Voets NL, Hough M, Mackay C, Roberts N, Suckling J, Bullmore E, James A, Fletcher PC. Consistency and interpretation of changes in millimeter-scale cortical intrinsic curvature across three independent datasets in schizophrenia. NeuroImage. 2012;63:611–621. doi: 10.1016/j.neuroimage.2012.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Satterthwaite TD, Connolly JJ, Ruparel K, Calkins ME, Jackson C, Elliott MA, Roalf DR, Ryan Hopsona KP, Behr M, Qiu H, Mentch FD, Chiavacci R, Sleiman PMA, Gur RC, Hakonarson H, Gur RE. The Philadelphia Neurodevelopmental Cohort: A publicly available resource for the study of normal and abnormal brain development in youth. NeuroImage. 2015 doi: 10.1016/j.neuroimage.2015.03.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Satterthwaite TD, Elliott MA, Ruparel K, Loughead J, Prabhakaran K, Calkins ME, Hopson R, Jackson C, Keefe J, Riley M, Mentch FD, Sleiman P, Verma R, Davatzikos C, Hakonarson H, Gur RC, Gur RE. Neuroimaging of the Philadelphia Neurodevelopmental Cohort. NeuroImage. 2014a;86:544–553. doi: 10.1016/j.neuroimage.2013.07.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Satterthwaite TD, Shinohara RT, Wolf DH, Hopson RD, Elliott MA, Vandekar SN, Ruparel K, Calkins ME, Roalf DR, Gennatas ED, et al. Impact of puberty on the evolution of cerebral perfusion during adolescence. Proc. Natl. Acad. Sci. 2014b:201400178. doi: 10.1073/pnas.1400178111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Scheipl F, Greven S, Küchenhoff H. Size and power of tests for a zero random effect variance or polynomial regression in additive and linear mixed models. Comput. Stat. Data Anal. 2008;52:3283–3299. [Google Scholar]
  33. Selemon LD, Rajkowska G, Goldman-Rakic PS. Elevated neuronal density in prefrontal area 46 in brains from schizophrenic patients: Application of a three-dimensional, stereologic counting method. J. Comp. Neurol. 1998;392:402–412. [PubMed] [Google Scholar]
  34. Shaw P, Kabani NJ, Lerch JP, Eckstrand K, Lenroot R, Gogtay N, Greenstein D, Clasen L, Evans A, Rapoport JL, Giedd JN, Wise SP. Neurodevelopmental trajectories of the human cerebral cortex. J. Neurosci. Off. J. Soc. Neurosci. 2008;28:3586–3594. doi: 10.1523/JNEUROSCI.5309-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Shaw P, Malek M, Watson B, Sharp W, Evans A, Greenstein D. Development of Cortical Surface Area and Gyrification in Attention-Deficit/Hyperactivity Disorder. Biol. Psychiatry, Oxytocin and Social Bonds in Development. 2012;72:191–197. doi: 10.1016/j.biopsych.2012.01.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sowell ER, Peterson BS, Kan E, Woods RP, Yoshii J, Bansal R, Xu D, Zhu H, Thompson PM, Toga AW. Sex Differences in Cortical Thickness Mapped in 176 Healthy Individuals between 7 and 87 Years of Age. Cereb. Cortex. 2007;17:1550–1560. doi: 10.1093/cercor/bhl066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Steen RG, Mull C, Mcclure R, Hamer RM, Lieberman JA. Brain volume in first-episode schizophrenia Systematic review and meta-analysis of magnetic resonance imaging studies. Br. J. Psychiatry. 2006;188:510–518. doi: 10.1192/bjp.188.6.510. [DOI] [PubMed] [Google Scholar]
  38. Toro R, Burnod Y. A Morphogenetic Model for the Development of Cortical Convolutions. Cereb. Cortex. 2005;15:1900–1913. doi: 10.1093/cercor/bhi068. [DOI] [PubMed] [Google Scholar]
  39. Vandekar SN, Shinohara RT, Raznahan A, Roalf DR, Ross M, DeLeo N, Ruparel K, Verma R, Wolf DH, Gur RC, Gur RE, Satterthwaite TD. Topologically Dissociable Patterns of Development of the Human Cerebral Cortex. J. Neurosci. 2015;35:599–609. doi: 10.1523/JNEUROSCI.3628-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385:313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
  41. von Economo C. In: The Cytoarchitectonics of the Human Cerebral Cortex. Parker S, translator. London: Oxford University Press; 1925. English translation, 1929. [Google Scholar]
  42. Wagstyl K. Non-uniform cortical thinning in schizophrenia: are sulci worse off?. Poster presented at: 21st Annual Meeting of the Organization for Human Brain Mapping; 2015 Jun 13–17; Honolulu, HI. 2015. [Google Scholar]
  43. Wagstyl K, Ronan L, Goodyer IM, Fletcher PC. Cortical thickness gradients in structural hierarchies. NeuroImage. 2015;111:241–250. doi: 10.1016/j.neuroimage.2015.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. White T, Andreasen NC, Nopoulos P, Magnotta V. Gyrification abnormalities in childhood- and adolescent-onset schizophrenia. Biol. Psychiatry. 2003;54:418–426. doi: 10.1016/s0006-3223(03)00065-9. [DOI] [PubMed] [Google Scholar]
  45. Wood SN. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011;73:3–36. [Google Scholar]
  46. Yun HJ, Im K, Jin-Ju Yang, Yoon U, Lee J-M. Automated Sulcal Depth Measurement on Cortical Surface Reflecting Geometrical Properties of Sulci. PLoS ONE. 2013;8:e55977. doi: 10.1371/journal.pone.0055977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Zilles K, Palomero-Gallagher N, Amunts K. Development of cortical folding during evolution and ontogeny. Trends Neurosci. 2013;36:275–284. doi: 10.1016/j.tins.2013.01.006. [DOI] [PubMed] [Google Scholar]
  48. Zilles K, Schleicher A, Langemann C, Amunts K, Morosan P, Palomero-Gallagher N, Schormann T, Mohlberg H, Bürgel U, Steinmetz H, Schlaug G, Roland PE. Quantitative analysis of sulci in the human cerebral cortex: Development, regional heterogeneity, gender difference, asymmetry, intersubject variability and cortical architecture. Hum. Brain Mapp. 1997;5:218–221. doi: 10.1002/(SICI)1097-0193(1997)5:4<218::AID-HBM2>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS776386-supplement-1.pdf (545.5KB, pdf)
2
NIHMS776386-supplement-2.pdf (1.1MB, pdf)
3
NIHMS776386-supplement-3.pdf (369.2KB, pdf)
4
NIHMS776386-supplement-4.pdf (586.9KB, pdf)
5
NIHMS776386-supplement-5.pdf (513.8KB, pdf)
6
NIHMS776386-supplement-6.pdf (536.2KB, pdf)
7
NIHMS776386-supplement-7.pdf (347.4KB, pdf)
8
NIHMS776386-supplement-8.docx (8.3MB, docx)

RESOURCES