On the Relationship between Cellular and Hemodynamic Properties of the Human Brain Cortex throughout Adult Lifespan

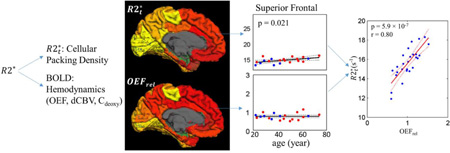
Abstract

Establishing baseline MRI biomarkers for normal brain aging is significant and valuable for separating normal changes in the brain structure and functioning from different neurological diseases. In this paper for the first time we have simultaneously measured a variety of tissue specific contributions defining R2* relaxation of the gradient recalled echo (GRE) MRI signal in human brains of healthy adults (ages 22 to 74 years) and related these measurements to tissue structural and functional properties. This was accomplished by separating tissue (${R2}_t^{*}$) and extravascular BOLD contributions to the total tissue specific GRE MRI signal decay (R2^*) using an advanced version of previously developed Gradient Echo Plural Contrast Imaging (GEPCI) approach and the acquisition and post-processing methods that allowed the minimization of artifacts related to macroscopic magnetic field inhomogeneities, and physiological fluctuations.

Our data (20 healthy subjects) show that in most cortical regions ${R2}_t^{*}$ increases with age while tissue hemodynamic parameters, i.e. relative oxygen extraction fraction (OEF_rel), deoxygenated cerebral blood volume (dCBV) and tissue concentration of deoxyhemoglobin (C_deoxy) remain practically constant. We also found the important correlations characterizing the relationships between brain structural and hemodynamic properties in different brain regions. Specifically, thicker cortical regions have lower ${R2}_t^{*}$ and these regions have lower OEF.

The comparison between GEPCI-derived tissue specific structural and functional metrics and literature information suggests that (a) regions in a brain characterized by higher ${R2}_t^{*}$ contain higher concentration of neurons with less developed cellular processes (dendrites, spines, etc.), (b) regions in a brain characterized by lower ${R2}_t^{*}$ represent regions with lower concentration of neurons but more developed cellular processes, (c) the age-related increases in the cortical ${R2}_t^{*}$ mostly reflect the age-related increases in the cellular packing density.

The baseline GEPCI-based biomarkers obtain herein could serve to help distinguishing age-related changes in brain cellular and hemodynamic properties from changes which occur due to the neurodegenerative diseases.

Graphical abstract

1. INTRODUCTION

Although it is well known that aging can cause functional cognitive impairments, the neurobiological effects of normal aging (i.e. changes in the cellular content and organizations, including the cerebral cortical thinning and atrophy) on functional and structural declines are still not well understood (1). A conventionally accepted idea dating back to 1950s is that the age-related cognitive functional decline is caused by the loss of neurons (2,3). However, quantitative studies with newly developed stereological methods suggest that neuron death is not sufficient to account for the age-related functional decline and the number of neurons in the neocortex remains largely the same over adult life (1). A more recent point of view is that relatively subtle alterations in the synaptic connectivity, dendritic spine density and neural plasticity (4–7) can be associated with age–related cognitive dysfunctions. Most of the cited studies related to neuronal structure were performed on non-human primates or other animals, or on post-mortem human tissues. To study neurodegenerative disorders, it is important to separate the normal aging effects from the underlying neurodegenerative pathologies. Hence it is essential to study the age-related cellular and functional alterations quantitatively in vivo and to establish a baseline for distinguishing normal aging from pathological effects.

Magnetic resonance imaging (MRI) is a well-established powerful non-invasive tool to study brain structure and function in vivo. For example, diffusion MRI can probe the tissue structure on a cellular scale and provide the information on the neural architecture and physiological changes (8), BOLD (Blood-Oxygen-Level-Dependent) MRI (9) provides information on brain functions (10–13) and high-field phase images allow in vivo visualization of the cortical substructures (14).

In this study, the MRI-based Gradient Echo Plural Contrast Imaging (GEPCI) technique (15–17) is utilized to establish quantitative in vivo biomarkers characterizing the evolution of tissue structural, cellular and functional properties throughout adult human lifespan. GEPCI is a post-processing method generating a multitude of quantitative and “weighted” images from a single acquisition of GRE signal with multiple gradient echoes. In this paper we mainly use GEPCI quantitative measurements of the transverse relaxation (R2*) of gradient echo MRI signal and GEPCI T1-weighted images. We also use a novel advanced approach (18) to separate the total R2* relaxation into tissue-specific (${R2}_t^{*}$) and BOLD-related contributions.

Previously we have published several studies to validate different aspects of the technique that we are using in the current paper. Specifically, we have developed a theoretical model of BOLD effect (19), validated it in phantom studies (20), conducted detailed measurements of blood magnetic susceptibility (21), validated our model in vivo using a rat model (22), provided analysis of systematic errors due to diffusion effects (23) and errors due to noise in the data (24). In the Appendix B of this paper, we provide additional analysis of errors specific to the method that is used in this paper.

Since the transverse relaxation of MRI signal is known to be affected by macroscopic field inhomogeneities (20), in this paper we use a newly-developed approach – voxel spread function method (25) – that allows minimizing the contribution of these adverse effects, thus providing measurements of tissue-specific R2^* -related relaxation properties. Further improvement in our measurements is achieved by utilizing another novel method (26) allowing the reduction of the artifacts resulting from physiological fluctuations and scanner instabilities. Both these advances improve the accuracy of our measurements.

Since ${R2}_t^{*}$ describes the part of the signal decay resulting from water molecule interactions with cellular and extracellular components of biological tissues, we hypothesize that in the normal brain it can serve as a biomarker of the cortical “cellular packing density” – a parameter mostly proportional to the number of neurons and glia cells in the unit tissue volume – and can potentially identify tissue alterations (see further comments in the Discussion section). BOLD effects (9,19,20) describe the relaxation due to the mesoscopic magnetic field inhomogeneities caused by the presence of a blood vessel network. Hence, separating BOLD effects from R2^* allows important information on tissue functional hemodynamic properties, such as, oxygen extraction fraction (OEF), deoxygenated cerebral blood volume (dCBV) and tissue concentration of deoxyhemoglobin (C_deoxy) (18).

In this paper, by comparing our results with the literature data we provide a support for the hypothesis that in a healthy adult brain the tissue-specific ${R2}_t^{*}$ can serve as a biomarker of the cortical cellular packing density. We also use this hypothesis to explain the relationships between ${R2}_t^{*}$ and the functional data, such as OEF and aerobic glycolysis. The baseline GEPCI-based biomarkers obtained herein could also serve to help distinguish age-related changes in brain cellular and hemodynamic properties from changes which occur due to neurodegenerative diseases, e.g. (27).

2. METHODS

2.1 Subjects

This study was approved by the Institutional Review Board of Washington University School of Medicine. Twenty participants aging from 22 to 74, including 7 male (ages: 22, 26, 29, 35, 37, 42, 65) and 13 female (ages: 23, 28, 33, 42, 45, 46, 50, 52, 56, 57, 61, 61, 74), were recruited in this study. None of the participants had any history of neurological diseases. All participants provided informed consent.

2.2 Data Acquisition

All subjects were scanned in a 3T Trio MRI scanner (Siemens, Erlangen, Germany). A 3D multi gradient echo sequence was used to obtain the data. Sequence parameters were: resolution 1×1×2 mm³ (read, phase, slab), FOV 256 mm×192 mm, repetition time TR = 50ms, flip angle 30°, 10 gradient echoes with first gradient echo time TE₁ = 4 ms, echo spacing ΔTE = 4ms. Additional phase stabilization echo (the navigator data) was collected for each line in k-space to correct for image artifacts due to the physiological fluctuations (26). The total acquisition time of GEPCI is 11 mins 30s. Field inhomogeneity effects were removed by using the voxel spread function (VSF) approach (25). Standard clinical Magnetization-Prepared Rapid Gradient Echo (MPRAGE) (28) images with TR/TI/TE = 2200/1100/3.37 ms and the resolution 0.9×0.9×1.5 mm³ were also collected for segmentation purposes. The total acquisition time of MPRAGE is 6 mins. After the data acquisition, the raw k-space data were read into MATLAB (The MathWorks, Inc.) for the post-processing.

2.3 Data Analysis and Image Generation

The image processing was finished in MATLAB (The MathWorks, Inc.) using previously developed algorithm (18). In brief, after correcting the k-space data for physiological artifacts (26), we apply FFT in the phase-encoding directions to get images. 3D spatial Hanning filter is then applied to the data in the image domain. To achieve an optimal signal-to-noise ratio, we use the following equation to combine the data of all channels (29):

$$S_n(TE)=\sum _{ch=1}^M{\lambda }_{ch}·{\overline{S}}_n^{ch}(T{E}_1)·S_n^{ch}(TE);\hspace{1em}{\lambda }_{ch}=\frac{1}{M·{\epsilon }_{ch}^2}\sum _{ch\prime =1}^M{\epsilon }_{ch\prime }^2$$ [1]

where the sum is taken over all M channels (ch), S̄ denotes complex conjugate of S, λ_ch are weighting parameters and ε_ch are noise amplitudes (r.m.s.). Index n corresponds to the voxel position (n=x,y,z). This algorithm allows for the optimal estimation of quantitative parameters, and also removes the initial phase incoherence among the channels (29,30).

The data are then analyzed on a voxel-by-voxel basis using the theoretical model (20):

$$S(TE)=A_0·\text{exp}[-R{2}_t^{*}·(TE-T{E}_1)+i·2\pi ·\mathrm{\Delta }f·(TE-T{E}_1)]·F_{\mathit{\text{BOLD}}}(TE)·F(TE)$$ [2]

where TE is the gradient echo time, $R{2}_t^{*}=1/T{2}_t^{*}$ is the tissue transverse relaxation rate constant (describing GRE signal decay in the absence of BOLD effect), Δf is the frequency shift (dependent on tissue structure and also macroscopic magnetic field created mostly by tissue/air interfaces), function F_BOLD(TE) describes GRE signal decay due to the presence of blood vessel network with deoxygenated blood (veins and the part of capillaries adjacent to veins), and function F(TE) describes the effects of macroscopic magnetic field inhomogeneities. In this paper we use voxel spread function (VSF) method (25) for calculating F(TE).

For the BOLD model we use a recently proposed expression (18):

$$F_{\mathit{\text{BOLD}}}(TE)=1-\frac{\zeta }{1-\zeta }·f_s(\delta \omega ·TE)+\frac{1}{1-\zeta }·f_s(\zeta ·\delta \omega ·TE)$$ [3]

that better accounts for the presence of large vessels in the voxel than traditional exponential function (19). In Eq.[4], ζ is the deoxygenated cerebral blood volume fraction (dCBV) and δω is the characteristic frequency determined by the susceptibility difference between deoxygenated blood and surrounding tissue(19):

$$\delta \omega =\frac{4}{3}\pi ·\gamma ·B_0·Hct·\mathrm{\Delta }{\chi }_0·(1-Y)$$ [4]

In this equation, Δχ_o = 0.27 ppm (21) is the susceptibility difference between fully oxygenated and fully deoxygenated blood, Y is the blood oxygenation level (with Y = 0 being fully deoxygenated), Hct is the blood hematocrit, and γ is the gyromagnetic ratio. Function f_s describes the signal decay due to the presence of the blood vessel network which was defined in (19). Herein we use a mathematical expression for the function f_s in terms of a generalized hypergeometric function ${}_1{F}_2$ (31):

$$f_s(\delta \omega ·TE){}_1{F}_2\left(\right[-\frac{1}{2}];[\frac{3}{4},\frac{5}{4}];-\frac{9}{10}{(\delta \omega ·TE)}^2)-1$$ [5]

By fitting equation [2] to the real and imaginary parts of the complex signal using nonlinear regression algorithm, we are able to find the five parameters: S₀, ${R2}_t^{*}$, Δf, ζ and δω for each voxel in the brain. Details of the fitting routine are described in great detail in (18). Based on the fitting results we can calculate BOLD-related R2′ :

$$R2\prime =\zeta ·\delta \omega$$ [6]

Oxygen Extraction Fraction (OEF)

$$OEF=1-Y=\delta \omega ·{(\frac{4}{3}\pi ·\gamma ·B_0·Hct·\mathrm{\Delta }{\chi }_0)}^{-1}$$ [7]

and the concentration of deoxyhemoglobin per unit tissue volume (32):

$$C_{\mathit{\text{deoxy}}}=\frac{3}{4}·\frac{\zeta ·\delta \omega ·n_{Hb}}{\gamma ·\pi ·\mathrm{\Delta }{\chi }_0·B_0}=\frac{3·n_{Hb}}{4·\gamma ·\pi ·\mathrm{\Delta }{\chi }_0·B_0}·R2\prime$$ [8]

where n_Hb is the total intracellular Hb concentration equal to 5.5×10⁻⁶mol / mL (32). Since Hct was not measured in our experiments, we will only report relative regional OEF (OEF_rel) values

$${OEF}_{\mathit{\text{rel}}}=\delta \omega /\delta {\omega }_{\mathit{\text{mean}}}$$ [9]

Note that conventionally, in a GRE experiment the total R2^* relaxation rate constant is considered to be a sum of two components – R2 relaxation rate constant representing the part of MR signal decay that cannot be reversed by a refocusing 180° RF pulse, and R2′ relaxation rate constant representing the part of the signal decay that can be reversed by a refocusing 180° RF pulse (usually attributed to BOLD effect in a static dephasing regime (19)) : R2^* = R2 + R2′. However, such a consideration would only be valid for a single compartment model. For a multi-compartment tissue, the part of R2^* remaining after the subtraction of BOLD effect can still have contributions from magnetic susceptibility effects resulting from the presence of different cell-building components. Hence, in our model, Eq. [2], we call it ${R2}_t^{*}$.

In this paper we also estimate the standard R2* values by fitting the following equation to the experimental data:

$$S(TE)=A_0·\text{exp}(-R{2}^{*}·TE+i·2\pi ·\mathrm{\Delta }f·TE)·F(TE)$$ [10]

2.4 Image segmentation

MPRAGE images were input into FreeSurfer (Laboratory for Computational Neuroimaging, Martinos Center for Biomedical Imaging) (33) to generate brain segmentations, calculate surfaces and cortical thickness. 26 cortical regions of interest (ROI), were chosen to represent frontal, temporal, parietal and occipital lobes. The thalamus, caudate, putamen, pallidum, hippocampus and amygdala were chosen to study the subcortical regions. MPRAGE images were registered to GEPCI-T1-weighted images using FMRIB’s Linear Image Registration Tool (34,35) in FSL and the transformation matrices of the registration were generated. Finally, these matrices were applied to the brain segmentations from FreeSurfer and transformed them to the space of GEPCI-T1-weighted images. Since GEPCI –T1-weighted images are naturally co-registered with all GEPCI maps (R2^*, ${R2}_t^{*}$, OEF_rel, C_deoxy, and dCBV), the segmentations were also naturally registered to all these maps. Cortical thicknesses in the cortical ROIs except cerebellar cortex generated by the FreeSurfer were also used for data analysis.

Even though the data were collected with rather high in-plane resolution – 1×1 mm², they are still susceptible to the partial volume effect. To minimize it we apply a CSF mask to further remove CSF signals from FreeSurfer segmentations, and we use the statistical measurement instead of voxel-wise analysis - for each of the FreeSurfer ROIs which usually contains thousands of voxels, we generated a single parameter – the median value of the corresponding measurement distribution (the median value is less sensitive to outliers that are related to partial volume effect). This procedure also minimizes the errors in the model parameters estimates discussed in the Appendix B.

2.5 Statistical analysis

The statistical analysis and correlations were established using the LinearModel class in MATLAB (The MathWorks, Inc.). All GEPCI parameters in each ROI were characterized by their median values and correlated with age across 20 subjects using the following equation:

$$\mathit{\text{parameter}}=a+k·(\mathit{\text{age}}-40)$$ [11]

Age 40 years was selected as the adult reference age for convenience. The cortical thicknesses were correlated with ages using the same equation. The p-values were calculated to evaluate each correlation and conventionally p < 0.05 is considered as a significant correlation. Multiple comparison analysis was not applied here because we only report individual correlations instead of comparing them across different ROIs.

3. RESULTS

3.1 Age-related changes in the cerebral cortex

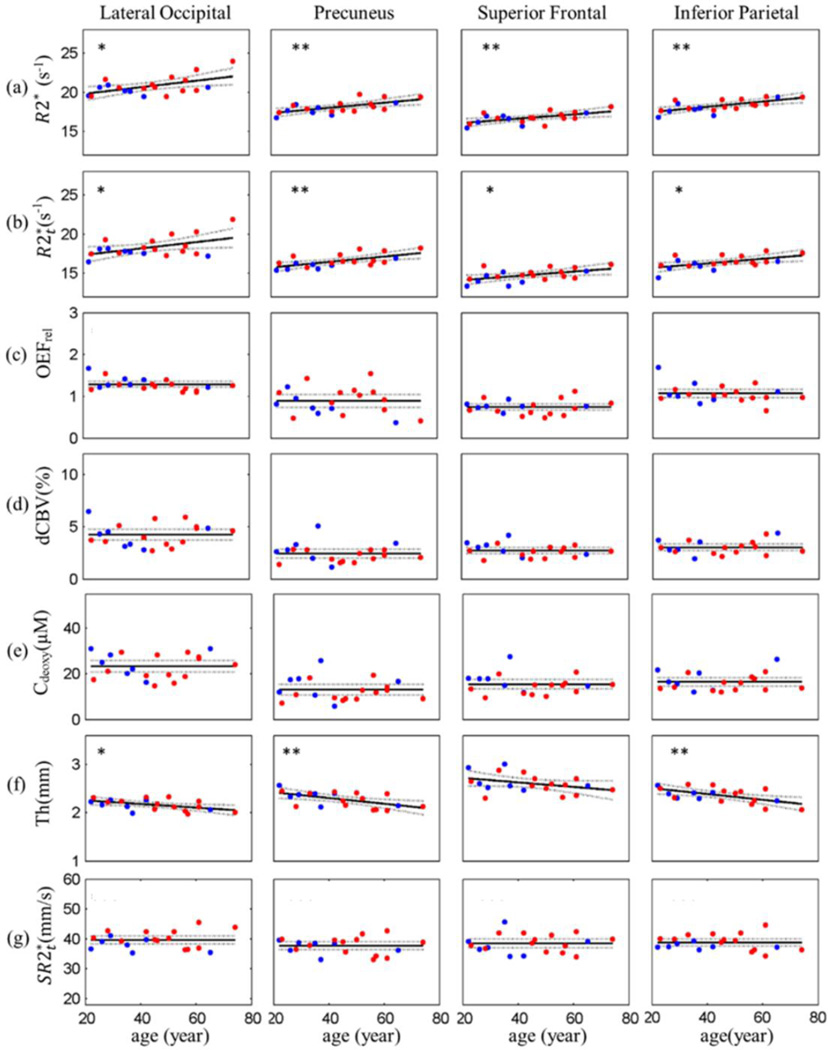
Our data (Figures 1 and 2, Tables A.1 and A.2) show that in most cortical regions R2^* and ${R2}_t^{*}$ increase with age, OEF_rel, dCBV and C_deoxy remain constant while cortical thickness, Th, decreases. In addition to parameters listed above, we have also introduced a parameter ${SR2}_t^{*}$ that represents an integrated characteristic of the ${R2}_t^{*}$ under a unit square of the cortex and is computed as a product of the median ${R2}_t^{*}$ and Th for each FreeSurfer region: ${SR2}_t^{*}={R2}_t^{*}·Th=$. The detailed role of this parameter will be addressed in the Discussion section.

Figure 1.

Age-related changes of parameters in selected cortical ROIs. Examples of the scatter plots of (a) R2^*, (b) ${R2}_t^{*}$, (c) OEF_rel (expressed as local-to-global ratios, see Methods), (d) dCBV, (e) C_deoxy, (f) cortical thickness (Th) and (g) ${SR2}_t^{*}$ versus age are shown across 4 selected cortical ROIs. Each plot represents the data from a single cortical region and each point in the plot represents a single subject. Male subjects are represented by blue points and female subjects by red points. For R2^*, ${R2}_t^{*}$ and cortical thickness, the solid lines are the regression curves and the p values evaluate the significance of the linear model. ${SR2}_t^{*}$, OEF_rel, dCBV and C_deoxy show no significant change with age and are represented by a constant model (the solid lines). The dashed lines in all plots represent the 95% confidence intervals. Number of stars (*) show significance level: p < 0.01 (**), p < 0.05 (*). The results of regression analysis from all other regions are listed in Table A.1 and Table A.2.

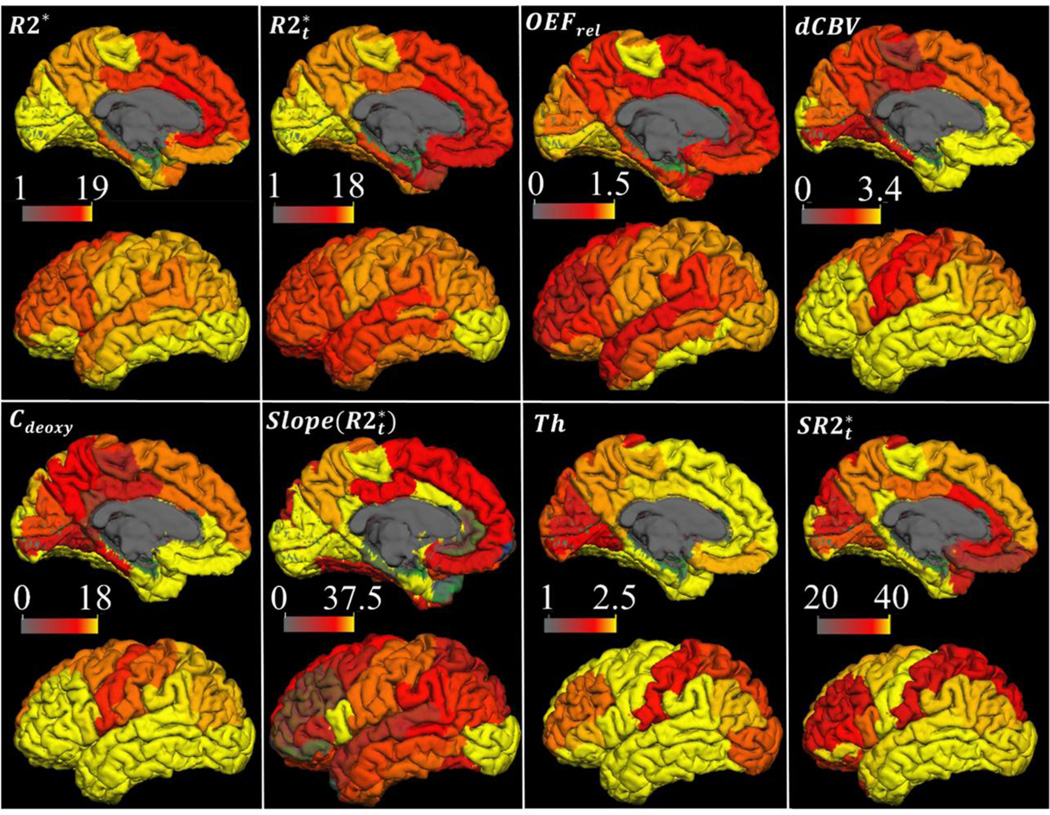
Figure 2.

Structural and hemodynamic parameters mapped on the cortical surface. The distributions of all GEPCI-derived parameters are presented on the lateral and medial cortical surfaces of the left hemisphere, including R2^* (s⁻¹), ${R2}_t^{*}(S^{-1})$, OEF_rel, dCBV(%), C_deoxy (µM), cortical thickness (Th) (mm), ${SR2}_t^{*}$ (mm/s), and the regression slope of ${R2}_t^{*}$ vs. age (s⁻¹/year). Images for R2^*, ${R2}_t^{*}$, and Th represent the regional mean values corresponding to an average 40-year old subject (parameter a in Eq. [11] and in Table A.1). Images for ${SR2}_t^{*}$, OEF_rel, dCBV and C_deoxy are the regional mean values averaged across all subjects (Table A.1). The surface of the cortex was generated by the FreeSurfer at the depth of 0.5 (the voxels in the center of gray matter were sampled). White matter, deep grey matter and ventricles were excluded.

Figure 1a shows that R2^* statistically significantly increased (p < 0.05) with age in all shown cortical ROIs. All other regions (see summary in Table A.1) also demonstrated increased R2^* with age though with different rates (slopes in Table A.1), e.g. rostral-anterior frontal and rostral middle frontal have the smallest slopes. ${R2}_t^{*}$ also significantly increased (p < 0.05) with age in the selected ROIs (Fig. 1b) and in most cortical regions in Table A.1 but with higher p values compared to R2^*. The regions with non-significant increases in R2^* with age showed even smaller changes in ${R2}_t^{*}$ with age. For instance, rostral middle frontal and rostral anterior frontal ${R2}_t^{*}$ did not significantly change with age, with p values of 0.42 and 0.76, respectively. In addition, a few regions with significant increases in R2^* with age showed non-significant but apparent increasing tendencies of ${R2}_t^{*}$ with age. For example, although ${R2}_t^{*}$ of the insula did not correlate significantly with age (p = 0.14), an increasing trend was seen.

Figure 1c shows that the relative OEF (OEF_rel) expressed as a local-to-global ratio, Eq. [9], showed no significant trend with age – the p values of the linear model were not significant (p > 0.05) in all cortical regions except the rostral-middle frontal (p= 0.013) and the lateral occipital (p= 0.026). To describe this data we use a constant model in all cortical regions. The mean values of OEF_rel are shown in Fig. 1 as solid lines with the 95% confidence intervals shown as dashed lines. These results indicate that OEF_rel remains relatively constant over adult lifespan. The mean values of OEF_rel ranged from 0.6 to 1.5 across the selected 26 ROIs with the regions in occipital lobe, such as cuneus, lingual and lateral occipital, having comparatively higher OEF_rel (Table A.2).

Results for dCBV (Fig. 1d and Table A.2) and C_deoxy (Fig. 1e and Table A.2) showed similar properties (no statistically significant dependence on age) as OEF_rel and were described with a constant model.

Cortical thickness significantly decreased (p<0.05) with age in most cortical regions (Fig. 1f, Table A.1). However, caudal anterior cingulate (p = 0.62), cuneus (p = 0.11), parsorbitalis (p = 0.23), isthmus of cingulate (p = 0.35), paracentral (p = 0.07), rostral anterior cingulate (p = 0.21), rostral middle frontal (p = 0.17), superior frontal (p = 0.11) and superior parietal (p = 0.09) cortex each showed less significant thinning with age. But trends toward decreasing thickness can be observed in some areas, such as, paracentral lobule, superior frontal and superior parietal cortex. Furthermore, the slopes, that show age-related differences in cortical thickness (mm/year), varied across different areas. These results indicated that age-related thinning varied in different regions of the brain.

Results for the integrated parameter ${SR2}_t^{*}$ were analyzed using the same procedure as OEF_rel and showed no significant linear relationships with age. They were presented using a constant model demonstrating no statistically significant changes over the studied human lifespans for each ROI except caudal anterior cingulate (Fig. 1g). The mean and standard deviation of the constant model can be found in Table A.2.

3.2 The distributions of parameters on the brain surfaces

The summary of the distributions of all the GEPCI-derived parameters is presented on the lateral and medial cortical surfaces of the left hemisphere in Fig. 2. The ventricles, white matter and deep gray matter are excluded. R2^* and ${R2}_t^{*}$ have a similar distributed network. Frontal lobe, inferior parietal, precuneus and posterior cingulate have relatively lower values than paracentral lobule, lateral occipital, cuneus and lingual. This distribution feature is consistent with the previously reported T2* mapping from 7 T resulting from the averaging of 14 subjects (36).

3.3 Correlations between structural and hemodynamic cortical tissue properties

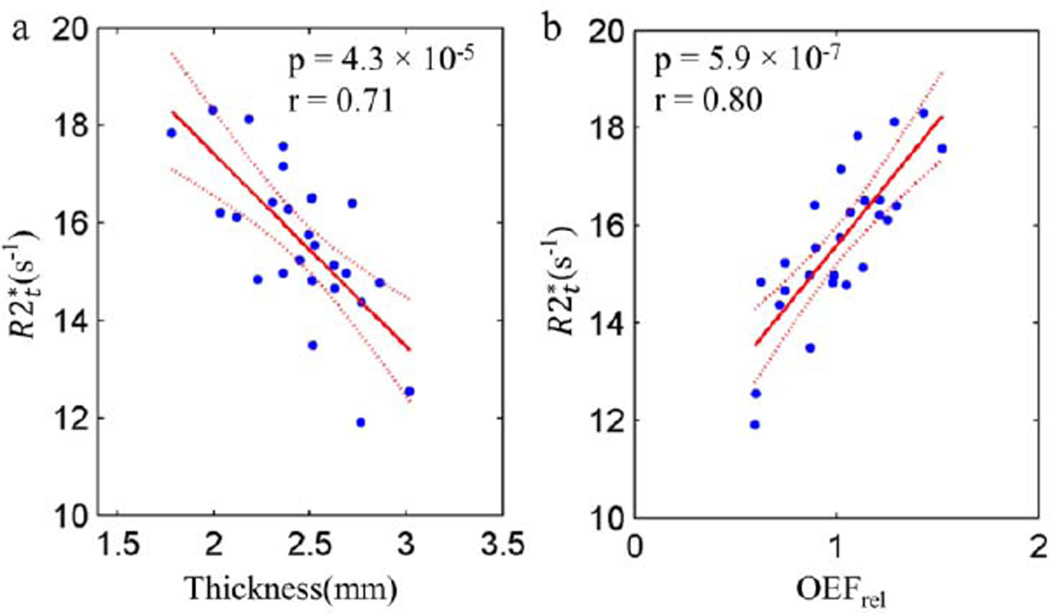
${R2}_t^{*}$ correlates negatively with the cortical thickness across 26 cortical ROIs (p < 0.05 and r = 0.71, Figure 3a). This correlation indicates that the thinner cortex has a relatively higher ${R2}_t^{*}$. Furthermore, ${R2}_t^{*}$ positively correlates with OEF_rel across 26 cortical ROIs (p < 0.05 and r = 0.8, Figure 3b). The regions extracting more oxygen also have higher ${R2}_t^{*}$. Implications of all these correlations will be discussed in detail in the Discussion section.

Figure 3.

The linear regression analysis of (a) ${R2}_t^{*}$ versus cortical thickness; (b) ${R2}_t^{*}$ versus OEF_rel; Each point represents one of the 26 FreeSurfer ROIs. The regional values of ${R2}_t^{*}$ and thickness correspond to the data evaluated at the age of 40 (parameter a in Eq. [11]). Since OEF_rel remains constant with age in the cortical regions, the values of OEF_rel are just the mean values across the subjects in the corresponding regions. All the coefficients from the linear regressions are listed in Table A.3 in the Appendix A.

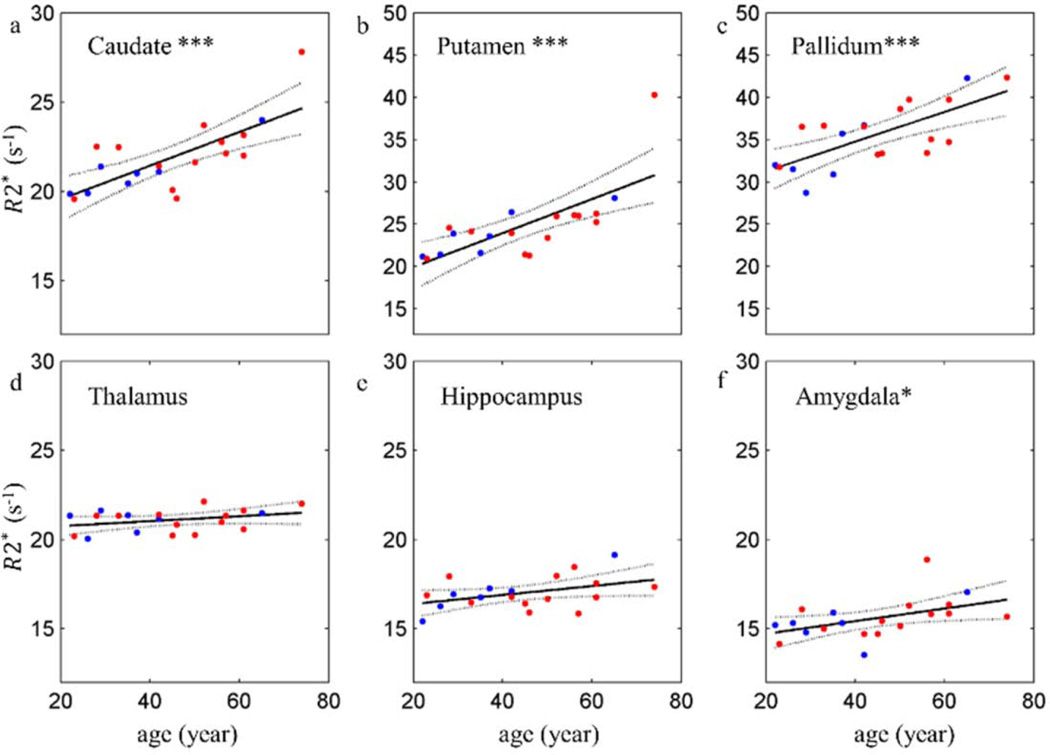
3.4 Age-related changes of R2* in subcortical regions

R2^* has statistically significant increases with age in basal ganglia (caudate, putamen and pallidum). Amygdala also shows significant increase of R2^* with age. Thalamus and hippocampus show less significant age-related changes.

3.5 Age-related changes of the R2* in cerebellar cortex

None of these parameters shows significant (p < 0.05) linear correlation with age in cerebellar cortex. OEF_rel, dCBV and C_deoxy are consistent with the tendencies in other cortical regions. However, R2^* and ${R2}_t^{*}$ showed no significant linear relationships with age which is reflected by non-significant p values of the linear model. The significant p values of the constant model for all the parameters indicated that all the measurements remain constant with age in the cerebellar cortex. Though, since the cerebellar cortex is very thin (< 1mm), this data may be affected by partial volume effect due to the resolution of the images.

4. DISCUSSION

In this paper for the first time we report the measurements of a variety of tissue specific contributions defining R2* relaxation of GRE MRI signal in adult human brain. This was accomplished by separating tissue (${R2}_t^{*}$) and extravascular BOLD contributions to the GRE MRI signal decay using our previously developed approach (18,20) and the acquisition and post-processing methods that allowed the minimization of artifacts related to macroscopic magnetic field inhomogeneities (25), and physiological fluctuations (26). Our major experimental findings can be summarized as follows:

1. We found that R2^* significantly increases with age in most cortical regions and this increase is mostly caused by the increase in ${R2}_t^{*}$ (Fig. 1b) since hemodynamic characteristics (OEF_rel and dCBV) do not change with age (Fig. 1e).

2. Our data show that while the cortex becomes thinner with normal aging (in agreement with previous reports (37,38)), the integrated ${R2}_t^{*}$, i.e. the product of ${R2}_t^{*}$ and cortical thickness (${SR2}_t^{*}={R2}_t^{*}·Th$), remains constant with age in most cortical regions – Fig. 1g.

3. We found that in the brain cortex ${R2}_t^{*}$ negatively correlates with the cortical thickness across 26 FreeSurfer regions – Fig. 3a.

4. We found that in the brain cortex ${R2}_t^{*}$ positively correlates with OEF_rel across 26 FreeSurfer regions – Fig. 3b.

5. The key questions are: why ${R2}_t^{*}$ increases with age in the cortex and what features of the brain cellular structure cause this increase and variability between different brain structures? Main contributions to ${R2}_t^{*}$ signal decay in different brain structures come from the water molecules interactions with cell structural proteins, lipids and iron (39–41). In the subcortical GM (i.e. the caudate, putamen and pallidum) a significant increase in R2^* with age that we observed (Fig. 4), is consistent with previous studies (41–46) and is usually attributed to the known iron deposition in those regions with the increasing age. However, iron is unlikely a contributor to the age-related increase of the cortical ${R2}_t^{*}$ because, according to Hallgren and Sourander (47), the iron content in the cortex remains nearly constant after the age of 30. The major contributions to the increased cortical ${R2}_t^{*}$ and its variability are likely to be attributed to the water molecule interactions with other cellular structural components such as lipids and proteins.

6. Another source of the variation in R2* potentially could be an anisotropic effect reported by Rudko et al (48). However, even at 9.4T field strength, R2* showed only 0.94 ± 0.32 s⁻¹ variation in GM of mice, which is a much smaller effect than the variation across different brain regions that we found in a human brain at 3T.

Figure 4.

The scatter plots and linear regressions of R2^* versus age in subcortical ROIs. Each plot represents the data from a single subcortical region and each point in the plot represents the median value in the region from a single subject. Male subjects are represented by blue points and female subjects by red points. The solid lines are the regression curves and the dashed lines are the 95% confidence intervals. All the coefficients from the linear regressions are listed in Table A.4 in the Appendix A. p < 0.001 ***, p < 0.01 **, p < 0.05 *.

The hypothesis that the changes of MR signal relaxation properties are related to the changes in the concentration of lipids and proteins has been useful in studying Central Nervous System (CNS) diseases, such as Multiple Sclerosis (e.g. (17,49)) where cellular damage is mostly attributed to the loss of myelin. However, this hypothesis might not be adequate to describe normal aging effects of a healthy tissue where MR signal relaxation properties are related not only to the concentration of the cellular structural components but also to their cellular structural arrangements (50). For example, lipids distributed as multiple small droplets would have much bigger water-accessible surface, hence cause substantially stronger relaxation effects than a single large lipid droplet with the same total amount of lipids.

Herein by comparing our results with the literature data we provide support for a hypothesis that in a healthy adult brain the tissue-specific ${R2}_t^{*}$ can serve as a biomarker of the cortical “cellular packing density” – a parameter mostly proportional to the number of neurons and glial cells in the unit tissue volume. We also use this hypothesis to explain the relationships between ${R2}_t^{*}$ and the functional data, such as OEF and aerobic glycolysis.

4.1 Cortical Cellular Packing Density correlates with ${R2}_t^{*}$ over adult lifespan

Our hypothesis is supported by the available literature data on the cellular changes in the aging brain. It was a common impression that the neuron loss (2,3) is an inevitable process of aging that leads to the cortical thinning and cognitive dysfunction. However, many studies have reported that the number of neurons in the human cortex remains the same over adult life (1,7,51–56) and that normal aging is accompanied by changes in the dendritic structures, spine density and synapse density. Significant reduction in dendritic arbors of pyramidal neurons located in prefrontal, superior temporal and precentral cortices and changes in dendritic spine size, shape and density across the neocortex in humans and animals were discussed by Dickstein (5). Hof and Morrison (6) argued that while neuron death predominates in Alzheimer’s disease, age-related cognitive impairment is probably mediated by changes in the synaptic communication rather than by neuron death. Fjell et al. (4) also argued that regions with a high degree of life-long plasticity are more affected by normal aging effects. Moreover, several hypotheses that do not include the loss of neurons have been proposed to explain the cortical thinning with the increasing age, including the shrinkage of the neuronal size and the reduction/loss of presynaptic terminals, dendritic complexity and neuropil (56). In addition to neurons, the number of other CNS cells such as glial cells did not show significant differences between elderly individuals with a mean age of 89 years and young individuals with a mean age of 26 years (55). Furthermore, the glia/neuron ratios of 1.32 for female and 1.49 for males showed no statistically significant correlation with age over adult life (57). Thus, the published studies indicate that the total number of neurons and glial cells in the cortex remains relatively constant over normal adult life.

The unchanged number of cells and the decreasing cortical volume imply the increasing cell density with age in the cortex, which is also supported by the results of Haug and Eggers (51,58) who concluded that the neuronal density significantly increases with age in Brodmann areas 6 and 11 in the frontal lobe and area 17 in the occipital lobe, with area 7 in parietal lobe and area 20 in inferior temporal gyrus showing non-significant but similar tendencies. Freeman et al (56) also found that frontal and temporal cortical neuronal density showed a small increase with increasing age.

This increasing age-related cortical cellular packing density within shrinking space in the cortex (due to shrinkage of the neuronal size and the reduction/loss of presynaptic terminals, dendritic complexity and neuropil (56)) is consistent with our interpretation of increased ${R2}_t^{*}$ reported herein as a biomarker of cellular packing density. In this context, the product of ${R2}_t^{*}$ and cortical thickness (${SR2}_t^{*}$) represents the cellular packing content underneath a unit surface (e.g., 1 square millimeter surface) of the cortex. Our finding that this product remains constant with age for all cortical regions (Fig. 1g, Table A.1), is in agreement with the published data discussed above indicating the preservation of cortical cellular content in healthy adults over their lifespan.

If both the number of neurons and the relative fraction of glial cells to neurons stay the same over age, the density of both neurons and glial cells would go up proportionally. Since axons and dendrites contain considerably larger concentration of macromolecules (i.e. lipids and proteins), their contribution to the ${R2}_t^{*}$ relaxation is expected to be prevailing compared to glial cells even though concentration of glia cells in the cortex is higher. Hence, we hypothesize that the increase of ${R2}_t^{*}$ is mainly due to the increased neuronal density.

4.2 Neuronal Packing Density correlates with ${R2}_t^{*}$ within individual human brains

Our data can also be compared with the direct measurements by Collins et al. (60) who provided detailed results on neuronal density in non-human primates. They found higher neuronal densities in primary visual cortex (V1), early extrastriate visual areas, primary auditory cortex (A1), primary somatosensory areas (S1) and middle temporal (MT), while lower neuronal densities in prefrontal cortex, premotor cortex, superior temporal sulcus, inferior parietal lobule and superior parietal lobule. In particular, Collins et al. reported the highest neuronal density in V1, the second highest in association visual areas and relatively higher density in S1 among all of the examined primates. Lowest neuronal densities were found in prefrontal cortex, premotor cortex or cortex ventral to S1 and motor cortex (M1) in different primates. Those distributions of neuronal density are in a very good qualitative correlation with the distributions of ${R2}_t^{*}$ found in our study. Indeed, in this study, the highest ${R2}_t^{*}$ were found in the visual cortex (cuneus, lateral occipital and lingual) and the lowest were found in the frontal areas (Fig.2 and Table A.1). Relatively higher ${R2}_t^{*}$ were also shown in S1 and M1 (paracentral, precentral and postcentral) and ${R2}_t^{*}$ values in these two regions were similar. Relatively lower ${R2}_t^{*}$ were found in regions close to S1 and M1. All in all, these data further support our hypothesis that ${R2}_t^{*}$ is related to neuronal density and can be considered as a biomarker of cellular packing density- the reported areas with lower neuronal density are the major areas with lower ${R2}_t^{*}$ and vice versa.

Elston et al. (61) found that cells in the prefrontal cortex of humans are more branched and more spinous than those in the temporal and occipital lobes. Comparing these results with the measurements of neuronal density by Collins et al. (60) we can conclude that regions with relatively lower neuronal density have more complex dendritic arbors, larger somas and dendritic field sizes and more spines than regions with higher neuronal density. This is in agreement with the line of consideration by Glasser and Van Essen (62) who utilized T1- and T2-weighted MRI to evaluate a distribution of the myelin content in the cortex. Hence, comparing the ${R2}_t^{*}$ maps with these literature data (60,61), we can further suggest that the areas with lower ${R2}_t^{*}$ represent regions with complex dendritic arbors, larger somas and dendritic field sizes and more spines than regions with higher ${R2}_t^{*}$.

4.3 Brain tissue hemodynamic properties

Besides ${R2}_t^{*}$, the relative OEF, dCBV and C_deoxy are also derived from our data and they are in agreement with previous literature results. The distribution of the relative OEF in Fig. 1 shows the uniformity across frontal area and precuneus but higher values in the visual cortex (cuneus and lingual) which is consistent with the findings of default mode network (63). The relative OEF shows no significant change with age (Fig. 2c), which is consistent with previous studies. Leenders et al. reported that oxygen extraction fraction (OER) didn’t change or showed a slight increase with age in the selected regions (64). Pantano et al. showed that OEF had no statistically significant changes with age, although a small upward trend was present (65). Yamaguchi et al. also demonstrated that OEF didn’t show any correlation with age (66). Our data on dCBV shows no significant change with age which is consistent with previous findings of no significant changes in the cerebral blood volume (which is a measure of both, dCBV and arterial blood volume) with age (64,66).

Our ${R2}_t^{*}$ map outlines practically the same structural features of the brain as the map of aerobic glycolysis (67) with areas of low ${R2}_t^{*}$ (complex dendritic and synaptic structure) corresponding to areas of high aerobic glycolysis and areas of high ${R2}_t^{*}$ corresponding to areas of low aerobic glycolysis. This fits well with our biophysical hypothesis of ${R2}_t^{*}$ reflecting cellular packing density. Indeed, the areas of complex dendritic and synaptic structures characterized by lower ${R2}_t^{*}$ are likely to require high aerobic glycolysis needed to support high synaptic activities (68). Moreover, since the correlation in brain regions between aerobic glycolysis and CBF is stronger than that between aerobic glycolysis and CMRO₂ (68), areas of high aerobic glycolytic activity may show relatively lower OEF. Hence, it is not surprising that we found a very strong correlation between ${R2}_t^{*}$ and OEF (p < 0.001, r = 0.71 in Figure 2b). It is also important to note that the regions with lower ${R2}_t^{*}$ are mostly located within the default mode network (63).

Although OEF and ${R2}_t^{*}$ are derived from the same data they are described by substantially different contributions in the model Eq. [2] and represent different properties of the system. Computer Monte-Carlo simulations (23) demonstrated that bias in the estimation of ${R2}_t^{*}$ due to using static dephasing regime model (19) does not exceed 0.3 s⁻¹ and biases in OEF and dCBV are smaller than 10%. Hence, the observed correlation is not due to the biases in the fitting routine. Besides, the results are consistent with the above listed literature data.

5. SUMMARY

Distinguishing the cognitive changes of normal aging from the initial stages of neurodegenerative disorders, such as Alzheimer’s disease, can be difficult. Hence, establishing baseline MRI biomarkers for normal aging is significant and valuable. In this paper we used an advanced GEPCI approach (18,25,26) allowing the quantitation of various tissue specific structural and functional metrics.

Comparison between our data and the available literature information suggests that the age-related changes in the cortical ${R2}_t^{*}$ mostly reflect the age-related changes in the cellular packing density. Our data also show that tissue hemodynamic parameters, i. e. relative OEF, dCBV and C_deoxy have no linear correlations with age and remain practically constant in most cortical regions. We found important correlations characterizing relationships between brain structural and hemodynamic properties in different brain regions. Specifically, thicker cortical regions have lower ${R2}_t^{*}$, reflecting less cellular packing density, and these regions extract less oxygen from the blood.

All our findings can be understood if we put forward the following hypotheses:

1. Regions in a brain characterized by a higher ${R2}_t^{*}$ contain higher concentration of neurons with less developed cellular processes and are characterized by lower glycolytic activity. Accordingly, they require less blood flow to maintain their structure. These areas have higher OEF.

2. Regions in a brain characterized by a lower ${R2}_t^{*}$ represent regions with lower concentration of neurons but more developed cellular processes (dendrites, spines, etc.). They display higher glycolytic activity, hence require higher blood flow to maintain and develop new structural elements responsible for “information storage”. These areas have lower OEF.

Figure 5.

The scatter plots of (a) R2^*, (b) ${R2}_t^{*}$, (c) OEF_rel (expressed as local-to-global ratios, see Methods), (d) dCBV, (e) C_deoxy versus age are shown in cerebellar cortex. Each point in the plot stands for the cerebellar cortex from a single subject. Male subjects are represented by blue points and female subjects by red points. For all the parameters the solid lines stand for the mean values. The dashed lines represent the 95% confidence intervals. The p values of the constant model are shown as well.

Highlights.

Transverse relaxation of MRI signal is separated in tissue (${R2}_t^{*}$) and BOLD contributions

We hypothesize that ${R2}_t^{*}$ can serve as a biomarker of the cortical cellular packing density

Cortical regions with lower ${R2}_t^{*}$ are thicker and have lower oxygen extraction fraction (OEF)

${R2}_t^{*}$ grows with age in most cortical regions while OEF remains constant

Age related increase in cortical ${R2}_t^{*}$ reflects increases in the cellular packing density

Abbreviations

GEPCI

Gradient Echo Plural Contrast Imaging

${R2}_t^{*}$

tissue specific R2*

Th

the cortical thickness

${SR2}_t^{*}$

the product of the median ${R2}_t^{*}$ and the cortical thickness

OEF

oxygen extraction fraction

dCBV

deoxygenated cerebral blood volume

C_deoxy

the concentration of deoxyhemoglobin

VSF

voxel spread function

APPENDIX A

Summary of results

Table A.1.

The parameters of Eq. [11] and p-values for R2^*, $R{2}_t^{*}$, and cortical thickness in 26 selected FreeSurfer ROIs across 20 healthy subjects.

	R2* (s−1)			$R{2}_t^{*}({\mathrm{s}}^{-1})$			Thickness (mm)
name	Slope (k)	Intercept (a)	p value	Slope (k)	Intercept (a)	p value	Intercept (a)	Slope (k)	p value
banksst	0.029	18.6	0.020	0.028	16.5	0.021	−0.0095	2.51	0.001
cauda-lanterior cingulate	0.031	15.6	0.011	0.052	13.5	0.004	−0.0018	2.52	0.617
caudal-middle-frontal	0.034	17.6	0.006	0.021	15.8	0.120	−0.0052	2.49	0.020
cuneus	0.040	19.7	0.005	0.043	17.8	0.007	−0.0035	1.78	0.112
fusiform	0.034	18.9	0.007	0.023	16.4	0.093	−0.0064	2.72	0.002
inferior parietal	0.034	18.2	0.002	0.029	16.3	0.012	−0.0060	2.39	0.007
isthmus cingulate	0.038	18.3	0.003	0.044	17.2	0.001	−0.0030	2.36	0.347
lateral occipital	0.041	20.6	0.015	0.040	18.1	0.032	−0.0038	2.18	0.023
lingual	0.048	19.9	0.005	0.051	18.3	0.009	−0.0043	2.00	0.022
middle temporal	0.037	18.5	0.002	0.030	14.8	0.060	−0.0082	2.86	0.007
parahippocampal	0.031	17.2	0.055	0.004	15.0	0.841	−0.0081	2.69	0.036
paracentral	0.043	19.0	0.001	0.039	17.6	0.027	−0.0050	2.36	0.072
parsopercularis	0.042	17.0	0.001	0.042	14.8	0.005	−0.0081	2.51	0.001
parsorbitalis	0.024	18.9	0.106	0.006	15.1	0.699	−0.0039	2.62	0.228
parstriangularis	0.033	17.6	0.010	0.019	15.0	0.392	−0.0053	2.36	0.028
postcentral	0.030	18.3	0.005	0.032	16.2	0.017	−0.0046	2.03	0.014
posterior cingulate	0.029	16.6	0.003	0.028	15.2	0.015	−0.0055	2.45	0.016
precentral	0.037	18.4	0.003	0.032	16.5	0.020	−0.0064	2.51	0.021
precuneus	0.033	18.0	0.004	0.034	16.4	0.003	−0.0060	2.31	0.009
rostral-anterior cingulate	0.014	15.6	0.227	0.006	11.9	0.762	−0.0040	2.76	0.212
rostral-middle-frontal	0.020	17.1	0.074	0.011	14.8	0.417	−0.0031	2.23	0.168
superior frontal	0.027	16.6	0.008	0.027	14.7	0.021	−0.0047	2.63	0.115
superior parietal	0.023	18.3	0.072	0.021	16.1	0.197	−0.0040	2.12	0.094
superior temporal	0.038	17.6	0.002	0.017	14.4	0.275	−0.0074	2.77	0.008
supramarginal	0.033	17.6	0.001	0.028	15.5	0.020	−0.0073	2.53	0.001
insula	0.022	15.5	0.036	0.020	12.5	0.143	−0.0051	3.02	0.002

Table A.2.

The mean values and standard deviations of the OEF, dCBV, Cdeoxy, and $SR{2}_t^{*}$ in 26 selected FreeSurfer ROIs across 20 healthy subjects.

ROI	OEFrel		dCBV(%)		Cdeoxy (µM)		$SR{2}_t^{*}(mm/s)$
name	mean	std	mean	std	mean	std	mean	std
banksst	1.14	0.30	3.23	1.22	18.2	6.0	41.0	3.2
caudal-anterior cingulate	0.87	0.54	2.79	1.99	15.2	10.2	34.3	3.4
caudal-middle-frontal	1.02	0.20	2.65	0.53	15.5	3.9	39.1	2.7
cuneus	1.10	0.31	2.70	1.69	14.4	8.5	31.9	3.4
fusiform	1.29	0.21	3.36	1.08	21.0	5.2	44.4	2.8
inferior parietal	1.07	0.22	3.03	0.68	16.5	4.0	38.7	2.5
isthmus cingulate	1.02	0.35	1.18	0.90	6.7	4.5	40.7	3.8
lateral occipital	1.29	0.14	4.25	1.10	23.4	5.4	39.6	2.9
lingual	1.43	0.42	1.88	1.41	10.5	6.5	36.6	2.8
middle temporal	1.05	0.29	6.45	1.59	37.8	9.0	42.1	3.0
parahippocampal	0.99	0.46	1.86	1.41	12.3	8.5	39.8	4.8
paracentral	1.52	0.52	1.12	0.99	8.1	6.6	41.5	4.3
parsopercularis	0.98	0.39	3.09	1.29	17.7	6.1	37.1	2.7
parsorbitalis	1.13	0.49	6.12	1.98	36.2	9.3	39.5	3.4
parstriangularis	0.87	0.36	4.48	2.29	25.1	11.2	35.2	3.9
postcentral	1.21	0.18	2.43	0.88	15.1	5.7	32.9	2.7
posterior cingulate	0.75	0.30	1.88	0.99	10.1	5.5	37.1	2.3
precentral	1.21	0.17	2.21	0.69	13.7	4.7	41.3	3.4
precuneus	0.89	0.33	2.44	0.89	13.0	5.0	37.7	2.8
rostral-anterior cingulate	0.60	0.17	6.25	2.36	34.3	11.1	32.9	5.0
rostral-middle-frontal	0.63	0.20	4.16	1.36	20.9	4.9	33.0	2.7
superior frontal	0.75	0.17	2.74	0.62	15.5	4.3	38.5	3.2
superior parietal	1.25	0.28	2.80	0.74	16.9	5.6	34.2	3.7
superior temporal	0.72	0.22	5.17	1.33	29.1	6.7	39.5	3.8
supramarginal	0.89	0.20	3.23	0.94	17.6	5.1	39.0	2.7
insula	0.60	0.22	3.46	1.04	20.7	6.0	37.8	2.7

Table A.3.

The regression coefficients, p values and Pearson correlation coefficients for $R{2}_t^{*}$ vs. Thickness and $R{2}_t^{*}(s^{-1})$ vs. OEF_rel. Data represent averages from 20 healthy subjects across 26 selected FreeSurfer ROIs displayed in Fig. 3.

	slope	intercept	p value	r
$R{2}_t^{*}(s^{-1})$ vs. Thickness (mm)	−3.96	25.3	4.34E-05	0.71
$R{2}_t^{*}(s^{-1})$ vs. OEF	5.09	10.5	6.94E-07	0.8

Table A.4.

The regression coefficients and p values of R2^* vs. age in 6 subcortical ROIs. Data represent results from 20 healthy subjects displayed in Fig. 4.

ROI		R2* (s−1)
name	slope	intercept	p value
caudate	0.094	21.4	0.0003
putamen	0.209	24.0	0.0003
pallidum	0.178	34.8	0.0004
thalamus	0.013	21.0	0.1635
hippocampus	0.024	16.9	0.0816
amygdala	0.035	15.4	0.0341

APPENDIX B

Error analysis

In previous publications we provided the analysis of the systematic errors due to the diffusion effects (23) and the errors due to the noise in the data (24). The additional restrictions of the model used in this study were also discussed in detail by Ulrich and Yablonskiy (18). In this Appendix we provide some additional analysis specific to this paper by using in silico data.

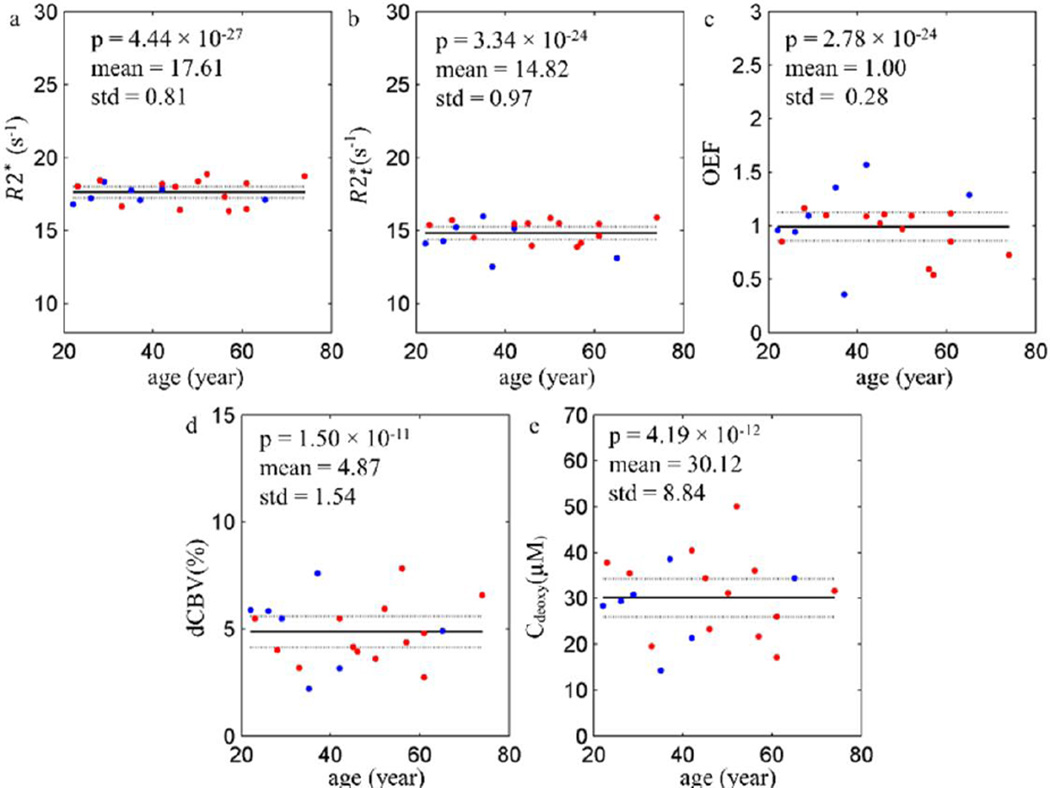
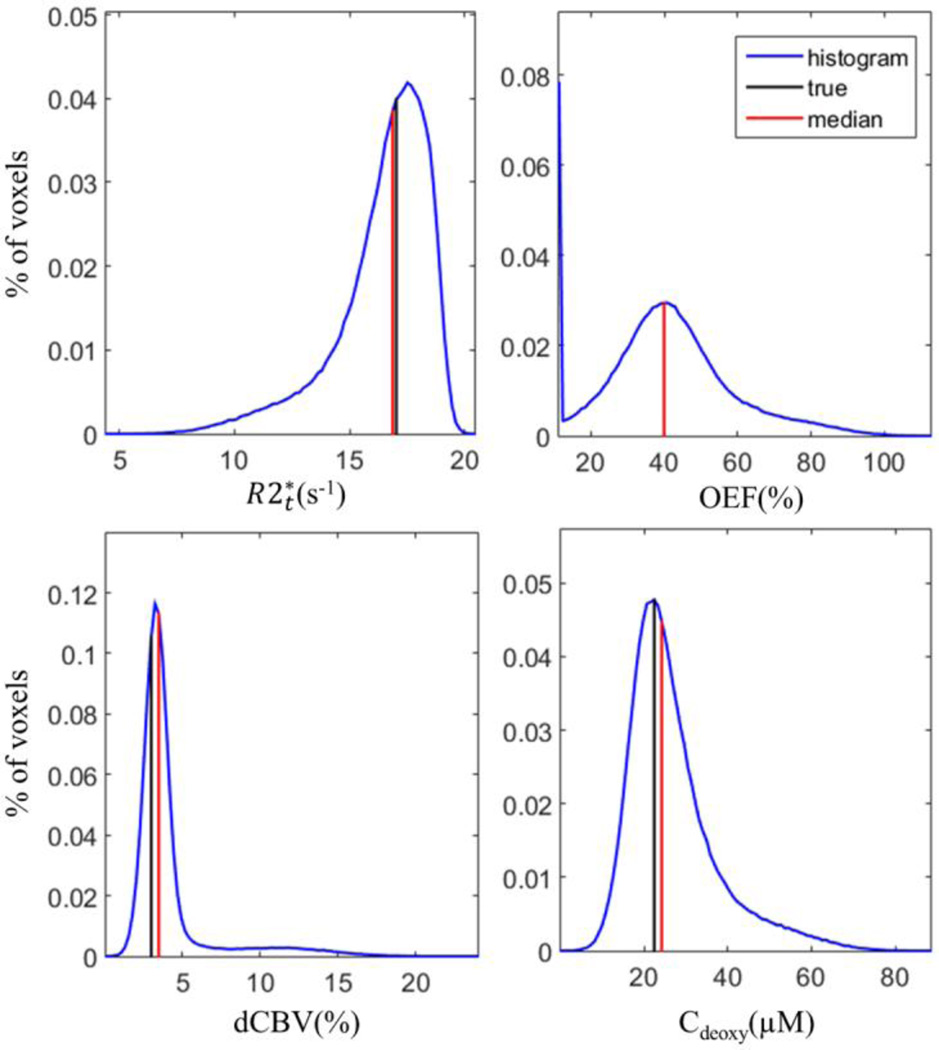
The simulated data were generated to test the accuracy of the theoretical model (Eq. [2]) used in this study. As the frequency (Δf) has minimal effects on the fitting process, only the amplitude of the signals were used in this simulation. First, the true values of the parameters were assigned based on our typical results: ${R2}_t^{*}=17$, OEF = 40%, and dCBV = 3%. Then the parameters were substituted into Eq. [2] to generate the “true” signals over 10 TEs from 4ms to 40ms. Second, a set of “real” signals over 10 TEs was generated by adding the random noise to the true signals. A typical SNR in our experiments is between 300 and 500 (for Hanning filtered data). In the simulated data we used the noise corresponding to SNR equal to 400. The random noise values were drawn from the standard normal distribution generated by a built-in function in MATLAB. In total, 500,000 sets of the simulated signals were generated in this way. Third, the same fitting routine used in the Method section was applied to each set of the simulated signals to calculate the output parameters. Finally, the medians, means and standard deviations of each parameter were calculated. The results are listed in Table B.1. The histograms of the output parameters, and the corresponding true and median values are shown in Figure B.1

The results show that the median values of ${R2}_t^{*}$, OEF, dCBV and C_deoxy better represent the true values than the means because the histograms are skewed and the median is less biased by the outliers.

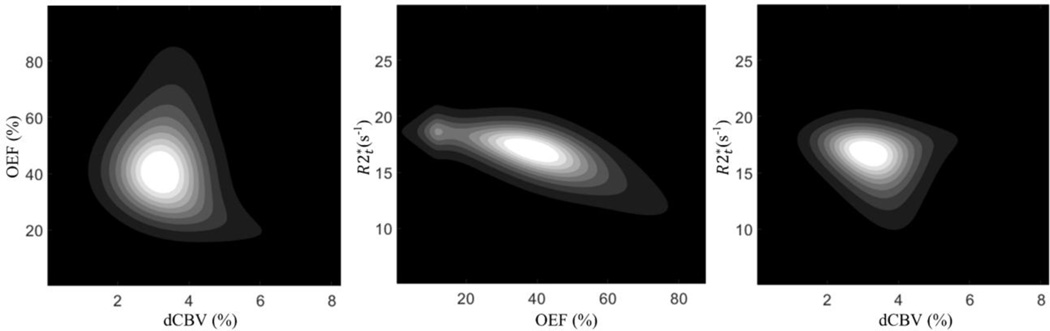
The 2D contour covariance maps of the relationships between ${R2}_t^{*}$, OEF and dCBV are shown in Fig. B.2. It demonstrates the peak value of ${R2}_t^{*}$ around 17, OEF around 40% and dCBV around 3%, well estimating the true values. The negative correlation between ${R2}_t^{*}$ and OEF (r = −0.88, p < 0.001) strengthens that the observed positive correlation between ${R2}_t^{*}$ and OEF_rel in our experimental data (Fig. 3) reflects the physiological relationship instead of errors.

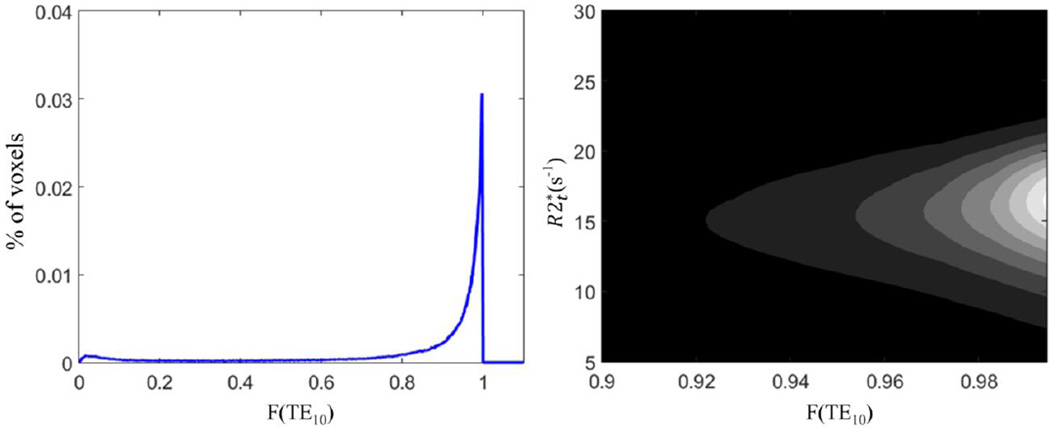
The detailed analysis of the correction for field inhomogeneity artifacts was provided in our previous paper where voxel spread function method (25) was introduced. Here we further demonstrate that VSF procedure does not create bias in parameters estimates in our data. We characterize signal decay due to the macroscopic field inhomogeneities by the F function at the last echo, F(TE₁₀), where the strongest signal decay is observed. Example of the distribution of F function at the last echo, F(TE₁₀), and the contour map of the joint covariance between ${R2}_t^{*}$ and F(TE₁₀), for the whole gray matter from an individual subject is shown in Figure B.3. No correlation is found between ${R2}_t^{*}$ and F(TE₁₀). The peak value of F(TE₁₀) is around 0.99 and most of values are located between 0.9 and 1 due to a good shimming procedure and rather small voxel size. The number of voxels with values lower than 0.8 is so small that they are not visible on the contour map. These voxels with lower F(TE₁₀) are mostly affected by the magnetic inhomogeneity due to the air/water interface around the sinuses and represent a very small fraction of the brain.

Table B.1.

The true values, medians, means and standard deviations of all the parameters in the simulations are listed here. The medians more accurately represent true values than the means for all the parameters.

	A0	$R{2}_t^{*}(s^{-1})$	OEF (%)	dCBV (%)	Cdeoxy (µM)
true values	100.00	17.00	40.00	3.00	22.44
median	99.94	16.91	40.01	3.43	24.63
mean	99.85	16.44	40.80	4.12	27.04
standard deviation	0.75	2.06	17.32	2.60	10.73

Figure B.1. The histograms of the simulated data for ${R2}_t^{*}$, OEF, dCBV and C_deoxy are shown with true values (black) and median values (red). The black and red lines overlap in the histogram of OEF. Note that the peak in OEF histogram at the lower boundary is due to the restriction set in the fitting routine (OEF > 10%).

Figure B.2. The contour covariance maps of the simulated data. The results show the peak values of ${R2}_t^{*}$ around 17, OEF around 40% and dCBV around 3%, well estimating the true values. The covariance between OEF and dCBV is consistent with the actual covariance map between the OEF and dCBV presented in Fig. 6 in the previous publication by Ulrich and Yablonskiy (18).

Figure B.3. Typical example of the distribution of F(TE₁₀) and the joint covariance contour of ${R2}_t^{*}$ and F(TE₁₀) are shown for a single subject. The range of F(TE₁₀) is from 0 to 1 and most of values are between 0.9 to 1. The number of voxels with F(TE₁₀) lower than 0.8 is quite small and they are not visible on the contour map. No covariance is found between ${R2}_t^{*}$ and F(TE₁₀) suggesting no bias in ${R2}_t^{*}$ estimate due to the field inhomogeneities.

One additional bias in the parameter estimates may be related to the estimation of OEF. Because our model of BOLD effect is developed under the assumption that the orientations of blood vessels are statistically random in each voxel, the actual variations of the blood vessel orientations may cause deviations in estimating OEF on a voxel by voxel basis. For example, if the blood vessels in some voxels have the predominant orientation parallel to the static magnetic field B₀, the BOLD effect is so minimal that the fitting routine will substantially underestimate OEF; conversely, OEF will be underestimated for the voxels with the predominant orientations of blood vessels perpendicular to B₀. However, as demonstrated in (20), the estimates of ${R2}_t^{*}$ and dCBV are not affected by this limitation. Besides, the use of median values for representing our results for very large regions, also minimizes these biases.

In conclusion, although substantial deviations from the true values of all parameters can be found in individual voxels and there are several restrictions on this model, the medians values of the parameters are very close to the true values. All in all, the simulations support that the methodology used in this study can generate the valid regional medians of ${R2}_t^{*}$ and hemodynamic parameters for large cortical regions. In our paper, we report results for cortical regions usually containing thousands of voxels.