f-divergence cutoff index to simultaneously identify differential expression in the integrated transcriptome and proteome

Abstract

The ability to integrate ‘omics’ (i.e. transcriptomics and proteomics) is becoming increasingly important to the understanding of regulatory mechanisms. There are currently no tools available to identify differentially expressed genes (DEGs) across different ‘omics’ data types or multi-dimensional data including time courses. We present fCI (f-divergence Cut-out Index), a model capable of simultaneously identifying DEGs from continuous and discrete transcriptomic, proteomic and integrated proteogenomic data. We show that fCI can be used across multiple diverse sets of data and can unambiguously find genes that show functional modulation, developmental changes or misregulation. Applying fCI to several proteogenomics datasets, we identified a number of important genes that showed distinctive regulation patterns. The package fCI is available at R Bioconductor and http://software.steenlab.org/fCI/.

INTRODUCTION

Data from ‘omics’ technologies, e.g. DNA microarray, Next-General Sequencing (NGS) and Mass Spectrometry (MS) based proteomics approaches, have become inexpensive and accessible. Yet, the vast majority of studies consider each data set independently. The ability to combine and synergistically integrate these different datasets will provide an understanding of gene expression and regulation across transcription and translation (1–9).

There is much literature that documents differences in transcript abundance and protein abundance in non-steady state systems. This difference is caused by several steps of regulation between the transcript and the protein. Every transcript has a particular stability and the regulation of this stability can be modulated by several mechanisms including miRNAs-mediated degradation. The translation of every transcript is regulated and has its own kinetics, thus the response of an increase in a particular transcript may not be reflected in an immediate increase in the protein. Furthermore, post-translational modifications such as ubiquitination can lead to the degradation of a particular proteins such that the protein levels are not reflective of mRNA levels. In the most extreme cases some proteins have very slow turnover such as eye lens crystallin and collagen have very long lifetimes or half-lives >70 and 117 years respectively (10) thus one cannot expect the measurement of the transcript to correlate with the measurement of protein abundance. Given this information, we need to understand regulation of expression at both the transcript and protein levels in biology and disease before we can intervene to cure disease.

Measuring and comparing gene expression and protein abundance is not trivial for a number of reasons related to instrumentation and data types used as explained here. Transcript expression using microarray technology has been used for decades. Microarrays quantify transcript expression by measuring probe hybridization signal intensity—a continuous number. Recent advances in sequencing technologies have ensured that NGS (i.e. RNA-Seq) is now the dominant high-throughput method to study transcript expression. NGS methods produce digital read counts for each gene which can be normalized as RPKM or FPKM (11). NGS methods exhibit low background noise and have a higher dynamic range (10⁵ compared to 10²) compared to microarray measurements (3,5,11,12). MS-based proteomics is currently the most sensitive and accurate method for the quantification of proteins. Protein expression using MS-based proteomics is measured by counting spectrum assigned to each protein or by measuring peak intensities of peptides that are found in those proteins (1). Thus, there are fundamental differences in the measurements and data types which require specialized statistical methods for comparing data from transcript to protein. However, we have devised the fCI method which allows us to compare across these different data type.

Currently, no tools exist to identify DEGs simultaneously and consistently across data types (6,13,14). Because each data type has unique properties, specialized statistical models have been developed to analyze each type of data. For example, a discrete negative binomial approach is used in DESeq and EdgeR to identify DEGs in RNA-Seq data, where the data type is characterized by discrete read counts (2–4,11). In contrast, the three major analysis approaches used for microarray data include the t-test, a regression model and mixture model, which are used to predict DEGs from continuous DNA probe intensity data (5,12,13). On the proteomics front, the G-test has been used to detect DEGs in spectrum count data (6,14–16). Given the wide variety of statistical tests across these various datasets, it is difficult to compare data from multiple ‘omics’ platforms despite the fact that these data are generated from the same samples. This paucity of a global method that can be used across data types to identify DEGs has been raised and the development of tools to analyze multiple data types from the same experimental paradigm is of general importance (17–20).

To overcome current limitations, we developed a novel approach, which is compatible with several data types from different ‘omics’ platforms and does not rely on frequency-based statistical learning methods. As a null hypothesis, we assume that the control samples, regardless of data types, do not contain DEGs and that the spread of the control data reflects the technical variance in the data. In contrast, the case samples contain a yet unknown number of DEGs. Removing DEGs from the case data leaves a set of non-DEGs whose distribution is identical to the control samples. Our method fCI identifies DEGs by computing the difference between the distribution of fold changes for the control–control data and remaining (non-differential) case-control gene expression ratio data (see Figure 1A and B) upon removal of genes with large fold changes. To do this we use the Hellinger distance measure or cross entropy methods (see ‘Materials and Methods’ section) (21–23). These approaches compute an optimal fold-change cutoff that minimizes the divergence. Thus, genes having a fold change larger than the chosen cutoff are treated as DEGs and are removed from the case data (see Figure 1C–E). Importantly, this fold-change-based divergence minimization algorithm can be used across multiple ‘omics’ datasets. The package fCI is available at R Bioconductor and also at http://software.steenlab.org/fCI/.

Figure 1.

Flowchart of fCI analysis. (A) Formation of replicate pairs in control and case samples. Gene expression levels from the control and case replicates are collected. Each replicate must contain the same number of genes. For the chosen control samples, fCI forms a list of the control–control combinations each containing two unique replicates from the full set of control replicates. Similarly, fCI forms a list of control-case combinations each containing a unique replicate from the control and a unique replicate from the case samples. (B) Generation of fCI pairwise combinations. fCI choose one control–control combination and one control-case combination to form a pair for a single fCI analysis. The total number of fCI analysis will be the product of control–control combinations and control-case combinations. In this figure, we choose one of the four fCI pairs for illustration purpose. (C) Formation of empirical and experimental distributions. The ratio of the chosen fCI control-control (or control-case) pair will undergo logarithm transformation and normalization (see ‘Materials and Methods’ section) if the pathological/experimental condition causes a number of genes to be upregulated or downregulated, a wider distribution which can be described by Gaussian distribution compared to the control–control empirical null distribution will be observed. fCI then gradually removes the genes from both tails (representing genes having larger fold changes) using the Hellinger Divergence or Cross Entropy estimation (Materials and Methods) until the remaining case-control distribution is very similar or identical to the empirical null distribution, as indicated by the Gaussian distribution. fCI then resume the iteration on the remaining fCI pairs. (D and E) Identification of fCI Differential Expressed Gens (DEGs) based on target frequency. (D) fCI combines all the pairwise analysis results each containing a list of misregulated genes in the chosen pair. (E) fCI produces a summary table which contains the total number of times a gene is found to be misregulated and the coverage percentage (total observations divided by all pairwise combinations considered) for each gene. (F) Formation of empirical and experimental distributions on integrated and/or multi-dimensional (i.e. time course data). In this example, gene expression values are recorded at c dimensions (c = 2 in this figure) with m replicates at each condition from a total of n genes. The ratio of the chosen fCI control–control (or control-case) on two-dimensional measurements will undergo logarithm transformation and normalization for the analysis. If the pathological/experimental condition causes a number of genes to be upregulated or downregulated, a wider distribution which can be described by kernel density distribution (indicated by the 3D ellipse in red) compared to the control–control empirical null distribution (indicated by the 3D ellipse in blue) will be observed.

MATERIALS AND METHODS

Our method considers transcriptomic (e.g. RPKM values from mapped reads of RNA-Seq experiment) and/or proteomic (e.g. protein peak intensities isobaric LC-MS/MS) data from two biological conditions (e.g. mutant and wild-type or case and control). The goal is to identify the set of genes whose RNA and/or protein levels are significantly changed in the case compared to the control.

In the basic scenario, we require each condition to have two replicates (e.g. transcript, protein or integrated transcript and protein expression data). To identify a set of DEGs in the case samples, the fCI method compares the similarity between the distribution of the case-control ratios (subject to logarithm transformation), denoted P, and similarly the control-control ratios (the empirical null), denoted Q (see Figure 1C and Supplementary Pseudocode). By construction, Q represents the empirical biological noise, i.e. the ratios from repeated measurements of the same sample. Under mild assumptions, the Almost Sure Central Limit Theorem ensures that P and Q will converge to a univariate/multivariate normal for large sample sizes as indicated by article ‘Almost sure central limit theorems for random ratios and applications to LSE for fractional Ornstein-Uhlenbeck processes’. Similarly, we could also construct distributions of P and Q from integrated/multi-dimensional data. In the simplest scenario of a time-course study consisting of two case and control replicates recorded at two time points, the empirical distribution P will be a matrix of two column vectors representing the technical noises, and Q will be a second matrix with case-control ratios, both measured at two time points respectively. Detail construction of these distributions are provided at Supplementary Pseudo-code, Figure 1A–F and Supplementary Figure S1.

To identify DEGs, we consider the difference between the distributions P and Q as quantified by the f-divergence (21). The f-divergence is a generalization of the Kullback-Leibler divergence, the Hellinger distance, the total variation distance and many other ways of comparing two distributions based on the odds ratio. Currently, we have implemented two different instances of f-divergence, but it is straightforward to extend the fCI code by adding additional divergences.

The Hellinger distance, H, is one of the most widely used metrics for quantifying the distance between two distributions and it is defined as:

The Hellinger distance has many advantageous properties such as being nonnegative, convex, monotone and symmetric (22,23). To calculate the Hellinger distance, we first use the maximum likelihood estimate to obtain the parameters of the distributions P and Q assuming Gaussian distributions. Let x₁, x₂, …, x_n be the individual case-control ratios with estimated mean μ₀ and variance ∑₀ from P, and μ₁ and variance ∑₁ from Q. The distance between two Gaussian distributions becomes:

Furthermore, we also consider the cross entropy, CE, for quantifying the differences between distributions,

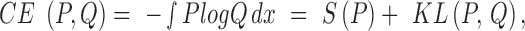where S is the entropy and KL is the Kullback-Leibler divergence. To calculate CE, we use and asymptotically unbiased non-parametric entropy estimator based on k-nearest neighbor approach (24).

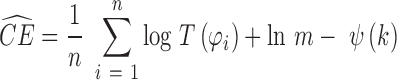where 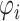is the distance from x_i to its k-th nearest neighbor in Q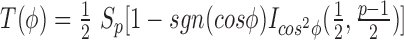, and and in the p-dimensional Euclidean space (sgn is the sign function, I_x(α, β) is the regularized incomplete beta function and p = 2 for univariate data), m is the number of observations and 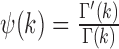is the digamma function (22,25,26).

If we divide the case-control ratio data into differential and non-differential genes, the remaining non-differential genes (upon the removal of DEGs) from the case-control data should be drawn from the same distribution as the empirical null (7). Therefore, the divergence will be at a global minimum close to 0.

When multiple biological/technical replicates are considered, the control–control ratio and case-control ratio can be formed in pair by mathematical combinations (see Figure 1B). Otherwise, if replicates are not available for control data, P and Q will be the direct logarithm-transformed distribution of the original gene expression. fCI uses Hellinger distance by default. Empirically, we have found that the cross entropy approach provides more conservative results compared to the Hellinger distance.

RESULTS AND DISCUSSIONS

In order to evaluate the model's performance, we considered multiple data sets that encompass commonly encountered multi-dimensional/integrated ‘omics’ data: (i) an experiment with both DNA microarray and isobaric-labeling LC/MS-MS expression measurements (multiple developmental stages of embryonic stem cells (ESCs) differentiated into beta cells); (ii) a proteogenomic dataset (embryonic cortical tissues from mice treated with rapamycin); (iii) and temporal mRNA-Seq dataset on the L4 dorsal root ganglion of rats. We then studied several distinctive omics datasets to directly compare fCI with existing methods including: (iv) a spiked-in microarray dataset; (v) an RNA-Seq dataset with known mRNA expression levels; (vi) an integrated proteogenomics dataset measured over a series of time points; (vii) a single-cell RNA-Seq dataset; and (viii) a simple RNA-Seq data where one gene was engineered to be over-expressed. Thus, we establish the validity of our methods by benchmarking them against standards in the field.

We first considered experiments for which multi-dimensional transcriptomic or proteomic data, and/or proteogenomic data were available. By multi-dimensional, we refer to data that has been generated for multiple related samples, i.e. time course and/or different tissue/cell types and/or in cases where both transcriptomic and proteomic data are available. Currently, multi-dimensional ‘omics’ data are analyzed separately using fundamentally different methods. Thus, we implemented a multi-dimensional fCI methodology, which for the first time allows the discovery of co-regulated genes that are changed jointly in multi-dimensional ‘omics’ data. fCI provides a coherent framework which can be used to analyze multi-dimensional datasets, even when the nature and type of the data are fundamentally different. We tested the algorithm in a time-course RNA-Seq data and a proteogenomic data.

We started with a bivariate fCI analysis on a dataset (see Supplementary Material 1-1) with expression levels measured in both DNA microarray and isobaric labeling LC-MS/MS experiments. In this dataset, both RNA and protein levels (ratios with respect to reference channel using TMT 6-plex isobaric tags) were recorded for six different time points (six cell differentiation stages) with three replicates in each time point. As ESCs differentiate, both RNA and protein contents were changed (see Supplementary Figure S2). However, the extent of change and the genes affected were not directly correlated. Nevertheless, fCI enabled us to find genes whose expression levels were significantly changed in both transcriptional and translational levels, and the changes across time points may be synchronized or delayed (see Figure 2A and B).

Figure 2.

Analysis of Transcriptomic and Proteomic dataset using fCI. (A and B) The box-plot of RNA and protein expression changes in gene AASS during five cell differentiation stages (see Supplementary Material 1-1). (A).RNA expression was measured by microarray hybridization intensity, and (B) the protein abundance was measured as the median log-2 ratio with respect to the reference channel (time-0). (C–E) Identification of DEGs in bivariate (2 time points) RNA-Seq data (see Supplementary Material 1-3). (C) The left panel shows the 3-way Venn diagram for the univariate fCI targets found in time-1 (orange), time-2 (red) and bivariate fCI targets found the two time points were analyzed jointly (green), using the time-course RNA-Seq dataset (Supplementary Material 1-5). (D) The scatterplot of the gene expression ratio from univariate fCI targets found at time-1 only (orange), time-2 only (red), for the bivariate analysis (green) and targets only found in bivariate fCI analysis (black). (E) The distribution of Hellinger divergence (log2)(z-axis) between case-control distribution and empirical null distribution after genes with a ratio greater than the cutoff specified in time-1 (x-axis) and time-2 (y-axis) were removed. The divergence scores would reach a global minimum point which manifests the optimal fold-change cutoff for transcript and protein (or in time point 1 and 2 respectively) in the integrated (or multi-dimensional) data set under study (F). The MA plot of empirical control–control and case-control (the first replicate of the pooled control and case samples respectively) ratios from microarray data (Supplementary Material 1-4). (G) The Gaussian kernel density plot of control–control (blue), the original case-control (red) and the remaining case-control (green) after misregulated genes are removed by fCI.

To give an unbiased estimate of fCI's performance, we benchmark fCI with limma (27), a widely used tool for differential expression analysis, on the same integrated proteogenomics dataset (see Supplementary Material 1-1). Although limma could be used to analyze continuous data type, it's not designed for LC-MS/MS data where proteins were measured by log2 ratios and RNAs by probe hybridization intensity. Therefore, we standardized all the transcript and protein expression with a mean of 0 and standard deviation of 1. Subsequently, we run limma on the standardized data, which contain transcript and protein expression measured on three replicates respectively. A total of 2828 genes were used for this analysis. The limma identified a total of 310 DEGs, and fCI identified 484 DEGs. An overlap of 116 genes was shared by the two software tools. The limma analyses requires that we combine the control microarray data and the MS data directly as well and the case MS and microarray data because the method compares the mean values of two populations. This is not ideal as the two dataset MS and microarray are vastly different in terms of magnitude and nature. For example, the gene Serpinb9 is 4-fold higher in experimental conditions for both the microarray data and LC-MS/MS data. However, limma was still not able to identify this gene. In addition, gene Alcam and Prdx3 have insignificant opposite changes in LC-MS/MS and microarray data, but limma treated them as a DEGs. For more genes identified by fCI and limma, see Supplementary Table S1.

Next, we performed a bivariate fCI analysis on a proteogenomic data (∼2500 genes) that was collected in-house (see Supplementary Material 1–2). Results showed that 103 significant DEGs were jointly changed. If a univariate fCI analysis was performed separately on the RNA-Seq and the proteomics dataset, 777 RNAs and 29 proteins are significantly misregulated respectively. A closer inspection of the results showed that the RNA and protein changes were not always directly correlated (see Supplementary Figure S3) as several studies have shown previously (28,21,22). For example, out of the 10 DEGs shown both in Proteomic data and RNA-Seq data, only five of them appeared in the bivariate data and the remaining five showed opposite regulations. Integration of the information from both expression levels in the same model enables the construction of a robust covariance matrix, thus reducing bias and error. Therefore, the combined proteogenomic analysis provided a unique perspective on the regulation of significant DEGs at the transcriptional and translational levels.

The third dataset is a time series bivariate RNA-Seq dataset (see Supplementary Material 1–3) with both control and treatment samples analyzed at two time points (23). In previous analysis, scientists need to perform two separate analyses to identify two sets of DEGs, and then find the commonly DEGs by intersecting the two DEG sets from the two time points respectively. A number of marginally changed genes that are chosen by only one or neither of the two analyses may be removed from subsequent analysis. However, such genes may be important targets for subsequence studies if they are closely co-regulated. In this study, we performed fCI analysis by two separate fCI analyses and a bivariate analysis to evaluate the model performance. Overall, fCI found a total of 2931 co-regulated DEGs when both time points were analyzed jointly using our multi-dimensional fCI, compared to only 1283 DEGs reported in individual analyses (see Figure 2C and D). In contrast, other algorithms, including DESeq, fail to find any targets jointly on the same bivariate data (see Supplementary Table S2), suggesting that more than half of the DEGs could not be effectively identified if the two time points were analyzed separately. Since the bivariate fCI analysis incorporated covariance information between the two time points, it was able to find marginal changes that were not significant in each of the univariate analysis. In addition, fCI also enabled us to identify the optimal cutoff ratios for both time points based on the three-dimensional divergence scores (see Figure 2E).

Having established the performance of the method on complex multi-dimensional datasets, we next benchmarked fCI with specialized tools that were developed for microarray, RNA-Seq or LC-MS/MS data analysis on the corresponding dataset respectively.

We first evaluated the applicability of fCI on a DNA microarray dataset (24) with normalized expression and known external spike-in standards (see Supplementary Material 1-4), which allowed us to validate the methods A common practice to evaluate and validate the software performance in spike datasets where DEGs are known in advance is to compute the true positive rate, false positive rate and area under the receiver operating characteristic (AUROC). In this analysis, we found that fCI achieved a AUROC of 98.9% (Supplementary Figure S4 and Supplementary Materials 1-4), thus outperforming current best microarray analysis methods (29) using AUROC by close to 10%. Subsequently, we chose only two replicates from the control samples and one replicate from the case samples to illustrate fCI's analysis workflow (see Figure 2F). Results showed that after DEGs are removed by fCI, the remaining non-differential case-control ratio distribution and control–control ratio distribution are nearly identical (see Figure 2F and G). Therefore, these spiked-in standards validated our assumption that the case sample (after DEGs are removed) displays a similar distribution as the control data.

We then applied the fCI on a second dataset (2) (see Supplementary Material 1-5) containing quantitative data for ∼1000 genes whose expression levels were measured using qRT-PCR to benchmark RNA-Seq technology and DEG algorithms. In this dataset (Supplementary Material 1-5), we have four replicates for control samples and four replicates for case (experimental) data. Therefore, a total of six empirical combinations and a total of 16 case-control combinations will be found (see Supplementary Figure S1 for details on constructing fCI combinations). In total, we run fCI for 6*16 (or 96) times. Each gene could be reported as a DEG from 0 to 96 times. Therefore, we assign a detection frequency (0–1) for each gene based on the number of times it is detected in the 96 fCI analyses. Again, we obtained similar results; fCI achieved a AUROC of 99.1% (see Supplementary Figure S5a). The AUROC for fCI was more than 10% higher (2) than DESeq (3), an R-Bioconductor package for RNA-Seq data analysis, showing the accuracy of fCI method on transcriptomic data with benchmarked expression measurements.

In fact, the true DEGs consistently have larger fCI detection frequencies than the genes that are not differentially expressed, and we created a histogram showing the distribution of fCI detection frequencies based on DEGs and not DEGs (Supplementary Figure S5b). The histogram shows that all fCI predicted DEGs with a detection score >0.7 are known(spiked) DEGs based on the validation labels. In addition, ∼80% of the known DEG genes have a detection score of 0.7. In other words, fCI achieved a detection specificity of 100% and a sensitivity of ∼80% under the threshold of 0.7. As the curve continues, the sensitivity keeps increasing (more spike-in known DEGs are identified) however the specificity decreases (some non-DEGs present with a detection frequency larger than the known standards). At the threshold score of 0.45, all real DEGs are found (sensitivity equals to 1) at the price of identifying ∼20% DEGs that are false positives.

In the above analysis, we compared fCI outcomes with true DEGs based on the log fold-change of 0.5. However, we investigated the performance of fCI when the log fold change is more stringent. In a previous analysis (2), scientists performed experiments using increasing log2 expression ratios (from 0.5 to 2 with increments of 0.10). Results showed that fCI's AUROC values dropped steadily with the increased cutoff ratios (Supplementary Figure S5c). However, fCI still produced the best results when compared with other methods.

We continued to tested our software on a published time-course dataset (see Supplementary Material 1-6) where mRNA and protein levels were obtained from bone marrow derived dendritic cells (DCs) growth in two conditions at six time points (25). DCs were treated either by LipoPolySaccharide (LPS) or Mock (no stimulation) for protein level estimations. We computed the genes that are differentially expressed for each time point with the reference time point, and then plotted the change in y-axis (a value of 0 will be given for time points showing no significant change with respect to reference time point) across different time points. Consistent with published results, we have shown that mRNA levels contributed to the changes of protein expression levels in genes such as Cebpb, Trafd1 (see Figure 3). Our analysis also suggested that LPS-induced and Mock cells show very distinctive (i.e. opposite) regulations in a number of genes (see Supplementary Figure S6).

Figure 3.

Analysis of protein and mRNA changes in the time-course data using fCI. Protein levels were measured in two treatment conditions (LPS and Mock) and two data recording methods (Heavy and Medium) respectively. Instead, mRNA levels were measured in only two treatment conditions (LPS and Mock) respectively. Both protein and mRNA levels were recorded at 0,1, 2, 4, 9 and 12 h. At each time point, fCI determined whether the given gene is differentially expressed or not compared to reference time point 0 h. If no significance was found, a fold change of 0 was assigned. Otherwise, the ratio will be reported at significantly changed time points. Effect of gene regulation with respect to the six time points were shown on gene ‘Cebpb’ and ‘Trafd1’ respectively.

Furthermore, we used fCI to investigate gene expression variability in mouse embryonic stem cells cultured in serum and in a two-inhibitor medium (30) (see Supplementary Materials 1-7). In single cell gene expression analysis we used a different approach with fCI. We analyzed the distribution of gene expression for individual genes across the individual cells, as opposed to the previous cases where we analyzed the distribution of multiple genes between samples (our reasoning for this approach is in the Supplementary Materials 1-7). With fCI, it is possible to monitor gene expression changes between cells undergoing different treatments (see Supplementary Figure S7). Results showed that gene expression values (878 out of 1492 genes) were more variable in cells cultured in traditional serum medium compared to genes (104 out of 1492 genes) from cells cultured in a two-inhibitor medium, which confirmed >80% of published results (31) (see Supplementary Table S3). For example, fCI confirmed that Pou5f1, Sox2 and Pcna were more variable in the serum condition compared to the two-inhibitor condition. In contrast, Ccna2 and Ccnb1 were both expressed similarly in the given conditions (31). This allowed us to utilize fCI and single cell RNA-Seq to evaluate sample variability and DEGs based on transcriptome similarities between cells.

In fact, a comparison of the spread of control–control and case-control distributions can already carry useful information whether DEGs should be expected in the case sample. For this reason, we performed the last fCI analysis using a dataset (see Supplementary Material 1-8) by both DESeq and fCI. The kernel density plot showed that the empirical null distribution had larger noise levels (see Supplementary Figure S8) compared with case-control distribution. Such an outcome should be the ground for concerns about the existence of large experimental noise levels (similar or larger than the treatment effect) and an indication of the absence of differential expression. fCI thus reported a large divergence value and failed to detect any targets within the defined maximum ratio (10-fold change), while DESeq reported 864 (∼5%) DEGs (3).

To know how confident fCI can identify ‘differentially expressed’ genes in the previous analyses, we calculated the approximate type-1 error rate in the following. Given a dataset containing multiple control replicates and experimental replicates, fCI computes the divergence scores between control–control (empirical null) and case-control distributions. fCI calculates the optimal fold-change cutoff that minimizes the divergence score between the empirical null and the case distribution. This cutoff allows the identification of truly DEGs which are then reported. Based on the assumption of fCI, we construct the following null hypothesis and alternative hypothesis. H0: no genes are differentially expressed between replicates of the control samples (the empirical null) and Ha: all genes are considered differentially expressed if their fold-change ratios between the case and controls are greater than the cutoff ratio defined by fCI's divergence estimation algorithm.

Ideally, if the fold-change cutoff is chosen without error (no false positives), we should not observe any gene in the control–control ratios (empirical null distribution) with a fold change larger than the chosen cutoff. However, in reality, with real world data there may be genes whose fold-change ratios are larger than the cutoff due to technical noise. The proportion of such genes in the empirical null distribution is equivalent to a type I error rate (incorrect rejection of a true null hypothesis). Using the RNA expression data (see Supplementary Material 1–5), we detected an optimal fold change of 1.3 using fCI (see Supplementary Figure S9). However, we noticed that in the empirical null distribution (computed from control replicates), there are 23 genes that have a fold change >1.3-fold in more than half of the six pairwise fCI empirical null combinations. The proportion of these 23 genes, divided by the total sample size of 1043 genes, is the type 1 error rate of 0.0221. In other words, the 2.21% DEGs are incorrectly rejected.

Furthermore, to evaluate the top DEGs according to the detection frequency whether they are false predictions or not, we provided the estimation of false discovery rate (FDR) below. We could estimate the FDR directly using spike-in samples which contained known DEGs. Let TP represents true positive matches and FP to be false positive matches, the number of all predicted DEGs is the sum of TP and FP, and the number of predicted DEGs that are not differentially spike-in genes is FP. The FDR is denoted as: (FDR) = FP/(FP + TP).

In the spiked-in RNA expression dataset (Supplementary Material 1-5), we already knew all the genes that were spiked-in to be differentially expressed based on the experimental design (2). Therefore, the FDR could be directly calculated. After conducting fCI analyses, we identified a total of 757 genes to be differentially expressed with a 1.3-fold change cutoff. After matching the 757 predicted DEGs with the known differential targets, we found a total of 19 genes to be incorrectly predicted as DEGs and 738 true predictions. The FDR thus become 19/(19 + 738) = 2.51%.

On the other hand, we could also obtain a permutation-based FDR approximation using the same dataset without relying on prior information about the true DEGs. To achieve this, we randomly permute the replicates between control and experimental samples (i.e. we form an empirical null distribution by computing the ratio between the second control replicate and the first experimental replicate), and then we computed the ‘DEGs’ from this permuted fCI combination. This concept is equivalent to the Target-Decoy database search that are widely used in proteomics study for FDR estimation (see Supplementary Figure S10). In theory, we do not expect to find any DEGs from the ‘decoy’ (permuted) sample. In contrast, the DEGs that are truly differentially expressed should be only found in the true (or target) database, which are constructed by real empirical null (a control–control pair) and the case-control (a case-control pair) distribution respectively.

In this experiment, we created a database consisting of 100 targeted fCI combinations and 100 permuted ‘decoy’ fCI combinations. According to our definition, we shouldn't find any true DEGs in the permuted ‘decoy’ fCI analysis. Results showed us that 921 DEGs were reported for a total of 71449 times (all identified DEGs) in the 200 fCI analysis. However, only 23 DEGs (the decoy DEGs) are identified in the 100 permuted fCI analysis. For the remaining 100 (target) fCI analyses, we consider a DEG to be a false positive if it has at least 50% detection frequency, and we ended up with 288 incorrect genes that showed up 3998 times (the false targets) as DEGs in these fCI analyses. Therefore, the FDR becomes (3998 + 23)/(71426 + 23), which become 5.63%. The analyses showed us that the permutation FDR is 2% higher than the true FDR. This could be due to the repeated sampling. In other words, it also showed us that the permutation FDR estimation is a conservative estimation.

Taken together, these results demonstrated fCI's versatile ability to identify DEGs using gene quantities in the form of probe hybridization signal intensity from microarrays, read counts from RNA-Seq and ion intensities from proteomic LC-MS/MS data.

CONCLUSIONS

In summary, we demonstrated that fCI is a tool that enables cross-omics data analyses which could not have been performed prior to its development. Firstly, it performed as well or better in finding DEGs across diverse data types (both discrete and continuous data) from various ‘omics’ technologies compared to methods that were specifically designed for the experiments. Secondly, it fulfills an urgent need in the ‘omics’ research arena by providing a means to analyze proteome and transcriptome data together. Thirdly, fCI does not rely on statistical methods that require sufficiently large numbers of replicates to evaluate DEGs. Instead fCI can effectively identify changes in samples with very few or no replicates. However, biological and/or technical replicates benefit the analyses as users not only can choose commonly regulated DEGs, but also can inspect uniquely changed genes in specific samples for validation. Furthermore, as we are excited about the cell specific data from single cell RNA-Seq experiments, fCI was tailored to process this type of data and show that it offered an understanding of specific gene expression levels in individual cells (32) (Supplementary Material 1-7). Compared to the formal cutoff index method (7,8), fCI has a completely different scope as it uses distinctive statistical methods, implementation and applications. In addition, fCI allows us to compute DEGs with various data types from transcriptomics, proteomics, integrated proteogenomics and time-series multi-dimensional data. In summary, the efficacy and applicability of fCI across experimental designs is rigorously tested and validated and fulfills a need in the rapidly evolving ‘omics’ landscape.

FUNDING

US National Institutes of Health [NINDS R01 NS066973 to H.S., J.S.]. Funding for open access charge: US National Institutes of Health [NINDS R01 NS066973].

Conflict of interest statement. None declared.