Summary
Objective
To test the hypothesis that individuals with patellofemoral pain (PFP) exhibit greater patellofemoral joint stress profiles compared to persons who are pain-free.
Methods
Ten females with PFP and ten gender, age, and activity-matched pain-free controls participated. Patella and femur stress profiles were quantified utilizing subject-specific finite element (FE) models of the patellofemoral joint at 15° and 45° of knee flexion. Input parameters for the FE model included: (1) joint geometry, (2) quadriceps muscle forces, and (3) weight-bearing patellofemoral joint kinematics. Using a nonlinear FE solver, quasi-static loading simulations were performed to quantify each subject’s patellofemoral joint stress profile during a static squatting maneuver. The patella and femur peak and mean hydrostatic pressure as well as the peak and mean octahedral shear stress for the elements representing the chondro-osseous interface were quantified.
Results
Compared to the pain-free controls, individuals with PFP consistently exhibited greater peak and mean hydrostatic pressure as well as peak and mean octahedral shear stress for the elements representing the patella and femur chondro-osseous interface across the two knee flexion angles tested (15° and 45°).
Conclusions
The combined finding of elevated hydrostatic pressure and octahedral shear stress across the two kneeflexion angles supports the premise that PFPmay be associated with elevated joint stress. Therefore, treatments aimed at decreasing patellofemoral joint stress may be indicated in this patient population.
Introduction
Disorders of the patellofemoral joint are among the most common and clinically challenging conditions encountered in orthopedic practice. Patellofemoral pain (PFP) affects a wide range of individuals, with higher incidence rates among women and those who are physically active1–5. Despite the high occurrence of PFP in society, there is considerable debate about the nature of this condition, including the pathologic process and the underlying risk factors central to its occurrence.
The most commonly cited hypothesis as to the cause of PFP is related to abnormal patella alignment and/or tracking, which increases patellofemoral joint stress and subsequent articular cartilage wear6–10. Since articular cartilage is aneural, it cannot be a source of pain6,11,12. However, it is feasible that the subchondral endplate, which contains pain receptors, may be exposed to stress variations that normally would be absorbed by healthy cartilage6,11,12
From a technical stand point, in-vivo evaluation of patellofemoral joint stress is a multifaceted challenge. Historically, quantification of patellofemoral joint stress has been made experimentally, using in-vitro cadaveric models13–15. Such studies have been valuable in providing information about the stress environment of the patellofemoral joint; however the use of non-physiologic muscle loading has made extrapolation to the in-vivo condition questionable. More recently, musculoskeletal modeling has been used to predict average contact stress to estimate the loads placed on the patellofemoral joint in-vivo.16–18 in these studies, average patellofemoral joint contact stress was estimated as the joint contact force divided by the total joint contact area as measured from magnetic resonance (MR) images. A limitation of this approach is the inability to provide information about peak stress and stress distribution patterns across the joint.
Current advancements in numerical approximation techniques have allowed for the integration of subject-specific musculoskeletal parameters and in-vivo experimental data to develop more elaborate computational models to investigate the stress environment of the patellofemoral joint19. The finite element (FE) approach is one such framework20. FE models have proven valuable for understanding stress distributions throughout complex biological structures when the use of analytical mathematical techniques is impractical21. Using a 3-dimensional (3D), subject-specific, FE modeling approach, the purpose of the current study was to test the hypothesis that individuals with PFP would demonstrate greater patellofemoral joint hydrostatic pressure and octahedral shear stress for the patella and femur cartilage compared to persons who are pain-free.
Methods
Subjects
Twenty subjects were recruited for this study, 10 females with PFP constituted the experimental group, while 10 pain-free females served as the control group (Table I). Prior to participation, all subjects were informed as to the nature of the study and signed a human subject’s consent form approved by the Health Sciences Institutional Review Board of the University of Southern California.
Table I.
Subject characteristics mean [standard deviation (SD)]
| PFP (N = 10) | Control (N = 10) | Significance | |
|---|---|---|---|
| Age (year) | 27.7 (4.3) | 27.0 (4.4) | P = 0.72 |
| Height (m) | 1.7 (0.1) | 1.6 (0.1) | P = 0.53 |
| Weight (Kg) | 63.3 (8.4) | 61.9 (8.7) | P = 0.72 |
| Activity level (MET. min/week) | 2804.0 (1830.1) | 2564.0 (1900.1) | P = 0.77 |
PFP = patellofemoral pain group.
Individuals with PFP were admitted to the study if their pain originated from behind the patella (i.e., retropatellar pain). Only subjects that reported an insidious onset of symptoms were accepted. Subjects were screened through physical examination to rule out evidence of large knee effusion and peri-patellar pain. The screening procedure also included a functional assessment of activities commonly associated with PFP (squatting, stair climbing, isometric quadriceps contraction). Subjects were included in the study if they reported pain of at least three out of 10 (based on a visual analog scale) with one or more of the aforementioned functional tasks. Individuals with PFP were excluded from participation if they reported any of the following: (1) previous history of knee surgery, (2) history of traumatic patella dislocation, (3) neurological involvement that would influence performance of various functional activities, and (4) implanted biological devices that could interact with a magnetic field.
Subjects in the control group were age, height, weight, and activity matched to those in the PFP group (Table I). Subjects’ physical activity levels were determined based on the World Health Organization’s Global Physical Activity Questionnaire (GPAQ). The GPAQ has been reported to provide a valid and reliable estimate of physical activity22. Subjects in the control group were selected based on the same criteria as the experimental group except that these individuals had no history or diagnosis of knee pain, pathology, or trauma.
Procedures
Subjects completed two data collection sessions. The first session consisted of MR assessment of the knee joint, whereas the second session consisted of biomechanical testing. For subjects with PFP, testing was performed on the painful side. To account for the potential influence of side-to-side differences among subjects (i.e., muscle volume, loading history, etc.), the side evaluated in the control subjects was matched to that of their counterpart in the PFP group.
MR assessment
Subject-specific cartilage morphology and bone geometry were obtained from sagittal plane MR images of the knee acquired with a 3.0 T MR scanner (General Electric Healthcare, Milwaukee, WI). Images were acquired with an eight-channel knee coil using a 3D, high-resolution, fat-suppressed, fast spoiled gradient recalled echo (SPGR) sequence (repetition time: 14.5 ms, echo time: 2.8 ms, flip angle: 10×, matrix: 320×320, field of view: 16 cm, slice thickness: 1.0 mm, scan time of 8:58 min). During this scan, subjects were positioned supine within the MR bore with the knee extended.
To obtain the relative weight-bearing positions and orientations of the patellofemoral joint, a custom made non-ferromagnetic loading apparatus providing a force equivalent to 25% of subjects’ body weight was utilized. Loaded MR images of the subjects’ knees were acquired at 15° and 45° of knee flexion, using a 3D, fast SPGR sequence (repetition time: 14.3 ms, echo time: 3.6 ms, flip angle: 10×, matrix: 320×160, field of view: 16 cm, slice thickness: 2.0 mm, scan time of 1:45 min).
Quadriceps muscle morphology was assessed from sagittal plane MR images of the thigh using a 3D SPGR protocol (repetition time: 9.4ms, echo time: 4.1 ms, flip angle: 20×, matrix: 384×384, field of view: 46 cm, slice thickness: 2 mm, scan time of 8:03 min). The sagittal plane images of the thigh were subsequently reconstructed in the coronal and axial planes and were used to estimate the 3D fiber orientation of each of the quadriceps muscles. The axial images of the thigh were utilized to measure the cross sectional area of the quadriceps muscles which was subsequently used as an input variable for our biomechanical model to estimate the magnitude of the muscle forces (see below for details).
Biomechanical testing
Subjects were instrumented for 3D motion and electromyography (EMG) analyses as described in previous publications16,18. Lower extremity kinematics was collected using an eight-camera motion analysis system at 60 Hz (Vicon, Oxford Metrics LTD. Oxford, England). Ground reaction forces were recorded at a rate of 1560 Hz using 2 AMTI force plates (Model #OR6-6-1, Newton, MA). Surface EMG signals of muscles crossing the knee joint were recorded at 1560 Hz, using pre-amplified, bipolar, surface electrodes (Motion Lab Systems, Baton Rouge, LA).
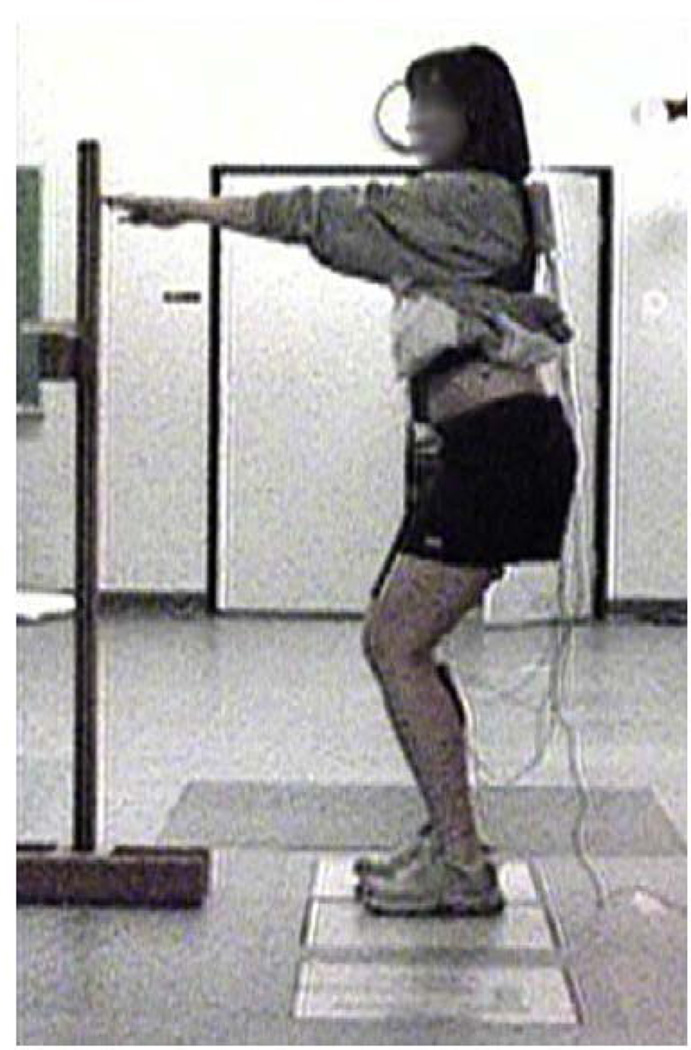
Following a standing calibration trial, subjects were asked to hold a bilateral squat position (10 s) at 15° and 45° of knee flexion with each foot positioned on a separate force plate. To account for the influence of the trunk position on the lower extremity demands during weightbearing23, the subjects’ trunk position was maintained upright by asking the subjects to flex their knees to the desired angle while keeping finger-tip contact with a pole placed at arm’s length (Fig. 1). While holding the desired squatting position, kinematics, kinetics, and EMG data were recorded simultaneously. This information was used for estimation of quadriceps muscle forces required as an input variable into the FE model.
Fig. 1.
The experimental set up for the squat maneuver used to estimate quadriceps muscle forces.
FE model development
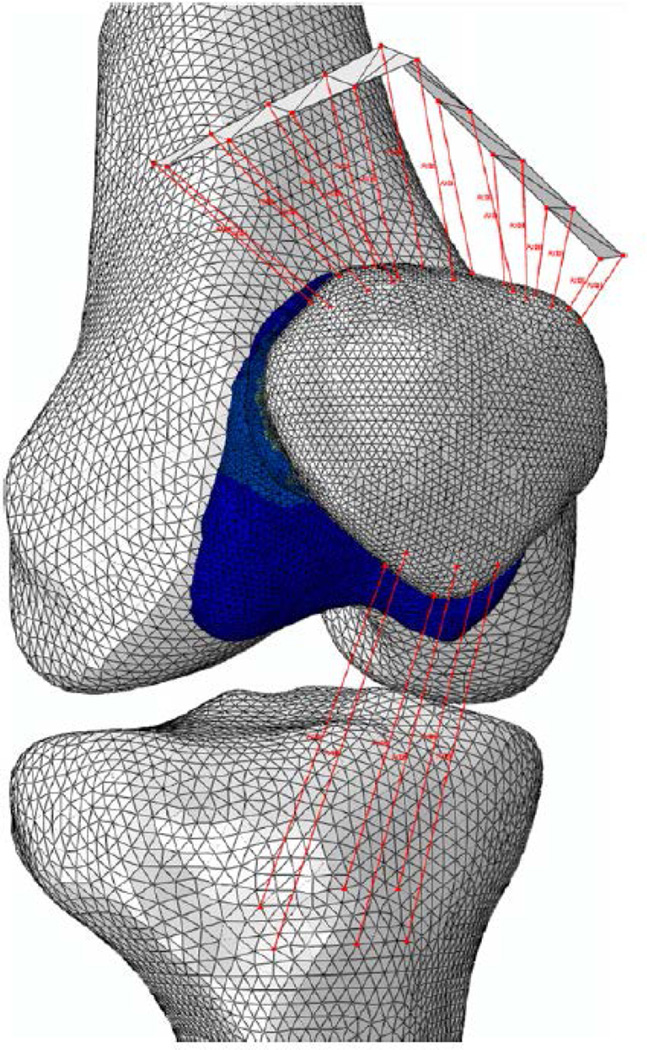
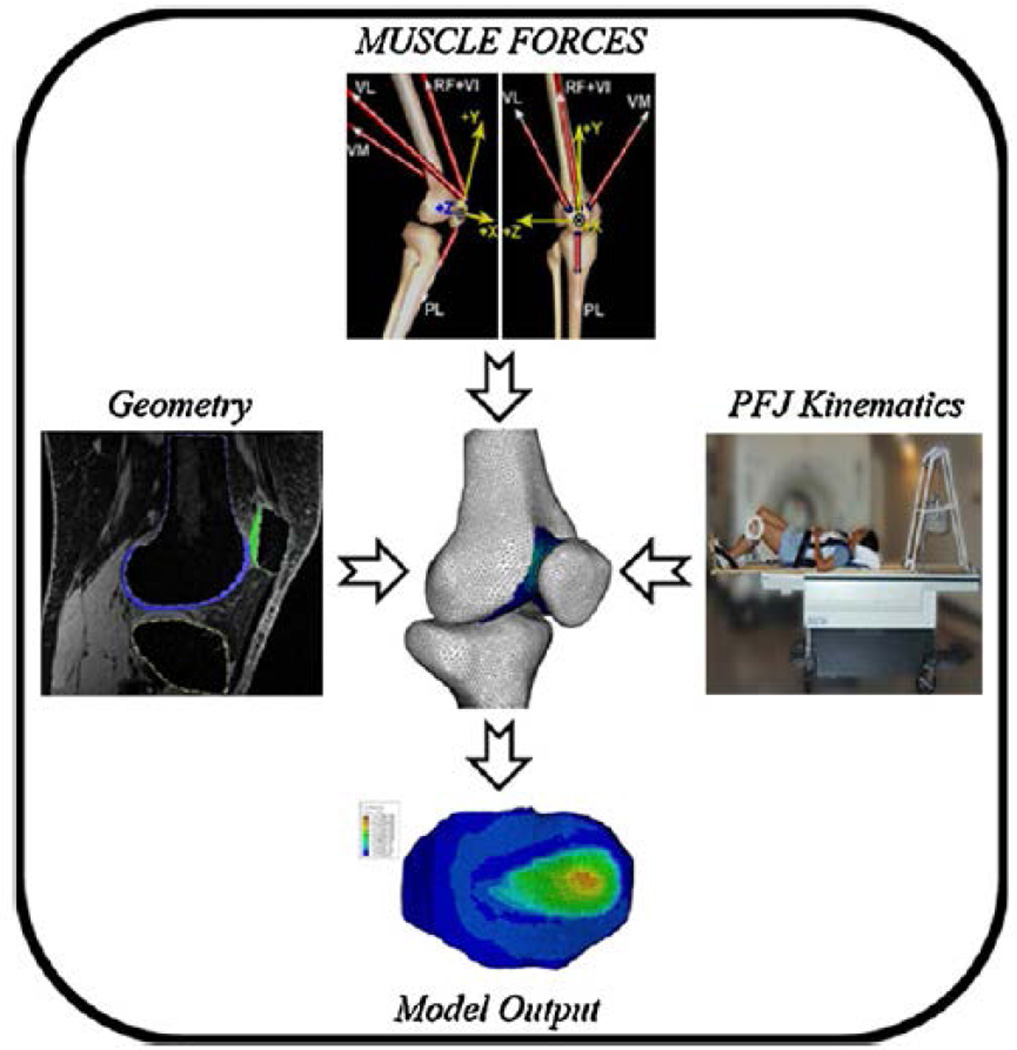
Forty subject-specific FEmodels (Fig. 2) were created to evaluate the stress fields in the patellofemoral joint cartilage (20 subjects×2 knee flexion angles). Subject-specific input parameters entered into the modeling pipeline included: joint geometry, quadriceps muscle forces, and weight-bearing patellofemoral joint kinematics (Fig. 3).
Fig. 2.
Representative FE model of the patellofemoral joint.
Fig. 3.
Subject-specific input parameters used to create FE models of the patellofemoral joint.
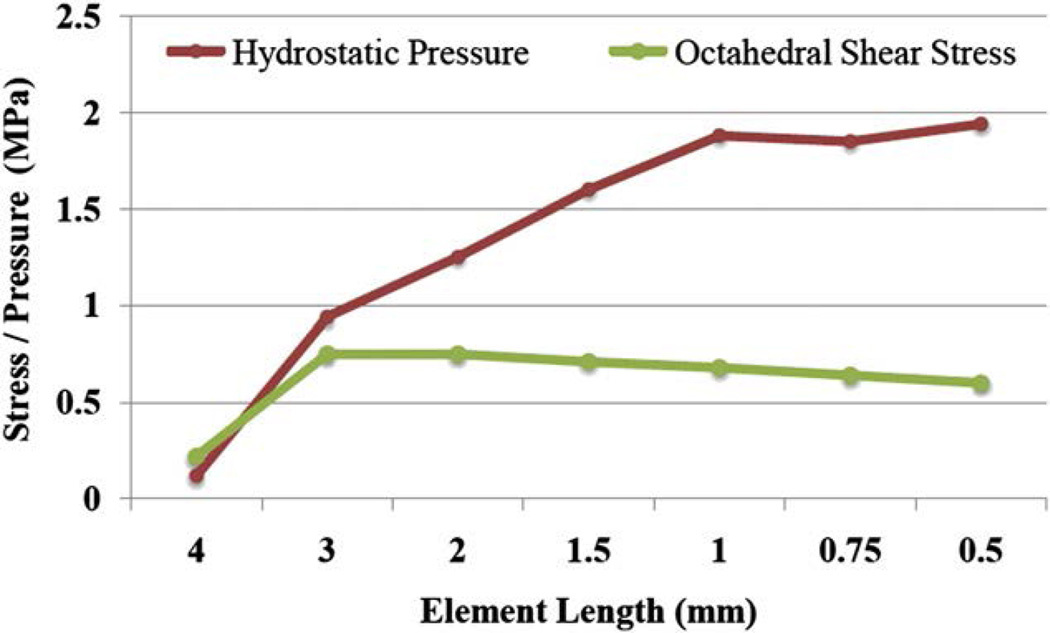
Using a commercial software package (Sliceomatic, Tomovision, Montreal, Quebec), the high resolution, sagittal plane MR images of the knee were manually segmented and 3D surfaces of the femur, tibia, patella, and articular cartilage covering of the femur and patella were created. Surfaces created for the femur, tibia, and patella were subsequently used to create rigid body shells of each bony structure using a proprietary FE pre-processor (Hypermesh, Altair Engineering Inc., Troy, MI). The articular cartilage of the patella and femur was modeled as homogeneous isotropic tetrahedral continuum elements with an elastic modulus of 4.0 MPa24 and a Poisson ratio of 0.47.25 An average element size of 0.75 mm was used after a mesh convergence analysis was performed. Mesh convergence was conducted on the patella cartilage elements through an iterative process of comparing the change in the outcome variables of interest (i.e., hydrostatic pressure and octahedral shear stress) as a function of decreasing average element length. Mesh convergence was tested for tetrahedral elements with average side lengths of 4.0, 3.0, 2.0, 1.5, 1.0, 0.75, and 0.50 mm (Fig. 4). Results of this convergence study revealed that peak stress values were similar between the 1 mm and 0.75 mm conditions (average peak difference of 3.7%). However, decreasing the element size from 0.75 mm to 0.5 mm did not result in a meaningful change in hydrostatic pressure and octahedral shear stress and resulted in a considerably longer computational time for the simulation.
Fig. 4.
Results for the mesh convergence analysis performed on the patella cartilage elements.
The methods used to estimate the individual quadriceps muscle forces from the biomechanical testing session have been described previously26. Briefly, a subject-specific representation of the extensor mechanism was created using SIMM modeling software (MusculoGraphics, Santa Rosa, CA). Subject-specific biomechanical data (kinematics, kinetics, EMG) were used to drive the model (via an optimization routine) and 3D quadriceps muscle forces were computed. The elements representing the quadriceps muscles were separated into three functional groups made up of six equivalent uniaxial force actuators (the rectus femoris/vastus intermedius, vastus medialis, and vastus lateralis muscles). The direction of muscle line of pull for the rectus femoris/vastus intermedius group was set parallel to the long axis of the femur27. The most lateral and medial borders of quadriceps line of pull (i.e., the vastus lateralis and vastus medialis) were determined from the sagittal and frontal plane fiber orientation of each muscle as measured from MR images of the subject’s thigh. Six connector elements representing each muscle group were then distributed uniformly from the medial to-lateral borders. In addition, six uniaxial, tension-only elements with total stiffness of 4334 N/mm were used to represent the patella tendon, which connected the patella and the tibia28.
Simulations were performed using a hard contact algorithm with a surface coefficient of friction of 0.02.25 Quasi-static loading simulations were performed using a nonlinear FE solver (Abaqus, SIMULIA, Providence, RI). For all simulations, the bony structures (i.e., femur, tibia, and patella) were modeled as rigid bodies. The initial orientations of the bony rigid bodies were determined from their loaded position captured from the weight-bearing MR images. To obtain the weight-bearing positioning of the femur, tibia, and patella at 15° and 45° of knee flexion, the FE mesh of each bone was registered to the corresponding bony surfaces obtained from the weight-bearing images. To simulate a stable weight-bearing condition, the femur and tibia were fixed in space. In order to represent an initial unloaded condition, the patella was moved anteriorly to create a gap between the articulating surfaces of the patellofemoral joint. Since the soft tissues controlling the rotation of the patellofemoral joint were not included in the models (i.e., ligaments and peri-patellar retinaculum), the three rotational degrees of freedom of the patella were constrained.
Model output & post-processing
The stress in the articular cartilage was quantified in terms of two invariants; (1) hydrostatic pressure, and (2) octahedral shear stress29–31. As scalar parameters, hydrostatic pressure and octahedral shear stress represent different aspects of the stress field30. The hydrostatic pressure reflects the magnitude of the portion of the stress tensor that tends to uniformly compress the cartilage, while the octahedral shear stress reflects the portion of the stress field that tends to distort the tissue30. A mesh surface was created to represent the chondro-osseous interface by selecting the element faces of the tetrahedral elements that were parallel to the subchondral bone surface. The stress values were then estimated at the centroids of cartilage element faces closest to the bone. Elements with only one node at the interface were not included in the analyses. To establish a clinically meaningful measure of mean patella and femur hydrostatic pressure and octahedral shear stress, only elements with stress values above a threshold of 271 kPa were considered when calculating the mean stress. This threshold corresponds to the minimum bone stress-pain threshold previously established for healthy subjects32. As an indirect assessment of the validity of each FE simulation, the estimated contact area and final patella position predicted by the models were compared to the actual contact area and patella position measured from the loaded MR images using previously published procedures33.
Statistical analyses
To test the hypothesis that cartilage stress differed between groups, a two-way repeated measures (group × knee angle) analysis of variance (ANOVA) was performed. In order to account for the matched design of the study, subject age, height, weight, and physical activity level were used as time-invariant covariates in all analyses. This analysis was repeated for peak and mean hydrostatic pressure and octahedral shear stress of the patella and the femur cartilage elements at the chondro-osseous interface. For all ANOVA tests, each analysis met the sphericity assumptions of the Mauchly’s sphericity test and significant main effects were reported only if there was no group knee angle interaction. The significance level for all analyses was set at 0.05.
Results
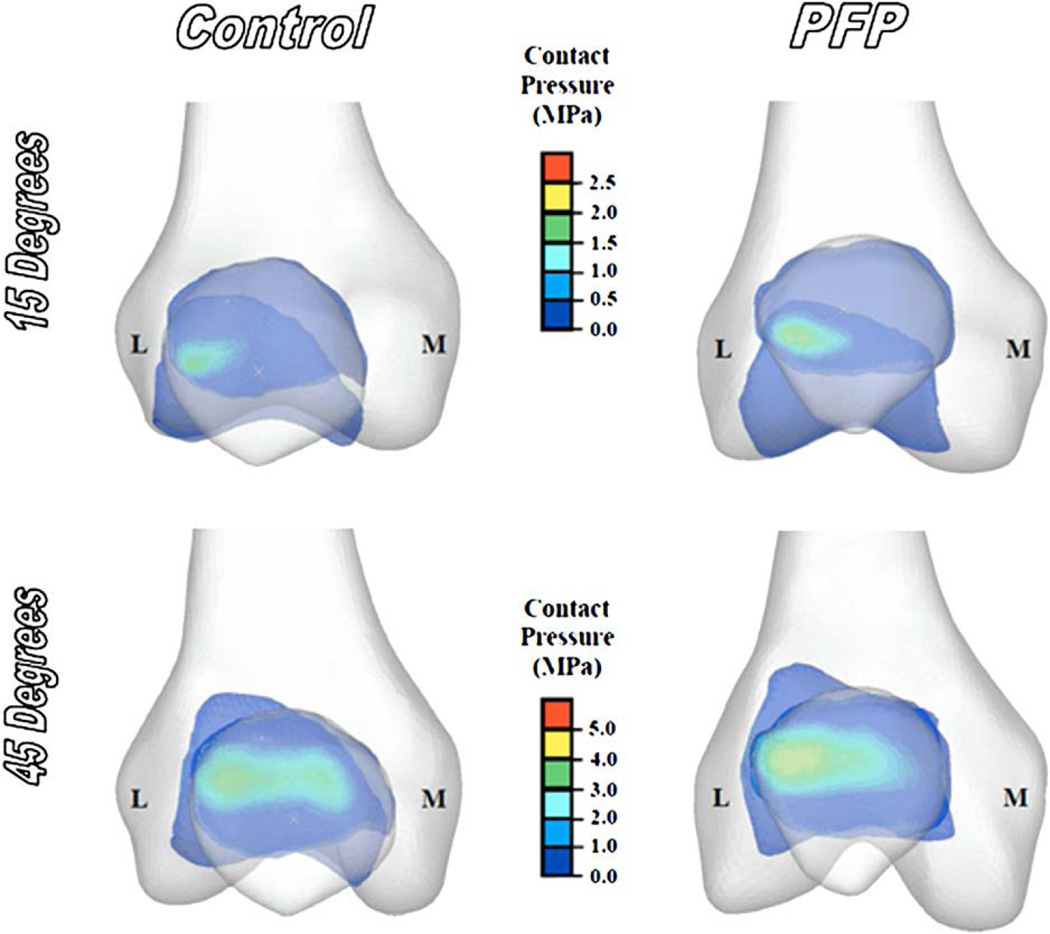
As a general trend, hydrostatic pressure and octahedral shear stress increased with increasing knee flexion angle (refer to Fig. 5 and Tables II and III). In addition, the highest peak and mean hydrostatic and octahedral shear stresses were observed on the lateral side of the patellofemoral joint (i.e., lateral patella facet and lateral femoral trochlea) (Fig. 5).
Fig. 5.
Representative patellofemoral joint contact pressure profiles of a control and a PFP subject at 15° and 45° of knee flexion. (L = lateral, M = medial).
Table II.
Group comparisons of the peak and mean hydrostatic pressure profiles of the elements representing the chondro-osseous interface of the patella and femur
| Patella | Femur | |||||
|---|---|---|---|---|---|---|
| PPP (SD) | Control (SD) | Mean difference (95% CI) | PPP (SD) | Control (SD) | Mean difference (95% CI) | |
| Peak hydrostatic pressure | ||||||
| Stress @ 15° | 2.0 (0.5) | 1.3 (0.5) | 0.6* (0.1–1.1) | 2.1 (0.5) | 1.4 (0.4) | 0.6* (0.2–1.1) |
| Stress @ 45° | 3.2 (0.8) | 2.7 (0.7) | 0.4 (−0.3–1.2) | 3.7 (1.2) | 3.0 (0.6) | 0.7 (−0.3–1.8) |
| Collapsed across angles (95% CI) | 2.6 (2.2–2.9) | 2.0 (1.7–2.3) | 0.5* (0.1–1.0) | 2.9 (2.5–3.3) | 2.2 (1.8–2.6) | 0.7* (0.1–1.3) |
| Mean hydrostatic pressure | ||||||
| Stress @ 15° | 0.8 (0.2) | 0.6 (0.2) | 0.2* (0.1–0.4) | 0.8 (0.1) | 0.6 (0.1) | 0.2* (0.1–0.3) |
| Stress @ 45° | 1.2 (0.3) | 0.9 (0.2) | 0.3* (0.1–0.5) | 1.3 (0.3) | 1.1 (0.2) | 0.2 (−0.1–0.5) |
| Collapsed across angles (95% CI) | 1.0 (0.9–1.1) | 0.8 (0.6–0.9) | 0.3* (0.1–0.4) | 1.1 (0.9–1.2) | 0.9 (0.7–1.0) | 0.2* (0.1–0.4) |
PFP = patellofemoral pain group.
Hydrostatic pressure is reported as mean value across all subjects, with units of MPa.
Denotes significant differences from the control group at P < 0.05.
Table III.
Group comparisons of the peak and mean octahedral shear stress profiles of the elements representing the chondro-osseous interface of the patella and femur
| Patella | Femur | |||||
|---|---|---|---|---|---|---|
| PFP (SD) |
Control (SD) |
Mean difference (95% CI) |
PFP (SD) |
Control (SD) |
Mean difference (95% CI) |
|
| Peak octahedral shear stress | ||||||
| Stress @ 15° | 0.6 (0.2) | 0.3 (0.1) | 0.2* (0.1–0.4) | 0.6 (0.2) | 0.4 (0.1) | 0.2* (0.1–0.4) |
| Stress @ 45° | 1.3 (0.7) | 0.9 (0.3) | 0.4 (−0.1–1.0) | 1.2 (0.4) | 1.0 (0.2) | 0.2 (−0.1–0.5) |
| Collapsed across angles (95% CI) |
1.0 (0.8– 1.1) |
0.6 (0.4– 0.8) |
0.3* (0.1–0.6) | 0.9 (0.8– 1.0) |
0.7 (0.6– 0.8) |
0.2* (0.1–0.4) |
| Mean octahedral shear stress | ||||||
| Stress @ 15° | 0.4 (0.1) | 0.2 (0.2) | 0.2* (0.1–0.3) | 0.4 (0.1) | 0.2 (0.2) | 0.2* (0.1–0.3) |
| Stress @ 45° | 0.6 (0.1) | 0.5 (0.1) | 0.1 (−0.1–0.2) | 0.6 (0.1) | 0.5 (0.1) | 0.1 (−0.1–0.2) |
| Collapsed across angles (95% CI) |
0.5 (0.4– 0.5) |
0.3 (0.3– 0.4) |
0.2* (0.1–0.2) | 0.5 (0.4– 0.5) |
0.4 (0.3– 0.4) |
0.1* (0.1–0.2) |
PFP = patellofemoral pain group.
Octahedral shear stress reported as mean value across all subjects, with units of MPa.
Denotes significant differences from the control group at P < 0.05.
Model validation
On average, contact areas estimated by the model were within 10.3 mm2 (3.0%) of contact areas measured from the weight bearing MR images. In addition, the average lateral patella displacements predicted by the FE models were within 0.02 (2.7%) of those measured from the weight-bearing images.
Hydrostatic pressure
Significant group main effects (no interactions) were found for mean and peak hydrostatic pressure values at both patella and femur chondro-osseous interface (Table II). When collapsed across knee flexion angles, individuals with PFP exhibited significantly greater peak patella hydrostatic pressure [mean difference = 0.5 MPa, 95% confidence interval (CI) = 0.1–1.0, P = 0.03], as well as significantly greater mean patella hydrostatic pressure (mean difference = 0.3 MPa, 95% CI = 0.1–0.4, P < 0.01) compared to the control group. When collapsed across knee flexion angles, individuals with PFP also exhibited significantly greater peak femur hydrostatic pressure (mean difference = 0.7 MPa, 95% CI = 0.1–1.3, P = 0.03), as well as significantly greater mean femur hydrostatic pressure (mean difference = 0.2 MPa, 95% CI = 0.1–0.4, P <0.04), compared to the control group.
Octahedral shear stress
Significant group main effects (no interactions) were found for mean and peak octahedral shear stress values at both patella and femur chondro-osseous interface (Table III). When collapsed across knee flexion angles, individuals with PFP demonstrated greater peak patella octahedral shear stress (mean difference = 0.3 MPa, 95% CI = 0.1–0.6, P = 0.01) and mean patella octahedral shear stress (mean difference = 0.2 MPa, 95% CI = 0.1–0.2, P < 0.01) compared to the control group. When collapsed across knee flexion angles, individuals with PFP also demonstrated significantly greater peak femur octahedral shear stress (mean difference = 0.2 MPa, 95% CI = 0.1–0.4, P< 0.03) and mean femur octahedral shear stress (mean difference = 0.1 MPa, 95% CI = 0.1–0.2, P = 0.01) compared to the control group.
Discussion
The purpose of this study was to evaluate whether individuals with PFP exhibit greater patellofemoral joint stress profiles compared to persons who are pain-free. Two scalar invariants, hydrostatic pressure and octahedral shear stress at the chondro-osseous interface of the patella and the femur were used to describe articular cartilage loading. Consistent with our hypothesis, cartilage stress values were significantly greater in the PFP group compared to the control group. On average, subjects in the PFP group exhibited increases of 33–35% in peak and mean patella cartilage hydrostatic pressure and 60–66% increases in peak and mean patella cartilage octahedral shear stress across the two knee flexion angles. Similarly, increases of 17–36% were found for peak and mean hydrostatic pressure and 35–60% increases in octahedral shear stress of the femoral cartilage across the two knee flexion angles were observed. Our findings support the premise that PFP may be associated with elevated joint stress.
From a mechanical perspective, the deformation caused by hydrostatic pressure leads to changes in tissue volume, creating fluid pressure within the cartilage extracellular matrix30. However, articular cartilage can tolerate hydrostatic pressures well since the incompressible fluid, rather than the fibrous matrix, supports external loading31. Nevertheless, it is conceivable that increased hydrostatic pressure at the chondro-osseous interface could be responsible for stimulating the highly innervated subchondral bone to cause pain32,34. Unlike the tissue volume changes created by the hydrostatic pressure, the octahedral shear stress reflects the portion of the stress environment that tends to distort tissue30. Since nociceptors respond to mechanical deformation, elevated octahedr shear stress at the chondro-osseous interface also could elicit pain. Although subjects in the current study did not report pain during the squatting procedure, the higher hydrostatic pressure and octahedral shear stress observed in the PFP group suggest that these individuals would likely reach their pain threshold more readily with higher demand activities (i.e., stair climbing, running, etc.).
It is assumed that excessive shear stress may contribute to patellofemoral joint cartilage pathology9,35, however this relationship has not been documented in humans. High levels of distortion caused by shear within the solid extracellular matrix can surpass the failure threshold of fibrous cartilage tissue, leading to its mechanical failure31. Based on the findings of the current study, it is plausible that the greater octahedral shear stresses documented in the PFP group may be a risk factor for cartilage breakdown in this population. The finding of greater octahedral shear stress in the PFP group also may have clinical relevance, as a long-term history of PFP has been linked to higher incidence of patellofemoral joint osteoarthritis36. Thus, understanding the mechanisms underlying elevated patellofemoral joint stress in this patient population may be an important step to prevent or delay long-term degenerative joint disease.
It is generally accepted that patellofemoral joint stress is influenced by a number of variables, including the forces acting on the joint, as well as the articulating geometry of the patella and femur20,25. A post-hoc analysis did not reveal a single dominant cause of the elevated stress fields observed in our PFP group. It is likely that elevated patellofemoral joint stress may represent a complex interaction of several factors and may vary from person-to-person. A larger study would be needed to identify potential risk factors associated with elevated patellofemoral joint stress in this population.
In light of the findings reported in the current investigation, there are several limitations that should be noted. From a mechanical perspective, the biomechanical function of articular cartilage is best understood when the tissue is viewed as multiphasic medium, with material properties that vary with location (inhomogeneity), direction (anisotropy), loading rate (viscoelasticity), and load magnitude (nonlinearity).31,37 That being said, the modeling approach used in the current study was based on the assumption that the cartilage material was homogeneously distributed, and the effects of anisotropy and viscoelasticity were not considered. Given that articular cartilage has been modeled previously as a single-phase, linear elastic, continuum material29,30,37, this simplification was deemed acceptable to assess the fundamental aspects of cartilage loading29.
In addition, the distribution of the quadriceps muscle forces used as input into the FEmodel was determined based on an optimization scheme that makes a number of assumptions regarding muscle activation and recruitment patterns38. However, based on the similarity of the predicted and measured contact areas and patella kinematics in our study, we feel that a reasonable estimation of quadriceps muscle force distribution was achieved. Also, while the quadriceps muscle forces in our study were estimated during a bilateral squat with each limb loaded at 50% of body weight, the weight-bearing positions and contact areas of the patellofemoral joint used in our simulations and for validation purposes were obtained during a leg press maneuver utilizing 25% of body weight. The difference in weight-bearing status of the lower limb during our testing procedures was deemed justified as our previous work has shown that once the patella engages the trochlear groove of the femur, increasing the level of quadriceps contraction does not have a significant influence on patellofemoral joint kinematics or the contact area39.
Another potential limitation of the current study was the use of tetrahedral elements to represent the patellofemoral joint cartilage. The best element type for FE analysis of complex structures has been long debated in the literature40–44, and the optimum approach is likely to be application-specific45. Although tetrahedral elements have been used for stress analyses of biological tissue in previous studies46–50, they typically are overly stiff and exhibit slow convergence44. On the other hand, hexahedral elements have been preferred over tetrahedral elements in terms of their convergence and accuracy43, but their application to model biological tissues is limited as creation of hexahedral meshes are time consuming when performed manually or semi-automatically and suffer from lack of robustness when performed automatically40. In addition, complex 3D domains cannot always be meshed into hexahedral elements42. Considering the limitations of hexahedral elements, highly refined tetrahedral elements have been suggested to provide a more anatomically realistic representation of volume data41,45, while producing results that are closer to theoretical solutions41. Using this approach, Yang and colleagues49,50 recently demonstrated that four-node tetrahedral elements could be used to investigate the role of knee alignment on the articular cartilage contact stresses and strains. In a similar fashion, the current study utilized highly refined tetrahedral meshes of the patellofemoral cartilage (approximately 100,000 elements/cartilage component). Although this approach substantially increased the computational cost of our simulations, it also permitted improved accuracy by allowing at least five rows of elements through the thickness of the patella and femoral articular cartilage at any point of contact. Additionally, given the comparative nature of this study, any systematic errors introduced by using tetrahedral elements would be similar between groups, and in turn, would allow our observed group differences to be preserved.
In summary, persons with PFP demonstrated greater patellofemoral joint cartilage stress during a static squatting maneuver at 15° and 45° of knee flexion compared to a group of pain-free controls. The finding of elevated patellofemoral joint stress supports the premise that PFP may be associated with abnormal joint loading. It stands to reason that interventions aimed at decreasing patellofemoral joint stress may be indicated in this patient population.
Acknowledgments
Financial support provided by Promotion of Doctoral Studies Level I & II awards from the Foundation for Physical Therapy. The funding source had no role in the study design, data collection, analysis or writing of this manuscript.
Footnotes
This study was approved by the Health Sciences Institutional Review Board, University of Southern California, Los Angeles, CA, USA.
Author contributions
All three authors contributed to the conception and design of the study, analysis and interpretation of data, as well as drafting and revising the manuscript for intellectual content. Dr. Farrokhi also contributed to the acquisition of the data and assumes responsibility for the integrity and accuracy of the data analysis.
Conflict of interest
The authors have no potential conflicts of interest.
References
- 1.Almeida SA, Trone DW, Leone DM, Shaffer RA, Patheal SL, Long K. Gender differences in musculoskeletal injury rates: a function of symptom reporting? Med Sci Sports Exerc. 1999;31:1807–1812. doi: 10.1097/00005768-199912000-00017. [DOI] [PubMed] [Google Scholar]
- 2.Devereaux MD, Lachmann SM. Patello-femoral arthralgia in athletes attending a Sports Injury Clinic. Br J Sports Med. 1984;18:18–21. doi: 10.1136/bjsm.18.1.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fairbank JCT, Pynsent PB, Vanpoortvliet JA, Phillips H. Mechanical factors in the incidence of knee pain in adolescents and young-adults. J Bone Joint Surg Br. 1984;66:685–693. doi: 10.1302/0301-620X.66B5.6501361. [DOI] [PubMed] [Google Scholar]
- 4.Levine J. Chondromalacia patellae. Physician Sportsmed. 1979;7:41–49. doi: 10.1080/00913847.1979.11948468. [DOI] [PubMed] [Google Scholar]
- 5.Loud KJ, Micheli LJ. Common athletic injuries in adolescent girls. Curr Opin Pediatr. 2001;13:317–322. doi: 10.1097/00008480-200108000-00005. [DOI] [PubMed] [Google Scholar]
- 6.Fulkerson JP, Buuck DA. Disorders of the patellofemoral joint Edited. Philadelphia: Lippincott Williams & Wilkins; 2004. p. xv.p. 374. [Google Scholar]
- 7.Heywood WB. Recurrent dislocation of the patella. J Bone Joint Surg. 1961;43-B:508–517. [Google Scholar]
- 8.Insall J, Falvo KA, Wise DW. Chondromalacia patellae. A prospective study. J Bone Joint Surg Am. 1976;58:1–8. [PubMed] [Google Scholar]
- 9.Moller BN, Moller-Larsen F, Frich LH. Chondromalacia induced by patellar subluxation in the rabbit. Acta Orthop Scand. 1989;60:188–191. doi: 10.3109/17453678909149251. [DOI] [PubMed] [Google Scholar]
- 10.Outerbridge RE. The etiology of chondromalacia patellae. J Bone Joint Surg Br. 1961;43-B:752–757. doi: 10.1302/0301-620X.43B4.752. [DOI] [PubMed] [Google Scholar]
- 11.Biedert RM, Sanchis-Alfonso V. Sources of anterior knee pain. Clin Sports Med. 2002;21:335–347. doi: 10.1016/s0278-5919(02)00026-1. [DOI] [PubMed] [Google Scholar]
- 12.Dye SF, Vaupel GL, Dye CC. Conscious neurosensory mapping of the internal structures of the human knee without intraarticular anesthesia. Am J Sports Med. 1998;26:773–777. doi: 10.1177/03635465980260060601. [DOI] [PubMed] [Google Scholar]
- 13.Ahmed AM, Burke DL, Yu A. In-vitro measurement of static pressure distribution in synovial joints e Part II: retropatellar surface. J Biomech Eng. 1983;105:226–236. doi: 10.1115/1.3138410. [DOI] [PubMed] [Google Scholar]
- 14.Huberti HH, Hayes WC. Patellofemoral contact pressures. The influence of q-angle and tendofemoral contact. J Bone Joint Surg Am. 1984;66:715–724. [PubMed] [Google Scholar]
- 15.Lee TQ, Morris G, Csintalan RP. The influence of tibial and femoral rotation on patellofemoral contact area and pressure. J Orthop Sports Phys Ther. 2003;33:686–693. doi: 10.2519/jospt.2003.33.11.686. [DOI] [PubMed] [Google Scholar]
- 16.Brechter JH, Powers CM. Patellofemoral stress during walking in persons with and without patellofemoral pain. Med Sci Sports Exerc. 2002;34:1582–1593. doi: 10.1097/00005768-200210000-00009. [DOI] [PubMed] [Google Scholar]
- 17.Powers CM, Ward SR, Chen YJ, Chan LD, Terk MR. Effect of bracing on patellofemoral joint stress while ascending and descending stairs. Clin J Sport Med. 2004;14:206–214. doi: 10.1097/00042752-200407000-00003. [DOI] [PubMed] [Google Scholar]
- 18.Ward SR, Powers CM. The influence of patella alta on patellofemoral joint stress during normal and fast walking. Clin Biomech. 2004;19:1040–1047. doi: 10.1016/j.clinbiomech.2004.07.009. [DOI] [PubMed] [Google Scholar]
- 19.Fernandez JW. Integrating modeling and experiments to assess dynamic musculoskeletal function in humans. Exp Physiol. 2006;91:371–382. doi: 10.1113/expphysiol.2005.031047. [DOI] [PubMed] [Google Scholar]
- 20.Besier TF, Gold GE, Beaupre GS, Delp SL. A modeling framework to estimate patellofemoral joint cartilage stress in vivo. Med Sci Sports Exerc. 2005;37:1924–1930. doi: 10.1249/01.mss.0000176686.18683.64. [DOI] [PubMed] [Google Scholar]
- 21.Brown TD. Finite element modeling in musculoskeletal biomechanics. J Appl Biomech. 2004;20:336–366. [Google Scholar]
- 22.Armstrong T, Bull F. Development of the World Health Organization Global Physical Activity Questionnaire (GPAQ) J Public Health. 2006;14:66–70. [Google Scholar]
- 23.Farrokhi S, Pollard CD, Souza RB, Chen YJ, Reischl S, Powers CM. Trunk position influences the kinematics, kinetics, and muscle activity of the lead lower extremity during the forward lunge exercise. J Orthop Sports Phys Ther. 2008;38:403–409. doi: 10.2519/jospt.2008.2634. [DOI] [PubMed] [Google Scholar]
- 24.Elias JJ, Bratton DR, Weinstein DM, Cosgarea AJ. Comparing two estimations of the quadriceps force distribution for use during patellofemoral simulation. J Biomech. 2006;39:865–872. doi: 10.1016/j.jbiomech.2005.01.030. [DOI] [PubMed] [Google Scholar]
- 25.Besier TF, Gold GE, Delp SL, Fredericson M, Beaupre GS. The influence of femoral internal and external rotation on cartilage stresses within the patellofemoral joint. J Orthop Res. 2008;26:1627–1635. doi: 10.1002/jor.20663. [DOI] [PubMed] [Google Scholar]
- 26.Chen YJ, Scher I, Powers CM. Quantification of patellofemoral joint reaction forces during functional activities using a subject specific, three-dimensional model. J Appl Biomech. 2010;26:415–423. doi: 10.1123/jab.26.4.415. [DOI] [PubMed] [Google Scholar]
- 27.Mesfar W, Shirazi-Adl A. Biomechanics of the knee joint inflexion under various quadriceps forces. Knee. 2005;12:424–434. doi: 10.1016/j.knee.2005.03.004. [DOI] [PubMed] [Google Scholar]
- 28.Hansen P, Bojsen-Moller J, Aagaard P, Kjaer M, Magnusson SP. Mechanical properties of the human patellar tendon, in vivo. Clin Biomech. 2006;21:54–58. doi: 10.1016/j.clinbiomech.2005.07.008. [DOI] [PubMed] [Google Scholar]
- 29.Carter DR, Beaupre GS. Linear elastic and poroelastic models of cartilage can produce comparable stress results: a comment on Tanck et al. (J Biomech 32:153–161, 1999) J Biomech. 1999;32:1255–1257. doi: 10.1016/s0021-9290(99)00123-2. [comment] [DOI] [PubMed] [Google Scholar]
- 30.Carter DR, Beaupré GS. Skeletal function and form Edited. Cambridge, UK; New York, NY: Cambridge University Press; 2001. p. xii.p. 318. [Google Scholar]
- 31.Carter DR, Beaupre GS, Wong M, Smith RL, Andriacchi TP, Schurman DJ. The mechanobiology of articular cartilage development and degeneration. Clin Orthop Relat Res. 2004;427(Suppl):S69–S77. doi: 10.1097/01.blo.0000144970.05107.7e. [DOI] [PubMed] [Google Scholar]
- 32.Rolke R, Andrews Campbell K, Magerl W, Treede RD. Deep pain thresholds in the distal limbs of healthy human subjects. Eur J Pain. 2005;9:39–48. doi: 10.1016/j.ejpain.2004.04.001. [DOI] [PubMed] [Google Scholar]
- 33.Powers CM, Ward SR, Chan LD, Chen YJ, Terk MR. The effect of bracing on patella alignment and patellofemoral joint contact area. Med Sci Sports Exerc. 2004;36:1226–1232. doi: 10.1249/01.mss.0000132376.50984.27. [DOI] [PubMed] [Google Scholar]
- 34.Nie H, Arendt-Nielsen L, Andersen H, Graven-Nielsen T. Temporal summation of pain evoked by mechanical stimulation in deep and superficial tissue. J Pain. 2005;6:348–355. doi: 10.1016/j.jpain.2005.01.352. [DOI] [PubMed] [Google Scholar]
- 35.Ryu J, Saito S, Yamamoto K. Changes in articular cartilage in experimentally induced patellar subluxation. Ann Rheum Dis. 1997;56:677–681. doi: 10.1136/ard.56.11.677. [DOI] [PMC free article] [PubMed] [Google Scholar]