Impulsivity and predictive control are associated with suboptimal action-selection and action-value learning in regular gamblers

Abstract

Heightened impulsivity and cognitive biases are risk factors for gambling problems. However, little is known about precisely how these factors increase the risks of gambling-related harm in vulnerable individuals. Here, we modelled the behaviour of eighty-seven community-recruited regular, but not clinically problematic, gamblers during a binary-choice reinforcement-learning game, to characterise the relationships between impulsivity, cognitive biases, and the capacity to make optimal action selections and learn about action-values. Impulsive gamblers showed diminished use of an optimal (Bayesian-derived) probability estimate when selecting between candidate actions, and showed slower learning rates and enhanced non-linear probability weighting while learning action values. Critically, gamblers who believed that it is possible to predict winning outcomes (as 'predictive control') failed to use the game's reinforcement history to guide their action selections. Extensive evidence attests to the ease with which gamblers can erroneously perceive structure in the reinforcement history of games when there is none. Our findings demonstrate that the generic and specific risk factors of impulsivity and cognitive biases can interfere with the capacity of some gamblers to utilise structure when it is available in the reinforcement history of games, potentially increasing their risks of sustaining gambling-related harms.

Introduction

Recent research and policy developments have highlighted the need to understand better the factors that increase the risk of gambling-related harms, broadly conceived of in terms of excessive expenditure of money and time on gambling and its adverse effects upon family, social and occupational functioning(Blaszczynski, 2009; Markham, Young, & Doran, 2014). One challenge is to elucidate the cognitive and emotional processes that translate these risk factors into actual harms.

Some risk factors for gambling-related harms are generic in that they are also appear to operate in related or co-occurring psychological difficulties. For example, trait impulsivity tends to be elevated in individuals who gamble frequently or who have problems controlling their gambling activities (Blaszczynski, Steel, & McConaghy, 1997; Steel, 1998). Impulsivity both complicates treatment delivery and diminishes the likelihood of good clinical outcomes in pathological gamblers (Adinoff et al., 2007; Goudriaan, Oosterlaan, De Beurs, & Van Den Brink, 2008). However, this is also the case in overlapping clinical populations such as those with alcohol or substance-related difficulties (Leeman & Potenza, 2012) and certain mood-related illnesses that can present with or without gambling problems (Di Nicola et al., 2010).

By contrast, other risk factors for gambling problems seem more specific. Cognitive perspectives emphasize the role of erroneous beliefs and reasoning about gambling games in sustaining gambling participation and facilitating the development of gambling problems (Robert Ladouceur, Paquet, & Dube, 1996; Toneatto, 1999). These biases include mistaken thinking about random outcomes – most famously, in the 'Hot-Hand' and 'Gambler's Fallacy' (Ayton & Fischer, 2004; Burns & Corpus, 2004; Croson & Sundali, 2005), but also beliefs that it is possible to predict, or even influence, the chance outcomes of gambling games (R. Ladouceur & Sevigny, 2005; Oei, Lin, & Raylu, 2008). Here, we investigated the relationships between the generic risk factor of impulsivity and the specific risk factors around cognitive biases and the abilities of gamblers to select between, and learn about, actions and probabilistic rewards. Learning more about disruptions to these cognitive operations can help us understand why some gamblers continue to gamble in the face accumulating losses, increasing the likelihood of gambling-related harm.

Actions-selection refers to the computational challenge of using the best available information to determine behavioural choices (Frank, 2011). In a gambling context, this challenge might be met by the adoption of (sometimes) sub-optimal strategies of persisting with previous winning game choices (e.g. positive recency in 'Hot-hand' fallacy) or shifting from losing choices in a sequence (e.g. negative recency in the 'Gambler's Fallacy') (Ayton & Fischer, 2004; Burns & Corpus, 2004; Croson & Sundali, 2005). Evidence attests to peoples' difficulties with randomness (A. Tversky & Kahneman, 1974) and the relative ease with which individuals (including gamblers) can be induced to perceive structure in the reinforcement history of games when none is available (Ayton & Fischer, 2004; Croson & Sundali, 2005). We know less about how effectively gamblers can use structure when it is available to optimise behaviour in chance games.

To explore this issue, we asked regular gamblers to complete a reinforcement-learning game in which two actions generated probabilistic outcomes of varying value. At different times, one action was more likely than the other action to deliver winning outcomes; at other times, these contingencies reversed (Behrens, Woolrich, Walton, & Rushworth, 2007). Optimal action-selection over successive choices should involve the comparison of approximate expected values, reflected in both the best cumulative estimate of actions' probabilities of reward – obtained through a Bayesian updating process – and the signalled values of the prospective outcomes. We tested whether variability in impulsivity and cognitive biases is associated with diminished use of these optimal information sources; but increased reliance upon decisional 'short-cuts' such as 'win-stay' strategies expressed in 'Hot Hand' phenomena (Ayton & Fischer, 2004).

Reinforcement-learning refers to the acquisition of knowledge about the stimuli or actions and their reward values (Cohen, 2008). Substantial computational and neurobiological research has demonstrated that reinforcement learning is mediated by dopaminergic modulation of cortico-limbic circuits known to show functional disturbances in samples of pathological gamblers (Glimcher, 2011; Reuter et al., 2005; Worhunsky, Malison, Rogers, & Potenza, 2014). In a simplified form, reinforcement-learning is captured by the Rescorla and Wagner (1972) Δ-rule in which the computed probability of an action producing a reward is updated on the basis of comparisons between the previous actual and expected outcomes: p_i+1 = p_i + α(r_i – p_i) where p is the estimated probability and r is the outcome (1, win; 0, no win). Positive differences augment the updated p_i+1 while negative differences – say, when an expected winning outcome is not delivered – diminishes p_i+1. The parameter α represents the learning rate; it captures the magnitude of adjustments made to the estimated probabilities, pi+1, following each outcome: larger values of α indicate larger adjustments (and rapid learning), smaller values indicate gradual adjustments (and slower learning). Trait impulsivity is associated with changes in D₂ receptor expression in mesolimbic structures that support reinforcement-learning (Buckholtz et al., 2010; Dalley et al., 2007). We tested whether variability in trait impulsivity and the strength of regular gamblers' cognitive biases is associated with smaller or large learning rates, indicating that some gamblers might learn more quickly or slowly than other gamblers.

We included three further elements in our reinforcement-learning model. Descriptive accounts of decision-making under conditions of risk, such as Prospect Theory (Kahneman & Tversky, 1979; Amos Tversky & Kahneman, 1992), describe how the relationship between nominal value and psychological value (or 'utility') often shows a concave function such that people tend to underweight larger increases in value rewards (as gains) compared to smaller increases. Similarly, people tend to overweight low probabilities of rewards in their choices but underweight high probabilities (Amos Tversky & Kahneman, 1992). However, this probability weighting may be disturbed in pathological gamblers in ways that promote preferences for risk across the range of probabilities (Ligneul, Sescousse, Barbalat, Domenech, & Dreher, 2013). Erroneous cognitions about probability are also a feature of gambling problems in some affected individuals (Toneatto, Blitz-Miller, Calderwood, Dragonetti, & Tsanos, 1997). Here, we tested whether the subjective evaluation of gains and probability weighting reflect variability in impulsivity and gambling-related cognitive biases in regular gamblers, linking risk factors for gambling-related harms to non-normative decisional processes that might sustain unhealthy gambling behaviours.

Finally, our reinforcement-learning model allowed the subjective value of gains, scaled by their probability weighting, to be used by a decisional ('softmax') rule (O'Doherty et al., 2004) to select probabilistically the action with the greater value. The rule incorporates a final parameter — the 'inverse temperature' — that captures the consistency with which the optimal actions are chosen, allowing us to assess, in an exploratory manner, the degree to which impulsivity — often conceived as the tendency to act without forethought (Evenden, 1999; Patton, Stanford, & Barratt, 1995) — and cognitive biases introduce an element of randomness in action-selection over and above changes in reward and probability weighting.

Methods

Participants

Ninety-two gamblers between 18-60 years of age with varying gambling involvement were recruited from the Oxford community using advertisements placed on a local website. All participants had gambled at least once in the past year; one gambler reported 4 problems and 6 reported three problems, as measured by the National Opinion Research Center (NORC) DSM-IV gambling screen (Wickwire, Burke, Brown, Parker, & May, 2008). None reported 5 or more problems with their gambling. Five gamblers were removed from the analysis because their parameter estimates on the probability-tracking task were greater than 3 SDs from the sample mean, leaving a final sample of 87 gamblers (see Table 1).

Table 1.

Demographic and psychometric characteristics of 87 regular (but non-pathological) participating gamblers

	N (%), Mean (SD)		Mean (SD)
Sex (male)	74(85.10)	Chasing Questionnaire
Age	32.78(11.49)	Big wins	13.47(5.92)
Years of education	14.47(2.92)	Big losses	10.38(5.23)
		Near-misses	4.45(1.85)
Gambling problems		Total	28.30(11.92)
Past year	0.76(1.01)
Lifetime	1.59(1.98)	Impulsivity
		Attentional	12.38(3.05)
Gambling losses (past year)		Motor	22.87(3.56)
< £100	61(70.1)	Non-planning	23.67(4.64)
£100 - £500	19(21.8)	Total score	59.26(9.61)
> £500	6(6.9)
		Gambling-related cognitive biases
Gambling frequency (past year)		Gambling expectancies	12.53(4.82)
Once or a few times	24(27.6)	Illusions of control	7.38(4.30)
1-3 times a month	12(13.8)	Predictive control	16.87(6.47)
1-3 times a week	40(46.0)	Perceived inability to stop	8.82(5.09)
Daily	11(12.6)	Interpretive control/bias	12.11(5.04)
		Total score	57.90(19.70)
Affect
State positive	33.01(6.29)
State negative	12.17(3.70)

Gambling problems - National Opinion Research Centre (NORC) DSM-IV gambling screen (Hodgins, 2004); Affect – Positive and Negative Affective Scales (PANAS; Watson et al., 1988); Chasing Questionnaire (CHQ; O'Connor & Dickerson, 2003); Impulsivity – Barratt's Impulsivity Scale (BIS-11; Patton et al., 1995); Gambling-related cognitive biases – Gambling Related Cognitions Scale (GRCS; Raylu & Oei, 2004).

In the previous year, 11 (12.6%) had gambled daily, 40 (46.0%) gambled 1-3 times a week, 12 (13.8%) gambled 1-3 times a month, and 24 (27.6%) gambled once to a few times a year. All gamblers were screened using a semi-structured interview to exclude any current DSM-IV psychological disorders including substance misuse disorders and pathological gambling (First, Spitzer, Gibbon, & Williams, 2002). The mean number of past year gambling problems, as measured by the NORC Gambling DSM-IV Screening instrument (Wickwire et al., 2008) was low at 0.76 (ranging from 0 to 4). Therefore, our observations about the impacts of impulsivity and cognitive biases upon action-values reported below cannot be attributed to the non-specific deleterious effects upon learning, attention and executive function of severe pathological gambling (Goudriaan, Oosterlaan, de Beurs, & van den Brink, 2005).

Demographic and psychometric measurements

Demographical information, including age and years of formal education, were collected. Participants also reported their past year gambling losses (scored 1, no losses; 2, less than £100; 3, between £100 to £500; 4, more than £500), and past year gambling frequency (1, once a year or less; 2, few times a year; 3, one to three times a month; 4, one to three times a week; 5, daily). Participants completed psychometric assessments of affective (Positive and Negative Affective Scales; Watson, Clark, & Tellegen, 1988) traits and loss-chasing behaviour (the Chasing Questionnaire; O'Connor & Dickerson, 2003) traits

Our gamblers also completed psychometrically-validated questionnaires to measure trait impulsivity and gambling-related cognitive biases (Patton et al., 1995; Raylu & Oei, 2004), before playing a simple binary-choice reinforcement-learning game for small monetary prizes (Behrens et al., 2007). In this experiment, we focused specifically upon impulsivity, as measured by the 'non-planning' subscale of the Barratt's Impulsivity Scale (BIS-11) (Patton et al., 1995). Non-planning impulsivity is characterized by a tendency to orient to the immediate results of actions rather than longer-term consequences. We reasoned that this expression of impulsivity is the most likely to impact on the way that gamblers select between, and learn about, actions with uncertain outcomes (Goudriaan et al., 2008). Our community sample of gamblers reported just slightly lower total BIS-scores (M = 59.26, SD = 9.61) relative to normative samples of (non-problem) gamblers described in the literature (e.g., M = 62.14, SD = 10.05; t(144) = 1.74, p = .09, d = 0.29)(Patton et al., 1995), but significantly lower than samples of pathological gamblers (M = 76.11, SD = 11.72; t(115) = 7.92, p < .0001, d = 1.42) (Loxton, Nguyen, Casey, & Dawe, 2008) and general psychiatric patients (M = 71.37, SD = 12.61; t(169) = 7.08, p< .001, d = 1.09) (Patton et al., 1995).

Finally, cognitive biases were measured using the Gambling-Related Cognitions Scale (GRCS) (Raylu & Oei, 2004). The GRCS has 5 subscales to capture: 'illusions of control' – the belief that prayer, lucky objects or rituals can enhance the likelihood of winning; 'interpretive biases' – the belief that past wins are due to personal ability whilst past losses are due to circumstance; 'gambling expectancies' – the belief that pleasure can be derived from gambling participation; 'predictive control' – the belief one has the skill to forecast wins; and finally, 'inability to stop gambling' – the belief that the desire to gamble is so strong that one will never be able to stop the habit. In comparative terms, the GRCS scores of our sample of gamblers (M = 57.90, SD = 19.70) were somewhat higher than that reported in an Australian general community sample (M = 35.28, SD = 16.81; t(705) = 11.49, p < .001, d = 0.87); but marginally lower than a sample of problem gamblers (M = 64.17, SD = 22.31; t(156) = 1.87, p = .06, d = 0.30) (Raylu & Oei, 2004).

Analysis of the psychometric data gathered from our sample demonstrated good internal reliability: all Cronbach's α > .82; whilst all subscales had at least moderate internal reliability: Cronbach's α > .65.

Probability-tracking game

Our probabilistic-learning task took the form of a two-armed bandit reinforcement-learning game that has previously been used successfully to identify the neural substrates of optimal estimations of probability while foraging in volatile reinforcement environments (see Fig. 1A; A full description of the task is available elsewhere; Behrens et al., 2007). Our participants were asked to choose between 2 actions ('blue' or 'green') to win 'points' prizes that were subsequently cashed out in monetary prizes. Sometimes, one action was more likely to win prizes than the alternative; at other times, the game offered a volatile reinforcement environment in which the reinforced and unreinforced actions swapped unpredictably.

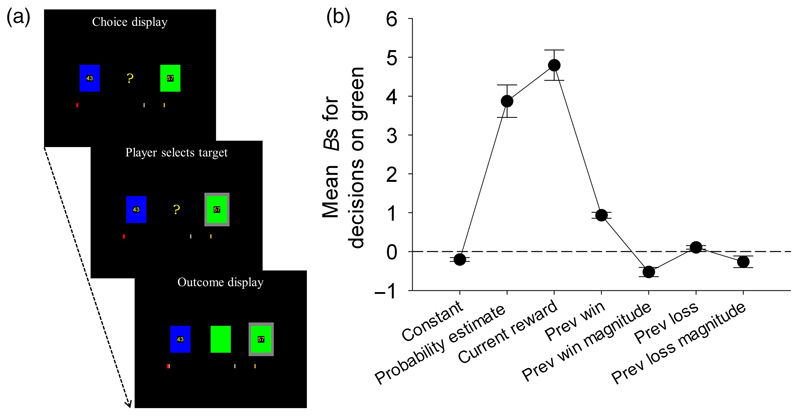
Fig. 1.

(A) An example of the probability-tracking task sequence (Behrens et al., 2007). In this instance, the player chose the green option (indicated by a grey background) and win the 57 points reward allotted to that option as signalled by the presentation of the correct option in the middle of the display; (B) Mean and S.E. of Bs for all regressors from the single participant GLMs of 87 regular (but non-pathological) participating gamblers. Regressors include: (i) a constant term (ii) tracked probability for the green option on the current choice; (iii) reward magnitude for the green option on the current choice; (iv-v) wins and the magnitude of the wins on the preceding choice (i.e., 'win-stay' or 'win-big-stay' strategies); and (vi-vii) loss and the magnitude of the losses on the preceding choice (i.e. 'lose-shift' or 'lose-big-shift' strategies).

Participants were told that one colour was more likely to be rewarded than the other but that this might vary over time. The probabilities of reward associated with each colour were not displayed so participants were required to estimate the likelihood of reward based on prior outcomes; i.e. this was choice under conditions of 'ambiguity' (Baron & Frisch, 1994). The number of points associated with each option was displayed within each coloured box (varying independently between 0 and 100), but participants were told that the probabilities of rewards were linked to the colours of the boxes and not the reward magnitudes.

If participants selected the rewarded colour, they won the points displayed in the box; however, if they selected the non-rewarded colour, they did not score any points and points were not deducted from their game total. A red bar at the bottom of the screen represented the cumulative sum of winnings over the course of the game. To increase participants' motivation, £10 was awarded if the red bar at the bottom of the display reached the silver mark and £15 if it crossed the gold mark. Unknown to the participants, blue was programmed to produce rewards 75% of the time over the course of the first 120 trials (stable condition). In subsequent 30-40 trial blocks, the winning colour alternated between blue and green, with the winning colour now rewarded 80% of the remaining trials (Behrens et al., 2007).

Statistical analysis

Participant-level analyses

We fit two models to participants' choice behaviour. First, individual decision parameters from the action-selection model were obtained by regressing (through a simple logistic General Linear Model) the selection of green option onto features of each choice across the sequence of trials (see below). Second, and separate to this, we fit a simple reinforcement-learning model to each participants' choices. Individual decision parameters for the reinforcement-learning model were obtained by direct numerical integration. The action-selection and reinforcement-learning models are described below:-

Action-selection model

Participants' choices (of the arbitrarily chosen option green) were regressed against: (i) a constant term; (ii) the optimally tracked probability of reward for the colour green (described in detail below); (iii) the value of reward on the green option for the current choice; (iv) winning on the green option with the preceding choice (coded as 1), winning on the blue option with the preceding choice (coded as -1) or losing on the previous choice (coded as 0); (v) the value of the reward on green on the previous choice if chosen and won (coded as positively), the value of the reward on blue on the previous choice if chosen and won (coded negatively) or losing on the previous trial (coded as 0); (vi) losing on the green option with the preceding choice (coded as a 1), losing on the blue option with the preceding choice (coded as a -1) or winning on the previous choice (coded as 0); and, finally, (vii) the value of the reward on the green option on the previous choice if chosen and lost (coded positively), the value of the reward on blue on the previous choice if chosen and lost (coded negatively), or losing on the previous choice (coded as 0).

Regressors were demeaned in 2 stages. To make regressors (iv) orthogonal to (v), and (vi) orthogonal to (vii), we centred regressors (v) and (vii) separately for each participant. Then, to reduce between-participant noise, regressors (ii) to (vii) were subsequently centred again for each participant.

Parameter (ii) is the optimal probability estimate that players would make if they tracked the fluctuating probability of reward across the game in order to use expected value to determine their choices. Using the forward (Markovian) model described in Behrens el al. (2007), we assumed that players following an optimal strategy do not take into account the whole reinforcement history at every play; rather, they update their prediction estimates using information from the preceding choice outcome (i.e. as a simple Bayesian learner). These prediction estimates are made by holding, in mind, the representations of rewards probability r_i, the variance of these reward probabilities v_i (i.e. estimating volatility), and the variance of this volatility k (i.e., estimating local changes in volatility). In Markovian terms, v_i controls the weight that decision outcome i+1 has on r_i; whilst k controls the weight that decision outcome i+1 has on v_i. The changeability of r and v from choice i to choice i+1 are probabilistic and are represented by Beta and Gaussian distributions respectively. (See Behrens et al. (2007) for the full algebraic description.) Therefore, in order to estimate the probability distribution at r_i+1 from the joint probability distribution of the 3 parameters r_i+1, v_i+1 and k, a numerical integration (marginalising) is done over v_i+1 and k. The optimal probability estimate at any point of the game (i.e., parameter (ii) of our action-selection model above) is then described by the mean value of the marginal probability distribution at r_i+1.

Reinforcement-learning model

We fitted a reinforcement learning model to each participant’s choices. The model contains four parameters: the learning rate, α; the probability distortion factor, γ; the reward magnitude weighting factor, η; and the softmax inverse 'temperature', β. Value for γ< 1 result in the typical Prospect Theory curvature with overweighting and underweighting of low and high probabilities (Amos Tversky & Kahneman, 1992). Values for η < 1 result the typical flattening of the utility curve, indicative of underweighting of higher magnitudes (Amos Tversky & Kahneman, 1992). Low values for β mean that even at very small differences between the option values, the model is highly likely to select the better option.

On each trial, the model updates the estimated probability of the chosen option according to a simple delta rule (Rescorla & Wagner, 1972):

$${\mathit{p}}_{\mathbf{\text{i}}\mathbf{+}\mathbf{1}}\mathbf{=}{\mathit{p}}_{\mathbf{\text{i}}}\mathbf{+}\mathit{\alpha }({\mathit{r}}_{\mathbf{\text{i}}}\mathbf{-}{\mathit{p}}_{\mathbf{\text{i}}})$$

where p is the estimated probability, r is the outcome (1, win; 0, no win). Only one outcome (green or blue) has to be tracked since p(Green) = 1 - p(Blue). From these estimates of reward probability, the subjectively distorted probabilities w were calculated as (Lattimore, Baker, & Witte, 1992):

$${\mathit{w}}_{\mathbf{\text{i}}}\mathbf{=}{\mathit{p}}_{\mathbf{\text{i}}}^{\mathit{\gamma }}\mathbf{/}\mathbf{[}{\mathit{p}}_{\mathbf{\text{i}}}^{\mathit{\gamma }}\mathbf{+}{\mathbf{(}\mathbf{1}\mathbf{-}{\mathit{p}}_{\mathbf{\text{i}}}\mathit{)}}^{\mathit{\gamma }}\mathbf{]}$$

Objective reward magnitudes were transformed into subjective magnitudes (A. Tversky & Kahneman, 1991), v:

$${\mathit{v}}_{\mathbf{\text{i}}}\mathbf{=}{\mathit{x}}_{\mathbf{\text{i}}}^{\mathit{\eta }}$$

where x_i is the objective reward magnitude on option i. Subjective expected values were then calculated as

$$\mathbf{\text{s}}\mathit{E}{\mathit{V}}_{\mathbf{\text{i}}}\mathbf{=}{{\mathit{v}}_{\mathbf{\text{i}}}}^{\mathbf{*}}{\mathit{w}}_{\mathbf{\text{i}}}$$

The model’s probability of selecting the option chosen by the subject on any given trial was then given by a softmax rule (O'Doherty et al., 2004):

$$\mathbf{\text{P}}\mathbf{(}\mathbf{\text{C}}\mathbf{=}\mathbf{\text{c}}\mathbf{)}\mathbf{=}\mathbf{1}\mathbf{/}\mathbf{(}\mathbf{1}\mathbf{+}\mathbf{\text{exp}}\mathbf{(}\mathbf{-}{\mathit{\delta }}^{\mathbf{*}}\mathbf{(}\mathbf{\text{s}}\mathit{E}{\mathit{V}}_{\mathbf{\text{c}}}\mathbf{-}\mathbf{\text{s}}\mathit{E}{\mathit{V}}_{\mathbf{\text{u}}}\mathbf{)}\mathbf{)}\mathbf{)}$$

where c and u denote the chosen and un-chosen option, respectively.

The parameters that provided the best fit of each participants' behaviour were estimated using a custom-implemented procedure in MATLAB. The parameter space was set up as a three-dimensional grid in log space with 30 points in each dimension. The joint posterior distribution of the unknown model parameters was specified as the product of choice probabilities over trials under each possible parameter combination in the grid. The marginal posterior distributions on each parameter were obtained by marginalizing (numerical integration) over the three dimensions of the grid. Optimal parameters were then taken as the distribution means of those marginal posterior distributions. (Note: comparison of a simple action-selection model assuming only an optimal Bayesian learner and one free parameter for inverse temperature provided a poorer fit to the sample data than an alternative reinforcement-learning model with 4 free parameters for (i) learning rate; (ii) magnitude distortion; (iii) probability distortion; and (iv) inverse temperature (see Table S3) (BIC= 293.64 vs BIC= 324.23), t(86) = 5.91, p< .001, r = .71.)

Group-level analyses

One-sample t-tests were performed on the obtained regression coefficients (Bs) from the single participant action selection GLMs to determine the significance of regression slopes across the population. These actions-selection parameters were entered into a Multivariate Analysis of Covariance (MANOVA) as dependent variables (DV), with participants' individual scores from the psychometric assessment as independent variables (IV), and controlling for differences in demography (i.e., age, sex, and years of education), gambling (i.e., past year gambling problems and the tendency to 'chase' winning outcomes, losing outcomes or near-misses), and affect (i.e., positive state affect). We included the latter covariates to show that any relationships between model parameters and psychometric scores were not confounded by gross differences in demographics, gambling severity, or affect. Follow-up univariate Analyses of Covariance (ANCOVAs) were performed to explore their associations between each of the action-selection parameters against the significant predictors from the above MANCOVA. These included scores for the 'non-planning' impulsivity sub-scale of the BIS-11 (Patton et al., 1995) and scores for the 'predictive control' sub-scale of the GRCS (Raylu & Oei, 2004); these being the psychometric subscale scores that showed consistent relationships with model parameters across the sample.

Next, reinforcement-learning decision parameters were normalised by a (natural) log transformation and entered into a MANCOVA as response variables with non-planning impulsivity and GRCS scores as predictor variables. Again, individual differences in demography, gambling, and affect were added as covariates. Follow-up univariate ANCOVAs were performed on the significant predictors from the above MANCOVA to explore their association with each of the reinforcement-learning decision parameters.

Results

Action-selection model

In order to model how gamblers selected between actions associated with uncertain outcomes, we fitted an action-selection model to each gambler’s choices (see Methods and Supplementary Materials for full details). At the single participant-level, each gambler's choice (of the colour 'green') was regressed against: (i) the optimally estimated probability of that option (as modelled by an ideal Bayesian learner (Behrens et al., 2007)); (ii) the magnitude of reward associated with that option; (iii-iv) the winning or winning magnitude of the preceding choice (i.e., 'win-stay' or 'win-big-stay' strategies); and, finally, (v-vi) the losing or losing magnitude on the preceding choice (i.e. 'lose-shift' or 'lose-big-shift' strategies).

Consistent with a previous report using this probabilistic-learning task in a student sample (Behrens et al., 2007), our gamblers used both the optimally-tracked probabilities of reward, (t(86) = 9.23, p < .001, d = 0.99), and their magnitudes when deciding between actions, (t(86) = 12.23, p < .001, d = 1.31; see Fig. 1B and Table S1). In addition, however, our gamblers tended to persist with a selection if it had been successful on the preceding choice , instantiating enhanced 'win-stay' behaviour; t(86) = 11.88, p < .001, d = 1.27), except when the prize won was large (instantiating diminished 'win-big-stay' behaviour; t(86) = -4.40, p < .001, d = 0.47). Gamblers also tended to stick with a selection if it had been unsuccessful on the preceding choice (illustrating decreased 'lose-shift' behaviour; t(86) = 2.33, p < .05, d = 0.25), but tended to switch responses if the loss was large (illustrating 'lose-big-shift' behaviour; t(86)= -1.78, p= .08, d = 0.19).

At the group level, we found that higher levels of impulsivity (β = -.34, p < .01) and stronger gambling-related cognitive biases (β = -.35, p < .01) both tended to go along with lower final scores on the game, suggesting that these features hampered effective action-selection (see Table S2). Additionally, gamblers' impulsivity scores (V = 0.19, F(6, 73) = 2.93, p = .01, η² = .19), their gambling-related cognitive biases (V = 0.15, F(6, 73) = 2.29, p < .05, η² = .16), and their age (V = 0.27, F(6, 73) = 4.52, p < .001, η² = .27) were all significant predictors of how much gamblers used different action-selection parameters. Impulsive gamblers (F(1,78) =14.73, p < .001, η² = .16; see Fig. 2A), as well as older gamblers (F(1,78) =8.66, p < .01, η² = .10), exhibited diminished use of the optimal (Bayesian) probability estimates when selecting actions. Rather, impulsive gamblers tended to persist with the same choices that had delivered larger rewards on preceding choices (i.e. increased 'win-big-stay' behaviour; F(1,78) =3.02, p = .09, η² = .04).

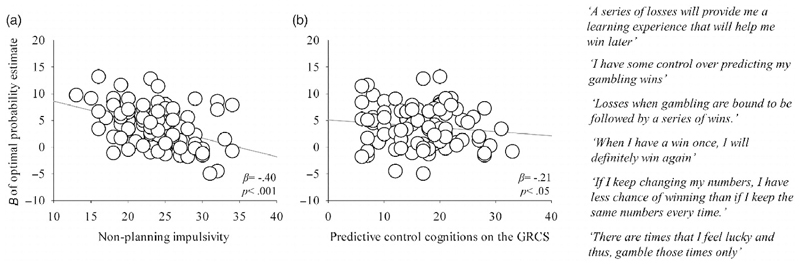
Fig. 2.

(A) Individual Bs indicating the use of the optimal (Bayesian) probability estimate in making choices as a function of non-planning impulsivity score from the Barratt's Impulsivity Scale (BIS-11) (Patton et al., 1995); (B) Individual Bs indicating the use of the optimal (Bayesian) probability estimate in making choices as a function of predictive control cognitions on the Gambling-related cognitions scale (GRCS) (Raylu & Oei, 2004) alongside items on the predictive control subscale displayed on the right of the figure.

Gambling-related cognitive biases also appear to impede the use of optimal probability estimates in action-selection. Gamblers who reported strong cognitive distortions about gambling exhibited diminished use of optimal probability estimates when deciding between the two response options in our game (F(1,78) =4.80, p < .05, η² = .06). Instead, gamblers with stronger cognitive biases tended to shift from options that they previously won (decreased 'win-stay' behaviour; F(1,78) =3.93, p = .05, η² = .05), and a tendency to shift from options that they previously lost (increased 'lose-shift' behaviour; F(1,78) = 6.67, p < .05, η² = .08).

Further analysis, regressing the optimal probability estimates against the predictive control subscale of the GRCS (as the belief that it is possible, within the context of commercial gambling games, to identify winning opportunities) (Raylu & Oei, 2004), indicated the failure to use the optimal (Bayesian) tracked probability of reward when making choices was particularly clear in those gamblers who endorsed cognitions associated with 'predictive control' (β = -.21, p < .05; see Fig. 2B and Table 2).

Table 2.

Group-level regression of Bs from the single participant GLMs (for optimal probability-tracking) against demographic and psychometric scores in 87 regular (but non-pathological) participating gamblers

	B	SE B	β
Constant	13.56	4.05
Education	0.30	0.13	.22*
Age	-0.10	0.03	-.29**
Sex	0.82	1.01	.08
Past year gambling problems	-0.13	0.38	-.03
Total score/CHQ	0.05	0.03	.16
State positive affect/PANAS	-0.08	0.06	-.17
Predictive control/GRCS	-0.13	0.06	-.21*
Non-planned impulsivity/BIS-11	-0.34	0.09	-.41***

Note: R² = .62 (p < .001); Covariates shaded in grey; *p < .05; **p < .01; ***p < .001 CHQ – Chasing Questionnaire (O'Connor & Dickerson, 2003); PANAS – Positive and Negative Affective Scales (Watson et al., 1988); GRCS – Gambling-related cognitions scale (Raylu & Oei, 2004); BIS-11 – Barratt's Impulsivity Scale (Patton et al., 1995).

Reinforcement-learning model

At the participant-level, our second model included four parameters: (i) the learning rate to indicate how much each outcome was used to update the estimated reward probabilities (i.e. the rapidity of adjusting action values); (ii) the subjective distortion of probabilities to demonstrate overweighting and underweighting of low and high probabilities (Amos Tversky & Kahneman, 1992); (iii) the underweighting of increasing magnitudes to describe a concave utility curve (Amos Tversky & Kahneman, 1992); and, finally, (iv) the consistency vs randomness (i.e., stochasticity) of gamblers' choices as quantified by the 'softmax' inverse 'temperature' (see Supplementary Materials for full details) (O'Doherty et al., 2004).

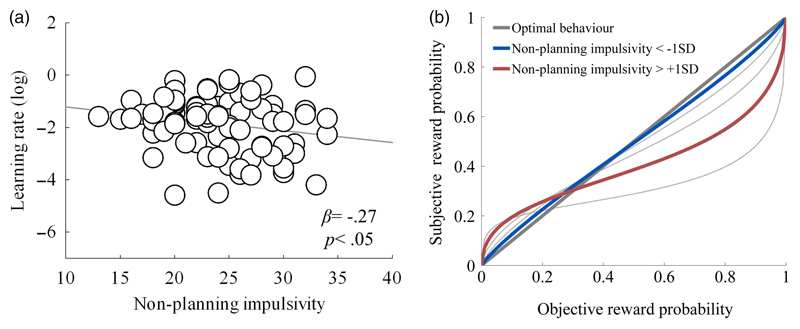
Entering the parameters of the reinforcement learning model into an MANCOVA revealed significant effects of impulsivity (V = 0.14, F(4,75) = 3.09, p < .05, η² = .14), but not cognitive biases (V = 0.04, F(4,75) = 0.82, p > .05). Gamblers who reported heightened non-planning impulsivity exhibited smaller learning rates compared to gamblers with lowered impulsivity (F(1,78) = 4.15, p < .05, η² = .05; see Fig. 3A). They also tended to overweight low probable outcomes and underweight high probable outcomes (F(1,78) = 4.87, p< .05, η² = .06; see Fig. 3B). Conversely, high impulsive gamblers did not under- or overweight larger value outcomes compared to low impulsive gamblers (see Fig. S1A and S1B); neither was there was any indication that impulsivity was associated with enhanced randomness in our gamblers' choices across the probability-tracking game (see Fig. S2A and S2B). Finally, in contrast to the clear associations between impulsivity and model parameters, there was no consistent evidence that gambling-related cognitive biases were associated with gamblers' learning rates, probability or reward magnitude weighting, or consistency or randomness of participants' choices (Fig. S1C and S2C).

Fig. 3.

(A) Learning rates (natural log) as a function of non-planning impulsivity score on the Barratt’s Impulsivity Scale (BIS-11)(Patton et al., 1995); (B) Probability distortions as indicated by overweighting and underweighting of low and high probabilities in participants with low and high non-planning impulsive participants (≈ +/- 1 S.D.).

Discussion

These data illustrate that one generic risk factor for gambling-related harm — namely, heightened (non-planning) impulsivity — and one specific risk factor — namely, predictive control — are associated with disruptions to action-selection and action-value learning mechanisms in a sample of regular gamblers. Extensive evidence attests to the ease with which regular gamblers can mistakenly perceive structure in the reinforcement history of games when there is none (Burns & Corpus, 2004; Croson & Sundali, 2005). These findings demonstrate that regular gamblers can find it difficult to use reinforcement structures to optimise their action selections or learn accurate action-value relationships in chance-based games.

The present effects were observed in a relatively large sample of gamblers who did not evidence of consistent gambling-related harms or satisfy the diagnostic criteria for DSM-IV (or V) problem or pathological gambling. The absence of problem gamblers from our sample mean that our findings cannot plausibly be attributed to the non-specific effects of gambling problems on risky decision-making per se (Goudriaan et al., 2005). Rather, our findings reflect the way that variability in generic and specific risk factors for gambling problems – specifically, heightened impulsivity and potent cognitive biases – operate to impair action-selection mechanisms and the acquisition of action-value associations.

Previous accounts of the way that impulsivity heightens the risk of addictive behaviours emphasize the tendency to act without forward planning as an expression of 'loss of control' over reward-seeking behaviours including heavy and broadened gambling participation , higher rates of comorbid alcohol and substance misuse (Petry, 2001a, 2001b), and poorer clinical outcomes . Such accounts are essentially descriptive, without any characterization of the mechanisms that mediate the link between impulsivity and gambling behaviours. Our data add to this picture by demonstrating that non-planning impulsivity in gamblers can be associated with diminished use of probability estimates that could be combined optimally with reward magnitudes to specify action (expected) values when selecting between candidate actions. This diminution in the use of probability estimates is accompanied by the use of 'short-cut' strategies such as persisting with action options that have produced large rewards previously (win-stay-large in Fig. 2), possibly reflecting 'Hot-Hand' behaviour (Ayton & Fischer, 2004; Burns & Corpus, 2004; Croson & Sundali, 2005). Finally, the additional finding that impulsive gamblers made smaller adjustments to action-values on the basis of their preceding outcomes (i.e. showed smaller learning rates) suggests that they are also vulnerable to believing, or at least behaving as if, the reward structures of chance-based games are more stable than they really are, possibly prolonging unhealthy gambling behaviours.

This interpretation complements the results of an earlier report that non-planning impulsivity (also scored with Barratt Impulsivity Scale (BIS-11)(Patton et al., 1995) is associated with increased uncertainty about the reinforcement structures available in a suite of slot machines (Paliwal, Petzschner, Schmitz, Tittgemeyer, & Stephan, 2014). In this experiment, Paliwal et al (2014) used Bayesian modelling to capture disrupted belief-updating as individuals completed a series of slot-machine games. Non-planning impulsivity was linked to increased uncertainty in the estimation of winning probabilities and game volatility, generating noisy (i.e. more random) choices. Other data have also linked heightened impulsivity with decision-related uncertainty (Averbeck et al., 2013). These observations and our own highlight the possibility that individuals with heightened non-planning impulsivity are not able to access, or choose not to access, updated probability estimates to help select optimal actions. On the other hand, unlike Paliwal et al (2014), we found no evidence that non-planning impulsivity increased the noise in our participants' choices. Rather, impulsivity was associated with increased win-stay behaviour following large winning outcomes suggesting that, in the face of uncertainty, impulsive gamblers default to heuristic strategies.

Our data also demonstrate enhanced probability weighting action-value learning in regular gamblers in the finding that impulsive gamblers further overweight low probable outcomes and underweight high probable outcomes as specified by descriptive accounts of choice under conditions of uncertainty; specifically 'Prospect Theory' (Kahneman & Tversky, 2000). This exaggerated bias might facilitate the adoption of more risky betting strategies through the tendency to overestimate the chances of winning outcomes but underestimate the greater likelihood of losing outcomes; and may be linked to recent evidence that pathological gambling is associated with altered neural representations of discounted probability within meisolimbic circuits (Miedl, Peters, & Buchel, 2012). Recently, Ligneul et al (2012) measured the probability weighting of a sample of pathological gamblers compared to samples of healthy and non-gambling controls. In contrast to our findings of enhanced overweighting of low probabilities and underweighting of high probabilities in regular but non-problematic gamblers, these authors found a general shift towards greater risk in pathological gamblers. Possibly, their data and ours indicate that transitions from moderate risk of gambling-related harm (as seen in our sample) towards severe risk of (as seen in individuals with a diagnosis of pathological gambling) involve shifts from enhanced under- and over-weighting of low and high probabilities into global preferences for risk with increasing severity.

The relationships between non-planning impulsivity on the one hand and diminished use of optimal probability estimates, low learning rates and enhanced probability weighting on the other hand shows some psychological specificity. There was no indication that heightened impulsivity in our sample of regular gamblers was associated with changes in the use of reward magnitude itself as specified in the action-selection model or in the underweighting of reward magnitudes in terms of their utilities (Kahneman & Tversky, 2000) as specified in our reinforcement-learning model. Lorains et al (2014) have reported that underweighting of reward magnitude, and consistency of choice ('inverse temperature') are disturbed in individuals with diagnoses of DSM-IV pathological gambling (Lorains et al., 2014), while the signaling of subjective value of delayed rewards within mesolimbic reinforcement circuits may also be distorted under at least some conditions (Miedl, Buchel, & Peters, 2014). Collectively, these data and our own suggest that some changes in action-value learning (e.g. discounting of reward magnitude/utilities and consistency of choice) emerge with increasing severity of gambling-related harm or gambling problems.

Complementing the impact of impulsivity upon the acquisition of action values, our data also indicate that gambling-related cognitive biases interfere with the use of estimated reward probabilities in action selection. Rather, cognitive biases promote the suboptimal strategy of placing more weight upon immediately preceding winning and losing outcomes to make further gambling decisions (i.e., decreased ‘win-stay’ and increased ‘lose-shift’ behaviours). In particular, we found that gamblers who endorsed items indicative of predictive control showed the lowest use of optimal probability estimates when selecting between actions. These items include statements such as 'A series of losses will provide me with a learning experience that will help me win later', 'Losses when gambling are bound to be followed by a series of wins', and 'There are times that I feel lucky and thus, gamble those times only', reflecting the conviction that, in the context of commercial gambling games, it is somehow possible to identify opportunities when winning outcomes are more or less likely. Our findings demonstrate that precisely those gamblers with the strongest predictive control biases tend not to use the reinforcement histories to estimate (reasonably) accurately reward probabilities. Such prior beliefs mean that gamblers with convictions of predictive control 'think they know best' and are unable to select between actions on the basis of their estimated expected value, potentially disrupting their ability to learn the value of gambling games (Turner, 2011).

There are at least some implications of our findings for treatment development. Impulsiveness can sometimes predict relapse in samples of treated pathological gamblers (Adinoff et al., 2007; Alvarez-Moya et al., 2011; Ramos-Grille, Goma-i-Freixanet, Aragay, Valero, & Valles, 2015). By contrast, shallow probability, though not delay, discounting is associated with reduced gambling participation during the delivery of psychosocial treatments and then increased likelihood of abstinence at 1-year follow-up (Petry, 2012). Our data suggest highlight one mechanism for these relationships; namely that heightened impulsiveness and, possibly, strengthened cognitive biases complicate treatment efficacy by blocking new learning about the reward contingencies of gambling games (Toneatto et al., 1997).

Finally, we acknowledge that our experiment has several limitations. First, our experiment was subject to one important limitation; it did not examine the effects of impulsivity and gambling-related cognitive biases in individuals with diagnoses of DSM-IV problem gambling or DSM-V disordered gambling, making it unclear whether our findings extend to individuals who have experienced severe or prolonged gambling harm. Similarly, our sample included a number of individual who only gambled only a few times a year, highlighting the relevance of our findings to those with limited to regular gambling participation. Second, our sample size was relatively small, highlighting the need for follow-up experiments to replicate our findings. Third, the patterns of gambling activities reported by our participants were relatively broad, raising the possibility that action-selection and action-value learning differs amongst gamblers with focused involvement in 'strategic' gambling forms; e.g. sports betting and poker (Lorains et al., 2014).

Notwithstanding these limitations, our data link the generic risk factor of impulsivity and the specific risk factor of predictive control to changes in action-selection and action-value learning. As such, these findings warrant further investigation as putative cognitive mechanisms that undermine the ability of vulnerable individuals to use the reward structure in gambling games to regulate participation and limit potential harm.