Analysis of Local Molecular Motions of Aromatic Sidechains in Proteins by 2D and 3D Fast MAS NMR Spectroscopy and Quantum Mechanical Calculations

Abstract

We report a new multidimensional magic angle spinning NMR methodology, which provides an accurate and detailed probe of molecular motions occurring on timescales of nano- to microseconds, in sidechains of proteins. The approach is based on a 3D CPVC-RFDR correlation experiment recorded under fast MAS conditions (ν_R = 62 kHz), where ¹³C-¹H CPVC dipolar lineshapes are recorded in a chemical shift resolved manner. The power of the technique is demonstrated in model tripeptide Tyr-(D)Ala-Phe and two nanocrystalline proteins, GB1 and LC8. We demonstrate that, through numerical simulations of dipolar lineshapes of aromatic sidechains, their detailed dynamic profile, i.e., the motional modes, is obtained. In GB1 and LC8 the results unequivocally indicate that a number of aromatic residues are dynamic, and using quantum mechanical calculations, we correlate the molecular motions of aromatic groups to their local environment in the crystal lattice. The approach presented here is general and can be readily extended to other biological systems.

Graphical abstract

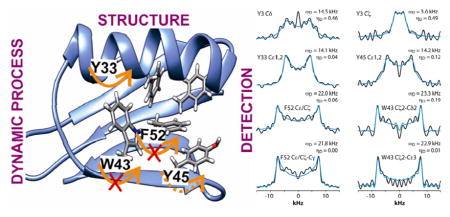
Introduction

In recent years solid-state Nuclear Magnetic Resonance (NMR) spectroscopy has become one of the most powerful techniques in structural studies of the condensed matter, in particular for synthetic polymers and biological systems.¹ A number of highly exciting applications have been reported for the latter group of samples including characterization of proteins and other biopolymers that are inaccessible to X-ray crystallography and solution-state NMR spectroscopy.² Today the palette of available methodological NMR approaches permitting to achieve general and specific information about local geometry, intra- and inter-molecular interactions, and higher order structure is very rich.³ The full assignment of resonances and determination of molecular structure can be done by employing different multi-dimensional solid-state NMR protocols. This issue was exhaustively discussed in recent review articles by us and by others.^4–7

To understand in detail the biological functions of proteins, the knowledge about molecular dynamics is crucial. It is well known that protein motions occurring on the pico- to millisecond time scales play important functional roles, and that dynamics modulates interactions between physiological partners. The unique feature of NMR spectroscopy is the possibility of analysis of dynamics of biomolecules at atomic resolution.⁸ Once signals are assigned, measurements can be made of relaxation rates, residual anisotropic interactions (dipolar, quadrupolar and chemical shift), relaxation dispersion profiles, magnetization- and hydrogen exchange rates; all yielding site-specific information about dynamics. However, one of the biggest achievement in the field of solid-state NMR spectroscopy is the introduction of fast magic angle spinning (MAS) probes delivering rotation frequencies higher than ν_R = 110 kHz presently.⁹ These very fast rates have opened new possibilities in studies of proteins.¹⁰ On the other hand, anisotropic tensorial interactions, e.g. dipolar and chemical shift, which are the source of crucial information about structure and dynamics of natural products are eliminated or averaged to their isotropic values due to very fast sample spinning. Hence, number of techniques have been developed during last years to reintroduce those interactions and a large variety of pulse schemes have been published.^11–15 Recoupling of anisotropic spin interactions is achieved by application of pulse sequences that are often based on symmetry rules introduced by Levitt.¹⁶ These sequences are called CNⁿ_ν and RNⁿ_ν, where the symbols N, n, and ν are small symmetry integer numbers that depend on the rotation properties of the spin angular moment during the rotor-synchronized train of radio frequency (RF) pulses. In this strategy the relationship between spins, space, rotation and radiofrequency pulses is used to amplify desired and suppress unwanted interactions. The recently published RN-CSA symmetry schemes are suitable for CSA recoupling under fast spinning speed (ν_R ≥ 40 kHz).¹⁷

Symmetry-based approaches were also employed by several research groups to study hetero-nuclear dipolar couplings in proteins.¹⁸ These sequences are highly effective in suppressing ¹H-¹H homonuclear dipolar couplings, which make them suitable in fully protonated systems. In these symmetry-based experiments the RF pulses have to be synchronized with the sample rotation, which is not always easy to achieve in case of very fast sample spinning (e.g. ν_R ≥ 100 kHz) due to the proportionality between the required RF fields and ν_R, and also to the transients which are not negligible with such small rotor periods.

In a recent article employing small molecules as model samples, we have shown that a simple Cross Polarization with Variable Contact (CPVC) experiment performed under fast MAS conditions is free from the discussed supra limitations and provides very accurate values of hetero-nuclear (¹³C-¹H, ¹⁵ N-¹H) dipolar couplings, D, which reflect the inter-atomic distances and/or molecular motions.¹⁹ We have also shown that CPVC methods are very robust with respect to RF-inhomogeneity, CSAs and offsets. Recent papers, from us and others, have fully confirmed the applicability of this approach.^20–22

In the current work we show that this methodology is a starting point for more advanced multi-dimensional techniques, which can be applied to study large biological systems. The power of this methodology is illustrated on ¹³C enriched models: tripeptide Tyr-(D)Ala-Phe and two proteins, GB1 and LC8. We demonstrate that using our approach, we can site-specifically assign the side-chain resonances of the aromatic residues, which is typically a challenge in proteins. With these assignments in hand, we infer the molecular dynamics of the aromatic residues. To do so, we employ an average Hamiltonian approach to simulate the dipolar lineshapes. This approach permits unequivocal identification of the motional modes of the aromatic sidechains undergoing nano- to microsecond time scale motions. Furthermore, by combining our experimental NMR results with theoretical calculations, we show that the motional modes correlate with the location of a particular amino acid in the context of the protein structure. The methodology reported here is general and readily extendable to other biological systems of interest, including non-crystalline proteins, protein assemblies, and other bio-macromolecules. At this stage of hardware development, 3D CPVC approach (as most of multidimensional solid-state NMR techniques) can only be applied to isotopically enriched samples. However, introducing new NMR concepts and techniques (e.g. very fast DNP CP/MAS) may shortly extend the applicability of the method to unlabeled samples.

Experimental

Materials

U-¹³C Tyr-(D)Ala-Phe (YAF) tripeptide was synthesized using labeled amino acids purchased from Sigma-Aldrich (D-Alanine-¹³C₃-99%) and Cambridge Isotope Laboratories, Inc. (L-Tyrosine-¹³C₉-99%, ¹⁵N-99% and L-Phenylalanine-¹³C₉-99%, ¹⁵N-99%). Its synthesis was carried out in solution according to procedure reported in our previous paper.²³

U-¹³C,¹⁵N-GB1 was bought from Giotto Biototech company as “ready-to-use” sample packed in 1.3 mm rotor. Dynein Light Chain 8 (LC8) protein was prepared according to the protocol reported by us previously.²⁴ 3 mg of U-¹³C,¹⁵N-LC8 prepared by controlled precipitation from polyethylene glycol were packed into a 1.3 mm rotor and used for subsequent MAS NMR experiments.

NMR spectroscopy

All experiments were measured on a Bruker Avance III spectrometer equipped with 1.3 mm ¹H/³¹P-¹⁵N probehead, spinning at ν_R = 62 kHz, and operated at frequencies of 600.1 and 150.9 MHz for ¹H and ¹³C, respectively. In all cases the π/2 pulse durations were of 2.5 μs for ¹H and 1.5 μs for ¹³C. We used a low power (RF = 10 kHz) swftppm decoupling^25,26 during acquisition.

2D ¹³C-¹³C RFDR-8m4¹ correlations²⁷ were measured with: (i) 166 kHz RF, (ii) mixing times of 8 or 16 ms, (iii) a matrix size of 2560×1024 points, and (iv) a spectral width of 220×220 ppm giving acquisition times of 38.4 and 15.4 ms in direct and indirect ¹³C dimensions. Experiments were measured with ramp CP from 70 to 100% on ¹H channel, with RF ≈ 100 kHz. We collected 40 scans for proteins and 8 scans for YAF.

3D CPVC-RFDR experiments used 8 ms mixing time and 166 kHz RF for RFDR-8m4¹. For proteins, we measured 16 scans matrix sizes of 2560×40×480 points, with spectral widths of 220 ppm×60 kHz×220 ppm giving acquisition times of 38.4×0.667×7.2 ms in ¹³C direct, dipolar and ¹³C indirect dimensions. For YAF, the 3D spectrum was measured with 8 scans, a matrix size of 1782×48×320 points, and spectral widths of 197 ppm×60 kHz×197 ppm giving acquisition times of 38.4×0.667×10.8 ms in ¹³C direct, dipolar and ¹³C indirect dimensions.

In all 3D CPVC-RFDR experiments, Hartmann-Hahn matching conditions were precisely calibrated on the sample by changing ¹H RF near to 104 kHz, while ¹³C RF was kept constant at 166 kHz.

Simulations of CPVC Dipolar Lineshapes

The simulations of CPVC dipolar lineshapes were performed in the time-domain mode. Based on the following considerations we could do it by application of the simple algebraic expressions quoted below instead of having to go through time-consuming full quantum mechanical calculations. The simulations of CPVC dipolar lineshapes were performed in the time-domain mode using simple algebraic expressions based on the following considerations. Under MAS, the CP magnetization transfer from the ¹H spin polarization to the to-be-detected ¹³C spin polarization can be performed either in zero-quantum (ZQ) or double-quantum (DQ) mode. ZQ-CP is optimized under a so-called Hartmann-Hahn-sideband condition requiring that the difference of the RF amplitudes applied to the two nuclei is equal to once or twice the spinning speed.²⁸ DQ-CP requires that the RF-amplitude sum equals once or twice the spinning speed.²⁹

CPVC method uses a sum or difference of RF-fields equal to the spinning rate as it reintroduces the maximum of dipolar interactions, hence leading to the maximum splitting of Δ = D/√2 in the case of static moieties. Moreover, it has been shown that ZQ-CP transfers perform better than DQ-CP ones, due to their larger possible RF fields.

In our recent publication²⁰ it was reported that spectra obtained under standard experimental conditions closely follow the results predicted under the assumption of ideal Hartmann-Hahn matching. It was also shown that non-ideal conditions, such as RF inhomogeneity, CSAs, resonance offsets, and homo-nuclear proton interactions, have very limited effects on the CPVC lineshape. Globally, the distortions are mainly observed in the region near zero frequency, leading us to exclude the central portion of the spectrum when performing the lineshape fittings. Another effect is a small increase of the apparent D value (less than 1 kHz), which is inconsequential and is neglected in our analysis.

These observations assured us that the current CPVC spectra can be analyzed in terms of the spin-evolution formalism of the idealized first-sideband Hartmann-Hahn situation, according to the intended RF-amplitude configuration. For a single ¹³C-¹H spin pair, the ¹³C signal after a CP contact time, τ, is given by

$$S(\tau )=1-cos({\omega }_{CP}\tau )$$

In the case of an immobile spin pair, the ω_CP frequency is given by

$${\omega }_{CP}=\frac{1}{4}\sqrt{2}{\omega }_{D}sin2\beta$$

ω_D being the dipolar coupling constant (DCC) in frequency unit and β the angle between the rotor axis and the CH vector.^30–31 In the case of a powder sample, two horns are observed in the dipolar spectrum, and their splitting is equal to Δ = ω_D/√2. As a result, the inter-nuclear distance is then directly determined from the splitting value without any lineshape fitting. In the absence of molecular motions, the dipolar-interaction tensor is axially symmetric, having components -ω_D/2, -ω_D/2, ω_D.

When the CH bond undergoes very fast orientational motions, the size of the effective dipolar tensor is reduced to one having principal components D_xx, D_yy, D_zz, thereby possibly losing its axial symmetry.³² In such a case, we identify the largest of the absolute values of the three components as ‘the’ DCC, represented by ω_D and the difference of the two other components divided by ω_D, as the asymmetry parameter η_D.

The ω_CP frequency is then given by

$${\omega }_{CP}=\frac{1}{6}{\omega }_{D}sin\beta \sqrt{2{cos}^2\beta {(3+{\eta }_{D}cos2\alpha )}^2+2{\eta }_D^2{sin}^{2}2\alpha }$$

where α and β are the azimuthal and polar angles of the rotor-axis direction with respect to the dipolar-tensor principal axes.

We simulated the CPVC signal in a home-written Fortran-95 program by summation of S(τ) over 2000 powder-averaged tensor orientations. This signal was then shifted by the experimental dead time, followed by Lorentzian apodization, and FT. Since the term 1 in the expression for S(τ) creates the large time-independent signal component that in the experimental spectra is eliminated by appropriate baseline correction prior to the FT, we simulated S(τ) simply as cos(ω_CPτ). The experimental CPVC spectra were obtained by FT of the time-domain signals extracted from the original 3D datasets for each well-resolved aromatic peak. The best-fit parameters for the dipolar coupling constant (ω_D), dipolar asymmetry parameter (η_D), and line broadening parameter (LB) were obtained by simplex least-squares minimization. Since experimental artifacts such as RF inhomogeneity and chemical-shift offsets often cause lineshape distortions in the central region, we disregard those regions in the fitting procedure. The width of this region is determined by the particular lineshape features in each individual case. We note that dipolar lineshapes corresponding to the desired carbon atom can be obtained using any cross peak with the frequency corresponding to this atom in the indirect or direct ¹³C dimension, and, as discussed in the Results section, the dipolar parameters derived from the different cross peaks corresponding to the same carbon atom are consistent to within the experimental error.

Quantum Mechanical Calculations

The energy of the infinite crystal of YAF tripeptide was calculated by the CASTEP program³³, which is a DFT-based code. Electron-correlation effects were modeled using the generalized gradient approximation of Perdew, Burke, and Ernzerhof.³⁴ The calculations were performed with ‘on-the-fly’ pseudopotentials, and a planewave cutoff energy of 600 eV with integrals taken over the Brillouin zone using a Monkhorst-Pack³⁵ grid with a minimum k-point sampling of 0.05 Å⁻¹. The atomic coordinates were derived from the Cambridge Crystallographic Database³⁶ (refcode IWANID²³). The positions of all atoms were optimized at the same computational level prior to the aromatic ring rotations. The energy dependence on the PHE/TYR rotation was calculated on a 2×2×1 supercell so that the rotation of one phenyl ring did not result in the same rotation of the neighboring rings under the periodic conditions. The energy calculations were performed with and without the dispersion correction.³⁷

For the cluster calculations, an aromatic ring was selected, then the selection was expanded to all atoms closer than 5 Å (including the atoms of the periodic images in the neighboring unit cells), and then the selection was expanded to include complete amino acid residues, and the aminoacid residues, which were terminated with amide (CONH₂) groups. The energy dependence on the phenyl ring rotation around the C_β–C_γ bond was calculated at Hartree-Fock level using a standard 6–31G* basis set within the Gaussian-09 program package.³⁸ The orientation of the OH group of TYR residues was kept fixed so that the hydrogen bond network of the crystal was not disturbed.

The same procedure for cluster constructions was used for the GB1 and LC8 proteins. Crystal structures 2QMT and 3DVT from Protein Data Bank³⁹ served as the starting structure.⁴⁰ Hydrogen atoms were added manually and their positions were optimized at the same computational level prior to the ring rotations and energy calculations.

Results and discussion

NMR Spectroscopy

2D CPVC Spectra

In the previous reports the 2D CPVC NMR approach was applied to study structural constraints in relatively simple model samples.^19,20 In these cases, very well resolved ¹³C isotropic signals have allowed unambiguous assignment of specific sites and analysis of C-H dipolar splittings. In the case of proteins, recording dipolar interactions site specifically requires at least one additional chemical shift dimension, to alleviate the signal overlap. This problem is illustrated here using two proteins under investigation, GB1 and LC8. GB1 is a 56-residue B1 binding domain of protein G, an immunoglobulin-binding protein expressed in group C and G Streptococcal bacteria. LC8 is an 89-residue microtubule-associated protein, dynein light chain 8 (LC8), which is an integral subunit of cytoplasmic dynein, a multi-subunit microtubule-based retrograde motor.

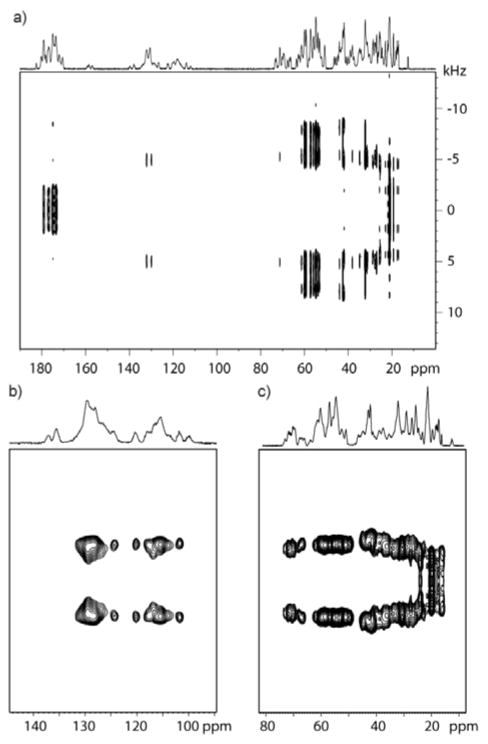
The 2D CPVC spectra of GB1 recorded with the spinning frequency of ω_R = 62 kHz are shown in Figures 1a (full spectrum) and 1b,c (expansions around aromatic and aliphatic regions). The appropriate spectra for LC8 protein are attached in Supporting Information (Figure S2).

Fig 1.

The 2D CPVC spectra of GB1 (a) and expansion around aromatic (b) and aliphatic (c) regions. 38.4 ms acquisition time, 2 s recycle delay, 40 transients per t1 step and 128 t1 steps were used, thus giving a total experiment time of 3h. Swept-Frequency TPPM decoupling with RF = 10 kHz was used.

On the first glance, the spectral resolution appears to be sufficiently high as to permit assignment of almost all ¹³C resonances. However, upon further inspection of the spectrum it becomes clear that we can only determine coarse values of dipolar splittings in the aromatic and aliphatic regions. Inspection of F1 slices indicates that peaks corresponding to the individual amino acid residues overlap, precluding extraction of site-specific information concerning the different motional modes. This overlap is further exacerbated in LC8, due to larger number of residues. As one can see in Figures 1b and 1c, both aromatic and aliphatic residues are overcrowded, and so the dipolar lineshapes for the individual carbon sites overlap.

3D CPVC-Based Experiments for Analysis of Aromatic Sidechain Dynamics: Validation in YAF Tripeptide

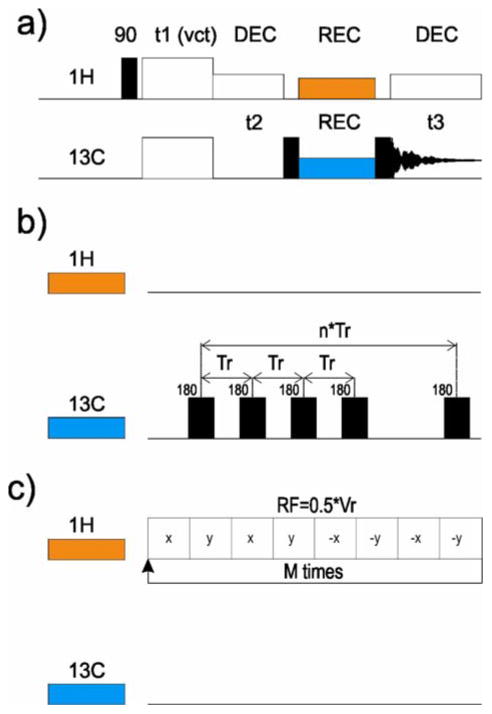
To overcome the spectral overlap problem, we introduced two new 3D experiments. As shown in Figure 2, we have combined CPVC with homonuclear ¹³C-¹³C sequences, RFDR (Figure 2b) and SHANGHAI (Figure 2c), which allow for the determination of short and long ¹³C-¹³C distances, respectively. In the current paper we focus on the 3D CPVC-RFDR approach.

Fig. 2.

Schematic drawing of the CPVC-based pulse sequences proposed in this work for ¹³C assignments and ¹³C-¹H dipolar coupling measurements: (a) full 3D sequence, and (b) RFDR or (c) SHANGHAI recoupling schemes.

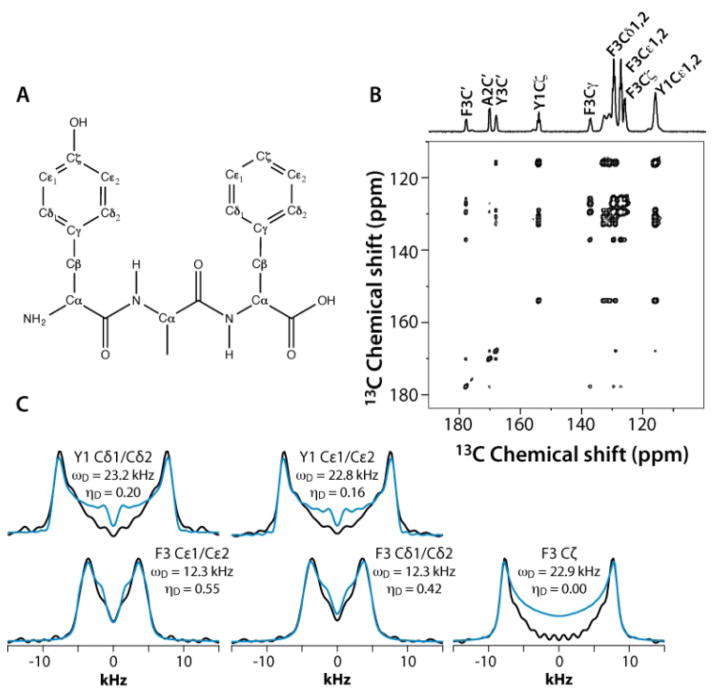
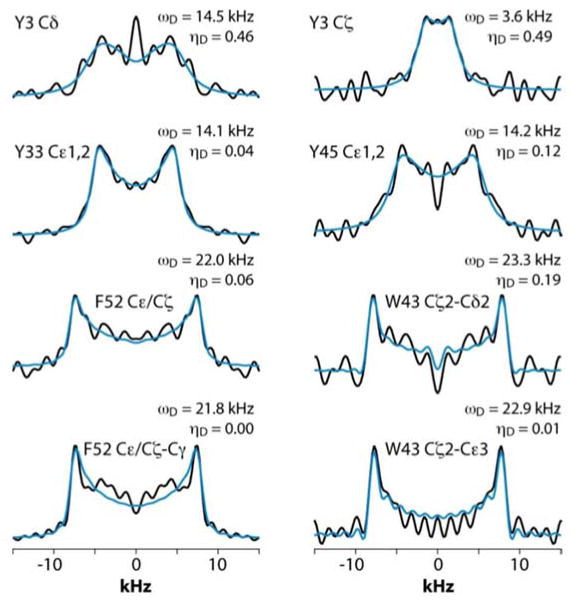
The applicability and accuracy of the CPVC-RFDR method were first validated using a simple model compound, the U-¹³C labeled YAF tripeptide. This sample is an excellent test case due to the well-defined and distinct dynamics of the two aromatic residues.⁴¹ Indeed, the phenyl ring of Tyr is rigid, while that of Phe is mobile and undergoes π jumps at the picosecond rate at room temperature⁴¹. These fast (on the NMR time scale) motions are expected to give rise to partial averaging of the Phe C-H dipolar tensors associated with the Cδ1,Cδ2 and Cε1,Cε2 carbon atoms (the two pairs of resonances overlap), resulting in a reduced dipolar frequency of ω_D = 11.25 kHz, which is ca. half of the rigid-limit value of 22.5 kHz, and a non-zero dipolar asymmetry parameter, η_D.

Figure 3 shows the 2D RFDR plane from the 3D CPVC-RFDR spectrum of the YAF peptide and five selected CPVC lineshapes extracted from the 3D spectrum. The dipolar interaction parameters, ω_D and η_D, extracted from the AHT-based simulations of the CPVC lineshapes in the time domain, are presented in the Figure 3 and in Table S2 of the Supporting information. The dipolar parameters for the Tyr and Phe residues are very different; the reduced dipolar frequency and non-zero dipolar asymmetry parameter for Phe indicate the presence of dynamics. The reduction of the dipolar splitting due to the molecular motions of phenyl rings in organic polymers and biological systems is well known and was discussed in prior reports including our previous paper.^41–44 The Cδ1,Cδ2 and Cε1,Cε2 carbons of the Phe residue exhibit motionally reduced dipolar interaction parameters: ω_D = 12.3/12.2 kHz and η_D = 0.42/0.45. These dipolar parameters suggest composite motions consisting of the π-jumps and additional motional modes, vide infra. In contrast, the Cζ carbon, whose dipolar tensor does not experience such motional averaging due to symmetry (Fig.3A), exhibits dipolar interaction parameters very close to the rigid limit values, ω_D = 22.9 kHz and η_D = 0.0. As discussed later in the text, this finding provides an important clue in defining the motional models for this residue. For the tyrosine residue, the dipolar interaction parameters for Cδ1,Cδ2 and Cε1,Cε2 carbons indicate an almost rigid phenyl ring, with ω_D = 23.2/22.8 kHz and η_D = 0.20/0.16, which is close (but not identical) to the rigid-limit values of 23 kHz and 0.0 respectively. That tyrosine’s Cδ1,Cδ2 and Cε1,Cε2 as well as the phenylalanine’s Cζ show slightly depressed dipolar couplings and non-zero dipolar asymmetry parameters (the deviations are well outside of the experimental errors) suggest the presence of some mobility in the ns-μs regime, likely small-amplitude out-of-plane wobbling motions.

Fig. 3.

A) The chemical structure of the YAF peptide. B) Aromatic region of the 2D ¹³C-¹³C RFDR spectrum of YAF. C) Dipolar lineshapes for cross peaks corresponding to the different aromatic carbons in Tyr and Phe residues of YAF, extracted from the 3D CPVC-RFDR spectrum. The experimental and best-fit simulated lineshapes are shown as black and blue lines, respectively.

Analysis of Aromatic Sidechain Dynamics in Proteins: GB1 and LC8

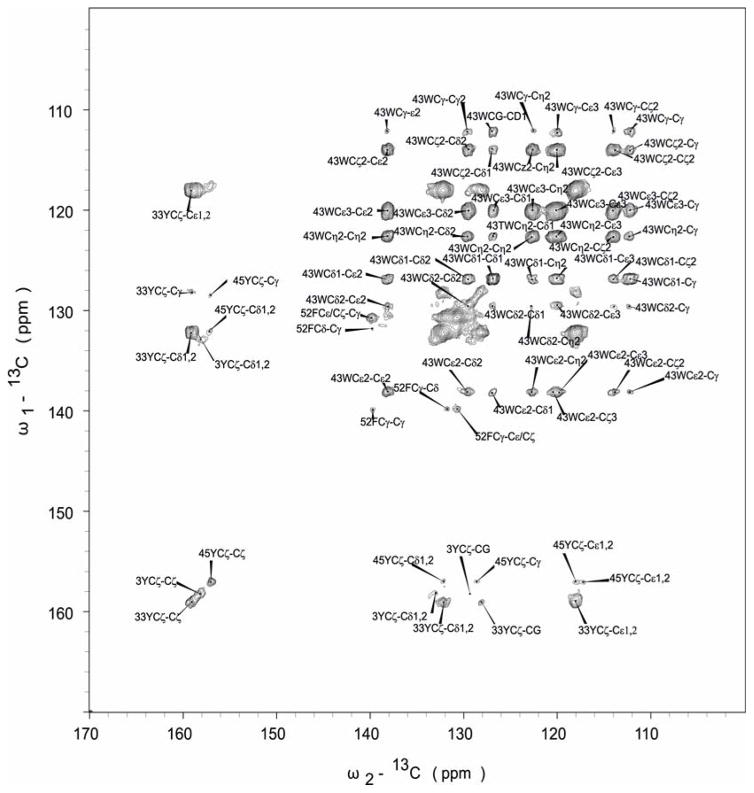
With the 3D CPVC-RFDR methodology validated on the model YAF tripeptide, we have next turned our attention to the analysis of aromatic sidechain dynamics in nanocrystalline GB1. The starting point of the analysis is the assignment of the ¹³C signals.^45–47 We note that GB1 has been extensively studied by MAS NMR, and resonance assignments have been established by the Rienstra group previously.⁴⁸ In this work, we focused attention on the dynamics of aromatic amino acids side groups. The molecular motion of other residues, e.g. Cα and Cβ carbons, can be probed using our approach (see supra) as well as other 3D MAS NMR methodologies discussed elsewhere.^49,50 To assign the aromatic sidechain carbons, we employed the ¹³C-¹³C 2D RFDR correlation, which yields one-bond C-C connectivities for all amino acid residues. Figure 4 shows the expanded aromatic region with labels corresponding to selected quaternary atoms. GB1 contains six aromatic residues: three tyrosines (Y3 and Y45 in β-sheets and Y33 in an α-helix), two phenylalanines (F30 in an α-helix and F52 in a β-sheet), and one tryptophan (W43, in a β-sheet). The quaternary carbons, which are separated from other signals, were assigned first, and the chemical shifts of Cζ carbons are δ = 158.5 (Y33Cζ), 158.0 (Y3Cζ), and 157.5 ppm (Y45Cζ). Using these Cζ resonances, the assignments of the aromatic sidechain spin systems for the three Tyr residues were straightforward.

Fig. 4.

2D ¹³C-¹³C RFDR correlation spectrum of GB1 acquired with the mixing time of 16 ms. 38.4 ms acquisition time, 2 s recycle delay, 40 transients per t1 step, 1024 t1 steps were used, giving a total experiment time of 24h. Swept-Frequency TPPM decoupling sequence with RF = 10 kHz was used.

The assignment of Phe-52 is also straightforward. The chemical shift of F52Cγ is 139.9 ppm, and it correlates with its Cε/Cζ whose shift is 131.0 ppm. Other correlations for Phe appear as intense overlapping signals found in the region of 130–132 ppm, and we could not unequivocally assign Phe-30 resonances. The assignment of resonances for Trp-43 is unambiguous. The correlation peaks between quaternary C43ε carbon (δ = 138.2 ppm) and other carbons are clearly present.

Figure 5 shows the CPVC dipolar lineshapes for the aromatic carbons in GB1 extracted from the 3D CPVC-RFDR spectrum. Indeed, the dipolar parameters were obtained as best fits by the AHT-based simulations of the lineshapes, and are summarized in Table S2 of the Supporting information. The results indicate that W43 does not undergo any significant dynamics. The dipolar interaction parameters extracted for all carbon atoms that have attached protons are very close to the rigid limit values, ω_D = 23 kHz and η_D = 0. The observed deviations from these parameters for GB1 are attributed to experimental errors, which are larger than in the YAF tripeptide because of lower signal-to-noise ratio in the spectra. The fact that the CPVC lineshapes for W43 and the corresponding dipolar interaction parameters extracted from 14 different diagonal and cross peaks are consistent is an important validation of the robustness of the CPVC-RFDR experiment. Similar to W43, F52 exhibits nearly rigid behavior with ω_D = 21.9 ± 0.1 kHz and η_D = 0.03 ± 0.03.

Fig. 5.

CPVC dipolar lineshapes for representative aromatic carbons in GB1 extracted from the 3D CPVC-RFDR spectra. The experimental and best-fit simulated lineshapes are shown as black and blue lines, respectively. The dipolar interaction parameters are indicated next to each lineshape and summarized in Table S2.

In contrast to W43 and F52, the tyrosine residues are dynamic. For Y33, the values for Cδ and Cε carbons, averaged over several cross peaks, are ω_D = 14.0 ± 0.2 kHz, and η_D = 0.03 ± 0.2. For Y45, they are ω_D = 14.2 kHz, and η_D = 0.12. These parameters are not consistent with simple fast π-jumps around the 1-4 axis where ω_D is expected to be 14.0 kHz and η_D = 0.6 (vide infra). The nearly axial dipolar interaction suggests that the aromatic ring undergoes a motion more complex than the π rotation around the Cγ-Cζ axis. Similarly, in Y3, more complex motions than the π rotations are observed: ω_D = 14.5 kHz and η_D = 0.46. We will discuss the possible nature of such complex motions later in the report.

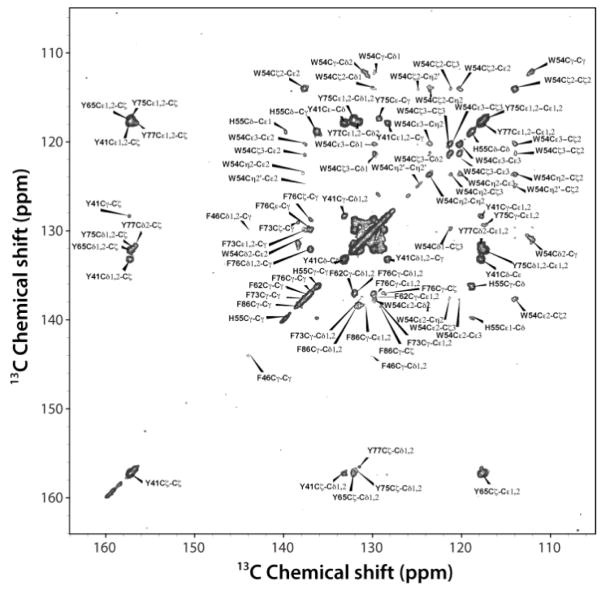
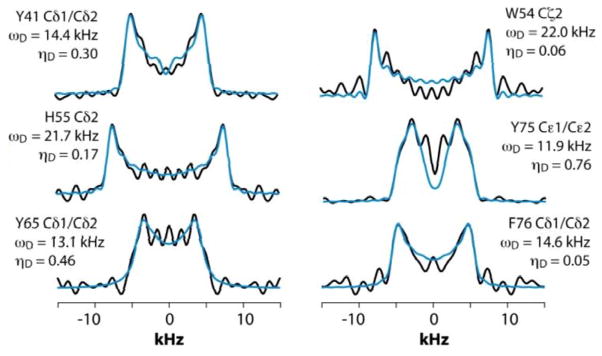
We next discuss the analysis of the molecular dynamics of the aromatic residues in LC8. Figure 6 shows the expansion around the aromatic region of the ¹³C-¹³C 2D RFDR correlation spectrum. The full spectrum is displayed in Figure S1 of the Supporting information. LC8 contains six tyrosines (Y32, Y41, Y50, Y65, Y75, and Y77), five phenylalanines (F46, F62, F73, F76, and F86), three histidines (H55, H68, and H72), and one tryptophan (W54). We have reported the residue-specific assignments of the aliphatic and carbonyl carbons of LC8 previously.^51,52 However, in those earlier data sets aromatic sidechain assignments could not be obtained. As shown in Figure 6, the quality of the 2D RFDR spectrum is such that the assignments of the majority of the aromatic sidechains were readily accomplished. The chemical shifts are summarized in Table S1 of the Supporting Information. With these assignments in hand, the analysis of the dipolar lineshapes from the 3D CPVC-RFDR spectra was straightforward for many of the aromatic residues in LC8. Figure 7 shows the experimental and simulated dipolar lineshapes for representative residues that yield resolved cross peaks. The corresponding dipolar parameters are summarized in Table S2 of the Supporting information.

Fig. 6.

2D ¹³C-¹³C RFDR spectrum of LC8 acquired with the mixing time of 16 ms. 38.4 ms acquisition time, 2 s recycle delay, 40 transients per t1 step, 1024 t1 steps were used, thus giving a total experiment time of 24h. For Swept-Frequency TPPM decoupling with RF = 10 kHz was used.

Fig. 7.

CPVC dipolar lineshapes for representative aromatic carbons in LC8 extracted from the 3D CPVC-RFDR spectrum. The experimental and best-fit simulated lineshapes are shown as black and blue lines, respectively. The dipolar interaction parameters are indicated next to each lineshape and summarized in Table S2.

The only tryptophan residue in LC8, W54, exhibits ω_D = 21.8–22.0 kHz and η_D = 0.06–0.20. These values indicate that W54 is nearly rigid in LC8, which is consistent with the fact it is located in a β-sheet and packed against several other aromatic residues: F46, Y50, and H70. Similarly, in H55 the field values of ω_D = 21.9 ± 0.2 kHz and η_D = 0.11 ± 0.05 indicate the lack of large-amplitude motions of the aromatic ring. This is not very surprising given the fact that H55 (i) belongs to a β-sheet, (ii) comprises the interface of the LC8 homodimer, and (iii) is packed against three aromatic residues: F86 located in the same LC8 monomer as well as F86 and H55 of the neighboring molecule.

F76, the only phenylalanine with non-overlapping signals whose dipolar lineshapes we have been able to analyze, is dynamic. The dipolar parameters recorded for Cδ1/Cδ2, ω_D = 14.6 kHz and η_D = 0.05, indicate complex motions similar to those related to our observations for Y33 of GB1, and the model that will be discussed in the next section apply.

For tyrosines, spectral overlap precludes analysis of dipolar lineshapes for Y32 and Y50. For the other four tyrosines, Y41, Y65, Y75, and Y77, the results unequivocally indicate the presence of dynamics. The dipolar parameters for all tyrosines suggest complex motional modes, the models for which are discussed in the next section.

Motional Models for Aromatic Groups

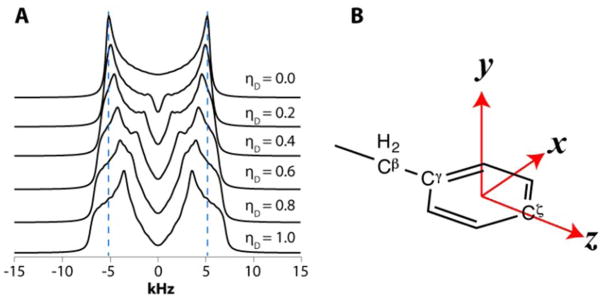
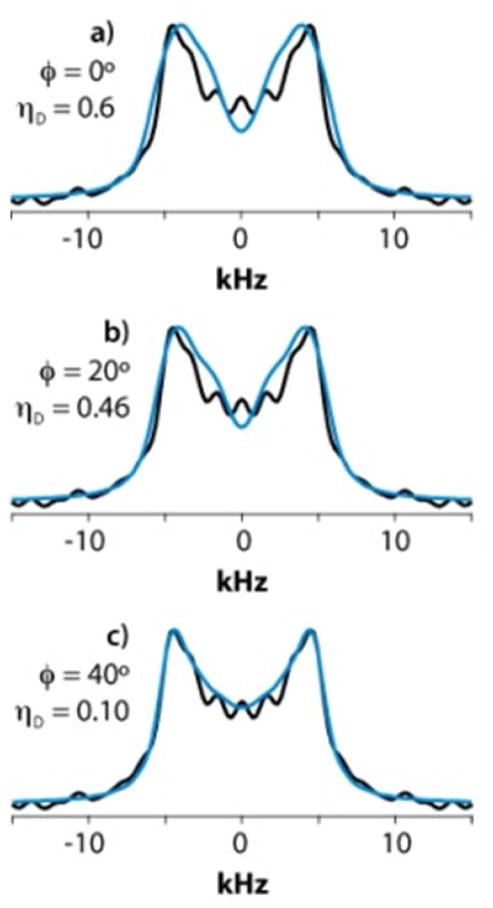
As discussed above, for several residues in GB1 and LC8 and for F3 in YAF we observed motionally reduced dipolar interaction parameters, namely ω_D smaller than the rigid limit value of 22.5 kHz and a non-zero η_D value. Non-zero dipolar asymmetry arising in the presence of dynamic averaging has profound effects on the lineshapes as it introduces an apparent broadening and it shifts the positions of the peak splittings, as illustrated in Figure 8A.

Fig. 8.

A. Simulated CPVC dipolar lineshapes for ωD = 15.0 kHz plotted as a function of ηD. Note the apparent broadening of the lines and decrease in the peak splitting as ηD increases. B. Rotational axes in the aromatic ring to describe motional models of aromatic sidechains.

Under such circumstances, it is not possible to determine the dipolar interaction parameters from the peak splittings alone, as has been suggested in prior studies,¹⁹ and lineshape simulations are required. As discussed earlier in the text, accurate dipolar interaction parameters are derived by simulations of CPVC spectra using the average Hamiltonian approach.

Interestingly, the dipolar interaction parameters for many carbon sites in our experiments are indicative of motions more complex than π-jumps around the Cγ-Cζ axis of the aromatic ring, where ω_D = 14.0 kHz and η_D = 0.6. To describe the possible motional models giving rise to such dipolar interaction parameters, we define an xyz axis system in the aromatic ring illustrated in Figure 8B: z- along the Cγ-Cζ axis; x- perpendicular to z in the aromatic plane; and y- perpendicular to the aromatic plane.

The models are kept as simple as possible by restricting them to rapid jumps of the dipolar tensor between two equally occupied orientations that are rotated away over angles ±ϕ_i from an unoccupied central orientation, whereby the rotation axis is parallel to one of the principal tensor axes (i = x, y or z). If the rotation is about the z axis, then the conversion of the dipolar tensor from the static central situation to the average of the rotated situations is given by

$$\left(\begin{array}{ccc}{D}_{xx}& 0& 0\\ 0& D_{yy}& 0\\ 0& 0& D_{zz}\end{array}\right)\to \left(\begin{array}{ccc}{D}_{xx}{cos}^2{\varphi }_z+D_{yy}{sin}^2{\varphi }_z& 0& 0\\ 0& D_{yy}{cos}^2{\varphi }_z+D_{xx}{sin}^2{\varphi }_z& 0\\ 0& 0& D_{zz}\end{array}\right)$$

A similar averaging is obtained for rotation about x or y axes.

The main motional process of the tyrosine ring is 180° flips about the z-axis. For the four carbons that are not along the z-axis, this can be viewed as rotational jumps about a central position consisting of an axially symmetric dipolar tensor with its main axis along z, making ϕ_y = ±60° jumps about y. From the CPVC spectra of immobile aromatic sites we know that the static dipolar frequency is ω_D ≈ 22.4 kHz. Hence, the ring flips lead to the following averaging of the tensor components (D_xx, D_yy, D_zz in kHz): (−11.2, −11.2, 22.4) → (14.0, −11.2, −2.8), i.e. ω_D = 14.0 kHz, η_D = 0.6.

These parameters deviate from the experimentally observed values by more than the experimental error.

Moreover, we cannot ascribe the deviations to π-ring flips that occur at correlation times between the extreme-narrowing limit of 10⁻⁷ s and the rigid limit of 10⁻⁴ s, thereby creating interesting transition lineshapes. Indeed, we have performed such simulations (not shown), and not only do the lineshapes poorly fit the experiment, but these intermediate correlation times also give rise to very short T_1ρ relaxation times that produce huge negative center peaks in the CPVC spectra. Those are not observed in our experimental data.

In the case of Y33 (GB1) and F76 (LC8), ω_D value found by the fit equals that of the two-site flip model, but η_D is nearly zero instead of the 0.6 predicated by the model. This suggests that there is an additional rotation about the x-axis (the orientation where the dipolar component is not affected). Such up-and-down flaps of varying angles give the following average dipolar tensors:

$$\begin{array}{l}{\mathrm{\varphi }}_{\mathrm{x}}=10°\to (14.0,-11.0,-3.1),i.e.,{\mathrm{\omega }}_{\mathrm{D}}=14.0\text{kHz},{\eta }_D=0.56\\ {\mathrm{\varphi }}_{\mathrm{x}}=20°\to (14.0,-10.2,-3.8),i.e.,{\mathrm{\omega }}_{\mathrm{D}}=14.0\text{kHz},{\eta }_D=0.46\\ {\mathrm{\varphi }}_{\mathrm{x}}=30°\to (14.0,-9.1,-4.9),i.e.,{\mathrm{\omega }}_{\mathrm{D}}=14.0\text{kHz},{\eta }_D=0.30\\ {\mathrm{\varphi }}_{\mathrm{x}}=40°\to (14.0,-6.3,-7.7),i.e.,{\mathrm{\omega }}_{\mathrm{D}}=14.0\text{kHz},{\eta }_D=0.10\end{array}$$

Keeping the line broadening equal to the fitted value of LB = 1.7 kHz, the resulting simulated spectra assuming the above flip angles, plotted on the experimental spectrum for Y33 of GB1, are illustrated in Figure 9.

Fig. 9.

Blue traces: simulated CPVC lineshapes assuming a motional model including the π-flips around the z axis and an additional rotation about the x-axis with ϕ_x angle of a) 0° (no rotation), b) 20°, and c) 40°. Black traces: experimental CPVC lineshape for Y33 in GB1. Note the excellent agreement observed between the experimental lineshape and the simulated lineshape with ϕ_x = 40°

A particular observation is that the peak splitting increases from 8.0 to 8.9 kHz when the rotation angle ϕ_x increases from 0 to 40°. This contradicts the conventional assumption that a smaller splitting implies a smaller "order parameter", i.e., a larger amplitude of molecular motion. This result, counterintuitive on the first glance, underscores the importance of fitting the lineshapes for deriving accurate dipolar tensor parameters.

The above result suggests that, in addition to the 180° flips, the phenyl rings in Y33 (GB1) and F76 (LC8) also flap up and down over an angle of about 2×40°. This could be related to trans-gauche-type transformations at C_β and be accommodated by bond-angle changes of the OH group and its hydrogen-bonding. We note that the relatively large line broadening parameter required to fit the spectra may either be a relaxation effect caused by these large-amplitude motions, or a distribution of the ϕ_x angles.

For F3 residue in YAF and for Y41, Y65, Y75, and Y77 in LC8, the CPVC lineshapes deviate in a different way from a simple π-jump model. In this case η_D is close to the predicted 0.6 but ω_D is reduced to 10.4–12.4 kHz. This can be reproduced by applying one additional small-angle two-site jump. In the case of F3 in YAF it is clear that the second rotation has to be about the z-axis, because the Cζ carbon exhibits rigid-limit dipolar interaction values, which would be inconsistent with rotations about either the x- or the y-axis. Incorporating the second rotation about the z-axis into our motional model for the YAF’s F3 residue, we obtain the best fit to the experimental results when the ring undergoes additional rotations by ±15° about the z-axis. So, we may conclude that when the phenyl ring makes π flips about the z-axis it has a wide range of possible orientations around its energy minimum, ca. 15° to each side, in agreement with the very shallow minimum around 0 and 180° found in the quantum mechanical calculations, vide infra.

For tyrosine residues in LC8, we cannot constrain the motional model in a similar way because Cζ carbons do not carry a proton. In the absence of such constraints, more than one motional profile is consistent with the experimental data.

Theoretical Calculations of the Energy Barriers for Mobile Aromatic Groups

To corroborate the motional models observed experimentally (vide supra) we have turned our attention to the quantum chemical calculations of rotational energy barriers. We have conducted these calculations on GB1, as the 3D structure of the polymorph used in our NMR experiments is known, in contrast to that of the LC8 sample used in the current work.

An alternative computational approach for the assessment of the side-chain motions could be molecular dynamics simulations with their tremendous advances in performance and applicability in recent years.^53–55 However, the size of the observed dipolar couplings suggests that micro- to millisecond simulation times would be required for a proper capturing of the molecular motions, which is still beyond the capability of conventional simulation techniques. The below described calculations of rotational barriers thus represent a computationally cheap and widely applicable approach for a qualitative link between observed NMR data and side-chain mobility.

In explaining the differences in the C-H dipolar splittings of aromatic groups in the crystal lattice we assumed that even subtle distinctions in the local environment will influence the energy barrier of free rotation around the 1–4 axis of phenyl rings. The aim of the study reported in this section is an analysis of energetic parameters employing the theoretical approach and their correlation with experimental values of the DCC. For testing the methodology we have used X-ray data for YAF peptide (refcode IWANID) constructing the appropriate cluster surrounding each phenyl residue. Figure 10 shows the crystal lattice motive with clearly seen the phenyl groups of Phe inside of a cage. The aromatic residue has enough space for free rotation. The molecular motion of phenyl ring of Tyr is more restricted due to presence of the neighboring methyl groups and hydrogen bondings.

Fig. 10.

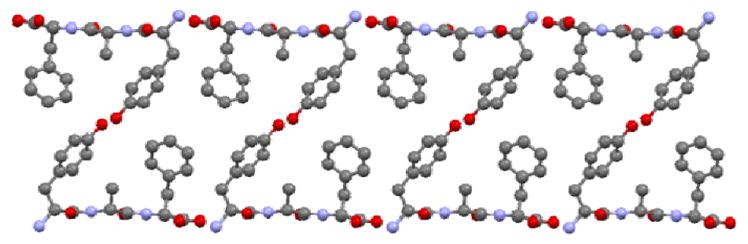
Visualization of the YAF supramolecular array. The coordinates are taken from ref.[23]

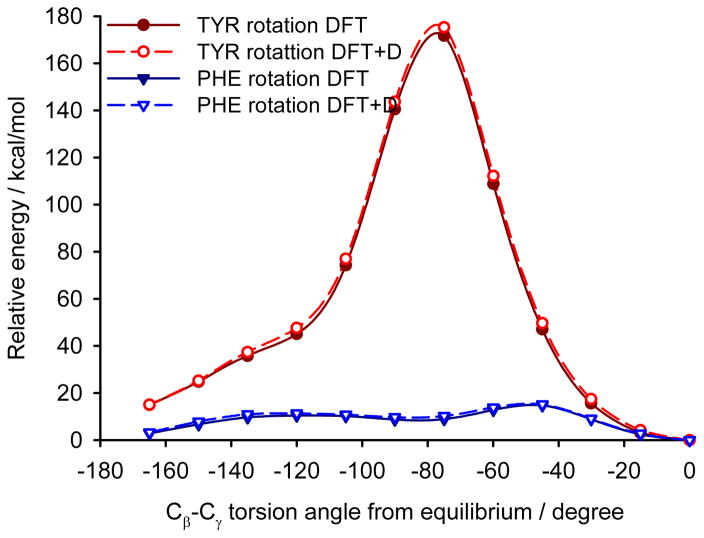
Two different computational approaches were used to estimate the mobility of the aromatic rings in YAF peptide. First, crystal calculations with fully periodic boundary conditions of the optimized YAF structure and of that with changed orientation of Phe or Tyr aromatic rings were used to estimate the barrier of aromatic ring rotation. Significant differences between the barriers of rotation of aromatic rings of Tyr and Phe are clearly visible in Figure 11.

Fig. 11.

The relative energy dependence on the rotation of Tyr and Phe aromatic rings in the YAF peptide. The calculations were performed with (DFT+D) and without (DFT) empirical dispersion correction.

Indeed, the rotation barrier of Phe is much lower than that of Tyr, which is in agreement with previous observations of significant differences in the mobility of these phenyl rings in the YAF peptide.^23,41 The rotation barriers in a real system will be probably slightly lower than the calculated ones for both rings because the surrounding molecules can adapt to the transition geometry.

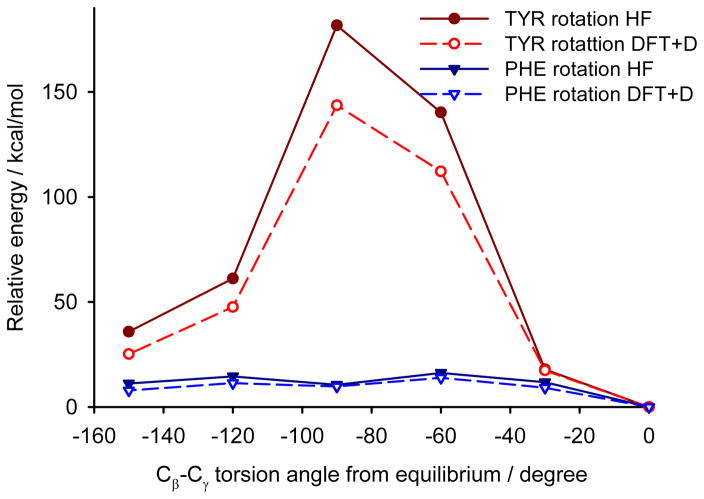
The second approach of the rotation barrier estimation consists in energy calculations for a cluster of molecules cut out of the infinite crystal structure with the studied aromatic ring in the center of the cluster. This approach is commonly used for prediction of NMR parameters of crystalline samples.⁵⁶ The Hartree-Fock energies calculated for the cluster models of YAF peptide overestimate the rotation barriers slightly (Figure 12), but for a qualitative insight into the mobility of aromatic residues within a polypeptide structure these calculations are sufficient. The advantage of the cluster approach is its applicability to protein structures where the calculations with periodic boundary conditions would be prohibitively computationally expensive. The comparison with the energies calculated with the periodic approach validates the cluster model, which is then applied for the GB1 proteins.

Fig. 12.

The comparison of cluster calculations (at Hartee-Fock level) with DFT periodic boundary calculations of rotation barriers of aromatic rings in the YAF peptide.

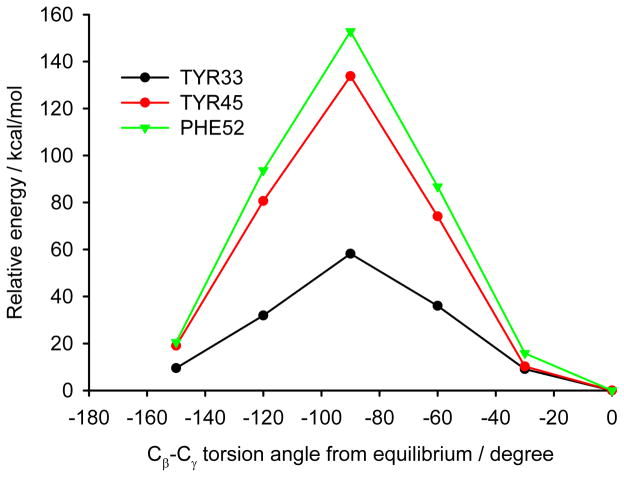
Analyzing the surrounding of aromatic residues we have found that the ring of Tyr33 faces the area between a helix and a sheet (Figure 13). In this position the phenyl ring has enough space for molecular motions, which is confirmed by the cluster calculations. The energy barrier for Tyr33 rotation was found to be less than half of that for Tyr45 and Phe52 (Figure 14). Tyr45 is located in the neighborhood of Phe52. The distance between the aromatic groups is below 4 Å and favors the π-π contacts. The rings under discussion are not aligned in one plane but form a small angle; and it is known from literature that small offset strengthens such interactions.⁵⁷

Fig. 13.

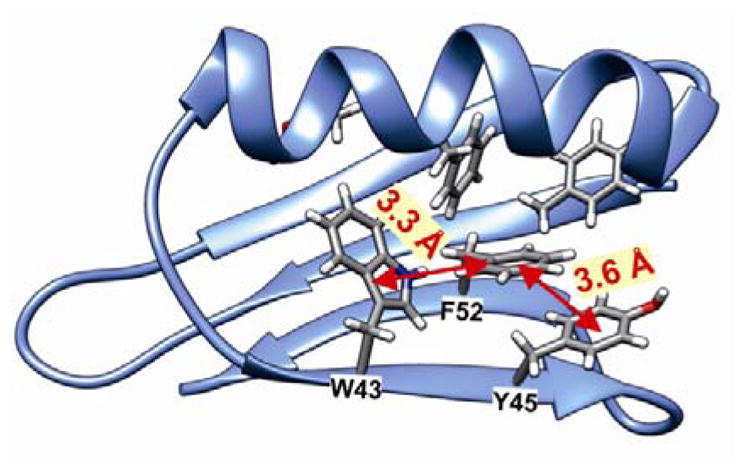
Visualization of GB1 protein with indicating of distances between selected aromatic residues.

Fig. 14.

The relative energy dependence on the rotation of aromatic rings in the GB1 protein. Tryptophan rotation would result in very close atomic contacts with the surrounding residues; therefore, it is not surprising that the aromatic ring of Trp43 is rigid.

Thus we can assume that molecular motions of Tyr45 and Phe52 are limited to small-amplitude wobbling around the 1–4 axis. Phe52 has an additional T-shape short-range contact (3.3 Å) with the adjacent tryptophan residue (Figure 14). The order of the calculated barrier heights agrees well with the order of experimental dipolar couplings (Figure 14) for these three residues. Tryptophan contains a bulky aromatic system, which cannot rotate freely in the GB1 protein.

We have tried to apply the same procedure for analysis of LC8 protein trying to find correlations between NMR measurements and quantum mechanical calculations of rotational barriers. Unfortunately, in the case of LC8 protein, the calculations are complicated by the fact that several polymorphic structures of LC8 are known. We have chosen 3DVT structure for the calculations, but the calculated rotational barriers were not fully consistent with the experiment, which indicates that 3DVT structure was not a good representative of the experimental structure. The knowledge of the 3D structure of the studied molecule is crucial for the understanding of its mobility. If, however, the structural data are missing, the calculations of rotational barriers might be possibly used to provide structural constraints or even to differentiate between several structural models.

Conclusions

In conclusion, under fast MAS conditions, the measurements of heteronuclear (¹⁵N-¹H and ¹³C-¹H) dipolar couplings in proteins can be obtained in a site-resolved way in a 3D experiment containing the CPVC dipolar dimension and two isotropic chemical shift dimensions. We have demonstrated that, for aromatic sidechains, ¹³C-¹H dipolar couplings can be accurately recorded and that they provide information on dynamic processes occurring on the timescales of dipolar interaction, as we have illustrated for two proteins, GB1 and LC8. Remarkably, by the analysis of dipolar lineshapes, specific motional modes can be inferred. Furthermore, in YAF, GB1, and LC8, the observed dynamic behavior could be readily accounted for by the analysis of tertiary contacts formed between the aromatic sidechains and other amino acids, and these observations are generally consistent with quantum mechanical calculations of the rotational energy barriers. Broadly, we expect that the methods introduced in this work will be useful for probing nano- to microsecond time scale motions in a variety of biological systems.