Accurate and precise plasma clearance measurement using four ^99mTc-DTPA plasma samples over 4 h

Abstract

Objectives

Glomerular filtration rate can be measured as the plasma clearance (CL) of a glomerular filtration rate marker despite body fluid disturbances using numerous, prolonged time samples. We desire a simplified technique without compromised accuracy and precision.

Materials and methods

We compared CL values derived from two plasma concentration curve area methods – (a) biexponential fitting [CL (E2)] and (b) Tikhonov adaptively regularized gamma variate fitting [CL (Tk-GV)] – for 4 versus 8 h time samplings from 412 ^99mTc-DTPA studies in 142 patients, mostly paediatric patients, with suspected fluid disturbances.

Results

CL (Tk-GV) from four samples/4 h and from nine samples/8 h, both accurately and precisely agreed with the standard, which was taken to be nine samples/8 h CL from (noncompartmental) numerical integration [CL (NI)]. The E2 method, four samples/4 h, and nine samples/8 h median CL values significantly overestimated the CL (NI) values by 4.9 and 3.8%, respectively.

Conclusion

Compared with the standard, CL (E2) from four samples/4 h and from nine samples/8 h proved to be the most inaccurate and imprecise method examined, and can be replaced by better methods for calculating CL. The CL (Tk-GV) can be used to reduce sampling time in half from 8 to 4 h and from nine to four samples for a precise and accurate, yet more easily tolerated and simplified test.

Introduction

Plasma clearance (CL) of a bolus injection of a radiopharmaceutical marker has been used for determining the glomerular filtration rate (GFR). CL measurement of GFR markers such as technetium-99m-diethylenetriaminepentaacetic acid (^99mTc-DTPA) has been shown to agree closely with renal clearance from inulin constant infusion, which is sometimes considered to be the gold standard technique 1,2. It is commonly understood that a full characterization of the plasma concentration curve provides the most accurate measure of GFR 3–7. For full characterization of the plasma concentration curve, the British Nuclear Medicine Society (BNMS) 5 recommends using a biexponential (E2) function to model the plasma disappearance curve created by the collection of 10 plasma samples over 4 h 5. The initial dose is then divided by the area under the plasma concentration curve (AUC) to give a value for CL, which, for ideal GFR markers, is considered a good measure of GFR 8. In recent times, it has been shown that the accuracy and precision of the E2 model can be further improved by increasing both the number of plasma samples and the duration over which they are collected 6. Although this extended sampling technique may have value for patients with impaired kidney function, or those with body fluid disturbance, it is rarely performed clinically because the large number of plasma samples places an excessive burden on both the patient and the clinical resources 7. Furthermore, it has been shown that the measurement of CL using the E2 model in patients with increased extracellular fluid can lead to clinically significant errors 9,10.

To minimize this burden, alternative methods that are less accurate and/or precise but require fewer plasma samples have been utilized. For example, in routine clinical practice, the BNMS and the Paediatric Committee of the European Association of Nuclear medicine guidelines recommend that the CL be calculated using the slope–intercept method, which is based on fitting of a single-exponential function to find the AUC of a plasma concentration curve comprising two to four plasma samples collected between 2 and 5 h after marker injection 3–5. However, reduced sampling techniques such as the slope–intercept method are known to overestimate the CL and require empirical correction factors to be applied to CL values 5,7. Even with correction, the slope–intercept method can produce systematic errors greater than 10%, depending on the post-hoc correction applied 11. It has also been shown to be insufficient for calculating CL in patients with body fluid disturbances, leading to reported errors in CL as high as 203% when compared with reference methods 12.

Improved abbreviated methods for determining GFR from CL should combine the accuracy and precision of extended plasma sampling techniques with the reduced frequency of sampling used in standard clinical techniques and should be applicable in patients with a wide range of clinical conditions. In this retrospective work, the data from a large cohort of patients who have undergone extended plasma sampling ^99mTc-DTPA GFR studies were examined with the aim of determining whether either the commonly recommended E2 model or the recently developed Tikhonov gamma variate (Tk-GV) model could satisfy the criteria for an improved method.

Materials and methods

Patient population

This retrospective study used data collected from extensive sampling GFR assessments referred to the Medical Physics Department of The Leeds Teaching Hospitals NHS Trust, between April 2003 and February 2013. Patients were referred from the Paediatric and Adult Oncology departments if they were suspected of having a ‘fluid disturbance’ such as ascites, pleural effusion or localized oedema associated with solid tumours 13. All participants or their guardians gave permission for their results to be used for research purposes. The work was considered by the local R&D department to be service evaluation and as such does not require either NHS research ethics or R&D approval. There were 412 studies in which nine plasma samples were collected from 54 female and 88 male patients over the course of 8 h. The patient population had a median age of 12 years, ranging from 0.6 to 56.0 years, and 346 studies (84%) were performed on patients less than 18 years of age. Patients were instructed to neither fast nor alter their diet before their GFR measurement.

Injection and blood sampling

In all studies, the clearance tracer used was ^99mTc-DTPA [TechneScan DTPA (Mallinckrodt Inc., St Louis, Missouri, USA) or Pentacis DTPA (IBA Molecular, Dulles, Virginia, USA)]. A bolus injection consisting of ∼2.5–50 MBq of ^99mTc-DTPA (patient weight adjusted) was administered either peripherally or through an indwelling central venous catheter with samples drawn from either a second line 14 or the contralateral arm. Some of the studies were carried out before the current British diagnostic reference level (ARSAC) of 10 MBq was adopted 15. For each patient, nine samples were drawn according to the sampling schedule 5, 10, 20, 60, 120, 180, 240, 360 and 480 min after injection, which yielded actual average sample-times of 6, 14, 23, 60, 122, 182, 243, 365 and 485 min. Because of the long time during which samples were collected, each sample was centrifuged the day after the procedure was performed.

Standard samples and plasma samples were prepared according to the BNMS guidelines 5 and counted for 50 min using either a Wallac 1470-10 Wizard or a Wizard2 (Perkin Elmer, Turku, Finland) 10-well gamma counter 16. The samples were counted in grouped trays – that is, the nine patient samples, three standards and 10 water-filled background samples. Each counter applied a well-specific sensitivity correction (determined from the normalization) before dividing by the counting time to convert the raw counts into normalized-counts per minute (cpm). The patient and standard sample cpm were manually corrected for background and decay.

Plasma clearance determination

CL of a marker is defined as the administered dose (D) divided by AUC of plasma concentration of that marker (i.e. D/AUC). However, when the actual concentrations C_obs(t) are approximated using fit functions symbolized as C(t), then the AUC value is an approximation. CL values are then calculated using this approximation:

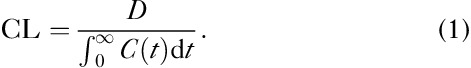The more exhaustive the time sampling is, the better this approximation becomes. The E2, Tk-GV and noncompartmental numerical integration (NI) methods were used to calculate CL as follows.

Biexponential (E2) method

In the biexponential method, plasma concentrations are fitted by sum of two exponential terms:

where c₁ and λ₁ are the coefficients from the early exponential term, and c₂ and λ₂ are from the late exponential term. These coefficients were more reliably obtained by 1/(concentration)²-weighted least-squares fitting of plasma concentration, which minimized the relative error of concentration as recommended elsewhere 17–19. The CL values from the biexponential curve fitting method were obtained from:

CL_E2 values calculated with all available sampling data (i.e. 8 h/nine sample data) using the E2_all method and CL values from the E2_all method are denoted as CL_E2all. In addition, CL values were calculated using the E2 method with four plasma samples obtained during the first 4 h. This had the distinction of providing exact solutions for all four of E2’s parameters, or definitely demonstrating that the only solutions that exist are in the complex field – that is, not every collection of four points has an E2 solution in real space. It has been observed that concentration is approximately linear on a concentration versus logarithm of time plot 20. Accordingly, the four time samples were selected to be in an approximately equal geometric progression of times so that the logarithms of those times are approximately equally spaced, in specific at 5, 20, 60 and 240 min (the E2_few method) and CL values from the E2_few method are denoted as CL_E2few. This was found to allow for the largest number of real-valued E2 solutions having four samples over the 4 h time scale.

Tikhonov adaptive regularized gamma variate (Tk-GV) method

The plasma concentration as a function of time can be modelled by means of gamma variate (GV) function:

where α, β and K are the three parameters of a GV function. The GV function can be rewritten as 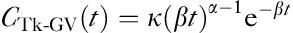, where 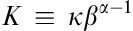and ĸ has units of concentration making it the GV function’s concentration scale parameter. α is the GV function’s shape parameter and is dimensionless. β is the GV’s per-unit-time scale-parameter, where βt is dimensionless. The three parameters of the GV function are obtained by means of Tikhonov regularized fitting of GV function to plasma data, which ensures that 0<α≤1 and β>0, and that the system volume of distribution is robust even when CL and β are vanishingly small 21. The fitting target for the Tk-GV method was modified to find the minimum relative error of the scale parameter, β. This produced slightly more aggressive smoothing compared with the minimization of relative clearance error of the classical Tk-GV method, but had the same property of robustness of volume of distribution for vanishingly small CL and β. CL was then calculated using the GV model equation 21:

where Γ(α) is gamma function of α. CL values calculated from extended sampling data – that is, 8 h, nine sample data (the Tk-GV_all method) – and CL values from the Tk-GV_all method are denoted as CL_Tk-GVall. CL values were also obtained from reduced sampling data – that is, same time samples selected for the 4 h E2 calculations (the Tk-GV_few method) – and CL values from the Tk-GV_few method are denoted as CL_Tk-GVfew.

Numerical integration method

Numerical integration (NI), a noncompartmental method and the most commonly used standard method for measuring drug clearances, was used here as the reference method, as it implies fewer kinetic assumptions compared with compartmental modelling, and given a sufficient number of samples and a long-enough elapsed time of sampling, it is known to accurately model the plasma concentration curve shape 12,17,21–23. Using the log-linear trapezoidal rule 24, NI consists of calculating the total AUC by adding areas under multiple curves interpolated between adjacent plasma concentration samples and includes two extrapolated areas, one from before the first sample and the other after the last sample 12,25. Adjacent time-sample concentrations were interpolated and/or extrapolated using exponential functions. The two extrapolated curves, backward-extrapolated to time zero from the earliest sample and forward-extrapolated to infinite time from the latest sample, used the single-exponential term solutions to the two earliest and two latest plasma time samples, respectively. Finally, CL was obtained by dividing the amount of dose by the AUC. CL values calculated from the NI method with 8 h, nine sample data were used as the reference CL values and denoted as CL_ref.

Statistical analysis

Passing–Bablok regression analysis was used to compare CL values and to test the significance of differences between methods 26. The regression analysis was applied to CL data that were transformed by taking their natural logarithms, as the logarithm of CL values are known to be more homoscedastic, which has been shown to improve the performance of the Passing–Bablok method comparison 21,27. Furthermore, taking the differences of the logarithms of the clearance values is similar to expressing the CL value differences as relative magnitudes, which reduces the effects of different CL values upon the error – that is, large errors at high CL and small errors at low CL. Logarithms of CL values calculated using the Tk-GV and E2 methods with all inclusive sampling were compared with the logarithms of the CL_ref values using the Passing–Bablok comparison method. It should be noted that CL values without taking logarithms were screened for significant intercepts of their Passing–Bablok regression lines. As all intercepts of these regressions were not significantly different from zero, this confirmed that the natural logarithms of the CL values could be taken without introducing bias.

The median differences between CL values from each trial method and the reference CL values were calculated. The same analyses were repeated to compare the Tk-GV and E2 methods performed with fewer samples with the reference method. In this study, clinical outliers were defined as those trial CL values that were greater than 10% different from their paired reference method CL values.

Results

The clearance values with inclusive sampling (8 h, nine samples) from the Tk-GV (CL_Tk-GVall), E2 (CL_E2all) and reference CL (CL_ref) methods, as well as with restricted sampling (4 h, four samples) from the Tk-GV (CL_Tk-GVfew) and E2 (CL_E2few) methods, were calculated from 412 GFR studies and compared pairwise for significance of difference.

CL values obtained from extended sampling (nine samples over 8 h)

A summary of the Passing–Bablok regression results comparing CL_Tk-GVall and CL_E2all with the CL_ref values are given in Table 1. Regression analysis shows good correlations between log-log CL values calculated using all three methods using all samples (all R²>0.99). All of the regression line slopes shown in Table 1 are statistically indistinguishable from 1, suggesting that a regression line slope is not necessary for comparing those CL values. In other words, all of the methods were collinear and no nonlinearity was detected by means of method comparison (as the power function exponents were statistically indistinguishable from 1). This allowed for more sensitive testing by means of direct comparison of the median of relative values between the methods and for a comparison of accuracy and precision between methods. As measures of accuracy and precision numbers, respectively, the median differences and the interquartile ranges (IQR) between CL values were obtained from each all inclusive sampling method and the CL_ref values (Fig. 1).

Table 1.

Passing–Bablok coefficients for logarithms of plasma clearance results for all samples for the E2, Tk-GV and NI reference methods

Fig. 1.

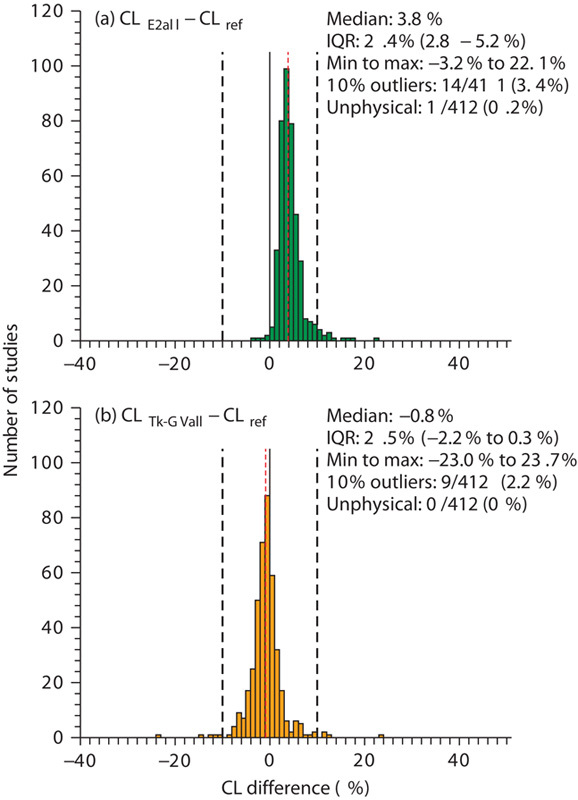
Histograms of (a) the differences between CL values obtained using the E2 (8 h, nine samples) method (CL_E2all) and reference clearance values (CL_ref), and (b) difference between CL values obtained using the Tk-GV (8 h, nine samples) method (CL_Tk-GVall) and reference clearance values (CL_ref) as a percentage of reference clearance values. The vertical red lines represent the median values. The black solid lines represent zero difference and the black dashed lines represent the −10% and 10% differences limits for outliers between the estimated and the reference values. CI, confidence interval; CL, plasma clearance; IQR, interquartile range.

As the CL_E2all versus CL_ref regression line’s intercept (Table 1) was significant [95% confidence interval (CI) is 0.018–0.045], the CL_E2all values and CL_ref values differed by a constant proportion (a constant intercept on a log–log regression line corresponds to a proportion as 1ny=m1nx−b has the form y′=mx′−b and implies y=e^−bx^m, which has the form y=b′x^m, where b′=e^−b is the proportionality constant). The positive intercept implies that the E2_all method overestimated the CL_ref values. As shown in Fig. 1, the median value of the overestimation was 3.8%. One study (0.2% of the total of 412 studies) of the E2_all method converged to unphysical values – that is, an unphysical exponential coefficient and clearance – and was discarded for the statistical comparisons. Of the remaining 411 studies, 3.4% had CL_E2all and CL_ref values that differed by more than 10%.

The results from regression testing in Table 1 show that the Tk-GV (8 h, nine samples) and the reference method did not statistically differ from each other (95% CI of intercept, −0.015 to 0.017). There was a –0.8% median difference between the CL_Tk-GVall and the CL_ref values. There were 2.2% of all studies having more than 10% difference between CL_Tk-GVall and CL_ref values. No failures consisting of out of bounds parameters were found for the Tk-GV_all method.

CL values obtained from reduced sampling (four samples over 4 h)

Table 2 presents the Passing–Bablok regression results comparing the CL_ref values with those CL values calculated using the Tk-GV_few and the E2_few method. The comparisons in Table 2 show good correlations between log–log CL values calculated using each trial method and the CL_ref values (all R²>0.98). All of the regression slopes were statistically indistinguishable from 1 and with the same argument as for the inclusive sampling study – only intercepts were necessary for comparing those regression results. Figure 3 presents the median and IQR of differences between CL values calculated from the reduced sampling trials and the CL_ref values.

Table 2.

Passing–Bablok coefficients for logarithms of plasma clearance results for 4 h, four samples for the E2, Tk-GV and NI reference methods

Fig. 3.

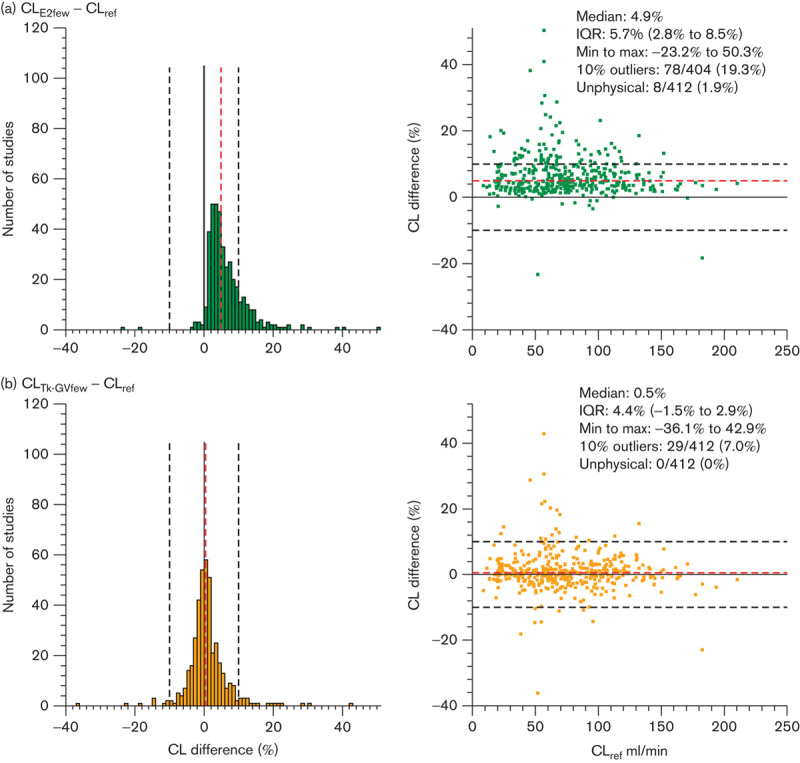
Histograms (left side) and Bland–Altman plots (right side) of (a) the differences between CL values obtained using the E2 (4 h, four samples) method (CL_E2few) and the reference clearance values (CL_ref, 8 h, nine samples) and (b) the difference between CL values obtained using the Tk-GV (4 h, four samples) method (CL_Tk-GVfew) and reference clearance values (CL_ref) as a percentage of reference clearance values. The dashed red lines represent the median values of the estimates. The black solid lines represent zero difference between methods and the black dashed lines represent the −10% and 10% difference limits for outliers between the estimated and reference values. CI, confidence interval; CL, plasma clearance; IQR, interquartile range.

The significant intercepts of CL_E2few versus CL_ref (95% CI is 0.017–0.071) implies that CL_E2few and CL_ref differed by a constant proportion. As shown in Fig. 3a and Table 2, the E2_few method overestimated the CL_ref values by a median difference of 4.9%. Eight studies (1.9%) with E2_few method results had unphysical exponential coefficients and/or CL values and were unavailable for statistical comparison. Of the remaining 404 studies, 19.3% were outliers, having CL_E2few and CL_ref values that differed by more than 10%.

Fig. 2.

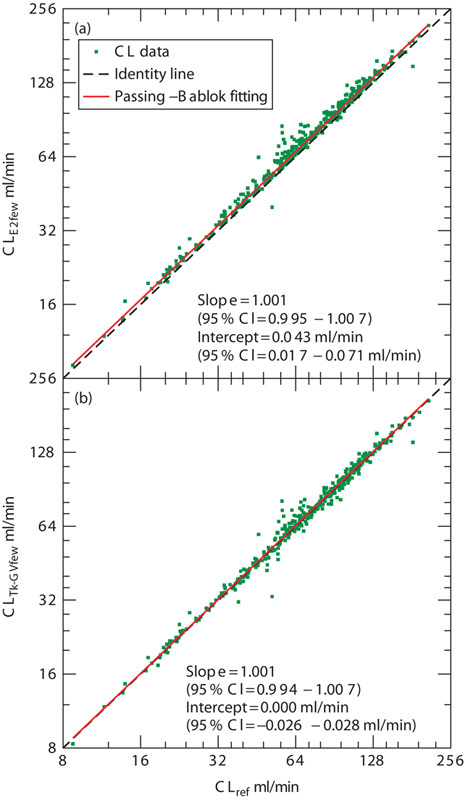
CL values obtained using (a) the E2 (4 h, four samples) method (CL_E2few) and (b) the Tk-GV (4 h, four samples) method (CL_Tk-GVfew) as a function of CL values obtained using the reference method (CL_ref). CI, confident interval; CL, plasma clearance.

As shown in Table 2 and Fig. 3b, the Tk-GV_few and reference methods were not significantly different (95% CI of intercept is −0.026 to 0.028). There was a 0.5% median difference between CL_Tk-GVfew and CL_ref values. Only 7% of all 412 studies comparing the CL_Tk-GVfew and CL_ref values differed by more than 10%. The Tk-GV_few method had neither out of bounds coefficients nor negative GFR-values (0 unphysical results) among the 412 studies.

Studies with CL values with larger deviation (>25%) from the reference CL values were individually examined. It was found that those large errors were introduced mainly due to larger noise of the plasma sample concentrations and no relationship was found for lower or higher CL values.

Discussion

It is clinically useful to minimize the number of blood samples required for testing and still obtain accurate and precise CL values. To determine CL after bolus injection of radiopharmaceutical and characterize the full plasma concentration curve, it is currently recommended to collect 10 samples over 4 h and model the resulting curve using E2 functions 3,5. In this study, the commonly recommended E2 and recently developed Tk-GV methods were tested for accuracy and precision for inclusive (8 h, nine samples) as well as restricted (4 h, four samples) plasma-sampling. A total of 412 studies were performed on 142 individuals suspected of having fluid disturbances from ascites, pleural effusions or localized oedema associated with solid tumours.

The results of this study implied that the completely inclusive E2_all method overestimated the reference CL values by a statistically significant median value of 3.8% and had an IQR of 2.4%. Even though 96% of the CL_E2all values in this patient population were found to be within 10% of the reference CL, it is important to note that the method failed outright in one patient study, or ∼0.2% of the study population. When the sample time period and number of samples were reduced from nine samples over 8 h to four samples over 4 h, the overestimation of the CL_ref values by the resulting E2_few method increased to a median value of 4.9% and showed the largest imprecision result in this study as measured using IQR (5.7%). Moreover, the percentage of studies in which there was less than 10% difference between the CL values from the E2_few and the reference method decreased from 96 to 79%, and the failure rate of obtaining physical results increased from 0.2 to 1.9% (eight patients) of the patient population. These results show that the E2 method was less accurate, produces CL values with more clinically significant errors and is prone to failure when reduced sampling is used to calculate CL. This confirms the results of a previous study, which demonstrated that the accuracy of CL measurements using the E2 model decreased when sampling time period decreased 6. However, that study did not propose a solution for that problem.

The results from the Passing–Bablok method comparison analysis showed that the Tk-GV method with both inclusive and restricted sampling produced statistically similar results to the reference method. Furthermore, more than 93% of the CL values from the Tk-GV method with both inclusive (98%) and restricted sampling (93%) were found to be within 10% of the reference CL values. No failures were found in the Tk-GV method with either inclusive or restricted sampling. When the elapsed sampling time was reduced from 8 to 4 h and the number of samples was reduced from nine to four samples, the median differences between the CL values from the Tk-GV method and CL_ref values changed from −0.8 to 0.5%, implying little change in accuracy. These results suggest that the Tk-GV_few method (with 50% of the sampling time and 44% of the number of samples) produced CL values similar to both the CL_ref values and the CL_Tk-GVall values.

The Tk-GV_few method demonstrated better method accuracy compared with E2_few (smaller median overestimation of reference CL) and precision (smaller IQR). The Tk-GV_few method even demonstrated better accuracy compared with the E2_all method. For both the inclusive and restricted sample study CL values, the Tk-GV method produced the least number of values that differed by more than 10% from the reference method. The findings show that fewer samples over a lesser time can be used to obtain CL values that are more precise and accurate when the Tk-GV method is used to calculate them. The Tk-GV method can also be a good alternative to the frequently used slope–intercept method as the slope–intercept method needs post-hoc corrections 5, which unlike the Tk-GV method, should not be used because of inappropriate overestimated CL results for fluid-disturbed patients 12,28.

Our results show that the Tk-GV method yielded accurate CL values for patients suspected of having fluid disturbances. Fluid disturbances alter the concentration curve shapes. GVs have a shape parameter, α, that can follow fluctuations in concentration curve shape, and biexponential functions do not. These shape changes are difficult to visualize on ordinary concentration versus time plotting. Concentration curve shapes are better appreciated on concentration versus logarithm of time plots, which have the effect of linearizing the early concentrations 20. It can be shown that, on such a plot, a GV will have two inflection points at 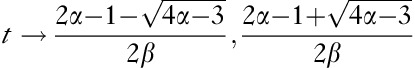, if the shape parameter is α>3/4, one inflection point for α=3/4, and none for α<3/4. For example, if α=0.85 and β=0.001, the inflection points would occur at 34 and 666 min. It is this mutability of shape that allows the GVs to follow concentration curves better compared with biexponentials, and to adjust to subtle alterations of curve shape, for which alterations of shape a biexponential model would optimistically require the addition of yet more compartments for their proper accommodation.

It is important to know how much a GFR measurement is likely to change in follow-up. For that purpose, precision is important, as a more precise measurement can be used to detect smaller interval differences. For example, monitoring of the change in kidney function is needed for patients with renal failure 29, for renal toxicity during cancer chemotherapy 30, for solitary kidney patients 5 or clinical trial kidney transplant recipients 31 and progression of renal damage in urinary obstructive disease, especially in children 5. This does not include conditions for which follow-up is not always needed but for which both accuracy and precision are still useful – for example, the evaluation of potential transplant donors, or to predict survival in cirrhosis and liver transplantation 32. Clinical indications such as these and potentially others may benefit from simple-to-obtain, precise and accurate GFR determinations. For many of the populations listed above, it may be of interest to study the applicability of the Tk-GV method. In the meanwhile, the Tk-GV method significantly outperformed the E2 method tested here in patients having suspected fluid disturbances.

The present study has a number of limitations. The study has been limited to individuals suspected of having fluid disturbances from ascites, pleural effusions or localized oedema associated with solid tumours. Furthermore, the reference method in this study – that is, the noncompartmental, numerical-integration method – implies that the terminal exponential occurs before 8 h. The advantage of the NI reference method is that the actual data, including any unusual fluctuations in that data, are used for quantification without making extraordinary assumptions concerning curve shape. Some authorities prefer the use of constant infusion of inulin as a standard 1,2,8, but comparison studies with bolus NI are lacking. However, when E2 models of bolus inulin were compared with constant infusion of inulin performed at different times in the same participants, differences strikingly similar to those seen here were produced, but without use of a control or a hypothetical explanation of those differences 18. Furthermore, the use of 24 h urine collection for the estimation of GFR is often less reliable compared with the CL measurement due to the collection errors and diurnal variation in GFR 33. In the current work, the NI control was used in the same participants using the same data, at the same times, such that the differences seen can only be due to the different analytic techniques.

Conclusion

This study has shown that using the Tk-GV method to calculate AUC reduces the intensive plasma sampling required to obtain accurate CLs for patients with suspected body fluid disturbances. The Tk-GV method using four plasma samples drawn over 4 h can be used to accurately replace with very good precision those CL values obtained from the E2 method, which is currently recommended by guidelines for accurate GFR when body fluid disturbances are suspected, for a much less traumatic and labour intensive test and is especially important for paediatric patients.