Calcium-channel number critically influences synaptic strength and plasticity at the active zone

Abstract

How synaptic-vesicle release is controlled at the basic release structure, the active zone, is poorly understood. By performing cell-attached current and capacitance recordings predominantly at single active zones in rat calyces, we found that single active zones contained 5-218 (mean, 42) calcium channels and 1–10 (mean, 5) readily releasable vesicles (RRVs) and released 0–5 vesicles during a 2-ms depolarization. Large variation in the number of calcium channels caused wide variation in release strength (measured during a 2-ms depolarization) by regulating the RRV release probability (P_RRV) and the RRV number. Consequently, an action potential opened ~1–35 (mean, ~7) channels, resulting in different release probabilities at different active zones. As the number of calcium-channels determined P_RRV, it critically influenced whether subsequent release would be facilitated or depressed. Regulating calcium channel density at active zones may thus be a major mechanism to yield synapses with different release properties and plasticity. These findings may explain large differences reported at synapses regarding release strength (release of 0, 1 or multiple vesicles), P_RRV, short-term plasticity, calcium transients and the requisite calcium-channel number for triggering release.

The function of the nervous system relies on trillions of synapses that display highly heterogeneous release strength and short-term plasticity. Different release strengths and short-term plasticity profiles of synapses^1–5 are used for distinct and essential forms of neural computation in brain circuits⁶. High-release-strength synapses may initially relay spikes from the presynaptic to the postsynaptic neuron with great reliability but tend to exhibit depressed release with ongoing repetitive firing^1–3,5. Such synapses may thereby mediate adaptation of cortical responses to sustained visual, olfactory or auditory stimuli⁶. By contrast, low-release-strength synapses may behave as silent synapses that can be activated during development, learning and memory formation⁶; these synapses may also mediate high-pass filtering of spikes owing to their propensity to facilitate during high-frequency firing⁶. More broadly, release impairment might contribute to the generation of various neurological disorders. All these factors emphasizing the importance of various release profiles have motivated two decades of extensive research of the mechanisms by which synapses elaborate different release strengths^1–5,7–23. However, the underlying mechanisms remain obscure, largely owing to the lack of techniques to access a single unit of the release structure, the active zone. Here we addressed this issue by developing a technique to patch predominantly single active zones at the release face of the nerve terminal, where we quantified the number of calcium channels and readily releasable vesicles, and their probability of opening or release.

RESULTS

Cell-attached patch recordings at single active zones

In brainstem slices pretreated with the protease papain (2.5 units ml⁻¹, in bath solution for 5–10 min), we partially exposed the calyx (nerve terminal) release face by applying a pressure (~0.5–1.0 p.s.i.) via a pipette between the calyx and the postsynaptic neuron (Fig. 1a). We used the same pipette to form the cell-attached patch at the release face in the ‘rim’ region within ~0–2 µm under the calyx surface (Fig. 1a). The patch was at the calyx because after whole-cell break-in (with an intracellular solution; Online Methods), a 20-ms depolarization to 0 mV induced a calcium current (I_Ca) of 1.95 ± 0.12 nA (mean ± s.e.m.) and a capacitance jump (ΔC_m ) of 371 ± 35 fF in 8 of 8 patches at 2 mM extracellular calcium, which were similar to those obtained without papain pretreatment and pressure application (I_Ca, 1.98 ± 0.16 nA; ΔC_m, 435 ± 35 fF, n = 5; P > 0.05; Supplementary Fig. 1). Thus, papain pretreatment, which made it easier to expose the release face, and the procedure to expose the release face did not affect I_Ca and release. Compared to our previously reported method, in which the release face was exposed via removal of the postsynaptic neuron²⁴, the present method detected I_Ca with far greater consistency, a feature essential for the extensive characterization of release profiles in this study.

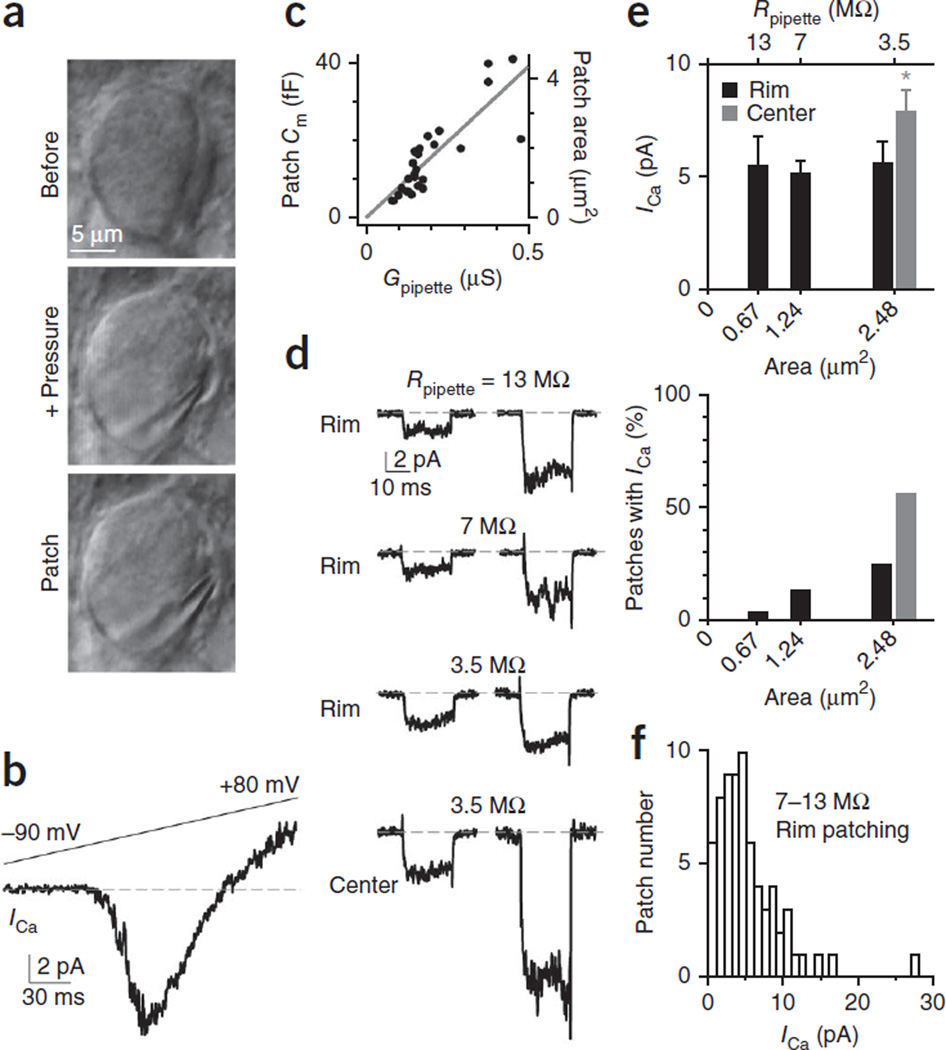
Figure 1.

Cell-attached patch recording of calcium currents at the calyx release face. (a) Differential infrared contrast (DIC) image of a calyx before (top) and after pressure application (middle) via a pipette that partially separated the calyx from the postsynaptic neuron, and after the cell-attached patch at the calyx release face (bottom, same pipette as in the middle). (b) Sampled current response to a ramp voltage from −90 to +80 mV at a cell-attached patch. Dashed line indicates the baseline. (c) Patch C_m and patch area plotted versus the pipette conductance (G_pipette = 1/resistance). The slope of the linear fit was 78 fF µS⁻¹. The specific C_m was 9 fF µ m⁻². (d) Sampled I_Ca induced by a 20-ms depolarization (from −90 to 0 mV) at the rim region (applies if not mentioned) with pipette resistance (R_pipette) of ~13 MΩ, 7 MΩ or 3.5 MΩ and at the central region with ~3.5 MΩ pipettes. All traces were low-pass-filtered at 2 kHz. Each trace was from a different patch. Dashed line indicates the baseline. (e) I_Ca amplitude (top, mean ± s.e.m.) and percentage (bottom) of patches exhibiting I_Ca at the calyx rim and central region (>2 µm deeper) are plotted versus the patch mean membrane area or pipette resistance (R_pipette). Top, rim patching: 13 MΩ, n = 12 patches; 7 MΩ, n = 57 patches; 3.5 MΩ, n = 22 patches. Top, central patching: 3.5 MΩ, n = 20. Bottom, rim patching: 13 MΩ, 12/353 patches; 7 MΩ, 57/425 patches; 3.5 MΩ, 22/88 patches. Bottom, central patching: 3.5 MΩn = 20/36 patches. (f) Patch I_Ca amplitude distribution from 6–8 (n = 57) and 12–14 MΩ (n = 12) pipettes. Patches with 3–4 MΩ (n = 22) pipettes were not included.

With 3–14 MΩ pipettes containing 10 mM calcium and a solution that isolated I_Ca, depolarization from −90 to 0 mV (these conditions apply in all cases unless mentioned otherwise) induced an inward current of 0.6–27.7 pA in 91 of 866 patches (for example, Fig. 1b). The current was mediated by voltage-dependent calcium channels based on multiple criteria¹⁵: current was activated at −37 ± 1 mV, peaked at 1 ± 2 mV, reversed direction at 45 ± 2 mV during a voltage ramp (n = 35 patches, Fig. 1b) and was abolished by including 50 µM cadmium in the pipette (n = 119 patches with no detectable currents, P < 0.001, χ² test; for example, Supplementary Fig. 2). Because only 11% (91 of 866) of the patches exhibited I_Ca, and we detected no inward currents at the calyx outer face (not apposing the postsynaptic neuron, n = 89 patches, P < 0.01, χ² test; Supplementary Fig. 3), calcium channels must be clustered at the release face. These results, together with the findings presented below that release only occurs at patches exhibiting I_Ca, suggest that patches with I_Ca contain at least one active zone, each with a cluster of calcium channels.

To gauge more precisely the number of active zones encompassed in a rim patch, we characterized I_Ca using patch pipettes of different sizes with resistances of ~13 MΩ (12–14 MΩ), 7 MΩ (6–8 MΩ) or 3.5 MΩ (3–4 MΩ). To estimate the patched membrane area of these different pipettes, we first measured the patch membrane capacitance of pipettes with different initial resistance (or conductance; Online Methods). We found a linear relation between the patch capacitance and the pipette conductance with a slope of 78 fF µS⁻¹ (Fig. 1c), consistent with previous measurements²⁵. With this slope and the specific membrane capacitance of 9 fF µm⁻² (ref. 26), the mean patch membrane areas for 13-MΩ, 7-MΩ and 3.5-MΩ pipettes were ~0.67 µm², 1.24 µm² and 2.48 µm², respectively. Despite a nearly fourfold increase in the patch area (from 0.67 µm² to 2.48 µm²), mean I_Ca amplitudes obtained with 13-MΩ, 7-MΩ and 3.5-MΩ pipettes remained essentially unchanged at 5.5 ± 1.3 pA (n = 12), 5.2 ± 0.6 pA (n = 57) and 5.6 ± 0.9 pA (n = 22), respectively (P = 0.89, ANOVA test, Fig. 1d,e); whereas the percentage of patches exhibiting I_Ca increased from 3.4% (12/353 patches) to 13.4% (57/425 patches) and 25% (22/88 patches, Fig. 1e). These results suggested that each I_Ca -containing patch encompassed only one active zone. Otherwise, the mean I_Ca amplitude should have increased with patch area. The I_Ca amplitude per patch varied widely (Fig. 1f).

Compared to rim patching with ~3.5-MΩ pipettes, patching at >2 µm below the surface (central region) with ~3.5-MΩ pipettes increased the fraction of patches exhibiting I_Ca from 25% (22/88 patches, rim patching) to 56% (20/36 patches, χ² test, P < 0.01) and increased the I_Ca amplitude from 5.6 ± 0.9 pA (n = 22) to 8.0 ± 0.8 pA (n = 20, Fig. 1d,e, P < 0.03). Thus, patches at the central region likely contain multiple active zones, suggesting that active-zone density is higher in central versus rim regions.

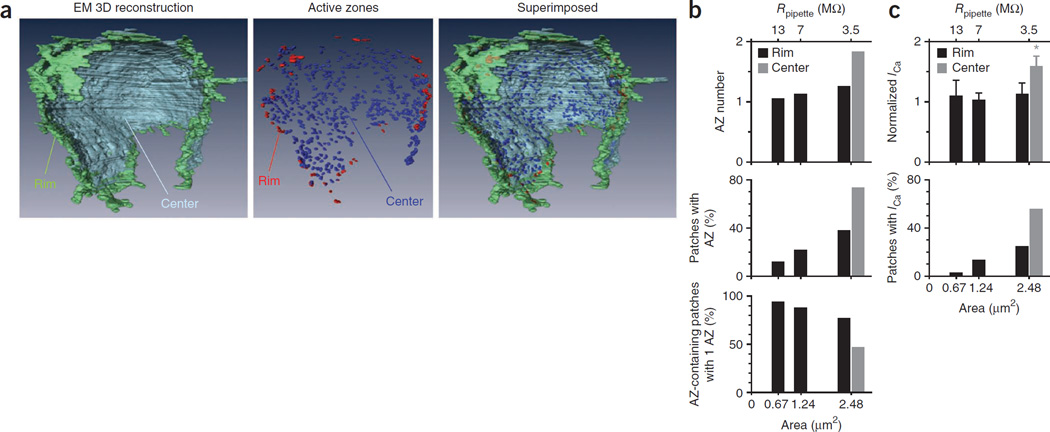
To corroborate these interpretations regarding active-zone prevalence, we analyzed previously published three-dimensional reconstructions of calyces obtained with electron microscopy (Fig. 2a)²⁷ or confocal microscopy (for example, Supplementary Fig. 4)²⁸. Computationally identifying the rim region in electron microscopy data as an ~2-µm-wide swath of calyceal release face abutting the outer face (Online Methods and Supplementary Fig. 5), we found an active-zone density of 0.20 active zones µm⁻² (Fig. 2a). By contrast, active-zone density in the central region was considerably larger at 0.56 active zones µm⁻² (Fig. 2a). We observed similar differences in active-zone density in confocal microscopy reconstruction of calyces (0.17 active zones µm⁻² at the rim area, 0.32 active zones µm⁻² at the center, n = 5 calyces, P = 0.012, Supplementary Table 1 and Supplementary Fig. 4).

Figure 2.

Active-zone density at the calyx release face matches patch electrophysiology. (a) A calyx three-dimentionally reconstructed with electron microscopy (EM; data from ref. 27) showing rim and center of the calyx release face (left), active zones at the rim and central region (middle; each spot represents an active zone) and the two images superimposed (right). The calyx vertical length is ~18 µm. (b) The mean active zone (AZ) number and percentage of patches containing one or more active zone, and the percentage of patching one active zone in patches containing one or more active zones plotted versus the patch membrane area of 13 MΩ, 7 MΩ and 3.5 MΩ pipettes. Data were obtained from simulation with the rim (0.20 active zone µm⁻²) or central (0.56 active zone µm⁻²) active-zone density measured from EM data in a. (c) Normalized I_Ca amplitude (mean ± s.e.m.) and percentage of patches exhibiting I_C at the calyx rim and central region (>2 µm deeper) plotted versus the patch mean membrane area or pipette resistance (R_pipette; 13 MΩ, n = 12; 7 MΩ, n = 57; 3.5 MΩ, n = 22). These plots are the same as those in Figure 1e, except that I_Ca amplitudes were normalized to the mean I_Ca obtained with 13-MΩ pipettes for comparison with data in b. We multiplied the normalized value by 1.1 so that the normalized I_Ca amplitude obtained by the 13-MΩ pipettes was the same as the predicted active-zone number of the corresponding pipette in b.

To determine the probability and the number of active zones being covered by a defined patch membrane size, we performed a numerical simulation using a rim active-zone density of 0.2 active zones µm⁻² as derived from the electron microscopy data (Online Methods and Supplementary Fig. 6). With random sampling, our simulation showed that as the patch membrane area increased from 0.67 µm² (the mean membrane area for 13-MΩ pipettes) to 1.24 µm² and 2.48 µm² (for 7-MΩ and 3.5-MΩ pipettes, respectively), the mean active-zone number at active zone-containing patches was rather stable, increasing from 1.1 to only 1.3 active zones per patch, whereas the percentage of patches containing active zones increased by about threefold, and the percentage of patches containing 1 active zone in active zone-containing patches decreased only modestly (Fig. 2b). With the central active-zone density of 0.56 µm⁻², simulation with a patch area of 2.48 µm² (for 3.5-MΩ pipette) predicted a higher percentage of patches containing active zones and higher active-zone number but a lower percentage of getting 1 active-zone in active zone-containing patches when compared to simulation at the active-zone density of 0.20 active zones µm⁻² (Fig. 2b). Overall, simulations based on the measured active-zone densities from the reconstructed calyx (Fig. 2a) resulted in outcomes (Fig. 2b) that were closely analogous to those obtained by patch electrophysiology (Fig. 2c, derived from Fig. 1e for side-by-side comparison). We observed a similar match when we used the confocal microscopy data for simulation (0.17 active zones µm⁻² at the rim area and 0.32 active zones µm⁻² at the center). In fact, the match was better (data not shown) because the active-zone density measured from confocal microscopy data was slightly lower than that measured from electron microscopy data.

The percentage of rim patches showing I_Ca was lower than the corresponding simulated results (Fig. 2b,c), suggesting that the active-zone density at the patch membrane may be lower than the measured value in the rim region, likely because some presumed rim patch may include the adjacent nonrelease face. This might explain why I_Ca did not increase, whereas the predicted active-zone number increased as the rim patch area increased (Fig. 2b,c). Alternatively, the increase in predicted active-zone number was too small (only ~18%, from 1.1 to 1.3 active zones) to detect given the large variation of I_Ca (Fig. 1d,f). Taken together, these results suggest that rim area patching with ~3.5–13-MΩ pipettes contained predominantly single active zones.

To be conservative, we examined single active zones with only ~7–13-MΩ pipettes at the rim region in subsequent experiments and data analysis because simulation predicted higher percentages of patching one active zone using 7–13-MΩ pipettes at the rim region (88–94%, Fig. 2b). I_Ca recorded with ~7–13 MΩ pipettes at the rim region was 5.3 ± 0.5 pA (n = 69) and ranged from 0.6 pA to 27.7 pA. The wide I_Ca amplitude distribution (Fig. 1f) reflected the large I_Ca variation from single active zones.

Single-calcium-channel properties at calyx release face

Knowing the I_Ca amplitude from the patched active zone (Fig. 1f), we sought to count the calcium-channel number (N_channel) at the patched active zone based on

$$N_{\text{channel}}=I_{\text{Ca}}/(i_{\text{mean\_channel}}\times P_{\text{mean\_channel}})$$ (1)

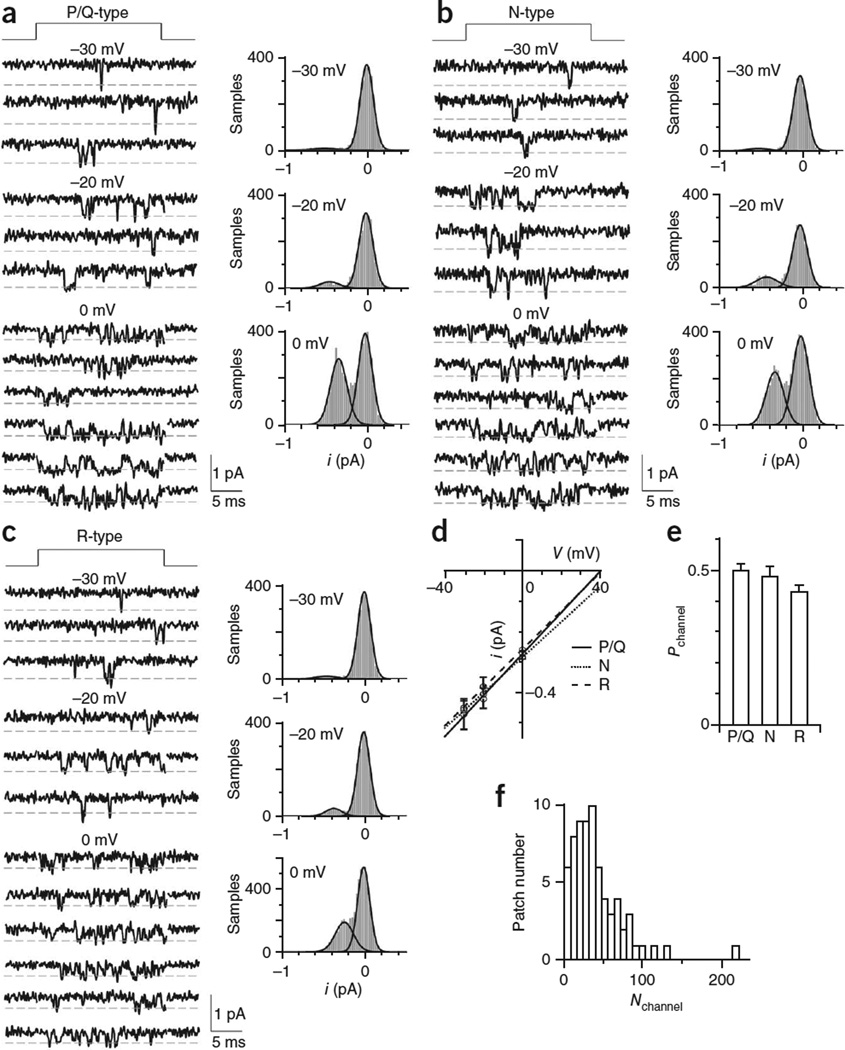
where N_channel refers to active, but not inactive channels, and i_{mean_ channel} (i refers to single-channel current, whereas I refers to current from a population of channels) and P_{mean_channel} (mean probability of a channel being open) were determined by the following single-channel experiments. In the calyces of postnatal day 8–10 rats we used, P/Q-, N- and R-type calcium channels are all present¹⁵. Thus, we used channel type–specific blockers to isolate each type of channel (Fig. 3a–c: see Online Methods for blocker names and concentrations). Depolarization for 20 ms elicited single-channel currents that flickered ‘open’ with durations mostly <3 ms (Fig. 3a–c). For P/Q-, N- and R-type channels, respective single-channel conductances (g_channel) were 6.8 ± 0.2 pS (n = 11 patches), 5.8 ± 0.2 pS (n = 6) and 6.3 ± 0.1 pS (n = 7, Fig. 3d); their elementary-current amplitudes (i_channel) at voltages (V) of 0 mV were 0.27 ± 0.01 pA (n = 11), 0.28 ± 0.01 pA (n = 6) and 0.26 ± 0.01 pA (n = 7, Fig. 3d); and their probabilities of being open (P_channel) were 0.50 ± 0.02 (51 traces from 11 patches), 0.48 ± 0.03 (33 traces from 6 patches) and 0.43 ± 0.02 (43 traces from 7 patches, Fig. 3e), respectively. As all three types were closely similar in g_channel, i_channel and P_channel, we obtained the i_{mean_channel} (0.27 ± 0.01 pA, n = 3 types) and P_{mean_channel} (0.47 ± 0.02, n = 3 types) at V = 0 mV without considering their differential contribution. N_channel, calculated from equation (1) with measured i_{mean_channel}, P_{mean_channel} and I_Ca, was 42 ± 4 but ranged widely from 5 to 218 (n = 69 patches, Fig. 3f). This distribution represents the active calcium channel distribution at individual active zones. We obtained similar distributions if i_{mean_channel} and P_{mean_channel} for each type were used (Supplementary Fig. 7), suggesting that data in Figure 3f would not be influenced by differential contributions of different types of calcium channels.

Figure 3.

Single calcium-channel conductance and probability of a channel being open (‘open probability’) at the release face. (a–c) Left, sampled single P/Q-type (a), N-type (b) and R-type (c) channel current at indicated voltages (the time of depolarization is shown at the top). Right, all-point histogram of the corresponding traces shown on the left. Curves are Gaussian fits of the data. All traces were low-pass-filtered at 2 kHz. (d) The single-channel i/V curve (mean ± s.e.m.) for P/Q-type (n = 6–11 patches for each data point), N-type (n = 3–6) and R-type (n = 3–7) channels. (e) P_channel (mean ± s.e.m.) for P/Q-type, N-type and R-type channels 0 mV. (f) Distribution of the patch N_channel, derived from data in Figure 1f, where I_Ca was converted to N_channel using equation (1).

Evoked release at cell-attached patch

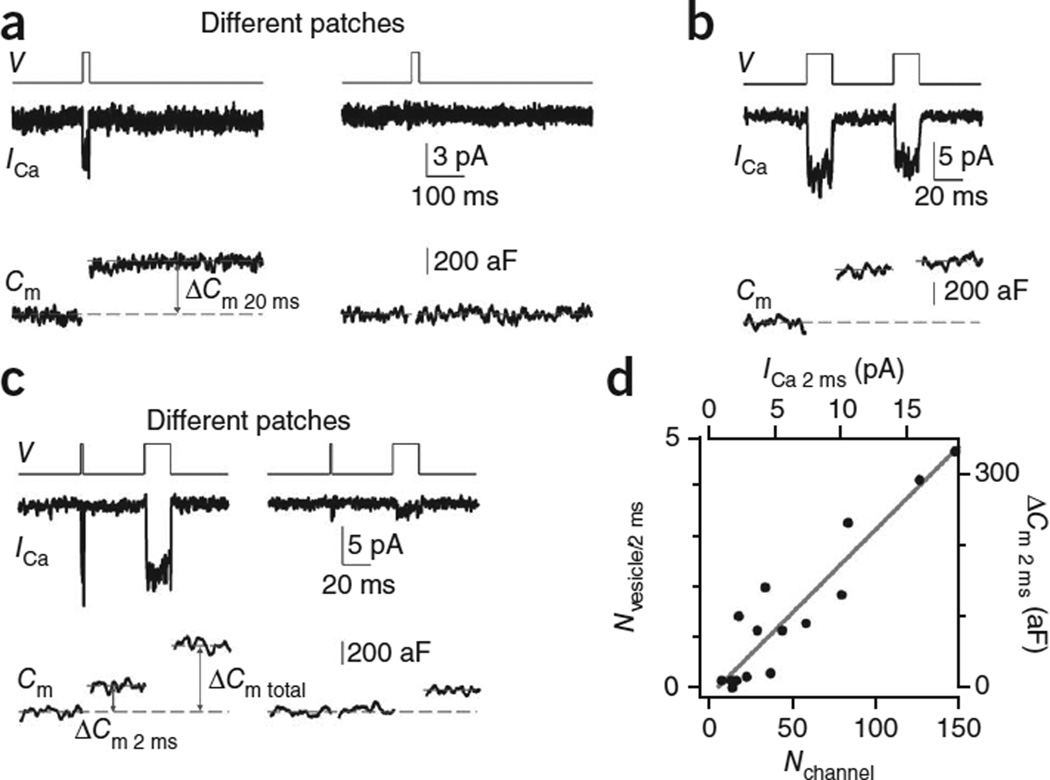
Knowing that N_channel varied widely at the patched active zone, we studied how this variation affects the release properties at the active zone. We did not include calcium-channel blockers in these experiments. Application of a 20-ms depolarization via the patch pipette induced a capacitance jump (ΔC_{m 20 ms}) of 323 ± 44 aF (n = 10) at patches with detectable I_Ca (I_{Ca 20 ms} ≥ 1 pA), but negligible ΔC_m (3 ± 2 aF, n = 226) at patches without detectable I_{Ca 20 ms} (< 1 pA, Fig. 4a). For these experiments, the noise in I_Ca recordings was higher owing to the concurrent capacitance recordings. Typically, we could only detect I_Ca with 1 pA or larger. However, this should not affect our conclusion, because I_Ca at most patches was larger than 1 pA when only I_Ca was measured in low-noise conditions (Fig. 1f). We concluded that release occurred only at patches containing calcium channels. This conclusion supports our suggestion that calcium channels are clustered at the active zone for triggering release.

Figure 4.

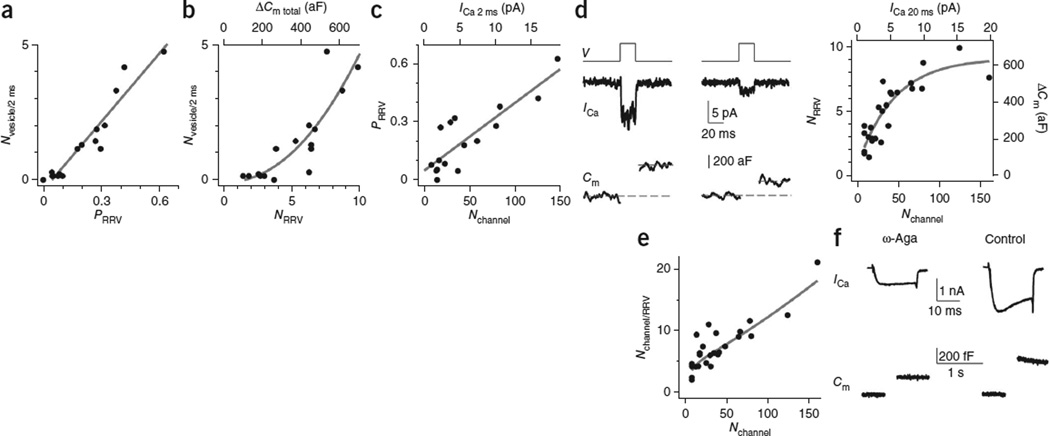
The impact of the calcium-channel number on release strength. (a) I_Ca (middle) and C_m (lower) induced by a 20 ms depolarization (upper, V) from two patches showing a detectable (left) or undetectable (right) I_Ca. Dashed lines show how we measured ΔC_m. Traces were low-pass–filtered at 1 kHz. The tail current was not as clear as in Figure 1 owing to the higher noise and lower-frequency filtering. (b) Sampled I_Ca and C_m induced by a pair of 20-ms depolarizations (interval, 50 ms). (c) Sampled I_Ca and C_m induced by a 2-ms depolarization followed 50 ms later by a 20-ms depolarization from two patches with large (left) and small (right) I_Ca. (d) N_{vesicles/2 ms} (ΔC_{m 2 ms}/70 aF) versus N_channel (calculated from I_{Ca 2 ms} using equation (1)). ΔC_{m 2 ms} and I_{Ca 2 ms} are also plotted. The line is a linear fit of data.

The 20-ms depolarization depleted the readily releasable vesicles (RRVs), because another 20-ms depolarization applied 50 ms later induced only 17 ± 5% (n = 10) of the first ΔC_m (Fig. 4b), similar to observations at the whole-cell configuration^16,19,29. As I_Ca did not decrease as much as the ΔC_m during the second depolarizing pulse (Fig. 4b), these results support our previous conclusion that the capacitance jump observed at the cell-attached patch is not a calcium-dependent artifact but reflects exocytosis^24,30.

Release strength critically depends on N_channel

To measure release strength, we applied a 2-ms depolarization to release a fraction of the RRV pool, and a 20-ms depolarization 50 ms later to deplete the remaining RRVs (Fig. 4c). We calculated number of vesicles released by the 2-ms depolarization (N_{vesicles/2 ms}) as ΔC_{m 2 ms} divided by 70 aF, the vesicle’s mean membrane capacitance at the calyx^24,31,32. N_{vesicles/2 ms}’ which reflected the release strength, ranged from 0 to 5 (Fig. 4d). N_{vesicles/2 ms} was approximately linearly proportional to the I_Ca induced by the 2-ms depolarization (I_{Ca 2 ms}) or N_channel (I_{Ca 2} ms/(i_{mean_channel} × P_{mean_channel})), suggesting that release strength may fundamentally depend on N_channel (n = 16 patches, Fig. 4d).

In theory, N_channel in that data shown in Figure 4d should be calculated from I_{Ca 20 ms} rather than from I_{Ca 2 ms}, because P_{mean_channel} was measured during a 20-ms depolarization (Fig. 3). However, the amplitude of the I_Ca during 2-ms depolarization was very similar to that during 20-ms depolarization. Thus, for simplicity of the plot, we used I_{Ca 2 ms} instead of the I_{Ca 20 ms}.

N_channel controls RRV release probability and number

How would N_channel affect the release strength (Fig. 4d)? As N_{vesicle/2 ms} was the product of the RRV number (N_RRV) and P_RRV, we addressed this question by first measuring N_RRV and P_RRV, and then by determining whether these two parameters depend on N_channel. For the measurement of N_RRV, owing to negligible vesicle replenishment, the total ΔC_m induced by a 2-ms depolarization and the subsequent 20-ms depolarization applied 50 ms later (ΔC_{m total} = 362 ± 44 aF, n = 16, for example, Fig. 4c) was similar to that induced by a 20-ms depolarization alone (323 ± 44 aF, n = 10; P > 0.1, Fig. 4a,b). Thus, N_RRV = ΔC_{m total}/70 aF or N_RRV = ΔC_{m 20 ms}/70 aF when the 20-ms depolarization was applied first. Pooling these measurements yielded N_RRV = 5.0 ± 0.5 (n = 26) with a range of ~1–10 (see also Fig. 5). For measurements of P_RRV, we calculated P_RRV as ΔC_{m 2 ms}/ΔC_{m total} from experiments such as those shown in Figure 4c. By analyzing these experiments, we found that N_{vesicle/2 ms} (or ΔC_{m 2 ms}) was approximately linearly proportional to P_RRV (Fig. 5a) and superlinearly proportional to N_RRV (Fig. 5b). Thus, N_{vesicle/2 ms}, an indicator of the release strength, depended on both P_RRV and N_RRV.

Figure 5.

Impact of calcium-channel number on the release probability and the number of RRVs. (a) N_{vesicle/2 ms} plotted versus P_RRV ( = ΔC_{m 2 ms}/ΔC_{m total}). The line is a linear fit of data from 16 patches like those shown in Figure 4c. (b) N_{vesicle/2 ms} plotted versus N_RRV (ΔC_{m total}/70 aF). ΔC_{m total} (ΔC_m induced by 2-ms and 20-ms depolarization) is also shown. The curve is an exponential fit of data (n = 16 patches). (c) P_RRV plotted versus N_channel (n = 16 patches). I_{Ca 2 ms} used to derive N_channel (with equation (1)) is also shown. (d) Left, sampled I_Ca and C_m induced by a 20-ms depolarization from two patches with different I_Ca values. Right, N_RRV plotted versus N_channel (n = 26). ΔC_m (right) and I_{Ca 20 ms} (upper) used to calculate N_RRV and N_channel are also shown. ΔC_m included ΔC_{m total} (for example, Fig. 4c, n = 16) and ΔC_{m 20 ms} (for example, left, n = 10) when the 20-ms depolarization was applied alone. The fitted curve (exponential function) shows that N_RRV approaches saturation. Dashed lines show how we measured ΔC_m. Traces were low-pass–filtered at 1 kHz. (e) N_channel/RRV plotted versus N_channel (n = 26, N_channel/RRV was derived from d, right). The curve was derived from the fitted curve in d, right. (f) Sampled whole-cell I_Ca and ΔC_m induced by a 20-ms depolarization from two calyces, one in the presence of ω-agatoxin-IVA (ω-Aga; 200 nM, bath, left) and the other in control (right). [Ca²⁺]_o = 2 mM.

A plot of P_RRV versus N_channel from 16 patches similar to those shown in Figure 4c revealed an approximately linear relation between P_RRV and N_channel (calculated from I_{Ca 2 ms}, Fig. 5c). Thus, increasing the calcium-channel number at the active zone increased the vesicle’s release probability. A plot of N_RRV versus N_channel from 26 patches such as those shown in Figure 4a–c (see also Fig. 5d) revealed a sub-linear relation between N_RRV (calculated from ΔC_{m total} or ΔC_{m 20 ms} alone) and N_channel (calculated from I_{Ca 20 ms}, Fig. 5d). Thus, N_RRV was larger as N_channel increased but approached saturation at larger N_channel (Fig. 5d). Taken together, N_channel may regulate release strength (N_{vesicle/2 ms}, Fig. 4d) by regulating both P_RRV and N_RRV (Fig. 5c,d).

Mechanisms by which N_channel regulates P_RRV and N_RRV

How would N_channel regulate P_RRV? A plot of the calcium-channel number per RRV (N_channel/RRV = N_channel/N_RRV’ calculated from Fig. 5d) versus N_channel revealed an approximately linear relation between them (Fig. 5e), suggesting that N_channel regulates P_RRV via influencing the calcium-channel number per RRV and thus the calcium microdomain near the RRV during depolarization.

The correlation between N_channel and N_RRV (Fig. 5d) may not necessarily reflect a causal relation but may suggest that more RRVs need more calcium channels to ensure that RRVs are near calcium channels for release. In support of this possibility, when we applied the high-affinity P/Q-type channel blocker ω-agatoxin IVA (200 nM, bath) to reduce the calcium-channel number³³, it reduced the whole-cell I_{Ca 20 ms} to 38 ± 5% (n = 5) and the whole-cell ΔC_{m 20 ms}, which reflected the RRV pool size^16,34, to 58 ± 5% (n = 5) of control at the extracellular calcium concentration ([Ca²⁺]_o) of 2 mM (Fig. 5f).

The relation between the ΔC_{m 20 ms} and the I_Ca during ω-agatoxin IVA application (Fig. 5f) did not follow the fourth power relation as demonstrated during brief action potential or 1-ms depolarization^15,35. This was because the stimulation was a 20-ms depolarization, which depletes nearly the whole RRV pool^{16,34,36–38}. Even when I_Ca was reduced by about half, which was similar to the I_Ca reduction in the presence of ω-agatoxin IVA, the RRV pool can still be depleted by a 20-ms depolarization¹⁶. Thus, the reduction of ΔC_{m 20 ms} in the presence of ω-agatoxin IVA (Fig. 5f) reflects a reduction of the RRV pool size. In other words, when ω-agatoxin IVA reduced the calcium-channel number³³, some readily releasable vesicles were not near functional calcium channels and thus could not be released by calcium influx during depolarization. We concluded that a larger number of calcium channels is needed to maintain a larger RRV pool.

In the whole-cell configuration, the RRV pool depleted by a 20-ms depolarization is composed of two kinetically different subpools of vesicles, a fast and a slow component^34,36,39. This raised the question as to whether a 20-ms depolarization could deplete the entire RRV pool. We included 50 µM 1,2-bis-(o-aminophenoxy)-ethane-N,N,N′,N′-tetraacetic acid (BAPTA) in the pipette solution, which was close to the endogenous calcium buffer capacity in the 8–10-day-old calyx^40,41. In this condition, the slow component of the RRV pool induced by a 20-ms depolarization was only a minor part (less than ~20%)³⁶. As a result, a 20-ms depolarization depleted nearly all vesicles in the RRV pool, which was mostly composed of the rapid component (see fig. 1 in ref. 36). These results are consistent with earlier findings that the slow release component is minor or even absent upon dialysis of the calyx with 50 µM ethylene glycol tetraacetic acid (EGTA)³⁹ but become more prominent in the presence of 200 µM³⁴ or 500 µM³⁹ EGTA. Even with 200 µM EGTA in the pipette solution, a 20-ms depolarization depleted all the rapid component and a large part of the slow component of the RRVs (see fig. 3 in ref. 34). We concluded that in our recording conditions, a 20-ms depolarization depletes nearly all vesicles in the RRV pool.

Calcium-channel number controls paired-pulse plasticity

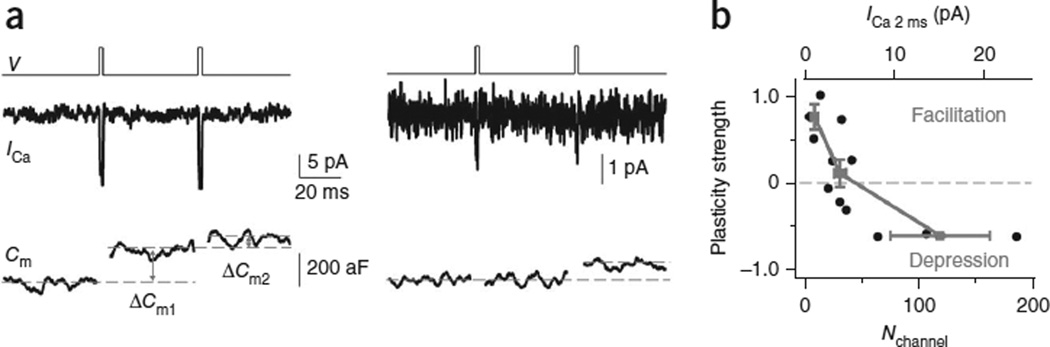
We showed that the release strength was controlled by N_channel (Fig. 4d) because P_RRV, N_channel/RRV and N_RRV depended on N_channel (Fig. 5c–f). Beyond these baseline release properties, we wondered whether N_channel would also impact short-term plasticity. Accordingly, we applied two 2-ms depolarizations 50 ms apart (Fig. 6a). We found that depression occurred when N_channel (or I_{Ca 2 ms}) was large (≥64 channels or 8.1 pA; Fig. 6a), facilitation occurred when N_channel was small (≤13 channels or 1.7 pA, Fig. 6a), and a mixture of depression or facilitation occurred with intermediate I_{Ca 2 ms} (Fig. 6b).

Figure 6.

The impact of N_channel on paired-pulse plasticity and the open channel number during an action potential. (a) I_Ca and C_m induced by a pair of 2-ms depolarization at 50-ms interval from two patches with large (left) and small (right) I_Ca (different vertical scales). Dashed lines show how we measured ΔC_m. Traces were low-pass-filtered at 1 kHz. (b) Paired-pulse strength plotted versus N_channel (or I_{Ca 2 ms}, top). The paired-pulse strength was calculated as (ΔC_m2 - ΔC_m1)/(ΔC_m2 + ΔC_m1), where ΔC_m1 and ΔC_m2 are the ΔC_m induced by the first and the second 2-ms depolarization. We did not use paired-pulse ratio because ΔC_m1 was 0 in some patches. Data were also divided into three groups based on I_{Ca 2 ms} (≤1.7 pA, 2.6 – 5.2 pA, ≥8.1 pA). Their average values (±s.e.m.) are shown (solid squares). The dashed line indicates zero paired-pulse strength, above which is facilitation and below which is depression.

Our observation that greater depression occurred with larger N_channel was because larger N_channel caused larger P_RRV (Fig. 5c), resulting in larger depletion of RRVs in the first stimulus (for example, Figs. 4c and 6a). Although we obtained this conclusion with 2-ms depolarization at [Ca²⁺]_o = 10 mM, the same principle should hold for action potential stimulation at [Ca²⁺]_o = 2 mM, except that the curve shown in Figure 6b would be shifted upwards and to the right.

Open calcium channels during an action potential

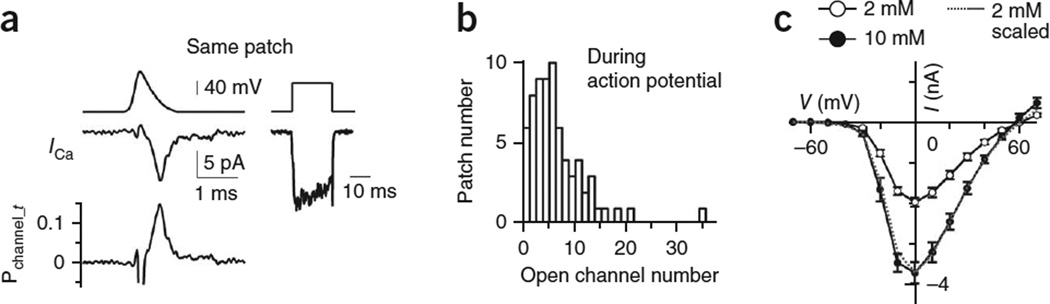
Using step depolarization to activate calcium channels, we observed a profound influence of N_channel on release properties and short-term plasticity (Figs. 4–6). In physiological conditions, calcium channels are activated by action potentials. To estimate how many calcium channels at an active zone are opened by an action potential, we used an action potential waveform¹⁴ to induce I_Ca (I_{Ca_t}, Fig. 7a). For these experiments, we did not record ΔC_m because it introduced more noise in I_Ca recordings and the ΔC_m was often too small to be measured reliably. The probability of a channel being open at time t (P_{channel_ t}) during the action-potential waveform was calculated based on

$$P_{\text{channel}\_t}=N_{\text{open}\_\text{channel}\_t}/N_{\text{channel}}=(I_{\text{Cat}}/((V_t-E_{\mathrm{r}})\times g_{\text{mean\_channel}}))/(I_{\text{Ca}V=0\text{mV}}/((0-E_{\mathrm{r}})\times g_{\text{mean\_channel}}\times P_{\text{mean}\_\text{channel}/\mathrm{V}=0\text{mV}}))=(I_{\text{Ca}\_\mathrm{t}}/(V_t-E_{\mathrm{r}}))/(I_{\text{CaV}=0\text{mV}}/((0-E_{\mathrm{r}})\times P_{\text{mean}\_\text{channel}/\mathrm{V}=0\text{mV}}))$$ (2)

where N_{open_channel_t} and V_t are the open channel number and voltage at time t during an action potential; E_r is the reversal potential (43 mV, Fig. 3d); P_{mean_channel/V = 0 mV} is the P_{mean_channel} at V = 0 mV (0.47, Fig. 3e); and I_{Ca V = 0 mV} is the I_Ca induced by a 20-ms depolarization to 0 mV, measured at ~5–10 s before or after the action potential stimulus (for example, Fig. 7a). With this method, we found that the peak P_{channel_t} was 0.16 ± 0.02 (n = 5) at V = −45 mV during the action potential-falling phase. With P_{channel_t} = 0.16, the data in Figure 3f were converted to the action potential–induced open channel number, which varied from ~0.8 to 35 with a mean of 6.7 per patch (Fig. 7b).

Figure 7.

The open calcium-channel number during an action potential. (a) Left, sampled I_Ca (middle) and P_{channel_t} (lower, calculated from equation (2)) during an action potential waveform stimulus (top). Right, I_Ca (bottom) induced by a 20-ms depolarization at 5 s after the action potential waveform stimulus (same patch as on the left). (b) Open N_channel distribution during an action potential, derived from data in Figure 3f (c) The calcium channel I/V curve (mean ± s.e.m.) obtained from whole-cell recordings at 2 mM (n = 5 calyces) and 10 mM (n = 5 calyces) extracellular calcium. The curve at 2 mM was also scaled to that at 10 mM to show similar I/V relation in these two conditions.

Although this action potential waveform measurement was made at [Ca²⁺]_o = 10 mM, we expect similar results at [Ca²⁺]_o = 2 mM because the whole-cell I_Ca-V curves at 2 mM (n = 5) and 10 mM (n = 5) calcium were amplitude-scale versions of each other (Fig. 7c), thereby excluding appreciable differences in surface-charge screening.

The action potential half-width at [Ca²⁺]_o = 10 mM had been reported to be ~35% wider than at [Ca²⁺]_o = 2 mM⁴². When we repeated the experiments shown in Figure 7a using a modified action potential waveform with a half-width (0.61 ms) 35% wider than that used for the experiments shown in Figure 7a (0.45 ms), the peak P_{channel_ t} was 0.25 ± 0.02 (n = 4, for example, Supplementary Fig. 8). Thus, regardless of the action-potential waveform used, the peak P_{channel_ t} was low. Our peak P_{channel_ t} (0.16–0.25) was smaller than a prior whole-cell estimate, which was ~69% of the maximum⁴³. However, the maximum probability of channels being open had not been measured in that whole-cell study⁴³. If it was 0.47, as measured here (Fig. 3e), the probability of a channel being open (0.32 = 0.69 × 0.47) was not far from our estimate (0.16–0.25).

DISCUSSION

The present work uncovers the fundamental properties of voltage-dependent calcium channels and transmitter release in single active zones. The work relied on a technique we established to patch predominantly one active zone at the calyx release face. The following arguments strengthen our suggestion that most cell-attached patches do not contain multiple active zones.

If larger N_RRV and N_channel were due to more active zones or a larger fraction of an active zone, N_RRV should have been linearly proportional to N_channel, and P_RRV should not have changed with increasing N_channel. Both predictions contradict our experimental findings (Fig. 5c,d). Furthermore, our patch area (1.24 µm², ~7 MΩ) was much larger than the area of an individual active zone (~0.05–0.1 µm²)^23,27,37, making it unlikely for a patch to contain a fraction of an active zone. Our measured N_RRV (5.0 ± 0.5) was similar to the number (~3.3–7) of vesicles anatomically docked within 20 nm from the calyx active-zone membrane^27,37. Dividing the whole-cell I_Ca (3.77 ± 0.25 nA, n = 5, 10 mM extracellular calcium, Fig. 7c) by the reported calyx active-zone number (550)²⁷ yielded a mean I_Ca per active zone of 6.9 pA, similar to the mean patch I_Ca we measured (5.3 ± 0.5 pA, Fig. 1f). In conclusion, the technique we developed opens the door to study presynaptic mechanisms at the single active-zone level.

Although only ~2 vesicles contacted the membrane at an active zone within 10 nm from the membrane²⁷, several studies considered vesicles within 20 nm from the membrane as docked vesicles^27,37. At the calyx, ~3–7 vesicles per active zone are docked within <20 nm from the plasma membrane^27,37, which matched N_RRV (~5 vesicles per patch) reported here. Furthermore, based on recordings from the whole calyx (including ~550 active zones), many previous studies showed that there are ~3,000–6,000 vesicles that can be released by a 10–50-ms depolarization, which correspond to ~5–10 RRVs per active zone (≈3,000/550 or 6,000/550)^38,39,44,45. This number is much larger than 2 docked vesicles within <10 nm from the active-zone membrane and closer to our estimate of 5 vesicles per patch. These studies suggest that the RRVs released by a 20-ms depolarization may not be identical to the docked vesicles within 10 nm from the plasma membrane, but likely included those docked within 20 nm from the plasma membrane at the calyx.

Calcium-channel number determines release and plasticity

We found that the number of calcium channels at an active zone varied widely from ~5 to 218. This number critically influences release strength (Fig. 4d) by two mechanisms. One mechanism is influence of the RRV release probability (Fig. 5c). As the N_channel increased, mean N_channel per RRV increased (Fig. 5e), resulting in an increase in the calcium concentration near the RRV during depolarization and thus an increase of the RRV’s release probability. The other mechanism is ensuring that RRVs are near calcium channels for release (Fig. 5d,f). With these two factors, the number of calcium channels at the active zone may determine whether an active-zone releases 0, 1 or multiple vesicles during a brief 2-ms depolarization (Fig. 4d). By influencing P_RRV, N_channel also critically adjusted the direction and the extent of paired-pulse plasticity at the active zone (Fig. 6). Thus, variation of N_channel is a major determinant of the heterogeneous release properties and short-term plasticity at single active zones. These results suggest a simple organizing feature of the synapse, whereby controlling N_channel specifies synapses with diverse release properties. The data shown in Supplementary Figure 9a help to illustrate this point schematically.

Some types of synapses behave like a silent synapse, barely releasing any vesicle, whereas others release multiple vesicles⁴. Some synapses display short-term facilitation, whereas others, short-term depression^9,10. The mechanisms underlying these differences have been intensely studied. At hippocampal and cortical synapses, release strength is proportional to the RRV number^1,2, the docked vesicle number and the active-zone area^7,8. However, different release strengths are accompanied by similar numbers of docked vesicles at cerebellar synapses³, questioning whether docked vesicles determine release strength. At cortical synapses, different release strengths are correlated with the volume-averaged calcium transient and depend on postsynaptic neurons¹⁰. Differences in the calcium transient at cerebellar synapses also have been reported¹¹. However, whether the volume-averaged calcium transient reflects calcium buffers or channel conductance/number remains unclear.

Our finding of N_channel variation at single active zones may provide an unifying mechanism to explain the heterogeneity of release and short-term plasticity profiles discussed above. Active zones with low N_channel may behave as a presynaptic silent synapse (Fig. 4d) and show subsequent short-term facilitation (Fig. 6). Active zones with high N_channel may release one or multiple vesicles (Fig. 4d) and show subsequent short-term depression owing to a large P_RRV that causes more depletion of RRVs during repetitive stimulation (Figs. 5c and 6). If N_channel is low, docked vesicles may not be surrounded by calcium channels and may thus not be releasable (Fig. 5d,f), explaining why release strength is not correlated with docked vesicles at some synapses³. Likewise, a large N_channel may make all docked vesicles releasable, explaining the correlation between release and docked vesicles^7,8.

Heterogeneous P_RRV^16,18,19 is attributed to the differential distance between calcium channels and RRVs¹⁹. Our work suggests that it is due to heterogeneity of active zones having different N_channel values, which results in different N_channel per RRV (Fig. 5c,e), and thus different calcium concentrations near the RRV. The seemingly linear relation between P_RRV and N_channel is different from the power relation between release and the calcium concentration⁵, suggesting that increasing N_channel raises the calcium concentration near RRVs sub-linearly. The underlying mechanism is unclear. One possibility is that as N_channel increases, more channels at a longer distance from a releasable vesicle may contribute to the release of it.

Given that N_channel variation may account for the synapse heterogeneity in releasing 0, 1 or multiple vesicles, calcium transients, short-term plasticity and P_RRV, we suggest that the regulation of N_channel would furnish a simple approach to achieving diverse heterogeneity in synaptic properties. How to regulate N_channel is not well understood. Recent studies shed light on this issue by showing that Rab3-interacting molecules (RIM) proteins may regulate calcium channels in a population of synapses^22,23. Our measurement of N_channel does not include inactive calcium channels that may be physically present at the active zone. Such inactive calcium channels might be due to regulation by many factors, such as G proteins, soluble N-ethylmaleimide-sensitive-factor attachment protein receptor (SNARE) proteins, protein kinases and lipids^46–48. For example, a recent study showed that reducing the membrane phosphatidylinositol 4,5-bisphosphate (PIP₂) may cause reduction of the voltage-dependent calcium current, likely by inactivating calcium channels, within ~100 ms⁴⁷. Such a dynamic conversion between active and inactive calcium channels might therefore be a potential mechanism to dynamically regulate N_channel and thus the properties of release and short-term plasticity at individual active zones.

Calcium-channel properties at the active zone

We directly measured and provided basic, yet critical parameters for calcium channels that are pivotal in controlling release at single active zones. How many open calcium channels are needed to trigger release has been debated for two decades: 1–125 channels have been proposed at different synapses^{11,13,14,20,21,49}. This large discrepancy might be partly due to the use of indirect techniques such as imaging and modeling. As a result, it has been unclear how many calcium channels are in an active zone and what fraction is activated by an action potential. The present work showed that an active zone contained ~5–218 calcium channels (mean, 42; Fig. 3f). An action potential opened ~16% or 0.8–35 (mean, 6.7) channels at an active zone (Fig. 7). Thus, one or more than ten channels may open depending on how many channels are at an active zone. They may all trigger release during an action potential, although the release probability with one channel should be much lower than that with more than 10 channels (Fig. 5c and Supplementary Fig. 9). This finding may help to reconcile the large differences or discrepancies in the estimate of the number of open calcium channels required to trigger release.

In addition to measuring N_channel, we measured the single-channel conductance and current amplitude for P/Q-, N- and R-type calcium channels at the active zone. The values were similar for different types of calcium channels, ranging from ~5.8 pS to 6.8 pS for the single-channel conductance and from ~0.26 to 0.28 pA for the single-channel current at 0 mV (Fig. 3). Given that the whole-cell I_Ca at 0 mV in 2 mM extracellular calcium was ~53% of that in 10 mM extracellular calcium (Fig. 7c), we can derive the single-channel conductance and current at 2 mM extracellular calcium, at which most previous studies of synaptic transmission were performed. The derived single-channel current at 0 mV in 2 mM extracellular calcium was ~0.14–0.15 pA. This value was on the order of those measured from somatic recordings for N- and L-type calcium channels⁵⁰, suggesting that the single-channel conductance may not be modified substantially by calcium-channel regulators localized at nerve terminals. In addition, calcium-channel currents flickered with a duration mostly less than 3 ms (Fig. 3). These basic properties of calcium channels at the active zone may help to constrain the parameters used in simulation studies of transmitter release in the calcium micro- or nanodomain.

ONLINE METHODS

Slice preparation and solutions

Animal care and use were carried out in accordance with US National Institutes of Health (NIH) guidelines and approved by the National Institute of Neurological Disorders and Stroke Animal Care and Use Committee. Parasagittal brainstem slices (200 µm thick) containing the medial nucleus of the trapezoid body were prepared from 8–10 d old Wistar rats using a vibratome²⁴. For preparing slices, we used a solution containing (in mM): 95 NaCl, 25 NaHCO₃, 25 glucose, 50 sucrose, 2.5 KCl, 1.25 NaH₂PO₄, 0.1 CaCl₂, and 3 MgCl₂, 0.4 ascorbic acid, 3 myo-inositol and 2 sodium pyruvate (95% O₂/5% CO₂). Slices were incubated for 30 min at 37 °C, during which the protease papain (2.5 unit/ml) was applied for 5–10 min and then held at room temperature (22–24 °C) for recordings with solutions described below.

For cell-attached recordings, the bath solution containing (in mM): 105 NaCl, 20 TEA-Cl, 2.5 KCl, 1 MgCl₂, 2 CaCl₂, 25 NaHCO₃, 1.25 NaH₂PO₄, 25 dextrose, 0.4 ascorbic acid, 3 myo-inositol, 2 sodium pyruvate, 0.001 tetrodotoxin (TTX; for preventing action potentials), pH 7.4 when bubbled with 95% O₂ and 5% CO₂. The cell-attached pipette contained (in mM): 10 CaCl₂, 10 HEPES and 145 TEA-Cl, pH 7.2, adjusted with TEA-OH (osmolarity was 290–310 milliOsm).

For whole-cell recordings of I_Ca and ΔC_m (Figs. 5f and 7c and Supplementary Fig. 1), the bath solution contained (in mM): 105 NaCl, 20 TEA-Cl, 2.5 KCl, 1 MgCl₂, 2 CaCl₂, 25 NaHCO₃, 1.25 NaH₂PO₄, 25 dextrose, 0.4 ascorbic acid, 3 myo-inositol, 2 sodium pyruvate, 0.001 TTX and 0.1 3,4-diaminopyridine, pH 7.4 when bubbled with 95% O₂ and 5% CO₂. The pipette contained (in mM): 125 Cs-gluconate, 20 CsCl, 4 MgATP, 10 Na₂-phosphocreatine, 0.3 GTP, 10 HEPES and 0.05 BAPTA, pH 7.2, adjusted with CsOH.

For whole-cell current clamp recordings, the bath solution contained (in mM): 105 NaCl, 20 TEA-Cl, 2.5 KCl, 1 MgCl₂, 2 CaCl₂, 25 NaHCO₃, 1.25 NaH₂PO₄, 25 dextrose, 0.4 ascorbic acid, 3 myo-inositol, 2 sodium pyruvate and 0.001 TTX, pH 7.4 when bubbled with 95% O₂ and 5% CO₂. The pipette contained (in mM): 125 K-gluconate, 20 KCl, 4 MgATP, 10 Na₂-phosphocreatine, 0.3 GTP, 10 HEPES and 0.05 BAPTA, pH 7.2, adjusted with KOH.

Electrophysiology

EPC-10 amplifier (HEKA electronics) was used for whole-cell recordings²⁹, whereas the Axopatch 200B (Molecular Devices) was used for cell-attached I_Ca recording, which provided a low noise for detection of single channel currents. To achieve low-noise recording, the gain was set at 100 pA/mV. Patch pipettes were pulled from Quartz glass (QF150-75-7.5, Sutter Instrument) with P2000 laser puller (Sutter Instrument) and coated with Sylgard.

For the cell-attached recording, the resting potential was assumed to be −65 mV which was the mean resting potential (-65 ± 2 mV, n = 7) measured at the whole-cell current-clamp mode with the same bath solution. The liquid junction potential was −5 mV, as calculated from the pCLAMP software (Molecular Devices). The resting holding potential was −90 mV at the patch, which took into account of the liquid junction potential (-5 mV) and the resting membrane potential (-65 mV).

For simultaneous I_Ca and C_m recordings, EPC-8 amplifier (HEKA) and SR830 2-phase lock-in amplifier (Stanford Research Systems) were used. A 20-kHz, 50–200-mV r.m.s. sine wave was superimposed on a command potential. The in-phase and 90°-out-of-phase current outputs of the lock-in amplifier were low-pass filtered at 0.3–1 ms (24 dB). Cell-attached capacitance recordings, phase adjustment, detection and measurement of capacitance up and down steps, and measurements of the patch membrane capacitance were performed as described previously²⁴.

Cell-attached recordings typically lasted for 30–60 s, after which I_Ca and/or ΔC_m ran down with an unknown reason. The fast rundown might explain why ΔC_m has never been induced by depolarization applied via the cell-attached patch at any secretory cell. The present work was, to our knowledge, the first to report the ΔC_m induced by depolarization via the cell-attached patch. We only analyzed the data collected in the first minute without substantial rundown. The interval between each stimulus was 3–5 s, at which calcium current inactivation was minimal²⁹. The limitation of the recording time, together with the requirement of high signal-to-noise ratio in recording, made our data collection a long and hard process. As a result, one patch could only be used for one type of experiments. For example, data shown in Figures 1, 3, 4, 5, 6 and 7 were from different experiments.

To measure the patch membrane (Fig. 1c), the electrode at the cell-attached configuration was retracted a few micrometers to achieve an inside-out configuration²⁴. A piece of Sylgard was moved toward the pipette, and the tip was pressed a few micrometers into the Sylgard, which resulted in a decrease of the capacitance. When the pipette was retracted from the Sylgard, the capacitance returned to the previous baseline level. The capacitance change during these manipulations was taken as the patch membrane capacitance²⁴.

Statistical analysis

Data are presented as mean ± s.e.m. Unless mentioned, the statistical test was the t-test.

Measurements of single channels and ‘open probability’

For recording single P/Q-type channel currents (Fig. 3a), the pipette contained 5 µM ω-conotoxin-GVIA, 1 µM SNX-482, and 10–50 nM ω-agatoxin-IVA, the latter of which blocked most, but not all P/Q-type channels, which increased the chance of detecting single channels. In addition, the bath contained 1 µM ω-conotoxin-GVIA, 200 nM SNX-482 and 10–50 nM ω-agatoxin-IVA. For recording single N-type channel currents (Fig. 3b), the pipette contained 1 µM ω-agatoxin-IVA and 1 µM SNX-482; the bath contained 200 nM ω-agatoxin-IVA and 200 nM SNX-482. For recording single R-type channel currents (Fig. 3c), the pipette contained 1 µM ω-agatoxin-IVA and 5 µM ω-conotoxin-GVIA; the bath contained 200 nM ω-agatoxin-IVA and 1 µM ω-conotoxin-GVIA.

When blockers of all three types were included in the pipette (1 µM ω-agatoxin-IVA, 5 µM ω-conotoxin-GVIA and 1 µM SNX-482) and in the bath (200 nM ω-agatoxin-IVA, 1 µM ω-conotoxin-GVIA and 200 nM SNX-482), we did not detect single inward channel currents in 91 patches at the release face. This confirmed that single inward channel currents observed in the presence of two types of voltage-dependent calcium channel (VDCC) blockers (Fig. 3) reflected the remaining type of VDCCs. Similar conductance for P/Q, N- and R-type channels observed in Figure 3 may not be surprising because similar ranges have been reported for these channel types (for example, N-type, 13 pS; P/Q-type, 9–19 pS in 110 mM barium)^51,52.

If the all-points frequency histogram taken from recorded current traces showed a clear single peak, the amplitude of which was similar to that judged by eye from recorded traces, the current was identified as the single-channel current, and the peak current (Fig. 3a–c) was i_channel. Otherwise, data were not used. The single-channel conductance ( g_channel) was obtained by linear regression fit of the single channel i/V curve (Fig. 3d). During single-channel recording, P_channel (Fig. 3e) was calculated as the mean current during 20-ms depolarization to 0 mV (integral of the current from 2 ms to 19.5 ms divided by 17.5 ms) divided by i_channel, the single channel current amplitude at V = 0 mV Owing to the limited time of patching, only 1–2 traces (one trace corresponded to currents in response to a 20-ms depolarization) were obtained in some patches. Thus, the mean P_channel was calculated from all traces in all patches, which was similar to the mean value from patches where more than four traces were collected.

Measurement of the active zone density

We measured the active zone density at the rim region, ~0–2 µm below the calyx surface where we patched (Fig. 1a), from two published data sets of 3D reconstructed calyces^27,28. One data set was based on calyces expressing mGFP to visualize the membrane and anti-Bassoon and anti-Piccolo three-dimensional immunolocalization to visualize the active zones with confocal microscopy²⁸. The other was derived from a serial sectioning electron microscopy reconstruction and manual tracing of the membrane and active zones. The latter data set was converted into a binary image stack to permit application of the same algorithms to both data sets.

The rim area was identified using a weakly supervised perceptual segmentation algorithm described below. Binary calyx image stacks generated by the algorithm were imported into the visualization software Amira 4.1.1 (Mercury Computer Systems). Active zones positioned in the central volume (including those with a larger fraction in the central region) were classified as central active zones, and those in the rim volume belonged to rim active zones. The active zone numbers were calculated using the ConnectedComponents function of Amira. The volume and surface were determined using the SurfaceGen function of Amira with no filtering. The surface of each compartment was subtracted by the connecting surface generated by cutting the original calyx into two compartments. The calyx surface oriented toward the postsynaptic cell was approximated by dividing the surface of center and rim by 2. Active-zone densities were calculated as the active zone number divided by the rim or the central surface area.

The weakly supervised perceptual segmentation algorithm was composed of three steps. First, using an image sequence of calyx sections, a sliding window was moved along both x-y and z directions in the image sequence to cluster and classify the whole image into two subgroups: the rim and the central group. The sliding window measures a set of properties for each labeled region on each calyx section. The measured properties were stored in a structured array, which denoted and described different measurements for each region (for example, perimeter, area and orientation). Then we applied a clustering method to classify the calyx sections into two subgroups corresponding to rim and central regions.

Second, we considered the labeled calyx region in each section as the composite of rim regions R and central regions C in linear blending of intensity values based on i^th pixel-level information. The sum of rim αR and central parts (1 - α)C was equal to the entire labeled calyx region (E),

$$E=\mathit{\text{aR}}+(1-a)C$$ (3)

where α is the fraction of the rim and (1 - α) is the remaining part of the central region. This equation simplifies computational complexity and avoids oversegmentation. The α is crucial to define the size of the rim regions and is derived from the size of the calyx section and its shape (Supplementary Fig. 5a).

To extract the correct position of two ending points for defining and segmenting the rim, we developed a skeleton-based ending point search algorithm that can identify ending points. A medial axis–based skeleton is a curve locally centered with respect to the shape boundary and the capture of the shape topology (Supplementary Fig. 5b). The smoothed medial axis along the shape of a calyx section was extracted by using anisotropic diffusion and morphological image processing (Supplementary Fig. 5c). This way, individual pieces of calyx regions can be connected into one continuous calyx region, which is useful for searching only two ending points.

Third, we applied the weakly supervised global visual quality control for segmenting rim and center. The weakly supervised control requires less human efforts and provides less bias than traditional supervised methods. In equation (3), α is controlled by measuring the size of neighborhood regions of each section. The α is then used to control the size of radius of a labeling circle (Supplementary Fig. 5d). The rim part is defined as the inside of the circle. However, owing to the variations and complexity of each calyx section, often more than two ending points were found per section (Supplementary Fig. 5c). To solve this problem, we manually selected the two correct ending points as labeled information and then propagated the label information along the z-direction through the whole image stack. The selected ending points were used as seed information to perceptually segment the rim and central parts.

Estimate of the probability of patching at the active zone

Simulation was performed using a custom-made Program (Igor Pro) with a square of 1,000 µm² (31.6 µm × 31.6 µm) to represent the calyx release face (Supplementary Fig. 6), whose surface area was reported to be ~1,000–1,400 µm² (refs. 27,28). We used a dot to represent an active zone (Supplementary Fig. 6) because our patch-membrane area (0.67 µm², 1.24 µm² or 2.48 µm²) was much larger than the active zone size (0.05–0.1 µm²) and the calcium channels might cluster in even a smaller area in the active zone⁵³. The active zone position was randomly generated inside the 1,000 µm² area. The mean active zone density was set as the measured mean active zone density at the calyx rim area or the center (Supplementary Table 1).

The patch membrane was set as round with an area of 0.67 µm², 1.24 µm² or 2.48 µm², the measured mean patch membrane area for the 12–14, 6–8 or 3–4 MΩ pipettes. The position (center) of the round patch membrane was generated randomly within the 1,000 µm² square for 100,000 times. For each time, if an active zone dot was within the round patch membrane, that active zone was counted as within the patch membrane. The results obtained from these 100,000 repeats were then summarized (Fig. 2b).