Texture feature extraction and analysis for polyp differentiation via computed tomography colonography

Abstract

Image textures in computed tomography colonography (CTC) have great potential for differentiating non-neoplastic from neoplastic polyps and thus can advance the current CTC detection-only paradigm to a new level toward optimal polyp management to prevent the deadly colorectal cancer. However, image textures are frequently compromised due to noise smoothing and other error-correction operations in most CT image reconstructions. Furthermore, because of polyp orientation variation in patient space, texture features extracted in that space can vary accordingly, resulting in variable results. To address these issues, this study proposes an adaptive approach to extract and analyze the texture features for polyp differentiation. Firstly, derivative operations are performed on the CT intensity image to amplify the textures, e.g. in the 1^st order derivative (gradient) and 2^nd order derivative (curvature) images, with adequate noise control. Then the Haralick co-occurrence matrix (CM) is used to calculate texture measures along each of the 13 directions (defined by the 1^st and 2^nd order image voxel neighbors) through the polyp volume in the intensity, gradient and curvature images. Instead of taking the mean and range of each CM measure over the 13 directions as the so-called Haralick texture features, the Karhunen-Loeve transform is performed to map the 13 directions into an orthogonal coordinate system where all the CM measures are projected onto the new coordinates so that the resulted texture features are less dependent on the polyp spatial orientation variation. While the ideas for amplifying textures and stabilizing spatial variation are simple, their impacts are significant for the task of differentiating non-neoplastic from neoplastic polyps as demonstrated by experiments using 384 polyp datasets, of which 52 are non-neoplastic polyps and the rest are neoplastic polyps. By the merit of area under the curve of receiver operating characteristic, the innovative ideas achieved differentiation capability of 0.8016, indicating the feasibility of advancing CTC toward personal healthcare for preventing colorectal cancer.

I. Introduction

According to the recent statistics from American Cancer Society (ACS), colorectal carcinoma (CRC) is the third most commonly diagnosed cancer and the second leading cause of cancer-related death in the United States [1]. It was estimated that 142,820 new cases would be diagnosed with 50,830 dying from the disease in 2014. Fortunately, most CRC arises from colorectal polyps, and the process could take 5–15 years for malignant transformation into cancer. Thus, early detection and removal of the polyps before or during the malignant transformation will effectively decrease the incidence rate of CRC [4, 15, 33, 40].

Clinical optical colonoscopy (OC) is currently the gold standard for detection and removal of the polyps. Because of its invasive nature, OC would demand a prohibitory resource to screen the large population with age over 50 [9, 16, 28]. Computed tomography colonography (CTC) has been under development over the past decades to relieve the burden of OC for the screening purpose and has shown comparable performance to OC with computer-aided detection (CADe) of the polyps sized 8mm and larger [12, 26, 42].

With an increasing number of polyps as detected by the CTC screening, the need for removal of the detected polyps will increase and eventually would also demand a great resource to reduce the incidence rate of CRC. Fortunately, in the screening population of age 50 and older, a significant amount of the polyps are non-neoplastic, named hyperplastic (H), [13, 14, 17, 18, 27, 29–33, 40], which are abnormal growths with no risk. Removal of these growths would gain nothing, but will consume a great resource.

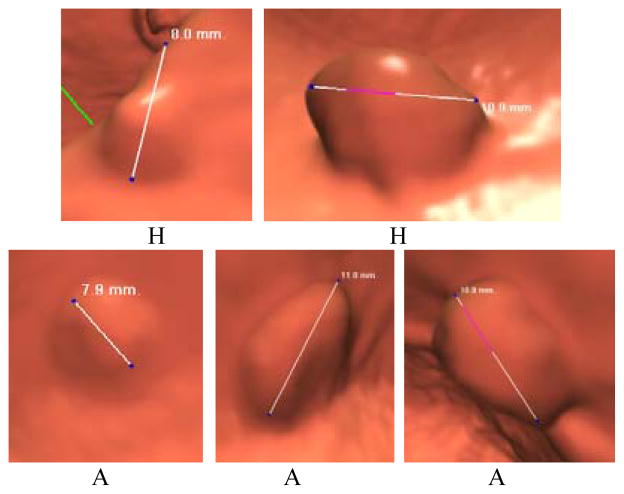
Efforts have been devoted to differentiate H from adenomatous (A) (or neoplastic) polyps in both OC and CTC fields by the measures of polyp size and surface characteristics, and the gain is limited, e.g. in the studies [27, 30, 32], where CTC was performed for polyp screening and followed by OC to resect the found polyps, more than 20% resections were hyperplastic. Fig. 1 illustrates five typical examples of polyps, of which two are H and three are A polyps. From the screenshots of endoscopic views of these polyps, it is clear the differentiation task is quite challenging if only the shape, surface property and size of the polyps are considered. More information is needed.

Fig. 1.

An illustration of five typical polyps, which were randomly selected from the database in this work. (H) – hyperplastic and (A) – adenomatous.

By the CTC screening, fully three-dimensional (3D) volume image data (also including the size and surface characteristics) are readily available not only for the purpose of polyp detection (by either human observer or computer observer–CADe) but also for the possibility of polyp differentiation and other clinical tasks beyond the detection purpose. This study aims to explore the feasibility of differentiating H from A polyps (by a computer-aided diagnosis–CADx strategy) using texture features derived from the 3D volumetric data.

While many texture features have been extracted and applied for various clinical purposes, e.g. [5, 36, 46], the feature extraction method of Haralick et al. [11] is attractive, because it gives a series of texture measures about the image intensity correlations among the image pixels on an image slice. Because of its attractiveness, efforts have been devoted to expand the Haralick’s method from 2D domain into 3D space to compute the texture measures among the image voxels and apply the 3D models for the CADe and CADx tasks [25, 39, 43, 47]. An important issue in the expansion is how to handle the spatial variation of computing the texture measures from the 2D domain to the 3D space where the shapes and orientations of the polyp volumes can change dramatically. This study presents a simple idea to handle this spatial variation.

To our knowledge, most (if not all) texture features are derived from intensity images. In producing the intensity images, various efforts have been devoted to smooth the image except at the objects’ borders in the image, because of inconsistence in acquired data due to noise and other measurement errors. During the piecewise smoothing, texture features would be sacrificed. To compensate for this loss, we have proposed a way to amplify the textures, similar to the spatial scale magnification in microscopy, by performing derivative operations on the intensity image [39]. This study will incorporate the simple idea of derivative amplification operations with the simple idea of handling spatial variation as an integrated adaptive approach to extract the volumetric texture features for the ultimate goal of differentiating H from A polyps.

The remainder of this paper is organized as follows. In Section II, a review of the Haralick method and its expansion from 2D to 3D space is given, followed by a presentation of our strategy of handling the 3D spatial variation. Then, a description of incorporating our texture amplification strategy to extract texture features in the derivative space is detailed. In Section III, experimental design for evaluating the extracted volumetric texture features is outlined and the results are reported with comparison to the previous method. Finally, discussion and conclusions are given in Section IV.

II. Methods

II.A. Review of the 2D Haralick Method for Texture Feature Extraction

In 1973, Haralick et al. introduced a method for texture feature extraction from 2D intensity or gray-level image [11]. By this method, a co-occurrence matrix (CM) is first defined and then applied to capture the gray-level correlations among resolution cells or image pixels in a 2D image slice. In implementation, a total of 14 texture measures along a direction through the image slice are calculated from the CM. The 14 texture measures are listed in [11]. A total of four directions (0, 45, 90 and 135 degrees) are defined on the image plane which are sufficient to span over the image slice, see Fig. 2. Assuming a similarity among the four directions, an average of each of the 14 measures over the four directions is computed as the corresponding texture feature, resulting in a total of 14 mean features. Additionally, the range of each of the 14 measures is also computed as another texture feature to reflect spatial variation, resulting in a total of 14 range features. Thus, a total of 28 texture features (14 means and 14 ranges) are obtained, which are usually called Haralick features in the literature. The definition of the CM and the computation of the average and range over the directions together reflect the core idea of the Haralick method. The core idea is called Haralick model hereafter.

Fig. 2.

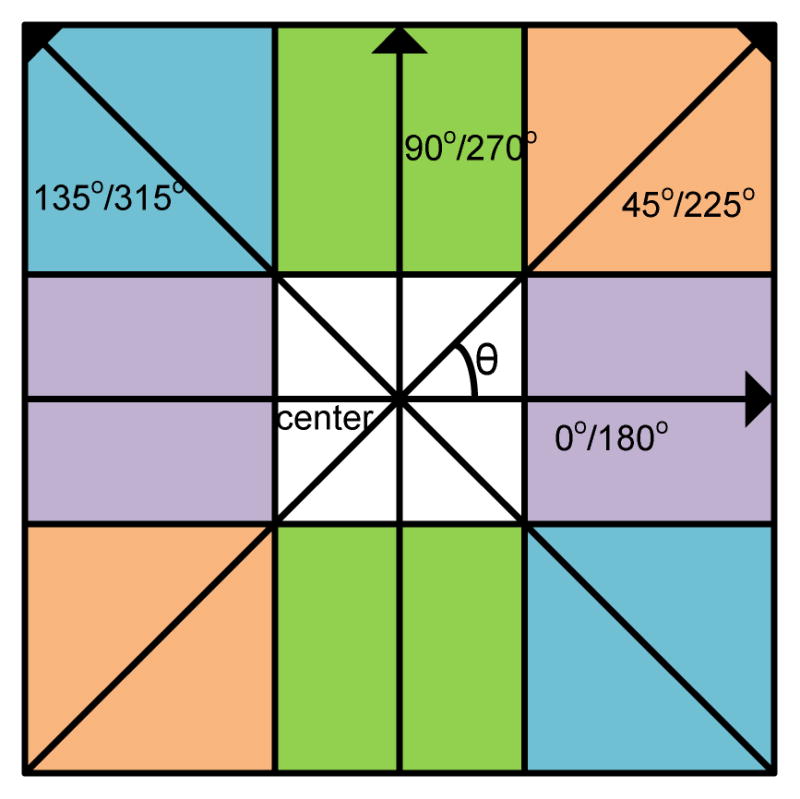
Illustration of the 2D Haralick method for extraction of texture features with image pixel size unit of d = 1 and four directions in an image slice.

II.B. Expansion of the Haralick Model from 2D to 3D Space

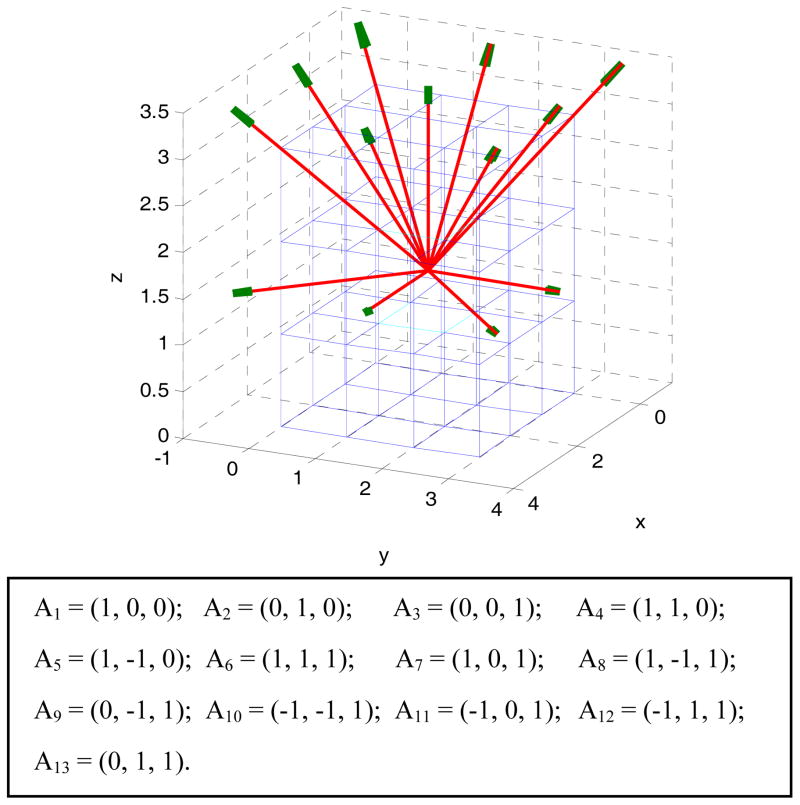
As mentioned above, because of the attractive nature in using the CM to capture the gray-level correlations, a great effort has been devoted to expand the Haralick model from 2D plane domain to 3D volume space [25, 39, 43, 47]. Similar to the selection of the four directions (from the 8 neighbors) in the 2D case of Fig. 2, a total of 13 directions (from the 26 neighbors) in the 3D space can be selected as shown by Fig. 3. Along each direction, 14 texture measures can be computed using the CM as defined by the Haralick model [11]. Using the same philosophy as the Haralick model did, the average and range values of each of the 14 measures over the 13 directions can be computed as the 3D texture features, resulting in a total of 28 features [25, 47]. The computed mean and range features are called 3D-Haralick features hereafter (in contrast to the 2D-Haralick features from a 2D image slice) or simply intensity features. While the mean and range can reflect some degree of the spatial variation of the texture measures along the 13 directions, a more adaptive strategy is desirable, e.g. Philips et al. [25] analyzed the directional variation on the CM measures within the liver. In this study, we explore an adaptive approach to extract and select the 3D texture features as detailed in the section of Feature Extraction below, instead of taking the mean and range features as the Haralick model did.

Fig. 3.

The 3D resolution cells or image voxels for one center voxel in 13 directions. The direction Ai (i=1, 2, …, 13) is equivalent to (x, y, z), which is a direction in the 3D coordinates. The center point is A0 = (1.5, 1.5, 1.5) and the 13 arrows beginning from this point is represented as A0+k* Ai, where k does not equals to 0.

II.C. Expansion of Volumetric Texture Measures

While the 14 texture measures of the Haralick model were designed to reflect some statistics or information about the pixel and pixel correlation, more measures can be designed to reflect a complete picture about the correlation. In this study, we introduce the following 16 new texture measures, which can be computed from each CM in the 3D space. (It is noted that the definitions of the notations in these new measures are the same as that of the 14 measures [11]:

Feature number	Description
$f_{15}=\underset{i,j}{max}p(i,j)$	15. Maximum probability.
$f_{16}=\underset{i,j}{\text{median}}p(i,j)$	16. Median probability.
$f_{17}=\underset{i,j}{\text{quartermedian}}p(i,j)$	17. First quartile probability
$f_{18}=\underset{i,j}{\text{threequartermedian}}p(i,j)$	18. Third quartile probability
$f_{19}=\frac{{\displaystyle \sum _{i=1}^{N_g}}{\displaystyle \sum _{j=1}^{N_g}}{\{p(i,j)\}}^2}{{N_g}^2}-{\left(\frac{{\displaystyle \sum _{i=1}^{N_g}}{\displaystyle \sum _{j=1}^{N_g}}p(i,j)}{{N_g}^2}\right)}^2$	19. Deviation of probability.
$f_{20}={\displaystyle \sum _{i=1}^{N_g}}{\displaystyle \sum _{j=1}^{N_g}}(i\ast j)p(i,j)$	20. Autocorrelation.
$f_{21}={\displaystyle \sum _{i=1}^{N_g}}{\displaystyle \sum _{j=1}^{N_g}}(i+j-{\mu }_x-{\mu }_y)p(i,j)$	21. Cluster average.
$f_{22}={\displaystyle \sum _{i=1}^{N_g}}{\displaystyle \sum _{j=1}^{N_g}}{(i+j-{\mu }_x-{\mu }_y)}^{2}p(i,j)$	22. Cluster variance.
$f_{23}={\displaystyle \sum _{i=1}^{N_g}}{\displaystyle \sum _{j=1}^{N_g}}{(i+j-{\mu }_x-{\mu }_y)}^{3}p(i,j)$	23. Cluster shade.
$f_{24}={\displaystyle \sum _{i=1}^{N_g}}{\displaystyle \sum _{j=1}^{N_g}}{(i+j-{\mu }_x-{\mu }_y)}^{4}p(i,j)$	24. Cluster prominence.
$f_{25}={\displaystyle \sum _{i=1}^{N_g}}{\displaystyle \sum _{j=1}^{N_g}}\mid i-j\mid p(i,j)$	25.Dissimilarity.
$f_{26}=\frac{p(i,j)}{1+\mid i-j\mid /N_g}$	26. Inverse difference.
$f_{27}=\frac{p(i,j)}{1+\mid i-j\mid }$	27.Homogeneity II.
$f_{28}=\frac{\mathit{HXY}-\mathit{HXY}2}{max\{HX,HY\}}$	28. Information measures of correlation III.
$f_{29}={(1-exp\left[-2.0(\mathit{HXY}1-\mathit{HXY})\right])}^{\frac{1}{2}}$	29. Information measures of correlation IV.
$f_{30}={\displaystyle \sum _{i=0}^{N_g-1}}i{p}_{x-y}(i)$	30. Difference average.

II.D. Texture Amplification

As mentioned above in the section of Introduction, when reconstructing the intensity images from acquired noise data, especially low-dose CT data, efforts have been devoted to ensure image smoothness except on the borders of objects in the image, sacrificing more or less textures in the reconstructed images. Performing derivative operations across the intensity image, similar to an amplification process, is a simple way to enhance or recover the textures. For example, in the 1^st derivative or gradient image, the voxels on the border of an object will have maximal values while the voxels within the object (or a very flat area) will have nearly zero values; and other voxels will have values ranging from nearly zero to the maximum value. Intuitively, in the 2^nd and higher derivative images, those voxels on the gradient regions in the intensity image will have non-zero values while others will have zero value. In this paper, we adopted our previous study [39] to include only the 1^st- and 2^nd- order derivative images to test our adaptive approach to handle the spatial variation in extracting the 3D texture features. The details of computing the derivative images are given in the reports [7, 22, 42, 45, 48]. Fig. 4 shows the different texture pattern characteristics in the three images of the original intensity, 1^st- and 2^nd- order derivatives about H and A polyps.

Fig. 4.

An illustration of two different polyp types (of H and A) and their corresponding endoscopic views and image slices, where the image slices are crossing vertically on the endoscopic view pictures, respectively. The sizes of the two polyps are around 10mm. The three slices from left to right are intensity, gradient and curvature images.

Given the acquired 3D intensity image I, and the computed 1^st-order derivative (or gradient) image I_g and the 2^nd-order derivative (or curvature) image I_c, the 3D-expanded texture feature extraction can be performed as follows.

II.E. Feature Extraction

Given the 3D gradient and curvature images, we can compute the 30 texture measures (14 from Haralick et al. [11] and 16 new ones from section II.C above) from the defined CM along each direction in each image as we did for the intensity image (in section II.B above), resulting in a vector of dimension of 2×30 = 60. By including the texture measures from the intensity image, we obtain a vector of dimension of 3×30 = 90. Repeating the calculation along all the 13 directions, we obtain a total of 13 vectors with a dimension of 90. By adopting the Haralick model of taking the average and range values of each of the 90 measures over the 13 directions as the texture features, we obtain total of 180 3D-texture features. These 180 3D-texture features (including 60 3D-Haralick features from the intensity image, 60 3D-features from the gradient image -- named gradient features, and 60 3D-features from the curvature image, -- named curvature features) are treated as the reference or baseline for comparison purpose in order to show the gain by the proposed adaptive approach in this study.

As we mentioned above that because of the spatial variation of polyp shapes and orientations in the 3D space, the average and range may not adequately reflect the entire volumetric texture features if the polyp shape is deviated from a sphere (such deviation is common in reality). Instead of computing the average and range of each texture measure over the 13 directions as the 3D-texture features, we would rather take an adaptive approach to address the spatial variation of the calculated CM measures over the 13 directions for the volumetric texture features of each polyp. In this exploratory study, we take the well-known principal component analysis, as an example, to address the spatial variation. Specifically, we take the Karhunen–Loève (KL) transform [51] on the 13 vectors along the angular axis of the 13 directions. In the KL domain, a new set of 13 directions (or 13 ordered eigenvectors) are obtained which are less dependent on the 3D shape orientation of the polyp in the original 3D patent space. We hypothesize that such adaptive approach will improve the feature extraction and analysis and, therefore, improve the classification or differentiation performance. The experiments of this study will be designed to test this hypothesis. In the KL domain, the volumetric texture features are selected along the 13 ordered eigenvectors. More details on the KL transform procedure are given below, followed by feature selection and classification.

The key procedure in the KL transform is to use an orthogonal transformation to convert a set of observations into a new coordinate system with uncorrelated variables. In the new coordinate system, the mean squared error between the given set of observations and their projections on the new coordinates is minimized. Moreover, a high degree of redundant data is compressed into a more compact form after the removal of the correlation between the observations. Suppose we have M variables and each variable can be described by N observations. Let the observations be represented as N column vectors, x₁, x₂,…, x_N, each of which has M elements or variables, making up the M row vectors. For this M×N matrix, named X, its covariance matrix, named T, can be computed. Since T is a symmetric matrix, an eigen decomposition can be perform on the matrix: T = VDV^τ, where τ is the transpose operator, D is a diagonal matrix with all the eigenvalues of T and each column in V is the eigenvector correspond to the eigenvalue in D. After the eigen decomposition, a new M×N matrix can be calculated, Y = V^τ X , which includes N new observations y₁, y₂,…, y_N, described by M new variables.

For each polyp, the observations or the CM texture measures in our case are obtained on the 13 directions or variables, so M = 13. Along each direction, 30 texture measures are computed from the intensity, gradient image and curvature images, respectively, so N = 3×30 = 90. If considering only one image for feature selection and analysis, e.g. intensity image, gradient image or curvature image, respectively, N = 30 (Int, Gra, or Cur). If considering two images, e.g. intensity image+gradient image, or intensity image+curvature image, or gradient image+curvature image, N = 60 (combinations of Int_Gra, Int_Cur, and Gra_Cur). If all the three images are considered together, N = 90 (Int_Gra_Cur).

Since a main goal in this study is to explore adaptive approach to address the spatial variation, instead of taking the average and range on the CM texture measures, therefore, our focus now is on the KL-transformed CM texture measures. The gain by the KL transform is that the KL operation relieves the correlation of the CM measures along the 13 directions. Without any a priori knowledge on the spatial variation of the CM measures, we take the KL transformed CM measures as our new volumetric texture features, and then develop a suitable feature selection and classification strategy to analyze the more compact-formatted texture features for the ultimate goal of differentiating hyperplastic from adenomatous polyps.

II.F. Feature Selection and Classification

After the KL operation, we obtain a new set of features with dimension of 13×N. For single image scenario N = 30, we have 390 features in 13 groups, and each group has 30 features. The 13 groups are called eigenvectors and are orderly arranged according to their eigenvalues in a decreasing manner. For the scenario of two image combinations N = 60, we have 780 features in 13 groups, and each group or each eigenvector has 60 features. For the scenario of all three image combined N = 90, we have 1,170 features in 13 groups, and each group or each eigenvector has 90 features. For each scenario, we adopt the Random Forest (RF) strategy [3], which has the advantage in solving the problems without any a priori knowledge on the problem, to select and classify the de-correlated and more compact-formatted features.

II.F.1 Feature Selection

RF is a popular and efficient algorithm for classification and regression problems as described by Breiman [3, 49]. Since the key problem in feature selection is the computation of the importance of the features, the RF algorithm provides us a model which is not only efficient in computation but also low over-fitting errors in accuracy.

In this application, we employ a function of the R-package “randomForest” [50] to construct the “forest” and select the importance order on the tree notes. An average of the total decrease in node impurities over all trees is computed, which is measured by the Gini impurity. According to the CART algorithm in [34], Gini impurity is a measure that reflects the mislabeled rate of a random element in the set:

$$\mathit{GINI}(t)=\sum _{i=1}^K{p}_i(1-p_i)=1-\sum _{i=1}^K{p_i}^2$$ (1)

where p_i is the probability that element t is correctly labeled as i, and K is the number of the descendent nodes of node t, specifically, K=2 in both the CART and RF algorithms. Each time, the Gini impurity of a node is greater than or equal to the sum of the Gini impurity of its two descendent nodes. With this property, the importance of the node t is calculated as [3]:

$$Im(t)=\frac{{\displaystyle \sum _{i=1}^L}{\mathit{GINI}}_i(t)-{\displaystyle \sum _{i=1}^L}{\mathit{GINI}}_i(t_{\mathit{des}})}{L}$$ (2)

where GINI_i(t) is the Gini impurity for node t of i-th tree in the forest, and t_des is the descendent nodes of t, and L is the number of trees in the RF algorithm [3], specifically, L=1,000 was set in our experiments.

By the above RF-embedded feature selection, we rank the importance of each feature in a decreasing order. The first feature in the order is most importance and the last one is least importance by the importance measure of Eq.(2).

Starting from the first feature on the order, we add the next ranked important feature to have a feature vector of dimension 2 and then perform classification on the feature vector to generate a measure of area under the curve (AUC) of the receiver operating characteristic (ROC) [8, 38]. By repeating the two steps of (i) adding next ranked feature on the order into the current feature vector and (ii) performing classification on the new feature vector of increased dimension (by 1) until reaching the maximum dimension (i.e. all features in the order have been added together), we obtain a plot of feature dimension vs. its corresponding AUC measure. From the plot, the feature vector with largest AUC value is the best feature vector and its dimension is called intrinsic dimension. The classification operation is detailed below.

II.F.2 Feature Classification

Similar as feature selection, the RF strategy [2] can be adopted for feature classification. In this study, we employ the R-package “randomForest” [50] again to serve the purpose of feature classification, called RF-embedded feature classification [21, 37]. For each classification experiment, since we have divided the data into training and testing datasets, we could build a classifier model with the training dataset information and then evaluate the model by the testing dataset. More details are given below.

As mentioned above in the Abstract, in total we have 384 polyp samples (half of them will be selected to be training set, i.e. 192 polyp samples of 26 H and 166 A), 390 features (in the scenario of individual images: Int / Gra / Cur), 780 features (in the scenario of two image combinations: Int_Gra / Int_Cur / Gra_Cur), and 1,170 features (in the scenario of all image combined: Int_Gra_Cur) for each polyp. By dividing the 384 polyp samples as training (192 polyp samples) and testing (192 polyp samples) datasets (the corresponding features of these samples are also divided), we first build up a RF model with the following initial parameter values: the number of trees L=1,000 and the number of features used in each splitting of a tree $N_f=\sqrt{M_f}$, where M_f is the total number of features in a feature set. Then when building an individual tree in the forest, we adjust N_f , which is randomly chosen to decide each node of the tree in, until the Out-of-bag error (OOB error) is stabilized to a low value [50]. Here for each tree we only use a bootstrap sample set of the whole training dataset and the OOB error could be calculated via the other part of the training dataset [3, 50]. The feature set is a feature vector, selected from all the features in the KL domain by the above described RF-embedded feature selection.

After building the RF model of Eq.(3) with training dataset, we could generate a single score (or posterior probability) for each test point based on the same RF model of Eq.(3) where the feature set is the testing dataset. The final classification decision is obtained by a majority vote law on all the classification trees (and an estimation of the probability of each class can also be deduced by calculating the proportion of each decision on all the classification trees). It is known that RF is an ensemble method and is constructed by a multitude of decision trees. Since each single decision tree can generate a result (0 or 1) during the classification, the final score of the test point will be decided by the votes (over all the trees in the forest).

Given the obtained scores, the ROC analysis [8, 38] can be used to obtain the AUC values for quantitative evaluation of the classification. By performing the ROC analysis on the scores, we can obtain the information about the best selection of feature subset and the highest AUC value of classification in all the three scenarios. The experimental design and outcomes are reported below.

III. Experimental Design and Results

III.A. Revision of the Original 14 Haralick Texture Measures

By examining the list of the original 14 Haralick texture measures [11], some discrepancies were found. The corresponding corrections and modifications are then made as follows.

Firstly, two typographical errors may have occurred in the 7^th and 14^th measures. In the 7^th measure of Sum of Variance, $f_7^{\ast }={\sum }_{i=2}^{2N_g}{(i-f_8)}^2{p}_{x+y}(i)$ was given in [11]. It is obvious that the expectation of f₆ in [11] should be used for $f_7^{\ast }={\sum }_{i=2}^{2N_g}{(i-f_6)}^2{p}_{x+y}(i)$, instead of the entropy measure of f₈ in [11]. By the 14^th measure of Maximum Correlation Coefficient, $f_{14}^{\ast }={(\text{second}\text{largest}\text{eigenvalue}\text{of}Q)}^{\frac{1}{2}}$ where $Q(i,j)={\displaystyle \sum _{k=1}^{N_g}}\frac{p(i,k)p(j,k)}{p_x(i)p_y(k)}$ in [11], it would reflect the correlation between the i-th row and the j-th column of the CM. Since the CM is symmetric, the correlation coefficient matrix Q(.) should be a symmetric matrix. So, a correction is made such that $Q(i,j)={\displaystyle \sum _{k=1}^{N_g}}\frac{p(i,k)p(j,k)}{p_x(i)p_y(j)}$ Secondly, for the 4^th measure of Sum of Squares or Variance, $f_4={\sum }_{i,j=1}^{N_g,N_g}{(i-\mu )}^{2}p(i,j)$, in [11], the definition of μ is missing, which poses an ambiguity in the interpretation of the “Variance”. Therefore, this measure is modified into a covariance measure in [11]: $f_4^{\ast }={\sum }_{i,j=1}^{N_g{N}_g,}(i-{\mu }_x)(j-{\mu }_y)p(i,j)$

III.B. Database for Experimental Studies

The above presented 3D volumetric texture features are extracted from the original intensity and high-order (gradient and curvature) images of a CTC database of 352 scans from 176 patients. The patient studies were performed during the time period from 2009 to 2013 by a standard CTC protocol [2, 30], i.e. a low-volume cathartic bowel preparation, oral fecal tagging, without IV contrast, and multi-detector CT scanners in adherence. The image data were acquired in helical mode with collimations of 1.0–3.0mm, pitch of 1–2, reconstruction intervals of 1.0–1.5mm, and modulated tube current–time products of 50–200mAs and tube voltages of 80–120kVp. The indication for CTC was screening for CRC in all individuals. The protocol was approved by appropriate ethical committee, and the studies were performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki and its later amendments. All patients gave their informed consent prior to their inclusion in the study and their identities were removed before the images were processed by the proposed texture extraction algorithms. Each patient was scanned at two positions, e.g. supine and prone, resulting in total of 352 scans. Due to some factors like the gravity, the two scans at supine and prone positions from the same patient might incur some changes in polyp shape and size, and thus these two scans were considered as two different datasets. The 352 scans include a total of 384 polyp datasets (polyp sizes ≥ 8mm: 52 are H and the rest 332 are A polyps according to their path reports, where the group A includes all types of adenomas: 32 serrated adenomas (SA), 200 tubular adenomas (TA), 67 tubulovillous adenomas (VA), 30 asenocarcinomas (AC) [6]. The clinical task here is to differentiate the 52 H from the 332 A polyps.

III.C. Semi-automatic Operation for Volume of Interests

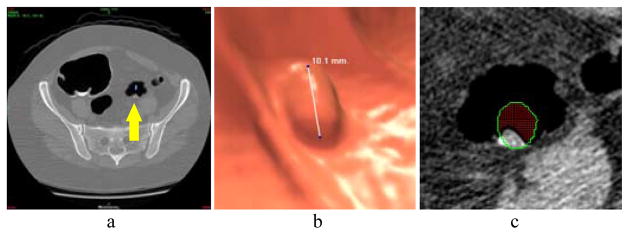
Before performing the CADx task of differentiating a polyp’s subtypes, that polyp should have been detected by a radiologist expert or a CADe pipeline with labeled coordinate (x,y,z) of that polyp in the CTC volume image data. For each detection with the labeled location (x,y,z), a volume of interest (VOI) for that polyp was first obtained so that texture features can be extracted from the VOI to determine its subtype. For that purpose, a semiautomatic technique, similar to those reported procedures [23, 32], was applied to extract the VOI. The semiautomatic technique can be outlined as follows. Firstly the detected polyp is roughly outlined manually on the 2D image slices according to the reported detection location (x,y,z) using a software, e.g. the CTC software (V3D Colon, Viatronix Inc., Stony Brook, NY, USA), and then an automatic air-cleaning algorithm, which is based on the segmentation results [44], is applied to the outlined volume to remove air voxels for an air-free 3D polyp VOI. Fig. 5 illustrates an example where the steps for the VOI extraction are shown. From the obtained VOI, texture features are extracted as described above.

Fig. 5.

Steps for semi-automatic extraction of VOI: (a): A report of polyp detected by a radiologist or a CADe algorithm (indicated by an arrow). (b): An endoscopic view of the polyp illustrated using the CTC software (V3D Colon, Viatronix Inc., Stony Brook, NY, USA). (c): A rough manual outline of the polyp on a 2D image slice (green circle), where the air voxels (red part within the outlines circle) is removed by our automatic air-cleaning algorithm.

III.D. Experimental Outcome

In this section, we will first evaluate the RF-embedded feature selection and then perform the RF-embedded feature classification on the newly extracted volumetric texture features with comparison to the baseline (or reference) volumetric texture features.

III.D.1. Performance of Feature Selection

From the Haralick’s original 14 and the newly presented 16 texture measures in section II.C above, we have the baseline texture measures or pre-KL texture measures:

1. 13×30 = 390 texture measures from the intensity image (Int); 390 measures from the gradient image (Gra), and 390 measures from the curvature image (Cur);

2. 2×390 = 780 measures from each combinations of Int_Gra, or Int_Cur, or Gra_Cur;

3. 3×390 = 1,170 measures from the combination of all the three images (Int_Gra_Cur).

The above pre-KL texture measures are also called pre-KL texture features hereafter. By computing the mean and range values of the above baseline measures over the 13 directions as the Haralick texture features, we have:

1. 60 Haralick texture features from each of the images, Int, Gra, or Cur;

2. 120 Haralick texture features from each combination of Int_Gra, or Int_Cur, or Gra_Cur;

3. 180 Haralick texture features from the combination of all the three images (Int_Gra_Cur).

By applying the KL transform on the above baseline measures (or pre-KL texture features) along the 13 directions, we have the following corresponding features in the KL domain or post-KL texture features:

1. 390 post-KL texture features from each of the images, Int, Gra, or Cur;

2. 780 post-KL texture features from the combinations of Int_Gra, or Int_Cur, or Gra_Cur;

3. 1,170 post-KL features from the combination of all the three images (Int_Gra_Cur).

Since there is no prior information on the ordering of the pre-KL texture features, the RF-embedded feature selection was performed randomly without any preference on any feature. After performing the selection, the features are ranked by their importance in a decreasing order for the three scenarios above: (1) 390 features for each individual image, (2) 780 measures for each two-image combination; and (3) 1,170 measures for all three image combination. For the post-KL features, the above presented RF-embedded feature selection was performed in the same way as in the selection of the pre-KL features.

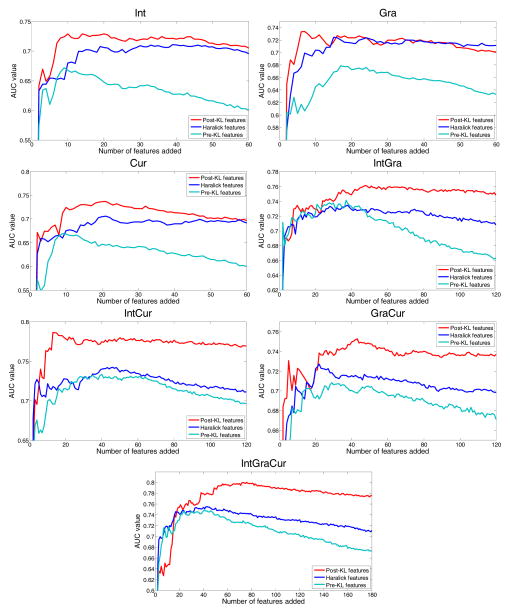
To show the performance of the ranked features, different feature sets or feature vectors were selected along the ordering, as described by the last paragraph of section II.F.1. The division of training and testing datasets was randomized 100 times for the purpose of increasing statistical confidence or minimizing the “random” (or statistical variation). In the division, the H and A polyps were equally distributed in training and testing sets, which means that the number of H and A polyps were the same in both datasets, respectively. Moreover, for each randomized case, which is one of 100 independent experiments, the training dataset was only used for feature selection and modeling, and the testing dataset was used for evaluation. Then the above presented RF-embedded classification in section II.F.2 was applied to each randomized case. The 100 classification outcomes were averaged for the final result. The final results can be plotted as a ROC curve for that selected feature set. The AUC value under that ROC curve is usually taken as a quantitative measure on the classification performance and, therefore, was used to indicate the quantitative measure on the repeated experimental outcomes. After all feature sets are processed, a plot can be drawn for the relationship between the AUC values and the selected feature sets. The plot is expected to increase from the feature set of smallest number of features (usually 1) up to reaching a peak at an optimal number of features (called intrinsic feature dimension), and then the plot generally drops down until the total feature set (including all features) was used. The higher the plot peak is, the richer the information embedded inside the features.

Fig. 6 shows the RF-embedded feature selection performance on the pre-KL features, the Haralick features (i.e. the mean and range over the 13 directions), and the post-KL features for three scenarios: (1) individual images of Int, Gra or Cur; (2) two image combinations of IntGra, IntCur, or GraCur; and (3) all three images together of IntGraCur. For each scenario, the performances of the three feature extraction methods were compared as shown by Fig. 6. It is observed that the performances of the three methods diversified quickly along the ordered feature sets. All the curves started by increasing the AUC value and then decreased the AUC value after reaching their maximum at the peak. This outcome indicates that the RF selection is effective. Except for the Gra feature set, the curves of the post-KL features are always on the top. Furthermore, the post-KL features reached higher AUC values than the other two types of the pre-KL features and the Haralick features in all the three scenarios of individual images and combinations of multiple images. This experimental outcome indicates the gain by the proposed adaptive approach to addressing the spatial variation of polyp volume orientation in the patient space and the texture amplification of CT images. The pre-KL features did not perform better than the Haralick features for a possible reason that the latter have much small number of features for classification (a gain in curse of dimensionality and computing efficiency). In other words, the texture measures from the 13 directions are correlated, and the selection of the mean and range of the texture measures over the 13 direction as the features is a reasonable choice. However, the simple KL operation is shown to be much better than the selection of the mean and range.

Fig. 6.

Plots of AUC values vs. selected number of features, which were ordered by the RF-embedded feature selection.

III.D.2. Performance of Feature Classification

The procedure of feature classification was described in the section II.F.2 above.

Table I shows the average classification results (AUC values) over 100 runs of the features extracted from the three methods. An obvious improvement of classification accuracy after considerations of the polyp orientation variation by the KL transform and the texture amplification by the derivative operation is seen for all the three scenarios of individual image and combinations of images. Moreover, a significant test was performed as shown in Table II by comparing the AUC values with and without considerations of the polyp orientation variation and texture amplification, where all of the P-values are <0.05, indicating that the proposed feature extraction model is significantly better than the Haralick feature extraction model. From Table I, it can be seen that the gain by the use of the KL transform for the polyp orientation variation is (0.8016–0.7553)/0.7553=6% over the Haralick’s average method. The gain by the use of the derivative operations for texture amplification is (0.8016–0.7288)/0.7288=10% for the KL transformed features. The performance in differentiating non-risk group (H) from the risk group (A) reached an AUC value of 0.8016 by the proposed adaptive approach.

TABLE I.

Averaged AUC information of the 100 runs before and after KL-transform

Group	AUC information
	Pre-KL Features	Haralick Features	Post-KL Features
Intensity	0.6716±0.0399	0.7105±0.0334	0.7288±0.0404
Gradient	0.6789±0.0384	0.7244±0.0348	0.7339±0.0368
Curvature	0.7057±0.0421	0.6693±0.0394	0.7369±0.0377
Int_Gra	0.7346±0.0369	0.7414±0.0443	0.7613±0.0393
Int_Cur	0.7330±0.0369	0.7421±0.0379	0.7862±0.0399
Gra_Cur	0.7082±0.0351	0.7270±0.0343	0.7528±0.0401
Int_Gra_Cur	0.7487±0.0436	0.7553±0.0377	0.8016±0.0352

Format: mean ± standard deviation

TABLE II.

Wilcoxon signed-rank test between the AUC of the post-KL features and the corresponding pre-KL and Haralick features

Post-KL features	Int	Gra	Cur	Int_Gra	Int_Cur	Gra_Cur	Int_Gra_Cur
Haralick features	≪0.05	0.0176	≪0.05	≪0.05	≪0.05	≪0.05	≪0.05
Pre-KL features	≪0.05	≪0.05	≪0.05	≪0.05	≪0.05	≪0.05	≪0.05

The p-value is the result of the Wilcoxon signed-rank test because the normality assumption for t-test is not hold.

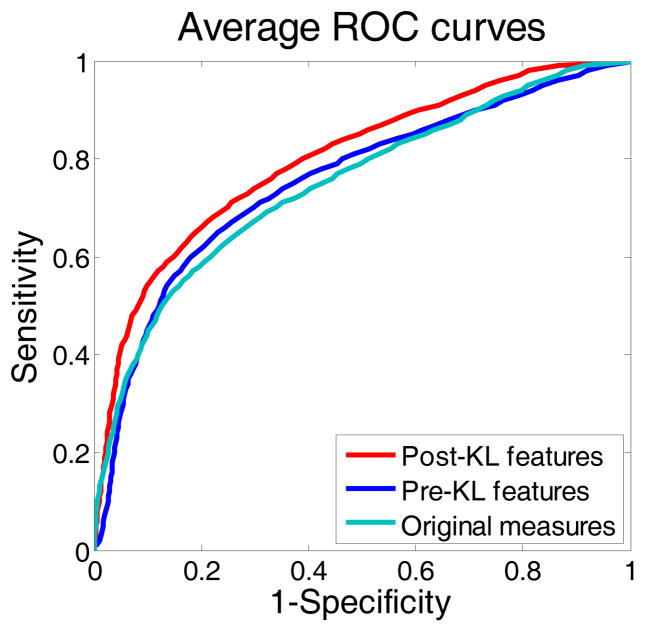
Since all the three feature extraction methods can reach their peak AUC values, their corresponding averaged ROC curves are plotted as shown by Fig. 7. The threshold averaging or operating point selection strategy was used to obtain the curves [8, 37, 38]. The curves are consistent with the AUC values in Table I. From these curves, it is seen that the post-KL features reached a higher sensitivity value, under the same specificity, than the other two methods. That is to say, the post-KL features could provide a better classification result than the other two methods.

Fig. 7.

The averaged ROC curves of the results from the three methods corresponding to their highest AUC values.

From the average ROC curves, different sensitivity-specificity paired values can be generated. Table III shows the average specificity levels for different fixed sensitivity levels and feature groups, based on the 52 H polyps and the 332 A polyps. For example, if we choose 0.75 sensitivity level for the post-KL feature group, its corresponding specificity will reach 0.6859. As a result, by employing a simple RF classifier, the number of correctly classified A polyps is 249 (of 332) and the number of H polyps is 35.67 (of 52) on an average. It is obvious that a higher specificity with the post-KL features can be always achieved for each fixed sensitivity value in the table, which indicates that the post-KL features do perform better than the other two feature extraction methods.

TABLE III.

Sensitivity-specificity pairs corresponding to the averaged ROC curves of the three methods in Fig. 7.

Group	Corresponding specificity with different sensitivity levels
	Sen=0.6	Sen=0.7	Sen=0.8	Sen=0.9
Post-KL features	0.8533	0.7509	0.6123	0.3955
Haralick features	0.8196	0.7009	0.5375	0.2884
Pre-KL features	0.7839	0.6594	0.4891	0.2865

In addition to the above investigations on the variation of polyp orientations and the texture amplification for the low tissue contrast CT images, we further performed experiments to show the gain by the 16 new texture measures of section II.C. The results are illustrated in Table IV, which have the similar notations as Table I. The highest AUC values are shown in Table V.

TABLE IV.

Averaged AUC information of the 100 runs before and after KL-transform

Group	AUC information
	Pre-KL Features	Haralick Features	Post-KL Features
Intensity	0.6295±0.0355	0.6855±0.0387	0.6998±0.0443
Gradient	0.6664±0.0329	0.7188±0.0376	0.7354±0.0421
Curvature	0.6544±0.0430	0.6376±0.0456	0.6801±0.0384
Int_Gra	0.7358±0.0388	0.7442±0.0410	0.7454±0.0379
Int_Cur	0.7300±0.0377	0.7389±0.0360	0.7601±0.0436
Gra_Cur	0.7021±0.0391	0.7005±0.0368	0.7436±0.0421
Int_Gra_Cur	0.7415±0.0351	0.7538±0.0383	0.7723±0.0413

Format: mean ± standard deviation

TABLE V.

Highest averaged AUC information of the 100 runs

	Post-KL features	Haralick features	Pre-KL features
30 measures	0.8016	0.7553	0.7487
14 measures	0.7723	0.7538	0.7415

By comparing Table I and Table IV, we can see that most of the feature sets have some gains by adding the 16 new texture measures into the corresponding feature sets. Using the post-KL feature extraction method as an example, the gain is (0.8016–0.7723)/0.7723=3.8% . The p-value under the Wilcoxon signed-rank test is less than 0.05, which indicates that adding the 16 new texture measures could provide more information than the original 14 texture measures.

IV. Discussion and Future work Conclusion

The spatial variation of polyp volume in the patient space is a common situation, thus an adaptive approach to address the variation is desired. The use of KL transform to address the variation in this exploratory study is just a simple example. Similarly, image reconstruction usually takes some penalties to smooth data noise, resulting in some loss of textures. The use of the derivative operation to amplify the textures is another simple example. Extracting more texture measures from the polyp volume is always desired. The addition of the 16 new texture measures in this study has shown a noticeable gain. Exploring other strategies for the spatial variation, texture amplification and extraction of more new texture measures are our future research interests.

Since screening the large population is the main purpose of developing CTC, the newly proposed technologies above remain the same screening purpose while aiming to advance the current CTC paradigm of detection-only capability to a new paradigm of not only detection but also characterization of the detections. By deviating from the screening purpose, efforts have been devoted to differentiating neoplastic from non-neoplastic lesions (polyps and masses) by the use of intravenous (IV) contrast-enhanced CTC protocol [20, 23, 24, 41]. The gain by the IV-contrast-enhanced CT image textures is at the cost of the complication of IV related procedure, which would compromise the screening purpose. An alternative attempt of gaining more CT image texture information is to use energy spectral CT (EsCT) [35] at the cost of increased radiation dose to the patient. Reducing the dose while retaining the EsCT image textures has been a topic of our research interests [19].

The database in this study includes polyps of size 8mm and larger. The size threshold of 8mm was chosen because it is currently believed to be clinically desired [26, 30]. Ideally, we would like to perform the classification on polyps with different size ranges, such as from (a) 5mm to 10mm, (b) 10mm to 15mm, (c) 15mm to 20mm, (d) 20mm to 30mm, and (e) 30mm and larger, where the size could be included as a feature in the feature set. Increasing the number of polyps and performing the classification on different polyp size ranges are another research interest of our future research effort.

By current CTC protocol, a patient is usually scanned at two positions of supine and prone, resulting in two sets of image data. Because the body turns over from supine to prone position, the entire colon changes significantly in shape, orientation and size due to mainly the gravity. Since the two image datasets are two statistically independent observations from a source, which changes significantly, researchers in the CTC field usually treat the varying source in the two datasets as two different sources, particularly when the number of sources is small (i.e. small sample size). In theory, there may be some bias in treating the same source as two different ones in the situation. However, for bi-classification, this concern would be relieved because the sample numbers of both hyperplastic and adenomatous polyps are doubled and the relative bias would be small. This hypothesis would be tested when the number of sources (or sample size) is large. This is one of our future research topics.

The simplicity and effectiveness of RF decision are attractive in theory and applications. In this study, RF was used for feature selection and classification separately. Integrating RF with ROC analysis for simultaneous feature selection and classification is another research interest of our future research effort.

V. Conclusion

In this paper, we first introduced some new texture measures according to the Haralick’s 3D model, and then took the well-known principal component analysis or KL transform, as an example, to explore an adaptive idea to address the spatial variation of polyp volume orientation in the patient space, and further integrated a mathematical derivative operation, as an example, for texture amplification to address the compromise of texture loss due to noise smoothing in many state-of-the-art CT image reconstruction algorithms. While the adaptive ideas and the tools (of mathematical derivatives and KL transform) used to realize the ideas for enhancing textures and stabilizing spatial variations are simple, their impacts to the clinical task of differentiating hyperplastic from adenomatous polyps are significant as evidenced by the above reported experiments, which rendered a gain in AUC value (i) from 0.7723 to 0.8016 by addition of 16 new texture measures; (ii) from 0.7553 to 0.8016 by the variation stabilization operation; and (iii) from 0.7288 to 0.8016 by the texture amplification operation. The differentiation capability of AUC = 0.8016 indicates quantitatively the feasibility of advancing CTC toward personal healthcare for preventing colorectal cancer. The ideas can be applied to other applications, such as differentiation of lung nodule malignancy [10].