Myocardial Infarct Segmentation from Magnetic Resonance Images for Personalized Modeling of Cardiac Electrophysiology

Abstract

Accurate representation of myocardial infarct geometry is crucial to patient-specific computational modeling of the heart in ischemic cardiomyopathy. We have developed a methodology for segmentation of left ventricular (LV) infarct from clinically acquired, two-dimensional (2D), late-gadolinium enhanced cardiac magnetic resonance (LGE-CMR) images, for personalized modeling of ventricular electrophysiology. The infarct segmentation was expressed as a continuous min-cut optimization problem, which was solved using its dual formulation, the continuous max-flow (CMF). The optimization objective comprised of a smoothness term, and a data term that quantified the similarity between image intensity histograms of segmented regions and those of a set of training images. A manual segmentation of the LV myocardium was used to initialize and constrain the developed method. The three-dimensional geometry of infarct was reconstructed from its segmentation using an implicit, shape-based interpolation method. The proposed methodology was extensively evaluated using metrics based on geometry, and outcomes of individualized electrophysiological simulations of cardiac dys(function). Several existing LV infarct segmentation approaches were implemented, and compared with the proposed method. Our results demonstrated that the CMF method was more accurate than the existing approaches in reproducing expert manual LV infarct segmentations, and in electrophysiological simulations. The infarct segmentation method we have developed and comprehensively evaluated in this study constitutes an important step in advancing clinical applications of personalized simulations of cardiac electrophysiology.

I. Introduction

Left-ventricular (LV) myocardial infarction, a medical condition in which regions of a patient’s LV lose viability due to prolonged ischemia, is a prominent cause of serious complications, including heart failure and ventricular arrhythmia [1], [2]. Central to the mechanisms underlying these complications is the structural and electrophysiological remodeling that occurs in the infarct regions during the healing process [1], [3], [4]. Recently, computational modeling of patient hearts has emerged as a promising non-invasive tool that can provide clinicians with personalized guidance in the treatment of post-infarct arrhythmias [5], [6], [7], [8], [9], [10]. However, to accurately represent the myocardial structural remodeling that occurs in ischemic cardiomyopathy, the computational models need to incorporate the patient-specific geometry of the infarct region [5], [11]. Presently, among the various imaging techniques used to acquire the infarct structure in the clinic [12], two-dimensional (2D) late-gadolinium enhanced cardiac magnetic resonance (LGE-CMR) scanning is the most widely used [13]. Therefore, accurate segmentation of the LV infarct regions from clinically acquired LGE-CMR images is paramount to patient-specific modeling of cardiac (dys)function in ischemic cardiomyopathy.

Existing approaches for LV infarct segmentation from LGE-CMR images can be broadly categorized into those based on image intensity thresholding, feature clustering, or energy minimization. Some of the techniques based on image intensity thresholding, including full width at half maximum (FWHM) [14] and signal threshold to reference mean (STRM) [15], [16], are the simplest to implement, and the most widely used in clinical studies. There are other approaches that employ intensity thresholding in the segmentation, e.g., the region growing [17], Otsu method [18], and watershed segmentation [19]; these are not as widely used as FWHM or STRM. Feature clustering techniques that have been utilized in the infarct segmentation include support vector machines [20], fuzzy c-mean clustering [21], and dictionary learning [22]. A drawback of the infarct segmentation methods based on intensity thresholding or feature clustering is that these methods do not incorporate any smoothness constraints, and therefore are highly influenced by image noise [23]. Accordingly, LV infarct segmentation methods based on energy minimization that incorporate smoothness constraints, along with region and boundary data terms, have been developed [24], [23]. Rajchl et al. [24] developed an interactive approach for the infarct segmentation based on a hierarchical convex max-flow method. However, this method was designed to operate on three-dimensional (3D) LGE-CMR images [24], which are not widely used in the clinic. Lu et al. [23] proposed to segment the infarct using a method based on graph cuts, but the performance evaluations they conducted were limited, in that a dataset of only ten patient images, and one accuracy metric, namely the infarct mass, was utilized [23]. Thus, there is a lack of a methodology that has been developed and thoroughly evaluated for robustly segmenting LV infarct from clinically acquired 2D LGE-CMR images. Additionally, no prior study has evaluated the efficacy of an infarct segmentation method based on computational simulations of cardiac (dys)function, for patient-specific modeling of the heart. Our goal was to address these needs.

We expressed LV infarct segmentation from clinically acquired 2D LGE-CMR images as a continuous min-cut optimization problem, and solved it using the dual formulation of the problem, namely the continuous max-flow (CMF). An image gradient-weighted smoothness term, along with a data term that quantified similarity between intensity histograms of segmented regions and those of a set of training images, was incorporated, for robustness, into the optimization objective. The 3D geometry of the infarct was reconstructed from the 2D segmentation using an interpolation technique we developed based on logarithm of odds (LogOdds). The developed methodology was extensively evaluated against expert manual LV infarct segmentations from 51 short-axis (SAX) LGECMR images, with metrics based on infarct geometry, and on outcomes of individualized simulations of cardiac electrophysiology. Several previously reported LV infarct segmentation methods were also implemented, and their performance was compared to that of our method.

Preliminary results from this study were published in conference proceedings very recently [25]. This paper substantially extends the conference publication, with a more detailed description of the methodology, 3D implementation of the CMF algorithm, use of several additional clinical LGE-CMR images in the evaluation, and importantly, a new assessment of the efficacy of the developed infarct segmentation method based on outcomes of individualized simulations of cardiac electrophysiology.

II. Methods

A. Overview of Our Methodology for Segmentation and Reconstruction of the LV Infarct

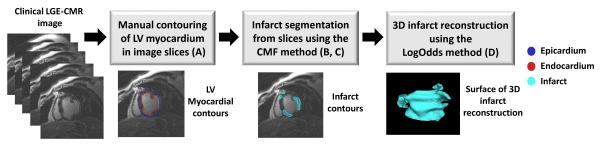
The workflow of our methodology for segmentation and 3D reconstruction of LV infarcts from clinically acquired SAX LGE-CMR images is illustrated in Fig. 1. Given an image, the epi- and endo-cardial boundaries of the LV were manually contoured in the image slices by an expert. The infarct was then segmented using the CMF method, for which the LV myocardium was used as the region of interest and the initialization region. We implemented two different versions of the CMF algorithm, namely a 2D approach, where each slice was segmented independently, and a 3D approach (CMF3D), where the entire stack of slices was segmented at once by means of an intermediate image with isotropic resolution that was created using nearest-neighbor interpolation method. Finally, the 3D geometry of the infarct was reconstructed from the infarct segmentations using an interpolation technique we developed based on LogOdds. Subsections B-D below describe in detail the components of the pipeline shown in Fig. 1. All image processing tasks were performed in the Matlab computing environment (Mathworks Inc., Natick, MA) installed on a personal computer equipped with a 2.3 GHz Intel Core i7 CPU, 12 GB of RAM, and the Windows operating system.

Fig. 1.

Block diagram of our processing pipeline to segment and reconstruct LV myocardial infarct from multi-slice clinical LGE-CMR images. The letter(s) in parenthesis in a block refer(s) to the corresponding subsection(s) of Section II, where the processing in the block is described. The pipeline involves delineation of the LV myocardium in 2D by an expert, segmentation of the infarct in 2D using the CMF algorithm, and reconstruction of 3D infarct geometry from the segmented slices using the LogOdds method.

B. LV Infarct Segmentation Expressed as a Continuous Min-Cut Problem

Let I(x) ϵ $\mathcal{Z}$ be the given image, where $\mathcal{Z}$ is the set of image intensities. Infarct segmentation was formulated as an optimization problem by iteratively evolving a contour $\mathcal{C}\left(s\right):[0,1]\to {\mathbb{R}}^2$ over time, where s is the arc-length parameterization of $\mathcal{C}\left(s\right)$, as illustrated in Fig. 2(a). Note that the mathematical formulations we provide here are for 2D segmentation, but the same concepts apply to surface evolution for 3D segmentation. The current contour ${\mathcal{C}}_t$ at time t is propagated to its new position ${\mathcal{C}}_{t+h}$ at time t + h such that ${\mathcal{C}}_{t+h}$ minimizes the following energy [26]:

$$\underset{\mathcal{C}}{\min }\left\{{\int }_{{\mathcal{C}}_f^{+}}{e}_f^{+}\left(x\right)\mathit{dx}+{\int }_{{\mathcal{C}}_b^{+}}{e}_b^{+}\left(x\right)\mathit{dx}+{\int }_{\partial \mathcal{C}}g\left(s\right)\mathit{ds}\right\}$$ (1)

where ${\mathcal{C}}_f^{+}$ and ${\mathcal{C}}_b^{+}$ are the foreground and background expansion regions with respect to ${\mathcal{C}}_t$, $e_f^{+}\left(x\right)$ and $e_b^{+}\left(x\right)$ are the corresponding cost functions, and g(s) is a boundary smoothness term [26]. Here, the foreground and background regions represent the LV infarct region and normal myocardium, respectively. Let u(x) ϵ {0, 1} be the function labeling the region enclosed by ${\mathcal{C}}_t$ such that u(x) = 1 when x is inside C_t and u(x) = 0 otherwise.

Fig. 2.

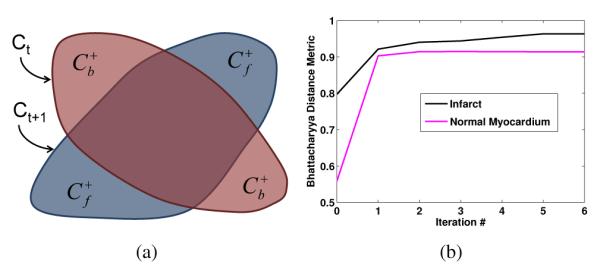
(a) Region changes arising from the evolution of the segmentation contour using the first-order approximation of the distribution matching based on Bhattacharyya distance metric. (b) Value of Bhattacharyya distance metric as a function of iteration number for an example segmentation.

In the present study, the cost functions were defined in terms of a data term E_Bh(u) comprising of the Bhattacharyya distance metric [27] between the intensity histograms h_i(z) of the segmented regions and intensity histograms ${\widehat{h}}_i\left(z\right)$ of a training dataset (target intensity histograms), where i = f; b and $z\in \mathcal{Z}$. The data term is defined as

$$E_{\text{Bh}}\left(u\right)=-\sum _{i=f,b}\sum _{z\in \mathcal{Z}}\sqrt{h_i\left(z\right){\widehat{h}}_i\left(z\right)}.$$ (2)

The target intensity histograms ${\widehat{h}}_{f,b}\left(z\right)$ were derived using the Parzen method [28] from the expert manual segmentations of the entire set of training images. Note that the intensity histogram of the infarct region varied substantially from one image to another, and therefore the incorporation of multiple images in the derivation of target intensity histograms was important. The region fidelity cost functions $e_f^{+}\left(x\right)$ and e⁺b(x) were given by the first-order derivatives of E(u) w.r.t. u_t(x) [27], i.e.,

$$e_i^{+}\left(x\right)=\frac{1}{2A_i}\sum _{z\in \mathcal{Z}}\left\{\sqrt{h_i\left(z\right){\widehat{h}}_i\left(z\right)}-\sqrt{\frac{{\widehat{h}}_i\left(z\right)}{h_i\left(z\right)}}K\left(z-I\left(x\right)\right)\right\},$$ (3)

where A_i = ∫_Ω u_i dx, i = f, b, is the area of the foreground and background and K(.) is the Gaussian kernel function [28].

To express Equation (1) as a continuous min-cut problem, let D₁(x) and D₂(x) be label assignment functions defined as follows:

$$D_1\left(x\right)≔\{\begin{array}{cc}{e}_b^{+}\left(x\right),\hfill & \text{where}x\in {\mathcal{C}}_t\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

$$D_2\left(x\right)≔\{\begin{array}{cc}{e}_f^{+}\left(x\right),\hfill & \text{where}x\notin {\mathcal{C}}_t\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (4)

The optimization problem in Equation (1) can then be expressed as the continuous min-cut formulation [26]

$$\underset{u\left(x\right)\in \{0,1\}}{\min }\langle 1-u,D_1\rangle +\langle u,D_2\rangle +{\int }_{\Omega }g\left(x\right)\mid \nabla u\mid \mathit{dx},$$ (5)

where u(x) ϵ {0, 1} is a binary constraint. We used an image gradient-weighted smoothness function, g(x) = λ₁ + λ₂ exp(−λ₃ ∣ ∇I(x)∣) in our formulation, where parameters λ₁; λ₂; λ₃ > 0.

It is challenging to solve the combinatorial optimization problem (5), because it is highly non-linear and non-convex. However, it has been proven, using the convex optimization theory [26], [29], that problem (5) can be solved globally and exactly via the following convex relaxation:

$$\underset{u\left(x\right)\in [0,1]}{\min }\langle 1-u,D_1\rangle +\langle u,D_2\rangle +{\int }_{\Omega }g\left(x\right)\mid \nabla u\mid \mathit{dx},$$ (6)

where the binary constraint u(x) ϵ {0, 1} in Equation (5) is now relaxed to u(x) ϵ [0, 1]. Thresholding the result of the convex relaxation in Equation (6) provides the exact and global optimum of (1). In other words, the continuous min-cut problem in Equation (5) can be solved globally.

C. CMF, the Dual Formulation of the continuous Min-Cut Problem

It is challenging to efficiently solve the continuous min-cut problem (6) directly. However, it can be efficiently solved via its dual, the max-flow formulation, using one of the global solvers available for this task [26], [30]. In the present study, we chose the CMF method described by Yuan et al. [26]. Note that the convex relaxation problem in Equation (6) is mathematically equivalent to the CMF formulation (Equation (12) in the previous study [26]). The CMF formulation was efficiently optimized using the classical augmented Lagrangian method [31] and implemented in the CUDA architecture (NVIDIA Corp., Santa Clara, CA).

Since a first order-approximation of the data term was used in the optimization, the value of energy function was not guaranteed to monotonically decrease with iterations. Accordingly, the iterations were stopped when either the incremental change in segmented region area between two successive iterations was smaller than 4 mm², or the number of iterations exceeded 8. These threshold values were determined heuristically. Figure 2(b) shows value of Bhattacharyya distance metric as a function of iteration number for an example segmentation.

D. Reconstruction of the 3D Infarct Geometry

To represent the LV infarct geometry in patient specific models of ventricular electrophysiology, the segmentation of the infarct from 2D LGE-CMR images needs to transformed into a 3D reconstruction [5], [32]. We have recently developed a technique called LogOdds method for this reconstruction [33]. The LogOdds method was shown to be significantly more accurate than several alternatives, including variational implicit, shape-based interpolation, and nearest neighbor methods [33]. LogOdds is an example of a class of functions that can be used to map binary image slices into the Euclidean space [34]. The mapped image slices can then be interpolated using linear combinations. Mathematically, let $p\in \mathbb{P}$ be the probability that a voxel is assigned to a particular anatomical structure. Then, the LogOdds of p, denoted as logit(p), is the logarithm of the ratio between p and its complement. i.e., $\mathit{logit}\left(p\right)=\mathit{log}\frac{p}{\left(1-p\right)}$. Let $\mathbb{L}=\{\mathit{logit}\left(p\right)\mid p\in \mathbb{P}\}$, and $P\left(t\right)=\frac{1}{1+e^{-t}}$, the inverse of logit(p). The functions logit(p) and P (t) make up a structure-preserving map between $\mathbb{P}$ and $\mathbb{L}$ [34]. Let s be the number of slices in the image, n the number of pixels per slice, and m the number of voxels in the interpolated image. The discrete probability maps $P:\Omega \to {\mathbb{P}}^n$, where $\Omega \subset {\mathbb{R}}^2$, are obtained from discrete label maps $B:\Omega \to {\mathbb{B}}^n$ of segmentation. LogOdds maps $L:\Omega \to {\mathbb{L}}^n$ are created from discrete probability maps using logit(.) function.

In this study, we used smoothing by spatial Gaussians with a standard deviation of two pixels, to convert binary image slices containing the infarct segmentations into probability maps. When a binary image slice representing the segmentation of an infarct region was smoothed using the Gaussian kernel, each pixel was assigned a value in the interval [0, 1], which we interpreted as the probability of that pixel belonging to the infarct region. Similarly to Pohl et al. [34] we used a probability value of 0.5, which maps to a LogOdds value to 0, to define the object boundary. The 2D probability maps resulting from Gaussian smoothing were converted into LogOdds maps using the logit(.) function. A cubic spline method was then used in the interpolation ${\mathbb{L}}^{\mathit{sn}}\to {\mathbb{L}}^m$, of the stack of 2D LogOdds maps into a 3D image. A 3D probability map $P:\Omega \to {\mathbb{P}}^m$ was generated from the interpolated image via logistic transformation. Finally, the 3D probability map was thresholded to generate a 3D reconstruction of the infarct region.

Even when the infarct segmentation is performed in 3D, the segmented regions need to be interpolated to obtain the final reconstruction. This is because the voxel size of the segmented image produced by CMF3D was 1.5–2.4 mm, which was coarser than the element size of 0.4 mm needed to resolve the electrical activation wavefront [32].

E. Data Acquisition

The data we utilized to train and evaluate the CMF method comprised of clinical LGE-CMR images of 61 patients with ischemic cardiomyopathy and LV dysfunction (LV ejection fraction ≤ 35%), randomly selected from the CMR arm of the PROSE-ICD study [35]. The images were acquired with an inversion recovery fast gradient echo pulse sequence, 15 to 30 minutes after a total injection of 0.2 mmol/kg gadodiamide (Omniscan, GE Healthcare Technologies). The patients were scanned in the SAX plane with a 1.5 Tesla whole-body scanner (Signa CV/I, GE Healthcare, Milwaukee, Wisconsin; or Siemens Avanto, Erlangen, Germany). The imaging parameters were as follows: TR 5.4 ms, echo time 1.3 ms, inversion time (TI) 175 to 250 ms, 2 excitations, 1 R-R interval imaging, flip angle 20, 350-ms time delay after the R wave, and 24 views per segment. In-plane resolution of the images was 1.5–2.4 mm, and the slice thickness was 8-10 mm, with 0-2 mm slice gap. The study protocol was approved by the Johns Hopkins Hospital Institutional Review Board, and all patients gave written informed consent. The LV myocardium and infarct were manually contoured by an expert in all images.

The data were divided into a training set and a testing set, consisting of 10 and 51 LGE-CMR images, respectively. The training dataset comprising of a total of 48 slices was used for sequentially optimizing the parameters of the CMF method (i.e., λ₁, λ₂, and λ₃), and generating the target intensity histograms. The testing dataset consisting of a total of 326 slices was used for evaluating the method. Note that, to maximize the testing set size, only a small subset of the data was used to form the training set.

F. Evaluation of Accuracy of Infarct Segmentation based on Outcomes of Electrophysiological Simulations

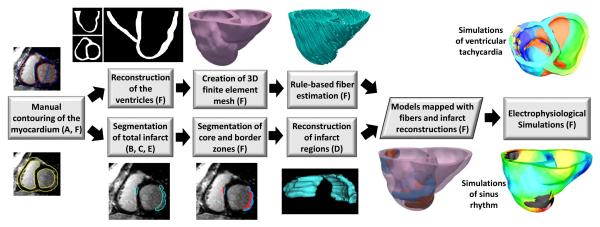
The block diagram for the evaluation of our infarct segmentation methodology based on outcomes of electrophysiological simulations is shown in Fig. 3. Simulations of both normal and abnormal cardiac function, in which cardiac electrical activity was modeled from ionic channels to the whole organ, were performed. As these multiscale simulation experiments were computationally very expensive, they were conducted with models generated from only a subset of 7 LGE-CMR images randomly chosen from our testing set. For each of these 7 images, the RV boundaries were also manually contoured in each 2D slice using the ImageJ software program (National Institutes of Health, Bethesda, MD), to incorporate the RV geometry in the ventricular models. Ventricular geometry was then reconstructed from the myocardial boundaries at an isotropic resolution of 0.4 mm using an interpolation method based on variational implicit functions [36]. The infarct region was segmented from the image using the CMF method, in addition to expert manual segmentation. Infarct tissue is known to comprise of scar (also referred to as infarct core zone) and semi-viable myocardium (or border zone) [35], and the two zones have different electrophysiological properties. Accordingly, we divided the infarct regions in the segmented image slices into the two zones, using a FWHM technique [35]. Three-dimensional geometry of the total infarct region and core zone were first reconstructed using the LogOdds method. The reconstruction for the border zone was then obtained as the relative complement of the infarct core, where total infarct reconstruction was considered as the union. Note that, the border zone geometry was not directly reconstructed from binary segmentations, because of larger errors encountered in this reconstruction than those in our approach [37]. These larger errors may be because the border zone is typically more complex in topology than the total infarct and core. Using the ventricular reconstruction, and the infarct reconstructions, two finite element models, one incorporating infarct zone geometries reconstructed from the manual segmentation, and the other with infarct zone geometries built from the computed segmentation, were created [38]. In this process, the 3D finite element meshes were generated from the reconstructions as described previously [39]. The fiber orientations for the models were estimated using a rule-based method [40]. The two models were identical except for the differences in tissue labels of some of the elements that reflected the differences in the infarct segmentations.

Fig. 3.

Block diagram of model generation, and execution of electrophysiological simulations, for the evaluation of our infarct segmentation method. the letter(s) in parenthesis in a block refer(s) to the corresponding subsection(s), of Section II, where the processing in the block is described. From each LGE-CMR image, two ventricular models, one incorporating infarct geometry reconstructed from manual segmentation, and the other with infarct geometry reconstructed from computed segmentation, were generated. Outcomes of electrophysiological simulations with the two models were then compared.

Electrical propagation was modeled using the monodomain formulation [32], which involves the solution of a reaction-diffusion equation coupled to a system of ordinary differential equations describing membrane kinetics. The governing equations were

$$C_m\frac{\delta V_m}{\delta t}+I_{\mathit{ion}}=\nabla .\left({\sigma }_i\nabla V_m\right),$$

and

$$I_{\mathit{ion}}=I_{\mathit{ion}}\left(v_m,\mu \right),\text{and}\frac{\delta \mu }{\delta t}=G\left(V_m,\mu \right),$$

where σ_i is the intracellular conductivity tensor; V_m is the transmembrane potential; C_m is the membrane specific capacitance; and I_ion is the density of the transmembrane current, which in turn depends on V_m and on a set of state variables μ describing the dynamics of ionic fluxes across the membrane. Intracellular conductivity σ_i assigned in the normal myocardium were such that the resulting conduction velocities matched those recorded in human ventricular experiments [41]. In the remodeled border zone, the transverse conductivity was decreased by 90% to represent connexin 43 remodeling and lateralization, which resulted in increased tissue anisotropy [42]. The infarct core was modeled as passive tissue with zero conductivity. The Ten Tusscher human ventricular action potential model was used to represent the membrane kinetics in the healthy myocardium [43]. For the border zone, this action potential model was modified to represent electrophysiological changes that have been observed experimentally [44], [45], [46]. These modifications resulted in a border zone action potential morphology that had decreased upstroke velocity, decreased amplitude, and increased duration, consistent with experimental recordings.

Sinus rhythm was simulated in all models by replicating activation originating from the Purkinje network. The models were activated at six locations on the endocardium by stimuli with a cycle length of 600 ms [47], [48]. The six locations included one on the RV free wall, three on the LV septum, and two on the LV free wall. Appropriate timings of the stimuli were chosen such that the resultant electrical propagation matched experimental data [49]. Since the electrophysiological remodeling within infarct tissue plays a crucial role in the initiation and sustenance of arrhythmias [45], [6], we expected the differences in infarct segmentations to affect the outcomes of simulations of abnormal cardiac function to a higher degree than those of simulations of normal electrical activity. As such, simulations of VT induction were conducted by applying, at the RV apex and the outflow tract in all models, a programmed electrical stimulation (PES) similar to that used in the clinic [50]. Our PES protocol consisted of 6 stimuli with a coupling interval of 350 ms, which were followed by a premature stimulus whose cycle length was shortened until sustained VT was initiated or the last stimulus failed to capture. If needed, two additional extrastimuli were delivered to attempt arrhythmia induction. An arrhythmia was classified as sustained if it persisted for at least 2 seconds. Pseudo-ECGs [51] were generated in all simulations by taking the difference between the extracellular potentials calculated at two points in an isotropic conductive medium surrounding the heart [49]. The activation maps in simulations were derived by determining, at each node of the finite element meshes, the instant in time at which the upstroke of the action potential at that node reached a threshold of 0 mV. All simulations were performed using the software package CARP (CardioSolv, LLC) [52], [53] on a parallel computing platform.

G. Metrics for Assessment of Infarct Segmentation Accuracy

The CMF method was evaluated using metrics based on infarct geometry as well as outcomes of individualized simulations of cardiac electrophysiology. The evaluation using the geometry-based metrics was done in two ways. First, the 2D infarct segmentations computed by the CMF method was compared to expert manual delineations, using metrics based on region overlap, boundary distance, and area. As the region overlap-based metric, we used the Dice similarity coefficient, DSC = 2∣R_A ∩ R_M∣/(∣R_A∣ + ∣R_M∣), where R_A and R_M, denote regions enclosed by computed and manual segmentations, respectively, and ∣.∣ denotes the volume of a region. The boundary distance-based metric was root meat square error (RMSE), calculated as the RMS of the shortest distance from each point on the boundary of the computed segmentation to the boundary of the manual delineation. Absolute area difference, δA = ∣A_A − A_M∣/A_M, where A_A and A_M are the areas of computed and manual segmentations, was used as the area-based metric. Second, we compared the 3D infarct reconstructions built from the segmentation by the CMF method to the ones generated from the manual delineations, using metrics based on region-overlap, boundary distance, volume, surface area, and topology. Note that these 3D metrics were important because they evaluated the performance of the segmentation methods in the estimation of indices such as infarct volume and surface area, which have shown to be predictive of clinical outcomes [35], [2]. Further, the generation of patient-specific models, for which the CMF method was developed, utilized the 3D infarct reconstructions. The boundary distance error in the 3D scenario was defined similarly to the 2D case, except that the calculation in the former was based on surfaces. As volume- and surface area-based metrics, we used volume difference (δV_sgn), absolute volume difference (δV), and surface area difference (δSA), expressed as a percentage of the volume or surface area of the infarct reconstructions built from the manual segmentation. The topology-based metric we employed was the absolute difference in Euler characteristic (δχ) between the infarct reconstructions built from segmentations by the CMF method and the manual segmentation.

The difference in pseudo-ECGs between simulations with models incorporating infarct reconstructions from segmentation by the CMF method and by manual delineation was calculated using RMSE, mean absolute deviation (MAD), and correlation coefficient (CORR) metrics. Note that the MAD and CORR metrics have been applied in prior clinical studies to compare ECGs of reentrant activity [54]. The MAD metric is defined as

$$\mathit{MAD}=\frac{\sum _{i=1}^{n_s}\mid \left(X_i-\stackrel{‒}{X}\right)-\left(Y_i-\stackrel{‒}{Y}\right)\mid }{\sum _{i=1}^{n_s}\mid \left(X_i-\stackrel{‒}{X}\right)+\left(Y_i-\stackrel{‒}{Y}\right)\mid },$$ (7)

where X and Y are two waveforms with length n_s [54]. The MAD metric varies between 0% and 100% corresponding to identical and completely different waveforms, respectively.

The difference in activation maps between simulations with models incorporating infarct reconstructions from segmentation by the CMF method and manual delineations were assessed as activation time difference, $\mathit{ATD}={\sum }_{i=1}^{n_n}\mid T_A^i-T_M^i\mid ∕n_n$, where n_n is the number of nodes in the finite element meshes of the models, and $T_i^A$ and $T_i^M$, respectively, are the activation times of node i in simulations with models incorporating infarct reconstructions from segmentations by the CMF method and manual delineation. The infarct core zone was excluded from ATD calculations, as the core was modeled as an insulator and did not activate. All metrics based on outcomes of electrophysiological simulations were computed in the steady state, when activation from beat to beat was stable.

H. Comparison of the CMF method with Existing Infarct Segmentation Methods

The CMF method was compared to several existing infarct segmentation techniques, including the FWHM method, the STRM approach with standard deviations one (STRM1), two (STRM2) and three (STRM3) from the reference mean, and the region growing (RG) algorithm. These methods were chosen due to their wide popularity in the clinical [35], [55], [56], [57] and modeling [6], [58] research communities. Also, previous studies have established high reproducibility and accuracy in infarct segmentation by the FWHM [15], [59], [60] and STRM methods [59]. In all the existing methods, the LV myocardium segmentation was used to constrain the infarct segmentation. The enhanced intensity region of the myocardium, normal region of the myocardium, and a seed point in the infarct region, for the FWHM, STRM, and RG methods respectively, were identified by an expert. To test whether incorporating a smoothing step into the threshold-based methods increased their accuracy, we re-evaluated these methods after applying connectivity filtering [18] to the infarct segmentations by these methods. The accuracy of the infarct segmentations by the existing methods was evaluated using metrics based on geometry, as in Fig. 1, and the results were compared to those of the CMF algorithm. Note that, in the evaluation of the various methods, the CMF method did not require any user inputs apart from the delineation of the LV myocardium, but the other methods did. Wilcoxon signed rank sum tests were performed to identify the statistically significant differences in DSC between the CMF method and the others. Paired t-tests were conducted to examine statistically significant difference between the log-transformed volumes of the infarct reconstructions built from segmentations by the CMF method and those by the existing approaches. All statistical analyses were performed using GraphPad Prism 6.2 (GraphPad Software Inc., CA), and an α of 0.05 was used as the level of significance.

To evaluate whether the poorer performance of an infarct segmentation method in geometry-based evaluations leads to inferiority in its performance in evaluations based on outcomes of simulations, we selected one representative method from the existing techniques, and evaluated its accuracy based on outcomes of electrophysiological simulations, as in Fig. 3. The representative method we chose was the best alternative approach in terms of DSC, which is widely regarded in the image processing community as an effective metric in evaluating 3D geometries. Note that, we used the same interpolation method, i.e., the LogOdds method, to reconstruct the 3D infarct geometry, regardless of the approach used to segment the infarct from the 2D images.

III. Results

A. Assessment of Infarct Segmentation Accuracies with Geometry-based Metrics

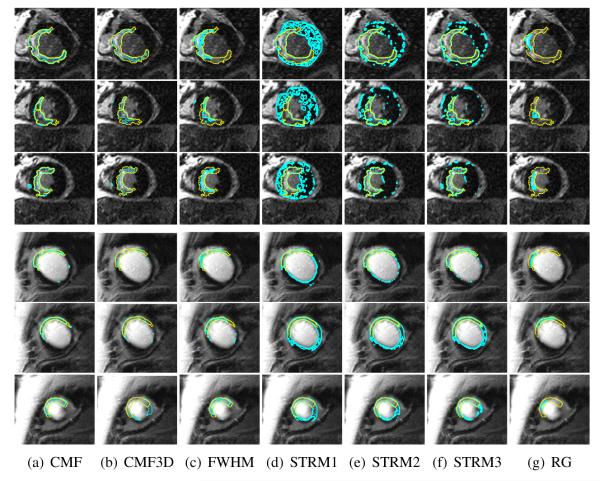
The optimal values of the parameters λ₁, λ₂, and λ₃ of the CMF method, obtained after the training, were 0.3, 0.1, and 10, respectively. For the CMF3D method, the optimal values of these parameters were 0.4, 0.3, and 5, respectively. The mean computation time for the execution of the CMF method was 0.8 ±0.3 s for a single slice, and 4.3±1.3 s for an LGE-CMR image. The CMF method converged within two iterations for a single slice. Results of the various infarct segmentation methods applied to an example LGE-CMR image are shown in Fig. 4. Qualitatively, between the various methods, infarct segmentations by the CMF method matched most closely with the manual delineations. Evidently, the segmentations by the CMF method had a substantially smaller number of isolated regions than those by the image intensity threshold-based techniques.

Fig. 4.

Exemplary results of the different infarct segmentation methods applied for two LGE-CMR images. Rows 1–3 correspond to the slices from the first image, rows 4–6 correspond to the slices from the second image, and columns correspond to the various methods. The expert manual delineation of the infarct in each of the slices is shown in yellow, and the contours computed by the different methods are displayed in cyan.

The summary of quantitative evaluation of the different infarct segmentation methods using 2D geometry-based metrics is shown in Table I. The CMF method outperformed all alternatives, in all accuracy metrics. In particular, mean DSC of the CMF method was significantly higher than those of alternatives. Among the existing methods, the STRM2 approach had the highest mean DSC. The summary of evaluation results for the core and border zones were reported separately in Table II. Between the infarct border zone and core, all the methods reported substantially higher accuracy in DSC for the latter. Compared to all the alternatives, the CMF method yielded significantly higher accuracy for the border zone. While the addition of connectivity filtering to the existing methods reduced the number of noise-induced false positive regions, and increased the DSC metrics of these methods by up to 2%, this improvement was not sufficient enough to make the threshold-based methods perform comparably to the CMF method.

TABLE I.

Summary of quantitative evaluation of accuracies of the various methods in segmenting the total LV infarct, using 2D geometry-based metrics. Significant differences between the DSC of CMF and those of other methods are indicated by asterisks.

Method	DSC (%)	RMSE (mm)	δA (%)
CMF	76.67±5.84	9.10±10.7	18.53±10.62
CMF3D	*73.21±10.04	11.07±8.77	33.45±29.23
FWHM	*63.57±10.38	13.6±14.4	43.41±24.14
STRM1	*65.63±10.04	18.03±12.05	61.7±54.00
STRM2	*67.40±12.64	14.3±14.6	34.92±34.92
STRM3	*65.88±15.61	13.64±13.7	25.32±24.04
RG	*43.92±14.23	11.88±19.6	97.217±119.8

TABLE II.

Summary of quantitative evaluation of the various methods for the infarct core and border zone segmentation using the DSC. Significant differences between the DSC of CMF and those of other methods are indicated by asterisks.

Method	Infarct Core DSC (%)	Border Zone DSC (%)
CMF	87.98±7.65	65.31±8.46
CMF3D	*85.92±10.51	*61.34±14.12
FWHM	88.13±8.54	*46.22±8.05
STRM1	87.60±8.61	*58.03±10.44
STRM2	*86.17±9.71	*58.64±12.8
STRM3	*83.99±11.95	*56.51±14.69
RG	*53.15±14.94	*14.96±13.68

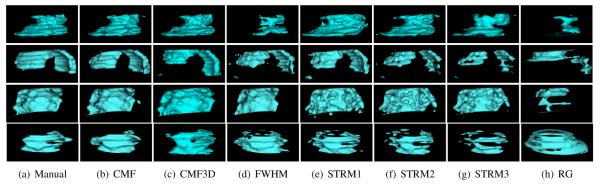
The surfaces of total infarct reconstructions generated from the segmentations of three example LGE-CMR images by the various methods are shown in Fig. 5. Qualitatively, between the various infarct segmentation methods, the reconstruction corresponding to the CMF method most closely resembled the one based on manual segmentation. Summary of the quantitative evaluation of the different infarct segmentation methods with metrics based on the 3D reconstructions is shown in Table III. Similarly to the results in Table I, the CMF method outperformed all alternatives, in all metrics. Particularly, the CMF method yielded significantly higher DSC, and significantly smaller volume errors than the existing techniques. On average, the CMF method underestimated the volume, as indicated by a δV_sgn of −8.5%. Note that, the ranking of different methods according to their DSC values was the same, regardless of whether the evaluation was done in 2D (Table I) or 3D (Table III).

Fig. 5.

Surfaces of total infarct reconstructions generated from the segmentations of four example LGE-CMR images using the various methods. Rows correspond to the images, and columns correspond to the various methods.

TABLE III.

Summary of quantitative evaluation of the various methods in segmenting the LV infarct, using 3D geometry-based metrics. Significant differences betweeen the DSC and δV of CMF and those of other methods are indicated by asterisks.

Method	DSC (%)	δV (%)	δVsgn (%)	RMSE (mm)	δSA (%)	Euler δχ
CMF	76.4±6.3	18.17±11.3	−8.5±20.4	2.22±2.55	17.1±11.8	6.2±4.8
CMF3D	72.7±11.3	22.31±18.4	2.5±43.7	3.76±3.10	25.6±29.3	8.3±10.5
FWHM	*62.6±12.1	*45.1±25.3	−31.6±41.1	3.10±2.96	33.3±24.8	13.3±11.8
STRM1	*67.1±9.75	*55.5±46.7	50.8±51.8	6.65±3.89	31.6±28.9	20.7±19.0
STRM2	*69.6±11.5	*30.8±26.3	14.5±38.06	5.21±3.44	33.1±27.3	15.7±13.6
STRM3	*68.9±15.1	*25.3±21.5	−8.8±32.2	4.09±3.03	36.5±29.7	16.1±13.1
RG	*45.8±15.4	*69.6±49.1	−37.7±76.8	6.22±3.58	51.3±23.9	7.2±6.1

B. Assessment of Infarct Segmentation Accuracy with Metrics based on Outcomes of Electrophysiological Simulations

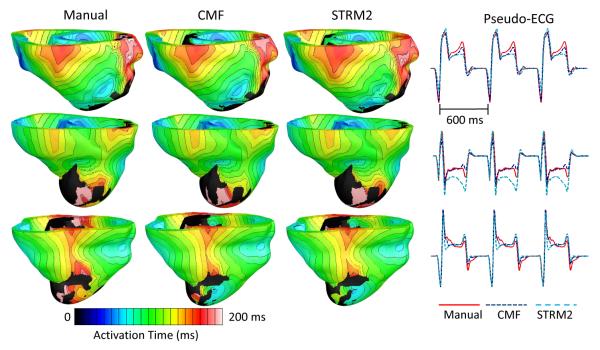
Since STRM2 was the existing method with the highest DSC, it was chosen as the representative alternative method for comparison with the CMF method in our electrophysiological simulation studies. The mean edge length of the finite element meshes generated for our ventricular models was 0.37 mm. Fig. 6 illustrates the activation maps, and corresponding pseudo-ECGs, from one beat of sinus rhythm simulated for three patient hearts. Visually, for a given patient heart, the activation maps simulated with models that incorporated infarct reconstructions built from manual and computed segmentations matched closely. However, between the pseudo-ECGs corresponding to the CMF and STRM2 methods, the former matched more closely with pseudo-ECGs corresponding to the manual segmentation. The summary of quantitative evaluation of the CMF and STRM2 methods based on outcomes of the sinus rhythm simulations are shown in Table IV. It was evident in the quantitative evaluation that, between the CMF and STRM2 methods, the outcomes of simulations corresponding to the former matched more closely with the ones corresponding to the manual segmentation.

Fig. 6.

Activation maps and pseudo-ECGs from one beat of sinus rhythm simulated for three patient hearts, with models that incorporated infarct reconstructions built from segmentations by different methods. The activation maps are displayed in anterior views of the ventricles.

TABLE IV.

Summary of quantitative evaluation of accuracies of the CMF and STRM2 infarct segmentation methods, based on outcomes of sinus rhythm simulations.

Method	RMSE (mV)	MAD (%)	CORR	ATD (ms)
CMF	0.031±0.027	14.3±7.3	0.95±0.06	3.95±2.35
STRM2	0.043±0.029	23.6±14.7	0.90±0.08	6.14±2.9

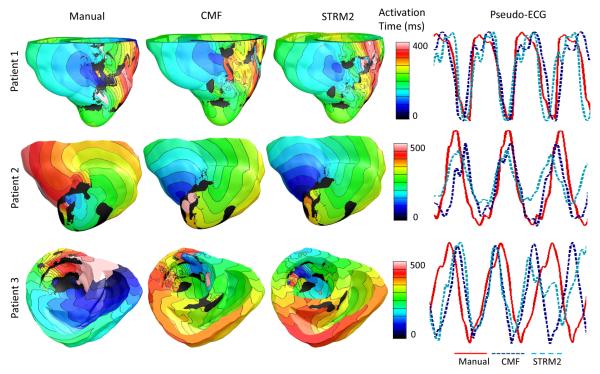
Table V presents the types of VTs initiated in our simulations of arrhythmia induction performed on all generated models. Between the CMF and STRM2 methods, the type of VT induced in models incorporating infarct segmentations with only the former perfectly matched those induced with models incorporating manual segmentations. Of the seven LGE-CMR images used in our simulation studies, VT was induced in models built from only three, for all three types of infarct segmentations. The infarct border zones delineated from these three images were larger than those from the rest, which is a major criterion for VT inducibility [45]. Thus, we were able to induce VT in the nine models regardless of the infarct segmentation method. Fig. 7 presents the simulated activation maps, and corresponding pseudo-ECGs, from one cycle of VTs simulated with models built from the three images. The activation maps of VT simulations matched closely across all three infarct segmentation methodologies in Patient 1. In VT simulations performed for Patient 2, between the activation maps corresponding to the STRM2 and manual segmentation methods, the activation map corresponding to the CMF method matched the former more closely. Although the direction of the simulated reentry circuit corresponding to the CMF method is opposite of that of the manual method in Patient 2, the simulations based on the CMF method will still be helpful in locating the organizing center of the reentrant circuit, for identifying target locations for catheter ablations in post-infarction patients, and stratifying the patient risk for ventricular arrhythmias post-infarct. For Patient 3, the VT simulated using the model incorporating segmentations by the STRM2 method was polymorphic, where the propagation pattern in the activation map shifted throughout the reentry period. In contrast, in simulations for Patient 3 with models incorporating CMF or manual segmentation, the VT was monomorphic. The pseudo-ECG corresponding to Patient 3 and STRM2 method illustrates that the morphology of the underlying VT was polymorphic, as listed in Table V. The RMSE, MAD, and CORR corresponding to the CMF method were 0.26 ± 0.11 mV, 33.1 ± 11.6%, and 0.69 ± 0.09, respectively. The values for the same metrics corresponding to the STRM2 were 0.36 ± 0.08 mV, 60.6 ± 8.6%, and 0.32 ± 0.24. Note that the differences in the RMSE, MAD, and CORR values between the CMF and STRM2 methods were 100 μV, 27.5%, and 0.37, respectively, in VT simulations. These differences were substantially larger than their corresponding values of 12 μV, 9.3%, and 0.05 in sinus rhythm simulations, underscoring the importance of employing accurate model reconstruction methodologies for individualized simulations of arrhythmia in patient hearts.

TABLE V.

Types of VTs initiated in our simulations of arrhythmia induction performed on all generated models. MVT, PVT, and _denote monomorphic VT, polymorphic VT, and no VT induced, respectively.

Patient #	Manual	CMF	STRM2
1	MVT	MVT	MVT
2	MVT	MVT	MVT
3	MVT	MVT	PVT
4	_	_	_
5	MVT	MVT	_
6	_	_	_
7	_	_	MVT

Fig. 7.

Activation maps and pseudo-ECGs from one beat of VTs simulated for three patient hearts, with models that incorporated infarct reconstructions built from segmentations by the different methods. The hearts are numbered the same way as they are in Table V. Activation maps are shown in anterior views of the ventricles for Patient 1 and 2, and in superior view of the ventricle for Patient 3. The VTs were monomorphic except for the one corresponding to Patient 3 and the STRM2 method.

IV. Discussion

The objective of this study was to develop and thoroughly evaluate a method for the segmentation of LV infarct from clinical LGE-CMR images, for patient-specific simulations of ventricular electrophysiology, and in particular, infarct-related VT. The CMF method we developed outperformed all alternative segmentation techniques, in terms of accuracy metrics based on geometry as well as outcomes of electrophysiological simulations. To our knowledge, this study is the first to evaluate the effect of inaccuracies in infarct segmentation on outcomes of simulations of cardiac function. Our study shows that inaccuracy in infarct segmentation affects the outcomes of VT simulations to a substantially higher degree than those of sinus rhythm simulations, and thereby underscores the significance of using accurate infarct segmentations in image-based simulations of infarct-related cardiac arrhythmia. The development of the CMF method, and its comprehensive evaluation constitute an important step in advancing clinical applications of image-based, patient-specific simulations of cardiac function. Additionally, the CMF algorithm is expected to improve automated, image-based measurements of infarct volume [35], surface area [2], spatial distribution [61], and transmurality [62], which have been shown to be predictive of clinical outcomes, including ventricular arrhythmia and sudden cardiac death.

To address the challenge of image intensity overlap between the infarct and the areas surrounding the myocardium, especially the blood pool, the CMF method, similarly to prior approaches, used a manual delineation of myocardial boundaries to define a region of interest [35], [15], [14]. However, unlike the existing infarct segmentation techniques implemented in this study, the CMF method performed the segmentation via an iterative minimization of an energy function, which comprised of an image gradient weighted-spatial regularization term, and a regional intensity histogram matching term. Due to the incorporation of this regularization term, infarct segmentation by the CMF method, in comparison with those by the existing approaches, were affected less by image noise, and resulted in fewer isolated regions.

Our methodology utilized intensity histogram matching based on the Bhattacharyya distance metric for contour evolution. Such an approach has been demonstrated to be robust by numerous previous studies. Freedman and Zhang [27] were the first to demonstrate that objects can be tracked in a level set framework using histogram matching with Bhattacharyya distance metric, and optimize the energy function using a first-order approximation. Although first-order approximations such as the one used in our study, do not guarantee convergence to global optimum, such approximations can yield accurate segmentations when a good initial solution is provided. More recently, several studies [63], [64] described histogram matching with Bhattacharyya metric for convex optimization. For instance, Punithakumar et al. [63] proposed a bound optimization scheme to optimize the highly nonlinear Bhattacharyya metric under a sequential convex/dual optimization perspective, which guarantees that the value of energy function monotonically decreases with each iteration. Within cardiac imaging, several recent studies have used a similar bound on the Bhattacharyya metric within a max-flow framework for automated segmentation [65], [66]. In particular, Nambakhsh et al. [65] described a method for LV segmentation from cardiac cine MR images based on a bound optimization scheme, which maximizes the Bhattacharyya distance metric between the estimated and model distributions of intensity and shape.

Preservation of the boundary between the border zone and the rest of the tissue is important for VT simulations. While some amount of detail in the border zone geometry will be lost due to the smoothing in the CMF method, our results demonstrated that the benefits of smoothing, e.g., minimizing the effects from noise, outweigh its limitations. Note that parts of the border zone boundary that coincide with the core zone boundary will not be affected by the smoothing in the CMF method. A potential alternative to our approach is to directly segment all three regions (i.e., normal myocardium, infarct core, and border zone) using a multi-region segmentation method based on energy minimization [24]. However, the drawback of multi-region segmentation methods is twofold: they may produce segmentations with artificial gaps between the core and border zone; and segmentation methods based on energy minimization suffer from shrinking bias, which may lead to shrinking of the relatively small border zone. In contrast with the multi-region segmentation methods, the developed two-step approach (i.e., binary segmentation based on energy minimization followed by thresholding) does not suffer from the above limitations, and is also simpler to implement. Out of the two implementations of the CMF method, the 2D approach outperformed the CMF3D. The decreased accuracy for the CMF3D method may be due to misalignment of slices during image acquisition, or artifacts introduced by the image interpolation method employed prior to 3D segmentation.

In our electrophysiological simulation studies, we observed that, irrespective of the infarct segmentation method, the same error in segmentation affected the outcomes of VT simulations to a substantially higher degree than those of sinus rhythm simulations. This was because, in VT, the morphology of the infarct zone largely determines the reentrant circuits that drive the pattern of wavefront propagation throughout the ventricles [45], [6]. Between the CMF and STRM2 methods, the outcomes of the simulations with models incorporating reconstructions built from infarct segmentations by the former were more similar to those with models generated using manual infarct segmentations. Thus, the inferior performance of the STRM2 approach compared to the CMF method in evaluations based on geometry translated into poorer performance of the former in evaluations based on simulations. Notably, between the CMF and STRM2 methods, the types of VTs induced with models built using infarct segmentations with only the former perfectly matched those induced with models generated using manual infarct segmentations. Since the STRM2 was the best among the existing methods in terms of DSC, we expect the CMF method to be more accurate in simulations than all the alternative methods used in our evaluation. All in all, our results indicate that the infarct segmentations by the CMF method, in comparison with those by the existing approaches, will be a better surrogate for manual infarct segmentations in the creation of patient specific models of ventricular electrophysiology that may be used to guide clinicians in therapeutic planning, and risk stratification [10], [6].

A limitation of our study is that the CMF methodology relied on manual delineation of myocardium to constrain the infarct segmentation. However, the amount of manual labor needed for the CMF method can be significantly decreased by utilizing myocardial boundaries segmented semi-automatically, either directly from the LGE-CMR images [16], [19] or from co-registered cinematic CMR images, as done previously [23], [20], [18]. As clinical LGE-CMR images are typically acquired with a large slice thickness, the data used in this study contain artifacts from partial volume averaging. As such, an improvement on the present study can be made in the future by utilizing data from high-resolution LGE-CMR methods [24].

V. Conclusion

We have developed a novel, semi-automated methodology for segmentation of LV infarct from clinical LGE-CMR images. The developed method has outperformed several alternative approaches in reproducing expert manual infarct segmentations, and in simulations of normal and abnormal ventricular electrophysiology. This study is the first that has evaluated a methodology for myocardial infarct segmentation based on outcomes of simulations of cardiac (dys)function, and constitutes an important step in advancing clinical applications of image-based, patient-specific simulations of ventricular electrophysiology.