Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jun 3;6:27134. doi: 10.1038/srep27134

Modeling adsorption with lattice Boltzmann equation

Long Guo 1, Lizhi Xiao 1,a, Xiaowen Shan 1,2, Xiaoling Zhang 3
PMCID: PMC4891696  PMID: 27256325

Abstract

The research of adsorption theory has recently gained renewed attention due to its critical relevance to a number of trending industrial applications, hydrogen storage and shale gas exploration for instance. The existing theoretical foundation, laid mostly in the early twentieth century, was largely based on simple heuristic molecular interaction models and static interaction potential which, although being insightful in illuminating the fundamental mechanisms, are insufficient for computations with realistic adsorbent structure and adsorbate hydrodynamics, both critical for real-life applications. Here we present and validate a novel lattice Boltzmann model incorporating both adsorbate-adsorbate and adsorbate-adsorbent interactions with hydrodynamics which, for the first time, allows adsorption to be computed with real-life details. Connection with the classic Ono-Kondo lattice theory is established and various adsorption isotherms, both within and beyond the IUPAC classification are observed as a pseudo-potential is varied. This new approach not only enables an important physical to be simulated for real-life applications, but also provides an enabling theoretical framework within which the fundamentals of adsorption can be studied.

Adsorption, and its counter process, desorption, are ubiquitous in nature and its understanding and modeling are crucial to many promising industrial applications ranging from the storage of gas fuel such as natural gas and hydrogen1 to the exploration of shale gases2. According to International Union of Pure and Applied Chemistry (IUPAC)3, the word adsorption describes “an increase in the concentration of a dissolved substance at the interface of a condensed and a liquid or gaseous phase due to the operation of surface forces”. In this process, a thin film of the dissolved substance, called adsorbate, forms on the surface of the condensed phase, called adsorbent, in contrary to the similar of absorption in which the adsorbate permeates into the bulk of the absorbent. It has been known for a long time that adsorption happens due to the interaction forces between the adsorbate and the adsorbent. According to the nature of the interaction force, adsorption is classified into physisorption (physical adsorption) where the binding force is the weak van der Waals force, and chemisorption when strong chemical bond between adsorbate and adsorbent forms. Here we restrict our attention to physisorption in this manuscript. Adsorption of methane is a key issues in shale gas development.

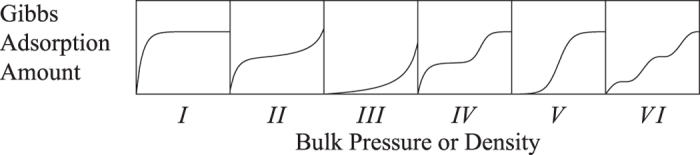
One of the main objectives in the study of adsorption is the prediction of the amount of substance that is adsorbed at an interface. Under the equilibrium condition, adsorption is usually characterized by the adsorption isotherm which is essentially the adsorbed amount as a function of the ambient pressure at the given temperature4. Due to the tremendous complexity associated with both the adsorbate and adsorbent, isotherms can vary greatly under different material and environmental conditions and the determination and analysis of them are mostly done experimentally with aid from theoretical models. Brunauer, Deming, Deming and Teller (BDDT)5 qualitatively summarized the experimental physisorption isotherms into five types which form the basis of the modern IUPAC classification6 shown in Fig. 1. Type I isotherm is typical of microporous (pore widths <2 nm per IUPAC definition7) adsorbent while isotherms of Types II and III are typical of macroporous (>50 nm) adsorbents with strong and weak adsorbate-adsorbent interactions respectively. Types IV and V occur for strong and weak interactions when the material is mesoporous (between 2 and 50 nm) and with capillary condensation. Type VI, added by IUPAC, has steps and occurs for some materials with strong interactions when the temperature is near the melting point for the adsorbed gas8,9.

Figure 1. The IUPAC recommended sub-critical adsorption isotherms classification.

Figure 1

Open in a new tab

Many empirical and semi-empirical adsorption theories have been developed, each based on its own assumptions and can interpret its own subset of the isotherms10. Among them, the most widely used ones are the Langmuir equation11 derived from kinetic studies based on a mono-layer adsorption model, and the Brunauer, Emmett and Teller (BET) equation12 which extends Langmuir’s theory to multi-layer adsorption. The Langmuir theory can interpret the Type I isotherm while Types II and III can be accounted for by the original BET theory and Types IV and V by its generalized version5.

Polanyi13 assumed that the adsorption of gases on solids is due to an attraction that derives from a potential which is uniquely determined by the spatial position of the gas molecule and therefore independent of the presence of any other molecules in the field of the adsorption potential. In another word, The molecular acceleration process has nothing to do with the environment except the spatial position. It is also assumed that the gas behaves in accordance with its normal equation of state in adsorbed phase. Dubinin assumed that the adsorption force field is independent from temperature14.

Results

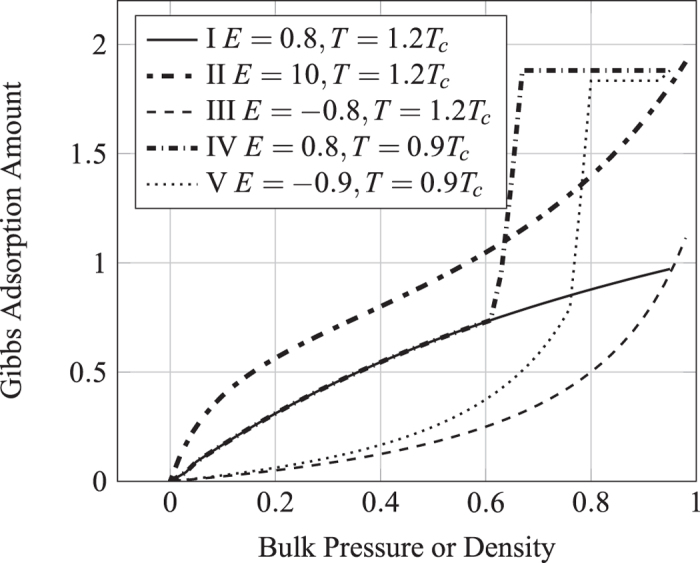
A lattice Boltzmann model for physisorption is presented. The adsorbate-adsorbent interaction is modeled via a pseudo-potential in a similar fashion to the non-ideal gas LBM model of Shan and Chen15. Various types of adsorption isotherms, both within and outside the IUPAC classification, are observed as the potential is adjusted. Quantitative correspondence with the classic Ono-Kondo theory of adsorption can also be established. When used as a boundary condition, this model compliments the existing LBM methodology and allows adsorption to be simulated together with the hydrodynamic flows of the adsorbate. The model directly associates the LB surface interaction with adsorption energy, and associate adsorption isotherms with Shan-Chen model, which can generate diffusion interface easily. The Shan-Chen model is a method which is very easy to achieve on programming, while introducing Shan-Chen model to adsorption simulation greatly reduces the difficulty of parameters selection for isotherms, as shown in Fig. 2. With this LB model, one just needs to know gas equation of state and the adsorption energy parameter E that can get the right type isotherms within the whole range.

Figure 2. The five adsorption isotherms reproduced by surface-force Shan-Chen model.

Figure 2

Open in a new tab

As in the present work, we only considered the adsorption of a adsorbate in a first lattice space. In reality, the situation is almost always affected by the fine structures of the adsorbent. Another important aspect that is not fully treated is the effect of the non-ideal gas. Here we only briefly showed that the adsorbate-adsorbate interaction can add greatly to the complicity of the macroscopic isotherms. It is worth pointing out that both of these additional physics can be handled within the LBM framework and we shall defer the treatments to future works.

Methods and Discussion

Based on thermodynamics and statistical physics, Ono and Kondo proposed a lattice theory to describe the surface tension and physical adsorption in pure liquids and solutions from the molecular standpoint16,17. Following Aranovich and Donahue18,19,20, gas molecules are envisioned to reside on a semi-infinite row of sites labeled starting from a solid wall by i = 1, ···, ∞. Let xi be the occupation fraction at site i which, at the macroscopic level, is the density measured with respect to a maximum density ρmax, e.g., xi ≡ ρi/ρmax. The molecules interact with those on the nearest-neighboring sites by the interaction energy, ε, and with the solid wall by the interaction energy, εs. The Ono-Kondo difference equation relates the occupation fraction at different layers by:

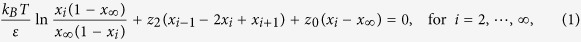graphic file with name srep27134-m1.jpg

which at i = 1 takes the following special form:

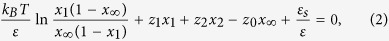graphic file with name srep27134-m2.jpg

where kB is the Boltzmann constant, T the temperature, z0 and z1 the volume and mono-layer coordination numbers respectively, and z2 ≡ (z0 − z1)/2. It is apparent that for a given bulk density, x∞, the density profile is solely determined by the interplay of the interaction energies of ε and εs, both with respect to the thermal energy of the gas particles. Analytical and numerical studies20,21 of Eqs (1) and (2) indicate that the Ono-Kondo model is able to predict all known types of adsorption behavior9. Particularly, at the low-density limit of xi → 0, Eq. (2) yields:

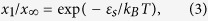graphic file with name srep27134-m3.jpg

which is Henry’s law as when the density profile drops rapidly to x∞ away from the wall, the adsorbed amount is solely given by x1. Next, without the low-density assumption, if the adsorbate-adsorbate interaction can be ignored, i.e., ε → 0, Eq. (2) gives:

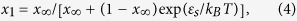graphic file with name srep27134-m4.jpg

which is the Langmuir isotherm22.

While owning its origin to the Lattice Gas Cellular Automaton (LGA) model for fluid mechanics simulation, the Lattice Boltzmann Equation (LBE) can be formulated as a special velocity-space discretization of the continuum Boltzmann equation (c.f., e.g. refs 23, 24, 25, 26). Since the early days of LGA, several attempts were made to include inter-particle interactions in the microscopic dynamics in order to simulate the complex behavior of multiphase flows. A number of schemes were afterwards suggested to incorporate the inter-particle interaction in the framework of LBE at the kinetic level among which, the pseudo-potential theory15,27 models the van der Waals interaction by introducing a momentum transfer among the particles within an interaction range (nearest-neighbors in most cases) in response to a pseudo-potential defined as a function of the local density. The pseudo-potential encapsulates at the microscopic level the details of the interaction that are normally characterized by the pairwise potential in continuum, and at the macroscopic level can be tailored to model many of the effects of a non-ideal gas fluid. Although the pseudo-potential model was first introduced rather intuitively, later analyses linked it to the mean-field theory in continuum28,29,30 by carrying out the BBGKY calculation to the next order.

In this article, we argue that the rich phenomenon of adsorption can be uniformly captured in the pseudo-potential LBE model. By varying the form of the pseudo-potential, a variety of adsorption isotherms manifest in macroscopic numerical simulations. With a few carefully chosen parameters, the wide spectrum of experimentally observed types of isotherms can be numerically reproduced.

The LBE is a special velocity-space discretization of the following Boltzmann-BGK equation:

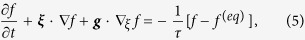graphic file with name srep27134-m5.jpg

where f = f(x, ξ, t) is the single-particle distribution function; x and ξ the coordinates in the configuration and velocity spaces respectively; g the acceleration of externally applied body force, including intermolecular interaction; ∇ξ the gradient operator in velocity space; and τ the relaxation time. On the right-hand-side is the BGK collision model31 with f (eq) being the dimensionless Maxwell-Boltzmann distribution26:

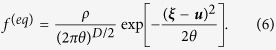graphic file with name srep27134-m6.jpg

Here, D is the spatial dimension; ρ, u, and θ are the thermo-hydrodynamic variables of density, velocity and temperature respectively, all dimensionless. It has been very well established that Eq. (5) describes the dynamics of a gas consisting of non-interacting particles so that at the various approximation levels, ρ, u, and θ satisfy the hydrodynamic equations such as the Euler and the Navier-Stokes equations32. In statistical mechanics, the Boltzmann equation is formally obtained as the lowest equation of the BBGKY hierarchy with inter-particle correlations completely ignored33. The kinetic effects of inter-particle interaction has to be modeled. In the pseudo-potential approach15, an interaction force between lattice sites x and x′ is defined as:

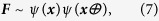graphic file with name srep27134-m7.jpg

where ψ(x) ≡ ψ(ρ(x)) plays the role of a potential which at the microscopic level dictates the details of the interaction, and at the macroscopic level result in a non-ideal-gas equation of state (EOS)15,27:

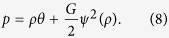graphic file with name srep27134-m8.jpg

By choosing a proper ψ, a wide variety of EOS’s, e.g., those of van der Waals, Carnahan-Starling, and Peng-Robinson, can be simulated34,35. The interaction force enters into the LBM dynamics by the following momentum increment at each time step and each site:

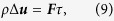graphic file with name srep27134-m9.jpg

and g ≡ F/ρ corresponds to the external acceleration in Eq. (5).

Interaction between the gas/liquid (adsorbate) and the solid (adsorbent) phases has been introduced into LBM by various authors36,37. Assuming the form of interaction by Eq. (7) still applies between a “fluid” site, x, and a boundary site, x′. The interaction force exerted on a fluid site in the vicinity of a boundary is proportional to ψ(ρ(x)). To account for the higher complicity in the gas-solid interaction, we allow the pseudo-potential to take a form different from that for the fluid sites, which we shall note by ψs.

We now investigate numerically the effects of such an interaction on the adsorption isotherms. We note that the amount of adsorption is customarily measured either by the absolute amount or the Gibbs excess amount38 which are defined respectively as:

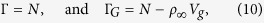graphic file with name srep27134-m10.jpg

where N is the total molar amount of gas, Vg the volume of the gas phase, and ρ∞ the number density of the bulk gas phase. Our simulation is carried out on a one-dimensional lattice as shown schematically in Fig. 3. The leftmost site, indexed 0, represents the solid wall where the interaction boundary condition is applied. All other sites i, 1 ≤ i ≤ K, are fluid sites with K being the index of the last site where we maintain the boundary condition:

Figure 3. Schematic plot of the one-dimensional lattice.

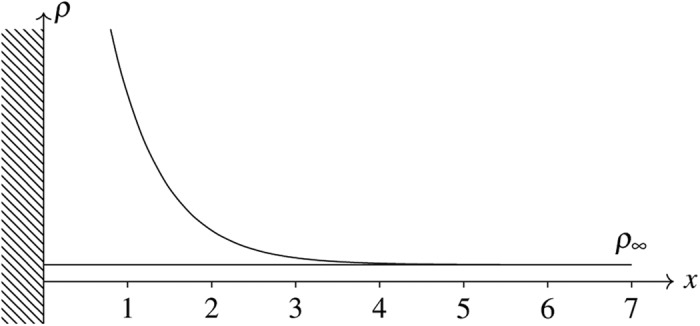
Figure 3

Open in a new tab

The area under the density profile is the absolute adsorption amount whereas that between the density profile and the ρ = ρ∞ line is the Gibbs amount.

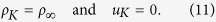graphic file with name srep27134-m11.jpg

The Gibbs adsorbed amount can be calculated as:

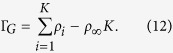graphic file with name srep27134-m12.jpg

Consider first the adsorption in the low-pressure (idea gas) limit in which the adsorbate-adsorbate interaction is absent. For wall-fluid interaction, the simplest model is to have an interaction force linearly proportional to the local density applied only to the first lattice site (nearest-neighbor interaction), i.e.:

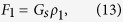graphic file with name srep27134-m13.jpg

where Gs is a constant interaction strength. Shown in Fig. 4 are the density profiles for a varying Gs with ρ∞ set at 0.01. To be seen is that only the density at the first lattice is affected. It can be further deduced that the shape of the profile is independent of ρ∞. By Eqs (9) and (13), Δu = Gsτ, and consequently the variation in the distribution function due to interaction, is independent of ρ1. The whole density profile therefore scales linearly with respect to ρ∞. In particular, the normalized quantity ρ1/ρ∞ is a function of Gs only but independent of ρ∞. We can therefore write:

Figure 4. Typical density profile with wall-fluid interaction only and the bulk density set at ρ∞ = 0.01.

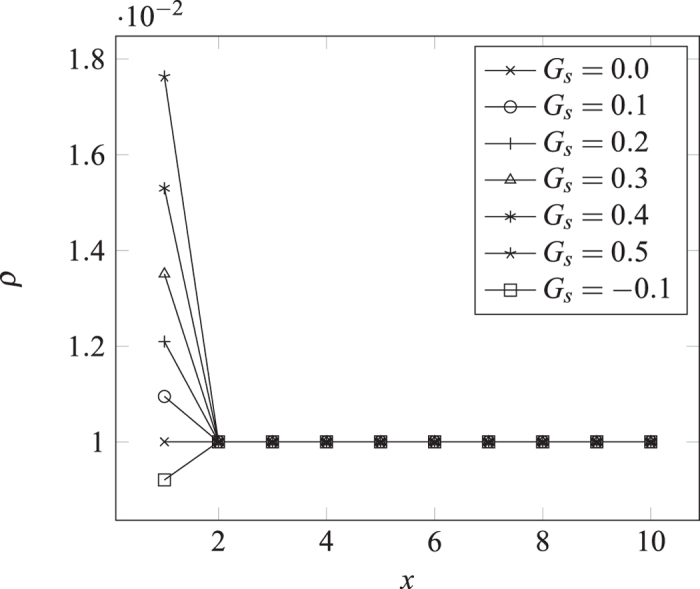
Figure 4

Open in a new tab

To be seen is that the effect of the fluid-wall interaction is confined to the very first lattice site.

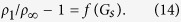graphic file with name srep27134-m14.jpg

Shown in Fig. 5 is the function f(Gs) obtained in numerical simulation with its independence on ρ∞ verified.

Figure 5. The normalized Gibbs amount vs. the interaction strength obtained by numerical simulation.

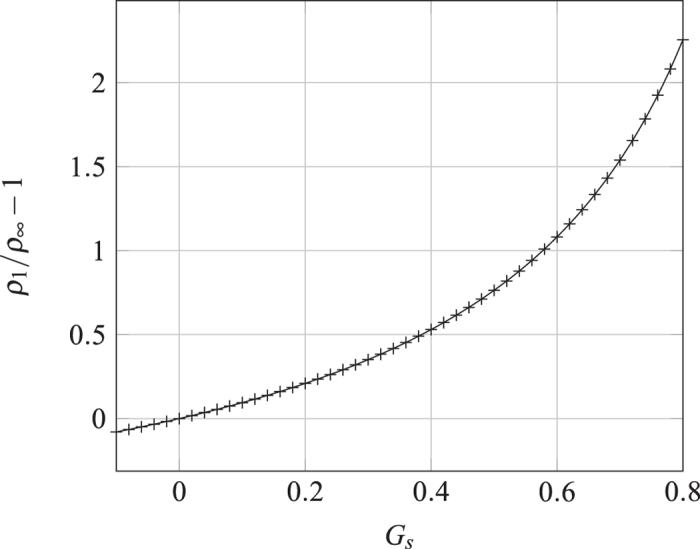
Figure 5

Open in a new tab

Note that the function form is independent of ρ∞.

A number of observations can be made. First, the left-hand-side of Eq. (14) is essentially the normalized Gibbs amount which should vanish in the absence of wall-fluid interaction. The numerical model correctly reproduces this feature. Second, ρ1 is linear in ρ∞, which is Henry’s law. Third, comparing Eq. (14) with Eq. (3), the following relation between the present LBM model and the Ono-Kondo lattice model can be identified:

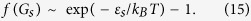graphic file with name srep27134-m15.jpg

Beyond the low-pressure limit, the more complex interaction is modeled via a pseudo-potential as in the bulk of the fluid15. To facilitate comparison with the Ono-Kondo theory, we rewrite Eq. (4) as:

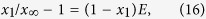graphic file with name srep27134-m16.jpg

where:

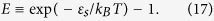graphic file with name srep27134-m17.jpg

Apparently Henry’s law (Equation (3)) is recovered as x1 → 0. Noticing f(Gs) ≅ Gs at small Gs, and comparing the equation above with Eq. (14), we let Gs ~ 1 − ρ1 and extend the linear force model of Eq. (13) by:

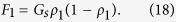graphic file with name srep27134-m18.jpg

Shown in Fig. 6 are the isotherms obtained from LBM simulation and Eq. (16). To be seen is that the LBM results agree well with the Ono-Kondo theory if the interaction is weak. The deviation at stronger interaction can be attribute to the approximation f(Gs) ≅ Gs. The discrepancy for E = −0.8 for high values of ρ∞ can be eliminated with simple approximate correction function. Depend on the signs of E or Gs, the isotherms exhibits the features of Types I and III respectively.

Figure 6. Comparison between the isotherms obtained in the LBM simulations with those predicted by the Ono-Kondo theory.

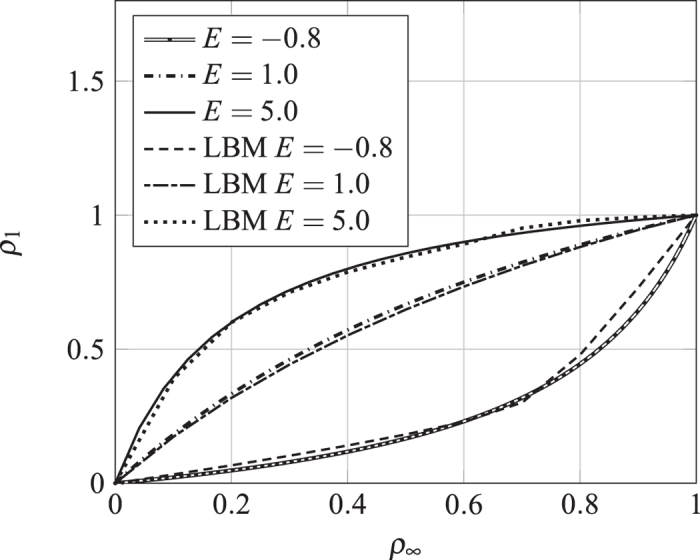
Figure 6

Open in a new tab

The lines are the solutions of Eq. (4) for different values of E.

Furthermore, isotherms with more interesting features can exhibit in the macroscopic level if more complicated pseudo-potential functions are used. Shown in Fig. 7 is a typical isotherm for the interaction:

Figure 7. Adsorption isotherm using the force model of Eq. (19).

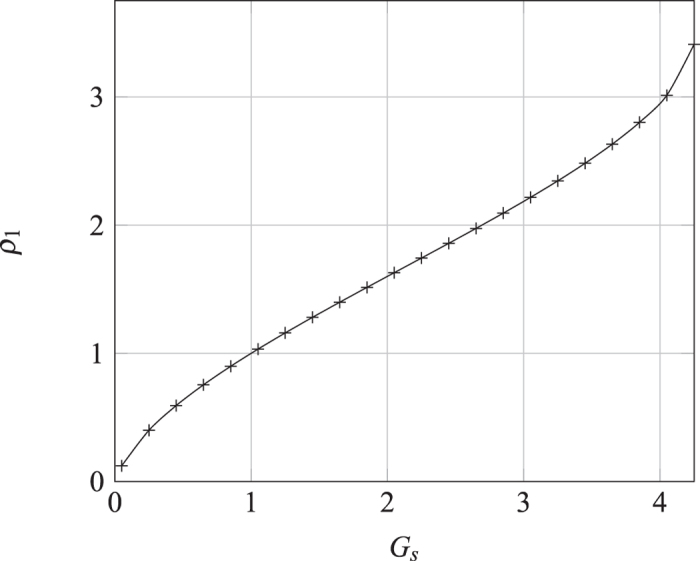
Figure 7

Open in a new tab

Certain features of Type II isotherms are exhibited.

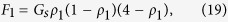graphic file with name srep27134-m19.jpg

which has the typical Type II features. Adsorbate-adsorbate interaction can be achieved by means of gas equation of state (EOS). The experimental data of diverse fluids analyses show near their critical point all fluids exhibit similar properties, so ratios of pressure, temperature and density of the absolute value and critical value can be used to export real gas equation of state. These ratios allow all parameters be dimensionless.

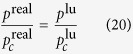graphic file with name srep27134-m20.jpg
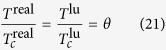graphic file with name srep27134-m21.jpg
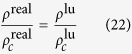graphic file with name srep27134-m22.jpg

For convenience, set lattice critical pressure 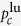Inline graphic, critical temperature 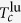Inline graphic and critical density 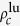Inline graphic to 1, thus, equation of state is presented by the potential function:

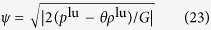graphic file with name srep27134-m26.jpg
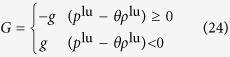graphic file with name srep27134-m27.jpg

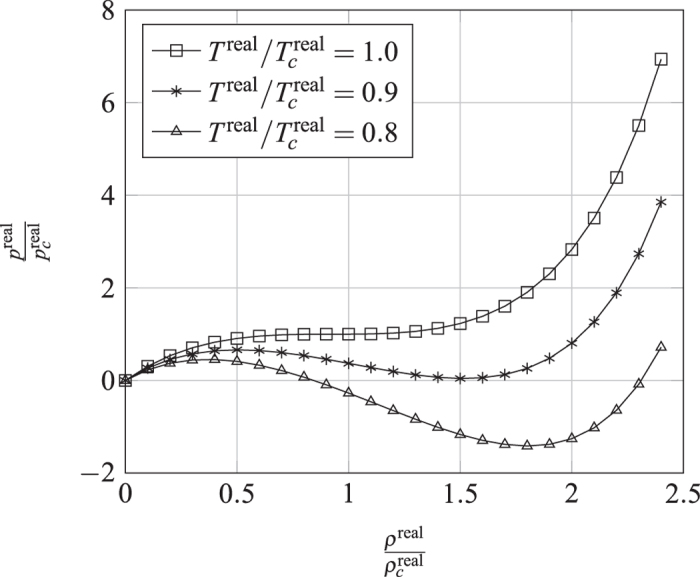
where g is a positive figure denoting the strength of the interaction force. Peng-Robinson39 (P-R) EOS is shown in Fig. 8:

Figure 8. P-R EOS system under the lattice units in Eq. (25).

Figure 8

Open in a new tab

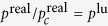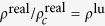Inline graphic, Inline graphic.

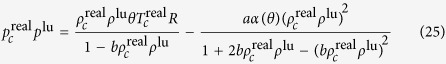graphic file with name srep27134-m28.jpg
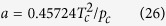graphic file with name srep27134-m29.jpg
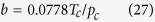graphic file with name srep27134-m30.jpg
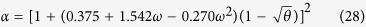graphic file with name srep27134-m31.jpg

where ω is the acentric factor of the species, for methane is 0.008. Insert Eqs (25, 26, 27, 28) in Eq. (23) to obtain ψ’s expression. Under the P-R EOS, the Eq. (18) still holds, and then it can simulate a non-ideal gas adsorption isotherm, as shown in Fig. 9.

Figure 9. The adsorption isotherm generated by P-R EOS in Fig. 8, E = 0.8.

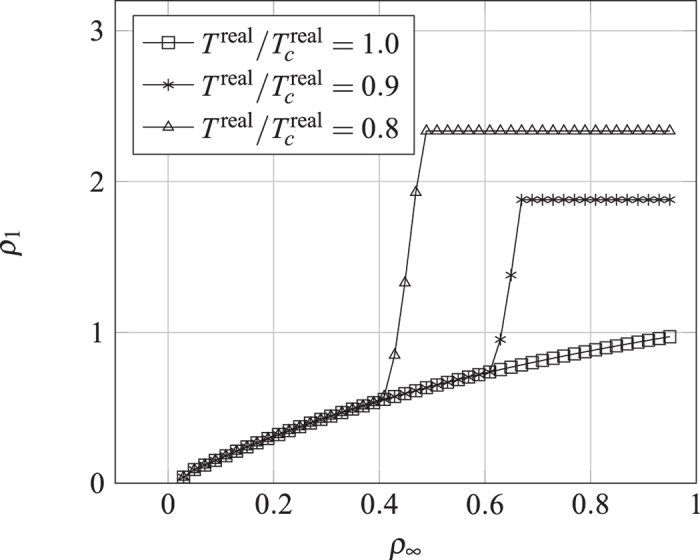
Figure 9

Open in a new tab

On the surface, if the temperature below the critical temperature, the condensation occurs, resulting in liquid film, E > 0 yield type IV isotherm, E < 0 yield type V isotherm, as shown in Fig. 9. When condensation does not occur, isotherm is mainly controled by Gs, but once condensation occurs, liquid film will soon occupy the entire surface, and the growth rate of adsorption amount in small pores reduce. Figure 9 can be seen as an adsorption isotherm in very close parallel plate, which can also be regarded as the micro pores. If the temperature is over the critical temperature, E > 0 yield type I isotherm, and E < 0 yield type III isotherm, and Eq. (19) yield type II isotherm. Since this model based on pseudo-potential, it is easy to be extended to three-dimensional. We use D3Q19 to achieve three-dimensional adsorption simulation, as shown in Fig. 10. Here a standard bounce back no-slip boundary condition is used to ensure conservation of mass. The adsorption is currently addressed in LBM as mass transfer process without directly linking to isotherms40,41, while our model can be used to reproduce five types of isotherms and gives the relationship between them and the adsorption energy. In addition, we also noted the new progresses on the EOS and interaction of fluid-solid interfaces42,43,44,45.

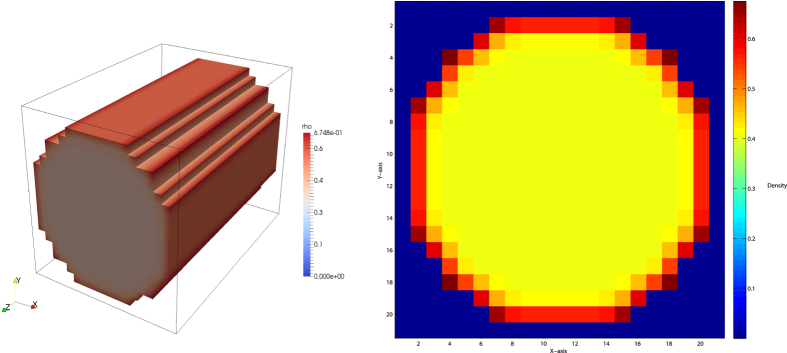
Figure 10. The adsorption density distribution on three-dimensional D3Q19 lattices tube with a size of 21 × 21 × 30.

Figure 10

Open in a new tab

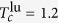Inline graphic, E = 1.0, Inline graphic.

Additional Information

How to cite this article: Guo, L. et al. Modeling adsorption with lattice Boltzmann equation. Sci. Rep. 6, 27134; doi: 10.1038/srep27134 (2016).

Acknowledgments

The authors thank financial supports from the National Natural Science Foundation of China (Grant Nos 41074102, 41130417), National Science and Technology Major Project (2011ZX05020-001) and “111 Program” (B13010), and Qunjie Du, Chuanhang He, Mingzhi Tian, Jie Wang for assistance.

Footnotes

Author Contributions L.X. and X.S. initialized the study and provided advice to L.G., L.X., L.G. and X.S. developed the numerical model. X.Z. provided the shale sample, digital core, adsorption experimental data. All authors contributed to the writing of the manuscript.

References

  1. Dillon A. C. et al. Storage of hydrogen in single-walled carbon nanotubes. Nature. 386, 377–379 (1997). [Google Scholar]
  2. Jarvie D. M., Hill R. J., Ruble T. E. & Pollastro R. M. Unconventional shale-gas systems: The Mississippian Barnett Shale of north-central texas as one model for thermogenic shale-gas assessment. Am. Assoc. Pet. Geol. Bull. 91, 475 (2007). [Google Scholar]
  3. Jenkins A. & McNaught A. Compendium of Chemical Terminology. (Blackwell Scientific Publications, Oxford, 1997), 2nd edn. [Google Scholar]
  4. Erbil H. Y. Surface Chemistry of Solid and Liquid Interfaces. (Blackwell Publications, 2006). [Google Scholar]
  5. Brunauer S., Deming L. S., Deming W. E. & Teller E. On a theory of the Van der Waals adsorption of gases. J. Am. Chem. Soc. 62, 1723 (1940). [Google Scholar]
  6. Sing K. et al. Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (recommendations 1984). Pure Appl. Chem. 57, 603 (1985). [Google Scholar]
  7. Everett D. H. Manual of symbols and terminology for physicochemical quantities and units, Appendix II: Definitions, terminology and symbols in colloid and surface chemistry. Pure Appl. Chem. 31, 577 (1972). [Google Scholar]
  8. Balbuena P. B. & Gubbins K. E. Theoretical interpretation of adsorption behavior of simple fluids in slit pores. Langmuir. 9, 1801 (1993). [Google Scholar]
  9. Donohue M. D. & Aranovich G. L. Classification of gibbs adsorption isotherms. Adv. Colloid Interface Sci. 76–77, 137 (1998). [Google Scholar]
  10. Dbrowski A. Adsorption - from theory to practice. Adv. Colloid Interface Sci. 93, 135 (2001). [DOI] [PubMed] [Google Scholar]
  11. Langmuir I. The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 38, 2221 (1916). [Google Scholar]
  12. Brunauer S., Emmett P. H. & Teller E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 60, 309 (1938). [Google Scholar]
  13. Polanyi M. The potential theory of adsorption. Science 141, 1010 (1963). [DOI] [PubMed] [Google Scholar]
  14. Dubinin M. M. The potential theory of adsorption of gases and vapors for adsorbents with energetically nonuniform surfaces. Chem. Rev. 60, 235 (1960). [Google Scholar]
  15. Shan X. & Chen H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E. 47, 1815 (1993). [DOI] [PubMed] [Google Scholar]
  16. Ono S. & Kondo S. Molecular theory of surface tension in liquids. In: structure of liquids, Encyclopedia of Physics 3/10, 134–280 (1960). [Google Scholar]
  17. Rowlinson J. S. & Widom B. Molecular Theory of Capillarity (Clarendon Press, 1982). [Google Scholar]
  18. Aranovich G. L. & Donohue M. D. Adsorption isotherms for microporous adsorbents. Carbon 33, 1369 (1995). [Google Scholar]
  19. Aranovich G. L. & Donohue M. D. Adsorption of supercritical fluids. J. Colloid Interface Sci. 180, 537 (1996). [DOI] [PubMed] [Google Scholar]
  20. Aranovich G. L. & Donohue M. D. Predictions of multilayer adsorption using lattice theory. J. Colloid Interface Sci. 189, 101 (1997). [Google Scholar]
  21. Bénard & Chahine R. Modeling of high-pressure adsorption isotherms above the critical temperature on microporous adsorbents: Application to methane. Langmuir. 13, 808 (1997). [Google Scholar]
  22. Langmuir I. The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 39, 1848 (1917). [Google Scholar]
  23. Benzi R., Succi S. & Vergassola M. The lattice Boltzmann equation: theory and applications. Phys. Rep. 222, 145 (1992). [Google Scholar]
  24. Chen S. & Doolen G. D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329 (1998). [Google Scholar]
  25. Shan X. & He X. Discretization of the velocity space in the solution of the Boltzmann equation. Phys. Rev. Lett. 80, 65 (1998). [Google Scholar]
  26. Shan X., Yuan X.-F. & Chen H. Kinetic theory representation of hydrodynamics: a way beyond the Navier-Stokes equation. J. Fluid Mech. 550, 413 (2006). [Google Scholar]
  27. Shan X. & Chen H. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys. Rev. E. 49, 2941 (1994). [DOI] [PubMed] [Google Scholar]
  28. He X., Shan X. & Doolen G. D. Discrete Boltzmann equation model for nonideal gases. Phys. Rev. E 57, 13 (1998). [Google Scholar]
  29. Martys N. S. Lattice Boltzmann simulation of two-dimensional wall bounded turbulent flow. Int. J. Mod. Phys. C. 12, 1169 (2001). [Google Scholar]
  30. He X. & Doolen G. D. Thermodynamic foundations of kinetic theory and lattice Boltzmann models for multiphase flows. J. Stat. Phys. 107, 309 (2002). [Google Scholar]
  31. Bhatnagar P., Gross E. P. & Krook M. A model for collision processes in gases. I. small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511 (1954). [Google Scholar]
  32. Chapman S. & Cowling T. G. The Mathematical Theory of Non-Uniform Gases (Cambridge University Press, : London, , 1970), 3ed ed. edn. [Google Scholar]
  33. Harris S. An Introduction to the theory of the Boltzmann equation (New York, 1971). [Google Scholar]
  34. Yuan P. & Schaefer L. Equations of state in a lattice Boltzmann model. Phys. Fluids 18, 042101 (2006). [Google Scholar]
  35. Kupershtokh A. L. A lattice Boltzmann equation method for real fluids with the equation of state known in tabular form only in regions of liquid and vapor phases. Comput. Math. 61, 3537 (2011). [Google Scholar]
  36. Martys N. S. & Chen H. Simulation of multicomponent fluids in complex three-dimensional geometries by the lattice Boltzmann method. Phys. Rev. E. 53, 743 (1996). [DOI] [PubMed] [Google Scholar]
  37. Briant A. J., Papatzacos P. & Yeomans J. M. Lattice Boltzmann simulations of contact line motion. I. liquid-gas systems. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 360, 485 (2002). [DOI] [PubMed] [Google Scholar]
  38. Myers A. L. & Monson P. A. Adsorption in porous materials at high pressure: Theory and experiment. Langmuir 18, 10261 (2002). [Google Scholar]
  39. Peng D. Y. & Robinson D. B. A new two-constant equation of state. Industrial and Engineering Chemistry: Fundamentals 15, 59–64 (1976). [Google Scholar]
  40. Levesque M., Duvail M., Pagonabarraga I., Frenkel D. & Rotenberg B. Accounting for adsorption and desorption in lattice Boltzmann simulations. Phy. Rev. E 88, 013308 (2013). [DOI] [PubMed] [Google Scholar]
  41. Zhou L., Qu Z. G., Chen L. & Tao W. Q. Lattice Boltzmann simulation of gas-olid adsorption processes at pore scale level. J. Comp. Phys. 300, 800–813 (2015). [Google Scholar]
  42. Zhang X. L., Xiao L. Z., Shan X. W. & Guo L. Lattice Boltzmann Simulation of Shale Gas Transport in Organic Nano-Pores. Sci. Rep. 4, 4843, doi:10.1038/srep04843 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Mazloomi M. Ali, Chikatamarla S. S. & Karlin I. V. Entropic lattice Boltzmann method for multiphase flows: Fluid-solid interfaces, Phys. Rev. E , 92, 023308 (2015). [DOI] [PubMed] [Google Scholar]
  44. Mazloomi M. A., Chikatamarla S. S. & Karlin I. V. Entropic Lattice Boltzmann Method for Multiphase Flows, Phys. Rev. Lett. 114, 174502 (2015). [DOI] [PubMed] [Google Scholar]
  45. Mazloomi M. A., Chikatamarla S. S. & Karlin I. V. Simulation of binary droplet collisions with the entropic lattice Boltzmann method, Phys. Fluids 28, 022106 (2016). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES