Cross-domain, soft-partition clustering with diversity measure and knowledge reference

Abstract

Conventional, soft-partition clustering approaches, such as fuzzy c-means (FCM), maximum entropy clustering (MEC) and fuzzy clustering by quadratic regularization (FC-QR), are usually incompetent in those situations where the data are quite insufficient or much polluted by underlying noise or outliers. In order to address this challenge, the quadratic weights and Gini-Simpson diversity based fuzzy clustering model (QWGSD-FC), is first proposed as a basis of our work. Based on QWGSD-FC and inspired by transfer learning, two types of cross-domain, soft-partition clustering frameworks and their corresponding algorithms, referred to as type-I/type-II knowledge-transfer-oriented c-means (TI-KT-CM and TII-KT-CM), are subsequently presented, respectively. The primary contributions of our work are four-fold: (1) The delicate QWGSD-FC model inherits the most merits of FCM, MEC and FC-QR. With the weight factors in the form of quadratic memberships, similar to FCM, it can more effectively calculate the total intra-cluster deviation than the linear form recruited in MEC and FC-QR. Meanwhile, via Gini-Simpson diversity index, like Shannon entropy in MEC, and equivalent to the quadratic regularization in FC-QR, QWGSD-FC is prone to achieving the unbiased probability assignments, (2) owing to the reference knowledge from the source domain, both TI-KT-CM and TII-KT-CM demonstrate high clustering effectiveness as well as strong parameter robustness in the target domain, (3) TI-KT-CM refers merely to the historical cluster centroids, whereas TII-KT-CM simultaneously uses the historical cluster centroids and their associated fuzzy memberships as the reference. This indicates that TII-KT-CM features more comprehensive knowledge learning capability than TI-KT-CM and TII-KT-CM consequently exhibits more perfect cross-domain clustering performance and (4) neither the historical cluster centroids nor the historical cluster centroid based fuzzy memberships involved in TI-KT-CM or TII-KT-CM can be inversely mapped into the raw data. This means that both TI-KT-CM and TII-KT-CM can work without disclosing the original data in the source domain, i.e. they are of good privacy protection for the source domain. In addition, the convergence analyses regarding both TI-KT-CM and TII-KT-CM are conducted in our research. The experimental studies thoroughly evaluated and demonstrated our contributions on both synthetic and real-life data scenarios.

1. Introduction

As we know well, partition clustering is one of the conventional clustering methods in pattern recognition which attempts to determine the optimal partition with minimum intra-cluster deviations as well as maximum inter-cluster separations according to the given cluster number and a distance measure criterion. The studies began with hard-partition clustering in this field, such as k-means [1-3] (also known as crisp c-means [3]), i.e., the ownership of one pattern to one cluster is definite, without any ambiguity. Then, benefiting from Zadeh’s fuzzy-set theory [4,5], soft-partition clustering [6-24,26-43] emerged, such as classic fuzzy c-means (FCM) [3,6], where the memberships regarding one data instance to all underlying clusters are in the form of uncertainties (generally measured by probabilities [6,17,18] or possibilities [7-9]), i.e. fuzzy memberships. So far soft-partition clustering has triggered extensive research and the representative work can be reviewed from the following four aspects: (1) FCM’s derivatives [6-14]. For improving the robustness against noise and outliers, two major families of derivatives of FCM, i.e., possibilistic c-means (PCM) [3,7-9] and evidential c-means (ECM) [10-13], were presented by relaxing the normalization constraint defined on the memberships of one pattern to all classes, and based on the concepts of possibilistic partition and credal partition, respectively. In addition, Pal and Sarkar [14] analyzed the conditions in which we can or should not use the kernel version of FCM; and the convergence analyses regarding FCM were studied in [15,16], (2) maximum entropy clustering (MEC) [3,17-23]. Karayiannis [17] and Li and Mukaidono [18] initially developed the MEC models by incorporating the Shannon entropy term into the total intra-cluster distortion measure. After that, Li and Mukaidono [19] further designed a complete Gaussian membership function for MEC; Wang et al. [20] incorporated the concepts of Vapnik’s ε-insensitive loss function as well as weight factor into the original MEC framework in order to improve the identification ability of outliers; Zhi et al. [21] presented a meaningful joint framework by combining the fuzzy linear discriminant analysis with the original MEC objective function; and the convergence of MEC was studied in [22,23], (3) hybrid rough-fuzzy clustering approaches [13,24-30]. Dubois and Prade [24] fundamentally addressed the rough-fuzzy and fuzzy-rough hybridization as early as 25 years ago. Then quite quantities of fuzzy and rough hybridization clustering approaches have been developed. For example, Mitra et al. [25] introduced a hybrid rough-fuzzy clustering algorithm with fuzzy lower approximations and fuzzy boundaries; Maji and Pal [26] varied Mitra’s et al. method [25] into the rough-fuzzy c-means with crisp lower approximations and fuzzy boundaries for heightening the impact of the lower approximation on clustering; Mitra et al. [27] suggested the shadowed c-means algorithm as an integration of fuzzy and rough clustering; and Zhou et al. [28] discussed shadowed sets in the characterization of rough-fuzzy clustering, (4) other fuzzy clustering models as well as applications. Aside from the above mentioned three aspects of literature, there exists a plenty of other work regarding soft-partition clustering. For example, Miyamoto and Umayahara [3,29] regarded FCM as a regularization of crisp c-means, and then via the quadratic regularization function of memberships they designed another regularization method named fuzzy clustering by quadratic regularization (FC-QR); Yu [30] devised the general c-means model by extending the definition of the mean from a statistical point of view; Gan and Wu [31] proposed a classic fuzzy subspace clustering model and further analyzed its convergence; Wang et al. [32] proposed another fuzzy subspace clustering method for handling high-dimensional, sparse data; and in addition, some application studies with respect to soft-partition clustering were also conducted, such as image compression [33,34], image segmentation [35-37], real-time target tracking [38,39], and gene expression data analysis [40].

As is well known, however, the effectiveness of usual soft-partition clustering methods in complex data situations still faces challenges. Specifically, their clustering performance depends to a great extent on the data quantity and quality in the target dataset. They can achieve desirable clustering performance only in relatively ideal situations where the data are comparatively sufficient and have not been distorted by lots of noise and outliers. Nevertheless, these conditions are usually difficult to be satisfied in reality. Particularly, new things frequently appear in modern high-technology society, e.g., load balancing in distributed systems [41] and attenuation correction in medical imaging [42], and it is difficult to accumulate abundant, reliable data in the beginning phase in these new applications. Therefore, this issue strictly restricts the practicability of partition clustering, in both cases of hard-partition and soft-partition. In our view, there exist two countermeasures to this challenge. That is, on one hand, we try our best to go on refining the self-formulations of partition clustering, like the trials from crisp c-means to FCM, PCM, MEC, and the others (e.g., [10,27,29]); on the other hand, the collaboration between partition clustering and fashionable techniques in pattern recognition should also be feasible, including semi-supervised learning [43-45], transfer learning [46-59], multi-task learning [60-62], multi-view learning [63,64], co-clustering [65-67], etc. Semi-supervised learning utilizes partial data labels or must-link/cannot-link constraints as the reference in order to improve the learning effectiveness on the target dataset. Transfer learning aims to enhance the processing performance on the target domain by migrating some auxiliary information from other correlative domains into the target domain. Multi-task learning concurrently performs multiple tasks with interactivities among them so that they can achieve better performance than that of each separate one. Multi-view learning regards as well as processing the data from multiple perspectives, and then eventually combines the result of each individual view according to a certain strategy. Co-clustering attempts to perform clustering on both the samples and the attributes of a dataset, i.e. it simultaneously processes the dataset from the perspectives of both row and column. As far as these techniques are concerned, however, we prefer transfer learning due to its specific mechanism. Transfer learning works in at least two, correlative data domains, i.e. one source domain and one target domain, and the case of more than one source domain is also allowed if necessary. Transfer learning first identifies useful information in the source domain, in the form of either raw data or knowledge, and then it handles the data in the target domain with such information acting as the reference and supplements. This usually enhances the learning quality of intelligent algorithms in the target domain. When current data are insufficient or impure (namely, polluted by noise or outliers), but some helpful information from other, related fields or previous studies is available, transfer learning is definitely the appropriate choice. Currently, many methodologies regarding transfer learning have also been deployed. For example, Pan and Yang [46] made an outstanding survey on transfer learning. The transfer learning based classification methods were investigated in [47-50], and the classification problem could currently be the most extensive research field on transfer learning. Several transfer regression models were proposed in [51-53]. Two dimension reduction approaches via transfer learning were presented in [54,55]. In addition, the trials connecting clustering problems with transfer learning were studied in [56-59], and several transfer clustering approaches were consequently put forward.

In this literature, we focus on the combination of the new soft-partition clustering model with transfer learning, due to the following two aspects of facts. First, conventional soft-partition clustering approaches, such as FCM and MEC, are prone to being confused by the apparent data distribution when the data in the target dataset are too sparse or distorted by noise or outliers. This usually causes their inefficient and even invalid results. Second, transfer learning offers us additional, supplemental information from other correlative domains in addition to these existing data in the target domain. With such auxiliary information acting as the reference, it is possible to approach the underlying, unknown data structure in the target domain. To this end, we conduct our work in two ways, i.e., refining the soft-partition clustering formulation as well as incorporating the transfer learning mechanism. In the first point, in light of the separate advantages in different, existing soft-partition models, e.g., FCM, MEC, and FC-QR, we first propose a new, concise, but meaningful fuzzy clustering model, referred to as quadratic weights and Gini-Simpson diversity based fuzzy clustering (QWGSD-FC), which aims at simultaneously inheriting the most merits of these existing methods. Then, based on this new model, by means of transfer learning, two types of cross-domain, soft-partition clustering frameworks and their corresponding algorithms, called Type-I/Type-II knowledge-transfer-oriented c-means (TI-KT-CM/TII-KT-CM), are separately developed. The primary contributions of our studies in this manuscript can be concluded as follows.

1. As a basis of our work, the delicate QWGSD-FC model concurrently has the advantages of FCM, MEC and FC-QR. That is, on one hand, similar to FCM, based on the weight factors in the form of quadratic, fuzzy memberships, this model can more effectively differentiate the individual influence of different patterns in the total intra-cluster deviation measure than that of the linear form adopted in MEC and FC-QR. On the other hand, in terms of the Gini-Simpson diversity measure, like Shannon entropy in MEC, and equivalent to the quadratic regularization function in FC-QR, QWGSD-FC is prone to attaining the unbiased probability assignments, based on the statistical maximum-entropy inference (MEI) principle [18,68].

2. Benefiting from the knowledge reference from the source domain, both TI-KT-CM and TII-KT-CM prove relatively high cross-domain clustering effectiveness as well as strong parameter robustness, which was demonstrated by comparing them with several state-of-the-art approaches on both artificial and real-life data scenarios.

3. Comparatively, TI-KT-CM only employs the historical cluster prototypes as the guidance, whereas TII-KT-CM refers simultaneously to the historical cluster prototypes and their associated fuzzy memberships. This indicates that TII-KT-CM features a more comprehensive knowledge learning capability than TI-KT-CM, and as a result, TII-KT-CM exhibits more excellent cross-domain, soft-partition clustering performance.

4. Either the historical cluster prototypes or the historical cluster prototype associated fuzzy memberships involved in TI-KT-CM or TII-KT-CM, belong to the advanced knowledge in transfer learning, and they cannot be mapped inversely into the raw data. This means that both TI-KT-CM and TII-KT-CM have the good capability of privacy protection for the data in the source domain.

The remainder of this manuscript is organized as follows. In Section 2, three, related, soft-partition clustering models (i.e., FCM, MEC and FC-QR) and the theory of transfer learning are briefly reviewed. In Section 3, the new QWGSD-FC model as well as the details of TI-KT-CM and TII-KT-CM are introduced step by step, such as the frameworks, the algorithm procedures, the convergence analyses and the parameter settings. In Section 4, the experimental studies and results are reported and discussed. In Section 5, the conclusions are presented.

2. Related work

2.1. FCM

Let X = {x_j ∣ x_j ∈ R^d, j = 1, …, N} denote a given dataset where x_j (j = 1, …, N) presents one data instance, and d and N are separately the data dimension and the data capacity. Suppose there exist C (1 < C < N) potential clusters in this dataset. The framework of FCM can be rewritten as

$$\begin{array}{l}\underset{\mathbf{V},\mathbf{U}}{\min }(J_{\mathit{FCM}}(\mathit{V},\mathit{U})=\sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^m{\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2),\\ \mathrm{s}.\mathrm{t}.0\le u_{ij}\le 1\mathrm{and}\sum _{i=1}^C{u}_{ij}=1,\end{array}$$ (1)

where V ∈ R^C×d denotes the cluster centroid matrix composed of the cluster centroids (also known as cluster prototypes), v_i ∈ R^d, i = 1, …, C; U ∈ R^C×N signifies the membership matrix and each entry u_ij denotes the fuzzy membership of data instance x_j to cluster centroid v_i; and m > 1 is a constant.

Using the Lagrange optimization, the update equations of cluster centroid v_i and membership u_ij in Eq. (1) can be separately derived as

$${\mathit{v}}_i=\frac{\sum _{j=1}^N{u}_{ij}^m{\mathit{x}}_j}{\sum _{j=1}^N{u}_{ij}^m},i=1,2,\dots ,C.$$ (2)

$$u_{ij}=\frac{1}{\sum _{k=1}^C{\left(\frac{\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }{\Vert {\mathit{x}}_j-{\mathit{v}}_k\Vert }\right)}^{\frac{2}{m-1}}},i=1,2,\dots ,C;j=1,2,\dots ,N.$$ (3)

2.2. Maximum entropy clustering (MEC)

In a broad sense, MEC refers to a category of clustering methods that contain a certain form of maximum entropy term in the objective functions. With the same notations as those in Eq. (1), the most classic MEC model [3,18] can be represented as

$$\begin{array}{l}\underset{\mathbf{V},\mathbf{U}}{\min }\left(J_{MEC}(\mathit{V},\mathit{U})=\sum _{i=1}^C\sum _{j=1}^N{u}_{ij}{\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2+\beta \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}\ln u_{ij}\right),\\ \mathrm{s}.\mathrm{t}.0\le u_{ij}\le 1\mathrm{and}\sum _{i=1}^C{u}_{ij}=1,\end{array}$$ (4)

where Σ_iju_ij ln u_ij is derived from Shannon entropy [17,18,69,70], $D{I}_s=-{\sum }_{i=1}^n{p}_i\ln p_i$, and β > 0 is the regularization coefficient.

Similarly, via the Lagrange optimization, the update equations of cluster centroid v_i and membership u_ij in Eq. (4) can be separately deduced as

$${\mathit{v}}_i=\frac{\sum _{j=1}^N{u}_{ij}{\mathit{x}}_j}{\sum _{j=1}^N{u}_{ij}},i=1,2,\dots ,C.$$ (5)

$$u_{ij}=\frac{\exp \left(\frac{{\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2}{\beta }\right)}{\sum _{k=1}^C\exp \left(\frac{{\Vert {\mathit{x}}_j-{\mathit{v}}_k\Vert }^2}{\beta }\right)},i=1,2,\dots ,C;j=1,2,\dots ,N.$$ (6)

2.3. Fuzzy clustering by quadratic regularization (FC-QR)

In [29], FCM was regarded as a regularization of crisp c-means via the fuzzy membership-based nonlinearity $u_{ij}^m$, and for presenting another regularization method, with MEC as the reference, in terms of the quadratic function ${\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^2$ as the new non-linearity, the FC-QR approach was proposed. With the same notations as those in Eq. (4), it can be reformulated as

$$\begin{array}{l}\underset{\mathbf{V},\mathbf{U}}{\min }\left(J_{QF-FC}(\mathit{V},\mathit{U})=\sum _{i=1}^C\sum _{j=1}^N{u}_{ij}{d}_{ij}+\frac{1}{2}\tau \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2\right),\\ \mathrm{s}.\mathrm{t}.0\le u_{ij}\le 1\mathrm{and}\sum _{i=1}^C{u}_{ij}=1,\end{array}$$ (7)

where d_ij = ∥x_j − v_i∥², and τ > 0 is the regularization parameter.

Based on the Lagrange optimization, it is easy to deduce that the update equation of cluster centroid v_i of FC-QR is the same as Eq. (5), whereas the derivation of fuzzy membership u_ij is a little complicated. Here we only quote the conclusions, and one can refer to [29] for the details. Let

$$J_{QF-FC}^{(k)}(\mathit{V},\mathit{U})=\sum _{i=1}^C{u}_{ik}{d}_{ik}+\frac{1}{2}\tau \sum _{i=1}^C{u}_{ik}^2,$$ (8)

i.e., $J_{QF-FC}^{(k)}$ in Eq. (8) is derived from J_{QF − FC} in Eq. (7) with a fixed x_k. Thus, $\min J_{QF-FC}=\min {\sum }_{k=1}^N{J}_{QF-FC}^{(k)}$ and each $J_{QF-FC}^{(k)}$ can independently be minimized from other $J_{QF-FC}^{(k^{\prime })}(k^{\prime }\ne k)$. Moreover let

$$f_{\ell }^L=\frac{1}{\tau }\left(\sum _{h=1}^L(d_{hk}-d_{\ell k})\right)+1,\ell \in [1,L].$$ (9)

Assume d_1k ≤ d_2k ≤ … ≤ d_Ck, then the solution of u_ik that minimizes $J_{QF-FC}^{(k)}$ is given by the following algorithm.

Algorithm for the optimal solution of u_ik in $J_{QF-FC}^{(k)}$

• Setp1Calculate $f_L^L$ for L = 1,…,C by Eq. (9). Let L̄ be the smallest number such that $f_{\overline{L}+1}^{\overline{L}+1}\le 0$.
• Step2For i = 1, …, L̄, put $u_{ik}=\frac{1}{\overline{L}}\left(\frac{1}{\tau }\sum _{\ell =1}^{\overline{L}}{d}_{\ell k}+1\right)-\frac{1}{\tau }{d}_{ik}$; and for i = L̄+1, …, C, put u_ik = 0.

2.4. Transfer learning

Transfer learning [46] works in at least two, correlative data domains, i.e. one source domain and one target domain, and sometimes there is more than one source domain in some complicated situations. Transfer learning usually aims to improve the learning performance of intelligent algorithms in the target domain, i.e. the target dataset, by means of the prior information obtained from the source domains. The overall modality of transfer learning is indicated in Fig. 1. As shown in Fig. 1, there are two possible types of prior information existing in transfer learning, i.e. raw data as well as knowledge.

Fig. 1.

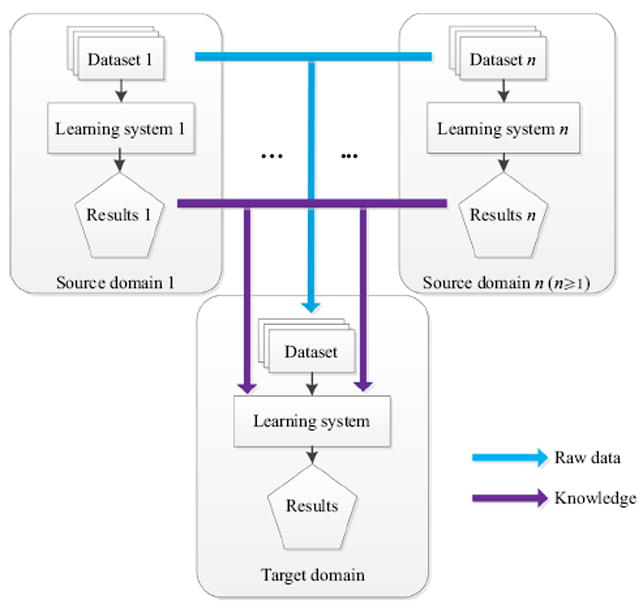
Overall framework of transfer learning.

Raw data in the source domain are the least sophisticated form of prior information. It may be the most common form to sample the source domain datasets in order to acquire lots of representatives and their labels. In contrast, knowledge in the source domains is one type of advanced information. The original data are not always available in the source domains; we sometimes need to draw knowledge from them. For example, for the purpose of privacy protection, some raw data might not be opened but the knowledge from the source domains without confidential information could be accessed. Other reasons also could cause the raw data not to be used directly even if they can be opened. For instance, if there are some potential drifts between the source and the target domain, an unexpected, negative influence may occur in the target domain if some improper data are adopted from the source domains. This is the so-called phenomenon of negative transfer. In order to avoid this underlying risk, it is a good choice to identify useful knowledge from the source domains rather than directly use raw data, e.g. the cluster prototypes in the source domain can be regarded as the good reference in the target domain.

3. Cross-domain soft-partition clustering based on Gini–Simpson diversity measure and knowledge transfer

Let us first recall and summarize some essences with respect to the relevant, soft-partition clustering models introduced in the previous section, i.e. FCM, MEC and FC-QR, before we introduce our own work.

1. As is evident, in FCM, the nonlinearity $u_{\mathit{ij}}^m$ consisting of fuzzy membership u_ij and the fuzzifier m is used to regularize crisp c-means, and the desirable, nontrivial fuzzy solution is achieved accordingly. However, it can also be expounded from the other perspective, i.e., it is equivalent to a weight factor for determining the individual influence of each d_ij = ∥x_j − v_i∥² to the total deviation measure ${\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^m{d}_{ij}$, in which d_ij evaluates the distortion of sample x_j (j = 1,…,N) to cluster prototype v_i (i = 1,…,C). Obviously, the larger the value of u_ij is, the more significantly d_ij impacts.

2. As uncovered in [3], both MEC and FC-QR were devised as other types of regularization methods of crisp c-means, and their formulations can be generalized as $J_r(\mathbf{V},\mathbf{U})={\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}{d}_{ij}+\beta k(\mathbf{U})$, in which k(U) signifies one nonlinear regularization function with respect to fuzzy memberships and β > 0 is a regularization parameter. In MEC, $k(\mathbf{U})={\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}\ln u_{ij}$ ln u_ij is derived from Shannon entropy, whereas in FC-QR, k(U) is instanced as the quadratic function ${\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^2$.

3. As we know, in FCM, the fuzzifier (i.e., constant power) m must be greater than 1, and it is set to 2 by default in most cases.

4. Differing from that in FCM, the weight of each d_ij = ∥x_j − v_i∥² is u_ij rather than $u_{ij}^m$ (m > 1) in both MEC and FC-QR, as shown in Eqs. (4) or (7).

We next present three aspects of our understanding regarding soft-partition clustering based on the above summaries.

1. As intuitively illustrated in Fig. 2, the common deviation measure in soft-partition clustering, $J={\sum }_{i=1}^C{\sum }_{j=1}^N{w}_{\mathit{ij}}{d}_{\mathit{ij}}={\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{\mathit{ij}}^m{\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2$ (m ≥ 1), is explicitly in the form of weighted sum, which measures the total distortion among all data instances and all cluster prototypes (i.e., cluster centroids). In this regard, we prefer the weighted modality enlisted in FCM (i.e., m > 1) rather than that in MEC and FC-QR (i.e., m = 1), as we consider that, comparatively, $w_{ij}=u_{ij}^m$ (m > 1) can more effectively distinguish the individual influence of each d_ij = ∥x_j − v_i∥² in J. Specifically, as is evident, in the membership matrix U, the greater the value of entry u_ij is, the higher the probability of x_j belonging to cluster i will be. That is, larger values of u_ij much convince us that individual x_j is a member of cluster i, thus their corresponding impacts of deviation measure in $J_i={{\sum }_{j=1}^N{w}_{ij}{d}_{ij}={\sum }_{j=1}^N{u}_{ij}^m\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2$ should be ensured. In contrast, the influences of much smaller values of u_ij should certainly be restricted and even neglected. This idea is a little similar to that in the shadowed c-means [27], in which the importance of different objects is differentiated by the regions, i. e., the members in the core of a shadowed set are weighted by 1, the objects in the shadowed region by $u_{ij}^m$, and the objects in the exclusion zones by $u_{ij}^{m^m}$ (i.e., double-powered by the fuzzifier parameter). To this end, we need a manner which can effectively convey the individual importance of each $w_{ij}{d}_{ij}=u_{ij}^m{\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2$. In the sense of power functions, w = u^m (m > 1), as indicated in Fig. 3 where m = 2 is taken as an example, compared with the linear one, w = u, in theory, the former is able to more reliably insure the impacts of larger values of u (e.g., u₂ in Fig. 3) as well as suppress those of much smaller ones (e.g., u₁ in Fig. 3).

2. It is clear that the second term, ${\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}\ln u_{ij}$, in MEC is derived from Shannon entropy, also termed as Shannon diversity index [70], $D{I}_S=-{\sum }_{i=1}^n{p}_i$ ln p_i. However, in our view, the quadratic regularization function, ${\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^2$, recruited in FC-QR can be regardedas another diversity index [69-72]: i.e., Gini–Simpson diversityindex [69-71]: $D{I}_{GS}=1-{\sum }_{i=1}^n{p}_i^2$. Under this consideration, in terms of the information theory, we can assign this term another more meaningful connotation, which is just explained in the following.

3. It is evident that the fuzzy clustering process conducted on a dataset can be regarded as probability assignment operations, i.e., determining the probability of each pattern x_j belonging to each cluster prototype v_i according to a quantity of accessible information, e.g., the mutual distances among all patterns. In the sense of information theory, the incorporation of the diversity index in the framework of fuzzy clustering, such as Shannon entropy or Gini–Simpson index, is to avoid bias while agreeing with whatever information is given, based on the statistical MEI principle [18,68]. As discussed in [68], as far as we know, this could be the only unbiased probability assignment mechanism that we can use, as the usage of any other would amount to arbitrary assumption of information which is sometimes hard to be validated in reality.

Fig. 2.

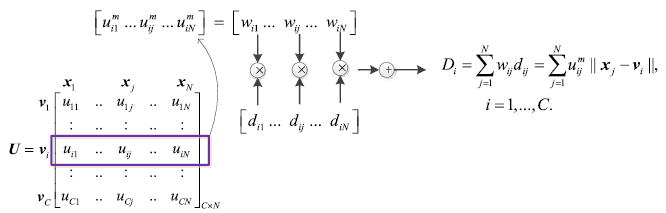
Interpretation of the deviation measure in soft-partition clustering from the perspective of weighted sum.

Fig. 3.

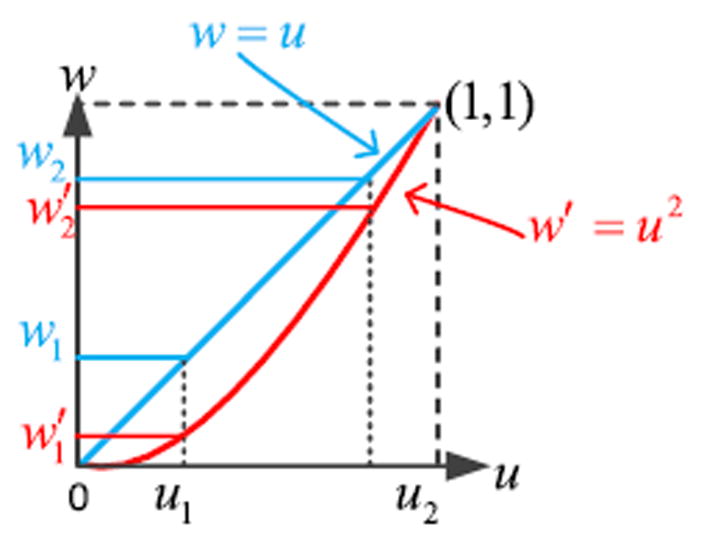
Impact distinction between m = 1 and m = 2 while u^m is used as the weight factor in deviation measure.

Based on the above understanding, we now first present a novel, delicate soft-partition clustering model as follows.

3.1. Soft-partition clustering based on quadratic weights and Gini–Simpson diversity

Definition 1

Using the same notations as those in Eqs. (1) and (4), the quadratic weights and Gini–Simpson diversity based fuzzy clustering model (QWGSD-FC) is defined as

$$\begin{array}{l}\underset{\mathbf{V},\mathbf{U}}{\min }\left(\Psi (\mathit{V},\mathit{U})=\sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2{\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2+\beta \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2\right),\\ \mathrm{s}.\mathrm{t}.0\le u_{ij}\le 1\mathrm{and}\sum _{i=1}^C{u}_{ij}=1.\end{array}$$ (10)

Using the Lagrange optimization, it is easy to prove that the update equations of cluster centroid v_i and membership μ_ij of QWGSD-FC can be straightforwardly derived as

$${\mathit{v}}_i=\frac{\sum _{j=1}^N{u}_{ij}^2{\mathit{x}}_j}{\sum _{j=1}^N{u}_{ij}^2},$$ (11)

$$u_{ij}=\frac{1}{(2{\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2+2\beta )\sum _{k=1}^C\frac{1}{2{\Vert x_j-v_k\Vert }^2+2\beta }}.$$ (12)

The motivation of the design of QWGSD-FC in this literature is to first figure out a concise but meaningful soft-partition clustering model that integrates the most merits of FCM, MEC and FC-QR, and then use it as a foundation to further propose our eventual, knowledge-transfer-oriented, soft-partition clustering methods below. For this purpose, QWGSD-FC is composed of two significant terms as usual. The first term, ${{\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^2\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2$, measures the total deviation of all data instances x_j, j =1,…,N, to all cluster prototypes v_i, i=1,…,C, with $u_{ij}^2$ being the weight factors. The second one, $\beta {\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^2$, derived from Gini–Simpson index, and equivalent to the quadratic function in FC-QR, pursues achieving unbiased probability assignments during the clustering process, based on the statistical MEI principle.

As for the quadratic weight $u_{ij}^2$ recruited in QWGSD-FC for the total intra-cluster deviation measure, this devisal arises from the following three aspects. First, as previously interpreted, we favor adopting $u_{ij}^m$ (m > 1) as the weight factor for the intra-cluster deviation measure, and as illustrated in Fig. 3, m = 2 meets our requirement that it is able to effectively convey the desired, individual impact regarding every d_ij = ∥x_j − v_i∥² in the total deviation measure. Second, compared with the combination of “linear weights+quadratic regularization function (equivalently, Gini–Simpson index)” in FC-QR, the pair of “quadratic weights+Gini–Simpson diversity” in QWGSD-FC appears more tractable, which can be demonstrated by the separate derivations of the update formulas of u_ij and v_i in FC-QR and QWGSD-FC. As uncovered in [3], the derivation process of FC-QR looks a little sophisticated, whereas via the ordinary Lagrange optimization, the update equations in QWGSD-FC are easily achieved. Last and most important, the practical performance of this model against the existing ones, e.g., FCM, MEC, and FC-QR, had been extensively, empirically validated before it was shaped in our research, which will be shown in detail in the experimental section.

It is still worth discussing the reason why we did not directly incorporate the Gini–Simpson diversity term into the framework of FCM, i.e., the formulation of ${\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^m{\Vert x_j-v_i\Vert }^2+\beta {\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^2$, m > 1. This formulation looks stronger than that of QWGSD-FC from the point of view of generalization. Nevertheless, it is easy to deduce that, in this way, the desirable, straightforward, analytical solutions of the cluster centroid and the fuzzy membership, like Eqs. (11) and (12), cannot be conveniently achieved in this case, and we could need other pathways to figure out the solutions of this issue, e.g., the gradient descent method [53]. This may bring us a distinct computing burden, which definitely, conversely weakens the practicability of this method.

Due to the above reasons, the form of “quadratic weights+Gini–Simpson diversity” in Eq. (10) is enlisted in our QWGSD-FC model, which can be regarded as a new improvement against these existing, classic, soft-partition clustering models.

3.2. Two types of cross-domain, soft-partition clustering frameworks via transfer learning

In order to improve the realistic performance of intelligent algorithms on the target dataset, i.e., the target domain, from the viewpoint of transfer learning, the prior knowledge from other correlative datasets, i.e., the source domains, is the reliable, beneficial supplement for these existing data. Based on such comprehension, we now present two types of cross-domain, soft-partition clustering strategies via the new QWGSD-FC model defined in Eq. (10). To facilitate interpreting and understanding, we suppose only one source domain and one target domain are involved throughout our research.

3.2.1. Type-I soft-partition transfer optimization formulation and corresponding knowledge-transfer-oriented c-means clustering framework

Definition 2

Let v̂(i = 1,…, C) denote the known cluster centroids in the source domain and other notations be the same as those in Eq. (10), then the type-I soft-partition transfer optimization formulation can be defined as

$$\underset{\mathbf{V},\mathbf{U}}{\min }\left({\Theta }_{T1}(\mathit{V},\mathit{U})=\gamma \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2{\Vert {\widehat{\mathit{v}}}_i-{\mathit{v}}_i\Vert }^2\right),$$ (13)

where γ ≥ 0 is the regularization coefficient.

Eq. (13) defines a transfer learning strategy in terms of the known cluster centroids v̂_i, i = 1, …, C, in the source domain. In our view, the cluster centroids, i.e. cluster prototypes, belong to a category of more reliable, prior information compared with a quantity of raw data drawn from the source domain. Because the raw data may contain certain uncertainties, e.g., data shortage, noise and outliers, whereas the cluster centroids are usually achieved by a certain, relatively precise procedure, which consequently insures their reliability. In Eq. (13), ${\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^2{\Vert {\widehat{\mathit{v}}}_i-{\mathit{v}}_i\Vert }^2$ is used to measure the total approximation between the estimated cluster centroids in the target domain and the historical ones in the source domain with $w_i{\sum }_{j=1}^N{u}_{ij}^2$ being the weight factors. As for the regularization coefficient γ, like other usual penalty parameters, it is used to control the overall impact of this regularization formulation. The composition of Definition 2 is illustrated in Fig. 4 intuitively.

Fig. 4.

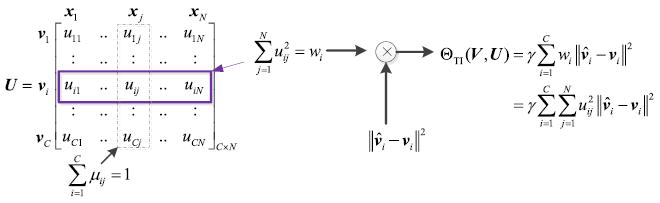
Illustration of the composition in Definition 2.

Although ordinary ${{\sum }_{i=1}^C\Vert {\widehat{\mathit{v}}}_i-{\mathit{v}}_i\Vert }^2$ is also able to evaluate the total deviation between the estimated cluster centroids in the target domain and the corresponding known ones in the source domain, it is more reasonable that the individual influence of each ∥v̂_i −v_i∥² is differentiated in the total measure, i.e., assigning each different weights. It is also well-accepted that major clusters composed of numerous data instances certainly play significant influences in this measure. Therefore, we attempt to devise a mechanism to effectively identify the major clusters. As we know well, each column u_j = [u_1j…u_ij…u_Cj]^T in the membership matrix U, as shown in Fig. 4, indicates all the probabilities of pattern x_j to every estimated cluster prototype. More precisely, the larger the value of u_ij, the higher the probability of x_j being a member of cluster i. Let us switch to the other point of view, i.e., each row u_i = [u_i1…u_ij…u_iN] in U. Cluster i necessarily contains a great quantity of data instances if many entries of u_i take values close to 1, which accordingly causes ${\sum }_{j=1}^N{u}_{ij}^2$ to take a large value. Therefore, with $w_i={\sum }_{j=1}^N{u}_{ij}^2$ being the weights, the major clusters are able to be highlighted as well as identified in the total deviation measure between these two types of cluster prototypes.

Based on Eqs. (10) and (13), we can present our first type of cross-domain, soft-partition clustering framework in the following definition.

Definition 3

If the notations are the same as those in Eqs. (10) or (13), the type-I knowledge-transfer-oriented c-means (TI-KT-CM) framework can be attained by incorporating Eq. (13) into Eq. (10) as follows:

$$\begin{array}{l}\underset{\mathbf{U},\mathbf{V}}{\min }\left({\Phi }_{TI-KT-CM}(\mathit{V},\mathit{U})=\sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2{\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2+\beta \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2+\gamma \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2{\Vert {\widehat{\mathit{v}}}_i-{\mathit{v}}_i\Vert }^2\right),\\ \mathrm{s}.\mathrm{t}.0\le u_{ij}\le 1\mathrm{and}\sum _{i=1}^C{u}_{ij}=1,\end{array}$$ (14)

where β > 0 and γ ≥ 0 are the coefficients of the Gini–Simpson diversity measure and the transfer optimization, respectively.

As previously mentioned, in TI-KT-CM, the parameter γ is adopted to control the whole impact of the transfer optimization ${\sum }_{i=1}^C{\sum }_{j=1}^N{u}_{ij}^2{\Vert {\widehat{\mathit{v}}}_i-{\mathit{v}}_i\Vert }^2$ to the entire framework. The greater the value of γ is, the more the transfer term contributes to the overall framework. Specially, γ→+∞ implies that the role of the transfer optimization term is significantly emphasized, i.e., the reference values of those historical cluster centroids are high in this case; therefore, the estimated cluster centroids in the target domain should be close to them. Conversely, γ→ 0 indicates that the importance of this transfer term is weakened, and the approximation between the known and the estimated cluster centroids in two different domains is consequently relaxed.

3.2.2. Type-II soft-partition transfer optimization formulation and corresponding knowledge-transfer-oriented c-means clustering framework

In terms of transfer learning again, we further extend Eq. (13) into the other, more delicate soft-partition transfer optimization formulation defined in Definition 4.

Definition 4

Let ũ_ij(i = 1, …, C; j = 1, …, N) signify the membership of individual x_j (j = 1, …, N) in the target domain to the known cluster centroid v̂_i(i = 1,…,C) in the source domain (referred to as historical cluster centroid-based memberships for short), and which can be computed by any fuzzy membership update equation in the source domain, e.g., Eqs. (3) or (6). Using the same notations as those in Eq. (13), the type-II soft-partition transfer optimization formulation can be defined as

$$\underset{\mathbf{V},\mathbf{U}}{\min }\left({\Theta }_{TII}(\mathit{V},\mathit{U})=\gamma \sum _{i=1}^C\sum _{j=1}^N(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2){\Vert {\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i\Vert }^2\right),$$ (15)

where η ∈ [0, 1] is one trade-off factor.

Obviously, the difference between Θ_TII(V, U) in Eq. (15) and Θ_TI(V, U) in Eq. (13) lies in the weight factors, i.e., we replace ${\sum }_{j=1}^N{u}_{ij}^2$ with ${\sum }_{j=1}^N(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2)$ as the weight of ∥v̂_i −v_i∥² in Θ_TII(V, U). For clearly interpreting the connotation in Eq. (15), the composition of Definition 4 is illustrated in Fig. 5. As shown in this figure, besides the current, estimated, fuzzy memberships in U in the target domain, the historical cluster centroid-based memberships in Ũ are also referenced for advanced transfer learning. More specifically, under the premise of transfer learning, there should be some similarity between v̂_i, v_i, i = 1,…,C, to a certain extent for any data instance x_j in the target domain. Therefore, the membership u_ij of x_j to v_i in the target domain and the membership ũ_ij of x_j−v̂_i in the source domain should also be close to each other to a certain extent, which means that ũ_ij can also be enlisted for appraising the importance of each ∥v̂_i−v_i∥² in the total approximation measure. As such, as indicated in Fig. 5, via the trade-off factor η ∈ [0, 1], the combination of $u_{ij}^2$ and ${\stackrel{\sim }{u}}_{ij}^2$ is used to constitute the new weight factor $w_i^{\text{'}}=\eta w_i+(1-\eta ){\stackrel{\sim }{w}}_i={\sum }_{j=1}^N(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2)$, and the value of η balances the individual impacts of these two types of fuzzy memberships. Specially, η→1 indicates that the importance of the estimated membership u_ij in the target domain is highlighted, whereas n→0 indicates that the historical cluster centroid-based membership ũ_ij is significantly referenced. As for the regularization coefficient γ, its role is the same as that in Θ_TII(V, U), i.e., it is recruited for controlling the whole impact of Θ_TII(V, U).

Fig. 5.

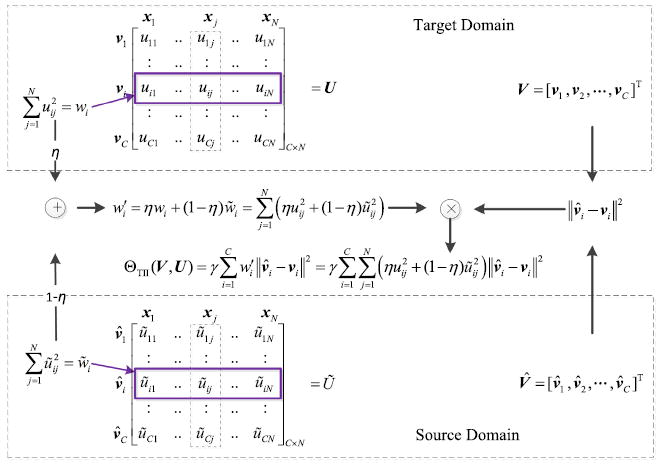
Illustration of the composition in Definition 4.

In addition, further inspired by Eq. (15), we extend Eq. (10) into the following transfer learning form:

$$\begin{array}{l}\underset{\mathbf{V},\mathbf{U}}{\min }\left({\Psi }^{\prime }(\mathit{V},\mathit{U})=\sum _{i=1}^C\sum _{j=1}^N(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2){\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2+\beta \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2\right),\\ \mathrm{s}.\mathrm{t}.0\le u_{ij}\le 1\mathrm{and}\sum _{i=1}^C{u}_{ij}=1.\end{array}$$ (16)

That is, in addition to the current estimated membership u_ij (i = 1, …, C; j = 1, …, N), the corresponding historical membership ũ_ij (i = 1, …, C; j = 1, …, N) can be recruited as the reference, and their combination via the trade-off factor η is eventually used as the joint weight for the intra-cluster deviation measure. Here the value of (1 − η) determines the reference degree of historical knowledge.

So far, we can propose the other type of cross-domain, soft-partition clustering framework by combining Eq. (16) with (15) as follows.

Definition 5

If the notations are the same as those in Eqs. (15) and (16), the type-II knowledge-transfer-oriented c-means (TII-KT-CM) framework is defined as

$$\begin{array}{c}\underset{\mathbf{V},\mathbf{U}}{\min }({\Phi }_{TII-KT-CM}(\mathit{V},\mathit{U})=\sum _{i=1}^C\sum _{j=1}^N(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2){\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2\\ +\beta \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2+\gamma \sum _{i=1}^C\sum _{j=1}^N\left(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right){\Vert {\widehat{\mathit{v}}}_i-{\mathit{v}}_i\Vert }^2),\\ \mathrm{s}.\mathrm{t}.00\le u_{ij}\le 1\mathrm{and}\sum _{i=1}^C{u}_{ij}=1,\end{array}$$ (17)

where η ∈ [0, 1], β > 0, and γ ≥ 0 are the transfer trade-off factor, the regularization parameter of Gini–Simpson diversity measure and the regularization parameter of transfer optimization, respectively.

3.2.3. Update equations of TI-KT-CM and TII-KT-CM

Theorem 1

The necessary conditions for minimizing the objective function Θ_TI−KT−CM in Eq. (14) yield the following update equations of cluster centroids and fuzzy memberships:

$${\mathit{v}}_i=\frac{\sum _{j=1}^N{u}_{ij}^2{\mathit{x}}_j+\gamma {\widehat{\mathit{v}}}_i\sum _{j=1}^N{u}_{ij}^2}{(1+\gamma )\sum _{j=1}^N{u}_{ij}^2},$$ (18)

$$u_{ij}=\frac{1}{(2{\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2+2\beta +2\gamma {\Vert {\widehat{\mathit{v}}}_i-{\mathit{v}}_i\Vert }^2)\sum _{k=1}^C\frac{1}{2{\Vert {\mathit{x}}_j-{\mathit{v}}_k\Vert }^2+2\beta +2\gamma {\Vert {\widehat{\mathit{v}}}_k-{\mathit{v}}_k\Vert }^2}}.$$ (19)

Theorem 2

The necessary conditions for minimizing the objective function Θ_{TII−KT−CM} in Eq. (17) yield the following cluster centroid and membership update equations:

$${\mathit{v}}_i=\frac{\sum _{j=1}^N\left(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right){\mathit{x}}_j+\gamma {\widehat{\mathit{v}}}_i\sum _{j=1}^N\left(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)}{(1+\gamma )\sum _{j=1}^N\left(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)},$$ (20)

$$u_{ij}=\frac{1}{(2\eta {\Vert {\mathit{x}}_j-{\mathit{v}}_i\Vert }^2+2\beta +2\gamma \eta {\Vert {\widehat{\mathit{v}}}_i-{\mathit{v}}_i\Vert }^2)\sum _{k=1}^C\frac{1}{2\eta {\Vert {\mathit{x}}_j-{\mathit{v}}_k\Vert }^2+2\beta +2\gamma \eta {\Vert {\widehat{\mathit{v}}}_k-{\mathit{v}}_k\Vert }^2}}.$$ (21)

For the proofs of Theorems 1 and 2, please see Appendix A.1 and A.2, respectively.

3.2.4. The TI-KT-CM and TII-KT-CM algorithms

We now depict the two, core, TI-KT-CM and TII-KT-CM clustering algorithms as follows

Algorithms: Type-I/Type-II knowledge-transfer-oriented c-means clustering (TI-KT-CM/TII-KT-CM)

Inputs:	The target dataset XT (the target domain), the number of clusters C, the known cluster centroids v̂i, i = 1, …, C, or the historical dataset XS (the source domain), the specific values of involved parameters in TI-KT-CM or TII-KT-CM, e.g. η, β, and γ, the maximum iteration number maxiter, the termination condition of iterations ε.
Outputs:	The memberships U, the cluster centroids V, and the labels of all patterns in XT.
Extracting knowledge from the source domain:
Setp1:	Generate the historical cluster centroids v̂i(i = 1, …, C) in the source domain XS via other soft-partition clustering methods, e.g., FCM or MEC (Skip this step if the historical cluster centroids v̂i(i = 1, …, C) are given).
Step2:	Compute the historical cluster centroid-based memberships ũij(i = 1, …, C; j = 1, …, N) of all data instances in XT to those historical cluster centroids v̂i(i = 1, …, C) via Eq. (3) or (6).
Performing clustering in the target domain:
Step 1:	Set the iteration counter t=0 and randomly initialize the memberships U(t) which satisfies 0 ≤ uij(t)≤ 1 and ${\sum }_{i=1}^C{u}_{ij}(t)=1$.
Step 2:	For TI-KT-CM, generate the cluster centroids V(t) via Eq.(18), U(t), and v̂i(i = 1, …, C).
	For TII-KT-CM, generate the cluster centroids V(t) via Eq. (20), U(t), v̂i(i = 1, …, C), and ũij(i = 1, …, C; j = 1, …, N).
Step 3:	For TI-KT-CM, calculate the memberships U(t + 1) via Eq. (19), V(t), and v̂i(i = 1, …, C).
	For TII-KT-CM, calculate the memberships U(t+1) via Eq. (21), V(t), and v̂i(i = 1, …, C).
Step 4:	If ∥ U(t + 1) − U(t)∥ < ε or t=maxiter go to Step 5, otherwise, =t+1 and go to Step 2;
Step 5:	Output the eventual cluster centroids V and memberships U in XT, and determine the label of each individual in XT according to U.

3.3. Convergence of TI-KT-CM and TII-KT-CM

For the convergence of iterative optimization issues, the well-known Zangwill’s convergence theorem [15,32] is extensively adopted as a standard pathway. Let us first review this theorem below.

Lemma 1

(Zangwill’s convergence theorem): Let D denote the domain of a continuous function J, and S ⊂ D be its solution set. Let Ω signify a map over D which generates an iterative sequence {z_(t+1) = Ω_{(t + 1)}(z_(t)), t = 0, 1, …} with z₍₀₎ ∈ D. Suppose that

1. {z_(t), t = 1, 2…} is a compact subset of D.

2. The continuous function, J : D→ R, satisfies that

   1. If z ∉ S, then for any y ∈ Ω(z), J(y) < J(z),

   2. if z ∈ S, then either the algorithm terminates or for any y ∈ Ω(z), J(y) ≤ J(z).

3. Ω is continuous on D–S.

   Then either the algorithm stops at a solution or the limit of any convergent subsequence is a solution.

   Likewise, we use this theorem to demonstrate the convergence of both TI-KT-CM and TII-KT-CM as follows.

3.3.1. Convergence analyses regarding TI-KT-CM

Definition 6

Let X = {x₁, …, x_N} denote one finite data set in the Euclidean space R^d, then the set composed of all soft C-partitions on X is defined as

$$M_c=\left\{U\in R^{CN}|\begin{array}{l}{u}_{ij}\in [0,1],1\le i\le C,1\le j\le N,\\ {\sum }_{i=1}^C{u}_{ij}=1,1\le j\le N.\end{array}\right\}.$$ (22)

Definition 7

A function F^I : R^Cd → M_C is defined as F^I(V^I) = U^I, where U^I ∈ M_C consists of $u_{\mathit{ij}}^{\mathrm{I}}$, 1 ≤ i ≤ C, 1 ≤ j ≤ N, and $u_{\mathit{ij}}^{\mathrm{I}}$ is calculated by Eq. (19) and V^I ∈ R^Cd.

Definition 8

A function G^I : M_C → R^Cd is defined as $G^{\mathrm{I}}({\mathbf{U}}^{\mathrm{I}})={\mathbf{V}}^{\mathrm{I}}={({\mathbf{v}}_1^{\mathrm{I}},\dots ,{\mathbf{v}}_C^{\mathrm{I}})}^{\mathrm{T}}$, where ${\mathbf{v}}_i^{\mathrm{I}}=(v_{i1}^{\mathrm{I}},\dots ,v_{id}^{\mathrm{I}})\in R^d$, 1 ≤ i ≤ C, are the estimated cluster centroids computed via Eq. (18) and U^I ∈ M_C.

Definition 9

A map T^I : R^Cd × M_C → R^Cd × M_C is defined as $T^{\mathrm{I}}=A_2^{\mathrm{I}}\circ A_1^{\mathrm{I}}$ for the iteration in TI-KT-CM, where $A_1^{\mathrm{I}}$ and $A_2^{\mathrm{I}}$ are further defined as $A_1^{\mathrm{I}}:R^{\mathit{Cd}}\times M_C\to M_C,A_1^{\mathrm{I}}({\mathit{V}}_{(t)}^{\mathrm{I}},{\mathit{U}}_{(t)}^{\mathrm{I}})=F^{\mathrm{I}}({\mathit{V}}_{(t)}^{\mathrm{I}})={\mathit{U}}_{(t+1)}^{\mathrm{I}},A_2^{\mathrm{I}}:M_C\to R^{\mathit{Cd}}\times M_C,A_2^{\mathrm{I}}({\mathit{U}}_{(t+1)}^{\mathrm{I}})=(G^{\mathrm{I}}({\mathit{U}}_{(t+1)}^{\mathrm{I}}),{\mathit{U}}_{(t+1)}^{\mathrm{I}})=({\mathit{V}}_{(t+1)}^{\mathrm{I}},{\mathit{U}}_{(t+1)}^{\mathrm{I}})$, i.e., T^I is a composition of two embedded maps: $A_1^{\mathrm{I}}$ and $A_2^{\mathrm{I}}$ and $T^{\mathrm{I}}({\mathit{V}}_{(t)}^{\mathrm{I}},{\mathit{U}}_{(t)}^{\mathrm{I}})=A_2^{\mathrm{I}}\circ A_1^{\mathrm{I}}({\mathit{V}}_{(t)}^{\mathrm{I}},{\mathit{U}}_{(t)}^{\mathrm{I}})=A_2^{\mathrm{I}}(F^{\mathit{I}}({\mathit{V}}_{(t)}^{\mathrm{I}}))=A_2^{\mathrm{I}}({\mathit{U}}_{(t+1)}^{\mathrm{I}})=(G^{\mathrm{I}}({\mathit{U}}_{(t+1)}^{\mathrm{I}}),{\mathit{U}}_{(t+1)}^{\mathrm{I}},)=({\mathit{V}}_{(t+1)}^{\mathrm{I}},{\mathit{U}}_{(t+1)}^{\mathrm{I}})$.

Theorem 3

Suppose X = {x₁, …, x_N} contains at least C (C < N) distinct points and $\left({\mathbf{V}}_{\left(0\right)}^{\mathrm{I}},{\mathbf{U}}_{\left(0\right)}^{\mathrm{I}}\right)$ is the start of the iteration of T^I with ${\mathit{U}}_{\left(0\right)}^{\mathrm{I}}\in {\mathrm{M}}_{\mathrm{C}}$ and ${\mathit{V}}_{\left(0\right)}^{\mathrm{I}}=G^{\mathrm{I}}\left({\mathit{U}}_{\left(0\right)}^{\mathrm{I}}\right)$, then the iteration sequence $\left\{\left({\mathit{V}}_{(t)}^{\mathrm{I}},{\mathit{U}}_{(t)}^{\mathrm{I}}\right),t=1,2,\cdots \right\}$ is contained in a compact subset of R^Cd × M_C.

The proof of Theorem 3 is given in Appendix A.3.

Proposition 1

If ${\mathit{V}}_{\ast }^{\mathrm{I}}\in R^{\mathit{Cd}}$, and γ ≥ 0 are fixed, and the function †^I: M_C → R is defined as ${†}^I({\mathbf{U}}^{\mathrm{I}})={\Phi }_{\mathrm{TI}-\mathrm{KT}-\mathrm{CM}}({\mathbf{U}}^{\mathrm{I}},{\mathbf{V}}_{\ast }^{\mathrm{I}})$, then ${\mathbf{U}}_{\ast }^{\mathrm{I}}$ is a global minimizer of †^I over M_C if and only if ${\mathit{U}}_{\ast }^{\mathrm{I}}=F^{\mathrm{I}}({\mathit{V}}_{\ast }^{\mathrm{I}})$.

Proof

It is easy to prove that †^I (U^I) is a strictly convex function when ${\mathit{V}}_{\ast }^{\mathrm{I}}\in R^{Cd}$, β > 0; and γ ≥ 0 are fixed. This means †^I (U^I) at most has one minimizer over M_C, and it is also a global minimizer. Furthermore, based on the Lagrange optimization, we know that ${\mathit{U}}_{\ast }^{\mathrm{I}}=F^{\mathrm{I}}({\mathit{V}}_{\ast }^{\mathrm{I}})$ is a global minimizer of †^I (U^I) over M_C.

Proposition 2

If ${\mathit{U}}_{\ast }^{\mathrm{I}}\in M_C$, β > 0; and γ ≥ 0 are fixed, and the function Γ^I: R^Cd → R is defined as ${\Gamma }^{\mathrm{I}}({\mathit{V}}^{\mathrm{I}})={\Phi }_{TI-KT-MC}({\mathit{U}}_{\ast }^{\mathrm{I}},{\mathit{V}}^{\mathrm{I}})$, then ${\mathbf{V}}_{\ast }^{\mathrm{I}}$ is a global minimizer of Γ^I over R^Cd if and only if ${\mathbf{V}}_{\ast }^{\mathrm{I}}=G^{\mathrm{I}}\left({\mathbf{U}}_{\ast }^{\mathrm{I}}\right)$.

Proof

It is easy to demonstrate that Γ^I(V^I) is a positive definite quadratic function when ${\mathit{U}}_{\ast }^{\mathrm{I}}\in M_C$, β > 0; and γ ≥ 0 are fixed, which means Γ^I(V^I) is also strictly convex in this situation. Likewise, by means of the Lagrange optimization, we consequently know that ${\mathit{V}}_{\ast }^{\mathrm{I}}=G^{\mathrm{I}}\left({\mathit{U}}_{\ast }^{\mathrm{I}}\right)$ is a global minimizer of Γ^I (V^I).

Theorem 4

Let

$$S^{\mathrm{I}}=\left\{({\mathit{V}}_{\ast }^{\mathrm{I}},{\mathit{U}}_{\ast }^{\mathrm{I}})\in R^{\mathit{Cd}}\times M_C|\begin{array}{l}{\Phi }_{TI-KT-CM}({\mathit{V}}_{\ast }^{\mathrm{I}},{\mathit{U}}_{\ast }^{\mathrm{I}})<{\Phi }_{TI-KT-CM}({\mathit{V}}_{\ast }^{\mathrm{I}},\mathit{U}),\forall \mathit{U}\in M_C\mathrm{and}\mathit{U}\ne {\mathit{U}}_{\ast }^{\mathrm{I}}\\ \mathrm{and}\\ {\Phi }_{TI-KT-CM}({\mathit{V}}_{\ast }^{\mathrm{I}},{\mathit{U}}_{\ast }^{\mathrm{I}})<{\Phi }_{TI-KT-CM}(\mathit{V},{\mathit{U}}_{\ast }^{\mathrm{I}}),\forall \mathbf{V}\in R^{\mathit{Cd}}\mathrm{and}\mathit{V}\ne {\mathit{V}}_{\ast }^{\mathrm{I}}\end{array}\right\}$$ (23)

denote the solution set of the optimization problem min Φ_TI–KT–CM(V, U). Let β > 0 and γ ≥ 0 take the specific values as well as v̂_i, i = 1, …, C, be known beforehand, suppose X = {x₁, …, x_N} contains at least C (C < N) distinct points. For (V̄, Ū) ∈ R^Cd × M_C, if (V̑, Ȗ) = T_I(V̄, Ū) then Φ_TI–KT–CM (V̑, Ȗ) ≤ Φ_TI–KT–CM (V̄, Ū) and the inequality is strict if (V̄, Ū)∉S^I.

The proof of Theorem 4 is given in Appendix A.4.

Theorem 5

Let β > 0 and γ ≥ 0 take the specific values as well as v̂_i, i = 1, …, C, be known beforehand, suppose X = {x₁, …, x_N} contains at least C (C < N) distinct points, then the map T^I : R^Cd × M_C → R^Cd × M_C is continuous on R^Cd × M_C.

The proof of Theorem 5 is given in Appendix A.5.

Theorem 6

(Convergence of TI-KT-CM). Let X = {x₁, …, x_N} contain at least C (C < N) distinct points and Φ_TI–KT–CM be in the form of Eq. (14), suppose (V₍₀₎, U₍₀₎) is the start of the iterations of T^I with U₍₀₎ ∈ M_C and V₍₀₎ = G^I(U₍₀₎), then the iteration sequence, $\left\{({\mathit{V}}_{(t+1)},{\mathit{U}}_{(t+1)})=T_{(t+1)}^{\mathrm{I}}({\mathit{V}}_{(t)},{\mathit{U}}_{(t)},t=0,1,\dots )\right\}$, either terminates at point (V*, U*) in the solution set S^I of Φ_TI–KT–CM or there is a subsequence converging to a point in S^I.

Based on Zangwill’s convergence theorem, Theorem 6 immediately holds under the premises of Theorems 3, 4, and 5.

3.3.2. Convergence analyses regarding TII-KT-CM

Definition 10

A function F^II : R^Cd → M_C is defined as F^II(V^II) = U^II, where U^II ∈ M_C consists of $u_{ij}^{\mathrm{II}}$, 1 ≤ i ≤ C, 1 ≤ j ≤ N, and $u_{ij}^{\mathrm{II}}$ is calculated by Eq. (21) and V^II ∈ R^Cd.

Definition 11

A function G^II : M_C → R^Cd is defined as $G^{\mathrm{II}}({\mathit{U}}^{\mathrm{II}})={\mathit{V}}^{\mathrm{II}}={({\mathit{v}}_1^{\mathrm{II}},\cdots ,{\mathit{v}}_C^{\mathrm{II}})}^{\mathrm{T}}$, where ${\mathbf{v}}_i^{\mathrm{II}}=(v_{i1}^{\mathrm{II}},\cdots ,v_{id}^{\mathrm{II}})\in R^d$, 1 ≤ i ≤ C are the estimated cluster centroids computed via Eq. (20) and U^II ∈ M_C.

Definition 12

A map T^II : R^Cd × M_C → R^Cd × M_C is defined as $T^{\mathrm{II}}=A_2^{\mathrm{II}}\circ A_1^{\mathrm{II}}$ for the iteration in TII-KT-CM, where $A_1^{\mathrm{II}}$ and $A_2^{\mathrm{II}}$ are defined as $A_1^{\mathrm{II}}:R^{\mathit{Cd}}\times M_C\to M_C,A_1^{\mathrm{II}}({\mathit{V}}_{(t)}^{\mathrm{II}},{\mathit{U}}_{(t)}^{\mathrm{II}})=F^{\mathrm{II}}({\mathit{V}}_{(t)}^{\mathrm{II}})={\mathit{U}}_{(t+1)}^{\mathrm{II}},A_2^{\mathrm{II}}:M_C\to R^{\mathit{Cd}}\times M_C,A_2^{\mathrm{II}}({\mathit{U}}_{(t+1)}^{\mathrm{II}})=(G^{\mathrm{II}}({\mathit{U}}_{(t+1)}^{\mathrm{II}}),{\mathit{U}}_{(t+1)}^{\mathrm{II}})=({\mathit{V}}_{(t+1)}^{\mathrm{II}},{\mathit{U}}_{(t+1)}^{\mathrm{II}})$, i.e., T^II is one composition of two embedded maps: $A_1^{\mathrm{II}}$ and $A_2^{\mathrm{II}}$, and $T^{\mathrm{II}}({\mathbf{V}}_{(t)}^{\mathrm{II}},{\mathit{U}}_{(t)}^{\mathrm{II}})=A_2^{\mathrm{II}}\circ A_1^{\mathrm{II}}({\mathit{V}}_{(t)}^{\mathrm{II}},{\mathit{U}}_{(t)}^{\mathrm{II}})=A_2^{\mathrm{II}}(F^{\mathrm{II}}({\mathit{V}}_{(t)}^{\mathrm{II}}))=A_2^{\mathrm{II}}({\mathbf{U}}_{(t+1)}^{\mathrm{II}})=(G^{\mathrm{II}}({\mathbf{U}}_{(t+1)}^{\mathrm{II}}),{\mathbf{U}}_{(t+1)}^{\mathrm{II}},)=({\mathbf{V}}_{(t+1)}^{\mathrm{II}},{\mathbf{U}}_{(t+1)}^{\mathrm{II}})$.

Theorem 7

Suppose X = {x₁, …, x_N} contains at least C (C < N) distinct points and $\left({\mathit{V}}_{(0)}^{\mathrm{II}},{\mathit{U}}_{(0)}^{\mathrm{II}}\right)$ is the start of the iteration of T^II with ${\mathbf{U}}_{(0)}^{\mathrm{II}}\in M_C$ and ${\mathit{V}}_{\left(0\right)}^{\mathrm{II}}=G^{\mathrm{II}}\left({\mathit{U}}_{(0)}^{\mathrm{II}}\right)$, then the iteration sequence $\left\{\left({\mathit{V}}_{(t)}^{\mathrm{II}},{\mathit{U}}_{(t)}^{\mathrm{II}}\right),t=1,2,\cdots \right\}$ is contained in a compact subset of R^Cd × M_C.

The proof of Theorem 7 is given in Appendix A.6.

Proposition 3

If ${\mathit{V}}_{\ast }^{\mathrm{II}}\in R^{Cd}$, β > 0, γ ≥ 0, and η ∈ [0, 1]s are fixed, and the function †^II : M_C → R is defined as ${†}^{II}({\mathit{U}}^{II})={\Phi }_{\mathrm{TII}-\mathrm{KT}-\mathrm{CM}}({\mathbf{U}}^{II},{\mathbf{V}}_{\ast }^{\mathrm{II}})$, then ${\mathbf{U}}_{\ast }^{\mathrm{II}}$ is a global minimizer of †^II over M_C if and only if ${\mathbf{U}}_{\ast }^{\mathrm{II}}=F^{\mathrm{II}}({\mathbf{V}}_{\ast }^{\mathrm{II}})$.

For the proof of this proposition, one can refer to that of Proposition 1.

Proposition 4

If ${\mathit{U}}_{\ast }^{\mathrm{II}}\in M_C$, β > 0, γ ≥ 0; and η ∈ [0, 1] are fixed, and the function Γ^II : R^Cd → R is defined as ${\Gamma }^{\mathrm{II}}({\mathit{V}}^{\mathrm{II}})={\Phi }_{\mathrm{TII}-}\mathrm{KT}-\mathrm{CM}({\mathit{U}}_{\ast }^{\mathrm{II}},{\mathit{V}}^{\mathrm{II}})$, then ${\mathbf{V}}_{\ast }^{\mathrm{II}}$ is a global minimizer of Γ^II over R^Cd if only if ${\mathit{V}}_{\ast }^{\mathrm{II}}=G^{\mathrm{II}}({\mathit{U}}_{\ast }^{\mathrm{II}})$.

For the proof of this proposition, one can refer to that of Proposition 2.

Theorem 8

Let

$$S^{\mathrm{II}}=\left\{({\mathit{V}}_{\ast }^{\mathrm{II}},{\mathit{U}}_{\ast }^{\mathrm{II}})\in R^{Cd}\times M_C|\begin{array}{l}{\Phi }_{\mathrm{TII}-\mathrm{KT}-\mathrm{CM}}\left({\mathit{V}}_{\ast }^{\mathrm{II}},{\mathit{U}}_{\ast }^{\mathrm{II}}\right)<{\Phi }_{\mathrm{TII}-\mathrm{KT}-\mathrm{CM}}\left({\mathit{V}}_{\ast }^{\mathrm{II}},\mathit{U}\right),\forall \mathit{U}\in M_C\mathrm{and}\mathit{U}\ne {\mathit{U}}_{\ast }^{\mathrm{II}}\\ \mathrm{and}\\ {\Phi }_{\mathrm{TII}-\mathrm{KT}-\mathrm{CM}}\left({\mathit{V}}_{\ast }^{\mathrm{II}},{\mathit{U}}_{\ast }^{\mathrm{II}}\right)<{\Phi }_{\mathrm{TII}-\mathrm{KT}-\mathrm{CM}}\left(\mathit{V},{\mathit{U}}_{\ast }^{\mathrm{II}}\right),\forall \mathit{V}\in R^{Cd}\mathrm{and}\mathit{V}\ne {\mathit{V}}_{\ast }^{\mathrm{II}}\end{array}\right\}$$ (24)

denote the solution set of the optimization problem min Φ_{TII–KT–CM}(V, U). Let η ∈ [0, 1], β > 0, and γ ≥ 0 be fixed as well as ũ_ij, i = 1, …, C, j = 1, …, N and v̂_i, i = 1, …, C, be known beforehand, suppose X = {x₁, …, x_N} contains at least C (C < N) distinct points. For (V̄,Ū) ∈ R^Cd × M_C, if (V̑,Ȗ) = T^II(V̄,Ū), then Φ_{TII–KT–CM} (V̑,Ȗ) ≤ Φ_{TII–KT–CM} (V̄,Ū) and the inequality is strict if (V̄,Ū)
S^II.

The proof of Theorem 8 is given in Appendix A.7.

Theorem 9

Let η ∈ [0, 1], β > 0, and γ ≥ 0 be fixed as well as ũ_ij, i = 1, …, C, j = 1, …, N and v̂_i, i = 1, …, C, be given beforehand, suppose X = {x₁, …, x_N} contains at least C (C < N) distinct points, then the map T^II : R^Cd × M_C → R^Cd × M_C is continuous on R^Cd × M_C.

For the proof of this theorem, one can refer to that of Theorem 5 in Appendix A.5.

Theorem 10

(Convergence of TII-KT-CM). Let X = {x₁, … x_N} contain at least C (C < N) distinct points and Φ_{TII–KT–CM} be in the form of Eq. (17), suppose (V₍₀₎, U₍₀₎) is the start of the iterations of T^II with U₍₀₎ ∈ M_C and V₍₀₎ = G^II(U₍₀₎), then the iteration sequence, $\left\{({\mathit{V}}_{(t+1)},{\mathit{U}}_{(t+1)})=T_{(t+1)}^{\mathrm{II}}({\mathit{V}}_{(t)},{\mathit{U}}_{(t)}),t=0,1,\dots \right\}$, either terminates at a point (V*, U*) in the solution set S^II of Φ_{TII–KT–CM} or there is a subsequence converging to a point in S^II.

Theorem 10 holds immediately based on Theorems 7, 8 and 9.

3.4. Parameter settings

There are two core parameters involved in TI-KT-CM, including the diversity measure coefficient β and the transfer regularization parameter γ in Eq. (14). As for TII-KT-CM in the form of Eq. (17), in addition to β and γ, the transfer trade-off factor η is also involved. We would like to explain the proper ranges regarding these parameters before we discuss how to effectively adjust them. As previously mentioned in Eqs. (14) or (17), the rough ranges of these parameters are η ∈ [0, 1] β > 0, and γ ≥ 0. Parameter η aims to balance the individual impacts of the current estimated memberships u_ij(i = 1, …, C; j = 1, …, N) and the historical memberships ũ_ij(i = 1, …, C; j = 1, …, N) in TII-KT-CM. In light of the possible values of both and u_ij and ũ_ij varying from 0 to 1, it is appropriate to let η also take values within interval [0, 1]. In order to make the Gini–Simpson diversity measure always play roles, β must take values larger than zero. Likewise, γ > 0 can make the transfer optimization term, i.e., Eqs. (14) or (17), impact in the framework of TI-KT-CM or TII-KT-CM. As for γ = 0, for TI-KT-CM, it indicates that our algorithm gives up the prior knowledge from other correlated data scenes and it degenerates thoroughly into QWGSD-FC in the form of Eq. (10), which usually occurs in such situations where the data distribution in the target domain greatly differs from that in the source domain; for TII-KT-CM, if γ = 0 and η ≠ 1, this indicates our algorithm only refers to the historical cluster centroid-based memberships for transfer learning, otherwise, i.e., γ = 0 and η = 1, TII-KT-CM also degenerates into QWGSD-FC in this case, and there is no historical knowledge which can be referenced at all.

As is well-known, nowadays the grid search strategy is extensively recruited for parameter setting in pattern recognition, and it is dependent on certain validity indices. Validity indices can be roughly divided into two categories, i.e., the label-based, external criterion as well as the label-free, internal criterion. The external criterion, e.g., NMI (Normalized Mutual Information) [45,73], RI (Rand Index) [73,74], and ACC (Clustering Accuracy) [45], evaluates the agreement degree between the estimated data structure and the known one, such as the clusters in the dataset. In contrast, the internal criterion, such as DBI (Davies Bouldin Index) [74] and DI (Dunn Index) [74], appraises the effectiveness of algorithms based purely on the inherent quantities or features in the dataset, such as the intra-cluster homogeneity as well as the inter-cluster separation.

Coming back to our work, in order to obtain the optimal parameter settings in TI-KT-CM or TII-KT-CM, the grid search was conducted as usual. Suppose the trial ranges of all involved parameters are given, the seeking procedure of best settings can be briefly depicted as follows. The range of each parameter was first evenly divided into several subintervals; after that, in the form of repeated implementations of the TI-KT-CM/TII-KT-CM algorithm, the multiple, nested loops were executed with one parameter locating in one loop and the subintervals of the parameter being the steps of the loop. Meanwhile, the clustering effectiveness in terms of the selected validity index, e.g., NMI or DBI, was recorded automatically. After the nested loops terminated, the best settings of all parameters can be obtained straightforwardly, i.e., the ones corresponding to the best clustering effectiveness within the given trial ranges. As for how to appraise the appropriate trial ranges of parameters in related algorithms, we will interpret this in the following experimental section.

4. Experimental results

4.1. Setup

In this section we focus on demonstrating the performance of our novel TI-KT-CM and TII-KT-CM algorithms. Besides TI-KT-CM and TII-KT-CM, several other correlative, state-of-the-art approaches are recruited as the competitors, i.e., LSSMTC (Learning Shared Subspace for Multitask Clustering) [62], CombKM (Combining K-means) [62], STC (Self-taught Clustering) [56], and TSC (Transfer Spectral Clustering) [59], in order to compare them with each other. Among them, TI-KT-CM and TII-KT-CM belong to soft-partition clustering, whereas LSSMTC and CombKM belong to hard-partition clustering; CombKM, LSSMTC and TSC belong to multi-task clustering; STC, TSC, TI-KT-CM, and TII-KT-CM belong to cross-domain clustering (i.e., transfer clustering); and STC as well as TSC belong to co-clustering essentially. The detailed, related categories regarding these methods are listed in Table 1. Definitely, these algorithms cover multiple categories and most of them belong to at least two categories. Therefore, the experiments performed by these approaches should be convincing. In addition, for verifying the practical performance of QWGSD-FC proposed as the foundation of our research, besides QWGSD-FC itself, other classic soft-partition clustering models, including FCM [3,6], MEC [3,18], FC-QR [3,29], PCM [3,7] and ECM [10], are also involved in our experimental studies.

Table 1.

Categories and parameter settings of involved algorithms.

Algorithms	Categories	Parameter values or trial ranges
FCM	Soft-partition clustering	Fuzzifier m ∈ [1.1 : 0.1 : 2.5]
MEC	Soft-partition clustering	Entropy regularization parameter β ∈[0.05:0.05:1, 10:10:100]
PCM	Soft-partition clustering	Fuzzifier m ∈[1.1 : 0.1 : 2:5]
		Parameter K=1
ECM	Soft-partition clustering	Parameter α ∈[1:1:10]
		Parameter β ∈[1.1:0.1:2.5]
		Parameter δ ∈[3:1:9]
FC-QR	Soft-partition clustering	Quadratic function regularizing coefficient γ ∈[0.1:0.1:2, 20:20:200]
QWGSD-FC	Soft-partition clustering	Diversity measure coefficient β ∈[0.05:0.05:1, 10:10:100]
LSSMTC	Hard-partition clustering; Multi-task clustering;	Task number T=2
		Regularization parameter l ∈{2; 22; 23; 24 ∪ [100 : 100 : 1000]
		Regularization parameter λ ∈{0.25, 0.5, 0.75}
ComKM	Hard-partition clustering; Multi-task clustering	K equals the number of cluster
STC	Transfer clustering; Co-clustering	Trade-off parameter λ = 1
TSC	Transfer clustering; Multi-task clustering; Co-clustering	Parameters K=27, λ = 3, and step=1
TI-KT-CM	Soft-partition clustering; Transfer clustering	Entropy regularization parameter β∈[0.05:0.05:1,10:10:100]
		Transfer regularization parameter γ∈[0:0.05:1,2:1:10,20:10:200]
TII-KT-CM	Soft-partition clustering; Transfer clustering	Entropy regularization parameter β∈[0.05:0.05:1,10:10:100]
		Transfer regularization parameter γ∈[0:0.05:1,2:1:10,20:10:200]
		Transfer trade-off factor η∈=[0 : 0:05 : 1]

Our experiments were conducted on both artificial and real-world data scenarios, and three popular validity indices, i.e., NMI, RI, and DBI, were enlisted for the clustering performance evaluation in our work. Among them, NMI and RI belong to external criteria, whereas DBI is one internal criterion. Before we introduce the details of our experiments, we first concisely review the definitions of these indices below.

4.1.1. NMI (normalized mutual information) [45,73]

$$NMI=\frac{{\sum }_{i=1}^k{\sum }_{j=1}^c{N}_{i,j}\log \left(\frac{N\cdot N_{i,j}}{N_i\cdot N_j}\right)}{\sqrt{\left({\sum }_{i=1}^k{N}_i\log \frac{N_i}{N}\right)\left({\sum }_{j=1}^c{N}_j\log \frac{N_j}{N}\right)}},$$ (25)

where N_i,j denotes the number of agreements between cluster i and class, N_i is the number of data instances in cluster, N_j is the number of data instances in class j, and N signifies the data capacity of the entire dataset.

4.1.2. RI (rand index) [73,74]

$$RI=\frac{f_{00}+f_{11}}{N(N-1)/2},$$ (26)

where f₀₀ signifies the number of any two data instances belonging to two different clusters, f₁₁ signifies the number of any two data instances belonging to the same cluster, and N is the total number of data instances.

4.1.3. DBI (Davies–Bouldin index) [74]

$$DBI=\frac{1}{C}\sum _{k=1}^C\underset{k\prime \ne k}{\max }\frac{{\delta }_k+{\delta }_{k\prime }}{\mathit{\Delta }kk\text{'}},$$ (27 – 1)

where

$${\delta }_k=\frac{1}{n_k}\sum _{{\mathbf{x}}_j^k\in C_k}\Vert {\mathit{x}}_j^k-{\mathit{v}}_k\Vert ,{\mathit{\Delta }}_{kk\prime }=\Vert {\mathit{v}}_k-{\mathit{v}}_{k\prime }\Vert ,$$ (27 – 2)

C denotes the cluster number in the dataset, ${\mathbf{x}}_j^k$ denotes the data instance belonging to cluster C_k, and nk and v_k separately signify the data size and the centroid of cluster C_k.

Both NMI and RI take values from 0 to 1, and larger values of NMI or RI indicate better clustering performance. Oppositely, smaller values of DBI are preferred, which convey that both the inter-cluster separation and the intra-cluster homogeneity are concurrently, relatively ideal in these situations. It is worth noticing that, however, similar to other internal criteria, DBI has the underlying drawback that smaller values do not necessarily indicate better information retrieval.

The trial ranges or the specific values of the core parameters in the involved algorithms are listed in Table 1 simultaneously. These trial ranges were also determined by the grid search strategy. Specifically, taking one algorithm running on one dataset as the example, in order to determine the appropriate parameter ranges, we first supposed a range for each parameter and evenly divided the initial range into several subintervals. Then, as depicted in Section 3.4, the nested loops, in which one parameter is located in one loop, were performed in order to implement the algorithm repeatedly with different parameter settings. Similarly, by means of the selected validity metric (e.g., NMI or DBI), the clustering effectiveness was recorded during the entire procedure. After the loops terminated, we attempted to change the current range of each parameter according to the following principles: (1) To gradually shrink the range, if the best score of the validity index located within the current range, (2) to gradually reduce the lower bound of the current range, if the best score of the validity index located in or near the lower bound, (3) to gradually increase the upper bound of the current range, if the best score of the validity index located in or near the upper bound. After several times of such trials, the appropriate parameter ranges of the algorithm on current dataset can be determined. Likewise, on other datasets, the above procedure was repeated similarly. By merging all the appropriate parameter ranges of the algorithm on all involved datasets, the eventual parameter trial ranges of the algorithm were achieved. For the specific parameter values recruited in those competitive algorithms, e.g. ECM, LSSMTC, STC and TSC, we referred generally to the authors’ recommendations in their literature as well as adjusting them according to our practices.

All of our experiments were performed on a PC with Intel Core i3-3240 3.4 GHz CPU and 4GB RAM, Microsoft Windows 7, and MATLAB 2010a. The experimental results are reported in the form of means and standard deviations of the adopted validity indices, which are the statistical results of running every algorithm 20 times on every dataset.

4.2. In artificial scenarios

To simulate the data scenarios for transfer clustering, we generated five artificial datasets: $X_S,X_T^{\mathrm{I}},X_T^{\mathrm{II}},X_T^{\mathrm{III}}$, and $X_T^{\mathrm{IV}}$. Among them, X_S simulates the only source domain dataset, and the others present four, target domain datasets with different data distributions. The supposed transfer scenarios are imagined as follows. The source domain dataset X_S is relatively pure and its data capacity is comparatively sufficient so that we can extract the intrinsic knowledge from it, i.e., the historical cluster centroids and the historical cluster centroid-based memberships of the patterns in the target domain. For this purpose, we generated X_S with four clusters and each cluster consisting of 250 samples, so its total capacity is 1000, as illustrated in Fig. 6. Let E_Ci and Σ_Ci denote the mean vector and the covariance matrix of the ith cluster in one dataset, respectively, then X_S was created via the MATLAB built-in function, mvnrnd(), with E_C1 [3 4], Σ_C1 = [10 0;0 10], E_C2 = [10 15], Σ_C2 = [25 0;0 7], E_C3 = [9 30], Σ_C3 = [30 0;0 20] and E_C4 = [20 5], Σ_C4 = [13 0;0 13]. As for the target domain datasets, we designed the following four particular scenes. $X_T^{\mathrm{I}}$ simulates the situation in which the data are rather insufficient and sparse, as indicated in Fig. 7(a). To this end, $X_T^1$ was generated with four clusters and each cluster merely including 20 data instances. More exactly, $X_T^{\mathrm{I}}$ was constituted with E_C1 = [3.5 4], Σ_C1 = [10 0;0 10], E_C2 = [11 13], Σ_C2 = [25 0;0 7], E_C3 = [9.5 29], Σ_C3 = [30 0;0 20], and E_C4 = [22 4.5], Σ_C4 = [13 0;0 13]. $X_T^{\mathrm{II}}$ depicts the case in which the data capacity is comparatively acceptable, although its data distribution differs from that in X_S to a great extent. For this purpose, we created $X_T^{\mathrm{II}}$ with E_Ci and Σ_Ci, i = 1, 2, 3, and 4, being the same as those in $X_T^{\mathrm{I}}$ despite each cluster being composed of 130 samples, as illustrated in Fig. 7(b). $X_T^{\mathrm{III}}$ and $X_T^{\mathrm{IV}}$ simulate the other, two, different scenes where the data are distorted by outliers and noise, respectively, although their capacities are also acceptable. Both $X_T^{\mathrm{III}}$ and $X_T^{\mathrm{IV}}$ were generated based on $X_T^{\mathrm{II}}$. More specifically, for $X_T^{\mathrm{III}}$, based on $X_T^{\mathrm{II}}$, we added another 35 data points by hand as the outliers, which were far away from all the existing individuals, as shown in Fig. 7(c) where the outliers are marked with the purple diamonds; for $X_T^{\mathrm{IV}}$, it was attained by adding the Gaussian noise with the mean and the deviation being 0 and 2.5, respectively, into $X_T^{\mathrm{II}}$, as shown in Fig. 7(d). Eventually, the data sizes of $X_T^{\mathrm{I}},X_T^{\mathrm{II}},X_T^{\mathrm{III}}$, and $X_T^{\mathrm{IV}}$ are separately 80, 520, 555, and 520 respectively.

Fig. 6.

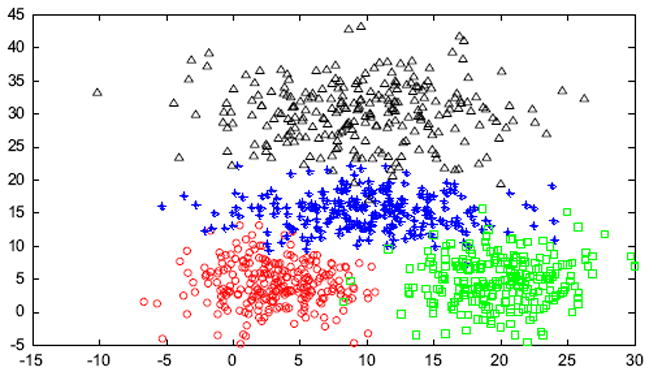
Artificial source domain dataset X_S.

Fig. 7.

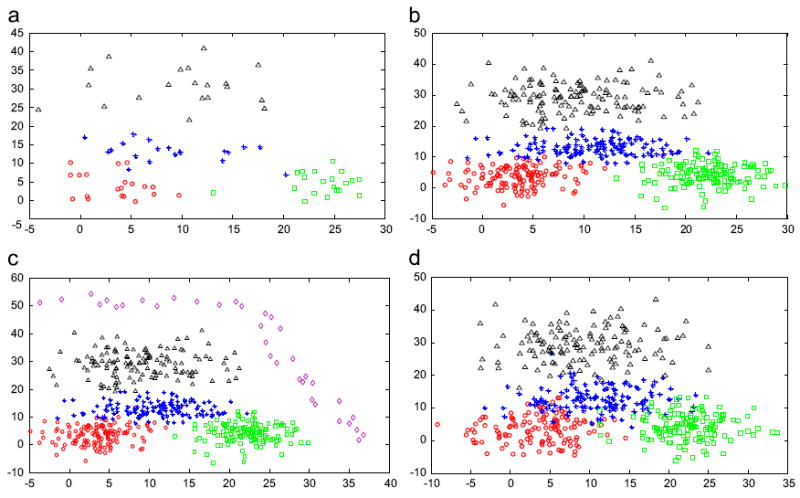
Artificial target domain datasets $X_T^{\mathrm{I}},X_T^{\mathrm{II}},X_T^{\mathrm{III}}$, and $X_T^{\mathrm{IV}}$.

Except for TSC, the other involved algorithms were separately implemented on these synthetic datasets. Among them, aside from the pure soft-partition clustering approaches, i.e., FCM, MEC, FC-QR, PCM, ECM, and QWGSD-FC, the other five algorithms need to use the source domain dataset X_S in different ways. Specifically, both TI-KT-CM and TII-KT-CM utilize the advanced knowledge drawn from X_S, i.e. the historical cluster centroids or the historical cluster centroid-based fuzzy memberships of the individuals in $X_T^{\mathrm{I}},X_T^{\mathrm{II}},X_T^{\mathrm{III}}$, and $X_T^{\mathrm{IV}}$, whereas the others directly use the raw data in X_S. As for TSC, it requires that the data dimension must be larger than the cluster number, and this condition cannot be satisfied in these synthetic data scenarios, therefore it did not run on these artificial datasets.

The clustering performance of each algorithm is listed in Table 2 in terms of the means and the standard deviations of NMI, RI, and DBI, where the top three scores of each index on each dataset are marked in the style of boldface and with “➀”, “➁” and “➂”, respectively. It should be mentioned that the experimental results of FCM with m = 2 and m taking the optimal settings within the given trial interval are separately listed in Table 2, due to the fact that the quadratic weight-based intra-cluster deviation measure in QWGSD-FC is equivalent to FCM’s formulation with m = 2. In this way, the practical regularization efficacy regarding Gini–Simpson diversity index in QWGSD-FC can be intuitively validated.

Table 2.

Clustering performance of the involved clustering algorithms on artificial datasets.

Dataset	Validity index	Algorithm
		FCM (m=2)	FCM	MEC	FC-QR	QWGSD-FC	PCM	ECM	LSSMTC	CombKM	STC	TI-KT-CM	TII-KT-CM
$X_T^{\mathrm{I}}$	NMI-mean	0.7747	0.8005	0.7669	0.8080	0.7978	0.8103	0.7373	0.7932	0.8426 ➂	0.7802	0.8926 ➁	0.9110 ➀
	NMI-std	5.23E-17	0	0.0743	0	1.17E-16	0	0.0349	0.0148	8.28E-17	0	0	0
	RI-mean	0.9177	0.9331 ➂	0.9066	0.9262	0.9288	0.866	0.859	0.9313	0.9116	0.9203	0.9639 ➁	0.9752 ➀
	RI-std	2.34E-16	0	0.0511	1.36E-16	1.17E-16	0	0.0404	0.0047	0	0	0	0
	DBI-mean	0.8011	0.8198	0.8059	0.7664	0.8088	0.6827 ➀	0.9079	0.8376	0.7646 ➂	0.8104	0.7641 ➁	0.7641 ➁
	DBI-std	9.79E-17	1.12E-16	0.0490	0	3.70E-17	0	0.055	0.0376	9.79E-16	0	0	0
$X_T^{\mathrm{II}}$	NMI-mean	0.8544	0.8544	0.8576	0.8539	0.8634 ➂	0.8571	0.7925	0.8059	0.8119	0.8500	0.8772 ➁	0.8977 ➀
	NMI-std	0	0	1.33E-16	0	0	1.36E-16	0	0	0.0011	0	0	0
	RI-mean	0.9510	0.9510	0.9528	0.9542	0.9534	0.9561 ➂	0.9181	0.9343	0.8814	0.9518	0.9600 ➁	0.9715 ➀
	RI-std	0	0	0	1.36E-16	0	0	0	0	0.0005	0	0	0
	DBI-mean	0.7499	0.7499	0.7407.3 ➂	0.7729	0.7272 ➀	0.777	0.7939	0.9316	0.7611	0.7437	0.7414	0.7324 ➁
	DBI-std	5.23E-17	5.23E-17	0	7.85E-17	0	0	1.11E-16	2.34E-16	7.49E-05	0	0	1.36E-16
$X_T^{\mathrm{III}}$	NMI-mean	0.7744	0.7839	0.7945	0.8022	0.8034	0.7949	0.8268 ➂	0.6715	0.7748	0.7871	0.8443 ➁	0.8763 ➀
	NMI-std	1.17E-16	0	0	1.17E-16	1.36E-16	0	0	0	0.0406	0	2.34E-16	0
	RI-mean	0.8724	0.8798	0.8932	0.9049	0.8972	0.8399	0.9097 ➂	0.8329	0.9025	0.9074	0.9180 ➁	0.9656 ➀
	RI-std	0	0	0	0	0	0	0	1.24E-16	0.0357	0	0	0
	DBI-mean	0.7782	0.7738	0.7945	0.7849	0.7637 ➂	0.7727	0.7384 ➀	0.9223	0.7912	0.7582 ➁	0.7982	0.7738
	DBI-std	0	0	0	0	1.17E-16	0	1.12E-16	0	0.0389	0	1.17E-16	0
$X_T^{\mathrm{IV}}$	NMI-mean	0.6913	0.7023	0.6464	0.7039	0.7108	0.7376 ➁	0.6958	0.6178	0.6265	0.6850	0.7212 ➂	0.7397 ➀
	NMI-std	1.48E-16	0	1.23E-16	0	1.17E-16	0	0.0848	1.17E-16	0.0026	0	0	0
	RI-mean	0.8880	0.8923	0.8006	0.8817	0.8969	0.9101 ➁	0.8594	0.8617	0.8286	0.8820	0.9010 ➂	0.9123 ➀
	RI-std	1.17E-16	0	0	0	0	0	0.0776	1.17E-16	0.0015	0	1.17E-16	0
	DBI-mean	0.8856	0.8734	0.8796	0.8556 ➀	0.8965	0.8718 ➂	0.956	1.1627	0.8705 ➁	0.8889	0.8899	0.8899
	DBI-std	1.17E-16	1.12E-16	0	0	2.34E-16	1.36E-16	0.088	1.17E-16	0.0029	0	1.17E-16	0

Based on these experimental results, we make some analyses as follows.

1. The data instances in $X_T^I$ are rather scarce and some clusters even partially overlap. In this case, the classic soft-partition clustering approaches usually cannot achieve desirable results as they are prone to being confused by the apparent data distribution, e.g. MEC and ECM. In addition, the data distribution in $X_T^I$ differs substantially from that in the source domain X_S such that the clustering effectiveness of LSSMTC, STC, and CombKM is distinctly worse than that of TI-KT-CM or TII-KT-CM, due to the poor entire reference value of the raw data in X_S in this case. In contrast, both TI- KT-CM and TII-KT-CM delicately utilize the concluded knowledge instead of the raw data in X_S as the guidance, i.e., the historical cluster centroids and their associated fuzzy memberships in X_S, and the reliability of these two types of knowledge is definitely stronger than that of raw data in $X_T^I$. As such, both TI-KT-CM and TII-KT-CM outperform the others easily.

2. Most algorithms achieve comparatively acceptable effectiveness on $X_T^{\mathrm{II}}$ as the data in $X_T^{\mathrm{II}}$ are relatively adequate and the data distribution in $X_T^{\mathrm{II}}$ is close to that in X_S, which conceals to a certain extent the dependence of related approaches to the source domain in this case.

3. In the situations of $X_T^{\mathrm{III}}$ and $X_T^{\mathrm{IV}}$ where the data are polluted by either the outliers or the noise, our proposed two transfer fuzzy clustering methods: TI-KT-CM and TII-KT-CM methods as well as the FCM’s derivative: ECM or PCM, exhibit more effective than the others, which demonstrates one of the merits of these methods, i.e., the better anti-interference capability.

4. As previously mentioned, the missions of multi-task clustering and transfer clustering are different. Specifically, multi-task clustering aims to simultaneously finish multiple tasks, and there should certainly be some interactivities between these tasks. However, transfer clustering focuses on enhancing the clustering effectiveness in the target domain by using some useful information from the source domain. Their different pursuits consequently cause the matching different clustering performances, as shown in Table 2. In summary, the clustering performance of those transfer clustering approaches, such as STC, TI-KT-CM, and TII-KT-CM, is generally better than that of the multi-task ones, e.g. LSSMTC and CombKM, in terms of the clustering results on the target domain datasets.

5. QWGSD-FC aims at integrating the most merits of FCM, MEC, and FC-QR as well as being concise in our research. As far as the results of the pure soft-partition clustering algorithms in Table 2 are concerned, it is clear that, in general, the performance of QWGSD-FC is better than or comparable to the others, even facing to PCM and ECM, two dedicated soft-partition clustering approaches devoted to coping with complex data situations. Particularly, the efficacy of the quadratically weighted intra-cluster deviation measure and the Gini–Simpson diversity measure can be verified by comparing the outcomes of QWGSD-FC with those of FC-QR and FCM (m = 2), respectively. Moreover, as described in Section 3, not only the framework but also the derivations regarding QWGSD-FC feature brief and straightforward. Therefore, putting them together, our intentions on QWGSD-FC are achieved.

6. Benefitting from the reliability of QWGSD-FC as well as the historical knowledge from the source domain, in general, both TI-KT-CM and TII-KT-CM exhibit relatively excellent clustering effectiveness on these synthetic datasets. Especially, owing to only relying on the advanced knowledge rather than the raw data in the source domain, they feature valuable stability in either the situation of data shortage or data impurity. As shown in Table 2, TII-KT-CM is always the best one and TI-KT-CM ranks at the top two or three, in terms of the well-accepted, authoritative NMI and RI indices.

7. Comparing TI-KT-CM with TII-KT-CM, the former refers to the historical cluster centroids solely, the latter, however, recruits the historical cluster centroids and their associated fuzzy memberships simultaneously. This means that TII-KT-CM has more distinctive, comprehensive learning capability with respect to historical knowledge than TI-KT-CM, which is directly responsible for its superiority to all the other candidates.

8. Both TI-KT-CM and TII-KT-CM overcome the others from the perspective of privacy protection as they only use the advanced knowledge in the source domain as the reference and this knowledge cannot be inversely mapped into the original data. Conversely, the other approaches thoroughly use the raw data in the source domain if needed.

In addition, based on Table 2, as previously mentioned, the instinctive flaw of the DBI index has been confirmed. That is, good clustering results in terms of the authoritative NMI and RI indices usually achieve relatively small DBI scores, whereas the smallest DBI value unnecessarily indicates the ground truth of data structure.

4.3. In real-life scenarios

In this subsection, we attempt to evaluate the performance of all involved algorithms in six, real-life transfer scenarios, i.e., texture image segmentation, text data clustering, human face recognition, dedicated KEEL datasets, human motion time series and email spam filtering. We first introduce the constructions regarding these data scenarios and then present the clustering results of all participants in them.

1. Texture image segmentation (Datasets: texture image segmentation 1 and 2, TIS-1 and TIS-2)

   We chose three different textures from the Brodatz texture database ¹ and constructed one texture image with 100 × 100 = 10,000 resolution as the source domain, as shown in Fig. 8(a). In order to simulate the target domains, we first composed another texture image, as indicated in Fig. 8(b), using the same textures and resolution as those in Fig. 8(a). Then we generated one derivative of Fig. 8(b) by adding noise, as shown in Fig. 8(c). With Fig. 8(a) acting as the source domain and Fig. 8(b) and (c) as the target domains, respectively, we generated two datasets for the scene of texture image segmentation, i.e., TIS-1 and TIS-2, by extracting the texture features from the corresponding images via the Gabor filter method [75]. The specific composition of TIS-1 and TIS-2 is listed in Table 3.

2. Text data clustering (Datasets: rec VS talk and comp VS sci)

   We selected four categories of text data: rec, talk, comp, and sci, as well as some of their sub-categories from the 20 News-groups text database ² in order to compose the two datasets, rec VS talk and comp VS sci, of the transfer scene of text data clustering. The categories and their sub-categories used in our experiments are listed in Table 4. Furthermore, the BOW toolkit [76] was adopted for data dimension reduction, which was originally up to 43,586. The eventual data dimension in both rec VS talk and comp VS sci is 350.

3. Human face recognition (Dataset: ORL)

   The famous ORL database of face ³ was enlisted in our work for constructing the transfer scene of human face recognition. Specifically, we selected 8 × 10 = 80 facial images from the original database, i.e., eight different faces and ten images per face. One frontal facial image of each person is illustrated in Fig. 9. We arbitrarily placed eight images per face in the source domain, and the remainder two in the target domain. In order to further widen the difference between the source and the target domain as well as enlarge the data capacity in each domain, we separately rotated each image anticlockwise with 10 and 20 degrees, then obtained two derivatives of each original image. Thus, the source domain and the target domain eventually contain 192 and 48 images, respectively. In view of the resolution of each image up to 92 × 112 = 10,304 pixels, we cannot directly use the pixel-gray values in each image as the features. Therefore, the principal component analysis (PCA) method was subsequently performed on the original features of pixel-gray values, and we obtained the eventual dataset with the dimension being 239.

4. The dedicated KEEL datasets (Datasets: cleveland and mammographic)

   In this scene, two dedicated datasets in the Knowledge Extraction based on Evolutionary Learning (KEEL) repository ⁴, i.e., cleveland and mammographic, were taken in our experiments. In each, the data capacity of the testing set is less than 90, whereas the data capacity in the training set is around nine times that in the testing set. Thus, one of our supposed transfer conditions is met, i.e., the data in the target domain are quite insufficient, and this data shortage in the target domain is prone to causing the data distribution inconsistence between the source domain and the target domain. Meanwhile, as real-life datasets, they usually contain uncertainties, such as noise and outliers. Putting them together, it should be suitable that these two real-life datasets are used to verify the effectiveness of all involved algorithms. As such, the testing set in cleveland or mammographic was regarded as the target domain and the training set as the source domain in our experiment.

5. Human motion time series (Dataset: HMTS)

   The dataset for ADL (Activities of Daily Living) recognition with wrist-worn accelerometer data set in the UCI machine learning repository ⁵ was recruited for the clustering on human motion time series. The initial dataset consisted of many three-variate time series recording three signal values of one sensor worn on 16 volunteers’ wrists while they conducted 14 categories of activities in daily living, including: climbing stairs, combing hair, drinking, sitting down, walking, etc. In order to simulate the transfer scene, the volunteers were divided into two groups via their genders, and 10 categories of activities, whose series number are greater than 15, were employed in our experiment. Due to the fact that the female’s total records are distinctly more than the male’s, we used all the female’s time series as the source domain and the male’s as the target domain. The initial properties of these involved activities and their affiliated time series are listed in Table 5. Because the time series dimensions (also, series lengths) of different categories of activities are inconsistent and they vary from hundreds to thousands, as shown in Table 5, the multi-scale discrete Haar wavelet decomposition [77] strategy was adopted in our study for dimensionality reduction. After three to six levels of Haar discrete wavelet transform (DWT) [77] performed on these raw time series, we truncated the intermediates with the same length being 17 and reshaped them into the forms of vectors, thus we attained the eventual dataset called human motion time series (HMTS) in our experiment with the final data dimension being 17 × 3 = 51.

6. Email spam filtering (Datasets: ESF-1 and ESF-2)

   The email spam repository, released by the ECML/PKDD Discovery Challenge 2006 ⁶, was adopted in our experiment. The data contains a set of publicly available messages as well as several sets of email messages from different users. As disclosed in [78], there exist distinct data distribution discrepancies between the publicly available messages and the ones collected by users, therefore these data are suited to construct our transfer learning domains. All messages in the repository were preprocessed and transformed into a bag-of-words vector space representation. Attributes were the term frequencies of the words. For our experiment, 4000 samples taken from the publicly available messages as well as separate 2500 samples obtained from two users’ email messages were recruited in order to construct our two transfer clustering datasets: ESF-1 and ESF-2. Due to the too high dimension in the original data (originally, as high as 206,908), the BOW toolkit [76] was adopted again for dimension reduction in our work, and the eventual data dimension in both ESF-1 and ESF-2 is 500, i.e., the 500 highest term frequencies of the words in each involved message were extracted as the eventual features in our experiment. The composition regarding ESF-1 and ESF-2 is listed in Table 6. Here, the task for all participating approaches is to identify the spam and non-spam emails.

Fig. 8.

Texture images adopted to construct TIS-1 and TIS-2. (a) Source domain in both TIS-1 and TIS-2 (b) Target domain in TIS-1 (c) Target domain in TIS-2.

Table 3.

Composition of texture image scenario.

Dataset	Source domain	Target domain
TIS-1	Fig. 8(a)	Fig. 8(b)
TIS-2	Fig. 8(a)	Fig. 8(c)

Table 4.

Categories and sub-categories of 20Newsgroups adopted in text data clustering.

Dataset	Source domain	Target domain
rec VS talk	rec.autos	rec.sport.baseball
	talk.politics.guns	talk.politics.mideast
comp VS sci	comp.sys.mac.hardware	comp.sys.ibm.pc.hardware
	sci.med	sci.electronics

Fig. 9.

Human facial dataset: ORL.

Table 5.

Raw properties of partial, involved activities and their af3liated time series in HMTS.

Property	Activity
	Climb_stairs		Comb_hair		Descend_stairs		Drink_glass		Getup_bed		Liedown_bed		Pour_water		Sitdown_chair		Standup_chair		Walk
	S	T	S	T	S	T	S	T	S	T	S	T	S	T	S	T	S	T	S	T
Series number	47	55	25	6	36	6	62	38	59	42	22	6	68	32	71	29	70	32	34	66
Max dimension	805	555	1282	734	594	507	1322	746	769	736	607	736	810	507	691	474	545	409	3153	1981
Min dimension	166	253	403	571	156	332	270	255	256	303	212	321	244	336	131	152	141	144	187	493

Note: S and T denote the source domain and the target domain, respectively.

Table 6.

Composition of email spam filtering scenario.

Dataset	Source domain	Target domain
ESF-1	Publicly available messages (size: 4000)	User 1’s messages (size: 2500)
ESF-2		User 2’s messages (size: 2500)

The details of all involved real-life datasets in our experiments are listed in Table 7. Based on our extensively empirical studies, for easily attaining the appropriate parameter ranges involved in each algorithm (particularly, for the regularization parameters), the data would better be normalized before being used in experiments. To this end, we transformed the range of each data dimension in all enlisted real-life datasets into the same interval [0,1] via the commonest data normalization equation, $x_{\mathit{id}}^{\prime }=(x_{\mathit{id}}-\min \{x_{\mathit{id}},\dots x_{\mathit{Nd}}\})/\max \{x_{1d},\dots x_{\mathit{Nd}}\}-\min \{x_{1d},\dots x_{\mathit{Nd}}\})$, where i and d denote the sample and the dimension indices, respectively.

Table 7.

Details of real-life datasets involved in our experiments.

Transfer scenario	Dataset	Transfer domain	Data size	Dimension	Cluster number
Texture image segmentation	TIS-1	Source domain	10,000	49	3
		Target domain	10,000	49
	TIS-2	Source domain	10,000	49	3
		Target domain	10,000	49
Text data clustering	rec VS talk	Source domain	1500	350	2
		Target domain	500	350
	comp VS sci	Source domain	1500	350	2
		Target domain	500	350
Human face recognition	ORL	Source domain	192	239	8
		Target domain	48	239
Dedicated KEEL datasets	cleveland	Source domain	267	13	5
		Target domain	30	13
	mammographic	Source domain	747	5	2
		Target domain	83	5
Human motion time series	HMTS	Source domain	494	51	10
		Target domain	312	51
Email spam 3ltering	ESF-1	Source domain	4000	500	2
		Target domain	2500	500
	ESF-1	Source domain	4000	500	2
		Target domain	2500	500

Table 8 reports the clustering performance of the 12 clustering algorithms running on these real-life datasets in terms of the NMI, RI and DBI metrics. As previously explained, among these approaches, FCM, MEC, FC-QR, PCM, ECM and QWGSD-FC, six pure soft-partition clustering approaches, ran directly on the target domain datasets, and the others worked by concurrently using both the source domain and the target domain datasets in different ways.

Table 8.

Clustering performance (NMI, RI, and DBI) of all involved algorithms on real-life datasets.

Dataset	Validity index	Algorithm
		FCM (m=2)	FCM	MEC	FC-QR	QWGSD-FC	PCM	ECM	LSSMTC	CombKM	STC	TSC	TI-KT-CM	TII-KT-CM
TIS-1	NMI-mean	0.4959	0.4965	0.5116	0.5306	0.5473	0.5044	0.4925	0.5757	0.5200	0.5148	0.6385 ➂	0.6419 ➁	0.6589 ➀
	NMI-std	0	0.0030	7.85E-17	0.0259	0	0.0004	0.0006	0	0	0	0	0	0
	RI-mean	0.7685	0.7760	0.8409	0.7838	0.7834	0.7834	0.7970	0.7965	0.7807	0.7680	0.8468 ➂	0.8713 ➀	0.8626 ➁
	RI-std	0	0.0039	1.36E-16	0.0223	0	0.0001	0.0002	0	0	0	0	0	0
	DBI-mean	1.8865 ➂	2.5104	2.6407	2.1269	2.2703	2.8019	2.3504	2.0075	1.8885	3.5779	2.8991	1.8782 ➀	1.8852 ➁
	DBI-std	0	0.9534	1.57E-16	0.2079	0	0.0035	0.0034	0	0	0	0	0	0
TIS-2	NMI-mean	0.4595	0.4641	0.4897	0.4767	0.5134	0.4501	0.4183	0.4630	0.4480	0.3237	0.5462 ➂	0.5885 ➁	0.6034 ➀
	NMI-std	0	3.37E-04	0	0.0387	0	0.0017	0.0234	0.1301	0	0	0	0	0
	RI-mean	0.7502	0/7497	0.7800	0.7766	0.7695	0.7420	0.7332	0.7587	0.7569	0.6577	0.7960 ➂	0.8231 ➁	0.8344 ➀
	RI-std	0	0.0013	0	0.0072	0	0.0025	0.0119	0.0594	1.36E-16	0	0	0	0
	DBI-mean	4.4014	3.8952	3.0241 ➁	4.5383	2.5411 ➀	3.9065	3.7990	3.4821	3.7441	3.2161	3.3464	3.1236 ➂	3.2931
	DBI-std	0	0.2034	0	0.6003	0	0.7946	0.2185	0.2656	0	0	0	0	0
rec VS talk	NMI-mean	0.2021	0.2021	0.2691	0.1021	0.2925	0.2047	0.2697	0.0818	0.0572	0.1865	0.4224 ➁	0.3767 ➂	0.4282 ➀
	NMI-std	5.85E-17	5.85E-17	0	1.70E-17	0.0377	0	0.0089	1.46E-17	0.0201	0.0055	0	1.17E-16	5.85E-17
	RI-mean	0.5925	0.5925	0.5960	0.5048	0.6124	0.5942	0.5856	0.5021	0.5002	0.5747	0.7359 ➀	0.6199 ➂	0.6842 ➁
	RI-std	0	0	0	0	0.0161	0	0.0142	0	0.0004	0.0078	0	1.17E-16	0
	DBI-mean	4.5510	4.5510	4.2649	2.7448	4.3947	4.5578	5.9097	2.2505 ➂	2.5320	3.9824	1.7190 ➁	2.8726	1.6871 ➀
	DBI-std	9.36E-16	9.36E-16	9.36E-16	5.44E-16	0.2925	0	0.1332	0	4.68E-16	0	0	0	9.36E-16
comp VS sci	NMI-mean	0.0509	0.0509	0.1049	0.1108	0.1216	0.0408	0.1015	0.0196	0.0021	0.1240	0.3073 ➀	0.1565 ➂	0.2065 ➁
	NMI-std	7.31E-18	0	0.0717	0.0942	0.0212	0	0.0149	1.83E-18	0	0.0027	0	7.31E-18	7.31E-18
	RI-mean	0.5160	0.5160	0.5321	0.5241	0.5272	0.5813	0.5534	0.4990	0.4990	0.5372	0.6781 ➀	0.6138 ➂	0.6238 ➁
	RI-std	1.17E-16	0	0.0262	0.0218	0.0056	0	0.0704	5.85E-17	5.85E-17	0.0140	0	0	0
	DBI-mean	6.1346	6.1346	6.1826	4.3646	5.6124	5.1346	5.3052	1.2699 ➀	2.0238 ➂	5.6792	1.8979 ➁	3.6788	2.8678
	DBI-std	9.36E-16	0	0.6981	2.6814	0.1901	0	0.0256	0	0.3801	0	0.01673	9.36E-16	9.36E-16
ORL	NMI-mean	0.3365	0.3563	0.3157	0.3663	0.3637	0.3812 ➂	0.3594	0.3582	0.2124	0.3310	0.2950	0.4979 ➁	0.7970 ➀
	NMI-std	0.0363	0	0.0593	0.0058	0.0388	0	0.0514	0	0.0954	0.0183	0.0054	5.85E-17	0
	RI-mean	0.8031	0.8129	0.8057	0.8168	0.8062	0.8200 ➁	0.7991	0.7748	0.5870	0.8116	0.8124 ➂	0.7730	0.9253 ➀
	RI-std	0.0108	0	0.0093	5.12E-4	0.0119	0	0.0100	0	0.1806	0.0034	0.0004	1.17E-16	0
	DBI-mean	3.3226	3.2060 ➁	3.3761	3.2942	3.3282	3.2974	3.3717	5.7024	6.1604	3.5186	3.2240 ➂	3.1844 ➀	3.4174
	DBI-std	0.0363	0	0.0551	0.0570	0.0774	5.44E-16	0.0229	0	9.36E-16	0.0361	0	4.68E-16	4.68E-16
cleveland	NMI-mean	0.2632	0.2832	0.3211	0.3250	0.3360 ➂	0.2527	0.3016	0.2598	0.2356	0.2252	0.1946	0.3432 ➁	0.3701 ➀
	NMI-std	0.0157	0	0.0063	0	5.85E-17	0	0.0276	0	0.0449	0	0.0006	0	5.85E-17
	RI-mean	0.6676 ➀	0.6023	0.6589 ➁	0.6207	0.6580 ➂	0.5862	0.6299	0.6138	0.5795	0.6137	0.6195	0.6506	0.6016
	RI-std	0.0047	0	0.0029	0	0	0	0.0033	0	0.0188	0	0.0008	0	0
	DBI-mean	2.5283	1.5314	1.6296	1.8426	1.8564	1.4324 ➁	1.9479	1.6003	1.6257	2.5723	0.9642 ➀	2.1132	1.5101 ➂
	DBI-std	0.2801	0	0.0069	0	0	2.72E-16	0.5797	0	0.0028	0	0.0081	4.68E-16	2.34E-16
mammographic	NMI-mean	0.5429	0.5429	0.5233	0.5512	0.5512	0.5544 ➂	0.5336	0.4723	0.5233	0.5233	0.3926	0.5920 ➁	0.6559 ➀
	NMI-std	1.17E-16	0	1.17E-16	0	1.17E-16	0	0	5.85E-17	1.17E-16	0	0	1.17E-16	1.17E-16
	RI-mean	0.8213	0.8213	0.7855	0.8043	0.8043	0.8234 ➂	0.8125	0.7496	0.7855	0.7881	0.7205	0.8424 ➁	0.8668 ➀
	RI-std	1.17E-16	1.17E-16	1.17E-16	0	1.17E-16	0	0	1.17E-16	1.17E-16	0	0	1.17E-16	1.17E-16
	DBI-mean	0.8706	0.8706	0.7051 ➂	0.7114	0.7114	0.7274	0.7601	0.7051 ➂	0.6883 ➁	0.7051 ➂	0.7658	0.6601 ➀	0.7051 ➂
	DBI-std	1.17E-16	1.17E-16	1.17E-16	0	0	0	0	1.17E-16	0	0	0	0	1.17E-16
HMTS	NMI-mean	0.5660	0.5771	0.5655	0.6203 ➂	0.6162	0.4287	0.6020	0.4491	0.5120	0.5914	0.5986	0.6549 ➁	0.6765 ➀
	NMI-std	0.0089	1/12E-16	0.0154	0.0225	0.0203	6.80E-16	0.0224	0	0	0.0101	0.0040	1.17E-16	0
	RI-mean	0.8671	0.8820	0.7929	0.8814	0.8829	0.6773	0.8847 ➂	0.7515	0.7745	0.8686	0.8862 ➁	0.8726	0.9020 ➀
	RI-std	0.0028	0	0.0065	0.0105	0.0106	1.36E-16	0.0109	0	1.17E-16	0.0003	0.0002	1.17E-16	0
	DBI-mean	1.6870	1.7065	1.4513	1.5514	1.4000	3.3071	2.1048	1.0867 ➁	1.0951 ➂	1.4873	0.7434 ➀	1.4931	1.3209
	DBI-std	0.1424	0	0.1386	0.1176	0.1515	5.44E-16	0.0861	2.34E-16	2.34E-16	0	0.0046	0	0
ESF-1	NMI-mean	0.2357	0.2811	0.3219	0.3607	0.3808 ➂	0.2473	0.2086	0.2654	0.2373	0.3072	0.2748	0.4624 ➁	0.5159 ➀
	NMI-std	0	0.0171	0.0092	6.80E-16	0	0	0.0034	0	0.0522	0	0	0	0
	RI-mean	0.5907	0.6073	0.6958 ➂	0.6359	0.6500	0.5785	0.5408	0.6704	0.6125	0.6556	0.5964	0.7518 ➁	0.8030 ➀
	RI-std	0	0.0152	0.0039	0	0	0	0.0016	0	0.0271	0	0	0	0
	DBI-mean	5.5604	5.0228	4.9623	4.1555 ➂	4.2210	6.3618	4.2102	5.2584	5.5093	4.2970	4.6440	3.8630 ➁	3.1765 ➀
	DBI-std	0	0.2583	0.0149	0	0	0	0.0220	0	0.3404	0	0	0	0
ESF-2	NMI-mean	0.3929	0.3946	0.4128	0.4595	0.4780 ➂	0.3445	0.3389	0.4121	0.3997	0.3895	0.3492	0.5218 ➁	0.5926 ➀
	NMI-std	0.0024	0	0	0	0	0	0.0719	6.20E-16	0.1747	0	0	0	0
	RI-mean	0.7427	0.7438	0.7067	0.7410	0.7791 ➂	07485	0.6901	0.7062	0.6840	0.6043	0.6498	0.8410 ➁	0.8467 ➀
	RI-std	0.0016	0	0	0	0	0	0.0220	0	0.0769	0	0	0	0
	DBI-mean	5.5225	5.5217	5.4036	5.4342	5.4882	5.7682	5.3934	5.4030	5.4648	4.7678	4.3788 ➂	3.9202 ➁	3.8236 ➀
	DBI-std	0.0011	0	0	0	0	0	0.6351	0	0.5785	0	0	0	0

As shown in Table 8, the reliability of QWGSD-FC has been verified once again. Specifically, as far as the clustering effectiveness of six pure soft-partition clustering methods is concerned, QWGSD-FC is better than or comparable with the others again. Especially, compared with that in previous artificial scenarios, the superiority of QWGSD-FC generally looks more obvious in these real-life data scenarios. Moreover, benefiting from the advanced knowledge from the source domain, both TI-KT-CM and TII-KT-CM also feature relatively excellent clustering effectiveness and stability. More exactly, in terms of the most authoritative NMI validity index, TII-KT-CM is always the best except on the comp VS sci dataset, and TI-KT-CM still ranks at the top 2 or top 3. In particular, referring to the NMI index again, compared with MEC, one conventional, soft-partition clustering method with maximum entropy optimization, the average performance improvement of TI-KT-CM is approximately 29.8%, and of TII-KT-CM is even up to 52.4%, in these real-life data scenarios. In addition, the other analyses and conclusions that we performed over those artificial datasets also hold on these real-life ones. In order to save paper space, we no longer repeat here.

It is worth discussing that neither TI-KT-CM nor TII-KT-CM achieved desirable scores on the comp VS sci dataset, despite the optimal parameter settings. In our view, the inherent data inhomogeneity existing in this dataset caused such phenomenon. As previously explained, both TI-KT-CM and TII-KT-CM need to use the knowledge from the source domain, i.e., the historical cluster centroids and their associated fuzzy memberships, and the knowledge is usually acquired by performing one, conventional, soft-partition clustering approach in the source domain, such as MEC in our work. However, we found the best NMI score of MEC was only approximately 0.1 in the source domain in comp VS sci, even at the optimal parameter settings, which indicates that both TI-KT-CM and TII-KT-CM cannot obtain desirable historical knowledge from the source domain in this situation. As the evidence shows in Table 8, all 12 algorithms failed on comp VS sci, and the best score of TSC is merely around 0.3. This distinctly demonstrates the data inconsistency existing in the dataset.

Moreover, the segmentation results of all the 12 algorithms in Fig. 8(b) and (c) are separately illustrated in Figs. 10 and 11 where the pixels belonging to the same clusters are shown in the same colors in each sub-figure of each algorithm. Intuitively, the last three algorithms, i.e., TSC, TI-KT-CM and TII-KT-CM, achieved better segmentations than the others.

Fig. 10.

Segmentation results of all involved algorithms on Fig. 8(b). (a) FCM(m=2) (b) MEC (c) FC-QR (d) QWGSD-FC (e) PCM (f) ECM (g) LSSMTC (h) CombKM (i) STC (j) TSC (k) TI-KT-CM and (l) TII-KT-CM.

Fig. 11.

Segmentation results of all involved algorithms on Fig. 8(c). (a) FCM(m=2) (b) MEC (c) FC-QR (d) QWGSD-FC (e) PCM (f) ECM (g) LSSMTC (h) CombKM (i) STC (j) TSC (k) TI-KT-CM and (l) TII-KT-CM.

4.4. Robustness analyses

Last but not the least, in order to completely demonstrate the reliability of our research, we have also appraised the parameter robustness of our proposed TI-KT-CM and TII-KT-CM algorithms with respect to their core parameters, i.e., in TI-KT-CM, the Gini–Simpson diversity measure parameter β and the transfer regularization parameter γ are involved, and in TII-KT-CM, in addition to β and γ, the transfer trade-off factors η is also included. For each algorithm on each dataset, either the synthetic or the real-life, we took turns selecting one parameter and then gradually varied its value with fixing the other parameters, meanwhile recorded the clustering performance of TI-KT-CM and TII-KT-CM in terms of NMI, RI and DBI. We attempt to exhibit the effectiveness curve of each validity index with respect to each approach on each dataset, based on these records. To save paper space, here we only separately report the experimental results of TI-KT-CM and TII-KT-CM on two synthetic datasets, $X_T^{\mathrm{I}}$ and $X_T^{\mathrm{IV}}$, and two real-life transfer datasets, i.e., ORL and cleveland..

On $X_T^{\mathrm{I}}$, TI-KT-CM achieved the optimum with β = 90 and γ = 0.35 during the grid-search procedure, on $X_T^{\mathrm{IV}}$ with β = 60 and γ = 0.05, on ORL with β = 0.05 and γ = 0.05, and on cleveland with β = 0.2 and γ = 0.05. As for TII-KT-CM, on $X_T^{\mathrm{I}}$ with β = 2, γ = 0.45 and η = 0.1, on $X_T^{\mathrm{IV}}$ with β = 60, γ = 0.05, and η = 0.9, on ORL with β = 0.05, γ = 0.2, and η = 0.05, and on cleveland with β = 30, γ = 2, and η = 0.7.

The performance curves of TI-KT-CM on these four datasets are illustrated in Fig. 12 where Fig 12(a) and (b) shows the cases on $X_T^{\mathrm{I}}$, Fig 12(c) and (d) is on $X_T^{\mathrm{IV}}$, Fig 12(e) and (f) is on ORL, and Fig 12 (g) and (h) is on cleveland. Likewise, Fig. 13 indicates the situations of TII-KT-CM with Fig 13(a)–(c) on $X_T^{\mathrm{I}}$, Fig 13(d)–(f) on $X_T^{\mathrm{IV}}$, Fig 13 (g)–(i) on ORL, and Fig 13(j)–(l) on cleveland.

Fig. 12.

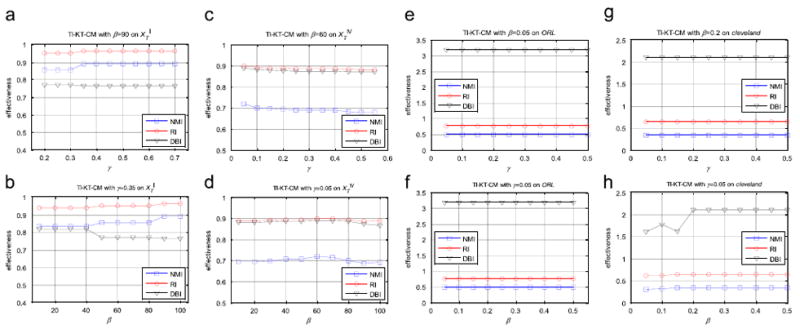
Performance curves of TI-KT-CM with respect to parameters γ and β on $X_T^{\mathrm{I}},X_T^{\mathrm{IV}}$, ORL, and Cleveland. (a) TI-KT-CM on $X_T^{\mathrm{I}}$, β is fixed and γ varies; (b) TI-KT-CM on $X_T^{\mathrm{I}}$, γ is fixed and β varies; (c) TI-KT-CM on $X_T^{\mathrm{IV}}$, β is fixed and γ varies; (d) TI-KT-CM on $X_T^{\mathrm{IV}}$, γ is fixed and β varies; (e) TI-KT-CM on ORL, β is fixed and γ varies; (f) TI-KT-CM on ORL, γ is fixed and β varies; (g) TI-KT-CM on cleveland, β is fixed and γ varies; (h) TI-KT-CM on cleveland, γ is fixed and β varies.

Fig. 13.

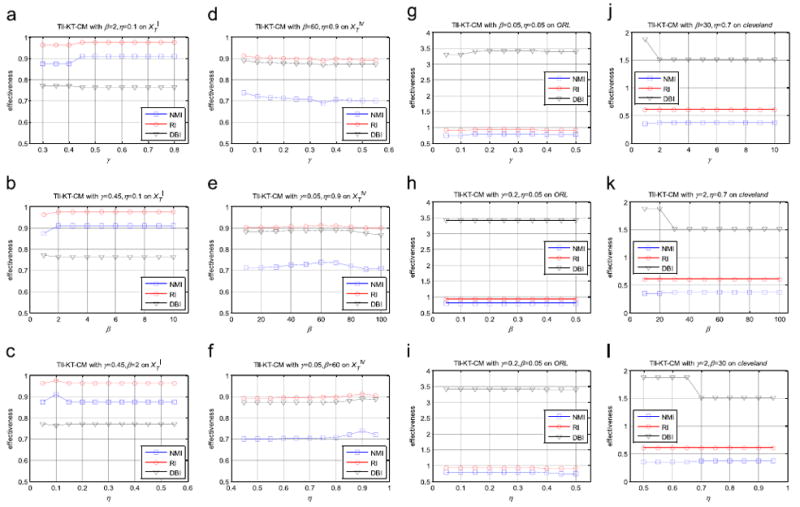
Performance curves of TII-KT-CM with respect to parameters γ, β, and η on $X_T^{\mathrm{I}},X_T^{\mathrm{IV}}$, ORL, and Cleveland. (a) TII-KT-CM on $X_T^{\mathrm{I}}$, β and η are fixed, and γ varies; (b) TII-KT-CM on $X_T^{\mathrm{I}}$, γ and η are fixed, and β varie; (c) TII-KT-CM on $X_T^{\mathrm{I}}$, and β are fixed, and η varies; (d) TII-KT-CM on $X_T^{\mathrm{IV}}$, β and η are fixed, and γ vari; (e) TII-KT-CM on $X_T^{\mathrm{IV}}$, γ and η are fixed, and β varies; (f) TII-KT-CM on $X_T^{\mathrm{IV}}$, γ and β are fixed, and η varies; (g) TII-KT-CM on ORL, β and η are fixed, and γ varies; (h) TII-KT-CM on ORL, γ and η are fixed, and β varie; (i) TII-KT-CM on ORL, γ and β are fixed, and η varie; (j) TII-KT-CM on cleveland, β and η are fixed, and γ varies; (k) TII-KT-CM on cleveland, γ and η are fixed, and β varies; (l) TII-KT-CM on cleveland, γ and β are fixed, and η varies.

As seen in Figs. 12 and 13, the clustering effectiveness of both TI-KT-CM and TII-KT-CM is relatively stable when their core parameters locate within proper ranges, which demonstrates that they both feature the quite excellent robustness against parameter settings.

5. Conclusions

To resolve the issue that existing soft-partition clustering approaches still cannot effectively cope with the situations where the data are quite insufficient or much distorted by plenty of noise or outliers, in this manuscript our work proceeds from three major aspects. (1) Based on the deep analyses regarding FCM, MEC and FC-QR, we first propose the delicate QWGSD-FC model which inherits the most merits of these three base models. (2) By means of two strategies of transfer learning, we devise two types of transfer optimization formulations in the forms of Eqs. (13) and (15), respectively. (3) Combining the previous two steps of work, we subsequently put forward two types of cross-domain, soft-partition clustering frameworks and their matching algorithms, i.e., type-I/type-II knowledge-transfer-oriented c-means (TI-KT-CM and TII-KT-CM). In addition, we prove the convergence of both TI-KT-CM and TII-KT-CM, and discuss the parameter settings involved in them. The experimental studies in both the artificial and the real-life transfer scenarios demonstrate that both TI-KT-CM and TII-KT-CM are of good cross-domain clustering effectiveness as well as parameter robustness, and, furthermore, that TII-KT-CM works better than TI-KT-CM benefiting from the more comprehensive ability of knowledge reference.

Biographies

Pengjiang Qian received his Ph.D. degree from Jiangnan University in March, 2011. He is an Associate Professor at the School of Digital Media, Jiangnan University, Wuxi, Jiangsu, China. He is now working at Case Western Reserve University, Cleveland, Ohio, USA as a research scholar and doing research in medical image processing. He has authored or co-authored more than 30 papers published in international/national journals and conferences. His research interests include data mining, pattern recognition, bioinformatics and their applications, such as analysis and processing for medical imaging, intelligent traffic dispatching, and advanced business intelligence in logistics.

Shouwei Sun is a M.S. candidate at the School of Digital Media, Jiangnan University, Wuxi, Jiangsu, China. His research interests include pattern recognition as well as bioinformatics and their applications.

Yizhang Jiang is a Ph.D. candidate at the School of Digital Media, Jiangnan University, Wuxi, Jiangsu, China. He is also now a research assistant in the computing department of the HongKong Polytechnic University and has been so for almost one year. He has published several papers in international journals including IEEE Trans. Fuzzy Systems and IEEE Trans. Neural Networks and Learning Systems. His research interests include pattern recognition, intelligent computation, and their applications.

Kuan-Hao Su received his Ph.D. from National Yang-Ming University in 2009, Taiwan (R.O.C.). He is now working as a research associate in the Department of radiology, Case Western Reserve University, Cleveland, Ohio, USA. His research interests include molecular imaging, tracer kinetic modeling, pattern recognition, and machine learning.

Tongguang Ni is a Ph.D. candidate at the School of Digital Media, Jiangnan University, Wuxi, Jiangsu, China. He has published nearly 10 papers in international/national journals, such as Information Science and the Journal of Information Science and Engineering. His research interest focuses on pattern recognition and its applications.

Shitong Wang received an M.S. degree in computer science from Nanjing University of Aeronautics and Astronautics, China, in 1987. He has visited London University and Bristol University in the U.K., Hiroshima International University, and Osaka Prefecture University in Japan, Hong Kong University of Science and Technology and Hong Kong Polytechnic University in Hong Kong, as a Research Scientist in recent 10 years. Currently, he is a Full Professor at the School of Digital Media, Jiangnan University, Wuxi, Jiangsu, China. His research interests include artificial intelligence, neuro-fuzzy systems, pattern recognition, and image processing. He has published nearly 100 papers in international/national journals and has authored seven books.

Raymond F. Muzic, Jr. earned his Ph.D. degree from Case Western Reserve University in 1991. He is currently an Associate Professor of Radiology, Biomedical Engineering, and General Medical Sciences – Oncology at Case Western Reserve University, Cleveland, Ohio, USA. His research focus has been on the development and application of quantitative methods for medical imaging. He has authored or co-authored approximately 50 peer-reviewed articles. He has lead or been a team member on numerous, funded research projects. He has also had the pleasure to serve as an advisor for doctoral students.

Appendix A. Proofs

A.1 Proof of Theorem 1

Proof

In terms of the Lagrange optimization, the minimization of Φ_TI–KT–CM in Eq. (14) can be converted to the following unconstrained minimization problem:

$$\begin{array}{l}{L}_1=\sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2{\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2+\beta \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2+\gamma \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2{\Vert {\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i\Vert }^2\\ +\sum _{j=1}^N{\alpha }_j(1-\sum _{i=1}^C{u}_{ij}),\end{array}$$ (A.1)

where α_j, j = 1, …, N, are the Lagrange multipliers.

By setting the derivatives of L₁ to zero with respect to v_i and u_ij, respectively, we arrive at:

$$\begin{array}{l}\frac{\partial L_1}{\partial {\mathbf{v}}_i}=\sum _{j=1}^N{u}_{ij}^2({\mathbf{x}}_j-{\mathbf{v}}_i)+\gamma \sum _{j=1}^N{u}_{ij}^2({\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i)=0\\ \iff v_i(1+\gamma )\sum _{j=1}^N{u}_{ij}^2=\sum _{j=1}^N{u}_{ij}^2{x}_j+\gamma {\widehat{v}}_i\sum _{j=1}^N{u}_{ij}^2.\end{array}$$ (A.2)

We can obtain Eq. (18) immediately by rearranging Eq. (A.2).

$$\begin{array}{l}\frac{\partial L_1}{\partial u_{ij}}=2u_{ij}{\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2+2\beta u_{ij}+2\gamma u_{ij}{\Vert {\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i\Vert }^2-{\alpha }_j=0\\ \iff u_{ij}=\frac{{\alpha }_j}{2{\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2+2\beta +2\gamma {\Vert {\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i\Vert }^2}.\end{array}$$ (A.3)

Because of ${\sum }_{k=1}^C{u}_{kj}=1$, according to Eq. (A.3), we have

$$\begin{array}{l}{\alpha }_j\sum _{k=1}^C\frac{1}{2{\Vert {\mathbf{x}}_j-{\mathbf{v}}_k\Vert }^2+2\beta +2\gamma {\Vert {\widehat{\mathbf{v}}}_k-{\mathbf{v}}_k\Vert }^2}=1\iff \\ {\alpha }_j=\frac{1}{\sum _{k=1}^C\frac{1}{2{\Vert {\mathbf{x}}_j-{\mathbf{v}}_k\Vert }^2+2\beta +2\gamma {\Vert {\widehat{\mathbf{v}}}_k-{\mathbf{v}}_k\Vert }^2}}.\end{array}$$ (A.4)

We then obtain Eq. (19) by substituting Eq. (A.4) into Eq. (A.3).

A.2 Proof of Theorem 2

Proof

Likewise, by using the Lagrange optimization, Eq. (17) can be converted to the following unconstrained minimization problem:

$$\begin{array}{l}{L}_2=\sum _{i=1}^C\sum _{j=1}^N\left(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right){\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2+\beta \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^2\\ +\gamma \sum _{i=1}^C\sum _{j=1}^N\left(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right){\Vert {\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i\Vert }^2+\sum _{j=1}^N{\alpha }_j(1-\sum _{i=1}^C{u}_{ij}),\end{array}$$ (A.5)

where α_j, j = 1, …, N, are the Lagrange multipliers.

We separately generate the derivatives of L₂ with respect to v_i and μ_ij and set them to 0:

$$\begin{array}{l}\frac{\partial L_2}{\partial {\mathbf{v}}_i}=\sum _{j=1}^N\left(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)\left({\mathbf{x}}_j-{\mathbf{v}}_i\right)\\ +\gamma \sum _{j=1}^N\left(\eta u_{ij}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)\left({\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i\right)=0,\end{array}$$ (A.6)

thus we can conveniently obtain Eq. (20) by reorganizing Eq. (A.6).

$$\begin{array}{l}\frac{\partial L_2}{\partial u_{ij}}=2\eta u_{ij}{\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2+2\beta u_{ij}+2\gamma \eta u_{ij}{\Vert {\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i\Vert }^2-{\alpha }_j=0\\ \iff u_{ij}=\frac{{\alpha }_j}{2\eta {\Vert {\mathbf{x}}_j-{\mathbf{v}}_i\Vert }^2+2\beta +2\gamma \eta {\Vert {\widehat{\mathbf{v}}}_i-{\mathbf{v}}_i\Vert }^2}.\end{array}$$ (A.7)

In light of $\sum _{k=1}^C{u}_{kj}=1$, based on Eq. (A.7), we attain

$$\begin{array}{l}{\alpha }_j\sum _{k=1}^C\frac{1}{2\eta {\Vert {\mathbf{x}}_j-{\mathbf{v}}_k\Vert }^2+2\beta +2\gamma \eta {\Vert {\widehat{\mathbf{v}}}_k-{\mathbf{v}}_k\Vert }^2}=1\iff \\ {\alpha }_j=\frac{1}{\sum _{k=1}^C\frac{1}{2\eta {\Vert {\mathbf{x}}_j-{\mathbf{v}}_k\Vert }^2+2\beta +2\gamma \eta {\Vert {\widehat{\mathbf{v}}}_k-{\mathbf{v}}_k\Vert }^2}}.\end{array}$$ (A.8)

We can eventually attain Eq. (21) by substituting Eq. (A.8) into Eq. (A.7).

A.3 Proof of Theorem 3

Proof

In light of the fact that the known, historical cluster centroids in the source domain, v̂_i, i = 1, …, C, are given and γ ≥ 0 is fixed, we can first define a new domain $E=\left\{{\mathbf{x}}_{\prime }^j=({\mathbf{x}}_j+\gamma {\widehat{\mathbf{v}}}_i)/(1+\gamma )|{\mathbf{x}}_j\in X,j=1,\dots ,N,i=1,\dots ,C\right\}$.

Suppose ${\mathbf{U}}_{(0)}^{\mathrm{I}}\in M_C$ is randomly initialized and γ ≥ 0 is fixed, then ${\mathbf{V}}_{(0)}^{\mathrm{I}}=G^{\mathrm{I}}\left({\mathbf{U}}_{(0)}^{\mathrm{I}}\right)$ can be calculated via Eq. (18) as

$$\begin{array}{l}{\mathbf{v}}_{i(0)}^{\mathrm{I}}=\frac{\sum _{j=1}^N{\left(u_{ij(0)}^{\mathrm{I}}\right)}^2{\mathbf{x}}_j+\gamma {\widehat{\mathbf{v}}}_i\sum _{j=1}^N{\left(u_{ij(0)}^{\mathrm{I}}\right)}^2}{(1+\gamma )\sum _{j=1}^N{\left(u_{ij(0)}^{\mathrm{I}}\right)}^2}\\ =\frac{\sum _{j=1}^N{\left(u_{ij(0)}^{\mathrm{I}}\right)}^2\left(({\mathbf{x}}_j+\gamma {\widehat{\mathbf{v}}}_i)/(1+\gamma )\right)}{\sum _{j=1}^N{\left(u_{ij(0)}^{\mathrm{I}}\right)}^2},i=1,\dots ,C,\end{array}$$ (A.9)

where v̂_i, i = 1, …, C, signify the known, historical cluster centroids in the source domain.

Let ${\rho }_{j(0)}^{\mathrm{I}}=\frac{{({\mu }_{ij(0)}^{\mathrm{I}})}^2}{\sum _{j=1}^N{({\mu }_{ij(0)}^{\mathrm{I}})}^2}$ and ${\mathbf{x}}_{\prime }^j=({\mathbf{x}}_j+\gamma {\widehat{\mathbf{v}}}_i)/(1+\gamma )$, j = 1, …, N, then Eq. (A.9) is equivalent to

$${\mathbf{v}}_{i(0)}^{\mathrm{I}}=\sum _{j=1}^N{\rho }_{j(0)}^{\mathrm{I}}{\mathbf{x}}_j^{\prime },i=1,\dots ,C,$$ (A.10 – 1)

with

$$\sum _{j=1}^N{\rho }_{j(0)}^{\mathrm{I}}=\sum _{j=1}^N\frac{{(u_{ij(0)}^{\mathrm{I}})}^2}{\sum _{j=1}^N{(u_{ij(0)}^{\mathrm{I}})}^2}=1.$$ (A.10 – 2)

Thus ${\mathbf{v}}_{i(0)}^{\mathrm{I}}\in \mathrm{conv}(E)$, i = 1, …, C, i.e. ${\mathbf{V}}_{I(0)}^{\mathrm{I}}\in {[\mathrm{conv}(E)]}^C$, where conv(E) and [conv(E)]^C denote the convex hull of E and the C-fold Cartesian product of the convex hull of E, respectively.

Iteratively, ${\mathbf{U}}_{(1)}^{\mathrm{I}}=F^{\mathrm{I}}\left({\mathbf{V}}_{(0)}^{\mathrm{I}}\right)$is computed via Eq. (19) and ${\mathbf{U}}_{\left(1\right)}^{\mathrm{I}}\in M_C$. Similar to the above analyses in Eqs. (A.9) and (A.10), we know that ${\mathbf{V}}_{(1)}^{\mathrm{I}}=G^{\mathrm{I}}\left({\mathbf{U}}_{\left(1\right)}^{\mathrm{I}}\right)$ also belongs to [conv(E)]^C. Therefore, as such, all iterations of T^I must belong to [conv(E)]^C × M_C.

Because M_C in the form of Eq. (22) is closed and bounded, and therefore compact. [conv(E)]^C is also compact [15,32]. Thus [conv(E)]^C × M_C is consequently compact in R^Cd × M_C.

A.4 Proof of Theorem 4

Proof

As (V̑, Ȗ) = T^I(V̄, Ū), we arrive immediately at Ȗ = F^I(V̄) and V̑ = G^I(Ȗ) according to Definition 9, and we have Φ_TI–KT–CM(T^I(V̄, Ū)) = Φ_TI–KT–CM(V̑, Ȗ) = Φ_TI–KT–CM(G^I(F^I(V̄)), F^I(V̄)). It is obvious that, if (V̄, Ū) ∈ S^I, the conditions, Ū = F^I(V̄) and V̄ = G^I(Ū), must simultaneously hold, otherwise, at least one of them does not hold. Specifically,

Combining the cases (1)–(3), we know Φ_TI–KT–CM (V̑, Ȗ) ≤ Φ_TI–KT–CM (V̄, Ū) and the inequality is strict if (V̄, Ū)∉S^I.

A.5 Proof of Theorem 5

1. For (V̄, Ū) 
 S^I, i.e., Ū = F^I(V̄) and V̄ = G^I(Ū), we have Φ_TI–KT–CM(V̑, Ȗ) = Φ_TI–KT–CM(G^I(F^I(V̄)), F^I(V̑)) = Φ_TI–KT–CM(G^I(Ū), Ū) = Φ_TI–KT–CM(V̄, Ū).

2. For Ū ≠ F^I(V̄), according to Proposition 1, we attain Φ_TI–KT–CM(V̄, Ū) > Φ_TI–KT–CM (V̄, F^I(V̄)) = Φ_TI–KT–CM(V̄, Ȗ). Further, based on Proposition 2, we have Φ_TI–KT–CM (V̄, Ȗ) ≥ Φ_TI–KT–CM (G^I(Ȗ), Ȗ) = Φ_TI–KT–CM(V̑, Ȗ). Thus we arrive at Φ_TI–KT–CM(V̑, Ȗ) < Φ_TI–KT–CM (V̄, Ū).

3. For Ū = F^I(V̄) and V̄ ≠ G^I (Ū), we arrive at Φ_TI–KT–CM(V̑, Ȗ) = Φ_TI–KT–CM(G^I(F^I(V̄)), F^I(V̄)) = Φ_TI–KT–CM(G^I(Ū), Ū). Further, according to Proposition 2, we have Φ_TI–KT–CM(V̑, Ȗ) = Φ_TI–KT–CM(G^I(Ū), Ū) < Φ_TI–KT–CM(V̄, Ū).

Proof

As defined in Definition 9, the map $T^{\mathrm{I}}=A_2^{\mathrm{I}}\circ A_1^{\mathrm{I}}$ is a composition of two, embedded maps, i.e. $A_1^{\mathrm{I}}$ and $A_2^{\mathrm{I}}$. Thus, if both $A_1^{\mathrm{I}}$ and $A_2^{\mathrm{I}}$ are continuous, $T^{\mathrm{I}}=A_2^{\mathrm{I}}\circ A_1^{\mathrm{I}}$ is consequently continuous. In order to prove $A_1^{\mathrm{I}}(V,\mathbf{U})=F^{\mathrm{I}}(\mathbf{V})$ is continuous, it equals to showing that F^I(V) is continuous. As F^I(V) is computed by Eq. (19) and it is continuous, $A_1^{\mathrm{I}}$ is reasonably continuous. Likewise, in order to prove $A_2^{\mathrm{I}}(\mathbf{U})=(G^{\mathrm{I}}(\mathbf{U}),\mathbf{U})$ is continuous, it amounts to (demonstrating that G^I(U) is continuous. As G^I(U) is calculated via Eq. (18), and Eq. (18) is definitely continuous when β and γ are fixed and v̂_i, i = 1, …, C, i, are given, G^I(U) is continuous, and so is $A_2^{\mathrm{I}}$. Combining them, this theorem can be proven.

A.6 Proof of Theorem 7

Proof

Similar to the proof of Theorem 3, we first define the domain $E=\left\{{{\mathbf{x}}^{\prime }}_j=({\mathbf{x}}_j+\gamma {\widehat{\mathbf{v}}}_i)/(1+\gamma )\mid {\mathbf{x}}_j\in X,j=1,\dots ,N,i=1,\dots ,C\right\}$.

Suppose ${\mathbf{U}}_{(0)}^{\mathrm{II}}\in M_C$ is randomly initialized and γ ≥ 0, η ∈ [0, 1] are fixed, then ${\mathbf{V}}_{(0)}^{\mathrm{II}}=G^{\mathrm{II}}\left({\mathbf{U}}_{(0)}^{\mathrm{II}}\right)$ can be calculated via Eq. (20) as

$$\begin{array}{l}{\mathbf{v}}_{i(0)}^{\mathrm{II}}=\frac{\sum _{j=1}^N\left(\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right){\mathbf{x}}_j+\gamma {\widehat{\mathbf{v}}}_i\sum _{j=1}^N\left(\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)}{(1+\gamma )\sum _{j=1}^N\left(\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)}\\ =\frac{\sum _{j=1}^N\left(\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)\left(({\mathbf{x}}_j+\gamma {\widehat{\mathbf{v}}}_i)/(1+\gamma )\right)}{\sum _{j=1}^N\left(\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)},i=1,\dots ,C,\end{array}$$ (A.11)

where v̂, i = 1, …, C, are the known, historical cluster centroids in the source domain, and ũ_ij, i = 1, …, C, j = 1, …, N, are the historical cluster centroid-based memberships of the data instances in the target domain. All the historical knowledge, both v̂_i and ũ_ij, is given or can be calculated in advance.

Let ${\rho }_{j(0)}^{\mathrm{II}}=\left(\left(\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)/\left({\sum }_{j=1}^N\left(\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)\right)\right)$ and ${\mathbf{x}}_{\prime }^j=({\mathbf{x}}_j+\gamma {\widehat{\mathbf{v}}}_i)/(1+\gamma )$ j = 1, …N, then Eq. (A.11) can be rewritten as

$${\mathbf{v}}_{i(0)}^{\mathrm{II}}=\sum _{j=1}^N{\rho }_{j(0)}^{\mathrm{II}}{\mathbf{x}}_{\prime }^j,i=1,\dots ,C,$$ (A.12 – 1)

with

$$\sum _{j=1}^N{\rho }_{j(0)}^{\mathrm{II}}=\sum _{j=1}^N\frac{\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2}{\sum _{j=1}^N\left(\eta {(u_{ij(0)}^{\mathrm{II}})}^2+(1-\eta ){\stackrel{\sim }{u}}_{ij}^2\right)}=1.$$ (A.12 –2)

Thus we know that ${\mathbf{V}}_{(0)}^{\mathrm{II}}$ belongs to [conv(E)]^C which denotes the C-fold Cartesian product of the convex hull of E.

Moreover, ${\mathbf{U}}_{(1)}^{\mathrm{II}}=F^{\mathrm{II}}\left({\mathbf{V}}_{(0)}^{\mathrm{II}}\right)$ is calculated via Eq. (21) and it definitely belongs to M_C. Referring to Eq. (A.12), we know that ${\mathbf{V}}_{(1)}^{\mathrm{II}}=G^{\mathrm{II}}\left({\mathbf{U}}_{(1)}^{\mathrm{II}}\right)$ also belongs to [conv(E)]^C. As such, all iterations of T^II belong to [conv(E)]^C × M_C. Likewise, due to both M_C [conv(E)]^C being compact, this theorem is proven.

A.7 Proof of Theorem 8

Proof

Because of (V̑, Ȗ) = T^II(V̄, Ū), we immediately obtain Ȗ = F^II(V̄) and V̑ = G^II(Ȗ) according to Definition 12, and we further arrive at Φ_{TII–KT–MC}(V̑, Ȗ) = Φ_{TII–KT–MC}(G^II(F^II(V̄)), F^II(V̄)). Clearly, if (V̄, Ū) ∈ S^II, the conditions, Ū = F^II(V̄) and V̄ = G^II(Ū), should concurrently hold, otherwise, at least one of them does not hold.

1. For (V̄,Ū) ∈ S^II, i.e., Ū = F^II(V̄) and V̄ = G^II(Ū), we have Φ_{TII–KT–MC}(V̑, Ȗ) = Φ_{TII–KT–MC}(G^II(F^II(V̄)), F^II(V̄)) = Φ_{TII–KT–MC}(G^II(Ū), Ū) = Φ_{TII–KT–MC}(V̄, Ū).

2. For Ū ≠ F^II(V̄), based on Proposition 3, we obtain Φ_{TII–KT–MC}(V̄,Ū) > Φ_{TII–KT–MC} (V̄, F^II(V̄)) = Φ_{TII–KT–MC}(V̄, Ū). Further, according to Proposition 4, we arrive at Φ_{TII–KT–MC}(V̄, Ȗ) ≥ Φ_{TII–KT–MC}(G^II(Ȗ), Ȗ) = Φ_{TII–KT–MC}(V̑, Ȗ). Thus we obtain Φ_{TII–KT–MC}(V̑, Ȗ) < Φ_{TII–KT–MC}(V̄, Ū).

3. For Ū = F^II(V̄) and V̄ ≠ G^II(Ū), we arrive at Φ_{TII–KT–MC}(V̑, Ȗ) = Φ_{TII–KT–MC}(G^II(F^II(V̄)), F^II(V̄) = Φ_{TII–KT–MC}(G^II(Ū), Ū. Further, according to Proposition 4, we have Φ_{TII–KT–MC}(V̑, Ȗ) = Φ_{TII–KT–MC}(G^II(Ū), Ū < Φ_{TII–KT–MC}(V̄, Ū).

As such, combining the cases (1)-(3), we know Φ_{TII–KT–MC}(V̑, Ȗ) and the inequality is strict if (V¯, Ū)
S^II.