Abstract
Mechanistic home range analysis (MHRA) is a highly effective tool for understanding spacing patterns of animal populations. It has hitherto focused on populations where animals defend their territories by communicating indirectly, e.g. via scent marks. However, many animal populations defend their territories using direct interactions, such as ritualized aggression. To enable application of MHRA to such populations, we construct a model of direct territorial interactions, using linear stability analysis and energy methods to understand when territorial patterns may form. We show that spatial memory of past interactions is vital for pattern formation, as is memory of ‘safe’ places, where the animal has visited but not suffered recent territorial encounters. Additionally, the spatial range over which animals make decisions to move is key to understanding the size and shape of their resulting territories. Analysis using energy methods, on a simplified version of our system, shows that stability in the nonlinear system corresponds well to predictions of linear analysis. We also uncover a hysteresis in the process of territory formation, so that formation may depend crucially on initial space-use. Our analysis, in one dimension and two dimensions, provides mathematical groundwork required for extending MHRA to situations where territories are defended by direct encounters.
Keywords: mathematical ecology, partial differential equations, pattern formation, ritualized aggression, territoriality
1. Introduction
Territorial conflicts occur in many different animal species, from birds to primates, insects to reptiles [1–4]. They sometimes take the form of physical fights, e.g. for monkeys [5] and humans [6,7]. However, to avoid costly injuries, animals often eschew fighting in favour of ‘ritualized aggression’, expressing dominance through displays, vocalizations and other non-violent interactions [8]. For example, ritualized aggression has been observed in many bird species, where plumages have often evolved to aid in displays of territorial dominance [9–11]. Likewise, bees have been observed to perform ‘perching and patrolling’ displays to highlight their territories [3]. In some cases, the line between non-violent and violent can become blurred, when ritualized displays turn into violent encounters (e.g. [2]). Nonetheless, be they violent or ritualized, the aim of territorial conflicts is to gain and defend parts of space for exclusive use by a select subset of the population, such as a flock, pack, tribe, nation or mating pair. Although aggressive interactions are sometimes non-territorial, here we focus on those that are, so may result in patterns of spatial segregation: interlocking territories that remain relatively stationary over time [12].
In this paper, we show mathematically how the process of territorial conflicts may give rise to spatial segregation patterns, and under what conditions these patterns may emerge or break down. This builds upon an established body of work on territorial pattern formation and home range analysis in scent-marking animals [13–15], which has been fruitful for accurate capture of home range patterns [16], predicting changes in territorial structure [17–19] and uncovering environmental drivers of spatial patterns [19,20]. However, such ‘mechanistic home range analysis’ (MHRA) studies all rely on there being a process of indirect interaction, whereby individuals mark the area throughout their terrain and then other individuals react to those marks. As noted in recent reviews [14,21], this constraint greatly limits the potential use of MHRA, as many populations instead use combats or ritualized aggression for territorial defence.
Here, we remedy this shortcoming by focusing on direct interactions (which we term ‘conflicts’), which of necessity can only occur at points on the borders between territories. Indeed, although MHRA has been used for understanding spatial structures of human gangs [4], where graffiti marking is used as a proxy for scent marking, that study also noted that direct confrontations between gangs may be influential in determining spatial structure. Similarly, the study of Potts et al. [22] demonstrated that memory of neighbouring vocalizations in bird populations may be modelled in an analogous way to scent-marking in canid populations. Yet, those bird populations are also known to engage in ritualized aggression for the purposes of territorial defence [23]. Therefore, both Smith et al. [4] and Potts et al. [22] would be improved by mechanistic models of direct territorial interactions. In general, by bringing direct interaction processes into the framework of MHRA [13,14], this paper expands the range of possible species and populations that may be studied using MHRA.
2. The model
We begin with some terminology, not intended to be definitive, but introduced purely for the purposes of this paper. Animals may move by themselves or as clusters of individuals (e.g. a pack or a flock), so we use the term ‘agent’ to mean either a lone-moving individual, or a cluster of individuals moving together. By ‘territorial conflict’, we mean any direct interaction that seeks to exclude certain agents from an area of space. For example, a territorial conflict could mean a physical fight, or a display of ritualized aggression.
To perform mathematical analysis, we start by describing a model of two agents living on a line segment. This analysis allows us to gain a rigorous understanding of the conditions under which territories can form. This understanding is then carried over into the more realistic two-dimensional (2D) situation, where we perform simulation analysis to provide evidence that our model can give rise to territory formation.
2.1. The one-dimensional model
First, we describe the model in discrete space and time, and then take the continuum limit. Let τ be the time between consecutive time steps and l the lattice spacing. We work on a one-dimensional (1D) line lattice. Parameters used in the model are listed in table 1.
Table 1.
Glossary of symbols. Note that some symbols are used either as dimensional quantities or their dimensionless equivalents, depending on the context (see §2.1.4).
| symbol | definition | model |
|---|---|---|
| n | arbitrary lattice site | discrete |
| s | arbitrary time step | discrete |
| τ | length of a single time step | discrete |
| l | lattice spacing | discrete |
| Ki(n,s) | probability that n is in agent i's conflict zone (CZ) at time s | discrete |
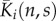 |
spatially averaged CZ | discrete |
| Ui(n, s) | probability that agent i is at site n at time s | discrete |
| ρτ,1 | probability that conflict occurs when agents meet | discrete |
| βl | rate at which CZ decays due to agents visiting without conflict | discrete |
| h | number of lattice sites for spatial averaging | discrete |
| d | perceptual radius of agent | discrete |
| q | strength of tendency to move away from CZ | discrete |
| μ | decay rate of CZ due to finite memory | both |
| x and t | space and time, respectively | continuous |
| ρ | rate at which conflicts occur when animals meet | continuous |
| β | rate at which CZ decays due to agents visiting without conflict | continuous |
| ki(x,t) | probability that x is in agent i's conflict zone at time t | continuous |
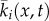 |
spatially averaged conflict zone | continuous |
| ui(x,t) | probability density of agent i at time t | continuous |
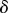 |
perceptual radius of agent | continuous |
| c | magnitude of advection | continuous |
| D | diffusion constant | continuous |
| L | width of terrain in 1D model | continuous |
| m | composite parameter μL2/ρ | continuous |
| a | composite parameter D/ρ | continuous |
| b | composite parameter βL/ρ | continuous |
| γ | composite parameter c/D | continuous |
2.1.1. The conflict zone
Roughly speaking, we wish say that the agent's ‘conflict zone’ is the place where it has a reasonably high expectation of experiencing a territorial conflict. Conflicts can only happen if agents are in the same place at the same time. So suppose that agents 1 and 2 meet at a lattice site n at time step s, and that ρτ,l is the probability that a conflict occurs during this time step. Then n becomes part of the conflict zone during this time step with probability ρτ,l.
As time passes without conflicts at point n, each agent gradually begins to view the point as being a less dangerous place to venture. This is bolstered by any visits it makes to n that do not result in a conflict. We model this by assuming that during a time step, the probability of site n being in the conflict zone changes by a factor of either 1 − μτ if the agent does not visit n, or 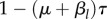 if the agent does visit n, where
if the agent does visit n, where 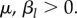 Here, μ models the memory decay of a conflict site that it has not visited for some time, while βl models the increase in expected safety incurred by visiting a site and not experiencing a conflict there. In summary, if we let Ki(n, s) be the probability that site n is in the conflict zone of agent i at timestep s, for
Here, μ models the memory decay of a conflict site that it has not visited for some time, while βl models the increase in expected safety incurred by visiting a site and not experiencing a conflict there. In summary, if we let Ki(n, s) be the probability that site n is in the conflict zone of agent i at timestep s, for 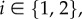 then
then
 |
2.1 |
2.1.2. A model of agent movement
As with the conflict zone, we begin by describing the agents' movement in discrete space and time. Each agent has a diffusive (i.e. random walk) aspect to its motion, to account for those aspects of movement within the territory that we are not explicitly modelling, such as foraging. It also has a tendency to move away from areas that are more likely to be part of the conflict zone and towards areas that are less likely to be in the conflict zone, which we model by biasing the random walk accordingly.
As an agent makes its decision to move, it will examine the area in its immediate vicinity, according to its perceptual capabilities. In other words, it makes its decision based on an average over certain nearby lattice sites. To be specific, we assume the probability of moving right (respectively, left) is determined by averaging the conflict zone over the 2h + 1 lattice sites centred d lattice sites to the right (respectively, left) of its location, where h ≥ 0, d ≥ 1 are integers. Therefore, we define the locally averaged conflict zone as follows:
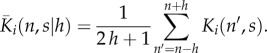 |
2.2 |
We then define the probability, 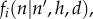 of agent i moving to a lattice site n, given that it was at site n′ in the previous time step, and given values of h and d, to be
of agent i moving to a lattice site n, given that it was at site n′ in the previous time step, and given values of h and d, to be
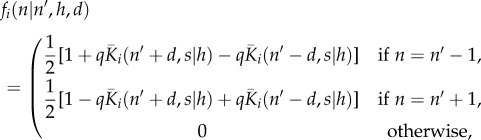 |
2.3 |
where 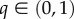 denotes the strength of bias away from the conflict zone.
denotes the strength of bias away from the conflict zone.
2.1.3. The continuum limit
One way to analyse the model given in equations (2.1) and (2.3) would be by performing stochastic simulations of the system. To gain mathematical insight, however, it is convenient to take a continuum limit in both space and time. This leads to the following system of partial differential equations (PDEs), defined on an interval [0, L], for i = 1, 2 (see the electronic supplementary material, appendix A for a derivation):
| 2.4 |
and
| 2.5 |
Here, ui(x,t) is the position probability density for agent i at time t, ki(x,t) is probability that position x is part of the conflict zone at time t, 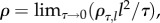
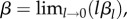
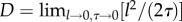 and c = 4dqD.
and c = 4dqD.
In equation (2.4),  is a local average of ki(x,t), given as follows:
is a local average of ki(x,t), given as follows:
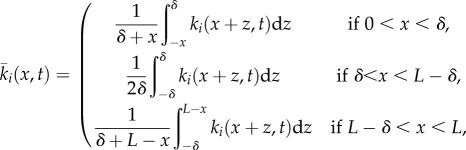 |
2.6 |
where 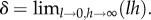 This local averaging arises from the biological considerations regarding the animal's perceptual capabilities, described at the start of §2.1.2. The precise mathematical form emerges from the limiting process given in the electronic supplementary material, appendix A.
This local averaging arises from the biological considerations regarding the animal's perceptual capabilities, described at the start of §2.1.2. The precise mathematical form emerges from the limiting process given in the electronic supplementary material, appendix A.
Finally, we impose the following boundary and integral conditions, respectively (see the electronic supplementary material, appendix A for details):
| 2.7 |
and
| 2.8 |
2.1.4. A dimensionless version of the model
To reduce the number of parameters in the system, we introduce the following dimensionless variables:
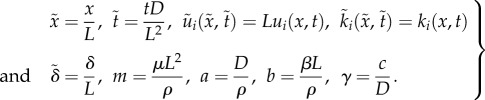 |
2.9 |
Dropping the tildes over the letters to ease notation, we arrive at the following dimensionless system of equations, which will be the object of 1D mathematical analysis in this paper, for 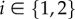 :
:
| 2.10 |
| 2.11 |
| 2.12 |
and
| 2.13 |
where the dimensionless version of  is
is
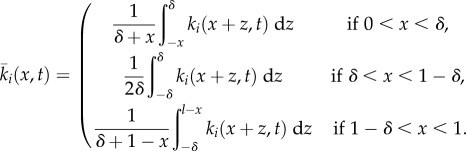 |
2.14 |
Unless otherwise stated, all parameter values are assumed to be non-negative.
2.2. The two-dimensional model
In two dimensions, we perform our analysis using the full, individual-based, stochastic model, to verify that territorial segregation occurs in the version of our model closest to reality. Simulations are performed on a 25 × 25 square lattice with reflecting boundary conditions, using four agents. At each time step, an agent at lattice site  moves to one of the four adjacent lattice sites with the following probabilities:
moves to one of the four adjacent lattice sites with the following probabilities:
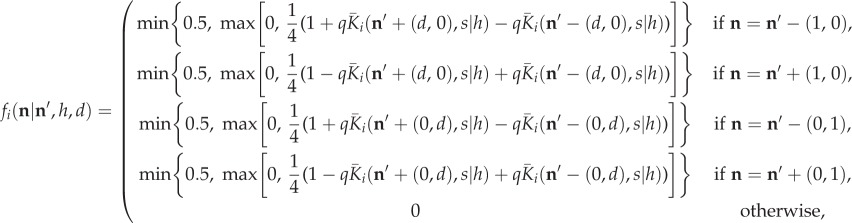 |
2.15 |
where q > 0 and d is a positive integer. When q < 1, this is the 2D analogue of equation (2.3). We extend our model for use when q ≥ 1 for extra flexibility. Here,  is the 2D analogue of equation (2.2), given as follows:
is the 2D analogue of equation (2.2), given as follows:
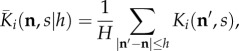 |
2.16 |
where H is the number of elements in the set  and Ki(n, s) is the probability that n is in the conflict zone of animal i at time step s. The evolution of Ki(n, s) is given by the following iterative equation (see equation (2.1) for the 1D version):
and Ki(n, s) is the probability that n is in the conflict zone of animal i at time step s. The evolution of Ki(n, s) is given by the following iterative equation (see equation (2.1) for the 1D version):
 |
2.17 |
We begin simulations with Ki(n, s) = 0 for every lattice site n and place individuals uniformly at random on the lattice grid. We allow 100 000 time steps ‘burn-in’ for the conflict zones to form, then run the simulations for a further 100 000 time steps to obtain the agents' utilization distribution. It turns out that, for the parameter values we tested, running the simulations for longer does not yield qualitatively significant change in the agents' utilization distribution (electronic supplementary material, figure S3).
3. Model analysis and results
3.1. Linear stability analysis
We use linear stability analysis to ascertain the conditions under which patterns may be expected to form in the 1D system described by equations (2.10)–(2.13) (e.g. [24], ch. 2). Owing to the integral conditions (equation (2.13)), the constant steady state for ui(x, t) is ui*(x). The constant steady state 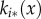 for ki(x, t) is calculated by setting equation (2.10) to zero so that
for ki(x, t) is calculated by setting equation (2.10) to zero so that
| 3.1 |
Plugging in the constant solution ui*(x) = 1 into equation (3.1), we find that 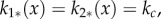 where
where
| 3.2 |
To linearize about this steady state, we define
| 3.3 |
We look for solutions of the form 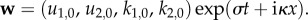 Then equations (2.10)–(2.11) imply the following linearized system of equations (as is standard, e.g. [24], ch. 2):
Then equations (2.10)–(2.11) imply the following linearized system of equations (as is standard, e.g. [24], ch. 2):
| 3.4 |
and
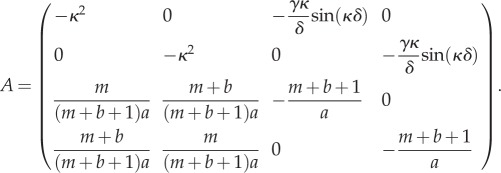 |
3.5 |
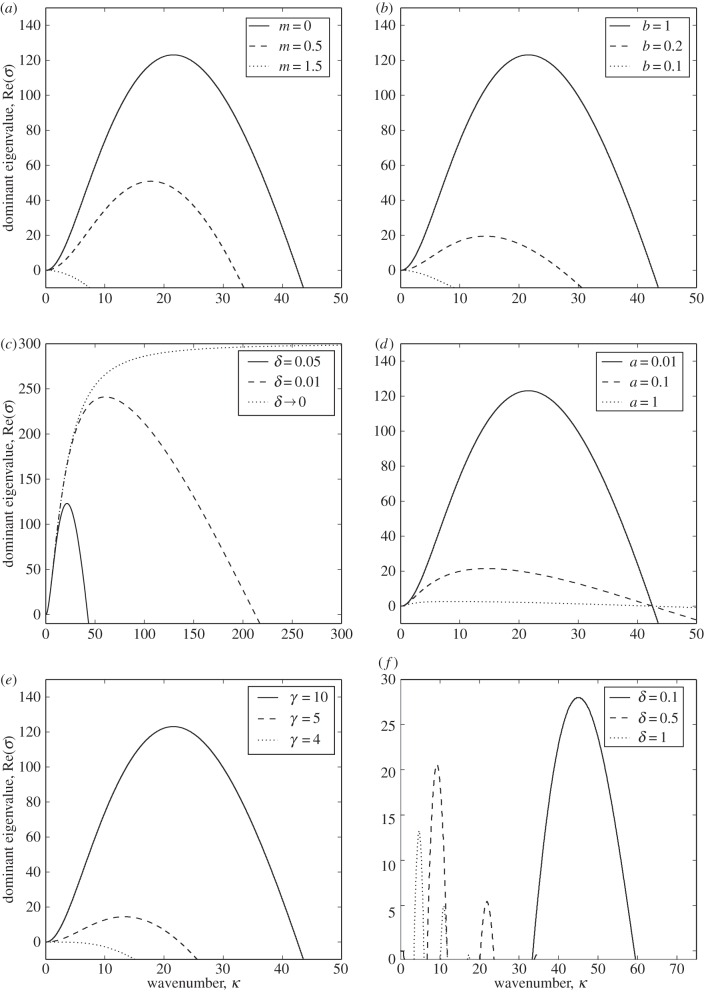
To determine whether patterns form in this system, we examine the dispersion relation. This plots the largest real value of σ as a function of the wavenumber κ, whenever det(A − σI) = 0. If the set of κ-values for which the curve lies above the axis is non-empty, then patterns may form with period 2π/κ from small perturbations of the constant steady state, for any κ in this set. Figure 1 shows the dispersion relation for various values of the parameter space (a, b, γ, δ, m). Though this five-dimensional space is too large to study exhaustively, we can ascertain certain general properties by varying one parameter at a time.
Figure 1.
Dispersion relations. Here, we examine the effect of each of the five parameters a, b, γ, δ, m on the dispersion relation for the system of equations (2.10)–(2.13). For panels (a–e), unless otherwise stated in the figure legend, a = 0.01, b = 1, γ = 10, δ = 0.05, m = 0. In panel (f), we examine the possibility of pattern formation when b = 0. Here, a = 0.1, m = 0.1, γ = 100 and δ varies according to the figure legend. See the electronic supplementary material, appendix B for an explanation of this choice of parameter values.
Figure 1a,b examines the effects of varying two aspects of the conflict zone decay: that which is proportional to the positional probability of the agent (b) and that which is not (m). If either m is too high or b is too low, then patterns cannot form. Therefore, the agents must have some process whereby they feel safer in places they have visited and not had territorial conflicts, so are less likely to view those places as part of the conflict zone. Moreover, this process must be relatively strong compared with the agents' tendency to forget about places they have not visited for a while. In the electronic supplementary material, appendix B, we show that if b = 0, then territories cannot form for biologically realistic parameter values. Nonetheless, there are parameter values where we observe pattern formation and some of these are explored in figure 1f (see also the electronic supplementary material, appendix C).
Figure 1c shows that as δ is decreased, the set of wavenumbers at which patterns may form increases in size. At the limit δ → 0, where agents only react to the conflict zone at the precise position they are located, patterns can form at arbitrarily high wavenumbers, so the problem is ill-posed. Therefore, it is necessary for territorial formation (in our model) that agents have a non-vanishing perceptive radius which they use to make movement decisions. Similar conditions were discovered in the studies of Briscoe et al. [25] and Potts & Lewis [26], regarding territorial scent-marking processes in canid populations.
From figure 1d, we see that the parameter a, measuring the relative effect of the agent's diffusion constant compared with the rate at which conflicts occur, appears to have no effect on the set of wavenumbers for which patterns form. However, the rate of growth of the resulting patterns is higher when a is lower. Lastly, figure 1e shows that patterns will only form if γ, the ratio of the advection rate (away from the conflict zone) to the diffusion rate, is sufficiently high.
3.2. Numerical analysis: patterns corresponding to territories
Having shown that patterns should form for certain choices of parameter values, we investigate whether the sort of patterns that correspond to territories may form in our system. Such patterns should result in u1(x) being predominantly concentrated on one side of the interval [0,1] with u2(x) on the other side. The steady state of equations (2.10)–(2.13) is a system of (ordinary) integro-differential equations that is too complicated for exact mathematical analysis. (That this is a system of integro-differential equations can be seen by expanding the 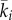 term in equation (2.11) using equation (2.14).) Therefore, we analyse this system numerically, using the method of false transients [27]. Details of the algorithm are in the electronic supplementary material, appendix D.
term in equation (2.11) using equation (2.14).) Therefore, we analyse this system numerically, using the method of false transients [27]. Details of the algorithm are in the electronic supplementary material, appendix D.
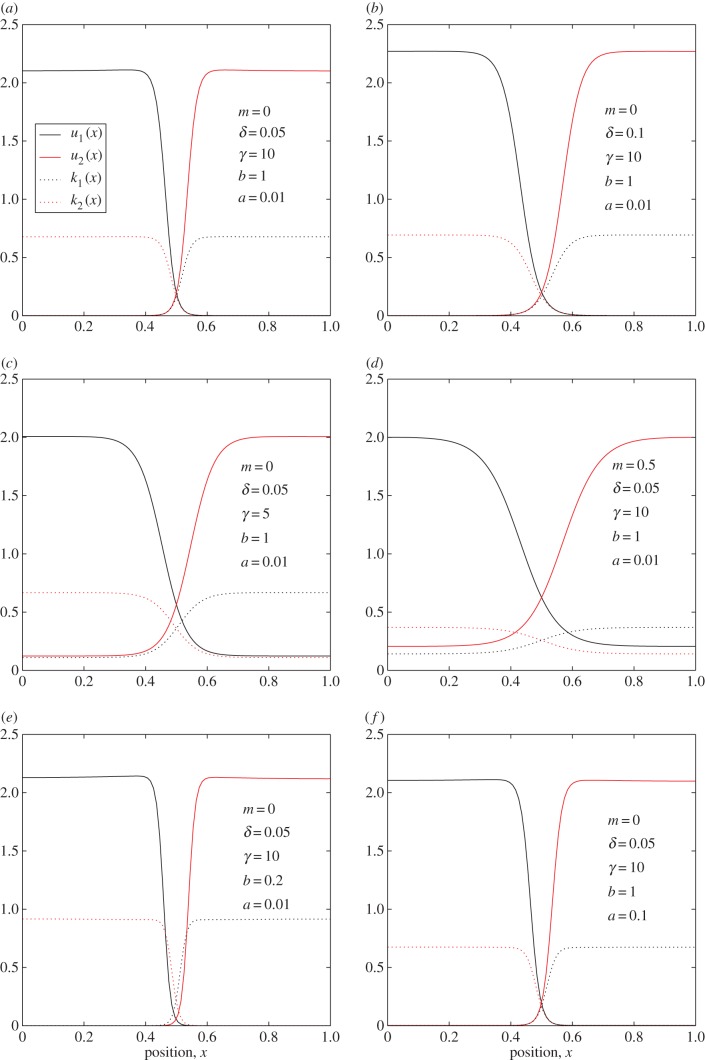
Numerical analysis reveals that patterns can form that look qualitatively like territories for certain parameter values (figure 2 and table 2). This analysis allows us to observe the qualitative effects of varying various parameters. By comparing figure 2a with b, we see that a lower perceptual range (δ) of the agent results in sharper territorial boundaries. Figure 2c shows that a lower drift tendency (γ) away from the conflict zone leads to less well-defined territories, with the position density being above about 0.1 across the whole range of the terrain (as compared with figure 2a where the drift tendency is higher). Similarly, comparing figure 2d and a shows that a tendency for the agents to forget about conflicts in areas they have not recently visited (m > 0) leads to less well-defined territories.
Figure 2.
Numerical solutions corresponding to territories. Here, numerical steady-state solutions to equations (2.10)–(2.13) are plotted. The respective parameter values are shown in the legends. Panel (a) can be considered as a base case, for comparison with panels (b), (c), (d), (e) and (f), which show the effect on territorial patterns of varying parameters δ, γ, m, b and a, respectively (also see table 2). (Online version in colour.)
Table 2.
Parameter combinations from figure 2.
| case | panel in figure 2 | δ | γ | m | b | a |
|---|---|---|---|---|---|---|
| base case | a | 0.05 | 10 | 0 | 1 | 0.01 |
| increased spatial averaging | b | 0.1 | 10 | 0 | 1 | 0.01 |
| less advection | c | 0.05 | 5 | 0 | 1 | 0.01 |
| higher memory decay rate | d | 0.05 | 10 | 0.5 | 1 | 0.01 |
| reduced safety from re-visits | e | 0.05 | 10 | 0 | 0.2 | 0.01 |
| greater diffusion/conflict-rate ratio | f | 0.05 | 10 | 0 | 1 | 0.1 |
Comparing figure 2a,e, we see that lowering b, the tendency for animals to feel safer in areas that they have recently visited and not had a conflict, leads to steeper sides of the conflict zone, and a reduced overall population density (i.e. lower u1(x) + u2(x)) in the centre of the territory. This reduced population density is analogous to the ‘buffer zones’ observed in [28], which can give a safe area for prey to exist between territories of predators. Finally, comparing figure 2f to a, we see that changing a (the relative effect of the agent's diffusion constant compared with the rate at which conflicts occur) has no effect on the resulting territorial patterns, as one would expect since a vanishes when the left-hand sides of equations (2.10)–(2.11) are set to zero.
3.3. Numerical analysis: transient dynamics
Although steady-state analysis is mathematically convenient and gives insight into the conditions under which territorial patterns may form, often natural systems are observed in a transient state away from equilibrium [18,29]. Therefore, it is important to examine the profile of the agents' utilization distributions before they have had time to reach a stable state.
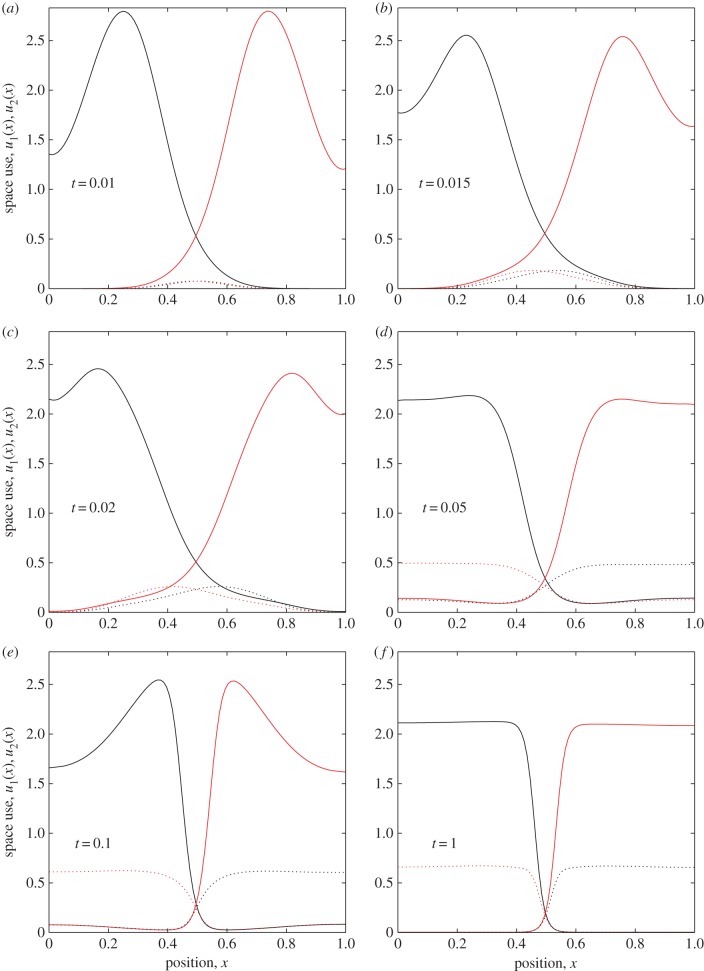
In the system studied here (equations (2.10)–(2.13)), the distributions of both the agents and the conflict zones have a rather interesting trajectory towards the steady state (figure 3). As the conflict zones emerge, they are initially almost identical in shape (figure 3a). Then they separate as each agent becomes more familiar with its side of the terrain (figure 3b,c). Eventually, patterns form that look somewhat like territories (figure 3d), but there is a relatively large probability of being found anywhere on the terrain compared with the eventual steady state. Next, the agents develop a tendency to spend time close to the territory boundary (figure 3e) causing the borders to sharpen. Once the borders have become sufficiently steep so that intrusion of agent 1 to the right-hand side (or agent 2 to the left-hand side) is very unlikely, the probability density within each territory flattens out to reveal a pattern similar to the eventual steady state (figure 3f). It is interesting to note that these varied dynamics occur as an outcome of behavioural rules that are, themselves, fixed through time.
Figure 3.
Transient territorial dynamics. Time-dependent solutions to equations (2.10)–(2.13) for a = 0.01, b = 1, γ = 10, δ = 0.05 and m = 0. The value of t is given in each plot, so time increases from panel (a) to (f). Analagous to figure 2, in each plot u1(x, t) (respectively, u2(x, t)) is given by a red (respectively, black) solid curve and k1(x, t) (respectively, k2(x, t)) by a red (respectively, black) dashed curve. (Online version in colour.)
3.4. Mathematical analysis when δ → 0: an energy method
Though the results of §3.1 suggest that patterns can form at arbitrary high wavelengths in the limit δ → 0, in this case the system is simple enough to perform some mathematical analysis. As δ → 0, the locally averaged integral  (equation (2.14)) tends to ki, so the system from equations (2.10)–(2.13) becomes
(equation (2.14)) tends to ki, so the system from equations (2.10)–(2.13) becomes
| 3.6 |
| 3.7 |
| 3.8 |
and
| 3.9 |
Note that these equations are identical to equations (2.10)–(2.13), except that the advection term in equation (3.7) contains the function ki in place of the function 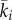 from equation (2.11).
from equation (2.11).
In this section, we analyse the system in equations (3.6)–(3.9) in the particular case where a, m = 0 and u1(x, t) + u2(x, t) = 2. Note that a = 0 means, in essence, that the conflict zones (ki) reach equilibrium much faster than the probability distributions of the individuals (ui). With these assumptions in place, the problem turns out to be simple enough for analysis of the full, time-dependent system, so we can gain some analytic insight into the features we have so far observed by linear analysis and numerics.
Plugging a, m = 0 and u1(x,t) + u2(x,t) = 2 into equation (3.6), we can write ki in terms of ui as follows, for i = 1, 2:
| 3.10 |
This means that equation (3.7) becomes
| 3.11 |
A direct calculation shows that equation (3.11) is equivalent to
| 3.12 |
where
| 3.13 |
From this, we construct an ‘energy’ functional
| 3.14 |
where Φ(ui) is the anti-derivative of ϕ(ui), i.e.
| 3.15 |
The reason for constructing the functional E(ui) is that it turns out to be a decreasing function of time, whose steady state occurs when the PDE in equation (3.11) is at steady state. To see this, observe the following calculation:
 |
3.16 |
where the third equality comes from equation (3.12) and the fifth from the zero-flux boundary conditions (equation (3.8)).
Note that the last term in equation (3.16) is always non-positive and is zero precisely when the flux,  is zero. Now, if equation (3.11) is at steady state, then the flux is constant across space, say
is zero. Now, if equation (3.11) is at steady state, then the flux is constant across space, say 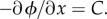 However, because the flux is zero at the boundaries (x = 0, 1), C must be zero. Thus, the flux is zero if and only if equation (3.11) is at steady state. Hence, by (3.16), E(ui) decreases over time unless equation (3.11) is at steady state. If the minima of E(ui) are finite, then E(ui) is bounded below and so the system will tend towards one of the minima as t → ∞. These minima can therefore be used to describe the eventual state of the system in equations (3.6)–(3.9). This approach is similar to that of Lyapunov's method for partial differential equations (e.g. [30]).
However, because the flux is zero at the boundaries (x = 0, 1), C must be zero. Thus, the flux is zero if and only if equation (3.11) is at steady state. Hence, by (3.16), E(ui) decreases over time unless equation (3.11) is at steady state. If the minima of E(ui) are finite, then E(ui) is bounded below and so the system will tend towards one of the minima as t → ∞. These minima can therefore be used to describe the eventual state of the system in equations (3.6)–(3.9). This approach is similar to that of Lyapunov's method for partial differential equations (e.g. [30]).
For the purposes of this paper, we are particularly interested in minima that correspond to territories. We show in electronic supplementary material, appendix E that when m = 0, classical, steady-state solutions to equations (3.6)–(3.9) must be constant. Hence weak steady-state solutions to equations (3.6)–(3.9) must be constant except possibly at a set of values with measure zero. As such, solutions that correspond to territories, i.e. with most of the density of the steady-state u1* concentrated on one side and most of the density of u2* on the other side, are such that 
 for
for 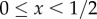 and
and 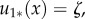
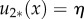 for
for 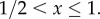
Furthermore, by the integral condition in equation (3.9), we must have  It follows that the local minimum energy solutions occur for values of η that minimize the following function, for 0 ≤ η ≤ 1:
It follows that the local minimum energy solutions occur for values of η that minimize the following function, for 0 ≤ η ≤ 1:
 |
3.17 |
Since b ≥ 0 and  we have
we have 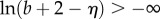 and
and 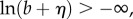 so that
so that 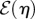 is finite. Thus, E(ui) is bounded below so the system does, indeed, tend towards a finite-valued minimum.
is finite. Thus, E(ui) is bounded below so the system does, indeed, tend towards a finite-valued minimum.
Analysing equation (3.17) numerically for various values of b and γ, we find that minima occur either when η = 0 or η = 1. The minimum η = 0 gives the following (weak) solution:
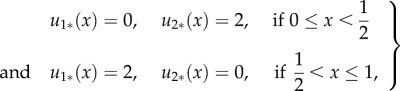 |
3.18 |
which corresponds to territory formation. The η = 1 case means that 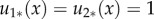 for all
for all 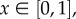 so that territories do not form.
so that territories do not form.
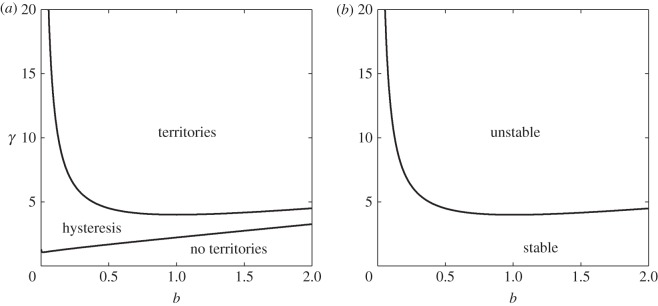
Interestingly, for certain values of b and γ, there are minima at both η = 0 and η = 1. This is an example of hysteresis, where territories only form if the initial conditions are sufficiently close to those in equation (3.18), but if initial conditions are close to a constant solution, then territories are not predicted to form. The regions of (b,γ)-space where we see territories, no territories or both (hysteresis) are shown in figure 4a.
Figure 4.
Predictions of territorial structures. Panel (a) gives the regions of (b,γ)-space where the (nonlinear) energy method (§3.4) predicts that territories should either form spontaneously (top-right region), decay to the constant steady state (bottom-left), or where the existence of territories depends upon the initial conditions (labelled ‘hysteresis’). Here, we assume a, m = 0 and δ → 0. Panel (b) shows the predictions of territory formation from linear analysis of the full system (equations (2.10)–(2.13)). In the ‘stable’ region, the analysis predicts that territories should not form from small perturbations of the constant steady state, whereas they may form in the ‘unstable’ region. In this case, m = 0 but the values of a and δ do not affect whether patterns will form for some wavenumber (figure 1c,d).
In figure 4b, these regions are compared with the regions where linear stability analysis predicts that small perturbations from the constant steady state will grow to non-constant patterns. Despite the various simplifying assumptions made in our energy-functional analysis, the results correspond almost identically to those from linear stability analysis of the full system. Furthermore, they suggest the places where the initial condition can have an effect on the appearance of territorial patterns, and so territories may exist in situations where the constant steady state is stable.
3.5. Simulation analysis in two dimensions
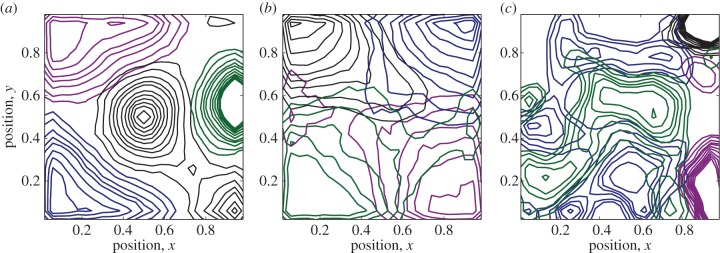
Figure 5 shows the results of 2D simulation analysis where ρ = 1, β = 0.1 and μ = 0. Note that by decreasing the parameter q, representing the strength of tendency to retreat, territories have greater overlap (see also the electronic supplementary material, figure S4). By decreasing d and h, the scale over which animals make movement decisions, territories become fragmented and less well defined (see also the electronic supplementary material, figure S5). This accords with our observation from 1D linear stability analysis that a lower spatial averaging means the system is susceptible to instabilities at higher wavelengths (figure 1c).
Figure 5.
Two-dimensional territories from stochastic IBM. Panel (a) shows four utilization distributions that emerge from stochastic simulations when d = 5, h = 5 and q = 3. Panel (b) shows the effect of reducing the agents' speed of retreat from conflict zones, by reducing q to q = 2 and keeping the other parameters constant. Panel (c) has d = 2, h = 2, q = 3, showing that by reducing the scale over which animals make movement decisions can cause greater territorial fragmentation. Contours are drawn at heights 0.5, 1, 2, 3, 4, 6, 8, 10, 12, 14, 16, from outer to inner. (Online version in colour.)
4. Discussion and conclusion
The aim of this paper is to show mathematically how territorial patterns can form from processes of direct interaction between animals. The reason behind studying this is to provide necessary mathematical background for extending the tools of MHRA [13,14] beyond the confines of scent-marking animals, for use with the many species that use direct interactions, such as ritualized aggression, to demarcate territories. We have shown that territories can form from such interactions if the following processes are present:
— spatial memory of both past territorial conflicts (encoded in ki(x, t)) and places where such conflicts have not recently occurred (encoded in the parameter b),
— a tendency to move away from places where territorial conflicts have recently occurred, and
— a reaction to spatial location averaged over a non-vanishing area centred on the animal.
Recently, spatial memory has been hypothesized as a key process behind many behavioural features in animal populations [31]. This is bolstered by copious studies of neurological ‘place cells’, which have explained the physiological processes underlying spatial memory in many animals (e.g. [32–34]). Therefore, it is reasonable to expect that such memory processes are at play in territorial formation.
Likewise, the other two above-listed processes are likely to be typical in most populations of territorial animals. The tendency to move away from the conflict zone is perhaps the most well-established process behind territory formation. For example, Wilson [35] defines the process of territorial defence as a ‘means of repulsion through overt defense or advertisement’ and Adams [12] explains how this has become a defining idea in territorial understanding.
The requirement for spatial averaging by an animal deciding where to move is less well documented, perhaps because it is taken as given that animals make movement decisions based on their immediate surroundings, not just their exact location. Nonetheless, many continuous-space models make the mathematical simplification that interactions only take place between the animal and its precise current location. This can lead to reasonable results in certain situations [17,28,36], but some studies have found that this simplification can dramatically change the nature of observed patterns [25,26]. The results here provide another example of this latter phenomenon.
We also demonstrate the possibility of a territorial hysteresis phenomenon occurring in animal populations (e.g. figure 4). Biologically, this means that animals need to have a certain set of behavioural properties to form territories (encoded in the parameters b and γ), but can relax them slightly once territories have formed and still maintain the territorial structure. Therefore, it is possible that animals exhibit slightly different territorial behaviour when forming new territories from that in situations where territorial borders have already been established. Such a phenomenon has been observed in a system of scent-marking animals (urban foxes), who respond to changes in territorial structures by altering their scent-marking behaviour [18]. We are, however, unaware of any similar studies regarding animals who perform ritualized aggression to demarcate territories.
The success of MHRA in shedding light on various spatial phenomena in ecology is well documented (see [14], for a recent review). However, its reliance on scent-marking and analogous processes of indirect interaction has been a severe limitation until now. The results from this study give the framework to make this extension, by explaining what processes need to be included in a model of territory formation from direct interactions. To apply this framework to positional data, one would either fit the steady-state solution of the 2D model to relocation data, using the techniques in [13], or parametrize the model from fine-scale movement, similar to the techniques described in [22]. Because the patterns that arise from direct interactions may be very similar to those from indirect ones, we would generally advocate using the latter, fine-scale techniques (or similar, e.g. [37]). On the scale of behavioural decisions, the difference between the two types of interaction (direct and indirect) is likely to be clearer than on the scale of long-term territorial patterns.
A programme of research that moves from mathematical analysis to data-driven studies has been successful for understanding scent-marking animals, as evidenced by initial papers containing 1D analysis [28,38] paving the theoretical groundwork for novel insights into real 2D systems [16,17,19]. We have thus followed suit for our study of direct interactions. However, as well as applications to real systems, there is also room for future mathematical investigation of more complicated, multi-agent, 2D systems of direct interactions. Furthermore, this study assumes that all agents in the system act in the same way, but this is often not true for real animal populations. It would be interesting for future investigations to modify the system to incorporate unequal agents, investigating the varying strategies that may be more or less beneficial for territorial gains, given different behavioural traits. Given the wide range of species that use direct interactions to determine territorial segregation, together with the well-developed statistical techniques for fitting positional data to such models, we hope that the modelling ideas presented here will have broad application to many situations in spatial ecology.
Supplementary Material
Acknowledgements
The authors would like to thank Thomas Hillen for many useful comments on the paper. We would also like to thank three anonymous reviewers whose comments helped improve the manuscript. M.A.L. also gratefully acknowledges a Canada Research Chair and a Killam Research Fellowship.
Authors' contributions
J.R.P. and M.A.L. jointly conceived, designed and performed the research. J.R.P. wrote the first draft and M.A.L. contributed substantially to revisions. Both authors approved the final version of the manuscript.
Competing interests
We declare we have no competing interests.
Funding
This study was partly funded by NSERC Discovery and Accelerator grants (M.A.L.).
References
- 1.King JA. 1973. The ecology of aggressive behavior. Annu. Rev. Ecol. Syst. 4, 117–138. ( 10.1146/annurev.es.04.110173.001001) [DOI] [Google Scholar]
- 2.Stamps JA. 1977. The relationship between resource competition, risk, and aggression in a tropical territorial lizard. Ecology 58, 349–358. ( 10.2307/1935609) [DOI] [Google Scholar]
- 3.Kimsey LS. 1980. The behaviour of male orchid bees (Apidae, Hymenoptera, Insecta) and the question of leks. Anim. Behav. 28, 996–1004. ( 10.1016/S0003-3472(80)80088-1) [DOI] [Google Scholar]
- 4.Smith LM, Bertozzi AL, Brantingham PJ, Tita GE, Valasik M. 2012. Adaptation of an ecological territorial model to street gang spatial patterns in Los Angeles. Disc. Cont. Dyn. Syst. 32, 3223–3244. ( 10.3934/dcds.2012.32.3223) [DOI] [Google Scholar]
- 5.Gros-Louis J, Perry S, Manson J. 2003. Violent coalitionary attacks and intraspecific killing in wild white-faced capuchin monkeys (Cebus capucinus). Primates 44, 341–346. ( 10.1007/s10329-003-0050-z) [DOI] [PubMed] [Google Scholar]
- 6.Sack RD. 1986. Human territoriality: its theory and history, vol. 7 Cambridge, UK: Cambridge University Press. [Google Scholar]
- 7.Gat A. 2006. War in human civilization. Oxford, UK: Oxford University Press. [Google Scholar]
- 8.Maynard-Smith J. 1982. Evolution and the theory of games. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 9.Price TD. 1984. Sexual selection on body size, territory and plumage variables in a population of Darwin's finches. Evolution 38, 327–341. ( 10.2307/2408491) [DOI] [PubMed] [Google Scholar]
- 10.Wegge P, Rolstad J. 1986. Size and spacing of capercaillie leks in relation to social behavior and habitat. Behav. Ecol. Sociobiol. 19, 401–408. ( 10.1007/BF00300542) [DOI] [Google Scholar]
- 11.Garamszegi LZ, Rosivall B, Hegyi G, Szöllösi E, Török J, Eens M. 2006. Determinants of male territorial behavior in a Hungarian collared flycatcher population: plumage traits of residents and challengers. Behav. Ecol. Sociobiol. 60, 663–671. ( 10.1007/s00265-006-0210-4) [DOI] [Google Scholar]
- 12.Adams ES. 2001. Approaches to the study of territory size and shape. Annu. Rev. Ecol. Syst. 32, 277–303. ( 10.1146/annurev.ecolsys.32.081501.114034) [DOI] [Google Scholar]
- 13.Lewis MA, Moorcroft PR. 2006. Mechanistic home range analysis. Princeton, NJ: Princeton University Press. [Google Scholar]
- 14.Potts JR, Lewis MA. 2014. How do animal territories form and change? Lessons from 20 years of mechanistic modelling. Proc. R. Soc. B 281, 20140231 ( 10.1098/rspb.2014.0231) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Potts JR, Lewis MA. 2014. A mathematical approach to territorial pattern formation. Am. Math. Mon. 121, 754–770. ( 10.4169/amer.math.monthly.121.09.754) [DOI] [Google Scholar]
- 16.Moorcroft PR, Lewis MA, Crabtree RL. 1999. Home range analysis using a mechanistic home range model. Ecology 80, 1656–1665. ( 10.1890/0012-9658(1999)080%5B1656:HRAUAM%5D2.0.CO;2) [DOI] [Google Scholar]
- 17.Moorcroft PR, Lewis MA, Crabtree RL. 2006. Mechanistic home range models capture spatial patterns and dynamics of coyote territories in Yellowstone. Proc. R. Soc. B 273, 1651–1659. ( 10.1098/rspb.2005.3439) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Potts JR, Harris S, Giuggioli L. 2013. Quantifying behavioral changes in territorial animals caused by sudden population declines. Am. Nat. 182, E73–E82. ( 10.1086/671260) [DOI] [PubMed] [Google Scholar]
- 19.Bateman AW, Lewis MA, Gall G, Manser MB, Clutton-Brock TH. 2015. Territoriality and home-range dynamics in meerkats, Suricata suricatta: a mechanistic modelling approach. J. Anim. Ecol. 84, 260–271. ( 10.1111/1365-2656.12267) [DOI] [PubMed] [Google Scholar]
- 20.Potts JR, Mokross K, Stouffer PC, Lewis MA. 2014. Step selection techniques uncover the environmental predictors of space use patterns in flocks of Amazonian birds. Ecol. Evol. 4, 4578–4588. ( 10.1002/ece3.1306) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kays R, Crofoot MC, Jetz W, Wikelski M. 2015. Terrestrial animal tracking as an eye on life and planet. Science 348, aaa2478. ( 10.1126/science.aaa2478) [DOI] [PubMed] [Google Scholar]
- 22.Potts JR, Mokross K, Lewis MA. 2014. A unifying framework for quantifying the nature of animal interactions. J. R. Soc. Interface 11, 20140333 ( 10.1098/rsif.2014.0333) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jullien M, Thiollay JM. 1998. Multi-species territoriality and dynamic of neotropical forest understorey bird flocks. J. Anim. Ecol. 67, 227–252. ( 10.1046/j.1365-2656.1998.00171.x) [DOI] [Google Scholar]
- 24.Murray JD. 2011. Mathematical biology II: spatial models and biomedical applications. Interdisciplinary Applied Mathematics New York, NY: Springer. [Google Scholar]
- 25.Briscoe B, Lewis M, Parrish S. 2002. Home range formation in wolves due to scent marking. Bull. Math. Biol. 64, 261–284. ( 10.1006/bulm.2001.0273) [DOI] [PubMed] [Google Scholar]
- 26.Potts JR, Lewis MA. 2015. Territorial pattern formation in the absence of an attractive potential. J. Math. Biol. 72, 25–46. ( 10.1007/s00285-015-0881-4) [DOI] [PubMed] [Google Scholar]
- 27.Mallinson GD, de Vahl Davis G. 1973. The method of the false transient for the solution of coupled elliptic equations. J. Comput. Phys. 12, 435–461. ( 10.1016/0021-9991(73)90097-1) [DOI] [Google Scholar]
- 28.Lewis MA, Murray JD. 1993. Modelling territoriality and wolf–deer interactions. Nature 366, 738–740. ( 10.1038/366738a0) [DOI] [Google Scholar]
- 29.Tao Y. 2014. On movement ecology: a study of dynamics. Davis, CA: University of California. [Google Scholar]
- 30.Hsu SB. 2005. A survey of constructing Lyapunov functions for mathematical models in population biology. Taiwan. J. Math. 9, 151. [Google Scholar]
- 31.Fagan WF, et al. 2013. Spatial memory and animal movement. Ecol. Lett. 16, 1316–1329. ( 10.1111/ele.12165) [DOI] [PubMed] [Google Scholar]
- 32.O'Keefe J, Dostrovsky J. 1971. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 34, 171–175. ( 10.1016/0006-8993(71)90358-1) [DOI] [PubMed] [Google Scholar]
- 33.Langston RF, Ainge JA, Couey JJ, Canto CB, Bjerknes TL, Witter MP, Moser EI, Moser MB. 2010. Development of the spatial representation system in the rat. Science 328, 1576–1580. ( 10.1126/science.1188210) [DOI] [PubMed] [Google Scholar]
- 34.Killian NJ, Jutras MJ, Buffalo EA. 2012. A map of visual space in the primate entorhinal cortex. Nature 491, 761–764. ( 10.1038/nature11587) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wilson EO. 2000. Sociobiology: the new synthesis. Cambridge, MA: Belknap Press of Harvard University Press. [Google Scholar]
- 36.Moorcroft PR, Barnett AH. 2008. Mechanistic home range models and resource selection analysis: a reconciliation and unification. Ecology 89, 1112–1119. ( 10.1890/06-1985.1) [DOI] [PubMed] [Google Scholar]
- 37.Niu M, Blackwell PG, Skarin A In press. Modeling interdependent animal movement in continuous time. Biometrics. ( 10.1111/biom.12454) [DOI] [PubMed] [Google Scholar]
- 38.Lewis MA, White KAJ, Murray JD. 1997. Analysis of a model for wolf territories. J. Math. Biol. 35, 749–774. ( 10.1007/s002850050075) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.