A ciliate memorizes the geometry of a swimming arena

Abstract

Previous studies on adaptive behaviour in single-celled organisms have given hints to the origin of their memorizing capacity. Here we report evidence that a protozoan ciliate Tetrahymena has the capacity to learn the shape and size of its swimming space. Cells confined in a small water droplet for a short period were found to recapitulate circular swimming trajectories upon release. The diameter of the circular trajectories and their duration reflected the size of the droplet and the period of confinement. We suggest a possible mechanism for this adaptive behaviour based on a Ca²⁺ channel. In our model, repeated collisions with the walls of a confining droplet result in a slow rise in intracellular calcium that leads to a long-term increase in the reversal frequency of the ciliary beat.

1. Introduction

The behaviour of protozoa has been examined for over a hundred years under various external conditions and has been compared with intelligent behaviour in higher animals [1–8]. It has long been observed that even protozoa behave in a highly adaptive way towards complicated environmental conditions [9–15]. These reports have repeatedly stimulated discussion on the possibility of something like primitive intelligence. The adaptability of protozoa and its ethological implications has become a classical topic, but much still remains to be understood.

Because of the relative simplicity of unicellular systems compared with multicellular organisms, the physical mechanism of adaptation may be easier to clarify. Insight has been provided by a number of studies such as solving a maze [16] and anticipating periodic environmental events by the slime mould Physarum [15]. These observations encourage us to rethink how this capacity for adaptation develops from the physical nature of the organism.

Concerning the capacity to learn the geometry of a space, impressive pioneering work on a protozoan ciliate Paramecium was performed by Bramstedt in 1935 [17]: after the organism was transferred from a tiny container to a large container, it swam freely but followed a trajectory that was similar to the shape of its previous container. Although this finding was striking, some other research groups carefully re-examined it and drew negative conclusions [18,19]. Here we attempt to throw more light on memory capacity of this type.

In this report, we design a new quantitative experiment and confirm that another species of ciliate Tetrahymena shows the capacity to learn spatial configurations. We first carry out a qualitative characterization of the adaptive behaviour. We then propose a possible physical mechanism for this type of memory capacity in ciliates, based on the regulation of electric phenomena in the membrane that are closely coupled with ciliary motion. Finally, we discuss the implications of this memorizing capacity from the perspective of comparative ethology.

2. Organism and methods

Protozoan ciliates Tetrahymena were cultured in a liquid medium (KCl 8 mg l⁻¹, MgSO₄ 8 mg l⁻¹, CaCl₂ 8 mg l⁻¹) and incubated in a dark room at room temperature (23–25°C). After being allowed to swim in a wide space freely for several tens of minutes, specimens of Tetrahymena were confined in a spherical droplet of culture medium (0.3–0.6 mm in diameter (ϕ), approximately 0.014–0.11 µl) embedded in mineral oil for 15 min. Next, the specimens were transferred to the much larger space of a Petri dish (35 mm in diameter, 3 ml of medium).

To minimize any space-dependent effects of unknown chemicals that may be released from the organism during swimming in the droplet, the liquid medium was thoroughly mixed just after the organism was transferred from the droplet to the Petri dish. The specimens then began to swim freely.

The swimming motion of Tetrahymena was monitored under dark-field illumination using a stereoscopic microscope (Olympus, SZX16). Microscopic images were captured using a CCD camera and recorded on video. The recorded images were transferred and saved on a personal computer. Using customized software, we analysed the swimming trajectories of Tetrahymena by the conventional method of video image analysis.

To characterize a swimming trajectory, the maximum distance (MD) was defined as 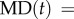max , where (x(t), y(t)) is the position of organism at time t. MD was plotted as a function of τ and could saturate at some value of diameter when the swimming trajectory was circular. At last, statistical occurrence of MD was plotted in the function of τ. Numbers of cells were 34 (ϕ = 0.3 mm), 31 (0.4 mm), 30 (0.5 mm) and 22 (0.6 mm).

For statistical confirmation of spatial extent of swimming trajectory after the confinement, the width of the circular shape of trajectory (approximate diameter) was measured for each circular shape on the whole trajectory of swimming, and the normalized frequency was plotted. The numbers of circles were 757 (ϕ = 0.3 mm), 292 (0.4 mm), 375 (0.5 mm) and 76 (0.6 mm).

3. Adaptive behaviour towards the shape and size of a swimming space in Tetrahymena

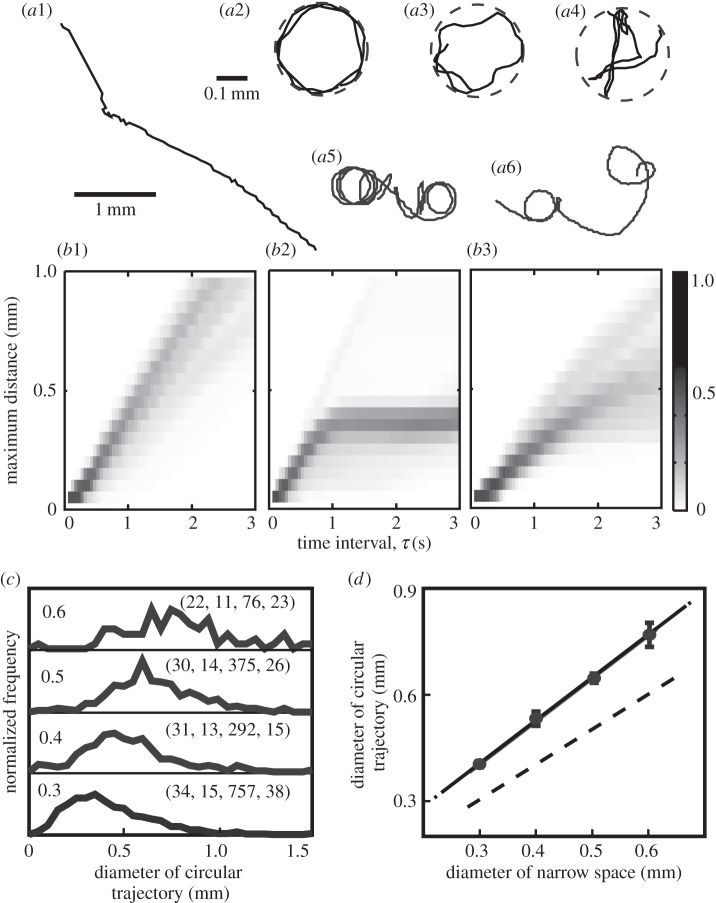
In an open space, Tetrahymena usually swam in a straight line at a velocity of 0.81 ± 0.27 mm s⁻¹ (mean ± s.d., N = 30), and changed the direction of swimming at a frequency of 0.01–0.1 Hz, as shown in figure 1a1.

Figure 1.

Typical swimming trajectories of Tetrahymena before and after the confinement: (a1) in a wide, open space before confinement in a small space; (a2–a4) in the confined space of a spherical droplet of diameter 0.3 mm; (a5, a6) in an open space after confinement. Solid and dashed lines show the trajectories of swimming and the shape of the confined space, respectively. (b1–b3) Statistical occurrence of maximum distance (MD) in the function of τ at the diameter of droplet, 0.3 mm. Grey level indicates a normalized frequency according to the grey chart on the right. (c,d) Dependence of the diameter of circular motion on the diameter of the confined space experienced, re-drawn from (c). The left numbers in each panel of (c) indicate the diameters of the confined space (mm), and the numbers in parentheses on the right indicate the number of experiments, number of results of type (a5), (a6), number of circular trajectories count, total observation time in minute for counting the circular trajectory. The error bars in (d) represent the standard error. The dashed line indicates where the two diameters are equal. Number of results of type (a5), (a6) (diameter of droplet, mm): 15(0.3), 13(0.4), 14(0.5), 11(0.6).

Figure 1a2–a4 shows the swimming trajectories observed in a tiny spherical droplet (the diameter, ϕ, is 0.3 mm): Tetrahymena repeatedly turned at the droplet wall and moved closely (figure 1a2) or approximately (figure 1a3) along the wall, and sometimes in a different manner (figure 1a4). The swimming patterns (figure 1a2 and figure 1a3) were often observed in this confined space over a few minutes. The pattern of swimming changed on a longer time scale.

After the organism was transferred from the confined space to a wide, open space, the swimming trajectory repeatedly traced a circular shape that was similar to the previous confined space (figure 1a5,a6). Sometimes the organism swam for a period of time almost in a straight line or in a large arc of much lower curvature; occurrences of these modes of swimming are apparent in the trajectories in figure 1a5,a6. The adaptive trajectory lasted from a few minutes to an hour, and the duration time differed from one individual to the next. The statistical occurrence of this type of trajectory was 45%, and the occurrence of swimming similar to figure 1a1, in which there was no adaptive change in the trajectory, was 53%, in a total of 117 specimens summing up the different ϕs (0.3, 0.4, 0.5, 0.6 mm). The remaining of cases were the other types. The duration of confinement was too short at 5 min to observe the type in figure 1a5,a6, and too long at 30 min (70% of organisms tended to stop moving).

Figure 1b1–b3 shows the characterization of swimming type. In a segment of swimming trajectory extracted in the time interval of 2τ, the statistical occurrence of MD of any two positions along the segment was measured with respect to τ. In the type in figure 1a5, MD was saturated at 0.4 mm as the trajectory is approximately circular at a diameter of 0.4 mm (figure 1b2). Such saturation was not observed in figure 1b1 when the trajectory was almost straight like figure 1a1. The trajectory was somewhere in between, like figure 1a6, as shown in figure 1b3.

For modes of swimming shown in figure 1a5 and a6, normalized frequencies of the diameters of the circular trajectories (excluding periods of time in which the organism swam in a straight line or wide arc) were determined and are shown in figure 1c. The diameter of the swimming trajectory increased with the diameter of the confined space experienced, which varied from 0.3 to 0.6 mm. The diameter of the swimming trajectory increased with ϕ and was approximately 1.3 times larger than ϕ (figure 1d). We are at present unable to explain this difference, and it is unclear whether the difference is physiologically significant.

In the control group that did not experience the confined space, only fewer than 10 times of the circular trajectories were counted when 80 individuals were traced for 1 min, and their diameters ranged from 1 to 2 mm. So the circular trajectory in the diameter of less than 1 mm was not observed at all for the accumulated 80 min of observation time. By contrast, after the experience of confined space, the numbers of circular trajectory (the diameter was mainly less than 1 mm) were 757, 292, 375 and 76 for the accumulated total observation time of 38 min, 15 min, 26 min and 23 min for droplet diameters of 0.3 mm, 0.4 mm, 0.5 mm and 0.6 mm, respectively. Therefore, we concluded that a circular trajectory less than 1 mm did not result from some stochastic fluctuations of swimming trajectory but was clearly induced by the confinement.

For the data of diameter distribution shown in figure 1c, the statistical significance tests of non-parametric type were done. It is because a precondition of equal variance for parametric ANOVA and multiple comparison tests was not satisfied: the variance of each group (different size of confined space) was not equal using Bartlett's test for equal variance. By means of non-parametric Kruskal–Wallis test, the medians varied significantly among the groups (p < 0.0001), and the rank sum differed significantly between any pair of groups (p < 0.05) by Dunn's multiple comparison test. Therefore, we concluded that the diameter of trajectory induced by the confinement differed significantly in the groups.

The swimming speed also changed while the swimming trajectory was circular: for instance, when ϕ = 0.3 mm, 0.39 ± 0.12 (mean ± s.d., N = 14) in the droplet and 0.56 ± 0.16 after the confinement. In the other diameters, the speeds after the confinement were 0.51 ± 0.09 (ϕ = 0.4 mm), 0.61 ± 0.13 (ϕ = 0.5 mm) and 0.49 ± 0.09 (ϕ = 0.6 mm).

4. A mathematical model for adaptive behaviour to a confined space

The swimming of a ciliate is driven by the collective motion of many cilia, which is controlled by the membrane potential and the Ca²⁺ current [6,20–22]. When the anterior part of a ciliate collides with an obstacle, Ca²⁺ ions flow into the cell and lead to reversal of the ciliary beat. The ciliate then changes direction and the turning angle depends on the period over which Ca²⁺ exceeds the threshold concentration [23]. A spontaneous turn sometimes occurs without collision with the wall due to excitation of the membrane evoked by internal and external fluctuations [24–28].

Based on the biochemical process that controls swimming, we propose a simple mathematical model. Let a ciliate be represented by a point particle with position (x(t), y(t)) at time t. The swimming motion can then be described as 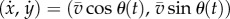, where 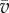is the speed (constant) and 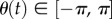is the measured angle of the swimming direction with respect to the x-axis, as shown in figure 2a1.

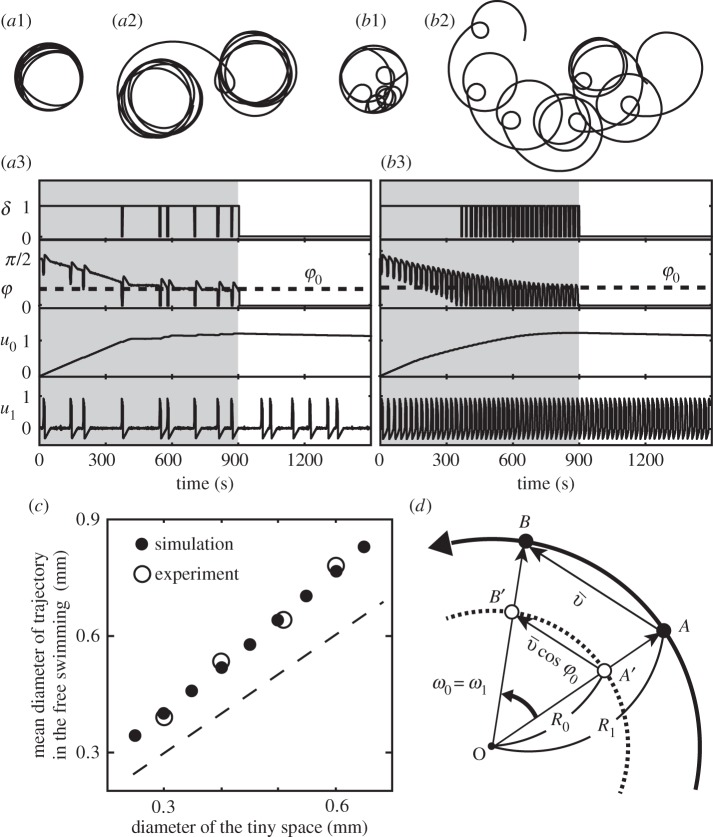
Figure 2.

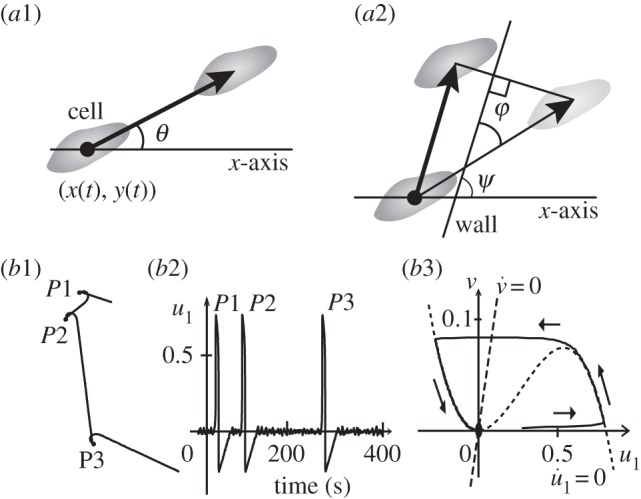
Schematic of mathematical description of swimming motion for free swimming (a1) and when in contact with the vessel wall (a2). Simulation of normal free swimming in the case of an excitable u₁ (b1–b3). (b1) Typical trajectory of swimming. (b2) Time course of u₁. The noise-induced spikes P1, P2 and P3 correspond to the turning events P1, P2 and P3, respectively, in (b1). (b3) A typical trajectory of a spike in the state space of u₁ and v. The solid line is the solution trajectory, and the dotted and the dashed lines are the null clines for u₁ and v, respectively.

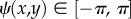Next, we describe the motion when the cell comes into contact with the vessel wall: the ciliate moves along the wall without any frictional resistance. That is, it slips along the wall. As shown in figure 2a2, the swimming trajectory is then given by the projection of the hypothetical free motion (in the case of no wall) onto the vessel wall, which is , where is the angle of the vessel wall at the contact point with the cell and φ(t) ∈ [0, π/2] is the contact angle between the vessel wall and the direction of hypothetical free motion of the cell.

Here we assume that the angle of turning is proportional to the Ca²⁺ influx such that 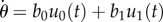, where u_0,u₁ are gating variables of the Ca²⁺ influx with slow and fast time scales, respectively. The existence of two such time scales for gating was suggested by experiment [29] and the molecular details have been well discussed for other types of cells such as neurons [30,31].

As the mechano-sensitive Ca²⁺ channel is located only at the anterior end in Paramecium [20], we set the threshold angle (φ₀) of collision sensitivity as the smallest angle at which the collision evokes a Ca²⁺ influx. However, the actual value of φ₀ is not well known although the estimated φ₀ could be within the range of 30° to 60° in Paramecium. Therefore, we examine the effects of φ₀ as a model parameter.

The slow variable u₀(t) is given by , where ɛ is a small positive value (ɛ = 0.0001). The parameter δ is the indicator of collision and takes a value of 1 (when colliding and sin(φ) > sin(φ₀)) or 0 (otherwise). The parameter s is a constant that expresses the small effect of a collision on the gating (s = 0.003). Because this slow gate opens a little in response to a collision and then closes slowly, a series of frequent collisions can be accumulated and a long-term effect on the regulation of the swimming direction appears. The dynamics of this slow variable is the new and most important idea in our model.

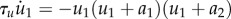
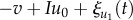
The fast variable u₁ shows excitable and oscillatory behaviour and is linked to another variable v(t) by FitzHugh–Nagumo type equations [32], 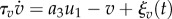. Here 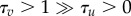, a₁, a₂ and I are the parameters and 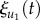, are random variables.

Lastly, we summarize the general framework of the model. The regulation of swimming direction is a function of Ca²⁺ influx that can be described by some of the gating variables of ion channels. It is likely that the full dynamics of the membrane potential includes many types of channel, but the effective modes of the dynamics can be described by just one or a few variables when the system is perturbed around the resting state of the potential by the stimulation of a collision. If the perturbed state is not far from the resting state (for free straight swimming, and (u₀, u₁) = (0, 0)), the linear approximation assumed in the u₀-equation of our model may be acceptable. Although the molecular machinery of the Ca²⁺ channels is not yet fully understood, it is expected that the mathematical description in our model is still plausible on a general level.

5. Numerical simulation of the model

Figure 2b shows the simulation of normal free swimming without any collision with the wall when u₁ is in an excitable regime. Typical trajectories of swimming look like a combination of straight motion and stochastic turning (figure 2b1). This turning results from a fluctuation-induced spike of u₁. The spikes P1, P2 and P3 in the time course of u₁ (figure 2b2) correspond to the three turning events P1, P2 and P3, respectively, in figure 2b1. A typical trajectory of a spike in the state space of u₁ and v is shown in figure 2b3.

Figure 3 shows the results of simulation (ϕ₀ = 40°) for two different sets of parameters: an excitable u₁ (figure 3a1–a3) and an oscillatory u₁ (figure 3b1–b3). The simulated trajectories of swimming are similar to the real ones (figure 1) during (figure 3a1,b1) and after (figure 3a2, b2) confinement in the small space.

Figure 3.

Mathematical modelling for swimming behaviour during and after confinement. Numerical simulations in the case of excitable u₁ (I = 0.0)(a1–a3) and in the case of oscillatory u₁ (I = 0.15)(b1–b3). Trajectories during (a1,b1) and after (a2,b2) the confinement. Time courses of key variables (a3,b3) and the confinement ended at time 900. The parameters for both cases were as follows: vessel size = 0.2 mm, 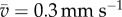, ɛ = 0.0001, s = 0.003, τ_u = 0.0025, τ_v = 20, a₁ = −0.3, a₂ = −1, a₃ = 4, b₀ = 1, b₁ = 5, φ₀ = 40° and . (a1,a2,b1,b2) Drawn to the same scale. (c) Simulated relationship between the diameter of the confined space and that of the circular trajectory just after confinement. The dashed line indicates where the two diameters are equal. All parameters were the same as (c). (d) Schematic of geometrical analysis of the relationship between the two diameters. See the main text for details.

At the initial condition (time 0), the organism contacts the wall at an angle of 90°, and the next time-step changes its direction of movement a little because φ > φ₀. This slight change in direction continues with further collisions as long as φ > φ₀, and the contact angle φ decreases to φ₀ (figure 3a3).

While the contact angle gradually decreases, u₀ increases by s (=0.003) at each change of direction and continues to increase over a series of frequent turning events as the decay rate of u₀ is slow. The increase in u₀ implies that the swimming trajectory becomes ever more curved.

Around the saturation level of u₀ at φ₀, the curvature of swimming becomes constant while the frequency of active turning and the decay speed of u₀ become balanced. This simulated trajectory (figure 3a1) is similar to that observed experimentally (figure 1a2). This saturated state of u₀ is maintained for some time after the vessel wall is removed at time 900 in the simulation, and the simulated (figure 3a2) and experimental (figure 1a5) trajectories remain similar.

Surprisingly, the diameter of circular motion after confinement is 1.3 times larger than that of the confined circular space, as also observed for the real organism. This relationship was reproduced for confined spaces with a range of sizes (figure 3c), provided that φ₀ = 40°. This adaptive circular motion slowly disappears (much later than time 1500) and straight motion is recovered (u₀ = 0, data not shown).

The simulation described above was performed in the excitable regime of u₁ and noise-induced spikes of u₁ were observed. These spikes result in a transient modulation of the curvature of swimming trajectory.

In the alternative regime of oscillatory u₁, the basic behaviour of u₀ observed for excitable u₁ was reproduced, even though regular oscillations of φ and u₁ are involved. The simulated trajectory during (figure 3b1) and after (figure 3b2) confinement are similar to the experimental trajectories in figure 1a3 and a6 with respect to the circular motion and its modulation.

As shown in figure 3c, the simulated diameters of free motion were approximately 1.3 times larger than the diameter of the confined space when φ₀ = 40°. This can be understood from the following geometrical analysis, as illustrated in figure 3d. Here we neglect u₁ because u₀ is essentially important to persist in the circular motion. As the trajectory of free swimming (the thick solid line in the figure) is circular due to the constant value of 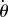(u₀ is nearly constant), we set the point O at the centre of this circle and denote the angular velocity as ω₁. When the organism is confined in the small space (indicated by the dashed line), the trajectory of free swimming is projected onto the dashed line. 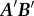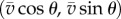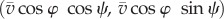The velocity vectors, AB between points A and B and between points A′ and B′, are and , respectively. 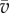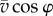The lengths |AB| and are thus given by and , respectively. The angular velocity shortly before and after the end of confinement can be approximated (for small Δt) by 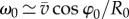and , respectively, where R₀ and R₁ are the radii of the circular trajectories during and after confinement. Because ω₁ is equal to ω₀, the ratio of the radii is given by 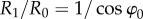, which is 1.3 in the case of φ₀ = 40°.

6. Discussion

As the confinement in a tiny droplet is an artificial condition, one may wonder if there indeed is such a space in the wild and if the circular swimming pattern observed is actually physiologically meaningful. Careful discussion on this matter is needed.

In stagnant waters like shallow rice paddy fields and ponds which are typical habitats for ciliates, there may be dense aggregates of fibrous algae like Spirogyra that form three-dimensional meshes with many tiny cavities. Or there may be aggregates of debris at the bottom of the paddy field or pond that look like media with many small-scale pores. Although the exactly spherical shape examined in this report is hardly possible under such natural conditions, cavities whose shape can be approximated by deformed spheres are to be expected. In this sense, a capacity to adapt to a confined spaces is not meaningless.

On the other hand, let us assume that there is no such cavity in the wild. Organism possess a high-enough capacity to adapt to a shape never experienced before. This, in turn, infers that Tetrahymena has generalized capacity for spatial memory. Whether or not spherical cavities occur naturally, the adaptive capacity reported here is of potential physiological usefulness.

When we confined them for more than 30 min, we observed that 70% of the individuals after exhibiting a circular trajectory stopped all movement. One may argue that the experimental conditions were stressful to the organisms. A different interpretation, however, is possible. In order to avoid frequent contacts with the wall, it may be favourable to cease movement, which would constitute an adaptive behaviour. As the organisms started to swim again sometime after the confinement, we can exclude a weakening of its physical condition by the confinement.

The adaptive behaviour reported here is of time scale shorter than a life span, and much shorter than multiple generations. It may be expected that complicated geometries of real micro-habitats are exerted in the wild. Possible advantages of this capacity will be examined in the future.

In the mathematical modelling performed in this paper, we assumed that Ca²⁺ and their Ca²⁺ channels played the key role, as many previous papers on the electrophysiological regulation of swimming behaviour in ciliates strongly suggested their importance [6,20,22,23]. This does not mean that Ca²⁺ and Ca²⁺ channels indeed contribute to the development of the adaptive behaviour reported in this paper. Therefore, this point awaits experimental verification.

The mathematical model proposed here, however, will still hold in a mathematical sense even if the key molecules are not Ca²⁺ and Ca²⁺ channels, because we assumed only two things (i) slower elicitation of a response that can accumulate their repetitive stimulation and (ii) dependency of the response sensitivity on the contact angle. The first assumption needs to be examined biologically and mathematically.

The key assumption in our model is the slow regulation of the Ca²⁺ channel, which is supported by reports that the shutdown of the Ca²⁺ current in Paramecium involves fast (10 ms range) and slow (10–100 s range) kinetics [29], and that such slow dynamics of the Ca²⁺ current is also widely found in both invertebrate and vertebrate neurons. It is thus plausible that adaptation and memorizing at the level of the cell might be embedded in the slow dynamics of channel motion. The adaptive capacity observed in this report is maintained for some time after the experience of confinement, and this might result in some benefit to the organism.

The swimming speed decreased down to 0.39 ± 0.12 in the droplet (the diameter is 0.3 mm) in comparison with 0.81 ± 0.27 in the wide-open space before being confined, and increased up a little to 0.56 ± 0.16 in the wide-open space after being confined. This change in the swimming speed is consistent with the well-known correlation between the swimming speed and curvature of swimming trajectory in Paramecium [21]: the swimming speed slows down while the curvature of swimming trajectory is larger, due to the increase in intracellular Ca²⁺ concentration which is induced by change in K⁺–Ca²⁺ composition of external medium. Although the species of organism is different from Tetrahymena, it is known that the swimming trajectory is circular in the diameter of 0.2–0.8 mm when the swimming speed is one-half or more slower than the normal speed (0.8–1.2 mm s⁻¹), and that the diameter is smaller at the slower swimming speed. This relationship of diameter and speed was very similar to the results observed in our experiment.

It is noted that a ciliate Paramecium is capable of swimming in a circular trajectory in a wide-open space under the specific conditions of external medium. This capacity can contribute to the space memory of spherical shape. Then a question arises: what kinds of shape other than spheres does the ciliate memorize? The original research done by F. Bramstedt showed a triangle was a possibility [17]. To test various shapes of arena is very interesting.

The capacities of adaptation and memory are of interest in basic biology and comparative ethology. In the field of neuroscience of higher animals, molecular events involved in the long- and short-term potentiation of synaptic connections in neural circuits have been studied in relation to the involvement of the N-methyl-d-aspartate receptor (NMDA receptor). Even in protozoa, like Paramecium and Tetrahymena, the NMDA receptor plays a key role in the regulation of swimming behaviour by modulating the membrane potential and the Ca²⁺ influx/efflux across the membrane [30,31]. This similarity implies a common evolutionally origin of capacity of memory and adaptation between ciliates and higher animals.

The range of time periods over which the real organisms exhibited the circular trajectories varied from minutes to hours. This large variation may be explained through the mathematical model. In the model, the time derivative of the slow variable u₀ is just proportional to −εu₀ as this is assumed to be the first order approximation of much more complicated dynamics for real channel molecules. The values of the proportional constant might be distributed over a range of 10-fold difference. Or, the complicated dynamics of real-world mechanism might be sensitive to internal and/or external noise through a nonlinear effect of dynamical motion.

Many types of smart behaviour in ciliates have been reported over the past 100 years. The capacity of conditioning (associative learning in response to two different stimulations) is one example. Even this type of higher learning capacity might be explained by a study of channel behaviour. This paper suggests a promising future direction for research on the physical ethology of ciliates.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by JSPS KAKENHI grant nos. 25730178 (I.K.), 24120709 (A.T.), 20300105 (T.N.) and 26310202 (T.N.), by a Grant-in-Aid for Scientific Research on Innovative Area from MEXT (25111726 (T.N.), 25103006 (T. N.)) and by the Strategic Japanese-Swedish Research Cooperative Program, Japan Science and Technology Agency (JST) (T.N.).