Identification of hierarchical chromatin domains

Abstract

Motivation: The three-dimensional structure of the genome is an important regulator of many cellular processes including differentiation and gene regulation. Recently, technologies such as Hi-C that combine proximity ligation with high-throughput sequencing have revealed domains of self-interacting chromatin, called topologically associating domains (TADs), in many organisms. Current methods for identifying TADs using Hi-C data assume that TADs are non-overlapping, despite evidence for a nested structure in which TADs and sub-TADs form a complex hierarchy.

Results: We introduce a model for decomposition of contact frequencies into a hierarchy of nested TADs. This model is based on empirical distributions of contact frequencies within TADs, where positions that are far apart have a greater enrichment of contacts than positions that are close together. We find that the increase in contact enrichment with distance is stronger for the inner TAD than for the outer TAD in a TAD/sub-TAD pair. Using this model, we develop the TADtree algorithm for detecting hierarchies of nested TADs. TADtree compares favorably with previous methods, finding TADs with a greater enrichment of chromatin marks such as CTCF at their boundaries.

Availability and implementation: A python implementation of TADtree is available at http://compbio.cs.brown.edu/software/

Contact: braphael@cs.brown.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

The 3D architecture of the genome influences key cellular processes such as gene regulation, replication timing and differentiation (Cavalli and Misteli, 2013). Chromosome conformation capture (3C) technologies use proximity ligation of DNA to elucidate genome structure at high resolution (De Wit and de Laat, 2012). Recently, techniques such as Hi-C that couple proximity ligation and high-throughput sequencing have revealed megabase-sized domains of self-interacting chromatin called topologically associating domains (TADs) in both mammals and fruit flies (Dixon et al., 2012; Hou et al., 2012; Nora et al., 2012; Sexton et al., 2012). Conserved across cell types and species, TADs may partition the genome into functional units and help regulate the distribution of epigenetic marks (Symmons et al., 2014; Tanay and Cavalli, 2013).

Hi-C uses proximity-based ligation to measure the frequency of physical interaction between pairs of genomic loci (Lieberman-Aiden et al., 2009). Typically, the raw read pairs generated by a Hi-C experiment are assigned to bins of fixed width (e.g. 40 kb), resulting in a contact matrix A, where A_ij is the number of contacts between bins i and j, normalized for experimental bias. Several methods have been developed for the identification of TADs from Hi-C data. These methods may be roughly classified into two categories: (i) methods that define a one-dimensional (1D) test statistic from the contact matrix A_ij and (2) methods that exploit the two-dimensional (2D) structure of the contact matrix.

Dixon et al. (2012) compute a 1D ‘directionality index’ (DI) from the contact matrix. This index defines whether contacts have an upstream bias, downstream bias or no bias. Next, they use a hidden Markov model (HMM) to partition the genome into regions defined by changes in the DI. Each transition into downstream bias marks the start of a domain and the next transition out of upstream bias marks its end. Sauria et al. (2014) introduce a 1D statistic called the ‘boundary index’ (BI) which captures sudden shifts in interaction preference. Sauria et al. (2014) identify domain boundaries by calling peaks in the BI, but do not explicitly pair these boundaries into domains, leaving the domain structure ambiguous.

Recently, a number of methods have been introduced to identify chromatin domains using the full 2D contact matrix. Filippova et al. (2014) use dynamic programing to find domains with maximal intra-domain contact frequency. This method includes a tunable size parameter and outputs the set of non-overlapping domains that are most robust to changes in the parameter value. More recently, Lévy-Leduc et al. (2014) developed a 2D model that fits a block diagonal matrix to observed contacts using maximum likelihood. This method is based on a generative model where the expected contact frequency across a TAD is uniform.

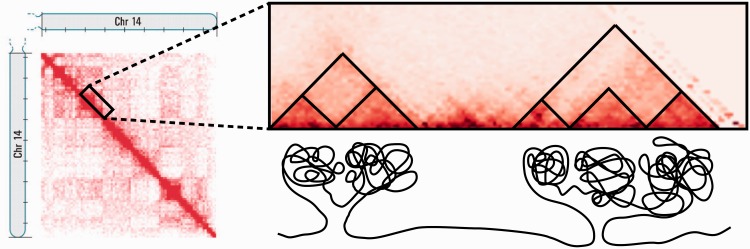
All the methods above assume that TADs are non-overlapping. However, several studies have observed a hierarchical chromatin organization including both TADs and sub-TADs within them (Fig. 1). Although TADs are conserved across cell types, sub-TADs are thought to vary between cell types and may facilitate changes in gene regulation during differentiation (Phillips-Cremins et al., 2013) and development (Berlivet et al., 2013). In addition, distinct combinations of proteins such as CTCF, Mediator and Cohesin may demarcate TAD and sub-TAD boundaries (Phillips-Cremins et al., 2013; Zuin et al., 2014). The distinct properties of TADs and sub-TADs highlight the need for methods that can detect both simultaneously. A very recent development in this direction is the ‘Arrowhead’ algorithm (Rao et al., 2014). Although this algorithm can identify overlapping domains, it does not explicitly require that overlapping domains be nested, and it is at present not publicly available.

Fig. 1.

Illustration of hierarchical TAD structure. A Hi-C contact map is shown on the left, with a close-up of the diagonal top-right. TADs and sub-TADs are annotated as triangles. The corresponding DNA structure is illustrated below

In this article, we introduce the TADtree algorithm, which detects nested hierarchies of TADs. In contrast to previously published methods that rely on ad hoc assumptions about the structure of TADs, we derive a straightforward model for the frequency of contacts within TADs. Our model is based on the empirical observation that within TADs, the enrichment of contacts over background grows linearly with the distance between bins, but at a rate that depends on the TAD length. Thus, every TAD can be characterized by two parameters: β, the baseline enrichment for contacts between adjacent bins within the TAD and δ, the rate at which contact frequency increases with distance between bins. Using reported TADs from previous studies, we derive relationships between the values of β and δ when one TAD is nested inside another. From these observations, we propose a model for TAD hierarchies.

We combine our model for contact enrichment within TADs with a 1D BI similar to the one used by Sauria et al. (2014). We formulate and optimize an objective function that scores a hierarchy of nested TAD trees according to both the fit to the observed contact matrix and the BI of each TAD and sub-TAD in the hierarchy. We demonstrate that our resulting TADtree algorithm outperforms existing methods on real data, predicting TADs that have greater enrichment for binding of factors known to delineate chromatin organization, and showing greater overlap with high-resolution data.

2 Methods

2.1 Model

Background contact frequencies

Consider a chromosome of length J (in bins) and a J × J symmetric matrix A, where A_ij is the frequency of contact between bins i and j. Typically, A_ij represents a normalized count of paired sequencing reads, where each read represents a ligation event between DNA fragments derived from bins i and j, respectively. Based on A, we form a ‘background’ function B giving the mean contact frequency for bins at each distance d. Formally,

$$B(d)=\frac{1}{J-d}{\displaystyle \sum _{i=1}^{J-d}{A}_{i,i+d}}.$$ (1)

Modeling TADs

A TAD, D, is modeled by the quadruple $D=(L_D,R_D,{\delta }_D,{\beta }_D)$, specifying an interval $[L_D,R_D]$ of bins and two parameters δ_D and β_D, which determine the expected contact frequency at each intra-TAD bin pair, as follows:

$${\tilde{A}}_D(l,k)=((k-l){\delta }_D+{\beta }_D)B(k-l)\hspace{0.17em}\text{for}\hspace{0.17em}{L}_D\le l\le k\le R_D.$$ (2)

${\tilde{A}}_D$ expresses the expected enrichment of contacts over background $\frac{{\tilde{A}}_D(l,k)}{B(k-l)}$ as a linear function of the distance $|k-l|$, having slope δ_D and intercept β_D.

This model is motivated by the observed properties of TADs identified by Dixon et al. (2012). We grouped TADs with similar sizes and computed the enrichment of contacts over background for bin pairs in each group. We observed that across many TAD groups, contact enrichment increases linearly with distance (Fig. 2A), with slope dependent on the size of the TAD. Although small deviations from linearity are observed for pairs of bins near TAD boundaries (Fig. 2B), a linear model is favored for the sake of simplicity. Because contact enrichment increases with distance, we require ${\delta }_D>0$. The positive correlation between contact enrichment and distance may arise from looping interactions between TAD boundaries, or because local interactions due to sequence proximity produce most of the contacts between closely spaced bins, drowning out the contacts that arise from the higher order structure imposed by TADs.

Fig. 2.

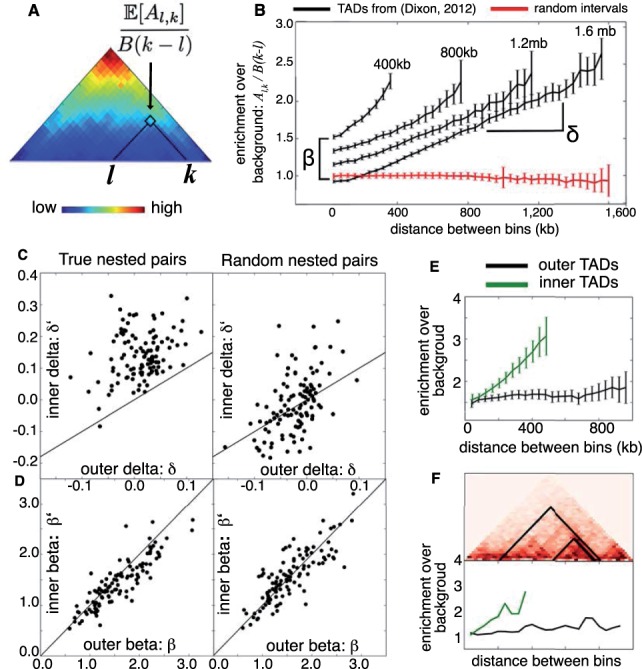
TADs from a previous study (Dixon et al., 2012) were each rescaled to match the closest of four sizes (400 kb, 800 kb, 1.2 Mb, 1.6 Mb) using bilinear interpolation. (A) The superposition of all TADs in the 1.2 Mb size class shows that contact enrichment increases with increasing distance between bins. (B) For each size class, the average enrichment of intra-TAD contacts increases linearly with distance. This linear function has slope δ and intercept β. Average enrichment for a set of random intervals is shown in red for comparison. Next, combining TADs from Filippova et al. (2014) and Dixon et al. (2012) revealed 114 nested pairs $D\prime \subset D$, where $D\prime$ had length 400–600 kb and D had length 800 kb to 1.2 Mb. (C) Nearly all nested pairs (black dots) had $\delta \prime \ge \delta$ (left), while this relationship was not true for nested pairs with randomized positions (right). (D) No similar inequality holds for values of β, although β and $\beta \prime$ are strongly correlated for both real and randomized nested pairs. (E) Rescaling nested TADs so that $D\prime$ was 500 kb and D was 1 Mb shows that average contact enrichment for $D\prime$ (green) and D (black) follows the linear model [Equation (2)] with $\delta \prime >\delta$ and $\beta \prime =\beta$. (F) Examples of nested pair (above) with contact enrichment plotted against distance (below)

Modeling sub-TADs

Consider two TADs, $D=(L_D,R_D,{\delta }_D,{\beta }_D)$ and $D\prime =(L_{D\prime },R_{D\prime },{\delta }_{D\prime },{\beta }_{D\prime })$, such that $D\prime$ lies within D (i.e. $L_D\le L_{D\prime }<R_{D\prime }\le R_D$). Because $D\prime$ represents a proper subset of the bins in D, the parameters ${\delta }_{D\prime },{\beta }_{D\prime }$ may differ from ${\delta }_D,{\beta }_D$. We investigated this difference systematically using pairs of TADs from Filippova et al. (2014) and Dixon et al. (2012) where a TAD from one dataset was contained by a TAD from the other dataset. We find that enrichment over background ($\frac{A_{lk}}{B(k-l)}$) rises with distance at a higher rate for inner TADs than for their respective outer TADs, that is ${\delta }_{D\prime }>{\delta }_D$ $(P<{10}^{-29}$; Fig. 2C). This inequality is not just a consequence of TAD size, because it does not hold for nested pairs with randomized positions (P = 0.3). In contrast, the values β_D and ${\beta }_{D\prime }$ for the outer and inner TADs show no systematic difference, but are strongly correlated $(r=0.88,P<{10}^{-35}$; Fig. 2D).

Based on these observations, we define $D\prime$ to be a sub-TAD of D provided

$$\begin{array}{l}{1.L}_D\le L_{D\prime }<R_{D\prime }\le R_D\hspace{0.17em}(\text{i}.\text{e}.\hspace{0.17em}D\prime \subset D).\\ {2.\delta }_{D\prime }>{\delta }_D.\end{array}$$

Thus, sub-TADs are defined as local regions within a larger TAD that have a different distribution of contacts, characterized by higher rate of increase in contact frequency with distance (Fig. 3A). In the same way that a single TAD D specifies an expected contact frequency function ${\tilde{A}}_D$, a TAD/sub-TAD pair $T=\{D,D\prime \}$ has an expected frequency function ${\tilde{A}}_T$, defined below. For convenience, we write $(l,k)\in D$ when $L_D\le l<k\le R_D$.

$${\tilde{A}}_T(l,k)=\{\begin{array}{ll}{\tilde{A}}_{D\prime }(l,k)\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}(l,k)\in D\prime \hfill \\ {\tilde{A}}_D(l,k)\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}(l,k)\in D\setminus D\prime \hfill \end{array}$$ (3)

Note that ${\tilde{A}}_T$ is defined for all bin pairs $(l,k)\in D$, because D is the union of the domains of ${\tilde{A}}_D$ and ${\tilde{A}}_{D\prime }$, respectively. ${\tilde{A}}_T$ is identical to ${\tilde{A}}_D$ outside the sub-region defined by $D\prime$, where it becomes identical to ${\tilde{A}}_{D\prime }$. This definition reflects the role of sub-TADs in capturing local regions within an existing TAD that have a distinct distribution of contacts, characterized by higher δ.

Fig. 3.

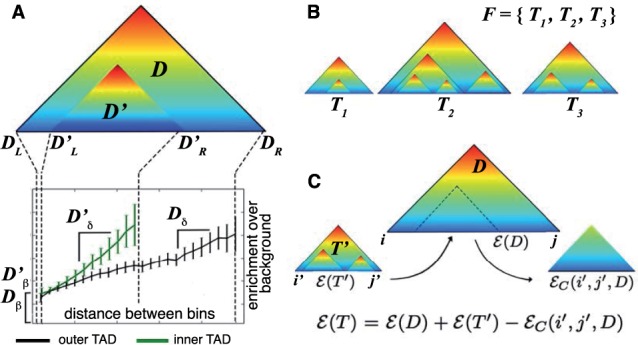
(A) When one TAD lies inside another, the enrichment of contacts increases at a faster rate for the inner TAD (green line) than for the outer TAD (black line), that is ${\delta }_{D\prime }>{\delta }_D$. (B) Example of a TAD forest containing TAD trees T₁, T₂ and T₃. (C) The squared error $\mathcal{E}(T)$ for a TAD tree T with root D and sub-tree $T\prime$ is obtained as $\mathcal{E}(T)=\mathcal{E}(D)+\mathcal{E}(T\prime )-{\mathcal{E}}_C$, where ${\mathcal{E}}_C$ is an ‘error compensation’ term that corrects double counting of the squared error over bin pairs in $T\prime$

Generalizing the TAD/sub-TAD arrangement shown in Figure 3A, we allow a single TAD to have multiple sub-TADs, and also allow sub-TADs to have their own sub-TADs. Formally, define a TAD tree T to be a rooted hierarchy of TADs, such that for each $D,D\prime \in T$ where $D\prime \subset D$, ${\delta }_{D\prime }>{\delta }_D$. A collection of disjoint TAD trees is called a TAD forest (Fig. 3B). Each TAD forest F specifies a map ${\tilde{A}}_F$ of expected contact frequencies. Because sub-TADs model the local distribution of contacts, which differs from that of the enclosing TAD, the expected contact frequency for each pair of bins in a TAD forest F is modeled using the minimal TAD $D\in F$ that contains them both or by background if there is no such TAD. Formally, let ${\min }_F(l,k)$ denote the minimal $D\in F$ such that $(l,k)\in D$, where ${\min }_F(l,k)=\varnothing$ if there is no such D. Then

$${\tilde{A}}_F(l,k)=\{\begin{array}{ll}{\tilde{A}}_D(l,k)\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\min }_F(l,k)=D\hfill \\ B(k-l)\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\min }_F(l,k)=\varnothing .\hfill \end{array}$$ (4)

Boundary index

So far we have described a model for the distribution of contacts within TADs, requiring that intra-TAD contact frequencies are enriched over background, especially for bins that are far apart. Another important feature of TADs is that their boundaries mark a shift in interaction preference. Dixon et al. (2012) use this feature as the basis for an HMM that predicts TADs by detecting shifts from upstream to downstream preference. Here, we define a 1D test statistic called the BI that measures local shifts in interaction preference. Note that Sauria et al. (2014) recently posted a preprint that also uses the term BI for their 1D statistic, which has a more complicated form. For constants p, q representing the scale and persistence of interaction shift, we define the BI ${\mathcal{B}}_{p,q}$ as follows:

$${\mathcal{B}}_{p,q}(i)={\displaystyle \sum _{l=i-q}^{i+q}|}{\displaystyle \sum _{k=1}^p{A}_{l,i+k}}-A_{l,i-k}|.$$ (5)

The BI measures the shift in contacts around an interval i. Specifically, in an interval of length p containing i, the BI ${\mathcal{B}}_{p,q}$ totals the differences in contact frequencies up to q bins upstream and downstream of i. Let ${\overline{\mathcal{B}}}_{p,q}(i):=({\mathcal{B}}_{p,q}(i)-\text{mean}({\mathcal{B}}_{p,q}))/\text{var}({\mathcal{B}}_{p,q})$ be the Z-score of ${\mathcal{B}}_{p,q}$, where mean and variance are taken over all bins on the given chromosome. We define ${\overline{\mathcal{B}}}_{p,q}$ for a TAD forest as follows:

$${\overline{\mathcal{B}}}_{p,q}(F)={\displaystyle \sum _{D\in F}{\overline{\mathcal{B}}}_{p,q}}(L_D)+{\overline{\mathcal{B}}}_{p,q}(R_D).$$ (6)

Because the end points of TADs should have high BI, we say that D has valid boundaries if ${\overline{\mathcal{B}}}_{p,q}(L_D)>0$ and ${\overline{\mathcal{B}}}_{p,q}(R_D)>0$.

2.2 Fitting TAD trees to data

Given a matrix A of observed contacts, we aim to find a TAD forest F that best fits the data. Specifically, we want a TAD forest F that has high BI and minimizes the error between A and the expected contact frequency function ${\tilde{A}}_F$. We measure the latter using the sum squared error,

$$\mathcal{E}(F)={\displaystyle \sum _{l,k}({\tilde{A}}_F(}l,k)-A_{lk}{)}^2$$ (7)

Finally, we require that F has valid boundaries in order to exclude false-positive TAD calls in regions of the genome that have high contact frequencies but low BI. We combine these criteria into the following optimization problem.

Problem 1 —

Given $N\in \mathbb{N}$ and $\gamma \in {\mathbb{R}}^{+}$, find a TAD forest F, with $|F|=N$ and each $D\in F$ having valid boundaries, that maximizes the objective function ${\mathcal{O}}_{\gamma }(F)=\gamma {\overline{\mathcal{B}}}_{p,q}(F)-\mathcal{E}(F)$.

Here, N and γ are user-defined parameters controlling the number of TADs and the balance between $\mathcal{E}$ and ${\overline{\mathcal{B}}}_{p,q}$, respectively.

We now define a recursive algorithm that solves Problem 1. First, we note that any TAD forest can be decomposed into a set of non-overlapping TAD trees. Thus, we will first show how to find TAD trees that locally maximize the objective ${\mathcal{O}}_{\gamma }$. To that end, we define an objective function $\Phi (i,j,N,\delta )$ over intervals $\left[i,j\right]$.

Definition 1 —

Given the interval $[i,j]$ and parameters $N\in \mathbb{N}$ and $\delta \in {\mathbb{R}}^{+}$, let $\Phi (i,j,N,\delta ):=\max {\mathcal{O}}_{\gamma }(T)$ over all TAD trees T such that (i) T is rooted at the interval $[i,j]$; (ii) T contains N TADs $(|T|=N)$; (iii) each $D\in T$ satisfies ${\delta }_D>\delta$ and (iv) each $D\in T$ has valid boundaries.

We will compute $\Phi (i,j,N,\delta )$ by dynamic programing. At each step, beginning with the interval $[i,j]$, we must make optimal choices of the following.

1. Parameters δ_D, β_D defining the root TAD $D=(i,j,{\delta }_D,{\beta }_D)$.

2. A collection of non-overlapping sub-intervals $[i_x,j_x]$ which define the locations of the top-level sub-trees in T.

3. For each interval $[i_x,j_x]$, a ‘multiplicity’ n_x representing the total number of TADs in that sub-tree. Note that in order for T to have N TADs, the multiplicities n_x must satisfy $\sum n_x=N-1$.

To implement the steps above, one must be able to compute the optimal score for a TAD tree having the specified root and first-level sub-trees. Recall that ${\mathcal{O}}_{\gamma }(T)=\gamma {\overline{\mathcal{B}}}_{p,q}(T)-\mathcal{E}(T)$, where $\mathcal{E}$ is the sum squared error defined in Equation (7). Suppose T is a TAD tree consisting of a root TAD D and a single sub-tree $T\prime$. From Equation (6), we have ${\overline{\mathcal{B}}}_{p,q}(T)={\overline{\mathcal{B}}}_{p,q}(D)+{\overline{\mathcal{B}}}_{p,q}(T\prime )$. However, $\mathcal{E}(T)\ne \mathcal{E}(D)+\mathcal{E}(T\prime )$, because pairs of bins within the sub-tree $T\prime$ contribute to both $\mathcal{E}(T\prime )$ and $\mathcal{E}(D)$, and are double counted when these terms are summed. Because the expected contact frequency for a pair of bins is modeled using the smallest TAD that contains them both [Equation (4)], we retain the contribution to squared error made by the sub-tree $T\prime$, and subtract the contribution to squared error from the root TAD D (Fig. 3C). Thus, if $T\prime$ spans the interval $[i\prime ,j\prime ]$, then $\mathcal{E}(T)=\mathcal{E}(D)+\mathcal{E}(T\prime )-{\mathcal{E}}_C(i\prime ,j\prime ,D)$, where ${\mathcal{E}}_C(i\prime ,j\prime ,D)$ is the error compensation term defined below.

Definition 2 —

Consider a TAD D and interval $[i,j]\subseteq [D_L,D_R]$. Let the error compensation ${\mathcal{E}}_C(i,j,D)$ be

$${\mathcal{E}}_C(i,j,D)={\displaystyle \sum _{l=i}^j{\displaystyle \sum _{k=l}^j(}}{\tilde{A}}_D(l,k)-A_{lk}{)}^2.$$ (8)

Using the error compensation, we derive an expression for the score of a TAD tree in terms of its root TAD and sub-trees.

Proposition 1 —

Let T be a TAD tree consisting of a root TAD D and a collection of non-overlapping sub-trees $T_1,\mathrm{...},T_m$, spanning the intervals $[i_1,j_1],\mathrm{...},[i_m,j_m]$. The score ${\mathcal{O}}_{\gamma }(T)$ can be decomposed as

$${\mathcal{O}}_{\gamma }(T)={\mathcal{O}}_{\gamma }(D)+{\displaystyle \sum _{x=1}^m(}{\mathcal{O}}_{\gamma }(T_x)+{\mathcal{E}}_C(i_x,j_x,D)).$$ (9)

We now describe Steps (1–3) above in greater detail. To perform step (1), recall that a TAD is defined by four parameters $(L_D,R_D,{\delta }_D,{\beta }_D)$. Thus, in choosing the root TAD D, two parameters are given ahead of time $([L_D,R_D]=[i,j])$, meaning we only need to select optimal values for δ_D and β_D. Next, for a given choice of δ_D and β_D, we must choose a set of non-overlapping sub-trees, defined by sub-intervals $[i_x,j_x]$ and multiplicities n_x (steps 2–3). To that end, let $\mathcal{I}(i,j,N)$ be the collection of sets $\{(i_x,j_x,n_x)\}$ that satisfy the following properties: (i) $[i_x,j_x]$ are non-overlapping sub-intervals of $[i,j]$; (ii) $\sum n_x=N-1$ and (iii) i_x and j_x are valid boundaries. Using $\mathcal{I}(i,j,N)$ as a search space, we evaluate $\Phi (i,j,N,\delta )$ as follows.

Proposition 2 —

For each interval $[i,j]$ and positive integer N,

$$\begin{array}{l}\Phi (i,j,N,\delta )={\displaystyle \underset{\{({\beta }_D,{\delta }_D)|{\delta }_D>\delta \}}{\max }}({\mathcal{O}}_{\gamma }(D)+{\displaystyle \underset{(i_x,j_x,n_x)\}\in \mathcal{I}(i,j,N)}{\max }}({\displaystyle \sum _x{\mathcal{W}}_x}\left)\right)\\ where\hspace{0.17em}{\mathcal{W}}_x=\Phi (i_x,j_x,n_x,{\delta }_D)+{\mathcal{E}}_C(i_x,j_x,D).\end{array}$$ (10)

To our knowledge, there is no efficient algorithm for evaluating Equation (10). To see why, note that ${\mathcal{W}}_x$ depends on both $(i_x,j_x,n_x)$ and $({\beta }_D,{\delta }_D)$, meaning the two maximizations cannot be performed independently. To perform the maximizations jointly, we could proceed in two directions. On the one hand, we could enumerate interval sets from the collection $\mathcal{I}(i,j,N)$ and optimize $({\beta }_D,{\delta }_D)$ for each. This is not practical, however, because $\mathcal{I}(i,j,N)$ is very large: $(|\mathcal{I}(i,j,N)|\sim \mathcal{O}({(j-i)}^N)$. Going in the other direction, we could discretize the space $\mathbb{R}\times {\mathbb{R}}^{+}$ and test a finite set of pairs $({\delta }_D,{\beta }_D)$, optimizing the interval set $\{(i_x,j_x,n_x)\}$ for each. This method has the advantage that the optimization over interval sets can be performed efficiently using a version of weighted interval scheduling (described below). However, there would still be a very large set of $({\delta }_D,{\beta }_D)$ pairs to check, making this approach impractical as well. Therefore, instead of evaluating $\Phi (i,j,N,\delta )$ exactly, we approximate it, using pre-computed values for $({\delta }_D,{\beta }_D)$ rather than true argmax. The pre-computed values are chosen to be optimal in the trivial case where D has no sub-TADs.

Definition 3 —

For each interval $[i,j]$, let

$$(\widehat{\beta }(i,j),\widehat{\delta }(i,j))=\underset{(\beta ,\delta )\in \mathbb{R}\times {\mathbb{R}}^{+}}{\mathrm{argmin}}\mathcal{E}((i,j,\delta ,\beta )).$$ (11)

We define a TAD D to be locally fitted if ${\delta }_D=\widehat{\delta }(L_D,R_D)$ and ${\beta }_D=\widehat{\beta }(L_D,R_D)$. Thus, D is locally fitted if its parameters are optimal in the case where D has no sub-TADs. We use ${\widehat{D}}_{ij}$ to denote the unique locally fitted TAD spanning $[i,j]$. Using $\widehat{\delta }(i,j)$ and $\widehat{\beta }(i,j)$ as pre-computed TAD parameters is convenient because they are easily found by linear regression. By restricting to locally fitted TADs, we obtain a simpler optimization problem which admits an efficient algorithm.

Problem 2 —

Given $N\in \mathbb{N}$ and $\gamma \in {\mathbb{R}}^{+}$, find the TAD forest F that maximizes the objective ${\mathcal{O}}_{\gamma }(F)=\gamma {\overline{\mathcal{B}}}_{p,q}(F)-\mathcal{E}(F)$ such that $|F|=N$, and each $D\in F$ is locally fitted and has valid boundaries.

Once again, our first step in solving Problem 2 will be to find optimal TAD trees over every interval.

Definition 4 —

Given $N\in \mathbb{N}$ and the interval $[i,j]$, define $\widehat{\Phi }(i,j,N):=\max {\mathcal{O}}_{\gamma }(T)$ over all TAD trees T such that (i) T is rooted at the interval $[i,j]$, (ii) T contains N TADs $(|T|=N)$ and (iii) each $D\in T$ is locally fitted has valid boundaries.

In contrast to $\Phi (i,j,N,\delta ),\hspace{0.17em}\widehat{\Phi }(i,j,N)$ does not take δ as an argument, because it maximizes over TAD trees whose δ values are fixed by the requirement that they be locally fitted. This leads to the following proposition, which shows how to evaluate $\widehat{\Phi }(i,j,N)$.

Proposition 3 —

For each interval $[i,j]$ and positive integer N,

$$\widehat{\Phi }(i,j,N)={\mathcal{O}}_{\gamma }({\widehat{D}}_{ij})+\underset{\{(i_x,j_x,n_x)\}\in \mathcal{I}(i,j,N)}{\max }\left({\displaystyle \sum _x{\mathcal{W}}_x}\right)$$ (12)

where

$${\mathcal{W}}_x=\{\begin{array}{ll}\widehat{\Phi }(i_x,j_x,n_x)+{\mathcal{E}}_C(i_x,j_x,{\widehat{D}}_{ij})\hfill & \hspace{0.17em}if\hspace{0.17em}\widehat{\delta }(i_x,j_x)\ge \widehat{\delta }(i,j)\hfill \\ -\infty \hfill & otherwise.\hspace{0.17em}\hfill \end{array}$$

2.3 Algorithm

To evaluate Equation (12), we must choose a set of non-overlapping intervals $[i_x,j_x]$ and multiplicities n_x that maximize $\sum _x{\mathcal{W}}_x$ and satisfy $\sum n_x=N-1$. Similarly, to assemble a TAD forest from TAD trees, we will likewise be choosing a non-overlapping set of intervals (leaves of TAD trees) with multiplicities (number of TADs in each tree) such that the sum of their scores is maximized and the multiplicities sum to a predefined N. These tasks are both similar to the weighed interval scheduling problem (Kleinberg and Tardos, 2005), which asks for the highest weight set of non-overlapping intervals from a given collection. However, the two tasks described above have the added requirement that the interval multiplicities sum to a predefined value. Therefore we define a variant of weighted interval scheduling called weighted interval scheduling with multiplicities (WISM).

Definition 5 —

WISM: Let $\{[i_{\alpha },j_{\alpha }]\hspace{0.17em}|\hspace{0.17em}\alpha \in A\}$ be a set of intervals with multiplicities $k_{\alpha }$ and weights $w_{\alpha }$. For a given integer N, the ${\mathit{\text{WISM}}}_N$ problem asks for the subset $B\subseteq A$ that maximizes ${\sum }_{\alpha \in B}{w}_{\alpha }$ subject to the following constrains: (i) the intervals $\{[i_{\alpha },j_{\alpha }]\hspace{0.17em}|\hspace{0.17em}\alpha \in B\}$ are non-overlapping and (ii) ${\sum }_{\alpha \in B}{k}_{\alpha }=N$.

We solve the WISM problem using a dynamic programing approach based on the following recurrence.

Proposition 4 —

Let N be an integer and let $\{[i_{\alpha },j_{\alpha }]\hspace{0.17em}|\hspace{0.17em}\alpha \in A\}$ be a set of intervals with multiplicities $k_{\alpha }$ and weights $w_{\alpha }$. Let ${\mathit{\text{WISM}}}_N(n)$ be the score of the solution to the ${\mathit{\text{WISM}}}_{\mathit{N}}$ problem, restricted to intervals that end before n. When $n<{\min }_{\alpha }{i}_{\alpha }$, then clearly ${\mathit{\text{WISM}}}_N(n)=0$. In all other cases

$${\text{WISM}}_N(n)=\max \{\begin{array}{l}{\max }_{\{\alpha |j_{\alpha }=n\}}({\mathcal{W}}_{\alpha }+WIS{M}_{(N-k_{\alpha })}(i_{\alpha }))\hfill \\ WIS{M}_N(n-1).\hfill \end{array}$$ (13)

TADtree algorithm

We now outline an algorithm for solving Problem 2, which we call TADtree. (Fig. 4) Consider a chromosome with a J × J contact matrix A. Let N be the number of TADs in the desired TAD forest. To constrain runtime, we limit the maximum TAD size to S and the number of TADs in each tree to M. The TADtree algorithm contains WISM as a subroutine, for which we do not provide pseudocode. The runtime of TADtree is $\mathcal{O}(J{N}^2+J{S}^3{M}^2+J{S}^5)$. Beyond the contact matrix A, TADtree accepts six user-defined parameters: $N,M,S,\gamma ,p$ and q. We do not provide a rigorous procedure for setting these parameters, but have detailed the rationale for our choices in Section 3.

Algorithm 1: $\text{TADtree}(A,N,M,S,\gamma ,p,q)$

Input: Matrix A of length J and parameters N, M, S, γ, p, q.

Output: TAD forest F representing solution to Problem 2.

$\mathcal{T}=[\hspace{0.17em}]$ // list of optimal TAD trees

for $i\in \{1,\mathrm{...},J-1\}$ do

  for $j\in \{i,\mathrm{...},i+S\}$ do

   compute $\widehat{\delta }(i,j)$ and $\widehat{\beta }(i,j)$ by linear regression

   if ${\overline{\mathcal{B}}}_{p,q}(i)>0,\hspace{0.17em}{\overline{\mathcal{B}}}_{p,q}(j)>0$ and $\widehat{\delta }(i,j)>0$ then

     $\widehat{\Phi }(i,j,1)\leftarrow {\mathcal{O}}_{\gamma }({\widehat{D}}_{ij})$

     $\mathcal{S}=[\hspace{0.17em}]$ // list of sub-trees

     for $i\prime \in \{i,\mathrm{...},j-1\}$ do

       for $j\prime \in \{i\prime +1,\mathrm{...},j\}$ do

        if ${\overline{\mathcal{B}}}_{p,q}(i\prime )>0,\hspace{0.17em}{\overline{\mathcal{B}}}_{p,q}(j\prime )>0$ and

        $\widehat{\delta }(i\prime ,j\prime )>\widehat{\delta }(i,j)$ then

          for $m\prime \in \{1,\mathrm{...},M-1\}$ do

           $\mathcal{W}\leftarrow \widehat{\Phi }(i\prime ,j\prime ,m\prime )+{\mathcal{E}}_C(i\prime ,j\prime ,{\widehat{D}}_{ij})$

           $\mathcal{S}\leftarrow$ append $(i\prime ,j\prime ,m\prime ,\mathcal{W})$

     for $m\in \{2,\mathrm{...},M\}$ do

       $\widehat{\Phi }(i,j,m)\leftarrow \text{WISM}(m,\mathcal{S})$

       $\mathcal{T}\leftarrow$append $(i,j,m,\widehat{\Phi }(i,j,m))$

return $\text{WISM}(N,\mathcal{T})$

Algorithm 2: $\text{WISM}(n,\mathcal{J})$

Input: $n\in \mathbb{N}$ and list $\mathcal{J}$ containing tuples $(i,j,m,\mathcal{W})$ representing intervals $[i,j]$ with multiplicity m and weight $\mathcal{W}$. Assume that $\mathcal{J}$ is ordered by the right end points of its constituent intervals.

Output: Highest weight subset of $\mathcal{J}$ with non-overlapping intervals whose multiplicities sum to n.

Fig. 4.

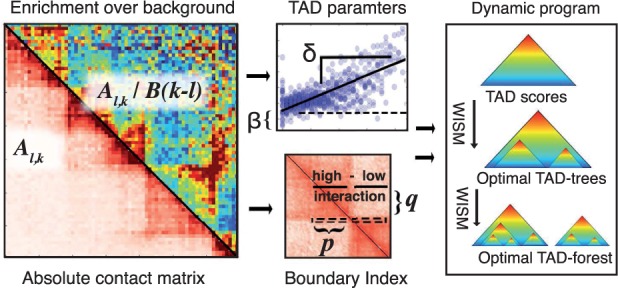
Overview of TADtree algorithm. (A) Beginning with contact matrix A, we compute the fold-enrichment over background for each pair of positions. (B) For each interval $[i,j]$, we estimate parameters $\widehat{\delta }(i,j),\widehat{\beta }(i,j)$. (C) Next, for each genomic position i we compute the BI, a 1D statistic that looks for local shifts in interaction frequency at TAD boundaries. (D) Finally, a dynamic program finds TAD trees that maximize the BI and best fit the contact matrix A, then selects an optimal set of TAD trees to form a TAD forest

3 Results

We used TADtree to analyze Hi-C data from Dixon et al. (2012) for mouse embryonic stem cells, which had been binned at 40 kb and normalized for sequencing bias using the method from Yaffe and Tanay (2011). This dataset included a matrix of contact frequencies for each chromosome (available at http://yuelab.org/hi-c/download.html).

3.1 TADtree parameters

For each contact matrix A, we ran TADtree (Algorithm 1) with the following parameters. We set the maximum TAD size to be 2 Mb (S = 50 bins), because TADs were originally defined at a scale of 1 Mb. We note that chromatin ‘megadomains’ larger than 2 Mb have been observed (Lieberman-Aiden et al., 2009), but the current focus is on TADs. In theory, it is desirable to use a large value of S in order to avoid biasing the solution by prior assumptions on TAD size. However, in practice, the $O(S^5)$ runtime of TADtree makes large values of S impractical.

We allowed at most M = 10 TADs per TAD tree. We find that TAD trees almost never attain this limit for the number of TADs (data not shown), implying that our choice for M did not limit the complexity of our output. We hypothesize that setting M = 10 allows our algorithm to detect the full complexity of TAD structure in the underlying Hi-C data used in this study, although higher resolution Hi-C data may warrant larger values of M.

For the remaining parameters, we used the following values: γ = 500, p = 3 (120 kb) and q = 12 (480 kb). These values were chosen based on visual inspection of output for small subsets of the full Hi-C contact maps. Although we do not have a rigorous procedure for choosing values of p and q, we observed that larger values of p and q make the BI insensitive to small-scale boundaries, while smaller values result in the algorithm outputting many TADs and sub-TADs, many of which are likely noise.

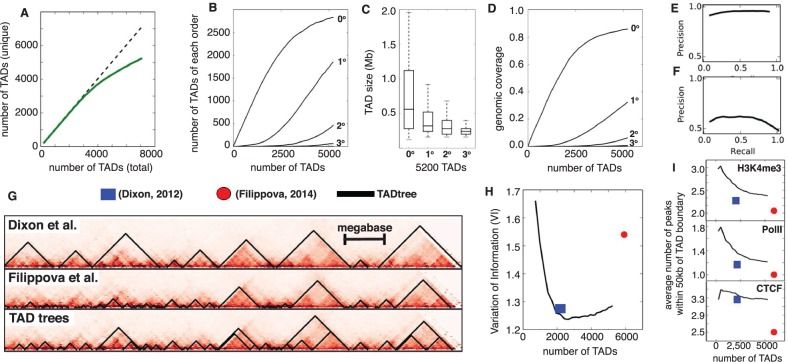
We varied the total number N of TADs to examine the tradeoffs in sensitivity and specificity (see below). Because TADtree runs independently on each chromosome, we chose N for each chromosome such that the number of TADs per megabase was consistent, using a range of densities (0 TADs/Mb, up to 6 TADs/Mb) across the different runs. For large values of N, we observed some duplicate TAD calls defined as pairs of TADs whose boundaries are both within 1 bin (40 kb) of each other (Fig. 5A). We filtered these duplicates by removing the inner TAD from each pair. Because of the dynamic programing approach used in TADtree, computing the optimal TAD forest for a given value N = N₀ also entails computing optimal TAD forests for all $N<N_0$. Thus our implementation of TADtree outputs a duplicate-filtered set of TADs (as well as the percentage of duplicates in the unfiltered set) across a user-specified range of values of N. Because a high percentage of duplicates suggests that TADtree is saturating the space of TAD forests, users can examine this percentage—or other relevant data—to choose a final value of N for downstream analysis.

Fig. 5.

(A) Total number of unique TAD output by TADtree (solid green curve) as a function of the value of N, the desired number of TADs. Dotted line is equality. (B) Number of TADs of each order as a function of total number of TADs. As the total number of TADs increases, the number of zero-order TADs (indicating new positions not covered by TADs) start to plateau and high order TADs appear. (C) Higher order TADs have smaller sizes and (D) lower coverage of the genome, consistent with their nesting inside larger TADs. (E, F) Precision-recall curves comparing TADs found by TADtree with those reported in Dixon et al. (2012). (G) Example of TADs from TADtree (bottom) and two previous studies (Dixon et al., 2012; Filippova et al., 2014). (H) TADs found by TADtree (black line) are more similar (lower VI) to those found in a recent analysis of higher resolution Hi-C data (Rao et al., 2014), compared with TADs reported in Dixon et al. (2012) (blue square) and Filippova et al. (2014) (red disk). (I) Number of ChIP-seq peaks for CTCF, PolII and the histone modification H3K4me3 within 50 kb of TAD boundary (y-axis) versus total number of TADs (x-axis) for TADtree TADs (black line), Dixon et al. (2012) (blue square) and Filippova et al. (2014) (red disk). TADtree shows greater enrichment for all four chromatin marks

3.2 TAD nesting

We found that the TADs returned by TADtree show extensive nesting. We define the order of a TAD as the number of TADs that contain it: TADs with no sub-TADs are order 0, sub-TADs have order 1, sub-sub-TADs have order 2 and so on. When we run TADtree with N = 2200 TADs, which is the number identified by Dixon et al. (2012), we find that 13% have order greater than 0. When we allow 5200 TADs, which is close to the number identified by Filippova et al. (2014), 45% have order greater than 0 (Fig. 5B). Although TADs of high order (up to 4) are observed, they are relatively rare. For example, with 5200 TADs, 10% have order $\ge 2$ and only 1.4% have order $\ge 3$. As expected, TADs of increasing order have decreasing size (Fig. 5C) and decreasing genomic coverage (Fig. 5D).

3.3 Comparison with previous studies

We compared the TADs from TADtree with those found in two previous studies (Dixon et al., 2012; Filippova et al., 2014) that analyzed the same contact matrices. To compare TADs from different approaches, we compared the partitions of bins determined by TAD end points using the variation of information (VI) measure (Meilă, 2003). The VI is a distance measure for set partitions, and thus lower values of VI mean that two partitions of bins into TADs are more similar. We find that the VI between TADtree TADs with N = 2200 and TADs from Dixon et al. (2012) was 0.82, compared to 1.72 when the positions of our TADs were randomly shuffled. Similarly, we find that VI = 0.99 between TADtree TADs with N = 5200 and those reported in Filippova et al. (2014), compared with 1.73 when our TADs were shuffled. Interestingly, the VI = 1.2 is much higher between Dixon et al. (2012) TADs and Filippova et al. (2014) TADs. This higher VI is likely a consequence of differing size preference. The method used by Dixon et al. (2012) tends to favor large TADs, while the approach used by Filippova et al. (2014) tends to favor small TADs. The greater similarity between our TADs and those from both Dixon et al. (2012) and Filippova et al. (2014) highlights the ability of TADtree to robustly identify TADs across a range of scales.

As an additional comparison between TADs from Dixon et al. (2012) and TADtree, we computed precision-recall curves, treating the Dixon et al. (2012) TADs as the true set. We performed the comparison in two ways: first counting bins inside TADs as true positives (Fig. 5E) and then counting the positions of TAD boundaries (Fig. 5F), where boundaries within one bin (40 kb) of each other were considered to match. TADtree obtained a recall of 89% at a precision of 95% in determining which bins were inside TADs, and a recall of 85% at a precision of 41% in determining TAD boundaries. Note that a low precision in the later comparison is expected since a large fraction of TAD boundaries predicted by TADtree belong to sub-TADs, and therefore lie between the boundaries of TADs called by Dixon et al. (2012).

As an independent measure of the quality of TADs output by the three approaches, we compared them to the TADs identified by Rao et al. (2014) in higher resolution Hi-C data. Specifically, Rao et al. (2014) generated Hi-C maps for mouse lymphoblasts at 5 kb resolution. Because this increased resolution allows significantly more data for estimating TADs, the TADs from these data are a useful benchmark for evaluating the accuracy of TAD calls based on the lower resolution (40 kb) contact maps used here. Fixing the number of TAD output by TADtree to the same as the other approaches, we find that the TADtree TADs are more similar to the TADs in the higher resolution (Rao et al., 2014) data than those from the other methods. The difference is relatively small in comparison with Dixon et al. (2012): VI = 1.24 for TADtree versus 1.27 for Dixon et al. (2012), and not statistically significant (P = 0.3) using a paired t-test that compares the values across individual chromosomes. A larger difference was observed in comparison with Filippova et al. (2014): VI = 1.28 for TADtree versus 1.54 for Filippova et al. (2014) ($P<{10}^{-6}$). Interestingly, we also observe that the lowest VI occurs when TADtree is run with N = 2600 TADs, a number in between the number of TADs in Dixon et al. (2012) and Filippova et al. (2014) (Fig. 5H).

3.4 Enrichment of chromatin marks

As another measure of the quality of TADs produced by each algorithm, we examined the enrichment of Chip-Seq derived binding sites of several proteins and chromatin marks that were shown by Dixon et al. (2012) to cluster at domain boundaries. Specifically, we examined binding sites of the transcription factor CTCF, an insulator protein that has been shown experimentally to contribute to TAD boundary formation (Zuin et al., 2014). We also examined the presence of PolII sites, as well as H3K4me3 marks—a transcription-associated chromatin mark—because TAD boundaries are frequently gene dense sites of active transcription (Hou et al., 2012) and have been shown to be enriched for housekeeping genes (Dixon et al., 2012). These marks were also used by Filippova et al. (2014) to validate their TAD predictions. We downloaded ChIP-Seq data for mES cells from ENCODE (GEO accession ID GSE29184). Peak calling for these data was performed in their initial publication (Shen et al., 2012). For each dataset, we counted the average number of ChIP-Seq peaks within 50 kb of a TAD boundary. Below, we present summary statistics for the whole genome, but compute P values using a paired t-test that compares the values across each chromosome. We found that TADs from TADtree show a significantly greater enrichment for all four ChIP-Seq signals than TADs from previous studies. For PolII and H3K4me3, our TADs have at least 14% more ChIP-seq peaks within 50 kb of a TAD boundary than the TADs from Dixon et al. (2012) and Filippova et al. (2014) when controlling for number of TADs (Fig. 5I) (P < 0.005 for 4/4 comparisons). Although our TAD boundaries show a similar enrichment of CTCF as those from Dixon et al. (2012), they have a 30% greater enrichment compared with TADs from Filippova et al. (2014) ($P<{10}^{-6}$). Enrichment of these marks decreases as we increase the total number of TADs, indicating a tradeoff between sensitivity and specificity. However, the robust improvement compared with previous methods over a large range of TAD numbers demonstrates the advantages of the hierarchical decomposition performed by TADtree.

4 Discussion

Hi-C and other approaches that combine high-throughput sequencing with 3C are becoming widely used to probe the 3D organization of the genome. There is increasing evidence that sub-TAD structure varies between cell types and contributes to changes in gene regulation during differentiation and development (Berlivet et al., 2013; Phillips-Cremins et al., 2013). TADtree is the first publicly available algorithm that detects nested hierarchies of TADs in Hi-C data. Thus, TADtree will enable further research into the organization of TADs and sub-TADs.

TADtree employs a straightforward linear model of contact enrichment that is derived from earlier annotations of TADs. TADtree finds the best TAD hierarchy via a dynamic programing algorithm, using an approximation of this model. We demonstrate that TADtree outperforms earlier methods on real Hi-C data. In particular, we show that TADs determined by TADtree on lower resolution (40 kb) data match more closely to TADs derived on higher resolution (5 kb) Hi-C data from Rao et al. (2014). Moreover, we find that TADtree-derived TADs have a higher enrichment at their boundaries for binding sites of factors such that CTCF than are known to demarcate chromatin boundaries.

Although the TADtree algorithm demonstrates that TAD hierarchies can be informative, there are several areas where the algorithm can be improved. First, TADtree finds only an approximate best fit to our model. Tests on smaller datasets using a brute force search suggest that the approximate solution differs little from the true solution (data not shown). Nonetheless, finding an exact solution in polynomial time—or proving that this cannot be done—may be an interesting problem for future research. A second limitation of TADtree is the rapid increase in runtime $\sim \mathcal{O}(S^5)$ with maximum TAD size S. Third, although our use of a parameter N specifying the number of TADs returned by TADtree is a novel contribution compared with previous methods, we have not included a procedure for model selection, leaving the choice of N to the user.

Chromatin structure is highly dynamic and varies widely from cell to cell (Lanctot et al., 2007). Because approaches such as Hi-C typically pool contacts from across a whole population, it is unclear to what extent the TAD trees identified in this article represent true chromosomal structures within individual cells. Although efforts have been made to deconvolve Hi-C contacts computationally (Sefer et al., 2015), this remains a challenging problem. In the future, advances in microscopy and single cell Hi-C (Nagano et al., 2013) may shed light on whether TAD trees are true chromosomal structures or artifacts of super position.

The emerging field of higher order chromatin organization is providing a new lens for viewing the regulatory landscape of cells. Chromatin structure may provide a missing link for understanding the regulatory changes that occur during differentiation and disease (Andrey et al., 2013; Jäger et al., 2015). Because megabase-scale TADs appear to be highly conserved across both cell types and species, it is likely that key changes in chromatin organization occur at the sub-TAD scale. For example, changes in the structure of sub-TADs could fine-tune opportunities for contact between genes and enhancers. Therefore, methods for deciphering the hierarchical structure of chromatin will be important for linking genome architecture to cellular state.