Abstract
Motivation: De novo transcriptome assembly is an integral part for many RNA-seq workflows. Common applications include sequencing of non-model organisms, cancer or meta transcriptomes. Most de novo transcriptome assemblers use the de Bruijn graph (DBG) as the underlying data structure. The quality of the assemblies produced by such assemblers is highly influenced by the exact word length k. As such no single kmer value leads to optimal results. Instead, DBGs over different kmer values are built and the assemblies are merged to improve sensitivity. However, no studies have investigated thoroughly the problem of automatically learning at which kmer value to stop the assembly. Instead a suboptimal selection of kmer values is often used in practice.
Results: Here we investigate the contribution of a single kmer value in a multi-kmer based assembly approach. We find that a comparative clustering of related assemblies can be used to estimate the importance of an additional kmer assembly. Using a model fit based algorithm we predict the kmer value at which no further assemblies are necessary. Our approach is tested with different de novo assemblers for datasets with different coverage values and read lengths. Further, we suggest a simple post processing step that significantly improves the quality of multi-kmer assemblies.
Conclusion: We provide an automatic method for limiting the number of kmer values without a significant loss in assembly quality but with savings in assembly time. This is a step forward to making multi-kmer methods more reliable and easier to use.
Availability and Implementation:A general implementation of our approach can be found under: https://github.com/SchulzLab/KREATION.
Supplementary information: Supplementary data are available at Bioinformatics online.
Contact: mschulz@mmci.uni-saarland.de
1 Introduction
With the massive amounts of RNA-seq data (Sultan et al., 2008) produced for many non-model organisms, the interest for de novo analyses of RNA-seq data has increased over the last few years. These analyses include the de novo assembly of full length transcripts, expression level computation of novel transcripts, detecting differentially expressed transcripts and detection of related genes in close species or polymorphism detection (Davidson and Oshlack, 2014; Haznedaroglu et al., 2012; Le et al., 2013; Sloan et al., 2012).
Due to the large number of applications, several methods have been proposed for the de novo transcriptome assembly. Most of these methods are based on building a de Bruijn graph (DBG) from the RNA-seq reads. The nodes of the DBG are substring of length k (also know as kmers) obtained from the reads and two nodes are connected if they have k-1 overlap. After obtaining the DBG, various heuristic algorithms are used to predict alternative transcripts from each DBG component. These algorithms either use a single kmer value (Chang et al., 2015; Grabherr et al., 2011; Xie et al., 2014) or merge transcripts generated from multiple kmer values to obtain a final non-redundant assembly (Peng et al., 2013; Robertson et al., 2010; Schulz et al., 2012; Surget-Groba and Montoya-Burgos, 2010). A multi-kmer based approach outperforms a single-kmer based approach as one kmer size rarely fits all genes (Chang et al., 2015; Peng et al., 2013; Schulz et al., 2012). Large kmer values resolve repeats and regions with many errors, whereas small kmer values are necessary to connect lowly expressed transcripts that have low-coverage regions. Hence even for most single kmer methods it is beneficial to run the assembler for different kmer values and merge the final results.
But the question about the core set of kmer sizes that are needed to achieve a good quality assembly has received little attention for multi-kmer methods. Currently, approaches (i) use the default kmer series of the assembler which is tuned on a limited number of datasets, (ii) select an arbitrary subset of kmer sizes or (iii) use all possible kmer sizes for the assembly. In practice that means that most often the resulting assembly is suboptimal. Either important kmer sizes are missed (cases 1–2) and therefore the sensitivity is reduced or the complete assembly contains more misassemblies than necessary and has wasted computational resources (case 3).
Selecting a suitable kmer size for de novo assembly has been previously explored in the context of genomic sequencing. For example (Chikhi and Medvedev, 2014) devised a method to select the best kmer size for de novo genome assembly. Simpson devised a method to estimate a number of interesting characteristics like paths with variations or repeats in the DBG for different kmer sizes from a FM-index over the reads (Simpson, 2014). Further, computing an optimal kmer range for de novo read error correction was also proposed (Ilie et al., 2011, Schulz et al., 2014). However, all these methods assume a uniform coverage distribution and are not applicable to non-uniform RNA-seq data.
Here we investigate in detail how the number of kmer assemblies can be minimized to save computational resources, without a large loss in sensitivity and without using a reference annotation for assembly quality assessment. We introduce the KREATION (Kmer Range EstimATION) algorithm that is based on two novel contributions: (i) a comparative clustering of single kmer assemblies to define extended clusters which gives a notion of the assembly quality and (ii) a heuristic model assessment that allows to predict the optimal stopping point for a multi-kmer assembly method. We show that our new de novo strategy automates the choice of kmer sizes to explore, while achieving close to optimal performance.
2 Methods
2.1 Evaluation of assemblies
We use standard metrics for the evaluation of our assembled transcripts. We align transcripts against the reference genome using Blat (Kent, 2002,version 36) and compare it with annotated Ensembl transcripts (Cunningham et al., 2014,version 65). Then we compute the number of Ensembl transcripts that are overlapped to at least 80 or 100% by an assembled transcript, and term them as 80 and 100%-hits, respectively. We defined 80%-hit improvement rate as the ratio of the 80%-hits obtained from the multi-kmer assembly compared to a single-kmer based assembly. Further, we compute misassemblies by counting the number of aligned transcripts whose aligned region is ≤ 95% of the total transcript length. All transcripts that are not misassemblies are considered to be correct. We also compute nucleotide sensitivity and specificity as explained by (Schulz et al., 2012).
2.2 Transcriptome assembly
We used the de novo transcriptome assemblers Oases (Schulz et al., 2012, version 0.2.08), SOAPdenovo-Trans (Xie et al., 2014, version 1.03) and Trans-ABySS (Robertson et al., 2010 version 1.5.3) for our analyses. All assemblers were run with default parameters except the kmer parameter for the DBG and insert length for the paired-end sequencing data sets. Transcripts shorter than 100bps were removed from the final assembly.
SOAPdenovo-Trans doesn’t have its own merge script and the merge script of Oases and TransABySS provides little information about the clusters obtained. Further, it was shown that the oases_merge script has suboptimal performance compared to CD-HIT-EST clustering (Haznedaroglu et al., 2012). Hence we used CD-HIT-EST (Fu et al., 2012, version 4.6.1-2012-08-07) for clustering individual kmer assemblies, as detailed in Section 2.3.
In order to analyze how selecting arbitrary kmer values influences assembly performance we created three sets of random kmers. All the sets contained kmers spread across the read length, see Table 1.
Table 1.
Sets of random kmer values used to analyze the effect of selecting arbitrary kmer values on the assembly. Rows represents the sets and columns represent the dataset with read length mentioned in brackets
| Brain (50) | TCell (45) | hESC (50) | HeLa (76) | |
|---|---|---|---|---|
| Set1 | 25,33,37,45 | 25,33,37,45 | 25,33,37,45 | 25,39,53,61 |
| Set2 | 25,31,35,43 | 25,31,35,43 | 25,31,35,43 | 35,43,57,69 |
| Set3 | 23,33,37,45 | 23,33,37,45 | 23,33,37,45 | 51,55,69,71 |
We denote as best-k the assembly where the highest number 80%-hits was achieved for a dataset. For the analyzed datasets these were assemblies obtained from k= 25 for brain, k= 23 for human Embryonic Stem Cell (hESC), k= 27 for T-cell and HeLa.
2.3 Clustering assembled transcripts
We use the CD-HIT-EST software, for clustering transcripts assembled by individual kmer sizes and merging sets of transcripts from distinct kmers. CD-HIT-EST is a fast clustering technique that reports final clusters with all sequences contained in the cluster. It uses a greedy algorithm to iteratively grow clusters and multicore parallelization for fast clustering. We run CD-HIT-EST with 10 threads.
Consider two sets of assembled transcripts, and with n and m many sequences respectively, each produced by running a de novo assembler for one or more kmer values. Let be the set of l sequence clusters obtained by applying a sequence clustering algorithm to and , denoted as ComputeClusters(). We define the following notions on clusters: a cluster is called unique with respect to if it holds that , namely that all sequences in c are only from assembly . Further we call the longest sequence of a cluster the representative of c, denoted as rep(c). A cluster is called extended by if and c is not unique. We denote e = extended() as the number of extended clusters in with respect to (See Supplementary Figure S1). Collectively we denote all clusters that are extended or unique with respect to as novel clusters with respect to . All remaining cluster are called old.
2.4 Predicting the assembly stopping point via assessment of model fit
We analyzed assemblies generated by different de novo assemblers and observed that with an increase in kmer size the number of correct transcripts produced by the assembler follows approximately an exponential distribution, see Results. We show that the number of extended clusters in consecutive assemblies behave similarly and can thus be used in a de novo setup. Our rationale was that once this exponential trend does not hold anymore for increasing kmer values, the number of extended clusters is not dominated by correct transcripts, but rather by missassemblies or redundant assemblies.
We summarize our approach for the above insight in algorithm 1: Given a set of reads and a minimal kmer, denoted kmin, the assembler explores an a priori fixed series of kmer values where . This series is computed using a function f. In our case we use the simple function: , as Oases and SOAPdenovo-Trans can use odd kmer values only and we wanted to use the same set of kmer values for all assemblers to maintain consistency. For each k an assembly is produced (line 7). All new transcripts in are clustered with the previous transcripts using the function ComputeClusters() to produce (line 8). The number of extended clusters ei with respect to is computed (using extended()) and its log count is stored in yi (line 9).
We then assume the following linear model:
| (1) |
where denotes the series, with . β0 and β1 are the constants representing slope and intercept of the line respectively. Gaussian noise is denoted by ϵ.
We are interested in analyzing the linear model fit with an increase in number of data points. More precisely, if we have a linear model fit on n − 1 datapoints (where n > 3, since we require at least three datapoints to model a line to avoid premature stopping of the assembly), we want to assess the error in predicting the nth datapoint using the line. We fit a line (lm) with and and estimate the coefficients by minimizing the residual sum of squares (line 10):
| (2) |
where is the predicted value of yi. Assuming that this line would also explain yn, we use the estimated coefficients to compute for kn (line 11). We compute the error between and its actual value:
| (3) |
We increment n and repeat the above procedure until n reaches the stopping point. For any given kmer series of length m, we define the deviation score (d_score) as the cumulative sum of point-wise error estimates:
| (4) |
The stopping point is determined by applying a threshold to the d_score (line 13). The is expected to remain close to zero for data points which follow a linear trend. It increases considerably and crosses the threshold value at a point where the quality of the linear fit degrades i.e. the fitted line is no longer able to explain the additional datapoint. If the is less than the cutoff, the algorithm continues and updates all the variables (line 16–18). Otherwise the algorithm terminates and produces the final assembly.
Algorithm 1.
Computation of largest kmer for a de novo transcriptome assembler with KREATION
1: Input: Reads , read length l, function f, kmin, threshold t
2:
3:
4:
5:
6: repeat
7:
8:
9:
10:
11:
12:
13: if
14: break
15: else
16:
17:
18: ▹ Compute next k value
19: end if
20: until
21: Output: transcripts
2.5 De novo removal of misassemblies
A disadvantage of merging several single kmer assemblies is the increased number of misassemblies in the final result. In principle, misassembled transcripts should only occur at kmer values that are shorter than repeat length and thus they are unlikely to occur at all different kmer values. To accommodate this idea we devised the following method. Assume we run our assembly for the values . After producing the final clustering of the transcripts of these four assemblies we consider the clusters c in which only transcripts of a certain exist, i.e. which are unique with respect to . We termed these clusters as single-k clusters. We classified all the single-k clusters and transcripts shorter than a predefined length threshold (300 bp for all datasets) as misassemblies.
For measuring the difference in misassemblies between multi-kmer assembly (say ) and single-kmer assembly (say ) we define:
| (5) |
where,
| (6) |
| (7) |
2.6 Data retrieval and preprocessing
All datasets were downloaded from the SRA (http://www.ncbi.nlm.nih.gov/sra). Five RNA-seq datasets were used for analysis: 147M paired-end reads of length 50 bps for human brain (Barbosa-Morais et al., 2012, SRR332171), 45M paired-end reads of length 45 bps for T-cell (Heap et al., 2010, SRX011545), 142M single-end reads of length 50 bps from hESCs (Au et al., 2013, SRR1020625), 64M paired-end reads of length 76 bps from HeLa cell lines (Cabili et al., 2011, SRR309265) and 60M, 101bp paired-end reads from IMR90 cell lines from ENCODE (http://genome.ucsc.edu/cgi-bin/hgFileUi?g=wgEncodeCshlLongRnaSeq).
The quality of transcriptome assembly is highly affected by the presence of sequencing errors (Le et al., 2013). Hence as a preprocessing step, all datasets were error corrected using SEECER version 0.2 (Le et al., 2013) with default parameters, except for HeLa where we used ks= 31 for SEECER. After each single kmer assembly we remove redundant transcripts in the same assembly by using CD-HIT-EST clustering (sequence identity 99%) (Fu et al., 2012) and only retaining the representative sequences of clusters.
3 Results
3.1 Common kmer selection strategies are suboptimal
Multi-kmer de novo transcriptome assemblers build the DBG for several kmer values. Conceptually, the task is to find the best multi-kmer assembly given a set of possible values and a set of reads . There are two problems to this: (i) which metric should be used to define optimal performance? (ii) how to efficiently find , such that achieves optimal performance for , given that there are many such subsets?
For the first problem, one performance measure used often in the literature is the number of annotated 80%-hits in a sequence database. This is determined by aligning the transcripts to a reference sequence and comparing it with existing gene annotation, (see ‘Methods’). This metric does not consider the specificity of the assembled transcripts and does not penalize for the amount of misassemblies. Here, we suggest to optimize the sensitivity of the multi-k assembly using the number of 80%-hits and use a misassembly removal strategy for the final assembly. We define the number of 80%-hits Ensembl transcripts that are obtained by running the assembler for all values in K for a dataset as optimal. With this notion, we can measure the performance of any multi-kmer assembly with in terms of % of optimal. For example, if the exhaustive assembly using K produces 2000 80%-hits, we set that as optimal. If another multi-k assembly produces 1500 80%-hits, then it reconstructed 75% of the optimal value.
The second problem is rarely addressed in the literature, in particular the problem of selecting a subset given . In practice, the following heuristics are common: (i) use the best single kmer assembly according to an evaluation criteria, e.g. the one with the most BlastX hits in a close species. Here we represent this strategy by an optimistic approach selecting the single kmer assembly that has the highest number of known reference transcripts assembled, termed Best-k. (ii) Select an arbitrary subset of possible kmer values. We created 3 such sets for each dataset, which are called Set 1–3 (see ‘Methods’). (iii) The last strategy is to run the assembly for the full set of values in K. In this work we introduce KREATION (Kmer Range EstimATION), a data-driven heuristic approach which tries to maximize sensitivity without running the full set of kmer assemblies.
In Figure 1, we show the performance of all three previous strategies using the Oases assembler (Schulz et al., 2012) on four different human RNA-seq datasets that have different read lengths and sequencing depth (see ‘Methods’). Compared to running the full set of kmers, which by definition is optimal, choosing a random set or picking the Best-k shows a loss in performance up to 30%. In particular, each setup outperforms the others on a different dataset, such that no one strategy can be recommended. KREATION achieves close to optimal performance (Fig. 1).
Fig. 1.
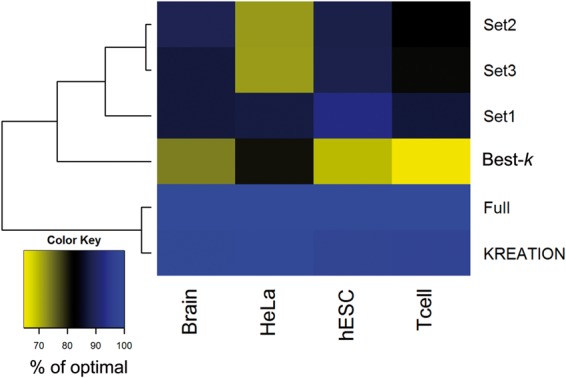
Comparison of kmer selection strategies: random selection of a set of kmers (Set 1-3), best possible single kmer based assembly (Best-k), using KREATION introduced here and merging assemblies over all possible kmers (Full). Each column denotes one of the datasets analyzed. The intensity of the heat map encodes how many of the optimal number of 80%-hits are achieved by the approach (% of optimal)
3.2 Clustering of consecutive kmer assemblies reveals assembly progress
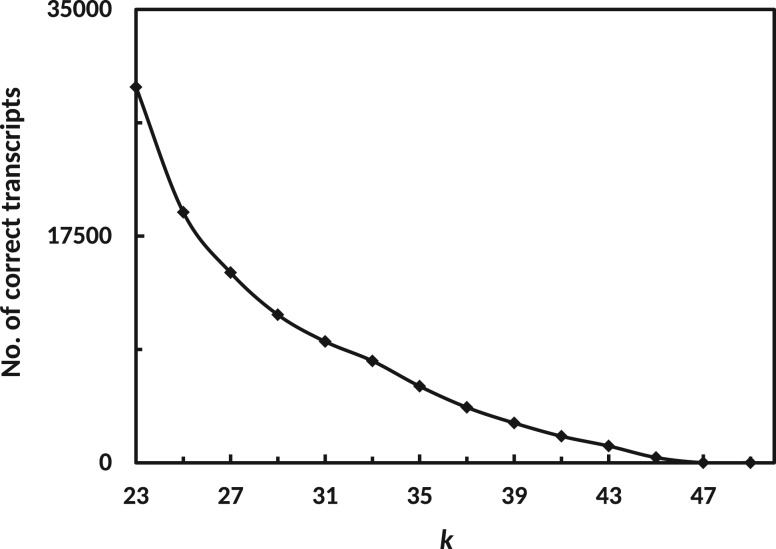
The main focus of this work is to define a data-driven procedure that predicts an optimal stopping point for a de novo multi-kmer assembler. As we mentioned earlier, we want to find a subset that shows a similar number of 80%-hits compared to the full assembly. First, we investigated the contribution of each single-kmer assembly to the performance of the full assembly using Oases. In Figure 2, we plot the number of correct transcripts that are assembled in their longest form in a particular single kmer assembly (x-axis). It can be seen that the assembly with the smallest kmer value contributes most of the correct transcripts and that a decreasing exponential trend can be observed, with higher kmer values being less important. From this we conclude that the problem of finding from all possible subsets can be simplified. We suggest to consider a series of increasing kmer values , where . In this work we used the series of kmers .
Fig. 2.
Total number of correct transcripts (y-axis) which were assembled during iteration of kmer k (x-axis) in the final merged assembly. Correctness of transcripts is determined through alignment to the genome, see ‘Methods’ section
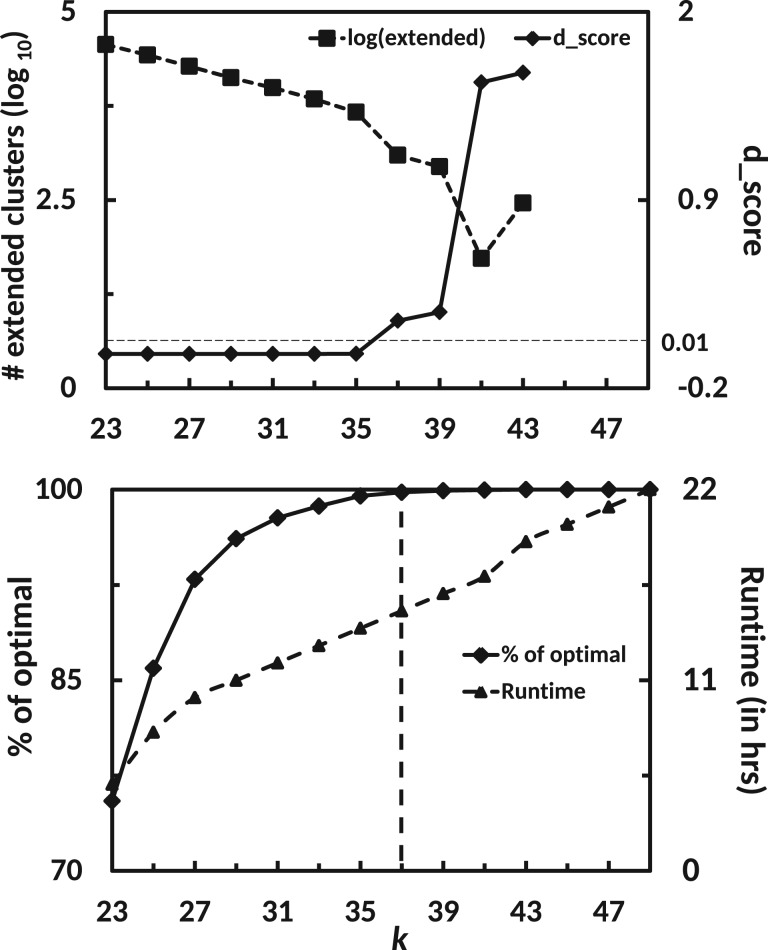
In Figure 3 (bottom) it is shown how the performance (% of optimal, left y-axis) changes when the multi-k assembly is constructed up to index i in the series, i.e. , by merging transcripts, (see ‘Methods’). Similar to our observation in Figure 2 we see that higher k values contribute little to the assembly, e.g. 99% of the optimal sensitivity is reached at k= 39.
Fig. 3.
Concordance between d_score, behaviour of extended clusters and the assembly of known transcripts. (top) The number of extended clusters (primary y-axis, log10 base) and d_score (secondary y-axis) is shown as a function of increasing k values in the multi-k assembly (x-axis), see text. The d_score crosses the threshold value (dotted horizontal line) at a k value after which no significant contribution is made to the assembly. This can be seen from the bottom plot which shows the contribution of each kmer (x-axis) towards assembly of optimal number of known 80%-hits (y-axis). The vertical dotted line represents the kmer where the assembly is stopped
In a de novo circumstance, how can we predict the index i such that the obtained sensitivity is close to optimal sensitivity? We observed that the number of transcripts going from i to i + 1 always increases, i.e. , illustrated for a dataset in Supplementary Table 1. However, we know from Figure 2 that for higher k values the number of correct transcripts decreases approximately exponentially. Correct transcripts, as in Figure 2, need to be novel. These novel transcripts in are the representative sequences of clusters that either extend transcripts in (extended clusters) or form unique clusters, without any transcript from (see ‘Methods’). For KREATION we use the CD-HIT-EST algorithm that preserves sequence to cluster memberships in its output and its clustering heuristic has an added advantage of being very fast in practice.
In our de novo setup some of the novel clusters will represent misassemblies. These misassemblies generally arise from the unique clusters (Supplementary Figure S2). Extended clusters constitute more 80%-hits than unique clusters (Supplementary Figure S3). Therefore, we can approximate the number of correct transcripts for by counting extended clusters.
In Figure 3 (top) we show how the logarithm of the number of extended clusters for the brain dataset behaves for different k values. As the number of extended clusters also contains misassemblies we observed the exponential trend, visible as a line in log space, only up to k = 35. Afterwards, when fewer genuine transcripts are contributed by , this trend changes. Hence, once the curve starts to deviate significantly from a straight line, dropping towards small cluster numbers, it may be advisable to stop the assembly as we do not expect contributions to the overall assembly.
3.3 Stopping the assembly by assessment of model fit
But how to measure if the exponential fit is worse after adding another kmer assembly?
We tested the following method. Suppose we run our assembly for values . We first fit a linear model to the log counts of extended clusters for all indices until n − 1, (see ‘Methods’). Assuming that the predicted linear model would also explain the response variable of the current index n, we predict the log count of extended clusters for n. We then deduce the error between the actual value and the predicted value. The process is repeated for all values of n and after each iteration errors are summed up defining our deviation score (). Normally the error is close to zero for data points which follow a linear trend and hence the resulting is very small. The error becomes significantly larger at a point where the curve starts to deviate from the straight line. This results in a noticeable increase in . As seen in Figure 3 (top), the value of remains close to zero until k = 37. Namely, until a kmer value where all the points are well approximated by a straight line. Beyond this kmer the increases significantly and goes above a pre-defined threshold (0.01 in our case). This point corresponds to a kmer that shows close to 99% of the optimal value (Fig. 3 bottom, dotted line). Therefore, stopping at this point results in almost no loss of assembly sensitivity and a significant reduction in runtime (Fig. 3 bottom, secondary axis). We tested this heuristics with other assemblers on the same dataset and found a similar behaviour (Fig. 4). Hence we used this heuristic to design the KREATION algorithm, see Algorithm 1.
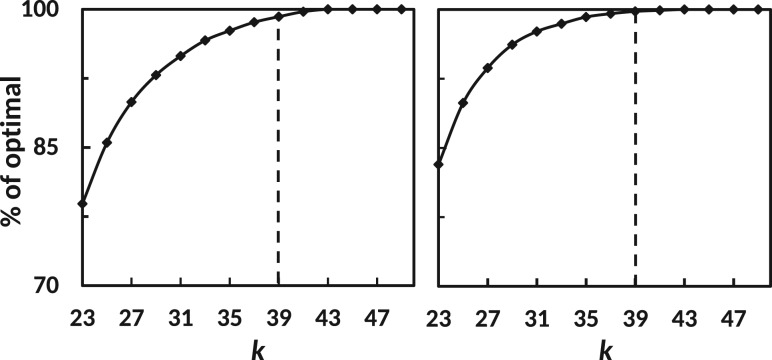
Fig. 4.
Analysis of optimal kmer value for Trans-ABySS (left) and SOAPdenovo-Trans (right) on the brain dataset. The points in the curve represents how much of the final 80% transcripts (final here means the 80% transcript discovered using all k-values and thus termed optimal) are predicted by a multi-k assembly up to the current kmer (x-axis). The dashed line in each plot represents the optimal kmer suggested by KREATION
3.3.1 Application to other datasets
In addition to the brain dataset, we tested KREATION on four other data sets with different read length and coverage (see ‘Methods’). In all cases the point where crosses the threshold value coincides with a kmer value close to the optimum (see Supplementary Figure S4–S7).
We list the complete numbers for all five datasets in Table 2. As the table shows, consistently for all datasets the stopping point only leads to a small decrease in the 100 and 80%-hits. Further the final number of transcripts is reduced without affecting the nucleotide sensitivity and specificity. We also show the number of kmer assemblies not computed and the time saved due to KREATION. In particular, for the longer read datasets (HeLa and IMR90) KREATION avoids a significant number of assemblies, saving up to days of computation on our computing cluster. Note that the clustering done after each kmer assembly, only takes in the order of a few minutes as CD-HIT-EST is parallelized and very fast (Fu et al., 2012).
Table 2.
Analysis of assembly results with all assemblers on the five datasets
| Oases | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Dataset | kmer range | No. Transcripts | Sens. (%) | Spec. (%) | 100%-hits | 80%-hits | Runs saved | %hrs reduced | Runtime (hrs) |
| Brain | KREATION | 462 896 | 46.59 | 68.98 | 6264 | 42 540 | 6 | 32 | 15 |
| Brain | Full | 468 056 | 46.74 | 68.94 | 6315 | 42 629 | — | — | 22 |
| hESC | KREATION | 196 824 | 37.58 | 73.13 | 12 783 | 42 899 | 8 | 31 | 9 |
| hESC | Full | 203 042 | 37.43 | 73.62 | 13 105 | 43 635 | — | — | 13 |
| HeLa | KREATION | 113 009 | 24.06 | 78.81 | 4243 | 25 625 | 15 | 10 | 162 |
| HeLa | Full | 119 009 | 24.1 | 77.43 | 4284 | 25 721 | — | — | 180 |
| TCell | KREATION | 129 868 | 19.11 | 77.91 | 3050 | 18 650 | 5 | 15 | 6 |
| TCell | Full | 132 975 | 19.05 | 75.42 | 3131 | 18 918 | — | — | 7 |
| IMR90 | KREATION | 1 362 744 | 49.65 | 37.21 | 22 165 | 59 253 | 14 | 34 | 600 |
| IMR90 | Full | 1 384 061 | 49.55 | 36.75 | 22 246 | 59 700 | — | — | 901 |
| SOAPdenovo-Trans | |||||||||
| Dataset | kmer range | No. Transcripts | Sens. (%) | Spec. (%) | 100%-hits | 80%-hits | Runs saved | %hrs reduced | Runtime (hrs) |
| Brain | KREATION | 295 870 | 33.28 | 63.08 | 4192 | 25 416 | 5 | 9 | 11 |
| Brain | Full | 298 286 | 33.28 | 63.35 | 4235 | 25 621 | — | — | 12 |
| hESC | KREATION | 226 974 | 35.52 | 60.34 | 8072 | 34 914 | 5 | 25 | 6 |
| hESC | Full | 229 635 | 35.45 | 60.27 | 8128 | 35 087 | — | — | 8 |
| HeLa | KREATION | 139 955 | 25.63 | 61.89 | 3413 | 23 308 | 15 | 20 | 60 |
| HeLa | Full | 144 909 | 25.63 | 60.3 | 3456 | 23 559 | — | — | 75 |
| TCell | KREATION | 94 233 | 18.79 | 73.37 | 2598 | 16 589 | 4 | 34 | 4 |
| TCell | Full | 94 925 | 18.8 | 73.48 | 2624 | 16 634 | — | — | 6 |
| IMR90 | KREATION | 1 836 920 | 38.58 | 8.65 | 11 936 | 45 276 | 17 | 10 | 573 |
| IMR90 | Full | 1 847 582 | 38.99 | 9.71 | 12 720 | 47 308 | — | — | 635 |
| TransABySS | |||||||||
| Dataset | kmer range | No. Transcripts | Sens. (%) | Spec. (%) | 100%-hits | 80%-hits | Runs saved | %hrs reduced | Runtime (hrs) |
| Brain | KREATION | 348 824 | 36.88 | 64.59 | 6715 | 36 531 | 5 | 10 | 18 |
| Brain | Full | 350 814 | 36.39 | 64.14 | 6766 | 36 629 | — | — | 20 |
| hESC | KREATION | 263 654 | 36.5 | 59.61 | 10 514 | 40 845 | 9 | 40 | 6 |
| hESC | Full | 274 615 | 36.72 | 57.95 | 10 975 | 41 618 | — | — | 10 |
| HeLa | KREATION | 143 423 | 26.8 | 68.56 | 4210 | 26 841 | 20 | 24 | 100 |
| HeLa | Full | 173 170 | 26.9 | 65.24 | 4402 | 27 460 | — | — | 130 |
| TCell | KREATION | 108 830 | 20.47 | 75.74 | 3572 | 212 347 | 4 | 25 | 4.5 |
| TCell | Full | 109 990 | 20.44 | 75.84 | 3608 | 21 409 | — | — | 6 |
| IMR90 | KREATION | 1 396 311 | 44.32 | 19.5 | 18 761 | 57 922 | 23 | 29 | 560 |
| IMR90 | Full | 1 470 188 | 46.03 | 22.8 | 20 653 | 60 095 | — | — | 780 |
The first row for each dataset analyses the transcripts obtained by running the assembly till the optimal kmer. The second row for each dataset represents the results obtained by running the assembly till a feasible kmer closest to the read length. KREATION used a threshold of 0.01 for all the cases.
3.3.2 Effect of d_score threshold
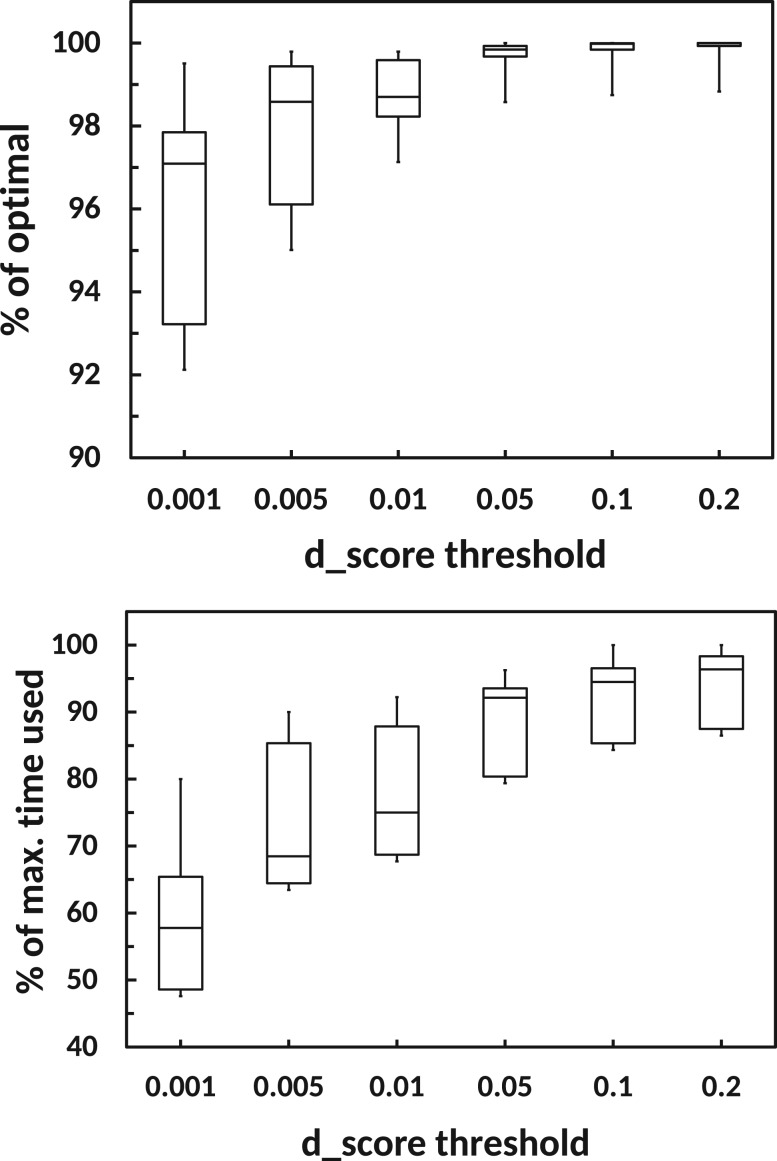
The threshold t for is an important parameter for KREATION. We tested our approach for various values of t = (0.001, 0.005, 0.01, 0.05, 0.1, 0.2) on all datasets and assemblers. We found that selecting a threshold of 0.001 leads to at least a 50% reduction in runtime, and at the same time a loss up to at most 9% in comparison to the full assembly. A high threshold value results in achieving an almost 100% optimal assembly, but results in insignificant reduction of runtime (Fig. 5). For our analyses we chose a threshold value of 0.01, which seems to be a good tradeoff between runtime and quality of the final assembly, but other values may be preferred by the user.
Fig. 5.
Analysis of KREATION performance with different d_score thresholds. (top, higher is better) Assembler performance is measured as % of optimal (y-axis) for different d_score thresholds (x-axis). (bottom, lower is better) KREATION runtime is shown in comparison to the time taken by the Full assembly (y-axis). Each box plot shows the results for all three assemblers applied to the five data sets
3.4 Single-k clusters are enriched in misassemblies
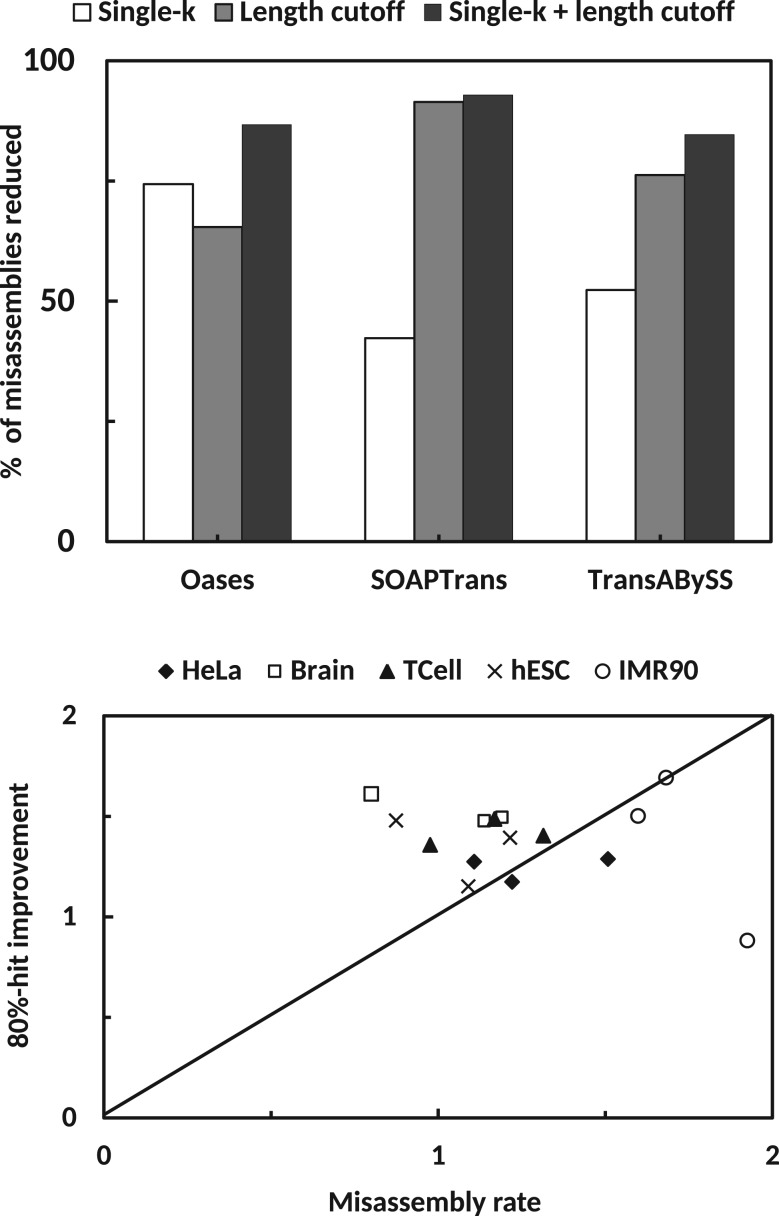
The major drawback of a multi-kmer based assembly is the generation of a high number of misassemblies. We observed, and also various studies have shown, that misassemblies are generally shorter in length (see Supplementary Figure S8) and hence a large percentage of them can be removed by applying a length cutoff (300 bp in our case) on the final transcripts (Fig. 6 top). As clustering transcripts produced by different kmer assemblies is an integral part of KREATION, we wondered how misassemblies are distributed over the clusters. We observed that clusters which contained transcripts from only one kmer value consisted of a large number of misassemblies. We termed these clusters single-k clusters (see ‘Methods’). Removing these clusters also reduces the number of misassemblies significantly (Fig. 6 top). We found that removing all transcripts which are either shorter than the length cutoff or which belong to single-k clusters reduces more misassemblies as compared to applying only one of the above mentioned filters (Fig. 6 top).
Fig. 6.
Analysis of different misassembly removal strategies. (top) The bar plot represents the performance of various removal strategy in terms of percentage of misassemblies removed on Brain dataset. Single-k cluster removal (white bar) and 300 bp length cutoff based removal (grey bar) removes a high percentage of misassemblies. A combination of both methods (black bar) performs better than applying only one strategy. (bottom) Comparison of 80%-hit improvement rate and misassembly rate for all computed assemblies (see ‘Methods’)
Further we wanted to check whether merging assemblies from multiple kmer values as done in KREATION is better than the single-kmer assembly with the highest sensitivity (k1 in our case). In other words, we wanted to check whether we are generating more misassemblies than useful transcripts, when we merge assemblies from multiple kmer values. For this, we define 80%-hit improvement rate as the fold-change of 80%-hits from the assembly generated by the lowest kmer and misassembly rate as the ratio of observed to the expected number of misassemblies. Figure 6 (bottom) shows the comparison between these two metrics for all KREATION assemblies computed, separated by dataset. In an ideal situation, the 80%-hit improvement rate should be better than the misassembly rate and hence all the points in the graph should be above the diagonal. We show that for most of the datasets the corresponding points are either above the diagonal or close to the diagonal, except for the HeLa dataset assembled by TransABySS, which has a misassembly rate of 1.93. We conclude that the multi-kmer based assembly approach followed by appropriate filtering of misassemblies is better than the single kmer based assembly.
4 Discussion and conclusion
We have presented KREATION, an algorithm that is able to automatically stop a de novo multi-k transcriptome assembly at a kmer value close to the optimal sensitivity. We showed that clustering newly assembled transcripts with all assemblies made in previous rounds can be used to estimate how many transcripts have been improved due to the last round, by counting extended clusters. We empirically found that the number of extended clusters falls exponentially with increasing k, when we consider to run the multi-k assembler from smaller kmer values to larger ones, as is most reasonable for transcriptome assemblies. This motivated us to predict the kmer value at which the assembly should stop by selecting the kmer where deviation to the expected exponential trend deviates considerably, as measured with the designed the d_score. We have shown that thresholding the d_score works well for three popular de novo assemblers, and datasets with different coverages and read lengths. For longer read datasets KREATION may save days of computation.
However, KREATION is a heuristic approach and there is no guarantee that the d_score threshold corresponds to a good stopping point or that there will be an optimum for the set of kmers tested, albeit both is true for the datasets and assemblers tested in this work. Still, we think that there is a theoretical connection that is worth exploring further. KREATION often selects different stopping kmer values for each assembler when applied to the same dataset. This points to a complex interplay between graph structure, transcriptome complexity, read coverage and assembler implementations. It may be the reason why simpler strategies for selecting kmers do not seem to generalize for datasets with different characteristics (cf. Fig. 1).
One disadvantage of merging the assemblies of several k values is the increased number of misassemblies as compared to using one kmer. However, recent studies have shown that appropriate filters (Yang and Smith, 2013) or a proper statistical treatment with replicate data (Davidson and Oshlack, 2014) allows to remove most misassemblies and therefore ease downstream analyses. Here we show that a large number of misassemblies stem from single-k clusters that can be removed easily. Together with a length cutoff on assembled transcripts this denotes a powerful approach to get rid of most of the misassemblies without removing genuine transcripts (Fig. 6, Supplementary Figure S9). We argue that this makes multi-kmer assembly strategies more useful for the community, but we think that there is still room for improvement for removing misassemblies.
In a recent work (Li et al., 2014) a reference free transcriptome assembly evaluation approach was introduced. Based on a graphical model of the RNA-sequencing process, an assembly quality estimate can be computed by aligning reads to the assembled transcripts. We note that in principle their method may be used as an alternative function to decide when to stop. However, this approach would constitute a serious runtime cost as read alignment, SAM file writing and model building would take in the order of hours for one kmer iteration. Instead, we see their work complementary to our work. We have focused on the question where to stop the assembly, but there are other parameters that are worth tuning. For example, we are currently assuming the k1 is given, which is partly due to the fact that it just needs to be chosen in such a way to avoid small kmers that produce misassemblies.
As a conclusion, we show that an informed kmer selection approach for de novo transcriptome assembly shows an improvement over simpler methods suggested so far. We believe that KREATION with the misassembly filters will be useful for the community and implemented the mentioned ideas in a software that currently supports the de novo assemblers tested in this work (https://github.com/SchulzLab/KREATION).
Supplementary Material
Acknowledgement
We like to thank the anonymous reviewers for their constructive comments.
Funding
This work was supported by the Cluster of Excellence on Multimodal Computing and Interaction (EXC284) of the German National Science Foundation (DFG).
References
- Au K.F. et al. (2013) Characterization of the human ESC transcriptome by hybrid sequencing. Proc.Natl. Acad. Sci. USA, 110, E4821–E4830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbosa-Morais N.L. et al. (2012) The evolutionary landscape of alternative splicing in vertebrate species. Science, 338, 1587–1593. [DOI] [PubMed] [Google Scholar]
- Cabili M.N. et al. (2011) Integrative annotation of human large intergenic noncoding RNAs reveals global properties and specific subclasses. Genes Dev., 25, 1915–1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang Z. et al. (2015) Bridger: a new framework for de novo transcriptome assembly using rna-seq data. Genome Biol., 16, 30. Zheng Chang and Guojun Li contributed equally to this work. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikhi R., Medvedev P. (2014) Informed and automated k-mer size selection for genome assembly. Bioinformatics, 30, 31–37. [DOI] [PubMed] [Google Scholar]
- Cunningham F. et al. (2014) Ensembl 2015. Nucleic Acids Res., 43, D662–D669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson N.M., Oshlack A. (2014) Corset: enabling differential gene expression analysis for de novo assembled transcriptomes. Genome Biol., 15, 410.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu L. et al. (2012) CD-HIT: accelerated for clustering the next-generation sequencing data. Bioinformatics, 28, 3150–3152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabherr M.G. et al. (2011) Full-length transcriptome assembly from RNA-Seq data without a reference genome. Nat. Biotechnol., 29, 644–652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haznedaroglu B.Z. et al. (2012) Optimization of de novo transcriptome assembly from high-throughput short read sequencing data improves functional annotation for non-model organisms. BMC Bioinformatics, 13, 170.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heap G.A. et al. (2010) Genome-wide analysis of allelic expression imbalance in human primary cells by high-throughput transcriptome resequencing. Hum. Mol. Genet., 19, 122–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilie L. et al. (2011) HiTEC: accurate error correction in high-throughput sequencing data. Bioinformatics, 27, 295–302. [DOI] [PubMed] [Google Scholar]
- Kent W.J. (2002) BLAT—The BLAST-Like alignment tool. Genome Res., 12, 656–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le H.S. et al. (2013) Probabilistic error correction for RNA sequencing. Nucleic Acids Res., 41, e109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B. et al. (2014) Evaluation of de novo transcriptome assemblies from RNA-Seq data. Genome Biol., 15, 553.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Y. et al. (2013) IDBA-tran: a more robust de novo de Bruijn graph assembler for transcriptomes with uneven expression levels. Bioinformatics, 29, i326–i334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson G. et al. (2010) De novo assembly and analysis of RNA-seq data. Nat. Methods, 7, 909–912. [DOI] [PubMed] [Google Scholar]
- Schulz M.H. et al. (2012) Oases: robust de novo RNA-seq assembly across the dynamic range of expression levels. Bioinformatics, 28, 1086–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulz M.H. et al. (2014) Fiona: a parallel and automatic strategy for read error correction. Bioinformatics, 30, i356–i363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson J.T. (2014) Exploring genome characteristics and sequence quality without a reference. Bioinformatics, 30, 1228–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sloan D.B. et al. (2012) De novo transcriptome assembly and polymorphism detection in the flowering plant Silene vulgaris (Caryophyllaceae). Mol. Ecol. Resour., 12, 333–343. [DOI] [PubMed] [Google Scholar]
- Sultan M. et al. (2008) A global view of gene activity and alternative splicing by deep sequencing of the human transcriptome. Science, 321, 956–960. [DOI] [PubMed] [Google Scholar]
- Surget-Groba Y., Montoya-Burgos J.I. (2010) Optimization of de novo transcriptome assembly from next-generation sequencing data. Genome Res., 20, 1432–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Y. et al. (2014) SOAPdenovo-Trans: de novo transcriptome assembly with short RNA-Seq reads. Bioinformatics, 30, 1660–1666. [DOI] [PubMed] [Google Scholar]
- Yang Y., Smith S.A. (2013) Optimizing de novo assembly of short-read RNA-seq data for phylogenomics. BMC Genomics, 14, 328.. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.