Abstract
The precision of human colour discrimination depends on the region of colour space in which measurements are made and on the direction in which the compared colours—the discriminanda—differ. Working in a MacLeod–Boynton chromaticity diagram scaled so that thresholds at the white point were equal for the two axes, we made measurements at reference points lying on lines that passed at 45° or −45° through the white point. At a given reference chromaticity, we measured thresholds either for saturation (i.e. for discriminanda lying radially along the line passing through the white point) or for hue (i.e. for discriminanda lying on a tangent of a circle passing through the reference point and centred on the white point). The discriminanda always straddled the reference point in chromaticity. The attraction of this arrangement is that the two thresholds can be expressed in common units. All that differs between saturation and hue measurements is the phase with which the short-wave signal is combined with the long-/middle-wave signal. Except for chromaticities very close to the white point, saturation thresholds were systematically higher than hue thresholds. We offer a possible explanation in terms of correlated neural noise.
Keywords: colour vision, colour discrimination, hue, saturation, correlated neural noise
1. Introduction
In the normal human retina, there are three classes of cone, maximally sensitive in different spectral regions [1]; and our perception of colour depends on neural comparisons of the rates at which photons are absorbed in the different classes [2]. Given three univariant signals, and thus two independent ratios, all visible colours can be represented on a two-dimensional surface. An example of such a ‘chromaticity diagram’ is the MacLeod–Boynton diagram (figure 1), whose ordinates are L/(L + M) and S/(L + M), where L, M and S are the excitations of the long-, middle- and short-wave cones, respectively [3]. The two ordinates of this diagram have physiological counterparts: they correspond to the signals extracted by retinal ganglion cells of the midget and the small bistratified types [2].
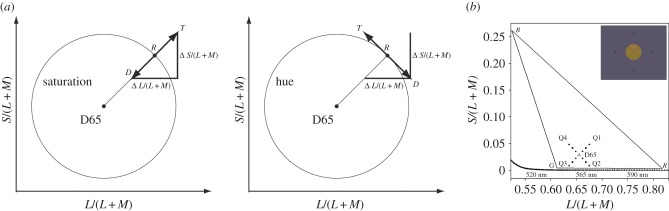
Figure 1.
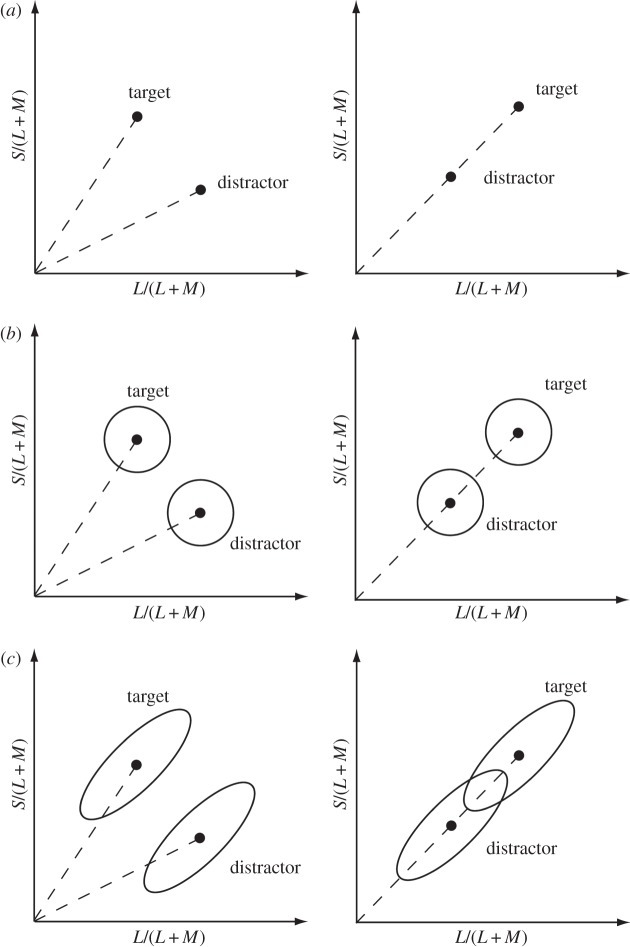
(a) The distinction between thresholds for saturation and for hue shown in a portion of the MacLeod–Boynton chromaticity diagram. R, T and D indicate the chromaticities of reference, target and distractor stiumuli respectively. (b) A section of the MacLeod–Boynton diagram showing the reference stimuli used in our main experiment. R, G and B indicate the chromaticities of the individual guns of our CRT monitor; and the solid triangle connecting these points shows the gamut of available chromaticities. Q1, Q2, Q3 and Q4 indicate our numbering of the four quadrants of the diagram. D65 indicates the white point, metameric to Illuminant D65. The dotted line at the bottom of the diagram indicates part of the spectrum locus. Inset: spatial configuration of the stimulus array. (Online version in colour.)
Although a chromaticity diagram represents all colours, such diagrams do not accurately predict the discriminability of pairs of colours. A pair of chromaticities separated by a given geometrical distance in the diagram may or may not have the same discriminability as a second pair separated by the same distance, depending on the region of the diagram in which the paired chromaticities lie, the direction in which the individual chromaticities differ and the state of adaptation of the eye [3–6]. Yet, in many civil and commercial domains, it is important to be able to predict when two samples will be noticeably different in colour; and several linear and nonlinear transformations of the CIE(1931) chromaticity diagram have been introduced, in successive attempts to achieve a ‘uniform colour space’ in which pairs of colours that are equally discriminable are separated by equal distances [7,8].
(a). The super-importance of hue differences and the problem of Mongean noise
In this study, we compare two fundamental subtypes of colour discrimination: discrimination of saturation and discrimination of hue. We define the two types of threshold in terms of the geometry of the chromaticity diagram and not in terms of subjective appearances (so we neglect the Abney effect [9]). We define the white point in the diagram as the chromaticity of the neutral illumination to which the eye is currently adapted (here, metameric to Daylight Illuminant D65). A pair of lights that differ in saturation are lights that lie along a line radiating from the white point. A circular set of chromaticities centred on the white point are described as varying in hue (figure 1a), and the hue thresholds measured here are along tangents to such a circle.
Rather little known in the modern literature on visual science, but much discussed in the mid-twentieth century by those concerned with practical tolerances for surface colours, is a phenomenon that Judd called the ‘super-importance of hue differences’ [7,8,10]. Colour differences measured along a radial line in colour space (i.e. saturation differences) are smaller than the ones that would be expected from differences in an orthogonal direction (i.e. hue differences). If we construct a circle in colour space that is centred on the white point and has a radius of n units of perceptual distance, then it is found that the circumference—a hue circle—does not have 2πn units of perceptual distance but more like 4πn units. Judd concluded that there was no possible Euclidean representation of colour space in which equal distances corresponded to equal discriminability [10].
Judd was primarily concerned with supra-threshold differences, but there is some indication that the super-importance of hue also applies at threshold [11]. It is curious that hue thresholds should be lower than saturation thresholds in this way. The neural channels that extract chromatic information at early stages of the visual system are usually thought of as signalling saturation. The channel is in equilibrium at the adapting chromaticity and it signals departures from this neutral state [12]. Thus, in a conventional view there might be four classes of units in the lateral geniculate nucleus, signalling either increments or decrements along the two cardinal axes of chromaticity space (figure 1b) [13]. To derive precise estimates of hues at angles between the cardinal axes, some form of comparator would be required more centrally to extract the ratios of the saturation signals generated in the distal channels. Estimates of saturation would depend on the vector sum of the same signals, and so it is not obvious why psychophysical thresholds for hue should be substantially lower than those for saturation. Below, we offer a possible explanation of this paradox.
The classical evidence for the super-importance of hue differences was largely derived from the viewing of surface colours, typically Munsell samples. Here, there is the possibility that physical noise contributes to any difference in discrimination. Real-world surfaces reflect to the eye a specular component (representing the illuminant) as well as a component (the body colour) that derives from selective absorption by pigment molecules within the material. This was first made explicit by Gaspard Monge in 1789 [14,15]; and in modern accounts of colour constancy [16,17], it has been identified as a way in which the visual system could recover the chromaticity of the illuminant by what could be called ‘chromatic triangulation’. Even a matte surface is represented not by a point in chromaticity space but by a distribution of chromaticities that extends from the body colour towards the chromaticity of the illuminant. Moreover, this variation will increase if the eye position is not fixed and changes occur in the angle of viewing the surface. We suggest the term ‘Mongean noise’ for this strictly physical noise. Because Mongean noise lies on a radial line in chromaticity space, it should raise thresholds for saturation but not for hue. It thus could contribute to the ‘super-importance of hue’ when discrimination is measured with material surfaces.
(b). The present measurements
In the work reported here, we use a self-luminous CRT display to compare hue discrimination and saturation discrimination while avoiding the problem of Mongean noise. We measure thresholds for hue and for saturation at reference chromaticities that lie on +45° and −45° radial lines passing through the white point in the MacLeod–Boynton diagram (figure 1a,b). Saturation measurements are made radially through the reference chromaticity, and hue measurements orthogonally through the same point. For each line, in each quadrant of the diagram, we make measurements at different distances from the neutral point.
An essential requirement is a common metric for expressing the two types of threshold. The salient feature of our design is that—for any given reference chromaticity—the same modulation of the S-cone signal is combined with the same modulation of the L/(L + M) signal, but in different phases for saturation and for hue. Thus, in the upper right quadrant of the MacLeod–Boynton diagram (Q1), saturation is measured when an increment in S/(L + M) is paired with an increment in L/(L + M), and hue is measured by pairing an increment in S/(L + M) with a decrement in L/(L + M). The target and distractor stimuli always lay symmetrically on opposite sides of the reference stimulus. The target always incorporated an increment in the S/(L + M) signal and the distractors incorporated a decrement in S/(L + M).
The scaling of the vertical axis of a MacLeod–Boynton diagram is arbitrary [18] and the angle taken as 45° will depend on this scaling. We followed recent tradition in the study of chromatic discrimination [19,20] and scaled the S/(L + M) ordinate so that thresholds for excursions around the white point were equal for the two cardinal axes. Thus, when below we refer to hue thresholds we formally mean thresholds measured along a line orthogonal to a radial line at 45° or −45° in the scaled space (figure 1).
In classical studies of colour discrimination, the observer was often able to inspect the surfaces or lights for an extended period before making a judgement (e.g. [11,21]), and this would allow the chromatic channels of the visual system to adapt towards the current chromaticity—‘self-adaptation’ to the target stimulus. Thus, measurements in different parts of chromaticity space might be made in different states of adaptation. This would be appropriate for setting tolerances for real-world surfaces, where viewing conditions would be similar; but it is inappropriate if the purpose is to analyse the visual mechanisms of discrimination. In this study, we set out to minimally perturb the observer's adaptation: a neutral adapting field was continuously present, and discrimination was probed with a brief array of target and distractor stimuli.
2. Material and methods
(a). Observers
The observers comprised the authors and three other, female observers who were highly practised but were naive as to the purpose of the experiments. All had normal colour vision as tested by the Cambridge Colour Test [22]. All observers gave informed consent according to the Declaration of Helsinki.
(b). Apparatus and stimuli
Two of the observers were tested in St Petersburg (Russia) and three in Cambridge (UK) using the same experimental programmes. In both laboratories, stimuli were presented on calibrated Mitsubishi CRT monitors (Diamond Pro 2070), controlled by Cambridge Research Systems (CRS) graphics systems (Visage in St Petersburg, VSG 2/3 in Cambridge). For calibration procedures and monitor settings, see [23].
The monitor was viewed binocularly from 57 cm. The steady white background field had a luminance of 10 cd m−2 and its chromaticity was that of Illuminant D65 [6]. A diamond array of black points guided fixation. The stimulus array was presented to the fovea and consisted of a disc divided into four sectors (inset, figure 1b). One sector, chosen at random on each presentation, was the target (T) and the remaining sectors were distractors (D). The array subtended 2° of visual angle.
The duration of the array was 200 ms. This value is a compromise between the self-adaptation that may occur at long exposures (see above) and the ‘tachistoscopic tritanopia’ known to affect very brief presentations [24]. In preliminary measurements, along the two cardinal axes at the white point, we observed tachistoscopic tritanopia below 200 ms, in that the ratio of S/(L + M) thresholds to L/(L + M) thresholds increased markedly. The ratio was relatively stable for durations greater than 200 ms.
We specified chromaticities in a MacLeod–Boynton diagram constructed from the cone sensitivities of DeMarco et al. [25]. The diagram represents a plane of equal luminance for the Judd1951 Observer, where luminance equals the sum of L- and M-cone signals [26]. We scaled the vertical ordinate so that thresholds for departures from the white point were equal on the two cardinal axes. In these preliminary measurements, we used the same configuration, duration and procedures as for the main experiments, and obtained thresholds for increments and decrements from the white point along the two axes for three of our observers. For each observer, there were five independent estimates of each threshold. On the basis of the average thresholds, we adopted the scaling factor 1.7054 relative to the ordinate of the classical MacLeod–Boynton diagram [27]. As a check, we repeated the measurements after scaling, obtaining a ratio of 1.02 (s.e.m.: 0.04) between thresholds on the two axes.
The test array had an average luminance 30% greater than that of the background when expressed in the L + M units of our space; but to ensure that observers could not discriminate the target from the distractors by differences in sensation luminance, we jittered independently the L + M value of each sector by ±1%.
(c). Procedure
Thresholds were measured along four lines radial to the chromaticity of D65 and at angles of either 45° or −45° (figure 1b). Along each line, measurements were centred on a reference chromaticity that differed from D65 in L/(L + M) value by 1, 2 or 3%. In the orange and green regions, a 3% shift in L/(L + M) brings the measurements close to the monitor gamut.
On any trial, the observer made a spatial forced choice, indicating by pushbuttons which sector of the test array differed in chromaticity from the remaining three. Auditory feedback was given. In any one experimental session, thresholds were measured for reference stimuli at one distance from D65 on all four lines. Within the session, hue and saturation thresholds at a given reference were measured in separate blocks of trials, thus giving a total of eight blocks in one session. The orders of blocks and of sessions were randomized.
During each threshold measurement, the reference chromaticity was never itself presented, but the discriminanda lay on a line passing through the reference and straddling the reference value. The chromatic separation of the discriminanda was increased or decreased symmetrically around the reference chromaticity according to the observer's accuracy. The staircase procedure tracked 79.4% correct [23]. The staircase terminated after 15 reversals, the last 10 being averaged to give the threshold. There were six sets of experimental runs, the first set being treated as practice. Thus, any given threshold for a given observer is based on five independent repetitions.
3. Results
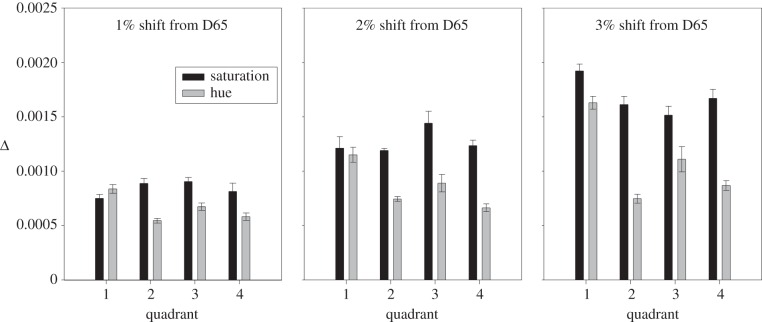
In the bar chart of figure 2, we show illustrative data for an observer who was unaware of the purpose of the experiments. The ordinate shows the difference (Δ) between the L/(L + M) coordinates of the target and distractors (as measurements are made at 45°, the difference in S/(L + M) is identical; see Material and methods). Each panel corresponds to measurements made at different distances from D65; and within each panel each pair of thresholds corresponds to one quadrant of the MacLeod–Boynton diagram (see figure 1b for the numbering of quadrants). In all but one case, the threshold for hue is lower than the threshold for saturation measured at the same reference chromaticity. The absolute size of the thresholds increases with distance from the adapting chromaticity (i.e. as one passes from the first to the third panel), and Q1 (the upper right quadrant) shows the weakest difference between hue and saturation.
Figure 2.
Results for an individual observer. The three panels show thresholds measured at three different distances from the white point. Within each panel, pairs of threshold (saturation and hue) are shown for the four quadrants of the MacLeod–Boynton diagram, numbered as in figure 1b. Thresholds are expressed as the difference (Δ) in L/(L + M) coordinate between target and distractors. Error bars show ±1 s.e.m. and are based on the variance of five independent measures of each threshold.
Figure 3 shows average results for all observers plotted directly in our scaled MacLeod–Boynton diagram after the manner of W. D. Wright's dashes [28]: the lengths of the line segments represent the separation of the discriminanda needed to sustain a performance of 79.4% correct. The pattern of results, in general, reflects that seen for an individual observer in figure 2: saturation thresholds at a given reference chromaticity are usually larger than for hue; the difference is least marked in Q1; and the absolute sizes of all thresholds increase with distance of the reference chromaticity from the white point. The latter is a classical finding (e.g. [19,20,29–33]). A repeated-measures ANOVA with factors hue versus saturation, distance from D65 and quadrant shows (after Greenhouse–Geisser correction) significant effects of hue versus saturation (F1,4 = 60.8, p < 0.001), distance from D65 (F1.22,4.92 = 46.1, p < 0.001) and quadrant (F1.67,6.66 = 12.7, p = 0.006). There was a highly significant interaction between hue versus saturation and distance from D65 (F1.64,6.57 = 29.1, p < 0.001), and a marginally significant interaction between distance from D65 and quadrant (F1.5,6 = 6.2, p = 0.04).
Figure 3.
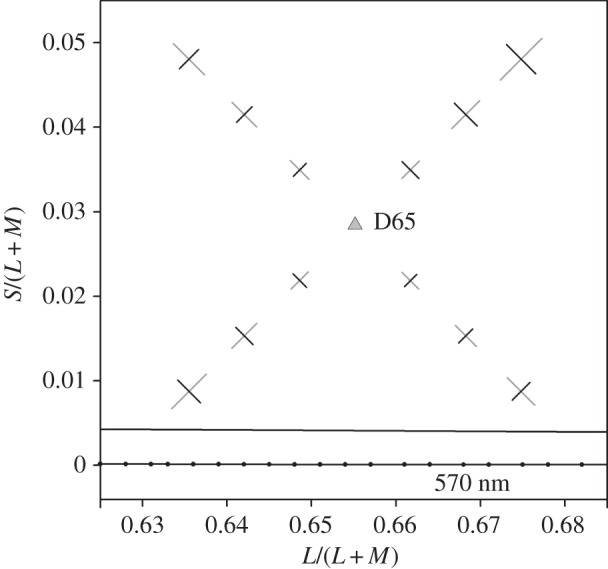
Average results for five observers, plotted in the MacLeod–Boynton diagram. The dashes directly show the separation of targets and distractors at threshold. D65 indicates the chromaticity of the neutral adapting field. The dotted line indicates part of the spectrum locus.
In figure 4, we plot ratios of saturation thresholds to hue thresholds for the separate quadrants of the MacLeod–Boynton diagram. All quadrants show an increasing ratio with increasing distance from the white point, but systematic differences between quadrants are apparent. The superiority of hue discrimination is most marked in Q4 (upper left) and least marked in Q1. However, the latter quadrant shows the strongest change in ratio.
Figure 4.
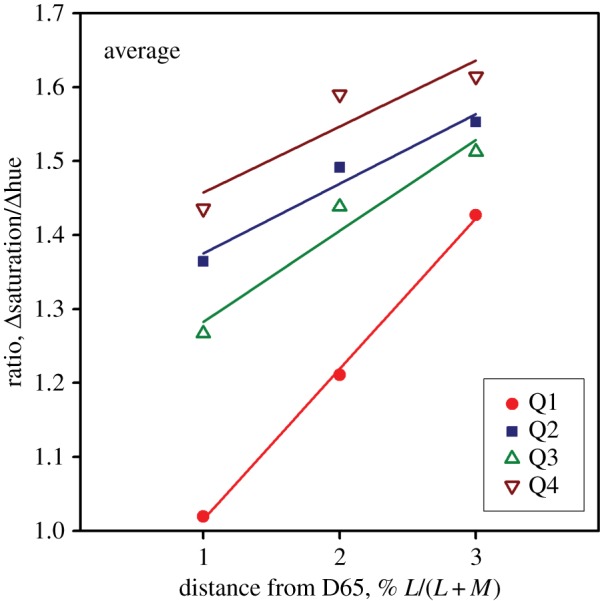
Ratios of saturation and hue thresholds. Ratios are shown separately for each quadrant of the MacLeod–Boynton diagram (numbered as in figure 1b). (Online version in colour.)
4. Control experiment: effects of luminance jitter
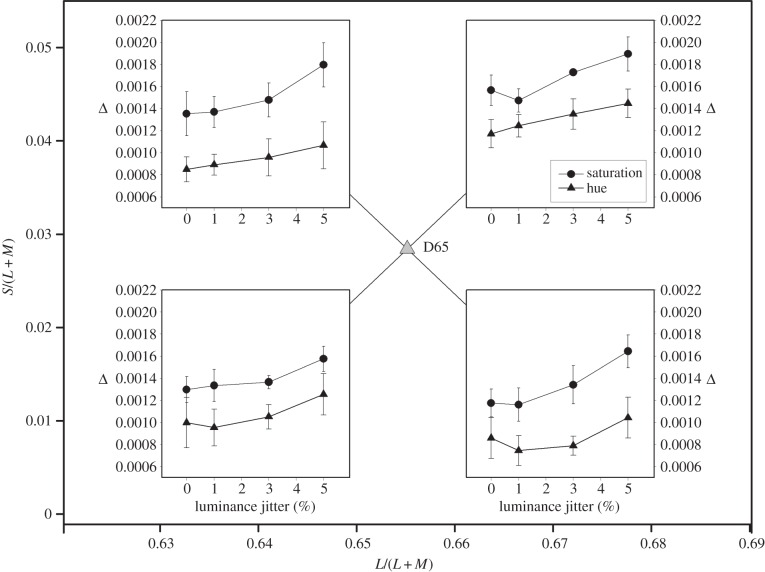
In our main experiment, we introduced a ±1% luminance jitter to ensure that observers used only chromatic cues. This was a conservative precaution, as chromatic discrimination typically surpasses luminance discrimination (e.g. [34]), and the small gaps between our fields would favour chromatic rather than luminance discrimination [35]. Is it possible, nevertheless, that the luminance jitter elevated saturation thresholds disproportionately? We performed a control experiment in which different levels of jitter (0, 1, 3 and 5%) were introduced in different blocks of trials. The observers and procedures were otherwise as for the main experiment, except that we tested at only one distance from the white point (2%).
Results for this control experiment are shown in figure 5. The four panels, corresponding to the four quadrants, are inset at their appropriate positions within the MacLeod–Boynton diagram. The ordinates of the inset panels show the distance between the discriminanda at threshold. It is clear that the superiority of hue discrimination survives when no jitter is present and that increasing jitter has similar effects on the two types of threshold. A repeated-measures ANOVA shows (after Greenhouse–Geisser correction) significant effects of hue versus saturation (F1,4 = 71.1, p < 0.001), jitter (F1.64,6.57 = 29.3, p < 0.001) and quadrant (F2.54,10.17 = 12.3, p < 0.001). There were no significant interactions.
Figure 5.
Average thresholds for hue (triangles) and for saturation (circles) as a function of luminance jitter. The four sets of data are symbolically placed within the appropriate quadrants of the MacLeod–Boynton diagram. These measurements were all made at reference chromaticities that differed from D65 by 2% in their L/(L + M) coordinate. Error bars show ±1 s.e.m. and are based on the inter-observer variance.
5. Hue and saturation thresholds very close to the white point
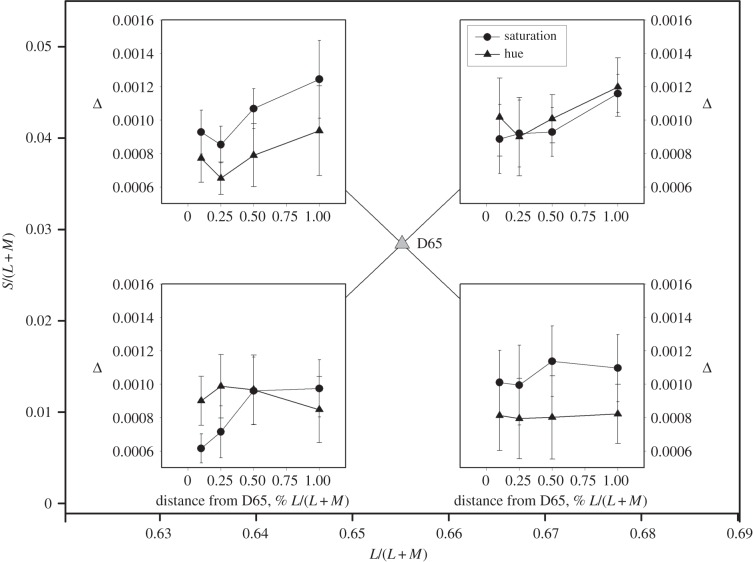
Figure 4 suggests that the ratio between the two types of threshold grows with distance from the white point. For three observers, we have made supplementary measurements very close to the white point, at reference chromaticities that differ from the L/(L + M) value of D65 by 0.1, 0.25, 0.6 and 1%. The reference chromaticities lay on +45° and −45° lines as before and the other experimental procedures were as for the main experiment.
Figure 6 shows results for this supplementary experiment. For quadrants 2 and 4 of the diagram, hue discrimination is superior even at the smallest distance from the white point, but for the remaining two quadrants the effect is attenuated or reversed. A repeated-measures ANOVA showed, as might be expected from figure 6, no significant effect of hue versus saturation, of distance from D65 or of quadrant, but (after Greenhouse–Geisser correction) significant interactions between hue versus saturation and quadrant (F1.07,2.15 = 30.49, p = 0.027), and hue versus saturation and distance from D65 (F1.93,3.85 = 18.65, p = 0.011).
Figure 6.
Supplementary measurements of hue and saturation thresholds very close to the white point. The abscissa of each panel shows the distance from the white point expressed as the percentage change in the L/(L + M) coordinate at the reference chromaticity at which the two types of threshold were measured. The four sets of data are symbolically placed within the appropriate quadrants of the MacLeod–Boynton diagram. Error bars show ±1 s.e.m.
6. Discussion
(a). The superiority of hue discrimination: a hypothesis in terms of correlated neural noise
Our main experiment reveals a general superiority for hue discrimination relative to discrimination of saturation. The experimental conditions ensured that the two types of measurement differed only in the signs with which modulations on the cardinal axes were combined, and the modulations were always centred on the same reference chromaticity, so the magnitudes of the two types of thresholds can be directly compared. Clearly, it would not be possible, from threshold measurements made under the present conditions, to construct a Euclidean colour space in which equal geometric distances corresponded to equal discriminability (see Introduction).
Why should thresholds for saturation systematically exceed those for hue? We offer a provisional theory in terms of correlated neural noise within the visual system.
In both the retina and the visual cortex, neurons are known to exhibit correlated variations in excitability [36–38]. Typically, the correlations are attenuated with increasing spatial separation of a given pair of neurons. Of special interest, for our present study, is the demonstration by Greschner and colleagues of correlation in the primate retina between neural firing in small bistratified ganglion cells (which draw ON input from S cones) and that in nearby ON midget cells (which draw ON input from either L or M cones) [38].
Figure 7 illustrates our hypothesis of how correlated neural noise might lead to superior hue discrimination. The axes of each panel represent the neural signals in the two chromatic channels of the early visual system. In each panel, T indicates the target and D the distractors in our forced-choice experiment. The left-hand panels represent the case of hue discrimination and the right-hand panels represent the case of saturation. The geometrical distance between T and D is equal in left and right panels.
Figure 7.
How correlated neural noise could explain the superiority of hue discrimination. In each panel, the x- and y-axes represent the signals in the two ‘cardinal’ chromatic channels of the early visual system. The left-hand panels correspond to hue discrimination and those on the right correspond to saturation discrimination. (a) No noise is assumed: the responses generated by the target and the distractors plot as points in the two-dimensional space. (b) The case where independent Gaussian noise is present in the two cardinal channels. The circles represent one contour of the probability density function produced by a given chromaticity. (c) It is assumed that noise in the two channels is correlated. Now the probability density distributions are elliptical with positive slopes. When the stimuli differ in saturation (right-hand panel) the distributions for the discriminanda overlap, but when the stimuli differ in hue—when a change on one axis is accompanied by an opposite change on the other axis—the overlap of the probability density distributions is less.
Figure 7a represents the case where there is no noise in the neural signals: the target and the distractors then plot as points. Figure 7b represents the case where independent, uncorrelated, Gaussian noise is present in the two neural channels. Each circle represents one contour of the probability density distribution of the neural responses produced by a given chromaticity. Figure 7c represents the case where the noise in the two channels is correlated. Now the probability density distributions are elliptical, since fluctuations in the two channels covary. The distributions overlap in the case of saturation shifts, but not in that of hue shifts, for the cardinal signals are combined with different signs in the two cases. In the case of hue, the S/(L + M) signal is higher for the target and lower for the distractors, whereas the opposite is true for the L/(L + M) signal. In the case of saturation, however, both the S/(L + M) signal and the L/(L + M) signal are higher for the target and lower for the distractors. Because the correlated neural noise causes the two probability density distributions to overlap, discrimination will be poorer for saturation.
The ‘super-importance of hue’ has sometimes led to the conclusion that hue and saturation are analysed by different systems. This view was classically expressed by Kuehni, who wrote: ‘In practical terms, there appear to be two independent systems: one that assesses changes in the ratio of two opponent color signals (assuming a two-process hue detection system) and the other changes in the size of the vector sum of the opponent color system (indicative of contrast) … The two seemingly operate independently of each other and are not connected in a euclidean sense’ ([8, p. 331]). Our hypothesis suggests how the two types of discrimination might depend on the same distal signals, although necessarily in one case it is the ratio of those signals that is identified and in the other, it is their sum.
An interesting analogy can be made between hue and saturation, on the one hand, and the auditory attributes of pitch and loudness on the other. In the classification of S. S. Stevens, hue is a metathetic sensory dimension like pitch, and saturation is prothetic like loudness [39]. In psychoacoustics, it has often been held that frequency discrimination could not depend on the same neural signals as intensity discrimination. The latter is thought to depend on the spike rate of cortical neurons, but the relatively high resolution observed for frequency suggested that pitch discrimination could not depend on the same signal and instead must depend on the timing of spikes. However, Micheyl et al. [40] explain the disparity of the two types of threshold by correlated noise in the same types of neuron.
In the case of vision, a hypothesis analogous to the present one was explored by Regan & Beverley [41] for the case of orientation discrimination. They point out the general principle that ‘Opponent processing has the feature that noise in the first-stage outputs…can be partially or even completely suppressed by the opponent element’ ([41, p. 153]).
(b). Intermediate colour channels?
For the purposes of the model outlined above, we took the primary signals to be S/(L + M) and L/(L + M), but chromatic channels tuned to intermediate, non-cardinal directions of colour space have often been postulated (e.g. [42]), channels that are usually taken to be central to the ‘cardinal’ channels but could conceivably be in parallel with them [43]. In principle, an explanation of the type offered above could still apply if hue discrimination depended on a comparison of the signals in channels tuned to intermediate directions in colour space.
Discrimination ellipses oriented obliquely have actually been taken as independent evidence for ‘intermediate’ chromatic channels. Our hypothesis of correlated noise offers an alternative explanation for such ellipses.
(c). Variation between quadrants of the MacLeod–Boynton diagram
For reference chromaticities at moderate distances from the white point, it appears to be a general rule that saturation thresholds exceed those for hue; and above we offered a possible explanation for this result. However, a complete explanation will need to take into account the differences of the strength of the effect in different quadrants of the MacLeod–Boynton diagram (figure 4). For Q2 (lower right) and Q4 (upper left), the ratios are largest, and the effect is maintained in regions very close to the white point (figure 6), whereas the effect is attenuated or reversed near the white point for quadrants Q1 and Q3. These results are consistent with earlier studies [19,20], where discrimination ellipses were measured in the different quadrants of DKL [13] space. A similar pattern is seen in the variance of thresholds for different observers in the results of Elliott et al. [42].
In this context, we note a provocative coincidence. In the present experiment, in equating cardinal axes to give equal thresholds at the white point, we found that we needed to scale the S/(L + M) ordinate of the MacLeod–Boynton diagram by a factor of approximately 1.71. Independently, in earlier experiments [43], we scaled this ordinate so that a line running between the wavelengths of unique yellow and unique blue ran at −45°: a very similar factor (1.64) was needed. The locus of unique yellows and blues in turn closely coincides with the ‘caerulean line’ in the outside world, the locus comprising mixtures of skylight and sunlight [15,44].
This means that in quadrants Q2 and Q4, the present saturation thresholds lie approximately along the locus of unique yellows and blues, while hue judgements in these quadrants coincide with the category boundary between reddish and greenish hues. We have earlier noted that an optimum of discrimination occurs in the latter case [43,45] (i.e. where thresholds are being measured orthogonally to the unique-blue locus). It remains possible that this region of enhanced discrimination does correspond to the equilibrium point of an intermediate neural channel that draws opposed inputs from M cones and from L + S cones (for discussion, see [43]).
7. Conclusion
Within the area of colour space that we have explored, thresholds for discriminating saturation are systematically higher than those for discriminating hue, except for chromaticities very close to the white point. We offer a possible explanation in terms of correlated neural noise in distal chromatic channels in the visual system. There is empirical evidence that noise in these two channels is indeed correlated [38].
Acknowledgement
We thank Sungmi Oh, the referees and the editors for valuable discussion.
Ethics
The experiments in both Cambridge and St Petersburg were approved by the Psychology Research Ethics Committee of the University of Cambridge.
Data accessibility
Authors' contributions
The authors contributed equally to the design and conduct of the experiments and to the preparation of the manuscript.
Competing interests
We declare we have no competing interests.
Funding
We received no funding for this study.
References
- 1.Dartnall HJA, Bowmaker JK, Mollon JD. 1983. Human visual pigments: microspectrophotometric results from the eyes of seven persons. Proc. R. Soc. Lond. B 220, 115–130. ( 10.1098/rspb.1983.0091) [DOI] [PubMed] [Google Scholar]
- 2.Dacey DM, Packer OS. 2003. Colour coding in the primate retina: diverse cell types and cone-specific circuitry. Curr. Opin. Neurobiol. 13, 421–427. ( 10.1016/S0959-4388(03)00103-X) [DOI] [PubMed] [Google Scholar]
- 3.MacLeod DIA, Boynton RM. 1979. Rectangular chromaticity diagram showing cone excitations at constant luminance. In Colour vision deficiencies V (ed. Verriest G.), pp. 65–68. Bristol, UK: Adam Hilger. [Google Scholar]
- 4.Tyndall EPT. 1933. Chromaticity sensibility to wave-length difference as a function of purity. J. Opt. Soc. Am. 23, 15–24. ( 10.1364/JOSA.23.000015) [DOI] [Google Scholar]
- 5.Le Grand Y. 1949. Les seuils différentiels de couleurs dans la théorie de Young. Revue d'Optique théor. exp. 28, 261–278. [PubMed] [Google Scholar]
- 6.Wyszecki G, Stiles WS. 1982. Color science, 2nd edn New York, NY: Wiley. [Google Scholar]
- 7.Judd DB. 1970. Ideal color space. Color Eng. 8, 37–52. [Google Scholar]
- 8.Kuehni RG. 2003. Color space and its divisions. Hoboken, NJ: Wiley. [Google Scholar]
- 9.Burns SA, Elsner AE, Pokorny J, Smith VC. 1984. The Abney effect: chromaticity coordinates of unique and other constant hues. Vis. Res. 24, 479–489. ( 10.1016/0042-6989(84)90045-2) [DOI] [PubMed] [Google Scholar]
- 10.Judd DB. 1969. Ideal color space: the super-importance of hue differences and its bearing on the geometry of color space. Palette 30, 21–28. [Google Scholar]
- 11.Brennan JG, Newhall SM. 1948. ICI specifications of difference limens for Munsell hue, value, and chroma. J. Opt. Soc. Am. 38, 696–702. ( 10.1364/JOSA.38.000696) [DOI] [PubMed] [Google Scholar]
- 12.DeValois RL, Marrocco RT. 1973. Single cell analysis of saturation discrimination in the macaque. Vis. Res. 13, 701–711. ( 10.1016/0042-6989(73)90033-3) [DOI] [PubMed] [Google Scholar]
- 13.Derrington AM, Krauskopf J, Lennie P. 1984. Chromatic mechanisms in lateral geniculate nucleus of macaque. J. Physiol. 357, 241–265. ( 10.1113/jphysiol.1984.sp015499) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Monge G. 1789. Mémoire sur quelques phénomènes de la vision. Ann. Chim. 3, 131–147. [Google Scholar]
- 15.Mollon JD. 2006. Monge. Visual Neurosci. 23, 297–309. ( 10.1017/S0952523806233479) [DOI] [PubMed] [Google Scholar]
- 16.Lee H-C. 1986. Method for computing the scene-illuminant chromaticity from specular highlights. J. Opt. Soc. Am. A 3, 1694–1699. ( 10.1364/JOSAA.3.001694) [DOI] [PubMed] [Google Scholar]
- 17.Hurlbert AC. 1998. Computational models of colour constancy. In Perceptual constancy: why things look as they do (eds Walsh V, Kulikowski J), pp. 283–322. Cambridge, UK: Cambridge Univerity Press. [Google Scholar]
- 18.Macleod DIA, Boynton RM. 1989. Remarks on the constant luminance chromaticity diagram. Color Res. Appl. 14, 157–158. ( 10.1002/col.5080140310) [DOI] [Google Scholar]
- 19.Krauskopf J, Gegenfurtner K. 1992. Color discrimination and adaptation. Vision Res. 32, 2165–2175. ( 10.1016/0042-6989(92)90077-V) [DOI] [PubMed] [Google Scholar]
- 20.Sankeralli MJ, Mullen KT. 1999. Ratio model for suprathreshold hue-increment detection. J. Opt. Soc. Am. A 16, 2625–2637. ( 10.1364/JOSAA.16.002625) [DOI] [PubMed] [Google Scholar]
- 21.MacAdam DL. 1942. Visual sensitivities to color differences in daylight. J. Opt. Soc. Am. 32, 247–281. ( 10.1364/JOSA.32.000247) [DOI] [Google Scholar]
- 22.Regan BC, Reffin JP, Mollon JD. 1994. Luminance noise and the rapid determination of discrimination ellipses in colour deficiency. Vis. Res. 34, 1279–1299. ( 10.1016/0042-6989(94)90203-8) [DOI] [PubMed] [Google Scholar]
- 23.Danilova MV, Mollon JD. 2014. Is discrimination enhanced at the boundaries of perceptual categories? A negative case. Proc. R. Soc. B, 281, 20140367 ( 10.1098/rspb.2014.0367) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mollon JD. 1982. A taxonomy of tritanopias. In Colour vision deficiencies VI (ed. Verriest G.), pp. 87–101. The Hague, The Netherlands: Dr. W. Junk. [Google Scholar]
- 25.DeMarco P, Pokorny J, Smith VC. 1992. Full-spectrum cone sensitivity functions for X-chromosome-linked anomalous trichromats. J. Opt. Soc. Am. A 9, 1465–1476. ( 10.1364/JOSAA.9.001465) [DOI] [PubMed] [Google Scholar]
- 26.Smith VC, Pokorny J. 1975. Spectral sensitivity of the foveal cone photopigments between 400 and 500 nm. Vis. Res. 15, 161–171. ( 10.1016/0042-6989(75)90203-5) [DOI] [PubMed] [Google Scholar]
- 27.MacLeod DIA, Boynton RM. 1979. Chromaticity diagram showing cone excitation by stimuli of equal luminance. J. Opt. Soc. Am. 69, 1183–1186. ( 10.1364/JOSA.69.001183) [DOI] [PubMed] [Google Scholar]
- 28.Wright WD. 1941. The sensitivity of the eye to small colour differences. Proc. Phys. Soc. London 53, 93–112. ( 10.1088/0959-5309/53/2/301) [DOI] [Google Scholar]
- 29.Schönfelder W. 1933. Der Einfluss des Umfeldes auf die Sicherheit der Einstellung von Farbengleichungen. Z. Sinnesphysiol. 63, 228–251. [Google Scholar]
- 30.Rautian GN, Solov'eva VP. 1954. Vlijanie svetlogo okrugenija na ostrotu cvetorazlochenija. Doklady Academii Nauk SSSR 95, 513–515. [PubMed] [Google Scholar]
- 31.Loomis JM, Berger T. 1979. Effects of chromatic adaptation on color discrimination and color appearance. Vis. Res. 19, 891–901. ( 10.1016/0042-6989(79)90023-3) [DOI] [PubMed] [Google Scholar]
- 32.Miyahara E, Smith VC, Pokorny J. 1993. How surrounds affect chromaticity discrimination. J. Opt. Soc. Am. A 10, 545–553. ( 10.1364/JOSAA.10.000545) [DOI] [PubMed] [Google Scholar]
- 33.Danilova MV, Mollon JD. 2014. Symmetries and asymmetries in chromatic discrimination. J. Opt. Soc. Am. A 31, A247–A253. ( 10.1364/JOSAA.31.00A247) [DOI] [PubMed] [Google Scholar]
- 34.Chaparro A, Stromeyer CF, Huang EP, Kronauer RE, Eskew RT. 1993. Colour is what the eye sees best. Nature 361, 348–350. ( 10.1038/361348a0) [DOI] [PubMed] [Google Scholar]
- 35.Boynton RM, Hayhoe MM, MacLeod DIA. 1977. The gap effect: chromatic and achromatic visual discrimination as affected by field separation. Opt. Acta, 24, 159–177. ( 10.1080/713819496) [DOI] [Google Scholar]
- 36.Smith MA, Sommer MA. 2013. Spatial and temporal scales of neuronal correlation in visual area V4. J. Neurosci. 33, 5422–5432. ( 10.1523/JNEUROSCI.4782-12.2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lin IC, Okun M, Carandini M, Harris KD. 2015. The nature of shared cortical variability. Neuron 87, 644–656. ( 10.1016/j.neuron.2015.06.035) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Greschner M, Shlens J, Bakolitsa C, Field GD, Gauthier JL, Jepson LH, Sher A, Litke AM, Chichilnisky EJ. 2011. Correlated firing among major ganglion cell types in primate retina. J. Physiol. 589, 75–86. ( 10.1113/jphysiol.2010.193888) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Panek DW, Stevens SS. 1966. Saturation of red—prothetic continuum. Percep. Psychophy. 1, 59–66. ( 10.3758/BF03207823) [DOI] [Google Scholar]
- 40.Micheyl C, Schrater PR, Oxenham AJ. 2013. Auditory frequency and intensity discrimination explained using a cortical population rate code. PLoS Comput. Biol. 9, e1003336 ( 10.1371/journal.pcbi.1003336) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Regan D, Beverley KI. 1985. Postadaptation orientation discrimination. J. Opt. Soc. Am. A 2, 147–155. ( 10.1364/JOSAA.2.000147) [DOI] [PubMed] [Google Scholar]
- 42.Elliott SL, Werner JS, Webster MA. 2012. Individual and age-related variation in chromatic contrast adaptation. J. Vis. 12, 8.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Danilova MV, Mollon JD. 2012. Foveal color perception: minimal thresholds at a boundary between perceptual categories. Vis. Res. 62, 162–172. ( 10.1016/j.visres.2012.04.006) [DOI] [PubMed] [Google Scholar]
- 44.Mollon JD, Lee RJ. 2008. Do unique hues originate within us or in the outside world? Perception 37, 127. [Google Scholar]
- 45.Danilova MV, Mollon JD. 2010. Parafoveal color discrimination: a chromaticity locus of enhanced discrimination. J. Vis. 10, 1.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.