Sensitivity to excluding treatments in network meta-analysis

Abstract

Network meta-analysis (NMA) of randomized controlled trials is increasingly used to combine both direct evidence comparing treatments within trials and indirect evidence comparing treatments across different trials. When the outcome is binary, the commonly used contrast-based NMA methods focus on relative treatment effects such as odds ratios comparing two treatments. As shown in a recent report, when using contrast-based NMA, the impact of excluding a treatment in the network can be substantial, suggesting a methodological limitation. In addition, relative treatment effects are sometimes not sufficient for patients to make decisions. For example, it can be challenging for patients to trade off efficacy and safety for two drugs if they only know the relative effects, not the absolute effects. A recently proposed arm-based NMA, based on a missing-data framework, provides an alternative approach. It focuses on estimating population-averaged treatment-specific absolute effects. This article examines the influence of treatment exclusion empirically using 14 published NMAs, for both arm-based and contrast-based approaches. The difference between these two NMA approaches is substantial, and it is almost entirely due to single-arm trials. When a treatment is removed from a contrast-based NMA, it is necessary to exclude other treatments in two-arm studies that investigated the excluded treatment; such exclusions are not necessary in arm-based NMA, leading to substantial gain in performance.

1. Introduction

Comparative effectiveness research is aimed at informing health care decisions concerning the benefits and risks of different diagnostic and intervention options. The growing number of treatment options for a given condition, as well as the rapid escalation in their cost, has created a greater need for rigorous comparisons of multiple treatments in clinical practice. To simultaneously compare multiple treatments for a given condition, network meta-analysis (NMA) methods have recently been developed, expanding the scope of conventional pairwise meta-analysis. NMA simultaneously synthesizes both direct comparisons of interventions within randomized controlled trials (RCTs) and indirect comparisons across RCTs^3-8. Currently, much effort in NMA has been devoted to contrast-based approaches, which focus on investigating relative treatment effects, such as odds ratios (ORs) when the outcome is binary. However, population-averaged absolute risks may be preferred in some situations such as cost-effectiveness analysis^9,10. In addition, relative treatment effects are sometimes insufficient for patients to make decisions. For instance, consider a patient's choice between treatments A and B with the following two sets of one-year survival rates: (i) π_A = 0.8 vs. π_B = 0.5; (ii) π_A = 0.004 vs. π_B = 0.001. Most likely, patients will strongly prefer treatment A in scenario (i) but have little preference in scenario (ii), yet both have odds ratio 4.0.

Contrast-based NMA can back-transform odds ratios to population-averaged absolute risks only if the absolute risk of a given reference treatment group can be accurately estimated from external data, or can be estimated using a separate model to analyze responses for the reference arm from the network^9,10. Both approaches depend on strong assumptions. For the approach using external data, even if such external data are available, they may come from a population different from the one represented in the NMA, and the assumption of transitivity of relative effects on the odds ratio scale (i.e., that treatment effects are independent of baseline risks) is rather strong. The choice of the odds ratio scale is generally arbitrary or conventional, and there is no particular reason to expect effects in different trials to be exchangeable on the odds ratio scale. For the approach using a distinct model for the reference arm, under the theory of missing data, this analysis is unbiased only under a strong assumption of missing completely at random, i.e., that each study randomly chooses which treatment arms to include. In addition, if the estimation of absolute effects uses a subset of the same trials used for the estimation of relative effects, then the estimated absolute and relative effects are not independent. Thus, one would need to model the correlations among the two sets of estimates, which is not straightforward. Finally, the back-transformed relative risks (RRs) and risk differences (RDs) can be noticeably different depending on which treatment is chosen as the reference group, even with exactly the same model and priors (Appendix A gives an example). These considerations suggest methodological limitations in contrast-based methods for estimating population-averaged absolute risks.

When performing an NMA, selecting appropriate treatments for the systematic review is crucial, as this will influence the validity and generalizability of both the direct and indirect evidence summarized in the analysis. However, no guidelines exist for treatment selection. Because the control treatment may not be defined consistently across trials, some have suggested excluding such control treatments from an NMA^11-13, but others have argued that having no comparison between an active intervention and placebo is problematic^14-16. Moreover, the treatments of interest may differ in different countries, and may vary over time due to introduction of new drugs¹⁷. Therefore, the treatment arms included in an NMA usually consist of a subset of a more extensive network. Using a contrast-based NMA^3,4, Mills et al.¹ examined the sensitivity of estimated effect sizes such as OR to removal of certain treatments. They concluded that excluding a treatment sometimes has substantial influence on estimated effect sizes. Consequently, selection of treatment arms should be carefully considered when applying NMA.

This article examines the sensitivity to treatment exclusion of an alternative approach to NMA, namely the arm-based (AB) approach, recently developed from the perspective of missing data analysis². The detailed model is briefly reviewed in Appendix B. This model assumes: 1) each study is independently chosen from a conceptual urn containing a large number of studies, and thus we can assign a joint distribution on the arm parameters independently across different studies; 2) each study hypothetically compares all treatments, many of which are missing at random. The arm-based model does not estimate the population-averaged absolute risk of each arm independently; instead, it respects the study randomization by accounting for the correlations between treatments within each study, which allows for “borrowing information” across treatment arms. This point is illustrated by an example in Appendix A, in which absolute risk estimates from the arm-based model differ from estimates from a simple logit random effects model using only studies with a specific treatment arm. In addition, simulation results and real data analyses have shown that in some cases the effect size estimates given by this arm-based method are less biased than those given by the contrast-based model².

Besides reporting changes due to treatment exclusion in the population-averaged absolute risk estimates from the arm-based model, we compare changes in relative effects (i.e., log odds ratio change) with those obtained from the contrast-based model. In this regard, the arm-based and contrast-based methods have a key difference: If a study only has two treatment arms and one of these arms is omitted from the NMA, a contrast-based analysis must omit the entire study, while an arm-based analysis can retain the single remaining arm. Note that single-arm studies do contribute information to estimation of relative effects from the perspective of missing data analysis, which is somewhat counter-intuitive. To give a simple illustration, consider paired bivariate normally distributed random variables X and Y with parameters $({\mu }_x,{\mu }_y,{\sigma }_x^2,{\sigma }_y^2,\rho )$, e.g., the probit-transformed absolute risks in the arm-based model. The expected value of Y given X is ${\mu }_y+\rho \frac{{\sigma }_y}{{\sigma }_x}(X-{\mu }_x)$. Once we observe a value X = x in a particular pair (with Y unobserved), the expected difference between Y and X for this pair becomes ${\mu }_y-x+\rho \frac{{\sigma }_y}{{\sigma }_x}(x-{\mu }_x)$, which does not equal μ_y – μ_x. Also, the variance of Y given X is $(1-{\rho }^2){\sigma }_y^2\le {\sigma }_y^2$. Therefore, even if Y is unobserved, modeling X and Y jointly, as in the arm-based model, helps reduce the standard error of a comparison. This point is illustrated by an example in Appendix A.

This article is organized as follows. Section 2 describes the specific NMA models being compared and the datasets to which we applied them. Section 3 presents results describing sensitivity of the NMA models to treatment exclusion. Section 4 closes with some suggestions on NMA and several limitations in our study.

2. Statistical analysis methods

2.1. Dataset selection

We reviewed forty network meta-analyses studied by Veroniki et al.¹⁸ and selected fourteen networks containing 567 randomized controlled trials with a total of 389,361 participants. Our selection criteria were that every treatment in the network should be evaluated in at least three studies; otherwise, the networks are poorly connected at that treatment node. We denote the fourteen networks as Ara 2009¹⁹, Ballesteros 2005²⁰, Bucher 1997²¹, Cipriani 2009¹³, Eisenberg 2008²², Elliott 2007²³, Lu 2006^5,24, Lu 2009^6,25,26, Middleton 2010²⁷, Mills 2009²⁸, Picard 2000²⁹, Puhan 2009³⁰, Thijs 2008³¹, and Trikalinos 2009³². Table 1 lists their characteristics including the outcomes, the investigated treatments with their weighted node degrees, and the total number of studies, participants, and events. For each node (treatment) in a network, the weighted degree is defined as the sum of weights on all edges incident to that node. In an NMA, the edge weight equals the number of pairwise comparisons between two treatments, so the weighted degree represents the frequency with which a particular treatment is investigated in all of the network's studies. The node with the greatest weighted degree can be considered the most well-connected. The online Supplemental Digital Material e-Figure 1 shows network plots for the 14 datasets.

Table 1.

Characteristics of the fourteen network meta-analyses.

Network	Outcome	No. of studies	No. of treatments	Treatment names (abbreviations) [weighted degree], sorted by weighted degree (largest to smallest)	Total no. of participants	Total no. of events	Naïve absolute risk#	Total no. of treatment groups	Total no. of treatment groups with zero events	Ineligible treatment removal		Smallest weighted degree*	Largest Weighted degree
										Arm-based model	Contrast- based model
Ara 200919	Adverse event leading to drug discontinuation	11	5	Atorvastatin 80 mg/day (ATO 80) [9]; Simvastatin 40 mg/day (SIM 40) [8]; Simvastatin 80 mg/day (SIM 80) [7]; Rosuvastatin 40 mg/day (ROS 40) [5]; Placebo [3].	24,793	1,155	0.047	24	2		SIM 40; ATO 80; SIM 80	3	9
Ballesteros 200520	Efficacy of antidepressants in dysthymia	9	4	Placebo [12]; Tricyclic antidepressant (TCA) [8]; Monoamine oxidase inhibitor (MAOI) [5]; Selective serotonin reuptake inhibitor (SSRI) [5].	1,386	663	0.478	21	0		Placebo	5	12
Bucher 199721	Number of Pneumocystis carinii pneumonia	18	4	Aerosolized pentamidine (AP) [14]; Trimethoprim-sulphamethoxazole (TMP-SMX) [13]; Dapsone/pyrimethamine (D/P) [5]; Dapsone (D) [4].	3,416	248	0.073	36	4		AP; TMP-SMX	4	14
Cipriani 200913	Unipolar major depression	111	12	Fluoxetine (FLU) [54]; Paroxetine (PAR) [32]; Sertraline (SER) [28]; Venlafaxine (VEN) [27]; Escitalopram (ESC) [17]; Citalopram (CIT) [14]; Mirtazapine (MIR) [13]; Bupropion (BUP) [12]; Fluvoxamine (FVX) [11]; Duloxetine (DUL) [8]; Reboxetine (REB) [8]; Milnacipran (MIL) [6].	24,595	13,951	0.567	224	0			6	54
Eisenberg 200822	Smoking abstinence	61	5	Placebo [64]; Transdermal nicotine (TN) [23]; Nicotine gum (NG) [20]; Bupropion (BUP) [18]; Varenicline (VAR) [9].	26,750	3,908	0.146	125	0	Placebo	Placebo	9(9)§	64(23)§
Elliott 200723	The proportion of patients who developed diabetes	22	6	β blocker (BB) [12]; Calcium-channel blocker (CCB) [12]; Angiotensin-converting enzyme inhibitor (ACEI) [11]; Placebo [10]; Thiazide diuretic (TD) [10]; Angiotensin-receptor blocker (ARB) [5].	154,176	10,962	0.071	48	0			5	12
Lu 20065,24	Smoking cessation	24	4	Individual counselling (IC) [21]; No contact [20]; Group counselling (GC) [8]; Self-help [7].	16,737	2,072	0.124	50	2			7	32
Lu 20096,25,26	Gastroesophageal reflux disease	40	6	H2 receptor antagonist (H2RA) [34]; Proton pump inhibitor (PPI) [17]; Placebo [14]; PPI double dose (PPI-D) [13]; Prokinetic agent (PA) [6]; H2RA double dose (H2RA-D) [4].	4,626	2,273	0.491	82	4		H2RA	4	34
Middleton 201027	Patients’ dissatisfaction	20	4	“First generation” endometrial destruction techniques (FG) [17]; “Second generation” endometrial destruction techniques (SG) [14]; Hysterectomy (HYST) [5]; Mirena (MIR) [4].	2,886	342	0.119	40	0	FG	FG; SG	4(4)§	17(14)§
Mills 200928	Smoking abstinence at at-least 4 weeks post-target quit date	89	4	Control [92]; Nicotine replacement therapy (NRT) [49]; Bupropion (BUP) [39]; Varenicline (VAR) [10].	29,525	10,847	0.367	181	1		Control	10	92
Picard 200029	Pain on injection with propofol	43	8	Placebo [48]; Lidocaine (mg) mixed with propofol 200 mg (LIDm) [26]; Lidocaine (mg) given before the injection of propofol (LIDb) [19]; No treatment (No Trt) [19]; Opioids (OPI) [19]; Lidocaine (mg) with tourniquet (LID+TOU) [13]; Temperature (TEM) [13]; Metoclopramide (MET) [7].	4,495	2,400	0.534	104	2			7	48
Puhan 200930	Exacerbation in patients with chronic obstructive pulmonary disease	34	5	Placebo [44]; Long-acting beta-agonists (BA) [33]; Inhaled corticosteroids (IC) [24]; Combined treatment with a long-acting beta-agonist and an inhaled corticosteroid (CT) [20]; Long-acting anticholinergics (AC) [11].	26,789	7,200	0.269	81	1			11	44
Thijs 200831	Efficacy of antiplatelet	23	5	Aspirin (ASA) [22]; Placebo [16]; Aspirin and dipyridamole (ASA+DP) [10]; Thienopyridines (ticlopidin or clopidogrel, THI) [7]; THI+ASA [3].	42,666	6,830	0.160	49	0		ASA; THI	3	22
Trikalinos 200932	Non-acute coronary artery disease	62	4	Bare-metal stents (BMS) [52]; Percutaneous transluminal balloon coronary angioplasty (PTCA) [43]; Drug-eluting stents (DES) [16]; Medical therapy (MT) [13].	26,521	821	0.031	124	22	BMS	BMS	13(13)§	52(43)§

^#Naïve absolute risk is calculated as the ratio of the total No. of Events compared to the total No. of Participants.

^*Weighted degree of a node (treatment) is the sum of weights (the number of pairwise comparisons between two treatments) on all edges incident to that node.

^§In each of these three networks, one particular treatment is not removed to remain network connectivity; the numbers in parentheses are given without accounting for these treatments.

2.2. Performing NMA and removing treatments

We fit the arm-based and contrast-based NMA Bayesian hierarchical models separately to each of the 14 network datasets. Appendix B gives details about these models. We used Markov chain Monte Carlo (MCMC) to compute posteriors for the effect sizes of interest, implemented using JAGS³³ via the R³⁴ package “rjags”³⁵.

Analyses with a treatment removed were performed as follows. Suppose a network includes K treatments. We first applied both the arm-based and contrast-based models to the complete network dataset (the full network) to estimate log ORs comparing each pair from the K treatments; we also estimated the population-averaged treatment-specific absolute risks using the arm-based model. Next, for each treatment, we excluded it from the network and applied the analyses to the remaining dataset (the reduced network) consisting of K – 1 treatments. The key difference between the arm-based and contrast-based models becomes pertinent at this point. If a treatment was removed from a network, then for any two-arm studies that included that treatment, only one treatment arm remained. For an analysis using the arm-based model, we could keep the single-arm studies as they still contribute to the likelihood function from the perspective of an analysis with missing data. However, for an analysis using the contrast-based model, because it uses information about contrasts, the single remaining arm no longer provides any information for estimation in the reduced network, so the whole two-arm study must be deleted if one of the treatments is excluded. Multi-arm studies – those comparing more than two treatments – that included the removed treatment were retained for analyses under both the arm-based and contrast-based models. For the present study, we did not consider any exclusion that creates a disconnected or poorly connected network, i.e., that resulted in at least one treatment in a network being evaluated in fewer than three studies. Table 1's “ineligible trt removal” column shows treatment exclusions that produce such ineligible reduced networks under analyses with the arm-based and contrast-based models. When comparing the arm-based and contrast-based models, we only considered treatment removals that were eligible under both models. Appendix C gives an example of which treatments were considered for exclusion.

2.3. Fold changes of estimated absolute risks in the arm-based model

For analysis using the arm-based model, we used fold changes of estimated population-averaged treatment-specific absolute risks to assess the impact of the treatment exclusion. Assume that the population-averaged absolute risk for a particular treatment is estimated as ${\widehat{\pi }}_f$ using the full network and ${\widehat{\pi }}_r$ using the reduced network. Then, the fold change for this treatment-specific absolute risk is defined as the maximum of ${\widehat{\pi }}_f∕{\widehat{\pi }}_r$ and ${\widehat{\pi }}_r∕{\widehat{\pi }}_f$. Thus, the fold change is never less than 1. Mills et al.¹ judged that a relative change not exceeding 1.03-fold is minor while a change greater than 1.10-fold is large, and over 1.20-fold is substantial, though such categorization is subjective and may need to be adapted to specific situations.

2.4. Comparison between arm-based and contrast-based methods

Without either external data or a separate model to estimate a reference treatment's absolute risk, the contrast-based method can only estimate ORs or their logarithms^2,10,17. We focused on the changes of log OR (LOR) when comparing the arm-based and contrast-based methods according to their sensitivity to treatment exclusion in the fourteen networks. For each network and treatment exclusion, we applied both models to the full and reduced networks. Then we calculated the LOR change (LORC) as the difference between the LOR estimates using the full and reduced networks: ${\mathrm{LORC}}_{ij}^{(-k)}={\widehat{\mathrm{LOR}}}_{ij}^{(-k)}-{\widehat{\mathrm{LOR}}}_{ij}$, where i, j index the treatments compared by this LOR and k indexes the treatment removed in the reduced network, i ≠ j ≠ k. ${\widehat{\mathrm{LOR}}}_{ij}$ and ${\widehat{\mathrm{LOR}}}_{ij}^{(-k)}$ are point estimates from the Bayesian analysis, which can be either the posterior means or medians; this article presents results for the posterior means.

Because of ${\mathrm{LORC}}_{ij}^{(-k)}+{\mathrm{LORC}}_{ji}^{(-k)}=0$ by the symmetry of LOR, when we used statistical tests to compare the arm-based and contrast-based models according to sensitivity to treatment exclusion, we considered the absolute LOR change, i.e., $\mid {\mathrm{LORC}}_{ij}^{(-k)}\mid$. Further, the average absolute LOR change is calculated for each model by averaging every $\mid {\mathrm{LORC}}_{ij}^{(-k)}\mid$ comparing all possible pairs of treatments based on all eligible treatment exclusions across all networks; a smaller average absolute change indicates a more robust NMA model with respect to treatment exclusion. To demonstrate that LOR changes resulting from an individual treatment exclusion in a network may be in opposite directions for the arm-based and contrast-based models, we present ${\mathrm{LORC}}_{ij}^{(-k)}$ with their directions in Figure 1, rather than their absolute values. To preserve any correlation structure between treatments in a network, when testing the difference between the arm-based and contrast-based methods, we used bootstrap resampling³⁶ at the network level (using 10,000 bootstrap samples); that is, each bootstrap sample consisted of fourteen resampled networks, drawn with replacement from the original fourteen networks. Based on the bootstrap samples, we calculated 95% confidence intervals (CIs) and p-values for each model's mean absolute LOR change and their difference.

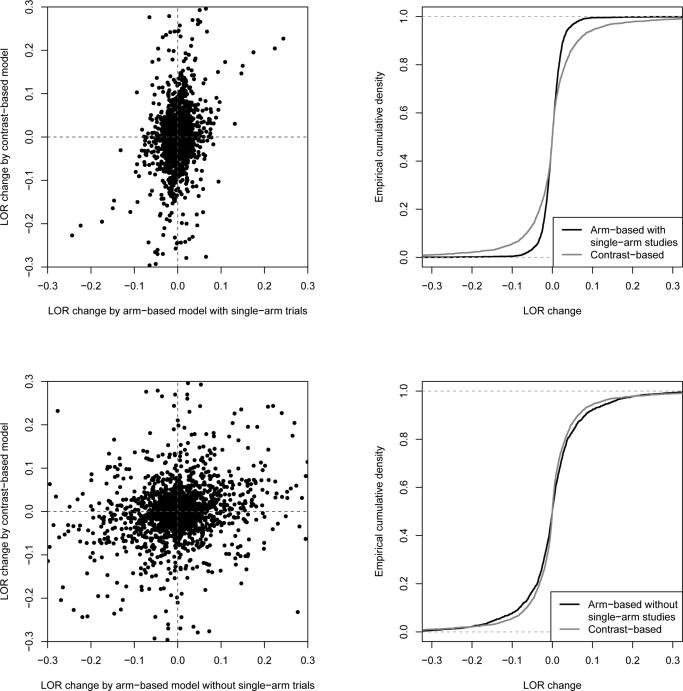
Figure 1.

Comparing the arm-based and contrast-based models according to log odds ratio changes. In the upper two panels, single-arm studies are kept in the reduced networks for the arm-based model; in the lower panels, the arm-based model is applied only to studies that can also be used by the contrast-based model, i.e., single-arm studies are excluded. Left panels are scatterplots of all log odds ratio changes (${\mathrm{LORC}}_{ij}^{(-k)}$) in the fourteen networks under the contrast-based model (vertical axis) vs. those under the arm-based model (horizontal axis). Right panels show the empirical cumulative distribution function of log odds ratio changes under the two models.

3. Results

3.1. Fold changes of estimated population-averaged absolute risks by the arm-based model

For the arm-based model, Table 2 reports the average and maximal fold changes of estimated population-averaged absolute risks and connectivity information about nodes associated with the maximal change for each network. The average fold changes in all networks are 1.05 or less; in 13 of 14 networks, the maximal change is below 1.10-fold. These small changes indicate the arm-based model's robustness to treatment exclusion. Although the arm-based model is robust in most cases, treatment exclusion can still produce significant changes (larger than 1.20-fold) for certain networks. For example, in the network Trikalinos 2009³², excluding the treatment PTCA results in a 1.39-fold change in the absolute risk estimate of the treatment MT. Referring to Tables 1 and 2, several potential factors affecting the fold changes are listed below.

Table 2.

Summary of fold changes of estimated population-averaged absolute risks using the arm-based model.

Network	Fold change		Removed treatment (weighted degree§) causing maximal fold change [Rank*/No. of eligible treatment removals]	Maximally affected treatment (weighted degree§) by the removal [Rank**/No. of treatments]
	Average	Maximal
Ara 200919	1.030	1.087	ATO 80 (9) [1/5]	ROS 40 (5) [2/5]
Ballesteros 200520	1.003	1.007	MAOI (5) [3/4]	Placebo (12) [4/4]
Bucher 199721	1.019	1.058	TMP-SMX (13) [2/4]	D (4) [1/4]
Cipriani 200913	1.005	1.033	SER (28) [3/12]	MIL (6) [1/12]
Eisenberg 2008 22	1.003	1.008	VAR (9) [4/4#]	BUP (18) [2/5]
Elliott 200723	1.015	1.056	Placebo (10) [4/6]	ACEI (11) [4/6]
Lu 2006 5,24	1.012	1.028	No contact (20) [2/4]	Self-help (7) [1/4]
Lu 2009 6,25,26	1.006	1.036	H2RA (34) [1/6]	Placebo (14) [4/6]
Middleton 2010 27	1.013	1.037	SG (14) [1/3#]	FG (17) [4/4]
Mills 200928	1.011	1.045	Control (92) [1/4]	VAR (10) [1/4]
Picard 200029	1.009	1.050	LIDb (19) [3/8]	MET (7) [1/8]
Puhan 2009 30	1.017	1.055	Placebo (44) [1/5]	BA (33) [4/5]
Thijs 2008 31	1.019	1.084	ASA+DP (10) [3/5]	THI+ASA (3) [1/5]
Trikalinos 200932	1.055	1.390	PTCA (43) [1/3#]	MT (13) [1/4]

^*Rank from largest to smallest according to the weighted degrees within the corresponding network.

^**Rank from smallest to largest according to the weighted degrees within the corresponding network.

^§The weighted degrees refer to the corresponding full network.

^#In each of these three networks, one particular treatment is not removed to remain network connectivity (See Table 1).

1. Removing treatments with larger weighted degree tends to cause larger fold changes, while the most affected treatment tends to have small weighted degree. In 6/14 networks, the maximal fold change is caused by the removal of treatment with the largest weighted degree; in 7/14 networks, the most affected treatment has the smallest weighted degree.

2. Including more studies and increasing network connectivity may help to reduce the impact of treatment exclusion. For example, Cipriani 2009¹³ examined 111 studies on 12 treatments, and each treatment is connected to at least three other treatments. All changes are smaller than 1.04-fold, and the average change is less than 1.01-fold. On the other hand, Ara 2009¹⁹ summarized only 11 studies on 5 treatments, and treatment exclusion caused changes as large as 1.09-fold.

3. NMA with low event rates may produce large fold changes. For example, the naïve absolute risk in Trikalinos 2009³² is only 3.1%, and 22/124 treatment groups reported zero events (Table 1). Although this network includes 62 studies, the maximal fold change is 1.39.

We should note that the factors above are not sufficient or necessary conditions when judging whether a network is robust to treatment exclusion. For example, Ballesteros 2005²⁰ has only 9 studies, but its average and maximal fold changes are smallest among the fourteen networks. The changes may be small in this network because it has a high naïve absolute risk.

3.2. Comparing the arm-based and contrast-based models

Figure 1 presents all LOR changes $\left({\mathrm{LORC}}_{ij}^{(-k)}\right)$ due to treatment exclusions in the fourteen networks under the arm-based and contrast-based models. In Figure 1's upper panels, the LOR changes under the arm-based model are estimated including single-arm studies. The scatterplot indicates that LOR changes for the arm-based model tend to be smaller in magnitude than those for the contrast-based model. The empirical cumulative distribution function (ECDF) in top right panel of Figure 1 supports this observation. Because ${\mathrm{LORC}}_{ij}^{(-k)}+{\mathrm{LORC}}_{ji}^{(-k)}=0$, the LOR changes between treatments i and j appear symmetrically in both the scatterplot and the ECDF graph. In addition, as each symmetric pair has the same absolute LOR change, we may only keep one value when we statistically test the difference between the arm-based and contrast-based models. (The resulting p-value remains the same if we include both values, as we use a nonparametric bootstrap resampling technique at the network level.)

Let μ_AB and μ_CB denote the true mean absolute LOR change (i.e., the expected value of $\mid {\mathrm{LORC}}_{ij}^{(-k)}\mid$ across all treatment exclusions in all networks) under the arm-based and contrast-based models, respectively. Based on 10,000 bootstrap samples, μ_AB is estimated as 0.020 with 95% CI (0.015, 0.031), and μ_CB is estimated as 0.047 with 95% CI (0.029, 0.100); μ_CB – μ_AB is estimated as 0.028 with 95% CI (0.011, 0.071) and two-sided p-value 0.005 for testing H₀: μ_AB = μ_CB vs. H_A: μ_AB ≠ μ_CB. Therefore, at 0.05 significance level, the absolute change under the contrast-based model is significantly larger than the change under the arm-based model, which suggests that the arm-based model is more robust than the contrast-based model to treatment exclusion.

To see whether the smaller average absolute LOR change caused by the arm-based model is due to the additional information it uses (that is, the retained single-arm studies), we applied the arm-based model to the same reduced networks that were used by the contrast-based model, in which single-arm studies were excluded. Figure 1's lower panels show the resulting LOR changes: the scatterplot and ECDF graph suggest that the arm-based and contrast-based models perform nearly the same when they use the same information. Let ${\tilde{\mu }}_{\mathrm{AB}}$ denote the true mean absolute LOR change when applying the arm-based model to the data used by the contrast-based model. Using the same bootstrap approach as above, the 95% CI for ${\tilde{\mu }}_{\mathrm{AB}}$ is (0.044, 0.089) with point estimate 0.054. The point estimate is comparable to that of the contrast-based model, but the 95% CI is slightly narrower; ${\mu }_{\mathrm{CB}}-{\tilde{\mu }}_{\mathrm{AB}}$ is estimated as −0.006 with 95% CI (−0.049, 0.027), with two-sided p -value 0.59 for testing $H_0:{\tilde{\mu }}_{\mathrm{AB}}={\mu }_{\mathrm{CB}}$ vs. $H_A:{\tilde{\mu }}_{\mathrm{AB}}\ne {\mu }_{\mathrm{CB}}$. These findings indicate that single-arm studies – which the arm-based model can use – provide valuable information.

The above conclusions are based on using posterior means as Bayesian point estimates. We also considered posterior medians as point estimates, with results similar to those presented here.

4. Discussion

This article examined the sensitivity of arm-based network meta-analysis to treatment exclusion, and compared that to the sensitivity of the contrast-based approach. For the arm-based model, we investigated the fold changes of estimated population-averaged absolute risks and found that the arm-based model is fairly robust for most networks. Because the changes of estimated population-averaged absolute risks were mostly less than 1.05-fold, relative effect sizes based on the marginal absolute risks, such as the odds ratio or relative risk, would also have small changes. Although in general the changes were minor, removing specific treatments can be influential, as in, e.g., Trikalinos 2009³². An influential treatment is typically investigated in many studies¹, while infrequently studied treatments are most likely to be affected by exclusion of other treatments to which they were compared. This suggests that when performing an NMA, researchers should be cautious if they only want to assess new treatments or if they want to exclude placebo arms or well-established treatments¹.

When comparing log odds ratio changes, the arm-based model generally outperformed the contrast-based model. Using bootstrap resampling, the difference between the arm-based and contrast-based models was statistically significant when single-arm studies were included in analyses using the arm-based model. However, when we dropped single-arm studies from reduced networks, the arm-based model performed almost the same as the contrast-based model. This implies that the arm-based model's greater robustness arises mainly from retaining single-arm studies. Some traditional pairwise meta-analyses have considered incorporating single-arm studies^37-40; when single-arm studies are available for NMA, the arm-based model can be an attractive alternative approach.

One might wonder why the arm-based and contrast-based models did not give identical results when the arm-based model was restricted by excluding single-arm studies in Section 3.2. The reason is that the two models involve different random-effect assumptions. Specifically, Shuster⁴¹ described two types of assumptions about random effects in meta-analysis. The first type of random effects, called “studies at random” (SR), assumes that the studies are independently chosen from a conceptual urn containing a large number of studies. The second type assumes that the relative effects in each study are randomly drawn from a conceptual urn while the studies are fixed; this is called “effects at random” (ER), which makes assumptions over and above SR, namely that the distribution of the random relative effects is independent of the study design. Arguably, the arm-based model requires the SR assumption, while the contrast-based model requires ER.

Our study has several limitations. First, we did not check evidence consistency in the investigated networks; detecting inconsistency in NMA is still an open question, which is partly discussed by Lu and Ades⁵. For the contrast-based model, this article assumes that the pairwise comparisons among any trio of treatments, say A, B, and C, are inter-related as θ_BC = θ_AC – θ_AB. If this consistency does not hold, we could use approaches based on an inconsistency model such as θ_BC = θ_AC – θ_AB + ϕ, which is discussed in Salanti et al.⁷ Here, ϕ represents the inconsistency between the direct evidence for treatment B vs. C and the indirect evidence from pairwise comparisons of A vs. B and A vs. C. For the arm-based model, one may consider detecting inconsistency between two treatments by comparing their absolute risk differences in direct comparisons versus indirect comparisons⁴². A large discrepancy implies potential inconsistency between these two treatments. The second limitation of our study is that we used a selection criterion requiring each treatment to be studied in at least three studies, mainly due to the need for an adequate number of studies to estimate parameters for the distribution of random effects. The literature has no well-established criterion serving this purpose.

In conclusion, arm-based methods can be an attractive alternative when data from some single-arm studies are available. For example, if we are interested in comparing treatments A, B, and C in an NMA, “single-arm” study data on A can come from two-arm studies comparing A vs. D or other treatments. Furthermore, although the arm-based model is generally more robust than the contrast-based model, for some NMAs, the contrast-based methods seem to be more robust to some treatment exclusions. For example, the LOR changes under the arm-based model can be fairly large, while the corresponding changes under the contrast-based model can be nearly zero (Figure 1). Therefore, analysts are advised to consider both the arm-based and contrast-based models for NMA, especially when making inference for a small or poorly connected network.

Appendix A. Estimating population-averaged absolute risks for the smoking cessation data

Consider using both the arm-based and contrast-based models to estimate absolute risks for the smoking cessation data presented in Hasselblad²⁴ and Lu and Ades⁵. This network meta-analysis dataset consists of 24 studies on a total of 16,737 participants, comparing the effects of self-help (B), individual counseling (C), and group counseling (D) versus no contact (A). It is straightforward to estimate the population-averaged absolute risks using the arm-based model.² To illustrate that the arm-based model does not simply estimate the population-averaged absolute risks for each treatment arm independently, we also consider separate logit and probit random effects models on each treatment to estimate the corresponding population-averaged absolute risks. Specifically, the random effects model for a treatment is $y_i\sim bin(n_i,p_i),g\left(p_i\right)=u+v_i,v_i\sim N(0,{\sigma }^2)$, where i indexes different studies, and y_i and n_i represent the number of events and participants on a given treatment arm. We used a vague prior for the fixed effect u and an inverse gamma prior for the variance σ². The link function g(·) is either the logit or probit link. The treatment's population-averaged absolute risk can be estimated for the logit link as $\pi =\frac{1}{1+\exp (-u∕\sqrt{1+C^2{\sigma }^2})}$ where $C=\frac{16\sqrt{3}}{15\pi }$, and for the probit link as $\pi =\Phi (u∕\sqrt{1+{\sigma }^2})$, where Φ(·) is the standard normal cumulative distribution function⁴³.

To estimate absolute risks using contrast-based NMA, we first selected a reference treatment group and used the above logit random effects model to estimate absolute risk distribution for the reference group, which was further used to estimate the population-averaged absolute risks of other treatment groups. The related WinBUGS code for the “random effect models for multiple arm trials” is available at http://www.bristol.ac.uk/social-community-medicine/projects/mpes/mtc/. Specifically, based on separate logit random effects models on each treatment, we used N(−2.62, 2.68⁻¹) as the prior of logit absolute risks for treatment A, N(−1.94, 1.23⁻¹) for treatment B, N(−1.69, 1.69⁻¹) for treatment C, and N(−1.44, 1.51⁻¹) for treatment D, when each is chosen as the reference group, respectively. The results were based on 500,000 MCMC iterations with 500,000 additional burn-in iterations, and are listed in Table A1.

Table A1 illustrates differences between the population-averaged absolute risks estimated by the arm-based model and by separate logit or probit models. In particular, because the arm-based approach models the absolute risks of treatment arms jointly to account for correlations among them within a study, the posterior of population-averaged absolute risks from the arm-based model generally have narrower 95% credible intervals than those from separate models. In addition, the contrast-based model leads to much wider 95% credible intervals. This may arise because the contrast-based model only uses the point estimates of u and σ² from the separate logit/probit random effects models as a “fixed” prior distribution for the reference group, and the absolute risk estimates of other treatments greatly depend on this prior information.

Appendix B. The arm-based and contrast-based models

Assume that a network meta-analysis reviews I studies on K treatments, where each study investigates a subset of the K treatments. Label the studies i = 1 to I and the treatments k = 1 to K. Let T_i be the subset of the K treatments that is compared in ith study. Further, in the ith study, let n_ik be the number of participants allocated to treatment k (k ∈ T_i), and let y_ik be the number of events. For binary outcome, both types of NMA models are based on the binomial likelihood y_ik ~ bin(n_ik, p_ik) for k ∈ T_i; they differ in the way they model the underlying absolute risks p_ik in each study’s treatment group.

The arm-based model² is specified as follows:

$$\begin{array}{c}\hfill g\left(p_{ik}\right)={\mu }_k+v_{ik};\hfill \\ \hfill {(v_{i1},v_{i2},\dots ,v_{iK})}^T\sim MVN(0,{\Sigma }_K),\hfill \end{array}$$

where g(·) is a link function and Σ_K is the variance-covariance matrix of the vector of random effects ${(v_{i1},v_{i2},\dots ,v_{iK})}^T$. Let ${\sigma }_k^2$, k = 1, 2, ... , K denote the diagonal elements of Σ_K. The μ_k's are fixed effects for the treatments. Notice that the v_ik's are correlated within each study via the multivariate normal distribution; thus the arm-based model respects within-study randomization. When the link function g(·) is the probit link (i.e., Φ⁻¹(·) ), the population-averaged absolute risk of treatment k is ${\pi }_k=E[p_{ik}\mid {\mu }_k,{\sigma }_k]=\Phi ({\mu }_k∕\sqrt{1+{\sigma }_k^2})$.⁴³ With this estimate for absolute risks, we can calculate ORs, RRs, and RDs. This article uses an inverse-Wishart prior for ${\Sigma }_K,{\Sigma }_K^{-1}\sim W({\mathbf{V}}_K,K)$, where V_K is a K × K matrix with diagonal elements 1 and off-diagonal elements 0.005. The inverse-Wishart prior is commonly used for variance-covariance matrices and is considered vague^44,45. Also, since it is conjugate, this prior allows some mathematical simplicity⁴⁶. Zhang et al.² gives practical computer code implementing MCMC for this model, and the R package pcnetmeta (http://cran.r-project.org/package=pcnetmeta) provides user-friendly functions.

A popular contrast-based model proposed by Lu and Ades^4,6 specifies a baseline treatment b(i) in the ith study. For convenience, we simply denote b(i) as b. The Bayesian hierarchical model for this approach is

$$\begin{array}{c}\hfill g\left(p_{ik}\right)={\mu }_i+X_{ik}{\delta }_{ibk};\hfill \\ \hfill {\delta }_{ibk}\sim N(d_{bk},{\sigma }_{bk}^2).\hfill \end{array}$$

In this model, X_ik is a dummy variable taking the value 1 if k ≠ b and 0 if k = b. Also, μ_i is the baseline effect for treatment b in the ith study, and δ_ibk is the relative effect of treatment k compared to the baseline b on the logit scale. This model treats the μ_i's as nuisances and uses non-informative priors for them. This model focuses on the treatment contrasts δ_ibk and the parameter of interest is the overall relative effect d_hk = d_bk – d_bh; therefore, this model is described as contrast-based. Practical computer code is available at http://www.bristol.ac.uk/social-community-medicine/projects/mpes/mtc/.

This article uses the two models as described above. Since the contrast-based model cannot estimate absolute effects, some authors have proposed the so-called “contrast-based + baseline” model¹⁰, which is specified as

$$\begin{array}{c}\hfill g\left(p_{ik}\right)={\mu }_i+X_{ik}{\delta }_{i1k};\hfill \\ \hfill {\delta }_{i1k}\sim N(d_{1k},{\sigma }_{1k}^2);\hfill \\ \hfill {\mu }_i\sim N(m,{\sigma }_m^2).\hfill \end{array}$$

Here, instead of being treated as a nuisance, μ_i is modeled as the absolute effect of the “reference” treatment 1. The absolute effect of treatment k is estimated by a_k = m + d_1k. This model not only assumes that the relative effects δ_i1k are exchangeable between studies, but also requires exchangeability between studies of the absolute effect μ_i for the “reference” treatment. Also, this model can be reduced to the arm-based model: we may rewrite $g\left(p_{ik}\right)=(m+d_{1k})+({\tilde{\mu }}_{i1}+{\tilde{\delta }}_{i,1k})$ for k ≠ 1, where ${\tilde{\mu }}_{i1}={\mu }_{i1}-m\sim N(0,{\tau }_m^2)$ and ${\tilde{\delta }}_{i,1k}={\delta }_{i,1k}-d_{1k}\sim N(0,{\sigma }_{1k}^2)$. Therefore, m + d_1k and ${\tilde{\mu }}_{i1}+{\tilde{\delta }}_{i,1k}$ correspond to the treatment-specific fixed effect μ_k and the random effect v_ik in the arm-based model, respectively. More details of NMA models can be found in the work by Hong et al. and discussions of it^47-49. Due to its similarity to the arm-based model and its strong assumptions, this article does not consider the “contrast-based + baseline” model.

Appendix C. An example of excluding a treatment to form a reduced network

Table A2 gives an example to illustrate the data available for arm-based and contrast-based models after excluding each treatment being considered. This network consists of six studies labelled A to F, which evaluate the efficacy of three treatments, labelled 1 to 3. Studies A to E are two-armed, while Study F is three-armed. The six rightmost columns show data that can be used by the arm-based and contrast-based methods if each of the three treatments is excluded. For the arm-based model, in the complete network and reduced networks each retained treatment is investigated in at least 3 studies. However, for the contrast-based model only exclusion of treatment 3 is eligible for consideration under our criteria (i.e., that each retained treatment is investigated in at least 3 studies).

The foregoing criterion would imply that no treatment exclusions need to be ruled out for the arm-based method. However, certain treatment exclusions, such as the removal of treatment placebo in Eisenberg 2008²², would create a disconnected network. Therefore, we ruled out such treatment exclusions in the present study.

Table A1.

Population-averaged absolute risks of the four treatments in the smoking cessation network meta-analysis studied by Hasselblad (1998) and Lu and Ades (2006). They are obtained by the arm-based model, contrast-based model using different reference treatments, and separate logit/probit random effects models on each treatment.

Treatment	Population-averaged absolute risks (posterior mean with 95% credible intervals)
	Contrast-based model Reference treatment (# of studies including this treatment)				Separate logit random effects models	Separate probit random effects models	Arm-based model (using probit link)
	A (19)	B (6)	C (19)	D (6)
A	0.078 (0.021, 0.194)	0.110 (0.012, 0.378)	0.093 (0.016, 0.280)	0.098 (0.013, 0.325)	0.075 (0.055, 0.104)	0.072 (0.045, 0.108)	0.083 (0.058, 0.117)
B	0.126 (0.027, 0.334)	0.156 (0.024, 0.456)	0.144 (0.023, 0.422)	0.147 (0.020, 0.454)	0.174 (0.084, 0.352)	0.182 (0.069, 0.384)	0.170 (0.086, 0.304)
C	0.162 (0.044, 0.379)	0.207 (0.028, 0.587)	0.180 (0.039, 0.455)	0.188 (0.029, 0.525)	0.175 (0.128, 0.241)	0.173 (0.118, 0.245)	0.185 (0.135, 0.248)
D	0.203 (0.048, 0.491)	0.248 (0.034, 0.665)	0.225 (0.042, 0.574)	0.220 (0.046, 0.540)	0.231 (0.125, 0.403)	0.244 (0.106, 0.450)	0.233 (0.127, 0.382)

Table A2.

An example for treatment exclusion.

Study ID	Treatment ID	Full network (no. of events / no. of participants)	Usable data
			Remove Treatment 1		Remove Treatment 2		Remove Treatment 3
			Arm-based	Contrast-based	Arm-based	Contrast-based	Arm-based	Contrast-based
A	1	yA1/nA1	–	–	yA1/nA1	–	yA1/nA1	yA1/nA1
A	2	yA2/nA2	yA2/nA2	–	–	–	yA2/nA2	yA2/nA2
B	1	yB1/nB1	–	–	yB1/nB1	–	yB1/nB1	yB1/nB1
B	2	yB2/nB2	yB2/nB2	–	–	–	yB2/nB2	yB2/nB2
C	1	yC1/nC1	–	–	yC1/nC1	–	yC1/nC1	yC1/nC1
C	2	yC2/nC2	yC2/nC2	–	–	–	yC2/nC2	yC2/nC2
D	2	yD2/nD2	yD2/nD2	yD2/nD2	–	–	yD2/nD2	–
D	3	yD3/nD3	yD3/nD3	yD3/nD3	yD3/nD3	–	–	–
E	1	yE1/nE1	–	–	yC1/nC1	yC1/nC1	yC1/nC1	–
E	3	yE3/nE3	yE3/nE3	–	yE3/nE3	yE3/nE3	–	–
F	1	yF1/nF1	–	–	yF1/nF1	yF1/nF1	yF1/nF1	yF1/nF1
F	2	yF2/nF2	yF2/nF2	yF2/nF2	–	–	yF2/nF2	yF2/nF2
F	3	yF3/nF3	yF3/nF3	yF3/nF3	yF3/nF3	yF3/nF3	–	–