Summary
Meta-analytic methods for combining data from multiple intervention trials are commonly used to estimate the effectiveness of an intervention. They can also be extended to study comparative effectiveness, testing which of several alternative interventions is expected to have the strongest effect. This often requires network meta-analysis (NMA), which combines trials involving direct comparison of two interventions within the same trial and indirect comparisons across trials. In this paper, we extend existing network methods for main effects to examining moderator effects, allowing for tests of whether intervention effects vary for different populations or when employed in different contexts. In addition, we study how the use of individual participant data (IPD) may increase the sensitivity of NMA for detecting moderator effects, as compared to aggregate data NMA that employs study-level effect sizes in a meta-regression framework. A new network meta-analysis diagram is proposed. We also develop a generalized multilevel model for NMA that takes into account within- and between-trial heterogeneity, and can include participant-level covariates. Within this framework we present definitions of homogeneity and consistency across trials. A simulation study based on this model is used to assess effects on power to detect both main and moderator effects. Results show that power to detect moderation is substantially greater when applied to IPD as compared to study-level effects. We illustrate the use of this method by applying it to data from a classroom-based randomized study that involved two sub-trials, each comparing interventions that were contrasted with separate control groups.
Keywords: Integrative data analysis, meta-analysis, moderation, network meta-analysis, participant level data, statistical power
1 Introduction
As intervention research advances, there is growing interest in moving from simple tests that compare intervention efficacy to more complex questions concerning which interventions work for whom and under what conditions. When analysts combine data from multiple trials using meta-analysis, they address these questions through meta-regression, testing whether study-level covariates predict systematic variation in intervention effects. In this paper we take up the question of how this work can be advanced through combining two general methods. These include network meta-analysis and the use of participant-level data.
Individual intervention trials randomly assign participants to controls and one or more interventions, testing whether outcomes differ between intervention and control, or among other forms of intervention. When an intervention has been tested in a number of trials, conventional meta-analysis techniques combine results across trials that have the same intervention arms, but test intervention effects across different contexts or populations. Meta-analysis techniques are available to combine summary measures such as effect sizes from a set of trials. Network meta-analysis, a more general method, allows for combining results across multiple trials that have varying intervention arms [1,2]. Two interventions of interest may be present in head-to-head trials, giving rise to a direct comparison, while other trials may only include one of these interventions, tested against a control. The overall effect that compares two active interventions can be estimated by taking into account both direct comparisons of the two interventions within the same trials, as well as indirect comparisons where one of these interventions is absent [3–6]. It is always helpful but not absolutely essential to have direct head-to-head comparisons. For example, consider two randomized trials where the first tests an intervention (B) against control (A) while the second tests a different intervention (C) against the same control. Even though there is no head-to-head comparison of B vs C, combining the comparisons of A vs B and A vs C should provide useful information on comparing B vs C. Provided nothing differs systematically between the two trials, the difference in these two estimates yields an unbiased estimate of the effect of B vs C. Extensions of this idea form the basis of network meta-analysis. Like pairwise meta-analysis, most network meta-analyses are based on aggregate data, generally from publications, to make comparisons between interventions.
Network meta-analysis has been used almost exclusively to study intervention main effects. However, as intervention research progresses, important questions emerge concerning which interventions work best for which populations, and under what general conditions. Such questions can only be answered through tests of moderation.
In pairwise meta-analysis, moderation is tested through meta-regression. Study effect sizes are regressed on study-level variables, such as type of intervention or percent of female participants. Although meta-regression techniques could in principle be used within network meta-analysis, we suggest that it will often be more pro table to employ new methods that combine participant-level data from multiple trials [7, 8]. As rich as network meta-analysis is, the use of summary statistics from reported findings limits its ability to examine more complex hypotheses involving moderators of intervention effects. As an example, consider the question of whether intervention effects may differ for participants who begin the trial with higher levels of targeted symptoms. This question is important as a growing number of studies suggest the importance of baseline moderators in determining who will benefit the most from an intervention [9]. The average estimates obtained from network meta-analysis say nothing about variation in the effects of an intervention across participants who differ on baseline characteristics.
Moderator effects in comparative effectiveness studies could be addressed by combining reports of moderator analyses of intervention effects in a pairwise meta-analytic framework. However, moderator analyses for single trials are not always reported in the published literature, especially when each individual trial has very low statistical power for detecting moderation. Such analyses in separate trials may be reported more often for those moderator variables that reach standard levels of statistical significance, and even when published in multiple trials the analyses may be based on different cutoff values (e.g., high or low risk). Thus selective reporting and lack of harmonization make it difficult to obtain useful syntheses of published moderation analyses. In many cases meta-analyses have used meta-regression based on trial-level covariates such as the percentage of high-risk individuals in a trial [10,11], to reflect how an individual covariate could moderate impact [12, 13]. Use of summarized participant-level covariates is problematic; it is well known that this approach can easily lead to erroneous conclusions when applied to participants (the ecological fallacy [14]).
The alternative we explore here involves testing for participant-level moderation of intervention effects [15] or more generally examining variation in impact by baseline characteristics [16, 17] by analyzing participant-level data across multiple trials. For this paper we assume that participant-level data from all trials are available and that the participant-level covariate and outcome are identical across trials. Analysis of individual-participant data (IPD) across multiple trials [12,18,19] is considered a type of integrative data analysis (IDA), which has seen extensive methodologic development in recent years both for combining data from passive longitudinal studies [20] as well as for randomized trials [21–23].
Analysis of IPD offers a number of advantages [24]. It allows for more precise harmonization of outcome measures, of particular importance when trials use somewhat different methods for measuring the same outcome [25, 26]. This may be less of an advantage when all trials use the same outcome measures, although even in this case IPD can be used to test the assumption that measurement is invariant over trials. IPD also makes maximal use of information on within-study variation in potential moderators, avoiding the ecological fallacy. The availability of IPD also facilitates a “one-stage” approach in the network meta-analysis. The use of IPD is limited to situations where participant-level data are available across trials. Federal policies now require that funded investigators make data available for other investigators, but obtaining and combining such data can require substantial resources (see Perrino et al. [9] for an in-depth discussion of methods for data sharing).
Recent work has established the benefits of studying whether participant characteristics moderate the effects of interventions with participant-level data as compared to aggregate data [15, 27–29]. This has recently been applied to network meta-analysis, with particular attention to combining trials when moderators are binary [1, 7]. We build on this work in 3 ways. Focusing on situations where IPD are available in all trials, we develop models for binary, categorical and continuous moderators. We also conduct simulations to assess how power is affected by this use of IPD.
In this article, we present multilevel models that allow for the analysis of moderator effects based on participant-level data aggregated across a pool of trials that involve both direct and indirect comparisons of interventions. This NMA framework is sufficiently general to allow the incorporation of non-randomized data such as additional samples of controls or intervened populations. It is noted that the NMA framework needs to adjust for confounders and other sources of heterogeneity when non-randomized data are included. We then use simulations to evaluate the statistical power for network meta-analytic comparisons of main effects and moderator effects for two interventions tested across the same and different trials. For main effect analyses that compare two active interventions, network meta-analysis with IPD is expected to improve statistical power slightly over network meta-regression, when variance estimates can be pooled [30]. For moderation analyses across multiple trials we anticipate greater statistical power when participant-level data are used compared with composite trial-level characteristics.
The remainder of this paper is structured as follows. Section 2 presents a two-level model specification of network meta-analysis based on IPD for both fixed and random effect modeling and provides a general definition of homogeneity and consistency, key concepts in network meta-analyses. Simulation results for power analyses for both main effect and moderation analyses are presented in Section 3. These models are then applied in Section 4 to two linked multilevel randomized trials in order to estimate an indirect comparison with two active interventions. Finally, Section 5 concludes with recommendations for this procedure's use and future work.
2 Modeling of network meta-analysis using individual-participant data
We consider how to make inferences about main effects and moderator effects across a collection of I studies (trials) each of which tests one or more intervention arms. In totality the trials involve K interventions, with K ≥ 3. We assume that all studies with more than one intervention are randomized at the participant level, and for convenience we use the term trial to refer to any single-arm or multi-arm study. Trials that are included need to be comparable, a term we use to refer to trials that involve similar populations (e.g., similar age group) and trial designs (e.g., similar follow-up time [31,32]). It is a basic premise of network meta-analysis that statistical comparisons of interventions across trials should be inferred only if the trials are clinically and methodologically comparable [33]. Inclusion/exclusion criteria for trials are often defined to identify eligible trials. It is not always easy to obtain participant-level data from multiple trials, but procedures for obtaining such data through a data sharing collaboration are discussed in Perrino et al. [34].
2.1. Modeling main effects and effect modifications in network meta-analysis
We begin with a generalized linear mixed model, accounting for different intervention arms in each trial. We assume that all trials have a common outcome measure Y and a common set of baseline covariates X. Measures need not be common, but issues of harmonizing different measures across trials raise tangential concerns to this paper's development and are discussed elsewhere [35]. Intervention moderator effects are given by the product of a subset Z of X covariates and these intervention indicators. We recommend following the standard practice of centering all moderator terms across trials at zero before calculating products, to reduce collinearity. In the generalized linear mixed model [36], defined in Equation (1) below with a link function g(·), we decompose each individual's response into a sum of three components corresponding to three sets of predictors X: intervention denoted by T, covariates Z, and effect modifiers2.
| (1) |
where i and j refer to participant j in trial i. The expectation of the outcome for participant j, in trial i when assigned to the kth intervention, Tij = k, is given by E[Yij|Tij = k]. α is a q × 1 vector of fixed effects associated with baseline covariates Xij which could also include trial-level covariates, although we focus here on individual-level covariates which extend the model when individual participant data is available, and a 1 × p row vector Zij are effect modifiers of intervention; ni is the number of participants in trial i. Here Tij = k indicates that participant j in trial i is assigned to intervention k, which can take at least one value in 1, ..., K. A scalar βk and a p × 1 vector γk are fixed effects to denote the main effect of intervention and the effect modifiers. and ci ~ Np(0, Σcc) are the corresponding random effects for trial i. Of note, we consider random effects of trials instead of fixed effects to capture variability among trials. Please also see Section 3 on an example of such data. Note that βk and bi are scalar while γk and ci are p-dimensional vectors of the same dimension as Zij. This generalized linear model can incorporate linear, logistic, and log-linear regression, as well as a wide range of other models.
Define the (p + 1) × (p + 1) covariance matrix of bi and ci as which does not vary with trial i. The vectors (bi, ci) are assumed to be independent across trials. In generalized fixed-effects modeling, we also assume that the variance in Y is some function of its mean, Var(Y) = ϕh(E(Y)).
We define the trial level mean and effect modifier
| (2) |
| (3) |
Note that in this first model the trial affects all interventions identically by shifting the overall intercept and moderator effect. It is also noted that Xijα in equation (1) produces an overall adjustment for the baseline values of the covariates in X.
As a final remark in this subsection on the level of moderator variables, we contrast our analyses with pairwise meta-analysis, which does not have access to participant-level data. Meta-analysis almost never includes participant level moderators as these analyses are generally not reported. In the absence of reported participant-level moderator analyses, meta- analysis sometimes resorts to the use of trial-level covariates, such as the average baseline level of risk, to provide some clues about how the intervention effect varies by, say participant level of risk. This can easily produce ecological fallacies, as we show later in the paper. But other subtleties arise when considering moderation both at participant level and trial level when IPD are available. For example, there are circumstances where it is appropriate to include trial-level covariates as having an effect on participants over and above participant- level covariates. As an illustration, it is possible that a trial conducted in hospitals that treat very sick children will use a more intensive behavioral intervention than one in a hospital with less sick children. We leave such investigations to a future paper.
2.2. Heterogeneity in interventions across trials
An extension to model (1) is to allow different random effects for each intervention arm in each trial, i.e., the trial by intervention interaction:
| (4) |
where α is a q × 1 vector of coefficients of baseline covariates Xij; as with all moderator models, the parameters for any covariate in Xij that also appears in Zij cannot be interpreted in isolation from its moderator effect. The random effects for trial by intervention interaction are distributed as and the random effects for trial × intervention × effect modifier are distributed as ci,k ~ Np(0, Σcc,k). Define the covariance matrix of bi,k and ci,k as . As before, these random effect vectors are assumed to be independent across trials. Random effects for the two interventions within the same trial can be correlated with one another, independent, or degenerate (e.g., bi,k = bi,k′ with probability one); however, we require that the covariance of bi,k and bi,k′ within a trial, Cov(k, k′), be the same across trials. Thus all the random effects for all trials are assumed to have the same underlying variance-covariance structure. The simplest case is to assume all the off-diagonal sub matrices are 0, but correlated random effects (e.g., random intercepts for control and active intervention) are often scientifically warranted [38] and also necessary for valid meta-analytic inferences for non-linear models [39]. It may be appropriate to equate some of the Σ elements, as we do in the example in Section 4.
The trial level main and modification effects for this more general model (4) are
| (5) |
| (6) |
The presence of random effects bi,k and ci,k allow heterogeneity in intervention effects across trials. Differences in these coefficients represent differences between interventions within a trial (e.g., mi,k – mi,k′) or differences between trials for the same intervention (e.g., mi,k – mi′,k). Contrasts involving mixed effects mi,k – mi,k′ over i correspond to moderation across trials, which are used in forming indirect comparative effectiveness estimates.
Model (4) can be specified in a number of ways. For example, one can replace fixed effects βk by βi,k and γk by γi,k and drop the random effects entirely. Other extensions, for example, introducing participant-level random effects as in growth modeling or random slopes for covariates X [40] are not discussed here as they add notational complexity without changing the underlying model.
2.3. Directly and indirectly estimable main effects and moderator effects
The realized model for a set of trials is determined by which interventions are available for each trial. We define an estimable direct effect as a simple contrast between two interventions that are realized in at least one trial. Define H to be the I × K indicator matrix of interventions for each trial. Then the contrast k, k′ is directly estimable if there exists at least one trial i such that Hi,k = Hi,k′ = 1.
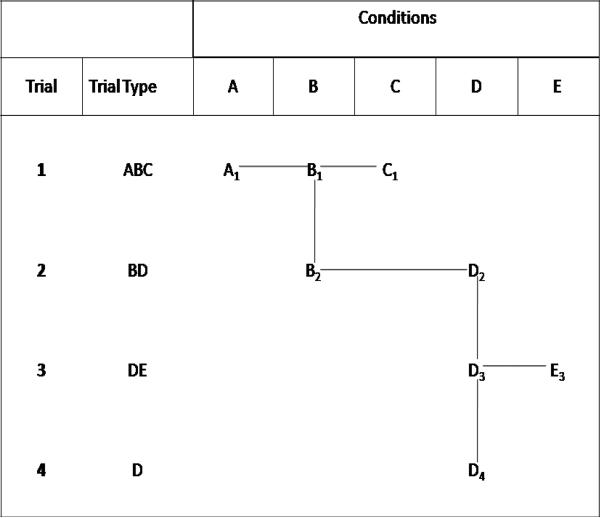
2.3.1. Derived Contrasts along a Path
In addition to basic contrast parameters within a trial, the patterns of interventions tested across the collection of trials can also provide additional information about contrasts. We define a contrast between interventions k and k′ to be indirectly estimable if there is at least one pathway involving two or more trials connecting these endpoints. In Figure 1 a step from one intervention to another is horizontal, and a step from one trial to another is vertical. Specifically, a path of length u > 1 starting in trial i at intervention k and ending in trial i′ at intervention k′ can be represented by the following steps: let k0 = k, i0 = i, ku = k′, and iu = i′ and then S0 = (i0, k0) and Su = (iu, ku), where each step is either horizontal, i.e., il = il–1 (and kl = kl–1 – 1 or kl–1 + 1), or vertical, i.e., kl = kl–1 (and il = il–1 – 1 or il–1 + 1), and all Hil,kl are 1, l = 1, . . ., u. The indirect value of the mean difference between k and k′ through a path S is defined in terms of the expected values mkj,
| (7) |
| (8) |
where the expectation is over the trial level random effects. Similarly the indirect response difference in k and k′ involving moderation at covariate level Z is
| (9) |
| (10) |
Note that the covariates in Z must be available and have the same definition in all trials. In addition, their joint distributions must have sufficient overlap across trials.
Figure 1.
A diagram of network with five interventions labeled A – E
Figure 1 provides a convenient way to represent the set of trials and interventions, using a connected, non-directed graph. Unlike other figures for network meta-analysis [41, 42], this figure retains information on which interventions are tested within each separate trial. Interventions are labeled A-E and subscripted by the trial number. Horizontal ties represent directly estimable contrasts in the same trial, for any pair of interventions on the same row. Vertical ties represent trials having the same intervention. Any pair of interventions not directly estimable but connected through some path has an indirectly estimable contrast. In this example the directly estimable contrasts are AB, BC, and AC (from Trial 1), BD (from Trial 2), and DE (from Trial 3). One indirectly estimable contrast is AD, where B serves as a common comparator [33] in the three-step path from A1 to B1, B1 to B2, and B2 to D2. Other indirectly estimable contrasts are AE, BE, CD, and CE. The last trial only includes intervention D.
2.4. Definitions of Homogeneity and Consistency
The terms homogeneity and consistency have been used in network meta-analysis [41] to refer to the assumptions required for interpreting contrasts across trials as causal effects. Violations of these conditions would imply that biases exist that would confound causal inferences of effects across trials. The term consistency is used by Lu and Ades [43] and Cooper et al. [44] to describe the condition where direct and indirect comparisons of two interventions do not differ. We have reviewed previous references to these concepts [41, 44] and applied these ideas to both main effects and moderation, including fixed-effects and mixed-effects models. Our own definitions follow.
Definition
Weak homogeneity for contrast k, k′ occurs if for all trials i that assign participants to interventions k or k′, E(mi,k – mi,k′) ≡ βk – βk′ does not vary with trial. We say there is strong homogeneity if in addition Var(mi,k – mi,k′) = 0 for all i. Similarly weak homogeneity of moderation comparing k and k′ is said to occur if E(wi,k – wi,k′) ≡ γk – γk′ does not depend on the trial. Strong homogeneity of moderation comparing k and k′ also requires that Var(wi,k – wi,k′) = 0. Likewise we say there is weak homogeneity for intervention k if E(mi,k) does not vary with trial and strong homogeneity for intervention k if Var(mi,k) = 0 for all i. Weak and strong homogeneity of moderation for intervention k are defined similarly.
When we use the terms “weak or strong homogeneity” without any modifiers (e.g., leaving off contrasts and conditioning), this shorthand will denote that all available contrasts k, k′ satisfy the conditions on mi,k – mi,k′ above. For clarity, if there are no trials or only one trial that assigns participants to interventions k or k′ we say homogeneity still holds.
Definition
There is weak consistency for contrast k, k′ in a collection of trials if there is the same expectation across any direct or indirect path. Weak consistency thus requires βk – βk′ to be the same for every trial having both k and k′ interventions, and that these are equal to δ(k, k′; S) for any realized path S. We use a similar definition of consistency for moderation involving k, k′, namely ρ(k, k′, Z, S) is constant over all paths S. Strong consistency requires no between-trial level variance in these quantities.
2.4.1. Testing for and estimation under homogeneity and consistency
Formal testing for homogeneity under model (4), e.g., verifying that E(mi,k – mi,k) ≡ βk – βk′ is constant over trials, can be done under certain circumstances where assumptions about trial level variance can be made. Define the subset of trials Jk,k′ = {i : Hi,k = Hi,k′ = 1} where two interventions are tested. By equation (5) the quantities mi,k – mi,k′ for i ∈ Jk,k′ have means βk – βk′ and between trial variance given by where Cov(k, k′) is the covariance of bi,k and bi,k′, which is the same across trials. Let m̂i,k – m̂i,k′ be an asymptotically unbiased estimate of mi,k – mi,k′ and sei its within-trial standard error. If we are willing to make the assumption that v2(k, k′) = 0, then the sum of squares (SSQ) ratio over trials Jk,k′, has asymptotically noncentral χ2 distribution with noncentrality proportional to . Thus a test of homogeneity for k, k′, i.e., SSQ(βk – βk′) = 0 can be made under the assumption of no trial-level random effects. If we make no assumptions about v2 we cannot distinguish between the variation in the fixed effects versus trial level random effects and thereby cannot form a test of weak homogeneity. But if we assume that v2(k, k′) = constant over all k, k′ we can compute its marginal maximum likelihood estimate and form such a test. Thus a rejection of the hypothesis that all v2(k, k′) are constant may suggest disconfirmation of weak homogeneity. In section 4 we investigate both of these tests in the context of a real example.
Similarly we can test for consistency by comparing the fit of a consistency restricted model with an unrestricted one. Again restrictions on the random effects distribution are required.
Estimation under strong or weak homogeneity and consistency in a frequentist approach is based on a generalized mixed model using marginal maximum likelihood (MML) [36] for the fixed participant-level effects as well as regression coefficients at the trial level, and restricted maximum likelihood (REML) for the variance-covariance parameters of the random effects, subject to restrictions.
3 Power analysis simulations
We pose two basic questions in this section. First, are there benefits in statistical power for examining a main effect contrast between two interventions when using participant-level data network analysis compared with aggregate data network meta-regression analysis that is based on combining summary statistics across multiple trials? Secondly, how is statistical power for contrasting moderation effects for two interventions affected when we combine participant-level data across multiple trials? Is the gain in power for moderation analysis using indirect estimates as large as that for direct estimates [17]? For both questions we examine a comparison of two interventions, B versus C, within a network of two-arm trials involving interventions A, B, and C. We consider two types of networks of trials. We call the first network an open loop because no trials compare B and C directly. In these open loop trial networks only indirect estimation of the B-C contrast is possible; see Figure 2. The second type involves trials that form a closed loop trial network with three interventions as in Figure 3; here trials directly compare interventions with each other so that both direct and indirect comparisons can be combined.
Figure 2.
A scheme of an open loop trial network with three interventions A, B, and C. The broken line indicates B and C are not tested head-to-head, though an indirect comparison is estimable by μBC = μBA – μCA.
Figure 3.
A scheme of a closed loop trial network with three Interventions A, B, and C. The solid lines indicate that any pair of interventions are tested head-to-head. For Interventions B and C, for example, there are direct μBC = μB – μC and indirect μBC = μBA – μCA estimates.
Monte Carlo simulations were conducted to investigate the added value of using IPD in the context of a network meta-analysis which involves three interventions, A, B, and C. Our task was to estimate both main effects of the comparison of B vs. C and the moderating effects of a binary covariate on the same B vs. C comparison. We simulated situations involving a continuous outcome (e.g., depression score) in analytic models with and without a two-level moderator variable at the participant level (e.g., gender) and varying numbers of trials. Some simulation conditions included trials with arms B and C (closed loop), and others did not (open loop). These simulations were designed to assess the gain in statistical power attained by using participant-level data compared with summarized trial-level data when either or both main effects and moderator effects were allowed to vary across trials. Global homogeneity and path homogeneity were assumed in this mixed-model framework. The following parameters were manipulated in the simulation: number of trials, effect sizes, distribution of moderation effects across trials, levels of trial heterogeneity and sample sizes. The number of trials of each type (AB), (AC), and (BC) was set to R = 2, 3, 4, 8; the closed loop designs included (BC) trials while the open loop designs excluded such trials. The effect sizes for both main and moderating effects were set to 0.25, 0.5, or 0.75, representing small, medium and large effects, respectively. Sample sizes were selected for each of these three effect sizes based on having 80% power to detect the main effect in a single trial.
Below we specify a model for generating the response Yrij from participant j in trial i (e.g., i = 1, . . ., 3 = I of trial types (AB), (AC), and (BC)) for the r-th replicate r = 1, . . ., R. For the main effects, we generate data according to the following model:
| (11) |
where , r = 1, . . ., R is the additional random effects for the ith trial for the rth replicate, and has one more subscript r to denote that it is repeated r times. The conditional mean mri,k for intervention k is αr + ari + βr,k + bri,k. We model the observed arm-level means for each intervention in the ith trial for the rth replicate, Ȳri,k as follows:
| (12) |
which is the same as model (11). The comparison between intervention arms, e.g., A vs. B, can be obtained by testing the contrast E[Ȳri,k] – E[Ȳri,k′] for k = A and k′ = B.
To investigate the differences between trial level and IDA under moderation, a binary covariate (gender) was used. Trial level analyses involved only the proportion of females in each trial; this proportion was set to π = 0.3, 0.5, 0.7 for trials that compared AB, AC and BC, respectively. For the moderation effect, the data were generated based on the following model:
| (13) |
where Zrij is an indicator for gender of participant j in the ith trial for the rth replicate. The values of Zrij are generated from a Bernoulli distribution with probability π. The fixed effect for gender main effect and effect modification are denoted by δr and γr,k, respectively; the random effects for the gender main effect and modification effect between intervention and gender are and , respectively. The remaining parameters were similarly defined in Model (4).
The trial-level moderator is the percent of female participants for each specific intervention arm within each trial. Thus the moderator is a continuous variable reflecting the percentage of females in each arm. However, in the participant-level analysis, the moderator is a dichotomous variable reflecting the gender of participant. The size of the aggregate dataset is twice the number of trials, each observation representing an arm-level mean of intervention within a trial. The arm-level aggregation allows us to fit a model which includes a trial effect, intervention effects, and the modification effects between interventions and gender proportion, and a mixed-effects model is specified as
| (14) |
where Z̄ri is a proportion of females in trial i at the rth replicate.
We also varied the level of variation in impact across trials from small to large [45], setting the values of σa = 0.10 and σb = 0.25, or σa = 0.25 and σb = 0.10. We also set the values of σc = σd = 0 to simplify the computation. Participant-level standard deviation is set at 1.0. Trial sample sizes were fixed based on the overall effect size. The required sample sizes to achieve at least 0.8 power for direct comparison of B versus C in a single trial were set at 250 for effect size of 0.25, 65 for effect size of 0.5, and 30 for effect size of 0.75. We used 1000 datasets for computing the statistical power for comparing B versus C under direct and indirect comparisons. Figures 2 and 3 depict the two types of comparisons of interest. The open loop network in Figure 2 allowed for only an indirect comparison of B versus C since the two interventions had not been compared head-to-head (broken line). The closed loop network in Figure 3 allowed for both indirect and direct estimates of comparison of B versus C.
3.1. Results
Based on the parameter specifications given above, we fit the proposed models using a marginal maximum likelihood approach. The simulation results for power calculations of main effects of Intervention B versus Intervention C are presented in Table 1. Power estimates for testing the main effects at the trial-level are only modestly lower than those at the participant-level for all conditions with more than one trial per type. This finding is not surprising because an analysis based on the intervention means at the trial level is close to the two-stage IPD model when the sample sizes are the same [46]. In particular, the small decline in power for trial level analyses is due to treating the within study sample variances as fixed and known, whereas the participant-level analyses pool these estimates. Also in Table 1 we found virtually identical power for both the trial-level and participant-level analyses for a main effect on the closed loop trial data. This is expected to occur because the arm-level means used in the trial-level analyses are sufficient statistics. There exist, however, measurable differences in power for the open-loop trials because of the fact that there is 50% more data for the closed loop trials, resulting in greater power in estimating individual variances.
Table 1.
Mean and standard error (SE) of estimate of power for main effects in the comparison of Intervention B against Intervention C across multiple trials when the ratio of SDtrial×treat(σb) to SDtrial(σa) is 0.4 in Model (11)
| Open Loop | Closed Loop | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Trial Level | Participant Level | Trial Level | Participant Level | ||||||
| Effect | Trials per Type | Mean | SE | Mean | SE | Mean | SE | Mean | SE |
| .25 (n = 250) | 2 | .11 | .01 | .18 | .012 | .30 | .015 | .29 | .015 |
| 3 | .41 | .015 | .59 | .015 | .75 | .014 | .75 | .014 | |
| 4 | .61 | .015 | .74 | .014 | .91 | .009 | .91 | .009 | |
| 8 | .92 | .009 | .97 | .006 | 1.0 | .001 | 1.0 | .001 | |
| .5 (n = 65) | 2 | .09 | .009 | .12 | .01 | .49 | .016 | .48 | .016 |
| 3 | .60 | .015 | .67 | .015 | .96 | .006 | .96 | .006 | |
| 4 | .83 | .012 | .88 | .01 | 1.0 | .001 | 1.0 | .002 | |
| 8 | .99 | .002 | 1.0 | .002 | 1.0 | 0 | 1.0 | 0 | |
| .75 (n = 30) | 2 | .09 | .009 | .11 | .01 | .56 | .016 | .55 | .016 |
| 3 | .67 | .015 | .73 | .014 | .98 | .004 | .98 | .004 | |
| 4 | .90 | .009 | .92 | .009 | 1.0 | 0 | 1.0 | 0 | |
| 8 | 1.0 | .001 | 1.0 | .001 | 1.0 | 0 | 1.0 | 0 | |
SD = standard deviation.
For Table 2, where the total variance is the same as in Table 1 but the trial by intervention variance is much higher than the trial variance, we find an overall decline in statistical power but more benefit from participant-level analysis compared with study-level analysis in the open loop case than we found for Table 1.
Table 2.
Mean and standard error (SE) of estimate of power for main effects in the comparison of Intervention B against Intervention C across multiple trials when the ratio of SDtrial×treat(σb) to SDtrial(σa) is 2.5
| Open Loop | Closed Loop | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Trial Level | Participant Level | Trial Level | Participant Level | ||||||
| Effect | Trials per Type | Mean | SE | Mean | SE | Mean | SE | Mean | SE |
| .25 (n = 250) | 2 | .11 | .01 | .27 | .014 | .14 | .011 | .14 | .011 |
| 3 | .23 | .013 | .50 | .016 | .27 | .014 | .27 | .014 | |
| 4 | .32 | .015 | .58 | .015 | .37 | .015 | .37 | .015 | |
| 8 | .47 | .016 | .73 | .014 | .69 | .015 | .69 | .015 | |
| .5 (n = 65) | 2 | .13 | .01 | .22 | .013 | .27 | .014 | .26 | .014 |
| 3 | .39 | .015 | .58 | .015 | .63 | .015 | .64 | .015 | |
| 4 | .55 | .016 | .72 | .014 | .82 | .012 | .82 | .012 | |
| 8 | .85 | .011 | .94 | .008 | .99 | .003 | .99 | .003 | |
| .75 (n = 30) | 2 | .11 | .01 | .17 | .012 | .37 | .015 | .37 | .015 |
| 3 | .52 | .016 | .65 | .015 | .86 | .011 | .86 | .011 | |
| 4 | .72 | .014 | .82 | .012 | .96 | .006 | .97 | .005 | |
| 8 | .95 | .007 | .98 | .004 | 1.0 | 0 | 1.0 | 0 | |
SD = standard deviation.
We also compared study-level and participant-level analyses without random effects of trial or trial by intervention. These simulations (not shown) produced identical results for study-level and participant-level analyses for both open loop and closed loop analyses, as one would expect.
We now summarize the findings on main effects, comparing study-level and participant-level main effects estimation. In terms of the utility of using participant-level data in estimating comparative effectiveness, we conclude that the only gain in power occurs when the number of trials of each type is small, there are no trials where the effect of interest (B vs. C) is directly estimable, and it is appropriate to pool variances.
Tables 3 and 4 show the calculated power of the test of moderation effects in the direct and indirect comparisons of B vs C. The results in these two tables show that the tests based on summary statistics at the trial level are very underpowered for both direct and indirect comparisons, and there is much higher power when participant-level data are used. When the number of trials of each type is increased, power increases much more rapidly for individual-level analysis, compared with that for study level. This implies that when conducting a network meta-analysis, one is almost certain to have substantially higher statistical power for detecting a moderation effect based on participant-level data compared with trial-level data. In addition, open-loop networks have somewhat lower power than closed-loop networks for the respective indirect and direct comparison of B and C.
Table 3.
Mean and standard error (SE) of estimate of power for moderation effects in the comparison of Intervention B against Intervention C across multiple trials (proportions of females: 0.3 (A vs B), 0.5 (A vs C), 0.7 (B vs C)) and the ratio of SDtrial×treat(σb) to SDtrial(σa) is 2.5
| Open Loop | Closed Loop | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Trial Level | Participant Level | Trial Level | Participant Level | ||||||
| Effect | Trials per Type | Mean | SE | Mean | SE | Mean | SE | Mean | SE |
| .25 (n = 250) | 2* | .04 | .006 | .49 | .016 | .06 | .007 | .76 | .014 |
| 3 | .10 | .009 | .29 | .014 | .58 | .015 | .64 | .015 | |
| 4 | .08 | .009 | .58 | .015 | .59 | .015 | .84 | .012 | |
| 8 | .07 | .008 | .94 | .007 | .60 | .015 | .99 | .012 | |
| .5 (n = 65) | 2* | .04 | .007 | .48 | .016 | .08 | .009 | .78 | .013 |
| 3 | .07 | .009 | .35 | .015 | .33 | .015 | .71 | .014 | |
| 4 | .08 | .009 | .62 | .015 | .35 | .015 | .90 | .009 | |
| 8 | .08 | .009 | .96 | .006 | .36 | .015 | 1.0 | 0 | |
| .75 (n = 30) | 2* | .04 | .006 | .47 | .016 | .08 | .009 | .80 | .013 |
| 3 | .05 | .007 | .33 | .015 | .17 | .012 | .69 | .015 | |
| 4 | .07 | .008 | .60 | .015 | .24 | .013 | .92 | .009 | |
| 8 | .09 | .009 | .96 | .007 | .32 | .015 | 1.0 | 0 | |
Calculated separately with fixed-effects assumptions.
SD = standard deviation.
Table 4.
Mean and standard error (SE) of estimate of power for moderation effects in the comparison of Intervention B against Intervention C across multiple trials (proportions of females: 0.3 (A vs B), 0.5 (A vs C), 0.7 (B vs C)) and the ratio of SDtrial×treat(σb) to SDtrial(σa) is 0.4
| Open Loop | Closed Loop | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Trial Level | Participant Level | Trial Level | Participant Level | ||||||
| Effect | Trials per Type | Mean | SE | Mean | SE | Mean | SE | Mean | SE |
| .25 (n = 250) | 2* | .04 | .006 | .49 | .016 | .06 | .007 | .76 | .014 |
| 3 | .03 | .006 | .30 | .015 | .21 | .013 | .70 | .015 | |
| 4 | .06 | .008 | .59 | .015 | .25 | .014 | .91 | .009 | |
| 8 | .07 | .008 | .95 | .007 | .27 | .014 | 1.0 | 0 | |
| .5 (n = 65) | 2* | .04 | .007 | .48 | .016 | .08 | .009 | .78 | .013 |
| 3 | .03 | .005 | .36 | .015 | .10 | .009 | .73 | .014 | |
| 4 | .05 | .007 | .63 | .015 | .13 | .01 | .93 | .008 | |
| 8 | .07 | .008 | .97 | .006 | .20 | .013 | 1.0 | 0 | |
| .75 (n = 30) | 2* | .04 | .006 | .47 | .016 | .08 | .009 | .80 | .013 |
| 3 | .04 | .006 | .34 | .015 | .08 | .009 | .72 | .014 | |
| 4 | .03 | .005 | .60 | .015 | .13 | .011 | .93 | .008 | |
| 8 | .06 | .007 | .96 | .006 | .24 | .014 | 1.0 | 0 | |
Calculated separately with fixed-effects assumptions.
SD = standard deviation.
4 Application to two simultaneous, parallel trials
In this section we present an example of network meta-analysis testing moderation of intervention effects using participant-level data. The data come from a large preventive field trial having two active interventions and one control. Interventions were assigned to first grade classrooms within schools in an imbalanced, incomplete block design where the two active interventions were never tested against one another. Each school can be considered a separate sub-trial as schools were randomly assigned to test classroom intervention B – the Good Behavior Game – against a control (A) or intervention C – Mastery Learning – against a control (A). First grade classes within schools were balanced on child's kindergarten grades and behavior prior to classes being randomly assigned to intervention within each school so that direct comparison of each intervention could be made against the control. Separate intervention teams provided training and supervision to teachers for both the Good Behavior Game and Mastery Learning. We chose not to allow two active interventions to be administered in classes within the same school as this would double the number of times intervention trainers would need to travel to that school [17]. In addition, having only one active intervention in a school reduces the possibility of leakage of intervention effects from one class to another.
Because there was no direct comparison of the two active interventions in the same school, this can be viewed as an open loop network where each school can be considered as if it were a separate cluster-randomized trial with classroom as the unit of randomization within school (see Figure 4). Random assignment of schools to the two trial designs, either A-B or A-C, allows us to treat the pool of schools as a collection of highly similar trials, thus permitting us to apply the methods for participant-level network meta-analysis. Interest here is on the indirect comparison of the two active interventions’ effects for the entire population of schools as well as testing whether these indirect effects were moderated by gender. Also of interest is the comparison of controls across schools as a test of partial homogeneity of this control; differences in these controls by type of design would suggest intervention contamination or leakage, which would complicate any findings. Network pathways allowing indirect comparisons of the Good Behavior Game and Mastery Learning all have vertical paths through the control classrooms. We have no direct comparisons of the two active interventions, so we cannot test consistency. Because of classrooms in the same school having the same intervention, it is possible to pool results for these similar classrooms to estimate the standard error at this level. We can use this to test for partial homogeneity of the contrast between the two active interventions, as well as assess their overall difference. If the test of weak heterogeneity indicated that control groups differed significantly, this would call into question inferences based on indirect comparisons.
Figure 4.
A diagram of network with three interventions labeled GBG (Good Behavior Game), ML (Mastery Learning), and Control.
More specifically, the Baltimore Prevention Trial (BPT) [16, 47] was a randomized controlled trial with two preventive interventions tested in parallel. The Good Behavior Game (GBG) is a group-contingent behavioral intervention aimed at reducing aggressive or disruptive behavior [48]. The second intervention, Mastery Learning (ML) is curriculum based and was aimed at improving reading achievement [49]. The study involved five large urban areas within Baltimore City, each having three or four similar elementary schools. The total number of students in the study was 1196. Assignment of school, and therefore of intervention trial type (GBG vs control, ML vs control) was equally balanced across these urban areas. The schools were randomly divided into 6 schools for testing GBG and 7 schools for ML. In the 13 schools with an active intervention, one first-grade classroom was randomly assigned to receive the control and the remaining one or two classes were given that particular intervention. A total of 8 GBG classes within the 6 GBG-testing schools received GBG, and 6 classrooms served as controls. Similarly, in the seven schools where ML was being tested, 9 classrooms were randomly selected to serve as ML intervention classrooms and 7 classrooms served as controls. Because GBG and ML were not compared head-to-head, our interest is to compare GBG and ML indirectly via an open-loop network meta-analysis method discussed in Section 2. For this paper we use as an outcome measure the proportion of 10-second time intervals that the child was observed to be off-task towards the end of first grade, obtained through direct observation of children during times where they were reading alone at their desks. Because of the relatively large number of observations available at the individual level (e.g., 40 minutes of 10-second observations), this estimated proportion is transformed with an arcsine square-root transformation [50] to stabilize variances and achieve approximate normality. Reduction of off-task behavior was a direct target of GBG and an indirect target of ML. Since some students were absent on some days during observation, we assumed missing at random for valid analysis using only observed data.
Below we present a multilevel model that is then used to make a partial test of weak and strong homogeneity. The results of this test are then used to conduct an appropriate analysis to compare both the main effect as well as a moderator effect of gender on the comparison of GBG and ML.
4.1. Multilevel model
We first fit a four-level mixed effects model with fixed intervention and random effects at the urban area, school, classroom and participant levels. Let Yrisj be an observation on off-task behavior from the rth urban area, ith school (or trial), in the sth class, and from the jth participant, where r = 1, . . ., R, i = 1, . . ., Ir, s = 1, . . ., Fri, and j = 1, . . ., nris. Let Xrisj represent a vector of baseline off-task behavior and gender (1 for male, 0 for female), and Zrisj is an indicator for gender. Following the same notational rule of Model (1), a multilevel model is given as
| (15) |
where the parameters have the same definitions as (1) with the exception that cri,k is now a fixed effect; the random effects are distributed as
and are assumed to be independent. Note that this model assumes that the variance for each intervention across schools, does not depend on the intervention.
In this example, neither of the assumptions of weak homogeneity for GBG versus its control and ML versus its control, can be tested directly because variation in these values across trials is confounded with a random effect that is used to capture variation in intervention differences across schools. This pooled variation at the school level, however, is quite small, , SE = 0.0123, suggesting that any departure from strong homogeneity is relatively small. We can conduct tests of weak homogeneity as well. The first of these tests whether the school level variation in GBG versus its control is the same as that for ML versus its control. If these variances differ, it may indicate one intervention in this parallel trial shows more variation in impact than the other. One possible cause for this could be some variation in leakage of an active intervention from one class into a control class in the same school, a potential that we have investigated elsewhere [51]. For this example the ratio of between school variances for ML and GBG effects relative to their own controls is F4,4 = .0240/.0027 = 8.89, p = .0289, where the number of degrees of freedom, 4, is based on 5 school error contrasts per intervention effect nested within 5 urban areas. This shows that there is more variation between ML schools as compared with those schools under the GBG intervention, suggesting greater leakage in ML schools. Another potential explanation is that greater variation in ML classrooms occurred compared to that for GBG, but we found no evidence for this in the data.
We have also tested for homogeneity of controls in schools assigned to test the Good Behavior Game versus controls assigned to test Mastery Learning. It is well known that tests of strong homogeneity where the variance estimate is based on a small number of trials (i.e., schools here) are often underpowered. Thus we consider an alternative test that is based on means rather than variances. Using our multilevel model above, this estimate of the mean difference between GBG control and ML control is 0.138, se = 0.090, df = 16.4, p = 0.142. Thus there is no evidence to reject homogeneity in the controls. This finding of equivalent controls allows us to consider the indirect comparison of GBG vs. ML.
4.2. Model results
Tables 5 and 6 present results of a multilevel model based on an IPD network meta-analysis approach for comparing the moderated effect of gender on the comparison of GBG against ML. Since the similarity of the GBG and ML controls was tested above, and it was found that there was not any significant difference between the controls, we have reasonable con dence that an indirect test of differences of differences between these two trials will provide useful inferences about the impact of the Good Behavior Game versus Mastery Learning.
Table 5.
Specific contrasts of levels of interventions (Good Behavior Game (GBG), Mastery Learning (ML) and Control) in network meta-analysis by off-task behavior occurrences after adjusting for baseline off-task behavior
| Effect | Estimate | Std Error | DF | Pvalue |
|---|---|---|---|---|
| Baseline off-task | .123 | .046 | 388 | .008 |
| Gender (male) | .088 | .033 | 379 | .004 |
| Intervention (contrasts) | ||||
| GBG vs. ML | −.239 | .084 | 8.96 | .020 |
| GBG vs. Control | −.287 | .076 | 11.6 | .003 |
| ML vs. Control | −.047 | .075 | 11.1 | .545 |
| Random effects | Variance (ICC) | |
|---|---|---|
| Urban | .009 (.080) | .011 |
| School | .004 (.037) | .013 |
| Classroom | .011 (.100) | .012 |
ICC = intra-class correlation coefficient.
Table 6.
Gender as effect modifier of interventions (Good Behavior Game (GBG), Mastery Learning (ML) and Control) in a network meta-analysis
| Effect | Estimate | Std Error | DF | Pvalue |
|---|---|---|---|---|
| Baseline off-task | .124 | .046 | 386 | .007 |
| Gender (male) | .103 | .048 | 377 | .031 |
| GBG vs. Control | −.247 | .086 | 18.7 | .003 |
| ML vs. Control | −.055 | .083 | 16.2 | .519 |
| GBG*Gender (male) | −.074 | .074 | 376 | .32 |
| ML*Gender (male) | .017 | .072 | 376 | .813 |
| Random effects | Variance (ICC) | |
|---|---|---|
| Urban | .009 (.080) | .011 |
| School | .003 (.031) | .013 |
| Classroom | .012 (.105) | .012 |
ICC = intra-class correlation coefficient.
After establishing the similarity between the two controls, we combined the effects for controls of GBG and ML, effectively allowing us to use them as a single control in estimating the indirect effect of GBG versus ML. As is depicted in Table 5, the estimated indirect effect of GBG versus ML is –.239 and a standard error of .084, providing strong evidence that GBG is more effective in reducing classroom off-task behavior compared with the ML intervention. We did not find any significant effect modifications involving gender (see Table 6).
5 Discussion
In this paper we examined how much power is needed to detect main and moderator effects in pairwise meta-analysis and network meta-analysis. We found that power is shaped by three factors: inclusion of both direct and indirect effects using network meta-analytic models, inclusion of moderator variables, and use of participant-level data. The findings indicate that the power of detecting effects depends on all three factors. Synthesis analyses have greater power when direct and indirect effects are combined, as compared with analyses that only include indirect effects. This holds for both main effect and moderator analyses, and occurs when analyses involve either summary (i.e., aggregate data meta-analytic) or participant-level data. Trials with participant-level data have a far greater statistical power for detecting moderator effects regardless of whether we are testing direct or indirect effects. Use of meta-regression with arm-level or trial-level summary data results in much lower power: under some conditions the ratio is on the order of 12:1 in favor of participant-level data. These power differences will also be in uenced by other factors including actual effect sizes, the number of trials, the number of participants per trial, and the amount of variability in the aggregated moderator across trials. In our example the empirically based power estimates are low for both methods, with a ratio favoring moderated IDA of only 1.5, largely because of the weak and nonsignificant moderator effects found here.
For comparative effectiveness using network meta-analysis, assessing homogeneity and consistency assumptions is very important. We used these assumptions in both main effects and moderation effects under mixed-effects models, separately for IPD and study-level analysis. In the case of main effects, trial-level and participant-level analyses of networks of trials give similar results. This is expected since the summary values are sufficient statistics [46].
The situation is quite different for testing participant-level moderator effects using participant-level data versus meta-regression that uses trial-averaged scores to test for moderation. Based on our simulations we urge extreme caution in interpreting trial-level moderation analysis at the participant level. We note that Donegan et al. [7] point out that IPD models can be specified such that within-trial moderation and between-trial moderation are forced to be equal. The model we present here does allow for tests of this equivalence across participant and trial level. They also note that this equivalence can be extended to other synthesis projects that integrate aggregate data and participant-level data. While this combining of IPD and aggregate data where some trials have IPD only and the remaining trials have only AD [1, 7] provides a valuable strategy for synthesis, we believe testing homogeneity in such hybrid pairwise meta-analysis and network meta-analysis warrants further study.
Our example included gender as a binary moderator, but the methods described here can also include continuous moderator variables. We have yet to investigate how these methods perform on two different moderator analyses, involving latent or unobserved measures at baseline. In particular, with multiple outcome measures we can analyze the data using growth models, which would summarize participant-level growth into a random or latent intercept term and one or more random or latent slope parameters. The moderating effect of interventions as a function of baseline then involves a effect modification term between intervention status and the latent intercept, as they predict changes in a latent slope over time. General methods for this type of analysis have been developed [52, 53], and can be readily extended to the case of multiple trials using multilevel growth models. Further work is necessary to investigate moderation of comparative effectiveness that may occur across interventions. In our example, the Good Behavior Game was hypothesized to affect aggressive/disruptive and off-task behavior in the classroom, and through the reduction of these disruptions to increase learning and comprehension. Mastery learning was designed to do the opposite, focusing first on reading improvement and its consequent outcomes. It is not surprising then that we concluded that the Good Behavior Game was superior to Mastery Learning in reducing off-task behavior. We also found no evidence that this differential effect of these two interventions differed by gender.
There are further approaches that deserve continued investigation. The presentation focuses on participant-level covariates, but we recognize that useful synthesis projects often examine arm-level and trial-level measured covariates. We have only examined unmeasured trial-level covariates in this paper. We employed a frequentist approach to modeling, but these estimation methods may be taxed as models grow more complex. In those instances it will likely be pro table to explore Bayesian methods [54]. In the example, we introduced a type of potential outcomes framework that could be used to represent outcomes for a participant on interventions not even tested in that particular trial. We believe this is a fruitful approach for future work in obtaining inferences generalized over the collection of trials; we chose not to introduce this framework at the beginning of this paper as it would have made the notation unwieldy. Finally, we focus on determining the power of detecting moderator effects as functions of network types, IPD or trial-level summaries. It is a topic of further research to investigate how to improve the precision of estimates.
In summary, this paper presented a formalized conceptualization of and methodology for investigating homogeneity and consistency that is quite general, allowing these terms to be examined in the context of an arbitrary set of trials whose participant-level data are used for data synthesis. Definitions of weak and strong homogeneity and consistency were introduced in the context of a generalized mixed model, and we applied these terms to both contrasts between interventions as well as single interventions themselves. Defining these terms for single interventions allows us to include non-randomized observational studies with randomized trials. In particular, a similar study of participants not exposed to an intervention can often serve as an external control group [55]; likewise when a program is scaled up and delivered to everyone as in an implementation study [56, 57], such data can potentially be combined with those in a trial who were randomly assigned to that intervention.
Supplementary Material
Acknowledgements
We would like to thank the editor, associate editor and two anonymous reviewers for their critiques that helped to improve the paper. Hendricks Brown, George Howe and Getachew Dagne were supported by the National Institute of Mental Health Grant No. R01MH040859. Lei Liu was supported by AHRQ R01HS020263.
Footnotes
From a counterfactual perspective, Vanderweele [37] distinguishes effect modification from interaction. In effect modification some variables condition the effect of the intervention, i.e. some other manipulated variables. VanderWeele reserves the term interaction for cases where the variable is itself an intervention with causal impact, such that the effects of combining the two interventions are different from those of the two interventions considered separately. Many social scientists do not make this distinction, using the term interaction to reference both situations. We follow VanderWeele's usage here, given that most trials research has focused on moderating variables such as gender or ethnicity rather than on combining sets of different interventions.
References
- 1.Jansen JP. Network meta-analysis of individual and aggregate level data. Research Synthesis Methods. 2012;3(2):177–190. doi: 10.1002/jrsm.1048. [DOI] [PubMed] [Google Scholar]
- 2.Saramago P, Sutton AJ, Cooper NJ, Manca A. Mixed treatment comparisons using aggregate and individual participant level data. Statistics in Medicine. 2012;31:3516–3536. doi: 10.1002/sim.5442. [DOI] [PubMed] [Google Scholar]
- 3.Lumley T. Network meta-analysis for indirect treatment comparisons. Statistics in Medicine. 2002;21:2313–2324. doi: 10.1002/sim.1201. [DOI] [PubMed] [Google Scholar]
- 4.Lu G, Ades AE. Combination of direct and indirect evidence in mixed treatment comparisons. Statistics in Medicine. 2004;23:3105–3124. doi: 10.1002/sim.1875. [DOI] [PubMed] [Google Scholar]
- 5.Caldwell DM, Ades AE, Higgins JPT. Simultaneous comparison of multiple treatments: combining direct and indirect evidence. BMJ. 2005;331:897–900. doi: 10.1136/bmj.331.7521.897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Song F, Loke YK, Walsh T, Glenny AM, Eastwood AJ, Altman DG. Methodological problems in the use of indirect comparisons for evaluating healthcare interventions: survey of published systematic reviews. BMJ. 2009;338:b1147. doi: 10.1136/bmj.b1147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Donegan S, Williamson P, D'Alessandro U, Garner P, Smith CT. Combining individual patient data and aggregate data in mixed treatment comparison meta-Analysis: Individual patient data may be beneficial if only for a subset of trials. Statistics in Medicine. 2013;32:914–930. doi: 10.1002/sim.5584. [DOI] [PubMed] [Google Scholar]
- 8.Ravva P, Karlsson MO, French JL. A linearization approach for the model-based analysis of combined aggregate and individual patient data. Statistics in Medicine. 2014;33(9):1460–1476. doi: 10.1002/sim.6045. [DOI] [PubMed] [Google Scholar]
- 9.Perrino T, Coatsworth JD, Briones E, Pantin H, Szapocznik J. Initial engagement in parent-centered preventive interventions: A family systems perspective. The Journal of Primary Prevention. 2001;22:21–44. [Google Scholar]
- 10.Berkey CS, Hoaglin DC, Mosteller F, Colditz GA. A random-effects regression model for meta-analysis. Statistics in Medicine. 1995;14(4):395–411. doi: 10.1002/sim.4780140406. [DOI] [PubMed] [Google Scholar]
- 11.Greenwood CMT, Midgley JP, Matthews AG, Logan AG. Statistical issues in a metaregression analysis of randomized trials: Impact on the dietary sodium intake and blood pressure relationship. Biometrics. 1999;55:630–636. doi: 10.1111/j.0006-341x.1999.00630.x. [DOI] [PubMed] [Google Scholar]
- 12.Lau J, Ioannidis JP, Schmid CH. Summing up evidence: one answer is not always enough. Lancet. 1998;351:123–127. doi: 10.1016/S0140-6736(97)08468-7. [DOI] [PubMed] [Google Scholar]
- 13.Hedges LV, Pigott TD. The power of statistical tests for moderators in meta-analysis. Psychological Methods. 2004;9:426–445. doi: 10.1037/1082-989X.9.4.426. [DOI] [PubMed] [Google Scholar]
- 14.Morgenstern H. Uses of ecologic analysis in epidemiologic research. American Journal of Public Health. 1982;72:1336–1344. doi: 10.2105/ajph.72.12.1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Berlin JA, Santanna J, Schmid CH, Szczech LA, Feldman HI. Individual patient–versus group–level data meta–regressions for the investigation of treatment effect modifiers: ecological bias rears its ugly head. Statistics in Medicine. 2002;21(3):371–387. doi: 10.1002/sim.1023. [DOI] [PubMed] [Google Scholar]
- 16.Brown CH, Wang W, Kellam SG, Muthén BO, Petras H, Toyinbo P, Poduska J, Ialongo N, Wyman PA, Chamberlain P, Sloboda Z, MacKinnon DP. Methods for testing theory and evaluating impact in randomized field trials: Intent-to-treat analyses for integrating the perspectives of person, place, and time. Drug and Alcohol Dependence. 2008;S95:S74–S104. doi: 10.1016/j.drugalcdep.2007.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brown CH, Sloboda Z, Faggiano F Teasdale B, Keller F, Burkhart G, Vigna-Taglianti F, Howe G, Masyn K, Wang W, Muthén B, Stephens P, Grey S, Perrino T. Prevention Science and Methodology Group. Methods for synthesizing findings on moderation effects across multiple randomized trials. Prevention Science. 2013;14(2):144–156. doi: 10.1007/s11121-011-0207-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stewart LA, Clarke MJ. Practical methodology of meta-analyses (overviews) using updated individual-patient data. Statistics in Medicine. 1995;14:2057–2079. doi: 10.1002/sim.4780141902. [DOI] [PubMed] [Google Scholar]
- 19.Higgins JP, Whitehead A, Turner RM, Omar RZ, Thompson SG. Meta-analysis of continuous outcome data from individual patients. Statistics in Medicine. 2001;20:2219–41. doi: 10.1002/sim.918. [DOI] [PubMed] [Google Scholar]
- 20.Rosenbaum PR. Observational Studies. 2nd edn. Springer-Verlag; New York: 2002. [Google Scholar]
- 21.Bradshaw CP, Zmuda JH, Kellam SG, Ialongo NS. Longitudinal impact of two universal preventive interventions in first grade on educational outcomes in high school. Journal of Educational Psychology. 2009;101(4):926–937. doi: 10.1037/a0016586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gibbons RD, Hur K, Brown CH, Davis JM, Mann JJ. Benefits from Antidepressants: Synthesis of 6-Week Patient-Level Outcomes from Double-Blind Placebo Controlled Randomized Trials of Fluoxetine and Venlafaxine. Archives of General Psychiatry. 2012;69(6):572–579. doi: 10.1001/archgenpsychiatry.2011.2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gibbons RD, Brown CH, Hur K, Davis JM, Mann JJ. Suicidal Thoughts and Behavior with Antidepressant Treatment: Reanalysis of the Randomized Placebo-Controlled Studies of Fluoxetine and Venlafaxine. Archives of General Psychiatry. 2012;69(6):580–587. doi: 10.1001/archgenpsychiatry.2011.2048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Curran PJ, Hussong AM. Integrative data analysis: The simultaneous analysis of multiple data sets. Psychological. Methods. 2009;14:81–100. doi: 10.1037/a0015914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bauer DJ, Hussong AM. Psychometric approaches for developing commensurate measures across independent studies: Traditional and new models. Psychological Methods. 2009;14:101–125. doi: 10.1037/a0015583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Siddique J, Chung JY, Brown CH, Miranda J. Comparative effectiveness of medication versus cognitive-behavioral therapy in a randomized controlled trial of low-income young minority women with depression. Journal of Consulting and Clinical Psychology. 2012;80(6):995–1006. doi: 10.1037/a0030452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lambert PC, Sutton A, Abrams KR, Jones DR. A comparison of summary patient-level covariates in mega-regression with individual patient data meta-analysis. Journal of Clinical Epidemiology. 2002;55:86–94. doi: 10.1016/s0895-4356(01)00414-0. [DOI] [PubMed] [Google Scholar]
- 28.Tudur SC, Williamson PR, Marson AG. Investigating heterogeneity in an individual patient data meta-analysis of time to event outcomes. Statistics in Medicine. 2005;24:1307–1319. doi: 10.1002/sim.2050. [DOI] [PubMed] [Google Scholar]
- 29.Simmonds MC, Higgins JPT. Covariate heterogeneity in meta-analysis: Criteria for deciding between meta-regression and individual patient data. Statistics in Medicine. 2007;26:2982–2999. doi: 10.1002/sim.2768. [DOI] [PubMed] [Google Scholar]
- 30.Jansen JP, Trikalinos T, Cappelleri JC, Daw J, Andes S, Eldessouki R, Salanti G. Indirect treatment comparison/network meta-analysis study questionnaire to assess relevance and credibility to inform health care decision making: An ISPOR-AMCPNPC Good Practice Task Force Report. Value in Health. 2014;17:157–173. doi: 10.1016/j.jval.2014.01.004. [DOI] [PubMed] [Google Scholar]
- 31.Brown CH, Liao J. Principles for designing randomized preventive trials in mental health: An emerging developmental epidemiologic paradigm. American Journal of Community Psychology. 1999;27:677–714. doi: 10.1023/A:1022142021441. [DOI] [PubMed] [Google Scholar]
- 32.Brown CH, Indurkhya A, Kellam SG. Power calculations for data missing by design with application to a follow-up study of exposure and attention. Journal of the American Statistics Association. 2000;95:383–395. [Google Scholar]
- 33.Hoaglin DC, Hawkins N, Jansen JP, Scott DA, Itzler R, Cappelleri JC, Boersma C, Thompson D, Larholt KM, Diaz M, Barrett A. Conducting indirect-treatment-comparison and network-meta-analysis studies: Report of the ISPOR task force on indirect treatment comparisons good research practices|Part 2. Value In Health. 2011;14:429–437. doi: 10.1016/j.jval.2011.01.011. [DOI] [PubMed] [Google Scholar]
- 34.Perrino T, Howe G, Sperling A, Beardslee A, Sandler I, Shern D, Pantin H, Kaupert S, Cano N, Cruden G, Bandiera F, Brown CH. Advancing science through collaborative data sharing and synthesis. Perspectives on Psychological Science. 2013;8(4):433–444. doi: 10.1177/1745691613491579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hofer SM, Piccinin AM. Integrative data analysis through coordination of measurement and analysis protocol across independent longitudinal studies. Psychological Methods. 2009;14(2):150–164. doi: 10.1037/a0015566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.McCullagh P, Nelder JA. Generalized Linear Models. 2nd ed. Chapman & Hall; New York: 1989. [Google Scholar]
- 37.VanderWeele TJ. On the distinction between interaction and effect modification. Epidemiology. 2009;20(6):863–871. doi: 10.1097/EDE.0b013e3181ba333c. [DOI] [PubMed] [Google Scholar]
- 38.Brown CH, Wang W, Sandler I. Examining how context changes intervention impact: The use of effect sizes in multilevel mixture meta-analysis. Child Develop Perspectives. 2008;2:198–205. doi: 10.1111/j.1750-8606.2008.00065.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bhaumik DK, Amatya A, Normand SL, Greenhouse J, Kaizer E, Neelon B, Gibbons RD. Meta-Analysis of Rare Binary Adverse Event Data. Journal of the American Statistical Association. 2012;107:555–567. doi: 10.1080/01621459.2012.664484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Becker BJ, Wu MJ. The Synthesis of regression slopes in meta-analysis. Statistical Science. 2007;22:414–429. [Google Scholar]
- 41.Salanti G, Higgins JPT, Ades AE, Ioannidis JPA. Evaluation of networks of randomized trials. Statistical Methods in Medical Research. 2008;17:279–301. doi: 10.1177/0962280207080643. [DOI] [PubMed] [Google Scholar]
- 42.Fisher DJ, Copas AJ, Tierney JF, Parmar MKB. A critical review of methods for the assessment of patient-level interactions in individual participant data meta-analysis of randomized trials, and guidance for practitioners. Journal of Clinical Epidemiology. 2011;64:949–967. doi: 10.1016/j.jclinepi.2010.11.016. [DOI] [PubMed] [Google Scholar]
- 43.Lu G, Ades AE. Assessing evidence inconsistency in mixed treatment comparisons. Journal of the American Statistical Association. 2006;101:447–459. [Google Scholar]
- 44.Cooper H, Patall EA. The Relative Benefits of Meta-Analysis Conducted With Individual-Participant Data Versus Aggregated Data. Psychological Methods. 2009;14:165–176. doi: 10.1037/a0015565. [DOI] [PubMed] [Google Scholar]
- 45.Higgins JPT, Thompson SG, Deeks JJ, Altman DG. Measuring inconsistency in meta-analyses. British Medical Journal. 2003;327:557–560. doi: 10.1136/bmj.327.7414.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Olkin I, Sampson A. Comparison of meta-analysis versus analysis of variance of individual-patient data. Biometrics. 1998;54:317–322. [PubMed] [Google Scholar]
- 47.Kellam SG, Brown CH, Poduska JM, Ialongo NS, Wang W, Toyinbo P, Petras H, Ford C, Windham A, Wilcox HC. Effects of a universal classroom behavior management program in first and second grades on young adult behavioral, psychiatric, and social outcomes. Drug and Alcohol Dependence. 2008;95(Suppl 1):S5–S28. doi: 10.1016/j.drugalcdep.2008.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Barrish HH, Saunders M, Wolf MM. Good behavior game: Effects of individual contingencies for group consequences on disruptive behavior in a classroom. Journal of Applied Behavior Analysis. 1969;2:119–124. doi: 10.1901/jaba.1969.2-119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Guskey TR, Gates S. Synthesis of research on the effects of mastery learning in elementary and secondary classrooms. Educational Leadership. 1986;43:73–80. [Google Scholar]
- 50.Zar JH. Biostatistical Analysis. Fourth edition. Prentice Hall; New Jersey: 1998. [Google Scholar]
- 51.Brown CH, Kellam SG, Ialongo N, Poduska J, Ford C. Prevention of aggressive behavior through middle school using a rst grade classroom-based intervention. In: Tsuang MT, Lyons MJ, Stone WS, editors. Recognition and Prevention of Major Mental and Substance Abuse Disorders (American Psychopathological Association Series) American Psychiatric Publishing, Inc; Arlington, VA: 2007. pp. 347–370. [Google Scholar]
- 52.Muthén BO, Brown CH, Leuchter A, Hunter A. General approaches to analysis of course: Applying growth mixture modeling to randomized trials of depression medication. In: Shrout PE, editor. Causality and Psychopathology: Finding the Determinants of Disorders and their Cures. American Psychiatric Publishing; Washington, DC: 2011. pp. 159–178. [Google Scholar]
- 53.Muthén BO, Brown CH, Masyn K, Jo B, Khoo ST, Yang CC, Wang CP, Kellam SG, Carlin JB, Liao J. General growth mixture modeling for randomized preventive interventions. Biostatistics. 2002;3:459–475. doi: 10.1093/biostatistics/3.4.459. [DOI] [PubMed] [Google Scholar]
- 54.Gelman A, Carlin J, Stern H, Dunson D, Vehtari A, Rubin D. Bayesian Data Analysis. 3rd ed. Chapman and Hall/CRC; New York: 2013. [Google Scholar]
- 55.Stuart EA, Marcus SM, Horvitz-Lennon MV, Gibbons RD, Normand S-LT. Using non-experimental data to estimate treatment effects. Psychiatric Annals. 2009;39(7):719–728. doi: 10.3928/00485713-20090625-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Landsverk J, Brown CH, Chamberlain P, Palinkas L, Horwitz SM, Ogihara M. Design and Analysis in Dissemination and Implementation Research. In: Brownson R, Colditz G, Proctor E, editors. Dissemination and Implementation Research in Health: Translating Science to Practice. Oxford University Press; 2012. [Google Scholar]
- 57.Brown CH, Chamberlain P, Saldana L, Wang W, Padgett C, Cruden G. Evaluation of two implementation strategies in fifty-one counties in two states: Results of a cluster randomized implementation trial. Implementation Science. 2014;9:134. doi: 10.1186/s13012-014-0134-8. doi:10.1186/s13012-014-0134-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.