How much training data for facial action unit detection?

Abstract

By systematically varying the number of subjects and the number of frames per subject, we explored the influence of training set size on appearance and shape-based approaches to facial action unit (AU) detection. Digital video and expert coding of spontaneous facial activity from 80 subjects (over 350,000 frames) were used to train and test support vector machine classifiers. Appearance features were shape-normalized SIFT descriptors and shape features were 66 facial landmarks. Ten-fold cross-validation was used in all evaluations. Number of subjects and number of frames per subject differentially affected appearance and shape-based classifiers. For appearance features, which are high-dimensional, increasing the number of training subjects from 8 to 64 incrementally improved performance, regardless of the number of frames taken from each subject (ranging from 450 through 3600). In contrast, for shape features, increases in the number of training subjects and frames were associated with mixed results. In summary, maximal performance was attained using appearance features from large numbers of subjects with as few as 450 frames per subject. These findings suggest that variation in the number of subjects rather than number of frames per subject yields most efficient performance.

I. Introduction

The face is an important avenue of emotional expression and social communication [10, 15]. Recent studies of facial expression have revealed striking insights into the psychology of affective disorders [17], addiction [18], and intergroup relations [12], among other topics. Numerous applications for technologies capable of analyzing facial expressions also exist: drowsy-driver detection in smart cars [11], smile detection in consumer cameras [6], and emotional response analysis in marketing [25, 34] are just some possibilities.

Given the time-consuming nature of manual facial expression coding and the alluring possibilities of the aforementioned applications, recent research has pursued computerized systems capable of automatically analyzing facial expressions. The predominant approach adopted by these researchers has been to locate the face and facial features in an image, derive a feature representation of the face, and then classify the presence or absence of a facial expression in that image using supervised learning algorithms.

The majority of previous research has focused on developing and adapting techniques for feature representation and classification [for reviews, see 2, 5, 36, 40]. Facial feature representations tend to fall into one of two categories: shape-based approaches focus on the deformation of geometric meshes anchored to facial landmark points (e.g., the mouth and eye corners), while appearance-based approaches focus on changes in facial texture (e.g., wrinkles and bulges). Classification techniques have included supervised learning algorithms such as neural networks [35], support vector machines [24], and hidden Markov models [37].

Conversely, very few studies have explored techniques for building training sets for supervised learning. In particular, most researchers seem to ignore the question of how much data to include in their training sets. However, several studies from related fields suggest that training set size may have important consequences. In a study on face detection, Osuna et al. [27] found that larger training sets required more time and iterations to converge and produced more complex models (i.e., more support vectors) than smaller training sets. In a study on object detection, Zhu et al. [42] found the counter-intuitive result that larger training sets sometimes led to worse classification performance than smaller training sets. Research is needed to explore these issues within automated facial expression analysis.

A great amount of effort has also gone into the creation of public facial expression databases. Examples include the CK+ database [23], the MMI database [28], the BINED database [32], and the BP4D-Spontaneous database [41]. Although the collection and labeling of a high quality database is highly resource-intensive, such efforts are necessary for the advancement of the field because they enable techniques to be compared using the same data.

While the number of subjects in some of these databases has been relatively large, no databases have included both a large number of subjects and large number of training frames per subject. In part for this reason, it remains unknown how large databases should be. Conventional wisdom suggests that bigger is always better, but the aforementioned object detection study [42] raises doubt about this conventional wisdom. It is thus important to quantify the effects of training set size on the performance of automated facial expression analysis systems. For anyone involved in the training of classifiers or the collection of facial expression data, it would be useful to know how much data is required for the training of an automated system and at what point the inclusion of additional training data will yield diminishing returns or even counter-productive results. Databases that are limited or extreme in size may be inadequate to evaluate classifier performance. Without knowing how much data is optimal, we have no way to gauge whether we need better features and classifiers or simply better training sets.

The current study explores these questions by varying the amount of training data fed to automated facial expression analysis systems in two ways. First, we varied the number of subjects in the training set. Second, we varied the number of training frames per subject. Digital video and expert coding of spontaneous facial activity from 80 subjects (over 350,000 frames) was used to train and test support vector machine classifiers. Two types of facial feature representations were compared: shape-based features and appearance-based features. The goal was to detect twelve distinct facial actions from the Facial Action Coding System (FACS) [9]. After presenting our methods and results, we offer recommendations for future data collections and for the selection of features in completed data collections.

Notations: Vectors (a) and matrices (A) are denoted by bold letters. B = [A₁; …; A_K] ∈ ℝ^{(d₁+…+d_K) × N} denotes the concatenation of matrices A_k ∈ ℝ^{d_k × N}.

II. Methods

A. Subjects

The current study used digital video from 80 subjects (53% male, 85% white, mean age 22.2 years) who were participating in a larger study on the impact of alcohol on group formation processes [30]. The video was collected to investigate social behavior and the influence of alcohol; it was not collected for the purpose of automated analysis. The subjects were randomly assigned to groups of three unacquainted subjects. Whenever possible, all three subjects in a group were analyzed; however, 14 groups contributed fewer than three subjects due to excessive occlusion from hair or head wear, being out of frame of the camera, or chewing gum. Subjects were randomly assigned to drink isovolumic alcoholic beverages (n=31), placebo beverages (n=21), or nonalcoholic control beverages (n=28); all subjects in a group drank the same type of beverage.

B. Setting and Equipment

All subjects were previously unacquainted. They first met only after entering the observation room where they were seated equidistant from each other around a circular table. We focus on a portion of the 36-minute unstructured observation period in which subjects became acquainted with each other (mean duration 2.69 minutes). The laboratory included a custom-designed video control system that permitted synchronized video output for each subject, as well as an overhead shot of the group (Figure 1). The individual view of each subject was used in this report. The video data collected by each camera had a standard frame rate of 29.97 frames per second and a resolution of 640 × 480 pixels.

Fig. 1.

Example of the overhead and individual camera views

C. Manual FACS Coding

The Facial Action Coding System (FACS) [8, 9] is an anatomically-based system for measuring nearly all visually-discernible facial movement. FACS describes facial activities in terms of unique action units (AUs), which correspond to the contraction of one or more facial muscles. FACS is recognized as the most comprehensive and objective means for measuring facial movement currently available, and it has become the standard tool for facial measurement [4, 10].

For each subject, one of two certified FACS coders manually annotated the presence (from onset to offset) of 34 AUs during a video segment using Observer XT software [26]. AU onsets were annotated when they reached slight or B level intensity. The corresponding offsets were annotated when they fell below B level intensity. All AUs were annotated during speech but not when the face was occluded.

Of the 34 coded AUs, twelve occurred in more than 5% of frames and were analyzed for this report; these AUs are described in (Table I). To assess inter-observer reliability, video from 17 subjects was annotated by both coders. Mean frame-level reliability was quantified with the Matthews Correlation Coefficient (MCC) [29]. The mean MCC was 0.80, with a low of 0.69 for AU 24 and a high of 0.88 for AU 12; according to convention, these numbers can be considered strong to very strong reliability [3].

TABLE I.

Descriptions, inter-observer reliability, and base rates (mean and std. dev.) for the analyzed FACS action units

			Base Rate
AU	Description	MCC	M	SD
1	Inner brow raiser	0.82	0.09	0.10
2	Outer brow raiser	0.85	0.12	0.13
6	Cheek raiser	0.85	0.34	0.21
7	Lid tightener	0.83	0.42	0.24
10	Upper Lip Raiser	0.82	0.40	0.23
11	Nasolabial Deepener	0.85	0.17	0.24
12	Lip Corner Puller	0.88	0.34	0.20
14	Dimpler	0.82	0.65	0.21
15	Lip Corner Depresser	0.72	0.10	0.10
17	Chin Raiser	0.74	0.29	0.19
23	Lip Tightener	0.74	0.21	0.16
24	Lip Presser	0.69	0.14	0.15

The mean base rate (i.e., the proportion of frames during which an AU was present) for AUs was 27.3% with a relatively wide range. AU 1 and AU 15 were least frequent, with each occurring in only 9.2% of frames; AU 12 and AU 14 occurred most often, in 34.3% and 63.9% of frames, respectively. Occlusion, defined as partial obstruction of the view of the face, occurred in 18.8% of all video frames.

D. Automated FACS Coding

1) Facial Landmark Tracking

The first step in automatically detecting AUs was to locate the face and facial landmarks. Landmarks refer to points that define the shape of permanent facial features, such as the eyes and lips. This step was accomplished using the LiveDriver SDK [20], which is a generic tracker that requires no individualized training to track facial landmarks of persons it has never seen before. It locates the two-dimensional coordinates of 64 facial landmarks in each image. These landmarks correspond to important facial points such as the eye and mouth corners, the tip of the nose, and the eyebrows.

2) SIFT Feature Extraction

Once the facial landmarks had been located, the next step was to measure the deformation of the face caused by expression. This was accomplished using two types of features: one focused on changes in facial texture and one focused on changes in facial shape. Separate classifiers were trained for each type of feature.

For the texture-based approach, Scale-Invariant Feature Transform (SIFT) descriptors [22] were used. Because subjects exhibited a great deal of rigid head motion during the group formation task, we first removed the influence of such motion on each image. Using a similarity transformation [33], the facial images were warped to the average pose and a size of 128 × 128 pixels, thereby creating a common space in which to compare them.

In this way, variation in head size and orientation would not confound the measurement of facial actions. SIFT descriptors were then extracted in localized regions surrounding each normalized facial landmark. SIFT applies a geometric descriptor to an image region and measures features that correspond to changes in facial texture and orientation (e.g., facial wrinkles, folds, and bulges). It is robust to changes in illumination and shares properties with neurons responsible for object recognition in primate vision [31]. SIFT feature extraction was implemented using the VLFeat open-source library [39]. Descriptors were set to a diameter of 24 pixels (parameters: scale=3, orientation=0). Each video frame yielded a SIFT feature vector with 8192 dimensions.

3) 3DS Feature Extraction

For the shape-based approach, three-dimensional shape (3DS) models were used. Using an iterative expectation-maximization algorithm [19], we constructed 3D shape models corresponding to LiveDriver’s landmarks. These models were defined by the coordinates of a 3D mesh’s vertices:

$$\mathbf{x}=[x_1;y_1;z_1;\dots ;x_M;y_M;z_M]$$ (1)

or, x = [x₁; …; x_M], where x_i = [x_i; y_i; z_i]. We have T samples: ${\{\mathbf{x}(t)\}}_{t=1}^T$. We assume that apart from scale, rotation, and translation all samples ${\{\mathbf{x}(t)\}}_{t=1}^T$ can be approximated by means of linear principal component analysis (PCA).

The 3D point distribution model (PDM) describes non-rigid shape variations linearly and composes them with a global rigid transformation, placing the shape in the image frame:

$${\mathbf{x}}_i={\mathbf{x}}_i(\mathbf{p})=s\mathbf{R}({\overline{\mathbf{x}}}_i+{\mathbf{\Phi }}_i\mathbf{q})+\mathbf{t}\hspace{1em}(i=1,\dots ,M)$$ (2)

where x_i(p) denotes the 3D location of the i^th landmark and p = {s, α, β, γ, q, t} denotes the parameters of the model, which consist of a global scaling s, angles of rotation in three dimensions (R = R₁(α)R₂(β)R₃(γ)), a translation t and non-rigid transformation q. Here x̄_i denotes the mean location of the i^th landmark (i.e., x̄_i = [x̄_i; ȳ_i; z̄_i] and x̄ = [x̄₁; …; x̄_M]).

We assume that the priors of the parameters follow a normal distribution with mean 0 and variance Λ at a parameter vector q: p(p) ∝ N(q; 0, Λ). We use PCA to determine the d pieces of 3M dimensional basis vectors (Φ = [Φ₁; …; Φ_M] ∈ ℝ^{3M × d}). Vector q represents the 3D distortion of the face in the 3M × d dimensional subspace.

To construct the 3D PDM, we used the BP4D-Spontaneous dataset [41]. An iterative EM-based method was used [19] to register face images. The algorithm iteratively refines the 3D shape and 3D pose until convergence, and estimates the rigid (s, α, β, γ, t) and non-rigid (q) transformations. The rigid transformations were removed from the faces and the resulting canonical 3D shapes (x̄_i+Φ_iq in Equation 2) were used as features for classification. Each video frame yielded a 3DS feature vector with 192 dimensions.

4) Classification

After we extracted the normalized 3D shape and the SIFT descriptors, we performed separate support vector machine (SVM) [38] binary-class classification on them using the different AUs as the class labels. Classification was implemented using the LIBLINEAR open-source library [13].

Support Vector Machines (SVMs) are very powerful for binary and multi-class classification as well as for regression problems. They are robust against outliers. For two-class separation, SVM estimates the optimal separating hyper-plane between the two classes by maximizing the margin between the hyper-plane and closest points of the classes. The closest points of the classes are called support vectors; they determine the optimal separating hyper-plane, which lies at half distance between them.

We used binary-class classification for each AU, where the positive class contains all samples labeled by the given AU, and the negative class contains every other shapes. In all cases, we used only linear classifiers and also vary the regularization parameter C from 2⁻⁹ to 2⁹.

5) Cross-Validation

The performance of a classifier is evaluated by testing the accuracy of its predictions. To ensure generalizability of the classifiers, they must be tested on examples from people they have not seen previously. This is often accomplished by cross-validation, which involves multiple rounds of training and testing on separate data. Stratified k-fold cross-validation [16] was used to partition subjects into 10 folds with roughly equal AU base rates. On each round of cross-validation, a classifier was trained using data (i.e., features and labels) from eight of the ten folds. The classifier’s regularization parameter C was optimized using one of the two remaining folds. The predictions of the optimized classifier were then tested using the final fold. This process was repeated so that each fold was used once for testing and parameter optimization; classifier performance was averaged over these 10 iterations. In this way, training and testing of the classifiers were independent.

6) Scaling Tests

In order to evaluate the impact of training set size on classifier performance, the cross-validation procedure was repeated while varying the number of subjects included in the training set and varying the number of training frames sampled from each subject. Because each training set was randomly sampled from eight of the ten folds, the maximum number of subjects that could be included in a given training set was 64 (i.e., 80 subjects × 8/10 folds). This number was then halved three times to generate the following vector for number of subjects: 8, 16, 32, or 64. Because some subjects had as few as two minutes of manual coding, the maximum number of video frames that could be randomly sampled from each subject was 3600 (i.e., 120 seconds × 29.97 frames per second). This number then was halved three times to generate the following vector for number of training frames per subject: 450, 900, 1800, 3600. A separate ‘scaling test’ was completed for each pairwise combination of number of subjects and number of frames per subject, resulting in a total of 16 tests.

7) Performance Metrics

Classifier performance was quantified using area under the curve (AUC) derived from receiver operating characteristic analysis [14]. AUC can be calculated from the true positive rate (TPR) and false positive rate (FPR) of each possible decision threshold (T):

$$AUC={\int }_{\infty }^{-\infty }TPR(T)FPR\prime (T)dT$$ (3)

When its assumptions are met, AUC corresponds to the probability that the classifier will rank a randomly chosen positive example higher than a randomly chosen negative example. As such, an AUC of 0.5 represents chance performance and an AUC of 1.0 represents perfect performance. AUC is threshold-independent and robust to highly-skewed classes, such as those of infrequent facial actions [21].

8) Data Analysis

The influence of training set size on classifier performance was analyzed using linear regression [7]. Regression models were built to predict the mean cross-validation performance (AUC) of a classifier from the number of subjects in its training set and the number of training frames per subject. Each scaling test was used as a separate data point, yielding 15 degrees of freedom for the regression models.

III. Results

A. SIFT-based Results

Using appearance-based SIFT features, mean classifier performance (AUC) across all AUs and scaling tests was 0.85 (SD = 0.06). Mean performance across all scaling tests was highest for AU 12 at 0.94 and lowest for AU 11 at 0.78.

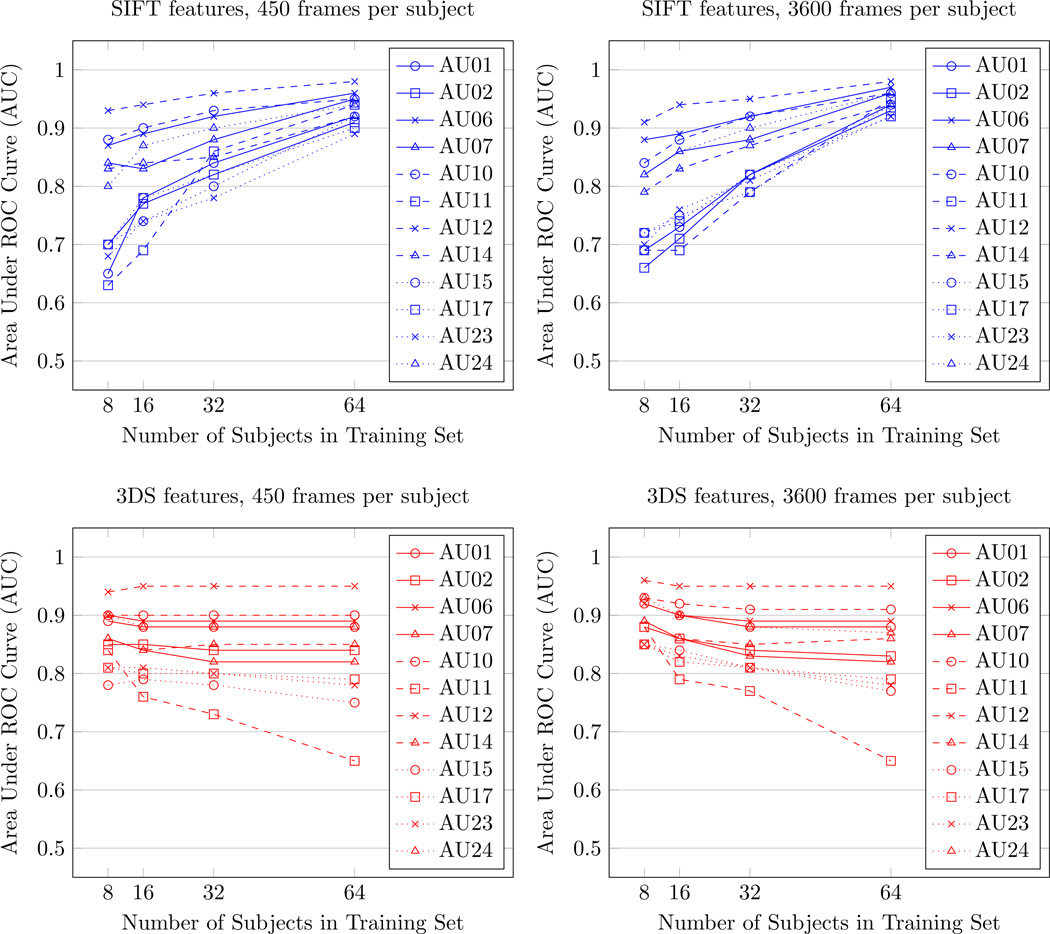
As shown in Figure 2, performance greatly increased as the number of subjects in the training set increased. The standardized regression coefficients in Table II show that increasing the number of subjects in the training set significantly increased classifier performance for all AUs (each p < .001). However, this increase was greater for some AUs than for others. For example, performance for AU 11 increased from 0.63 to 0.94 as the training set increased from 8 to 64 subjects (using 450 frames per subject), while performance for AU 12 increased from 0.93 to 0.98.

Fig. 2.

Classifier performance as a function of number of subjects in the training set

TABLE II.

Standardized regression coefficients for predicting the performance of SIFT-based classifiers

	Number of subjects			Frames/subject
AU	β	t	Sig.	β	t	Sig.
1	0.95	11.75	<.001	−0.06	−0.76	.46
2	0.97	15.02	<.001	−0.04	−0.63	.54
6	0.99	26.64	<.001	0.01	0.28	.78
7	0.98	18.72	<.001	0.01	0.22	.83
10	0.88	7.73	<.001	−0.24	−2.08	.06
11	0.96	11.95	<.001	−0.04	−0.52	.61
12	0.96	12.35	<.001	−0.06	−0.74	.45
14	0.98	16.61	<.001	−0.06	−0.96	.36
15	0.97	14.21	<.001	−0.01	−0.13	.90
17	0.98	18.98	<.001	0.01	0.12	.90
23	0.98	17.39	<.001	0.08	1.50	.16
24	0.96	12.46	<.001	0.02	0.32	.76

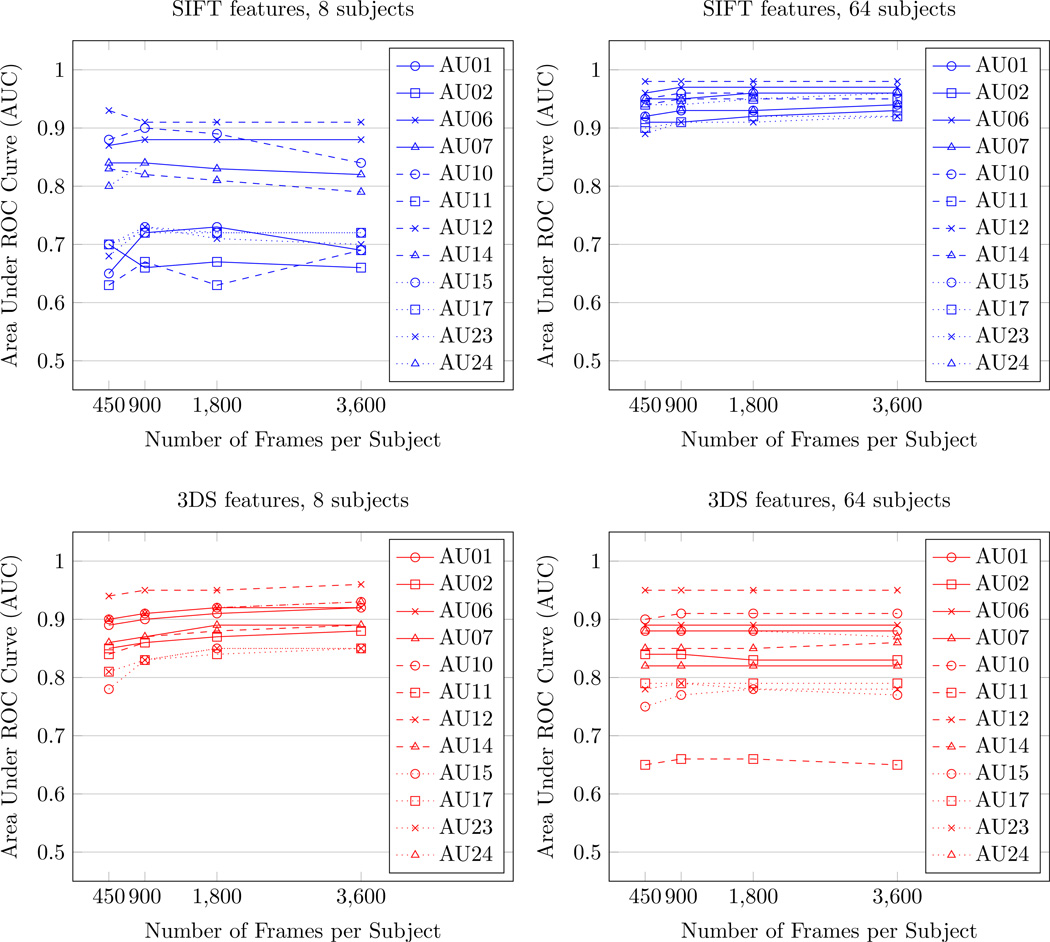
As shown in Figure 3, performance did not change as the number of training frames per subject increased. The standardized regression coefficients in Table II show that increasing the number of training frames per subject did not yield a significant change in performance for any AU.

Fig. 3.

Classifier performance as a function of number training frames per subject

B. 3DS-based Results

Using shape-based 3DS features, mean classifier performance (AUC) across all AUs and scaling tests was 0.86 (SD = 0.05). Mean performance across all scaling tests was highest for AU 12 at 0.95 and lowest for AU 10 at 0.76.

As shown in Figure 2, mean performance slightly decreased as the number of subjects in the training set increased. The standardized regression coefficients in Table III show that increasing the number of subjects in the training set significantly decreased classifier performance for all AUs (each p < .05) except AU 10 and AU 12, which did not change. This reduction was most dramatic for AU 11, which dropped from 0.84 to 0.65 as the training set increased from 8 to 64 subjects (using 450 frames per subject).

TABLE III.

Standardized regression coefficients for predicting the performance of 3DS-based classifiers

	Number of subjects			Frames/subject
AU	β	t	Sig.	β	t	Sig.
1	−0.74	−4.82	<.001	0.37	2.40	<.05
2	−0.84	−5.69	<.001	0.14	0.94	.36
6	−0.68	−3.81	<.01	0.35	1.95	.07
7	−0.82	−5.96	<.001	0.27	1.94	.07
10	−0.25	−1.42	.18	0.72	4.05	<.01
11	−0.94	−10.83	<.001	0.11	1.31	.21
12	−0.26	−1.31	.21	0.65	3.27	<.01
14	−0.47	−2.23	<.05	0.44	2.07	.06
15	−0.77	−5.95	<.001	0.43	3.31	<.01
17	−0.79	−5.69	<.001	0.34	2.45	<.05
23	−0.90	−8.36	<.001	0.21	1.99	.07
24	−0.74	−4.15	<.01	0.22	1.23	.24

As shown in Figure 3, mean performance slightly increased for some AUs as the number of training frames per subject increased. The standardized regression coefficients in Table III show that increasing the number of training frames per subject significantly increased classifier performance for AU 1, AU 10, AU 12, AU 15, and AU 17 (each p < .05). The other seven AUs did not change as the number of training frames per subject increased.

IV. Discussion

We investigated the importance of training set size on the performance of an automated facial expression analysis system by systematically varying the number of subjects in the training set and the number of training frames per subject. Classifiers were trained using two different types of feature representations – one based on facial shape and one based on facial texture – to detect the presence or absence of twelve facial action units.

Results suggest that only the number of subjects was important when using appearance (i.e., SIFT) features; specifically, classification performance significantly improved for all action units as the number of subjects in the training set increased. This result may be due to the high dimensionality of the SIFT features. High dimensional features allow for the description of more variance in the data, but also require more varied training data to do so. This explanation would account for the finding that, on average, SIFT features performed worse than 3DS features with 8 and 16 subjects in the training set, but better than 3DS features with 64 subjects in the training set.

The connection between number of subjects in the training set and classifier performance was statistically significant for all action units; however, it was stronger for some action units than others. For instance, classifier performance increased an average of 0.23 for AU 1, AU 2, AU 11, AU 15, AU 17, and AU 23 as the number of subjects in the training set increased from 8 to 64, whereas it only increased an average of 0.10 for AU 6, AU 7, AU 10, AU 12, AU 14, and AU 24. This result may be because the former group of action units are more varied in their production and thus require more varied training data. It may also be related the relative occurrence of these action units; the average base rate of the former group of action units was 15.76%, while the average base rate of the latter group was 38.67%. Thus, more frequent facial actions may require fewer subjects in the training set to provide the necessary data variety.

Increasing the number of training frames per subject did not significantly change classification performance when using SIFT features. This result may suggest that subjects are highly consistent in producing facial actions. If so, then adding more frames per subject would only be adding more data points close to existing support vectors and classification performance would not change.

When using shape (i.e., 3DS) features, on the other hand, both the number of subjects and the number of frames per subject had some effect on classification performance. Similar to the finding of Zhu et al. [42], we found that performance slightly but consistently lowered for most action units as the number of subjects in the training set increased. This effect was marked for one action unit in particular (i.e., AU 11), which may be due to the fact that many subjects never made that expression. As such, adding more subjects to the training set may have skewed the class distribution. Overall, however, this pattern of results was unexpected and is difficult to explain. Due to the conservative nature of our cross-validation procedure, we are confident that it is not an anomaly related to sampling bias. Further research will be required to explore why appearance but not shape features behaved as expected with regard to the number of subjects in the training set.

For shape-based features, the results of increasing the number of training frames per subject were mixed. For five of the twelve action units, performance significantly increased with the number of frames per subject. This may be due to the relative insensitivity of shape-based features to the facial changes engendered by certain action units. The action units that did improve with more frames per subject (i.e., AU 1, AU 10, AU 12, AU 15, and AU 17) all produce conspicuous changes in the shape of the brows or mouth, whereas the action units that did not improve produce more subtle shape-based changes or appearance changes.

Neither shape nor appearance features needed much data from each subject to achieve competitive classification performance. The minimum amount of training data sampled per subject was 450 frames, which corresponds to just over 15 seconds of video. These results align with the “thin slice” literature, which claims that it is possible to draw valid inferences from small amounts of information [1].

It will be important to replicate these findings with additional large spontaneous facial expression databases as they become available. Databases may differ in context, subject demographics, and recording conditions; these and other factors may affect how much training data is required. Future studies should also explore how training set size affects the performance of classifiers other than support vector machines. Finally, the question of how to best select positive and negative training frames is still open. Competitive performance was achieved in the current study by making these selections randomly; however, it is possible that we could do even better with more deliberate choices. As frames from the same expression events are likely to be more similar than frames from different events, future work may also explore the effect of including different numbers of events.

In conclusion, we found that the amount and variability of training data fed to a classifier can have important consequences for its performance. When using appearance features, increasing the number of subjects in the training set significantly improved performance while increasing the number of training frames per subject did not. For shape-based features, a different pattern emerged. Increasing the number of subjects and training frames led to unexpected results that warrant further research. Overall, the best performance was attained using high dimensional appearance features from a large number of subjects. Large numbers of training frames were not necessary. When comparing the results of different appearance-based approaches in the literature, it is important to consider differences in number of subjects. Failure to include sufficient subjects may have attenuated performance in previous studies. On a practical note, if you are starting a new data collection, our findings support a recommendation to collect a small amount of high quality data from many subjects and use high dimensional appearance features such as SIFT.