Abstract
Cadmium arsenide (Cd3As2) is known for its inverted band structure and ultra-high electron mobility. It has been theoretically predicted and also confirmed by ARPES experiments to exhibit a 3D Dirac semimetal phase containing degenerate Weyl nodes. From magneto-transport measurements in high quality single crystals of Cd3As2, a small effective mass m* ≈ 0.05 me is determined from the Shubnikov-de Haas (SdH) oscillations. In certain field orientations, we find a splitting of the SdH oscillation frequency in the FFT spectrum suggesting a possible lifting of the double degeneracy in accord with the helical spin texture at outer and inner Fermi surfaces with opposite chirality predicted by our ab initio calculations. Strikingly, a large antisymmetric magnetoresistance with respect to the applied magnetic fields is uncovered over a wide temperature range in needle crystal of Cd3As2 with its long axis along [112] crystal direction. It reveals a possible contribution of intrinsic anomalous velocity term in the transport equation resulting from a unique 3D Rashba-like spin splitted bands that can be obtained from band calculations with the inclusion of Cd antisite defects.
Topological materials have attracted great attention recently in condensed matter physics and material science. Non-trivial topology in a bulk band along with certain crystal symmetry can give rise to a novel material phase with unusual surface states, such as topological insulator1,2, topological crystalline insulator3,4 and Weyl semimetal (WS)5,6,7. Recently, a 3D Dirac semimetal (DS) phase has been theoretically predicted to exist in Na3Bi8, BiO29, and Cd3As210, where angle-resolved photoemission spectroscopy (ARPES) has provided direct evidences for such a 3D Dirac semimetal band11,12. As opposed to a WS, a DS contains overlapping Weyl nodes with opposite chirality in momentum space and typically requires a special crystal symmetry to protect the nodes against the gap-opening. The breaking of either time reversal symmetry or inversion symmetry in a DS is, therefore, a route toward realizing a WS phase, where a special magneto-electric coupling effect13 due to the non-conserving chiral current between separated Weyl nodes can lead to novel transport phenomena14,15,16,17,18. Cd3As2 contains inverted bands with ultra-high electron mobility, which were reported decades ago19,20, but only recently it revives as an example of 3D topological Dirac semimetals. It has been shown in experiments that a WS phase can be realized in Cd3As2 by applying intense magnetic field along the [001] crystal direction21,22. However, when the magnetic field is tilted away from [001] direction, the four-fold rotational symmetry is broken giving rise to gapped Dirac nodes in Cd3As223. More recently, an exotic superconducting phase was discovered in point contact measurements on the surface of Cd3As2, which was attributed to the possible tip-induced symmetry-lowering or density variation near the point contact region24,25. Those results all point to an important fact that the system’s symmetry plays a crucial role dictating the details of Dirac band structures in Cd3As2.
In this study, we performed magnetotransport measurements on needle crystals of pure Cd3As2 grown by chemical vapor transport26,27. Compared to flux growth single crystals16,28, the CVT needle crystals have lower residual resistivity ratio suggesting higher defect level, which enables us to investigate the influence of defects to the Dirac band structures in Cd3As2. By introducing the Cd antisite defects into the band calculations, both the inversion symmetry and rotational symmetry were broken giving rise to a unique 3D Rashba-like spin splitted bands in Cd3As2, which may provide a qualitative explanation to the observed splitting in SdH frequency at various field angles and also a huge antisymmetric magnetoresistance (MR) with respect to magnetic fields in Cd3As2. Nevertheless, a possible current-jetting effect29,30 due to disorder and inhomogeneous conductivity, which has been reported in several narrow band-gap semiconductors31,32, will be discussed and compared to our transport data in Cd3As2.
Results and Discussions
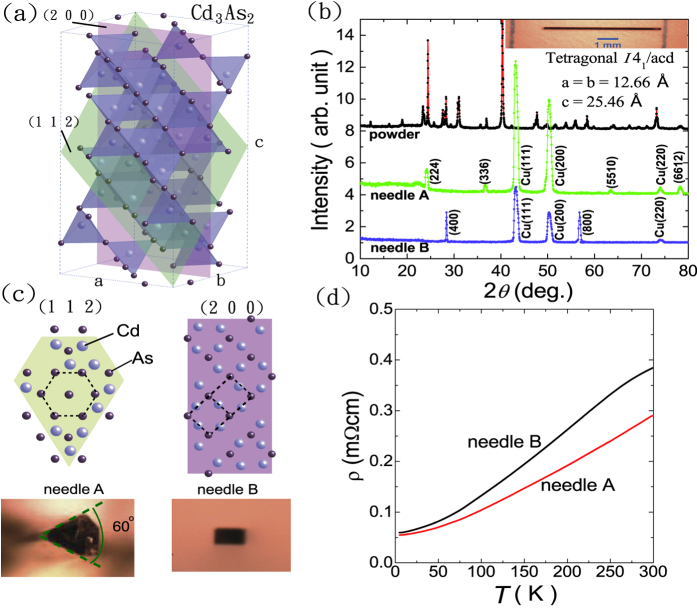
The crystal structure of Cd3As2 as shown in Fig. 1(a) comprises a distorted antifluorite structure with ordered Cd vacancies, and it contains 80 atoms within a unit cell. For the phase stabilized at the lowest temperature, the Cd vacancies could be arranged orderly within a large tetragonal cell composed of corner-sharing CdAs4 tetrahedral units. The symmetry of Cd3As2 generated at the lowest temperature has been controversially indexed with either noncentrosymmetric space group I41cd33 or I41/acd with centrosymmetry34. While the indexing based on powder X-ray diffraction (XRD) is nearly equally satisfactory, and the initial Cd vacancy ordering is determinative on the final symmetry, the growth condition and crystal morphology could also play a role34. In the same batch of crystals, two types of needles can be identified. Needle A has nearly triangular-shape cross-section, while needle B has rectangle-shape cross-section as demonstrated in Fig. 1(c). Figure 1(b) shows the powder XRD pattern of the needle B crystal, which can be indexed with the space group I41/acd with centrosymmetry. For needle A, the same space group of I41/acd can be indexed in the X-ray diffraction. In order to identify the crystalline direction along the long axes of the needle crystals, a 4-circle diffractometer was used, and the corresponding single-crystal XRD of needle A and B are shown in Fig. 1(b), where the long axis directions of needle A and B were confirmed to be along [112] and [200], respectively. In addition, the full-width half maximum of the XRD peaks is merely about 0.2–0.4 degrees indicating good single crystalline quality with a small mosaic spread in our needle-like crystals. Crystallographically, it is reasonable to have stable phase of large (112) plane for Cd3As2, because (112) plane corresponds to a plane of pseudo-hexagonal close packing for a tetragonal unit cell with c ≈ 2a. The resistivity data shown in Fig. 1(d) indicate a metallic behavior with residual resistivity ratios (RRR ≡ ρ300K/ρ5K) of 4.4 and 5.6 for needle A and needle B, respectively. The corresponding electron density and the estimated Drude mobility are listed in Table 1. For needle B, the carrier density equals 9.2 × 1017 cm−3, and the corresponding Hall mobility μD is as high as 113,567 cm2V−1 s−1 at T = 5 K.
Figure 1.
(a) An illustration of Cd3As2 crystal structure, where the (112) and (200) planes are shown. (b) Powder XRD pattern with preferred orientation fitted by I41/acd space group symmetry. The single crystal XRD of needle A and B are also included to verify the corresponding needle long-axis directions to be along [112] and [200], respectively. The additional copper peaks come from the sample holder contribution. The upper inset shows the optical image of a 6 mm-long needle crystal of Cd3As2. (c) Optical images of needle A and B, showing triangular and rectangle cross-sections, where the corresponding (112) and (200) planes are illustrated in the upper panel. (d) Temperature dependence of the resistivity for needle A and needle B, showing similar metallic behavior.
Table 1. Major SdH frequency F1(T), secondary SdH frequency F2(T), effective mass m*(me), and Drude mobility μD (cm2V−1 s−1) obtained from SdH oscillation measurements and calculated band structure.
| ne × 1018 (cm−3) | F1 (T) | F2 (T) |
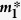 (me) (me) |
μD at 5 K (cm2V−1 s−1) | |
|---|---|---|---|---|---|
| needle A | 2.4 | 61.5 | 49.8 | 0.0498 | 45,577 |
| needle B | 0.92 | 27.3 | 20.4 | 0.0232 | 113,567 |
| Calculation | 2.4 | 52 | 35 | – | – |
| 0.92 | 31 | 18 | – | – |
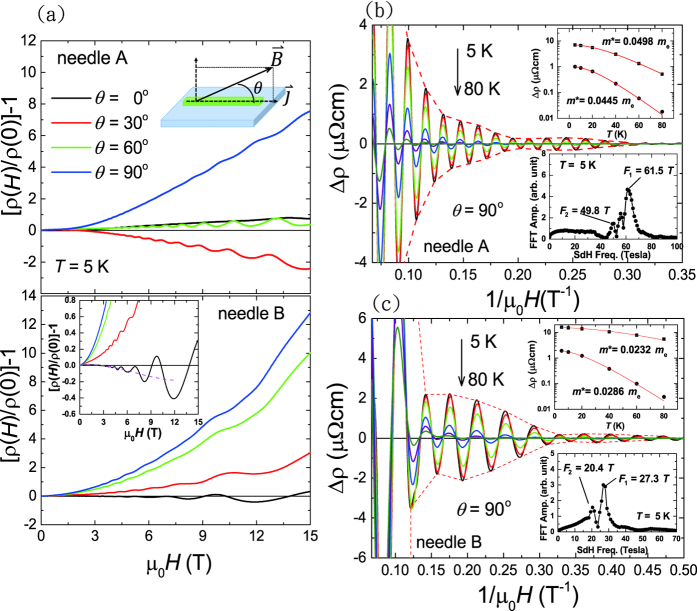
Figure 2(a) shows the symmetrized MR (MR = [MR(H) + MR(−H)]/2) at four different θ values ranging from zero to 90 degrees, where θ is defined as the angle between the current and the applied magnetic field (upper inset cartoon). At T = 5 K, the magnitude of MR in needle B progressively decreases from a large positive value of MR ≡ [ρ(H)/ρ(0)] − 1 = 12.8 at θ = 90° to a small negative MR at θ = 0° angle (shown in the lower inset of Fig. 2(a)). On the contrary, the MR in needle A shows non-monotonic variation with θ values as demonstrated in the upper panel of Fig. 2(a). The unusual high μH enables the determination of band parameters via SdH oscillations in transport measurements. A large amplitude of SdH oscillation was found in MR at low T, which remains observable up to T ≥ 100 K. Figure 2(b) shows the pure oscillatory component of the resistivity Δρ versus 1/μ0H for needle A at 6 different temperatures ranging from 5 K to 80 K. The magnetic field is normal to the [112] direction. The damping of the SdH oscillation by temperature and magnetic field can be described by the following equation based on Lifshitz-Kosevich formula.
Figure 2.
(a) Symmetrized MR in needle A (upper) and B (lower) at four different θ angles. The inset figure of lower panel is an enlarged view, showing a small negative MR at θ = 0°. (b,c) Plot the pure oscillatory component in MR versus 1/μ0H for needle A and B, respectively, at θ = 90° and various temperatures ranging from 5 to 80 K. The upper and lower insets are the corresponding effective masses fitting using Lifshitz-Kosevich formula and FFT spectra. Both needle A and B exhibit beating patterns in SdH oscillations with multiple closely-spaced peaks in the FFT spectra at θ = 90°.
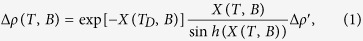 |
where X(T, B) ≡ 2π2kBTm*/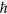 eB, m* is the effective cyclotron mass and TD is the Dingle temperature. Δρ′ refers to the undamped oscillatory component. By fitting the peak values of Δρ-T and log(Δρ ⋅ sin hX/X) − 1/μ0H according to Eq. 1, we determined m* = 0.0498 me for needle A as demonstrated in the upper inset of Fig. 2(b). Two resolvable SdH frequencies of 49.8 and 61.5 Tesla were identified in the Fast Fourier transform (FFT) spectrum shown in the lower inset of Fig. 2(b). On the other hand, the pure oscillatory component of resistivity for needle B is shown in Fig. 2(c), where two SdH frequencies of 20.4 and 27.3 Tesla and m* = 0.0232 me were determined. The calculated band for I41/acd structure with Cd antisites in (112) plane at similar ne gives two close SdH frequencies F1 and F2, which is in relatively good agreement with the experimental data. A summary of the band parameters for needle A and needle B from SdH experiments and calculation is given in Table 1.
eB, m* is the effective cyclotron mass and TD is the Dingle temperature. Δρ′ refers to the undamped oscillatory component. By fitting the peak values of Δρ-T and log(Δρ ⋅ sin hX/X) − 1/μ0H according to Eq. 1, we determined m* = 0.0498 me for needle A as demonstrated in the upper inset of Fig. 2(b). Two resolvable SdH frequencies of 49.8 and 61.5 Tesla were identified in the Fast Fourier transform (FFT) spectrum shown in the lower inset of Fig. 2(b). On the other hand, the pure oscillatory component of resistivity for needle B is shown in Fig. 2(c), where two SdH frequencies of 20.4 and 27.3 Tesla and m* = 0.0232 me were determined. The calculated band for I41/acd structure with Cd antisites in (112) plane at similar ne gives two close SdH frequencies F1 and F2, which is in relatively good agreement with the experimental data. A summary of the band parameters for needle A and needle B from SdH experiments and calculation is given in Table 1.
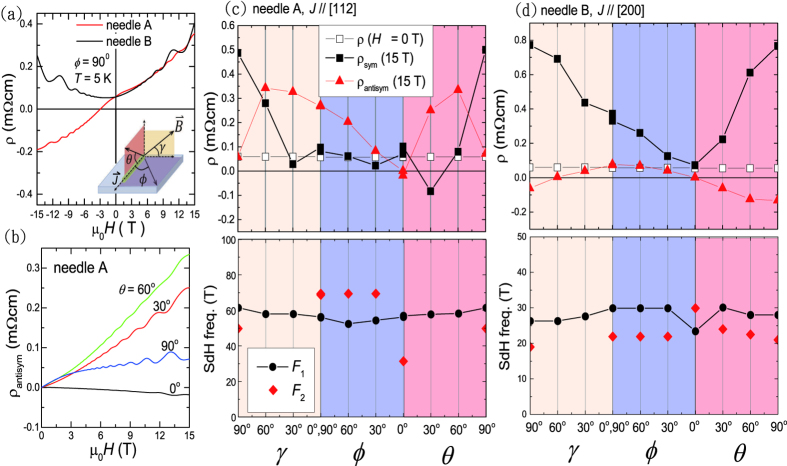
Figure 3(a) shows the resistivity versus magnetic field applied along ϕ = 90°, where the definition of corresponding angles of γ, ϕ, and θ are illustrated in the lower inset cartoon. Both needle A and needle B exhibit noticeable antisymmetric component in the MR regardless of the large aspect ratio (≡ length/width) of ≅3.9 (15.7) in needle A (B). By using the formula of ρsym ≡ [ρ(H) + ρ(−H)]/2 and ρantisym ≡ [ρ(H) − ρ(−H)]/2, symmetric (ρsym) and antisymmetric (ρantisym) components of the MR can be extracted. The resulting field dependence of ρantisym in needle A at four different θ angles is shown in Fig. 3(b), where the corresponding ρsym has been shown in Fig. 2(a). The upper panels of Fig. 3(c,d) are the angular dependence of the extracted ρsym and ρantisym at μ0H = 15 T for needle A and needle B, respectively. We remark that, for needle B with current along the [200] crystal direction, ρantisym at some angles can be even larger than ρsym, and the magnitude of ρantisym appears to be at minimum when ϕ = 0° or θ = 0°. The SdH frequencies determined from the FFT spectra for needle A and needle B are shown in the lower panels of Fig. 3(c,d), respectively, where apparent multiple SdH frequencies can be identified. The major SdH frequencies F1 (black circles) being the location of largest peak in the FFT spectrum were determined to be about 61 Tesla and 27 Tesla in needle A and needle B, respectively, exhibiting weak dependency on γ, ϕ, and θ values. We also note that secondary SdH frequencies (red diamonds) can be clearly observed at some angles in both needle A and needle B.
Figure 3.
(a) Resistivity ρ versus field μ0H shows significant antisymmetric component in needle A and B. The lower inset cartoon illustrates the geometric definition for angles of γ, ϕ, and θ. (b) Extracted antisymmetric components (ρantisym) in MR of needle A at four different θ angles. At μ0H = 15 Tesla, the angular dependence of extracted symmetric (ρsym) and antisymmetric (ρantisym) components of needle A and B are shown in (c,d), respectively. The lower panel shows the corresponding SdH frequencies that can be identified from the FFT spectra. The major SdH frequencies F1 (black circles) at about 61 Tesla and 27 Tesla for needle A and B, respectively, both show weak angular dependence. Secondary SdH frequencies F2 appear at some angles shown as red diamonds.
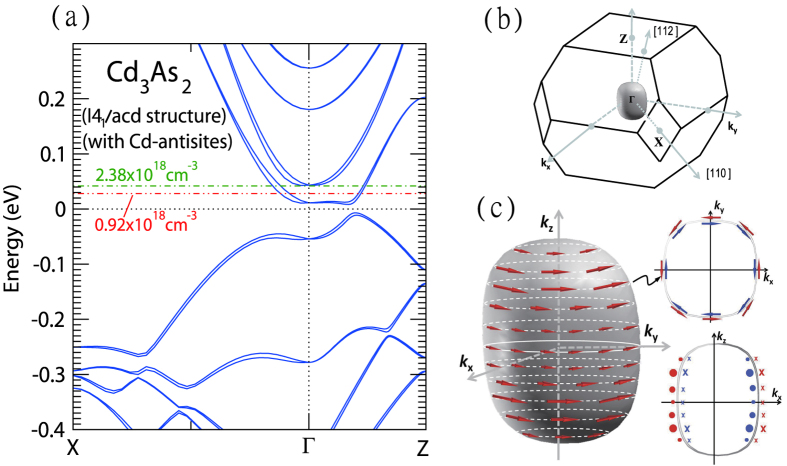
Figure 4(a) shows the calculated band structure based on I41/acd space group symmetry with Cd antisite defects. The dotted-dash lines represent two Fermi level locations set by experimental SdH frequencies within the rigid band approximation. For needle B with a density of ne = 0.92 × 1018 cm−3, the Fermi level is about 30 meV above the Dirac node. As described previously, the Cd vacancies are ordered in the manner to keep the inversion symmetry in the defect-free I41/acd lattice. The inversion symmetry then leads to the spin degenerate Dirac bands, which can not explain the observed splitted SdH frequencies. Inspired by our calculated spin splitted Dirac bands of the noncentrosymmetric I41/cd lattice (see supplementary information), we thus introduce ≈1% Cd antisite defect in the centrosymmetric I41/acd lattice by moving one Cd ions to one of the Cd vacancies so as to break the inversion symmetry and split the centrosymmetry protected spin degenerate Dirac bands. As shown in the figure, a lifting of spin degeneracy in the calculated band in the kx − ky plane is successfully obtained from breaking of the inversion center of I41/acd structure by the Cd antisite defects and thus gives rise to the two calculated SdH frequencies listed in Table 1. This is in accord with the observed beating patterns and multiple closely-spaced SdH frequencies shown in Fig. 2(b,c) (see also supplementary information). However, we note that a small gap about 10 meV is opened at the Dirac node due to the rotational symmetry breaking by the Cd antisites. In addition, the band width was reduced causing a flatter Dirac bands, which results in a somewhat lower Fermi level location in our band calculations compared to previous reports based on defect-free band calculations12,28. In the lower panels of Fig. 3(c,d), the variation of the SdH Frequency with γ, θ, and ϕ is less than 15%. The Fermi surface can, therefore, be regarded as a slightly distorted sphere as illustrated in Fig. 4(b) obtained from a calculated band with a Fermi level at ≈0.04 eV above the gapped Dirac node for the I41/acd structure with ≈1% Cd antisite defects. The shape of the Fermi surfaces and the spin chirality are similar to those of the defect-free noncentrosymmetric I41cd lattice at 0.1 eV with smaller band splittings. This remains well above the Lifshitz transition occurring at around 0.01 eV. Hence, the two Fermi pockets corresponding to two gapped Dirac nodes along the Γ − Z line merged together into a bigger Fermi surface centered at Γ. The [112] and [200] directions corresponding to the long axes of needle A and needle B, respectively, are also indicated in Fig. 4(b). We further performed calculation on spin texture of the 3D Fermi surface shown in Fig. 4(c), where the electrons over the Fermi surfaces possess chirality with a spin-momentum lock in-plane spin texture. Furthermore, due to the broken centrosymmetry by the Cd antisites, the spin texture on the inner and outer Fermi surfaces revolve in the opposite direction as shown in the upper inset of Fig. 4(c) similar to a Rashba-like band-splitting. The difference in the area of the two Fermi surfaces over the ab-plane is about 29%, which is compatible with the experimental value (≈20%) from splitted SdH frequencies shown in Fig. 2(b,c). We remark that such an unusual 3D Rashba-like spin splitted band is a direct consequence of the large spin-orbit coupling and also Cd-antisites induced inversion symmetry breaking in Cd3As2 while the time reversal symmetry remains valid.
Figure 4.
(a) A calculated band structure of Cd3As2 with I41/acd space group symmetry and Cd antisite defects. The two dotted lines correspond to the Fermi level locations for needle A and B, respectively, determined from the experimental values of Fermi surface area. (b) The calculated 3D Fermi surface with an energy of ≈0.04 eV above the gapped Dirac node close to the Fermi level of our samples suggests a slightly distorted Fermi sphere in Cd3As2. [112] and [200] crystal directions are indicated corresponding to the long-axis directions for needle A and B, respectively. (c) The spin texture over an outer Fermi surface. Red and blue arrows indicate spin texture on the outer and inner Fermi surfaces, respectively, where the size of the arrows indicates the spin polarization. The lower inset shows the spin texture profile on kx − kz plane, while the upper inset is a top view of the Fermi surfaces at finite kz indicated by the black arrows.
The raw data of the resistivity shows an antisymmetric behavior with respect to the in-plane magnetic field inferring a large transverse Hall-like signal picked up by the voltage leads due to the leads misalignment. The estimation of normal Hall signal due to leads misalignment is difficult due to unknown distance W′ between leads normal to the current direction. A rough estimation of normal Hall contribution can be given using ρxy,norm = ρxy × (W′/W)/(AR), where W is the needle width and AR = L/W is the aspect ratio of the needle. If we take W′/W ≈ 10% and AR = 3.9 (15.7) for needle A(B), ρxy,norm (15 T) = 0.1 mΩcm (0.06 mΩcm), which is at least 4-fold smaller in magnitude compared to the observed ρantisym shown in Fig. 3(c,d). In addition, ρxy,norm should grow monotonically with increasing magnetic field strength normal to the current direction (i.e., the θ and ϕ angles go from zero to 90 degrees), which contradicts with the non-monotonic variation of ρantisym with θ values observed in needle A shown in Fig. 3(c).
Now we turn to discuss the possible current-jetting effect. It was shown that the inhomogeneous conductivity can cause a distortion in the current path giving rise to a perpendicular current component 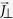 that flows normal to the major current direction
that flows normal to the major current direction 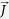 30,31. In Cd3As2, high resistivity anisotropy and relatively short quantum scattering lifetime of ~10−14 s as determined from SdH oscillations were reported16,35 making the current jetting effect a likely source of unusual magnetotransport behavior. In general,
30,31. In Cd3As2, high resistivity anisotropy and relatively short quantum scattering lifetime of ~10−14 s as determined from SdH oscillations were reported16,35 making the current jetting effect a likely source of unusual magnetotransport behavior. In general, 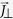 contributes a normal Hall signal to MR resulting in a B-linear and non-saturating MR in transverse field with
contributes a normal Hall signal to MR resulting in a B-linear and non-saturating MR in transverse field with 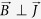 . For longitudinal field geometry of
. For longitudinal field geometry of 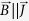 , further bending in
, further bending in 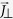 by
by 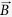 results in a decrease in potential drop between voltage electrodes and hence a negative MR. Compared to the MR data of Cd3As2 shown in Fig. 2(a), a nearly B-linear MR at θ = 90° (
results in a decrease in potential drop between voltage electrodes and hence a negative MR. Compared to the MR data of Cd3As2 shown in Fig. 2(a), a nearly B-linear MR at θ = 90° (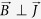 ) only appeared at fields higher than about 10 Tesla. In addition, a positive MR at θ = 0° (
) only appeared at fields higher than about 10 Tesla. In addition, a positive MR at θ = 0° (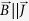 ) with vanishing ρantisym up to 15 Tesla (Fig. 3(b)) was observed in needle A instead. Those phenomena cannot be fully understood via the current-jetting mechanism alone. We also note the large negative MR found in needle A at θ = 30°, where its origin is unclear and requires further investigation. On the other hand, ρantisym remains finite at low-field diffusive limit and grows larger in higher fields without saturation as shown in Fig. 3(b). In particular, the ρantisym − μ0H curve at θ = 90° exhibits a slower increase of ρantisym at higher fields, which is different from others being nearly linear with field. Those findings strongly suggests that there is additional contribution to the antisymmetric MR other than the normal Hall contribution and the high field effect in quantum limit. We also find that such an antisymmetric behavior in MR persists up to room temperature and shows relatively weak T dependence (see supplementary information), which supports for a more intrinsic origin rather than due to impurity effect at low T.
) with vanishing ρantisym up to 15 Tesla (Fig. 3(b)) was observed in needle A instead. Those phenomena cannot be fully understood via the current-jetting mechanism alone. We also note the large negative MR found in needle A at θ = 30°, where its origin is unclear and requires further investigation. On the other hand, ρantisym remains finite at low-field diffusive limit and grows larger in higher fields without saturation as shown in Fig. 3(b). In particular, the ρantisym − μ0H curve at θ = 90° exhibits a slower increase of ρantisym at higher fields, which is different from others being nearly linear with field. Those findings strongly suggests that there is additional contribution to the antisymmetric MR other than the normal Hall contribution and the high field effect in quantum limit. We also find that such an antisymmetric behavior in MR persists up to room temperature and shows relatively weak T dependence (see supplementary information), which supports for a more intrinsic origin rather than due to impurity effect at low T.
Another likely mechanism is the anomalous velocity term associated with the non-zero Berry curvature of the bulk band36,37. In a general formalism, the electron velocity can be expressed as 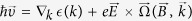 , where
, where 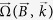 is the Berry curvature. In a diffusive transport14, it can be shown to give a total current of
is the Berry curvature. In a diffusive transport14, it can be shown to give a total current of
 |
where 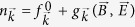 is the electron distribution function.
is the electron distribution function. 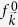 and
and 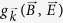 are the equilibrium and non-equilibrium distribution function, respectively. In zero field, time reversal symmetry ensures that the integration of anomalous velocity term (
are the equilibrium and non-equilibrium distribution function, respectively. In zero field, time reversal symmetry ensures that the integration of anomalous velocity term (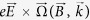 ) with
) with 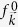 over the whole Fermi surface gives zero contribution to the total current. However, in the presence of magnetic field and electric bias, the induced
over the whole Fermi surface gives zero contribution to the total current. However, in the presence of magnetic field and electric bias, the induced 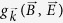 can result in non-vanishing anomalous velocity contribution to the total current as shown in Eq. 2. It is known that the electric current and spin polarization can couple with each other in a 2D electron gas system with Rashba spin splitting38,39. For example, current-induced spin polarization has been demonstrated providing a strong support for the observable effects originating from non-equilibrium
can result in non-vanishing anomalous velocity contribution to the total current as shown in Eq. 2. It is known that the electric current and spin polarization can couple with each other in a 2D electron gas system with Rashba spin splitting38,39. For example, current-induced spin polarization has been demonstrated providing a strong support for the observable effects originating from non-equilibrium 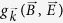 term. In the case of a 3D Rashba-like spin splitted band shown in Fig. 4(c),
term. In the case of a 3D Rashba-like spin splitted band shown in Fig. 4(c), 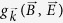 value can have nontrivial dependence on the orientation of
value can have nontrivial dependence on the orientation of 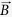 and
and 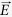 , which results in anomalous angular dependence in the transport phenomena.
, which results in anomalous angular dependence in the transport phenomena.
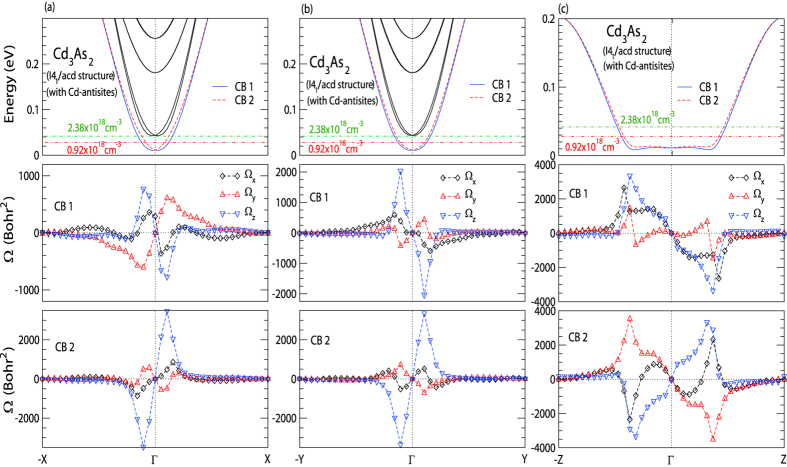
In order to look into the anomalous velocity contribution, Berry curvature 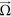 based on the band structure shown in Fig. 4(a) was calculated. Figure 5(a–c) shows the results along Γ − X, Γ − Y, and Γ − Z, respectively. We note that
based on the band structure shown in Fig. 4(a) was calculated. Figure 5(a–c) shows the results along Γ − X, Γ − Y, and Γ − Z, respectively. We note that 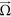 for the two conduction bands of CB1 (middle panel) and CB2 (lower panel) have non-zero magnitudes along all three principle axes indicating a 3D nature of the Rashba-like spin-splitted band.
for the two conduction bands of CB1 (middle panel) and CB2 (lower panel) have non-zero magnitudes along all three principle axes indicating a 3D nature of the Rashba-like spin-splitted band. 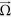 is antisymmetric with respect to the Γ point as expected for a system with time reversal symmetry. We remark that the calculated
is antisymmetric with respect to the Γ point as expected for a system with time reversal symmetry. We remark that the calculated 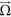 gives the largest non-zero value along Γ − Z direction, which is nearly 4-fold bigger compared to that along Γ − X. Such a difference can provide qualitative explanation on the observation of a larger ρantisym in needle A sample with current applied along [112], where a non-zero electric bias along Γ − Z is present. We note that similar splitting in SdH frequency was also reported in flux-growth Cd3As2 crystals28. It was attributed to the two nested ellipsoidal Fermi surface along the Γ − Z, showing single SdH frequency when the magnetic field is along [112] direction, which is not compatible with our observation in needle A that shows two distinct SdH frequencies at θ = 0°. It is also not clear how the spin-degenerate and nested ellipsoidal Fermi surface can lead to a large transverse current response in the charge transport.
gives the largest non-zero value along Γ − Z direction, which is nearly 4-fold bigger compared to that along Γ − X. Such a difference can provide qualitative explanation on the observation of a larger ρantisym in needle A sample with current applied along [112], where a non-zero electric bias along Γ − Z is present. We note that similar splitting in SdH frequency was also reported in flux-growth Cd3As2 crystals28. It was attributed to the two nested ellipsoidal Fermi surface along the Γ − Z, showing single SdH frequency when the magnetic field is along [112] direction, which is not compatible with our observation in needle A that shows two distinct SdH frequencies at θ = 0°. It is also not clear how the spin-degenerate and nested ellipsoidal Fermi surface can lead to a large transverse current response in the charge transport.
Figure 5.
Berry curvature calculations along Γ − X (a), Γ − Y (b), and Γ − Z (c) using the band structure show in Fig. 4(a). The upper panels show the band structures. The corresponding Berry curvature 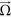 for CB 1 and CB 2 bands are shown in the middle and lower panels, respectively. Non-zero Berry curvatures were found along all three principle axes in accord with a 3D nature of the Rashba-like spin-splitted band in Cd3As2 with Cd antisites.
for CB 1 and CB 2 bands are shown in the middle and lower panels, respectively. Non-zero Berry curvatures were found along all three principle axes in accord with a 3D nature of the Rashba-like spin-splitted band in Cd3As2 with Cd antisites.
In conclusion, Cd3As2 exhibits a 3D topological Dirac semimetal phase with ultra-high electron mobility. According to our band calculations, Cd antisite defects can be an effective symmetry-breaking mechanism giving rise to a unique 3D Rashba-like spin splitting in the kx − ky plane. This is also supported by our angular SdH measurements, showing splitted Fermi surface. By comparing the transport data in needle A and B with long axes along [112] and [200], respectively, we uncover significant transverse Hall-like signals in MR, which can not be simply attributed to the normal Hall-effect-related mechanisms. Particularly, we found that such a transverse Hall-like signal is much more pronounced in needle A with current bias along [112] direction. This can be qualitatively understood from our calculated Berry curvature, showing a 4-fold enhancement in magnitude along Γ − Z, and the corresponding non-equilibrium electron distribution due to the external magnetic field and electric bias can lead to an unusual large anomalous velocity contribution to the electron transport.
Additional Information
How to cite this article: Guo, S.-T. et al. Large transverse Hall-like signal in topological Dirac semimetal Cd3As2. Sci. Rep. 6, 27487; doi: 10.1038/srep27487 (2016).
Supplementary Material
Acknowledgments
The authors acknowledge the funding support from the nanoprogram at Academia Sinica and Ministry of Science and Technology (MOST) in Taiwan. W.L.L. acknowledges the funding support from the Academia Sinica 2012 career development award in Taiwan. G.Y.G. acknowledges the support from the Academia Sinica thematic research program. H.T.J. and G.Y.G. also thank NCHC, CINC-NTU and NCTS, Taiwan for supports. F.C.C. acknowledges support from TCECM under MOST-Taiwan.
Footnotes
Author Contributions W.-L.L., H.-T.J., G.-Y.G. and F.C.C. designed the experiment. R.S. and F.C.C. are responsible for single-crystal growth and crystal structural characterizations. T.-R.C., H.-T.J. and G.-Y.G. performed the theoretical band calculations. S.-T.G., Y.-Y.C. and W.-L.L. carried out the low temperature transport measurements and data analysis. W.-L.L. wrote the manuscript.
References
- Fu L. & Kane C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007). [Google Scholar]
- Hasan M. Z. & Kane C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
- Fu L. Topological Crystalline Insulators. Phys. Rev. Lett. 106, 106802 (2011). [DOI] [PubMed] [Google Scholar]
- Dziawa P. et al. Topological crystalline insulator states in Pb1−xSnxSe. Nat. Mater. 11, 1023–1027 (2012). [DOI] [PubMed] [Google Scholar]
- Wan X., Turner A. M., Vishwanath A. & Savrasov S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011). [Google Scholar]
- Burkov A. A., Hook M. D. & Balents L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011). [Google Scholar]
- Weng H., Fang C., Fang Z., Bernevig B. A. & Dai X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 5, 011029 (2015). [Google Scholar]
- Wang Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012). [Google Scholar]
- Young S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012). [DOI] [PubMed] [Google Scholar]
- Wang Z., Weng H., Wu Q., Dai X. & Fang Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B 88, 125427 (2013). [Google Scholar]
- Liu Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal, A3Bi. Science 343, 864–867 (2014). [DOI] [PubMed] [Google Scholar]
- Neupane M. et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat. Commun. 5, 3786 (2014). [DOI] [PubMed] [Google Scholar]
- Zyuzin A. A. & Burkov A. A. Topological response in Weyl semimetals and the chiral anomaly. Phys. Rev. B 86, 115133 (2012). [Google Scholar]
- Son D. T. & Spivak B. Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 88, 104412 (2013). [Google Scholar]
- Kim H. J. et al. Dirac versus Weyl fermions in topological insulators: Adler-Bell-Jackiw anomaly in transport phenomena. Phys. Rev. Lett. 111, 246603 (2013). [DOI] [PubMed] [Google Scholar]
- Liang T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 14, 280 (2014). [DOI] [PubMed] [Google Scholar]
- Burkov A. A. Anomalous Hall effect in Weyl metals. Phys. Rev. Lett. 113, 187202 (2014). [DOI] [PubMed] [Google Scholar]
- Li C. Z. et al. Giant negative magnetoresistance induced by the chiral anomaly in individual Cd3As2 nanowires. Nat. Commun. 6, 10137 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aubin M. J., Caron L. G. & Jay-Gerin J. P. Energy-band structure of Cd3As2 at low temperatures and the dependence of the direct gap on temperature and pressure. Phys. Rev. B 15, 3872–3878 (1977). [Google Scholar]
- Rosenberg A. J. & Harman T. C. Cd3As2, A noncubic semiconductor with unusually high electron mobility. J. Appl. Phys. 30, 1621–1622 (1959). [Google Scholar]
- Jeon S. et al. Landau quantization and quasiparticle interference in the three-dimensional Dirac semimetal Cd3As2. Nat. Mater. 13, 851 (2014). [DOI] [PubMed] [Google Scholar]
- Cao J. et al. Landau level splitting in Cd3As2 under high magnetic fields. Nat. Commun. 6, 7779 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang Z. J. et al. Angular-dependent phase factor of Shubnikov de Haas oscillations in the Dirac semimetal Cd3As2. Phys. Rev. Lett. 115, 226401 (2015). [DOI] [PubMed] [Google Scholar]
- Aggarwal L. et al. Unconventional superconductivity at mesoscopic point contacts on the 3D Dirac semimetal Cd3As2. Nat. Mater. 15, 32 (2016). [DOI] [PubMed] [Google Scholar]
- Wang H. et al. Observation of superconductivity induced by a point contact on 3D Dirac semimetal Cd3As2 crystals. Nat. Mater. 15, 38 (2016). [DOI] [PubMed] [Google Scholar]
- Sankar R. et al. Large single crystal growth, transport property, and spectroscopic characterizations of three-dimensional Dirac semimetal Cd3As2. Sci. Rep. 5, 12966 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng J. et al. Large linear magnetoresistance in Dirac semimetal Cd3As2 with Fermi surfaces close to the Dirac points. Phys. Rev. B 92, 081306(R) (2015). [Google Scholar]
- Zhao Y. et al. Anisotropic Fermi surface and quantum limit transport in high mobility three-dimensional Dirac semimetal Cd3As2. Phys. Rev. X 5, 031037 (2015). [Google Scholar]
- Yoshida K. Transport of spatially inhomogeneous current in a compensated metal under magnetic fields. III. A case of bismuth in longitudinal and transverse magnetic fields. J. Appl. Phys 51, 4226 (1980). [Google Scholar]
- Parish M. M. & Littlewood P. B. Non-saturating magnetoresistance in heavily disordered semiconductors. Nature 426, 162 (2003). [DOI] [PubMed] [Google Scholar]
- Hu J., Rosenbaum T. F. & Betts J. B. Current jets, disorder, and linear magnetoresistance in the silver chalcogenides. Phys. Rev. Lett. 95, 186603 (2005). [DOI] [PubMed] [Google Scholar]
- Hu J. & Rosenbaum T. F. Classical and quantum routes to linear magnetoresistance. Nat. Mater. 7, 697 (2008). [DOI] [PubMed] [Google Scholar]
- Steigmann G. A. & Goodyear J. The crystal structure of Cd3As2. J. Acta Cryst. B 24, 1062–1067 (1968). [Google Scholar]
- Ali M. N. et al. The crystal and electronic structures of Cd3As2, the three-dimensional electronic analogue of graphene. Inorg. Chem. 53, 4062 (2014). [DOI] [PubMed] [Google Scholar]
- Novak M. et al. Large linear magnetoresistance in the Dirac semimetal TlBiSSe. Phys. Rev. B 91, 041203(R) (2015). [Google Scholar]
- Karplus R. & Luttinger J. M. Hall effect in ferromagnetics. Phys. Rev. 95, 1154 (1954). [Google Scholar]
- Luttinger J. M. Theory of the Hall effect in ferromagnetic substances. Phys. Rev. 112, 739 (1958). [Google Scholar]
- Hammar P. R. & Johnson M. Potentiometric measurements of the spin-split subbands in a two-dimensional electron gas. Phys. Rev. B 61, 7207 (2000). [Google Scholar]
- Silsbee R. H. Theory of the detection of current-induced spin polarization in a two-dimensional electron gas. Phys. Rev. B 63, 155305 (2001). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.