Adaptive Anisotropic Gaussian Filtering to Reduce Acquisition Time in Cardiac Diffusion Tensor Imaging

Abstract

Purpose

Diffusion tensor imaging (DTI) is used to quantify myocardial-fiber-orientation based on helical-angles (HA). Accurate HA measurements require multiple excitations (NEX) and/or several diffusion encoding directions (DED). Increasing NEX and/or DED increases acquisition time (TA). In this study, we reduce TA by implementing 3D adaptive anisotropic Gaussian filter (AAGF) on DTI data in ex-vivo normal and infarcted porcine hearts.

Methods

DTI was performed on ex-vivo hearts (9-healthy, 3-myocardial infarction (MI)) with several combinations of DED and NEX. AAGF, mean (AVF) and median filters (MF) were applied on primary eigenvectors prior to HA estimation. The performance of AAGF was compared against AVF and MF. Root mean square error (RMSE), concordance correlation-coefficients and Bland-Altman's technique was used to determine optimal combination of DED and NEX that generated best HA maps in least possible TA. Lastly, effect of AAGF on MI model was evaluated.

Results

RMSE in HA of AAGF was lower compared to AVF or MF. Post AAGF filtering fewer DED and NEX were required to achieve HA maps with similar integrity as those obtained from higher NEX and/or DED. Alterations caused in HA orientation in MI model were preserved post-filtering.

Conclusion

Our results demonstrate that AAGF reduces TA without affecting the integrity of myocardial microstructure.

INTRODUCTION

Myocardial fiber orientation governs electrical conduction and mechanical activation of the left ventricle (LV) [1]. The propagation of electrical impulses responsible for rhythmic contraction of the LV exhibits anisotropy, and occurs predominantly along the longitudinal axis of the myocardial fibers [2, 3]. Furthermore, the counter-directional helical organization of the myocardial fibers influences the torsional motion of the LV and assists in regulating stress and strain during systole and diastole [4, 5]. Remodeling of fiber orientation can result from either functional (arrhythmia [6]) or structural (myocardial infarction [7] and ventricular hypertrophy [8]) abnormalities. Therefore, a quantitative estimate of fiber orientation is important in order to investigate the influence of the orientation on the electromechanical properties of the heart.

In recent years, diffusion tensor imaging (DTI) has emerged as a non-invasive quantitative tool to characterize the orientation of myocardial fibers using helical angle (HA) measurement [9]. HA is defined as the measure of the angle between the short-axis imaging plane and the projection of the primary eigenvector onto the epicardial tangent plane [10]. It has been observed that a variety of pathological conditions, such as myocardial infarction (MI) and hypertrophic cardiomyopathy, effect myocardial fiber orientation [11, 12] rendering HA to be a potentially relevant quantitative diagnostic parameter.

The accuracy of HA measurements depends on the estimate of the diffusion tensor $\underset{̱}{\underset{¯}{\mathbf{D}}}$, which is very sensitive to noise. This sensitivity arises because the diffusion-weighted magnitude images (DWI) are degraded by Rician noise which leads to distorted estimates of the diffusion ellipsoids. Noise effects are further amplified as spatial resolution of the DWI is increased. $\underset{̱}{\underset{¯}{\mathbf{D}}}$ can be improved by i) acquiring more measurement directions for the anisotropic ellipsoid and ii) improving signal to noise ratio (SNR) of the DWI. The former can be achieved by increasing diffusion-encoding directions (DED) while the latter can be achieved by averaging the DWI over a number of excitations (NEX). However, an increase in either DED or NEX is directly proportional to an increase in acquisition time (TA). Previous ex-vivo cardiac DTI studies have used different DED-NEX combinations, and based on the spatial resolution the corresponding TA has ranged anywhere from between 30 minutes to 60 hours [13-16]. To the best of our knowledge, there is no extensive cardiac DTI literature that explores the optimal DED-NEX combination (in a minimal TA setting) required for accurate tensor estimation. A potential solution to improve tensor estimation is to implement post-acquisition filters during different stages of data processing. Various regularization and filtering techniques have been implemented in the past to improve image quality and to reduce noise primarily with respect to brain applications. These include sequential anisotropic Wiener filtering [17], bilateral filtering [18], Perona-Malik based filtering [19], wavelet based filtering [20], non-linear diffusion filtering [21, 22] and Riemannian based approach to anisotropic filtering [23]. Based on the implementation stage of these filters, filtering can be broadly categorized into three groups. In the first category, the filter is applied directly on raw DWI data prior to tensor estimation [17, 19, 21, 24]. In the second category, filtering is performed in conjunction with tensor estimation [25, 26], while in the last category, the filter is implemented directly on the diffusion tensors [27, 28].

In our investigation, we extend the concept of anisotropic filtering and develop a three-dimensional (3D) adaptive anisotropic Gaussian filter (AAGF) to smooth the eigenvectors of $\underset{̱}{\underset{¯}{\mathrm{D}}}$ specifically for myocardial applications. The filter is designed to preserve the structural information of myocardial fibers by taking into consideration the inherent curvature of the myocardium (caused by the transmurally rotating fibers) and smoothing primarily along the direction of the principle eigenvector. This specific adaptive anisotropic nature of the filter preserves the integrity of the underlying microstructure and prevents blurring which could potentially mask pathological changes. We hypothesize that the eigenvectors obtained from rapidly acquired DWI data with fewer NEX and DED, when filtered with our proposed technique, will generate HA with similar accuracy as that achieved from longer DWI acquisitions obtained with increased NEX and DED. Additionally, the competence of the filtering technique in identifying microstructural alterations in a diseased myocardium needed to be investigated (performed using a MI model).

THEORY

The general 3D Gaussian filtering uses a 3D spatially varying window with weights defined as:

$$G=\frac{1}{{\left(2\pi \right)}^{3∕2}\left({\sigma }_x\right)\left({\sigma }_y\right)\left({\sigma }_z\right)}{e}^{-[\frac{{(x-x_0)}^2}{{{\sigma }_x}^2}+\frac{{(y-y_0)}^2}{{{\sigma }_y}^2}+\frac{{(z-z_0)}^2}{{{\sigma }_z}^2}}$$ (1)

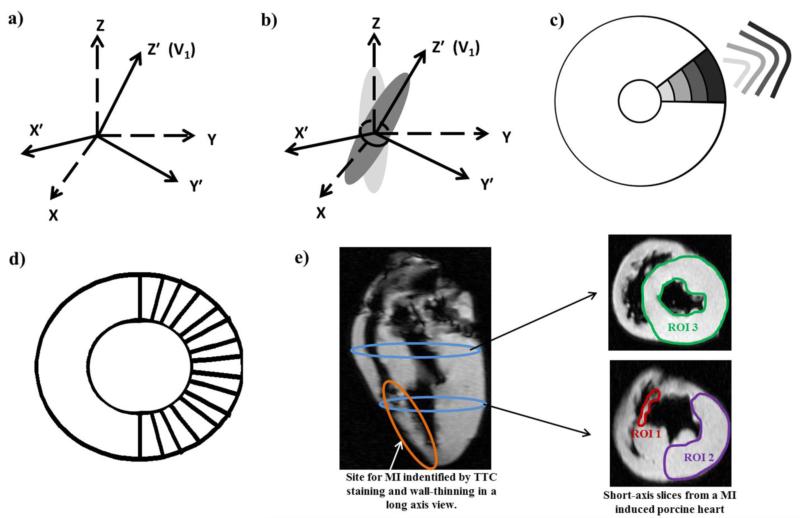
where σ_x, σ_y and σ_z represent the spread of the Gaussian function in x, y and z directions, respectively. G demonstrates anisotropic characteristics when the spread in one of the three directions is greater than the others. To preserve the structural information of the diffusion tensor, it needs to be ensured that the direction with the largest spread coincides with the direction of the primary eigenvector V₁. Therefore, for each imaging voxel an orthonormal local rotated coordinate system (x′, y′, z′) is defined, such that the rotated axis (z′) on which the maximum spread will be assigned aligns with the primary eigenvector V₁ (Fig 1a.).

Fig 1. Schematic of filter design and analysis.

a) Local coordinate system for each voxel, defining the orientation of the Gaussian filter for that particular voxel. b) Rotated anisotropic Gaussian kernel G′. c) σ_z′ of the rotated Gaussian kernel G′ increases with increasing radial distance as shown by the Gaussian profiles. d) Sixteen radial transmural profiles were examined to investigate the HA line profiles. e) Location of MI on a long axis view with arrows indicating the location of the 2 short axis slices used to perform filter sensitivity analysis on 3 ROIs (red, purple and green).

Based on this rotated coordinate system for each imaging voxel a rotated Gaussian window G′ is defined. As stated, the spread (σ_z′) of G′ in the z′ direction (designed to align with V₁) is greater than the spread (σ_x′, σ_y′) in the other two directions (Fig 1b.). G′ can be mathematically described by the following relation:

$$G^{\prime }(x^{\prime },y^{\prime },z^{\prime })=\mathit{R}\mathrm{G}(\mathrm{x},\mathrm{y},\mathrm{z})$$ (2)

where R is the rotation matrix given by:

$$\mathbf{R}=\left(\begin{array}{cccc}\hfill {x^{\prime }}_x\hfill & \hfill {x^{\prime }}_y\hfill & \hfill {x^{\prime }}_z\hfill & \hfill 0\hfill \\ \hfill {y^{\prime }}_x\hfill & \hfill {y^{\prime }}_y\hfill & \hfill {y^{\prime }}_z\hfill & \hfill 0\hfill \\ \hfill {z^{\prime }}_x\hfill & \hfill {z^{\prime }}_y\hfill & \hfill {z^{\prime }}_z\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$ (3)

Since G′ is the Gaussian window with respect to the rotated frame, it is defined as:

$$G^{\prime }=\frac{1}{{\left(2\pi \right)}^{3∕2}\left({\sigma }_{x^{\prime }}\right)\left({\sigma }_{y^{\prime }}\right)\left({\sigma }_{z^{\prime }}\right)}{e}^{-[\frac{{(x^{\prime }-x_0^{\prime })}^2}{{{\sigma }_{x^{\prime }}}^2}+\frac{{(y^{\prime }-y_0^{\prime })}^2}{\sigma {y^{\prime }}^2}+\frac{{(z^{\prime }-z_0^{\prime })}^2}{{{\sigma }_{z^{\prime }}}^2}]}$$ (4)

where (x₀′, y₀′, z₀′) = (x₀, y₀, z₀) is the centroid of the window and the point of rotation.

Furthermore, in order to account for the transmurally rotating fibers along the LV, σ_z′ is defined as a function of the radial distance (as shown in the short axis imaging plane in Fig 1c.). That is, as the Gaussian window moves away from the centroid of the lumen the spread in the V₁ direction increases with increasing radius. This is done to approximate the curvature of the heart (i.e. arc of a fiber) with a straight line (Fig 1c.).

Finally, the filtered eigenvector is obtained by applying the rotated kernel Gi′ on the eigenvector V_1i over a specific window length. The subscript i corresponds to a specific window occurrence as the window is scanned through the image space. To accommodate changes in V_1i, Gi′ is redefined each time the window is relocated, making the filter spatially variant.

METHODS

Animal Preparation

Preparation of Healthy Myocardium to Determine Optimal DED-NEX Combination Required to Generate Optimum HA Maps in Minimum TA

Nine ex-vivo porcine hearts were used to determine the optimal NEX and DED combination needed to estimate HA. The animals were euthanized and the hearts were extracted, flushed with saline and immersed in a 10% neutral buffered formalin solution at room temperature. Prior to scanning, the hearts were washed under running cold water and then immersed in water bath for 15 minutes to hydrate the myocardium.

Preparation of MI-Induced Myocardium to Evaluate Sensitivity of Filter

Three ex-vivo porcine hearts were used to evaluate the effectiveness of the filtering technique in preserving abnormal myocardial fiber orientation in MI-induced hearts. Infarction was created using ethanol injection in the left anterior descending artery (LAD) [29]. Post-infarction the animals were monitored for three weeks to allow maximum fibrosis and remodeling in the infarcted region [30]. After 22 days, the animals were euthanized and the hearts were removed, flushed with saline, stained using tetrazolium chloride to delineate the area of infarction and finally placed in a 10% neutral buffered formalin solution at room temperature. Prior to scanning, the same hydration procedure performed in the healthy hearts was followed in the MI-induced hearts.

Image Acquisition

Ex-vivo DTI was performed in 12 hearts (9 healthy, 3 MI) in a 3T MRI scanner (Tim Trio, Siemens Healthcare, Erlangen, Germany). A two-dimensional bipolar diffusion-weighted echo planar imaging sequence was used to acquire multi-slice short-axis views of the heart. Twenty one scans were performed with different combinations of NEX and DED as detailed in Table 1. The maximum NEX acquired in each DED (12, 30, and 64) group was limited by the maximum allowable TA which was fixed at ~ 30 mins. Other imaging parameters included: repetition time (TR)=7000 ms; echo time (TE)=90 ms; echo train length=128; echo spacing=0.7ms; bandwidth=1628 Hz/pixel; slice thickness=2 mm; imaging matrix=128×128; field of view (FOV)=256×256 mm²; isotropic voxel resolution=2×2×2 mm³ and b₀/b₁ value for diffusion encoding=0/1000 s/mm². Number of slices acquired ranged anywhere between 32 and 42, based on the individual heart size.

Table 1.

Acquisition parameters and AAGF analysis results.

Diffusion Encoding Direction (DED)	Number of Excitations (NEX)	Acquisition Time per Slice (TA in ms)	Mean RMSE from all 9 animals (HAUF)	Mean RMSE from all 9 animals (HAAAGF)	Concordance correlation-coefficients (ρc for 95% CI)	Mean Diff from reference standard (± 1SD) 95% Confidence Limits of Agreement
12	1	2,329	19.11 ± 1.9	16.68 ± 2.5	0.66 (0.64, 0.68)	0.82 (−24.57, 26.14)
	2	4,643	16.52 ± 1.8	14.30± 2.0	0.75 (0.74, 0.76)	1.29 (−19.8, 22.4)
	3	6,971	15.36 ± 1.7	13.52 ± 1.53	0.80 (0.79, 0.81)	1.2 (−17.6, 20.0)
	4	9,300	14.19 ± 1.8	12.57 ± 1.6	0.83 (0.82, 0.84)	1.47 (−15.4, 18.35)
	6	13,943	12.95 ± 1.7	11.97 ± 1.5	0.85 (0.84, 0.86)	1.65 (−14.19, 17.49)
	8	18,600	11.60 ± 1.7	11.26 ± 1.2	0.87 (0.86, 0.873)	1.71 (−13.27, 16.68)
	12	27,886	10.14 ± 1.4	10.71 ± 1.1	0.88 (0.87. 0.884)	1.79 (−12.33, 15.91)
	16	37,186	8.91 ± 1.3	10.19 ± 1.0	0.89 (0.88, 0.894)	1.8 (−11.64, 15.24)
	20	46,486	NA	NA	0.906 (0.9, 0.911)	1.81 (−10.37, 14)
30	1	5,586	16.05 ± 2.4	14.22 ± 2.5	0.76 (0.75, 0.77)	1.4 (−18.9, 21.72)
	2	11,157	13.70 ± 2.1	12.44 ± 2.1	0.817(0.81, 0.83)	1.15 (−16.81, 19.1)
	3	16,743	12.00 ± 2.0	11.76 ± 2.2	0.87 (0.86, 0.88)	1.64 (−13.18, 16.47)
	4	22,314	10.83 ± 2.2	11.02 ± 1.9	0.88 (0.876, 0.89)	1.48 (−12.47, 15.44)
	5	27,900	9.56 ± 1.6	10.30 ± 1.3	0.89 (0.887, 0.9)	1.53 (−11.73, 14.8)
	6	33,471	8.96 ± 2.2	10.25 ± 1.7	0.90 (0.89, 0.904)	1.54 (−11.36, 14.44)
	7	39,057	8.19 ± 1.7	9.98 ± 1.5	0.90 (0.89, 0.904)	1.71 (−11.05, 14.46)
	8	44,629	NA	NA	0.92 (0.91, 0.924)	1.66 (−9.7, 13)
64	1	11,629	13.92 ± 2.7	12.93 ± 2.8	0.82 (0.81, 0.83)	1.32 (−16.26, 18.9)
	2	23,243	10.61 ± 2.0	10.73 ± 1.7	0.88 (0.87, 0.884)	1.62 (−12.57, 15.81)
	3	34,871	8.81 ± 1.6	9.96 ± 1.4	0.89 (0.88, 0.92)	1.84 (−11.36, 15.04)
	4	46,486	NA	NA	0.92 (0.91, 0.921)	1.69 (−9.76, 13.13)

DED-NEX combination, corresponding acquisition time and mean normalized RMSE for unfiltered and AAGF filtered maps. The average time required to implement AAGF was 0.6 seconds per slice.

Image Analysis

The acquired images were masked to segment the LV. A pixel from the edge was left out of the mask from both the epicardium and endocardium to avoid boundary effects caused due to air-tissue interface. Custom-built software written in Matlab (Mathworks, Natick, MA) was used to process the masked images. Diffusion tensors were generated for all 21 acquisitions shown in Table 1 and subsequently diagonalized to determine the eigenvalues and eigenvectors. These eigenvectors were used to estimate unfiltered HA (HA_UF) maps.

Reference Standard

Due to the lack of direct histopathological correlation the maximum acquired NEX (20, 8 and 4 for DED 12, 30 and 64 respectively) in each group which was limited by the maximum allowable TA (~30 minutes) was used as the reference HA value.

Optimization of Filter Parameters and Analysis of Filter Performance using Healthy Myocardium (Comparison with Isotropic Filters)

The performance of AAGF was compared to 2 different 3D isotropic filters, a mean or averaging filter (AVF) and a median filter (MF). The primary eigenvectors were filtered using AAGF, AVF and MF, and these filtered eigenvectors were used to estimate HA maps (HA_AAGF, HA_AVF and HA_MF respectively) for every NEX in each DED group. AAGF filter specifications were as follows: Radial thickness of the myocardium was divided into 4 segments and the spread in the direction of maximum anisotropy (σ_z′) was incremented from 1.5 (endocardium) in steps of 0.5 for each segment to 3.0 (epicardium). The spreads in the other two directions (σ_x′ and σ_y′) were kept constant at 1. All units were defined based on pixel length. Several 3D filter window-lengths were explored on a randomly selected heart to find the optimal filter length. This optimal length was selected based on minimum normalized root mean square error (RMSE) in HA between the reference standard to that of each NEX for all DEDs. The same optimal window length was used for the isotropic filters. A normalized RMSE estimation of unfiltered and filtered HA from all 9 healthy hearts was plotted using SAS 9.4 software (SAS, Inc, Cary, NC). The mean normalized RMSE for unfiltered and filtered maps for each DED-NEX setting was estimated and plotted in the same figure to compare the performance of our proposed filtering technique.

Determining acquisition Parameters (DED, NEX) for Minimum TA

To determine acquisition parameters for measuring minimum TA, in each of the 3 DED settings (12, 30 and 64) a cut-off NEX (NEX_{F_C}) was established. This cut-off was based on the minimum NEX required by AAGF filter to produce robust HA_AAGF maps. Robustness of the filtered maps was determined by simultaneously considering normalized RMSE, concordance correlation-coefficient (ρ_c) [31] and Bland-Altman's limits of agreement [32]. Based on generated plots (mean RMSE from the 9 hearts) normalized RMSE from HA_AAGF map was regarded acceptable if it was within 5% of the minimum normalized RMSE obtained for that particular DED setting. Concordance coefficients and Bland-Altman's analysis (pooling the midventricular slices from all the animals) with a 95% confidence interval (CI) was generated using STATA 13 (StataCorp LP, College Station, Texas) by comparing HA_AAGF maps to the reference standard (in each DED group). To evaluate the minimum required NEX in each DED group a ρ_c greater than 0.8 was considered permissible. Additionally, narrow limits of agreement from the Bland Altman's plot were taken into account to assess agreement between HA_AAGF and reference standard maps.

Once NEX_{F_C} was established, HA line profiles were generated in three different slices of the LV (apex, mid and base), along 16 equally spaced (11.25° apart) transmural regions on the free wall (Fig 1d.) for both NEX_{F_C} based and reference HA maps. A comparison was performed to verify if the linear variation of HA line profiles from the epicardium to endocardium in the reference maps were comparable to the line profiles from the NEX_{F_C} maps. Finally, an inter-DED group assessment of the entire myocardium was performed to estimate the optimal combination of DED and NEX that generated the best HA_AAGF maps in the least possible TA.

SNR Analysis

SNR (ratio of mean signal to the standard deviation (SD) of noise in the b₀ image) was investigated in order to understand the relationship between reductions in normalized RMSE versus normalized SNR. The SNR from the reference image (in each DED group) was used for normalization in each DED-NEX combination. Additionally, we investigated the response of the filter at NEX_{F_C} in terms of available normalized SNR and reduction in normalized RMSE.

Analysis of Sensitivity of Filter in Diseased Myocardium (MI-Induced Hearts)

Once NEX_{F_C} was determined in the normal porcine hearts this value was used to generate HA_AAGF maps for each DED setting in the MI-induced porcine hearts. A pixel-wise comparison was performed (between the HA_AAGF maps and HA_UF maps generated from the reference standard) by estimating the percentage difference between the two HA measurements. Three ROIs were investigated in the diseased myocardium; one corresponded to the infarcted area (ROI 1), the second corresponded to a remote region on the same slice as the infarct (ROI 2), and the third (ROI 3) corresponded to a slice remote from the site of the infarct (Fig 1e.). Mean and SD for error in HA was determined in the 3 ROIs from the percentage difference maps and the result was used to evaluate the sensitivity of the filter to pathology influenced remodeling.

RESULTS

Optimizing Filter Length

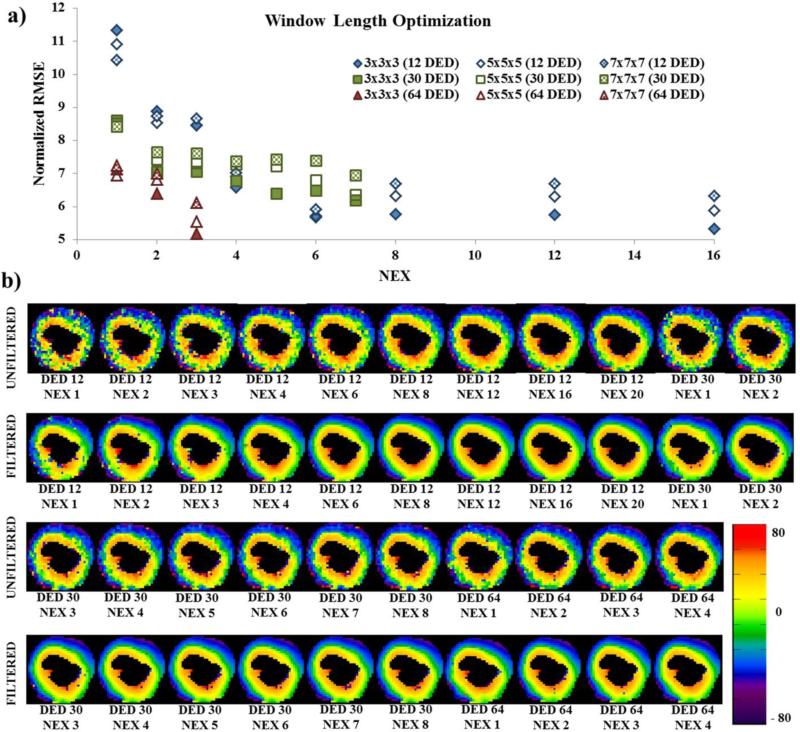
Optimization of filter length was performed by randomly selecting one porcine heart for all DED-NEX combinations, which was then used as a sample representation for further analysis in all the other hearts. AAGF was applied on the eigenvectors and HA maps were generated using 3 different window sizes, 3×3×3, 5×5×5 and 7×7×7. The normalized RMSE between the control and HA_AAGF (filtered using the 3 different window sizes) for each NEX is plotted in Fig 2a. We observed that in all the 3 DED groups the window length 3×3×3 led to the minimal normalized RMSE. Hence, the filter window 3×3×3 was used for all further processing. A representation of HA maps from a mid-ventricular slice of the myocardium in the same animal using the optimal window size (3×3×3) is shown in Fig 2b. The 1^st and 3^rd rows show HA_UF maps and its corresponding HA_AAGF maps are shown in the 2^nd and 4^th rows. The maps indicate that at each NEX, the HA_AAGF map obtained is a smoothed version of the corresponding HA_UF map. These maps represent the trend observed in all the other hearts.

Fig 2. AAGF window length optimization in the entire heart and HA map of a single slice for all 21 acquisitions.

a) Plot of NEX vs normalized RMSE of HA maps obtained with three filter windows 3×3×3, 5×5×5 and 7×7×7 for all the 21 acquisition to determine optimal window length. b) Unfiltered and filtered (filter window length used: 3×3×3) HA maps from a mid-ventricular 2 mm slice for all 21 acquisitions (labelled below each image). 1^st and 3^rd Row: HA_UF. 2^nd and 4^th Row: H_AAAGF.

Analyzing Filter Performance using Healthy Myocardium (Comparison with Isotropic Filters)

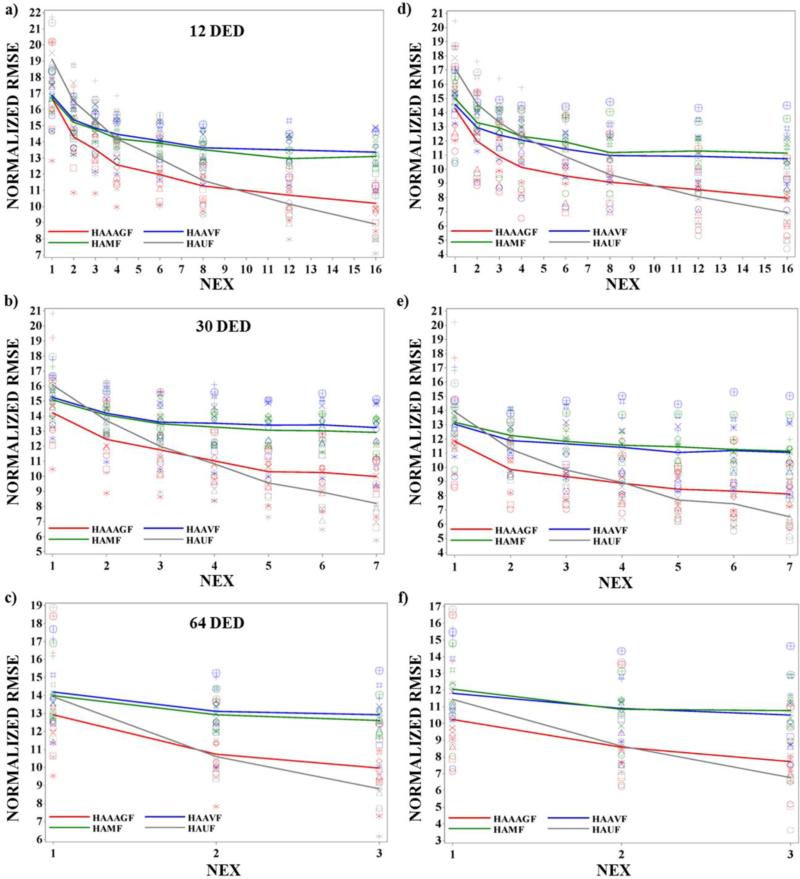
Eigenvectors were filtered with 3D 3×3×3 AAGF, AVF and MF and subsequently filtered HA maps were generated. For comparing the performance of each filter a NEX vs normalized RMSE graph for the entire heart in 9 animals was plotted (Fig 3(a-c)) and the mean (shown as colored lines on the plot) from all animals for each NEX was connected. A further assessment was performed on the central slices of the myocardium where transition in HA both in plane and through plane was subtle and less critical compared to the apex. Normalized RMSE estimation was performed for only 5 mid-ventricular slices and again the mean was generated for all the 9 animals (Fig 3(d-f)). We observed that the normalized RMSE for all NEX in the five mid-ventricular slices was lower than the normalized RMSE from the entire heart suggesting that the filter functioned better in the mid-ventricular slices. In both set of plots between the 3 filters (red (AAGF), green (MF) and blue (AVF)), AAGF had lower normalized RMSE throughout when compared to the isotropic filters indicating that AAGF filtering technique is superior to a regular mean or median filter.

Fig 3. Normalized RMSE vs NEX for the entire heart and 5 center slices for all the 9 healthy hearts.

Plot of normalized RMSE vs NEX for unfiltered HA maps and HA maps filtered using the 3 different filtering techniques (AAGF, AVF and MF) for a) 12 DED b) 30 DED and c) 64 DED for the entire heart and for d) 12 DED e) 30 DED f) 64 DED for the center slices in 9 healthy animals. The different markers represent normalized RMSE from each animal. The mean normalized RMSE profile for each filtering technique (AAGF (red), AVF (blue) and MF (green)) and the unfiltered maps (gray) is shown on the plot.

Determining acquisition Parameters (DED, NEX) for Minimum TA

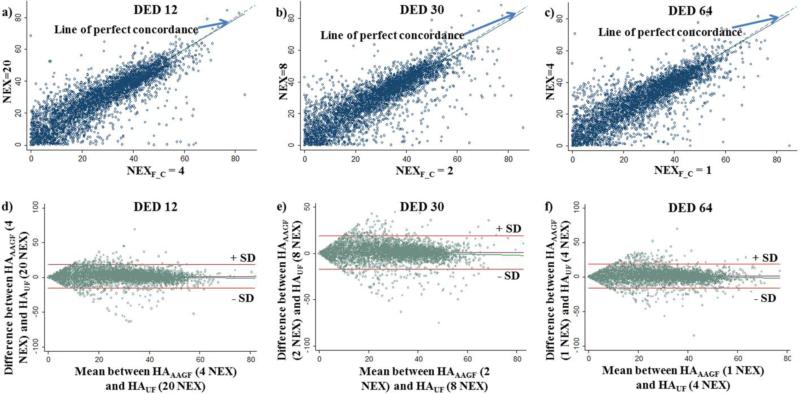
To determine the best acquisition parameters that provided the least TA we first needed to establish NEX_{F_C}. From Table 1 we see that the minimum normalized RMSE for the HA_UF maps for 12, 30 and 64 DED were 8.9%, 8.2% and 8.8% respectively. Therefore, the acceptable range of RMSE (<5% from the minimum) for 12, 30 and 64 DED would be 13.9%, 13.2% and 13.8% respectively. From the RMSE of the HA_AAGF maps, we observed that for 12 DED, any NEX above 3 (RMSE=13.5%) falls under the acceptable range (<13.9%) but going above 8 NEX does not provide any advantage (above 8 NEX normalized RMSE of the unfiltered maps is equal to or lower than the filtered maps). Furthermore, any NEX above 3 has a ρ_c (0.80 (95% CI: [0.79, 0.81]) which is within the permissible threshold (>0.8). Hence, any NEX from 3 to 8 can be defined as NEX_{F_C}, since they meet the set criterion. Now each of these NEX (3, 4, 6 and 8) reduced RMSE by 1.9%, 2.4%, 0.9% and 0.3% respectively, when compared to their unfiltered counterparts. We observe that increasing the NEX to 6 or 8 increases TA considerably (TA_NEX=6: 13.9s, TA_NEX=8:18.6s) while causing a marginal reduction (<1%) in RMSE. Additionally, between 3 and 4 NEX although both the reduction in RMSE and ρ_c is almost comparable, NEX=4 (1.47[−15.4, 18.35]) has a much narrower Bland-Altman's limits of agreement as compared to NEX=3 (1.2 [−17.6, 20.0]). Therefore, after simultaneously considering reduced normalized RMSE, good ρ_c and narrow limits of agreement NEX_{F_C} for a 12 DED acquisition was set to 4. The concordance plot and Bland-Altman's plot for NEX_{F_C}=4 shown in Fig 4(a, d) demonstrates that there is good agreement between HA_AAGF and the reference standard. A similar analysis was performed for 30 and 64 DED and the cut-offs were defined as 2 (RMSE=12.41% (Fig 3b), ρ_c=0.82[0.81, 0.83] (Fig 4b) and limits of agreement: 1.15[−16.81, 19.1] (Fig 4e)) and 1 (RMSE=12.9% (Fig 3c), ρ_c=0.82[0.81, 0.83] (Fig 4c) and limits of agreement: 1.32[−16.26, 18.9] (Fig 4f)) NEX, respectively. This reduced TA by approximately 5, 4 and 4 times for 12, 30 and 64 DED, respectively as shown in Table 1. In addition to the TA reported in Table 1 the average post-processing time required to implement AAGF was 0.6 seconds per slice, which was constant for the different DED-NEX combinations.

Fig 4. Concordance-correlation and Bland-Altman's Analysis.

Plot of Concordance-correlation between reference standard and NEX_{F_C} for a) 12 DED, b) 30 DED, c) 64 DED acquisition. The solid line corresponds to the reduced major axis and the dashed line corresponds to the line of perfect concordance. Bland-Altman's analysis was performed between reference standard and NEX_{F_C} generated maps for a) 12 DED, b) 30 DED, c) 64 DED acquisition. The solid lines show mean ± 1 SD.

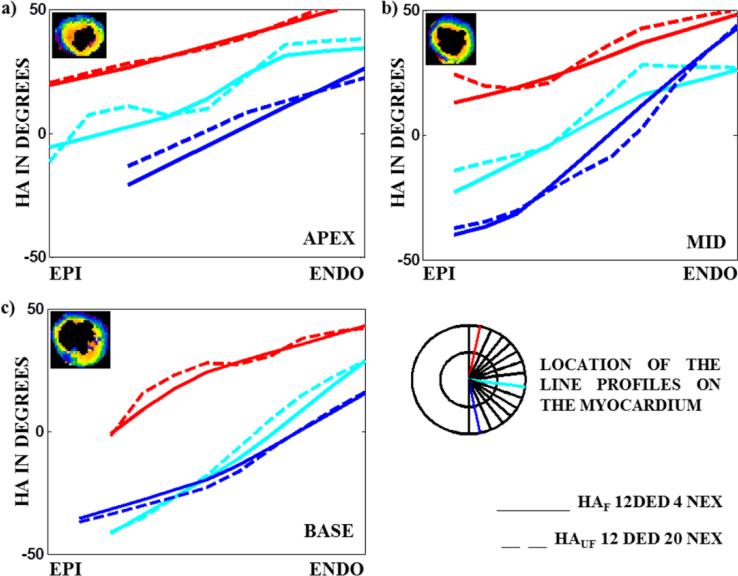
Once NEX_{F_C} was established, slices each from the apex, mid-ventricle and base were selected and line profiles were generated for HA_AAGF maps obtained from the cut-offs and HA_UF maps obtained from the reference standard. Three line profiles from a slice of the apex, mid and base sections of the LV with 12 DED acquisition in an animal is shown in Fig 5. The line profiles in the apex, mid-ventricle and base shows smooth transition from the epicardium to the endocardium. From the figure we also observe that the filtered profiles in all the cases are a good approximation of the unfiltered counterparts obtained from the reference standard. Similar trends were observed in all the other animals. Therefore, we can conclude that the structural information of the LV obtained with higher NEX can be approximated by filtering the lower NEX principal eigenvectors with our proposed technique, thereby causing a reduction in TA.

Fig 5. Three line profiles (the location of the profiles are shown in the cartoon of the LV) showing HA transition on a slice from the apex, mid-ventricle and base of the LV comparing HA maps obtained from NEX_{F_C} to the reference standard in a 12 DED acquisition.

HA maps of the slice in the a) apex b) mid and c) base for which the profiles have been generated are shown in the top left hand corner of each image. Line profiles generated from filtered HA maps obtained from NEX_{F_C} (4 NEX, solid line) show a smooth transition from the epicardium to the endocardium and are in agreement with the reference standard (20 NEX, dotted line).

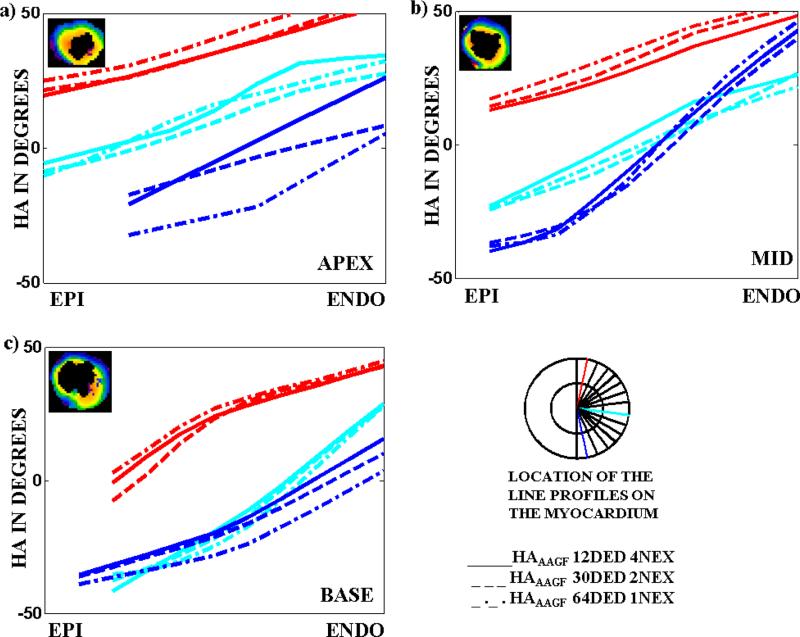
Finally, an inter-DED group comparison was performed to establish the best DED-NEX combination that provided the least TA. Fig 6(a-c) compares different line profiles in the apex, mid-ventricle and base of a myocardium for the 3 DED settings (12, 30 and 64) with their respective NEX_{F_C} (4, 2 and 1). The comparison establishes that HA_AAGF maps from the different encoding groups agree well with each other. However, TA for HA_AAGF with 12 DED and 4 NEX was minimum (9.3s for a single slice) indicating that this combination of DED-NEX generates the best HA_AAGF maps in the least possible time.

Fig 6. Three line profiles (the location of the profiles are shown in the cartoon of the LV) showing HA transition on a slice from the apex, mid-ventricle and base of the LV comparing HA maps obtained from NEX_{F_C} for all the 3 DED settings (12, 30 and 64).

HA maps of the slice in the a) apex b) mid and c) base for which the profiles have been generated are shown in the top left hand corner of each image. Line profiles generated from filtered HA maps obtained from NEX_{F_C}, for 12 (solid), 30 (dashed) and 64 (dashed-dotted) DED show a smooth transition from the epicardium to the endocardium and are in agreement with the each other.

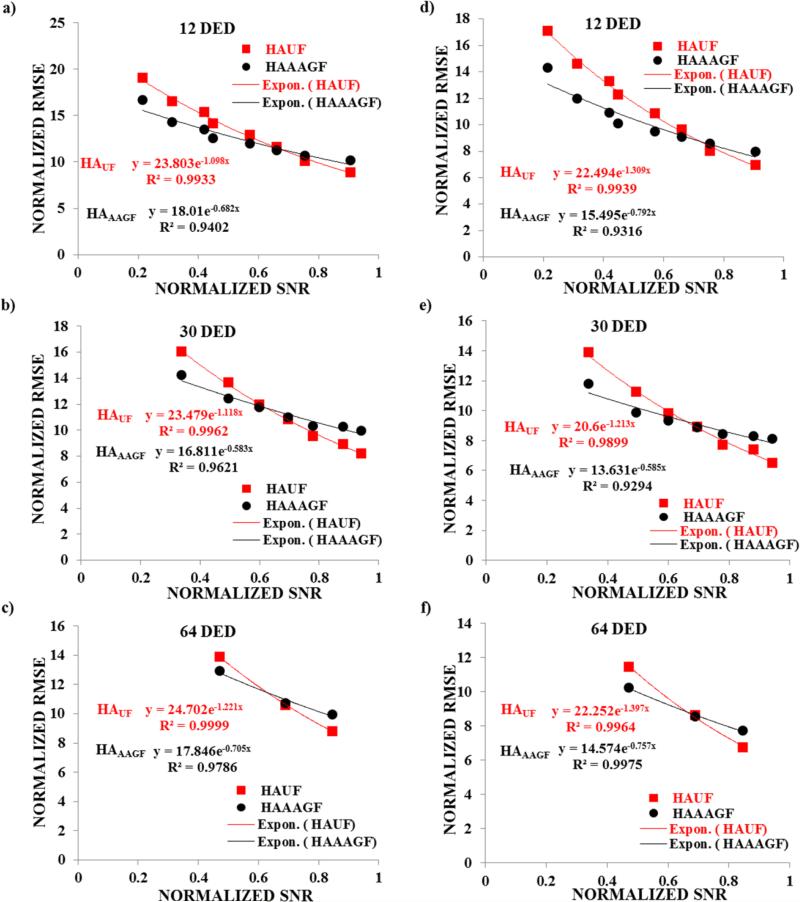
SNR Analysis

We next evaluated the association between RMSE and SNR. Fig 7. shows a plot of normalized RMSE (HA_AAGF and HA_UF) versus normalized SNR in all the 3 DED settings both for the entire heart and the 5 center slices. It was observed that with increasing normalized SNR (increasing NEX) the normalized RMSE exhibited an exponential decrease for both the AAGF filtered and unfiltered maps. An exponential regression analysis demonstrated that R² values in all the cases was greater than 0.93 (as shown in the Fig 7) displaying a strong inverse correlation between increasing SNR and RMSE (i.e., RMSE decreased with increasing SNR). A further assessment showed that at NEX_{F_C} the available SNR for all 3 DED groups is less than 50% of the reference standard. As mentioned earlier, it was observed that HA_AAGF provides reduced normalized RMSE compared to HA_UF at this SNR (less than 50%) indicating that at low SNR AAGF provides better estimates of DTI. This shows that AAGF allows lower SNR acquisitions to produce better vector estimates thereby assisting in decreasing TA.

Fig 7. Regression analysis of normalized RMSE (both from AAGF filtered and unfiltered) vs normalized SNR for the entire heart and center slices.

Plot of normalized RMSE vs normalized SNR for HA_UF maps and HA_AAGF for a) 12 DED b) 30 DED and c) 64 DED for the entire heart and for d) 12 DED e) 30 DED f) 64 DED for the center slices in 9 healthy animals. The R² values for each correlation for the exponential regression analysis is shown in each figure and the fit is denoted by a solid lines for both HA_UF (red) and HA_AAGF (black).

Analyzing Sensitivity of Filter in Diseased Myocardium (MI-Induced Hearts)

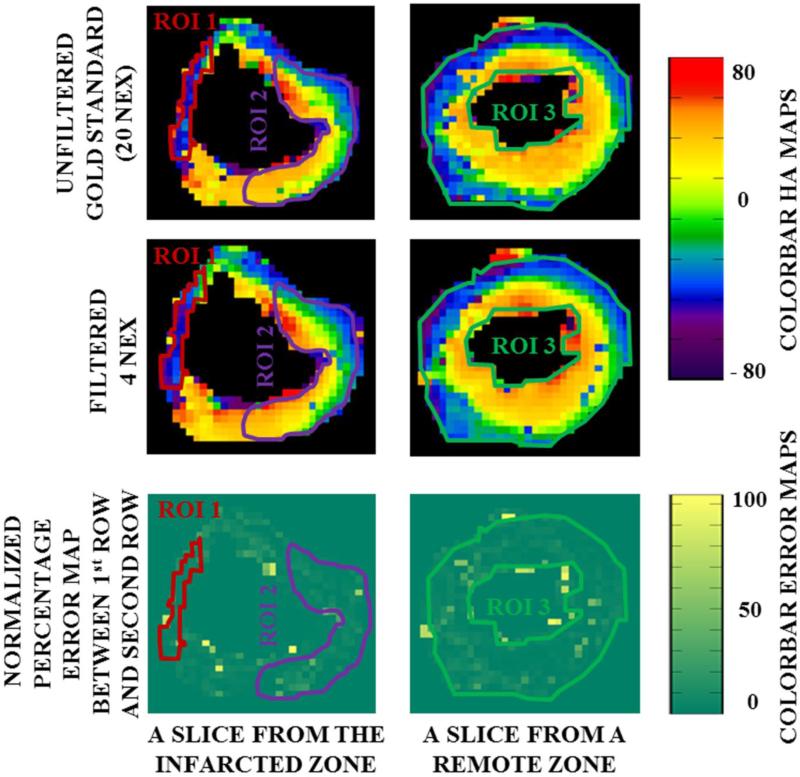
Fig 8 shows HA maps obtained from 12 DED AAGF data with NEX=4 (top row) and from the reference standard (NEX=20, 2^nd row) in a porcine myocardium induced with MI. The percentage difference between the AAGF data and the reference standard is shown in the 3^rd row of the figure. This animal had a prominent infarct in the septal wall of the apex, which extended into the mid-ventricular region. As mentioned earlier, 3 distinct ROIs were investigated. Since the infarct was observed in the septal wall (area approximated in TTC staining, confirmed by myocardial wall thinning in MRI scout images), ROI 1 corresponds to the infarct region on the septal wall as shown by the red contour. On the same slice a region ROI 2 was selected on the free-wall far from the infarct denoted by the purple contour. A third region remote to the site of the infarct was defined in a basal slice as indicated by the green contour. From ROI 1 we can conclude that the infarcted region demonstrated a distinct loss in endocardial layer and mid-myocardial layer, as majority of the myocardium within the red contour (infarcted region) has HA values corresponding to the epicardial layer. ROI 2 had the usual trend of a smooth transition of HA from the endocardium to the epicardium indicating that this region was not affected by the remodeling process caused due to MI. HA transition in ROI 3 was consistent with that from a healthy heart suggesting that the basal slices were unaffected by the pathological changes. The error maps demonstrated uniformity throughout the LV except for a few pixels near the epicardium and endocardium mostly due to air/tissue interface causing susceptibility artifact. These few pixels in the error maps have been deliberately left out of the contour while calculating the mean percentage error in each ROI since it appears primarily to be an edge/susceptibility artifact. The mean percentage error and the SD in ROI 1, ROI 2 and ROI 3 for the 3 DED setting in the 3 MI-induced pigs is shown in Table 2. A mean error percentage less than 10% suggests that there was good agreement between the filtered and reference maps, thereby indicating that the filtering technique is sensitive to disease conditions and can successfully preserve pathological anomalies caused on the micro-structure of the myocardium.

Fig 8. HA maps and error profiles for infarcted myocardium. 1^st Row.

HA_UF map Left: From an infarcted region Right: From a basal slice, remote to the infarction site. 2^nd Row: HA_AAGF mapLeft: From an infarcted region Right: From a basal slice, remote to the infarction site. 3^rd Row: Percentage difference between HA_UF and HA_AAGF Left: From an infarcted region Right: From a basal slice, remote to the infarction site. Error map is very uniform within the three different ROI under investigation.

Table 2.

Error Percentage Measurements.

DED	ERROR PERCENTAGE
	MI Pig 1			MI Pig 2			MI Pig 3
	ROI 1	ROI 2	ROI 3	ROI 1	ROI 2	ROI 3	ROI 1	ROI 2	ROI 3
12	1.85±1.5	5.18±5.4	4.03±5.2	2.68±5.6	7.01±9.7	5.10±7.6	3.03±2.9	3.2±3.7	4.4±6.7
30	2.48±2.3	4.60±4.8	3.71±7.2	6.39±6.3	6.93±6.8	6.47±8.1	3.82±3.3	3.05±3.0	4.2±6.5
64	2.38±1.9	5.62±7.6	2.44±2.7	6.79±7.7	7.88±10.6	6.83±9.3	5.09±7.6	3.10±3.5	4.5±6.9

Mean and SD of the percentage error between HA_AAGF maps obtained from NEX_{F_C} and corresponding HA_UF reference maps for the 3 DED settings in the 3 different ROI measured in all the 3 MI-induced pigs.

DISCUSSION

Our results demonstrate that a potential alternative approach towards improving LV HA estimation from diffusion tensor imaging is to apply post-processing AAGF on the principal eigenvectors. Currently, AAGF is implemented offline, however, if tensors are estimated during reconstruction AAGF can be added to the reconstruction pipeline of the MR scanner. Applying AAGF allows a significant reduction in scan time by making additional image acquisition unnecessary. The average time required to implement AAGF is approximately 0.6 seconds per slice which is insignificant compared to the improvement in TA. Since AAGF is applied on the eigenvectors the processing time is constant for any DED-NEX combination and is only dependent on the number of pixels containing in the data. The locally modified anisotropy of the AAGF is an important improvement over isotropic mean or median filtering because it reduces transmural blurring. This conservative smoothing scheme preserves pathological anomalies as demonstrated by the feasibility study in a MI model.

We observed that the RMSE estimate was higher for the entire heart as compared to the central slices. This higher error can be attributed to the characteristic spiral geometry that forms a partial loop-8 structure at the apex [33, 34]. Due to this sharp turn in the helical angles at the tip of the apex, and a low image resolution (voxel dimensions: 2×2×2 mm³), voxels near the apex had mixed tissue types which contributed to partial volume effects, thereby corrupting the tensor estimation. Furthermore, the number of pixels available in the apical slices was fewer compared to the mid-ventricular slices and hence the same straight line approximation of the Gaussian function that works in the mid-ventricular regions may fail for the apical slices. This can be partially resolved by modifying AAGF, and making it adaptive such that the filter specifications are varied as a function of the axial length. That is, the window size would increase with increasing distance from the apex to the base of the heart and the radial variation of the Gaussian function would also be dependent on location of the window on the long axis. However, this investigation is beyond the scope of this paper.

Most of the anisotropic DTI filters in the literature have been developed for brain applications. Since white matter tracts are long and relatively straight fibrous structures, these filters are not suited to encounter the curved myocardial anatomy. The AAGF approach uses the curvature of the myocardium and the organization of fibers to implement a spatially dependent filter shape that adapts to the orientation and curvature of the fiber.

Currently, AAGF is implemented directly on the primary eigenvectors to estimate HA. However, its application is not restricted to HA estimation, but can potentially be extended to all myocardial DTI metrics derived from the primary eigenvectors. For example, the filtered eigenvectors could be used for myocardial fiber tracking applications.

To the best of our knowledge, there is no gold standard for the ideal DED-NEX combination in literature and all protocols are built on individual applications restricted by TA. In our current study, we observed that if AAGF is applied, 12DED-4NEX is sufficient to generate robust HA maps. This conclusion was drawn from the mean of 9 ex-vivo porcine hearts. Individual analysis of the heart yielded the same results ensuring that the conclusions were not biased by the effect of a single myocardium. However, since a previous study has shown that at least 30DED is necessary for fiber tracking applications [35], if the application of AAGF is further extended for fiber tracking, additional investigation is necessary to analyze the effect of the filtering technique on fiber tracts.

The cut-off DED-NEX combination established in this manuscript may not directly relate to in-vivo imaging since imaging parameters would be completely different (TE, TR, spatial resolution) and presence of ECG trigger and cardiac motion would generate a very different SNR response. However, with respect to in-vivo cardiac DTI sequences available in literature [36-39], we can analyze the potential impact of the filtering technique on improving DTI vector estimates and scan time. The stimulated echo acquisition mode (STEAM) sequence [37, 40] use 6DED-1NEX acquisition to estimate eigenvectors. Although 6 DED was not investigated in this study but 1NEX acquisition was explored for all the 3 DED settings. Based on that we can conclude that in each case HA estimated from AAGF for 1 NEX had a lower RMSE compared to unfiltered HA indicating that filtering in-vivo images could potentially improve eigenvector estimation and in turn improve HA measurements and fiber tracking. The motion compensated spin echo approach [38] used 6DED-30NEX which takes 7 mins at an average heart rate of 60 bpm. Considering the results from 12DED-20NEX data, we can conclude that improvement in tensor estimation with increasing averages plateaus (marginal improvement with increasing averages) after a certain NEX (Fig 3) and 12DED-4NEX was sufficient to estimate HA when the eigenvectors were filtered using AAGF. Therefore, assuming that the same trend prevails for in-vivo imaging, acquiring so many averages may not be necessary thereby decreasing the scan time considerably.

Literature reports contradictory effect on HA transitions as a result of MI. One group reported a distinct shift towards negative helix [15, 41] in regions both adjacent and remote to the infarction, while another group reported a noticeable rightward/positive shift [16]. We have not noticed any specific trend as such in the three MI models we investigated; exploring further on the trend of HA due to MI remodeling is beyond the scope of this work. However, this study ensured that the filtering technique proposed could well preserve the abnormal fiber orientation observed in a diseased myocardium. In the 3 MI-induced myocardium examined here, anomalies noticed in pre-filtered reference HA maps existed in post-filtered maps.

There are a few limitations in our study. First, using histology as the gold standard to validate HA was not feasible since the hearts were borrowed from another study. However, range of HA observed in our study and the trend of HA transition from epicardium (left-handed helix) to endocardium (right-handed helix) is consistent with the literature [16, 42] which has been previously validated histologically [9].Second, higher NEX at higher DED was not performed in order to limit maximum scan time to be ~30 minutes for each encoding direction. Third, since reference standard was based on the maximum scan time (~30 minutes), RMSE, ρ_c and Bland-Altman's analysis obtained in this study is not absolute and dependent on the reference standard. However, since the reference standard between the unfiltered and filtered image was kept constant, the results obtained in this study is unbiased. Fourth, lower spatial resolution which was limited by our maximum acquisition time might have compromised the true estimation of HA at the apex due to sharp turn angles. Fifth, it is known that formalin-fixation causes de-hydration in tissues, which was mitigated by soaking the hearts in a water-bath for 15 minutes prior to each scan [43]. Finally, since all the acquisitions were performed in one scan session, signal obtained from later acquisitions can vary due to loss of moisture content in the sample, however it was compensated by repeatedly spraying saline water on the tissue. Despite of these limitations we have demonstrated that AAGF is superior to the isotropic filters thereby reducing TA.

CONCLUSION

In this study, an AAGF was implemented to smooth the eigenvectors generated from DTI. The subsequent effect of filtering the primary eigenvectors obtained both by fewer NEX and DED produced robust HA similar to that derived from primary eigenvectors of higher NEX with increased DED, thereby reducing TA considerably. The filtering technique could also successfully preserve pathological differences.