Abstract
During level-ground walking, mechanical work from each leg is required to redirect and accelerate the center of mass. Previous studies show a linear correlation between net metabolic power and the rate of step-to-step transition work during level-ground walking with changing step lengths. However, correlations between metabolic power and individual leg power during step-to-step transitions while walking on uphill/downhill slopes and at different velocities are not known. This basic understanding of these relationships between metabolic demands and biomechanical tasks can provide important information for design and control of biomimetic assistive devices such as leg prostheses and orthoses. Thus, we compared changes in metabolic power and mechanical power during step-to-step transitions while 19 subjects walked at seven slopes (0°, +/−3°, +/−6°, and +/−9°) and three velocities (1.00, 1.25, and 1.50 m/s). A quadratic model explained more of the variance (R2=0.58–0.61) than a linear model (R2=0.37–0.52) between metabolic power and individual leg mechanical power during step-to-step transitions across all velocities. A quadratic model explained more of the variance (R2=0.57–0.76) than a linear model (R2=0.52–0.59) between metabolic power and individual leg mechanical power during step-to-step transitions at each velocity for all slopes, and explained more of the variance (R2=0.12–0.54) than a linear model (R2=0.07–0.49) at each slope for all velocities. Our results suggest that it is important to consider the mechanical function of each leg in the design of biomimetic assistive devices aimed at reducing metabolic costs when walking at different slopes and velocities.
Keywords: Locomotion, Biomechanics, Metabolic, Step-to-step transition, Slope
1. Introduction
To walk, humans utilize metabolic energy to perform mechanical tasks such as generating force to support weight and performing work to redirect/accelerate the center of mass (COM) from step-to-step. COM dynamics have been well represented by an inverted pendulum model during single leg support for level-ground walking at constant velocities (Cavagna et al., 1977; Gottschall and Kram, 2006). This model suggests minimal mechanical work to sustain steady-speed locomotion because of a constant phasic exchange of potential and kinetic energy (Cavagna et al., 1977, 2000). However, during step-to-step transitions, the leading leg absorbs mechanical work to slow downward movement of the COM while the trailing leg generates mechanical work to redirect the COM upward and forward (Alexander, 1980; Donelan et al., 2002a, b; Kuo, 2007; Adamczyk and Kuo, 2009).
Individual leg mechanical power during step-to-step transitions changes with velocity over level-ground (Donelan et al., 2002a, b; Adamczyk and Kuo, 2009; Franz et al., 2012), such that the leading leg absorbs and trailing leg generates work simultaneously during step-to-step transitions. However, both legs generate work while walking on uphill slopes greater than 0° and absorb work when walking on downhill slopes less than 0° at 1.25 m/s (Franz et al., 2012). Similarly, metabolic power increases with uphill slopes greater than and decreases with downhill slopes less than −3° (Kang et al., 2002; Minetti et al., 2002; Sawicki and Ferris, 2009; Silder et al., 2012). However, step-to-step transition work and metabolic demands for the combined effects of slope and velocity have not been examined.
Previous research has shown strong correlations between metabolic power and individual leg mechanical power performed during step-to-step transitions for level-ground walking at 0.72–1.97 m/s with varying step lengths (Donelan et al., 2002a). Donelan et al. found that when step length is varied, 79–89% of the variance in metabolic power is explained by individual leg mechanical power during the step-to-step transition (Donelan et al., 2002a). This strong correlation between metabolic and individual leg step-to-step transition power during level-ground walking suggests a correlation may exist when walking uphill and downhill at different velocities. However, these correlations have not been established. Further, because previous research has shown that the ankle accounts for 46–89% of the external power required for level-ground walking (Winter, 1983; Farris and Sawicki, 2012), understanding the correlations between metabolic and mechanical power is important for design, development, and control of robust biomimetic assistive devices such as leg prostheses and orthoses (Ferris et al., 2007). Previous studies suggest that prosthetic ankle power plays an important role in reducing metabolic demands during level-ground walking (Herr and Grabowski, 2012; Caputo and Collins, 2014).
Our purpose was to determine the correlations between metabolic power and individual leg step-to-step transition mechanical power during walking across a wide range of slopes and velocities. We sought to better understand the basic biomechanics and metabolic costs of unimpaired human walking. Metabolic power increases and leading (Plead) and trailing (Ptrail) leg mechanical powers are more positive on steeper uphill slopes compared to level-ground walking. Metabolic power decreases, and Plead and Ptrail are more negative on steeper downhill slopes compared to level-ground walking. Further, metabolic power increases, Plead is more negative and Ptrail is more positive at faster velocities (Minetti et al., 1993, 2002; Franz et al., 2012). We hypothesized that metabolic power would be correlated with Plead and Ptrail for all slopes (−9° to 9°) and velocities (1.00 m/s, 1.25 m/s and 1.50 m/s). We also hypothesized that the ratio of individual leg mechanical power during step-to-step transitions to the overall metabolic power, indicated as the individual limb power ratio (ILPR), would be similar across all slopes and velocities.
2. Methods
Nineteen subjects with no lower extremity or neurological injuries or pathologies volunteered [13 M, 6 F, mean 29.2 years (8.4 years); 69.6 kg (13.2 kg)] and gave informed written consent prior to participating in accordance with a protocol approved by the Department of Veteran Affairs’ Human Subjects Institutional Review Board. Subjects walked on a dual-belt force-measuring treadmill (Bertec Corp., Columbus, OH) at seven slopes (0°, +/−3°, +/−6°, and +/−9°) and three velocities (1.00, 1.25, and 1.50 m/s). We used constant speeds for comparisons across conditions and with other studies (Franz et al., 2012). First, we measured each subject’s mass and metabolic rate while standing. Then, we measured metabolic rates and ground reaction forces during each six-minute walking trial. Trial order was randomized, and at least two minutes rest was enforced between trials. Data collection occurred over three sessions at the same time each day to account for potential day-to-day variability in metabolic rates. Seven walking conditions were tested each day.
2.1. Metabolic power
We measured rates of oxygen consumption (; ml/min/kg) and carbon dioxide production (; ml/min/kg) using indirect calorimetry (Parvo Medics TrueOne 2400, Sandy, UT). We averaged and from the last two minutes of each trial and calculated metabolic power using a standard equation (Brockway, 1987). We determined net metabolic power by subtracting standing from each trial’s metabolic power.
2.2. Step-to-step transition power
We measured ground reaction forces (F) at 1500 Hz from each leg and normalized all data to body mass (m). We filtered F with a fourth order low-pass Butterworth filter and 20 Hz cutoff frequency using a custom program (Matlab, Natick, MA). COM acceleration (a) with respect to time (t) was calculated as follows:
| (1) |
| (2) |
| (3) |
where medio-lateral (ML), parallel (parallel), and perpendicular (perp) components of force were calculated relative to the treadmill slope (θ). COM velocity (ν) was calculated as the integral of acceleration with respect to time
| (4) |
We determined integration constants (ν0) for perpendicular (νperp) and medio-lateral (νML) velocities by assuming that average ν over a stride equaled zero. We determined ν0 for parallel velocity (νparallel) by assuming that average ν over a stride equaled treadmill velocity. We calculated external mechanical power performed by each leg during step-to-step transitions using the method described by Donelan et al. (2002a). We calculated step-to-step transition power absorbed and generated by each leg (Plead and Ptrail) on the COM as the sum of the products of ground reaction force (F) and COM velocity (νcom) during the step-to-step transition
| (5) |
| (6) |
We defined step-to-step transition as the time when both legs were on the ground (Donelan et al., 2002a). We detected heel-strike and toe-off with a force threshold of twice the average signal noise when nothing was in contact with the treadmill. Step-to-step transitions may extend beyond double support (Adamczyk and Kuo, 2009), but our primary interest was to understand correlations between metabolic power and mechanical power absorbed at initial contact and produced during late stance, thus we defined the step-to-step transition as the time of double support. We calculated each subject’s average individual leg powers during step-to-step transitions from approximately 75 steps per subject. Then, we calculated the average and standard deviation of individual leg power from all subjects.
2.3. Relationship between individual leg mechanical power and metabolic power
Based on research by Donelan et al. (2002a, b), we quantified correlations between metabolic and individual leg mechanical power using linear models. Because leg muscles must produce force to move the COM forward during walking and thereby incur a metabolic cost, musculoskeletal models have optimized muscle activation squared to accurately predict biomechanical data for a walking gait cycle (Crowninshield and Brand Richard, 1981; Anderson and Pandy, 2001; Thelen, et al., 2003) and approximate metabolic cost (Umberger and Rubenson, 2011). Based on this research, we also investigated quadratic models when correlating metabolic power and individual leg mechanical power. Further, we analyzed data for all slopes at individual speeds based on work by Farris and Sawicki (2012) that demonstrated a quadratic change in individual leg work with faster constant speed.
2.4. Individual limb power ratio (ILPR)
We quantified ILPR as the ratio between average individual leg mechanical power during step-to-step transitions and average metabolic power for the entire walking task. We acknowledge that other mechanical tasks account for the metabolic power required during the entire gait cycle, but sought to specifically understand how relative changes in step-to-step transition power affected metabolic power at different slopes and velocities. As such, ILPR shows the effect of each leg’s step-to-step transition power on overall metabolic power, but underestimates ILPR for the entire walking task
| (7) |
| (8) |
2.5. Statistics
We used two-way repeated measures ANOVAs (P<0.05) to compare metabolic power and step-to-step transition power of each leg at different slopes and velocities. Our within subject variables were slope with seven levels: 0°, ±3°, ±6°, and ±9° and velocity with three levels: 1.00, 1.25, and 1.50 m/s. We correlated average metabolic power with average step-to-step transition power of each leg using linear and quadratic curve fitting regression models (RStudio, Boston, MA), where the strongest correlation delineated the best model.
3. Results
3.1. Metabolic power
Average metabolic power was statistically different between all slopes except between −6° and −3° (F(6,114)= 1161.69, P<0.001). Greater metabolic power was required to walk with increasing slopes from −3° to 9° and decreasing slopes from −6° to −9° (Fig. 1). At all velocities, metabolic power was 20% greater at −9° compared to −6° (1.97 W/kg to 1.63 W/kg) and over five times greater at 9° compared to −3° (10.38 W/kg to 1.69 W/kg). On all slopes, metabolic power was statistically different between all velocities (F(2,38)=734.00, P<0.001). We found a significant interaction effect between slope and velocity (F(12,228)=109.527, P<0.001). At 1.00 and 1.25 m/s, metabolic power was statistically different for each slope, except for −6° and −3° (Fig. 1). At 1.50 m/s metabolic power was statistically different for each slope, except −9° and −6° compared to −3°.
Fig.1.
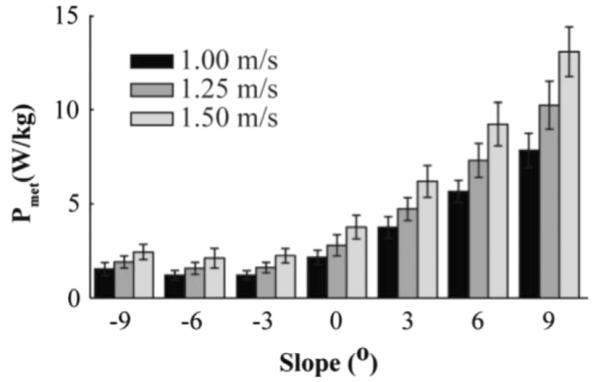
Average (S.D.) metabolic power (Pmet) for seven slopes and three velocities (n=19). In general, Pmet increased at slopes greater or less than −3° and increased with velocity within each slope condition. Specific pairwise comparisons are described in Section 3.
3.2. Step-to-step transition power
Leading leg step-to-step transition power (Plead) decreased significantly with decreasing slopes and faster velocities (F(6,114)=186.34, P<0.001; F(2,38)=261.01, P<0.001; Fig. 2b). Plead from all velocities decreased by 118% from 9° to −9° (0.76 W/kg to −4.31 W/kg). Plead from all slopes was over two-fold more negative at 1.50 m/s compared to 1.00 m/s (−2.11 W/kg to −0.66 W/kg). There was also a significant interaction effect between velocity and slope (F(12,228)=8.75, P < 0.001). At slopes of −9° and −6°, Plead was more negative between 1.00 and 1.50 m/s and between 1.25 and 1.50 m/s. At −3°, Plead was more negative with faster velocities and all velocities were significantly different from each other. At 1.00 m/s, Plead was more positive with increasing slopes between −9° and 0°, 3°, 6°, 9°, between −6° and 0°, 3°, 6°, 9°, between −3° and 3°, 6°, 9°, between 0° and 6°, 9°, and between 3° and 9°. At 1.25 m/s, Plead was more positive with steeper uphill slopes, except between 3° and 6°. At 1.50 m/s, Plead was more positive with steeper uphill slopes, except between 0° and 3°, 3° and 6°, and 6° and 9°.
Fig. 2.
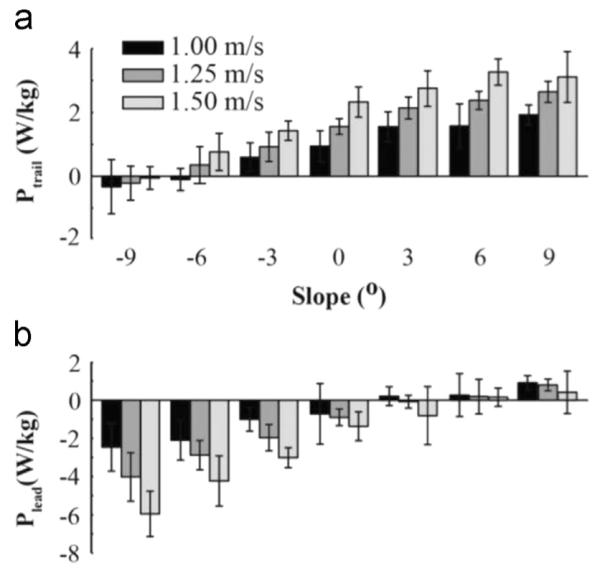
Average (S.D.) mechanical work of individual legs during step-to-step transitions. (a) Mechanical work of the trailing leg (Ptrail) during the step-to-step transition at each slope and velocity. Ptrail was more positive with increasing slope from −9° to 9° and at faster velocities. (b) Mechanical work of the leading leg (Plead) during the step-to-step transition at each slope and velocity condition. Plead was more positive with increasing slope from −9° to 9° and at slower velocities.
Trailing leg step-to-step transition power (Ptrail) increased significantly with increasing slopes and faster velocities (F(6,114)=311.15, P < 0.001; F(2,38)=330.19, P < 0.001; Fig. 2a). Ptrail from all velocities increased nine-fold from −9° to 9° (−0.31 W/kg to 2.58 W/kg). Ptrail from all slopes was 125% greater at 1.50 m/s compared to 1.00 m/s (1.80 W/kg to 0.86 W/kg). At each slope from −6° to 9°, we found a significant interaction effect for Ptrail between velocity and slope (F(12,228)=4.898, P < 0.001). Ptrail increased significantly with faster velocities, except for between 1.00 and 1.25 m/s at −6° and between 1.25 and 1.50 m/s at 9°. Ptrail did not change with velocity at −9°. More specifically, at 1.00 m/s, Ptrail increased with slope, except between −9° and −6°, −3° and 0°, 0° and 3°, 3° and 6°, and 6° and 9°. At 1.25 m/s, Ptrail increased with slope, except between 3° and 6°, and 6° and 9°. At 1.50 m/s, Ptrail increased with slope, except between 0° and 3°, 0° and 9°, 3° and 6°, and 6° and 9°.
3.3. Relationship between metabolic power and step-to-step transition power
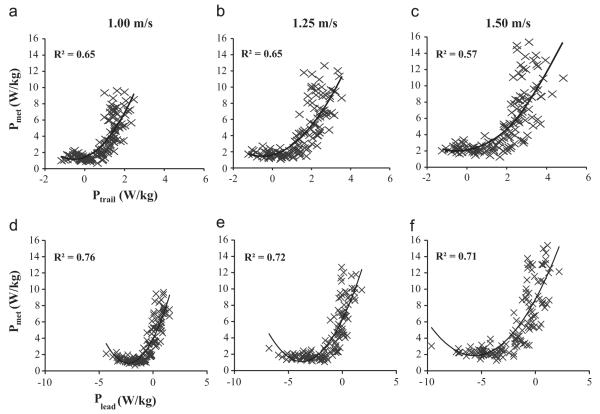
We fit our data with linear and quadratic models and found that 37% and 52%, respectively, of the variance in metabolic power was explained by Plead. Ptrail explained 58% and 61% of the variance in metabolic power with linear and quadratic models, respectively. Specifically, at each velocity across all slopes we found significant correlations between metabolic power and Plead and Ptrail using linear and quadratic models (Fig. 3, R2≥0.52). At each velocity across all slopes, a quadratic model best described the relationship between overall metabolic power and Plead; R2=0.76, 0.72, and 0.71 for 1.00, 1.25, and 1.50 m/s, respectively and overall metabolic power and Ptrail; R2=0.65, 0.65, and 0.57 for 1.00, 1.25, and 1.50 m/s, respectively (Table 1). At each slope across all velocities, a quadratic model best described the relationship between overall metabolic power and Plead and overall metabolic power and Ptrail (R2=0.12–0.54, Table 2). The strongest correlations were between metabolic power and Plead, and metabolic power and Ptrail at each velocity across all slopes. Thus, subsequent analyses were performed at each velocity across all slopes.
Fig. 3.
Relationship between metabolic power (Pmet) and mechanical power of the individual legs during the step-to-step transition phase. For both the trailing leg (Ptrail) (A–C) and leading leg (Plead) (D–F), data are presented for all slopes for all subjects at each velocity tested. We found that a quadratic model best described the correlation between Pmet and Ptrail for all three velocities (R2=0.57 to 0.65) and the correlation between Pmet and Plead for all three velocities (R2=0.71 to 0.76).
Table 1.
R2 values for model fits at each velocity for all slopes.
|
Pmet vs. Ptrail |
Pmet vs. Plead |
|||||
|---|---|---|---|---|---|---|
| 1.00m/s | 1.25m/s | 1.50m/s | 1.00m/s | 1.25m/s | 1.50m/s | |
| Linear | 0.58* | 0.59* | 0.52* | 0.56* | 0.54* | 0.58* |
| Quadratic | 0.65* | 0.65* | 0.57* | 0.76* | 0.72* | 0.71* |
Linear and quadratic models describe the correlation between metabolic power (Pmet) and trailing (Ptrail) or leading (Plead) leg mechanical power. All models yielded significant correlations (P<0.05). We determined the best fit from the highest R2 values (indicated in bold).
indicates p<0.01.
Table 2.
R2 values for model fits at each slope for all velocities.
| −9° | −6° | −3° | 0° | 3° | 6° | 9° | ||
|---|---|---|---|---|---|---|---|---|
| Pmet vs. Ptrail | Linear | 0.09# | 0.27* | 0.38* | 0.41* | 0.48* | 0.39* | 0.33* |
| Quadratic | 0.09 | 0.28* | 0.38* | 0.46* | 0.54* | 0.40* | 0.39* | |
| Pmet vs. Plead | Linear | 0.35* | 0.41* | 0.47* | 0.49* | 0.25* | 0.15* | 0.07# |
| Quadratic | 0.36* | 0.41* | 0.50* | 0.53* | 0.25* | 0.20* | 0.12# |
Linear and quadratic models describe the correlation between metabolic power (Pmet) and trailing (Ptrail) or leading (Plead) leg mechanical power. We determined the best fit from the highest R2 values (indicated in bold).
indicates p<0.05,
indicates p<0.01.
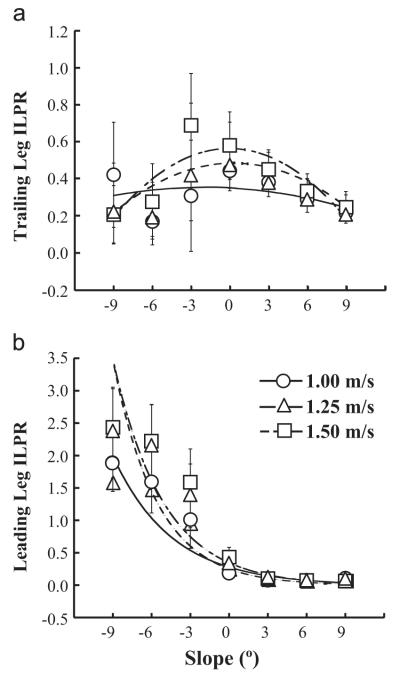
ILPR describes the extent that total metabolic power was affected by each leg’s mechanical power during step-to-step transitions (Fig. 4). At all velocities, trailing leg ILPR (ILPRtrail) decreased by 33–41% during uphill compared to level-ground walking (Fig. 4a) and by 32–40%, during downhill compared to level-ground walking (Fig. 4a). At all slopes, there were no differences in ILPRtrail between velocities (Fig. 4a). ILPRtrail was maximized at 0° and decreased at slopes greater or less than 0° at 1.00 m/s and 1.25 m/s. At 1.50 m/s, ILPRtrail was maximized at −3°. Quadratic regression models best described ILPRtrail at each velocity across all slopes (R2=0.21, 0.71, and 0.78 for 1.00 m/s, 1.25 m/s, and 1.50 m/s). At all velocities, leading leg ILPR (ILPRlead) decreased by 51–82% during uphill compared to level-ground walking. On downhill slopes, ILPRlead increased four- to seven-fold compared to level-ground walking (Fig. 4b). There were no differences in ILPRlead between velocities at all slopes (Fig. 4b). Exponential regression models best described the ILPRlead data with R2=0.71, 0.78, and 0.77 for 1.00 m/s, 1.25 m/s, and 1.50 m/s, respectively.
Fig. 4.
Average (S.D.) individual limb power ratio (ILPR) of the trailing and leading legs during step-to-step transitions at each slope and velocity. ILPR is calculated as the ratio of individual leg mechanical power during the step-to-step transition and overall metabolic power. (a) Trailing leg ILPR was maximized at 0° and decreased at slopes greater or less than 0° at 1.00 m/s and 1.25 m/s. At 1.50 m/s, trailing leg ILPR was maximized at −3°. Regression models were ILPR= −0.0009s2−0.0036s+0.3506 at 1.00 m/s (R2=0.21), ILPR= −0.0031s2+0.0019s+0.4851 at 1.25 m/s (R2=0.72), and ILPR=−0.0046s2− 0.0002s+0.5642 at 1.50 m/s (R2=0.78), where s is slope (deg). (b) Leading leg ILPR increased up to six-fold and decreased by up to 73% at −9° and 9°, respectively, compared to 0°. There were no differences in ILPR due to changes in velocity. Regression models were ILPR=0.2783e−0.219s at 1.00 m/s (R2=0.71), ILPR=0.2511e−0.292s at 1.25 m/s (R2=0.78), and ILPR=0.3458e−0.257s at 1.50 m/s (R2=0.77).
4. Discussion
We determined correlations between metabolic power and individual leg mechanical power associated with step-to-step transitions when walking on level-ground, and a range of uphill and downhill slopes at three velocities. Metabolic power was greater for walking on slopes greater and less than −3°, results supported by previous findings (15, 19, 21, 22). At steeper uphill slopes, Plead and Ptrail were more positive compared to level-ground walking (Fig. 3a and b) and in agreement with previous research (Franz et al., 2012). Similar to previous results (Franz et al., 2012), Plead and Ptrail were more negative with steeper downhill slopes compared to level-ground walking (Fig. 3a and b). At faster velocities, metabolic power increased, the leading leg absorbed more power, and the trailing leg generated more power compared to slower velocities. With faster velocities across all slopes, Plead became more negative while Ptrail became more positive. Our findings of step-to-step transition mechanical power are consistent with previous research (Franz et al., 2012), while changes in metabolic and mechanical power due to velocity at each slope are novel. Finally, we found that Plead or Ptrail accounted for 57–76% of the variance in overall metabolic power over a wide range of slopes and velocities. Donelan et al. (2002a) found strong linear correlations between metabolic and mechanical power during step-to-step transitions due to varied step lengths over level-ground. However, we found that a quadratic model best described metabolic power and Plead, and metabolic power and Ptrail over a wide range of slopes and velocities.
In support of our hypothesis, we found that metabolic power was correlated with Plead and Ptrail (R2≥0.57) for all slopes at each velocity. Specifically, when we applied a linear model to our data, we found that 52–59% of the variance in metabolic power could be explained by changes in Plead and Ptrail over all slopes at each velocity (Table 1). Using a curve estimation regression with metabolic power as the dependent variable and Plead or Ptrail as the independent variable, we compared results of quadratic and linear models. We found that a quadratic model best described the correlation between metabolic power and Plead, (R2=0.71–0.76) and between metabolic power and Ptrail (R2=0.57–0.65). The use of a quadratic model to correlate metabolic and mechanical power is supported by previous research (van Bolhuis and Gielen, 1999; Anderson and Pandy, 2001; Thelen et al., 2003) that estimates metabolic cost from muscle activation squared.
We calculated ILPR based on quadratic models to determine the influence of mechanical power on metabolic power (Fig. 4). Metabolic power increased more than the mechanical power generated by both legs during the step-to-step transition while walking up steeper slopes, resulting in a lower ILPR compared to level-ground. At steeper downhill slopes, Plead influenced overall metabolic power more than Ptrail. When walking on steeper downhill slopes, the leading leg absorbed most of the power (Fig. 2b), while the trailing leg absorbed relatively little power (Fig. 2a). Previous research suggests that eccentric muscle action associated with power absorption is more efficient than concentric muscle action (Margaria, 1968; Ryschon et al., 1997). For example, an ILPRlead of 2.5 suggests that a large amount of mechanical power is being absorbed during the step-to-step transition relative to the cheap metabolic cost of absorbing that power. Thus, the leading leg was more efficient than the trailing leg when walking down steeper slopes.
The underlying reason for quadratic models better explaining the variance in metabolic power at each velocity across slopes may result from each leg’s role during step-to-step transitions. At steeper uphill slopes, both legs produced power to move the COM forward and up. Walking up steeper slopes required greater propulsive force and positive work by the leading and trailing legs (Franz et al., 2012). Both legs generated more positive power and the muscles presumably performed concentric work at steeper uphill slopes, which likely explains the decrease in ILPR, as concentric muscle action is less efficient (i.e. more metabolically costly) than eccentric muscle action (Margaria, 1968; Ryschon et al., 1997). At steeper downhill slopes, increased metabolic power was mostly due to changes in Plead and not Ptrail. The leading leg absorbed most of the power and performed eccentric work while walking downhill compared to the trailing leg, which could explain why further increases in metabolic power with steeper downhill slopes are more strongly correlated with Plead than with Ptrail. Further, ILPRlead increased exponentially while ILPRtrail decreased with steeper downhill slopes (Fig. 4). We predict that at downhill slopes steeper than −9°, the magnitude of work absorbed by the leading leg would presumably continue to increase and metabolic power would continue to increase (Minetti et al., 2002).
Trailing leg propulsive forces become negligible at −9° (Franz et al., 2012), suggesting that there are no propulsive forces at downhill slopes steeper than −9°. As propulsive forces decrease, the trailing leg’s contribution is small during step-to-step transitions. Thus, the exponential relationship showed little change in metabolic power due to changes in Ptrail on downhill slopes. The trailing leg was less efficient at steeper downhill slopes; therefore the smaller trailing leg contribution likely explains the low correlation between metabolic power and Ptrail on downhill slopes.
4.1. Implications for lower leg assistive device design
A non-linear model best describes the relationship between metabolic and mechanical power across all slopes at each velocity. These relationships suggest that biomimetic assistive devices such as prostheses and orthoses need power, dampening, and robust control for sloped walking. Such devices should specifically consider the role of the trailing and leading legs. Advances in leg prostheses allow for powered plantarflexion through use of a battery, actuators, and springs (Au et al., 2008, 2009; Au and Herr, 2008). People with leg amputations using such powered ankle-foot prostheses have significantly lower metabolic demands compared to using passive-elastic prostheses and equivalent metabolic demands compared to non-amputees during level-ground walking at 0.75–1.75 m/s (Herr and Grabowski, 2012; Malcolm et al., 2013). Non-amputees using ankle-foot orthoses that provide powered plantarflexion during walking reduced their metabolic demand in all assisted compared to unassisted orthotic conditions on level-ground and uphill slopes (Sawicki and Ferris, 2009). These results suggest that changes in ankle power significantly affect individual leg power and the metabolic cost of walking. Previous studies show that biological ankle power generation during level-ground walking accounts for 46–89% of the total mechanical power (Winter, 1983; Farris and Sawicki, 2012). Thus, future studies are needed to understand how joint-level power affects the metabolic cost of walking at different slopes and velocities.
Based on our results, effective assistive device control should consider the type of walking condition, total mechanical power output of the leg, and temporal control at different phases of the gait cycle. Our results suggest that the mechanical power demands of an assistive device would differ and depend on whether the affected leg is leading or trailing in a phase of the gait cycle during sloped walking at different velocities. Given the greater ILPRlead compared to ILPRtrail during downhill walking, a robust assistive device must be capable of power production, and significant power absorption to minimize metabolic costs.
5. Conclusions
We quantified metabolic power and step-to-step transition power of the leading and trailing legs during walking over a wide range of slopes and velocities. We found that individual leg mechanical power during step-to-step transitions accounts for ~65% of the metabolic power needed to walk at 21 combinations of slope and velocity, and that quadratic models best described the relationships between each leg’s power and metabolic power. Future studies are needed to explore extreme slopes and slower and faster velocities. Our results provide a foundation for the design of powered leg assistive devices for robust constraints such as varied slopes and velocities during walking. Understanding the contributions of individual joints during walking at different slopes and velocities will advance prosthetic and orthotic designs. Future work will examine joint dynamics at similar slopes and velocities.
Acknowledgments
This study was sponsored by a Department of Veterans Affairs Career Development Award granted to AMG from the Rehabilitation Research and Development Service, and Eastern Colorado Healthcare System VAMC (VA RR&D Career Development Award-2 A7972-W).
Footnotes
Conflict of interest
The authors have no financial affiliation or involvement with any commercial organization that has a direct financial interest in any matter included in this article.
References
- Adamczyk PG, Kuo AD. Redirection of center-of-mass velocity during the step-to-step transition of human walking. J. Exp. Biol. 2009;212(Pt 16):2668–2678. doi: 10.1242/jeb.027581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander RM. Optimum walking techniques for quadrupeds and bipeds. J. Zool. 1980;192:97–117. [Google Scholar]
- Anderson FC, Pandy MG. Dynamic optimization of human walking. J. Biomech. Eng. 2001;123(5):381–390. doi: 10.1115/1.1392310. [DOI] [PubMed] [Google Scholar]
- Au S, Berniker M, Herr H. Powered ankle-foot prosthesis to assist level-ground and stair-descent gaits. Neural Netw. 2008;21(4):654–666. doi: 10.1016/j.neunet.2008.03.006. [DOI] [PubMed] [Google Scholar]
- Au SK, Herr HM. Powered ankle-foot prosthesis—the importance of series and parallel motor elasticity. IEEE Robot. Autom. Mag. 2008;15(3):52–59. [Google Scholar]
- Au SK, Weber J, Herr H. Powered ankle–foot prosthesis improves walking metabolic economy. IEEE Trans. Robot. 2009;25(1):51–66. [Google Scholar]
- van Bolhuis BM, Gielen CCAM. A comparison of models explaining muscle activation patterns for isometric contractions. Biol. Cybern. 1999;81:249–261. doi: 10.1007/s004220050560. [DOI] [PubMed] [Google Scholar]
- Umberger Brian R., Rubenson J. Understanding muscle energetics in locomotion: new modeling and experimental approaches. Exerc. Sport Sci. Rev. 2011;39(2):59–67. doi: 10.1097/JES.0b013e31820d7bc5. [DOI] [PubMed] [Google Scholar]
- Brockway JM. Derivation of formulae used to calculate energy expenditure in man. Hum. Nutr. Clin. Nutr. 1987;41C:463–471. [PubMed] [Google Scholar]
- Caputo JM, Collins SH. A universal ankle–foot prosthesis emulator for human locomotion experiments. J. Biomech. Eng. 2014;136(3):035002. doi: 10.1115/1.4026225. [DOI] [PubMed] [Google Scholar]
- Cavagna GA, Heglund NC, Taylor CR. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am. J. Physiol. 1977;233(5):R243–261. doi: 10.1152/ajpregu.1977.233.5.R243. [DOI] [PubMed] [Google Scholar]
- Cavagna GA, Willems PA, Heglund NC. The role of gravity in human walking: pendular energy exchange, external work and optimal speed. J. Physiol. 2000;528(3):657–668. doi: 10.1111/j.1469-7793.2000.00657.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donelan JM, Kram R, Kuo AD. Mechanical work for step-to-step transitions is a major determinant of the metabolic cost of human walking. J. Exp. Biol. 2002a;205:3717–3727. doi: 10.1242/jeb.205.23.3717. [DOI] [PubMed] [Google Scholar]
- Donelan JM, Kram R, Kuo AD. Simultaneous positive and negative external mechanical work in human walking. J. Biomech. 2002b;35(1):117–124. doi: 10.1016/s0021-9290(01)00169-5. [DOI] [PubMed] [Google Scholar]
- Farris DJ, Sawicki GS. The mechanics and energetics of human walking and running: a joint level perspective. J. R. Soc. Interface. 2012;9(66):110–118. doi: 10.1098/rsif.2011.0182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferris DP, Sawicki GS, Daley MA. A physiologist's perspective on robotic exoskeletons for human locomotion. Int. J. Humanoid Robot. 2007;4(3):507–528. doi: 10.1142/S0219843607001138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franz JR, Lyddon NE, Kram R. Mechanical work performed by the individual legs during uphill and downhill walking. J. Biomech. 2012;45(2):257–262. doi: 10.1016/j.jbiomech.2011.10.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottschall JS, Kram R. Mechanical energy fluctuations during hill walking: the effects of slope on inverted pendulum exchange. J. Exp. Biol. 2006;209(Pt 24):4895–4900. doi: 10.1242/jeb.02584. [DOI] [PubMed] [Google Scholar]
- Herr HM, Grabowski AM. Bionic ankle–foot prosthesis normalizes walking gait for persons with leg amputation. Proc. Biol. Sci. 2012;279(1728):457–464. doi: 10.1098/rspb.2011.1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang J, Chaloupka EC, Mastrangelo MA, Hoffman JR. Physiological and biomechanical analysis of treadmill walking up various gradients in men and women. Eur. J. Appl. Physiol. 2002;86(6):503–508. doi: 10.1007/s00421-002-0583-7. [DOI] [PubMed] [Google Scholar]
- Kuo AD. The six determinants of gait and the inverted pendulum analogy: a dynamic walking perspective. Hum. Mov. Sci. 2007;26(4):617–656. doi: 10.1016/j.humov.2007.04.003. [DOI] [PubMed] [Google Scholar]
- Malcolm P, Derave W, Galle S, De Clercq D. A simple exoskeleton that assists plantarflexion can reduce the metabolic cost of human walking. PloS One. 2013;8(2):e56137. doi: 10.1371/journal.pone.0056137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margaria R. Positive and negative work performances and their efficiencies in human locomotion. Int. Z. Angew. Physiol. 1968;25(4):339–351. doi: 10.1007/BF00699624. [DOI] [PubMed] [Google Scholar]
- Minetti AE, Ardigo LP, Saibene F. Mechanical determinants of gradient walking energetics in man. J. Physiol. 1993;471:725–735. doi: 10.1113/jphysiol.1993.sp019969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minetti AE, Moia C, Roi GS, Susta D, Ferretti G. Energy cost of walking and running at extreme uphill and downhill slopes. J. Appl. Physiol. 2002;93:1039–1046. doi: 10.1152/japplphysiol.01177.2001. [DOI] [PubMed] [Google Scholar]
- Crowninshield Roy D., Brand Richard A. A physiologically based criterion of muscle force prediction in locomotion. J. Biomech. 1981;14(11):793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
- Ryschon TW, Fowler MD, Wysong RE, Anthony A, Balaban RS. Efficiency of human skeletal muscle in vivo: comparison of isometric, concentric, and eccentric muscle action. J. Appl. Physiol. 1997;83(3):867–874. doi: 10.1152/jappl.1997.83.3.867. [DOI] [PubMed] [Google Scholar]
- Sawicki GS, Ferris DP. Mechanics and energetics of incline walking with robotic ankle exoskeletons. J. Exp. Biol. 2009;212(Pt 1):32–41. doi: 10.1242/jeb.017277. [DOI] [PubMed] [Google Scholar]
- Silder A, Besier T, Delp SL. Predicting the metabolic cost of incline walking from muscle activity and walking mechanics. J. Biomech. 2012;45(10):1842–1849. doi: 10.1016/j.jbiomech.2012.03.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thelen DG, Anderson FC, Delp SL. Generating dynamic simulations of movement using computed muscle control. J. Biomech. 2003;36(3):321–328. doi: 10.1016/s0021-9290(02)00432-3. [DOI] [PubMed] [Google Scholar]
- Winter D. Energy generation and absorption at the ankle and knee during fast, natural, and slow cadences. Clin. Orthop. Relat. Res. 1983;175:147–154. [PubMed] [Google Scholar]