Transport across Schlemm’s canal endothelium and the blood-aqueous barrier

Abstract

The majority of trabecular outflow likely crosses Schlemm’s canal (SC) endothelium through micron-sized pores, and SC endothelium provides the only continuous cell layer between the anterior chamber and episcleral venous blood. SC endothelium must therefore be sufficiently porous to facilitate outflow, while also being sufficiently restrictive to preserve the blood-aqueous barrier and prevent blood and serum proteins from entering the eye. To understand how SC endothelium satisfies these apparently incompatible functions, we examined how the diameter and density of SC pores affects retrograde diffusion of serum proteins across SC endothelium, i.e. from SC lumen into the juxtacanalicular tissue (JCT). Opposing retrograde diffusion is anterograde bulk flow velocity of aqueous humor passing through pores, estimated to be approximately 5 mm/s. As a result of this relatively large through-pore velocity, a mass transport model predicts that upstream (JCT) concentrations of larger solutes such as albumin are less than 1% of the concentration in SC lumen. However, smaller solutes such as glucose are predicted to have nearly the same concentration in the JCT and SC. In the hypothetical case that, rather than micron-sized pores, SC formed 65 nm fenestrae, as commonly observed in other filtration-active endothelia, the predicted concentration of albumin in the JCT would increase to approximately 50% of that in SC. These results suggest that the size and density of SC pores may have developed to allow SC endothelium to maintain the blood-aqueous barrier while simultaneously facilitating aqueous humor outflow.

Introduction

The inner wall endothelium of Schlemm’s canal (SC) serves a dual purpose. On one hand, it must be sufficiently conductive to allow conventional aqueous humor (AH) outflow to enter SC and drain from the eye. AH most likely crosses SC endothelium through micron-sized pores (Johnson, 2006; Braakman et al., 2015). On the other hand, the inner wall must prevent blood and serum proteins, sometimes present within SC, from refluxing into the trabecular meshwork and anterior chamber. Since the inner wall of SC is the only endothelium separating AH in the anterior chamber from blood in the episcleral veins, SC endothelium is an integral part of the blood-aqueous barrier (BAB). Unidirectional flow through the outflow pathway is known to preserve the BAB (Raviola, 1976; Raviola 1977), but it is unclear how SC endothelium can maintain barrier function while also being sufficiently porous to facilitate outflow.

To better understand this issue, we developed a theoretical model describing the transport of solutes, such as serum proteins, through an individual pore in SC endothelium. We considered both retrograde diffusion of solute (from SC lumen into the juxtacanalicular tissue (JCT) immediately underlying SC endothelium) and the opposing anterograde bulk flow of solute (advection) resulting from AH drainage through the pore (Figure 1). This model, appropriate for non-lipophilic solutes and serum proteins that cross SC endothelium primarily through pores, allows us to quantify the effectiveness of the BAB by determining solute concentrations in the JCT relative to that in SC.

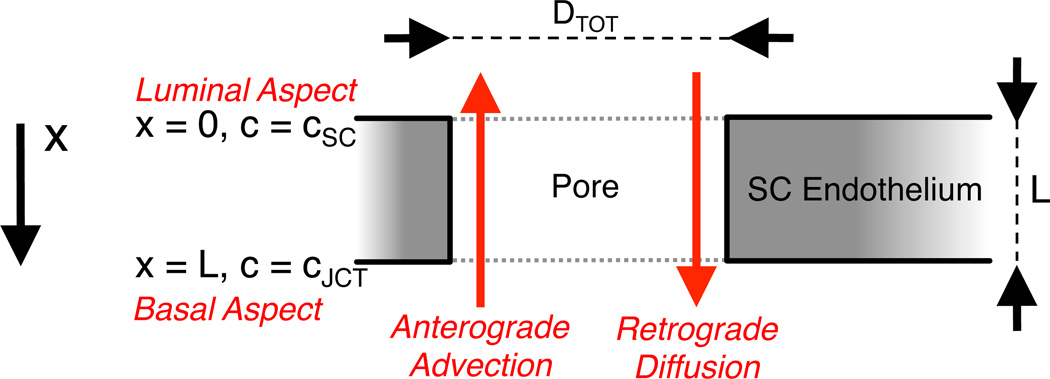
Figure 1.

A schematic representation of a pore through the inner wall endothelium of Schlemm’s canal. Aqueous humor passes through the pore in the basal-to-apical direction, which contributes to anterograde mass transport due to advection. Retrograde mass transport occurs via diffusion in the opposite (apical-to-basal) direction. The luminal aspect of the pore coincides with x = 0 and the luminal concentration is assumed to be c_SC. The cell thickness at the pore is L and the diameter of the pore is D_tot.

Model

We assume one-dimensional solute transport occurring along the axis of the pore within the domain x ∈ [0, L], where L is the basal-apical length of a pore through the inner wall endothelium of SC (Figure 1). The anterograde (basal-to-apical) solute transport rate due to AH advection is equal to A_pU_SC c, where A_p is the pore cross-sectional area, U_SC is the average velocity of AH within the pore, and c is the solute concentration within the pore. Note that c is a function of position x. The retrograde (apical-to-basal) solute transport rate due to diffusion is described by Fick’s first law and is equal to $-A_p𝒟\frac{dc}{dx}$, where 𝒟 is the effective diffusion coefficient of the solute in the pore. At steady state, the mass transport provided by anterograde advection and retrograde diffusion must balance, such that:

$$U_{SC}c=-𝒟\frac{dc}{dx}$$ (1)

Neglecting solute concentration gradients within SC lumen, the solute concentration at the apical end of the pore is c(x = 0)=c_sc, where c_sc is the solute concentration in SC lumen. Equation 1 can then be solved for c(x) to yield:

$$c(x)=c_{SC}{e}^{-U_{SC}x/𝒟}$$ (2)

The predicted solute concentration within the pore thus decays exponentially as a function of distance x from the apical end of the pore. The concentration at the basal end of the pore, c(x = L) = c_JCT, yields a reasonable upper limit for the solute concentration in the JCT. The ratio of the solute concentration in the JCT to that in SC is given by

$$\frac{c_{JCT}}{c_{SC}}=e^{-P{e}_L}$$ (3)

where

$$P{e}_L=\frac{U_{SC}L}{𝒟}$$ (4)

is the dimensionless Péclet number that expresses the ratio of the rates of advection to diffusion across a pore of length L. For large Péclet numbers (Pe_L ≫ 1), advection dominates over diffusion, and c_JCT is small compared to c_SC. This corresponds to an effective BAB. For small Péclet numbers (Pe_L ≪ 1), diffusion dominates over advection, and c_JCT approaches the value of c_SC, implying an ineffective BAB. Thus, the value of Pe_L determines the effectiveness of the BAB attributable to the inner wall of SC. A similar approach was taken by Aukland and Reed (1993) in their analysis of transcapillary filtration and protein transport into the interstitial space.

To evaluate the situation in the eye, we estimated Pe_L by choosing typical parameter values for U_SC, L and 𝒟 from the literature. We specifically examined two important solutes, albumin and glucose, selected to explore how molecular size (and hence 𝒟) affects BAB effectiveness. We also considered two pore diameters, 0.88 µm and 65 nm. Although 0.88 µm is a typical pore size for SC endothelium (Ethier et al., 1998), consideration of the smaller pore size allowed us to examine how the BAB effectiveness would change if, rather than micron-sized pores, SC endothelium expressed 65 nm fenestrae typical of most other filtration-active endothelia (Tamm, 2009). To ensure a fair comparison between these two scenarios, we held the AH drainage characteristics (i.e., hydraulic resistance) of the inner wall constant across these two pore sizes.

Parameter Estimates

Parameter values suitable for human eyes were obtained from the literature (Table 1; see below) as follows. Several studies were consulted to obtain an estimate for the range of each parameter. From these studies, a single study was chosen that used an experimental setup that, in our judgment, was best suited to the determination of the parameter of interest, and, where possible, presented both a population average and standard deviation (SD). The standard error of the mean (SEM) was calculated for each parameter as $SEM=\frac{SD}{\sqrt{N}}$ where N was the number of observations in that study. Propagation of error was used to calculate the SD and SEM of quantities that were estimated from literature values. Specifically, we used Kline and McClintock’s (1953) method based on the chain rule of differentiation.

Table 1.

Parameters used to derive tde filtration and tdrough-pore velocities across SC endotdelium.

Literature Parameter Values	Units	Mean	SDa	SEMa	References
Total Outflow (Qtot)*	mm3/min	2.75	0.63	0.04	McLaren and Brubaker, 1985; Brubaker, 1991
Conventional Outflow Fraction (pcon)	%	83.2%	6.7%	2.7%	Jocson and Sears, 1971
Schlemm’s Canal Widtd (w)†	mm	0.258	0.033	0.013	ten Hulzen and Johnson, 1996
Corneal Diameter (Dcor)‡	mm	12.02	0.38	0.038	Baumeister et al., 2004
Pore Density (ntot)	mm−2	1289	751	129	Ethier et al., 1998
Pore Diameter (Dtot)°	mm	0.00088	0.00027	0.00005	Ethier et al., 1998
Derived Parameters	Unit	Mean	SDa	SEMa	Derivation
Conventional Outflow (Qcon)	mm3/min	2.29	0.56	0.08	Qtot • pcon
Filtration Area (ASC)	mm2	9.7	1.28	0.51	π • Dcor • w
Porosity (εSC)	%	0.078%	0.065%	0.011%	ntot • Dtot2 • π/4
Filtration Velocity (VSC)	mm/s	0.0039	0.0011	0.0002	Qcon/(60 • ASC)
Through-Pore Velocity (USC)	mm/s	5.05	4.47	0.80	100 • VSC / εSC

^(a): Calculated using Kline and McClintock, 1953.

^(*): Based on fluorescein clearance measurements;

^(†): Anterior/Posterior lengtd;

^(‡): Measured at limbus;

^(°)Weighted average of geometric mean diameter of all pore subtypes, SD from total pore major axis.

Denoting total AH outflow by Q_tot, the fraction of outflow leaving the eye through the conventional outflow pathway by p_con, and the filtering area of the inner wall endothelium by A_SC, we can compute the average filtration velocity across the endothelium (also referred to as the superficial velocity), V_SC, as $V_{SC}=\frac{Q_{\mathit{\text{tot}}}{p}_{\mathit{\text{con}}}}{A_{SC}}$. The numerical value of V_SC (3.9 ± 1.1 µm/s; Table 1) is noteworthy because it is approximately 3-fold larger than the superficial filtration velocity across the renal glomerulus (1.2 µm/s^†), suggesting that the inner wall accommodates possibly the largest transendothelial filtration velocity of any endothelium in the body. Furthermore, for an average SC endothelial cell thickness of 0.5 µm (Vargas-Pinto et al., 2014), the value of V_SC indicates that on average each SC cell facilitates flow at a rate nearly eight times its own volume each second. These observations strongly argue for a highly conductive pathway for flow across the inner wall, namely through pores (Johnson, 2006), and imply that active AH transport (e.g., via ‘macro pinocytosis’ (Tripathi, 1972)) cannot be the primary mechanism of AH flow across the inner wall.

With a total pore density of n_tot and an average pore diameter of D_tot, the porosity of SC inner wall is ${\epsilon }_{SC}=n_{\mathit{\text{tot}}}\pi \frac{D_{\mathit{\text{tot}}}^2}{4}=0.078\pm 0.065\%$. Because of this small porosity, the through-pore velocity $U_{SC}=\frac{V_{SC}}{{\epsilon }_{SC}}$ of AH flowing through each pore is much greater than V_SC. Indeed, the remarkably large value of U_SC (5.1 ± 4.5 mm/s; Table 1) suggests that basal-to-apical advection could provide a significant barrier against retrograde diffusion.

Molecular diffusivity generally decreases with increasing molecular weight. All else being equal, anterograde advection will more strongly oppose retrograde diffusion for solutes of larger molecular weight. Values for the diffusion coefficient of glucose and albumin in water at 37°C (𝒟₀) are listed in Table 2; these diffusion coefficients are known based on direct measurements. As the diffusion coefficient may not be known for all solutes of interest, Young et al. (1980) have provided an empirical relationship between molecular weight and diffusion coefficient based on experimental data from 143 proteins,

$${𝒟}_0=8.34\times {10}^{-16}\frac{T}{\mu M^{\frac{1}{3}}}$$ (5)

where 𝒟₀ is given in units of m²/s, T is the absolute temperature in Kelvin (T = 310 K at physiological temperature), μ is AH viscosity expressed in Pascal-seconds (μ = 6.92 × 10⁻⁴ Pa s at 37°C), and M is solute molecular weight in Daltons. Note that Equation 5 is valid primarily for globular proteins, and tends to overestimate the true diffusion coefficient for non-globular proteins. Predictions based on Equation 5 thus provide a reasonable upper limit for $\frac{c_{JCT}}{c_{SC}}$ and a conservative estimate of the effectiveness of the BAB.

Table 2.

Parameters used to estimate the solute concentration in the JCT versus that in SC as an indicator of the effectiveness of the BAB under conditions of micron-sized pores versus fenestrae for small (glucose) and large (albumin) solutes.

		Scenarios:
	Unit	Glucose through pores	Albumin through pores	Glucose through fenestrae	Albumin through fenestrae
Diffusion Coefficient in H2O at 37°C (D0)	mm2/s	9.1×10−4	8.5×10−5	9.1×10−4	8.5×10−5
Radius of Solute (a)	mm	3.6×10−7	3.6×10−6	3.6×10−7	3.6×10−6
Radius of Pore (r)	mm	4.4×10−4	4.4×10−4	3.3×10−5	3.3×10−5
Renkin Correction	-	0.998	0.983	0.976	0.745
Corrected Diffusion Coefficient (D)	mm2/s	9.1×10−4	8.4×10−5	8.9×10−4	6.3×10−5
Through-Pore Velocity (USC)	mm/s	5.05	5.05	0.38	0.38
Basal-Apical Pore Length (L)	mm	1.0×10−4	1.0×10−4	1.0×10−4	1.0×10−4
Péclet Number (PeL)	-	0.56	6.0	0.042	0.59
cJCT/cSC	%	57%	0.24%	96%	55%

As all solutes have a finite molecular radius, the effective diffusion coefficient within a pore is reduced due to steric hindrance and additional fluidic drag caused by interactions between the solute and the wall of the pore. To compute the effective diffusion coefficient of a solute of radius a in a pore of radius $r=\frac{D_{\mathit{\text{tot}}}}{2}$, we used Renkin’s correction (1954)

$$\frac{𝒟}{{𝒟}_0}=[2{(1-\frac{a}{r})}^2-{(1-\frac{a}{r})}^4][1-2.104(\frac{a}{r})+2.09{\left(\frac{a}{r}\right)}^3-0.95{\left(\frac{a}{r}\right)}^5]$$ (6)

where 𝒟₀ is the uncorrected diffusion coefficient of the solute in free solution obtained either from direct experimental measurements or from estimates given by Equation 5. The corrected diffusion coefficient 𝒟 was used to calculate Pe_L in Table 2.

BAB Effectiveness for SC Inner Wall

For glucose transport through a typical SC pore, Pe_L is 0.56 and, according to Equation 3, $\frac{c_{JCT}}{c_{SC}}$ is 0.57, indicating that retrograde diffusion is comparable in magnitude to advection, such that the predicted glucose concentration in the JCT reaches 57% of that in SC lumen. On the other hand, Pe_L for albumin is 6.0 and $\frac{c_{JCT}}{c_{SC}}$ is 0.0024, indicating that advection dominates over diffusion for the case of albumin transport through a typical SC pore, such that the predicted albumin concentration in the JCT is only 0.24% of that in SC lumen (Table 2). These predictions are broadly consistent with measured concentrations in the anterior chamber of glucose (~60% of that in plasma (Davies et al., 1984)) and serum proteins (<1% of that in plasma (Tripathi et al., 1989)). However, protein within the anterior chamber likely originates from ciliary body capillaries via diffusion through the iris root (Freddo et al., 1990; Barsotti et al., 1992), and due to proximity to the iris root the concentration in the trabecular meshwork or JCT may differ from that in the central anterior chamber (Freddo, 2013).

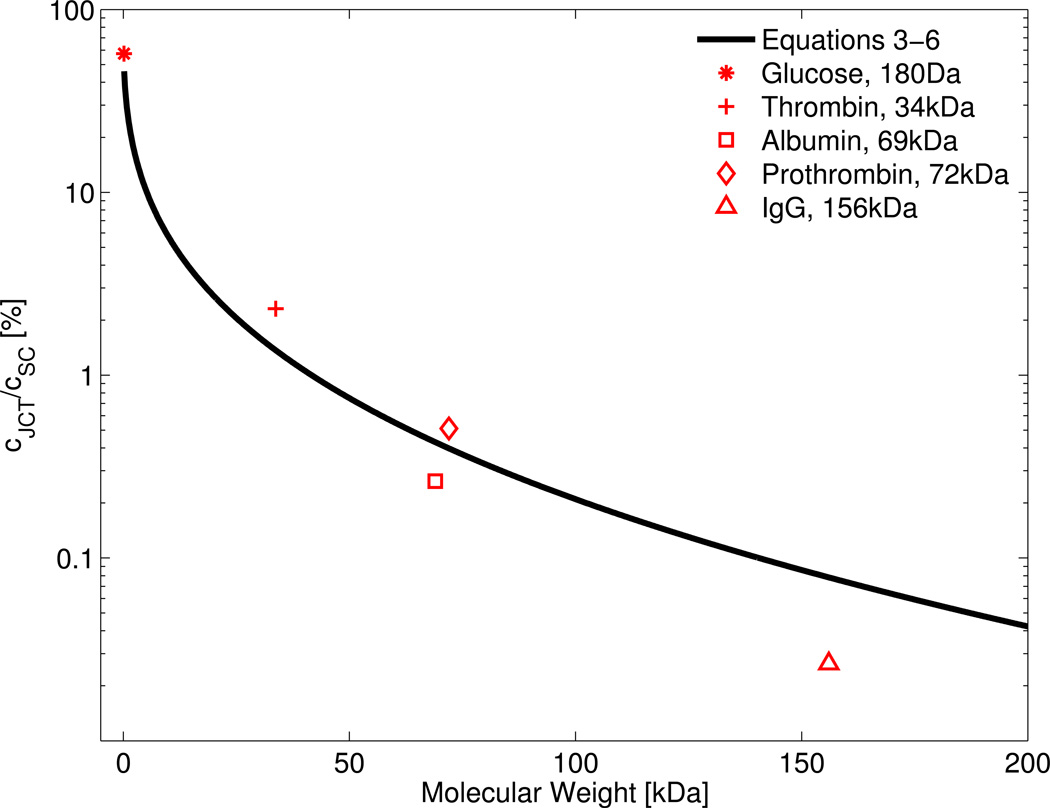
Combining Equations 3 to 6 yields an analytic expression for the ratio $\frac{c_{JCT}}{c_{SC}}$ as a function of solute molecular weight, which is plotted in Figure 2. As Equation 5 provides only an estimated value of 𝒟₀, the ratio $\frac{c_{JCT}}{c_{SC}}$ was also calculated using direct experimental measurements of 𝒟₀ for glucose, albumin, thrombin (bovine), prothrombin (bovine) and γG-immunoglobulin (IgG) in water at 37°C (these estimates are shown by the symbols in Figure 2). Figure 2 shows that for solutes smaller than approximately 10 kDa, the $\frac{c_{JCT}}{c_{SC}}$ ratio is 10% or more. For larger proteins, such as albumin, prothrombin and IgG, the $\frac{c_{JCT}}{c_{SC}}$ ratio is 1% or less. This suggests that, despite maintaining patent pores, SC endothelium functions as an effective barrier against retrograde transport of large molecular weight solutes and serum proteins, in line with its role as part of the BAB.

Figure 2.

The predicted relationship between the solute concentration ratio across a pore $\left(\frac{c_{JCT}}{c_{SC}}\right)$ versus the molecular weight of the diffusing solute, as determined by combining Equations 3–6 (black curve). Red points show the $\frac{c_{JCT}}{c_{SC}}$ ratio using the experimentally-determined values for the diffusion coefficient for glucose, thrombin (bovine), albumin, prothrombin (bovine) and γG-immunoglobulin (IgG), values of which were obtained from Harmison et al., 1961, Lamy and Waugh, 1953, Levick and Smaje, 1987 and Tyn and Gusek, 1990. Deviations from the curve are due to differences between the estimate provided by Equation 5 and the true diffusion coefficient. For solutes smaller than 10 kDa, the $\frac{c_{JCT}}{c_{SC}}$ ratio is 10% or more, while for larger proteins, such as albumin, prothrombin and IgG, the $\frac{c_{JCT}}{c_{SC}}$ ratio is 1% or less. This suggests that SC endothelium forms an effective barrier against retrograde transport of large molecular weight solutes and serum proteins into the JCT, consistent with its role as part of the BAB.

BAB Effectiveness for SC Inner Wall with Hypothetical Fenestrae Rather than Micron-Sized Pores

Fenestrae are occasionally observed in SC inner wall and have been referred to as “mini-pores” (Inomata et al., 1972; Tamm, 2009), although the large majority of transendothelial openings are micron-sized pores. Here we investigate the effectiveness of the BAB in the hypothetical case that SC endothelium contained only 65 nm fenestrae rather than micron-sized pores. To allow a fair comparison, both micron-sized pores and fenestrae were assumed to generate the same overall flow resistance as estimated by Sampson’s law for flow through an aperture. Sampson’s law states that the hydrodynamic resistance ℛ of n_tot apertures per unit area with diameter D_tot is given by $ℛ=\frac{\beta }{n_{\mathit{\text{tot}}}{D}_{\mathit{\text{tot}}}^3}$, where β is a coefficient that is the same for both types of transendothelial openings (Bill and Svedbergh, 1972; Ethier et al., 1998; Happel and Brenner, 1983). In order for 65 nm fenestrae to generate the same hydrodynamic resistance ℛ as the micron-sized pores, the fenestral porosity must be 1.0%, resulting in a through-pore velocity U_SC of 0.38 mm/s. This is more than ten-fold lower than our estimate of U_SC for micron-sized pores. The smaller through-pore velocity for fenestrae decreases the Péclet number to below 1 for both solutes, indicating that diffusion dominates under these conditions, and the predicted $\frac{c_{JCT}}{c_{SC}}$ ratio is 0.96 and 0.55 for glucose and albumin, respectively (Table 2). Thus, for the case of 65 nm fenestrae, we predict that the inner wall of SC would not function as an effective barrier against retrograde diffusion of large molecular weight solutes or serum proteins into the JCT.

Limitations and Assumptions

Our model is based on a number of assumptions. First, we assume steady flow within the pore. In reality, the pressure in the eye varies over the cardiac cycle by 1–2 mmHg (known as the ocular pulse) and larger changes in pressure are attributable to blinking and ocular motion (Coleman and Trokel, 1969; Dastiridou et al., 2009). Any pressure pulsations would introduce velocity pulsations within the pore and may thereby affect mass transport. Flows over cellular dimensions are, however, typically dominated by viscosity, such that inertial effects are negligible and the flow remains laminar and kinematically reversible without turbulent mixing. The ratio of inertial to viscous forces for pulsatile flow is given by the Womersley parameter, expressed as $D_{\mathit{\text{tot}}}\sqrt{\frac{\omega \rho }{\mu }}$, where ω is the angular frequency of pulsations ($~2\pi \frac{rads}{s}$ for humans), and ρ and μ are the fluid density and viscosity, respectively. Because the value of the Womersley parameter is much smaller than unity for both pores and fenestrae (0.003 and 0.0002, respectively), viscosity dominates and the flow through the pore is quasi-static, meaning that despite the pulsatility, the flow achieves instantaneous equilibrium (and is therefore in phase) with the pressure gradient for all times during the pulse. Under these conditions, mass transport through the pore is determined by integrating Equation 1 over the pulse waveform, such that U_SC becomes equal to the mean through-pore velocity. This is consistent with the calculations presented in Table 2. As a potential worse-case scenario, calculations could be based on the minimum through-pore velocity, estimated to be 4.3 mm/s (equal to 6/7^ths of 5.05 mm/s) based on an ocular pulse amplitude of 1 mmHg superimposed on a mean pressure drop of 7 mmHg across the outflow pathway. (Note that the flow never reverses because IOP is always greater than episcleral venous pressure under normal conditions). Using the minimum through-pore velocity, the predicted values of $\frac{c_{JCT}}{c_{SC}}$ change by less than 5%, leading to the same conclusions regarding the effectiveness of the BAB. Hence, the assumption of steady flow is reasonable in the context of mass transport through the pore.

A second assumption is that the inner wall endothelium of SC is stationary. In reality, the inner wall is under constant motion due to transient changes in IOP associated with the ocular pulse, blinking and ocular motion. The inner wall cells themselves experience continuous deformation during giant vacuole formation and inner wall ‘ballooning’. The velocity of the trabecular meshwork attributable to the ocular pulse, which we assume to be similar to the velocity of the inner wall, is on the order of ~3 µm/s (Li et al., 2013), roughly 1000-fold smaller than the through-pore velocity (~5 mm/s). Similarly, the velocity of SC cells during giant vacuole formation is even smaller and on the order of µm/min based on histological estimates (Brilakis and Johnson, 2001) and in vitro observations (Pedrigi et al., 2011). Because the inner wall velocity is negligibly small compared to the through-pore velocity, from the point of view of mass transport through the pore, the inner wall can be reasonably assumed to be stationary for purposes of this study.

A third assumption is in regards to Equation 5 that is most appropriate for globular proteins. Many serum proteins are globular, such as albumin (the main protein of blood plasma), hemoglobin and immunoglobulins, and the diffusion coefficient of such proteins is reasonably well approximated by Equation 5. However, for non-globular proteins, such as fibrinogen or collagen that are rod-shaped or linear, the diffusion coefficient deviates from that predicted by Equation 5. This is because a larger aspect ratio and larger radius of gyration presents a larger surface area for solute-solvent interactions that slows molecular motion relative to a spherical molecule of same molecular weight. Other factors such as the intrinsic viscosity of the protein and amount of bound water also introduce deviations from Equation 5. All else being equal, however, Equation 5 presents a reasonable upper limit for the diffusion coefficient for a protein of given molecular weight. Because the $\frac{c_{JCT}}{c_{SC}}$ increases with 𝒟, predictions based on Equation 5 provide an upper estimate for the effectiveness of the BAB attributable to the inner wall of SC.

Conclusion

We conclude that the diameter and density of inner wall pores, combined with the typical outflow rate of AH, effectively oppose retrograde diffusion of large molecular weight solutes and serum proteins across the inner wall of Schlemm’s canal in the human eye. This mechanism may allow the inner wall to preserve the blood-aqueous barrier while simultaneously providing a highly conductive pathway for AH outflow.