Accuracy of Functional and Predictive Methods to Calculate the Hip Joint Center in Young Non-pathologic Asymptomatic Adults with Dual Fluoroscopy as a Reference Standard

Abstract

Predictions from biomechanical models of gait may be sensitive to joint center locations. Most often, the hip joint center (HJC) is derived from locations of reflective markers adhered to the skin. Here, predictive techniques use regression equations of pelvic anatomy to estimate the HJC, whereas functional methods track motion of markers placed at the pelvis and femur during a coordinated motion. Skin motion artifact may introduce errors in the estimate of HJC for both techniques. Quantifying the accuracy of these methods is an area of open investigation. In this study, we used dual fluoroscopy (DF) (a dynamic x-ray imaging technique) and three-dimensional reconstructions from computed tomography (CT) images, to measure HJC locations in-vivo. Using dual fluoroscopy as the reference standard, we then assessed the accuracy of three predictive and two functional methods. Eleven non-pathologic subjects were imaged with DF and reflective skin marker motion capture. Additionally, DF-based solutions generated virtual markers placed on bony landmarks, which were input to the predictive and functional methods to determine if estimates of the HJC improved. Using skin markers, functional methods had better mean agreement with the HJC measured by DF (11.0 ± 3.3 mm) than predictive methods (18.1 ± 9.5 mm); estimates from functional and predictive methods improved when using the DF-based solutions (1.3 ± 0.9 and 17.5 ± 8.6 mm, respectively). The Harrington method was the best predictive technique using both skin markers (13.2 ± 6.5 mm) and DF-based solutions (10.6 ± 2.5 mm). The two functional methods had similar accuracy using skin makers (11.1 ± 3.6 and 10.8 ± 3.2 mm) and DF-based solutions (1.2 ± 0.8 and 1.4 ± 1.0 mm). Overall, functional methods were superior to predictive methods for HJC estimation. However, the improvements observed when using the DF-based solutions suggest that skin motion artifact is a large source of error for the functional methods.

Introduction

Biomechanical models of human gait provide valuable insight into the pathophysiology of diseases that are believed to alter locomotion. Model predictions of joint kinematics and kinetics have demonstrated particular sensitivity to the location of the hip joint center (HJC)¹⁸. Most gait studies calculate the HJC based on the location of reflective markers adhered to the skin at identifiable landmarks during a static trial or from the trajectories of skin markers measured during a coordinated motion. These approaches may yield biomechanical models that have sufficient accuracy to detect gross differences in gait parameters of interest. However, depending on the research question, errors due to skin marker placement and/or motion artifact may lead to mismeasurement of the HJC and subsequent inaccuracies in those parameters that rely on the HJC. Knowing the positional accuracy of the HJC would be useful when interpreting results from models of gait. As one example, biomechanists could calculate the sensitivity of hip joint angles by relocating the HJC within previously-measured error bounds.

The hip joint, in particular, presents a challenge to analyze using biomechanical models derived from trajectories of skin markers. First, the hip lies deep within the body, and thus, the true location of the HJC cannot be measured directly from landmarks visible at the surface of the skin. Second, the hip is surrounded by capsular tissue, muscle and fat. Motion of the soft-tissue bulk relative to the underlying bony anatomy can introduce errors of 20 mm or more^{9, 10}.

Two primary approaches, with variations thereof, have been used to estimate the HJC from skin markers. Predictive methods estimate the location of the HJC using anthropometric measurements and accompanying regression equations, with varying levels of complexity. For example, Bell et al. predicted the HJC based on the distance between the anterior superior iliac spine (ASIS) markers². Davis and colleagues utilized a regression that also includes the ASIS distance, but they incorporated leg length as an additional variable⁶. More recently, Harrington et al. used a leave-one-out-cross-validation method to determine which anatomical dimensions were the best predictors of the HJC location, including pelvis width, pelvis depth and leg length¹².

Functional methods are similar to predictive methods in that they use body segment positions to calculate the HJC. However, in contrast to predictive methods, the algorithms used by functional approaches incorporate the dynamic motion of a segment relative to its parent body to calculate the HJC. As with predictive methods, variations of the functional method have been developed. In this study, two techniques were chosen because of their widespread availability in commercial software programs. However, other functional approaches have been described in the literature. Schwartz and Rozumalski presented a transformational technique²⁵, and Ehrig and colleagues developed a faster and more robust algorithm termed symmetric center of rotation estimation (SCoRE)⁸.

Studies have attempted to assess the in-vivo accuracy of the aforementioned functional and predictive methods using digitized locations of the HJC from radiographs, ultrasound images or magnetic resonance images^{12, 15, 24}. Yet, studies have lacked a reference standard capable of measuring the three-dimensional (3D) motion of the pelvis and femur in-vivo (i.e. with respect to subject-specific bone anatomy) in the absence of skin motion artifact. Thus, the accuracy of functional and predictive methods to estimate the HJC remains a topic of debate, as evidenced by a recent review article¹⁶.

Dual fluoroscopy (DF) imaging, in conjunction with model-based tracking (MBT), enables calculation of the 3D positions of bones in-vivo without the limitations imposed by standard skin marker motion capture techniques³. We have previously validated DF and MBT to measure hip kinematics to a positional error less than 0.48 mm and rotational error less than 0.58°¹⁷. Use of DF and MBT affords the opportunity for a reference standard by which to calculate the accuracy of the functional and predictive methods to estimate the HJC.

The first objective of this study was to assess the accuracy of predictive and functional skin marker-based methods to estimate the HJC. Our second objective was to determine if estimates of the HJC made by predictive and functional methods improved when the DF solutions for bony landmark locations were used in-lieu of those calculated from skin markers. Although many HJC calculation methods have been proposed, this study focused on the assessment of accuracy for three predictive and two functional methods that are commercially available. Given that functional methods incorporate motion of each individual subject, which is governed by the anatomy and articulation of the hip, we hypothesized that functional methods would result in lower errors than predictive methods. Furthermore, given the presence of skin motion artifact, we hypothesized that errors for functional methods would decrease when using the DF-based solutions.

Materials and Methods

Subjects

Eighteen subjects provided written informed consent to volunteer for this University of Utah Internal Review Board approved study (IRB #: 51053). All subjects were screened for radiographic signs of hip pathoanatomy, such as femoroacetabular impingement (FAI) and hip dysplasia with a standing anteroposterior (AP) radiograph. Screening excluded seven subjects, leaving eleven subjects. Participants were active, young adults (Age: 23 ± 2 years, BMI: 21 ± 2 kg/m²) who were pain free at the time of testing (Table 1).

Table 1.

Subject demographics, body segment dimensions used in regression equations for the dual fluoroscopy analysis, and the absolute femur joint center location measured by dual fluoroscopy. The femur joint center was expressed in the pelvis anatomical coordinate system and was used as the reference standard for this study. Note that the pelvis width (PW) and pelvis depth (PD) listed here were measured from bony landmark positions with dual fluoroscopy. The leg length (LL) reflects the value used for the Harrington analysis. BMI = body mass index.

Subject	Age (years)	BMI (kg/m2)	Gender	PW (mm)	PD (mm)	LL (mm)	Femur Joint Center
							Lateral (mm)	Posterior (mm)	Inferior (mm)
1	23	21	Male	247.9	151.8	977.4	83.3	46.5	82.1
2	24	21	Male	212.3	146.8	950.6	91.1	49.8	87.8
3	23	21	Male	236.2	136.8	949.0	83.0	38.0	74.5
4	20	21	Female	207.7	134.7	867.6	92.6	43.1	76.7
5	23	22	Male	249.8	141.4	941.5	81.3	38.0	89.5
6	23	22	Female	248.5	132.0	878.9	89.1	37.8	84.9
7	23	24	Male	240.2	143.4	955.9	96.2	52.4	80.2
8	28	17	Female	226.9	128.1	865.4	79.6	36.7	65.8
9	22	21	Female	203.9	136.5	881.2	88.5	47.5	78.8
10	26	21	Female	215.3	142.5	857.3	86.0	38.0	78.5
11	21	19	Male	227.8	139.1	971.1	82.6	54.0	84.3
Mean	23	21	-	228.8	139.4	917.8	86.7	43.8	80.3
SD	2	2	-	17.0	6.8	47.2	5.3	6.5	6.7

Computed Tomography Scans and 3D Reconstruction

Computed Tomography (CT) arthrography images were acquired of each subject using a 128-section single-source CT machine (SOMATOM Definition™, Siemens Healthcare, Munich, Bavaria, Germany) following a published protocol^{14, 17}. The scan included the entire pelvis and proximal femurs (1 mm slices, 120 kVp, 200-400 mAs) as well as the distal femur and proximal tibia (3 mm slices, 120 kVp, 150 mAs). Though arthrography (i.e. contrast enhancement) was not required to obtain 3D reconstructions of bone, it was performed to provide images of hip cartilage and labrum for ongoing studies. The CT images were semi-automatically segmented to generate 3D reconstructions of the pelvis and femur (Fig. 1A) using commercial software (Amira, v5.6, Visage Imaging, San Diego, CA). To ensure possible inflammation and pain from the arthrography procedure did not influence the motion analysis portion of the study, all CT scans were acquired after motion capture or at least four days prior to motion capture.

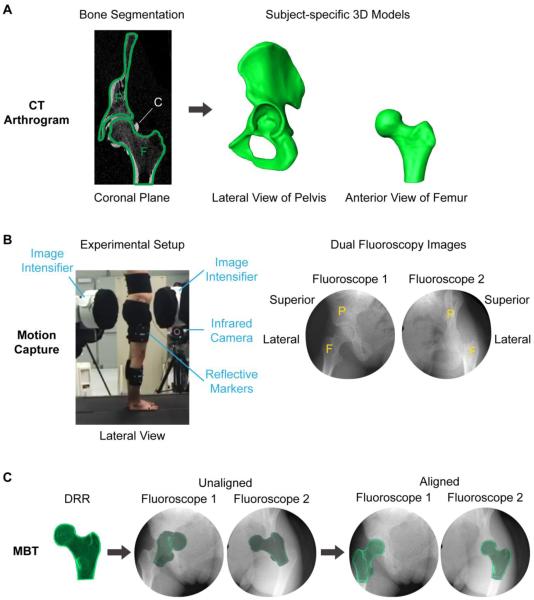
Figure 1.

Experimental methods for skin marker and dual fluoroscopy measurements. Subject-specific 3D models of the pelvis and femur were generated by segmentation of computed tomography (CT) arthrography images (A). Pelvis and femur positions were measured simultaneously with dual fluoroscopy and infrared light reflective markers (i.e., stereophotogrammetry) (B). The dual fluoroscopy system, which consisted of two pairs of x-ray emitters (not pictured) and image intensifiers mounted to four separate bases, was arranged around an instrumented treadmill. Model-based tracking (MBT) determined the 3D position of the femur and pelvis in the dual fluoroscopy reference frame (only femur shown) (C). To define 3D bone position, MBT semi-automatically aligned a digitally reconstructed radiograph (DRR), which was generated by ray-cast projection through a subject-specific 3D model, with the image from each fluoroscope. P=pelvis. F=femur. C=contrast.

Skin Marker and Dual Fluoroscopy Data Collection

Reflective skin markers, 14 mm in diameter, were placed on the pelvis and femur to track each body segment. A licensed physical therapist (KBF) trained team members (NF, PA, MK) to palpate anatomical landmarks on the pelvis and femur to facilitate consistent and accurate placement of markers. For the pelvis, markers were placed on the left and right ASIS, posterior superior iliac spines (PSIS) and superior borders of the iliac crest. The ASIS anatomical landmark was identified by palpating along the iliac crest until the most anterior aspect of the pelvis was reached. The PSIS anatomical landmark was identified by palpating the posterior pelvis until a bony protuberance was found. The PSIS landmark was confirmed by palpating the medial sacro-iliac joint and inferior posterior inferior iliac spine landmark. The superior border of the iliac crest markers’ base was placed at the inferior location of the most lateral aspect of the iliac crest. For the femur, a rigid plate with four markers was secured to the thigh with a Velcro strap. The Velcro strap was wrapped around the thigh at the most superior location possible, and the plate was placed on the most lateral aspect of the thigh. Additional markers were placed on the knee epicondyles and ankle malleoli for segment orientation and length calculations.

Subjects were imaged simultaneously using near-infrared cameras and DF at 100 Hz for the two trials described below (Fig. 1B). The custom DF system consisted of two pairs of x-ray emitters and image intensifiers mounted to four separate bases (Radiological Imaging Services, Hamburg, PA, USA). The x-ray emitters and image intensifiers were arranged around an instrumented treadmill (Bertec Corporation, Columbus, OH, USA) to image the hip joint. Settings for the DF system were adjusted manually on a per-subject basis to produce images with high contrast and signal-to-noise ratio. Settings ranged from 78-92 kVp and 1.9-3.2 mAs with a camera exposure of 5-7 ms under continuous fluoroscopy, similar to those reported in our previous DF validation study¹⁷. The trajectories of the reflective markers were acquired with a 10-camera Vicon motion capture system running Nexus 1.8.5 (Vicon Motion Systems; Oxford, UK). The Vicon motion capture system was calibrated with the active calibration wand according to manufacturer recommendations. Two trials were acquired. The subject stood in a neutral stance (i.e., static) during the first trial and performed a functional hip joint center movement during the second. For the static trial, subjects were instructed to stand upright with their feet hip width apart and slightly externally rotated. The star-arc pattern was performed once for the functional hip joint center trial as described previously⁵. The star-arc pattern included hip flexion-extension, abduction-adduction and circumduction. The pelvis of one of the subjects left the combined FOV of the DF system, and thus, the functional joint centers could not be measured based on DF solutions for this individual. Due to time constraints on the use of fluoroscopy for the data capture, an additional trial was not acquired.

Post-processing of Motion Data

Marker positions were reconstructed and processed in Nexus to fill any gaps in the markers’ trajectory and correct any unlabeled or mislabeled markers. Gap filling and marker labeling were performed according to Vicon recommendations²⁸. Based on a residual analysis of each system’s data, the skin marker data were low-pass filtered at 6 Hz and the DF solutions were filtered at 15 Hz²⁹. Model-based tracking followed the protocol validated for the hip by Kapron et al.¹⁷, using software described previously³. Briefly, the MBT software created digitally reconstructed radiographs (DRRs) by ray cast projection through the 3D surface models generated from segmentation of CT images. The DRRs were then initially oriented in the MBT virtual alignment interface by the user; the final position was calculated automatically by the software to optimize agreement between the DRRs and fluoroscope images (Fig. 1C)³. By aligning each fluoroscope image with its corresponding DRR, the 3D position of the bones was calculated in the calibrated DF coordinate system.

Bony Landmark Selection

The locations of bony landmarks were defined from the 3D CT model reconstruction and then transformed into the DF coordinate system via the MBT solutions. The bony landmark locations in the DF coordinate system were used to calculate all HJCs. To measure the reference HJC, the region of the femoral head presumed to articulate within the acetabulum was automatically isolated using principal curvature in PostView¹⁹. The nodes that defined the surface of the isolated region were then fit to a sphere as described previously¹³. The center of the best-fit sphere defined the femoral joint center (FJC), which we assumed to be the center of the hip for this study.

Additional bony landmarks were identified for the femur and pelvis based on a previous study that found an intra-observer and inter-observer repeatability of 0.18 ± 0.44 mm and 0.24 ± 0.38 mm for the ASIS and 0.12 ± 0.37 mm and 0.24 ± 0.38 for the PSIS¹⁷. For the current study, the femur landmarks included the greater trochanter, lesser trochanter, knee midpoint and a point along the lateral line extending from the knee midpoint. The knee midpoint and mediolateral axis of the femur were defined from the femoral epicondyles and a cylinder fit to the posterior femoral condyles as previously described¹⁷. The line that connected the FJC and knee midpoint defined the long (superior-inferior) axis of the femur, and a point along the lateral line from the knee midpoint defined the lateral direction. Anterior was defined as the cross product of the superior and lateral directions. The greater and lesser trochanters, which were only used to track the femur during dynamic motion, were initially isolated with 1^st principal curvature, and the apex surface node was selected as the trochanter. Application of principal curvature and subsequent selection of the surface node were performed in PostView¹⁹.

The ASIS and PSIS locations were identified in the 3D CT model to coincide with the bony protuberances that were palpated for skin marker placement³⁰. The ASIS bony protuberance was initially isolated using 1^st principal curvature, and the most anterior surface node was selected as the ASIS landmark. The PSIS bony protuberance was initially isolated using 2^nd principal curvature, and the most posterior surface node was selected as the PSIS landmark.

Transformations between Vicon and Dual Fluoroscopy Systems

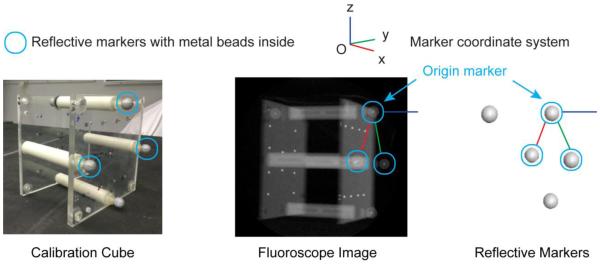
To directly compare data, the Vicon and DF systems had to be synced temporally and spatially. Temporal syncing was accomplished via an external trigger that was registered by both systems. Spatial syncing was achieved via custom skin markers that housed a metal bead at the center. These modified skin markers were fixed to posts extending from an acrylic calibration cube used to calibrate the DF system, which contained metal beads at known locations (Fig. 2). Three of a total of five modified skin markers visible by both the DF and Vicon systems were selected. These markers defined an intermediate coordinate system from which Vicon measurements were transformed to the DF coordinate system and vice-a-versa. The offset between coordinate systems was defined by the location of the Origin marker in Figure 2. The x-direction was defined by a vector towards the marker on the left, and the y-direction was initially defined by a vector towards the marker on the right. The z-direction was defined as the cross product of x and y. To ensure orthogonality, the y-direction was then redefined as the cross product between z and x. To check the transformation between systems, cube marker positions in the DF system were compared to the transformed positions from the Vicon system (excluding the origin marker that by definition will transform to the same position in the other system). The maximum and average ± standard deviation difference between the DF and Vicon systems was 0.9 mm and 0.3 ± 0.2 mm, respectively.

Figure 2.

Spatial transformation between dual fluoroscopy and skin markers. Custom skin markers were manufactured with a metal bead at the center and affixed to a calibration cube with metal beads located at known positions. The cube was imaged simultaneously with dual fluoroscopy and Vicon. The markers served as an intermediate coordinate system for transformation from the Vicon lab coordinate system to the dual fluoroscopy coordinate system and vice-a-versa. The offset between coordinate systems was defined by the location of the top Origin marker. The x-direction was defined by a vector towards the marker on the left, and the y-direction was initially defined by a vector towards the marker on the right. The z-direction was defined as the cross product of x and y. To ensure orthogonality, the y-direction was then redefined as the cross product between z and x. O: origin.

Calculation of the HJCs

The reference standard for this study was the center of the femoral head, FJC, as determined by dual fluoroscopy solutions. Five HJCs from the literature were quantified from reflective skin marker positions. Calculations for these five HJCs were readily available in commonly used biomechanical software programs. Three HJCs were calculated from regression equations in the literature, herein referred to as predictive methods, and two were calculated with functional methods. In addition, bony landmark locations from DF solutions were used to re-calculate each of the five aforementioned literature-based HJCs.

The HJCs from predictive methods were calculated using Visual3D software (C-Motion, Germantown, MD, USA). After marker positions were imported into Visual3D, each marker that was placed over an anatomical landmark was offset towards the bone based on the marker radius (7 mm) and base height (2 mm). The Bell method calculated the HJC at distances from the pelvis anatomical origin, defined at the midway point between the left and right ASIS markers, based on percentages of the inter-ASIS distance². The second method, developed by Davis and colleagues⁶, defined the HJC based on inter-ASIS distance and leg length. The Bell and Davis methods were calculated automatically in Visual 3D with CODA and Helen Hayes pelvis segment definitions, respectively. The last predictive method was described by Harrington et al.¹², and the Harrington HJC was defined manually in the pelvis anatomical coordinate system at percentage distances based on the inter-ASIS distance, pelvis depth and leg length. For the Harrington method, leg length was calculated as the sum of the linear distance between the ipsilateral (i.e., DF imaged) ASIS marker, medial knee marker and medial ankle marker. Pelvis depth was defined as the distance between the midpoints between the left and right ASIS and PSIS markers.

One of the functional methods to determine the HJC was also calculated in Visual3D. Visual3D software quantified functional joint positions using a transformational technique presented by Schwartz and Rozumalski²⁵, hereafter referred to as STT. To take advantage of new algorithms in Vicon, marker data were also imported into recently released Vicon Nexus 2.0, which has algorithms for tracking body segments and calculation of functional joint centers. The tracking algorithm, optimum common shape technique (OCST), defined the position of each body segment relative to the segment’s marker positions²⁷. A second algorithm, SCoRE, calculated the functional joint center⁸.

HJC Comparisons

All HJC locations calculated from skin marker positions were transformed into the DF coordinate system for direct comparison with the FJC. The HJCs for the predictive methods based on the DF solutions were calculated in MATLAB (Version 7.10, The Mathworks, Inc., Natick, MA, USA) using equations in C-Motion’s online documentation (http://c-motion.com/v3dwiki/index.php?title=Hip_Joint_Landmarks; Harrington 2 equation for the Harrington HJC). All HJCs were calculated in the static trial and expressed in the pelvis anatomical coordinate system. All comparisons were made at a single time frame during the static trial and ensemble averaged across subjects. The location of each HJC was displayed relative to the subject’s hemipelvis reconstructed from CT images. This facilitated a qualitative assessment of the positional accuracy of each method relative to the underlying pelvic anatomy.

All statistical tests and calculations were performed in MATLAB with significance set at p < 0.05. A Lilliefors test indicated that the data did not exhibit a normal distribution. Thus, the non-parametric signed rank test was completed to investigate which anatomical directions exhibited a difference between the DF-determined FJC and the predictive and functional methods. To assess the overall agreement between methods, the mean linear distance and limits of agreement between each method and the FJC were calculated. Here, the mean linear distance represented the bias in each measurement relative to the FJC, and the limits of agreement represented the bounds in which 95% of the differences would lie⁴.

Results

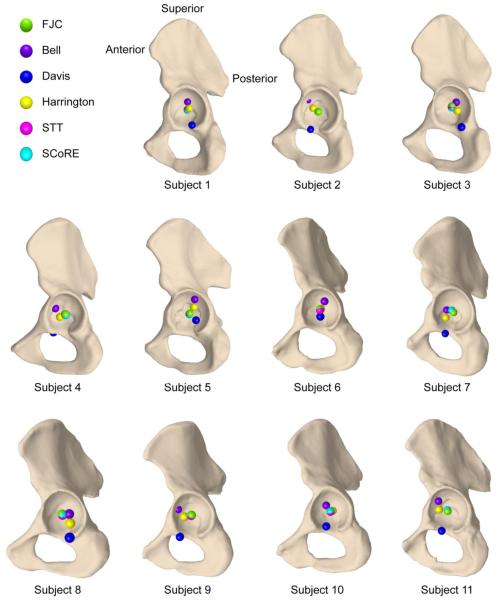
For all subjects the FJC visually appeared most centrally located within the acetabulum when the HJCs were calculated from skin markers (Fig. 3) and DF bony landmarks (Fig. 4). Almost all HJCs from skin marker positions were located within the acetabular rim (Fig. 3). Only the Davis (Subjects 1, 2, 3, 4, 6 and 9), Bell (Subjects 4, 9 and 11) and Harrington (Subject 9) HJCs visually exhibited overlap with bone or were located outside the acetabular rim. For the HJCs from DF landmarks (Fig. 4), Davis (Subjects 2, 3, 4, 7, 8, 9 and 11) and Bell (2, 4 and 9) HJCs were located outside the acetabular rim or overlapped with bone. The functional methods HJCs were all located inside the acetabular rim and did not overlap with bone for the skin marker and DF measurements.

Figure 3.

Hip joint center locations plotted relative to the 3D reconstruction of each subject’s pelvis. The Bell, Davis, Harrington, Schwartz Transformation Technique (STT), and Symmetrical Center of Rotation Estimation (SCoRE) were estimated from skin marker positions, whereas the femoral joint center (FJC) was calculated directly from the 3D reconstruction of the femoral head center in the dual fluoroscopy system. The view was set manually to a perspective centered in the acetabulum. For visualization purposes, the hemipelvi were scaled to approximately the same height, and right hemipelvi (subjects 6-11) were reflected to match the anatomical directions of left hemipelvi. Some of the HJCs overlapped one another as they were in close proximity, obscuring neighboring HJCs in certain instances.

Figure 4.

Hip joint center locations calculated from DF plotted relative to the 3D reconstruction of each subject’s hemipelvis. The Bell, Davis, Harrington, Schwartz Transformation Technique (STT), Symmetrical Center of Rotation Estimation (SCoRE) and femur joint center (FJC) were calculated with DF solutions of bony landmark positions. The view was set manually to a perspective centered in the acetabulum. For visualization purposes, the hemipelvi were scaled to approximately the same height, and right hemipelvi (subjects 6-11) were reflected to match the anatomical directions of left hemipelvi. Some of the HJCs overlapped one another as they were in close proximity, obscuring neighboring HJCs in certain instances. Note that the hemipelvis for Subject 2 exited the combined view of the fluoroscopes during the functional hip joint center trial; thus, Subject 2 has only predictive method HJCs derived from bony landmark locations during the static trial.

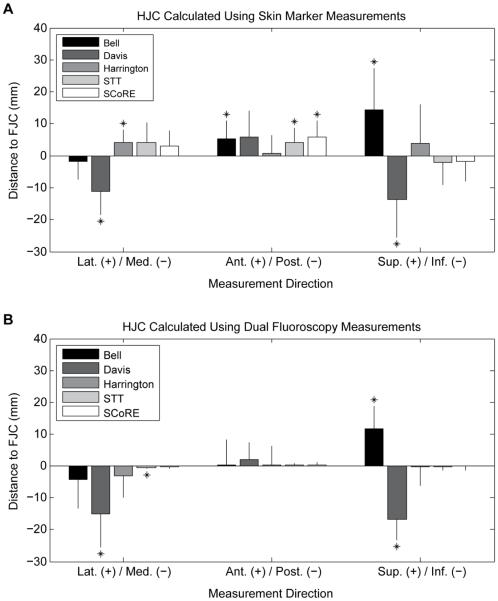
For the HJCs calculated from skin marker positions, each method was significantly different than the FJC in at least one anatomical direction (Fig. 5A). More specifically, the Bell method HJC was significantly anterior (P<0.02) and superior (P<0.01) to the FJC. The Davis HJC was significantly medial (P<0.01) and inferior (P<0.02) to the FJC. The Harrington HJC was significantly lateral (P<0.01). Finally, the STT and SCoRE HJCs were significantly anterior (P<0.01 and P<0.01, respectively).

Figure 5.

Difference in hip joint center locations relative to the dual fluoroscopy measured femur joint center (FJC). Hip joint center locations were generated from reflective skin marker locations (A) and from dual fluoroscopy solutions of the bony landmark locations (B). Significant difference from FJC indicated with an asterisk, * (p<0.05). STT=Schwartz Transformation Technique. SCoRE=Symmetrical center of rotation estimation. Lat.=Lateral. Med.=Medial. Ant.=Anterior. Post.=Posterior. Sup.=Superior. Inf.=Inferior.

For the HJCs calculated from the DF solutions, the number of significant findings decreased, suggesting an overall improvement in the estimation of the HJC among the five methods (Fig. 5B). Still, the Bell HJC was significantly superior (P<0.01) to the FJC, and the Davis HJC was significantly medial (P<0.001) and inferior (P<0.001) to the FJC. Although a marginal difference, the STT HJC was significantly medial (P<0.05) to the FJC. The Harrington and SCoRE methods were not different in any anatomical direction when using the DF solutions.

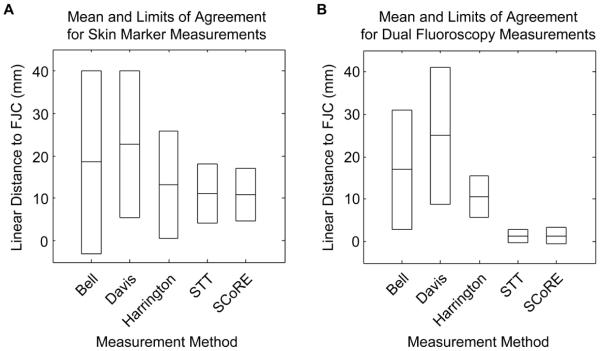
The linear distance from the HJCs estimated by skin markers to the FJC indicated a larger error for the predictive methods than functional techniques (Fig. 6A). More specifically, the Bell, Davis and Harrington HJCs had a mean linear distance of 18.5 mm, 22.7 mm and 13.2 mm, and the STT and SCoRE HJCs had a mean distance of 11.1 mm and 10.8 mm, respectively. For all methods except Davis, the error decreased when the HJCs were calculated from the DF solutions (Fig. 6B). When using the DF solutions, the relative ranking of each method was similar. Specifically, the mean linear distance to the FJC for the Bell, Davis, and Harrington HJCs was 16.9 mm, 24.9 mm and 10.6 mm, and the mean distance for STT and SCoRE HJCs was 1.2 mm and 1.4 mm, respectively. The improvements in mean linear distance with DF-based HJCs relative to skin marker-based HJCs were 1.6 mm for Bell, 2.6 mm for Harrington, 9.8 mm for STT and 9.4 mm for SCoRE. Davis was 2.2 mm further from the FJC with DF as compared to skin markers. Therefore, our hypothesis was confirmed for all methods except for the Davis method.

Figure 6.

Mean and 95% limits of agreement for the linear distance between hip joint center locations relative to the dual fluoroscopy measured femur joint center (FJC). Hip joint center locations were generated from reflective skin marker locations (A) and from bony landmark locations measured with dual fluoroscopy (B). STT=Schwartz Transformation Technique. SCoRE=Symmetrical center of rotation estimation.

Discussion

The first objective of this study was to assess the accuracy of five predictive and functional skin marker-based methods to estimate the HJC. Each of the five methods estimated a HJC that was significantly different in at least one anatomical direction from that measured directly in-vivo using DF. Overall, compared to predictive methods, functional techniques provided a better approximation of the actual HJC location. Our second objective was to determine if estimates of the HJC made by predictive and functional methods improved when the DF solutions for bony landmark locations were used in-lieu of those calculated from skin markers. In general, improvements were observed, especially for the functional methods. Collectively, our results in young adults without hip pathologies or movement disorders support the use of functional methods to obtain the HJC.

Both predictive and functional methods to estimate the HJC rely on assumptions made from the position of skin markers. Thus, some level of error in the estimation of the HJC would be expected, independent of the applied technique. However, functional methods may be advantageous in that they do not require palpation of bony landmarks and thus do not necessarily require accurate placement of skin markers. Furthermore, by estimating the HJC from a pre-defined movement, functional methods may inherently account for the anatomy of each subject’s pelvis and femur as hip articulation is likely governed by the shape of the contact interface. Although predictive methods do consider the anatomy, the final estimate of the HJC is a linear approximation that does not necessarily account for inter-subject variation, such as the curvature of bone representing the medial-lateral width of the ilium for a given ASIS width. Also, the appropriateness of predictive methods will depend on the independent variable(s) included in the equations. In this regard, the Bell method only inputs the ASIS width, while the Harrington method depends on the ASIS width as well as the pelvis depth and leg length. Finally, as discussed by Croce et al.⁷, bony landmark identification relies on identification of a point (not just a surface), quantification of the soft tissue layer between the skin marker and bone, and the palpation procedure used. Thus, there may be more potential sources of error when using predictive methods as compared to functional techniques to estimate the HJC. It is for these reasons that we believe the functional methods were able to provide a more accurate estimate of the FJC measured directly in-vivo by DF.

While the functional methods do not require accurate placement of markers, skin motion artifact, previously estimated to be approximately 2 cm for the pelvis¹¹, is thought to introduce errors in functional HJC measurement by erroneously tracking of the femur and/or pelvis⁹. When using the DF solutions to re-estimate the HJC with the functional methods, the mean agreement, as assessed by the linear distance between the HJCs, improved by almost 1 cm for both the STT (9.9 mm) and SCoRE (9.4 mm) HJCs. In addition, the functional HJC’s mean and limits of agreement, which represent the bounds in which one would expect 95% of measurements to lie, overlapped with zero (STT: 1.2 [−0.4 2.8] mm, SCoRE: 1.4 [−0.6 3.4]), indicating that the variation of the difference is greater than the observed mean difference. These results indirectly suggest that skin motion artifact is primarily responsible for the errors in location of the functional hip joint center, as DF measures in-vivo bone motion directly, thereby eliminating skin motion artifact.

For the functional methods, estimates of the HJC have been shown to be influenced by the total range of motion at the joint^{20, 24}. According to the authors of the study that described the star-arc pattern used herein⁵, hip range of motion (ROM) for the subjects in our study was sufficient. In particular, Camomilla et al. stated that 15° in neutral to flexed, neutral to extended and neutral to abduction positions would suffice⁵. The mean ± standard deviation for range of motion in our study was 41.6 ± 6.6° in flexion-extension and 34.3 ± 9.4° in adduction-abduction. Another study, using a mechanical linkage, showed that errors from 30° ROM were significantly greater than errors from 60° ROM²¹. The 60° ROM was suggested as a goal for future studies of HJC locations¹⁶. However, our study demonstrated that functional methods provided a more accurate estimation of the HJC when using DF solutions that eliminated skin marker error. Indirectly, this would imply that skin motion artifact, which has been shown to increase at larger hip joint angles¹¹, worsens the functional HJC measurement. Indeed, a previous study that utilized skin marker analysis did demonstrate increased error when using a larger ROM compared to a limited motion profile¹. The effect of ROM on HJC position has not been explored with DF and presents a focus for future work. This is important because many patient populations suffer from hip pain and weakness and therefore cannot complete the functional hip joint trial.

Although this is the first study to measure the in-vivo position of the HJC with DF, our results are similar to previous research that compared predictive and functional HJCs. Ultrasound has been previously used to assess HJC errors in the gait laboratory, with 2D ultrasound measuring errors of 13.4 mm for functional and 21.6 mm for predictive methods¹⁵. Our study’s skin marker analysis reported 11 mm for functional methods and 13 - 23 mm for predictive methods, which is in agreement with that quantified by 2D ultrasound. Three-dimensional ultrasound measurements found similar results, with the Harrington method performing best of the predictive methods (mean error 16 mm) and the geometric sphere fit functional method the best of the functional methods (mean error 15 mm)²³. An EOS system, which is a low-dose biplane imaging system capable of HJC registration based on standing x-rays, found the geometric sphere fit functional method to localize the HJC within 11 mm and the Harrington method to put the HJC within 17 mm²⁴. A recent review of the available HJC studies determined that a functional method should be used when sufficient range of motion is available and that the Harrington equations had the smallest error of all the predictive methods¹⁶. While the previous study and review suggested that the geometric sphere fit method performed the best of the functional methods, the mean agreement of the STT and SCoRE techniques in our study fell below or within the range of error values listed for in-vivo studies that used a geometric sphere fit.

While all HJCs were statistically different than the FJC in at least one direction, the question remains whether or not the differences were clinically relevant. Ultimately, the need for accurate measurements of the HJC, and their influence on clinical parameters of gait, will depend on the objective of that given study. However, a previous modeling study found the clinically relevant threshold for HJC mislocation error to be 30 mm²⁶. Given this threshold, only the Bell and Davis HJCs exhibited clinically relevant differences. For Bell, two of 11 subjects (18%) had HJCs more than 30 mm from the FJC, and these were both for skin marker-based HJCs. The Davis HJCs were also 30 mm or more from the FJC on two of 11 subjects with skin marker-based HJCs, and the number of subjects increased to four of 11 subjects (36%) for the the DF-based HJCs. All of the Harrington, STT and SCoRE HJCs were within the 30 mm threshold for both skin markers and DF. Based on the clinically relevant threshold defined by Stagni et al., our data confirm that the Harrington and functional methods are most appropriate for clinical use. However, the effect of different HJC definitions on joint mechanics has yet to be determined, as the previous modeling work was based on nominal perturbation of an HJC in each anatomical direction²⁶. Future studies could use the errors reported in our study as baseline data to assess the sensitivity of biomechanical measurements that rely on the HJC. From these calculations, investigators could then determine if errors introduced by calculations of the HJC are clinically important for the research question at hand.

The advantages of coupling DF with MBT are that they allow for submillimeter and subdegree measurement accuracy and visualization of the calculated HJC relative to the 3D reconstructed anatomy of each subject’s pelvis and femur. In contrast, almost all previous studies traced only the femoral head on a single image or stack of images and then calculated the joint center from these outlines^{15, 23}. Furthermore, we identified bony landmarks in a semi-automatic fashion using principal curvature, as opposed to manual identification in medical image data¹². Moreover, we could visualize the HJC calculated using the various methods relative to the subject’s pelvis. Finally, for both static poses and dynamic functional hip joint motions, we were able to isolate the influence of soft tissue motion relative to errors from other sources such as inaccuracies in the regression equation by using the DF solutions to recalculate the HJC.

There are disadvantages to using DF and MBT. The screening x-ray, CT scan and dual fluoroscopy motion capture exposed subjects to ionizing radiation. The effective dose equivalent for the study was 10.72 mSv. This is equal to approximately 0.21 times the yearly radiation exposure limit allowed for a radiation worker, or roughly 3 years of background radiation. In addition, segmentation of the 3D model and MBT was a laborious process. Thus, while DF and MBT provided submillimeter accuracy for measuring the HJC, this approach may not be efficient for analysis of studies including a larger sample size.

This study included factors that potentially influenced the results reported herein. First, we did not obtain an accurate estimate of the thickness of soft tissue between the marker base and bone. Neglecting soft tissue thickness above the ASIS and PSIS bony landmarks would result in overestimation of the pelvis depth; ignoring the pelvis depth component of the Harrington HJC calculation has been shown to improve HJC estimates by 3 mm²². However, we suspect soft tissue thickness would not influence our results substantially because our study subjects had a low BMI (21 ± 2 kg/m²). While the lower BMI of study subjects helped reduce errors from soft tissue thickness, results from lower BMI subjects may or may not extend to subjects with higher BMI. Errors in the estimation of the HJC could increase for subjects with higher BMI due to increased soft tissue artifact. Thus, caution should be exercised when interpreting our HJC errors for studies that enroll subjects with a larger BMI. Furthermore, patients with limited joint strength or other disabilities may not be able to complete the functional joint center trial and thus, only predictive methods could be used to estimate the HJC in these subjects. Nonetheless, our reported errors for predictive methods would still apply for subjects without abnormal hip anatomy that were within the age and BMI of our subjects. In addition, there is variation in hip joint between male and female anatomy, but with our sample size, it was not practical to assess gender as a covariate when assessing statistical differences between HJC calculations. Along these lines, a larger sample size would increase statistical power and possibly alter the number of significant findings between different predictive/functional methods and the FJC. Nevertheless, the purpose of this study was not to establish statistical significance between two or more methods, but rather to report baseline errors one could anticipate when evaluating gait in adults with relatively low BMI who did not have abnormal hip anatomy.

An additional potential limitation was the ability of the authors to accurately place markers at the same anatomical location across subjects. We aimed to reduce radiation exposure, and thus, we did not examine inter/intra-rater repeatability for this study. Discrepancies in the placement of skin markers could have altered differences from the skin marker-based HJCs as compared to the DF-based HJCs. Another potential limitation is that the methods we evaluated were only those available in Visual3D and Vicon Nexus. We did not assess the errors in estimating the HJC from a marker placed on the greater trochanter. Moreover, a geometric or algebraic algorithm for the functional joint calculation may yield a HJC closer to the FJC measured by DF. Nevertheless, there were close mean agreements between the FJC and STT and SCoRE algorithms when using the DF solutions at 1.2 mm and 1.4 mm, respectively. Future research could explore additional fitting algorithms or develop novel approaches to determine the HJC, using the data herein.

To summarize, using DF and MBT, we found that functional methods had better overall agreement with the FJC than predictive methods. Both the functional and predictive methods (except Davis) improved when using the DF solutions, especially the functional methods, which suggests that skin motion artifact plays a major role in causing inaccuracies in the estimation of the HJC. This study highlights the need to use caution when interpreting biomechanical variables dependent on the spatial location of the HJC, especially when predictive methods are employed. Future work will use the data collected herein, and analysis of forthcoming dynamic activities of daily living, to determine the influence of soft tissue artifact (STA) on estimates of the HJC as well as predictions of joint angles, joint moments and joint reaction forces from biomechanical models. However, in the current study the overall influence of STA can be deduced from the comparisons of the HJC calculated from skin-markers to those derived from the DF-based solutions.