Abstract
Molecular dynamics (MD) trajectories based on a classical equation of motion provide a straightforward, albeit somewhat inefficient approach, to explore and sample the configurational space of a complex molecular system. While a broad range of techniques can be used to accelerate and enhance the sampling efficiency of classical simulations, only algorithms that are consistent with the Boltzmann equilibrium distribution yield a proper statistical mechanical computational framework. Here, a multiscale hybrid algorithm relying simultaneously on all-atom fine-grained (FG) and coarse-grained (CG) representations of a system is designed to improve sampling efficiency by combining the strength of nonequilibrium molecular dynamics (neMD) and Metropolis Monte Carlo (MC). This CG-guided hybrid neMD-MC algorithm comprises six steps: (1) a FG configuration of an atomic system is dynamically propagated for some period of time using equilibrium MD; (2) the resulting FG configuration is mapped onto a simplified CG model; (3) the CG model is propagated for a brief time interval to yield a new CG configuration; (4) the resulting CG configuration is used as a target to guide the evolution of the FG system; (5) the FG configuration (from step 1) is driven via a nonequilibrium MD (neMD) simulation toward the CG target; (6) the resulting FG configuration at the end of the neMD trajectory is then accepted or rejected according to a Metropolis criterion before returning to step 1. A symmetric two-ends momentum reversal prescription is used for the neMD trajectories of the FG system to guarantee that the CG-guided hybrid neMD-MC algorithm obeys microscopic detailed balance and rigorously yields the equilibrium Boltzmann distribution. The enhanced sampling achieved with the method is illustrated with a model system with hindered diffusion and explicit-solvent peptide simulations. Illustrative tests indicate that the method can yield a speedup of about 80 times for the model system and up to 21 times for polyalanine and (AAQAA)3 in water.
I. Introduction
Molecular dynamics (MD) simulations of detailed atomic models is a powerful tool to study the properties of complex biomolecular systems.1−3 However, while simulations based on realistic all-atom (AA) models arguably offer the most detailed information, such models evolve on a complex and rugged energy surface, and their dynamics is often burdened by a host of slow processes. For this reason, achieving an adequate sampling of all the relevant configurations of a system from straight MD simulations is often challenging. Most proposed approaches to enhance sampling by accelerating the exploration of configurational space are either not guarantied to yield Boltzmann equilibrium or only applicable to a small subset of degrees of freedom;4−13 see refs (14−17) for reviews. The Metropolis Monte Carlo (MC) algorithm, which consists of generating a random walk in configuration space from a set of proposed moves that are attempted and then accepted or rejected,18,19 also offers a powerful method to generate a Boltzmann equilibrium distribution that is not, in principle, limited by dynamical processes. In practice, its application is only limited by the richness of the set of proposed moves that are attempted for generating a random walk in configurational space. Nevertheless, attempts to sample large conformational changes with MC remain completely ineffective for complex molecular systems in the presence of explicit solvent due to the rejection of all proposed new configurations.
An appealing alternative approach is to consider a simplified coarse-grained (CG) model that relies on an effective many-body potential of mean force (PMF) associated with a reduced set of degrees of freedom.20−23 Because the many-body PMF governing a CG model is expected to be generally smoother than the energy surface of its AA counterpart, its dynamics is often intrinsically simpler and faster. However, except for the simplest situations, the effective many-body PMF associated with the CG degrees of freedom is not known exactly. Commonly, an approximate PMF is constructed, which affects many thermodynamic and kinetic results. Force-matching, whereby information extracted from the fine-grained (FG) model via the mapping function is transferred toward the CG model, provides a formal route to improve the many-body PMF underlying a CG model.22,23 However, the accuracy of the resulting CG model remains inherently limited by the functional form chosen to represent the many-body PMF.
Even assuming that a long trajectory of a CG model has been generated, exploiting this information to enhance the configurational sampling of the FG model is not straightforward. In principle, a set of configurations for the FG model could be generated by reconstructing, via a “reverse coarse-graining” (rCG) operation, the missing degrees of freedom onto snapshots extracted from a CG trajectory. Unfortunately, rCG generally involves mostly ad hoc empirical modeling procedures that do not yield a Boltzmann equilibrium distribution. In this sense, the information does not flow from the CG to the FG model. More rigorous approaches allowing the information to flow back and forth between a FG model and its associated CG model have sought to couple the two levels via a resolution-exchange strategy.24−30 In particular, resolution-exchange with incremental coarsening relies on a potential energy that interpolates between the FG and CG models according to a parameter λ.24−26,28 The hope of resolution-exchange is to combine the efficiency of CG simulation and the accuracy of a FG model by swapping configurations between the two representations, although achieving considerable gains in computational efficiency remains a challenge. One proposed route to improve the efficiency of the algorithm has been to first relax configurations before an exchange is attempted, but this procedure yields the correct canonical sampling only if the rate of exchanges is sufficiently low.27 An alternative avenue is the multiscale enhanced sampling (MSES) method of Zhang and Chen, in which a small set of CG auxiliary particles evolving on a simplified potential energy surface is coupled to an all-atom system via harmonic springs of variable strength within a replica-exchange simulation framework.31
Despite these previous efforts, a robust framework that exploits the information from a CG model to generate the proper Boltzmann equilibrium distribution for a FG model is still needed. A promising avenue to address these issues is presented by the recent extensions to the MC algorithm that combines the strength of nonequilibrium molecular dynamics (neMD) and MC.32−36 In hybrid neMD-MC, the value of some chosen variable is altered gradually in a time-dependent controlled manner, while the remaining degrees of freedom are allowed to evolve freely according to the dynamical equations of motion. The configuration generated by the nonequilibrium switching process is then treated as a candidate that must be either accepted or rejected via a Metropolis criterion to generate the equilibrium Boltzmann distribution. This hybrid neMD-MC framework has most notably been used to formulate a constant-pH simulation algorithm.32,33,37
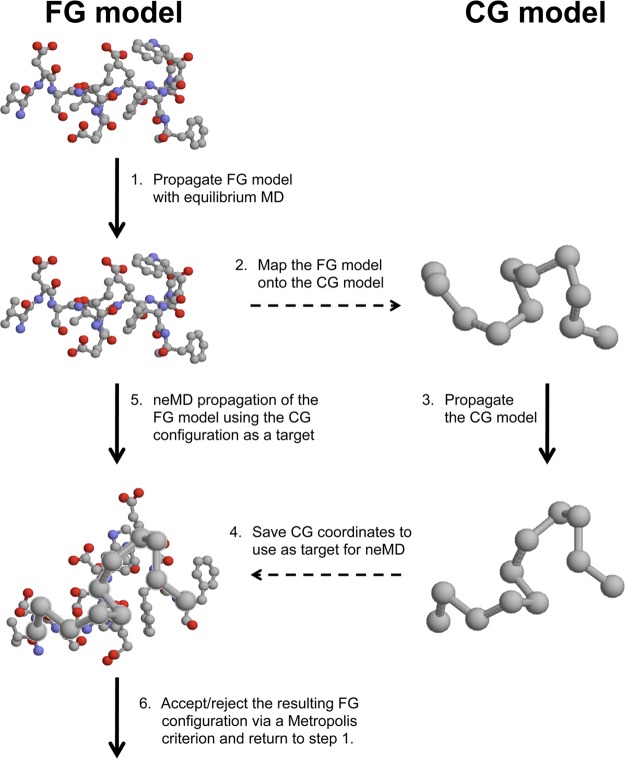
Here, this idea is pursued further to design a novel multiscale method that exploits the evolution of a CG model to help generate target candidate configurations that are then used to guide the FG model during the neMD switching trajectories. The coarse-grained guided hybrid nonequilibrium molecular dynamics—Monte Carlo (CG-guided hybrid neMD-MC) algorithm, comprises six steps, illustrated schematically in Figure 1: (1) a FG configuration of an atomic system is dynamically propagated for some period of time using equilibrium MD; (2) the resulting FG configuration is mapped onto a simplified CG model; (3) the CG model is propagated for a brief time interval to yield a new CG configuration; (4) the resulting CG configuration is used as a target to guide the evolution of FG system; (5) the FG configuration (from step 1) is driven via a nonequilibrium MD (neMD) simulation toward the CG target; (6) the resulting FG configuration at the end of the neMD trajectory is then accepted or rejected according to a Metropolis criterion before returning to step 1. A symmetric two-ends momentum reversal prescription is used for the neMD trajectories of the FG system to guarantee that the CG-guided hybrid neMD-MC algorithm obeys microscopic detailed balance and rigorously yields the equilibrium Boltzmann distribution.33,36 It is shown that the CG-guided hybrid neMD-MC algorithm can be carefully engineered to achieve a reasonably high acceptance probability, even when using fairly short neMD switching trajectories. More importantly, because the transition probabilities are constructed to satisfy detailed balance, the CG-guided hybrid neMD-MC is guaranteed to yield the equilibrium Boltzmann distribution. In the next section, we formulate the theoretical basis of CG-guided hybrid neMD-MC. The performance of the method is illustrated with applications to simple model systems and solvated polypeptides.
Figure 1.
Flowchart of the CG-guided hybrid neMD-MC simulation method.
II. Theoretical Developments
Let the total energy of a system be E(x) = U(r) + K(p), where U is the potential energy, K is the kinetic energy, and x represents all of the degrees of freedom, including the coordinates r and the momenta p. In Metropolis Monte Carlo, we seek to generate a stochastic random walk process that moves the system from a configuration x to a configuration x′ and ensure that the random walk will obey detailed balance for the Boltzmann distribution:
| 1 |
where π(x) = Q–1 exp[−βE(x)] is the equilibrium probability (β = 1/kBT), and 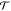 is the
transition probability. One common
approach to construct such a random walk is to separate the transition
probability into two stages: (1) the probability to generate a proposed
move and (2) the probability to accept (or reject) this move,
is the
transition probability. One common
approach to construct such a random walk is to separate the transition
probability into two stages: (1) the probability to generate a proposed
move and (2) the probability to accept (or reject) this move,
| 2 |
which leads to the condition
| 3 |
The probability of a proposed move
describes
the probability of reaction coordinates moving toward the target value.
The probability to accept or reject the proposed move, however, is
determined after the switch. The most common approach is when the
transition probability of the proposed move is inherently symmetric,
i.e., 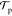 (x → x′) =
(x → x′) = 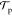 (x′ → x), leading to the
condition for the acceptance probability
(x′ → x), leading to the
condition for the acceptance probability
| 4 |
that is formally satisfied by the Metropolis criterion,
| 5 |
Examples include constant-pH simulation or
biminima simulation, where the reaction coordinates of the neMD-MC
can only choose predetermined values. For example, in a hybrid MD/neMD-MC
constant-pH simulation, the reaction coordinate for neMD-MC is the
protonation state. Therefore, the target value is always the deprotonated
state when the initial value is the protonated state and vice versa.
As a result, 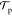 is always 1.
In the biminima simulation,
the reaction coordinates are usually shifted for a fixed amount, and
therefore
is always 1.
In the biminima simulation,
the reaction coordinates are usually shifted for a fixed amount, and
therefore 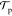 is also 1. By
substitution, it can be readily
shown that
is also 1. By
substitution, it can be readily
shown that
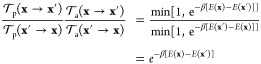 |
6 |
and therefore the Metropolis construct satisfies eq 1. In this case, if the constraint schedule is time reversible and the momentum is properly treated, the neMD-MC will generate the correct Boltzmann distribution.33,35,36
If the long time scale
relaxation of the system is known to be
dominated by the dynamics along a set of coarse-grained (CG) variables, R, it is possible to exploit this information to increase
the efficiency of the hybrid neMD-MC algorithm. First, it is assumed
that at any time, the CG variables R(t) are uniquely defined from x(t) through
a mapping function as, R = M[x]. The general idea is to separate the transition probability 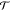 (x → x′)
into two distinct steps,
(x → x′)
into two distinct steps,
| 7 |
where 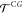 represents the transition probability for
a set of CG variables R, and latter
represents the transition probability for
a set of CG variables R, and latter 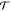 is the
transition probability for the FG
variables x, conditional on the transition R → R′ taking place. Here, the
first step only involves changes in the CG variables. The transition
probability,
is the
transition probability for the FG
variables x, conditional on the transition R → R′ taking place. Here, the
first step only involves changes in the CG variables. The transition
probability, 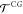 , is constructed such that it obeys the
CG detailed balance relationship,
, is constructed such that it obeys the
CG detailed balance relationship,
| 8 |
where πCG(R) is the equilibrium probability of the R coordinates associated with the CG model. Assuming that the CG model is constructed on the basis of a potential of mean force W(R), the probability ratio is,
| 9 |
In practice, a
number of methods could be
used to fulfill these conditions while propagating the CG coordinates
(e.g., Brownian dynamics, Langevin dynamics, Metropolis MC, etc.).
In the second step, the transition R → R′ in CG space must be used to guide the changes in the remaining
atomic FG degrees of freedom. To formalize this idea, it is useful
to rewrite the transition probability 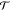 as the
product of the probability of a proposed move
as the
product of the probability of a proposed move 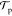 , and the probability
to accept
or reject the proposed move
, and the probability
to accept
or reject the proposed move 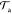 ,
,
| 10 |
In principle,
generating the transition probability 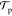 for the proposed move in x, conditional on the transition R → R′, could be a daunting task.
Even simply mapping the set of
FG variables x that is consistent with the CG variables R, a problem that is commonly referred to as “reverse
coarse graining”, can be extremely difficult in general. However,
all issues with such a reverse mapping problem are resolved naturally
and rigorously if the system’s degrees of freedom x(t) are generated from a neMD propagation under
the influence of a time-dependent constraint dragging the CG variables
from their initial R to the final R′
value. During the neMD dynamical R → R′ switching process, the evolution of the CG coordinates R(t) is externally controlled and follows
a fixed time-dependent schedule over a time interval τneMD, while the remaining degrees of freedom are propagated freely
for the proposed move in x, conditional on the transition R → R′, could be a daunting task.
Even simply mapping the set of
FG variables x that is consistent with the CG variables R, a problem that is commonly referred to as “reverse
coarse graining”, can be extremely difficult in general. However,
all issues with such a reverse mapping problem are resolved naturally
and rigorously if the system’s degrees of freedom x(t) are generated from a neMD propagation under
the influence of a time-dependent constraint dragging the CG variables
from their initial R to the final R′
value. During the neMD dynamical R → R′ switching process, the evolution of the CG coordinates R(t) is externally controlled and follows
a fixed time-dependent schedule over a time interval τneMD, while the remaining degrees of freedom are propagated freely
| 11 |
The CG coordinates start in the initial state R at the beginning of the neMD switch and are gradually altered in a time-dependent manner to reach the final state R′ at a time interval τneMD later. This process can be implemented by evolving the system under a time-dependent holonomic constraint, or by applying stiff harmonic restraints centered on R(t). Finally, the CG-guided scheme must satisfy the global detailed balance relationship,
| 12 |
To guarantee detailed balance, the time-dependent R(t) for the forward and backward switching, R → R′ and R′ →R, must be consistent. This is automatically satisfied if R(t) is constructed from the linear form eq 11. A nonlinear form could also be used for the switching, as long as it is symmetric and time-reversible. Assuming that the transition probability of the proposed move is symmetric,
| 13 |
which is verified if the dynamical propagation used to generate the neMD trajectory is deterministic and reversible (e.g., using a symplectic integrator), we obtain,
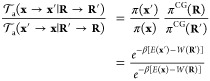 |
14 |
It follows that in the
CG-guided hybrid neMD-MC
scheme, the Metropolis acceptance probability, 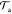 , is
, is
| 15 |
In the present development, it is assumed that the CG model is propagated via a thermalized dynamics satisfying the detailed balance condition eq 8. This is the reason why the energy difference between the CG configurations (W(R) −W(R′)) appears in the acceptance criterion eq 15. Alternatively, one could carry out the dynamics of the CG system with a propagator that conserves energy, consistent with a microcanonical ensemble. In this case, the energy difference of CG configurations would not appear in the Metropolis criterion. It is also worth pointing out that the CG coordinates R correspond to a subspace of the FG coordinate x that is generated via the mapping function M[x] through eq 11. In this sense, the acceptance criterion operates only in the FG space and this is the reason why the acceptance criterion does not involve a joint distribution in terms of (x,R).
As illustrated in Figure 1, the CG-guided hybrid neMD-MC algorithm comprises the following steps: (1) Propagate the FG system with equilibrium MD using the potential energy U(x) for a period of time τMD; (2) extract the CG coordinates R from x via the mapping function M; (3) propagate the simple CG on the free energy surface W(R) (for a predetermined time τCG or until a chosen stopping criterion is met) to yield the new CG configuration R′; (4) save the final CG coordinates R′ to use as a target for the neMD trajectory; (5) propagate the FG model from x to x′ under the time-dependent constraint that M[x] changes linearly from R to R′ over an interval τneMD; and (6) accept or reject the final configuration of the FG system according to the Metropolis probability eq 15 before returning to step 1.
By construction, the CG-guided hybrid algorithm yields the correct Boltzmann equilibrium distribution for the FG model, regardless of the underlying CG model that is chosen to generate the attempted moves. Nonetheless, the choice of an optimal CG model to achieve the highest efficiency is an important issue that needs further consideration. Generally, important sampling techniques aim at achieving variance reduction in computer simulations by sampling high and low probability regions with equal frequency while recovering a correct distribution by assigning a proper statistical weight to the different regions. The CG-guided hybrid algorithm can be designed according to the same guiding principles by recognizing that the potential energy driving the CG model actually governs the statistical weight attributed to the coordinates R. For a given FG model, the “exact” PMF with respect to the CG degrees of freedom is defined as,
| 16 |
where C is some constant. If Wexact(R) were known, then using it in the algorithm would result in an optimal CG model. This is because the CG-guided neMD simulation would sample all regions with equal probability, as demonstrated by the following development:
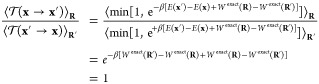 |
17 |
This relationship is valid for any R and R′ within the CG space. In addition, the average acceptance probability for neMD transitions between R and R′, which also affects the simulation efficiency, is
| 18 |
When increasing W(R) relative to W(R′), ⟨ (x′ → x)⟩R′ increases while ⟨
(x′ → x)⟩R′ increases while ⟨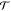 (x → x′)⟩R decreases and vice versa; eq 18 reaches a maximum if the average acceptance
probability is roughly equal, when using Wexact(R) for the CG model. In practice, the exact PMF with
respect to the CG degrees of freedom is not known, but the above argument
shows that, in an importance sampling sense, the optimal efficiency
will be achieved if one chooses a reasonable approximation to Wexact(R) that accurately captures
the dominant effects.
(x → x′)⟩R decreases and vice versa; eq 18 reaches a maximum if the average acceptance
probability is roughly equal, when using Wexact(R) for the CG model. In practice, the exact PMF with
respect to the CG degrees of freedom is not known, but the above argument
shows that, in an importance sampling sense, the optimal efficiency
will be achieved if one chooses a reasonable approximation to Wexact(R) that accurately captures
the dominant effects.
III. Illustrative Simulations
(a). Linear Chain of Linked Particles
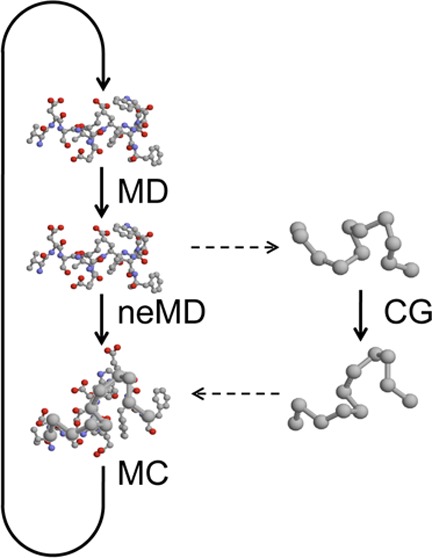
A one-dimensional linear chain system with 12 particles linked together in a periodic potential was designed to test and illustrate the enhanced sampling from the CG-guided hybrid neMD-MC. The system is shown in Figure 2. The FG system comprises 12 particles, each with a mass of 1, and each pair of adjacent particles is connected by a bond. The only two types of forces acting on each particles are the bond force and the potential force. The potential force, shown in Figure 3, is defined by U(i) = cos(2π xi) – cos(10π xi)/2, where x is the coordinate, and i is the index of the particle (going from 1 to 12). The first part of U(i) defines the periodicity. The second part introduces additional ruggedness on the energy surface. The bond force is defined by Ebond(i,j) = 20(rij – 1)2δ(|i – j| – 1), where rij is the distance of the two particles, and the function δ indicates that only adjacent particles are connected by a bond. The periodic potential energy divides the configuration space into infinite number of wells along the x axis, with the width of each well being 1 and the energy barrier between adjacent wells being around 2.6. The vertical dashed line in Figure 3 shows the boundary of each well. Since the optimal bond length is also 1, the most stable configuration of the molecule is to occupy 12 adjacent wells, each with one particle. To diffuse along the x axis, a couple of particles, if not all, have to cross the energy barrier at the same time. Therefore, the diffusion constant from MD simulations is extremely low (see Figure 6a). The CG system contains only three effective particles, each with a mass of 4. No additional potential force is applied in the CG system. The bond force for the CG system is given by EbondCG(i,j) = 20 (rij – 4)2 δ(|i – j| – 1). The CG particles 1, 2, and 3 correspond to the centers of mass of FG particles 1–4, 5–8, and 9–12, respectively. The simulation of this system is carried out using an in-house code written in c++. The temperature kBT is set to 1; diffusion constant to 0.5; time step to 0.005; and collision rate to 2.0. The lengths of equilibrium MD, CG, and neMD simulations are all 1000 steps. A flowchart of the simulation for this system is shown in Figure 2. Each simulation is carried out for 106 rounds.
Figure 2.
Flowchart of CG-guided hybrid neMD-MC for a 12 particle model system. Big (small) spheres represent the particles in the CG (FG) system. Springs represent bonds. Configuration of the CG (FG) system is represented using R (x). Groups of particles are circled using a blue box. The solid lines between the FG and CG system represent the center-of-mass constraints applied on the FG system using the position of the CG particles. The arrows between the FG and CG system represent the mapping function M. (a) From the initial FG structure x, the CG structure R is built. (b) Dynamical propagation is performed on the CG model, generating a new configuration R′. (c) Dynamical propagation is performed on the FG model, generating a new configuration x′. During this propagation, the position of the CG model is used to constrain the center-of-mass for the FG system. The time-dependent constraints vary linearly in accord with eq 11.
Figure 3.
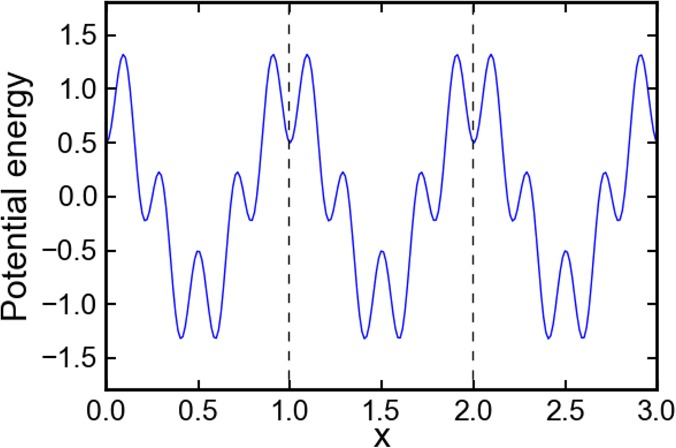
Potential energy surface for the 12 particle model system. The blue solid line presents the potential energy along the x axis. Its analytic form is U = cos(2πx) −cos(10πx)/2. The potential energy is periodic and extends to infinity. This figure only shows three wells. The width of each well is 1. The dotted lines mark the boundaries of each well.
Figure 6.
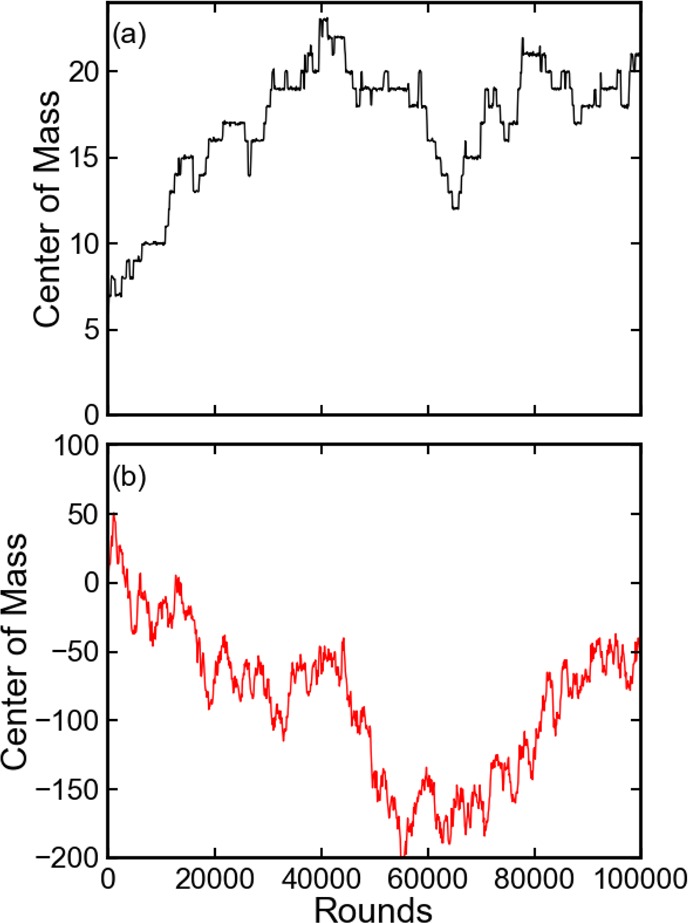
Evolution of the center-of-mass of the entire linked chain molecule. The center-of-mass is sampled every 100 rounds. (a) Equilibrium MD. Each round contains a MD of 2000 steps. (b) CG-guided hybrid neMD-MC. Each round contains MD, CG simulation, and neMD-MC, each for 1000 steps. The linear regression generates a coefficient of determination R2 value above 0.99 for either scheme.
(b). Solvated Peptide System
The algorithm was tested on four different AA peptide systems with explicit solvent: trialanine(Ala3), penta-alanine(Ala5), deca-alanine(Ala10), and (AAQAA)3. (AAQAA)3 is a 15 residue peptide, with residues 3, 8, and 13 as glutamine and the rest as alanine. The polyalanines have all α-helical initial structures. For (AAQAA)3, two different initial structures were prepared, one β-sheet like and another α-helix like, as shown in Figure 4. Ala3 and (AAQAA)3 have an acetylated N-terminus and an N-methylamide C-terminus. Ala5 and Ala10 have unblocked, charged termini. The potential energy of the solvated peptide systems is represented by the CHARMM36 force field38 and TIP3 water potential.39 Ala3 is solvated in a 24 Å cubic box: Ala5, 30 Å; Ala10, 40 Å; and (AAQAA)3, 60 Å. The solvent for the Ala5 and Ala10 systems is a 1 M KCl aqueous solution. The CG systems for polyalanines and (AAQAA)3 systems include only a single atom type for the backbone α carbon (CGC). It has the atom mass of a normal carbon, 12.01. Each α carbon in the AA system is associated with one CGC atom. The total number of CGC atoms depends on the length of the peptide. Unless mentioned otherwise, the bond, angle and dihedral energy terms for CGC are empirically set as Ebond = 100 (r – 3.83)2, Eangle = 94.84 (θ – 100.0)2, and Edihedral = 0.1 (χ – 55.0)2, where r, θ, and χ are the bond length, angle, and dihedral, respectively. There is no water and no periodic boundary conditions (PBC) for the CG system.
Figure 4.
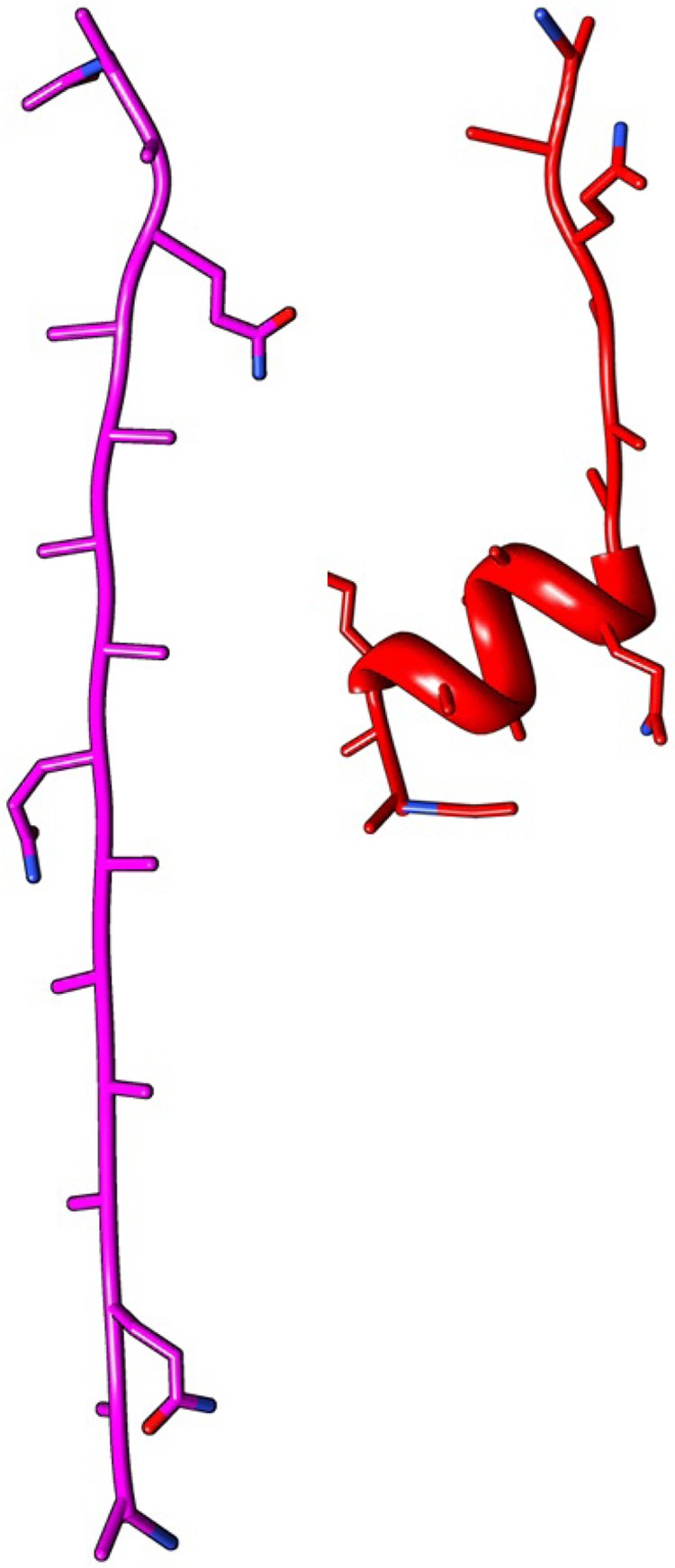
Two initial structures of (AAQAA)3. The magenta one has an all β-sheet configuration. The red one has an α-helix for the first 10 residues and β-sheet for the rest of the 5 residues.
The CHARMM program version c36b140 is used for MD simulations for both the AA and CG system. In-house Python scripts are used for the general control flow of the algorithm (generating CHARMM input files, controlling MC acceptance, etc.). Input files are generated at each attempted move with the newest parameters and constraints. Unbiased brute-force MD simulations were also performed with the same systems to provide a comparison.
For the AA simulations with explicit solvent (MD and neMD), the system is subjected to PBC. Particle-Mesh Ewald (PME) summation41 is used to treat the electrostatic interactions, with a real-space cutoff set to 14 Å and grid spacing smaller than 0.5 Å. The Lennard-Jones (LJ) interactions are smoothly truncated with a switching function from 10 to 12 Å. The equations of motion are integrated with a time-step of 2 fs, and SHAKE42 is used to constrain covalent bonds involving hydrogen atoms. For MD, the peptide is kept near the center of the PBC box with a weak global center-of-mass restraint. The leapfrog varlet integrator is used with constant temperature and pressure control (CPT) based on Berendsen’s method. Temperature is controlled at 300 K and pressure at 1 atm. For neMD, the leapfrog verlet integrator is used without CPT. The position of carbon-α is harmonically and strongly constrained. The constraint target positions vary linearly during the switch. The initial constraint position is mapped from the AA structure, and the final constraint position is generated by CG simulations. Theoretically, there could be a small “tracking” error between R and M[x] when harmonic restraints are used instead of holonomic constraints, but the tracking error is expected to be small with strong restraints, and does not affect the accuracy or the foundation of the theory. To propagate the CG system, a Langevin dynamics is used with a temperature of 300 K. The overall rotation and transition are removed from the CG configuration. In each cycle, the initial velocities of the CG model were generated according to the Maxwell distribution.
In the present implementation, the MD and neMD trajectories have a fixed length while the propagation of the CG coordinates is controlled by a “stopping criterion”. Choosing carefully the stopping criterion to control the magnitude of the displacement R → R′ can greatly increase the efficiency of the method (see the Discussion section). Here, two different stopping criteria were tested. The first criterion is based on the root-mean-square-deviation (RMSD) of the set of CG coordinates; the CG simulation is stopped when the difference ∥R–R′∥ exceeds a preset maximum allowed value, ΔRMSD. The second criterion is based on the deviation of angles within the set of CG coordinates and works also with a preset maximum allowed value, Δθ. Taking the (AAQAA)3 system as an example, the CG system comprises 15 atoms and therefore 13 angles formed by adjacent atoms. The initial angles are recorded, the absolute change in degrees (between −180 to 180) for each is monitored, and the CG simulation is stopped when the average absolute change exceeds the preset maximum allowed value. For Ala3, Ala5, Ala10, and (AAQAA)3, both were tested. The difference of efficiency is examined in the Discussion section. Lastly, to prevent sampling of the cis-peptide bond conformation, all target configurations generated by CG simulation with bond lengths shorter than 3.5 Å were discarded.
IV. Results and Discussion
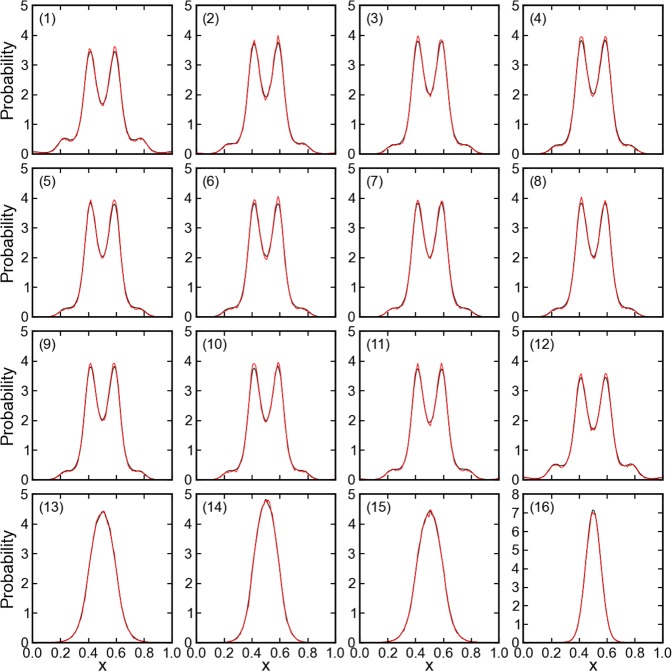
The general validity of the CG-guided hybrid neMD-MC was first ascertained using a simple model of a linear chain of linked particles in a one-dimensional periodic potential (Figure 2). In Figure 5, the distribution of each single particle, the center-of-mass of each particle group, and of the entire linear chain are plotted. For all degrees of freedom, the CG-guided hybrid neMD-MC and the equilibrium MD generate the exact same distributions. The global diffusion constant of the linked chain is a good indicator of the overall sampling efficiency of the simulation. For each scheme, 10 independent trajectories were generated. The diffusion constant along the x axis is calculated as ⟨∥xt – x0∥2⟩= Dt, where ⟨...⟩ denotes the average of 10 trajectories. The evolution of the center-of-mass for the entire chain is shown in Figure 6. The diffusion constant is 0.53 per 1000 rounds for equilibrium MD and 43 for CG-guided hybrid neMD-MC. According to this estimator, the CG-guided hybrid neMD-MC gives a speedup of 80 times for this system. While the CG-guided hybrid neMD-MC algorithm can rigorously yield the proper Boltzmann equilibrium distributions, it is absolutely critical to satisfy all conditions of microscopic reversibility for a valid algorithm. For example, using a time-dependent constraint that is not symmetric with respect to R and R′ for the switching schedule fails to reproduce the correct equilibrium distributions of each particle and particle group (results not shown).
Figure 5.
Distribution along x for the linked chain model system. Black lines show the distribution simulated using equilibrium MD simulation; red lines show the CG-guided hybrid neMD-MC. The subplot (1–12) presents the distribution for each atom; (13–15) for the center-of-mass of each atom group; and (16) for the center-of-mass of the entire molecule. The molecule moves along the entire x axis. However, the potential energy surface is periodic. This figure presents the relative position of the atom or center-of-mass inside each well, no matter which well it is residing in. The boundary of the well is defined in Figure 3.
The overall performance of the CG-guided hybrid neMD-MC algorithm was then examined for realistic atomic models of biomolecules with explicit solvent. Those include tri-, penta-, and deca-alanine peptides solvated in water. To ascertain the formal correctness of the method, the population of the various conformations was calculated. The results of the simulation are summarized in Table 1. According to this analysis, CG-guided hybrid neMD-MC and equilibrium MD generate the same distributions. For a valid comparison, however, it is important that the equilibrium MD simulations be sufficiently long to reach proper convergence. The accuracy of the method was further examined for Ala3 using a set of simulation parameters for the CG-guided hybrid neMD-MC simulations (τMD = 2ps, τneMD = 4ps, and ΔRMSD = 1.5). The histogram of distances and angles of adjacent carbon-α is shown in Figure 7. The PMF along ϕ or ψ is shown in Figure 8, and the 2D-PMF along ϕ and ψ angles is shown in Figure 9. According to this analysis, the histograms and PMFs generated by CG-guided hybrid neMD-MC are very similar to those obtained from long equilibrium MD simulations. The similarity of the PMFs along ϕ or ψ angles with previous results from Mu et al.43 provides additional confirmation of the validity of the CG-guided hybrid neMD-MC.
Table 1. Results of Multi-alanine and (AAQAA)3.
| peptide/source | Δa | nMD (ps) | nneMD (ps) | total (ns) | αd % | β % | ppII % | L-α % | ηGf | ηL |
|---|---|---|---|---|---|---|---|---|---|---|
| Ala3 | ||||||||||
| CG-guided hybrid neMD-MC | 1.5 | 1 | 1 | 100 | 33 | 18 | 46 | 2 | 1.9 | 2.4 |
| 1.5 | 2 | 4 | 120 | 35 | 18 | 43 | 2 | 1.4 | 0.7 | |
| 3 | 2 | 4 | 90 | 35 | 18 | 44 | 1 | 5.0 | 1.1 | |
| equilibrium | 120 | 32 | 18 | 46 | 2 | |||||
| Ala5 | ||||||||||
| CG-guided hybrid neMD-MC | 10 | 2 | 4 | 160 | 24 | 18 | 50 | 6 | 5.0 | 0.7 |
| 7 | 2 | 4 | 160 | 19 | 20 | 56 | 2 | 1.5 | 0.7 | |
| 15 | 2 | 8 | 160 | 31 | 17 | 41 | 9 | 6.9 | 0.4 | |
| equilibrium | 120 | 13 | 22 | 62 | 1 | |||||
| refc | 13 | 31 | 52 | |||||||
| Ala10 | ||||||||||
| CG-guided hybrid neMD-MC | 5 | 2 | 2 | 20 | e | 5.7 | 2.3 | |||
| 5 | 2 | 4 | 20 | 6.7 | 2.6 | |||||
| 10 | 2 | 2 | 20 | 10 | 2.0 | |||||
| 10 | 2 | 4 | 20 | 15 | 1.3 | |||||
| equilibrium | 20 | |||||||||
| (AAQAA)3 | ||||||||||
| CG-guided hybrid neMD-MCb | 15 | 4 | 8 | 120 | 30 | 20 | 41 | 8 | 8.7 | 9.8 |
| 15 | 4 | 8 | 120 | 32 | 20 | 34 | 12 | 21 | 5.9 | |
| equilibrium | 100 | 82 | 4 | 12 | 2 | |||||
| refc | 44 | 19 | 30 | |||||||
Using ΔRMSD for Ala3 and Δθ for others.
This simulation of (AAQAA)3 had an initial structure with an α-helix (Figure 4, right). The following row presents result for CG-guided hybrid neMD-MC of (AAQAA)3 with an initial structure with a β-sheet (Figure 4, left). Equilibrium MD simulation has initial structure with an α-helix.
Paper of Best et al.38
α is defined as −160 < ϕ < −20, −120 < ψ < 50 (Figure 9b, blue box); β −180 < ϕ < −90, 50 < ψ < 180, or −180 < ϕ < −90, −180 < ψ < −120, or 160 < ϕ < 180, 110 < ψ < 180 (Figure 9b, cyan box); ppII −90 < ϕ < −20, 50 < ψ < 180, or −90 < ϕ < −20, −180 < ψ < −120 (Figure 9b, magenta box); L-α 0 < ϕ < 120, −30 < ψ < 90 (Figure 9b, yellow box). For Ala3 and (AAQAA)3, termini are blocked, and the averages of all residues are shown; for Ala5 and Ala10, averages of all but two terminal residues are shown.
Trajectories are too short to generate useful statistics.
For Ala3 and Ala5, only transitions of the middle residue are counted. For Ala10, the average of transitions of residues 3–8 is counted. For (AAQAA)3, the average of transitions of residues 3–13 is counted.
Figure 7.
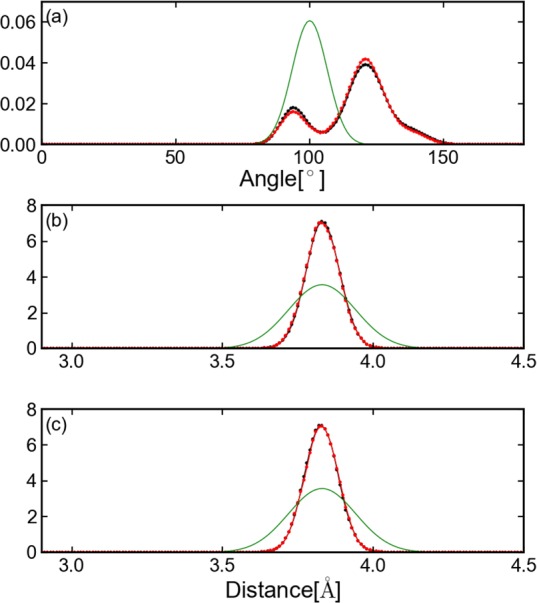
Distribution of distances and angles of adjacent carbon-α for Ala3. The black line presents the results from equilibrium MD; the red line from CG-guided hybrid neMD-MC; and the green line the theoretical distribution calculated from CG parameters. Three carbon-α atoms are defined as CA1, CA2, and CA3. Subplot a presents a histogram of the angle of CA1-CA2-CA3; b the distance between CA1 and CA2; and c the distance between CA2 and CA3.
Figure 8.
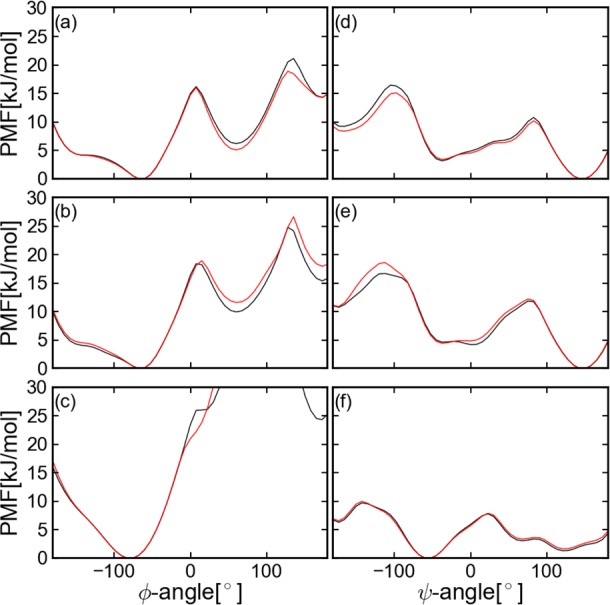
PMF along ϕ and ψ angles for Ala3. The black line presents the results from equilibrium MD and the red line from CG-guided hybrid neMD-MC. Subplots a and d present PMF along the ϕ and ψ angles of residue 1; b and e of residue 2; and c and f of residue 3. The lowest value for each PMF is always set to 0.
Figure 9.
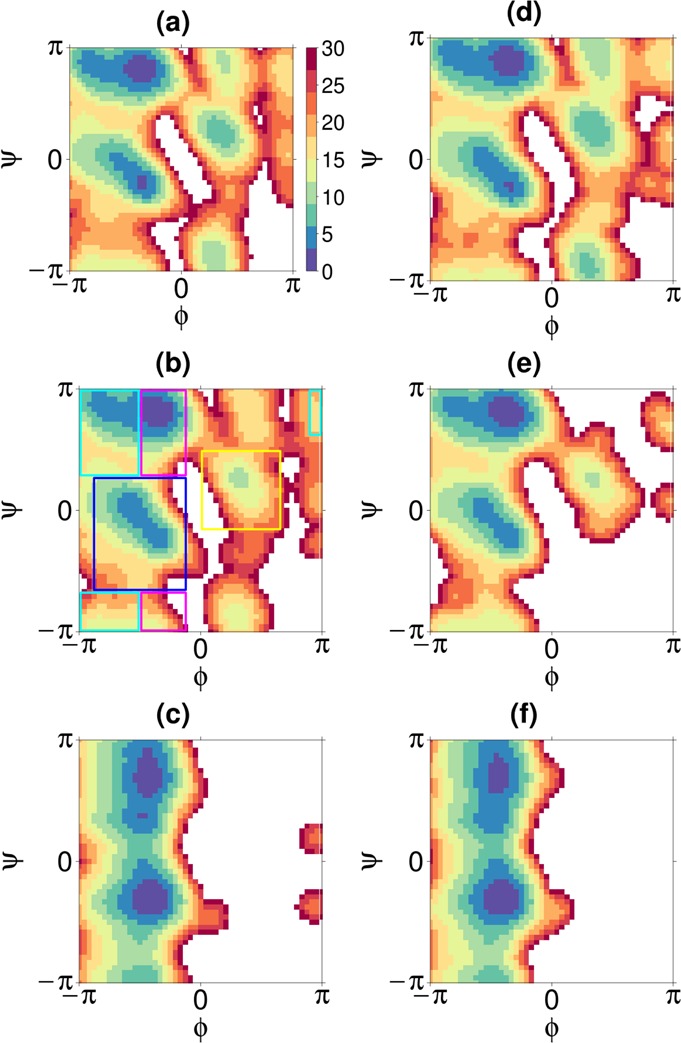
2D PMF along ϕ and ψ angles for Ala3. The x axis is ϕ-angle and the y axis ψ-angle. Subplots a–c present the PMF calculated from the simulation results of equilibrium MD; d–f of CG-guided hybrid neMD-MC. Subplots a and d present the PMF of residue 1; b and e of residue 2; and c and f of residue 3. The color key is shown in a. Definitions of α (blue box), β (cyan box), ppII (magenta box), and L-α (yellow box) are shown in b.
Transitions between the α, β, ppII, and L-α backbone conformers are expected to be representative of the slowest motions of polyalanine peptides in solvent. To quantify the kinetic acceleration gained by the CG-guided hybrid neMD-MC algorithm, we define the speedup factor, η, as the ratio of the number of transition events from the CG-guided hybrid neMD-MC simulation, relative to that from the equilibrium MD simulation. For the sake of the comparison, the total simulation length ascribed to the CG-guided hybrid neMD-MC algorithm comprises the length of both the equilibrium MD and all of the attempted neMD switches (whether they are accepted or rejected). To facilitate the discussion, it is useful to distinguish “global transitions”, corresponding to interconversions between the α, L-α, β, and ppII conformers (not including interconversions between β and ppII), and “local transition”, corresponding to the interconversion between β and ppII. In polyalanine, transitions from α to β are opposed by a large energy barrier. However, the energy barrier for transitions from ppII to β is relatively small. Accordingly, we determined the global and local speedup factors, ηglobal and ηlocal, from the simulation data. On the basis of this analysis, the sampling efficiency appears to vary with the length of MD, τMD, length of neMD, τneMD, and the maximum allowed displacements Δθ or ΔRMSD. In almost all of the cases examined here, CG-guided hybrid neMD-MC has higher efficiency than straight equilibrium MD, going up to 15-fold acceleration.
According to eq 17, the accuracy of the underlying CG model affects the overall efficiency of the CG-guided hybrid neMD-MC algorithm. Specifically, optimal efficiency is achieved if the effective energy surface of the CG model is a reasonably good approximation to the exact PMF with respect to those degrees of freedom. To illustrate this important point, we examined the impact of an improved CG model on the sampling efficiency of the Ala5 peptide. The energy terms of the improved CG model were set to Ebond = 400 (r – 3.83)2, Eangle = 30 (θ −115.0)2, and Edihedral = 0.1 (χ – 55.0)2, in order to better match the distribution from unbiased MD simulation (Figure 10). The other parameters were the same as that in the first row for Ala5 in Table 1. Under these conditions, the average acceptance ratio increases from 35% to 45%, demonstrating the additional gain in sampling efficiency with an improved CG model.
Figure 10.
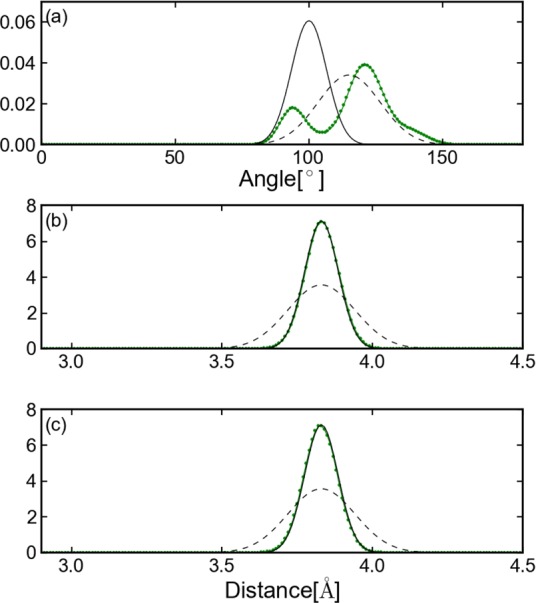
Distribution of distance and angles for Ala5. The green dotted line presents the distribution sampled from equilibrium MD. The black solid line presents the distribution defined by Ebond = 100 (r – 3.83)2, Eangle = 94.84 (θ – 100.0)2, and Edihedral = 0.1 (χ – 55.0)2. The black dotted line presents the distribution defined by Ebond = 400 (r – 3.83)2, Eangle = 30 (θ – 115.0)2, and Edihedral = 0.1 (χ – 55.0)2. Subplot a presents the angle between the carbon-α of residues 2, 3, and 4. Subplot b presents the distance between carbon-α of residues 2 and 3. Subplot c presents the distance between carbon-α of residues 3 and 4.
Finally, the accuracy and sampling efficiency of the CG-guided hybrid neMD-MC algorithm was examined for the solvated (AAQAA)3 peptide (Figure 4). All results are given in Table 1. Compared with equilibrium MD, an estimated speedup on the order of 21 times is achieved with the CG-guided hybrid neMD-MC. The evolution of ϕ or ψ angles for residues 1, 4, and 8 is shown in Figure 11. For residue 1, the number of total transitions are comparable for equilibrium MD simulation and CG-guided hybrid neMD-MC. For residues 4 and 8, no global or local transitions were observed using equilibrium MD, while many were observed using CG-guided hybrid neMD-MC. The reason is that the α-helix of the initial structure did not unfold during equilibrium MD simulations but unfolded and refolded with CG-guided hybrid neMD-MC. The evolution of average population of α, β, ppII, L-α, and helix is shown in Figure 12. The CG-guided hybrid neMD-MC simulations starting from different conformations appear to quickly converge toward unique results. In contrast, the configurational exploration from equilibrium MD does not converge.
Figure 11.
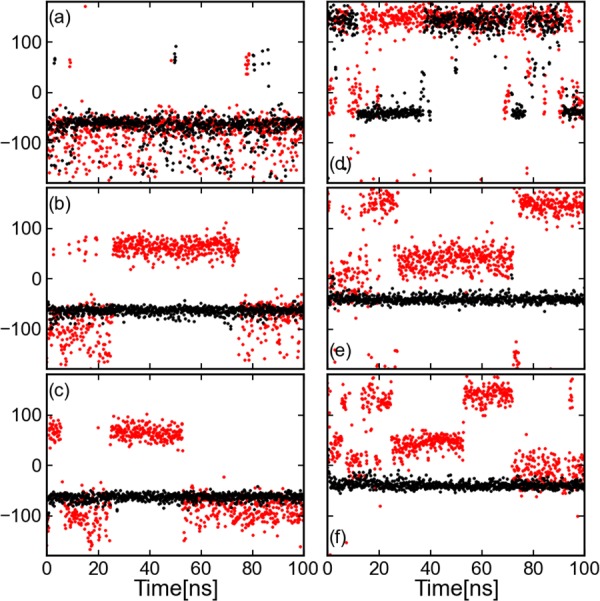
Evolution of ϕ and ψ angles for (AAQAA)3. The black line presents the results from equilibrium MD and the red line from CG-guided hybrid neMD-MC. Both simulations had an initial structure with an α-helix (Figure 4, right). Subplots a and d present the evolution of ϕ and ψ angles of residues 1; b and e of residue 4; and c and f of residue 8.
Figure 12.
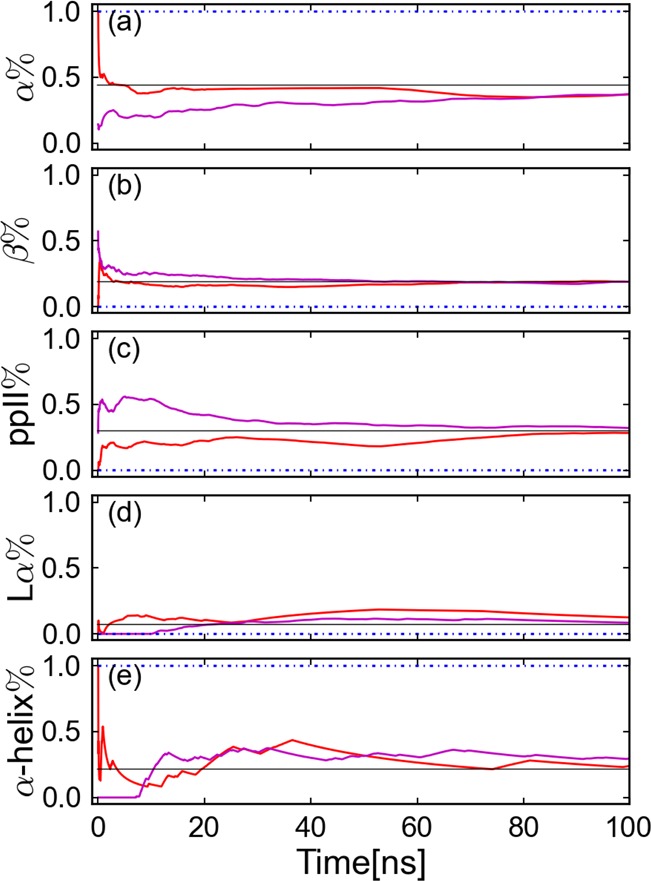
Evolution of the percentage of different conformations. The solid lines present the results from a CG-guided hybrid neMD-MC; the dashed lines are from equilibrium MD. The black solid line presents the reference percentage from Best et al.38 The red and blue lines present simulations where the initial structure has an α-helix (Figure 4, right); magenta β sheet (Figure 4, left). Subplots a–d present the percentage of α, β, ppII, and L-α. The average percentage of residues 6–10 is shown. Subplot e presents the percentage of the α-helix. The structure contains an α-helix secondary structure when three successive residues are in α conformation.
One process observed in the CG-guided hybrid neMD-MC simulations of the solvated peptides is the cis–trans isomerization of the peptide linkages. This was somewhat unexpected because this process, opposed by a high energy barrier, is commonly never observed in equilibrium MD simulations at room temperature. In retrospect, however, it is clear that the occurrence of some cis configuration is entirely consistent with the Boltzmann equilibrium distribution of the polypeptide system. In this sense, long equilibrium MD simulations only explore a fraction of all possible configurational space; they generate the equilibrium distribution of a polypeptide that is kinetically trapped in the trans state. In contrast, CG-guided hybrid neMD-MC simulations aim at achieving a full configurational sampling of the system and thus are not limited by slow kinetic processes that are opposed by large energy barriers. This observation illustrates vividly the power unleashed by a simulation method that truly seeks to enhance configurational sampling. However, there are certainly circumstances where one would realistically want to restrict the conformational sampling to the subspace that is explored by equilibrium MD. In particular, in the present simulations we explicitly prevented cis–trans isomerization at the level of the CG model. More generally, one could restrict the conformational sampling to the subspace accessible to equilibrium MD in various ways, for example, by introducing confinement potentials on different degrees of freedom.
The present set of simulations allows us to draw some general principles regarding the main factors affecting the performance of the CG-guided hybrid neMD-MC algorithm. The magnitude of the displacement R → R′ that should be taken from the CG model to generated proposed MC moves for the AA system is one particularly important factor to consider. Generally, one should avoid using a target configuration R′ corresponding to an exceedingly large conformational transition since the proposed move is unlikely to be accepted during the Metropolis step. However, using a target configuration R′ corresponding to a minuscule conformational transition is clearly unproductive and should also be avoided. The magnitude of the displacement can be controlled by using a fixed propagation time of the CG model (τCG) or by using a “stopping criterion” based on a maximum allowed displacement. One of the stopping criteria used here was based on a maximum allowed value for RMSD of the CG coordinates, ΔRMSD. For all of the solvated peptide systems examined here, the sampling performance was better with a RMSD-based stopping criterion than with a fixed propagation time (results not shown). The reason is that the change in conformation can vary substantially for CG simulation propagated by a fixed amount of time. However, RMSD-based stopping criteria can also become suboptimal for long peptides like Ala10 or (AAQAA)3 because global transitions for residues near the middle of the chain are not well sampled. The latter do not occur during the brief CG simulations as they correspond to RMSD values that greatly exceed the stopping criterion ΔRMSD. This observation led us to introduce an angle-based stopping criterion with a maximum allowed change in the angle, Δθ. The CG-guided hybrid neMD-MC simulations of deca-alanine and (AAQAA)3 using the angle-dependent stopping criterion outperformed the ones with RMSD-dependent stopping criterion, by at least 2-fold (results not shown). The angle-based stopping criterion succeeds in enhancing the sampling of these transitions because it treats the conformational change within each residue more uniformly than a RMSD-based stopping criterion. Consequently, a broad range of motions is accelerated, including large conformational change transition involving residues that are in the middle of the chain. It might be possible to design alternative stopping criterion to further accelerate global transition near the middle of the chain.
Ultimately, the performance of the CG-guided hybrid neMD-MC algorithm is sensitive to both the magnitude of the CG displacement, R → R′, and the length of the neMD switching trajectory, τneMD. A large τneMD is definitely required to obtain a reasonably high acceptance probability for large proposed MC moves. The simulations reported in Table 1 were designed so that a large τneMD was always used when a large displacement is allowed. In the final analysis, while the optimal combination of τneMD and maximum allowed CG displacement is probably system-dependent, it should be possible to adaptively refine the value of these parameters depending on the type of conformational change that needs to be enhanced. Nevertheless, in trying to optimize the performance of the method, it is crucial to make sure that the microscopic reversibility of the CG simulation imposed by eq 8 is rigorously maintained.
V. Conclusions
A typical AA model of a complex bimolecular system often contains a very large number of degrees of freedom. Straight unbiased MD simulations progress very slowly in this high dimensional space and are often inefficient to adequately sample all of the meaningful configurations. The CG-guided hybrid neMD-MC simulation described here offers a promising departure from equilibrium MD. It aims to increase the sampling efficiency by using the evolution of the simpler CG model as a guide to drive any chosen motions with the AA system that are thought to be intrinsically slow.
The CG-guided hybrid neMD-MC method produces a Boltzmann equilibrium sampling that is rigorously valid, for any reasonable choice of effective energy surface for the CG model. Technically, the CG model is used only as a guide to generate proposed MC moves that are then accepted or rejected via a Metropolis probability eq 15. Thus, a key feature of the CG-guided hybrid neMD-MC method is that the imperfections and inaccuracies of the CG model do not formally affect the ultimate outcome of the simulation. For example, the parameters of the CG model of polyalanine were not optimized, and the latter is clearly imperfect and inaccurate, as shown from the differences between the distributions with respect to the CG coordinates (Figure 7). Notwithstanding these imperfections of the CG model, the CG-guided hybrid neMD-MC nonetheless yields the correct distributions, identical to those obtained from equilibrium MD of the AA model. Of particular importance, the CG-guided hybrid neMD-MC method does not rely on a multicopy replica-exchange framework, which can become very costly from a computational point of view.24,31
A wide range of avenues could be explored to build on the present CG-guided hybrid neMD-MC framework. Of paramount importance is the choice of CG degrees of freedom and how they relate to slow motions within the AA system. To investigate a novel AA system with unknown properties, a sound strategy would be to first try to detect the relevant slow modes from the limited information from AA simulation data in order to construct a meaningful CG model, which could then be progressively refined. Another practical aspect that also affects the efficiency of the algorithm is the magnitude of the motion from the CG simulation that is utilized to generate proposed MC moves. Clearly, no substantial gain in sampling efficiency can be expected if the CG model is used only to generate very small displacements. However, being overly ambitious has also some drawbacks; the acceptance probability may become vanishingly small if very large displacements of the CG coordinates are used to drive the AA system with neMD simulations. To resolve this issue, one may conceive of an adaptive procedure aimed at maximizing the acceptance probability and the sampling efficacy of the CG-guided hybrid neMD-MC. In practice, the motion of the CG variables may be controlled either via the length of the CG trajectory or be determined on the basis of some maximum displacement criterion. For the solvated Ala5, Ala10, and (AAQAA)3 systems, the best results were obtained with an angle dependent criterion; the CG simulations were stopped when the average difference of the angle was larger than a certain cutoff. This was chosen such that all residues were treated equivalently in terms of transition size.
Ultimately, while the CG-guided hybrid neMD-MC is rigorously valid for any CG model, the overall efficiency will be better if the effective energy surface of the CG model is reasonably accurate. For example, the average acceptance ratio in Figure 10 and Table 1 shows the additional gains in sampling efficiency with an improved CG model. However, if the CG model always generates proposed moves that are energetically forbidden for the AA model then most will be rejected, and the method becomes very inefficient. Our formal analysis based on eq 17 shows that the optimal choice is formally achieved when the effective energy surface of the CG model corresponds to the exact many-body PMF computed with respect to the CG degrees of freedom within the AA system. While the exact PMF with respect to the CG degrees of freedom is generally unknown, this analysis offers a direct route to improve efficiency by progressively constructing a reasonable approximation that captures the dominant effects. To achieve maximum sampling efficiency with the CG-guided hybrid neMD-MC algorithm, one could adopt an adaptive procedure in which the information accumulated from the AA simulation would serve to progressively improve the parameters of the CG model. For example, one could adjust the function Wexact(R) “on-the-fly” during the simulation using a force-matching algorithm.22,23 Future work will explore this avenue in more detail.
This work was supported by the National Institutes of Health (grant U54-GM087519) and by National Science Foundation (grant CHE-1136709). The authors are grateful to Greg Voth for his support.
The authors declare no competing financial interest.
References
- Karplus M.; McCammon J. A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- Karplus M.; Kuriyan J. Molecular dynamics and protein function. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 6679–6685. 10.1073/pnas.0408930102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perilla J. R.; Goh B. C.; Cassidy C. K.; Liu B.; Bernardi R. C.; Rudack T.; Yu H.; Wu Z.; Schulten K. Molecular dynamics simulations of large macromolecular complexes. Curr. Opin. Struct. Biol. 2015, 31, 64–74. 10.1016/j.sbi.2015.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber T.; Torda A. E.; van Gunsteren W. F. Local elevation: a method for improving the searching properties of molecular dynamics simulation. J. Comput.-Aided Mol. Des. 1994, 8, 695–708. 10.1007/BF00124016. [DOI] [PubMed] [Google Scholar]
- Leone V.; Marinelli F.; Carloni P.; Parrinello M. Targeting biomolecular flexibility with metadynamics. Curr. Opin. Struct. Biol. 2010, 20, 148–154. 10.1016/j.sbi.2010.01.011. [DOI] [PubMed] [Google Scholar]
- Wu X.; Brooks B. R. Self-guided Langevin dynamics simulation method. Chem. Phys. Lett. 2003, 381, 512–518. 10.1016/j.cplett.2003.10.013. [DOI] [Google Scholar]
- Damjanovic A.; Wu X.; Garcia-Moreno E B.; Brooks B. R. Backbone relaxation coupled to the ionization of internal groups in proteins: a self-guided Langevin dynamics study. Biophys. J. 2008, 95, 4091–4101. 10.1529/biophysj.108.130906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu X.; Brooks B. Toward canonical ensemble distribution from self-guided Langevin dynamics simulation. J. Chem. Phys. 2011, 134, 134108. 10.1063/1.3574397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voter A. F. Hyperdynamics: Accelerated molecular dynamics of infrequent events. Phys. Rev. Lett. 1997, 78, 3908. 10.1103/PhysRevLett.78.3908. [DOI] [Google Scholar]
- Hamelberg D.; Mongan J.; McCammon J. A. Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
- Fajer M.; Hamelberg D.; McCammon J. A. Replica-exchange accelerated molecular dynamics (REXAMD) applied to thermodynamic integration. J. Chem. Theory Comput. 2008, 4, 1565–1569. 10.1021/ct800250m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang W.; Roux B. Free energy perturbation Hamiltonian replica-exchange molecular dynamics (FEP/H-REMD) for absolute ligand binding free energy calculations. J. Chem. Theory Comput. 2010, 6, 2559–2565. 10.1021/ct1001768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maragliano L.; Vanden-Eijnden E. A temperature accelerated method for sampling free energy and determining reaction pathways in rare events simulations. Chem. Phys. Lett. 2006, 426, 168–175. 10.1016/j.cplett.2006.05.062. [DOI] [Google Scholar]
- Lei H.; Duan Y. Improved sampling methods for molecular simulation. Curr. Opin. Struct. Biol. 2007, 17, 187–191. 10.1016/j.sbi.2007.03.003. [DOI] [PubMed] [Google Scholar]
- Christen M.; van Gunsteren W. F. On searching in, sampling of, and dynamically moving through conformational space of biomolecular systems: A review. J. Comput. Chem. 2008, 29, 157–166. 10.1002/jcc.20725. [DOI] [PubMed] [Google Scholar]
- Mitsutake A.; Mori Y.; Okamoto Y. Enhanced sampling algorithms. Methods Mol. Biol. 2013, 924, 153–195. [DOI] [PubMed] [Google Scholar]
- Bernardi R. C.; Melo M. C.; Schulten K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta, Gen. Subj. 2015, 1850, 872–877. 10.1016/j.bbagen.2014.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metropolis N.; Rosenbluth A. W.; Rosenbluth M. N.; Teller A. H.; Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087. 10.1063/1.1699114. [DOI] [Google Scholar]
- Hastings W. K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. 10.1093/biomet/57.1.97. [DOI] [Google Scholar]
- Riniker S.; Allison J. R.; van Gunsteren W. F. On developing coarse-grained models for biomolecular simulation: a review. Phys. Chem. Chem. Phys. 2012, 14, 12423–12430. 10.1039/c2cp40934h. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Tieleman D. P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. 10.1039/c3cs60093a. [DOI] [PubMed] [Google Scholar]
- Izvekov S.; Parrinello M.; Burnham C. J.; Voth G. A. Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: a new method for force-matching. J. Chem. Phys. 2004, 120, 10896–10913. 10.1063/1.1739396. [DOI] [PubMed] [Google Scholar]
- Izvekov S.; Voth G. A. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B 2005, 109, 2469–2473. 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- Christen M.; van Gunsteren W. Multigraining: An algorithm for simultaneous fine-grained and coarse-grained simulation of molecular systems. J. Chem. Phys. 2006, 124, 154106. 10.1063/1.2187488. [DOI] [PubMed] [Google Scholar]
- Lyman E.; Ytreberg F.; Zuckerman D. Resolution exchange simulation. Phys. Rev. Lett. 2006, 96, 028105. 10.1103/PhysRevLett.96.028105. [DOI] [PubMed] [Google Scholar]
- Lyman E.; Zuckerman D. Resolution exchange simulation with incremental coarsening. J. Chem. Theory Comput. 2006, 2, 656–666. 10.1021/ct050337x. [DOI] [PubMed] [Google Scholar]
- Liu P.; Voth G. A. Smart resolution replica exchange: An efficient algorithm for exploring complex energy landscapes. J. Chem. Phys. 2007, 126, 045106. 10.1063/1.2408415. [DOI] [PubMed] [Google Scholar]
- Liu P.; Shi Q.; Lyman E.; Voth G. Reconstructing atomistic detail for coarse-grained models with resolution exchange. J. Chem. Phys. 2008, 129, 114103. 10.1063/1.2976663. [DOI] [PubMed] [Google Scholar]
- Cheluvaraja S.; Ortoleva P. Thermal nanostructure: An order parameter multiscale ensemble approach. J. Chem. Phys. 2010, 132, 075102. 10.1063/1.3316793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao Y.; Ortoleva P. J. Molecular dynamics/order parameter extrapolation for bionanosystem simulations. J. Comput. Chem. 2009, 30, 423–437. 10.1002/jcc.21071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W.; Chen J. Accelerate Sampling in Atomistic Energy Landscapes Using Topology-Based Coarse-Grained Models. J. Chem. Theory Comput. 2014, 10, 918–923. 10.1021/ct500031v. [DOI] [PubMed] [Google Scholar]
- Stern H. A. Molecular simulation with variable protonation states at constant pH. J. Chem. Phys. 2007, 126, 164112. 10.1063/1.2731781. [DOI] [PubMed] [Google Scholar]
- Stern H. A. Erratum: “Molecular simulation with variable protonation states at constant pH” [J. Chem. Phys.126, 164112 (2007)]. J. Chem. Phys. 2007, 127, 079901. 10.1063/1.2768942. [DOI] [PubMed] [Google Scholar]
- Ballard A. J.; Jarzynski C. Replica exchange with nonequilibrium switches. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 12224–12229. 10.1073/pnas.0900406106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilmeier J. P.; Crooks G. E.; Minh D. D. L.; Chodera J. D. Nonequilibrium candidate Monte Carlo is an efficient tool for equilibrium simulation. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, E1009–E1018. 10.1073/pnas.1106094108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y.; Roux B. Efficient hybrid non-equilibrium molecular dynamics-Monte Carlo simulations with symmetric momentum reversal. J. Chem. Phys. 2014, 141, 114107. 10.1063/1.4895516. [DOI] [PubMed] [Google Scholar]
- Chen Y.; Roux B. A Constant-pH Hybrid Non-Equilibrium Molecular Dynamics - Monte Carlo Simulation Method. J. Chem. Theory Comput. 2015, 10.1021/acs.jctc.5b00372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B.; Zhu X.; Shim J.; Lopes P. E. M.; Mittal J.; Feig M.; MacKerell A. D. Jr Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ 1 and χ 2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Madura J. D.; Swenson C. J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6646. 10.1021/ja00334a030. [DOI] [Google Scholar]
- Brooks B. R.; Brooks C. L. III; Mackerell A. D. Jr.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; Caves L.; Cui Q.; Dinner A. R.; Feig M.; Fischer S.; Gao J.; Hodoscek M.; Im W.; Kuczera K.; Lazaridis T.; Ma J.; Ovchinnikov V.; Paci E.; Pastor R. W.; Post C. B.; Pu J. Z.; Schaefer M.; Tidor B.; Venable R. M.; Woodcock H. L.; Wu X.; Yang W.; York D. M.; Karplus M. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30, 1545–1614. 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- York D. M.; Darden T. A.; Pedersen L. G. The effect of long-range electrostatic interactions in simulations of macromolecular crystals: A comparison of the Ewald and truncated list methods. J. Chem. Phys. 1993, 99, 8345. 10.1063/1.465608. [DOI] [Google Scholar]
- Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Mu Y.; Kosov D. S.; Stock G. Conformational dynamics of trialanine in water. 2. Comparison of AMBER, CHARMM, GROMOS, and OPLS force fields to NMR and infrared experiments. J. Phys. Chem. B 2003, 107, 5064–5073. 10.1021/jp022445a. [DOI] [Google Scholar]