Large-Scale Multiple Testing of Correlations

Abstract

Multiple testing of correlations arises in many applications including gene coexpression network analysis and brain connectivity analysis. In this paper, we consider large scale simultaneous testing for correlations in both the one-sample and two-sample settings. New multiple testing procedures are proposed and a bootstrap method is introduced for estimating the proportion of the nulls falsely rejected among all the true nulls.

The properties of the proposed procedures are investigated both theoretically and numerically. It is shown that the procedures asymptotically control the overall false discovery rate and false discovery proportion at the nominal level. Simulation results show that the methods perform well numerically in terms of both the size and power of the test and it significantly outperforms two alternative methods. The two-sample procedure is also illustrated by an analysis of a prostate cancer dataset for the detection of changes in coexpression patterns between gene expression levels.

1 Introduction

Knowledge of the correlation structure is essential for a wide range of statistical methodologies and applications. For example, gene coexpression network plays an important role in genomics and understanding the correlations between the genes is critical for the construction of such a network. See, for example, Kostka and Spang (2004), Carterm et al. (2004), Lai, et al. (2004), and de la Fuente (2010). In this paper, we consider large scale multiple testing of correlations in both one- and two-sample cases. A particular focus is on the high dimensional setting where the dimension can be much larger than the sample size.

Multiple testing of correlations arises in many applications, including brain connectivity analysis (Shaw, et al. 2006) and gene coexpression network analysis (Zhang, et al. 2008 and de la Fuente, 2010), where one tests thousands or millions of hypotheses on the changes of the correlations between genes. Multiple testing of correlations also has important applications in the selection of the significant gene pairs and in correlation analysis of factors that interact to shape children's language development and reading ability; see Lee, et al. (2004), Carter, et al (2004), Zhu, et al. (2005), Dubois, et al. (2010) Hirai, et al. (2007), and Raizada et al. (2008).

A common goal in multiple testing is to control the false discovery rate (FDR), which is defined to be the expected proportion of false positives among all rejections. This testing problem has been well studied in the literature, especially in the case where the test statistics are independent. The well-known step-up procedure of Benjamini and Hochberg (1995), which guarantees the control of the FDR, thresholds the p-values of the individual tests. Sun and Cai (2007) developed under a mixture model an optimal and adaptive multiple testing procedure that minimizes the false nondiscovery rate subject to a constraint on the FDR. See also Storey (2002), Genovese and Wasserman (2004), and Efron (2004), among many others. The multiple testing problem is more complicated when the test statistics are dependent. The effects of dependency on FDR procedures have been considered, for example, in Benjamini and Yekutieli (2001), Storey, Taylor and Siegmund (2004), Qiu et al. (2005) Farcomeni (2007), Wu (2008), Efron (2007), and Sun and Cai (2009). In particular, Qiu et al. (2005) demonstrated that the dependency effects can significantly deteriorate the performance of many FDR procedures. Farcomeni (2007) and Wu (2008) showed that the FDR is controlled at the nominal level by the Benjamini-Hochberg step-up procedure under some stringent dependency assumptions. The procedure in Benjamini and Yekutieli (2001) allows the general dependency by paying a logarithmic term loss on the FDR which makes the method very conservative.

For large scale multiple testing of correlations, a natural starting point is the sample correlation matrix, whose entries are intrinsically dependent even if the original observations are independent. The dependence structure among these sample correlations is rather complicated. The difficulties of this multiple testing problem lie in the construction of suitable test statistics for testing the individual hypotheses and more importantly in constructing a good procedure to account for the multiplicity of the tests so that the overall FDR is controlled. To the best of our knowledge, existing procedures cannot be readily applied to this testing problem to have a solid theoretical guarantee on the FDR level while maintaining good power.

In the one-sample case, let X = (X₁, . . . , X_p)′ be a p dimensional random vector with mean μ and correlation matrix R = (ρ_ij)_p×p, and one wishes to simultaneously test the hypotheses

$$H_{0ij}:{\rho }_{ij}=0\text{versus}{H}_{1ij}:{\rho }_{ij}\ne 0,,\text{for}1\le i<j\le p,$$ (1)

based on a random sample X₁, ..., X_n from the distribution of X. In the two-sample case, let X = (X₁, . . . , X_p)′ and Y = (Y₁, . . . , Y_p)′ be two p dimensional random vectors with means μ₁ and μ₂ and correlation matrices R₁ = (ρ_ij1)_p×p and R₂ = (ρ_ij2)_p×p respectively, and we are interested in the simultaneous testing of correlation changes,

$$H_{0ij}:{\rho }_{ij1}={\rho }_{ij2}\text{versus}{H}_{1ij}:{\rho }_{ij1}\ne {\rho }_{ij2},\text{for}1\le i<j\le p,$$ (2)

based on two independent random samples, X₁, ..., X_n1 from the distribution of X and Y₁, ..., Y_n2 from the distribution of Y, where c₁ ≤ n₁/n₂ ≤ c₂ for some c₁, c₂ > 0.

We shall focus on the two-sample case in the following discussion. The one-sample case is slightly simpler and will be considered in Section 4. The classical statistics for correlation detection are based on the sample correlations. For the two independent and identically distributed random samples {X₁, . . . , X_n1} and {Y₁, . . . , Y_n2}, denote by X_k = (X_k,1, . . . , X_k,p)′ and Y_k = (Y_k,1, . . . , Y_k,p)′. The sample correlations are defined by

$${\widehat{\rho }}_{ij1}=\frac{{\sum }_{k=1}^{n_1}(X_{k,i}-{\stackrel{‒}{X}}_i)(X_{k,j}-{\stackrel{‒}{X}}_j)}{\sqrt{{\sum }_{k=1}^{n_1}{(X_{k,i}-{\stackrel{‒}{X}}_i)}^2{\sum }_{k=1}^{n_1}{(X_{k,j}-{\stackrel{‒}{X}}_j)}^2}},$$

and

$${\widehat{\rho }}_{ij2}=\frac{{\sum }_{k=1}^{n_2}(Y_{k,i}-{\stackrel{‒}{Y}}_i)(Y_{k,j}-{\stackrel{‒}{Y}}_j)}{\sqrt{{\sum }_{k=1}^{n_2}{(Y_{k,i}-{\stackrel{‒}{Y}}_i)}^2{\sum }_{k=1}^{n_2}{(Y_{k,j}-{\stackrel{‒}{Y}}_j)}^2}},$$

where ${\stackrel{‒}{X}}_i=\frac{1}{n_1}{\sum }_{k=1}^{n_1}{X}_{k,i}$ and ${\stackrel{‒}{Y}}_i=\frac{1}{n_2}{\sum }_{k=1}^{n_2}{Y}_{k,i}$. The sample correlations ${\widehat{\rho }}_{ij1}$ and ${\widehat{\rho }}_{ij2}$ are heteroscedastic and the null distribution of ${\widehat{\rho }}_{ij1}$ and ${\widehat{\rho }}_{ij2}$ depends on unknown parameters. A well known variance stabilization method is Fisher's z-transformation,

$$\widehat{Z}=\frac{1}{2}\ln \frac{1+\widehat{\rho }}{1-\widehat{\rho }},$$

where $\widehat{\rho }$ is a sample correlation coefficient. In the two-sample case, it is easy to see that under the null hypothesis H_0ij : ρ_ij1 = ρ_ij2 and the bivariate normal assumptions on (X_i, X_j) and (Y_i, Y_j),

$$F_{ij}\equiv \frac{\sqrt{n_1{n}_2}}{2\sqrt{n_1+n_2}}\left[\ln \left(\frac{1-{\widehat{\rho }}_{ij1}}{1-{\widehat{\rho }}_{ij1}}\right)-\ln \left(\frac{1+{\widehat{\rho }}_{ij2}}{1-{\widehat{\rho }}_{ij2}}\right)\right]\to N(0,1).$$ (3)

See, e.g., Anderson (2003). To perform multiple testing (2), a natural approach is to use F_ij as the test statistics and then apply a multiple testing method such as the Benjamini-Hochberg procedure or the Benjamini-Yekutieli procedure to the p-values calculated from F_ij. See, for example, Shaw, et al. (2006) and Zhang, et al. (2008). However, the asymptotic normality result in (3) heavily depends on the bivariate normality assumptions on (X_i, X_j) and (Y_i, Y_j). The behavior of F_ij in the non-normal case is complicated with the asymptotic variance of F_ij depending on $\mathsf{E}{X}_i^2{X}_j^2$ and $\mathsf{E}{Y}_i^2{Y}_j^2$ even when ρ_ij1 = ρ_ij2 = 0; see Hawkins (1989). As will be seen in Section 5, the combination of Fisher's z-transformation with either the Benjamini-Hochberg procedure or the Benjamini-Yekutieli procedure, does not in general perform well numerically.

In this paper, we propose a large scale multiple testing procedure for correlations that controls the FDR and the false discovery proportion (FDP) asymptotically at any prespecified level 0 < α < 1. The multiple testing procedure is developed in two stages. We first construct a test statistic for testing the equality of each individual pair of correlations, H_0ij : ρ_ij1 = ρ_ij2. It is shown that the test statistic has standard normal distribution asymptotically under the null hypothesis H_0ij and it is robust against a class of non-normal population distributions of X and Y. We then develop a procedure to account for the multiplicity in testing a large number of hypotheses so that the overall FDR and FDP levels are under control. A key step is the estimation of the proportion of the nulls falsely rejected by the procedure among all the true nulls at any given threshold level. A bootstrap method is introduced for estimating this proportion.

The properties of the proposed procedure are investigated both theoretically and numerically. It is shown that, under regularity conditions, the multiple testing procedure controls the overall FDR and FDP at the pre-specified level asymptotically. The proposed procedure works well even when the components of the random vectors are strongly dependent and hence provides theoretical guarantees for a large class of correlation matrices.

In addition to the theoretical properties, the numerical performance of the proposed multiple testing procedure is also studied using both simulated and real data. A simulation study is carried out in Section 5.1, which shows that this procedure performs well numerically in terms of both the size and power of the test. In particular, the procedure significantly outperforms the methods using Fisher's z-transformation together with either the Benjamini-Hochberg procedure or the Benjamini-Yekutieli procedure, especially in the non-normal case. The simulation study also shows that the numerical performance of the proposed procedure is not sensitive to the choice of the bootstrap replication number. We also illustrate our procedure with an analysis of a prostate cancer dataset for the detection of changes in the coexpression patterns between gene expression levels. The procedure identifies 1341 pairs of coexpression genes (out of a total of 124,750 pairs) and 1.07% nonzero entries of the coexpression matrix. Our method leads to a clear and easily interpretable coexpression network.

The rest of the paper is organized as follows. Section 2 gives a detailed description of the proposed multiple testing procedure. Theoretical properties of the procedure is investigated in Section 3. It is shown that, under some regularity conditions, the procedure controls the FDR and FDP at the nominal level asymptotically. Section 4 discusses the one-sample case. Numerical properties of the proposed testing procedure are studied in Section 5. The performance of the procedure is compared to that of the methods based on the combination of Fisher's z-transformation with either the Benjamini-Hochberg procedure or the Benjamini-Yekutieli procedure. A real dataset is analyzed in Section 5.2. A discussion on extensions and related problems is given in Section 6 and all the proofs are contained in the supplementary material Cai and Liu (2014).

2 FDR control procedure

In this section we present a detailed description of the multiple testing procedure for correlations in the two-sample case. The theoretical results given in Section 3 show that the procedure controls the FDR and FDP at the pre-specified level asymptotically.

We begin by constructing a test statistic for testing each individual pair of correlations, H_0ij : ρ_ij1 = ρ_ij2. In this paper, we shall focus on the class of populations with the elliptically contoured distributions (see Condition (C2) in Section 3) which is more general than the multivariate normal distributions. The test statistic for general population distributions is introduced in Section 6.3. Under Condition (C2) and the null hypothesis H_0ij : ρ_ij1 = ρ_ij2, as (n₁, n₂) → ∞,

$$\frac{{\widehat{\rho }}_{ij1}-{\widehat{\rho }}_{ij2}}{\sqrt{\frac{{\kappa }_1}{n_1}{(1-{\rho }_{ij1}^2)}^2+\frac{{\kappa }_1}{n_2}{(1-{\rho }_{ij2}^2)}^2}}\to N(0,1)$$ (4)

with

$${\kappa }_1\equiv \frac{1}{3}\frac{\mathsf{E}{(X_i-{\mu }_{i1})}^4}{{\left[\mathsf{E}{(X_i-{\mu }_{i1})}^2\right]}^2}\text{and}{\kappa }_2\equiv \frac{1}{3}\frac{\mathsf{E}{(Y_i-{\mu }_{i2})}^4}{{\left[\mathsf{E}{(Y_i-{\mu }_{i2})}^2\right]}^2},$$

where (μ₁₁, . . . , μ_p1)′ = μ₁ and (μ₁₂, . . . , μ_p2)′ = μ₂. Note that ${\kappa }_i\ge \frac{1}{3}$ for i = 1, 2 and they are related to the kurtosis with ${\kappa }_1=\frac{1}{3}{\kappa }_X+1$ where ${\kappa }_X=\frac{\mathsf{E}{(X_i-{\mu }_{i1})}^4}{{\left[\mathsf{E}{(X_i-{\mu }_{i1})}^2\right]}^2}-3$ is the kurtosis of X. For multivariate normal distributions, κ₁ = κ₂ = 1.

In general, the parameters ρ_ij1, ρ_ij2, κ₁ and κ₂ in the denominator are unknown and need to be estimated. In this paper we estimated κ₁ and κ₂ respectively by

$${\widehat{\kappa }}_1=\frac{1}{3p}\sum _{i=1}^p\frac{n_1{\sum }_{k=1}^{n_1}{(X_{k,i}-{\stackrel{‒}{X}}_i)}^4}{{\left[{\sum }_{k=1}^{n_1}{(X_{k,i}-{\stackrel{‒}{X}}_i)}^2\right]}^2}\text{and}{\widehat{\kappa }}_2=\frac{1}{3p}\sum _{i=1}^p\frac{n_2{\sum }_{k=1}^{n_2}{(Y_{k,i}-{\stackrel{‒}{Y}}_i)}^4}{{\left[{\sum }_{k=1}^{n_2}{(Y_{k,i}-{\stackrel{‒}{Y}}_i)}^2\right]}^2}.$$

To estimate ρ_ij1 and ρ_ij2, taking into account of possible sparsity of the correlation matrices, we use the thresholded version of the sample correlation coefficients

$${\tilde{\rho }}_{ijl}={\widehat{\rho }}_{ijl}I\left\{\frac{\mid {\widehat{\rho }}_{ijl}\mid }{\sqrt{\frac{{\widehat{\kappa }}_l}{n_l}{(1-{\widehat{\rho }}_{ijl}^2)}^2}}\ge 2\sqrt{\frac{\log p}{n_l}}\right\},l=1,2,$$

where I{·} denotes the indicator function. Let ${\tilde{\rho }}_{ij}^2=\max \{{\tilde{\rho }}_{ij1}^2,{\tilde{\rho }}_{ij2}^2\}$ and we use ${\tilde{\rho }}_{ij}^2$ to replace ${\rho }_{ij1}^2$ and ${\rho }_{ij2}^2$ in (4). We propose the test statistic

$$T_{ij}=\frac{{\widehat{\rho }}_{ij1}-{\widehat{\rho }}_{ij2}}{\sqrt{\frac{{\widehat{\kappa }}_1}{n_1}{(1-{\tilde{\rho }}_{ij}^2)}^2+\frac{{\widehat{\kappa }}_2}{n_2}{(1-{\tilde{\rho }}_{ij}^2)}^2}}$$ (5)

for testing the individual hypotheses H_0ij : ρ_ij1 = ρ_ij2. Note that under H_0ij, ${\tilde{\rho }}_{ij}^2$ is a consistent estimator of ρ_ij1 and ρ_ij2. On the other hand, under the alternative H_1ij, $\sqrt{\frac{{\widehat{\kappa }}_1}{n_1}{(1-{\tilde{\rho }}_{ij}^2)}^2+\frac{{\widehat{\kappa }}_2}{n_2}{(1-{\tilde{\rho }}_{ij}^2)}^2}\le \sqrt{\frac{{\widehat{\kappa }}_1}{n_1}{(1-{\tilde{\rho }}_{ij1}^2)}^2+\frac{{\widehat{\kappa }}_2}{n_2}{(1-{\tilde{\rho }}_{ij2}^2)}^2}$. Hence, T_ij will be more powerful than the test statistic using ${\tilde{\rho }}_{ij1}$ and ${\tilde{\rho }}_{ij2}$ to estimate ρ_ij1 and ρ_ij2 respectively.

Before introducing the multiple testing procedure, it is helpful to understand the basic properties of the test statistics T_ij which are in general correlated. It can be proved that, under the null hypothesis H_0ij and certain regularity conditions,

$$\underset{0\le t\le b\sqrt{\log }p}{\sup }\mid \frac{\mathsf{P}(\mid T_{ij}\mid \ge t)}{2-2\Phi \left(t\right)}-1\mid \to 0\text{as}(n_1,n_2)\to \infty$$

uniformly in 1 ≤ i < j ≤ p and p ≤ n^r for any b > 0 and r > 0, where Φ is the cumulative distribution function of the standard normal distribution; see Proposition 1 in Section 3.

Denote the set of true null hypotheses by

$${\mathcal{H}}_0=\{(i,j):1\le i<j\le p,{\rho }_{ij1}={\rho }_{ij2}\}.$$

Since the asymptotic null distribution of each test statistic T_ij is standard normal, it is easy to see that

$$\mathsf{P}(\underset{(i,j)\in {\mathcal{H}}_0}{\max }\mid T_{ij}\mid \ge 2\sqrt{\log p})\to 0\text{as}(n_1,n_2,p)\to \infty .$$ (6)

We now develop the multiple testing procedure. Let t be the threshold level such that the null hypotheses H_0ij are rejected whenever |T_ij| ≥ t. Then the false discovery proportion (FDP) of the procedure is

$$\frac{{\sum }_{(i,j)\in {\mathcal{H}}_0}I\{\mid T_{ij}\mid \ge t\}}{\max \{{\sum }_{1\le i<j\le p}I\{\mid T_{ij}\mid \ge t\},1\}}.$$

An ideal threshold level for controlling the false discovery proportion at a pre-specified level 0 < α < 1 is

$${\tilde{t}}_1=\inf \{0\le t\le 2\sqrt{\log p}:\frac{{\sum }_{(i,j)\in {\mathcal{H}}_0}I\{\mid T_{ij}\mid \ge t\}}{\max \{{\sum }_{1\le i<j\le p}I\{\mid T_{ij}\mid \ge t\},1\}}\le \alpha \},$$

where the constraint $0\le t\le 2\sqrt{\log p}$ is used here due to the tail bound (6).

The ideal threshold ${\tilde{t}}_1$ is unknown and needs to be estimated because it depends on the knowledge of the set of the true null hypotheses ${\mathcal{H}}_0$. A key step in developing the FDR procedure is the estimation of G₀(t) defined by

$$G_0\left(t\right)≔\frac{1}{q_0}\sum _{(i,j)\in {\mathcal{H}}_0}I\{\mid T_{ij}\mid \ge t\}$$ (7)

where q₀ = Card(${\mathcal{H}}_0$). Note that G₀(t) is the true proportion of the nulls falsely rejected by the procedure among all the true nulls at the threshold level t. In some applications such as the PheWAS problem in genomics, the sample sizes can be very large. In this case, it is natural to use the tail of normal distribution G(t) = 2 – 2Φ(t) to approximate G₀(t). In fact, we have

$$\underset{0\le t\le b_p}{\sup }\mid \frac{G_0\left(t\right)}{G\left(t\right)}-1\mid \to 0$$ (8)

in probability as (n₁, n₂, p) → ∞, where $b_p=\sqrt{4\log p-a_p}$ and a_p = 2 log(log p). The range 0 ≤ t ≤ b_p is nearly optimal for (8) to hold in the sense that a_p cannot be replaced by any constant in general.

Large-scale Correlation Tests with Normal approximation (LCT-N)

Let 0 < α < 1 and define

$$\widehat{t}=\inf \{0\le t\le b_p:\frac{G\left(t\right)(p^2-p)∕2}{\max \{{\sum }_{1\le i<j\le p}I\{\mid T_{ij}\mid \ge t\},1\}}\le \alpha \},$$ (9)

where G(t) = 2 – 2Φ(t). If $\widehat{t}$ does not exist, then set $\widehat{t}=\sqrt{4\log p}$. We reject H_0ij whenever |T_ij} ≥ $\widehat{t}$.

Remark 1

In the above procedure, we use G(t) to estimate G₀(t) when 0 ≤ t ≤ b_p. For t > b_p, G(t) is not a good approximation of G₀(t) because the convergence rate of G₀(t)/G(t) → 1 is very slow. Furthermore, G(t) is not even a consistent estimator of G₀(t) when $t\ge \sqrt{4\log p-\log \left(\log p\right)+O\left(1\right)}$ since $p^{2}G\left(t\right)$ is bounded. Thus, we threshold the test |T_ij| with $\sqrt{4\log p}$ directly to control the FDP.

Note that Benjamini-Hochberg procedure with p-values G(|T_ij|) is equivalent to re-jecting H_0ij if |T_ij| ≥ ${\widehat{t}}_{BH}$, where

$${\widehat{t}}_{BH}=\inf \{t\ge 0:\frac{G\left(t\right)(p^2-p)∕2}{\max \{{\sum }_{1\le i<j\le p}I\{\mid T_{ij}\mid \ge t\},1\}}\le \alpha \}.$$

It is important to restrict the range of t to [0, b_p] in (9). The B-H procedure uses G(t) to estimate G₀(t) for all t ≥ 0. As a result, when the number of true alternatives $\mid {\mathcal{H}}_0^c\mid$ is fixed as p → ∞, the B-H method is unable to control the FDP with some positive probability, even in the independent case. To see this, we let H₀₁, . . . , H_0m be m null hypotheses and m₁ be the number of true alternatives. Let FDP_BH be the true FDP of the B-H method with independent true p-values and the target FDR = α. If m₁ is fixed as m → ∞, then Proposition 2.1 in Liu and Shao (2014) proved that, for any 0 < β < 1, there exists some constant c > 0 such that ${\underset{¯}{\lim }}_{m\to \infty }\mathsf{P}({\mathrm{FDP}}_{BH}\ge \beta )\ge c$.

Remark 2

In the multiple testing procedure given above, we use p(p – 1)/2 as the estimate for the number q₀ of the true nulls. In many applications, the number of the true significant alternatives is relatively small. In such “sparse” settings, one has q₀/((p² – p)/2) ≈ 1 and the true FDR level of the testing procedure would be close to the nominal level α. See Section 5 for discussions on the numerical performance of the procedure.

The normal approximation is suitable when the sample sizes are large. On the other hand, when the sample sizes are small, the following bootstrap procedure can be used to improve the accuracy of the approximation. Let ${\mathcal{X}}^{\ast }=\{{\mathit{X}}_k^{\ast },1\le k\le n_1\}$ and ${\mathcal{Y}}^{\ast }=\{{\mathit{Y}}_k^{\ast },1\le k\le n_2\}$ be resamples drawn randomly with replacement from {X_k, 1 ≤ k ≤ n₁} and {Y_k, 1 ≤ k ≤ n₂} respectively. Set ${\mathit{X}}_k^{\ast }={(X_{k,1}^{\ast },\dots ,X_{k,p}^{\ast })}^{\prime },1\le k\le n_1$ and ${\mathit{Y}}_k^{\ast }={(Y_{k,1}^{\ast },\dots ,Y_{k,p}^{\ast })}^{\prime },1\le k\le n_2$. Let

$${\widehat{\rho }}_{ij1}^{\ast }=\frac{{\sum }_{k=1}^{n_1}(X_{k,i}^{\ast }-{\stackrel{‒}{X}}_i^{\ast })(X_{k,j}^{\ast }-{\stackrel{‒}{X}}_j^{\ast })}{\sqrt{{\sum }_{k=1}^{n_1}{(X_{k,i}^{\ast }-{\stackrel{‒}{X}}_i^{\ast })}^2{\sum }_{k=1}^{n_1}{(X_{k,j}^{\ast }-{\widehat{X}}_j^{\ast })}^2}},$$

where ${\stackrel{‒}{X}}_i^{\ast }=\frac{1}{n_1}{\sum }_{k=1}^{n_1}{X}_{k,i}^{\ast }$ and ${\stackrel{‒}{Y}}_j^{\ast }=\frac{1}{n_2}{\sum }_{k=1}^{n_2}{Y}_{k,j}^{\ast }$. We define ${\widehat{\rho }}_{ij2}^{\ast }$ in a similar way. Let

$$T_{ij}^{\ast }=\frac{{\widehat{\rho }}_{ij1}^{\ast }-{\widehat{\rho }}_{ij2}^{\ast }-({\widehat{\rho }}_{ij1}-{\widehat{\rho }}_{ij2})}{\sqrt{\frac{{\widehat{\kappa }}_1}{n_1}{(1-{\widehat{\rho }}_{ij1}^{\ast 2})}^2+\frac{{\widehat{\kappa }}_2}{n_2}{(1-{\widehat{\rho }}_{ij2}^{\ast 2})}^2}}.$$ (10)

For some given positive integer N, we replicate the above procedure N times independently and obtain $T_{ij,1}^{\ast },\dots ,T_{ij,N}^{\ast }$. Let

$$G_{N,n}^{\ast }\left(t\right)=\frac{2}{N(p^2-p)}\sum _{k=1}^N\sum _{1\le i<j\le p}I\{\mid T_{ij,k}^{\ast }\mid \ge t\}.$$

In the bootstrap procedure, we use the conditional (given the data) distribution of ${\widehat{\rho }}_{ij1}^{\ast }-{\widehat{\rho }}_{ij2}^{\ast }-({\widehat{\rho }}_{ij1}-{\widehat{\rho }}_{ij2})$ to approximate the null distribution. The signal is not present because the conditional mean of $({\widehat{\rho }}_{ij1}^{\ast }-{\widehat{\rho }}_{ij2}^{\ast })-({\widehat{\rho }}_{ij1}-{\widehat{\rho }}_{ij2})$ is zero. Proposition 1 in Section 3 shows that, under some regularity conditions,

$$\underset{0\le t\le b_p}{\sup }\mid \frac{G_{N,n}^{\ast }\left(t\right)}{G_0\left(t\right)}-1\mid \to 0$$ (11)

in probability. Equation (11) leads us to propose the following multiple testing procedure for correlations.

Large-scale Correlation Tests with Bootstrap (LCT-B)

Let 0 < α < 1 and define

$$\widehat{t}=\inf \{0\le t\le b_p:\frac{G_{n,N}^{\ast }\left(t\right)(p^2-p)∕2}{\max \{{\sum }_{1\le i<j\le p}I\{\mid T_{ij}\mid \ge t\},1\}}\le \alpha \}.$$ (12)

If $\widehat{t}$ does not exist, then let $\widehat{t}=\sqrt{4\log p}$. We reject H_0ij whenever $\mid T_{ij}\mid \ge \widehat{t}$.

The procedure requires to choose the bootstrap replication time N. The theoretical analysis in Section 3 shows that it can be taken to be any positive integer. The simulation shows that the performance of the procedure is quite insensitive to the choice of N.

3 Theoretical properties

We now investigate the properties of the multiple testing procedure for correlations introduced in Section 2. It will be shown that, under mild regularity conditions, the procedure controls the FDR asymptotically at any pre-specified level 0 < α < 1. In addition, it also controls the FDP accurately.

Let FDP$\left(\widehat{t}\right)$ and FDR$\left(\widehat{t}\right)$ be respectively the false discovery proportion and the false discovery rate of the multiple testing procedure defined in (9) and (12),

$$\mathrm{FDP}\left(\widehat{t}\right)=\frac{{\sum }_{(i,j)\in {\mathcal{H}}_0}I\{\mid T_{ij}\mid \ge \widehat{t}\}}{\max ({\sum }_{1\le i<j\le p}I\{\mid T_{ij}\mid \ge \widehat{t}\},1)}\text{and}\mathrm{FDR}\left(\widehat{t}\right)=\mathsf{E}\left(\mathrm{EDP}\left(\widehat{t}\right)\right).$$

For given positive numbers k_p and s_p, define the collection of symmetric matrices $\mathcal{A}(k_p,s_p)$ by

$$\mathcal{A}(k_p,s_p)=\{{\left(a_{ij}\right)}_{p\times p}:a_{ij}=a_{ji},\text{Card}\{1\le i\le p:\mid a_{ij}\mid \ge k_p\}\le s_p,\forall 1\le j\le p\}.$$ (13)

We introduce some conditions on the dependence structure of X and Y.

(C1). Suppose that, for some 0 < θ < 1, γ > 0 and 0 < ξ < min}(1 – θ)/(1 + θ), 1/3}, we have ${\max }_{1\le i<j\le p}\mid {\rho }_{ijh}\mid \le \theta$, h = 1, 2, and ${\mathit{R}}_h\in \mathcal{A}(k_p,s_p)$. h = 1, 2, for some k_p = log p)^−2–γ and $s_p=O\left(p^{\xi }\right)$.

The assumption max_1≤i<j≤p|ρ_ijh| ≤ θ, h = 1, 2, is natural as the correlation matrix would be singular if max_1≤i<j≤p|ρ_ijh| = 1. The assumption ${\mathit{R}}_h\in \mathcal{A}(k_p,s_p)$ means that every variable can be highly correlated (i.e., ρ_ijl ≥ k_p) with at most s_p other variables. The conditions on the correlations in (C1) are quite weak.

Besides the above dependence conditions, we also need an assumption on the covariance structures of X and Y. Let (σ_ij1)_p×p and (σ_ij2)_p×p be the covariance matrices of X and Y respectively.

(C2). Suppose that there exist constants ${\kappa }_1\ge \frac{1}{3}$ and ${\kappa }_2\ge \frac{1}{3}$ such that for any i, j, k, l ∈ {1, 2, . . . , p},

$$\begin{array}{cc}\hfill \mathsf{E}(X_i-{\mu }_{i1})(X_j-{\mu }_{j1})(X_k-{\mu }_{k1})(X_l-{\mu }_{l1})=& {\kappa }_1({\sigma }_{ij1}{\sigma }_{kl1}+{\sigma }_{ik1}{\sigma }_{jl1}+{\sigma }_{il1}{\sigma }_{jk1}),\hfill \\ \hfill \mathsf{E}(Y_i-{\mu }_{i2})(Y_j-{\mu }_{j2})(Y_k-{\mu }_{k2})(Y_l-{\mu }_{l2})=& {\kappa }_2({\sigma }_{ij2}{\sigma }_{kl2}+{\sigma }_{ik2}{\sigma }_{jl2}+{\sigma }_{il2}{\sigma }_{jk2}).\hfill \end{array}$$ (14)

It is easy to see that ${\kappa }_1\equiv \frac{1}{3}\mathsf{E}{(X_i-{\mu }_{i1})}^4∕{\left[\mathsf{E}{(X_i-{\mu }_{i1})}^2\right]}^2$ and ${\kappa }_2\equiv \frac{1}{3}\mathsf{E}{(Y_i-{\mu }_{i2})}^4∕{\left[\mathsf{E}{(Y_i-{\mu }_{i2})}^2\right]}^2$. Condition (C2) holds, for example, for all the elliptically contoured distributions (Anderson, 2003). Note that the asymptotically normality result (4) holds under Condition (C2) and the null H_0ij : ρ_ij1 = ρ_ij2.

We also impose exponential type tail conditions on X and Y.

(C3). Exponential tails: There exist some constants η > 0 and K > 0 such that

$$\mathsf{E}\exp (\eta \mid X_i-{\mu }_{i1}\mid ∕{\sigma }_{ii1}^{1∕2})\le K\text{and}\mathsf{E}\exp (\eta \mid Y_i-{\mu }_{i2}\mid ∕{\sigma }_{ii2}^{1∕2})\le K\text{for all}i.$$

Let n = n₁ + n₂. We first show that under p ≤ n^r for some r > 0, (C2) and (C3), the distributions of T_ij and $G_{n,N}^{\ast }\left(t\right)$ are asymptotic normally distributed and G₀(t) is well approximated by $G_{N,n}^{\ast }\left(t\right)$.

Proposition 1

Suppose p ≤ n^r for some constant r > 0. Under Conditions (C2) and(C3), we have for any r > 0 and b > 0, as (n, p) → ∞,

$$\underset{(i,j)\in {\mathcal{H}}_0}{\sup }\underset{0\le t\le b\sqrt{\log p}}{\sup }\mid \frac{\mathit{P}(\mid T_{ij}\mid \ge t)}{2-2\Phi \left(t\right)}-1\mid \to 0,$$ (15)

$$\underset{0\le t\le b_p}{\sup }\mid \frac{G_{N,n}^{\ast }\left(t\right)}{2-2\Phi \left(t\right)}-1\mid \to 0,$$ (16)

and

$$\underset{0\le t\le b_p}{\sup }\mid \frac{G_{N,n}^{\ast }\left(t\right)}{G_0\left(t\right)}-1\mid \to 0$$ (17)

in probability, where Φ is the cumulative distribution function of the standard normal distribution.

We are now ready to state our main results. For ease of notation, we use FDP and FDR to denote FDP$\left(\widehat{t}\right)$ and FDR$\left(\widehat{t}\right)$ respectively. Recall that ${\mathcal{H}}_0=\{(i,j):1\le i<j\le p,{\rho }_{ij1}={\rho }_{ij2}\}$ and q₀ = Card(H₀). Let ${\mathcal{H}}_1=\{(i,j):1\le i<j\le p,{\rho }_{ij1}\ne {\rho }_{ij2}\},q_1=\text{Card}\left({\mathcal{H}}_1\right)\text{and}q=(p^2-p)∕2$.

Theorem 1

Assume that p ≤ n^r for some r > 0 and q₁ ≤ cq for some 0 < c < 1. Under (C1)-(C3),

$$\underset{(n,p)\to \infty }{\overline{\lim }}\mathrm{FDR}\le \alpha ,\underset{(n,p)\to \infty }{\lim }\mathit{P}(\mathrm{FDP}\le \alpha +\epsilon )=1$$ (18)

for any ε > 0.

Theorem 1 shows that the procedures proposed in Section 2 control the FDR and FDP at the desired level asymptotically. It is quite natural to assume q₁ ≤ cq. For example, if q₁/q → 1, then the number of the zero entries of R₁ – R₂ is negligible compared with the number of the nonzero entries and the trivial procedure of rejecting all of the null hypotheses controls FDR at level 0 asymptotically. Note that r in Theorem 1 can be arbitrarily large so that p can be much larger than $n(p\gg n)$.

A weak condition to ensure t̂ in (9) and (12) exists is Equation (19) below, which imposes the condition on the number of significant true alternatives. The next theorem shows that, when t̂ in (9) and (12) exists, the FDR and FDP tend to αq₀/q, where q = (p² – p)/2.

Theorem 2

Suppose that for some δ > 0,

$$\text{Card}\left\{(i,j):\frac{\mid {\rho }_{ij1}-{\rho }_{ij2}\mid }{\sqrt{{\kappa }_1+{\kappa }_2}}\ge 4\sqrt{\frac{(n_1+n_2)\log p}{n_1{n}_2}}\right\}\ge \left(\frac{1}{\sqrt{8\pi }\alpha }+\delta \right)\sqrt{\log \left(\log p\right)}.$$ (19)

Then, under the conditions of Theorem 1, we have

$$\underset{(n,p)\to \infty }{\lim }\frac{\mathrm{FDR}}{\alpha q_0∕q}=1and\frac{\mathrm{FDP}}{\alpha q_0∕q}\to 1inprobabilityas(n,p)\to \infty .$$ (20)

From Theorem 2, we see that if R₁ – R₂ is sparse such that the number of nonzero entries is of order o(p²), then q₀/q → 1. So the FDR tends to asymptotically. The sparsity assumption is commonly imposed in the literature on estimation of high dimensional covariance matrix. See, for example, Bickel and Levina (2008), and Cai and Liu (2011).

The multiple testing procedure in this paper is related to that in Storey, Taylor and Siegmund (2004). Let p₁, . . . , p_q be the p-values. Storey, Taylor and Siegmund (2004) estimated the number of true null hypotheses q₀ ${\widehat{q}}_0={\sum }_{k=1}^{q}I\{p_i\ge \lambda \}∕(1-\lambda )$ with some well-chosen λ and then incorporate q̂₀ into the B-H method for FDR control. It is possible to use similar idea to estimate q₀ and improve the power in our problem. However, the theoretical results in Storey, Taylor and Siegmund (2004) are not applicable in our setting. In their Theorem 4, to control FDR, they required ${\widehat{FDR}}_{\lambda }^{\infty }\left(t\right)<\alpha$ which implies the number of true alternative hypotheses q₁/q → π₁ with some positive π₁ > 0. This excludes the sparse setting q₁ = o(q) which is of particular interesting in this paper. They assumed that the true p-values are known. This is a very strong condition and will not be satisfied in our setting. Moreover, their dependence condition is imposed on the p-values by assuming the law of large numbers (7) in Storey, Taylor and Siegmund (2004). Note that we only have the asymptotic distributions $G_{n,N}^{\ast }\left(t\right)$ and N(0, 1) for the test statistic. Our dependence condition is imposed on the correlation matrix which is more natural.

4 One-Sample Case

As mentioned in the introduction, multiple testing of correlations in the one-sample case also has important applications. In this section, we consider the one-sample testing problem where we observe a random sample X₁, ..., X_n from a p dimensional distribution with mean μ and correlation matrix R = (ρ_ij)_p×p, and wish to simultaneously test the hypotheses

$$H_{0ij}:{\rho }_{ij}=0\text{versus}{H}_{1ij}:{\rho }_{ij}\ne 0,\text{for}1\le i<j\le p.$$ (21)

As mentioned in the introduction, Fisher's z-transformation does not work well for non-Gaussian data in general. Using the same argument as in the two-sample case, we may use the following test statistic for testing each H_0ij : ρ_ij = 0,

$$\frac{\mid {\widehat{\rho }}_{ij}\mid }{\sqrt{\frac{\widehat{\kappa }}{n}}(1-{\widehat{\rho }}_{ij}^2)},$$

where $\widehat{\kappa }=\frac{1}{3p}{\sum }_{i=1}^p\frac{n{\sum }_{k=1}^n{(X_{k,i}-{\stackrel{‒}{X}}_i)}^4}{{\left({\sum }_{k=1}^n{(X_{k,i}-{\stackrel{‒}{X}}_i)}^2\right)}^2}$ is an estimate of $\kappa \equiv \frac{1}{3}\frac{\mathsf{E}{(X_i-{\mu }_i)}^4}{{\left[\mathsf{E}{(X_i-{\mu }_i)}^2\right]}^2}$. The false discovery rate can be controlled in a similar way as in Section 2 and all the theoretical results in Section 3 also hold in the one-sample case.

There is in fact a di erent test statistic that requires weaker conditions for the asymptotic normality for the one-sample testing problem (21). Note that (21) is equivalent to

$$H_{0ij}:{\sigma }_{ij}=0\text{versus}{H}_{1ij}:{\sigma }_{ij}\ne 0,\text{for}1\le i<j\le p.$$ (22)

Hence, we propose to use the following normalized sample covariance as the test statistic

$$T_{ij}=\frac{{\sum }_{k=1}^n(X_{ki}-{\stackrel{‒}{X}}_i)(X_{kj}-{\stackrel{‒}{X}}_j)}{\sqrt{n{\widehat{\theta }}_{ij}}},$$ (23)

where

$${\widehat{\theta }}_{ij}=\frac{1}{n}\sum _{k=1}^n{[(X_{ki}-{\stackrel{‒}{X}}_i)(X_{kj}-{\stackrel{‒}{X}}_j)-{\widehat{\sigma }}_{ij}]}^2$$

is a consistent estimator of the variance θ_ij = Var((X_i – μ_i)(X_j – μ_j)). Note that Cai and Liu (2011) used a similar idea to construct an adaptive thresholding procedure for estimation of sparse covariance matrix. By the central limit theorem and the law of large numbers, we have T_ij converging in law to N(0, 1) under the null H_0ij and the finite fourth moment condition, $\mathsf{E}{(X_i-{\mu }_i)}^4∕{\sigma }_{ii}^2<\infty$.

When the sample size is large, the normal approximation can be used as in (9). On the other hand, if the sample size is small, then we can use a similar bootstrap method to estimate the proportion of the nulls falsely rejected among all the true nulls,

$$\frac{1}{q_0}\sum _{(i,j)\in {\mathcal{H}}_0}I\{\mid T_{ij}\mid \ge t\},$$

where ${\mathcal{H}}_0=\{(i,j):1\le i<j\le p,{\rho }_{ij}=0\}$ and $q_0=\text{Card}\left({\mathcal{H}}_0\right)$. Let ${\mathcal{X}}_j^{\ast }=\{X_{kj}^{\ast },1\le k\le n\}$ be a resample drawn randomly with replacement from $\{X_{kj},1\le k\le n\}$. Let the re-samples ${\mathcal{X}}_j^{\ast },1\le j\le p$, be independent given $\{X_{kj},1\le k\le n,1\le j\le p\}$ and set ${\mathit{X}}_k^{\ast }={(X_{k1}^{\ast }-{\stackrel{‒}{X}}_1,\dots ,X_{kp}^{\ast }-{\stackrel{‒}{X}}_p)}^{\prime },1\le k\le n$. We construct the bootstrap test statistics $T_{ij}^{\ast }$ from ${\mathit{X}}_1^{\ast },\dots ,{\mathit{X}}_n^{\ast }$ as in (23). The above procedure is replicated N times independently which yield $T_{ij,1}^{\ast },\dots ,T_{ij,N}^{\ast }$. Let

$$G_{n,N}^{\ast }\left(t\right)=\frac{2}{N(p^2-p)}\sum _{k=1}^N\sum _{1\le i<j\le p}I\{\mid T_{ij,k}^{\ast }\mid \ge t\}.$$ (24)

Finally, we use the same FDR control procedure as defined in (12).

In the one sample case, the dependence condition (C1) can be weakened significantly. (C1*). Suppose that for some γ > 0 and ξ > 0 we have

$$\text{Card}\{(i,j):1\le i<j\le p,\mid {\rho }_{ij}\mid \ge {\left(\log p\right)}^{-2-\gamma }\}\le C{p}^2∕{\left(\log p\right)}^{1+\xi }.$$

In (C1*), the number of pairs of strong correlated variables can be as large as p²/(log p)^1+ξ. Similar to Theorems 1 and 2 in the two-sample case, we have the following results for the one-sample case. Let ${\mathcal{H}}_1=\{(i,j):1\le i<j\le p,{\rho }_{ij}\ne 0\}$, q₁ = Card(${\mathcal{H}}_1$) and q = (p² – p)/2.

Theorem 3

Assume that p ≤ n^r for some r > 0 and q₁ ≤ cq for some 0 < c < 1. Suppose the distribution of X satisfies Condition (C1*), (C2) and (C3), then

$$\underset{(n,p)\to \infty }{\overline{\lim }}\mathrm{FDR}\le \alpha and\underset{(n,p)\to \infty }{\lim }\mathit{P}(\mathrm{FDP}\le \alpha +\epsilon )=1$$ (25)

for any ε > 0.

Theorem 3 shows that for simultaneous testing of the correlations in the one-sample case, the dependence condition (C1) can be substantially weakened to (C1*). As in Theorem 2, if the number of significant true alternatives is at least of order $\sqrt{\log \left(\log p\right)}$, then Theorem 4 below shows that the FDR and FDP will converge to αq₀/q

Theorem 4

Suppose that for some δ > 0,

$$\text{Card}\left\{(i,j):\frac{\mid {\sigma }_{ij}\mid }{\sqrt{{\theta }_{ij}}}\ge 4\sqrt{\frac{\log p}{n}}\right\}\ge \left(\frac{1}{\sqrt{8\pi }\alpha }+\delta \right)\sqrt{\log \left(\log p\right)}.$$

Then, under conditions of Theorem 3,

$$\underset{(n,p)\to \infty }{\lim }\frac{\mathrm{FDR}}{\alpha q_0∕q}=1and\frac{\mathrm{FDP}}{\alpha q_0∕q}\to 1inprobabilityas(n,p)\to \infty .$$ (26)

5 Numerical study

In this section, we study the numerical properties of the multiple testing procedure defined in Section 2 through the analysis of both simulated and real data. Section 5.1 examines the performance of the multiple testing procedure by simulations. A real data analysis is discussed in Section 5.2.

5.1 Simulation

We study in this section the performance of the testing procedure by a simulation study. In particular, the numerical performance of the proposed procedure is compared with that of the procedures based on Fisher's z transformation (3) together with the Benjamini-Hochberg method (Benjamini and Hochberg, 1995) and Benjamini-Yekutieli method (Benjamini and Yekutieli, 2001). We denote these two procedures by F_z-B-H and F_z-B-Y, respectively.

5.1.1 Two sample case: comparison with F_z-B-H and F_z-B-Y

The sample correlation matrix is invariant to the variances. Hence, we only consider the simulation for σ_ii1 = σ_ii2 = 1, i = 1, ..., p. Two covariance matrix models are considered.

• Model 1. R₁ = Σ₁ = diag(D₁, D₂ . . . , D_p/5), where D_k is a 5 × 5 matrix with 1 on the diagonal and ρ for all the off-diagonal entries. R₂ = Σ₂ = diag(I, A), where I is a (p/4) × (p/4) identity matrix and A = diag(D_p/20+1, . . . ,D_p/5).

• Model 2. R₁ = Σ₁ = diag(D̂₁, D̂₂, . . ., D̂_[p/m2], Î), where D̂_k is a m₁ × m₁ matrix with 1 on the diagonal and ρ for all the off-diagonal entries. Î is a (p – m₁[p/m₁]) × (p – m₁[p/m₁]) identity matrix. R₂ = Σ₂ = diag(D̂₁, D̂₂, . . ., D̂_[p/m2], Î), where D̃_k is a m₂ × m₂ matrix with 1 on the diagonal and ρ for all the off-diagonal entries. Ĩ is a (p – m₂[p/m₂]) × (p – m₂[p/m₂]) identity matrix.

The value of ρ will be specified in different distributions for the population. We will take (m₁, m₂) = (80, 40) in Model 2 to consider the strong correlation case. The following four distributions are considered.

• Normal mixture distribution. X = U₁Z₁ and Y = U₂Z₂, where U₁ and U₂ are independent uniform random variables on (0, 1) and Z₁ and Z₂ are independent random vectors with distributions N(0, Σ₁) and N(0, Σ₂) respectively. Let ρ = 0.8.

• Normal distribution. X and Y are independent random vectors with distributions N(0, Σ₁) and N(0, Σ₂) respectively. Let ρ = 0.6.

• t distribution. Z₁ and Z₂ are independent random vectors with i.i.d. components having t₆ distributions. Let $\mathit{X}={\Sigma }_1^{1∕2}{\mathit{Z}}_1$ and $\mathit{Y}={\Sigma }_2^{1∕2}{\mathit{Z}}_2$ with ρ = 0.6.

• Exponential distribution. Z₁ and Z₂ are independent random vectors with i.i.d. components having exponential distributions with parameter 1. Let $\mathit{X}={\Sigma }_1^{1∕2}{\mathit{Z}}_1$ and $\mathit{Y}={\Sigma }_2^{1∕2}{\mathit{Z}}_2$ with ρ = 0.6.

The normal mixture distribution (κ₁ ≠ 1 and κ₂ ≠ 1) allows us to check the influence of non-normality of the data on the procedures based on Fisher's z transformation. We also give the comparison between our procedure and the one based on Fisher's z transformation when the distribution is truly multivariate normal distributed. Note that the normal mixture distribution and the normal distribution satisfy the elliptically contoured distributions condition. On the other hand, the t distribution and exponential distribution generated by the above way do not satisfy (C2) and the t distribution does not satisfy (C3) either. So it allows us to check the influence of conditions (C2) and (C3) on our method.

In the simulation, we generate two groups of independent samples from X and Y . Let the sample sizes n₁ = n₂ = 50 and n₁ = n₂ = 100 and let the dimension p = 250, 500 and 1000. The number of the bootstrap re-samples is taken to be N = 50 and the nominal false discovery rate α = 0.2. Based on 100 replications, we calculate the average empirical false discovery rates

$$\text{Average}\left\{\frac{{\sum }_{(i,j)\in {\mathcal{H}}_0}I\{\mid T_{ij}\mid \ge \widehat{t}\}}{\max \{{\sum }_{1\le i<j\le p}\{\mid T_{ij}\mid \ge \widehat{t}\},1\}}\right\}$$

and the average empirical powers

$$\text{Average}\left\{\frac{{\sum }_{(i,j)\in {\mathcal{H}}_1}I\{\mid T_{ij}\mid \ge \widehat{t}\}}{{\sum }_{1\le i<j\le p}I\{{\rho }_{ij1}\ne {\rho }_{ij2}\}}\right\},$$

where ${\mathcal{H}}_1=\{(i,j):1\le i<j\le p,{\rho }_{ij1}\ne {\rho }_{ij2}\}$.

The simulation results for Model 1 in terms of the empirical FDR are summarized in Table 1 and the results on the empirical powers are given in Table 2. It can be seen from the two tables that, for the normal mixture distribution, the proposed procedure with bootstrap approximation (LCT-B) has significant advantages on controlling the FDR. It performs much better than the proposed procedure with normal approximation (LCT-N) when the sample size is small. Note that the performance of LCT-N becomes better as n increases. Both procedures in (9) and (12) outperform the one based on Fisher's z transformation (3) on FDR control. For the multivariate normal distribution, our methods have more power than F_z-B-H and F_z-B-Y. The latter method is also quite conservative. For the other two distributions which do not satisfy (C2), the empirical FDRs of F_z-B-H are larger than α while the empirical FDRs of our method are smaller than α. However, the powers of our method are quite close to those of F_z-B-H. Note that F_z-B-Y has the lowest powers although it is able to control the FDR.

Table 1.

Empirical false discovery rates (α = 0.2), Model 1.

		Normal mixture		N(0,1)
p\n1 = n2		50	100	50	100
250	Fz-B-H	0.9519	0.9479	0.3084	0.2511
	Fz-B-Y	0.6400	0.6136	0.0411	0.0256
	LCT-B	0.2267	0.1096	0.1068	0.1045
	LCT-N	0.4897	0.3065	0.3270	0.2450
500	Fz-B-H	0.9750	0.9721	0.3253	0.2511
	Fz-B-Y	0.7293	0.6714	0.0341	0.0249
	LCT-B	0.2368	0.0935	0.1039	0.0834
	LCT-N	0.5137	0.2977	0.3204	0.2334
1000	Fz-B-H	0.9871	0.9861	0.3669	0.2594
	Fz-B-Y	0.8052	0.7629	0.0428	0.0226
	LCT-B	0.2420	0.0620	0.1012	0.0567
	LCT-N	0.5479	0.2804	0.3304	0.2227
		t 6		Exp(1)
250	Fz-B-H	0.3204	0.2473	0.3738	0.2846
	Fz-B-Y	0.0430	0.0278	0.0693	0.0351
	LCT-B	0.0703	0.0890	0.0943	0.0817
	LCT-N	0.0903	0.0323	0.0721	0.0097
500	Fz-B-H	0.3487	0.2530	0.4328	0.3040
	Fz-B-Y	0.0384	0.0255	0.0768	0.0345
	LCT-B	0.0612	0.0639	0.0915	0.0568
	LCT-N	0.0868	0.0228	0.0845	0.0065
1000	Fz-B-H	0.3870	0.2711	0.4975	0.3309
	Fz-B-Y	0.0523	0.0261	0.0958	0.0396
	LCT-B	0.0565	0.0434	0.1050	0.0355
	LCT-N	0.0907	0.0165	0.1018	0.0046

Table 2.

Empirical powers (α = 0.2), Model 1.

		Normal mixture		N(0,1)
p\n1 = n2		50	100	50	100
250	Fz-B-H	0.9889	1.0000	0.5375	0.9405
	Fz-B-Y	0.9113	0.8782	0.2125	0.8072
	LCT-B	0.9245	0.9968	0.6445	0.9712
	LCT-N	0.9729	0.9995	0.7798	0.9792
500	Fz-B-H	0.9906	1.0000	0.4433	0.9247
	Fz-B-Y	0.8945	0.9985	0.1521	0.7576
	LCT-B	0.9074	0.9944	0.5741	0.9572
	LCT-N	0.9671	0.9996	0.7268	0.9751
1000	Fz-B-H	0.9894	1.0000	0.3593	0.8866
	Fz-B-Y	0.8768	0.9977	0.1027	0.6876
	LCT-B	0.8920	0.9979	0.5048	0.9381
	LCT-N	0.9583	0.9992	0.6784	0.9646
		t 6		Exp(1)
250	Fz-B-H	0.5465	0.9477	0.5981	0.9565
	Fz-B-Y	0.2329	0.8252	0.2762	0.8432
	LCT-B	0.6397	0.9647	0.5593	0.9525
	LCT-N	0.6562	0.9462	0.5357	0.8806
500	Fz-B-H	0.4679	0.9228	0.5104	0.9273
	Fz-B-Y	0.1684	0.7645	0.1884	0.7763
	LCT-B	0.5536	0.9490	0.4781	0.9206
	LCT-N	0.6047	0.9244	0.4656	0.8300
1000	Fz-B-H	0.4717	0.8925	0.4405	0.9049
	Fz-B-Y	0.1134	0.6965	0.1334	0.7208
	LCT-B	0.4699	0.9273	0.4118	0.8754
	LCT-N	0.5373	0.8984	0.4067	0.7873

The correlation in Model 2 is much stronger than that in Model 1 and the number of true alternatives is also larger. As we can see from Table 3, our method can still control the FDR e ciently and the powers are comparable to those of F_z-B-H and much higher than those of F_z-B-Y. As the numerical results for Model 1, the empirical FDRs of F_z-B-H are much larger than α for the normal mixture distribution. The performance of F_z-B-H is improved on the other three distributions although its empirical FDRs are somewhat higher than α when p = 1000 and n = 50.

Table 3.

Empirical false discovery rates (α = 0.2), Model 2.

		Normal mixture		N(0,1)
p\n1 = n2		50	100	50	100
250	Fz-B-H	0.4582	0.4476	0.1944	0.1797
	Fz-B-Y	0.1406	0.1356	0.0212	0.0189
	LCT-B	0.2095	0.2063	0.1845	0.1824
	LCT-N	0.2934	0.2433	0.2454	0.2163
500	Fz-B-H	0.6264	0.5993	0.2226	0.1968
	Fz-B-Y	0.2187	0.1924	0.0239	0.0174
	LCT-B	0.1722	0.1951	0.1612	0.1836
	LCT-N	0.3309	0.2694	0.2607	0.2214
1000	Fz-B-H	0.7275	0.7174	0.2436	0.2131
	Fz-B-Y	0.2700	0.2456	0.0245	0.0177
	LCT-B	0.1349	0.1632	0.1222	0.1600
	LCT-N	0.3297	0.2698	0.2626	0.2278
		t 6		Exp(1)
250	Fz-B-H	0.1976	0.1753	0.2058	0.2051
	Fz-B-Y	0.0242	0.0171	0.0257	0.0253
	LCT-B	0.1928	0.1924	0.2111	0.2039
	LCT-N	0.1924	0.1398	0.1497	0.1100
500	Fz-B-H	0.2340	0.2067	0.2372	0.2163
	Fz-B-Y	0.0253	0.0201	0.0282	0.0215
	LCT-B	0.1694	0.1745	0.1699	0.1945
	LCT-N	0.1883	0.1377	0.1313	0.0810
1000	Fz-B-H	0.2425	0.2171	0.2597	0.2255
	Fz-B-Y	0.0234	0.0181	0.0275	0.0201
	LCT-B	0.1235	0.1675	0.1343	0.1667
	LCT-N	0.1644	0.1211	0.1101	0.0640

5.1.2 One sample case

To examine the performance of our method in the one-sample case, we consider the following model.

• Model 3. R = Σ = diag(D₁, D₂ . . . , D_p/5), where D_k is a 5 × 5 matrix with 1 on the diagonal and ρ for all the off-diagonal entries.

We consider four types of distributions and ρ is taken to be the same values as in the two-sample case. In the simulation we let n = 50 and p = 500. The number of the bootstrap re-samples is taken to be N = 50 and the nominal false discovery rate α = 0.2. The empirical FDRs of three methods based on 100 replications are summarized in Table 5. As we can see from Table 5, the empirical FDRs of F_z-B-H are higher than α, especially for the normal mixture distribution. F_z-B-Y is also unable to control the FDR for the normal mixture distribution. Our method controls FDR quite well for all four distributions. Even when (C2) is not satisfied, our method can still control FDR efficiently.

Table 5.

Empirical FDRs for one sample tests (α = 0.2), Model 3.

	U*N(0,1)	N(0,1)	t(6)	Exp(1)
Fz-B-H	0.9093	0.2923	0.3019	0.3601
Fz-B-Y	0.5304	0.0339	0.0361	0.0714
LCT-B	0.1733	0.1895	0.1859	0.1769

We now carry out a simulation study to verify that the FDP control in the one sample case can be get benefit from the correlation. Consider the following matrix model.

• Model 4. Σ = diag(D₁, D₂ . . . ,D_k, I), where D_k is a 5 × 5 matrix with 1 on the diagonal and 0.6 for all the off-diagonal entries.

We take k = 1, 5, 10, 20, 40, 80 such that the correlation increases as k grows. Let X = ${\Sigma }^{1∕2}\mathit{Z}$, where Z is the standard normal random vector. We take n = 50 and p = 500. The procedure in Section 4 with the bootstrap approximation is used in the simulation. To evaluate the performance of the FDP control, we use the l₂ distance $SD≔\sqrt{{\sum }_{i=1}^{100}{(FD{P}_i-\alpha q_0∕q)}^2∕100}$, where FDP_i is the FDP in the i-th replication. As we can see from Table 5, the distance between FDP and αq₀/q becomes small as k increases.

5.2 Real data analysis

Kostka and Spang (2004), Carter et al. (2004) and Lai, et al. (2004) studied gene-gene coexpression patterns based on cancer gene expression datasets. Their analyses showed that several transcriptional regulators, which are known to be involved in cancer, had no significant changes in their mean expression levels but were highly differentially coexpressed. As pointed out in de la Fuente (2010), these results strongly indicated that, besides differential mean expressions, coexpression changes are also highly relevant when comparing gene expression datasets.

In this section we illustrate the proposed multiple testing procedure with an application to the detection of the changes in coexpression patterns between gene expression levels using a prostate cancer dataset (Singh et al. 2002). The dataset is available at http://www.broad.mit.edu/cgi-bin/cancer/datasets.cgi.

This dataset consists of two classes of gene expression data that came from 52 prostate tumor patients and 50 prostate normal patients. There are a total of 12600 genes. We first choose 500 genes with the smallest absolute values of the two-sample t test statistics for the comparison of the means

$$t_i=\mid {\stackrel{‒}{X}}_i-{\stackrel{‒}{Y}}_i\mid \sqrt{{\widehat{s}}_{1i}^2∕n_1+{\widehat{s}}_{2i}^2∕n_2},$$

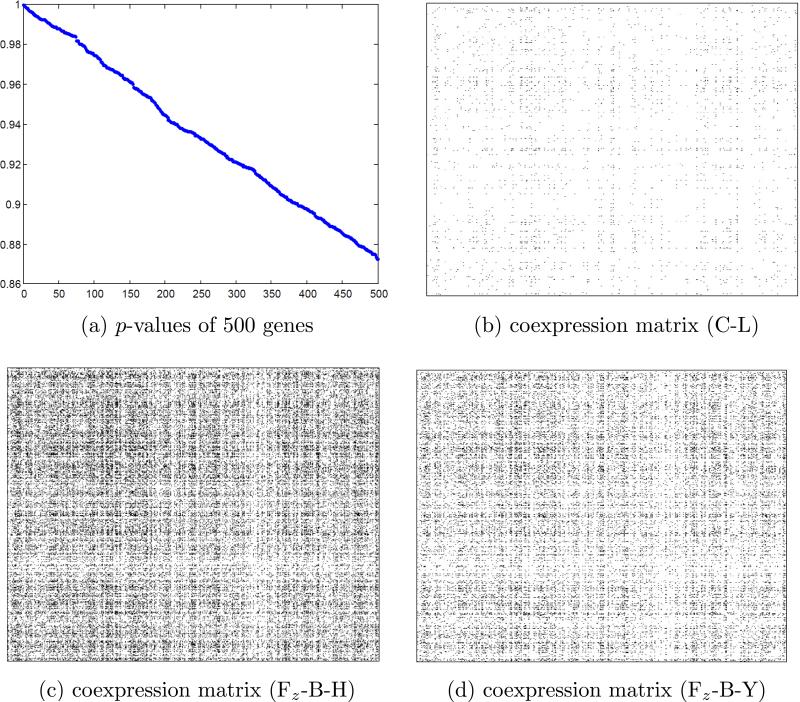
where ${\widehat{s}}_{1i}^2$ and ${\widehat{s}}_{2i}^2$ are the sample variances of the i-th gene. All of the p-values P(|N(0, 1)| ≥ |t_i|) of 500 genes are greater than 0.87; see Figure (a). Hence, it is very likely that all of the 500 genes are not differentially expressed in the means. The proposed multiple testing procedure is applied to investigate whether there are differentially coexpressed gene pairs between these 500 genes. As in Kostka and Spang (2004), Carter et al. (2004) and Lai, et al. (2004), the aim of this analysis is to verify the phenomenon that additional information can be gained from the coexpressions even when the genes are not differentially expressed in the means.

Figure 1.

(a) p-Values of 500 genes. (b) Coexpression matrix (C-L). (c) Coexpression matrix (Fz-B-H). (d) Coexpression matrix (Fz-B-Y).

Let $r_{ij}^N\left(r_{ij}^T\right)$ denote the Pearson correlation coefficient between the expression levels of gene i and gene j of the prostate normal (tumor) patients. We wish to test the hypotheses $H_{0ij}:r_{ij}^N=r_{ij}^T$, 1 ≤ i < j ≤ 500. The pair of genes i and j is identified to be differentially coexpressed if the hypothesis H_0ij is rejected. See de la Fuente (2010). We compare the performance between our procedure (the number of the bootstrap re-samples N = 50) and those based on Fisher's z transformation with the nominal FDR level α = 0.05. Our procedure (Figure (b)) identifies 1341 pairs of coexpression genes and 1.07% nonzero entries of the coexpression matrix (estimation of support of R₁ – R₂). As noted by Yeung, et al. (2002), gene regulatory networks in most biological systems are expected to be sparse. Our method thus leads to a clear and easily interpretable coexpression network. In comparison, F_z-B-H and F_z-B-Y identify respectively 26373 (21.14%) and 13794 (11.06%) pairs of coexpression genes and the estimates of the support of R₁ – R₂ are very dense and difficult to interpret (Figures (c) and (d)). This is likely due to the non-normality of the dataset so that (3) fails to hold. As a result, the true FDR level of F_z-B-H and F_z-B-Y may be much larger than the nominal level which leads to the large number of rejections.

6 Discussion

In this paper, we introduced a large scale multiple testing procedure for correlations and showed that the procedure performs well both theoretically and numerically under certain regularity conditions. The method can also be used for testing the cross-correlations, and some of the conditions can be further weakened. We discuss in the section some of the extensions and the connections to other work.

6.1 Multiple Testing of Cross-Correlations

In some applications, it is of interest to carry out multiple testing of cross-correlations between two high dimensional random vectors, which is closely related to the one-sample case considered in this paper. Let X = (X₁, . . . , X_p1)′ and Y = (Y₁, . . . , Y_p2) be two random vectors with dimension p₁ and p₂ respectively. We consider multiple correlation tests between X_i and Y_j

$$H_{0ij}:\mathsf{Cov}(X_i,Y_j)=0\text{versus}{H}_{1ij}:\mathsf{Cov}(X_i,Y_j)\ne 0$$

for 1 ≤ i ≤ p₁ and 1 ≤ j ≤ p₂. We can construct similar test statistics

$$T_{ij}=\frac{{\sum }_{k=1}^n(X_{ki}-{\stackrel{‒}{X}}_i)(Y_{kj}-{\stackrel{‒}{Y}}_j)}{\sqrt{n{\widehat{\theta }}_{ij}}},$$

where

$${\widehat{\theta }}_{ij}=\frac{1}{n}\sum _{k=1}^n{[(X_{ki}-{\stackrel{‒}{X}}_i)(Y_{kj}-{\stackrel{‒}{Y}}_j)-{\widehat{\sigma }}_{ijXY}]}^2,{\widehat{\sigma }}_{ijXY}=\frac{1}{n}\sum _{k=1}^n(X_{ki}-{\stackrel{‒}{X}}_i)(Y_{kj}-{\stackrel{‒}{Y}}_j).$$

The normal distribution can be used to approximate the null distribution of T_ij when the sample size is large. If the sample size is small, we can use $G_{n,N}^{\ast }\left(t\right)$ to approximate the null distribution of T_ij, where

$$G_{n,N}^{\ast }\left(t\right)=\frac{1}{N{p}_1{p}_2}\sum _{k=1}^N\sum _{i=1}^{p_1}\sum _{j=1}^{p_2}I\{\mid T_{ij,k}^{\ast }\mid \ge t\}.$$

Here $T_{ij,k}^{\ast }$ are constructed by the bootstrap method as in (24). The multiple testing procedure is as follows.

FDR control procedure

Let 0 < α < 1 and define

$$\widehat{t}=\inf \{0\le t\le b_p:\frac{G_{n,N}^{\ast }\left(t\right)p_1∕p_2}{\max \{{\sum }_{i=1}^{p_1}{\sum }_{j=1}^{p_2}I\{\mid T_{ij}\mid \ge t\},1\}}\le \alpha \}.$$

If t̂ does not exist, then let $\widehat{t}=\sqrt{2\log \left(p_1{p}_2\right)}$. We reject H_0ij whenever |T_ij| ≥ $\widehat{t}$.

Let ${\mathcal{H}}_0=\{(i,j):\mathsf{Cov}(X_i,Y_j)=0\}$ and ${\mathcal{H}}_1=\{(i,j):\mathsf{Cov}(X_i,Y_j)\ne 0\}$. We assume the following condition holds for X and Y.

(C4). For any $\mathcal{A}=\{i,j,k,l\}$, if $(i,j)\in {\mathcal{H}}_0$ and $(k,l)\in {\mathcal{H}}_0$, then

$$\mathsf{E}\left[(X_i-\mathsf{E}{X}_i)(Y_j-\mathsf{E}{Y}_j)(X_k-\mathsf{E}{X}_k)(Y_l-\mathsf{E}{Y}_l)\right]={\tau }_{\mathcal{A}}\mathsf{E}\left[(X_i-\mathsf{E}{X}_i)(X_k-\mathsf{E}{X}_k)\right]\mathsf{E}\left[(Y_j-\mathsf{E}{Y}_j)(Y_l-\mathsf{E}{Y}_l)\right]$$

for some positive constant ${\tau }_{\mathcal{A}}$.

Let R₁ and R₂ be the correlation matrices of X and Y respectively. Denote p = p₁ + p₂, q = p₁p₂, q₀ = Card(${\mathcal{H}}_0$) and q₁ = Card(${\mathcal{H}}_1$). Suppose that $p_1\asymp p_2$. Then the following theorem holds.

Theorem 5

Assume that p ≤ n^r for some r > 0 and q₁ ≤ cq for some 0 < c < 1. Under (C1), (C3) and (C4),

$$\underset{(n,p)\to \infty }{\overline{\lim }}\mathrm{FDR}\le \alpha ,\underset{(n,p)\to \infty }{\lim }\mathit{P}(\mathrm{FDP}\le \alpha +\epsilon )=1$$

for any ε > 0. Furthermore, if

$$\text{Card}\left\{(i,j):\frac{\mid \mathit{Cov}(X_i,Y_j)\mid }{\sqrt{{\theta }_{ij,XY}}}\ge 4\sqrt{\frac{\log p}{n}}\right\}\ge \left(\frac{1}{\sqrt{8\pi }\alpha }+\delta \right)\sqrt{\log \left(\log p\right)},$$

then

$$\underset{(n,p)\to \infty }{\lim }\frac{\mathrm{FDR}}{\alpha q_0∕q}=1and\frac{\mathrm{FDP}}{\alpha q_0∕q}\to 1inprobabilityas(n,p)\to \infty ,$$

where θ_ij,XY = Var[(X_i – EX_i)(Y_j – EY_j)].

6.2 Relations to Owen (2005)

A related work to the one-sample correlation test is Owen (2005), which studied the variance of the number of false discoveries in the tests on the correlations between a single response and p covariates. It was shown that the correlation would greatly a ect the variance of the number of false discoveries. The goal in our paper is different from that in Owen (2005). Here we study the FDR control on the correlation tests between all pairs of variables. In our problem, the impact of correlation is much less serious and is even beneficial to the FDP control under the sparse setting (C1*). To see this, set $\mathcal{N}=\{(i,j):1\le i<j\le p,\mid {\rho }_{ij}\mid \ge {\left(\log p\right)}^{-2-\gamma }\}$ for some γ > 0. In other words, N denotes the pairs with strong correlations. Suppose that Card($\mathcal{N}$) = p^τ for some 0 < τ < 2. The larger τ indicates the stronger correlations among the variables. It follows from the proof of Theorem 2 that $\mathsf{P}(0\le \widehat{t}\le \sqrt{(4-2\tau )\log p})\to 1$ 1. By the proof in Section 7, we can see that the di erence FDP – αq₀/q depends on the accuracy of the approximation

$$\underset{0\le t\le \sqrt{(4-2\tau )\log p}}{\sup }\mid \frac{{\sum }_{(i,j)\in {\mathcal{H}}_0}I\{\mid T_{ij}\mid \ge t\}}{\mid {\mathcal{H}}_0\mid G_{n,N}^{\ast }\left(t\right)}-1\mid .$$

Generally, a larger τ provides a better approximation because the range 0 ≤ t ≤ $\sqrt{(4-2\tau )\log p}$ becomes smaller and $\mid {\mathcal{H}}_0\mid G_{n,N}^{\ast }\left(\sqrt{(4-2\tau )\log p}\right)$ becomes larger. Hence, as τ increases, the FDP is better controlled. Simulation results in Section 5.1.2 also support this observation.

6.3 Relax the Conditions

In Sections 2 and 3, we require the distributions to satisfy the moment condition (C2), which is essential for the validity of the testing procedure. An important example is the class of the elliptically contoured distributions. This is clearly a much larger class than the class of multivariate normal distributions. However, in real applications, (C2) can still be violated. It is desirable to develop test statistics that can be used for more general distributions. To this end, we introduce the following test statistics that do not need the condition (C2).

Let $X_{ki}^{\prime }=(X_{ki}-{\mu }_i)∕{\sigma }_{ii1}^{1∕2}$. It can be proved that, under the finite 4th moment condition $\mathsf{E}{(X_{ki}-{\mu }_{i1})}^4∕{\sigma }_{ii1}^2<\infty$,

$$2\sqrt{\frac{n_1}{{\theta }_{ij1}}}({\widehat{\rho }}_{ij1}-{\rho }_{ij1})\to N(0,1),$$ (27)

where i ≠ j and

$${\theta }_{ij1}=\frac{1}{n_1}\sum _{k=1}^{n_1}{(2X_{ki}^{\prime }{X}_{kj}^{\prime }-{\widehat{\rho }}_{ij1}{X^{\prime }}_{ki}^2-{\widehat{\rho }}_{ij1}{X^{\prime }}_{kj}^2)}^2.$$

We can estimate μ_i and σ_ii1 in θ_ij1 by their sample versions. Let ${\widehat{X}}_{ki}=(X_{ki}-{\stackrel{‒}{X}}_i)∕{\widehat{\sigma }}_{ii1}^{1∕2}$ where ${\widehat{\sigma }}_{ii1}=\frac{1}{n_1}{\sum }_{k=1}^{n_1}{(X_{ki}-{\stackrel{‒}{X}}_i)}^2$, and let

$${\widehat{\theta }}_{ij1}=\frac{1}{n_1}\sum _{k=1}^{n_1}{(2{\widehat{X}}_{ki},{\widehat{X}}_{kj}-{\widehat{\rho }}_{ij1}{\widehat{X}}_{ki}^2-{\widehat{\rho }}_{ij1}{\widehat{X}}_{kj}^2)}^2.$$

${\widehat{\theta }}_{ij2}$ is defined in the same way by replacing X with Y . So the test statistic

$$T_{ij}^{\prime }=\frac{2({\widehat{\rho }}_{ij1}-{\widehat{\rho }}_{ij2})}{\sqrt{{\widehat{\theta }}_{ij1}∕n_1+{\widehat{\theta }}_{ij2}∕n_2}}$$ (28)

can be used to test the individual hypothesis H_0ij : ρ_ij1 = ρ_ij2. We have the following proposition.

Proposition 2

• (1).Suppose that $\mathit{E}{(X_{ki}-{\mu }_{i1})}^4∕{\sigma }_{ii1}^2<\infty$ and $\mathit{E}{(Y_{ki}-{\mu }_{i2})}^4∕{\sigma }_{ii2}^2<\infty$. Under the null hypothesis H_0ij : ρ_ij1 = ρ_ij2, we have $T_{ij}^{\prime }\Rightarrow N(0,1)$.
• (2).
  Suppose that p ≤ n^r for some r > 0 and (C3) holds. For any b > 0, we have

  $$\underset{(i,j)\in {\mathcal{H}}_0}{\sup }\underset{0\le t\le b\sqrt{\log p}}{\sup }\mid \frac{\mathit{P}(\mid T_{ij}^{\prime }\mid \ge t)}{2-2\Phi \left(t\right)}-1\mid \to 0,$$

Proposition 2 can be used to establish the FDR control result for multiple tests (2) by assuming some dependence condition between the test statistics $T_{ij}^{\prime }$. However, we should point out that, although $T_{ij}^{\prime }$ does not require (C2), numerical results show that it is less powerful than the test statistic T_ij in Section 2.

Table 4.

Empirical powers (α = 0.2), Model 2.

		Normal mixture		N(0,1)
p\n1 = n2		50	100	50	100
250	Fz-B-H	0.9970	1.0000	0.9208	0.9963
	Fz-B-Y	0.9730	0.9997	0.6640	0.9658
	LCT-B	0.9879	1.0000	0.9096	0.9977
	LCT-N	0.9932	0.9999	0.9381	0.9978
500	Fz-B-H	0.9955	1.0000	0.8637	0.9941
	Fz-B-Y	0.9658	0.9996	0.5482	0.9506
	LCT-B	0.9819	0.9999	0.8482	0.9943
	LCT-N	0.9901	0.9999	0.8954	0.9967
1000	Fz-B-H	0.9936	1.0000	0.8037	0.9900
	Fz-B-Y	0.9498	0.9996	0.4479	0.9257
	LCT-B	0.9753	0.9999	0.7920	0.9926
	LCT-N	0.9836	0.9999	0.8492	0.9947
		t 6		Exp(1)
250	Fz-B-H	0.9136	0.9965	0.9165	0.9971
	Fz-B-Y	0.6548	0.9678	0.6861	0.9704
	LCT-B	0.9047	0.9972	0.8710	0.9957
	LCT-N	0.9013	0.9957	0.8607	0.9920
500	Fz-B-H	0.8576	0.9924	0.8641	0.9929
	Fz-B-Y	0.5498	0.9430	0.5771	0.9467
	LCT-B	0.8441	0.9946	0.8000	0.9912
	LCT-N	0.8394	0.9907	0.7774	0.9813
1000	Fz-B-H	0.8015	0.9881	0.8105	0.9875
	Fz-B-Y	0.4639	0.9232	0.4890	0.9196
	LCT-B	0.7655	0.9886	0.7254	0.9827
	LCT-N	0.7857	0.9856	0.7110	0.9679

Table 6.

Empirical distance between FDP and αq₀/q (α = 0.2).

k	1	5	10	20	40	80
SD	0.3426	0.1784	0.0836	0.0433	0.0281	0.0221