Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jan 24;4:3845. doi: 10.1038/srep03845

Separation of photo-induced radical pair in cryptochrome to a functionally critical distance

Ilia A Solov'yov 1,2,a, Tatiana Domratcheva 3,b, Klaus Schulten 1,4,c
PMCID: PMC4894384  PMID: 24457842

Abstract

Cryptochrome is a blue light receptor that acts as a sensor for the geomagnetic field and assists many animals in long-range navigation. The magnetoreceptor function arises from light-induced formation of a radical pair through electron transfer between a flavin cofactor (FAD) and a triad of tryptophan residues. Here, this electron transfer is investigated by quantum chemical and classical molecular dynamics calculations. The results reveal how sequential electron transfer, assisted by rearrangement of polar side groups in the cryptochrome interior, can yield a FAD-Trp radical pair state with the FAD and Trp partners separated beyond a critical distance. The large radical pair separation reached establishes cryptochrome's sensitivity to the geomagnetic field through weakening of distance-dependent exchange and dipole-dipole interactions. It is estimated that the key secondary electron transfer step can overcome in speed both recombination (electron back-transfer) and proton transfer involving the radical pair reached after primary electron transfer.

Key biological processes involve the conversion of energy into forms that are usable for chemical transformations or cellular signaling. This conversion often involves electronic degrees of freedom and occurs through chemical reaction, light absorption, excitation energy transfer, and electron or proton transfer. Such processes can only be appropriately understood and adequately modeled using the concept and methods of quantum physics. A particularly striking example of a quantum mechanical process in biology apparently is magnetoreception, which assists navigation in animals, for example in migratory birds1,2,3. Magnetoreception is suggested to arise through photoactivation of cryptochromes4,5,6,7,8, blue light photoreceptors contained in the eye9,10, the photoactivation being influenced by the Earth's magnetic field. The protein's name was chosen as the receptor hid for a long time from the instruments of researchers. The name, though, seems still appropriate today as the physical mechanism of the receptor is still hidden. Interestingly, cryptochrome is controlling in many species a tidal rhythm based on a circalunar internal clock driven by night light and many birds, indeed, are nocturnal migrants11,12,13.

The magnetoreception function of cryptochrome is postulated to arise from a radical pair formed through intra-protein electron transfer14,15,16,17. The quantum evolution of a nonequilibrium electron spin state of initially spin-correlated radicals in the pair is conjectured to change the yield of the reaction products of the radical pair in wet, warm and noisy biological surroundings, even though the Zeeman interaction with the geomagnetic field is more than seven orders of magnitude smaller than the thermal energy kBT. The thermodynamic effect of such minuscule interactions on chemical equilibria is entirely negligible, yet the intermediate reaction rates are strongly influenced due to quantum effects. 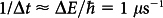This can be understood readily on the basis of the well known uncertainty relationship of quantum mechanics, Inline graphic, according to which an energy as small as ΔE = 10−9 eV can bring about an electronic state change with a rate of Inline graphic.

The radical pair mechanism is the only well-established way in which an external magnetic field influences a chemical reaction18,19,20. To form the basis of an effective compass magnetoreceptor, a radical pair reaction, however, must match a number of conditions. These conditions fall into five broad overlapping areas: chemical, magnetic, kinetic, structural and dynamic18,21. A critical condition is that the exchange and dipole-dipole interactions between the unpaired electron spins on the radical partners must be even smaller than the Zeeman interaction, a condition which is realized only for a sufficiently large separation between the radical pair partners22. It is still unclear to what extent these conditions are satisfied in cryptochrome, as the physical mechanism of cryptochrome photoactivation has yet to be unraveled in atomistic detail.

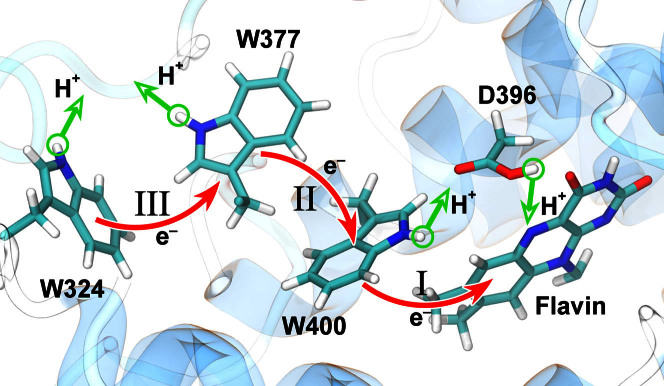
Transient absorption measurements provide invaluable insight into the photodynamical properties of cryptochrome, but due to spectral overlap of electron donor and acceptor groups and their various redox states the spectra cannot be interpreted directly in terms of concrete transient states or of a physical photoactivation mechanism23,24. The studies of the last decade indicate that formation of the signaling state in cryptochrome from the plant Arabidopsis thaliana involves photoinduced electron transfer to isoalloxazine, the key moiety of the flavin adenine nucleotide (FAD) cofactor of cryptochrome. The electrons are transferred from a tryptophan triad (W400, W377, W324), highly conserved among cryptochromes from many species, that bridges the space between flavin and the protein surface15,16,25,26,27,28, as depicted in Fig. 1. Recently, alternative electron transfer schemes were suggested that involve other amino acid residues in the protein29,30,31. However, all proposed pathways consider a sequence of electron transfer steps resulting in increasing distance separation in the radical pair and eventually leading to the formation of the cryptochrome's signaling state.

Figure 1. Electron and proton transfers in cryptochrome.

Figure 1

Open in a new tab

Shown is the flavin cofactor, the tryptophan triad (W400, W377, W324) and the D396 residue forming the active site of cryptochrome-1 from Arabidopsis thaliana. Electron (red) and proton (green) transfer processes that likely govern cryptochrome activation are presented by arrows. The three electron transfers W400 → flavin, W377 → W400·+, and W324 → W377·+ are labeled I, II, and III, respectively. Electron transfer following flavin photo-excitation leads to a radical pair state of cryptochrome: transfer I to [FAD·− + W400·+] with the averaged pair separation of 7.4 Å, sequential transfer I + II to [FAD·− + W377·+] with pair separation of 12.2 Å, sequential transfer I + II + III to [FAD·− + W324·+] with pair separation of 18.2 Å.

Here we investigate the structurally known plant cryptochrome from Arabidopsis thaliana32, as it is highly homologous in sequence to the structurally unknown avian cryptochrome33, as well as homologous in sequence and structure to cryptochromes from insect34 and mouse35, studied recently through crystallography. Variation of cryptochrome photoactivation in different species is naturally expected due to structural differences in the proteins; however, the conserved flavin and tryptophan triad suggest that the physical mechanism of cryptochrome activation, resolved below, is general and our findings in A. thaliana cryptochrome should also apply to animal cryptochromes.

Recently23, we have combined ab initio quantum chemistry and classical all-atom molecular dynamics (MD) simulations to investigate the primary photoreaction of plant cryptochrome that triggers radical pair formation, denoted in Fig. 1 as electron transfer I. We demonstrated that a radical pair [FAD·− + W400(H)·+] involving flavin and the closest tryptophan residue, W400, is formed in the course of this first electron transfer. In our notation W400(H)·+ and W400·+ are equivalent, “(H)” denoting explicitly a protein carrying the positive charge of the tryptophan radical.

The [FAD·− + W400(H)·+] radical pair can be rapidly stabilized through proton transfer between positively charged W400(H)·+ and negatively charged flavin FAD·−, involving as an intermediate proton transfer stepping stone the aspartic acid D396 shown in Fig. 1. This proton transfer was seen to be favorable energetically, as the estimated activation energy of the process is negligibly small, but it requires a local rearrangement of D396, which was estimated to happen in less than 1 ns23, leading to the [FADH· + W400·] radical pair, i.e., a radical pair with the protonated flavin radical. The calculations also suggested that recombination, i.e., backward electron transfer, of the latter radical pair occurs on the microsecond time scale, hence allowing within this time range a subsequent forward electron transfer that would increase the radical-pair separation distance. For the sake of simple notation W400(H)·+ will be denoted from now on simply as W400·+, except when the W400(H)·+ → FAD·− proton transfer reaction is considered.

Interpretation of experimental data30,36, however, suggests that a second electron transfer, W377 → W400·+, depicted in Fig. 1 as transition II, and also a third electron transfer W324 → W377·+ (electron transfer III) take place prior to the stabilization of the radical pair by protonation, i.e., from [FAD·− + W400·]. To accurately evaluate the energy requirements for such W377 → W400·+ electron transfer, we need to consider the role of the molecular environment in formation of a [FAD·− + W377·] radical pair, which was considered previously only to a very limited extent23. The sequential electron transfers I, II, and III are considered to be crucial for cryptochrome's magnetoreceptor role28,33,37, as pointed out above, since a critical condition for a geomagnetic field-sensitive radical pair behavior is a sufficiently large separation distance between the transferred electron (on FAD) and its hole (on either W400, W377 or W324), the latter two positions being preferable for magnetoreception due to a larger distance value as can be recognized in Fig. 118,21,33.

In the present study we investigate the possibility of W377 → W400·+ electron transfer (transfer II) succeeding W400 → flavin electron transfer (transfer I) in plant cryptochrome from Arabidopsis thaliana. Of particular interest is the question of whether transfer II can occur fast enough. The speed of the transfer is crucial as the transfer has to outrun flavin protonation; once flavin protonation takes place the closely spaced [FAD·− + W400·+] radical pair becomes stabilized and impedes energetically transfer II. To address the stated question we investigate in the present study in how far electron transfer II can be induced through fast enough conformational transitions in cryptochrome; such transitions are needed to render transfer II energetically feasible.

Results

Model for W377 active site

The primary electron transfer in cryptochrome, W400 → flavin, is facilitated through amino acids that surround the electronic donor and acceptor sites of the protein23. In particular, as demonstrated computationally23, the presence of an aspartic acid, residue D396, in close vicinity to W400 as shown in Fig. 1, stabilizes the primary [FAD·− + W400·+] radical pair through flavin protonation to become [FADH· + W400·]. W400(H)·+ deprotonation by D396 prevents the W377 → W400(H)·+ electron transfer, which however is crucial for cryptochrome magnetoreception. D396 is expected to be protonated in the cryptochrome resting state and, therefore, available for the suggested protonation reaction; the protonation state is concluded from the crystallographic structure (PDB code 1U3C)32, in which the distance between the OD2 atom of D396 and the backbone oxygen of the M381 residue is only 2.7 Å; availability of D396 for flavin protonation is also consistent with the side group's in situ pKa value as determined through a propKa calculation38.

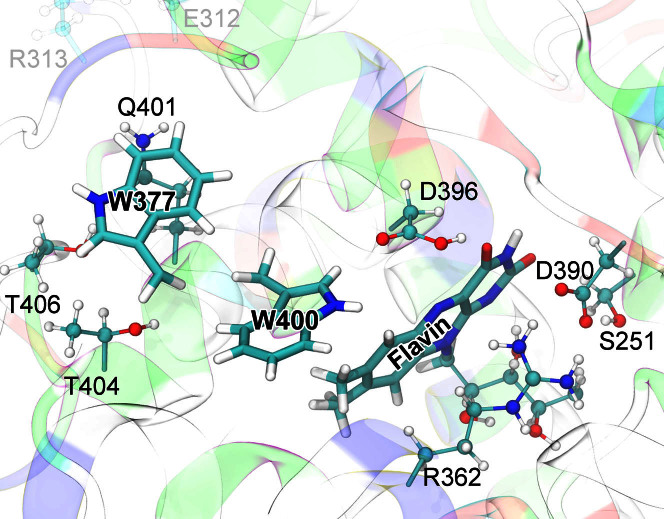
The second tryptophan of the electron transfer triad, W377, is located 4.8 Å further away from the flavin (see Fig. 1) as compared to W400. Additionally, W377 does not have any charged, or transiently charged, amino acids in its immediate vicinity that could stabilize the [FAD·− + W377·+] radical pair, suggesting right off the bat an energetically uphill and, therefore, fairly slow W377 → W400·+ electron transfer23. However, in order to judge the actual rate of a W377 → W400·+ electron transfer an account of amino acids surrounding W377 is called for. Inspecting the cryptochrome structure, one identifies several polar amino acid residues that are about ~4–6 Å away from W377 in the equilibrated structure of the protein. These side groups could accelerate W377 → W400·+ electron transfer by rearranging themselves. Figure 2 illustrates the charge distribution in cryptochrome's active site. The polar amino acids that surround W377 are Q401, T404, and T406, while the charged amino acids, E312 and R313, are directed away from W377 and, therefore, likely irrelevant for the electron transfer rate.

Figure 2. Cryptochrome active site model.

Figure 2

Open in a new tab

The quantum chemical description of the W377 → W400·+ electron transfer in cryptochrome (electron transfer II in Fig. 1) includes electronic degrees of freedom of riboflavin and of the side chains of amino acid residues S251, R362, W377, D390, D396, Q401, W400, T404, and T406. Residues donating and accepting the electrons (flavin, W400, W377) are shown in licorice representation, while the atoms of coordinating side chains are shown as balls and sticks. The coloring of cryptochrome secondary structure illustrates the charge distribution of the protein's amino acids: positive (blue), negative (red), polar uncharged (green), and hydrophobic uncharged (white). Sidechain groups of all polar, positively and negatively charged amino acids surrounding flavin, W400, and W377 were included into the active site model to describe environmental effects on the W377 → W400·+ electron transfer; distant charged sidechains, e.g., E312, R313 (transparent), were not included in the quantum chemical description.

Electron transfer through the W400 + W377 diad

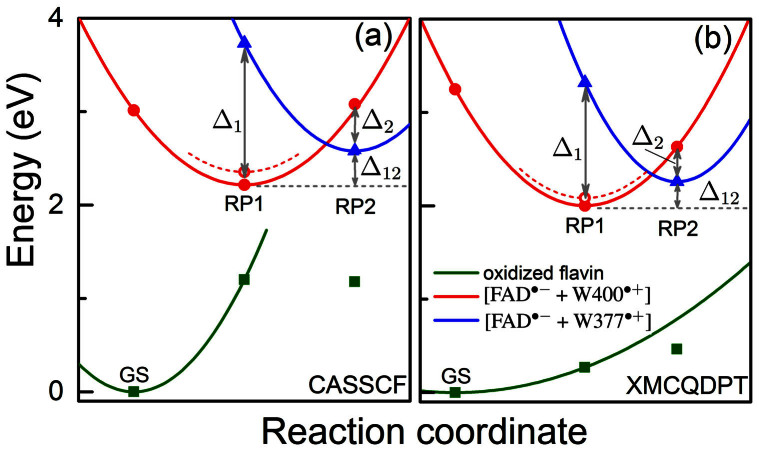
The electronic states of the cryptochrome active site with the lowest energies are shown in Fig. 3. The energy profiles were calculated using the CASSCF (Fig. 3a) and the perturbation theory-based XMCQDPT-2 (Fig. 3b) approaches as outlined in Methods. The total energies, computed using either approach, are compiled in Tab. 1. Three different electronic states are shown in Fig. 3: (i) the resting state, characterized by an oxidized flavin, namely by FAD + W400 + W377 (green squares); (ii) the radical pair state FAD·− + W400·+ + W377 = [FAD·− + W400·+] (red circles); and (iii) the radical pair state FAD·− + W400 + W377·+ = [FAD·− + W377·+] (blue triangles). The geometry of the model system introduced in Fig. 2 was optimized for these three states and the excitation spectra for the geometries obtained were computed. The energy-optimized configurations are denoted in Fig. 3 as GS, RP1, and RP2. GS and RP1 correspond to the S0 and S2(0) energy minima, respectively, described in a previous paper23. Associated with RP1 and RP2, in particular, are the energy differences Δ1, Δ2 and Δ12 defined in Fig. 3.

Figure 3. Potential energy profiles of the key electronic states in cryptochrome.

Figure 3

Open in a new tab

The energy for oxidized flavin is shown in green, for radical pair state [FAD·− + W400·+] in red and for radical pair state [FAD·− + W377·+] in blue. Solid symbols represent calculated energies, while lines represent schematic potential energy surfaces. The energies were computed using the CASSCF method (a) and the perturbation theory-based XMCQDPT-2 method (b). Open circles denote the energies calculated for the optimized [FAD·− + W400·+] radical pair after the rearrangement of the W377 residue shown in Fig. 4. Δ1 is the energy difference between the RP2 and the RP1 state calculated for the RP1-optimized geometry and Δ2 is the energy difference between the RP1 and the RP2 state calculated for the RP2-optimized geometry; Δ12 is the energy difference between geometry optimized RP2 state and geometry optimized RP1 state. The values of the energies Δ1, Δ2, Δ12, according to the data in Tab. 1, are 1.52 eV, 0.50 eV, 0.36 eV, respectively, for the CASSCF method and 1.32 eV, 0.38 eV, 0.26 eV, respectively, for the XMCQDPT-2 method.

Table 1. Total energies of electronic states in the cryptochrome active site. Energies were calculated for the cryptochrome active site model shown in Fig. 2. Geometry optimization in the electronic ground and excited states was performed with the state-averaged CASSCF and XMCQDPT-2 methods using the program Firefly51. Three electronic states were considered. The labels in the first column denote states marked in Fig. 3. The energy of the FAD·− + W377·+ state for the optimized GS geometry, in fact, is higher than the energy of the excited FAD·− + W400*·+ state, and, therefore, does not appear in the table. The calculated energies (CASSCF and XMCQDPT-2 values) of the second excited state for the GS geometry correspond to the FAD·− + W400*·+ state and are marked with an asterisk.

state oxidized flavin FAD·− + W400·+ FAD·− + W377·+
CASSCF total energies (a.u.)
GS, optimized −3612.751899 −3612.641151 −3612.624968*
RP1, optimized −3612.707732 −3612.670458 −3612.614731
RP1, with W377 rearrangement −3612.705990 −3612.665373 −3612.622435
RP2, optimized −3612.708593 −3612.638732 −3612.657125
XMCQDPT-2 total energies (a.u.)
GS, optimized −3623.670253 −3623.550927 −3623.524985*
RP1, optimized −3623.660373 −3623.596712 −3623.548341
RP1, with W377 rearrangement −3623.651291 −3623.593714 −3623.559870
RP2, optimized −3623.653140 −3623.573561 −3623.587278
Open in a new tab

Energies of [FAD·− + W400·+] and [FAD·− + W377·+] radical pair states

The previous study23 demonstrated that the [FAD·− + W400·+] radical pair forms rapidly upon flavin photoexcitation, in agreement with experimental observations16. The [FAD·− + W377·+] radical pair state results from subsequent W377 → W400·+ electron transfer II (see Fig. 1). The W377 → W400·+ electron transfer, however, is inhibited once FAD·− acquires a proton from W400·+ via D39623. Figure 3 shows the energy minimum corresponding to the [FAD·− + W400·+] radical pair formed prior to flavin protonation. In this configuration the aspartic acid D396 is in its rearranged configuration23 that it assumes upon the W400 → FAD* electron transfer I (see Fig. 1).

The energy of the cryptochrome active site with the optimized [FAD·− + W400·+] radical pair (state of optimal geometry RP1) is Δ1 = 1.32 eV lower than the energy of the active site with the [FAD·− + W377·+] radical pair, both energies calculated for the RP1 geometry and shown in Fig. 3b (XMCQDPT-2 result). Optimization of the [FAD·− + W377·+] radical pair leads to a crossing of the energy surfaces characterizing the two radical pairs and a lowering of the energy-optimized RP2 state by Δ1 – Δ12 = 1.06 eV as seen in Fig. 3. The molecular environment of W377 is essential for lowering the energy of the respective radical pair. Previously23, we considered W377 without an account for this environment and, therefore, did not observe crossing of the energy surfaces describing the two radical pair states; instead, the [FAD·− + W377·+] radical pair energy minimum was located on an excited potential energy surface with respect to the [FAD·− + W400·+] radical pair.

In the present study, the crossing of the surfaces comes about through the rearrangement of W377 as well as of side groups T404, T406 and Q401 as shown in Fig. 4. The computed peaked crossing of the radical pair surfaces in Fig. 3 suggests that the respective electron transfer belongs to the regime where the activation energy hardly exceeds the driving force and, therefore, according to Marcus theory39 is feasible. Yet, the energy of the RP2-optimized state is higher than the energy of the RP1-optimized state by Δ12 = 0.26 eV. The RP2-optimized state is, thus, at best an intermediate state of photo-excited cryptochrome that would need to be stabilized through, for instance, deprotonation of W377·+ or further down-hill electron transfer. The formation of a short lived, metastable [FAD·− + W377·+] radical pair is, however, necessary for cryptochrome magnetoreception, as it enables a likely, subsequent W324 → W377·+ electron transfer, leading to formation of the highly separated [FAD·− + W324·+] radical pair. In fact, an uphill electron transfer is not unusual, it occurs frequently in proteins40.

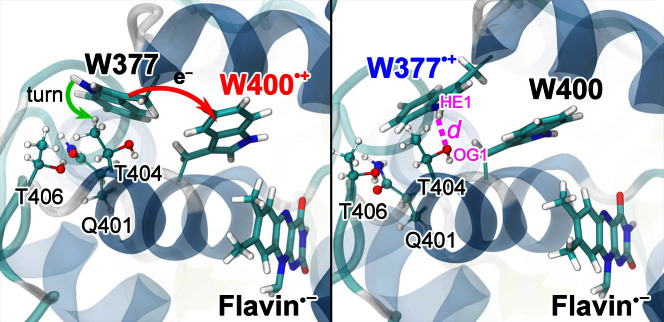
Figure 4. Turn of W377 upon electron transfer.

Figure 4

Open in a new tab

Shown is a rearrangement of the W377 residue in Arabidopsis thaliana cryptochrome, namely a turn of the side group that is coupled to W377 → W400·+ electron transfer. The turn comes about in the quantum chemical geometry optimization calculations depicted in Fig. 3 and involves also the positive W400·+ radical and the polar environment of the W377 residue made up of residues Q401, T404, and T406. A T404OG1 …W377HE1 hydrogen bond (right panel, magenta) is formed upon the turn of W377.

Factors stabilizing the [FAD·− + W377·+] radical pair state

As pointed out, a lowering of the [FAD·− + W377·+] radical pair energy by Δ1 − Δ12 = 1.06 eV in going from the RP1-optimized geometry to the RP2-optimized geometry comes about, as shown in our quantum chemical calculations, due to a rearrangement, illustrated in Fig. 4, of the polar Q401, T404, and T406 amino acids that surround the W377 residue. These three amino acids can create an environment for W377 that is energetically favorable for transfer of an electron. Interestingly, in order to enable the second, i.e., W377 → W400·+ electron transfer, the polar Q401, T404, and T406 amino acids force the W377 residue to turn, once W400 has donated its electron to the flavin. This turn is strongly coupled to the W377 → W400·+ electron transfer and arises nearly instantaneously as the [FAD·− + W377·+] radical pair is formed. Figure 4 illustrates the turn of the W377 residue in cryptochrome, which leads to T404OG1 …W377HE1 hydrogen bond formation.

Rearrangement of the molecular environment around W377 is critical for bringing about the W377 → W400·+ electron transfer as the energy of the [FAD·− + W377·+] radical pair without movement of W377 from its crystal structure arrangement is higher than the energy of the [FAD·− + W400·+] radical pair23. The rearrangement of W377 has a minor impact on the energy of the RP1 state, as demonstrated in Fig. 3; the energy values shown (open circles) were determined for the optimized RP1 state, where W377 was assumed to be in its rearranged configuration, i.e., as in the energy optimized RP2 state. Thus, the polar Q401, T404, and T406 amino acids induce a strong, but mainly local, effect upon formation of the [FAD·− + W377·+] radical pair.

Estimate of W377 → W400·+ electron transfer kinetics

The calculated energy profiles of the radical pair states in cryptochrome, shown in Fig. 3, allow one to estimate the rate constant k for the W377 → W400·+ electron transfer employing Marcus' formula39

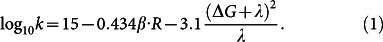graphic file with name srep03845-m1.jpg

Here ΔG (in eV) is the driving force of the electron transfer, λ (in eV) denotes the protein reorganization energy, β (in Å−1) is the so-called electronic coupling factor, and R (in Å) is the contact distance between donor and acceptor molecules (W377 and W400·+). The formula in Eq. (1) holds at temperature T = 300 K, which enters the expression through the coefficient 3.1. The energy diagram in Fig. 3 suggests that W377 → W400·+ electron transfer is energetically uphill with driving force ΔG ≡ Δ12 = 0.26 eV. The value of λ is estimated as the energy difference Δ1 between the [FAD·− + W400·+] and [FAD·− + W377·+] states in Fig. 3, taken at the equilibrium geometry RP1, i.e, we set λ ≡ Δ1 = 1.32 eV. Δ1 represents the reorganization energy required to perturb the chemical structure of the cryptochrome active site and its coordinating residues upon W377 → W400·+ electron transfer. In other words, the reorganization energy describes the energy associated with changes in bond lengths and valence angles that are required for the oxidant and reductant to switch their oxidation states. Upon the W377 → W400·+ electron transfer, the residues D396, Q401, T404, and T406 (see Fig. 2), included in the quantum chemistry calculation, experience structural perturbations as these residues are neighboring W377 and W400. More distant residue neighbors of W400 and W377 are less involved in the W377 → W400·+ electron transfer, as the W377 and W400 residues are screened through the polar residues already included in the quantum chemical calculations. The negligible effect of distant residues on the electronic excitation spectrum has also been demonstrated through a combined QM/MM calculations performed earlier for cryptochrome23 and for the homologous DNA photolyase41.

After W377 rearrangement the contact distance R between W377 and W400·+ is lowered to 2.8 Å, suggesting an electron transfer rate of 108–109 s−1, assuming in Eq. (1) the value β = 1.5–2.3 Å−1, which is a value consistent with earlier studies33. The stated electron transfer rate is comparable with the rate of W400·+ deprotonation and higher than the rate of the [FADH· + W400·] radical-pair recombination23. The rate value 108–109 s−1 suggests that formation of [FAD·− + W377·+] is possible on kinetic grounds. Without stabilizing interactions in the cryptochrome interior, W377 → W400·+ electron transfer would be too slow, as follows from comparison of energies in Fig. 3 with those computed for an in vacuo model of electron transfer chain in cryptochrome in Fig. S1.

Comparison of CASSCF and XMCQDPT-2 energies

It is worth noting the close comparison of CASSCF and XMCQDPT-2 results in Fig. 3, demonstrating that the W377 → W400·+ electron transfer in cryptochrome can be described using either approach since the respective relative energies of the radical pairs are in close agreement with each other. This observation reveals that, with respect to the ground state, the radical pairs in cryptochrome do not have a strong differential dynamic correlation, which is neglected in the CASSCF approach and included in the XMCQDPT2 method.

Tryptophan rearrangement seen also in MD simulation

As pointed out, the turn of W377 as shown in Fig. 4, is driven by W377 → W400·+ electron transfer, denoted in Fig. 1 as electron transfer II, and the corresponding change in geometry comes about as the result of the quantum-chemical geometry optimization. However, significant motion of W377 has been observed also in our classical MD simulations, where atomic partial charges corresponding to the [FAD·− + W400·+] radical pair state were assumed, i.e., for the molecular state of the protein prior to W377 → W400·+ electron transfer. In fact, the MD simulations can complement the quantum chemical calculations and show in how far cryptochrome conformational fluctuations preceding W377 → W400·+ electron transfer can generate energetically favorable conditions for the transfer to actually take place.

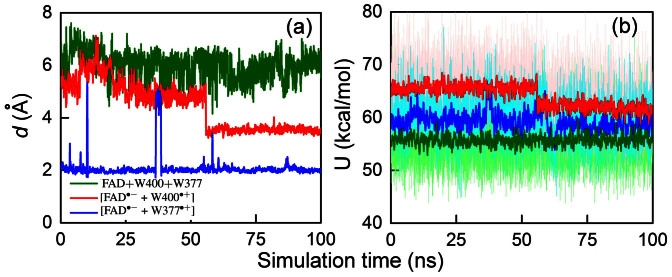
Figure 5a shows the time evolution of the distance d between the OG1 atom of the T404 residue and the HE1 atom of the W377 residue (red line in Fig. 5, see also Fig. 4). In Fig. 5a a step-like decrease of d from ~5.2 Å down to ~3.5 Å is observed. This transition happens after 50 ns of simulation and corresponds to the structural rearrangement shown in Fig. 4. We note that the rearrangement occurs for cryptochrome in the radical pair state [FAD·− + W400·+] and is not seen in the simulation of the resting cryptochrome with the oxidized flavin, i.e., characterized by FAD + W400 + W377 (see Fig. 5a (green line)); in the latter case the hydrogen bond length d is fluctuating around 6 Å throughout the entire simulation. In other words, completion of the primary electron transfer, transfer I, permits fast (namely ns-scale, see below) protein conformational changes that are favorable for fast secondary and tertiary electron transfers II and III.

Figure 5. Spontaneous rearrangement of W377 seen in classical MD simulation.

Figure 5

Open in a new tab

(a) Time evolution of the distance d between the OG1 atom of the T404 residue and the HE1 atom of the W377 residue (see Fig. 4) calculated for cryptochrome with oxidized flavin, i.e., in the FAD + W400 + W377 state (green), cryptochrome in the radical pair state [FAD·− + W400·+] (red), and cryptochrome in the radical pair state [FAD·− + W377·+] (blue). (b) Total energy in Arabidopsis thaliana cryptochrome of the neutral W400…W377 diad (green), the diad with the W400·+ radical (red), and of the diad with the W377·+ radical (blue). The distances in (a) and the corresponding energies in (b) for the three redox states of cryptochrome are measured for the same MD trajectories. The energies calculated for each step of the simulation are shown with the shaded colors, while intense colors show energies averaged over 50 steps.

W377·+ stabilization through hydrogen bond seen in MD simulation

MD simulation of cryptochrome after W377 → W400·+ electron transfer, i.e., in the radical pair state [FAD·− + W377·+], was seen to increase the stability of a key hydrogen bond between the W377 and T404 residues. In fact, seen in Fig. 5a (blue line), the distance T404OG1…W377HE1 between atoms HE1 and OG1 fluctuates around 2.1 Å throughout the entire MD simulation with infrequent short increases up to 5 Å. The distance is very close in value to the value of 2.0 Å found in quantum chemical geometry optimization. Remarkably, the rearrangement of the W377 residue, which results in the quantum chemical optimization, arises in the MD simulation of the radical pair state [FAD·− + W377·+] on a nanosecond time scale.

Molecular dynamics energies of whole and partial tryptophan triad

To characterize the W377 rearrangement further, Fig. 5b shows the total energy of the neutral tryptophan W400…W377 diad (green line), the diad with the W400·+ radical (red line), and the diad with the W377·+ radical (blue line). For the respective three simulations the total energy is defined as

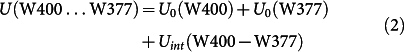graphic file with name srep03845-m2.jpg
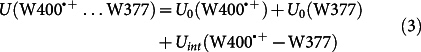graphic file with name srep03845-m3.jpg
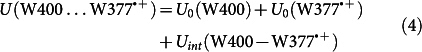graphic file with name srep03845-m4.jpg

where U0(…) is the internal energy of a given residue (W400, W400·+, W377, or W377·+), and Uint(…) denotes the interaction energy between two residues.

Figure 5b illustrates that in the case of the cryptochrome resting state (green line), the total energy of the diad fluctuates around a value of 55.7 kcal/mol. Transferring an electron from W400 to the flavin results in an energy increase of ~10 kcal/mol (red line in Fig. 5b), indicating that the W400·+…W377 diad has become energetically less favorable than in the FAD + W400 + W377 resting state. The rearrangement of W377 at 50 ns aims to improve the interaction between W377 and W400·+, leading to a decrease of the total energy of the diad by ~3.7 kcal/mol. W377 → W400·+ electron transfer leads to a further energy decrease of the W400…W377·+ diad by ~3 kcal/mol as shown in Fig. 5b (blue line). This decrease indicates that reorientation of W377, shown in Fig. 4, allows optimization of interactions in the tryptophan diad and, thus, contributes to the stabilization of the radical pair with the longer distance separation, both before and after electron transfer II.

[FAD·− + W377·+] stabilization through solvent

In order for cryptochrome to function as a magnetoreceptor the magnetic field sensitive radical pair should be stabilized on the timescale on which magnetic field effects are expected to arise. For a geomagnetic field of 0.5 G the latter timescale is 1 μs−1, as estimated in Introduction. The energetic stabilization of the [FAD·− + W377·+] radical pair needed to assure a sufficiently long life time most likely comes about through W377·+ deprotonation to ions bound to cryptochrome's surface. Alternatively, the [FAD·− + W377·+] radical pair could transform into the [FAD·− + W324·+] radical pair, which is also suitable for magnetoreception and could in turn also be stabilized through W324·+ deprotonation. Both deprotonation processes are indicated in Fig. 1.

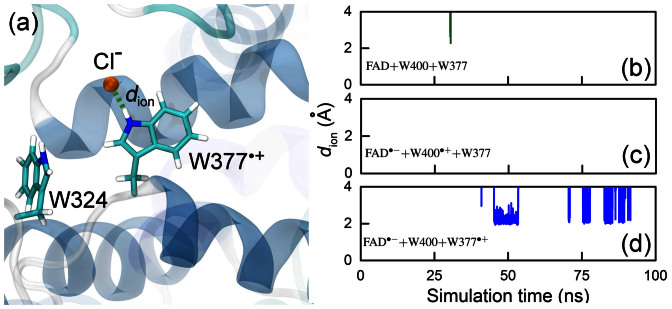
To investigate W377·+ deprotonation, MD simulations of the three different redox states of cryptochrome were performed, namely for FAD + W400 + W377, [FAD·− + W400·+], and [FAD·− + W377·+]. The simulations were performed for cryptochrome in solution with 50 mM of NaCl. In the simulations the distances between W377 and chlorine anions were monitored as shown in Figs. 6b–d. Interestingly, chlorine anions barely interact with the cryptochrome active site in its resting state or in the [FAD·− + W400·+] radical pair state, but were seen to bind spontaneously to the W377·+ radical in the simulation of cryptochrome in the [FAD·− + W377·+] radical pair state. Figure 6a shows a typical MD simulation snapshot, illustrating chlorine anion binding, which leads to stabilization of W377·+. Since W377 and W324 residues are in close proximity to each other, as shown in Fig. 6, the binding of Cl− may facilitate the subsequent W324 → W377·+ electron transfer.

Figure 6. Interaction of W377 radical with environment.

Figure 6

Open in a new tab

(a) Chlorine anion, Cl−, spontaneously binding from the bulk solvent to the positively charged W377·+ residue, as seen in MD simulation. The binding of Cl− is characterized by the hydrogen bond length dion which has been analysed for three redox states of the cryptochrome active site: FAD + W400 + W377 (b), [FAD·− + W400·+] (c), and FAD·− + W377·+] (d).

Conclusions and Discussion

The present study continues earlier investigations of cryptochrome photoactivation. Cryptochrome is thought to host, upon light absorption, a radical pair that allows the protein to sense a very weak magnetic field, endowing migratory birds1,2,3,21 and many other animals42,43 as well as insects44,45 with a magnetic compass sense. A radical pair is formed in cryptochrome through a series of electron transfer reactions involving three strictly conserved tryptophan residues. Ab initio quantum chemistry and all-atom MD simulations revealed now that amino acid residues in cryptochrome bring about, after initial absorption of blue light by its flavin cofactor, sequential electron transfers and steer cryptochrome to the radical pair state [FAD·− + W377·+] or [FAD·− + W324·+] (see Fig. 1), in which radical partners are separated by 12.2 Å or 18.2 Å, respectively, in either case likely far enough to exhibit exchange and dipole-dipole interactions low enough for reception of the weak Earth magnetic field to become feasible33.

Sequential electron transfer through the tryptophan triad is critical for cryptochrome to achieve the large separation between radical partners18,21. In this respect the [FAD·− + W324·+] radical pair is thought to be optimal15,16,25,26,27,28, as it assumes the largest separation distance between flavin and tryptophan radicals, namely about 18.2 Å (see Fig. 1). The [FAD·− + W324·+] radical pair in cryptochrome is formed through the series of W400 → flavin, W377 → W400·+, and W324 → W377·+ electron transfers, requiring prior formation of the W377·+ radical. In this respect, fast formation and energetic stabilization of the [FAD·− + W377·+] radical pair studied here is essential. The formation of the [FAD·− + W377·+] radical pair through W377 → W400·+ electron transfer requires prior formation of the [FAD·− + W400·+] radical pair; it is essential that the latter transfer is faster than deprotonation of W400·+.

The rate of W377 → W400·+ electron transfer is estimated to be about 108–109 s−1, a value which results from Eq. (1) for a choice of typical system parameters; the actual value will differ as the calculated energy profiles of the electronic states in cryptochrome do not account for the complete protein environment, an inclusion of which may actually further shift the relative energies of the [FAD·− + W400·+] and [FAD·− + W377·+] radical pairs. The estimated energy difference between the [FAD·− + W400·+] and [FAD·− + W377·+] radical pairs is, however, fairly small and lies within the accuracy of our model, therefore, suggesting that the energetics of the W377 → W400·+ electron transfer is described here already rather well. According to Marcus theory39,46, the electron transfer rate depends on the electronic coupling factor β, which is governed by the protein environment and is difficult to calculate precisely. It typically ranges from 0.9 Å−1 for covalently bridged redox centers in synthetic systems47 to 3.5 Å−1 in vacuum48,49. The exact value of β for the various electron transfer steps in cryptochrome is still not known.

Once the [FAD·− + W377·+] radical pair has formed, W324 → W377·+ electron transfer becomes feasible, leading to formation of a well-separated [FAD·− + W324·+] radical pair suitable for magnetoreception. The rate of the W324 → W377·+ electron transfer is critical here; if this process is sufficiently slow, binding of negatively charged ions, e.g., of Cl−, can bring about deprotonation of W377·+ before W324 → W377·+ electron transfer takes place. However, it is also possible that a deprotonated state of [FAD·− + W324·+], namely [FAD·− + W324·], is formed from a deprotonated [FAD·− + W377·+], namely [FAD·− + W377·] through coupled electron-proton transfer [FAD·− + W377·] → [FAD·− + W324·].

Upon [FAD·− + W324·+] formation, the W324·+ radical is expected to deprotonate into solution or to be reduced by an external electron donor, leaving cryptochrome in its signaling state6,18,24,31,33. W324 → W377·+ electron transfer accompanied by W324·+ deprotonation needs to be investigated in the future. This investigation is extremely challenging, though, as it requires inclusion of even more electronic degrees of freedom than accomplished in our previous23 and current study.

A description of W324 → W377·+ electron transfer, W377·+, W324·+ deprotonation and possibly coupled electron-proton transfer between W377 and W324 is still called for to complete theoretical modeling of cryptochrome's entire photoactivation reaction. Either of these processes stabilizes the [FAD·− + W377·+] and [FAD·− + W324·+] radical pairs, making them long-lived enough for magnetoreception. The [FAD·− + W377·+] and [FAD·− + W324·+] radical pairs, with the [FAD·− + W324·+] state being more favorable, have a large enough separation between the radical pair partners to exhibit exchange and dipole-dipole interactions that are sufficiently weak for reception of the Earth magnetic field by cryptochrome to be feasible.

Methods

Calculations were performed employing a variety of theoretical methods. Quantum chemical calculations of the cryptochrome active site model were performed with the CASSCF and XMCQDPT-250 methods available in the program Firefly51 which is partially based on the GAMESS (US)52 source code. MD simulations were performed using NAMD 2.953 with the CHARMM22 force field54,55. All images were rendered with VMD56.

Quantum chemistry calculations

The cryptochrome active site, shown in Fig. 2, was constructed from the Arabidopsis thaliana cryptochrome crystal structure (PDB code 1U3C)32. The flavin adenine nucleotide chromophore, modeled by riboflavin, and several amino-acid side chains (S251, R362, W377, D390, D396, Q401, W400, T404, and T406) were included into the quantum chemical description of electron transfer II. The respective moieties are highlighted in Fig. 2. The Cα-atoms of the amino acid side chains in the quantum chemical description were terminated by hydrogens and were fixed to the position that they assumed in cryptochrome taken from a previous study23. The riboflavin was terminated by a CH3- group with the C-atom fixed. The studied structure corresponds to the S2(0) energy minimum established in the earlier publication23 with a rearranged COOH- group of the D396 residue and had been obtained in the course of a 5 ns MD equilibration simulation of cryptochrome with the [FAD·− + W400·+] radical pair.

Geometry optimization of the active site models involved the different redox states of the cryptochrome active site characterized through (i) the oxidized flavin, FAD, with neutral (reduced) W377 and W400 residues, (ii) the radical pair [FAD·− + W400·+] with reduced W377 and (iii) the radical pair [FAD·− + W377·+] with reduced W400. The optimization was performed with the state-averaged CASSCF(4,3) method employing the protocol developed earlier23,57, assuming equal weights for the three states considered; the LUMO of the flavin and the HOMOs of W377 and W400 were included in the CASSCF active space. The CASSCF wave-functions were selected according to the principal-orbital complete active space approach23,57,58,59, where the single-electron excitations, corresponding to the radical pair states [FAD·− + W400·+] and [FAD·− + W377·+], are described by including two molecular orbitals in the CASSCF active space. At the optimized geometries, the excitation spectra were computed using the perturbation theory-based XMCQDPT-2 method50. The electronic wavefunction was expanded in all calculations using the 6-31G* basis set.

Molecular dynamics simulations

We performed MD simulations for three modifications of the Arabidopsis thaliana cryptochrome-1 crystal structure32, which correspond to the states (i), (ii) and (iii) defined above. MD simulations were performed using NAMD 2.953 with the CHARMM22 force field for proteins with CMAP corrections54,55 and the TIP3P water model. In all simulations cryptochrome was neutralized by a 50 mM solution of NaCl. The CHARMM force-field parameters for FAD, FAD·−, and W·+ assumed in this study were developed earlier23 and are available as supporting material in an earlier publication23.

Periodic boundary conditions were adopted in all MD simulations and the particle-mesh Ewald (PME) summation method was employed for evaluating Coulomb forces. The van der Waals (vdW) energy was calculated using a smooth cutoff of 12 Å. The integration time step was 2 fs; temperature was kept at 300 K by applying Langevin forces with a damping coefficient of 1.0 ps−1 to all atoms in the system, except hydrogens. Each simulated system was first energy-minimized, then heated to 300 K. After heating, each simulated system was equilibrated for 2 ns with harmonic restraints applied to the protein under NPT ensemble conditions and using Nosé-Andersen Langevin piston pressure control60, allowing the systems to acquire a constant volume at 1 atm pressure. With restraints turned off, each system was then subjected to 5 ns equilibration under NPT ensemble conditions. Finally, a 100 ns MD simulation was carried out in the NVT ensemble for each simulated system.

Supplementary Material

Supplementary Information

SI Figure 1 and an in vacuo model for studying electron transfer in the isoalloxazine moiety and the tryptophan triad complex

srep03845-s1.pdf (1.6MB, pdf)

Acknowledgments

This work has been supported by National Science Foundation grants NSF MCB-1157615 and NSF PHY0822613 as well as by National Institute of Health grant NIH 9P41GM104601. The authors gladly acknowledge supercomputer time provided by the Texas Advanced Computing Center and the National Center for Supercomputing Applications via XSEDE (grant MCA93S028). K.S. thanks the Alexander von Humboldt Foundation for support and I.S. acknowledges support as a Beckman Fellow. T.D. acknowledges the financial support form the MPG Minerva-program.

Footnotes

Author Contributions I.S. and K.S. have designed the study. I.S. has performed the calculations and analysis with advice from T.D. All authors contributed to the writing of the paper.

References

  1. Ball P. Physics of life: The dawn of quantum biology. Nature 474, 272–274 (2011). [DOI] [PubMed] [Google Scholar]
  2. Wiltschko W. & Wiltschko R. Magnetic compass of European robins. Science 176, 62–64 (1972). [DOI] [PubMed] [Google Scholar]
  3. Hein C. M., Engels S., Kishkinev D. & Mouritsen H. Robins have a magnetic compass in both eyes. Nature 471, E11–E12 (2011). [DOI] [PubMed] [Google Scholar]
  4. Ritz T., Adem S. & Schulten K. A model for photoreceptor-based magnetoreception in birds. Biophys. J. 78, 707–718 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Solov'yov I. A., Mouritsen H. & Schulten K. Acuity of a cryptochrome and visionbased magnetoreception system in birds. Biophys. J. 99, 40–49 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Solov'yov I. A., Schulten K. & Greiner W. Nur dem Schnabel nach? Physik Journal 5, 23–28 (2010). [PMC free article] [PubMed] [Google Scholar]
  7. Solov'yov I. A. & Schulten K. Magnetoreception through cryptochrome may involve superoxide. Biophys. J. 96, 4804–4813 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Liedvogel M. & Mouritsen H. Cryptochromes - a potential magnetoreceptor: what do we know and what do we want to know? J. R. Soc. Interface 7, S147–S162 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Mouritsen H. et al. Cryptochromes and neuronal-activity markers colocalize in the retina of migratory birds during magnetic orientation. Proc. Natl. Acad. Sci. USA 101(39), 14294–14299 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Nieβner C. et al. Avian ultraviolet/violet cones identified as probable magnetoreceptors. PLoS ONE 6, e20091 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Zantke J. et al. Circadian and circalunar clock interactions in a marine annelid. Cell Rep. 5, http://dx.doi.org/10.1016/j.celrep.2013.08.031 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Levy O. et al. Light-responsive cryptochromes from a simple multicellular animal, the coral Acropora millepora. Science 318, 467–470 (2007). [DOI] [PubMed] [Google Scholar]
  13. Fukushiro M. et al. Lunar phase-dependent expression of cryptochrome and a photoperiodic mechanism for lunar phase-recognition in a reef fish, goldlined spinefoot. PLoS ONE 6, e28643 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Sancar A. Structure and function of DNA photolyase and cryptochrome blue-light photoreceptors. Chem. Rev. 103(6), 2203–2237 (2003). [DOI] [PubMed] [Google Scholar]
  15. Giovani B., Byrdin M., Ahmad M. & Brettel K. Light-induced electronic transfer in a cryptochrome blue-light photoreceptor. Nat. Struct. Biol. 10, 489–490 (2003). [DOI] [PubMed] [Google Scholar]
  16. Zeugner A. et al. Light-induced electron transfer in Arabidopsis cryptochrome-1 correlates with in-vivo function. J. Biol. Chem. 280(20), 19437–19440 (2005). [DOI] [PubMed] [Google Scholar]
  17. Bouly J.-P. et al. Cryptochrome blue light photoreceptors are activated through inter-conversion of flavin redox states. J. Biol. Chem. 282, 9383–9391 (2007). [DOI] [PubMed] [Google Scholar]
  18. Rodgers C. Magnetic field effects in chemical systems. Pure Appl. Chem 81, 19–43 (2009). [Google Scholar]
  19. Maeda K. et al. Chemical compass model of avian magnetoreception. Nature 453, 387–390 (2008). [DOI] [PubMed] [Google Scholar]
  20. Henbest K. et al. Radio frequency magnetic field effects on radical recombination reaction: a diagnostic test for the radical pair mechanism. J. Am. Chem. Soc. 126, 8102–8103 (2004). [DOI] [PubMed] [Google Scholar]
  21. Solov'yov I. A., Hore P. J., Ritz T. & Schulten K. Quantum Effects in Biology, chapter Chemical compass for bird navigation. Masoud Mohseni, Yasser Omar, Greg Engel, Martin B. Plenio. in Print Cambridge University Press (2014). [Google Scholar]
  22. O'Dea A. R., Curtis A. F., Green N. J. B., Timmel C. R. & Hore P. Influence of dipolar interactions on radical pair recombination reactions subject to weak magnetic fields. J. Phys. Chem. A 109, 869–973 (2005). [DOI] [PubMed] [Google Scholar]
  23. Solov'yov I. A., Domratcheva T., Moughal Shahi A. R. & Schulten K. Decrypting cryptochrome: Revealing the molecular identity of the photoactivation reaction. J. Am. Chem. Soc. 134, 18046–18052 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Solov'yov I. A. & Schulten K. Reaction kinetics and mechanism of magnetic field effects in cryptochrome. J. Phys. Chem. B 116, 1089–1099 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kottke T., Batschauer A., Ahmad M. & Heberle J. Blue-light-induced changes in Arabidopsis cryptochrome 1 probed by FTIR difference spectroscopy. Biochem. 45, 2472–2479 (2006). [DOI] [PubMed] [Google Scholar]
  26. Chaves I. et al. The cryptochromes: Blue light photoreceptors in plants and animals. Annu. Rev. Plant Biol. 62, 335–364 (2011). [DOI] [PubMed] [Google Scholar]
  27. Biskup T. et al. Direct observation of a photoinduced radical pair in a cryptochrome blue-light photoreceptor. Angew. Chem. Int. Ed. Engl. 48, 404–407 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Maeda K. et al. Magnetically sensitive light-induced reactions in cryptochrome are consistent with its proposed role as a magnetoreceptor. Proc. Natl. Acad. Sci. USA 109, 4774–4779 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Biskup T. et al. Variable electron transfer pathways in an amphibian cryptochrome: tryptophan versus tyrosine-based radical pairs. J. Biol. Chem. 288, 9249–9260 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Immeln D., Weigel A., Kottke T. & Lustres J. L. P. Primary events in the blue light sensor plant cryptochrome: Intraprotein electron and proton transfer revealed by femtosecond spectroscopy. J. Am. Chem. Soc. 134(30), 12536–12546 (2012). [DOI] [PubMed] [Google Scholar]
  31. Biskup T. et al. Unexpected electron transfer in cryptochrome identified by time-resolved EPR spectroscopy. Angew. Chem. Int. Ed. Engl. 50, 12647–12651 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Brautigam C. A. et al. Structure of the photolyase-like domain of cryptochrome 1 from Arabidopsis thaliana. Proc. Natl. Acad. Sci. USA 101, 12142–12147 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Solov'yov I. A., Chandler D. E. & Schulten K. Magnetic field effects in arabidopsis thaliana cryptochrome-1. Biophys. J. 92, 2711–2726 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zoltowski B. et al. Structure of full-length drosophila cryptochrome. Nature 480, 396–399 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Czarna A. et al. Structures of drosophila cryptochrome and mouse cryptochrome1 provide insight into circadian function. Cell 153, 13941405 (2013). [DOI] [PubMed] [Google Scholar]
  36. Langenbacher T., Immeln D., Dick B. & Kottke T. Microsecond light-induced proton transfer to flavin in the blue light sensor plant cryptochrome. J. Am. Chem. Soc. 131, 14274–14280 (2009). [DOI] [PubMed] [Google Scholar]
  37. Henbest K. B. et al. Magnetic-field effect on the photoactivation reaction of Escherichia coli DNA photolyase. Proc. Natl. Acad. Sci. USA 105, 14395–14399 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Olsson M. H., Sondergard C. R., Rostkowski M. & Jensen J. H. PROPKA3: consistent treatment of internal and surface residues in empirical pKa predictions. J. Chem. Theory Comput. 7, 525–537 (2011). [DOI] [PubMed] [Google Scholar]
  39. Marcus R. & Sutin N. Electron transfer in chemistry and biology. Biochim. Biophys. Acta 811, 265–322 (1985). [Google Scholar]
  40. Ransaca S., Pariseya N. & Mazat J.-P. The loneliness of the electrons in the bc1 complex. Biochim. Biophys. Acta 1777, 1053–1059 (2008). [DOI] [PubMed] [Google Scholar]
  41. Shahi A. R. M. & Domratcheva T. Challenges in computing electron-transfer energies of DNA repair using hybrid QM/MM models. J. Chem. Theory Comput. 9, 4644–4652 (2013). [DOI] [PubMed] [Google Scholar]
  42. Lohmann J. & Johnsen S. The neurobiology of magnetoreception in vertebrate animals. Trends Neurosci. 23, 153–159 (2000). [DOI] [PubMed] [Google Scholar]
  43. Johnsen S. & Lohmann K. J. The physics and neurobiology of magnetoreception. Neuroscience 6, 703–712 (2005). [DOI] [PubMed] [Google Scholar]
  44. Gegear R. J., Casselman A., Waddell S. & Reppert S. M. Cryptochrome mediates light-dependent magnetosensitivity in drosophila. Nature 454, 1014–1018 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Foley L. E., Gegear R. J. & Reppert S. M. Human cryptochrome exhibits light-dependent magnetosensitivity. Nature 10.1038/ncomms1364 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Solov'yov I. A., Chang P.-Y. & Schulten K. Vibrationally assisted electron transfer mechanism of olfaction: Myth or reality? Phys. Chem. Chem. Phys. 14, 13861–13871 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Smalley J. et al. The kinetics of electron-transfer through ferrocene-terminated alkenethiol monolayers on gold. J. Phys. Chem. 99, 13141–13149 (1995). [Google Scholar]
  48. Moser C., Keske J., Warncke K., Farid R. & Dutton P. Nature of biological electron transfer. Nature 355, 796–802 (1992). [DOI] [PubMed] [Google Scholar]
  49. Bertran D., Onuchic J., Winkler J. & Gray H. Electron-tunneling pathways in proteins. Science 258, 1740–1741 (1992). [DOI] [PubMed] [Google Scholar]
  50. Granovsky A. A. Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory. J. Chem. Phys. 134, 214113–(1–14) (2011). [DOI] [PubMed] [Google Scholar]
  51. Granovsky A. A. Firefly version 8.0.0. http://classic.chem.msu.su/gran/firefly/index.html.
  52. Schmidt M., Baldridge K., Boatz J., Elbert S., Gordon M., Jensen J., Koseki S., Matsunaga N., Nguyen K., Su S., Windus T., Dupuis M. & Montgomery J. J. Comp. Chem. 14, 1347–1363 (1993). [Google Scholar]
  53. Phillips J. C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R. D., Kale L. & Schulten K. Scalable molecular dynamics with NAMD. J. Comp. Chem. 26, 1781–1802 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. MacKerell, Jr et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 102, 3586–3616 (1998). [DOI] [PubMed] [Google Scholar]
  55. MacKerell A. D. Jr, Feig M. & Brooks C. L. III Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comp. Chem. 25, 1400–1415 (2004). [DOI] [PubMed] [Google Scholar]
  56. Humphrey W., Dalke A. & Schulten K. VMD – visual molecular dynamics. J. Molec. Graphics 14, 33–38 (1996). [DOI] [PubMed] [Google Scholar]
  57. Udvarhelyi A. & Domratcheva T. Photoreaction in BLUF receptors: Proton-coupled electron transfer in the Flavin-Gln-Tyr system. Photochem. & Photobiol. 87, 554–563 (2011). [DOI] [PubMed] [Google Scholar]
  58. Domratcheva T. Neutral histidine and photoinduced electron transfer in DNA photolyases. J. Am. Chem. Soc. 133, 18172–18182 (2011). [DOI] [PubMed] [Google Scholar]
  59. Domratcheva T., Fedorov R. & Schlichting I. Analysis of the primary photocycle reactions occurring in the light, oxygen, and voltage blue-light receptor by multiconfigurational quantum-chemical methods. J. Chem. Theory Comput. 2, 1565–1574 (2006). [DOI] [PubMed] [Google Scholar]
  60. Feller S. E., Zhang Y. H., Pastor R. W. & Brooks B. R. Constant pressure molecular dynamics simulation – the Langevin piston method. J. Chem. Phys. 103(11), 4613–4621 (1995). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

SI Figure 1 and an in vacuo model for studying electron transfer in the isoalloxazine moiety and the tryptophan triad complex

srep03845-s1.pdf (1.6MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES