Channelrhodopsin2 Current During the Action Potential: “Optical AP Clamp” and Approximation

Abstract

The most widely used optogenetic tool, Channelrhodopsin2 (ChR2), is both light- and voltage-sensitive. A light-triggered action potential or light-driven perturbations of ongoing electrical activity provide instant voltage feedback, shaping ChR2 current. Therefore, depending on the cell type and the light pulse duration, the typically reported voltage-clamp-measured ChR2 current traces are often not a good surrogate for the ChR2 current during optically-triggered action potentials. We discuss two experimental methods to reveal ChR2 current during an action potential: an “optical AP clamp” and its approximation employing measured current-voltage curve for ChR2. The methods are applicable to voltage- and light-sensitive ion currents operating in excitable cells, e.g. cardiomyocytes or neurons.

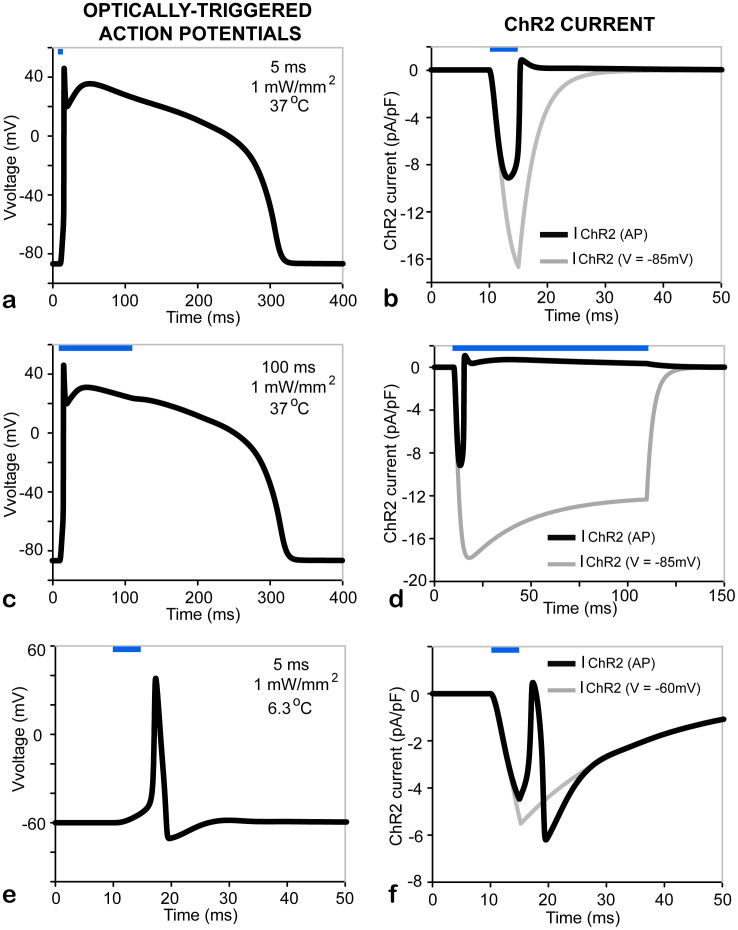
This brief note concerns the underlying opsin currents during light-triggered action potentials in excitable cells and tissues in optogenetics experiments. The most widely used excitatory opsin, Channelrhodopsin2 (ChR2), is both light- and voltage-sensitive¹,². This implies that during an optically-triggered action potential, the ChR2 current will experience instant feedback from the ensuing change in membrane voltage. Many optogenetics studies²,³,⁴,⁵,⁶ show side-by-side independent records of the light-triggered ChR2 current (in voltage-clamp mode using a constant voltage setting), I_ChR2(Vclamp), and the light-triggered change in membrane voltage (action potential, AP) obtained in current-clamp mode. Occasionally, the AP record and I_ChR2(Vclamp) are shown in a paired manner⁵,⁶. However, the actual ChR2 current during the displayed action potential, I_ChR2(AP), is never measured nor reported in the literature. We stress here that I_ChR2(Vclamp) and I_ChR2(AP) can be very different, especially for longer light pulses and/or longer action potentials, as seen in cardiomyocytes, for example. This is illustrated in the simulated examples in Figure 1, using a computer model of ChR2(H134R)⁷ inserted in a human ventricular cardiomyocyte model⁸ and in a modified Hodgkin-Huxley model of squid giant axon⁹. The action potential provides instant feedback and shapes the ChR2 current through voltage according to our model⁷,¹⁰ and our experimental data for I_ChR2(AP) in cardiomyocytes⁷.

Figure 1. ChR2 current during a light-triggered action potential is different from the ChR2 current in response to a constant voltage clamp using the same light pulse parameters (here 470 nm, 1 mW/mm²).

(a–b). The response of a ventricular cardiomyocyte to a 5 ms light pulse. (c–d). The response of a ventricular cardiomyocyte to a 100 ms light pulse. (e–f). The response of a squid giant axon to a 5 ms light pulse. Panels a, c and e show the lighttriggered APs, while (b), (d) and (f) show I_ChR2(AP). For comparison, I_{IChR2(Vclamp)} in response to identical light pulses is overlaid (grey) in (b), (d) and (f) (Vclamp5285 mV or 260 mV). Cardiomyocyte simulations (a–d) were at 37°C, while the squid giant axon model (e–f) was run at 6.3°C. Blue bars indicate timing of light pulse application.

The classic way to experimentally extract the contribution of a voltage-dependent current during an action potential is to apply an action potential clamp (APclamp)¹¹,¹² in conjunction with specific pharmacological blocking agents. Typically, a pre-recorded action potential (obtained under current-clamp regime, I_total = 0) is used as voltage input to clamp the cell and two records are obtained – in the absence (“no drug”) and in the presence (“drug”) of a selective pharmacological blocker. The difference in total current between the two conditions is interpreted as the current of interest.

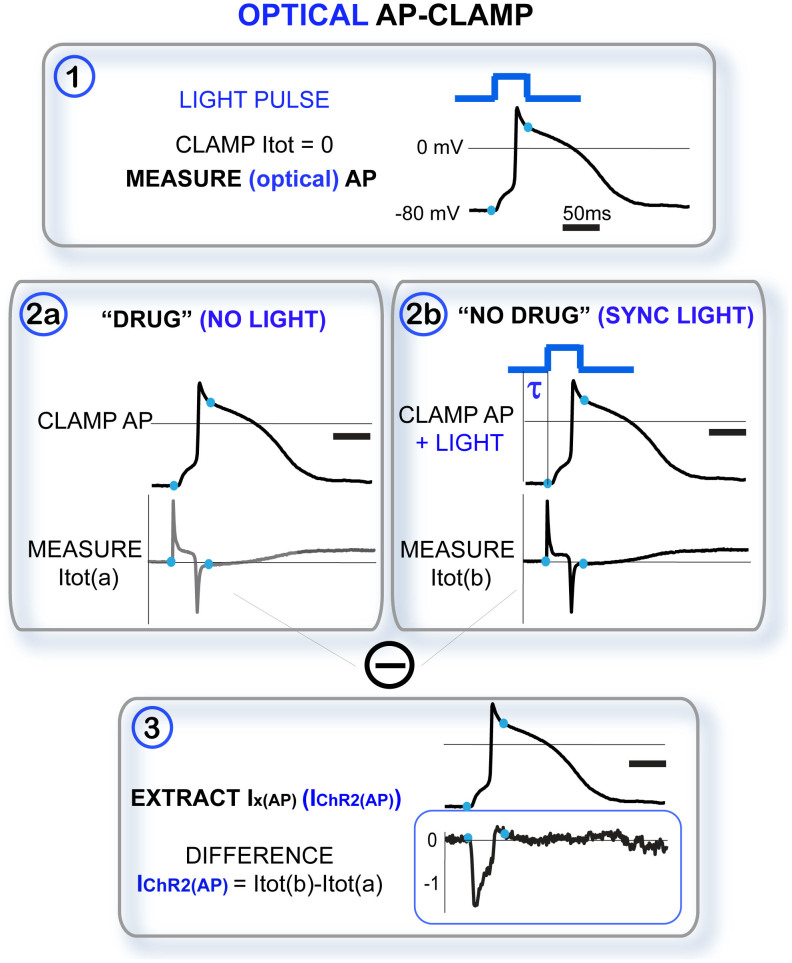
Light-sensitive ion channels add a twist to this approach. The “drug” condition can be easily captured by a record of total current in the dark, which yields a very selective blocking of the opsin contribution. However, the “no drug” record of a light- and voltage-sensitive ion channel is non-trivial. While the action of pharmacological blockers is slow (compared to the action potential kinetics) and steady-state records are appropriate, the response to a light pulse(s) is instantaneous and it elicits an important fast transient component in ChR2 that needs to be preserved in the current record. Hence, constant “light on” condition will not be equivalent to “no drug”. Recently, we presented a modified version of the APclamp that uses precisely synchronized optical pulse(s) to extract I_ChR2(AP) during optically-triggered APs⁷ – an “optical APclamp” method explained in Figure 2.

Figure 2. The “optical APclamp”: Experimental protocol to extract opsin current during an optically-triggered action potential.

The schematic illustrates the three steps in a classical APclamp (in black) and the added elements to achieve an “optical APclamp” (in blue). Importantly, in step 2b, identical light pulse(s) to the one(s) used in step 1 must be delivered synchronously (lag time τ) with the action potential clamp. The traces are used for illustration only but they are actual recordings from ChR2-expressing adult guinea pig cardiomyocytes, as shown in⁷.

Additionally, here we propose an alternative scaling method for extracting I_ChR2(AP) that corrects the measured I_ChR2(Vclamp) using an empirical current-voltage (I–V) curve, fed by voltage values from the measured optically-triggered APs. The idea is inspired by the relatively mild voltage dependence of ChR2 kinetics⁷ and therefore ability to separate⁷,¹³,¹⁴,¹⁵ its light-dependence (L) and its voltage-dependence (a measured I–V curve). We begin with a general expression for I_ChR2 as a function of irradiance E[t], transmembrane voltage V[t], and time t:

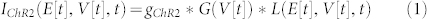where G(V[t]) is the voltage-dependent channel conductance (a nonlinear inward rectifying function for ChR2), L(E[t],V[t],t) is the irradiance- and voltage-dependent kinetic response of the channel to light, and g_ChR2 is a scaling factor for expression levels.

Then, for the ChR2 current during time-invariant clamp voltage, V_clamp, we obtain:

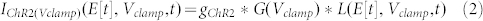The mild voltage-dependence of the ChR2 kinetic parameters⁷ permits the approximation of the kinetic response (in L) during dynamically changing voltage (e.g. action potentials) with the response during a voltage clamp, if in both cases an identical optical stimulation protocol is used, i.e. identical light pulse sequence is applied with the same irradiance, pulse morphology and duration, E[t]:

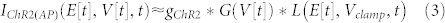Therefore, from (2) and (3), a scaler function can be derived, which is purely voltage-dependent and independent of the light response (L) of the tissue:

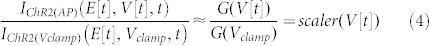In sum, any opsin current, I_ChR2(AP), during optically-triggered dynamic voltage response, e.g. action potential(s), can be recovered using:

• a known I–V curve, G(V[t])

• measured light-triggered voltage response, V[t], and

• measured I_ChR2(Vclamp)[t] under voltage-clamp and identical light-pulsing protocol E[t], used to obtain V[t]; I_ChR2(Vclamp)[t] intrinsically carries information about the expression levels and light-dependent kinetics

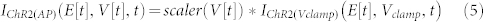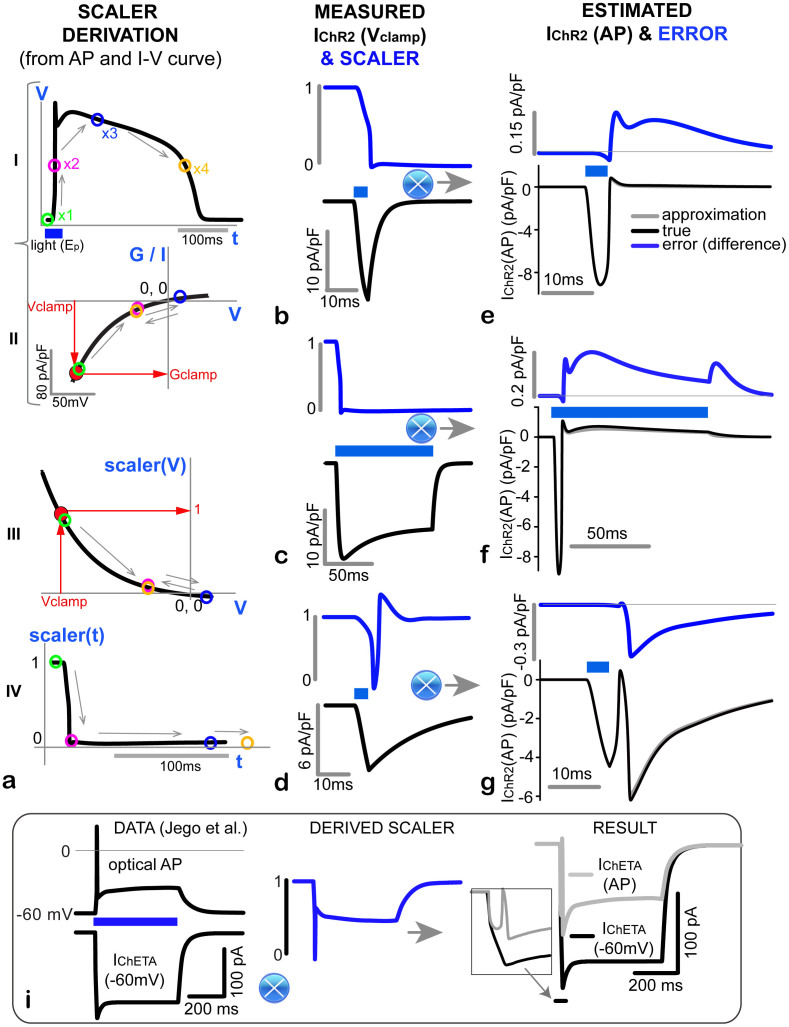
Step-by-step graphical illustration of this scaling method is shown in Figure 3, including derivation of the scaler function and application to model data from Figure 1. Furthermore, in Figure 3i, we apply this method to an example of published neuroscience data⁶, using ChETA (a ChR2 mutant¹⁶,¹⁷). We computationally recover I_ChETA(AP) in ChETA-expressing melanin-concentrating hormone (MCH) neurons, based on the published AP and I_{ChETA(Vclamp)} records, and assuming similar rectification function as for ChR2(H134R), as implied in¹⁶,¹⁷. The predicted current I_ChETA(AP) is substantially smaller and with different (biphasic) morphology than the I_{ChETA(Vclamp)}; this may explain the lack of secondary spikes compared to equivalent electrical current injection⁶.

Figure 3. Approximation to an “optical APclamp”: Scaling I_ChR2(Vclamp) by an experimental ChR2 I-V curve to obtain I_ChR2(AP).

(a). Derivation of a scaler, using an example light-triggered ventricular cell AP (a-I) and an empirical ChR2 I-V curve (a-II, here, the fit to the I-V curve had the form G(V) = (10.64 - 14.64*exp(-V/42.77))⁷). The position of four color-coded points (x1 to x4) from the AP is mapped onto the I–V curve and then onto the derived scaler as a function of voltage (a-III) and as a function of time (a-IV). Note the different time scales in a-I and a-IV. (b-g). Using the time-dependent scaler (middle column, (b–d), blue), derived for each of the three simulated cases from Figure 1, here we multiply the typically measured and reported I_ChR2(Vclamp) (middle column, (b–d), black) to obtain an excellent approximation of the I_ChR2(AP) (right column, (e–g)). Superimposed in (e–g) are the “true” (black) and approximated/scaled I_ChR2(AP) (grey); the small error (difference between the two currents) is enhanced in blue for each case. The bottom panel (i) illustrates the application of the method to published data on ChETA-MCH neurons⁶; inset on the right shows the first 50 ms of measured I_{ChETA(Vclamp)} and estimated I_ChETA(AP).

Errors in the proposed approximation approach come from: 1) uncertainties in the ChR2 I–V curve for the particular cell; and 2) from ignored voltage-dependence of the kinetic parameters of the light response (L), i.e. assumption (3). Errors of the first kind may occur primarily if the opsin (I–V) response varies significantly depending on the cell environment and the I–V curve was obtained in a different cell type than the one in which voltage is measured; importantly however, other conditions of the experiment, e.g. irradiance and pulse protocols, are captured independently of the I–V curve, through I_ChR2(Vclamp) in Eqn. (5). Errors of the second type are relatively small for ChR2/H134R as displayed in Figure 3. This method is applicable to any opsin with a well-characterized I–V curve, and the accuracy of approximating I_ChR2(AP) is inversely related to the level of voltage-dependence in the opsin's kinetics (in the L-function). In ChR2 mutants with relatively voltage-independent kinetics such as ChETA (E123T)¹⁶ and ET/TC (E123T/T159C)¹⁷, the method will be highly accurate, with even smaller approximation errors when compared with H134R. The use of this technique with such opsins renders the approximation in Eqn. (3) very accurate, as the kinetics of ChETA and ET/TC are completely recovered by measuring the current under voltage clamp (through I_ChR2(Vclamp)), and the scaler fully corrects for the rectification-induced nonlinearlity in voltage. Furthermore, with knowledge of an opsin's selective ionic permeability, this method provides an effective tool for determining an opsin's transient ionic flux during ongoing electrical activity and therefore its contribution to intracellular ionic concentrations. This is particularly important for those with greater permeability to Ca²⁺ such as CatCh (L123C)¹⁸ or when trying to predict an opsin's effect on intracellular pH¹⁹. Similar to H134R discussed here, ChETA, ET/TC, and CatCh all retain the strong inward rectification displayed by wild-type ChR2¹⁶,¹⁷,¹⁸, thus it is similarly necessary to perform either this approximation or the aforementioned optical AP clamp to recover the true ChR2 current (I_ChR2(AP)) during dynamically changing voltage.

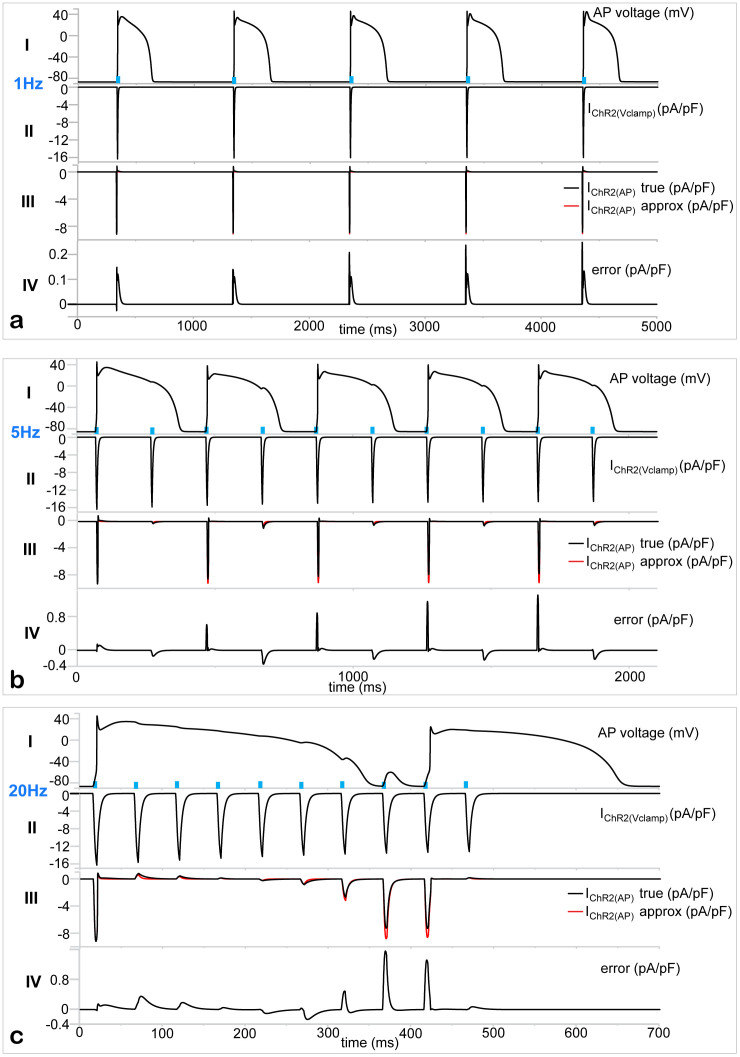
We expect the accuracy of the approximation method to be somewhat reduced for more complex light-pulsing protocols when recovery from inactivation is engaged, as the latter depends on voltage⁷. To test the performance of the proposed approach for multi-pulse protocols, we analyzed optical pacing of cardiomyocytes at different frequencies: 1 Hz, 5 Hz and 20 Hz in silico (Figures 4 and 5). Human ventricular cardiomyocytes show full capture, i.e. 1:1 response, during 1 Hz optical pacing at 5 ms pulses, 1 mW/mm² (Figure 4a). Same pulse parameters induce 2:1 block at 5 Hz pacing, i.e. every other pulse triggers an action potential (Figure 4b), and result in a higher-level block (8:1) at a very fast, unphysiological pacing rate of 20 Hz (Figure 4c). In all cases, the voltage-clamp recorded current, I_ChR2(Vclamp), shown in rows II of all panels, is a poor surrogate for the “true” I_ChR2(AP), shown as a black trace in rows III, Figure 4a–c. In contrast, our approximation/scaling approach fully captures the morphology of the true I_ChR2(AP) (red vs. black trace in rows III), and tracks it quantitatively even at high pacing rates, with instantaneous maximum errors mostly less than 1 pA/pF (rows IV in Figure 4a–c).

Figure 4. Optical pacing of cardiomyocytes at various frequencies and the underlying I_ChR2(AP) – example traces and approximation errors.

Human ventricular cardiomyocytes were paced by 5 ms, 1 mW/mm² light pulses (blue), delivered at 1 Hz (panel a, 5 pulses shown), 5 Hz (panel b, 10 pulses shown) or 20 Hz (panel c, 10 pulses shown). Note the different time scales. In panels (a–c), row I shows the triggered voltage changes (action potentials); row II shows the I_ChR2(Vclamp) in response to the light pulses, if the voltage is clamped at 285 mV; row III shows overlaid, highly similar true I_ChR2(AP) (black) and approximated I_ChR2(AP) (red) by the proposed method in Figure 3; and row IV shows the error (difference) between the overlaid black and red traces in row III.

Figure 5.

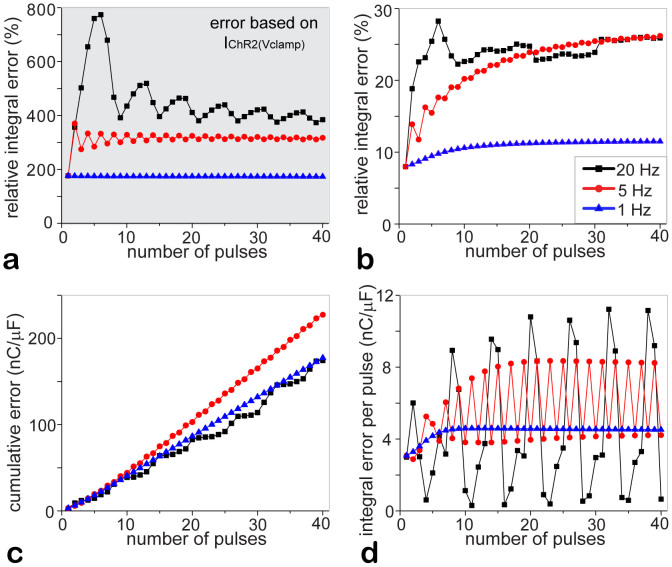
Summary of error estimates as function of stimulation frequency and pulse number: (a) (shaded). Relative time-integrated error (as % of the time-integrated I_ChR2(AP), cumulative over the indicated number of light pulses/beats) if I_ChR2(Vclamp) is used to estimate the true I_ChR2(AP) (i.e. error between rows II and III in Figure 4a–c). (b–d). Errors if the new (I–V curve-based) approximation is used to estimate the true I_ChR2(AP) (compare the overlaid traces in rows III of Figure 4a–c, as well as the resultant difference errors displayed in rows IV of Figure 4a–c). (b). Relative time-integrated error (in % of the time-integrated I_ChR2(AP)); (c). Cumulative absolute time-integrated error (in units of charge nC/μF); (d). Absolute time-integrated error per pacing period (in nC/μF). Light pulses were 5 ms at 1 mW/mm², delivered at 1 Hz (blue), 5 Hz (red) or 20 Hz (black), as indicated by example traces in Figure 4. Note that 40 pulses correspond to 40 s, 8 s and 2 s time interval for the three pacing frequencies.

The contrast in performance between the I_ChR2(Vclamp) and our approximation of the true I_ChR2(AP) is further quantified in Figure 5a vs. 5b. The relative time-integrated errors (δ(n) as per Eqn. (7)) for the former are unacceptably high even at 1 Hz pacing, and are more than 20 times higher than those seen with the proposed approximation.

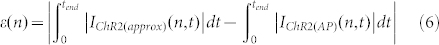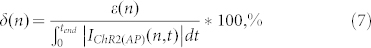where n is the number of delivered optical pulses, t_end is the time when the (n-th) pulse period ends, I_ChR2(approx) represents either I_ChR2(Vclamp) (Figure 5a) or the approximated/scaled I_ChR2(AP) (Figure 5b), and ε(n) is the cumulative time-integrated absolute error (in units of charge, nC/μF) for n pulses (Figure 5c).

We also show the time-integrated absolute error per pulse (also in nC/μF), ε_pulse(n), in Figure 5d:

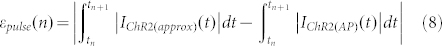where t_n is the onset of the n-th pulse and t_{n + 1} is the start time of the following pulse.

With lack of full capture at higher pacing rates, i.e. 2:1 response at 5 Hz and 8:1 response at 20 Hz, the errors per pulse vary accordingly (Figure 5d), changing with the membrane potential and the level of ChR2 current engagement. Therefore, for a given number of pulses, the cumulative errors for very high pacing rates (20 Hz) can be lower than the errors seen for 1 Hz pacing, for example (Figure 5c). Nevertheless, in all cases, the approximation captures the morphology of I_ChR2(AP) with small instantaneous errors (Figure 4).

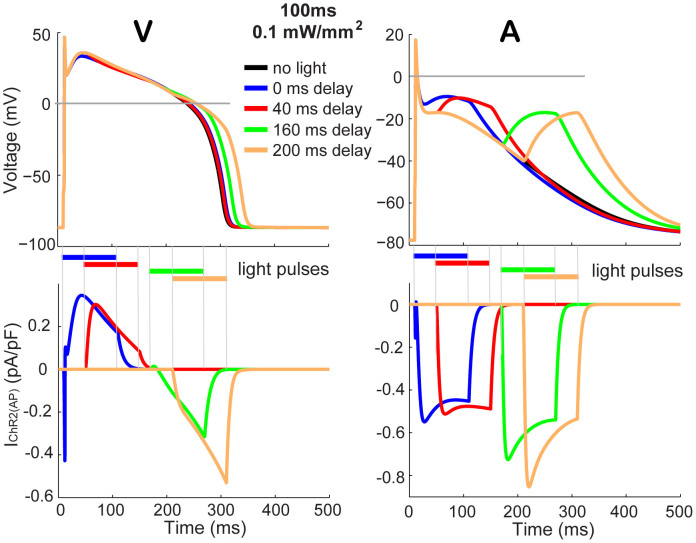
When a light pulse triggers ChR2 response during an ongoing action potential, the contribution of this opsin-provided current strongly depends on the respective action potential shape, and hence on the voltage feedback provided by the cell. For example, in a ventricular cardiomyocyte, it is very difficult to alter an ongoing action potential if light stimulation is applied during the earlier AP phases, Figure 6, left, due to the strong inward rectification of ChR2 at the depolarized voltage levels maintained during the ventricular AP plateau. Furthermore, because of the rapid nonlinear voltage changes in the later repolarization AP phases, the observed I_ChR2(AP) is very different in shape compared to I_ChR2(Vclamp). At the same time, in an atrial cell AP, which operates extensively at voltages below 0mV and has a more gradual repolarization, a light pulse delivered during an ongoing AP produces higher magnitude inward I_ChR2(AP) and has a better chance at influencing the electrical state of the cell, i.e. altering the action potential shape (Figure 6, right). The two approaches outlined here in Figures 2 and 3 are applicable in uncovering the underlying opsin currents (Figure 6, bottom row) during such optical perturbations of ongoing electrical activity in different cell types. Such information can be useful in designing optical cardioversion strategies²⁰,²¹ or feedback strategies for suppression of ongoing pathological neural excitations²².

Figure 6. Light pulses, applied during an ongoing action potential, trigger distinct I_ChR2(AP) in different cardiac cell types due to instant voltage feedback.

Electrically-triggered action potentials in human ventricular cells⁸ (V, left) and in atrial cells²³ (A, right), and the effect of a light pulse (470 nm, 100 ms, 0.1 mW/mm²), applied at variable delay with respect to the electrical stimulus (current injection was 0.5 ms. 50 pA/pF). The respective underlying I_ChR2(AP) currents are shown for V and A on the bottom. Timing of the light pulses is indicated by color-coded horizontal bars.

In summary, using the “optical APclamp” or its proposed simple approximation, one can reveal the true nature of the opsin contribution during light-triggered action potentials or during optical perturbation of ongoing electrical activity in different cells and appreciate the feedback exerted on the opsin current during membrane voltage changes. These aspects of the ChR2 action are important in better understanding its function in mammalian excitable tissue, including brain and heart, and evaluating differences between optical and electrical stimulation. The approaches discussed here are potentially applicable to other opsins with separable light- and voltage dependencies; they can be used to rationally improve and optimize the performance of engineered opsins for operation in specific cells and tissues.