Abstract
Electron-impact total ionization cross sections for the CH radical and C2H2 (acetylene) have been calculated using the Binary-Encounter-Bethe (BEB) model. The BEB model combines the Mott cross section and the asymptotic form of the Bethe theory, and has been shown to generate reliable ionization cross sections for a large variety of molecules. The BEB cross sections for CH and C2H2 are in good agreement with the available experimental data from ionization thresholds to hundreds of eV in incident energies.
Keywords: acetylene, hydrocarbon, radical, total ionization cross section
1. Introduction
The Binary-Encounter-Bethe (BEB) model [1] has been successfully used to calculate the total ionization cross sections of a wide range of molecules [2–4] including H2, O3, and SF6. The BEB model combines a modified form of the Mott cross section with the asymptotic form of the Bethe theory (i.e., high incident energy) for electron-impact ionization of an atom.
These two theories are combined in such a way that not only the ionization cross section has the proper asymptotic form but so does the stopping cross section, which is the product of the cross section and the energy transfer from the incident particle to the target [1]. Although the theoretical model in its differential form requires the knowledge of continuum dipole oscillator strengths df/dE, we assumed a simple form for df/dE to facilitate the integration over the ejected electron energy. The resulting expression for the ionization cross section per molecular orbital, which we refer to as the BEB model, has a remarkably simple form [1]:
| (1) |
where t = T/B, u = U/B, S = 4πa02NR2/B2, a0 is the Bohr radius (= 0.5292 Å), R is the rydberg energy (= 13.6057 eV), T is the incident electron energy, and N, B, and U are the electron occupation number, the binding energy, and the average kinetic energy of the orbital, respectively.
In this article, we compare the BEB cross sections for the CH radical in its ground state 2P and C2H2 also in the ground state 1Ʃg+ with available experimental data. Both molecules are used in modeling the behavior of edge plasmas in the divertor region of a tokamak [5].
2. Results and Discussion
The molecular constants B and U were calculated using the 6-311+G(d,p) basis set in the GAMESS code [6]. Although one can in principle use theoretical values for all B’s, theoretical values for the lowest ionization potential (IP) are usually inaccurate. Therefore, we used experimental values [7] only for the lowest IP to match the observed thresholds. Theoretical results and comparisons to experimental data presented below are also available on a NIST web page for electron-impact ionization cross sections at:
http://physics.nist.gov/PhysRefData/Ionization/Xsection.html
Note that the above address is case sensitive.
2.1 CH (2II)
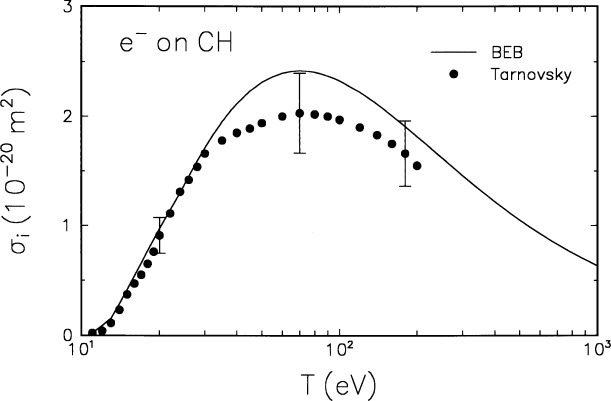
The molecular orbital constants B, U, and N for the CH radical are listed in Table 1, and the BEB model is compared in Fig. 1 to the only available experimental data by Tarnovsky et al. [8]. Although the experiment was performed using deuterium instead of hydrogen, i.e., with CD, our theory is insensitive to the use of the isotope. As Tarnovsky et al. [8] have pointed out, their experiment did not detect fast deuterons produced, which may partly account for the difference between theory and experiment near the peak. Otherwise, theory and experiment are in excellent agreement, particularly for T < 30 eV. This is the region of T for which most other theories have difficulty in reproducing observed cross sections. The BEB model produces reliable cross sections for many molecules at low T (≈ 50 eV or less) [2–4].
Table 1.
Molecular orbital (MO) constants for CH (2II): B = binding energy, U = kinetic energy, N = occupation number. The B value marked by * is an experimental value
| MO | B (eV) | U (eV) | N |
|---|---|---|---|
| 1σ | 309.23 | 436.80 | 2 |
| 2σ | 23.48 | 36.40 | 2 |
| 3σ | 13.03 | 32.96 | 2 |
| 1π | 10.64* | 26.19 | 1 |
Fig. 1.
Comparison of the BEB cross section to experiment for CH. Solid curve, BEB cross section; circles, experimental data by Tarnovsky et al. (for CD) [8]. The ordinate is the ionization cross section, and the abscissa is the incident energy.
2.2 Acetylene, C2H2 (1Ʃg+)
The molecular orbital constants for acetylene are listed in Table 2, and the BEB model is compared in Fig. 2 to the available experimental data [9–11]. The experimental data by Zheng and Srivastava [9] and those by Tate and Smith [10] agree well with each other but they are approximately 15 % higher than the theory at the peak. On the other hand, the data by Gaudin and Hagemann [11] are in excellent agreement with the theory from T = 100 eV to 2 keV. Since the BEB model provides a convenient analytic form for the ionization cross section for the entire range of T shown in Fig. 2, and the data by Tate and Smith agree well with the theory for T < 30 eV, we are confident that the BEB cross sections will be appropriate and useful for plasma modeling applications.
Table 2.
Molecular orbital (MO) constants for C2H2 (1Ʃg+): B = binding energy, U = kinetic energy, N = occupation number. The B value marked by * is an experimental value
| MO | B (eV) | U (eV) | N |
|---|---|---|---|
| 1σg | 305.62 | 435.15 | 2 |
| 1σu | 305.50 | 436.31 | 2 |
| 2σg | 28.18 | 49.60 | 2 |
| 2σu | 20.80 | 32.79 | 2 |
| 3σg | 18.55 | 33.64 | 2 |
| 1πu | 11.4* | 28.99 | 4 |
Fig. 2.
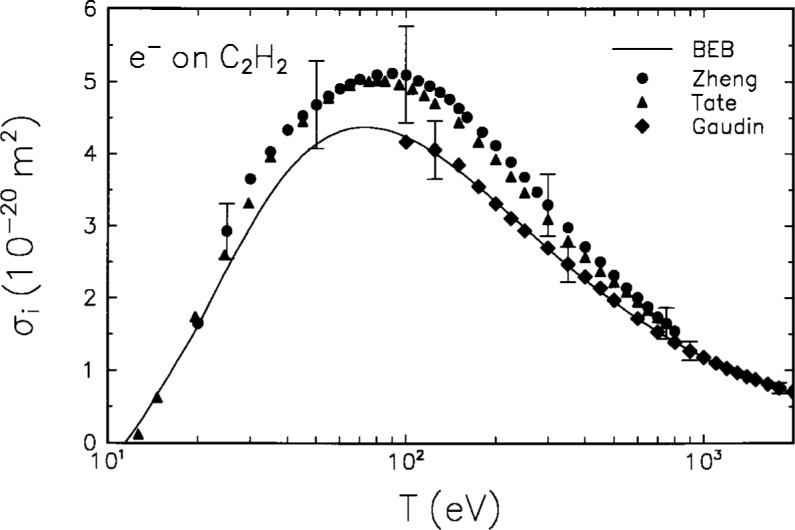
Comparison of BEB cross section to experiments for C2H2. Solid curve, BEB cross section; circles, experimental data by Zheng and Srivastava [9]; triangles, data by Tate and Smith [10]; diamonds, data by Gaudin and Hagemann [11]. The ordinate is the ionization cross section, and the abscissa is the incident energy.
Acknowledgments
The work at NIST was supported in part by the Office of Fusion Energy Science of the U.S. Department of Energy.
Biography
About the authors: Yong-Ki Kim is a physicist in the Atomic Physics Division of the NIST Physics Laboratory. M. Asgar Ali is a professor in the Chemistry Department at Howard University. M. Eugene Rudd is a professor emeritus in the Department of Physics and Astronomy at the University of Nebraska-Lincoln. The National Institute of Standards and Technology is an agency of the Technology Administration, U.S. Department of Commerce.
3. References
- 1.Kim YK, Rudd ME. Phys Rev A. 1994;50:3954. doi: 10.1103/physreva.50.3954. [DOI] [PubMed] [Google Scholar]
- 2.Hwang W, Kim Y-K, Rudd ME. J Chem Phys. 1996;104:2956. [Google Scholar]
- 3.Kim YK, Hwang W, Weinberger NM, Ali MA, Rudd ME. J Chem Phys. 1997;106:1026. [Google Scholar]
- 4.Ali MA, Kim Y-K, Hwang W, Weinberger NM, Rudd ME. J Chem Phys. 1997;106:9602. [Google Scholar]
- 5.Tawara H. In: Chap. 16 in Atomic and Molecular Processes in Fusion Edge Plasmas. Janev RK, editor. Plenum Press; New York: 1995. [Google Scholar]
- 6.Schmidt MW, Baldridge KK, Boatz JA, Elbert ST, Gordon MS, Jensen JH, Koseki S, Matsunaga N, Nguyen KA, Su SJ, Windus TL, Dupuis M, Montgomery JA. J Comput Chem. 1993;14:1347. [Google Scholar]
- 7.S.G. Lias, J.F. Liebman, R.D. Levin, and S.A. Kafafi, NIST Positive Ion Energetics Database, Version 20, Standard Reference Database 19A, National Institute of Standards and Technology, Oct. 1993. This database lists adiabatic IPs.
- 8.Tarnovsky V, Levin A, Deutsch H, Becker K. J Phys B. 1996;29:139. [Google Scholar]
- 9.Zheng SH, Srivastava SK. J Phys B. 1996;29:3235. [Google Scholar]
- 10.Tate JT, Smith PT. Phys Rev. 1932;39:270. [Google Scholar]
- 11.Gaudin A, Hagemann R. J Chim Phys. 1967;64:1209. [Google Scholar]