A Stochastic Solution to the Unbinned WHAM Equations

Abstract

The Weighted Histogram Analysis Method (WHAM) and unbinned versions such as the Multistate Bennett Acceptance Ratio (MBAR) and Unbinned WHAM (UWHAM) are widely used to compute free energies and expectations from data generated by independent or coupled parallel simulations. Here we introduce a Replica Exchange-like algorithm (RE-SWHAM) that can be used to solve the UWHAM equations stochastically. This method is capable of analyzing large data sets generated by hundreds or even thousands of parallel simulations that are too large to be “WHAMMED” using standard methods. We illustrate the method by applying it to obtain free energy weights for each of the 240 states in a simulation of host-guest ligand binding containing ~ 3.5 × 10⁷ data elements collected from 16 parallel Hamiltonian Replica Exchange simulations, performed at 15 temperatures. In addition to using much less memory, RE-SWHAM showed a nearly eighty fold improvement in computational time compared with UWHAM.

Graphical Abstract

The Weighted Histogram Analysis Method (WHAM) is used to compute free energies and expectations from data generated by multi-canonical simulations and independent simulations at multiple Hamiltonian or thermodynamic states^1–13 For example, after running Umbrella Sampling, the standard procedure is to use WHAM to combine the pieces of the free energy profile along chosen reaction coordinates.⁴ After running Replica Exchange (RE) simulations,^14,15 WHAM is used to estimate the free energy differences between Hamiltonian states, or to obtain expectation values at the targeted thermodynamic states from the simulation data at all of the thermodynamic states.^6,7 In this letter we describe a RE-like algorithm we have developed that corresponds to a stochastic solution of the UWHAM equations. We refer to this algorithm as Replica Exchange Stochastic WHAM or RE-SWHAM. Since running RE-SWHAM requires much less computing power compared with present WHAM-based analysis tools such as MBAR⁸ and UWHAM,^5,9 we believe RE-SWHAM is a promising method for analyzing very large ensembles of data generated by multi-canonical simulations or massively parallel but independent datasets generated on very large computer grids.^16,17

Before introducing RE-SWHAM, we review the binless WHAM (UWHAM) equations.⁹ In parallel simulations, if each simulation has different thermodynamic parameters such as temperature and pressure, they are referred to as simulations at different thermodynamic states; if each simulation has different potential energy functions, such as in Hamiltonian RE simulations, they can be referred to as simulations at different alchemical Hamiltonian states. Moreover, parallel simulations can differ in both thermodynamic parameters and potential energy functions such as in two dimensional RE simulations. For simplicity we refer to each of these states, which is characterized by a specific combination of thermodynamic parameters and potential energy functions, as a thermodynamic state, in order to avoid confusion with our description of the UP and DOWN conformational states. Consider a system of M parallel simulations labeled by Greek letters. Each thermodynamic state has a biased potential w_α(u), where u is the reduced coordinate of the observation. Suppose u_αi is the i^th observation at the α^th thermodynamic state, and N_α is the total number of observations at the α^th thermodynamic state. The UWHAM estimates of the density of states Ω(u_γi) and the partition function Z_α are (up to a multiplicative constant):^6,9

$${Ẑ}_{\alpha }=\sum _{\gamma =1}^M\sum _{i=1}^{N_{\gamma }}{c}_{\alpha }(u_{\gamma i})\hat{\mathrm{\Omega }}(u_{\gamma i}),$$ (1)

$$\hat{\mathrm{\Omega }}(u_{\gamma i})=\frac{1}{{\sum }_{\kappa =1}^M{N}_{\kappa }{Ẑ}_{\kappa }^{-1}{c}_{\kappa }(u_{\gamma i})},$$ (2)

where

$$c_{\alpha }(u_{\gamma i})=\text{exp}[-{\beta }_{\alpha }{w}_{\alpha }(u_{\gamma i})],$$ (3)

is the bias factor. Equation (1), (2) and (3) constitute a coupled set of equations which can by solved by Newton iteration⁸ or optimization.^9,10 The UWHAM estimate of the probability of the observation u_γi at the α^th state is

$${\hat{p}}_{\alpha }(u_{\gamma i})={Ẑ}_{\alpha }^{-1}\hat{\mathrm{\Omega }}(u_{\gamma i})c_{\alpha }(u_{\gamma i}).$$ (4)

We note that although the solution to the UWHAM equations depends on the number of observations at each thermodynamic state N_α, it does not depend on the original thermodynamic state at which each sample u_γi is observed.

We now describe a stochastic Monte-Carlo approach to solve the coupled equation (1), (2) and (3) inspired by the Replica Exchange algorithm. Consider a system of M parallel simulations labeled by Greek letters. Suppose there are N_α observations at the α^th thermodynamic state and N is the total number of observations, namely $N={\sum }_{\alpha =1}^M{N}_{\alpha }$. To initialize RE-SWHAM we first construct a weight array of N elements for each thermodynamic state, corresponding to the N observations. (A computationally efficient algorithm implementing RE-SWHAM is presented later and illustrated by Fig. 1.) There are M arrays of N elements, one for each thermodynamic state. The individual elements of the weight array have value 0 or 1 at every iteration. Initially, we set all the elements corresponding to the data actually observed at this thermodynamic state to 1, and the others to 0. Consider the α^th thermodynamic state, the initial weight array is

$$X_{\alpha }(t=0)=\{{\delta }_{\alpha }(u_{11},t=0)=0,\cdots ,{\delta }_{\alpha }(u_{\alpha 1},t=0)=1,{\delta }_{\alpha }(u_{\alpha 2},t=0)=1,\cdots ,{\delta }_{\alpha }(u_{\alpha N_{\alpha }},t=0)=1,\cdots ,{\delta }_{\alpha }(u_{\gamma i},t=0)=0,\cdots ,{\delta }_{\alpha }(u_{M{N}_M},t=0)=0\},$$ (5)

where γ ≠ α, and it has N_α nonzero elements. For simplicity, we reindex the N observations and omit the label of the original thermodynamic state at which each data element was observed since that information is not required. The weight array for the α^th thermodynamic state at time t is referred to as X_α(t) = {δ_α(u₁, t), δ_α(u₂, t), ⋯, δ_α(u_i, t), ⋯, δ_α(u_N, t)}, where δ_α(u_i, t) = 1 if the observation u_i occupies the α^th thermodynamic state at t, δ_α(u_i, t) = 0 otherwise.

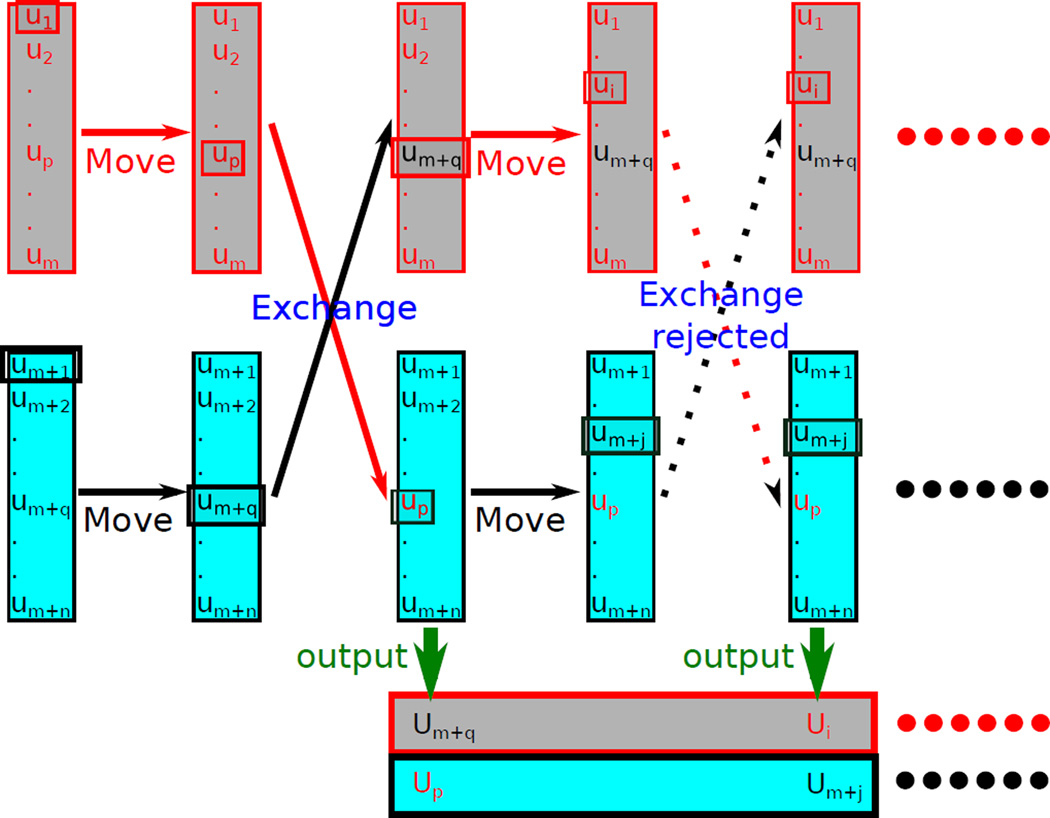
Figure 1.

An illustration of the RE-SWHAM algorithm. This drawing illustrates two replica exchange cycles of the RE-SWHAM method, and shows only two thermodynamic states with “grey” or “cyan” color. In each cycle one data element is chosen from each thermodynamic state first, then a replica exchange is performed. In the first cycle since the swap is accepted, the data associated with the two replicas is swapped to the other thermodynamic state’s data array. At the end of each cycle, the data associated with replicas are recorded as the output like explicit RE simulations..

The Metropolis Monte-Carlo RE-SWHAM algorithm resembles running explicit replica exchange simulations, which consists of cycles. There are two components in each cycle: i) the MD or MC simulation of each replica at a fixed thermodynamic state (the “move” process), which includes comformational relaxation at that thermodynamic state; ii) the attempted swaps of replicas (the “exchange” process), which is the relaxation in the replica and thermodynamic state permutation space. The RE-SWHAM algorithm also runs by replica exchange cycles. At each cycle, a data element at each thermodynamic state is chosen based on the current normalized weights, ${\delta }_{\alpha }(u_i,t)/{\sum }_{j=1}^N{\delta }_{\alpha }(u_j,t)={\delta }_{\alpha }(u_i,t)/N_{\alpha }$. Since in RE-SWHAM the elements of the weight array at each iteration represent the set of N_α out of N data elements that currently occupy that thermodynamic state, randomly choosing the next data element is analogous to the move process of an explicit RE simulation when its MD simulation period per cycle is so long that two adjacent configurations chosen for replica exchange have no correlations. Then a set of replica exchanges is performed which follows the same exchange criterion as in explicit replica exchange simulations (see the Metropolis function in Eq. (9)). In this letter we use the independence sampling algorithm as the proposal scheme,¹⁸ which attempts to exchange replicas from two thermodynamic states chosen at random.

RE-SWHAM updates the weights of observations of thermodynamic states based on the exchange process. When an exchange attempt is accepted, RE-SWHAM swaps the thermodynamic states of the two replicas, and changes the weights of the observations associated with the replicas at both thermodynamic states. For example, if one replica associated with the observation u_i at the α^th thermodynamic state hops to the γ^th thermodynamic state at time t, RE-SWHAM changes the weight of u_i to 0 at the α^th thermodynamic state, namely δ_α (u_i, t) = 0, and to 1 at the γ^th thermodynamic state, namely δ_γ (u_i, t) = 1. As part of this exchange move, a corresponding data element u_j moves from the γ^th to the α^th thermodynamic state. Notice that in RE-SWHAM algorithm the number of nonzero weights remains the same at each thermodynamic state and each observation has a nonzero weight at one and only one thermodynamic state. Following this procedure, the instantaneous weight of each data element at each thermodynamic state oscillates as 0 and 1, but the normalized time-average of the weight converges to the unbiased estimate of the probability of the data element, p̂_α(u_i), in Eq(4).

The RE-SWHAM algorithm performs a random walk in the space of the weight arrays of observations. In each cycle, RE-SWHAM moves from one set of weight arrays, or a configuration, to another following the same exchange criterion as that for multi-canonical replica exchange simulations:

$$\mathbf{X}(0)\stackrel{\mathrm{R}\mathrm{E}\text{ cycle}}{\to }\mathbf{X}(1)\stackrel{\mathrm{R}\mathrm{E}\text{ cycle}}{\to }\cdots \mathbf{X}(t)\stackrel{\mathrm{R}\mathrm{E}\text{ cycle}}{\to }\cdots ,$$ (6)

where X(t) is a set of weight arrays {X₁(t), X₂(t), ⋯, X_α(t), ⋯, X_M(t)} with X_α(t) corresponding to the weight array at the α^th thermodynamic state as described earlier. The total number of configurations of this Markov chain corresponds to the total number of ways to assign N non-zero instantaneous weights to M thermodynamic states, with the number of observations at each thermodynamic state fixed at {N₁, N₂, ⋯, N_α, ⋯, N_M} which is: $N!/({\prod }_{\alpha =1}^M{N}_{\alpha }!)$. The equivalent Master equation perspective for this random walk is

$$\frac{d{\mathbf{P}}_{\mathbf{X}}(t)}{dt}=\mathbf{A}·{\mathbf{P}}_{\mathbf{X}}(t),$$ (7)

where A is the rate matrix and P_X(t) represents the vector probability of all the possible configurations. The solution of Eq. (7) can be written as

$${\mathbf{P}}_{\mathbf{X}}(t+\mathrm{\Delta }t)={\mathbf{P}}_{\mathbf{X}}(t)·\mathbf{T},$$ (8)

where T is the row-normalized transition matrix.

It is possible to write down the transition matrix for RE-SWHAM when one exchange is attempted per cycle. Suppose at the beginning of a cycle, RE-SWHAM is at the i^th configuration (which corresponds to a specification of the N instantaneous weights at each of the M thermodynamic states), and two replicas are chosen at random to attempt an exchange. Consider the trial move in RE-SWHAM which attempts to exchange one observation u_m at the α^th thermodynamic state and the other observation u_n at the γ^th thermodynamic state. The new configuration will be called the j^th configuration, which is the same as the i^th configuration except that the weights of u_m and u_n are exchanged in the weight arrays at the α^th and the γ^th thermodynamic states. The probability that this trial move is accepted, namely, the exchange from the i^th configuration to the j^th configuration is accepted is

$$T_{ij}=\frac{2}{M(M-1))}\frac{1}{N_{\alpha }}\frac{1}{N_{\gamma }}\text{min }(1,\frac{\text{exp}[-{\beta }_{\alpha }{w}_{\alpha }(u_n)]\text{exp}[-{\beta }_{\gamma }{w}_{\gamma }(u_m)]}{\text{exp}[-{\beta }_{\alpha }{w}_{\alpha }(u_m)]\text{exp}[-{\beta }_{\gamma }{w}_{\gamma }(u_n)]})=\frac{2}{M(M-1))}\frac{1}{N_{\alpha }}\frac{1}{N_{\gamma }}\mathrm{\Psi }\left(\text{log }\right[\frac{c_{\alpha }(u_m)c_{\gamma }(u_n)}{c_{\alpha }(u_n)c_{\gamma }(u_m)}\left]\right).$$ (9)

where the first factor 2/(M(M − 1))) is the probability of choosing the replicas at the α^th and the γ^th thermodynamic states from the M replicas, and the factors 1/N_α and 1/N_γ are the probabilities of choosing one observation from the respective thermodynamic states. Throughout, Ψ is the Metropolis function¹⁹

$$\mathrm{\Psi }(x)=\text{min}(1,\text{exp}[-x]).$$ (10)

Consider the reverse trial exchange move from the j^th configuration to the i^th configuration, in other words, the swap of the observation u_n at the α^th state and the observation u_m in at the γ^th state with all other weights in configuration i and j having the same values. The probability of this move is

$$T_{ji}=\frac{2}{M(M-1))}\frac{1}{N_{\alpha }}\frac{1}{N_{\gamma }}\mathrm{\Psi }\left(\text{log }\right[\frac{c_{\alpha }(u_n)c_{\gamma }(u_m)}{c_{\alpha }(u_m)c_{\gamma }(u_n)}\left]\right).$$ (11)

By construction the stationary probabilities of the i^th and j^th configurations, denoted by p_i and p_j, satisfy the detailed balance condition:

$$p_i{T}_{ij}=p_j{T}_{ji}.$$ (12)

Next consider a subgroup I including all the configurations which have the observation u_m at the α^th thermodynamic state and the other observation u_n at the γ^th thermodynamic state, and another subgroup J including all the configurations which have the observation u_n at the α^th thermodynamic state and the other observation u_m at the γ^th thermodynamic state. For each configuration k in the subgroup I, there exists one configuration l in the subgroup J for which the only difference between these two configurations are the thermodynamic state the observation u_m and u_n belongs to. Every pair of such configurations, (k, l) with k ∈ I and l ∈ J, satisfies p_kT_ij = p_lT_ji, where T_ij and T_ji remain the same regardless of (k, l). Then the total probabilities of these two subgroups satisfy

$$\left(\sum _{k\in I}{p}_k\right)T_{ij}=\left(\sum _{l\in J}{p}_l\right)T_{ji}.$$ (13)

Theoretically the correlation is nonzero between the occurrence of the m^th observation at the α^th thermodynamic state and the occurrence of the n^th observation at the γ^th thermodynamic state (or the occurrence of the m^th observation at the γ^th thermodynamic state and the occurrence of the n^th observation at the α^th thermodynamic state). However, such correlations become negligible when the total number of observations at each thermodynamic state is large. Therefore, the total probabilities of the subgroup I and J are

$$\sum _{k\in I}{p}_k=\langle {\delta }_{\alpha }(u_m,t){\delta }_{\gamma }(u_n,t)\rangle \approx \langle {\delta }_{\alpha }(u_m,t)\rangle \langle {\delta }_{\gamma }(u_n,t)\rangle =N_{\alpha }{\tilde{p}}_{\alpha }(u_m)N_{\gamma }{\tilde{p}}_{\gamma }(u_n)$$

$$\sum _{l\in J}{p}_l=\langle {\delta }_{\alpha }(u_n,t){\delta }_{\gamma }(u_m,t)\rangle \approx \langle {\delta }_{\alpha }(u_n,t)\rangle \langle {\delta }_{\gamma }(u_m,t)\rangle =N_{\alpha }{\tilde{p}}_{\alpha }(u_n)N_{\gamma }{\tilde{p}}_{\gamma }(u_m),$$ (14)

where 〈δ_α(u_m, t)〉 is the time-average weight of the observation u_m at the α^th thermodynamic state, and p̃_α(u_m) is the normalized RE-SWHAM time-average weight, namely p̃_α(u_m) = 〈δ_α(u_m, t)〉/N_α. Combining Eq. (9), (11), (13), (14) and applying the property Φ(x)/Φ(−x) = exp(−x) lead to the detailed balance relation

$$\frac{{\tilde{p}}_{\alpha }(u_m)/c_{\alpha }(u_m)}{{\tilde{p}}_{\gamma }(u_m)/c_{\gamma }(u_m)}=\frac{{\tilde{p}}_{\alpha }(u_n)/c_{\alpha }(u_n)}{{\tilde{p}}_{\gamma }(u_n)/c_{\gamma }(u_n)},\text{ for all }(u_m,u_n)\text{ and }(\alpha ,\gamma ).$$ (15)

Denote the common value of the ratios in Eq. (15) by f(α, γ) which depends on (α, γ), but not (u_m, u_n), and fix γ at a baseline thermodynamic state, say α⁰. Then Eq. (15) gives

$${\tilde{p}}_{\alpha }(u_m)/c_{\alpha }(u_m)=f(\alpha ,{\alpha }^0)({\tilde{p}}_{{\alpha }^0}(u_m)/c_{{\alpha }^0}(u_m)).$$ (16)

That is, the probability p̃_α(u_m) can be expressed in the form

$${\tilde{p}}_{\alpha }(u_m)={\tilde{Z}}_{\alpha }^{-1}\tilde{\mathrm{\Omega }}(u_m)c_{\alpha }(u_m),\text{ for all }{u}_m\text{ and }\alpha ,$$ (17)

where Z̃_α = 1/f(α, α⁰) and Ω̃(u_m) = p̃_α⁰(u_m)/c_α⁰(u_m). Since ${\sum }_{m=1}^N{\tilde{p}}_{\alpha }(u_m)=1$ at each thermodynamic state, summing both sides of Eq. (17) over m yields

$${\tilde{Z}}_{\alpha }=\sum _{m=1}^N{c}_{\alpha }(u_m)\tilde{\mathrm{\Omega }}(u_m).$$ (18)

As mentioned previously, the RE-SWHAM algorithm keeps the total number of observations, N_α, unchanged at each thermodynamic state; the normalized time-average weight of every observation p̃_α(u_m) satisfies ${\sum }_{\alpha =1}^M{N}_{\alpha }{\tilde{p}}_{\alpha }(u_m)={\sum }_{\alpha =1}^M\langle {\delta }_{\alpha }(u_m,t)\rangle =1$, because each observation appears at one and only one thermodynamic state at one time. Multiplying both sides of Eq. (17) by N_α and summing over α yields

$$\tilde{\mathrm{\Omega }}(u_m)=\frac{1}{{\sum }_{\alpha =1}^M{N}_{\alpha }{\tilde{Z}}_{\alpha }^{-1}{c}_{\alpha }(u_m)}.$$ (19)

Thus the RE-SWHAM estimates {Ω̃(u_m) : m = 1, …, N} and {Z̃_α: α = 1, …, M} satisfy the array of equations (18)–(19), which are equivalent to the UWHAM equations Eq. (1)–(2). But the UWHAM estimates {Ω̂(u_m) : m = 1, …, N} and {Ẑ_α : α = 1, …, M} are, up to a multiplicative constant, unique solutions to Eq. (1)–(2).^5,9 Then Ω̃(u_m) = Ω̂(u_m) for all m = 1, …, N and Z̃_α = Ẑ_α for all α = 1, …, M provided that the same baseline thermodynamic state α⁰ is used in UWHAM and RE-SWHAM. Therefore by Eq. (4) and (17), the estimated probabilities from RE-SWHAM agree with those from UWHAM: p̃_α(u_m) = p̂_α(u_m).

In the previous discussion, we showed how to write any element of the transition matrix T for RE-SWHAM with one exchange attempt per cycle. Theoretically one can obtain the UWHAM solution by diagonalizing the transition matrix T and solving the equilibrium probabilities of all the possible configurations. This is impractical because of the overwhelming size of the transition matrix; however, RE-SWHAM provides a Markov Chain Monte Carlo solution to the problem.

RE-SWHAM, described conceptually above, can be implemented in practice as a computationally efficient algorithm. See Fig. 1 for an illustration of RE-SWHAM for a problem containing two thermodynamic states. To initialize RE-SWHAM, instead of constructing a weight array, we construct a current data array for each thermodynamic state using all the data elements observed from that thermodynamic state. In Fig. 1, there are m observations originally from the “grey” state and n observations from the “cyan” state. Then RE-SWHAM is run by cycles: first, one of the data elements is chosen with equal probability from each thermodynamic state. Second, a replica exchange attempt is performed following the multi-canonical exchange criterion. When an exchange attempt is accepted, the thermodynamic states of the two replicas are swapped, and the observations (data elements) associated with these two replicas are also swapped to the other thermodynamic state’s data array. As shown by the first replica exchange cycle in Fig. 1, the observation u_p is swapped to the “cyan” state and the observation “u_m+q” is swapped to the “grey” state. At the end of each cycle, no matter whether or not the exchange attempt is accepted, the observation associated with the replica at each thermodynamic state is recorded as the output like explicit RE simulations. Notice our implementation does not track the weight array but tracks the explicit observations with non-zero weights for each thermodynamic state to save the memory, since the total number of weights, $(M\times {\sum }_{\alpha =1}^M{N}_{\alpha })$, increases rapidly with the number of thermodynamic states M. Although the illustration shows only one exchange attempt per cycle, in practice performing multiple exchange attempts per cycle accelerates the convergence of RE-SWHAM.¹⁸

The output of RE-SWHAM at each thermodynamic state is a sample of all observations according to their UWHAM weights from Eq. (4) or RE-SWHAM weights from Eq. (17). The free energy difference between two adjacent thermodynamic states can be obtained by the standard “free energy perturbation formula” (FEP),²⁰ but note that unlike standard FEP, in Eq. (20) the reweighted (i.e. maximum likelihood) density of states appears. For instance, the free energy difference between the α^th and (α + 1)^th thermodynamic states is

$$-k_{B}T\text{ ln }\left(\frac{{\tilde{Z}}_{\alpha +1}}{{\tilde{Z}}_{\alpha }}\right)=-k_{B}T\text{ ln}\frac{{\sum }_{i=1}^N\tilde{\mathrm{\Omega }}(u_i)c_{\alpha +1}(u_i)}{{\sum }_{i=1}^N\tilde{\mathrm{\Omega }}(u_i)c_{\alpha }(u_i)}=-k_{B}T\text{ ln}\frac{{\sum }_{i=1}^N\tilde{\mathrm{\Omega }}(u_i)c_{\alpha }(u_i)\left(\frac{c_{\alpha +1}(u_i)}{c_{\alpha }(u_i)}\right)}{{\sum }_{i=1}^N\tilde{\mathrm{\Omega }}(u_i)c_{\alpha }(u_i)}=-k_{B}T\text{ ln}{\langle \frac{c_{\alpha +1}(u_i)}{c_{\alpha }(u_i)}\rangle }_{\alpha },$$ (20)

where the triangular brackets denote an average over the u_i values sampled at the α^th thermodynamic state according to their converged RE-SWHAM probabilities p̃_α(u_i).

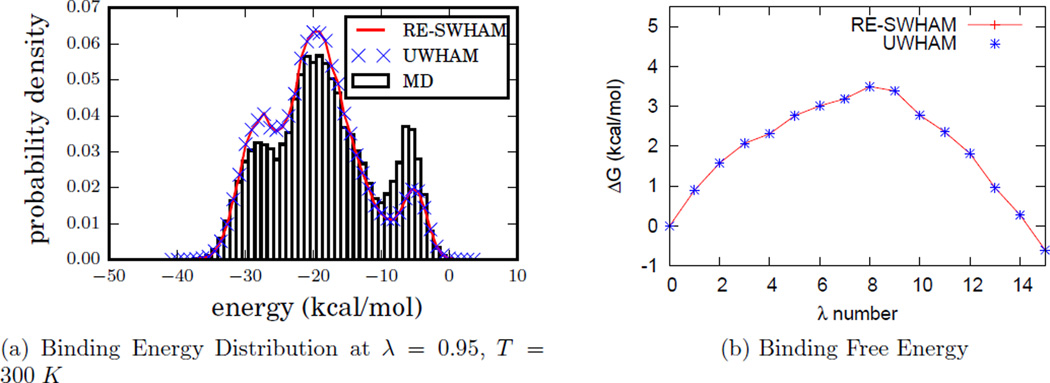
We include three numerical examples of the application of RE-SWHAM in this letter. The first example is to estimate the binding of a guest molecule to a host at 300 K from 16 independent 12 ns long MD simulations with different Hamiltonians for which the coupling between the guest and the host is varied. See Supporting Information and Simulation Methods section for more details. We deliberately chose this set of short unconverged independent parallel simulations to guarantee the obvious differences between the raw data and their RE-SWHAM estimates. The second example is to calculate the free energy differences between the 16 λ states at 300 K from a 72 ns one dimensional RE simulation using the same 16 Hamiltonians used in the first example. In both examples we applied UWHAM to analyze the data as the benchmark. As shown in Fig. 2(a) and (b), the binding energy distribution at the λ = 0.95 thermodynamic state and the free energy differences estimated by UWHAM and RE-SWHAM are indistinguishable. (see the Supporting Information for the distribution of binding energy at each λ thermodynamic state.)

Figure 2.

Numerical comparisons between UWHAM and RE-SWHAM. Plot (a) shows the Heptanoate-β-cyclodextrin binding energy distribution of λ = 0.95 state at 300 K obtained from a 12 ns independent MD simulation, and the UWHAM and RE-SWHAM estimates calculated from 16 independent 12 ns MD simulations run at different λ states. Plot (b) shows the free energy differences between these 16 λ states at 300 K estimated by UWHAM and RE-SWHAM from a 72 ns RE simulation. In both plots the UWHAM and RE-SWHAM results are indistinguishable.

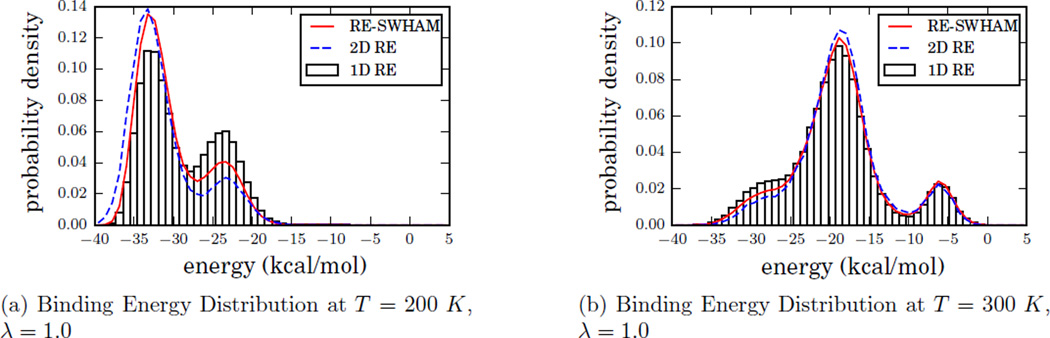
To illustrate the ability of RE-SWHAM to analyze a very large data set which is difficult to analyze using standard UWHAM or MBAR methods, we applied RE-SWHAM to estimate the binding energy distributions from the data generated by a set of independent one dimensional RE simulations (each with 16 replicas, using the same 16 Hamiltonians used in the first two examples) run at 15 different temperatures. The data ensemble in this example contains 240 thermodynamic states varying in λ values and temperatures, and a total 3.456 × 10⁷ data elements. Fig. 3 shows the raw data and the RE-SWHAM estimates of the binding energy distributions of λ = 1.0 state at 200 K and 300 K. We also plotted the results obtained from an asynchronous two dimensional 240 state RE simulation reported previously.¹⁶ These results serve as a converged benchmark. As can be seen, at low temperature (200 K), even the one dimensional RE simulations are not converged after 72 ns. However, compared with the two dimensional asynchronous RE simulation results, applying RE-SWHAM to this unconverged two dimensional (λ, T) data set led to significant improvements for the binding energy distribution at 200 K by using information from the simulations at higher temperature. At 300 K, RE-SWHAM estimates also show some improvements compared with the raw data. (see the Supporting Information for more discussion including the distribution of binding energy of λ = 1.0 state at each of 15 temperatures and the corresponding UWHAM estimate.) The RE-SWHAM estimates in Fig. 3 are the statistical results from the output stream of RE-SWHAM run for 12 minutes (2.0 × 10⁶ RE cycles), however it took 15.7 hours to obtain similar converged estimates with UWHAM.

Figure 3.

An application of RE-SWHAM to analyze a very large data set containing 240 thermodynamic states and 3.456 × 10⁷ data elements. These plots show the binding energy distributions of λ = 1.0 state at 200 k and 300 K obtained from one dimensional RE simulations and the respective RE-SWHAM estimates calculated from 15 independent one dimensional RE simulations run at 15 different temperatures. The blue dash lines are the binding energy distributions obtained from an asynchronous two dimensional 240 state RE simulation, which serve as a converged benchmark. The estimates from RE-SWHAM run for 12 minutes agree with those obtained from UWHAM (not shown) which required 15.7 hours to converge. The RE-SWHAM results show significant improvements for the binding energy distribution at 200 K compared with the unconverged one dimensional RE simulation data. At 300 K the one dimensional RE simulation data are better converged, but even for this data set, reweighting with RE-SWHAM leads to some improvements in the estimates of the low energy tail of the distribution.

As far as we aware this is the first time that the WHAM equations have been solved stochastically. More importantly, we believe RE-SWHAM is a promising tool to handle very large data sets. Over the last decade, hardware and software developments made it possible to run enhanced sampling simulations with hundreds of thermodynamic states, or Umbrella Sampling with thousands of windows.^{16,17,21–23} These kinds of large-scale simulations provide significant sampling power to study complex biological systems, however they also pose a challenge for reweighting techniques like UWHAM to analyze the large raw data sets. For example, for the data obtained from a multicanonical simulation with M thermodynamic states and $\overline{N_{\alpha }}$ observations per state, UWHAM needs to manipulate a matrix with $\overline{N_{\alpha }}\times M^2$ elements, and the size of this matrix increases rapidly with the number of thermodynamic states M. Instead the RE-SWHAM algorithm is a better choice for such scenario because it only manipulates $\overline{N_{\alpha }}\times M$ data elements, and performs simple replica exchange processes during the analysis. We have developed another algorithm called “local WHAM” (LWHAM) to analyze very large data sets which is based on the idea of only “WHAMMing” the data elements in the local neighborhood for each thermodynamic state (manuscript in preparation). Finally, we note a recent study by Meng and Roux who proposed an algorithm based on a multivariate linear regression, to process large data sets generated by Umbrella Sampling along a chosen reaction coordinate without solving the WHAM equations.²³ RE-SWHAM can also be used to construct potentials of mean force from data generated by Umbrella Sampling.

Simulation Methods

The biological system used to generate simulation data is the binding of a guest molecule (Heptanoate) to a host molecule (β-cyclodextrins) — a problem we studied previously.^24,25 The binding energy distribution analysis method (BEDAM) was applied to study the binding of Heptanoate/BCD complex.²⁶ BEDAM is a free energy method based on RE simulations in which the interaction between ligand and acceptor is scaled by the factor λ changing gradually from zero to one, namely (H = H₀ + λV ; 0 ≤ λ ≤ 1). Here we chose 16 λ values: (0.0, 0.001, 0.002, 0.004, 0.01, 0.04, 0.07, 0.1, 0.2, 0.4, 0.6, 0.7, 0.8, 0.9, 0.95, 1.0). For the two dimensional problem we “RE-SWHAMED” data from 240 states with different (λ, T) values. One dimensional replica exchange simulations each with 16 λ values were carried out independently at 15 temperatures: (200 K, 206 K, 212 K, 218 K, 225 K, 231 K, 238 K, 245 K, 252 K, 260 K, 267 K, 275 K, 283 K, 291 K, 300 K). There are replica exchanges between simulations of different λ states at each temperature but no replica exchanges allowed between simulations at different temperatures. Each one dimensional replica exchange simulation lasted 72 ns. (See Supporting Information for more details.)