Abstract
Direct 17O NMR structural studies of bound water in crystalline hydrates and biological macromolecules are challenging due to the low natural abundance and quadrupolar nature of 17O nuclei. However, the advent of high field NMR positions 17O NMR to become an important tool to address structural problems in biological solids. We show herein that the NMR properties of 17O in a series of amino acids and dipeptides can be determined by a combination of non-spinning and magic-angle spinning experiments using a range of magnetic field strengths from 9.4 to 21.1 T. Furthermore, we propose a 17O chemical shift fingerprint region for bound water molecules in biological solids that is well outside the previously determined ranges for carbonyl, carboxylic, and hydroxyl oxygens, thereby offering the ability to resolve multiple 17O environments using rapid one-dimensional NMR techniques. Finally, we compare our experimental data against quantum chemical calculations using GIPAW and hybrid-DFT, finding intriguing discrepancies between the electric field gradients calculated from structures determined by x-ray and neutron diffraction.
Keywords: NMR, 17O, GIPAW, hydrates, water, amino acids, biophysical
Graphical abstract
Introduction
Although its molecular struc8ture is simple, water impacts the structure and dynamics of both biological and inorganic chemical systems and its functions are vast and diverse. At the atomic level water molecules play crucial roles in directing protein folding, ion transport, and structural stability.1 The ability of water to form strong intermolecular hydrogen bonds makes it key to the secondary and tertiary structural formation of proteins, as well as a transport medium for various ion-channels. As an example, a water molecule (W402) has been found to be important in the H+/OH− photocycle in bacteriorhodopsin.2,3 These internal water molecules influence the storage and transfer of protons, as well as the orientation of the proton donor and acceptor.2 In a second recent example, cryo-electron microscopy and magic-angle spinning (MAS) nuclear magnetic resonance (NMR) studies of amyloid fibrils suggest that the amyloid fibril architecture consists of long fibrils, where two β-sheets of peptide are arranged in an antiparallel manner. A space of ~8–10Å located between two sheets likely contains a bilayer of water molecules that stabilizes the structure of the fibrils.4–7 Despite extensively studied with various structural models having been proposed, little is known about the interactions and the forces that are responsible for enabling the formation of fibrils.7,8 In particular, traditional techniques such as x-ray diffraction and solution NMR have thus far been unable to elucidate the role of these water molecules and the ability to use 17O NMR as a probe in the solid state could add significantly to our knowledge of these systems.
In contrast to other biologically relevant NMR-active nuclei (e.g., 13C, 15N), NMR studies of 17O have progressed slowly due to its low natural abundance (0.037%), small gyromagnetic ratio (−5.774 × 107 MHz T−1, approximately 1/7 to that of 1H), and quadrupolar nature (I=5/2, Q = −2.558 fm2).9 These physical characteristics lead to inherently low sensitivity (~1/15 to that of 13C), and its spectra are poorly resolved due to second-order quadrupolar line broadening. Specifically, 17O MAS NMR spectra typically display residual second-order broadening not averaged to zero by MAS.10,11 Modest sensitivity gains for studying 17O NMR have been achieved in the past by using isotopic enrichment12–15, performing the experiments in magnetic fields greater than 16.4 T16–20, and applying population transfer techniques.21,22 Recently dynamic nuclear polarization (DNP) of 17O has provided effective gains in sensitivity in a series of biological and inorganic chemical systems.23–26 While it is also possible to remove the second-order quadrupolar interaction to obtain simplified isotropic spectra, doing so requires advanced techniques and special instrumentation such as double rotation (DOR) or dynamic-angle spinning (DAS) probes.27,28 More accessible approaches involve two-dimensional spectroscopic techniques such as multiple-quantum magic-angle spinning (MQMAS)29 and satellite-transition magic-angle spinning (STMAS)30. In cases where the quadrupole coupling is large (> 5 MHz), the excitation efficiency of these latter approaches is reduced dramatically; for example, in MQMAS experiments, to about ~5%.31,32 Thus, although there are a number of promising MQMAS studies of 17O-labeled biological samples, the experimental results are limited by signal-to-noise and therefore require long acquisition times.33–42
Despite these inherent difficulties, 17O remains an appealing nucleus to study by NMR because, like nitrogen, it is directly involved in hydrogen bonding and the chemical shifts are quite sensitive to the chemical environment.43–45 Furthermore, it possesses a large chemical shift range (~1000 ppm), and as an added benefit, a quadrupolar interaction that could offer further structural constraints.13,46,47 It is therefore important to develop the spectroscopic fingerprinting techniques that will allow the interpretation of 17O NMR parameters in various hydrated chemical environments. In this study, we examine a series of hydrated amino acids in order to understand the effect of the local environments on the 17O chemical shift and quadrupolar coupling parameters. Using spectra recorded at multiple magnetic fields, we were able to extract the NMR parameters as well as resolve multiple sites within hydrated biological molecules by one-dimensional (1D) spectroscopy without recourse to complex 2D methods. The structural relation between 17O chemical shifts and structural water are further investigated using quantum chemical calculations by gauge-including projector augmented waves (GIPAW) and hybrid-density functional theory (DFT) methods for crystalline structures and cluster models, respectively.
Terminology and Definitions
A 17O NMR spectrum typically shows the central transition (1/2 ↔ −1/2) peak, with its shape determined by a second-order quadrupolar interaction that can be described by the quadrupolar coupling constant, CQ, and the asymmetry parameter, η:
| (1) |
| (2) |
where e is the charge of an electron, Q is the quadrupolar moment intrinsic to the nucleus of interest, h is Planck’s constant, and Vnn are eigenvalues of the electric field gradient (EFG) tensor (|Vzz| ≥ |Vyy| ≥ |Vxx|). A more comprehensive explanation of the quadrupolar interactions in solids can be found elsewhere.48–51
Chemical shift anisotropy (CSA) can also influence the spectral appearance of 17O NMR spectra, particularly at high magnetic fields (≥ 11.7 T).52,53 Using multiple magnetic field strengths, one can deconvolute the magnetic shielding parameters from the electric field gradient tensor. The isotropic chemical shift (δiso) is given by the trace of the chemical shift tensor components (i.e., δ11, δ22 and δ33)
| (3) |
The overall breadth of the shielding tensor is described by the span, Ω, and the relative magnitude of the components by the skew, κ, using the Herzfeld-Berger54 convention.
| (4) |
| (5) |
Experimental
a.) Materials and Synthesis
Seven crystalline amino acid hydrates were prepared by mixing 100–300 mg of crystalline powders (L-asparagine monohydrate, sodium L-aspartic acid monohydrate, L-cysteine HCl, L-histidine HCl, L-glycylglycine HCl, L-glycylglutamine HCl and L-arginine HCl) purchased from Sigma-Aldrich (St. Louis, MO) and 150–300 μl of 30% 17O-enriched water diluted from concentrated stock purchased from Cambridge Isotope Laboratories (40% 17O, Andover, MA) or Sigma-Aldrich (45% 17O, Miamisburg, OH). Samples were heated to 40–65 °C for 30 minutes in 1.5 mL Eppendorf vials until all solid residues were dissolved, and then cooled to room temperature. The Eppendorf vials were left sealed for 2–8 days without further agitation. Upon small crystal formation (i.e., nucleation), vials were opened to the atmosphere over a period of 24 to 48 hours allowing partial evaporation, and then sealed until crystals precipitated from solution over 3 to 21 days. Crystals were removed from the remaining solvent and dried in order to remove excess physisorbed water on the crystalline surface. All crystals were transparent and clear in color with sizes varying between 1 and 6 mm. The single crystals were ground using an agate mortar and pestle, and placed into ZrO2 rotors for all NMR experiments. Residual water trapped within small crystalline pockets due to crystalline twinning or a large excess of a water layer physisorbed onto the outer surface results in a sharp 17O water resonance due to isotropic tumbling. In these cases, the samples were re-crystallized. Final samples were visually inspected in their single-crystalline form and confirmed via powder x-ray diffraction and 13C[1H] cross polarization MAS NMR with reference to known NMR spectra.
b.) Nuclear magnetic resonance
17O solid-state NMR experiments were performed using magnetic fields ranging from 9.4 to 21.1 T. Experiments performed at 9.4 T (400 MHz, 1H, Francis Bitter Magnet Laboratory, Massachusetts Institute of Technology (FBML-MIT)), 16.4 T (698 MHz, 1H, FBML-MIT) and 17.6 T (748 MHz, 1H, FBML-MIT) were acquired using home-built spectrometers (courtesy of Dr. David Ruben, FBML-MIT). Experiments performed at 9.4 T (400 MHz, 1H, University of Manitoba), 11.7 T (500 MHz, 1H, University of Manitoba), 18.8 T (800 MHz, 1H, FBML-MIT) and 21.1 T (900 MHz, 1H, FBML-MIT) were acquired using either Bruker Avance II or III spectrometers. Recycle delays were optimized for each sample at each field. 17O γB1/2π values were between 50 and 80 kHz as determined from liquid water. Non-spinning spectra were acquired using continuous-wave high-power 1H decoupling (γB1/2π between 50 and 100 kHz). All spectra were referenced to 0 ppm using water (18 % H2 17O). Acquisition details for each spectrometer are given below (Table 1).
Table 1.
17O solid state nuclear magnetic resonance acquisition parameters
| Bo (T) | ωL/2π(MHz) | Pulse Sequence | Spinning Frequency (ωr/2π, kHz) | Recycle Delay (s) | Scans (× 1,000) | Rotor Size (mm, o.d.) |
|---|---|---|---|---|---|---|
| Hahn-echo | ||||||
| 9.4 | 53.8 | 0, 18 & 20 | 1 to 3 | 64 to 512 | 3.2 & 4 | |
| Solid-echo | ||||||
| 11.7 | 67.3 | Hahn-echo | 0 & 60 | 1 to 3 | 32 to 256 | 1.3 |
| 16.4 | 94.2 | Hahn-echo | 0 & 15 | 0.8 to 3 | 24 to 512 | 3.2 |
| 17.5 | 101.2 | Hahn-echo | 0 & 12 | 1 to 3 | 24 to 256 | 3.2 |
| Hahn-echo | ||||||
| 18.7 | 107.6 | 0 & 18 | 1 to 3 | 8 to 128 | 3.2 | |
| Bloch | ||||||
| Hahn-echo | ||||||
| 21.1 | 121.1 | 0, 16 & 20 | 1 to 3 | 8 to 96 | 3.2 | |
| Bloch |
c.) Quantum chemical calculations
Electric field gradient and chemical shielding calculations for crystalline monohydrates were performed using a density functional theoretical method implemented in CASTEP, a plane-wave basis set ideal for computing properties in periodic systems. The Perdew-Burke-Ernzerhof (PBE) functionals are used in the generalized gradient approximation (GGA) for the exchange-correlation energy55,56 and ultrasoft pseudopotentials57 generated on the fly. All calculations were performed using an ultrafine accuracy basis set and a maximum plane-wave energy of > 550 eV using the gauge-including projector-augmented wave method (GIPAW).58 The Monkhorst-Pack grid had a maximum density of up to 4 × 8 × 4 k points. Convergence was tested using crystalline, hydrogen and full-atom energy optimizations, as well as various basis set levels (i.e., medium to ultra-fine) as illustrated in the supporting information Figure S1. Due to the high-energy cutoffs of the x-ray crystalline structures (due to an inability to measure H positions) all crystalline structures59–69 underwent a hydrogen geometry optimization (unless otherwise stated); these refined structures were then used for the NMR calculations of chemical shieldings and electric field gradients. Calculated chemical shieldings were converted to chemical shifts using the following equation, δiso = (σref – σiso), whereby σref = 275.69 ppm (vide infra).
17O electric field gradient calculations were performed on model crystalline superstructures using the hybrid density functional theory approach implemented within Gaussian03.70 The Becke, 3-parameter, Lee-Yang-Parr (B3LYP)71–73 hybrid functional was used with basis sets varying from 3–21 to 6–311++g(d,p). Superstructure clusters were assembled using Gaussview 3.09 from both neutron and x-ray diffraction data. Each charge-neutral cluster contained three or four full amino acid units surrounding a single water molecule (extended models are shown in the supporting information, Figure S7). The Vzz electric field gradient component from the central water molecule was converted to the quadrupolar coupling constant using a quadrupolar moment of −2.558 fm−2.
d.) 17O Spectral Processing and Simulations
All spectra were processed by RNMR (Dr. D. Ruben, FBML-MIT) or TOPSPIN (Bruker, Billerica, USA). Exponential line broadening between 50 and 500 Hz was applied to all spectra. 17O NMR spectra were simulated using either WSOLIDS74, DMFIT75 or SPINEVOLUTION76 software packages in order to determine the quadrupolar and chemical shift parameters. The Euler angles from GIPAW calculations were extracted using the EFGShield software.77
Results
Seven amino acid monohydrates were studied using multiple magnetic field 17O NMR experiments (9.4 to 21 T) under MAS and non-spinning conditions, as shown in Figures 1 to 4, with additional figures in the supplementary information (supporting figures S2 to S6). Spectral simulations, shown only at 21.1 T in Figures 1 to 4, provided accurate chemical shift and quadrupolar coupling parameters for crystalline oxygen water environments with 17O experimental and GIPAW parameters summarized in Tables 2 and 3. Crystal structure details and full GIPAW calculated parameters for all oxygen environments are summarized in Tables S1 to S3.
Figure 1.
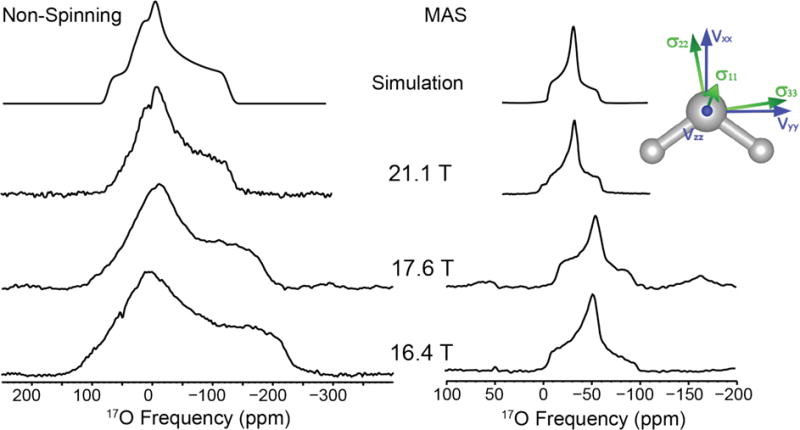
17O NMR of L-asparagine•H2O at 16.4, 17.6 and 21.1 T. Simulation of non-spinning data: CQ = 7.0 MHz, η = 0.95, δiso = 0.5 ppm, Ω = 45 ppm, κ = 0.0 and simulation of MAS data: CQ = 7.0 MHz, η = 0.95, δiso = 0.5 ppm
Figure 4.
17O MAS NMR of L-glycyl-glycine HCl monohydrate – (a) Three-site simulation of the two carboxylic oxygens (COOH) and the bound water oxygen (H2O); (b) experimental data acquired at 21.1 T. The molecular structure (inset) depicts that 17O labels and assignments based on 17O isotropic chemical shift. All 17O NMR parameters for each site are located in Table 2.
Table 2.
Experimental 17O NMR parameters for crystalline amino acid monohydrates
| Sample | 17O Site | CQ, MHz (± 0.1) |
η (± 0.05) |
δiso, ppm (± 1) |
Ω, ppm (± 10) |
κ |
|---|---|---|---|---|---|---|
|
| ||||||
| Arg | H2Oi | 7.0 | 0.88 | 26 | n.d. | n.d. |
|
| ||||||
| Asn | H2Oi | 7.0 | 0.95 | 0.5 | 45 | 0 (0.2) |
|
| ||||||
| Asp | H2Oi | 6.9 | 0.92 | −4 | 50 | −0.7(0.2) |
|
| ||||||
| Cys | H2Oi | 7.0 | 0.90 | 31 | 40 | 0.6(0.3) |
| C=O | 8.45 | 0.05 | 345 | n.d. | n.d. | |
| C-OH | 7.2 | 0.26 | 176 | n.d. | n.d. | |
|
| ||||||
| Gly-Gly | H2Oi | 6.9 | 0.9 | 28.5 | 45 | −0.8(0.2) |
| C=O | 8.5 | 0.1 | 343 | n.d. | n.d. | |
| C-OH | 7.4 | 0.3 | 166 | n.d. | n.d. | |
|
| ||||||
| Gly-Gln | H2Oi | 7.1 | 0.95 | 8.5 | 40 | −0.4(0.2) |
|
| ||||||
| His | H2Oi | 7.1 | 0.95 | 14 | 45 | 0.5(0.5) |
Fitted parameters determined from non-spinning and MAS data acquired between 9.4 and 21.1 T, Euler angles set to calculated parameters from GIPAW calculations using energy minimized structures where only the hydrogen positions were allowed to move within the crystal structure (neutron structures were used when available).
Back-exchanged in acid to label the carboxyl group with 17O.
n.d. – not determined
Table 3.
Quantum chemical calculations (GIPAW) of 17O NMR parameters for crystalline amino acid monohydrates
| Sample | Site | CQ, MHz | η | δiso, ppm† | Ω, ppm | κ |
|---|---|---|---|---|---|---|
|
| ||||||
| Arg | H2Ox | 8.254 | 0.82 | 27.18 | 55.895 | −0.324 |
| H2Ox | 8.248 | 0.78 | 28.55 | 54.648 | −0.636 | |
|
| ||||||
| Asn | H2On | 8.267 | 0.80 | 2.60 | 59.544 | −0.33 |
| H2Ox | 8.274 | 0.80 | −1.35 | 54.359 | −0.361 | |
|
| ||||||
| Asp | H2Ox | 8.326 | 0.82 | 0.27 | 53.868 | −0.333 |
|
| ||||||
| Cys | H2Ox | 8.252 | 0.75 | 37.98 | 32.61 | 0.235 |
| COx | 8.508 | 0.06 | 348.48 | 509.477 | −0.39 | |
| C-OHx | −7.559 | 0.26 | 201.21 | 366.088 | −0.085 | |
|
| ||||||
| Gly-Gly | H2On | 7.248 | 0.98 | 15.44 | 49.657 | −0.478 |
| H2Ox | 7.367 | 0.87 | 30.66 | 53.68 | −0.604 | |
| COn | 8.558 | 0.05 | 341.44 | 588.503 | −0.55 | |
| COx | 8.553 | 0.02 | 342.31 | 582.602 | −0.509 | |
| C-OHn | −7.582 | 0.25 | 178.06 | 241.001 | 0.947 | |
| C-OHx | −7.549 | 0.24 | 185.33 | 244.051 | 0.947 | |
|
| ||||||
| Gly-Gln | H2Ox | 7.748 | 0.87 | 7.07 | 50.321 | −0.448 |
|
| ||||||
| His | H2On | 8.620 | 0.73 | 14.24 | 49.961 | 0.306 |
| H2Ox | 8.544 | 0.72 | 14.80 | 50.592 | 0.235 | |
NB: All crystal structures underwent a H geometry optimization step to reduce the overall energy/symmetrized forces, x – x-ray and n – neutron determined crystal structures,
referenced using σref of 275.69 ppm.
a.) Crystalline Amino Acid Monohydrates
i.) C4H8N2O3·H217O (Asn)
L-asparagine monohydrate has an orthorhombic unit cell with a P212121 space group containing a single crystallographic water molecule. The MAS and non-spinning NMR spectra are shown in Figure 1. The 17O quadrupolar coupling constant of the water is 7.0 MHz, larger than the CQ observed for ice.23,78 The asymmetry parameter is 0.95, which is characteristic of a water molecule lying on a two-fold axis of rotation (i.e., C2v local symmetry).47 The GIPAW calculation (neutron) overestimates the CQ (8.267 MHz), and predicts the EFG tensor principal component Vxx on the C2 axis, Vyy within the HOH vertical plane, and Vzz perpendicular to Vxx and Vyy, coming out of the plane of the molecule (Figure 1, inset). The chemical shift parameters are an isotropic shift, δiso of 0.5 ppm, a span, Ω of 45 ppm, and a skew, κ of 0 (Table 2). GIPAW-calculated Euler angles are 83°, 83°, 346°. These values are close to the 90°, 90°, 0° values expected from the crystal structure and the C2 axis of the water molecule.
ii.) C4H7NNaO4·H217O (Asp)
Sodium L-aspartic acid monohydrate contains a single water molecule site within an orthorhombic unit cell (P212121, space group) identical to L-asparagine monohydrate. The water site has a CQ of 6.9 MHz and an η of 0.92. Figure 2 shows the MAS NMR spectra acquired at various magnetic fields from 11.7 to 21.1 T, illustrating the advantage of high field NMR for quadrupolar nuclei (non-spinning NMR spectra are shown in Figure S2). The experimentally determined chemical shift is δiso = −4 ppm. A Ω of 50 ppm and κ of 0.9 were determined using non-spinning high field data (Table 2). The GIPAW calculated (x-ray) Euler angles of L-aspartic acid monohydrate are α=276°, β=82°, γ=15°.
Figure 2.
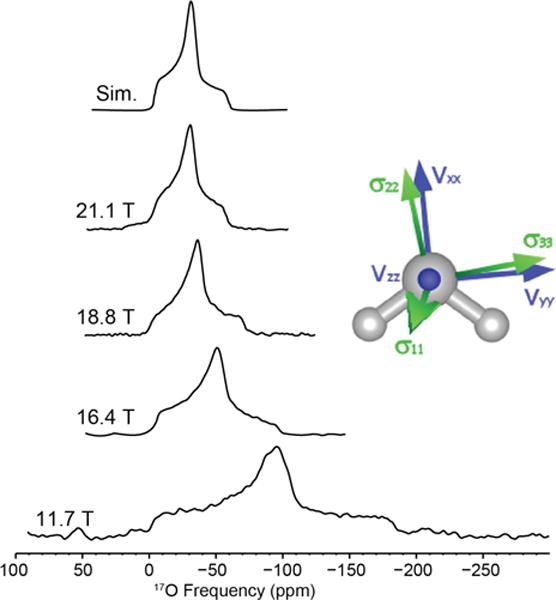
17O MAS NMR of sodium L-aspartic acid monohydrate acquired at various magnetic fields. Simulation parameters: CQ = 6.9 MHz, η = 0.92, δiso = −4 ppm.
iii.) C6H14N4O2·HCl·H217O (Arg)
L-Arginine HCl monohydrate is monoclinic with a P21 space group. The water oxygen is shifted to higher frequency with δiso = 26 ppm. The CQ is 7.0 MHz with an η of 0.88 (Table 2). The electric field gradient principal components calculated using GIPAW (x-ray) are comparable to Asn and Asp, with the Euler angles being 120°, 83° and 198°. The MAS NMR spectrum is shown in Figure S3.
iv.) C6H9N3O2·HCl·H217O (His)
L-histidine HCl monohydrate shows a single water site with a CQ = 7.1 MHz, η = 0.95, and δiso = 14 ppm (Table 2). The single water site is present within an orthorhombic cell (space group, P212121). GIPAW calculation (neutron) overestimates the CQ (8.62 MHz) but underestimates η (0.73). The GIPAW-calculated EFG tensors are in similar orientations with respect to the other H2O molecules, whereas the Euler angles for the chemical shift tensors with respect to the EFG tensors are 188°, 87°, and 334°. The MAS and non-spinning NMR spectra are shown in Figure S4.
v.) C3H7SNO2·HCl·H217O (Cys)
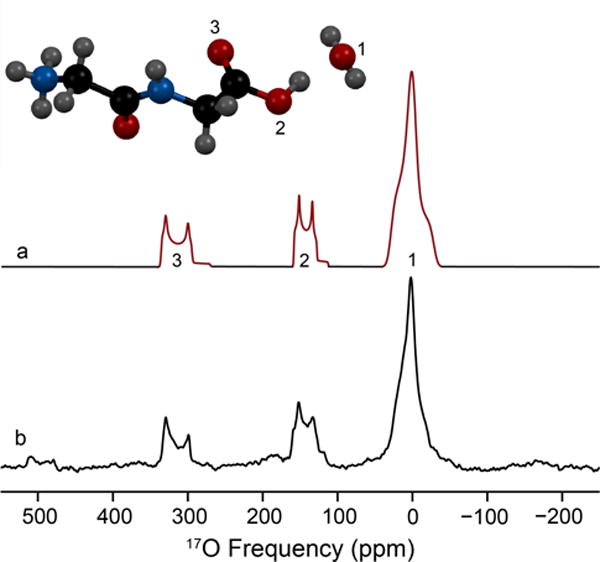
L-cysteine HCl monohydrate is orthorhombic with a space group of P212121. The experimentally determined quadrupolar coupling constant and asymmetry parameter are CQ = 7.0 MHz and η = 0.90 (Table 2). The chemical shift parameters determined from MAS and non-spinning NMR experiments are δiso = 31 ppm, Ω = 40 ppm and κ = 0.6 (Figure S5). Euler angles calculated from GIPAW (x-ray) are α=92°, β=87°, and γ=351°, consistent with the crystallographic constraints of 90°, 90°, 0°, respectively. Two additional 17O sites are resolved using acid exchange (Figure 3) and assigned to the carbonyl (C=17O) and carboxylic acid (CO17OH). The fitted quadrupolar coupling constants, asymmetry parameters and isotropic chemical shifts are CQ = 8.45 MHz, η = 0.05 and δiso = 345 ppm (C=17O) and CQ = 7.2 MHz, η = 0.26 and δiso = 176 ppm (CO17OH) (Table S1).
Figure 3.
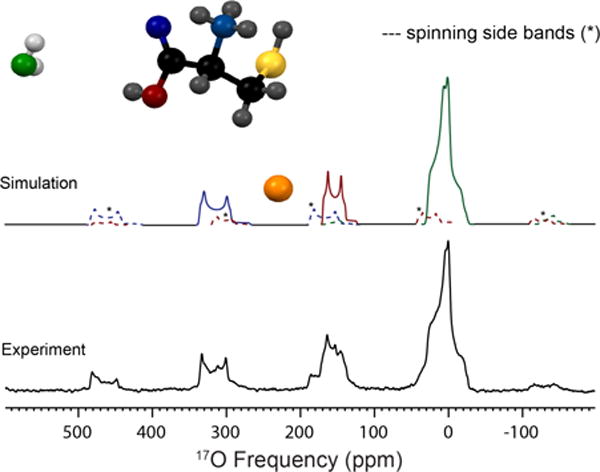
17O MAS NMR spectrum of three resolved oxygen sites present in L-cysteine · HCl · H2O acquired at 21.1 T (bottom). Simulation of the experimental data (top) is illustrated with the associated spinning sidebands marked in dotted lines; simulated parameters are located in Table 2. The three oxygen environments were assigned by chemical shift and are labeled in color: green (H2O), red (CO-OH) and blue (C=O).
b.) Crystalline dipeptide monohydrates
vi.) C7H13N3O4·H217O (Gly-Gln)
L-glycyl-glutamine monohydrate has an orthorhombic unit cell (P212121) with a single crystallographic water site. The 17O quadrupolar coupling constant for the water is CQ = 7.1 MHz and η = 0.95, constrained by the local C2V point group symmetry at the water site. The chemical shift parameters were determined using various magnetic field measurements: δiso = 8.5, Ω = 40 ppm, and κ = −0.4. GIPAW-calculated Euler angles (neutron structure) were 254°, 86°, 0° for α, β and γ, respectively. Figure S6 shows the MAS and non-spinning spectra.
vii.) C4H8N2O3·HCl·H217O (Gly-Gly)
L-glycyl-glycine HCl monohydrate is monoclinic with a P 21/c space group. Three distinct oxygen sites were resolved at 21.1 T and assigned to water, carbonyl and carboxylic acid oxygen environments. Simulating the experimental data allows the quadrupolar coupling constant (and asymmetry parameter) for each site to be measured at 6.9 (0.9, H2O), 8.5 (0.1, C=O), and 7.4 (0.3, COOH) MHz, respectively (Table S4). The calculated quadrupolar coupling constant (and asymmetry parameter) from GIPAW using neutron diffraction data are 7.2 (0.93, H2O), 8.6 (0.05, C=O) and −7.6 (0.25, COOH) MHz (Table 3), Euler angles for the water site were 100°, 84° and 205° (α, β and γ). The chemical shifts for each site were also determined (δiso = 28.5, 343 and 166 ppm, Table 2) with good resolution between the three sites due to the reduction of the second order quadrupolar broadened central transition at ultrahigh magnetic fields (i.e, 21.1 T) as shown in Figure 4.
Discussion
The second-order quadrupolar lineshape of the central transition can be an informative structural probe of the vicinity near the oxygen site. The magnitudes of the quadrupolar interaction and the asymmetry parameter reveal local symmetry information about the oxygen nucleus. The 17O quadrupolar coupling constants of all water sites within the various crystalline solids were determined experimentally to be between 6.9 and 7.1 MHz (Table 2). These results agree reasonably well with previous studies of various forms of ice23,78 and other hydrates79, which have reported quadrupolar coupling constants between 6.6 and 7.0 MHz.
Sternberg47 has shown that the asymmetry parameter is a sensitive indicator of the 17O bond angle. In theory it is possible to extract the ∠HOH angle from the experimentally determined η, and a true tetrahedral ∠HOH should give rise to a η = 1. However, since the function is non-linear, any asymmetry parameter of < 1 results in two possible answers, one above and one below 109.47°. Further complications arise when we consider that the error of the experimentally determined asymmetry parameter needs to be ≤ 0.01 units in order to reduce the error in bond angle to < 0.4°. Although our data are of high quality (~ ± 0.05 units), a large range of angles is still possible (~4° span) according to the equations determined by Sternberg.47
The EFG tensor components for all water molecules studied here have similar positions with respect to the water molecule. The smallest EFG component (Vxx) is oriented along the C2 axis bisecting the two electron lone-pairs, similar to the overall dipole of the molecule. Vyy is located perpendicular to the plane of the lone-pairs, aligned within the HOH plane of the molecule. Both of these lie parallel to the plane of the water molecule depicted in Figure 1, while the largest component of the electric field gradient (Vzz) projects out of the plane of the molecule. As the overall structural variation of water is fairly limited in amino acids, with minor deviations due to the small forces and crystallization, it should not be surprising that the magnitude and shape of the EFG tensors for all structures presented have nearly identical parameters and are representative of a C2v local symmetry.
The magnitude of the quadrupolar coupling constant reflects structural details of various environments. For example, an oxygen atom located in a cubic (i.e., Td or Oh) environment has a quadrupolar coupling of zero. Since the oxygen environments in biologically relevant systems deviate from a cubic lattice, the coupling constants are typically found between 6.5 and 8.5 MHz but have been reported to be as large as 11 MHz.12–14 The observed quadrupolar couplings of 7 MHz are characteristic of bound water environments, while rapid isotropic motion of free (unbound) water averages the interaction. The large difference in the magnitude of the quadrupolar coupling constants and asymmetries allows these parameters to be used to identify different oxygen sites in biological solids including carbonyl (C=O, CQ between 7.8 and 8.7 MHz, η < 0.3)80–84, carboxylic acid (−COOH, CQ between 5.9 and 7.7 MHz, η < 0.65)80–84, alcohol oxygens (−COH, CQ between 8.0 and 10, η > 0.7)24,85 and bound water (this work).12–14
An intriguing issue arises in the theoretical calculation of 17O quadrupolar coupling constants by GIPAW (Figure 5a) for hydrated environments. The calculations consistently overestimate the quadrupolar coupling constant by 0.7 to 1.7 MHz, irrespective of whether the crystal structure was determined by neutron or x-ray diffraction data. This means there is a 10 to 25 % overestimation depending on the hydrate crystalline system. Unlike the CQ calculations, the calculated 17O asymmetry parameters for all hydrated environments studied were consistently underestimated by a small amount, ~ 0.1. This discrepancy between GIPAW and 17O experimental NMR data (Table 2 and 3, Figure 5) is unique, as this approach has shown very good agreement with other chemical systems in recent years, including carboxylic (C17O17OH) oxygen of amino acids86,87, inorganic oxides15,88,89, and small organic molecules18,41,90.
Figure 5.
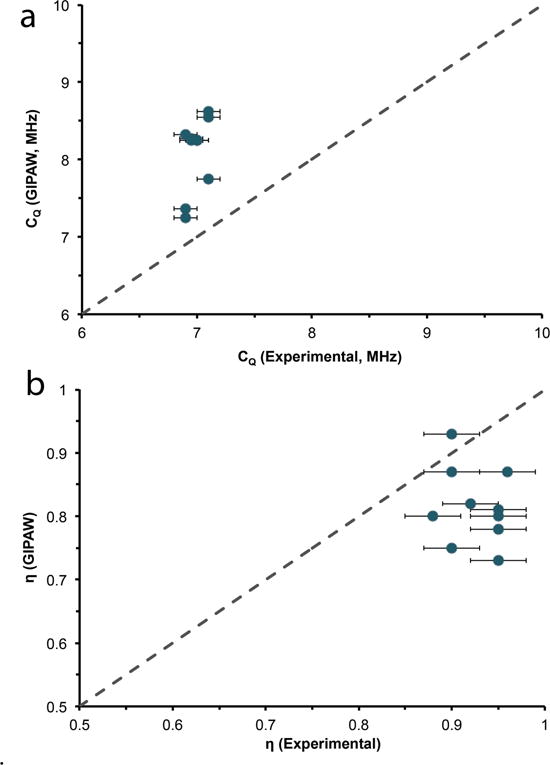
17O Experimental and GIPAW calculated quadrupolar coupling constants (a) and asymmetry (b) parameters for various crystalline hydrates. Dotted line is the 1:1 relation between experimental and calculated results.
In all of our test cases, GIPAW had difficulty calculating the proper quadrupolar coupling constants for water environments, with the exceptions of glycylglycine-HCl-H2O and ice from a previous study.24 Although the reason for this discrepancy is not yet understood, two possibilities may be suggested. The first is the difficulty of precisely locating the H positions of the water molecule (i.e., inaccuracy in the crystal structures). Although our H-optimizations did have an effect on the calculated quadrupolar coupling constants, significant changes in the H positions resulted in only a ~10% change in the CQ. Second, a recent report by Rees et al.91, looking at hydrogen bonding in hydrogen dibenzoates, suggested that dynamics affected their calculated 17O parameters when using the GIPAW software CASTEP. As CASTEP treats the calculated NMR parameters at 0 K (i.e., inhibiting motional averaging) our experimental results (as well as Rees et al.) were collected at room temperature, where partial averaging could occur. While oxygen dynamics could affect the observed quadrupolar couplings,90 with previous studies23–26,92,93 indicating small effects on both the lineshape and magnitude of the quadrupolar coupling interaction, closer examination of our chemical environments shows that the symmetry of the water itself restricts dynamics in any direction that would reduce the Vzz component. The medium-range structure (i.e., hydrogen bonding network) will, however, be disrupted by the oscillations about the HOH bisector of the water molecule, leading to a reduction in the observable quadrupolar coupling constant at room temperature.94–96
The discrepancy (≤ 25%) in calculating the 17O quadrupolar couplings by GIPAW warranted further investigation to determine whether overestimates are also found with other theoretical approaches. Cluster calculations using hybrid-DFT were implemented within Gaussian03© to calculate the quadrupolar coupling constants on single molecular units and large amino acid clusters (Figures S7–S10). Models were built upon x-ray and neutron diffraction structures (where available). The clusters were constructed to contain an isolated water molecule surrounded by 3 to 4 amino acid units. This approach allows us to consider local and medium-range order effects on the 17O EFG, while minimizing the computational cost (i.e. full unit cells). Figure 6 illustrates the quadrupolar coupling constants determined from x-ray and neutron structures for Asp, Gly-Gly, His, and Arg. It is clear that the calculations, which describe clusters from x-ray structures, accurately reproduce the experimentally determined 17O quadrupolar coupling constants, whereas the clusters from a neutron source consistently overestimate the constants. We hypothesize that the DFT functional for water molecules was parameterized using experimental x-ray crystal structure data. The only exception we observed was Gly-Gly-HCl-H2O, where the neutron62 and x-ray61 structures resulted in identical unit cell dimensions so that the calculated values by GIPAW and hybrid-DFT clusters were nearly identical.
Figure 6.
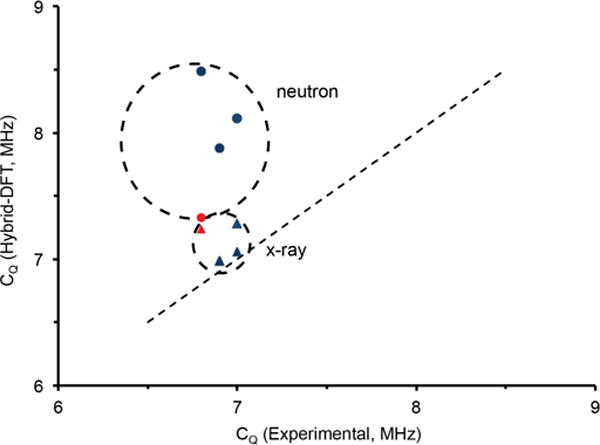
Relationship of calculated (hybrid-DFT) vs. experimental CQ of amino acid monohydrate clusters using a matching series of neutron (circle) and x-ray (triangle) crystalline structures. The red circle and diamond depict the neutron and x-ray structures of Gly-Gly.61,62
It is important to note that GIPAW calculations for the carboxylic acid oxygens (−COOH) in the amino acid structures studied here agree well with experimentally determined 17O quadrupolar coupling constants (vide supra) and chemical shifts (vide infra) determined in this work and elsewhere81,86 (Figure S11–S13). Furthermore, using x-ray, neutron and H-optimized structures did not lead to a significant improvement in the CQ values calculated using GIPAW.
For biological solids, 13C and 15N chemical shift information has been extensively tabulated and used to assign various functional groups, amino acid residues, and intra- and intermolecular interactions in proteins.97–99 17O NMR offers a new perspective with an extensive chemical shift range of over 500 ppm for oxygen environments associated with biologically relevant systems. However, unlike 13C and 15N, 17O NMR is still in a developmental stage for biological systems, and significant efforts have been expended characterizing various oxygen environments.12–14 As a result, many oxygen species can be readily identified by their 17O chemical shift signatures, including carbonyl oxygens (C=17O), which are located between 270 to 350 ppm, and carboxylic acid oxygens (CO17OH) between 160 to 260 ppm. Alcohol (−17OH) oxygens can be found in a chemical shift range of 50 to 110 ppm.80,81,86
The 17O NMR chemical shifts of bound water were determined experimentally and are located between −4 and +31 ppm, revealing a ~ 40 ppm chemical shift range for the various hydrated crystalline solids studied here and offering an eight-fold increase in chemical shift dispersion over that of 1H NMR (~ 5 ppm range) for structural water. Due to the 17O isotropic chemical shifts of hydrates being shifted to lower frequency with respect to other biologically relevant oxygen sites (Figure 7), multiple 17O sites within various chemical environments can be readily resolved using high magnetic fields, as shown in Figures 4 and 7.
Figure 7.
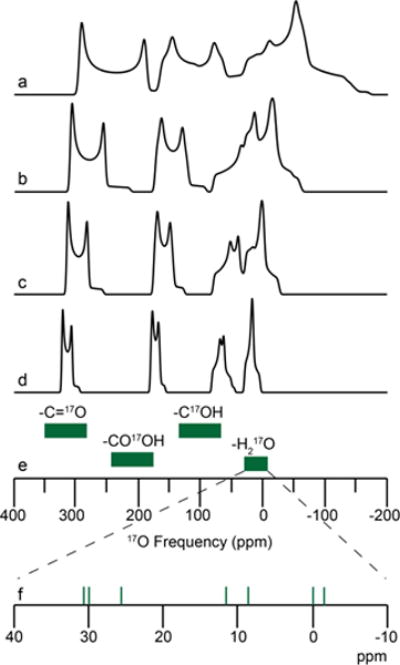
17O chemical shift ranges (green, e) and MAS simulations (above) for various biologically relevant oxygen environments at (a) 11.7 T, (b) 16.4 T, (c) 21.1 T, and (d) 30.5 T (1.3 GHz 1H, in development at FBML-MIT100) using parameters for L-tyrosine • HCl for the carbonyl, carboxylic acid, and phenol oxygen environments81 and L-glycyl-glycine HCl monohydrate for the bound water environment (this work). (f) Green vertical lines are the isotropic 17O chemical shift determined within this study.
The dependence of NMR chemical shifts on local structure is fundamental to the use of NMR in structure determination. 17O quantum-chemical calculations using GIPAW have performed extremely well in predicting the 17O chemical shielding interactions of various oxygen-containing environments.84–89,101,102 Two previous studies of 17O chemical shifts in the polymorphs of SiO289 and the carboxylic acid oxygens (−COOH) of various amino acids86 have offered reference shielding values to convert calculated shieldings to chemical shifts of 262.6 ppm and 261.5 ppm, respectively. Although our calculations exhibit a linear correlation with the experimental values, a clear offset is observed when using these suggested reference values. As addressed above, the observed offset may be due to the difficulty in treating water molecules in GIPAW, although convergence is easily achieved with the use of hydrogen-optimized crystal structures and medium-to-ultrafine level basis sets (Figure S1). Experimentally determined 17O isotropic chemical shifts and calculated chemical shifts (i.e., corrected chemical shifts from GIPAW using our new reference shielding (σref) value of 275.69 ppm) are displayed in Figure 8a. Excellent agreement is achieved using the hydrogen-refined crystal structures between GIPAW and experimentally determined 17O NMR parameters.
Figure 8.
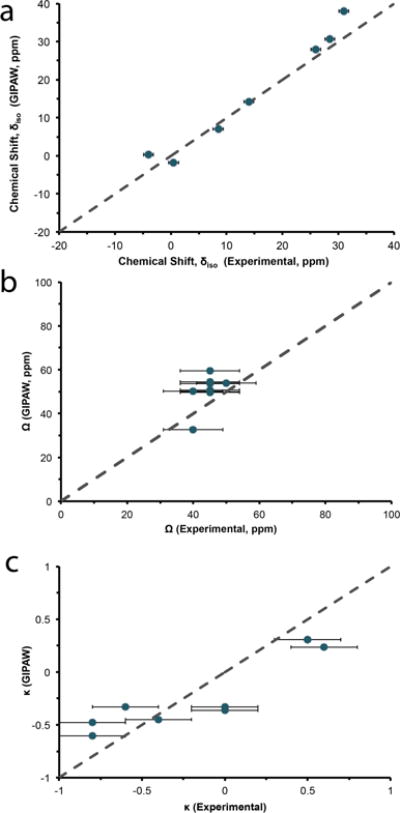
Experimental and GIPAW-calculated 17O isotropic chemical shift (a), span (b) and skew (c) for bound water in the amino acid monohydrates. Dotted line is the 1:1 relation between experimental and calculated results.
The ~40 ppm chemical shift range in bound water molecules is brought about by changes in the overall electronic environment and thus could be related to important structural elements. In previous studies, hydrogen bonding was correlated with 15N103,104 and 17O105–107 chemical shifts in various biological solids. 17O chemical shifts have also been shown to be sensitive to the C—O bond length in carbonyl functional groups.81 A significant issue is the subtle structural differences observed for water molecules in different bound environments (i.e., bond distance (O-H) and angle (∠HOH)). Nevertheless, these small geometrical changes108 could lead to significant effects on the 17O shielding. Detecting these dependencies has traditionally been challenging as many known crystalline hydrate structures are determined from x-ray diffraction which cannot effectively determine the H positions, leading to sizeable reported variations in bond distance and angles (i.e., 0.774 to 0.914 Å and 97.72° to 121.57°) that could be further complicated by dynamics. Neutron structures, which identify H positions, show a much smaller range of values (e.g., 0.96 to 0.97 Å and 104.96° to 109.52°). Comparing the experimentally determined isotropic chemical shift and structural parameters (i.e., H-O, ∠HOH and H2O — NH2) measured from both x-ray and neutron diffraction does not lead to any clear correlation (Figure S14).
Due to the absence of a complete set of neutron structures and the large residual forces observed in the calculations for all x-ray and neutron structures, a crystal structure refinement of the H-positions using GIPAW was performed. Utilizing the geometry-optimized crystal structures, the amino acid monohydrates have three common features involving the water H-O bond distance and ∠HOH bond angle, and the H2O — NH2 hydrogen-bonding interaction to the nearest amine (Table S2). As illustrated in Figure 9, a qualitative trend seems to be present when focusing on the optimized bond angle and O-H distance in both the 17O δiso of the experimental and GIPAW calculated data. 17O chemical shifts are sensitive to the molecular structure of water within these amino acids and may prove to be valuable for difficult measurements using other NMR techniques. There is no clear trend relating H2O — NH3 hydrogen bonding with respect to isotropic chemical shift, however the 17O GIPAW-calculated CQ and η are sensitive to this hydrogen bonding interaction (Figure S15). The monohydrate dipeptide Gly-Gly-HCl•H2O contains the longest H2O — NH3 hydrogen bonding interaction of 3.03 Å. Interestingly, the GIPAW and hybrid-DFT calculated CQ and η values for both x-ray and neutron diffraction data agree within ~5% of the experimental values reported here for this dipeptide. This is the only monohydrate complex that we examined containing a hydrogen bond >2.9 Å, providing further evidence that quadrupolar coupling parameters are sensitive to the secondary coordination environment.
Figure 9.
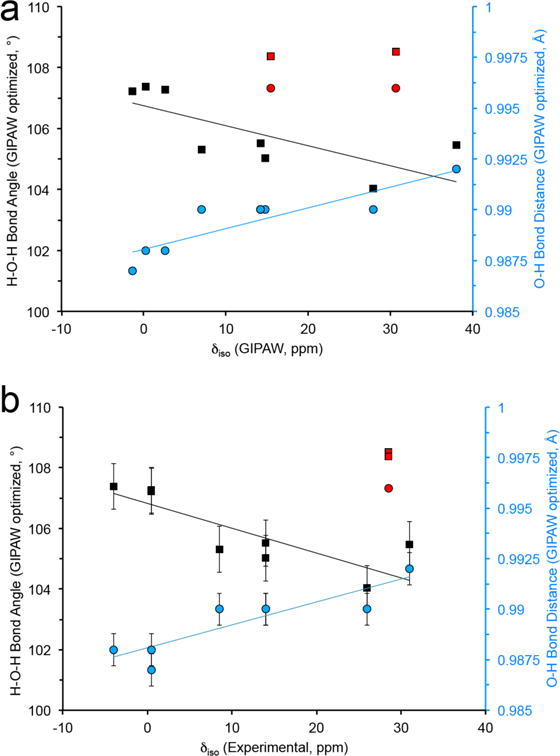
Relationship between HOH bond angle and average O-H bond distance (from GIPAW optimized crystalline structures) and (a) GIPAW and (b) experimentally determined 17O isotropic chemical shift, δiso. Data points in red are from the x-ray and neutron crystal structure of L-glycylglycine-HCl-H2O. The thin lines are a guide for the eye.
In order to obtain information regarding the chemical shift anisotropy of the various water environments, non-spinning 17O NMR spectra were obtained for all samples. As an example, the non-spinning spectrum of histidine spans ~54 kHz (~1000 ppm) at 9.4 T (Figure S4). Due to the significant second-order quadrupolar broadening of the central transition, high-field NMR measurements were required to observe and measure the effects of chemical shift anisotropy, since second-order quadrupolar broadening is inversely proportional to Bo, while chemical shift anisotropy scales linearly with Bo. Nine independent variables are required to fit the non-spinning data, including: CQ, η, δiso, Ω, κ, Euler angles (α, β, Ɣ), and the dipolar interaction. The quadrupolar coupling constant, quadrupolar asymmetry parameter and isotropic chemical shift (δiso, CQ and η) can be measured by MAS NMR experiments. To remove any effects due to the strong 1H-17O dipolar coupling, continuous-wave 1H decoupling (i.e., ≥ 50 kHz) was applied during acquisition of the non-spinning spectra. These dipolar coupling effects were only observable at higher magnetic fields and were negligible during MAS for all magnetic fields. As magnetic fields strengths continue to increase (i.e., ≥ 1.3 GHz) and high-resolution 1D and 2D (i.e., MQMAS and STMAS) experiments involving quadrupolar nuclei become more common, 1H-decoupling may become necessary even in MAS experiments as resonances become even narrower, no longer dominated by quadrupolar broadening.81,109–112
The local symmetry of the water molecule (C2v) forces certain constraints on both CSA and EFG tensors. As the tensors need to be aligned, the Euler angles must be increments of ~90°. As indicated above, the EFG tensor component Vxx lies along the C2 axis, bisecting the HOH angle and in the HOH plane, and Vzz is perpendicular to the HOH plane. Vyy is perpendicular to these two directions (Figures 1–5). Similarly, the chemical shift tensor orientations calculated by GIPAW approximately obey these symmetry constraints, with σ11 lying approximately parallel to the Vzz tensor component and σ22 along the C2 axis approximately parallel with Vxx. σ33 is perpendicular to these two directions.
The span and skew were adjusted to effectively simulate the non-spinning data at 21.1 T. The spans were determined to be between 30 and 50 ppm. These spans mirror the measured 17O chemical shift range determined for water environments in hydrated amino acids. Although our experimental errors for the measured CSA are moderate (± 25%), a significant shift anisotropy clearly contributes to the observed lineshapes. The paucity of higher magnetic fields currently restricts us from establishing a clear relationship between structural components of water and the individual chemical shift tensor components (δ11, δ22, and δ33), which has been documented for other 17O shift tensors in biological solids.105,113 Nevertheless, this is the first time the 17O CSA of water has been observed and we believe these CSA interactions will offer further structural information in the near future as higher magnetic fields become available (Figure S16).
Conclusion
The quadrupolar and chemical shift parameters of 17O in various hydrated crystalline amino acids were determined using a range of magnetic fields, revealing markers for structural identification. The quadrupolar coupling constants are approximately 7 MHz for all water environments. A new chemical shift range (~ 40 ppm) for 17O of bound water has been determined and offers the possibility to resolve multiple 17O water sites at high magnetic fields.
Experimental 17O chemical shift and quadrupole parameters were compared with GIPAW and hybrid-DFT quantum chemical calculations. GIPAW-based calculations consistently overestimated CQ, while η was slightly underestimated, but hybrid-DFT calculations from x-ray structures were consistent with our experimental 17O NMR results. The agreement with x-ray crystal structures suggest that the functionals for the hybrid-DFT calculations may not been optimized using neutron diffraction data. The calculated chemical shieldings from GIPAW are consistent with our experimental NMR data, although a new scaling factor of 275.69 ppm is required to effectively convert the calculated shieldings to chemical shifts for room temperature data. The hydrogen-optimized structures reveal that the 17O chemical shifts of these hydrates are linearly correlated with bond distances and angles. Further studies are underway in an attempt to determine what effects long-range hydrogen bonding and water dynamics may have on the experimental quadrupolar coupling parameters and how high-field dynamic nuclear polarization may be able to assist in these studies.
High magnetic fields offer the capacity to systematically characterize 17O chemical shift for bound water environments, which have been hampered at lower magnetic fields due to imprecise δiso values. Combining our experimental data on L-cysteine · HCl · H2O and L-glycyl-glycine · HCl · H2O, the use of high magnetic fields could even be further extended to resolve four biologically relevant oxygen environments (i.e., C=O, CO-OH, C-OH and H2O), as observed in our simulation of L-Tyr-HCl-H2O (Figure 7), offering great opportunities for advancing the application of 17O NMR to the structural characterization of biological solids.
Supplementary Material
Acknowledgments
This work was supported by the National Institute of Biomedical Imaging and Bioengineering (NIBIB), National Institutes of Health (NIH) through grant numbers: EB-002804, EB-003151, EB-001960 and EB-002026. VKM is grateful to the Natural Sciences and Engineering Research Council (NSERC) of Canada and the Government of Canada for a Banting Postdoctoral Fellowship. SK is supported by an NSERC Discovery Grant and Canada Foundation for Innovation infrastructure funds. The authors would like to thank Mr. A. Thakkar (FBML-MIT) for technical assistance and Dr. V. Terskikh (National Ultrahigh-Field NMR Facility for Solids, NRC, Ottawa, Canada) for scientific discussions and access to the CASTEP software.
References
- 1.Levy Y, Onuchic JN. Proceedings of the National Academy of Sciences. 2004;101:3325. doi: 10.1073/pnas.0400157101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bondar A-N, Fischer S, Smith JC. Journal of Membrane Biology. 2011;239:73. doi: 10.1007/s00232-010-9329-3. [DOI] [PubMed] [Google Scholar]
- 3.Luecke H, Schobert B, Richter HT, Cartailler JP, Lanyi JK. Journal of Molecular Biology. 1999;291:899. doi: 10.1006/jmbi.1999.3027. [DOI] [PubMed] [Google Scholar]
- 4.Debelouchina GT, Bayro MJ, van der Wel PCA, Caporini MA, Barnes AB, Rosay M, Maas WE, Griffin RG. Physical Chemistry Chemical Physics. 2010;12:5911. doi: 10.1039/c003661g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.van der Wel PCA, Hu KN, Lewandowski J, Griffin RG. Journal of the American Chemical Society. 2006;128:10840. doi: 10.1021/ja0626685. [DOI] [PubMed] [Google Scholar]
- 6.Caporini MA, Bajaj VS, Veshtort M, Fitzpatrick A, MacPhee CE, Vendruscolo M, Dobson CM, Griffin RG. Journal of Physical Chemistry B. 2010;114:13555. doi: 10.1021/jp106675h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Debelouchina GT, Bayro MJ, Fitzpatrick AW, Ladizhansky V, Colvin MT, Caporini MA, Jaroniec CP, Bajaj VS, Rosay M, MacPhee CE, Vendruscolo M, Maas WE, Dobson CM, Griffin RG. Journal of the American Chemical Society. 2013;135:19237. doi: 10.1021/ja409050a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fitzpatrick AWP, Debelouchina GT, Bayro MJ, Clare DK, Caporini MA, Bajaj VS, Jaroniec CP, Wang L, Ladizhansky V, Müller SA, MacPhee CE, Waudby CA, Mott HR, De Simone A, Knowles TPJ, Saibil HR, Vendruscolo M, Orlova EV, Griffin RG, Dobson CM. Proceedings of the National Academy of Sciences. 2013;110:5468. doi: 10.1073/pnas.1219476110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Harris RK, Becker ED. Journal of Magnetic Resonance. 2002;156:323. [Google Scholar]
- 10.Grandinetti PJ, Trease NM, Ash JT. Progress in NMR Spectroscopy. 2011;59:121. doi: 10.1016/j.pnmrs.2010.11.003. [DOI] [PubMed] [Google Scholar]
- 11.Grandinetti PJ. In 48th Experimental NMR Conference, Daytona Beach, FL. 2007 Apr 22–27;:138. [Google Scholar]
- 12.Wong A, Poli F. Annual Reports on NMR Spectroscopy. 2014;83:145. [Google Scholar]
- 13.Wu G. Progress in Nuclear Magnetic Resonance Spectroscopy. 2008;52:118. [Google Scholar]
- 14.Wu G. Encyclopedia of Magnetic Resonance. Wiley; 2011. [Google Scholar]
- 15.Ashbrook SE, Smith ME. Chemical Society Reviews. 2006;35:718. doi: 10.1039/b514051j. [DOI] [PubMed] [Google Scholar]
- 16.Zhu J, Ye E, Terskikh V, Wu G. Angewandte Chimie. 2010;49:8399. doi: 10.1002/anie.201002041. [DOI] [PubMed] [Google Scholar]
- 17.Aguiar PM, Michaelis VK, McKinley CM, Kroeker S. Journal of Non-Crystalline Solids. 2013;363:50. [Google Scholar]
- 18.Kong X, Shan M, Terskikh V, Hung I, Gan Z, Wu G. Journal of Physical Chemistry B. 2013;117:9643. doi: 10.1021/jp405233f. [DOI] [PubMed] [Google Scholar]
- 19.Kwan I, Mo X, Wu G. Journal of the American Chemical Society. 2007;129:2398. doi: 10.1021/ja067991m. [DOI] [PubMed] [Google Scholar]
- 20.Antzutkin ON, Iuga D, Filippov AV, Kelly RT, Becker-Baldus J, Brown SP, Dupree R. Angewandte Chemie International Edition. 2012;51:10289. doi: 10.1002/anie.201203595. [DOI] [PubMed] [Google Scholar]
- 21.Prasad S, Clark TM, Sharma R, Kwak HT, Grandinetti PJ, Zimmermann H. Solid State Nuclear Magnetic Resonance. 2006;29:119. doi: 10.1016/j.ssnmr.2005.10.007. [DOI] [PubMed] [Google Scholar]
- 22.Brinkmann A, Kentgens APM. Journal of the American Chemical Society. 2006;128 doi: 10.1021/ja065415k. [DOI] [PubMed] [Google Scholar]
- 23.Michaelis VK, Markhasin E, Daviso E, Herzfeld J, Griffin RG. The Journal of Physical Chemistry Letters. 2012;3:2030. doi: 10.1021/jz300742w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Michaelis VK, Corzilius B, Smith AA, Griffin RG. Journal of Physical Chemistry B. 2013 doi: 10.1021/jp408440z. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Michaelis VK, Ong T-C, Kiesewetter MK, Frantz DK, Walish JJ, Ravera E, Luchinat C, Swager TM, Griffin RG. Israel Journal of Chemistry. 2014;54:207. doi: 10.1002/ijch.201300126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Blanc F, Sperrin L, Jefferson DA, Pawsey S, Rosay M, Grey CP. Journal of the American Chemical Society. 2013;135:2975. doi: 10.1021/ja4004377. [DOI] [PubMed] [Google Scholar]
- 27.Chmelka B, Mueller K, Pines A, Stebbins J, Wu Y, Zwanziger J. Nature. 1989;339:42. [Google Scholar]
- 28.Baltisberger JH, Gann SL, Grandinetti PJ, Pines A. Mol Phys. 1994;81:1109. [Google Scholar]
- 29.Frydman L, Harwood JS. J Am Chem Soc. 1995;117:5367. [Google Scholar]
- 30.Gan Z. J Am Chem Soc. 2000;122:3242. [Google Scholar]
- 31.Wu G, Rovnyak D, Griffin RG. Journal of the American Chemical Society. 1996;118:9326. [Google Scholar]
- 32.Wu G, Rovnyak D, Huang PC, Griffin RG. Chem Phys Lett. 1997;277:79. [Google Scholar]
- 33.Brinkmann A, Kentgens APM. The Journal of Physical Chemistry B. 2006;110:16089. doi: 10.1021/jp062809p. [DOI] [PubMed] [Google Scholar]
- 34.Gullion T, Yamauchi K, Okonogi M, Asakura T. Macromolecules. 2007;40:1363. [Google Scholar]
- 35.Hung I, Uldry A-C, Becker-Baldus J, Webber AL, Wong A, Smith ME, Joyce SA, Yates JR, Pickard CJ, Dupree R, Brown SP. Journal of the American Chemical Society. 2009;131:1820. doi: 10.1021/ja805898d. [DOI] [PubMed] [Google Scholar]
- 36.Sefzik TH, Houseknecht JB, Clark TM, Prasad S, Lowary TL, Gan Z, Grandinetti PJ. Chem Phys Lett. 2007;434:312. [Google Scholar]
- 37.Wong A, Beevers AJ, Kukol A, Dupree R, Smith ME. Solid State Nuclear Magnetic Resonance. 2008;33:72. doi: 10.1016/j.ssnmr.2008.04.003. [DOI] [PubMed] [Google Scholar]
- 38.Wu G, Dong S, Ida R, Reen N. JAmChemSoc. 2002;124:1768. doi: 10.1021/ja011625f. [DOI] [PubMed] [Google Scholar]
- 39.Yamauchi K, Okonogi M, Kurosu H, Tansho M, Shimizu T, Gullion T, Asakura T. Journal of Magnetic Resonance. 2008;190:327. doi: 10.1016/j.jmr.2007.11.006. [DOI] [PubMed] [Google Scholar]
- 40.Zhu J, Ye E, Terskikh V, Wu G. Angewandte Chemie, International Edition. 2010;49:8399. doi: 10.1002/anie.201002041. [DOI] [PubMed] [Google Scholar]
- 41.O’Dell LA, Ratcliffe CI, Kong X, Wu G. The Journal of Physical Chemistry A. 2012;116:1008. doi: 10.1021/jp210844t. [DOI] [PubMed] [Google Scholar]
- 42.Wong A, Howes AP, Yates JR, Watts A, Anupold T, Past J, Samoson A, Dupree R, Smith ME. Physical Chemistry Chemical Physics. 2011;13:12213. doi: 10.1039/c1cp20629j. [DOI] [PubMed] [Google Scholar]
- 43.Degroot HJM, Harbison GS, Herzfeld J, Griffin RG. Biochemistry. 1989;28:3346. doi: 10.1021/bi00434a033. [DOI] [PubMed] [Google Scholar]
- 44.Harbison G, Herzfeld J, Griffin RG. Journal of the American Chemical Society. 1981;103:4752. [Google Scholar]
- 45.Munowitz M, Bachovchin WW, Herzfeld J, Dobson CM, Griffin RG. Journal of the American Chemical Society. 1982;104:1192. [Google Scholar]
- 46.Mackenzie KJD, Smith ME. Multinuclear Solid-State NMR of Inorganic Materials. Vol. 6 Pergamon; London: 2002. [Google Scholar]
- 47.Sternberg U. Solid State Nuclear Magnetic Resonance. 1993;2:181. doi: 10.1016/0926-2040(93)90023-g. [DOI] [PubMed] [Google Scholar]
- 48.Slichter CP. Principles of Magnetic Resonance. Harper & Row; New York: 1963. [Google Scholar]
- 49.Taulelle F. NMR of Quadrupolar Nuclei in the Solid State. Vol. 322 Kluwer Academic Publishers; London: 1988. [Google Scholar]
- 50.Man PP. Encyclopedia of Analytical Chemistry. John Wiley and Sons; Chichester: 2000. [Google Scholar]
- 51.Ashbrook SE, Wimperis S. eMagRes. John Wiley & Sons, Ltd; 2007. [Google Scholar]
- 52.Wu G, Hook A, Dong S, Yamada K. The Journal of Physical Chemistry A. 2000;104:4102. [Google Scholar]
- 53.Wu G, Yamada K. Solid State Nuclear Magnetic Resonance. 2003;24:196. doi: 10.1016/s0926-2040(03)00046-8. [DOI] [PubMed] [Google Scholar]
- 54.Herzfeld J, Berger AE. Journal of Chemical Physics. 1980;73:6021. [Google Scholar]
- 55.Perdew JP, Burke K, Ernzerhof M. Physical Review Letters. 1996;77 doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 56.Perdew JP, Burke K, Ernzerhof M. Physical Review Letters. 1998;80 doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 57.Vanderbilt D. Physical Review B. 1990;41:7892. doi: 10.1103/physrevb.41.7892. [DOI] [PubMed] [Google Scholar]
- 58.Yates JR, Pickard CJ, Payne MC, Mauri F. Journal of Chemical Physics. 2003;118:5746. [Google Scholar]
- 59.Fuess H, Hohlwein D, Mason SA. Acta Crystallographica. 1977;B33:654. [Google Scholar]
- 60.Madhaven J, Aruna S, Thomas PC, Vimalan M, Rajasekar SA, Sagayaraj P. Crystal Research and Technology. 2007;42:59. [Google Scholar]
- 61.Parthasarathy R. Acta Crystallographica. 1969;B25:509. [Google Scholar]
- 62.Koetzle TF, Hamilton WC, Parthasarathy R. Acta Crystallographica. 1972;B28:2083. [Google Scholar]
- 63.Xian L, Lu G-X. Chemical Research and Application. 2007;19:474. [Google Scholar]
- 64.Flaig R, Koritsanszky T, Dittrich B, Wagner A, Luger P. Journal of the American Chemical Society. 2002;124:3407. doi: 10.1021/ja011492y. [DOI] [PubMed] [Google Scholar]
- 65.Ramanadham M, Sikka SK, Chidambaram R. Acta Crystallographica. 1972;B28:3000. [Google Scholar]
- 66.Ayyar RR, Srinivasan R. Current Science. 1965;34:449. [Google Scholar]
- 67.Chapman RP, Bryce DL. Physical Chemistry Chemical Physics. 2007;9:6219. doi: 10.1039/b712688c. [DOI] [PubMed] [Google Scholar]
- 68.Panneerselvam K, Soriano-Garcia M. Acta Crystallographica. 1995;C51:2718. [Google Scholar]
- 69.Umadevi K, Anitha K, Sridhar B, Srinivasan N, RK R. Acta Crystallographica. 2003;E59:01073. [Google Scholar]
- 70.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JJA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox J, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RK, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Conzalez C, Pople JA. G03 ed.; Gaussian. 2003 [Google Scholar]
- 71.Lee C, Yang W, Parr RG. Physical Review B: Condensed Matter. 1988;37:785. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 72.Becke AD. Journal of Chemical Physics. 1993;98:5648. [Google Scholar]
- 73.Becke AD. Journal of Chemical Physics. 1996;107:8554. [Google Scholar]
- 74.Eichele, K.; 1.20.21 ed. 2013.
- 75.Massiot D, Fayon F, Capron M, King I, Le Calve S, Alonso B, Durand JO, Bujoli B, Gan Z, Hoatson G. Magnetic Resonance in Chemistry. 2002;40:70. [Google Scholar]
- 76.Veshtort M, Griffin RG. Journal of Magnetic Resonance. 2006;178:248. doi: 10.1016/j.jmr.2005.07.018. [DOI] [PubMed] [Google Scholar]
- 77.Adiga S, Aebi D, Bryce DL. Canadian Journal of Chemistry. 2007;85:496. [Google Scholar]
- 78.Spiess HW, Garrett BB, Sheline RK. Journal of Chemical Physics. 1969;51:1201. [Google Scholar]
- 79.Zhang QW, Zhang HM, Usha MG, Wittebort RJ. Solid State Nuclear Magnetic Resonance. 1996;7:147. doi: 10.1016/s0926-2040(96)01258-1. [DOI] [PubMed] [Google Scholar]
- 80.Lemaitre V, Smith ME, Watts A. Solid State Nucl Magn Reson. 2004;26:215. doi: 10.1016/j.ssnmr.2004.04.004. [DOI] [PubMed] [Google Scholar]
- 81.Pike KJ, Lemaitre V, Kukol A, Anupold T, Samoson A, Howes AP, Watts A, Smith ME, Dupree R. J Phys Chem B. 2004;108:9256. [Google Scholar]
- 82.Goc R, Ponnusamy E, Tritt-Goc J, Fiat D. International Journal of Peptide and Protein Research. 1988;31:130. doi: 10.1111/j.1399-3011.1988.tb00015.x. [DOI] [PubMed] [Google Scholar]
- 83.Kuroki S, Ando I, Shoji A, Ozaki T. Chemical Communications. 1992;433 [Google Scholar]
- 84.Wong A, Howes AP, Yates JR, Watts A, Anupold T, Past J, Samoson A, Dupree R, Smith ME. Physical Chemistry Chemical Physics. 2011;13:12213. doi: 10.1039/c1cp20629j. [DOI] [PubMed] [Google Scholar]
- 85.Zhu J, Lau JYC, Wu G. The Journal of Physical Chemistry B. 2010;114:11681. doi: 10.1021/jp1055123. [DOI] [PubMed] [Google Scholar]
- 86.Gervais C, Dupree R, Pike KJ, Bonhomme C, Profeta M, Pickard CJ, Mauri F. The Journal of Physical Chemistry A. 2005;109:6960. doi: 10.1021/jp0513925. [DOI] [PubMed] [Google Scholar]
- 87.Yates JR, Pickard CJ, Payne MC, Dupree R, Profeta M, Mauri F. Journal of Physical Chemistry A. 2004;108:6032. [Google Scholar]
- 88.Profeta M, Benoit M, Mauri F, Pickard CJ. Journal of the American Chemical Society. 2004;126:12628. doi: 10.1021/ja0490830. [DOI] [PubMed] [Google Scholar]
- 89.Profeta M, Mauri F, Pickard CJ. Journal of the American Chemical Society. 2003;125:541. doi: 10.1021/ja027124r. [DOI] [PubMed] [Google Scholar]
- 90.Kong X, O’Dell LA, Terskikh V, Ye E, Wang R, Wu G. Journal of the American Chemical Society. 2012;134:14609. doi: 10.1021/ja306227p. [DOI] [PubMed] [Google Scholar]
- 91.Rees GJ, Day SP, Lari A, Howes AP, Iuga D, Pitak MB, Coles SJ, Threlfall TL, Light ME, Smith ME, Quigley D, Wallis JD, Hanna JV. CrystEngComm. 2013;15:8823. [Google Scholar]
- 92.Long JR, Ebelhäuser R, Griffin RG. The Journal of Physical Chemistry A. 1997;101:988. [Google Scholar]
- 93.Maly T, Andreas LB, Smith AA, Griffin RG. Physical Chemistry Chemical Physics. 2010;12:5872. doi: 10.1039/c003705b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Chiba T. Journal of Chemical Physics. 1963;39:947. [Google Scholar]
- 95.Eriksson A, Hussein MA, Berglund B, Tegenfeldt J, Lindgren J. Journal of Molecular Structue. 1979;52:95. [Google Scholar]
- 96.Millar JM, Thayer AM, Zax DB, Pines A. Journal of the American Chemical Society. 1986;108:5113. [Google Scholar]
- 97.De Paepe G. Annual Review on Physical Chemistry. 2012;63:661. doi: 10.1146/annurev-physchem-032511-143726. [DOI] [PubMed] [Google Scholar]
- 98.Griffin RG. Nature Structural Biology. 1998;5:508. doi: 10.1038/749. [DOI] [PubMed] [Google Scholar]
- 99.Wylie BJ, Sperling LJ, Nieuwkoop AJ, Franks WT, Oldfield E, Rienstra CM. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:16974. doi: 10.1073/pnas.1103728108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Bascunan J, Hahn S, Park D-K, Iwasa Y. IEEE Transactions Applied Superconductivity. 2011;21:2092. doi: 10.1109/TASC.2010.2086995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Benoit M, Profeta M, Mauri F, Pickard CJ, Tuckerman ME. Journal of Physical Chemistry B. 2005;109:6052. doi: 10.1021/jp0492570. [DOI] [PubMed] [Google Scholar]
- 102.Wong A, Thurgood G, Dupree R, Smith ME. Chemical Physics. 2007;337:144. [Google Scholar]
- 103.Kuroki S, Ando S, Ando I, Shoji A, Ozaki T, Webb GA. Journal of Molecular Structure. 1990;240:19. [Google Scholar]
- 104.Kuroki S, Asakawa N, Ando S, Ando I, Shoji A, Ozaki T. Journal of Molecular Structure. 1991;245:69. [Google Scholar]
- 105.Wong A, Pike KJ, Jenkins R, Clarkson GJ, Anupold T, Howes AP, Crout DHG, Samoson A, Dupree R, Smith ME. Journal of Physical Chemistry A. 2006;110:1824. doi: 10.1021/jp055807y. [DOI] [PubMed] [Google Scholar]
- 106.Takahashi A, Kuroki S, Ando I, Ozaki T, Shoji A. Journal of Molecular Structure. 1998;442:195. [Google Scholar]
- 107.Kuroki S, Yamauchi K, Ando I, Shoji A, Ozaki T. Current Organic Chemistry. 2001;5:1001. [Google Scholar]
- 108.Chiari G, Ferraris G. Acta Crystallographica. 1982;B 38:2331. [Google Scholar]
- 109.Goswami M, Madhu PK. Journal of Magnetic Resonance. 2012;219:4. doi: 10.1016/j.jmr.2012.03.018. [DOI] [PubMed] [Google Scholar]
- 110.Ganapathy S, Delevoye L, Arnoureux JP, Madhu PK. Magnetic Resonance in Chemistry. 2008;46:948. doi: 10.1002/mrc.2286. [DOI] [PubMed] [Google Scholar]
- 111.Keeler EG, Michaelis VK, Griffin RG. Submitted. 2015 [Google Scholar]
- 112.Wong A, Howes AP, Pike KJ, Lemaitre V, Watts A, Anupold T, Past J, Samoson A, Dupree R, Smith ME. Journal of the American Chemical Society. 2006;128:7744. doi: 10.1021/ja062031l. [DOI] [PubMed] [Google Scholar]
- 113.Dong S, Ida R, Wu G. The Journal of Physical Chemistry A. 2000;104:11194. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


