Integrated protein function prediction by mining function associations, sequences, and protein–protein and gene–gene interaction networks

Abstract

Motivations

Protein function prediction is an important and challenging problem in bioinformatics and computational biology. Functionally relevant biological information such as protein sequences, gene expression, and protein–protein interactions has been used mostly separately for protein function prediction. One of the major challenges is how to effectively integrate multiple sources of both traditional and new information such as spatial gene–gene interaction networks generated from chromosomal conformation data together to improve protein function prediction.

Results

In this work, we developed three different probabilistic scores (MIS, SEQ, and NET score) to combine protein sequence, function associations, and protein–protein interaction and spatial gene–gene interaction networks for protein function prediction. The MIS score is mainly generated from homologous proteins found by PSI-BLAST search, and also association rules between Gene Ontology terms, which are learned by mining the Swiss-Prot database. The SEQ score is generated from protein sequences. The NET score is generated from protein–protein interaction and spatial gene–gene interaction networks. These three scores were combined in a new Statistical Multiple Integrative Scoring System (SMISS) to predict protein function. We tested SMISS on the data set of 2011 Critical Assessment of Function Annotation (CAFA). The method performed substantially better than three base-line methods and an advanced method based on protein profile–sequence comparison, profile–profile comparison, and domain co-occurrence networks according to the maximum F-measure.

1. Introduction

Protein function prediction is important for understanding life at the molecular level and therefore is highly demanded by biomedical research and pharmaceutical applications [1]. There are a large amount of sequence data generated by next generation sequencing every day. However, the annotation of the function of these sequences by experimental is still a big challenge because of the inherent difficulty and considerable expense [2]. In addition, some experiments in vitro may not faithfully reflect a protein’s activity in vivo [3]. Therefore, accurately predicting protein function from sequence using computational methods is a useful way to solve the problem at large scale and low cost.

A number of computational protein function prediction methods had been developed in the last few decades [4–11]. The most commonly used method is to use the tool Basic Local Alignment Search Tool (BLAST) [12] to search a query sequence against protein databases containing experimentally determined function annotations to retrieve the hits based on the sequence homology. The function of homologous hits is used as the prediction of the query sequence. Some of this kind of methods are GOtch [13], OntoBlast [14], and Goblet [15]. However, the prediction coverage of BLAST based methods may be low because BLAST is not sensitive enough to find many remote homologous hits. Some other methods such as PFP [16] use profile–sequence alignment tool PSI-BLAST [12] to get more sensitive predictions.

In addition to sequence homology, some methods use other information to predict protein function. In order to incorporate the prediction of functional residues into the prediction of protein function at the whole molecular level [17,18], some methods predict protein function based on amino acid sequences [19,20]. Some other methods make function prediction based on protein–protein interaction networks [9,21–25] assuming that interacted proteins may share the similar function. Others make function prediction by using protein structure data [18,26,27], microarray gene expression data [28], or combination of several sources of information [29–32]. One of the biggest challenges of protein function prediction is how to obtain diverse relevant biological data, such as protein amino acid sequence, gene–gene interaction data, protein–protein interaction data, protein structure from multiple reliable sources efficiently, and how to integrate these biological data to make protein function prediction [33].

Besides the development of function prediction methods, unbiased benchmarking of different method is also very important for the community to identify the strengths and weaknesses of different methods in order to develop more accurate function prediction methods. The Critical Assessment of Function Annotation (CAFA, http://biofunctionprediction.org/) is an experiment designed to provide such a large-scale assessment of protein function prediction methods, and it has benefited the whole community by involving a significant number of groups to blindly test their function prediction methods on the same set of proteins within a specific time frame [1], which also provide a test ground for benchmarking new methods including our method developed in this work. During CAFA in 2011, 30 teams associated with 23 research groups participated in the effort, and several new methods have been developed to achieve high accuracy of protein function prediction [1]. For example, sequence-based function prediction methods PFP [16,34] and ESG [35] from professor Kihara’s lab use PSI-BLAST one time and recursively against the target sequence to get the hits for protein function prediction [36,37], the method from the team Jones-UCL integrates a wide variety of biological information sources into a framework for protein function prediction [38], Argot2 annotates protein sequence with GO terms from the UniProtKB-GOA database weighted by their semantic relationship for protein function prediction [39,40], GOstruct uses co-mention and bag-of-words features mined from the biomedical literature for protein structure prediction [41], PANNZER uses weighted k-nearest neighbor methods with statistical testing to maximize the reliability of a functional annotation [42], and MS-kNN method finds k-nearest neighbors of a query protein based on different types of similarity measures and predicts its function by weighted averaging of its neighbors’ functions [43].

In this work, we develop a novel Statistical Multiple Integrative Scoring System (SMISS) for protein function prediction. SMISS integrates the information from homologs found by PSI-BLAST, protein–protein interaction networks, spatial gene–gene interaction networks derived from chromosomal conformation capturing data, and amino acid sequence information, and calculates three different probability scores (MIS score, NET score, and SEQ score) for each GO term based on these information, and makes function prediction based on the combination of these three scores. SMISS is a very open system, which can be easily expanded to include more biological information to enhance the accuracy of protein function prediction.

The rest of the paper is organized as follows. In Section 2, we describe how to calculate three different scores and integrate them to make protein function prediction. In Section 3, we blindly test our method and compare it with three base-line methods and three network-based protein function prediction methods. In Section 4, we summarize the work and discuss the direction of future work.

2. Methods

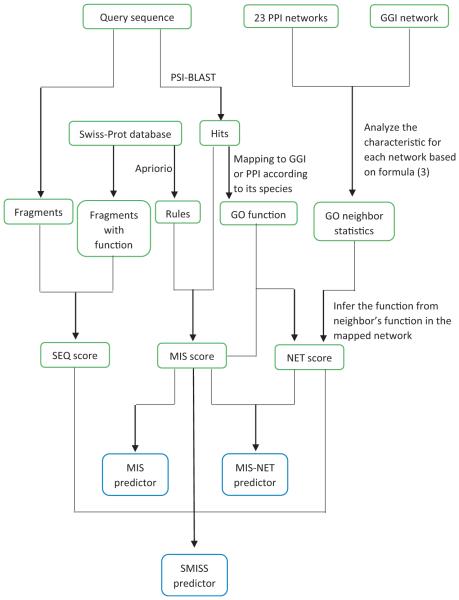
The SMISS (Statistical multiple integrative scoring system for protein function prediction) method uses three different scores: the MIS score (Multiple Integrated Score) which is calculated based on the PSI-BLAST hits and their GO terms inferred from the Swiss-Prot database by data mining techniques, the NET score (Network score) which is calculated from spatial gene–gene interaction networks and protein–protein interaction networks, and the SEQ score (Sequence score) which is calculated from the amino acid sequence of a query protein. We test three different predictors by combining these three scores in different ways. The first one is SMISS-predictor, which combines all three scores. The second one is MIS-predictor, which only use the MIS score. The third one is MIS–NET-predictor, which combines the MIS score and the NET score. Fig. 1 shows the overall flowchart of our three predictors. We introduce the method to calculate each score in the following section.

Fig. 1.

The overall flowchart of our method.

2.1. MIS score

The calculation of MIS score is different for two types of GO functions. For the first type, the MIS score is calculated from the PSI-BLAST results while searching against Swiss-Prot [44] database. The default setting of PSI-BLAST has been used with 3 iterations on Swiss-Prot databased released on Jul. 2010 for benchmark on CAFA1, the default e-value threshold (i.e. 10) is applied for prediction, and the predictions with e-value larger than 0.01 are ignored since their confidence score is 0 based on formula (1). All the potential distantly homologous protein hits and their e-values are retrieved and stored. The e-value of each protein hit is converted into a probabilistic confidence score using the following formula:

$$S=\frac{-{\log }_{10}t}{200}-0.01$$ (1)

In this formula, t is the e-value of the protein, and S is the probabilistic confidence score. We constrain the confidence score to be in the range of 0 and 1. That is, the confidence score is set to 0 for all hits with e-value (t) larger than 0.01, and all hits with e-value less than e-202 have confidence score 1. Assuming that N protein hits have confidence score larger than 0, and P_i is the number i protein (i ϵ [1;N]), we can get all gene ontology (GO) terms from the Swiss-Prot database for each P_i. The n_i GO terms for P_i are denoted as $G_{i_1},G_{i_2},\cdots ,G_{i_{n_i}}$. By applying formula (1), we can calculate the confidence score P(P_i ) of each GO term associated with P_i. The same confidence score is assigned to each GO term of P_i , such that $P\left(G_{i_j}\right)=P\left(P_i\right)$, where j ϵ [1; n_i]. Given the GO terms lists $\left(G_{i_j}\right)$ with the probabilistic confidence scores $\left(P\left(G_{i_j}\right)\right)$, we combine them to generate a list of unique GO terms $\left(G_k^{\prime }\right)$ and calculate the confidence scores $\left(P\left(G_k^{\prime }\right)\right)$, while i ϵ [1; N], j ϵ [1; n_i], and k ≥ 0 as follows. Assuming the same GO term G_x appears in the GO term lists of two different proteins i and j with confidence scores P_i (G_x) and P_j (G_x), respectively, the following formula is used to update the combined confidence score of the GO term G_x :

$$P\left(G_x\right)=1-(1-P_i\left(G_x\right))\ast (1-P_j\left(G_x\right))$$ (2)

We continuously update the confidence score of any two same GO terms existing in different proteins by formula (2), and it can be proved (details omitted) that the final confidence score for each GO term G_x is: $P\left(G_x\right)=1-{\prod }_{i=1}^{i=N}(1-P_i\left(G_x\right))$ where P_i (G_x) is the confidence score of the GO term G_x in the ith protein (P_i). After applying formula (2), we can finally get a list of unique GO terms $\left(G_k^{\prime }\right)$ with the calculated confidence score $P\left(G_k^{\prime }\right)$.

For the second type of GO terms, the MIS score is assigned as 1. The GO terms are inferred from the protein hits with confidence score 1. To infer the unobserved GO terms, we first apply Apriori algorithm [45] to mine the association rules from Swiss-Prot database. Apriori algorithm is used for association rule mining in transaction database, and here we apply it to get the association rules for protein function prediction. First, we extract the GO function from the Swiss-Prot database for each protein sequence. Assuming there are N different GO terms, G₁, ..., G_N, N is the total number of GO terms in the database, and each protein’s GO functions are considered as a transaction. Secondly, the Apriori algorithm is used to generate the association rules, G_i, ..., G_j → G_k, i, j, and k are all integers equal or less than N. In our case, that is the association rules between different GO terms. There are two parameters for Apriori algorithm for us to tune: the minimum support and minimum confidence. To decide these two parameters, five cross validation techniques are used, while dividing all GO function transactions into five folds, four of them are used for training, and the other one for testing. The precision and recall are used to evaluate the performance. The minimum support is set to 0.05, and minimum confidence is set to 90 based on the five cross validation result, while 51,512 association rules are generated. More details of tuning the parameters are included in Section 3. Finally, after generating the association rules by data mining technique, we check all combination of GO terms with confidence 1, and apply the association rules mined from Swiss-Prot database to infer more GO terms. The MIS score of all inferred GO terms are set as 1. In summary, the MIS score is calculated from PSI-BLAST results by formula (2), and is set as 1 for GO terms inferred by Apriori algorithm.

2.2. NET score

Protein–protein interaction networks and spatial gene–gene interaction networks have been used for generating the NET score, irefindex network [46] is used for generating 23 protein–protein interaction networks of multiple species. irefindex provides an index of protein interactions available in a number of primary interaction databases, and we parse it for 22 different species to get 22 protein–protein interaction networks, and another network for remaining proteins. The gene–gene interaction network [47] is generated from Hi-C contact data of the normal B-cell [48]. We consider two genes are interacting when the total number of Hi-C contact between them is more than a contact threshold [48]. We want to mention that this gene–gene interaction network is used for proteins in Homo sapiens that can be mapped to it. Otherwise, the 23 protein–protein interaction networks are used. Here, if two genes/proteins are connected in a network, their GO terms are assumed to interact. For any two interacted GO terms G_i and G_j from gene–gene/protein–protein interaction networks, we calculate the probability score between them for statistical analysis as follows:

$$P(G_i\mid G_j)=\frac{F(G_i\mid G_j)}{\sum _{k=1}^{k=N}F(G_i\mid G_k)}$$ (3)

In formula (3), F(G_i|G_j) is the total number of interactions for the GO term G_j interacting with GO term G_i. N is the total number of GO terms interacting with GO term G_i. We calculate the scores by this formula for all neighboring GO terms of each 23 protein– protein interaction networks and gene–gene interaction network, and store them for protein function prediction. Given a query sequence, first, we retrieve the protein hits lists with e-values by PSI-BLAST for it. Second, we search each protein from the protein hits lists starting from lowest e-value until we find one which has GO functions. To predict the GO functions, we map the protein to our generated gene–gene interaction/protein–protein interaction networks. Given that this protein is in H. sapiens and the gene encoding it exists in our generated gene–gene interaction network, we use the gene–gene interaction network to predict the GO functions, otherwise, the protein–protein interaction network for species of this protein is used for the function prediction. We store the MIS score of the selected mapped gene/protein as M_map. Thirdly, we obtain the neighbors of the mapped gene/protein in the networks, and get all GO terms (G_k) from each neighbor gene/protein, while k ϵ [1; N], and N is the total number of GO terms from all neighbors. Finally, we generate all possible GO term neighbors GN_l for each GO term from the statistics calculated on the gene–gene interaction network/protein–protein interaction network. The probability score for each GO term neighbor GN_l is calculated as M_map times the score generated by applying formula (3) to the whole gene–gene/protein–protein interaction network between GN_l and G_k. We combine all GO term neighbors GN_l by formula (2), and generate the final GO term list. The final probability score for each GO term is the NET score. Here, l ϵ [1; NN], and NN is the total number of GO term neighbors.

2.3. SEQ score

We calculate the SEQ score from the protein sequence itself. We retrieve all protein sequences and the protein function GO terms in the Swiss-Prot database. We use a 5-residue sliding window technique to divide each sequence into sequence fragment with a length of 5. The reason to use a length of 5 is because we want to include more GO terms and fragments smaller than or equal to 4 cannot represent the structural information accurately [49]. So given the protein sequence with length N, there are in total (N-5) sequence fragments. Let’s assume a protein has a number of GO function terms G_i , while i ϵ [1; M], and M is the total number of GO terms. The sequence of that protein can be divided into (N-5) sequence fragments, and for one specific sequence fragment S_j, the conditional probability of GO term G_i inferred from it can be calculated in the following formula:

$$P(G_i\mid S_j)=\frac{F\left(S_j\right)}{(N-5)}$$ (4)

N is the sequence length, and F(S_j) is the frequency of the sequence fragment S_j extracted from the sequence by the 5-residue sliding window technique. The frequency could be more than one since one sequence fragment may exist more than one time in the protein sequence. Secondly, we calculate the probability of GO term G_i inferred from sequence fragment S_j for each sequence by applying formula (4). Thirdly, we combine all GO terms with the following formula when the same GO term G_i inferred from the same sequence fragment S_j in different sequence:

$$P(G_i\mid S_j)=1-(1-P_1(G_i\mid S_j))\ast (1-P_2(G_i\mid S_j))$$ (5)

P₁ (G_i|S_j) and P₂ (G_i|S_j) are the probability from the two different sequences. In the prediction phase, for each query protein sequence, we divide it into sequence fragment with 5-residue sliding window technique, and for each sequence fragment, we search against the sequence fragment database built from the Swiss-Prot database by formula (5), and get all possible GO terms G_i with the probability score P(G_i). The formula (2) is used to combine all same GO terms from different sequence fragment. Finally, we generate a GO term list for the query protein sequence and the SEQ probability score for each GO term.

2.4. Score combination

We develop three different predictors with different combination of these three scores. The first predictor is SMISS-predictor that combines all three different GO term lists calculated from MIS, NET and SEQ scores, respectively. The following formula is used to calculate the finally combined score for each GO term G_i :

$$\begin{array}{cc}\hfill P\left(G_i\right)& =1-(1-W_{\mathrm{MIS}}\ast P_{\mathrm{MIS}}\left(G_x\right))\ast (1-W_{\mathrm{NET}}\ast P_{\mathrm{NET}\left(G_x\right)})\hfill \\ \hfill & \ast (1-W_{\mathrm{SEQ}}\ast P_{\mathrm{SEQ}}\left(G_x\right))\hfill \end{array}$$ (6)

p_MIS(G_x)is the MIS score of this GO term, P_NET (G_x) is the NET score of this GO term, P_SEQ (G_x) is the SEQ score of this GO term, W_MIS is the weight for MIS score, W_NET is the weight for NET score, and W_SEQ is the weight for SEQ score. We set the weight 0.5 for MIS score, 0.22 for NET score, and 0.28 for SEQ score empirically, which is based on their accuracy on our local benchmark for each score. The second predictor is MIS-predictor, which only uses the GO term list calculated by the MIS score. And the third predictor is MIS–NET-predictor, which generate two different GO term lists by calculating the MIS score and NET score, and finally combines these two GO term lists for the final prediction. The formula (6) is used to combine them while the P_SEQ (G_x) is set to 0 for MIS– NET-predictor.

2.5. Score scaling

The combined scores may be hard to analyze and evaluate when several GO term predictions have very similar scores close to 1 or when there are no predictions with relatively high confidence score. In order to avoid the problem, the combined scores are rescaled. For all predicted GO terms of a query sequence, we rank them based on the confidence score. Each prediction gets a ranking R_i. A new score (S + 0:01 - 0:01 * R_i) is assigned to all predictions. S is the initial score, S can be set as 1 or the max confidence score. In our method, we set it to 1. Two predictions with the same confidence score have the same ranking. For the predictions with the non-positive scaled score, we reset the score to 0.01.

3. Results and discussion

3.1. Parameters in Apriori algorithm for calculating MIS score

We apply data mining technique Apriori algorithm to obtain more GO terms as the predictions. There are two parameters for the Apriori algorithm: minimum support and minimum confidence. Given a rule X ⇒ Y regarding two GO terms X and Y, the minimum support is the minimum probability of an arbitrary transaction (e.g. the set of GO terms of a protein) contains both X and Y, and the minimum confidence is a conditional probability that a transaction having X also contains Y. We use the fivefold cross-validation on the GO terms in the Swiss-Prot database to optimize the two parameters. The performance of using different values of minimum support and minimum confidence is shown in Table 1. We first fix the minimum confidence at 60, and try different minimum support, and the multiplication of precision and recall is maximized when minimum support is 0.1, and it decreases as the minimum support increases. Then we increase the minimum confidence to 70, and try minimum support values less than 0.1, and the multiplication of precision and recall decreases as the minimum support increases. Another finding is that the minimum confidence actually does not influence the multiplication of precision and recall too much. For the same minimum support 0.1, with minimum confidence 60 and 70, the multiplication of precision and recall is 0.079669 and 0.079751, respectively. So we decide to try larger minimum confidence score, such as 90, and the result shows smaller minimum support has better performance. The number of rules generating for different minimum support values such as 0.02, 0.03, 0.04 is 171,817, 120,114, 62,707, 51,356, respectively. Considering the computation complexity related to the number of rules and their similar performance, we finally decide to set minimum support as 0.05 and minimum confidence as 90.

Table 1.

The precision, recall, and multiplication of precision and recall for different values of minimum support and confidence according to fivefold cross validation.

Min support	Min confidence	Precision	Recall	Multiplication
0.1	60	0.175247	0.454611	0.079669
0.2	60	0.175762	0.294839	0.051821
0.3	60	0.178529	0.240628	0.042959
0.4	60	0.178	0.217349	0.038688
0.5	60	0.180751	0.203954	0.036865
0.6	60	0.184234	0.194982	0.035922
0.7	60	0.185663	0.179099	0.033252
0.8	60	0.187923	0.176552	0.033178
0.9	60	0.191136	0.166148	0.031757
1	60	0.193348	0.155527	0.030071
0.02	70	0.189585	0.575122	0.109035
0.03	70	0.19235	0.552382	0.10625
0.05	70	0.19523	0.504344	0.098463
0.1	70	0.193433	0.41229	0.079751
0.15	70	0.19347	0.296692	0.057401
0.1	80	0.205309	0.357896	0.073479
0.15	80	0.206317	0.242143	0.049958
0.02	90	0.218213	0.48637	0.106133
0.03	90	0.219549	0.461519	0.101326
0.04	90	0.220407	0.4356	0.096009
0.05	90	0.221515	0.415496	0.092039
0.06	90	0.221194	0.392394	0.086795
0.07	90	0.221575	0.378077	0.083773
0.08	90	0.22069	0.361477	0.079774
0.09	90	0.219519	0.339378	0.0745
0.1	90	0.219174	0.320815	0.070314
0.15	90	0.223325	0.207827	0.046413

3.2. Prediction performance

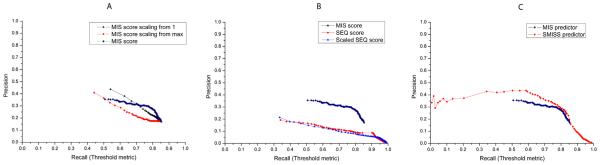
We evaluate the performance of our method on CAFA1 datasets. CAFA released 48,298 protein targets in total, and 436 of them whose function deposited in Swiss-Prot database are used for our evaluation. Different threshold from 1 to 0.01 decreased by 0.01 is used as thresholds on predicted GO term scores. The predictions with confidence score higher than the threshold will be selected to compare with the true GO terms (threshold metric). Based on this metric, we evaluate the performance of MIS score and how the score scaling technique influences the performance. The precision and recall metrics are used to evaluate the performance of the prediction. Here, in evaluating the performance of our methods on CAFA1 datasets, all predicted and actual GO terms are propagated to the root of the Gene Ontology Directed Acyclic Graph (DAG). All the GO terms in the paths of predicted GO terms toward the root were considered as predicted GO terms, and all the GO terms present in the paths of the actual GO terms toward the root were considered as true GO terms. The overlapping GO terms between predicted and true GO terms are considered as correct predictions. The precision is calculated by the total number of correct predictions divided by the total number of predicted GO terms, and the recall is calculated by the total number of correction predictions divided by the total number of true GO terms [10]. These two metrics are complementary to evaluate the performance of a method from different perspective. The result is shown in Fig. 2A. We test two different score scaling techniques. One is scaled from 1, which sets the starting score to 1. Another is scaled from max, which sets the starting score to the maximum score among all predictions. Fig. 2A shows that the MIS score gets similar precision for the recalls in the range of 0.5 and 0.75, but the precision drops drastically when the recall is larger than 0.75. That is because a lot of false-positive predictions are made at a low threshold. Comparing the two score scaling techniques, scaling from 1 has better performance with higher precision, and finally they both can reach a similar high recall 0.85. Comparing the MIS score with and without score scaling, they both can reach a high recall, but the one with score scaling can reach a higher precision, and the precision decreases more smoothly as recall increases. We calculate the maximum multiplication of precision and recall. MIS score with and without score scaling get 0.239 and 0.231, respectively, suggesting applying score scaling technique slightly improve the performance.

Fig. 2.

The performance comparison for MIS, SEQ, and SMISS using scaled technique benchmarked on CAFA1. X-axis shows the recall of the prediction, and y-axis shows the precision of the prediction. (A) The performance of original MIS score and the score with score scaling technique start from 1 or max. (B) The performance of MIS score, original SEQ score, and the scaled SEQ score. (C) The comparison between MIS predictor and SMISS predictor.

It is interesting to compare the performance of the MIS score and the SEQ score. Fig. 2B demonstrates the performance difference of between the two scores. The SEQ score has relatively low precision because it usually makes more predictions and at the same time it can reach a relatively high recall for the same reason. And the SEQ scores with and without scaling techniques have similar performance. Fig. 2C illustrates the performance of combining all three different scores by the SMISS predictor. The SMISS predictor outperforms the MIS predictor in both recall and precision. The SMISS can reach a very high recall probably because of the contribution of the SEQ score.

Moreover, we compare the SMISS predictor with three standard baseline methods (Prediction 57, Prediction 58, and Prediction 59) and three predictors (Prediction 1, Prediction 2, and Prediction 3) that integrates profile–sequence homology search, profile–profile homology search and domain co-occurrence network [10]. Prior method is used for Prediction 57, which selects 836 most frequent GO terms counted from the Swiss-Prot database for each target as prediction [10]. Prediction 58 is based on BLAST method, which uses the tool BLAST [12] to search the target protein against groups of proteins for predictions [10]. The third baseline method for Prediction 59 is GOtcha method [13], which generates the sum of the negative logarithm of the e-values resulted from the BLAST search (GOtcha I-Scores) as the confidence score for GO terms selection [10]. The result is shown in Fig. 2B. The three predictors (Prediction 1, Prediction 2, and Prediction 3) perform better mostly than the standard baseline methods (Prediction 57, Prediction 58, and Prediction 59). Although the precision of the SMISS predictor is not as high as other methods, it can reach a higher recall than other methods because it can make more GO term predictions. In order to balance both precision and recall, we use F-measure to compare these methods. The maximum F-measure of our SMISS predictor is 0.500, much higher than 0.269, 0.211, and 0.289 of Prediction 57, Prediction 58, and Prediction 59. In addition, it is also higher than 0.347, 0.302, and 0.310 of Prediction 1, Prediction 2, and Prediction 3 (see Fig. 3).

Fig. 3.

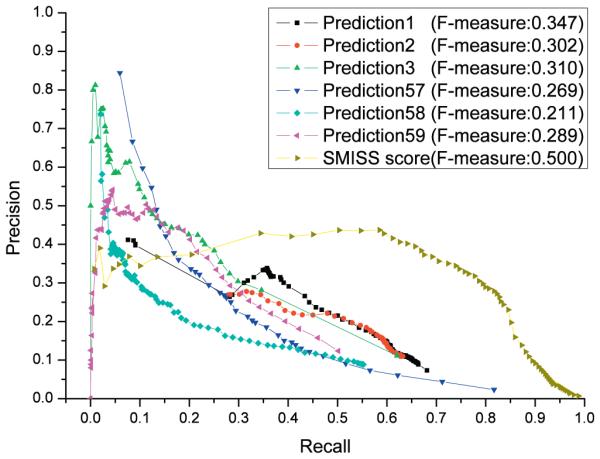
The performance of our SMISS with three standard baseline method and three predictors from an automated three-level method. Prediction 57, 58, 59 is the standard baseline method, and Predictors 1, 2, 3 is three predictors from an automated three-level method. X-axis shows the recall for each predictor, and y-axis shows the precision for each predictor.

3.3. Case study

We randomly select few proteins whose function is released recently, and submit the query protein sequence in our protein function prediction website to test the usefulness of our method. We only keep the predictions which have confidence score more than 0.9, so that our prediction is not influenced by some random predictions which has low confidence score. Table 2 shows the summary of PDB ids with their true functions and the protein function predictions made by our methods in the case study. The first case is 4OPY, which is released at 05/20/2015, and the UniProtKB id is Q9AGJ5. This protein has four GO functions: GO:0030655, GO:0046677, GO:0008800, and GO:0016787. Our SMISS predictor successfully predict three of them (GO:0030655, GO:0046677, and GO:0008800), so that the precision is 1, and recall is 0.75. In addition to the three GO function predicted by SMISS predictor, the MIS predictor also predicts the function GO:0033251, which is considered as true while propagating the function GO:0016787 to the root. The MIS predictor predicts 12 functions in total for this protein, so that the precision is 0.33, and recall is 1. The MIS–NET predictor only predicts 8 functions, including all true prediction by MIS predictor, so the precision is 0.5, and recall is 1. The SMISS predictor actually makes more function predictions, but only few of them could have confidence score more than 0.9, since our combination process finally assigns high confidence score to the predictions which are predicted from different sources on consensus. The defect for SMISS predictor is that it sometimes misses few true predictions because of its high standard, for example, the function GO:0033251 is not assigned as confidence score more than 0.9 for SMISS predictor, but it is predicted by MIS and MIS–NET predictor. The second case is 4O7V, which is released at 12/31/2014, and the UniProtKB is O57978. There are five GO functions: GO:0006164, GO:0006189, GO:0000166, GO:0004639, and GO:0005524. The MIS predictor successfully predicts four of them (GO:0006164, GO:0006189, GO:0004639, and GO:0005524), missing the function GO:0000166. It makes 15 function predictions, so the precision is 0.27, and recall is 0.80. The MIS–NET predictor has 14 function predictions for this protein, and three of them (GO:0006189, GO:0004639, and GO:0005524) are correct. The confidence score of GO:0006164 by MIS–NET predictor is not more than 0.9 since it is not found from the network, making the precision as 0.6, and recall as 0.21. The SMISS predictor combines the prediction from three different sources, so it also misses the function GO:0006164. It only makes three function predictions with confidence score more than 0.9, and successfully predicts the function GO:0006189, GO:0004639, and GO:0005524. The precision for SMISS predictor is 1, and recall is 0.60. Once we consider the F-measure, which is the multiplication of precision and recall, we can see that the F-measure for MIS, MIS–NET, and SMISS predictor is 0.22, 0.13, and 0.6, respectively. As is shown, the SMISS predictor combines different sources, even though it may miss some true functions, it is still very useful considering both precision and recall. The MIS and MIS–NET predict more functions with high confidence score, so that it can cover more true GO functions.

Table 2.

Summary of PDB ids with their true functions and the protein function predictions made by our methods in the case study.

PDB id	True functions (GO ID: description)	SMISS prediction/ score	MIS prediction/ score	MIS–NET prediction/ score
4OPY	GO:0030655: beta-lactam antibiotic catabolic process	GO:0030655/1.00	GO:0030655/1.00	GO:0030655/1.00
	GO:0046677: response to antibiotic	GO:0046677/1.00	GO:0046677/1.00	GO:0046677/1.00
	GO:0008800: beta-lactamase activity	GO:0008800/1.00	GO:0008800/0.99	GO:0008800/1.00
	GO:0016787: hydrolase activity		GO:0005886/0.98	GO:0005886/0.99
			GO:0005576/0.97	GO:0005576/0.98
			GO:0042597/0.96	GO:0042597/0.97
			GO:0033251/0.95	GO:0033251/0.96
			GO:0033250/0.95	GO:0033250/0.96
			GO:0008360/0.94
			GO:0009252/0.94
			GO:0006508/0.94
			GO:0009002/0.94
4O7V	GO:0006164: purine nucleotide biosynthetic process	GO:0006189/1.00	GO:0006189/1.00	GO:0006189/1.00
	GO:0006189: ’de novo’ IMP biosynthetic process	GO:0004639/1.00	GO:0004639/1.00	GO:0004639/1.00
	GO:0000166: nucleotide binding	GO:0005524/1.00	GO:0005524/1.00	GO:0005524/1.00
	GO:0004639: Phosphoribosylaminoimidazolesu-ccinocarboxamide synthase activity		GO:0004638/0.99	GO:0005737/0.99
	GO:0005524: ATP binding		GO:0034023/0.99	GO:0005829/0.98
			GO:0005829/0.98	GO:0016020/0.97
			GO:0006144/0.97	GO:0003735/0.96
			GO:0006164/0.96	GO:0006412/0.96
			GO:0009113/0.95	GO:0005886/0.95
			GO:0005737/0.94	GO:0003677/0.94
			GO:0004357/0.93	GO:0006351/0.93
			GO:0006163/0.93	GO:0019843/0.92
			GO:0005634/0.92	GO:0008270/0.91
			GO:0016020/0.91	GO:0046872/0.90
			GO:0000082/0.90

4. Conclusion

In this work, we develop a novel protein function prediction system – SMISS. SMISS integrates information from different sources to improve protein function prediction. Given a protein sequence, it generates a list of Gene Ontology (GO) function terms based on the known function annotations of the homologous proteins found by PSI-BLAST. The set of GO terms is then expanded according to the association rules between GO terms learned by mining the Swiss-Prot database, and then the GO terms are further augmented by the function annotations of the neighboring proteins or genes found in protein–protein interaction networks and the novel spatial gene–gene interaction networks of the human genome constructed from the Hi-C chromosomal conformation data of the genome. Finally, the protein sequence is cut into sequence fragments with a length of 5, and more GO terms are predicted from these fragments. The information is measured by three different probabilistic scores (MIS, SEQ, and NET score), respectively and is combined by SMISS for protein function prediction. Based on the test on the protein targets in the 2011 Critical Assessment of Function Annotation (CAFA), SMISS performs better than the baseline methods and other methods of combining profile–sequence search, profile–profile search, and domain co-occurrence networks. SMISS is an open system, which can combine the information from other sources not used in this work. Our future direction is to expand our current system to include other information such as gene expression and genomic location information, and also improve the current method, for example, control potential degeneration of created profiles in PSI-BLAST to improve the MIS score (we randomly select 225 sequences inserting into the database, and 98 of them keeps e-value 0 when search against itself, and the maximum e-value for the rest is e-12), and search better weight to combine different scores to improve the method.