Network burst dynamics under heterogeneous cholinergic modulation of neural firing properties and heterogeneous synaptic connectivity

Abstract

The characteristics of neural network activity depend on intrinsic neural properties and synaptic connectivity in the network. In brain networks, both of these properties are critically affected by the type and levels of neuromodulators present. The expression of many of the most powerful neuromodulators, including acetylcholine (ACh), varies tonically and phasically with behavioural state, leading to dynamic, heterogeneous changes in intrinsic neural properties and synaptic connectivity properties. Namely, ACh significantly alters neural firing properties as measured by the phase response curve in a manner that has been shown to alter the propensity for network synchronization. The aim of this simulation study was to build an understanding of how heterogeneity in cholinergic modulation of neural firing properties and heterogeneity in synaptic connectivity affect the initiation and maintenance of synchronous network bursting in excitatory networks. We show that cells that display different levels of ACh modulation have differential roles in generating network activity: weakly modulated cells are necessary for burst initiation and provide synchronizing drive to the rest of the network, whereas strongly modulated cells provide the overall activity level necessary to sustain burst firing. By applying several quantitative measures of network activity, we further show that the existence of network bursting and its characteristics, such as burst duration and intraburst synchrony, are dependent on the fraction of cell types providing the synaptic connections in the network. These results suggest mechanisms underlying ACh modulation of brain oscillations and the modulation of seizure activity during sleep states.

Introduction

One of the difficulties in understanding the mechanisms generating brain network activity is the significant heterogeneity in both neuronal firing characteristics and synaptic connectivity structure. Both of these properties can dynamically vary, in normal and pathological conditions, owing to a number of different short-term and long-term mechanisms, including neuromodulation and synaptic plasticity mechanisms (Zucker, 1989; Stevens & Wang, 1995; Marder & Thirumalai, 2002; Beverlin et al., 2012). Computational modelling has provided insights into how neuronal characteristics contribute to network behaviour; however, less is understood about the situation when neuronal properties vary significantly across a network, as can occur in neuromodulation by some of the brain’s most potent neuromodulators. This study was motivated by the aim to build an understanding of specific contributions of neuromodulator-induced heterogeneity in neural firing properties and in synaptic connectivity to the generation of neural network activity patterns.

Acetylcholine (ACh) expression in cortical and hippocampal regions varies tonically and phasically with behaviour. Its release is high during waking, decreases during non-rapid eye movement (REM) sleep, and increases to its highest levels during REM sleep (Marrosu et al., 1995); phasic ACh increases have been measured during cognitive and memory tasks (Stancampiano et al., 1999; Bianchi et al., 2003). Previous work has shown that ACh modulation significantly increases neural excitability and alters neural firing properties as measured by the phase response curve (PRC) (Cole & Nicoll, 1983; Stiefel et al., 2008). Theoretical and modelling studies have illustrated that ACh-induced changes in the neuronal PRC alter the propensity for network synchronization (Hansel et al., 1995; Ermentrout, 1996; Bogaard et al., 2009).

In this simulation study, we investigated how heterogeneity in the cholinergic modulation of neural firing properties and the resulting heterogeneity of the cell types supporting synaptic connectivity in the network affected the characteristics of network spatiotemporal activity. We considered the simplified context of excitatory networks in order to fully identify the underlying mechanisms; however, excitatory synaptic signalling can dominate in brain networks under some conditions. For example, under seizure conditions, inhibitory interneurons have been observed to enter depolarization block and not participate in network firing activity (Ziburkus et al., 2006; Shin et al., 2010). During these episodes, interactions among excitatory cells would be the primary drivers of firing activity. Generally, purely excitatory networks tend to show population bursts composed of episodes of higher-frequency firing by a large population of the neurons, separated by periods of relative quiescence across the network. Our results show that different network bursting patterns can result from variations in the heterogeneous makeup of individual neural firing properties and the resultant heterogeneity in synaptic connectivity of the underlying network. Namely, we show that cells that are strongly and weakly modulated by ACh contribute differentially to the existence of population bursts and to their initiation, maintenance, and intraburst synchronization. Furthermore, variations in network connectivity among strongly and weakly modulated cells can lead to the abolition of population bursts. Although the networks that we investigated are biophysically simple, our results identify fundamental mechanisms that participate in the generation of observed brain network activity, including ACh-induced modulation of the power of hippocampal theta rhythms and the dependence of sleep state on seizure activity.

Materials and methods

Cortical neuron model

All model cells in this study were implemented with a Hodgkin–Huxley-based model that included a fast Na⁺ current, a delayed rectifier K⁺ current, a leakage current, and a slow, low-threshold M-type K⁺ current (Stiefel et al., 2009; Fink et al., 2013). The cellular response to the presence of ACh was modelled by varying the maximum conductance g_Ks of this low-threshold K⁺ current. Specifically, ACh blocks the M current as a result of activation of muscarinic ACh receptors (Brown, 1988). As described below, weak ACh modulation, simulated by g_Ks = 0.6 mS/cm², endows these model cells with a Type II PRC, whereas strong ACh modulation, simulated with g_Ks = 0.2 mS/cm², leads to a Type I PRC (Stiefel et al., 2008, 2009). Therefore, we refer to weakly modulated cells as Type II and strongly modulated cells as Type I. The current balance equation for the ith cell was given by:

$$\begin{array}{r}C\frac{\mathrm{d}{V}_i}{\mathrm{d}t}=-[g_{\text{Na}}{m}_{\infty }^3(V_i)h(V_i-V_{\text{Na}})+g_{\text{Kdr}}{n}^4(V_i-V_{\mathrm{K}})\\ +g_{\text{Ks}}z(V_i-V_{\mathrm{K}})+g_L(V_i-V_L)]+I_I^{\text{drive}}-I_i^{\text{syn}}\end{array}$$

with C = 1 μF/cm², V_i in mV, and t in ms. $I_i^{\text{syn}}$ was the synaptic current input to the cell.

$I_i^{\text{drive}}$, the intrinsic driving current for the ith cell, was set such that it would induce firing at a frequency f_i in the range 15–21 Hz when isolated from the network (the particular choice for f_i was made uniformly at random within this range for each cell). In order to accomplish this, frequency–current responses were obtained and then subjected to polynomial fitting. For Type I neurons, this results in the function:

$$I_i^{\text{drive}}=-0.0003\cdot f_i^2+0.0372\cdot f_i-0.1934.$$

Type II neurons have a minimal firing frequency (~3.3 Hz), and their frequency–current relationship is well approximated above threshold with the continuous function:

$$I_i^{\text{drive}}=0.0003\cdot f_i^2+0.0542\cdot f_i.$$

Activation of the Na⁺ channel was instantaneous and modelled by the steady-state activation function m_∞ (V), whereas the inactivation variable h evolved in time. Likewise, the gating variables n and z, respective to the delayed rectifier K⁺ current and the M-type K⁺ current, also evolved in time according to the relationship:

$$\frac{\mathrm{d}x}{\mathrm{d}t}=\frac{x_{\infty }\left(V\right)-x}{{\tau }_x\left(V\right)}\text{for}x=h,n,z.$$

With the exception of the previously detailed variation in the maximum conductance constant g_Ks, all parameters were constant across the network. The steady-state activation and time constant functions for the gating variables and parameter values used were as follows:

$$\begin{array}{l}{m}_{\infty }\left(V\right)={\left\{1+\exp \left[\left(-V-30.0\right)/9.5\right]\right\}}^{-1}\\ \begin{array}{l}{h}_{\infty }(V)={\{1+\exp [(V+53.0)/7.0]\}}^{-1}\hfill \\ {\tau }_h(V)=0.37+2.78{\{1+\exp [(V+40.5)/6.0]\}}^{-1}\hfill \end{array}\\ \begin{array}{l}{n}_{\infty }(V)={\{1+\exp [(-V-30.0)/10.0]\}}^{-1}\hfill \\ {\tau }_n(V)=0.37+1.85{\{1+\exp [(V+27.0)/15.0]\}}^{-1}\hfill \end{array}\\ z_{\infty }\left(V\right)={\left\{1+\exp \left[\left(-V-39.0\right)/5.0\right]\right\}}^{-1}{\tau }_z\left(V\right)=75.0\end{array}$$

Parameter values were as follows: g_Na = 24.0 mS/cm², g_Kdr = 3.0 mS/cm², g_L = 0.02 mS/cm², V_Na = 55 mV, V_K = −90 mV, and V_L = −60 mV.

Network simulations

Networks were composed of 250 Type I neurons and 250 Type II neurons, and the synaptic connectivity structure was generated in a manner similar to the algorithm defined by Watts and Strogatz for the formation of ‘small-world’ networks (Watts & Strogatz, 1998). First, a one-dimensional ring network consisting of N cells was constructed, with each cell synapsing onto its 1st to kth nearest neighbours. Second, by use of the randomness parameter p constrained to the interval [0, 1], kp outgoing synapses from each cell i were chosen uniformly at random and removed. Finally, kp synapses were returned to each cell I, and were wired to any cell j, also chosen uniformly at random, provided that a synapse from i to j did not already exist and that i ≠ j. We considered networks with N = 500 and k = 20, corresponding to 4% synaptic connectivity, which is within reported measurements of 2–5% connectivity in brain networks (Sporns, 2011). For Fig. 2, the rewiring parameter p was varied between simulations.

Fig. 2.

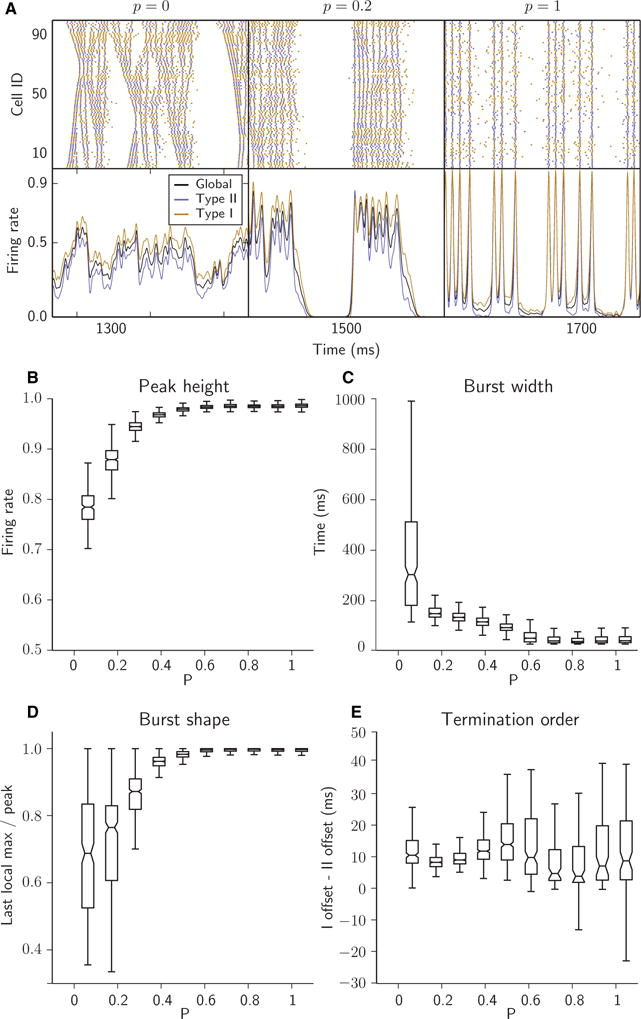
Randomness of synaptic connectivity promoted population bursting and synchrony. (A) Raster plots (top panels) and time-dependent firing rates (bottom panels; see Materials and methods) for networks with different degrees of randomness in synaptic connectivity controlled by parameter p. All networks are composed of 250 Type I and 250 Type II cells, each with 4% connectivity (synaptic out-degree k = 20). (B–E) Tukey boxplots showing the relationship between randomness in network connectivity (parameter p) and four bursting metrics (p = 0 not included, owing to absence of bursting). The bottom, midline and top of each box represent the lower quartile (25th percentile, or Q1), median (50th percentile, or Q2), and upper quartile (75th percentile, or Q3), respectively; whiskers extend down from Q1 and up from Q3 to cover 1.5 times the interquartile range (Q3–Q1) of the samples. (B) Peak height of network firing rate during the burst. (C) Burst width. (D) Ratio of the last local maximum of network firing rate before termination to the highest peak in firing rate within the burst. (E) Difference in offset times of Type I and Type II firing rates at burst termination.

For simulations corresponding to Figs 3–7, we first formed a network with parameters N = 500, k = 20, and P = 0.5. This network was then used as a template for the formation of all networks in which synapses of a particular type were removed. We refer to this network as the ‘fully connected’ or ‘0% removed’ network. To generate a network in which 5% of synapses were removed, all of Type T (e.g. Type I–Type II), 500 synapses of Type T were selected uniformly at random and removed from the network. To generate a network with 10% synapses of Type T removed, we repeated the process above with the 5% removed network as the template. Removal of 25% of synapses of Type T resulted in removal of approximately all Type T synapses, as there are four types of synapse. This recursive method of generating increasingly sparse networks was conceived in order to control for the architectural variation that would arise if each network were generated independently from the others. Networks referred to as having ‘uniform’ removal were generated by successively removing (5%)/4 synapses of each of the four synapse types rather than by the successive removal of 5% synapses of all the same type. As the degree of connectivity in and of itself has a dramatic effect on network dynamics, these simulations are meant to provide a frame of reference for comparing networks with the same connectivity density but different distributions of synapses between the heterogeneous cell types.

Fig. 3.

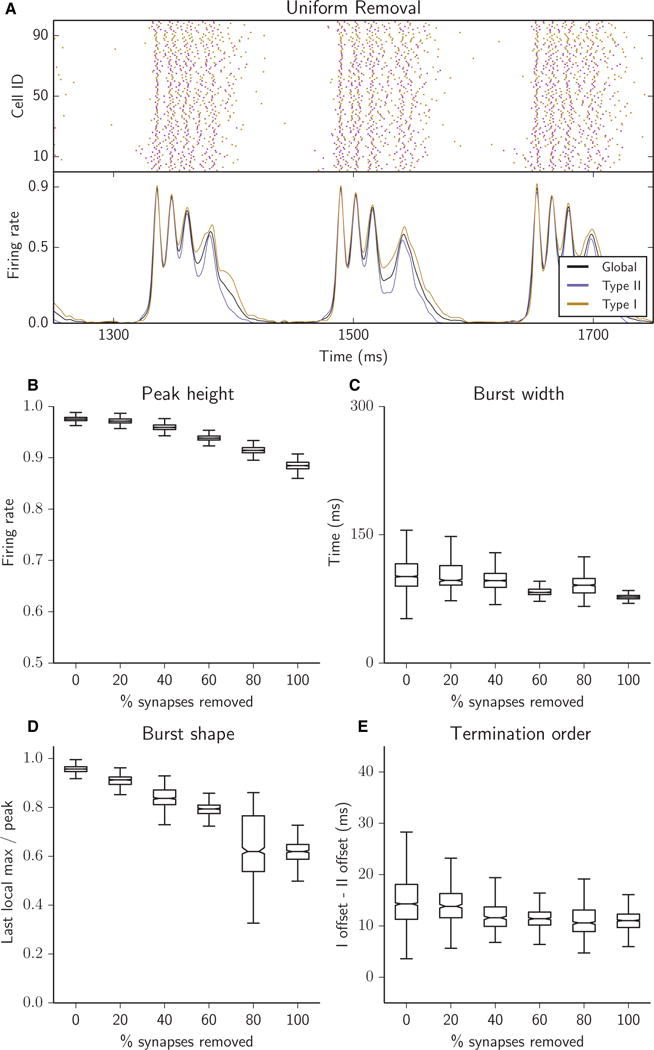
Reducing the overall connectivity of the network resulted in bursts with reduced peak height (B), shorter duration (C), a falling ceiling as intraburst oscillations decreased in magnitude with successive synaptic removal (D), and closely matched firing rates of Type I and Type II cells during burst termination (E). (A–E) Raster plots (A, top panel), network firing rates (A, bottom panel) and bursting metrics (B–E, boxplots as in Fig. 2) for an excitatory heterogeneous network with 25% of synapses removed (A) or with 5% of synapses successively removed (B–E), for synapses randomly chosen uniformly among the four synapse types (see Materials and methods).

Fig. 7.

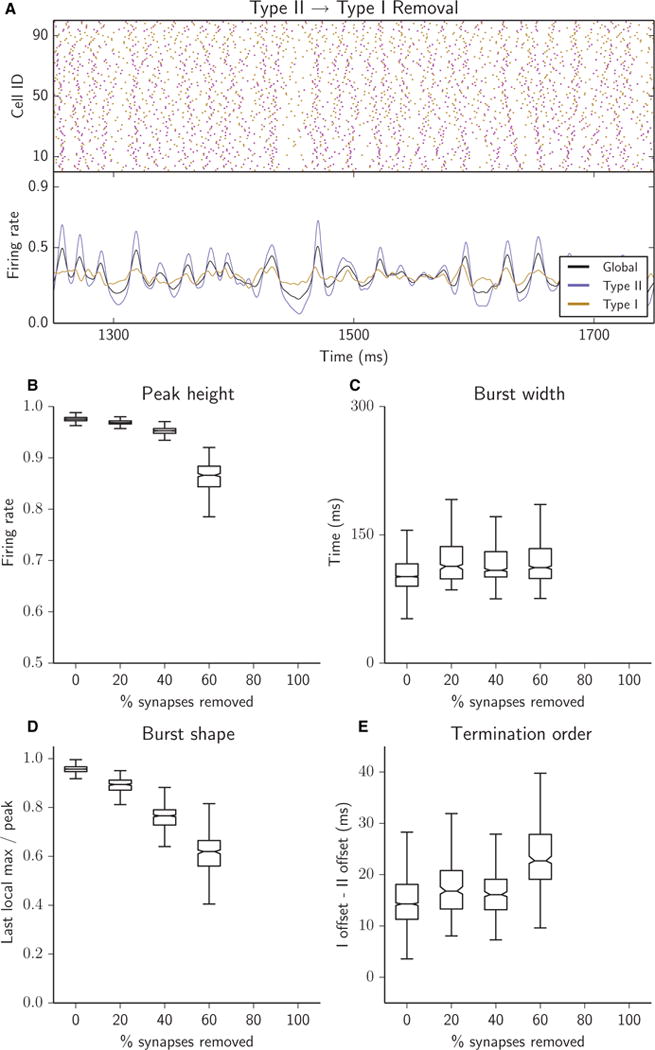
Removal of Type II–I synapses abolished network bursting. No bursting was obtained when > 15% of the Type II–I synapses were removed. (A–E) Raster plots (A, top panel), network firing rates (A, bottom panel) and bursting metrics (B–E, boxplots as in Fig. 2) for an excitatory heterogeneous network with 25% of synapses removed (A) or with 5% of synapses successively removed (B–E); all removed synapses were Type II–I.

Synaptic current was transmitted from presynaptic neuron i to postsynaptic neuron j at time t according to the equation:

$$I_{ij}^{\text{syn}}=w\text{exp}\left(-\frac{t-t_{\text{spike}}}{\tau }\right)\left(V_j-E_{\text{syn}}\right),$$

where, for AMPA-like synaptic currents, w = 0.08 mS/cm², τ = 0.5 ms, and E_syn = 0 mV. Variable V_j represents the membrane potential of postsynaptic neuron j, and variable t_spike represents the most recent time when the membrane potential of presynaptic neuron i breached 0.0 mV from below.

For N-methyl-D-aspartate (NMDA)-like synaptic currents, τ = 180.0 ms, and the current was activated only when the postsynaptic cell’s voltage was above −30 mV. The minimum value of synaptic strength w was calculated so that the total synaptic current matched that of the AMPA-like synapse, and was set to w = 0.000266 mS/cm². This value was doubled and quadrupled in some simulations.

Addition of cellular noise

For a subset of simulations, we added external random noise stimulation to each cell. Noise was modelled by applying brief (1 ms) current pulses I_noise to each cell at randomly determined times. The minimum I_noise amplitude was set to 1.4 μA, which corresponds to the pulse amplitude needed for the Type I cell to spike from resting membrane potential. I_noise amplitude was increased up to 6 μA. The probability of a current pulse being delivered at a given time step was linked to the intrinsic (uncoupled) firing frequency of a cell. The baseline frequency of the noise pulses, on average, matched the spiking frequency of the neurons. Noise frequency was increased up to four times this value.

Networks were simulated for a total of 25 s, including an initial 500-ms transient period. Each series of simulations was completed five times, each time generating a new synaptic connectivity template to introduce topological variation. In Figs 2–7, boxplots represent the complete set of data obtained from all simulations. For numerical integration of the network, we employed the fourth-order Runge–Kutta algorithm with a time step of 0.025 ms. All networks were generated and simulated with custom C++ code.

PRCs

To compute the neuronal PRC, a single cell was numerically simulated at a constant intrinsic driving current until it reached a stable 15-Hz spiking pattern (‘stable’ here means that the standard deviation of 10 successive interspike intervals was below 0.1). The cell was then perturbed at 100 equally spaced times (or phases) during the interspike interval with a current pulse of 3.0 μA/cm² for a duration of 0.1 ms. The subsequent spike time was recorded and compared with the projected spike time in the absence of the perturbation. The normalized phase shift was computed by dividing the difference between the projected and actual spike times by the duration of the interspike interval. Figure 1 shows this phase shift plotted against the phase of the perturbation within the interspike interval where the spike occurs at phases 0 and 1.

Fig. 1.

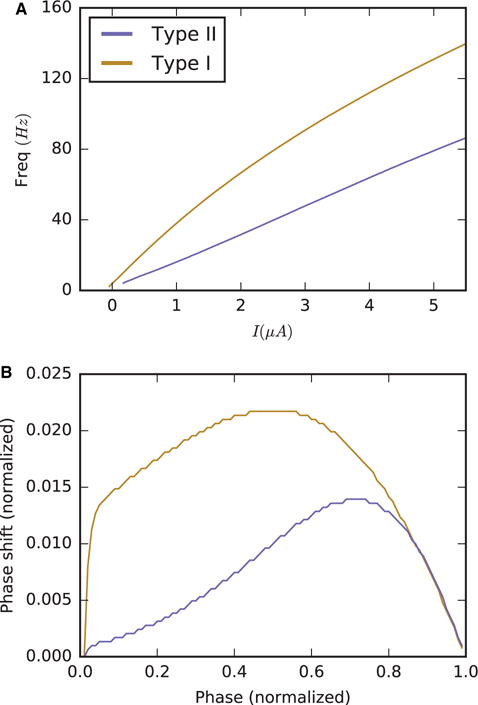
ACh modulation changes the excitability and response properties of a cortical pyramidal cell model: frequency–current curves (A) and PRCs (B) under strong ACh modulation (Type I, gold curves) and under weak ACh modulation (Type II, blue curves).

Firing rates

Curves representing the collective firing rate of a neural population p (e.g. all Type I cells) were generated by averaging the firing rate functions r_i (t) for each neuron i in population p, where r_i (t) is the linear filter:

$$r_i\left(t\right)={\displaystyle \sum _{k=1}^{n}D\left(t-t_k\right),}$$

where t_k is the time of the kth spike time, and D (t − t_k) refers to the window function.

$$D\left(\tau \right)=\text{exp}\left(\frac{{\tau }^2}{2{\sigma }^2}\right).$$

Thus, the firing rate function R_p (t) for population p can be expressed as.

$$R_p\left(t\right)=\frac{1}{\left|p\right|}{\displaystyle \sum _{i=1}^{\left|p\right|}{r}_i\left(t\right).}$$

Our choice of the parameter σ = 2 for the kernel was motivated by its impact on the function R_p (t); in particular, our value of r generated r_i (t) curves that were sufficiently wide to form relatively smooth R_p (t) curves (thus making the curve more amenable to finding robust local maxima or minima), but were sufficiently narrow to avoid the possibility that r_i (t) might exceed the value r_i (t) = 1. Additionally, this implies that R_p (t) will also be confined to the interval [0, 1].

Bursting metrics

To quantify network bursting patterns, we computed several burst measures from the profiles of the firing rate curves averaged across bursts, including peak burst height, burst width, a measure of burst shape, and termination order. Individual bursts were isolated by determining their onset and offset times. The onset of a burst was defined as the event in which the instantaneous global firing rate breached the bursting threshold, here taken to be 0.1 spikes/cell/ms. Likewise, burst offset was defined by the firing rate dropping below that same threshold. To guard against erroneously categorizing small perturbations above and below the threshold as bursts, we enforced two constraints: the firing rate must reach at least 0.5 spikes/cell/ms, and the time duration above threshold must exceed 25 ms. Peak burst height was the highest local maximum obtained during the burst, and burst width was calculated by taking the difference between the two trans-threshold events. Burst shape was computed as the ratio of the last local maximum in global firing rate before burst termination to the highest peak within the burst, and termination order was the difference between the offset times of the Type I and Type II firing rate curves.

We additionally computed power spectral density (PSD) functions and cross-correlations of the firing rate traces for each simulation. PSD functions were computed by Welch’s method, with a sample rate of 40 000 Hz and a 15 000-sample segment length, and averaged over five realizations of the simulation for every synapse removal case.

Intraburst causality diagrams

The intraburst causality diagrams in Fig. 10 illustrate which population initiated the burst and its intraburst oscillations. This was computed by determining which population first began to increase in activity following the previous oscillation by comparing the timing of local minima in Type I and Type II firing rate curves, as shown in Figs 3A–6A (lower panels). For example, to determine which population typically initiated an intraburst oscillation, for each burst we found the times of the preceding local minima for Type I and Type II firing rates, and registered a score in the following manner. If the Type I local minimum occurred before the Type II local minimum, then a score of 1.0 was recorded for that oscillation (conversely, a score of 2.0 was recorded if the Type II local minimum occurred first; ties were marked as 1.5). Once a score for every intraburst oscillation of each burst had been obtained, we took the average of these values across all analysed bursts. The opacity of each point reflects the fraction of bursts that contained its corresponding number of intraburst oscillations (that is, the first few points are quite opaque, as nearly all bursts have at least a few intraburst oscillations; conversely, relatively few bursts contained > 10 oscillations, and these points are therefore relatively transparent). Note that the 0th local minimum was defined as the initiation of the burst, and the score in this case was determined by which population had the greater firing rate at the time of onset.

Fig. 10.

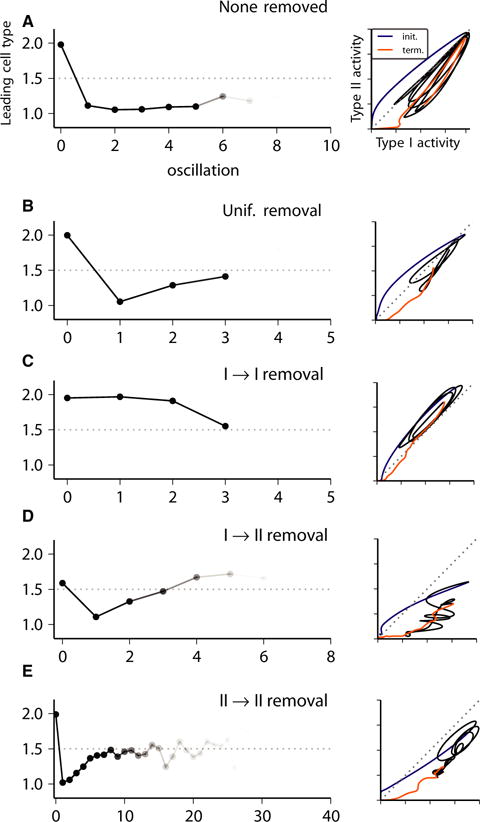
Phase diagrams of Type I vs. Type II firing rate curves during a single representative burst (right panels) and intraburst causality diagrams (left panels; see Materials and methods) for network bursting activity in excitatory heterogeneous networks with no synapses removed (A) or with 25% of synapses removed, randomly chosen uniformly among the four synapse types (B), and all Type I–I (C), all Type I–II (D), or all Type II–II (E). In the phase diagrams (left), the different time intervals of the burst trajectory are indicated by curve colour: blue, burst initiation; black, intraburst activity; gold, burst termination. The intraburst causality diagram (right) indicates the average of the cell type (1.0, Type I; 2.0, Type II) whose firing rate curve, shown in the lower panels of Figs 3A, 4A, 5A and 6A, led activation of burst initiation (0th oscillation) and subsequent intraburst oscillations in activity. Decreased opacity of the curve reflects the fraction of bursts in the simulation showing the number of oscillations.

Fig. 6.

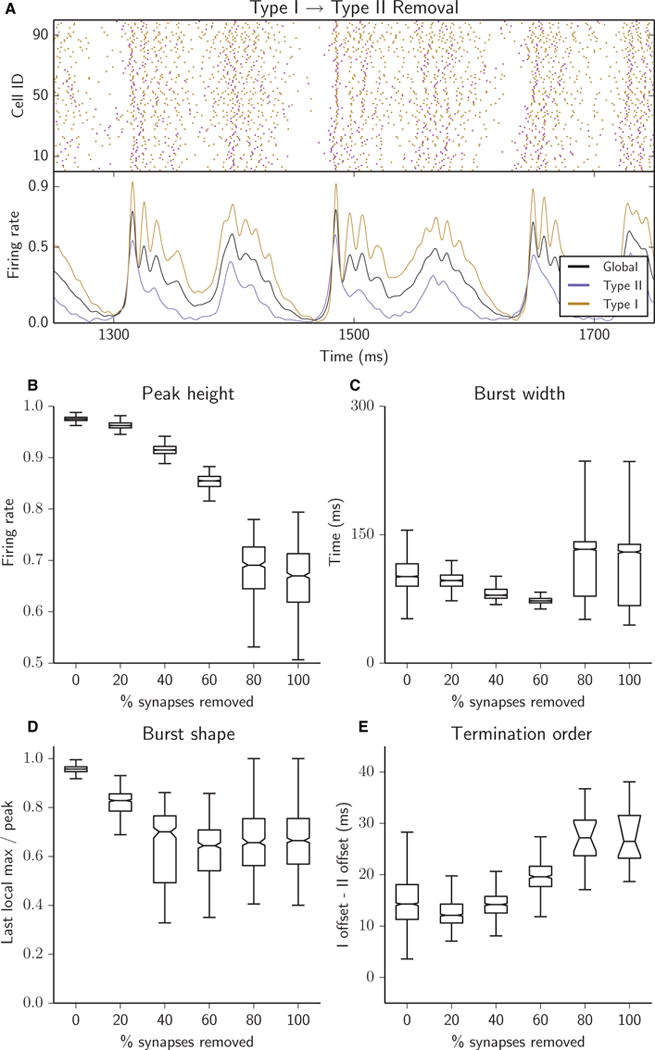
Removing Type I–II synapses degraded synchrony and burst structure. Peak height decreased (B), burst width narrowed until 80% of Type I–II synapses were removed, when Type I activity was not completely silenced and bursts became bimodal (C), burst shape became more sloped (D), and Type I cells maintained their activity long after Type II cells were silenced (E). (A–E) Raster plots (A, top panel), network firing rates (A, bottom panel) and bursting metrics (B–E, boxplots as in Fig. 2) for an excitatory heterogeneous network with 25% of synapses removed (A) or with 5% of synapses successively removed (B–E); all removed synapses were Type I–II.

Results

PRCs and synchrony

In hippocampal and cortical pyramidal cells, ACh blocks a slow, M-type K⁺ current through its action on muscarinic ACh receptors (Brown, 1988). Blockade of this current has been shown to increase neuronal excitability and to induce a shift in neuronal response properties as measured by the PRC (Stiefel et al., 2008). Generally, the PRC measures how external stimuli change the timing or phase of an oscillating system. In the context of neurons, the PRC measures the change in spike timing of a repetitively firing neuron in response to a synaptic input or an applied current. PRCs of most neuron models and from experimental measurements fall into two primary types of shape, Type I and Type II. Neurons with Type II PRCs respond with either a delay or an advance in spike firing in response to an excitatory stimulus; firing is delayed if the stimulus arrives at early phases of the firing cycle, and is advanced if the stimulus is delivered at later phases of the cycle. Neurons with Type I PRCs exclusively show advances in spike firing, and the magnitude of the advances is generally symmetric about a peak advance near the middle of the cycle. In the neuron model used in our simulation study (Stiefel et al., 2009) and in similar neuron models (Pfeuty et al., 2003), decreasing the magnitude of the maximum conductance of the M-type K⁺ current, g_Ks, as a simulation of ACh modulation, varies the frequency–current curve, reflecting an increase in excitability, and switches the PRC from Type II-like to Type I-like (Fig. 1).

The significance of this switch in PRC shape is a change in the propensity for synchronization among cells coupled together in a network. Analysis of models of two coupled neurons with Type I and Type II PRCs by employing the theory of weakly coupled oscillators has shown that Type II neurons have a higher propensity to synchronize than Type I neurons (Hansel et al., 1995; Ermentrout, 1996). This property of Type II cells was also shown to hold in simulation studies of large networks with varying connectivity structures (Bogaard et al., 2009; Fink et al., 2011). We note that the higher synchronization propensity of Type II neurons does not seem to depend on the existence of an explicit delay region at early phases of the PRC; in numerical studies, networks of neurons with PRCs showing little response to stimuli at early phases and an asymmetry towards later phases in the peak of phase advances synchronized more readily than networks whose cells had more symmetric Type I-like PRCs (Pfeuty et al., 2003; Fink et al., 2011; Beverlin et al., 2012).

Network bursting in heterogeneous excitatory networks

In the context of cholinergic neuromodulation of a neural network, heterogeneous modulation of cell excitability type is expected, as different cells have different expression profiles of muscarinic ACh receptors, and ACh levels have been shown to increase slowly with changes in network activity and behaviour (Zhang et al., 2010). The aim of this study was to understand the contributions of cellular heterogeneity, and thus heterogeneity in the propensity for synchronization, to the formation of spatiotemporal activity in the simplified context of a solely excitatory network. We considered 500-cell networks composed of 50% Type I and 50% Type II cells, to avoid biasing cellular properties within the network, and 4% synaptic connectivity.

First, to establish baseline network activity, we measured the properties of activity patterns for heterogeneous excitatory networks with varying connectivity topology (ranging continuously from local to random connectivity). As the synaptic rewiring parameter p was varied from 0 to 1, network activity transitioned from intermittent global or local propagating activity to synchronous bursting activity (Fig. 2A). Network bursting occurred for p ≥ 0.1, with synchrony within bursts increasing with p. We quantified these changing burst characteristics by using metrics based on the collective network firing rate (Fig. 2A, lower panel). As synaptic rewiring increased, peak burst height quickly tended toward its maximum value, reflecting the increase in synchronous recruitment of cells, resulting in nearly all cells firing simultaneously when p > 0.5 (Fig. 2B). Rewiring also opposed variability in peak height. The width of bursts decreased with increasing randomness in synaptic connectivity (Fig. 2C), as increasing synchronous firing promoted more synchrony in termination of firing.

Many bursts for values of p < 0.5 were characterized by a strong initial peak followed by a series of intraburst population spikes of diminishing magnitude (e.g. p = 0.2 in Fig. 2A). This behaviour represents a reduction in total spiking activity during the burst and/or a progressive desynchronization of network activity. This burst characteristic may be important, because either or both of these phenomena may be closely linked to a mechanism for the termination of longer bursts. We quantified this pattern by taking the ratio of the last local maximum in global firing rate before burst termination to the highest peak within the burst. Here, we see that more locally connected networks promoted this tapering behaviour far more strongly than random networks (Fig. 2D).

Although both types of cells must necessarily cease firing for a burst to terminate, we observed a strong tendency for Type I cells to maintain firing for longer than Type II cells. To quantify this behaviour, we compared the offset times of Type I and Type II firing rates during burst termination (Fig. 2E). Type II cells reliably ceased firing before Type I cells for most p-values; for the largest p-values, the variance in this measure increased as all cells ceased firing more simultaneously with more synchrony across the network.

Changes in network burst properties as a function of targeted synaptic removal

To determine the nature of interactions between Type I and Type II cells and how these interactions generated the dynamics of the network as a whole, we varied the degree to which Type I and Type II cells were able to communicate with other cells of the same and opposing types. This variation in connectivity structure was achieved by first categorizing each synapse on the basis of the types of its presynaptic and postsynaptic cells (for example, all synapses delivering current from Type I cells to Type II cells are of the same synapse type, namely Type I–II). This resulted in four synapse types: I–I, I–II, II–I, and II–II. The degree of connectivity for each synapse type was then varied by deleting some number n of its connections. This targeted synapse deletion can, in theory, mimic slower changes in the fraction of population type, but also dynamic changes happening on much faster timescales related to short-term facilitation or depression of synapses.

As removing synapses of any kind necessarily reduces the connectivity density of the network (and thus changes its dynamics), we also simulated networks in which n/4 synapses of each type were removed uniformly rather than removing all n synapses from a single category. The effects on network burst dynamics for this uniform synapse removal case and for each single-type synapse removal case are shown in Figs 3–7 for 500-cell networks consisting of 50% Type I and 50% Type II neurons with 4% initial synaptic connectivity. As we were primarily interested in changes in stereotypic bursting dynamics as a function of synaptic removal, we performed the described study for networks with rewiring parameter p = 0.5. Note that network bursting when p = 0.5 with no synapses removed is similar to the case when p = 1, shown in Fig. 2A, as indicated by similar values of all burst measures (Fig. 2B–E).

Reducing the overall synaptic connectivity of the network resulted in bursts with only moderately reduced peak height (Fig. 3B) and shorter duration (Fig. 3C). With successive uniform removal of synapses, we observed more significant but still limited progressive degeneration of intraburst structure, illustrated by the falling ceiling as intraburst oscillations decreased in magnitude (Fig. 3D). Although Type I cells continued to fire beyond the cessation of Type II cells at burst termination, the variation in this offset time difference was reduced (Fig. 3E). In summary, when synaptic connectivity was reduced but the proportions of each synapse type remained constant, burst characteristics did not change qualitatively: burst width and termination order were not greatly affected and variability was reduced in these measures, whereas variation in burst shape and peak height increased slightly.

In contrast, when synaptic connectivity was reduced by removing synapses of specific types, the characteristics of network bursts, i.e. their generation, duration, internal structure, and termination, changed significantly. These results indicated that the distinct, qualitative differences in burst characteristics can enable the identification of the underlying composition of synapses in the network.

Removing Type I–I synapses resulted in highly stereotypic, regular network bursts with increased synchronization of intraburst activity (Fig. 4). This was reflected by the decrease in variance of all burst measures as synapses were successively removed (Fig. 4B–E). Burst peak height remained high (Fig. 4B) and burst width became consistently narrower (Fig. 4C). The recruitment of the cells in each intraburst oscillation changed only slightly during burst duration, indicating that, throughout the burst, cells fired synchronously. The burst shape was much less sloped and with less variance than with uniform removal of the same number of synapses (Fig. 4D). Thus, in this case, burst termination was not attributable to a drop in synchrony during the burst. With little or no synaptic activity between Type I cells, these cells lost their characteristic tendency to continue activity far past the terminal drop in Type II cell activity (Fig. 4E), thus aiding in a synchronized fall into global silence.

Fig. 4.

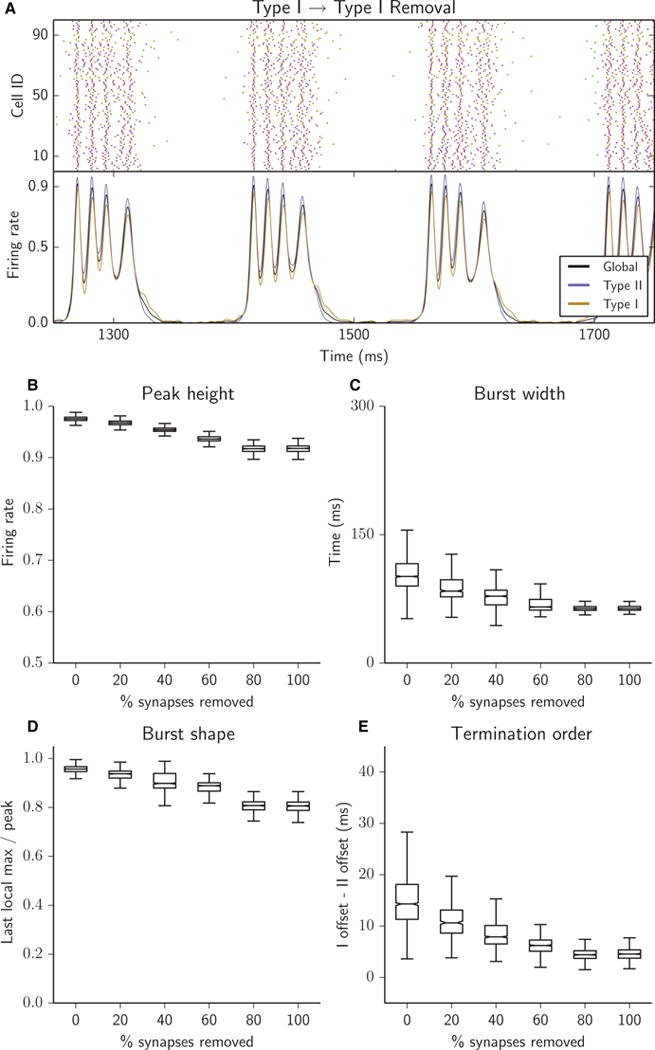
Removing Type I–I synapses resulted in a highly regular network bursting structure and highly synchronized population bursts. Peak height decreased (B), burst width became consistently narrower (C), burst shape became more sloped (D), and bursts terminated with similar firing cessation of each cell type (E). (A–E) Raster plots (A, top panel), network firing rates (A, bottom panel) and bursting metrics (B–E, boxplots as in Fig. 2) for an excitatory heterogeneous network with 25% of synapses removed (A) or with 5% of synapses successively removed (B–E); all removed synapses were Type I–I.

To better compare the intraburst activity across removal of different synapse types, we computed the PSD of the global network firing rate curves (Fig. 8). When Type I–I synapses were removed (Fig. 8A), bursting was maintained as reflected by the consistent peak near 10 Hz, which captures the interburst frequency. Higher-frequency oscillations (~80 Hz) gained more power and became more focused as Type I–I synapses were removed (red and blue curves), reflecting increased synchrony of intraburst activity as compared with uniform synaptic removal (grey curve) and with full synaptic connectivity (black curve).

Fig. 8.

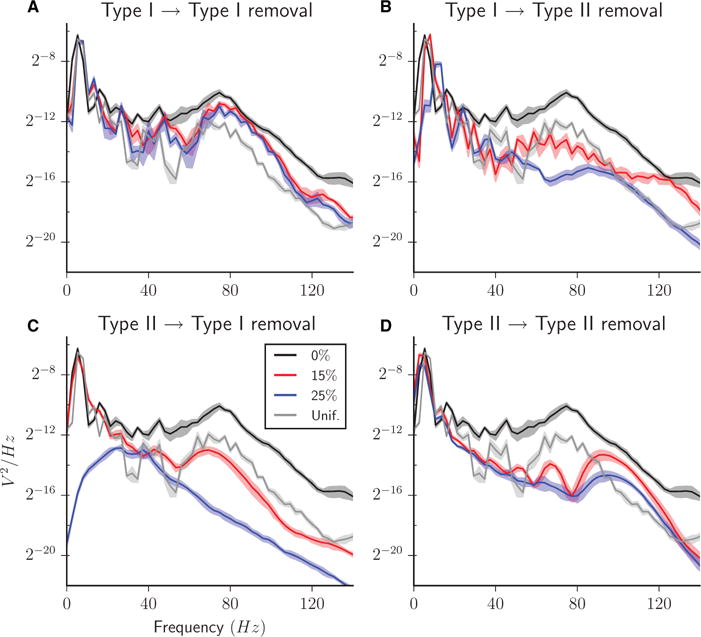
PSD functions of the global network firing rate curves for heterogeneous excitatory networks with 0% (black curve), 15% (red curve) and 25% (blue curve) of synapses removed, all Type I–I (A), Type I–II (B), Type II–I (C), or Type II–II (D). PSD for networks with 25% of synapses removed randomly chosen uniformly among the four synapse types is shown for comparison in each panel (grey curve). In all curves, the centre curve is the average across five simulation runs, and the shadow region indicates the standard deviation interval.

In contrast, removal of Type II–II synapses led to bursts with completely asynchronous intraburst activity (Fig. 5). The lack of Type II–II connections did not prevent Type II cells from initiating bursts, as shown by the higher Type II collective firing rate at the onset of burst initiation (Fig. 5A, lower panel). Moreover, the initial peak burst height was comparable to that in the uniform removal case, indicating a well-synchronized initiation (Fig. 5B). However, the synchronization of Type II cells quickly degraded (Fig. 5D). Firing rates of Type II cells remained high; however, the intraburst temporal structure was effectively abolished, allowing for a large increase in burst duration (Fig. 5C) (that is, the burst does not terminate because of lack of activity or because of highly synchronous discharges). The variance of burst width greatly increased (note the change of scale in Fig. 5C as compared with Figs 3C, 4C, 6C, and 7C) as the collective silencing of Type II cells, which usually preceded burst termination, became more dependent on fluctuations in Type I cell activity. The degradation of intraburst synchrony is reflected in the heavily sloped shape of the bursts (Fig. 5D) and the larger difference in offset times of Type I and Type II cells (Fig. 5E) as synapses were removed. The PSD plot for this case reflects the maintenance of longer bursts (Fig. 8D); the low-frequency peak is skewed towards lower frequencies with increasing synapse removal. At the same time, intraburst synchronous activity disappeared, as reflected in a loss of power in the ~80-Hz range. Power increased in higher frequencies (~100 Hz), owing to intraburst asynchronous fluctuations.

Fig. 5.

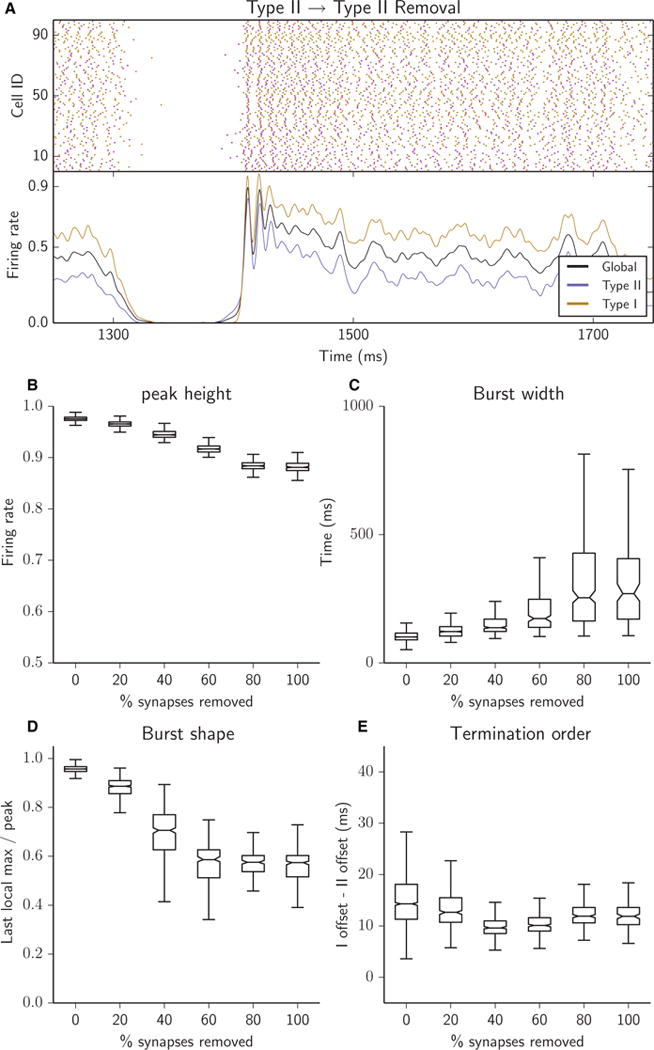
Removing Type II–II synapses desynchronized intraburst activity. Peak height was high, indicating strong synchronization at initiation (B), burst width increased greatly and became highly variable (C), burst shape was heavily sloped, reflecting long, slowly terminating tails of activity (D), and termination order was not affected (E). (A–E) Raster plots (A, top panel), network firing rates (A, bottom panel) and bursting metrics (B–E, boxplots as in Fig. 2) for an excitatory heterogeneous network with 25% of synapses removed (A) or with 5% of synapses successively removed (B–E); all removed synapses were Type II–II.

Removing Type I–II synapses degraded network bursting and reduced intraburst synchronization (Fig. 6). Peak burst height decreased, reflecting less synchronization at burst initiation (Fig. 6B), and the increased slope and variance of burst shape indicated a loss of intraburst synchrony (Fig. 6D). The collective firing rate of Type II cells (Fig. 6A, lower panel) was lower in these networks than in the uniform synaptic removal case (Fig. 3A, lower panel) and was consistently lower than that of Type I cells, indicating that removal of Type I–II synapses degraded not only their frequency but also the ability of Type II cells to synchronize with each other and thus provide a synchronized signal to Type I cells. This led to an interesting effect on burst width: up to 15% synaptic removal, bursts narrowed (Fig. 6C), while at the same time Type I cells became less able to follow Type II cells into a global silent period, as shown by the increase in termination order (Fig. 6D). As more synapses were removed, the lingering tail of Type I activity at the end of a burst merged with the beginning of the next burst, thus conjoining consecutive bursts and forming a bi-peaked burst structure (Fig. 6A, lower panel). This transition caused the jump in burst width after 15% removal. Degraded bursting activity was reflected in the decrease and rightward shift of the peak near 10 Hz in PSD (Fig. 8B) as Type I–II synapses were removed, with the shift that occurred between the 15% removal and 25% removal cases capturing the transition from typical single burst dynamics to the less synchronous bi-peaked burst dynamics. Additionally, the high-frequency peak generated by intraburst synchronous activity was lost as these synapses were selectively removed. At the same time, it is worth noting that bursts still originated with Type II cell activity (Fig. 6A, lower panel), as Type II activity drove recruitment of Type I cells that, in turn, propelled burst initiation.

Finally, removal of Type II–I synapses completely destroyed network bursting (Fig. 7). As these synapses were removed, peak burst height decreased (Fig. 7B) and the burst shape became more sloped (Fig. 7D). When > 15% of synapses were removed, there were no periods of global silence, and continuous asynchronous activity was shown, as indicated by the absence of burst measures. The synchronizing propensity of Type II cells was still evident in the higher peaks in the Type II collective firing rate in response to small rises in the Type I rate (Fig. 7A, lower panel). However, the lack of sufficient synaptic signalling from Type II to Type I cells made it impossible to recruit Type I cells into synchronized activity. The loss of bursting was clearly reflected by the loss of the PSD peak near 10 Hz when these synapses were absent (Fig. 8C).

Understanding qualitative interactions between Type I and Type II neurons during bursting dynamics

The above results identify the contributions of Type I and Type II cells to generating network bursting, and in particular indicate the role of Type II cells in synchronization. Intuitively, it makes sense that the Type II cells, by synchronizing among themselves, would provide a synchronizing drive to the Type I cells in the network. This effect of Type II cell activity was evident in our results by the promotion of asynchronous activity when either Type II–I synapses were removed (Fig. 7) or Type II–II synapses were removed (Fig. 5). However, synaptic signalling from Type I cells was also critical in generating well-synchronized burst dynamics, as burst synchrony degraded when Type I–II synapses were removed (Fig. 6). Our results indicate that the synaptic drive provided by the Type I cells to the Type II cells is necessary for the Type II cells to generate a coherent synchronizing signal to the entire network. In a qualitative way, we can think of the Type II cells as promoting synchronization in the network, and the Type I cells as providing the necessary excitation to generate a coherent synchronizing signal.

These roles for the two cell types were clarified in measures that revealed the temporal relationship between their firing activities during network bursting, including the cross-correlation between Type II and Type I firing rate curves (Fig. 9), the intraburst causality measure (Fig. 10, left panels), and plots of typical burst trajectories in the phase space of the firing rate curves (Fig. 10, right panels). To avoid repetition, we show burst characteristics revealed by these measures in Figs 9 and 10 simultaneously.

Fig. 9.

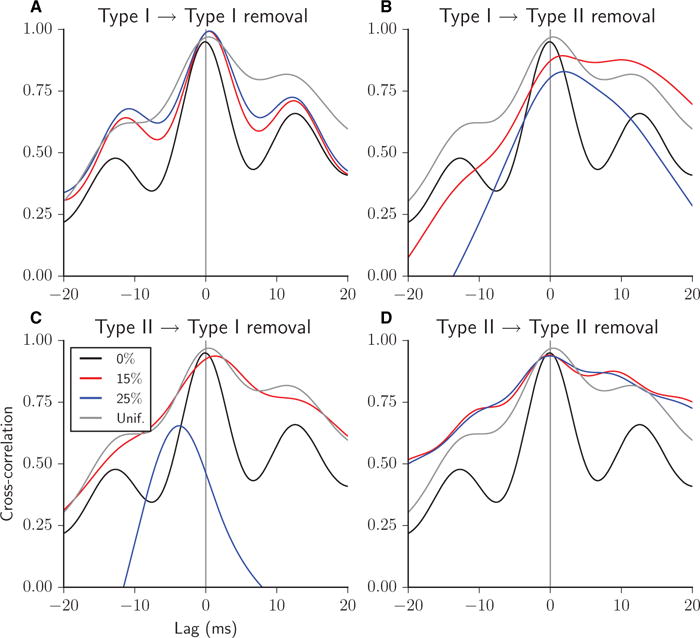
Cross-correlation between the Type I and Type II firing rate curves for heterogeneous excitatory networks with 0% (thin black curve), 15% (thick red curve) and 25% (thick blue curve) of synapses removed, all Type I–I (A), Type I–II (B), Type II–I (C), or Type II–II (D). Cross-correlation for networks with 25% of synapses removed randomly chosen uniformly among the four synapse types is shown for comparison in each panel (thin grey curve). A positive time lag corresponds to Type II leading.

The cross-correlation between the Type II and Type I firing rate curves revealed which cell type led, on average, the overall activity within the burst by the offset of the peak relative to zero lag (Fig. 9; positive lag corresponds to Type II leading). In the full network, with no synapses removed, the cross-correlation peak was slightly negative, indicating a slight tendency for Type I cells to drive behaviour (Fig. 9, all panels, black curves). This can be explained by the generally higher excitability of Type I neurons. Note also that this does not contradict the fact that, generally, Type II cells initiate the burst; leading Type II neurons at burst initiation are quickly overtaken by Type I cells during subsequent burst evolution. To illustrate these changing temporal relationships, we plot the firing rate trajectories during a typical burst in the Type I–Type II phase space (Fig. 10A, right panel). In the phase space, clockwise motion indicates Type II activity leading Type I activity. During burst initiation (blue portion of the curve), motion was clockwise, but it quickly reversed to counter-clockwise motion for the remainder of the burst. To further quantify these temporal relationships, Fig. 10 also displays an intraburst causality measure (left panels; see Materials and methods) that identifies the cell type leading each intraburst oscillation in firing rate activity (identified by local minima) averaged over all bursts in the simulation. In the full network, Type II cells reliably led activity at burst initiation, but Type I cells took over leading the intraburst oscillations.

Bursts after uniform synaptic removal were generated by similar interactions between the cell types as in the case of full connectivity. The peak in cross-correlation was shifted slightly positively (Fig. 9, all panels, grey curve), reflecting Type II cells leading behaviour at burst initiation. The shift in peak was positive in this case, because the bursts were shorter, with fewer intraburst oscillations led by Type I cells than in the full network, owing to the decrease in synaptic density. The leading behaviour of Type I cells in the intraburst oscillations was also evident by the counter-clockwise motion of the intraburst trajectory in the Type I–Type II phase space (Fig. 10B, right panel, black and gold portions of the curve) and in the intraburst causality measure (left panel).

When Type I–I synapses were removed, Type II cells became the primary drivers of the regular, more synchronous bursting observed in these networks. The cross-correlation peak was shifted positively (Fig. 9A) and the motion of the trajectories was clockwise throughout the burst in the Type I–Type II phase space (Fig. 10C, right panel). Average behaviour over all bursts in the simulation, shown in the intraburst causality measure (Fig. 10C, left panel), indicated that Type I cells led some of the final intraburst oscillations.

The importance of the synaptic signalling from Type I cells to Type II cells in promoting their coherent synchronizing signal was revealed in the cross-correlation plot when those connections were removed. Here, the positively shifted peak indicated that Type II cells were leading activity, but the broad peak reflects the lack of synchronized intraburst oscillations [Fig. 9B; compare with the well-defined peaks in full network (black curve) and when Type I–I synapses were removed (Fig. 9A)]. The phase space plot of the burst trajectory, on the other hand, shows that, whereas Type II cell activity led the initial rise in activity at burst onset, Type I cell activity outpaced Type II activity by the peak of the onset (Fig. 10D, right panel; note that the blue portion of the trajectory crossed the y = x line). This lack of coherence of Type II activity in driving burst initiation was further reflected in a value of < 2 in the intraburst causality measure (Fig. 10D, left panel).

Although Type II cells continued to lead activity at the onset of burst initiation when Type II–II synapses were removed, as reflected in the initial portion of the trajectory in the phase space (Fig. 10F, right panel) and in the intraburst causality measure (left panel), neither cell type consistently led the asynchronous intraburst activity, as reflected in the symmetric, broad shape of the cross-correlation curves (Fig. 9D). This more uniform temporal relationship between cell types was also clear from the approach to a value of 1.5 in the intraburst causality measure during burst progression.

The cross-correlation plot clearly showed that removal of Type II–I synapses weakened intraburst structure (Fig. 9C; note the broad peak with 15% synapses removed, red curve) before their complete removal caused loss of network bursting altogether. The resulting asynchronous activity was led by Type I cells, as reflected in the leftward shift in the peak of the cross-correlation, owing to their random fluctuations in activity propelling a synchronous response in Type II cells.

Stability of the network bursting in the presence of noise

We also investigated how the network bursting behaviours responded to the introduction of external random noise stimulation to the cells. To do so, we applied rectangular current pulses of fixed amplitude at randomly chosen time points to each cell individually. The average frequency of pulse delivery was varied from a baseline frequency such that each cell received an average of 1.5 pulses per spiking cycle. Pulse amplitude was varied from a minimal amplitude such that a Type I cell (at resting potential) receiving pulses at this baseline frequency would be driven to fire an action potential.

The observed burst characteristics observed were very robust even for relatively high noise levels (Fig. 11). For the lowest pulse amplitude and frequency values up to intermediate values (i.e. twice the minimal amplitude and four times the baseline frequency), there were no major differences as compared with the no-noise results for the different cases of synapse removal (middle column). As expected, network burst characteristics did show changes under high noise levels (amplitude and frequency both four times the minimal values; right column). The major differences were observed for networks with uniform or Type I–II synapse removal, in which bursting was abolished. The high noise levels promoted high activity of the Type I cells that could be maintained during decreases in Type II firing activity that sculpt the envelope of burst firing. This effect was also apparent in the Type I–I removal case, where bursting still occurred with high noise levels but Type I firing rates did not decay to zero during the quiescent periods between bursts. These results indicate that the observed bursting dynamics are extremely robust to noise, and the ability of Type II cells to gate network firing into bursting activity can be retained under extreme noise levels when recurrent excitation among Type I cells is limited.

Fig. 11.

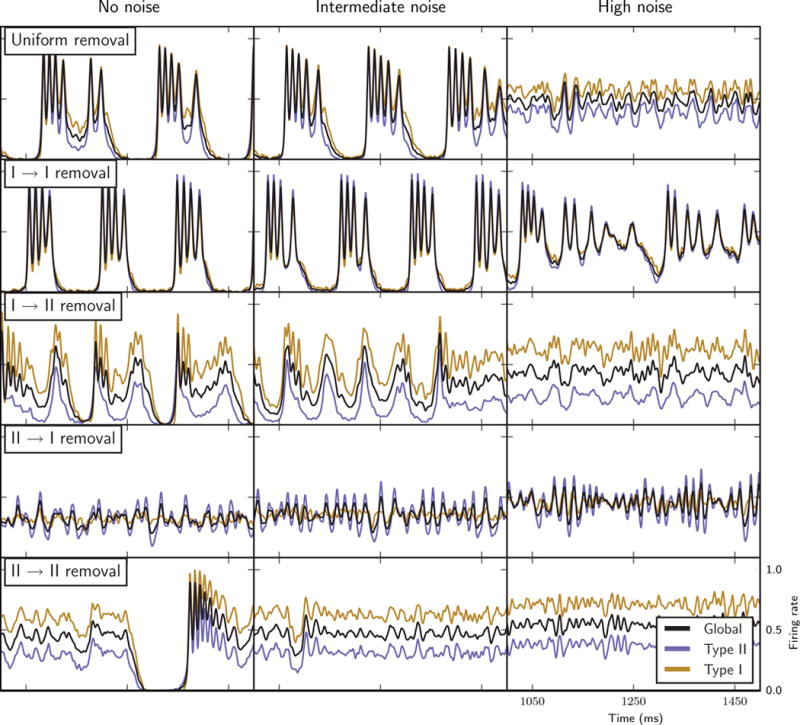
Network bursting behaviours with the introduction of external random noise stimulation to individual cells (see Materials and methods): firing rate curves of the entire network (black curves), Type I cells only (gold curves) and Type II cells only (blue curves) in the different synapse removal cases (labelled rows) with no noise added (left column, similar to the results shown in Figs 3–7), with intermediate noise stimulation amplitude and frequency (middle column, twice minimal amplitude and four times baseline frequency), and high noise stimulation amplitude and frequency (right column, four times minimal amplitude and baseline frequency).

Network bursting in the presence of long-lasting synaptic currents

It is hypothesized that NMDA synapses play an important role in the generation of bursting in networks (Bonansco & Buno, 2003; Bland et al., 2007). NMDA synaptic currents are characterized by significantly longer time constants and Mg²⁺ blockade at cell voltage levels below −30 mV. We investigated how the addition of long-lasting synaptic currents affect network burst characteristics in the cases of different synapse removal (Fig. 12). In addition to the fast, AMPA-like synaptic currents, we included an NMDA-like synaptic current with a longer synaptic decay time constant, and restricted activation to when the postsynaptic cell voltage was above −30 mV (see Materials and methods). The amplitude of the NMDA synaptic current was varied from a baseline level such that the total current released by these synapses in response to a presynaptic action potential matched that of the AMPA current. The introduction of strong NMDA-like currents (amplitude twice that of the AMPA current; middle column) resulted in prolongation of bursts driven by maintained activity levels of both cell types. With Type I–II synapses removed, bursting was degraded, as Type I cell activity remained high during decreases in Type II cell activity. These trends continued for stronger NMDA-like currents (amplitude four times that of the AMPA current; right column) except for in the uniform removal case, where the longer-lasting synaptic currents maintained almost continuous Type II cell activity levels. These results are similar to those for networks with external random noise added, in that bursting was maintained only in networks with Type I–I synapses removed, suggesting that Type II cells are able to gate network firing into bursts when the underlying connectivity limits Type I cell recurrent excitation.

Fig. 12.

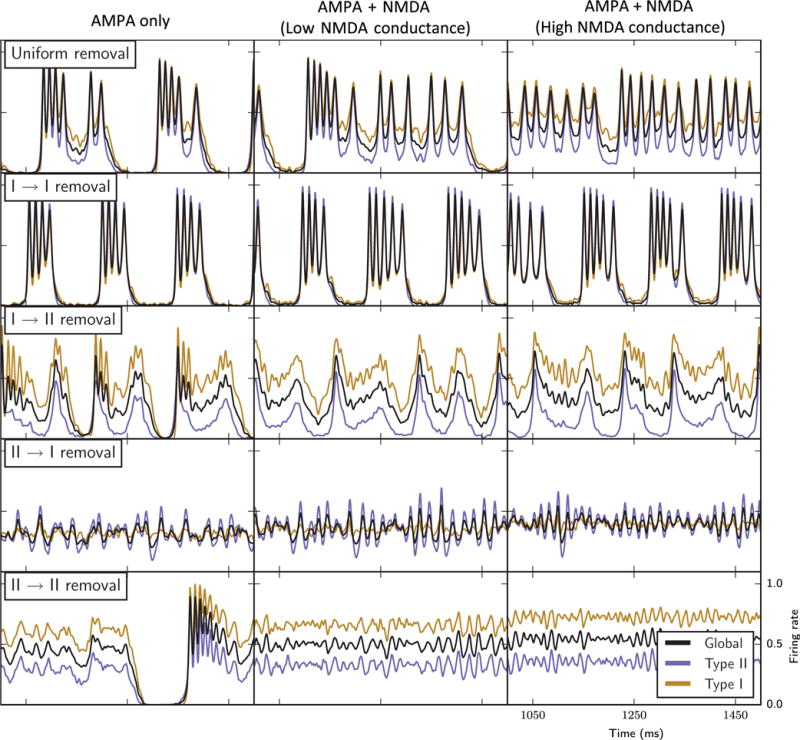
Network bursting behaviours with the inclusion of slower NMDA-like synaptic currents in addition to fast AMPA-like synaptic currents (see Materials and methods): firing rate curves of the entire network (black curves), Type I cells only (gold curves) and Type II cells only (blue curves) in the different synapse removal cases (labelled rows) with only AMPA synapses (left column, similar to the results shown in Figs 3–7), with NMDA synaptic conductance twice that of AMPA synaptic conductance (middle column), and with NMDA synaptic conductance four times that of AMPA synaptic conductance (right conductance).

Discussion

In brain networks, cellular properties and network structure are influenced by numerous factors during normal brain states, such as by neuromodulation, and in pathological brain states. In this study, we focused on the interaction of both cellular and network properties that can underlie changes in activity patterns. Specifically, we constructed networks composed of neurons having two types of membrane excitability properties, as measured by their frequency–current curves and PRCs, as a result of different responses to the neuromodulator ACh. PRCs provide a powerful theoretical framework for understanding the synchronization propensity of neural networks, and at the same time can be measured experimentally (Smeal et al., 2010; Schultheiss et al., 2012). We identified synapses as belonging to one of four groups depending on the types of the presynaptic and postsynaptic neurons. Through systematic removal of specific synapse types, we constructed networks with the same connectivity density but with varied distributions of synapse types. Comparing dynamics in these different networks elucidated differential roles for the two cell types in the formation, maintenance and termination of synchronous bursts in network activity, as summarized in the Graphical Abstract. Generally, as predicted by other studies (Hansel et al., 1995; Ermentrout, 1996; Bogaard et al., 2009), Type II neurons promoted synchronized activity, whereas Type I cells were more excitable and provided overall network excitation. Although these roles are not surprising, given the known changes in frequency–current relationships and PRCs resulting from cholinergic modulation, how these roles determined overall network activity depended on the distribution of synapse types. Our results showed that variations in the balance of the interactions between cell types caused dramatic changes in the stereotypic properties of network bursts.

Fewer synaptic connections originating from Type I cells generally lowered the amount of recurrent excitation in the network. However, the effect of deleting these connections depended on their postsynaptic target. Deletion of Type I–I connections generally lowered recurrent excitation between Type I cells. In this case, Type II cells continued to receive a significant amount of Type I input, and thus could generate synchronized population spikes. However, owing to limited recurrent excitation, the pool of Type I cells available to maintain bursting activity was diminished, leading to short bursts with well-defined internal structure. In contrast, when Type I–II connections were deleted, the Type II cells could not generate well-synchronized population spikes or maintain high levels of overall activity, owing to lowered input. This, in turn, reduced the population of Type I cells that could fire in response to synchronous input from Type II cells. The resulting diminished feedforward and feedback interactions between the cell types led to short variable bursts with a low degree of intraburst structure.

Fewer synaptic connections originating from Type II cells, on the other hand, generated drastically different bursting activity, depending on the target of those connections. If Type II–I connections were deleted, bursting was abolished. This was because the Type I cells did not receive synchronous drive that could force them to fire together. Type II cells continued to fire somewhat synchronously, but their coherence was low, because the feedback input from the Type I cells was asynchronous. A completely different scenario occurred when Type II–II connections were abolished. In this case, the Type II cells had limited ability to form synchronized bursts in response to Type I recurrent input. Thus, except for the initial spike at the onset of the burst, the network showed moderate levels of asynchronous activity. The average cellular firing rate was sufficiently high for recurrent excitation to maintain network activity, and synchronization was sufficiently low to avoid episodes in which a large fraction of cells were in the refractory phase of their cycle, leading to the quiescent periods between bursts. Thus, in this case, the network achieved a delicate balance of relatively low levels of synchrony and moderate levels of recurrent excitation that allowed the burst to continue for a long time.

These roles for cells with Type I and Type II excitability properties in generating network burst activity were also evident in related results regarding synaptic plasticity dynamics in similar heterogeneous excitatory networks (Knudstrup et al., 2016). In that study, synaptic weights were allowed to evolve according to a spike-timing-dependent plasticity rule (Dan & Poo, 2004). The role of Type II neurons as drivers of the synchronizing signal to Type I cells was revealed by the maximal potentiation of Type II–I synapses and the almost complete weakening of Type I–II synapses, owing to Type II cells, on average, firing before Type I cells. In neither that study nor the current study did we include short-term synaptic plasticity mechanisms, such as short-term depression or facilitation of synaptic efficacy, in the networks. However, our results may point to possible effects of such activity-dependent plasticity. Generally, Type I neurons have higher firing rates in the networks considered here, suggesting that Type I–I and Type I–II synapses would be most susceptible to depression or facilitation. Facilitation of Type I–I synapses would lead to longer bursts but perhaps less synchrony within bursts, whereas facilitation of Type I–II synapses may increase intraburst synchrony, owing to heightened drive to the Type II cells. The effects of depression of these synapses is harder to predict, as burst synchrony may be promoted by depression of Type I–I synapses but degraded by depression of Type I–II synapses.

Our simplified network model does not include many components of actual neurons and brain networks that can also contribute to synchronized network bursting. For example, we have not included inhibitory neurons in our networks. Inhibitory interneurons are well known to contribute to synchronized firing in cortical and hippocampal networks by gating the firing times of excitatory pyramidal cells through the ING and PING mechanisms (Whittington et al., 1995, 2000). In these mechanisms, during the time windows of firing opportunities for pyramidal cells, their intrinsic firing properties and the synaptic connectivity among them, as investigated here, will affect their activity patterns. Interestingly, some types of inhibitory interneuron, such as oriens-lacunosum moleculare cells, contain M-type K⁺ currents, which would also be targets of cholinergic modulation (Lawrence et al., 2006). Current work by our group is investigating the effects of such cholinergic modulation on the activity of coupled inhibitory cell networks, including synchronization, which would affect ING/PING network mechanisms. In our neuronal model, we have also not included the Ca²⁺-dependent K⁺ current, I_AHP, which is modulated by ACh (Madison et al., 1987). Modelling studies have shown, however, that modulation of I_AHP does not affect the neuronal PRC and thus the cell’s propensity for synchronization (Stiefel et al., 2009). Because we have concentrated on the effects of cholinergic modulation leading to heterogeneous cellular dynamics, we have focused on its modulation of the M-type K⁺ current, which has the primary effect on the PRC (Stiefel et al., 2009).

Although ACh has effects on synaptic transmission and plasticity, especially in hippocampal networks (Hasselmo, 2006), we have focused on its influence on intrinsic neuronal response properties. Our thorough dissection of the contributions of these different cellular properties provides a detailed understanding of the mechanisms generating population activity. These insights, although provided by a simplified network model, can translate to more biophysically realistic settings. For example, in the hippocampus, ACh is strongly implicated in the generation and modulation of theta rhythms (Vertes & Kocsis, 1997; Hasselmo, 2006; Alger et al., 2014). Both ACh and theta rhythms are essential for normal hippocampal function, and their disruption leads to impairment of learning and memory (Jerusalinsky et al., 1997; Buzsaki, 2002; Power et al., 2003). Simultaneous in vivo measurements of ACh levels and extracellular local field potentials by amperometry have shown slow phasic increases in ACh during episodes of theta rhythm activity (Zhang et al., 2010; Santos et al., 2015) generated by a population of slow-firing, putatively cholinergic neurons in the medial septum (Zhang et al., 2011). The activity of these slow-firing cells precedes increases in the power of hippocampal theta rhythms (Zhang et al., 2011). Our simulation results provide an explanation for such an increase in theta rhythm power, as phasic increases in ACh will increase the proportion of pyramidal cells with Type I-like excitability properties that can drive network activity to promote the synchronization coordinated by theta-generating mechanisms, including interneuron activity and projections from the medial septum (Buzsaki, 2002).

Persistent firing of prefrontal cortical neurons during working memory tasks is another example where the cholinergic-induced effects on neuronal activity reported here may be contributing. As has been clearly shown during delayed match-to-sample tasks in primates, certain neurons show persistent, maintained firing during the delay period following the brief presentation of the sample cue, and the rate of this persistent firing directly correlates with task performance (Goldman-Rakic, 1996; Funahashi, 2006). Further studies have suggested that persistent firing of recurrently connected clusters of pyramidal cells codes for the location of sample cues in the visual field (Goldman-Rakic, 1995). Scopolamine, an antagonist of muscarinic receptors that mediate ACh’s effect on the M-type K⁺ current, degrades performance on working memory tasks and reduces the rate of persistent firing during the delay period (Zhou et al., 2011). Our results suggest that, in control conditions, ACh would contribute to persistent firing in the delay period by promoting Type I properties that enhance activity within the pyramidal cell clusters.

ACh has been implicated in the generation of hippocampal sharp waves (SPWs), which are large-amplitude deflections in local field potential recordings caused by highly synchronous population firing events (Buzsaki, 2015). SPWs occur in all behavioural states but are more frequent during non-REM or slow-wave sleep (SWS) and during extended periods of immobility during waking, when ACh levels are lower. Although the suppressive effects of ACh on synaptic transmission may have the biggest influence on inhibiting the synchronous firing underlying SPWs (Hasselmo, 2006), its cellular effects may also contribute to limiting synchronization. Pyramidal cells in both the CA3 and CA1 hippocampal regions contain M-type K⁺ currents, and cholinergic modulation results in increased cellular excitability (Vervaeke et al., 2006; Hu et al., 2007). Although not explicitly measured, CA1 pyramidal cells are more likely to show changes in neuronal PRCs, as ACh acts to increase burst firing in CA3 pyramidal cells (Vervaeke et al., 2006). Our results suggest that recruitment of pyramidal cells into synchronous SPW events may be attenuated by high ACh levels, when Type I cellular properties would be most prevalent. This effect, in addition to suppression of synaptic transmission, would limit the extent of propagation and thus the amplitude of the SPW. These effects may particularly contribute to the different activity patterns of SPWs across sleep and wake states (Buzsaki, 2015).

Pathological brain states are caused by disease-driven changes to both network structure and to the properties of a propotion of neurons. Whereas changes in cellular properties, which depend on a cell’s receptor and channel repertoire and extracellular molecular milieu, have been studied extensively (Lerche et al., 2001; Catterall et al., 2008), changes to underlying network properties are less well understood. Under seizure conditions, inhibitory interneurons have been observed to enter depolarization block (Ziburkus et al., 2006; Shin et al., 2010), making excitatory synapses the dominant connection type, as in our network models. Stereotypical seizures evolve from the fast oscillatory activity observed at onset to sequences of lower-frequency, population burst events as the seizure terminates (Netoff & Schiff, 2002; Jirsa et al., 2014). These evolving dynamics are certainly generated by dynamic changes to the underlying cellular and connectivity properties of the neural network. Our results predict that cellular or synaptic plasticity mechanisms that lead to a dominance of Type II cellular responses and of Type II synaptic efficacy would promote the transition to shorter, more synchronized population burst activity. More generally, the distinct characteristics of burst activity obtained with different distributions of synaptic connections could enable predictions of properties of the dominant synapse type within the underlying network. Additionally, experimental recordings of single cell activity during interictal discharges in epileptic patients have identified classes of neurons with different firing patterns during the discharge, with some neurons showing high firing rates only at the onset of the discharge, and other neurons whose firing increases only after discharge onset (Keller et al., 2010). Our results predict that these firing patterns would correspond to cells with Type II and Type I response profiles, respectively.

Our results also relate to the modulation of epileptic activity during sleep states. ACh levels are state-dependent, with high levels occurring during wakefulness, very low levels during non-REM movement or SWS, and the highest levels during REM sleep (Marrosu et al., 1995). These differences in the neuromodulatory environment can significantly change the cellular properties in a given network, with Type II cellular responses dominating during SWS, and Type I responses dominating during REM sleep. It has been established that REM sleep in humans is largely seizure-free, even though neuronal activity levels are high (Herman et al., 2001; Minecan et al., 2002; Rocamora et al., 2013). Our results support the hypothesis that the lack of seizures is attributable to the domination of Type I cellular properties induced by high ACh levels. We have shown that activity of Type II neurons underlies seizure onset, and the lack of Type II–I connections leads to abolition of seizures. On the other hand, interictal epileptic discharges are common during deep-stage SWS, but they often do not lead to seizure onset (Malow et al., 1998; Minecan et al., 2002). Our results predict that, because of low ACh levels, Type II cellular properties dominate and promote synchronized bursts, but they do not convert to seizure activity, owing to the lack of cells with Type I response properties. Furthermore, our results provide an explanation for the higher propensity for there to be seizure onset during the lighter sleep stages that occur during the early stages of a sleep episode (Herman et al., 2001; Minecan et al., 2002; Rocamora et al., 2013). During these stages, ACh levels are also changing, so it is more likely that cells are heterogeneously modulated, leading to a mixture of Type I and Type II responses. Our simulations show that the feedforward and feedback interactions between synchronizing signals generated by Type II cells and the overall excitability of Type I cells generate the perfect conditions for seizure activity.

Abbreviations

ACh

acetylcholine

NMDA

N-methyl-D-aspartate

PRC

phase response curve

PSD

power spectral density

REM

rapid eye movement

SPW

sharp wave

SWS

slow-wave sleep