Using a continuum model to predict closure time of gaps in intestinal epithelial cell layers

Abstract

A two-dimensional continuum model of collective cell migration is used to predict the closure of gaps in intestinal epithelial cell layers. The model assumes cell migration is governed by lamellipodia formation, cell-cell adhesion, and cell-substrate adhesion. Model predictions of the gap edge position and complete gap closure time are compared with experimental measures from cell layer scratch assays (also called scratch wound assays). The goal of the study is to combine experimental observations with mathematical descriptions of cell motion to identify effects of gap shape and area on closure time and to propose a method that uses a simple measure (e.g., area) to predict overall gap closure time early in the closure process. Gap closure time is shown to increase linearly with increasing gap area; however, gaps of equal areas but different aspect ratios differ greatly in healing time. Previous methods that calculate overall healing time according to the absolute or percent change in gap area assume that the gap area changes at a constant rate and typically underestimate gap closure time. In this study, data from scratch assays suggest that the rate of change of area is proportional to the first power or square root power of area.

Introduction

Tissue injuries, which may result from trauma, surgery, or disease, are associated with disrupted functionality of a tissue and an increased risk of infection. For example, injuries to the skin compromise the body’s ability to protect itself against the environment [1] and injuries to the intestinal epithelial layer could result in bacterial sepsis. Tissue repair requires the migration of cells into the wounded region and the proliferation of new cells to restore the original density of the tissue. A wound is considered healed once tissue functionality has been fully restored [2].

The ability to predict wound healing time accurately could allow clinicians to quantify the benefit of various treatment strategies and identify procedures that accelerate healing [3]. To achieve this, simple and informative measurements to assess wounds during the healing process are needed. Mathematical descriptions of wound healing may be useful in determining quantifiable indicators of complete wound closure. As expected, the size and location of a wound are factors that affect healing rates. Deep wounds heal more slowly than superficial wounds since several cell layers and blood vessels are interrupted, requiring the formation of a blood clot and the contraction of cells [4]. Superficial wounds, such as wounds in the intestinal epithelial cell layer, disrupt only a single layer of cells and rely primarily on cell migration in the initial stages of healing. A combination of clinical observations with mathematical explanations of wound healing may help to elucidate important factors and methods for predicting overall healing time for a variety of wound types.

Observations of wound closure

To assess the progression of a wound, quantities such as absolute wound area remaining, percentage of initial wound area remaining, wound volume remaining, wound perimeter remaining, wound healing velocity, and mean adjusted healing rates have been measured [3, 5]. Some of these measurements can be difficult to obtain clinically, and there is currently no universally accepted measure of wound healing [2]. While wound area is an obvious measure of wound closure, predicting healing time based on the percent of wound area healed tends to bias small wounds and based on the absolute wound area healed tends to bias large wounds [6, 7].

Gilman [8] proposed an alternate measure, called the linear healing parameter, that represents the average distance the wound margin has advanced over a given time period. Gorin et al. [7] showed that healing rates calculated according to the linear healing parameter had no correlation to initial wound area. The linear healing parameter tends to remain relatively constant over time and thus may be a reliable forecaster of total healing time [9].

In [6], three methods for calculating healing times based on wound area and the linear healing parameter are described and compared. The healing times for a theoretical circular wound of radius 50 mm were calculated using the three methods. It was observed that calculating the absolute area or percent area will almost always underestimate the healing time for a wound, whereas the linear healing rate of the wound was constant and provided the most accurate measure of healing time. It should be noted that these methods give accurate predictions only if the rate of change of area or of the linear healing parameter is nearly constant.

The principle of the “greatest inscribed circle” has also been used to explain wound closure via epithelialization in the absence of wound contraction [10]. According to this theory, the time for epithelialization of a wound is directly proportional to the radius of the largest circle that can fit within the boundary of the original wound. It was observed that two rectangular wounds with the same area but with different inscribed circle radii did not close in the same amount of time; the rectangle with the larger inscribed circle radius closed more slowly since the radius represents the greatest distance over which the epithelium must migrate [10].

Wounds exhibit a wide variety of geometries, including concave, convex, and highly irregular shapes. In [11], the change in shape of venous leg ulcers was evaluated over time, and a regression analysis was used to conclude that wounds that shifted to a convex shape over time were more likely to heal than those that did not change shape. In another study involving venous leg ulcers, wound surface area decreased exponentially with time early in the treatment phase [11]. However, it was noted that an exponential function is not accurate over a long time period and thus may only be appropriate when describing the contraction phase of wound closure.

Zahm et al. [12] examined in vitro wound repair of the respiratory surface epithelium. Unlike the exponential healing time observed in venus leg ulcers, the wounded area of the respiratory epithelium was observed to decrease linearly with time during the first half of wound closure (~50 h). During the second half of closure, the repair process slowed, but the number of proliferative cells in the repairing area increased dramatically until wound closure was complete (~day 4). Video recordings of the wound culture showed lamellipodia formation at the wound edge. This protrusion mechanism was observed to be accompanied by cell-cell and cell-matrix interactions governing the migration of the remaining cell layer [12].

The observations from these multiple wound scenarios demonstrate that healing time predictions are affected by multiple factors such as wound geometry, tissue type, cell-cell interactions, and the stage of the healing process (epithelialization, contraction, or proliferation). In this paper, we analyze the influence of these factors on the closure time of a gap in a cell layer using a recently developed two-dimensional continuum model [13] of collective cell migration based on data from cell layer scratch assays (also known as scratch wound assays, in other contexts). Using a mathematical model to assess these factors can allow us to make predictions and derive analytical results that are not biased by experimental uncertainty.

Mathematical modeling of wound healing

Many mathematical models have used reaction diffusion equations to describe wound healing [14, 15]. For example, Sherratt and Murray [15] investigated planar epidermal movement controlled by diffusion and a mitotic regulator that activates or inhibits migration. Model predictions of the decrease in the radius of a circular wound were consistent with experimental data from wounds of a similar diameter for a range of species and wound locations [14]. The model was also used to predict healing times for multiple wound geometries, including cusped, diamond, and ovate-shaped wounds. Healing time was predicted to decrease as the side-to-length ratio of rectangular wounds was increased, regardless of activation or inhibition. In the presence of the regulation of mitosis via an inhibitor mechanism, wounds with an initially cusped shape progressed into a rounded wound during healing, whereas initially ovate wounds flattened and healed faster [14]. Sadovsky and Wan [16] also studied epidermal wound closure. They developed a continuum mechanical model in which the circumferential contraction of the epidermis surrounding the wound is governed by laws of mechanics and cell-cell signaling. They note that different expressions for elastic strain or active stress may be necessary to explain the dynamics of the wound closure process near complete closure, and they did not include proliferation or differentiation in the current version of the model.

Javierre et al. [17] developed a two-dimensional model for wound closure of the epidermal basal membrane; closure was mediated by cell mitosis and lamellipodia-induced cell migration in the presence of a generic epidermal growth factor. Multiple wounds on planar surfaces were considered, and wound morphology was identified as a key parameter affecting healing kinetics. The model was used to predict that healing is initiated at regions with high convexity and is delayed if the diffusion of the growth factor is slower than the rate of cell migration. Lee and Wolgemuth [18] provided a biophysical description of collective migration of epithelial cells based on the motility of single cells. They considered four types of forces that act throughout an epithelial monolayer: intercellular stress, polarization stresses generated inside of the cells by the action of the cytoskeleton, actin, and molecular motors, thrust forces against the substrate, cell-cell adhesion forces, and drag forces due to cell-substrate adhesions. Their seven-parameter model showed that the mechanical process that drives single cell crawling is sufficient to drive motion of a layer if cell-cell adhesion is taken into account.

Along the same lines, we have recently developed a two-dimensional continuum model to describe the collective migration of an intestinal epithelial cell layer in response to a gap [13]. Three mechanisms are assumed to govern gap closure: lamellipodia formation, substrate adhesion, and cell-cell adhesion. The model includes the contribution of cell migration to gap closure but neglects proliferation because the model was calibrated to experimental data from scratch assays of intestinal epithelial cells over relatively short time periods during which proliferation was balanced by apoptosis. The model parameters were optimized according to the density of the cell layer and location of the gap edge in scratch assays [13].

The model is used to track the closure of both hypothetical and experimentally-based geometries of gaps in cell layers. Model parameters are varied to demonstrate the effect of model assumptions and tissue type on the predicted healing time. The evolution of multiple gaps is predicted, and different phases of gap edge velocity are identified. The effects of initial gap geometry on gap closure characteristics are investigated, and gap closure time is shown to differ for gaps of equal areas but different initial shapes. Closure time as a function of inscribed circle radii is also determined. The suitability of three common methods for calculating healing time is explored by comparing model predictions with experimental time measurements for intestinal epithelial cell scratch assays, and two new methods for calculating healing time are proposed.

Materials and Methods

Experimental gap edge

In a scratch assay, rat intestinal enterocytes (IEC-6 cells) obtained by the Hackam Lab at the University of Pittsburgh from ATTC are cultured on a glass coverslip, grown to 100% confluence, serum-starved for 12 hours, and scraped with a pipette to induce an injured region within the cell sheet. The cell sheet is one cell thick, and the motion and deformation of the cells are captured at 5 minute intervals using differential interference contrast imaging. Multiple points along the experimental gap edges are recorded by hand and used to determine the area and perimeter of each experimental gap at multiple time points.

Computational gap edge

Migration of a two-dimensional cell layer with a gap is predicted using a previously-developed continuum model [13]. The cell layer is defined by a density of cells, ρ(x,y,t), given as a function of the spatial coordinates x and y and time t. A relaxed (unstressed) cell layer is given by ρ₀. In the scratch assay, the initial cell layer is assumed to be pre-stressed due to the forces generated by the lamellipodia of the cells throughout the entire layer. The motion of the cell layer is assumed to be driven by the force of the lamellipodia (F) acting in the direction normal to the gap edge, the stretching of the layer described by the elastic modulus (k), and the friction between the cells and the substrate, which includes the effects of the release of the trailing cell edge and is described by an adhesion constant b. For simplicity, we neglect higher order effects such as adhesion of neighboring cells to each other, which can be described as viscosity of the layer, and dipole moments arising from cell polarizations. Such effects have been implemented in other models, such as [18]. Ratios of these parameters are represented by two constants: ϕ = F/k and κ = k/b.

In [13], it was shown that the model reduces to the following free boundary problem:

$${\partial }_t\rho =\kappa \Delta \rho +g(\rho )\hspace{1em}\text{in }{\mathrm{\Omega }}^{\mathrm{t}}$$

$${\nu }_n=\kappa {\rho }^{-\mathit{1}}\nabla \rho \hspace{1em}\hspace{1em}\text{on }\partial {\mathrm{\Omega }}_1^{\mathrm{t}}$$

$$\rho ={\rho }_{\mathit{0}}{e}^{-\phi }\hspace{1em}\hspace{1em}\hspace{1em}\text{on }\partial {\mathrm{\Omega }}_1^{\mathrm{t}}$$ (1)

$$\rho \mathit{(}x,\mathit{0}\mathit{)}={\rho }_{\mathit{0}}{e}^{\phi }\hspace{1em}\hspace{1em}\text{in }{\mathrm{\Omega }}^0$$

$$\nabla \rho ·n=\mathit{0}\text{ or }\rho ={\rho }_{\mathit{0}}\hspace{1em}\text{on }\partial {\mathrm{\Omega }}_2$$

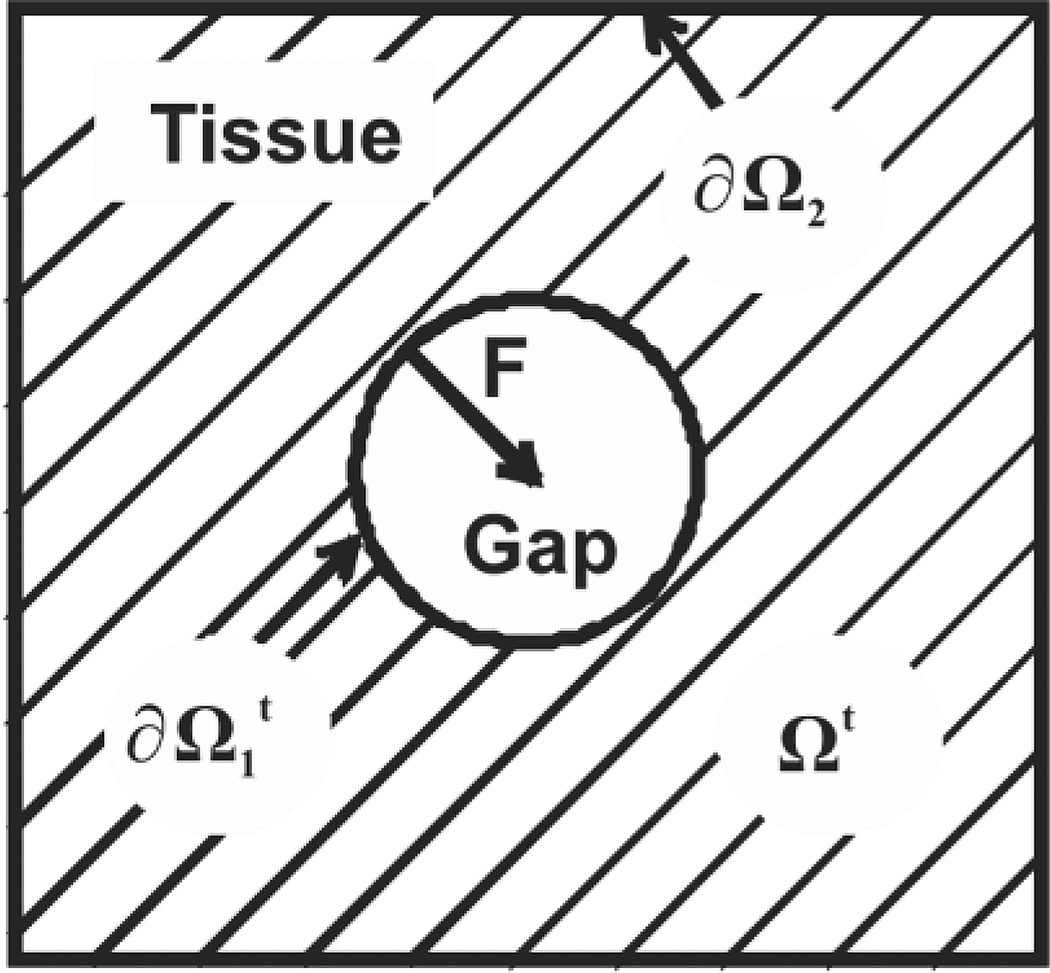
where g(ρ) defines the proliferation of cells in the layer, Ω^t represents the time-dependent tissue area, $\partial {\mathrm{\Omega }}_1^{\mathrm{t}}$ is the gap boundary, and ∂Ω₂ is the boundary of the observed area (see Figure 1). In the development of the model, the cell sheet is represented as a compressible inviscid fluid. The form of Eq. 1 results from the choice of the constitutive equation for material elasticity (see [19] for details) and does not arise from any underlying diffusion process. The free boundary problem with g = 0 and the defined initial and boundary conditions is known as the Stefan problem, which has been extensively studied in many contexts [20, 21]. A numerical solution is found for a given gap geometry using a variation of a level set method that was developed in [22] and applied to Stefan problems in [23, 24].

Figure 1.

Computational domain of the moving boundary initial value problem. Hatched area (Ω^t) represents the cell layer, and the white area is a cell-free region. Two boundaries of Ω^t are labeled: $\partial {\mathrm{\Omega }}_1^{\mathrm{t}}$ (gap edge) and ∂Ω₂ (exterior tissue edge). F is the force exerted by cells at the gap edge.

Optimal values of ϕ, κ, and ρ₀ were found by minimizing the sum of the mean square difference between the experimental and predicted cell density values and gap edge positions. The values ϕ = 0.19, κ = 72.53 µm²/h, and ρ₀ = 0.63 cells/µm² were optimized according to gap closure data from IEC-6 cells [13].

We analyze gaps of different geometries defined within a 100 µm by 100 µm region of cells representing intact tissue. Predicted closure times and shapes of the gap contours would be affected by the choice of Dirichlet or Neumann boundary conditions, as described in [13]. In this study, the critical size for the computational domain was determined so that model predictions were not affected by changes in domain size. Dirichlet boundary conditions are chosen on the boundary of the tissue region since cells are assumed to extend far beyond the gap edge. The time-dependent position of the gap edge is predicted using the model, and the area and perimeter of the gap are calculated at multiple time points. The gap is considered completely closed once the area of the gap falls below twice the area of a numerical grid space (1 µm).

The computational representation of the gap edge consists of a discrete set of points. To obtain the average instantaneous velocity along the computed gap edge, the normal velocity at each point on the gap contour is calculated. Arc lengths between each consecutive pair of points are calculated, and the velocity along each segment is estimated.

Healing time calculations

Three commonly used methods for estimating wound closure time are the Absolute Area Reduction method, Percent Area Reduction method, and Linear Parameter method [6]. The Area Reduction methods are based on the assumption that the time rate of change in wound area, c, is constant. The Absolute Area Reduction method estimates the constant c in the average sense as the ratio of the difference between the current wound area and original wound area to the total change in time. The Percent Area Reduction method estimates c as the instantaneous change by calculating the difference in wound areas between two consecutive time points. The Linear Parameter method assumes that the average velocity of the wound edge over the wound contour is constant in time [6]. The linear healing parameter, d, is defined as the ratio of the difference in wound areas to the average perimeter for two consecutive time points:

$$d=\frac{A_{i-1}-A_i}{\frac{1}{2}(P_{i-1}+P_i)}$$ (2)

where A_i is wound area and P_i is wound perimeter at time t_i. The Linear Parameter method was developed to remove the bias in the Area Reduction methods to wound size. Gilman [6] used the Linear Parameter method to predict healing time for a circular wound in the following way:

$$d_i=\frac{\pi {R_{i-\mathit{1}}}^{\mathit{2}}-\pi {R_i}^{\mathit{2}}}{\frac{1}{2}(2\pi R_{i-\mathit{1}}+2\pi R_i)}=R_{i-\mathit{1}}-R_i$$ (3)

Since the rate of change of the radius is assumed to be constant,

$$\frac{dR}{dt}=c=\frac{d_i}{t_i-t_{i-\mathit{1}}}$$ (4)

Solving Eq. 4 for R(t) with initial condition (0, R₀) gives

$$R\mathit{(}t\mathit{)}=R_{\mathit{0}}+ct$$ (5)

Closure time (t_f) is calculated using this method by solving for t in Eq. 5 with R(t_f) = R_min:

$$t_f=\frac{\mathit{(}{R}_{\mathit{0}}-R_{\mathit{\text{min}}}\mathit{)}\mathit{(}{t}_i-t_{i-\mathit{1}}\mathit{)}}{d_i}$$ (6)

For noncircular wound shapes, R₀ is the radius of the inscribed circle of the initial wound shape.

In addition to these three methods, we investigate two methods of calculating healing time in which the time rate of change of area is not constant but is proportional to the square root of area (Square Root Area method) or the first power of area (Proportional Area method).

The Square Root Area method is motivated by the observation that if wound area is assumed to be proportional to the square of the inscribed radius and if the rate of change of the inscribed radius is assumed constant (as in the Linear Parameter method), then the rate of change of wound area will be proportional to the square root of area, which is consistent with some experimental findings [25]. The Proportional Area method was hypothesized according to area measurements obtained from the scratch assays examined in this study.

The assumed relationship for each method is listed in row 1 of Table 1. The estimates of the rates of change are given in row 2. In row 3, the solution to the differential equation from row 1 is given in terms of c_i and initial conditions. Finally, in row 4, healing time is found by solving for the value of t in row 3 when A = A_min (or R = R_min). A_min (or R_min) represents the minimal wound area (or radius) at which a wound is considered closed.

Table 1.

A comparison of five methods for predicting gap closure time

Method	1. Absolute Area	2. Percent Area	3. Linear Parameter	4. Square Root	5. Proportional Area
Relation	$\frac{dA}{dt}=c_{\mathit{1}}$	$\frac{dA}{dt}=c_{\mathit{2}}$	$\frac{dR}{dt}=c_{\mathit{3}}$	$\frac{dA}{dt}=c_{\mathit{4}}\sqrt{A}$	$\frac{dA}{dt}=c_{\mathit{5}}A$
Constant, c	$c_1=\frac{A_{\mathit{0}}-A_i}{\mathit{0}-t_i}$	$c_{\mathit{2}}=\frac{A_{i-\mathit{1}}-A_i}{t_{i-\mathit{1}}-t_i}$	$c_{\mathit{3}}=\frac{\mathit{2}\mathit{(}{A}_{i-\mathit{1}}-A_i\mathit{)}}{\mathit{(}{P}_{i-\mathit{1}}+P_i\mathit{)}\mathit{(}{t}_{i-\mathit{1}}-t_i\mathit{)}}$	$c_{\mathit{4}}=\frac{A_{i+\mathit{1}}-A_{i-\mathit{1}}}{\sqrt{A_i}\mathit{(}{t}_{i+\mathit{1}}-t_{i-\mathit{1}}\mathit{)}}$	$c_{\mathit{5}}=\frac{A_{i-1}-A_{i-\mathit{1}}}{A_i\mathit{(}{t}_{i-\mathit{1}}-t_i\mathit{)}}$
Area, A or Radius, R	A0 + c1t	Ai−1 + c2(t−ti−1)	R0 + c3t	${(\sqrt{A_i}+\frac{c_{\mathrm{4}}}{\mathit{2}}\mathit{(}t-t_{i-\mathit{1}}\mathit{)})}^{\mathit{2}}$	Ai−1ec5(t−ti−l)
Closure time, tf	$\frac{A_{\mathit{\text{min}}}-A_{\mathit{0}}}{c_{\mathit{1}}}$	$\frac{A_{\mathit{\text{min}}}-A_{\mathit{0}}}{c_{\mathit{2}}}+t_{i-\mathit{1}}$	$\frac{R_{\mathit{0}}-R_{\mathit{\text{min}}}}{c_{\mathit{3}}}$	$\frac{2(\sqrt{A_{min}}-\sqrt{A_i})}{c_4}+t_i$	$\frac{1}{c_5}ln\left(\frac{A_{min}}{A_{i-1}}\right)+t_{i-1}$

Results

Effect of model parameters on gap closure time

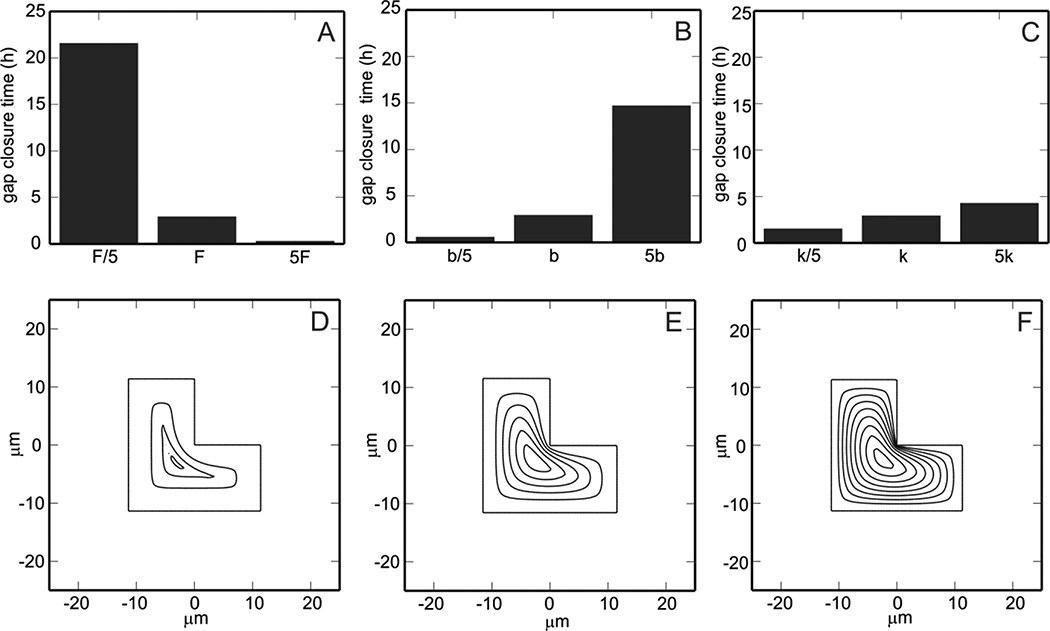
In Fig. 2, the optimized values of ϕ and κ (ϕ₀ = 0.19 and κ₀= 72.53 µm²/h) are varied to illustrate the dependence of model predictions on parameter values. Recalling that ϕ = F/k and κ = k/b, it is evident that a change in F only affects the value of ϕ and a change in b only affects the value of κ whereas a change in k alters both ϕand κ. The top row of Fig. 2 shows that increasing the force of the lamellipodia (F), decreasing the frictional coefficient (b), or decreasing the elastic modulus of the layer (k) can reduce gap closure time predictions.

Figure 2.

Model predicted healing times and evolution of L-shaped gap edge while varying parameter values. Optimized parameter values for ϕ=F/k and κ=k/b are ϕ₀ = 0.19 and κ₀= 72.53 µm²/h. A. Effect of increasing parameter F = F₀/5, F₀, 5F₀ on gap closure time. B. Effect of increasing parameter b = b₀/5, b₀, 5b₀ on gap closure time. C. Effect of increasing parameter k = k₀/5, k₀, 5k₀ on gap closure time. In the bottom row, the evolution of the gap edge is shown for the three values of k in (C) at half hour increments. D. ϕ=5ϕ₀ and κ=κ₀/5. E. ϕ=ϕ₀ and κ=κ₀. F. ϕ=ϕ₀/5 and κ =5κ₀.

In the second row of Fig. 2, parameter k is varied by factors of 5 (as in Fig. 2C). These k values correspond to ϕ=5ϕ₀ and κ=κ₀/5 (Fig. 2D, k = k₀/5), ϕ=ϕ₀ and κ=κ₀ (Fig. 2E, k = k₀), and ϕ=ϕ₀/5 and κ=5κ₀ (Fig. 2F, k = 5k₀). In panel D, the velocity of the edge is observed to be independent of the curvature of the gap and slows with time. In panel F, the gap edge velocity decreases with decreasing curvature (the velocity is effectively zero if the curvature is negative, corresponding to an inside corner) and is uniform with time. Differences in these parameters correspond to differences in tissue type, suggesting that closure times can differ widely with location of a wound. For example, MDCK cells (used in [18]) and IEC-6 enterocytes (used here) exhibit different cell-cell adhesion and migration properties; IEC-6 cells do not show the complex wound edge evolution (oscillations) known to occur in MDCK cells.

It follows from Eq. 1 that any change in can be accommodated by a change in the units of time without affecting the solutions of the model. In other words if ρ(x,t) is a solution of the boundary value problem in Eq. 1, then ρ̃(x,t) = ρ(x,tτ) is a solution of the BVP with kappa replaced by κτ and v_n replaced by v_n,τ. Thus, solutions of the BVP with different κ values but the same ϕ will give rise to the same sequence of shapes for the gap edge, only with different times of progression through those shapes; the higher the κ, the faster the closure. In the remaining results presented in this study, the optimized values of ϕ₀ = 0.19 and κ₀= 72.53 µm²/h [13] (shown in Fig. 2E) are used to describe the motion of the intestinal epithelial cell layer.

Effect of gap geometry on gap closure time

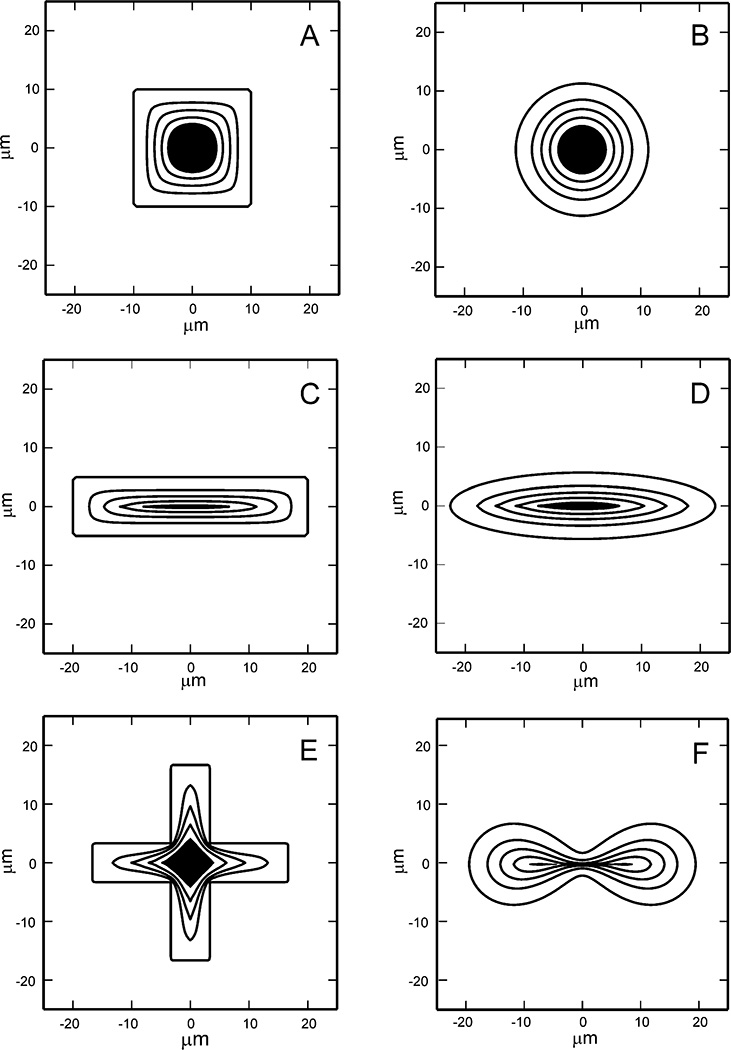
Numerical computation of the evolution of the gap edge for various initial gap geometries (Fig. 3) predicts that motion of the gap edge is always in the direction that closes the gap, i.e., the edge never retracts to make the gap larger, even at the extreme corners. The model predicts that convex gaps with more than one axis of symmetry, such as a square (Fig. 3A) or circle (Fig. 3B), close symmetrically. Gap shapes with unequal dimensions, such as a rectangle (Fig. 3C) or ellipse (Fig. 3D), tend to close faster in the direction perpendicular to the smallest dimension. Corners are generally smoothed out during the evolution except for gaps with large initial aspect ratio where a sharp corner with high edge curvature forms as the gap retreats from the area (Fig. 3E). The model predicts that the gap edge ultimately converges toward a convex shape, even though convexity may be attained fairly late in the closure process. In rare instances, the topology of the cell layer may change from an annulus to a region with 2 or more holes (Fig. 3F), which has also been observed in experiments. The six gaps in Fig. 3 have an initial area of 400 µm². The plotted contours correspond to the position of the gap edge at half hour intervals, and the gap area remaining after 2 hours has been shaded. Similar images are provided in Figure 4, but with the initial geometry corresponding to the positions of the gap edges in the epithelial cell layer scratch wound assays. The contours represent positions of the gap edge every 30 minutes.

Figure 3.

Evolution of the gap edge of 6 different initial gap shapes. Each gap has an initial area of 400 µm² and is defined within a 100 µm × 100 µm tissue region. Gap contours are shown at 30 minute intervals, and the gap area remaining after 2 hours has been shaded. A. Square. B. Circle. C. Rectangle. D. Ellipse. E. Cross. F. Cassini oval

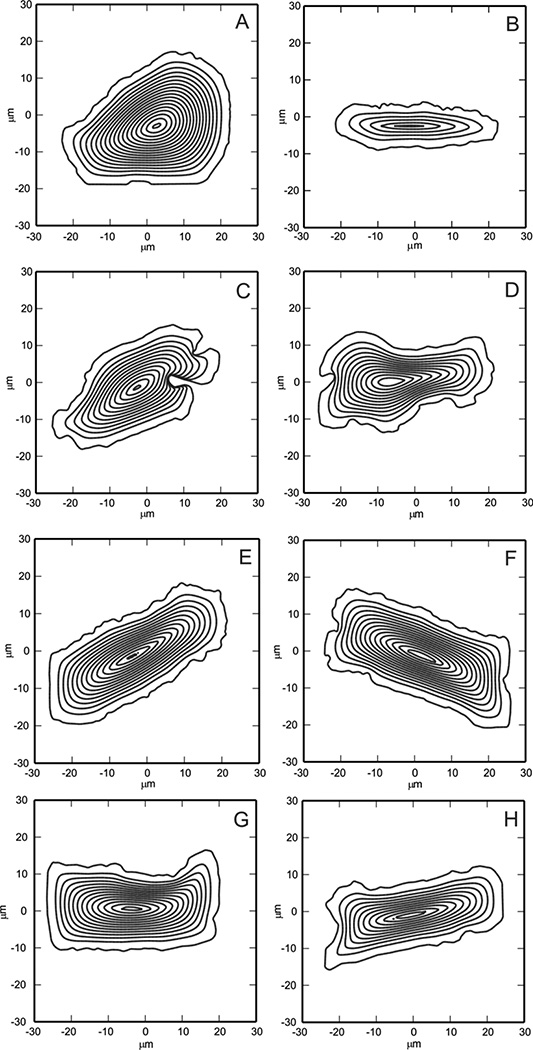
Figure 4.

Evolution of the gap edge of 8 different scratch assays. Each gap is defined within a 100 µm × 100 µm tissue region. Gap contours are shown at 30 minute intervals until closure.

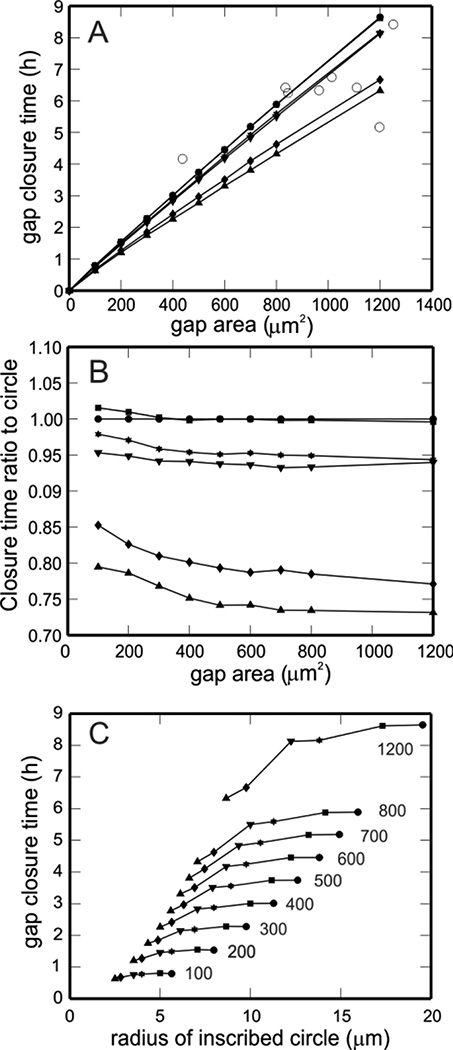
Model predictions of gap closure time as a function of initial gap area are shown in Fig. 5A for multiple initial gap geometries with initial areas between 100 and 1200 µm², including squares, circles, and rectangles and ellipses with different aspect ratios. In addition, experimentally measured closure times for the eight scratch assays shown in Fig. 4 are included (Fig. 5A, open circles). As expected, closure time increases with initial gap area but is not the same for all gap shapes of equal area. Gaps with an aspect ratio of one close in approximately the same amount of time (e.g., circle and square gaps). However, as this aspect ratio deviates from one, the time for gap closure predicted by the model decreases. The ratios of the closure times of various gaps to the closure time of a circular gap are shown in Fig. 5B to highlight how the difference in gap shape affects predicted closure time. In addition, gap closure time as a function of inscribed circle radius is shown in Fig. 5C. Gaps of equal area are connected by solid curves and labeled. As observed by Watts [10], gaps with the same area but with different inscribed circle radii do not heal at the same rate.

Figure 5.

A. Gap closure time as a function of initial gap area for multiple gap shapes: 4×1 rectangle (upward triangle), 2×1 rectangle (downward triangle), square (closed square), circle (closed circle), 4×1 ellipse (hexagon), and 2×1 ellipse (diamond). Closure times are calculated for all of these shapes with initial areas of 100, 200, 300, 400, 500, 600, 700, 800, and 1200 µm². Actual closure times for 8 different experimental scratch assays are also included in the figure (open circles). B. Ratio of closure time of each shape in panel A to the closure time of a circle of the same initial area. Symbols as in panel A. C. Gap closure time as a function of inscribed circle radii. Gaps of equal area are connected by solid curves and labeled (values in µm²). Symbols as in panel A.

Predicting closure time using area and perimeter measurements

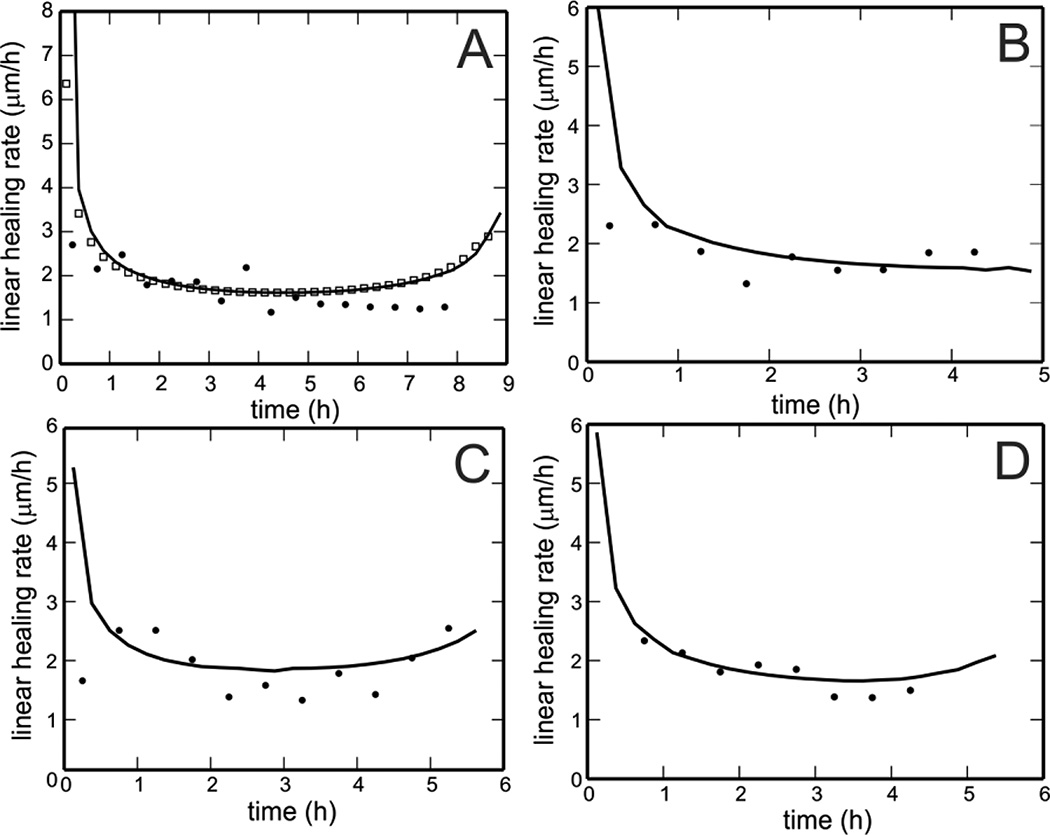
In the limit of small ΔA, the ratio of the linear healing parameter to the time difference converges to the mean normal velocity of gap closure when averaged over the gap edge. The average instantaneous gap edge velocity predicted by the model for the experimental scratch assay in Fig. 4A is denoted by the solid curve in Fig. 6A and is shown to be approximately equal to the time rate of change of the linear healing parameter when calculated for the same gap using Eq. 2 (Fig. 6A, open squares). This verifies that average instantaneous velocity can be directly compared with the rate of change of linear healing parameters. The linear healing rate calculated from the area and perimeter data for the experimental gap in Fig. 4A is also shown (black dots) for Δt = 30 minutes. In Fig. 5B–D, the linear healing rate is calculated for three additional experimental gaps from Fig. 4 (black dots) with Δt = 30 minutes and compared with the model predictions of average instantaneous velocity for those gaps (solid curves).

Figure 6.

A. Model computed average instantaneous gap edge velocity for the experimental wound shown in Fig. 4A (curve) is directly comparable to the time rate of change of the linear healing parameter computed from the areas and perimeters of the gap contours (open squares). The experimental values of time rate of change of the linear healing parameter are also shown at half hour intervals (dots). B–D. The time rates of change of the linear healing parameter is shown for three experimental scratch assays (dots) with Δt = 30 minutes and are compared with model predictions of average instantaneous velocity for those gaps (curves). Panel B shows good agreement between model predictions and experimental results. Panel C shows the occasional speed-up that is predicted by the model at the end of closure. Panel D shows that the model predictions overestimate gap closure times in some cases.

The average instantaneous velocity of the gap edge, as predicted by the model, exhibits different phases of behavior. Initially, the gap edge velocity is maximal; it then steadily decreases to a lower value at which it remains relatively constant for the majority of the closure process. In some cases, the velocity is predicted to increase slightly at the final stage of gap closure. We hypothesize that this slight increase may be due to the increasing curvature of the gap edge at the final time steps. These phases have been observed in some of the scratch assays, although the final increase is not always observed experimentally.

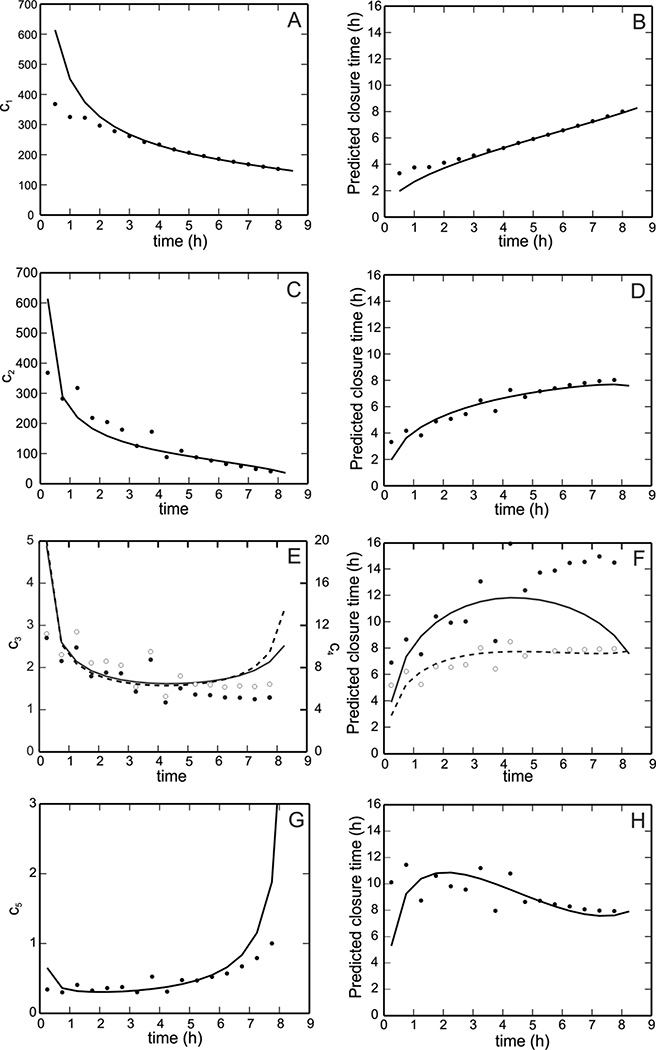
The Absolute Area, Percent Area, and Linear Parameter methods as well as the Square Root and Proportional Area methods are used to predict the healing time of an experimental cell layer scratch assay (Fig. 7, right column), which was found experimentally to be nearly 8.5 hours. In the left column of Fig. 7, the proportionality constants for all of the methods are plotted as a function of time. These plots are used to investigate whether or not the assumed proportionality constants indeed remain constant. In all panels, solid curves correspond to model calculations and dots correspond to the measurements from the assay. The dashed curve in Fig. 7F represents the closure time prediction according to the Square Root method, which is based on the linear healing parameter but assumes gap area is always proportional to the square of the radius. The results in Fig. 7 indicate that the Absolute and Percent Area methods underestimate the closure time, verifying Gilman’s conclusions [6]. However, unlike Gilman’s findings, the linear healing rate is not predicted to be constant for this scratch assay, and thus the Linear Parameter method gives both an overestimate and underestimate of the closure time during the different phases of closure instead of converging to the actual closure time. The Square Root and Proportional Area methods are shown to provide better overall predictions of total closure time.

Figure 7.

Comparison of predicted healing times for an experimental scratch assay using five different methods (see text). In column 1 (panels A, C, E, G), the constant c_i for each method (see Table 1) is plotted as a function of time. In column 2 (panels B, D, F, H), the predicted healing time for each method is shown as a function of time. A, B: Absolute Area Reduction method. C, D: Percent Area Reduction method. E, F: Linear Parameter method (solid line, black dots) and Square Root method (dashed line, open dots). G, H: Proportional Area method. In all panels, solid lines correspond to model calculations and dots correspond to experimental measures.

Discussion

In this paper we use a previously developed two-dimensional continuum mechanical model of gap closure [13] to study the dependence of gap closure times on initial gap shape, gap area, and parameters reflecting tissue type and cell-cell interactions. In addition we employ the model to evaluate the commonly used methods for predicting gap closure time and propose two new alternative methods which show better accuracy of predictions.

The model we employ [13] describes all of the characteristic features of a migrating intestinal epithelial cell layer in response to a gap: it predicts motion of the gap edge in the direction of the gap (no retractions of the edge), faster motion of the edge in regions with higher curvature, and a change in the topology of the gap from one to multiple holes under certain conditions (Fig. 3F). The methods developed here can be applied to any wound healing model; it would be illustrative to examine whether more complex models (such as [18], which includes effects of cell polarization, dipole stress, and shear force) give similar predictions as our model.

Effect of model parameters on gap closure time

The model indicates that the time for gap closure increases with decreasing lamellipod force, increasing adhesion, or increasing elastic modulus of the cell layer. This is in accord with observations that if lamellipod formation at the gap edge is inhibited, gap closure is slowed or even stalled [26]. Throughout the paper we used a single pair of constants obtained by fitting IEC-6 cell migration scratch assay results [13]. However, we have observed that fitting model parameters to data is difficult due to the insensitivity of the gap shape to the parameters. As seen in Fig. 2D–F, a ten-fold difference in parameter values gives rise to solutions with similar gap shapes. In general, the prediction of the gap closure time is much more sensitive than the prediction of the gap shape. This significant error in the gap shape results in an ill-posed optimization problem in the space of the two parameters, κ and ϕ.

The numerical solution of the gap closure contour in Fig. 3E was sensitive to the grid spacing, and the closure progress slowed down severely as the program attempted to smooth out any sharp corners that developed during the closure process. We are working to resolve this issue by using a finite element method approach. For this study, we ran model simulations on a refined mesh for the gap shapes shown in Fig. 3 (except panel E), and the closure times and contours were not different. We also note that the Square Root and Proportional Area Methods proposed in this study (see Table 1) were based on the closure of cell layer scratch assays for which model predictions of gap closure did not depend on the grid spacing. In addition, complete closure of gaps with aspect ratios that deviate from one does not occur until the gap also closes in the longest dimension. This behavior differs from behavior observed in vitro or in vivo in which wounds may be able to close along a seam instead of being required to close to a single point. Therefore, the numerical implementation of the model causes an overestimation of the closure time for gap with aspect ratios that are different from one.

Effect of gap geometry on gap closure time

The ability to accurately quantify wound healing time is of crucial importance to both clinicians and patients. Clinicians need to assess whether or not a particular treatment strategy is optimal, and patients appreciate any indication of their expected recovery time. An advantage of using a mathematical model to predict wound closure is the potential ability to predict healing times without conducting a closely monitored study over several months [3]. However, as illustrated in the present study (Fig. 5), it is important to be mindful that model predictions of closure time are sensitive to wound shape, size, and type.

The results in Fig. 5A suggest that closure time increases linearly with increasing gap area, although gaps of equal area do not necessarily close in the same amount of time (Fig. 5B). Multiple initial gap geometries are explored in Fig. 5 to give a potential range of gap closure time for gaps of a given initial area; as initial gap area increases, the range of possible closure time varies more substantially (e.g., 4–9 hours for a gap with an initial area of 1200 µm²). Since it is impossible to predict all possible gap shapes, the time ranges provided here are lower bounds on the actual closure time ranges for intestinal epithelial gap closure. As a general rule, as the aspect ratio of the gap deviates from one, the time for gap closure predicted by the model decreases (e.g., rectangles and ellipses). This prediction is consistent with previous findings in an epidermal migration model [14]. Gap closure times for scratch assays are included on the plot (open circles, Fig. 5A) to illustrate that the ranges of closure times predicted by this model provide fairly good estimates of actual closure time of two-dimensional gap within an epithelial cell layer. While a few of the points lie outside of the predicted range, this is likely due to the position of the experimental gap (e.g., Neumann boundary conditions may be more appropriate when tracking gaps located near the edge of the cell layer) or due to uncertainty of the true initial gap area (e.g., the initial gap edges were not always visible in the microscope image).

The model accurately captures the edge velocity of actual experimental gaps in many cases (Fig. 6B) but overestimates the time to gap closure in others (Fig. 6D). This may result from overestimating the original gap dimension if the edges of the gap were not entirely within the microscope viewing area. Also, some of the experimental gaps are observed to pinch off into multiple pieces, while the model predicts the evolution of a single gap contour till closure. By not predicting a pinch off, the model assigns a larger area to the gap, thereby contributing to the overestimation of total gap closure time.

It is important to note that these predictions are based on a model calibrated to a particular line of intestinal epithelial cells. Actual closure times for wounds in other tissue types may differ significantly from the values given in this study. The model could be adapted to data from different tissues (provided they can be approximated as two-dimensional) to provide more appropriate healing time estimates in other tissue types. In addition, factors such as cell proliferation, wound contraction, tissue growth factors, or blood supply are not modeled here but could be added to the model to determine their impact on closure time in other situations. For example, including a variable for growth factors can help to quantify which mechanisms are most significantly impacted by growth factors. A viscous term is not included in the current version of the model, but future work should include viscous effects, as in [18], to take into account the viscous stress resulting from differences in velocity between neighboring cells.

Predicting closure time using area and perimeter measurements

Given the observed variance of closure time with gap area, a method of predicting gap closure times independent of wound geometry or initial area has important application in the clinical setting. It is especially important to have a simple mathematical formula for predicting wound closure time based on readily available measurements of wound characteristics, such as wound area and wound perimeter. We found that the Absolute Area method and Percent Area method underestimate closure times and fail to provide accurate estimates until the very end of the closure process, which is in agreement with previously established conclusions [6].

Gilman [6] claims that a Linear Parameter method provides a better estimate of the actual healing time because the linear healing parameter is constant during the closure. However, the scratch assays in this study did not exhibit this behavior. By definition, the ratio of the linear healing parameter to time difference is equivalent to the average instantaneous normal velocity of the gap edge (Fig. 6A). In the scratch assays, gap edge velocity was observed to vary during the initial closure process but to be nearly constant after the first hour of closure. Velocity is maximal at the beginning of closure, which Zahm et al. [12] hypothesized is due to the availability of new space for the cells to occupy. For some gaps, the model predicts a slight speed-up near the end of closure (Fig. 6C); this speed-up also occurs in some experimental assays but is not seen consistently for all gaps. A comparison of the average instantaneous velocity predictions for multiple gap shapes (including squares, circles, rectangles, triangles, and ellipses) suggests that the speed-up occurs for gaps with multiple axes of symmetry. We hypothesize that the presence or absence of this final speed-up stage may be a function of initial gap geometry and the curvature of the evolving gap edge.

We propose two additional methods for computing the closure time, the Square Root method and Proportional Area method, which are based on the assumptions that the dependence of the time-rate of change of the gap area is proportional to the square root of area or the first power of area, respectively. These methods provide better estimates of gap closure time than the three previously established methods since they both converge to the correct gap closure time as more data is available and they provide accurate predictions at early stages of the closure process. Thus, the model predictions support the use of a simple measure, such as gap area, to provide a relatively accurate prediction of healing time after only the first few steps of gap closure. The Square Root method slightly underestimates the closure time initially, while the Proportional Area method slightly overestimates this time. It is possible that a method with time-rate of change of the gap area proportional to some power p of the area, where ½ < p < 1, would fit the data better, but we found that the estimation of this parameter is very difficult. As a compromise one could simply average the predictions of both methods to obtain a more accurate estimate. These two methods are useful for predicting a range of closure times for superficial wounds; however, other clinical aspects may be required to obtain accurate closure time predictions for wounds of various types and sizes. In summary, using mathematical modeling to predict how factors such as wound geometry and tissue type can affect closure time has an important application in studying wound healing and other disorders that are affected by the presence of injured tissue.