Powerful and Adaptive Testing for Multi-trait and Multi-SNP Associations with GWAS and Sequencing Data

Abstract

Testing for genetic association with multiple traits has become increasingly important, not only because of its potential to boost statistical power, but also for its direct relevance to applications. For example, there is accumulating evidence showing that some complex neurodegenerative and psychiatric diseases like Alzheimer’s disease are due to disrupted brain networks, for which it would be natural to identify genetic variants associated with a disrupted brain network, represented as a set of multiple traits, one for each of multiple brain regions of interest. In spite of its promise, testing for multivariate trait associations is challenging: if not appropriately used, its power can be much lower than testing on each univariate trait separately (with a proper control for multiple testing). Furthermore, differing from most existing methods for single-SNP–multiple-trait associations, we consider SNP set-based association testing to decipher complicated joint effects of multiple SNPs on multiple traits. Because the power of a test critically depends on several unknown factors such as the proportions of associated SNPs and of traits, we propose a highly adaptive test at both the SNP and trait levels, giving higher weights to those likely associated SNPs and traits, to yield high power across a wide spectrum of situations. We illuminate relationships among the proposed and some existing tests, showing that the proposed test covers several existing tests as special cases. We compare the performance of the new test with that of several existing tests, using both simulated and real data. The methods were applied to structural magnetic resonance imaging data drawn from the Alzheimer’s Disease Neuroimaging Initiative to identify genes associated with gray matter atrophy in the human brain default mode network (DMN). For genome-wide association studies (GWAS), genes AMOTL1 on chromosome 11 and APOE on chromosome 19 were discovered by the new test to be significantly associated with the DMN. Notably, gene AMOTL1 was not detected by single SNP-based analyses. To our knowledge, AMOTL1 has not been highlighted in other Alzheimer’s disease studies before, although it was indicated to be related to cognitive impairment. The proposed method is also applicable to rare variants in sequencing data and can be extended to pathway analysis.

ALZHEIMER’S disease (AD) (MIM 104300) is the most common neurodegenerative disease, and every 67 sec, someone in the United States develops AD (Alzheimer’s Association 2015a). Currently there is no cure for AD, and most cases are diagnosed in the late stage of the disease. It is projected that the number of Americans of age 65 years and older with AD will increase from 5.1 million in 2015 to 13.5 million in 2050, a growth from an estimated 11% of the U.S. senior population in 2015 to 16% in 2050, costing >$1.1 trillion in 2050 (Alzheimer’s Association 2015b). To advance our understanding of the initiation, progression, and etiology of AD, the Alzheimer’s Disease Neuroimaging Initiative (ADNI) was started in 2004 and continues to the present, collecting extensive clinical, genomic, and multimodal imaging data (Shen et al. 2014). Many other genetic studies have been conducted, identifying multiple common and rare variants, shedding light on pathogenic mechanisms of AD (Marei et al. 2015; Saykin et al. 2015). In particular, the APOE$\mathit{\epsilon }4$ allele has been consistently shown to be associated with AD. However, only 50% of AD patients carry an APOE$\mathit{\epsilon }4$ allele, suggesting the existence of other genetic variants contributing to risk for the disease (Karch et al. 2014). A recent study indicates that 33% of total AD phenotypic variance is explained by common variants; APOE alone explains 6% and other known markers 2%, meaning >25% of phenotypic variance remains unexplained by known common variants (Ridge et al. 2013). Hence, as for other common and complex diseases and traits, many more genetic factors underlying late-onset AD are yet to be discovered. One obvious but costly approach is to have a larger sample size. Alternatively, more powerful analysis methods are urgently needed. For example, in contrast to the popular single single-nucleotide polymorphism (SNP)-based analysis, novel gene- and pathway-based analyses may be more powerful in discovering additional causal variants. As demonstrated by Jones et al. (2010), jointly analyzing functionally related SNPs sheds new light on the relatedness of immune regulation, energy metabolism, and protein degradation to the etiology of AD. The reason is due to the well-known genetic heterogeneity and small effect sizes of individual common variants, as observed from published genome-wide association study (GWAS) results (Manolio et al. 2009). To boost power in identifying aggregate effects of multiple SNPs, it may be promising to conduct association analysis at the SNP-set (or gene) level, rather than at the individual SNP level.

Another strategy is to use multiple endophenotypes, intermediate between genetics and the disease, for their potential to have stronger associations with genetic variants. In addition to boosting power, the use of intermediate phenotypes may provide important clues about causal pathways to the disease (Maity et al. 2012; Schifano et al. 2013). A recent GWAS demonstrated the effectiveness of the strategy: some risk genes such as FRMD6 were first identified to be associated with some neuroimaging intermediate phenotypes (e.g., hippocampal atrophy) (Shen et al. 2014) and then were later validated to be associated with AD (Hong et al. 2012; Sherva et al. 2014). A possibly useful but underutilized intermediate phenotype is the brain default mode network (DMN), consisting of several brain regions of interest (ROIs) remaining active in the resting state. Brain activity in the DMN may explain the etiology of AD (Metin et al. 2015) and is a plausible indicator for incipient AD (Damoiseaux et al. 2012; Greicius et al. 2004; He et al. 2009; Jones et al. 2011; Balthazar et al. 2014). Since there is growing evidence that genetic factors play a role in aberrant default mode connectivity (Glahn et al. 2010), it may be substantially more powerful to detect genetic variants associated with the DMN, a set of multiple intermediate phenotypes, than with AD.

Here we discuss gene-based multitrait analysis, aiming at discovering genes associated with multiple traits such as the DMN. To date, several but not many methods have been proposed for gene-based multitrait analysis (Maity et al. 2012; Guo et al. 2013; Van der Sluis et al. 2015; Wang et al. 2015). The simplest way is to use the minimum P-value (minP) test based on the most significant single-SNP–single-trait association, which, however, may lose power in the presence of multiple weak associations between multiple SNPs and multiple traits. Some methods, such as that in Van der Sluis et al. (2015) and M-TopQ25Stat (Guo et al. 2013), utilize only a few top association signals among the pairwise single-SNP–single-trait associations. Some methods based on principal components analysis (PCA) or principal components of heritability (PCH), originally proposed for multiple SNPs and a single trait (Wang and Abbott 2007; Klei et al. 2008), may be also applied. However, these methods and canonical correlation analysis (CCA) (Tang and Ferreira 2012) make use of only one or a few top components, and thus they share the same weakness of power loss in the presence of multiple associations; furthermore, the number of principal components (PCs) may be difficult to determine (Aschard et al. 2014). Another extreme is the burden test (Shen et al. 2010; Guo et al. 2013; Mukherjee et al. 2014), which is powerful in the presence of a dense association pattern, in which most SNP–trait pairs are associated with almost equal effect sizes and directions; otherwise, e.g., when the association directions of some SNP–trait pairs are different, it does not perform well (as is well known for analysis of rare variants). A compromise between the above two extremes is a variance-component test (Maity et al. 2012; Wang et al. 2013), which is more robust to association density/sparsity and varying association directions. Nevertheless, as shown in the context of multiple rare variants and a single trait (Pan et al. 2014), it may still suffer from power loss in the presence of more sparse association patterns (i.e., when there are fewer associated SNP–trait pairs). A fundamental challenge in multivariate analysis is the lack of a uniformly most powerful test: nonadaptive test may be powerful in some situations, but not in others. Nevertheless, we aim to construct an adaptive test such that it can maintain high power, not necessarily highest power, across a wide range of scenarios. In particular, the proposed test is adaptive at both the SNP and trait levels. Its key feature is the use of a weighting scheme to yield robust statistical power no matter whether the true and unknown association pattern is dense or sparse (or in whatever directions), and the weight is determined data adaptively. In addition, some chosen weights correspond to several existing tests, including a burden test and a variance-component test. Therefore, the high power range of the proposed test covers those of the burden test and the variance-component test. Moreover, the proposed test is based on the general framework of the generalized estimating equations (GEE), and hence it is flexible with the capability to incorporate covariates and various types of traits (Liang and Zeger 1986). It also avoids a difficulty in correctly specifying a joint multivariate distribution or likelihood for a set of multiple traits. Furthermore, we extend the proposed method to pathway analysis, in which it is adaptive to possibly varying gene-level associations.

We compare the performance of the new test with that of several existing tests, using both simulated and real data. The methods were applied to structural magnetic resonance imaging (MRI) data drawn from the ADNI to identify genes associated with the DMN. In the GWAS, 277,527 SNPs were mapped to 17,557 genes, among which genes AMOTL1 on chromosome 11 and APOE on chromosome 19 were discovered by the new test to be significantly associated with the DMN. Notably, gene AMOTL1 was not detected by single SNP-based analyses. We also illustrate the application of the methods to the ADNI whole-genome sequencing (WGS) data, although no significant genes were identified, presumably due to a relatively small sample size.

In the following, we briefly review GEE and an existing method before introducing the new test in Materials and Methods. In Results, the new and several existing methods are compared with applications to the ADNI data and simulated data mimicking the ADNI data. We end with a short summary of the conclusions.

Materials and Methods

Review

Generalized estimating equations:

Suppose for each individual $i=1,\dots ,n,$ we observe k traits $Y_i={\left({\mathit{y}}_{i1},\dots ,y_{ik}\right)}^{\prime },$ q covariates $z_i={\left(z_{i1},\dots ,z_{iq}\right)}^{\prime },$ and a set of SNPs $x_i={\left(x_{i1},\dots ,x_{ip}\right)}^{\prime },$ with $x_{ij}\in \left\{0,1,2\right\}.$ Denote $X_i=\mathit{I}\otimes {\mathit{x}}_i^{\prime }$ and $Z_i=I\otimes \left(1,z_i^{\prime }\right),$ where I is a $k\times k$ identity matrix, and ⊗ represents the Kronecker product. We model the mean of the phenotypes $E\left(Y_i|X_i,Z_i\right)={\mu }_i,$ using a marginal generalized linear model

$$g\left({\mu }_i\right)=Z_i\mathit{\varphi }+X_i\mathit{\beta }=H_i\mathit{\theta }$$ (1)

with $H_i=\left(Z_i\hspace{0.17em}{X}_i\right),$ parameters $\theta ={\left({\varphi }^{\prime },{\beta }^{\prime }\right)}^{\prime },$ and a link function $g(.).$ The regression coefficients $\beta ={\left({\beta }_{11},\dots ,{\beta }_{p1},\dots ,{\beta }_{1k},\dots ,{\beta }_{pk}\right)}^{\prime }$ are a $pk\times 1$ vector, in which ${\beta }_{jt}$ represents the effect of the jth SNP on the tth trait, while the element ${\varphi }_{st}$ of $\varphi ={\left({\varphi }_{11},\dots ,{\varphi }_{\left(q+1\right)1},\dots ,{\varphi }_{1k},\dots ,{\varphi }_{\left(q+1\right)k}\right)}^{\prime }$ is the effect size of the sth covariate on the tth trait. Liang and Zeger (1986) proposed estimating φ and β by solving the GEE

$$U_{\theta }={\displaystyle \sum _{i=1}^n{D^{\prime }}_i{V}_i^{-1}\left(Y_i-{\mu }_i\right)=0}$$ (2)

with $D_i=\partial {\mu }_i/\partial {\theta }^{\prime }$ and $V_i=\phi A_i^{1/2}{R}_w\left(\alpha \right)A_i^{1/2},$ where φ is a dispersion parameter, $A_i=\text{diag}\left\{v\left({\mu }_{i1}\right),\dots ,v\left({\mu }_{ik}\right)\right\}$ models the variances with a variance function $v\left({\mu }_i\right),$ and $R_w\left(\alpha \right)$ is a working correlation matrix with possibly some unknown parameters α. Specifically, for quantitative traits ($Y_i$) with the identity link function (or more generally, for any generalized linear model with a canonical link function), the score vector $U_{\theta }$ and its variance–covariance matrix $\mathrm{Cov}\left(U_{\theta }\right)$ are

$$U_{\theta }={\left({U^{\prime }}_{\varphi },{U^{\prime }}_{\beta }\right)}^{\prime }={\displaystyle \sum _{i=1}^n{\left(Z_i\hspace{0.17em}{X}_i\right)}^{\prime }{R}_w^{-1}\left(Y_i-{\mu }_i\right)},$$

$$\mathrm{Cov}\left(U_{\theta }\right)={\displaystyle \sum _{i=1}^n{\left(Z_i\hspace{0.17em}{X}_i\right)}^{\prime }{R}_w^{-1}\left(Y_i-{\mu }_i\right){\left(Y_i-{\mu }_i\right)}^{\prime }{R}_w^{-1}\left(Z_i\hspace{0.17em}{X}_i\right)}.$$

The covariance matrix can be partitioned according to the score components for ϕ and β: $\mathrm{Cov}\left(U_{\theta }\right)=\left(\begin{array}{cc}{V}_{11}& V_{12}\\ V_{21}& V_{22}\end{array}\right).$ For convenience, the working independence model is often used with $R_w$ as an identity matrix $I_{k\times k},$ as done in this article unless specified otherwise.

Our primary concern is to test for overall genetic effects with $H_0:$ $\beta =0,$ while treating ϕ as nuisance parameters. To perform the score test, we evaluate Equation 1 under $H_0.$ Under $H_0,$ we have $g\left({\mu }_i\right)=Z_i\varphi ,$ and the estimate of ϕ, denoted as $\widehat{\varphi },$ is the solution to the generalized score equation $U_{\varphi ,\beta =0}={\displaystyle {\sum }_{i=1}^n{Z^{\prime }}_i\left(Y_i-{\mu }_i\right)=0}.$ The marginal mean is estimated by ${\widehat{\mu }}_i=g{\left(Z_i\widehat{\varphi }\right)}^{-1}.$

For testing SNP-set effects, we consider the subcomponents of the score vector for β:

$$U_{\beta }={\displaystyle \sum _{i=1}^n{X^{\prime }}_i\left(Y_i-{\widehat{\mu }}_i\right)}.$$ (3)

$U_{\beta }$ asymptotically follows a multivariate normal distribution $\mathcal{ℳN}\left(0,{\tilde{\Sigma }}_{\beta }\right)$ under $H_0,$ where ${\tilde{\Sigma }}_{\beta }=V_{22}-V_{21}{V}_{11}^{-1}{V}_{12}.$ $U_{\beta }$ can be written as $U_{\beta }={\left(U_{11},\dots ,U_{p1},\dots ,U_{1k},\dots ,U_{pk}\right)}^{\prime }.$ Each element $U_{jt}$ measures the association strength between SNP j and trait k for $j=1,\dots ,p$ and $t=1,\dots ,k$ and is asymptotically proportional to ${\beta }_{jt}$ in Equation 1. ${\beta }_{jt}=0$ implies there is no association between SNP j and trait k; similarly $U_{jt}=0$ (or small) indicates no (or weak) association between SNP j and trait k.

For testing $H_0,$ the GEE-Score test statistic is defined by

$$\text{GEE-Score}={U^{\prime }}_{\beta }{\tilde{\Sigma }}_{\beta }^{-1}{U}_{\beta }.$$

Under $H_0$, the GEE-Score statistic asymptotically follows a central chi-square distribution with $pk$ degrees of freedom. When $pk$ is large, this standard score test loses power for large degrees of freedom. Another way to draw inference, especially convenient when combining the score test with other tests as discussed later, is to simulate $U_{\beta }^{\left(b\right)}\mathcal{\sim ℳN}\left(0,{\tilde{\Sigma }}_{\beta }\right)$ for $b=1,\dots ,B$ and obtain the null statistics $\text{GEE-}{\text{Score}}^{\left(b\right)}=U_{\beta }^{{\left(b\right)}^{\prime }}{\tilde{\Sigma }}_{\beta }^{-1}{U}_{\beta }^{\left(b\right)}.$ The P-value can be calculated as $P_{\text{Score}}={\displaystyle {\sum }_{b=1}^{B}I\left(\text{GEE-Score}\le \text{GEE-}{\text{Score}}^{\left(b\right)}\right)/\left(B+1\right)},$ where $I(\cdot )$ denotes the indicator function.

For ease of notation, we suppress β and take $U=U_{\beta }$ and $V={\tilde{\Sigma }}_{\beta }$ hereafter.

An adaptive association test for a single SNP:

Zhang et al. (2014) proposed a class of sum of powered score (SPU) tests for testing association between an individual SNP and multiple traits, along with its data-adaptive version (aSPU). The SPU tests are a family of association tests based on the (generalized) score vector in the GEE framework, aiming for at least one of them to be powerful in any given situation. With only a single SNP j, then the score vector reduces to $U={\left(U_{j1},\dots ,U_{jk}\right)}^{\prime }.$ The association between the SNP and k traits can be quantified with a test statistic

$$\text{SPU}\left(\gamma \right)={\displaystyle \sum _{t=1}^k{\left(U_{jt}\right)}^{\gamma }},$$

where a candidate integer $\gamma \ge 1$ is chosen from a preselected parameter set $\mathrm{\Gamma };$ e.g., $\mathrm{\Gamma }=\left\{1,2,\dots ,8,\mathrm{\infty }\right\}.$ The statistical power of an SPU(γ) test depends on the choice of $\gamma \in \mathrm{\Gamma }.$ When γ is an odd integer, the SPU(γ) test sums up the association signals across all the traits, retaining high power if all or most of the multiple traits have an almost equal effect size in the same association direction. A special case is $\gamma =1,$ giving a burden test commonly used for rare variants. With an even γ, the SPU(γ) test will be more powerful when some traits have different association directions. In particular, the SPU(2) test is the same as the sum of squared score (SSU) test (Pan 2011), closely related to multivariate distance matrix regression (MDMR) (McArdle and Anderson 2001), kernel machine regression (KMR) (Liu et al. 2007), and variance-component tests (Tzeng et al. 2011). Furthermore, as γ increases, the SPU test upweights the more strongly associated traits, while reducing the weights on other ones. In particular, when $\gamma \to \mathrm{\infty }$ (as an even integer), only the maximum component of the score vector is used and the test statistic is defined as $\text{SPU}\left(\mathrm{\infty }\right)={\max }_{t=1}^k\left|U_{jt}\right|.$ The SPU$\left(\mathrm{\infty }\right)$ test is similar to the UminP test (when the variances of the score components are almost equal). To compute the significance of an SPU test, Monte Carlo (MC) simulations (or alternatively, permutations) are used; for $b=1,\dots ,B,$ the null score $U^{\left(b\right)}={\left(U_{j1}^{\left(b\right)},\dots ,U_{jk}^{\left(b\right)}\right)}^{\prime }$ is generated from $\mathcal{ℳN}\left(0,V\right),$ from which the null statistics SPU${\left(\gamma \right)}^{\left(b\right)}={\displaystyle {\sum }_{t=1}^k{\left(U_{jt}^{\left(b\right)}\right)}^{\gamma }}$ can be obtained for each γ. Then the P-value can be calculated as $p_{\gamma }=\left[{\displaystyle {\sum }_{b=1}^{B}I\left(\text{SPU}\left(\gamma \right)\le \text{SPU}{\left(\gamma \right)}^{\left(b\right)}\right)+1}\right]/\left(B+1\right).$

However, it is not clear how to choose an optimal γ a priori for given data. Hence, Zhang et al. (2014) proposed an aSPU test to extract association evidence from multiple SPU(γ) tests. The statistic of the aSPU test is the minimum P-value of SPU$\left(\gamma \right)$s for some candidate values of γ,

$$\text{aSPU}=\underset{\gamma \in \mathrm{\Gamma }}{\min }{p}_{\gamma },$$

where $p_{\gamma }$ is the P-value of SPU$\left(\gamma \right).$ By MC simulations (or permutations), the P-value of aSPU, along with those of all SPU(γ) tests, can be efficiently calculated based on the same set of the null statistics in a single layer.

Existing gene-based tests:

We compare the proposed test with several existing gene-based tests for multiple traits, including multivariate analysis of variance (MANOVA), MDMR with the Euclidean distance (McArdle and Anderson 2001), multivariate KMR under linear kernel (Maity et al. 2012), and a multivariate functional linear model (MFLM) (Wang et al. 2015). We note that KMR can be derived based on a random-effects model while MFLM is built on a fixed-effect model. For implementation, the R package vegan was used for MDMR; R code for KMR and MFLM was downloaded from the authors’ websites, http://www4.stat.ncsu.edu/∼maity/software.html and https://www.nichd.nih.gov/about/org/diphr/bbb/software/fan/Pages/default.aspx, respectively. Since KMR (Maity et al. 2012) was computationally slow, it was excluded from the simulation studies.

New methods

An adaptive test:

We introduce a novel gene-based adaptive sum of powered score test for a set of multiple traits, denoted as aSPUset, by extending the single SNP-based test of Zhang et al. (2014). Suppose that there are p SNPs in a gene and k traits of interests. Recall that $U={\left(U_{11},\dots ,U_{p1},\dots ,U_{1k},\dots ,U_{pk}\right)}^{\prime }$ is the generalized score vector of length $pk$ in GEE, and V is the $pk\times pk$ covariance matrix of the score vector; each element of the score, $U_{jt}$ quantifies the association between SNP j and trait t. In practice, the true and unknown association patterns across multiple SNPs and multiple traits are complex: some SNPs may be associated with some traits, but not with other traits; different SNPs may be associated with different subsets of the traits with varying association strengths and directions. Since the use of nonassociated SNPs and traits in a test statistic could reduce the power of the test, we may want to give higher weights to more likely associated SNPs and traits. However, how much to optimally overweight these likely associated SNPs and traits depends on the true association pattern, which is unknown. The aSPUset test employs two positive integer parameters, ${\gamma }_1$ and ${\gamma }_2,$ to control the degrees of weighting over the SNPs and over the traits, respectively, and the two parameters are chosen data adaptively. A larger ${\gamma }_1$ puts more weights on the SNPs more likely to be associated with a given trait, while a larger ${\gamma }_2$ upweights the traits more strongly associated with the SNPs.

We build the test statistic as follows. For each trait t, $S\left({\gamma }_1;t\right)$ quantifies the association between the single trait and multiple SNPs, and then $\text{SPU}\left({\gamma }_1,{\gamma }_2\right)$ combines the single trait-based statistics:

$$S\left({\gamma }_1;t\right)={\left({\displaystyle \sum _{j=1}^p{\left(U_{jt}\right)}^{{\gamma }_1}}\right)}^{1/{\gamma }_1},\hspace{1em}\text{SPU}\left({\gamma }_1,{\gamma }_2\right)={\displaystyle \sum _{t=1}^k{\left(S\left({\gamma }_1;t\right)\right)}^{{\gamma }_2}}.$$ (4)

Here candidate integers ${\gamma }_1\ge 1$ and ${\gamma }_2\ge 1$ are chosen from two preselected parameter sets ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2.$ We used ${\mathrm{\Gamma }}_1={\mathrm{\Gamma }}_2=\left\{1,2,\dots ,8,\mathrm{\infty }\right\},$ due to the good performance in our numerical studies.

In $S\left({\gamma }_1;t\right),$ ${\left(U_{jt}\right)}^{{\gamma }_1}$ can be rewritten by an alternative form ${\left(U_{jt}\right)}^{{\gamma }_1}=U_{jt}^{{\gamma }_1-1}{U}_{jt}=w_{jt}{U}_{jt}.$ $w_{jt}=U_{jt}^{{\gamma }_1-1}$ is a weight for each score element, which reflects the association strength (and direction) between SNP j and trait t of the given data. With ${\gamma }_1=1,$ the SPU test weights each SNP equally and yields the highest power if all the SNPs are associated with the trait t with similar effect sizes and association direction (i.e., all positive or all negative). When the subsets of SNPs are associated with the trait t, or their association directions are different, SPU(${\gamma }_1=2,{\gamma }_2$) is often more powerful. As ${\gamma }_1$ increases, SPU(${\gamma }_1,{\gamma }_2$) puts heavier weights on the SNPs that are more strongly associated with the trait t. At the end, as the parameter approaches ∞ (as an even integer), it considers the only most significant SNP; i.e., $\text{SPU}\left({\gamma }_1=\mathrm{\infty },{\gamma }_2\right)={\displaystyle {\sum }_{t=1}^k{\left({\max }_{j=1}^p\left|U_{jt}\right|\right)}^{{\gamma }_2}}.$

Similarly, ${\gamma }_2$ controls how much to upweight the traits that are more likely to be associated with SNPs. SPU$\left({\gamma }_1,{\gamma }_2=1\right)$ weights all traits equally and performs best when each trait is equally associated with the SNPs. Similarly, as ${\gamma }_2$ increases, the SPU test overweights larger trait-based statistics $S\left(.;t\right);$ in an extreme case, as ${\gamma }_2\to \mathrm{\infty },$ we define $\text{SPU}\left({\gamma }_1,{\gamma }_2=\mathrm{\infty }\right)={\max }_{t=1}^k\left|S\left({\gamma }_1;\hspace{0.17em}t\right)\right|.$ If one is more interested in the most significantly associated single-SNP–single-trait pair, $\text{SPU}\left({\gamma }_1=\mathrm{\infty },{\gamma }_2=\mathrm{\infty }\right)={\max }_{j,t}\left|U_{jt}\right|$ can be considered. Using various combinations of ${\gamma }_1$ and ${\gamma }_2,$ one can target and fit different association patterns across multiple SNPs and multiple traits, including their varying sparsity levels. As a result, the SPU(${\gamma }_1,{\gamma }_2$) tests cover several existing tests as special cases as will be shown.

The aSPUset test chooses (${\gamma }_1,{\gamma }_2$) data adaptively by taking the minimum P-value of SPU(${\gamma }_1,{\gamma }_2$)s as the test statistic for candidates ${\gamma }_1\in {\Gamma }_1$ and ${\gamma }_2\in {\mathrm{\Gamma }}_2,$

$$\text{aSPUset}=\underset{{\gamma }_1,{\gamma }_2}{\min }{p}_{{\gamma }_1,{\gamma }_2}.$$

To assess the significance of all the $\text{SPU}\left({\gamma }_1,{\gamma }_2\right)\text{s}$ and the aSPUset test, we use either permutations or MC simulations in a single layer to obtain their P-values. The permutation-based method is useful when the covariance matrix (V) is not easy to estimate (e.g., in a high-dimensional setting) or when the usual Normal asymptotics may not hold (e.g., n is not large compared to $pk$); in contrast, the simulation-based method is more restrictive but computationally more efficient. For the permutation-based method, residual terms $\text{re}{\text{s}}_i=Y_i-{\widehat{\mu }}_i$ in Equation 3 are permuted to generate ${\text{res}}_i^{\left(b\right)}$ for $b=1,\dots B,$ from which the null score vector $U^{\left(b\right)}$ is computed as $U^{\left(b\right)}={\displaystyle {\sum }_{i=1}^n{X^{\prime }}_i\text{re}{\text{s}}_i^{\left(b\right)}}.$ Alternatively, for the simulation method, we simulate the null score vectors independently from the null distribution: $U^{\left(b\right)}\sim \mathcal{MN}\left(0,V\right)$ for $b=1,\dots B.$

In either case, the null statistics $\text{SPU}{\left({\gamma }_1,{\gamma }_2\right)}^{\left(b\right)}$ can be calculated from the null score vectors $U^{\left(b\right)}$ for $b=1,\dots ,B.$ Because all SPU(${\gamma }_1,{\gamma }_2$) tests are based on the same null score vectors $U^{\left(b\right)},$ we just need to simulate one set of null scores and efficiently compute the null statistics, $\text{SPU}{\left({\gamma }_1,{\gamma }_2\right)}^{\left(b\right)}$ tests simultaneously for candidate ${\gamma }_1,{\gamma }_2$’s. Then the P-value of $\text{SPU}\left({\gamma }_1,{\gamma }_2\right)$ is

$$p_{{\gamma }_1,{\gamma }_2}=\frac{1+{\displaystyle {\sum }_{b=1}^B(I\left(\left|\text{SPU}{\left({\gamma }_1,{\gamma }_2\right)}^{\left(b\right)}\right|\ge \left|\text{SPU}\left({\gamma }_1,{\gamma }_2\right)\right|\right)}}{B+1}.$$

We can also simultaneously and efficiently compute the P-value of the aSPUset test based on the same set of the null statistics being used for the SPU tests. Note that for each $\text{SPU}{\left({\gamma }_1,{\gamma }_2\right)}^{\left(b\right)},$ we can calculate its P-value as $p_{{\gamma }_1,{\gamma }_2}^{\left(b\right)}=\left[{\displaystyle {\sum }_{l\ne b}(I\left(\left|\text{SPU}{\left({\gamma }_1,{\gamma }_2\right)}^l\right|\ge \left|\text{SPU}{\left({\gamma }_1,{\gamma }_2\right)}^{\left(b\right)}\right|\right)+1}\right]/B.$ Denote its minimum as $p^{\left(b\right)}={\min }_{{\gamma }_1,{\gamma }_2}{p}_{{\gamma }_1,{\gamma }_2}^{\left(b\right)}.$ Then the significance of the aSPUset test is obtained as

$$P_{\text{aSPUset}}=\frac{{\displaystyle {\sum }_{b=1}^{B}I\left(\left|p^{\left(b\right)}\right|\le \left|\text{aSPUset}\right|\right)+1}}{B+1}.$$

Extensions:

As shown by Zhang et al. (2014), in some but not all situations, the GEE-Score test may perform better than the aSPU test for a single SNP and multiple traits; the opposite is true too. Hence, to take advantage of both tests, we combine them by taking their minimum P-value to form a new test statistic,

$$\text{aSPUset-Score}=\min \left(P_{\text{aSPUset}},P_{\text{Score}}\right).$$ (5)

Its P-value can be calculated using simulations or permutations as for aSPUset. The null statistic GEE-Score^(b) is obtained from the same score $U^{\left(b\right)}$ that is used for $\text{SPU}{\left({\gamma }_1,{\gamma }_2\right)}^{\left(b\right)}.$ Hence the null statistics for $\text{SPU}{\left({\gamma }_1,{\gamma }_2\right)}^{\left(b\right)}$ and GEE-Score^(b) can be computed simultaneously.

We can also consider a variance-weighted version of the SPU and aSPUset tests, called the SPUw and aSPUw-set, respectively. Each diagonal element of the covariance matrix (V) corresponds to the variance of the individual score element $U_{jt};$ denote the variance of $U_{jt}$ as $V_{jt}.$ The SPUw test is defined with the statistic

$$\text{SPUw}\left({\gamma }_1,{\gamma }_2\right)={\displaystyle \sum _{t=1}^k{\left\{{\left[{\displaystyle \sum _{j=1}^p{\left(U_{jt}/\sqrt{V_{jt}}\right)}^{{\gamma }_1}}\right]}^{1/{\gamma }_1}\right\}}^{{\gamma }_2}}.$$

The aSPUw-set test statistic is defined as the one taking the minimum P-value of the multiple-SPUw$\left({\gamma }_1,{\gamma }_2\right)$ tests in the same way as that for aSPUset and SPU$\left({\gamma }_1,{\gamma }_2\right).$ The SPUw and aSPUw-set tests are invariant to the scale of each trait and hence may be useful when it is unclear how to standardize multiple traits that are in different scales. However, standardizing the traits (such that their sample variances are all equal to one) may or may not be beneficial; often, the power of the unweighted SPU tests and that of the weighted ones are similar as shown before in other contexts (Pan et al. 2014; Zhang et al. 2014).

Relationships with other methods:

The SPU tests are closely related to some existing tests, covering some as special cases. Guo et al. (2013) proposed a set of nonparametric methods for gene-based multiple-trait association analysis, called M-MeanStat, M-MaxStat, and M-TopQ25Stat. Each of the methods of Guo et al. (2013) is built on a generalized Kendall’s τ, which quantifies the pairwise association between a single SNP and a single trait. Comparing two sets of statistics, M-MeanStat vs. $\text{SPUw}\left(2,2\right)$ and M-Max vs. $\text{SPUw}\left(\mathrm{\infty },1\right)$, we see their equivalence as described in Appendix A.

It is obvious that the SPU(1,1) test is a burden test, which is optimal if its implicit assumption that each SNP–trait pair is equally associated (with the same association direction) holds. The SPU(2,2) test has connections to several other tests. Zhang et al. (2014) showed that when testing on a single SNP, the SPU(2,2) test under the GEE working independence model is equivalent to MDMR with the Euclidean distance. However, for testing multiple SNPs, the equivalence does not hold (Appendix B). KMR with the linear kernel has the same test statistic as SPU(2,2) if the working correlation matrix $R_{\text{w}}$ of the latter in GEE is correctly specified as the true correlation matrix of $Y_i$ [i.e., $R_{\text{w}}=\text{Corr}\left(Y_i|H_0\right)$]; see Appendix C for derivation. This illustrates the flexibility of our proposed test under GEE, in contrast to the stronger modeling assumption in KMR. Since KMR can be derived based on a random-effects model while the burden test is formulated based on a fixed-effects model, our proposed method can be regarded as combining results from both fixed- and random-effects models.

As is shown in our numerical studies, the GEE-Score test and MANOVA performed similarly; we establish the equivalence between the GEE-Score test and MANOVA with the Pillai–Bartlett trace (Appendix D). Muller and Peterson (1984) discussed the close relationships among four versions of MANOVA (i.e., with the Pillai–Bartlett trace, Hotelling–Lawley’s trace, Wilk’s λ, and Roy’s largest root), each of which can be written as a function of generalized canonical correlations (CCA). Hence the GEE-Score test is directly related to MANOVA and CCA.

Pathway analysis:

We extend the adaptive test for association analysis of a single trait and a pathway (i.e., a set of genes) (Pan et al. 2015) to that of multiple traits and a pathway. The main idea is to allow adaptive weighting at the gene level, in addition to at the SNP and trait levels. Given a pathway S with $\left|S\right|$ genes and a single trait t, we partition the score vector according to the genes in S as $U={\left({U^{\prime }}_{1t},\dots ,{U^{\prime }}_{\left|S\right|,t}\right)}^{\prime }$ with a subvector for gene g (with $h_g$ SNPs) as $U_{gt}={\left(U_{g,1,t},\dots ,U_{g,h_g,t}\right)}^{\prime }.$ Denote $\text{SPU}\left({\gamma }_1;\hspace{0.17em}g,\hspace{0.17em}t\right)$ and $\text{SPUpath}\left({\gamma }_1,{\gamma }_2;t\right)$ as the gene-specific SPU and the pathway-based SPU test statistics for a single trait t, respectively. Define a new test statistic $\text{GEE-SPUpath}\left({\gamma }_1,{\gamma }_2,{\gamma }_3\right)$ as the pathway analysis for multiple traits,

$$\begin{array}{c}\text{SPU}\left({\gamma }_1,w_1;g,t\right)={\left({\displaystyle \sum _{j=1}^{h_g}{\left(w_{1,g,j}{U}_{g,j,t}\right)}^{{\gamma }_1}/h_g}\right)}^{1/{\gamma }_1},\\ \text{SPUpath}\left({\gamma }_1,{\gamma }_2,w_1,w_2;\hspace{0.17em}t\right)={\left({\displaystyle \sum _{g=1}^{\left|S\right|}{\left(w_{2,g}\text{SPU}\left({\gamma }_1,w_{1,g};g,t\right)\right)}^{{\gamma }_2}}\right)}^{1/{\gamma }_2},\\ \text{GEE-SPUpath}\left({\gamma }_1,{\gamma }_2,{\gamma }_3,w_1,w_2\right)={\displaystyle \sum _{t=1}^k{\left(\text{SPUpath}\left({\gamma }_1,{\gamma }_2,w_1,w_2;t\right)\right)}^{{\gamma }_3}},\end{array}$$

where the three scalars ${\gamma }_1,{\gamma }_2,{\gamma }_3>0$ are specified to control the degrees of weighting the SNPs, genes, and traits, respectively; $w_1={\left({w^{\prime }}_{1,1},\dots ,{w^{\prime }}_{1,\left|S\right|}\right)}^{\prime }$ gives gene-specific weights for the SNPs in gene g as $w_{1,g}={\left(w_{1,g,1},\dots ,w_{1,g,h_g}\right)}^{\prime },$ and $w_2={\left(w_{2,1},\dots ,w_{2,\left|S\right|}\right)}^{\prime }$ gives gene-specific weights for each gene in the pathway S. These weights are specified based on some prior knowledge on the importance of the genes and SNPs; without prior knowledge, we can simply use an equal weight 1 on each gene and each SNP, as used in our later simulations. We employed ${\gamma }_1\in {\mathrm{\Gamma }}_1=\left\{1,2,\dots ,8\right\}$ and ${\gamma }_2,{\gamma }_3\in {\mathrm{\Gamma }}_2={\mathrm{\Gamma }}_3=\left\{1,2,4,8\right\}$ in later simulations.

Finally, a new adaptive test for pathway analysis, denoted the GEE-aSPUpath test, is defined as

$$\text{GEE-aSPUpath}=\underset{{\gamma }_1\in {\mathrm{\Gamma }}_1,{\gamma }_2\in {\mathrm{\Gamma }}_2,{\gamma }_3\in {\mathrm{\Gamma }}_3}{\min }{p}_{{\gamma }_1,{\gamma }_2,{\gamma }_3},$$

where $p_{{\gamma }_1,{\gamma }_2,{\gamma }_3}$ is the P-value of the GEE-SPUpath$\left({\gamma }_1,{\gamma }_2,{\gamma }_3\right)$ test. The simulation or permutation procedure for generating the null statistics and calculating P-values for all the GEE-SPUpath and GEE-aSPUpath tests is similar to that for the GEE-aSPUset test.

Due to the limited space, we will not discuss the pathway-based tests in the sequel; some simulation results are presented in Supplemental Materials, File S4.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article. The R code for the proposed tests and simulations is available in Supplemental Materials, File S5. An R package GEEaSPU is to be uploaded to CRAN.

Results

Real data example

ADNI data:

Data used in the preparation of this article were obtained from the ADNI database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies, and nonprofit organizations, as a $60 million, 5-year public–private partnership. The primary goal of ADNI has been to test whether serial MRI, positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, VA Medical Center and University of California, San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from >50 sites across the United States and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited >1500 adults, ages 55–90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow-up duration of each group is specified in the protocols for ADNI-1, ADNI-2, and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.

GWAS with ADNI-1 data:

One objective of ADNI is to elucidate genetic susceptibility to AD. We conducted a gene-based multitrait analysis for ADNI-1 data, by using gray matter volumes in the 12 ROIs corresponding to the DMN as intermediate phenotypes. The DMN is a network of brain regions that are active when an individual is at wakeful rest, which includes inferior temporal, medial orbitofrontal, parahippocampal, precuneus, and posterior cingulate ROIs (Greicius et al. 2004). Importantly, DMN activity distinguishes cognitively impaired patients such as with Alzheimer’s, attention deficit hyperactivity disorder (ADHD), or bipolar disorder from healthy controls (Greicius et al. 2004; Buckner et al. 2008; Meda et al. 2014; Metin et al. 2015). The gray matter volumetric measures related to the DMN were extracted from the ADNI-1 baseline data.

We included all SNPs with minor allele frequency (MAF) ≥ 0.05, with genotyping rate >90%, and surviving the Hardy–Weinberg equilibrium test at a significance threshold of 0.001. After all rounds of quality control, 519,286 SNPs remained, among which 277,527 SNPs were mapped to 17,557 genes. To consider SNPs in promoter or regulatory regions for each gene, we included SNPs upstream and downstream within 20 kb of each gene. Subjects with >10% missing genotypes were excluded, and only non-Hispanic Caucasians whose 12 gray matter volumes in the DMN were all measured at baseline were included, resulting in 144 patients with AD, 311 subjects with MCI, and 180 healthy elderly controls. For covariates, gender, years of education, handedness, age, and intracranial volume (ICV) measured at baseline were included.

To demonstrate the applicability and power of our approach, we applied MANOVA, MDMR (McArdle and Anderson 2001), KMR (Maity et al. 2012), MFLM (Wang et al. 2015) and GEE-based tests, GEE-Score, and aSPUset and aSPUset-Score tests. The number of MC simulations or permutations for each method was set at $B={10}^3$ at the beginning, but was increased to $B={10}^8$ if an obtained P-value was $<5/B,$ which ensured the identification of the genes at the genome-wide significance level (P-value $<2.8\times {10}^{-6}$ with a Bonferroni adjustment). When any obtained P-value was <1.0e-8, we reported it as 1.0e-8. The P-values of permutation-based aSPUset and of simulation-based aSPUset agreed well (with a Pearson correlation of 0.98), and thus we reported only permutation-based results. For MFLM, we used β-smooth basis functions with the Pillai–Bartlett trace as a representative.

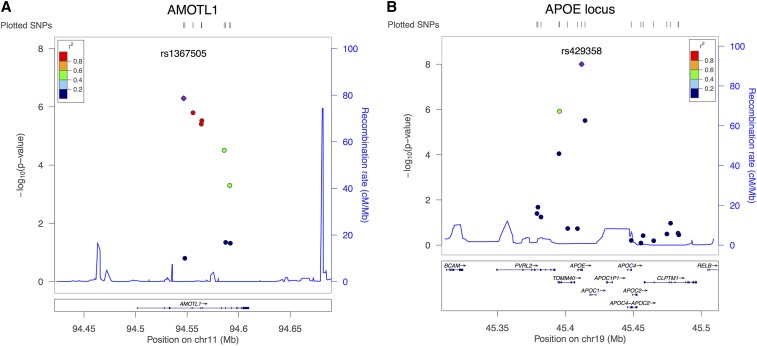
The aSPUset and MDMR tests uncovered two loci associated with the DMN. Table 1 lists the genes with the highest significance levels. Genes $AMOTL\mathit{1}$ (on chromosome 11) and APOC1, APOE (on chromosome 19) were identified by both aSPUset and MDMR, but not by other tests, while TOMM40 (on chromosome 19) was detected only by aSPUset. AMOTL1 is known to be involved in cell adhesion and cell signaling (Hamatani et al. 2004). A recent study using a pathway-enrichment strategy showed that the genes involved in neuronal cell adhesion and cell signaling are overrepresented in schizophrenia and bipolar disorder (Meda et al. 2014). Anney et al. (2008) identified AMOTL1 as a gene associated with ADHD. The gene was also highly expressed in thalamus, a brain region implicated in the cognitive impairment of early stage Huntington’s disease (Schmouth et al. 2013). Three genes (APOC1, APOE, TOMM40) in chromosome 19 could not be readily discerned due to their physical closeness, although their gene sizes (i.e., the numbers of SNPs) varied. The P-values of MDMR became less significant as the gene size increased, while the aSPUset was robust to the number of SNPs. This locus containing APOE is well known to be related to Alzheimer’s disease and cognitive impairment disorder (Seshadri et al. 2010; Kamboh et al. 2012; Liu et al. 2014).

Table 1. P-values of the gene-based association tests for the DMN with the ADNI-1 data.

					GEE
Gene region	No. SNPs	Chr	Position		Score	aSPUset	aSPUset-Score	MANOVA	MDMR	KMR	MFLM
AMOTL1	6	11	94,121,155	94,269,566	1.18e0-4	1.0e-08	1.0e-08	7.73e-05	3.48e-07	0.451	7.73e-05
APOC1	4	19	50,089,760	50,134,446	6.14e-04	1.0e-08	1.0e-08	3.45e-04	4.42e-08	0.342	2.30e-04
APOE	6	19	50,080,878	50,124,490	1.27e-03	1.0e-08	1.0e-08	7.93e-04	2.21e-07	0.268	5.97e-04
TOMM40	10	19	50,066,316	50,118,786	0.023	1.0e-08	1.0e-08	1.86e-02	6.99e-06	0.569	1.04e-03

Chr, chromosome.

Table 2 lists the SNPs included in the significant genes. We applied several single SNP-based tests for association with the default mode network. For each method, the permutation or simulation number was increased up to ${10}^8$ to satisfy the genome-wise significance level. As shown in Table 2, none of the SNPs in gene AMOTL1 was significant, suggesting that a strong association signal was retained only in the gene level, rather than in the SNP level. On the other hand, SNP rs429358 contained in three genes (APOC1, APOE, TOMM40) was highly significant with a P-value of 1.0e-8. These results lend support to the proposed aSPUset test’s potential to be able to recover both multiple weak effects and single strong effects, due to its adaptiveness.

Table 2. P-values of the single SNP-based association tests for the DMN for the significant gene regions ($\mathrm{\pm }20$ kb) with the ADNI-1 data.

					GEE
Gene	Chr	aSPUset	SNP	Position	Score	SPU(2)	SPU(∞)	aSPU	MANOVA	MDMR
AMOTL1	11	1.0e-08	rs1367505	94,186,285	8.0e-05	2.4e-07	2.8e-05	5.1e-07	5.1e-05	2.1e-07
			rs10501816	94,187,396	0.417	0.151	0.237	0.158	0.432	0.186
			rs2033367	94,195,356	1.2e-04	8.0e-07	6.5e-05	1.6e-06	9.1e-05	3.01e-07
			rs2241667	94,203,379	8.0e-04	1.6e-06	1.3e-04	3.9e-06	1.8e-04	8.0e-06
			rs333027	94,225,561	5.0e-04	1.6e-05	9.5e-05	3.1e-05	4.6e-04	6.9e-05
			rs333025	94,227,040	0.02	0.025	0.030	0.045	0.015	0.022
APOC1	19	1.0e-08	rs8106922	50,093,506	0.236	0.116	0.212	0.183	0.244	0.128
			rs405509	50,100,676	0.420	0.156	0.207	0.186	0.422	0.184
			rs439401	50,106,291	7.0e-04	2.3e-06	1.2e-05	3.1e-06	4.1e-04	2.2e-05
			rs429358	50,103,781	1.0e-05	4e-08	8.3e-06	1.0e-08	2.1e-06	1.25e-08
APOE	19	1.0e-08	rs157580	50,087,106	3.1e-03	1.4e-04	8.8e-04	9.0e-05	3.1e-03	3.9e-4
			rs2075650	50,087,459	9.0e-04	3.8e-06	2.2e-03	1.2e-06	2.9e-04	1.5e-05
			rs8106922	50,093,506	0.236	0.116	0.212	0.183	0.244	0.128
			rs405509	50,100,676	0.420	0.156	0.207	0.186	0.422	0.184
			rs439401	50,106,291	7.0e-04	2.3e-06	1.2e-05	3.1e-06	4.1e-04	2.2e-05
			rs429358	50,103,781	1.0e-05	4e-08	8.3e-06	1.0e-08	2.1e-06	1.25e-08
TOMM40	19	1.0e-08	rs2075642	50,069,307	0.842	0.711	0.471	0.629	0.840	0.662
			rs387976	50,070,900	0.073	0.031	0.036	0.040	0.068	0.067
			rs11667640	50,071,631	0.262	0.034	0.012	0.021	0.265	0.035
			rs6859	50,073,874	0.728	0.076	0.299	0.057	0.729	0.072
			rs157580	50,087,106	3.1e-03	1.4e-04	8.8e-04	9.0e-05	3.1e-03	3.9e-4
			rs2075650	50,087,459	9.0e-04	3.8e-06	2.2e-03	1.2e-06	2.9e-04	1.5e-05
			rs8106922	50,093,506	0.236	0.116	0.212	0.183	0.244	0.128
			rs405509	50,100,676	0.420	0.156	0.207	0.186	0.422	0.184
			rs439401	50,106,291	7.0e-04	2.3e-06	1.2e-05	3.1e-06	4.1e-04	2.2e-05
			rs429358	50,103,781	1.0e-05	4e-08	8.3e-06	1.0e-08	2.1e-06	1.25e-08

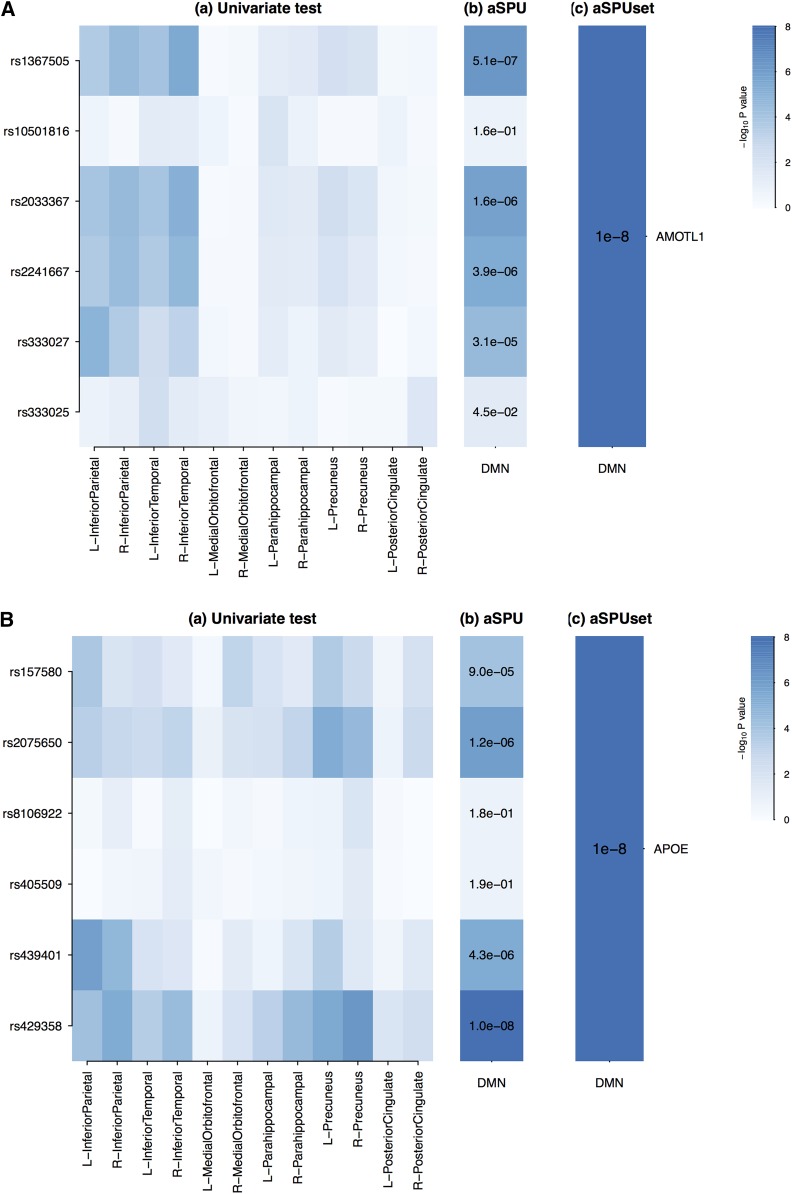
We explored each identified locus in detail in Figure 1 and Figure 2. In Figure 1, a LocusZoom plot (Pruim et al. 2010) illustrates local linkage disequilibrium (LD), recombination patterns, and P-values obtained from the single SNP-based aSPU test for the DMN. Figure 2 illustrates the association analyses for genes AMOTL1 and APOE, respectively. First, we obtained P-values from the univariate test between each SNP and each individual trait composing the DMN, and then we applied the SNP-based test (aSPU) between each SNP and DMN (12 traits). Finally, we applied the aSPUset test at the gene level for the DMN. The SNPs contained in AMOTL1 showed strong LD (Figure 1A), and their aggregate effects turned out to be significant at the gene level (Figure 2A). Among the SPU$\left({\gamma }_1,{\gamma }_2\right)$ tests applied with ${\gamma }_1,{\gamma }_2\in \left\{1,\dots ,8,\mathrm{\infty }\right\},$ SPU(3,2) showed the minimum P-value, implying that weak effects were aggregated for an overall association. In Figure 2B, only one variant (rs429358) in APOE was significant, but the significance level of aSPUset did not diminish in the gene-level analysis. In testing APOE, the P-values of SPU(2,1), SPU(4,1), SPU(6,1), SPU(8,1), and SPU($\mathrm{\infty },$1) were tied and the most significant; this suggested that one SNP (rs429358) dominated in the gene level across all the traits.

Figure 1.

LocusZoom for two loci (A AMOTL1 and B APOE) identified by aSPUset and MDMR. LD structure in each locus and P-values obtained from the single SNP-based aSPU test are presented.

Figure 2.

P-values of the association tests for the DMN and SNPs for genes AMOTL1 and APOE. (A,a and B,a) Univariate test for single-SNP–single-trait association; (A,b and B,b) aSPU test for single-SNP–multitrait association; (A,c and B,c) aSPUset test for gene–multitrait association.

Since the proposed test is based on combining all possible single-SNP–single-trait association pairs, if one wants to identify which pairs contribute most to an overall association, one can simply examine the significance levels of the univariate single-SNP–single-trait association tests. For example, Figure 2, A,a and B,a, illustrates the contribution of each SNP–trait pair for AMOTL1 and APOE. In the gene AMOTL1, the SNP–trait pairs, (rs1367505, R-InferiorTemporal), (rs2033367, R-InferiorTemporal), and (rs333027, L-InferiorParietal), were ranked highest; for APOE, the top three significant pairs were (rs429358, R-Precuneus), (rs2075650, L-Precuneus), and (rs429358, L-InferiorParietal).

As shown in File S1, we conducted a single SNP-based GWAS scan for the ADNI-1 data. Interestingly, no SNP was significant from univariate single-SNP–single-trait analyses as shown in File S1, Figure A and Figure B. Furthermore, only one SNP, rs429358, was significant in single SNP-based multitrait analyses as shown in File S1, Figure C and Figure D. In contrast, two loci (AMOTL1 and APOE) were uncovered by gene-based multitrait analyses by our proposed new test (File S1, Figure E and Figure F). In all analyses, covariates considered included gender, years of education, handedness, age, and ICV measured at baseline. Taken together, these results clearly demonstrated the advantage and power gain of our proposed gene-based multitrait analysis.

Validation with ADNI-GO/2 data:

Using the ADNI-1 data as the discovery sample, our GWAS identified two loci associated with the DMN. To validate the results, each method was applied to the two genes AMOTL1 and APOE, using the ADNI-GO/2 data as the validation sample (with $n=754$). We applied the same SNP-filtering criteria as applied to ADNI-1. Table 3 presents the P-values obtained from each method; no significant association was identified. Due to different genotyping arrays, ADNI-GO/2 data contain different sets of SNPs from those of ADNI-1; we imputed missing SNPs that were originally included in the analysis of ADNI-1, based on the reference samples of HapMap 3 with MaCH (Liu et al. 2013), to apply each method to the identical SNP sets of ADNI-1. The aSPUset and aSPUset-Score tests identified gene APOE with P-values of 0.019 and 0.024, respectively, which passed the significance threshold of 0.05/2 as shown in Table 3, but gene AMOTL1 was not significant by any test. File S2, Figure A illustrates P-values from single SNP-based testing after adjusting for covariates; SNP rs429358 was associated with the DMN (P-value 1.9e-3) by passing the Bonferroni-adjusted significance level of 0.05/12. File S2, Figure B presents P-values for the two candidate gene regions based on the ADNI-GO/2 data; the methods include the univariate single-SNP–single-trait test, the single SNP-based multitrait aSPU test, and the gene-based multitrait aSPUset test.

Table 3. P-values of the gene-based association tests with the ADNI-GO/2 and ADNI-1/GO/2 data.

Data	Gene region	No. SNPs	Chr			GEE
				Position		Score	aSPUset	aSPUset-Score	MANOVA	MDMR	MFLM
ADNI-GO/2	AMOTL1	13	11	94,481,507	94,629,918	0.723	0.896	0.940	0.698	0.716	0.638
	APOE	13	19	45,389,277	45,432,652	0.083	0.042	0.056	0.097	0.366	0.974
ADNI-GO/2 with identical SNP sets of ADNI-1	AMOTL1	6	11	—		0.639	0.552	0.576	0.638	0.918	0.638
	APOE	6	19	—		0.308	0.019	0.024	0.292	0.065	0.292
ADNI-1/GO/2 with identical SNP sets of ADNI-1	AMOTL1	6	11	—		1.0e-08	1.0e-08	1.0e-08	1.0e-08	1.0e-08	1.0e-08
	APOE	6	19	—		1.0e-08	1.0e-08	4.45e-06	1.0e-08	1.0e-08	4.45e-06

We should mention possible sample differences between ADNI-1 and ADNI-GO/2 cohorts. The ADNI-1 cohort includes three subject groups consisting of 25% patients with AD, 50% subjects with MCI, and 25% cognitively normal (CN) subjects; in contrast, the ADN-GO/2 study assigns 754 subjects into five groups: 20% CN, 12% significant memory concern (SMC), 35% early mild cognitive impairment (EMCI), 17% late mild cognitive impairment (LMCI), and 16% AD. At least the proportions of the CN subjects and patients with AD in the two cohorts are different, which might lead to different association results.

Finally, we combined the two cohorts to form ADNI-1/GO/2 with a larger sample size (∼1400 subjects) and obtained the P-values from the tests for the two candidate gene regions. The two genes were highly significantly associated with the default mode network as shown in Table 3.

Gene-based rare variant analysis of the ADNI sequencing data:

The proposed method was applied to analysis of rare variants with the ADNI WGS data, consisting of 254 and 500 subjects from ADNI-1 and ADNI-GO/2, respectively. In total, 26,142 genes were included for analyses; all variants inside a gene and those located 25 kb of upstream and downstream of the gene were mapped to the gene. Five covariates were adjusted: gender, years of education, handedness, age, and ICV. Due to the low frequency of rare variants, the asymptotic assumption for some tests may not hold; we modified each method to avoid using asymptotics. For MANOVA, rather than using the usual F distribution, we permuted residuals (under the null model) to estimate its null distribution; for aSPUset and MFLM, similarly the permutation-based method was applied. We included all rare variants within each gene region; the number of variants within each region ranged from 3 to 750. Sometimes permutation-based MANOVA suffered from rank deficiency when constructing the test statistic and could not be applied to ∼600 genes; MFLM also failed for some genes due to rank deficiency.

First, we included only rare variants (with MAF < 0.01) and then, both rare and low-frequency variants (with MAF < 0.05). No gene passed the genome-wide Bonferroni-adjusted significance threshold of $2.8\times {10}^{-6}.$ The results for each set of rare variants are illustrated in File S3, Figure A and Figure B. MFLM was problematic with an inflation factor ∼1.5 in both analyses.

Given that two gene regions were significantly associated with DMN in the previous GWAS analysis, it would be of interest to see whether the rare variants in the two genes were associated. Table 4 reports the P-values for the two candidate genes. No significant associations were detected. File S3, Figure C depicts the P-values from single trait-based tests, including SKAT, SKAT-O, T1 (a burden test for rare variants with MAF < 0.01), T5 (a burden test for rare and low-frequency variants with MAF < 0.05), minP, and aSPU tests (Wu et al. 2011; Pan et al. 2014). T1 and T5 are equivalent to the SPU(1) test with MAF thresholds 0.01 and 0.05, respectively. The minP test is similar to the SPU(∞) test.

Table 4. P-values of the gene-based tests for rare variant–DMN association with the ADNI sequencing data.

Filtering criteria	Gene region	No. SNPs	Chr	Position		aSPUset	MANOVA	MFLM
MAF $<0.05$	AMOTL1	536	11	94,481,507	94,629,918	0.298	0.176	0.148
	APOE	153	19	45,389,277	45,432,652	0.104	0.837	0.476
MAF $<0.01$	AMOTL1	265	11	94,481,507	94,629,918	0.835	0.193	0.151
	APOE	84	19	45,389,277	45,432,652	0.874	0.833	0.189

Simulations

Simulation setups:

We evaluated the performance of our method along with several existing methods in simulation studies. The simulated data mimicked the association structures for the two genes (AMOTL1 on chromosome 11 and TOMM40 on chromosome 19) and the DMN in ADNI-1 data. Two factors were considered: association effect size (setup 1) and sparsity of association patterns (setup 2). For setup 1, various effect sizes were created by scaling the regression coefficient estimates obtained from a multivariate linear model (MLM) fitted to the original data. On each gene, an MLM was fitted to the ADNI-1 data, including the covariates ($z_i$), SNPs ($x_i$), and DMN ($Y_i$). For covariates, we included gender, education, handedness, age, and ICV as in the original data analysis. Denote the parameter estimates in an MLM as follows: $G_0$ is a vector for intercepts; $G=\left(g_{jt}\right)$ is a $p\times k$ matrix, in which $g_{jt}$ represents the effect size of SNP j on trait t; the element $h_{qt}$ in matrix $H=\left(h_{qt}\right)$ stands for the qth covariate effect on the tth trait; and ∑ is the covariance estimate for the multivariate error term. To maintain the true correlation structures among genotype scores $x_i={\left(x_{i1},\dots ,x_{ip}\right)}^{\prime }$ and five covariates $z_i={\left(z_{i1},\dots ,z_{i5}\right)}^{\prime },$ we sampled pairs $\left(x_i,z_i\right)$ from the ADNI-1 data in each simulation. The multiple traits for subject i were generated from a multivariate normal distribution:

$$Y_i\sim \mathcal{ℳN}\left(G_0+\phi \cdot G^{\prime }{x}_i+H^{\prime }{z}_i,\sum \right).$$ (6)

Here φ was a scaling parameter controlling the effect sizes of the SNPs ($x_i$): with $\phi =0,$ the null hypothesis held and type I error rates were evaluated; at $\phi =1,$ the effect sizes were set to be equal to the estimated ones from the ADNI-1 data.

For setup 2, we varied the sparsity level of the association structure. At a fixed $\phi =0.5,$ we increased the gene size by adding some null SNPs to gene AMOTL1. For the null SNPs, the genotype data adjacent to AMOTL1 were used. As before, $\left(x_i,z_i\right)$ pairs were sampled from the ADNI-1 data. Throughout simulations, 10,000 replicates were used for each setup and the tests were conducted at the significance level $\alpha =\mathrm{0.05.}$

Type I error and power:

All the tests showed type I error rates controlled under the nominal level of 0.05 (Table 5). Of note, MDMR resulted in conservative type I error rates. In setup 1 (Table 5), as the association effect size (φ) decreased, the aSPUset and aSPUset-Score tests were more powerful than other tests, suggesting the potential usefulness of the proposed tests in identifying causal SNPs with weak effects. Since MFLM was proposed to reduce the dimensionality of the SNP data, it might not be desirable to use MFLM here; it might perform better with larger numbers of SNPs.

Table 5. Simulation setup 1: type I errors ($\phi =0$) and power ($\phi \ne 0$) under varying genetic effect sizes.

	GEE
φ	Score	SPU(2,2)	aSPUset	aSPUset-Score	MANOVA	MDMR	MFLM
AMOTL1 (6 SNPs)
0	0.0479	0.0528	0.0530	0.0522	0.0490	0.0353	0.0490
0.2	0.1078	0.1837	0.1659	0.1654	0.1128	0.0964	0.1128
0.3	0.2325	0.3494	0.3159	0.3328	0.2394	0.2135	0.2394
0.4	0.4657	0.5571	0.5079	0.5559	0.4764	0.4130	0.4764
0.5	0.7436	0.7614	0.7156	0.7967	0.7528	0.6607	0.7528
0.6	0.9288	0.9008	0.8722	0.9452	0.9341	0.8608	0.9341
0.7	0.9913	0.9677	0.9550	0.9926	0.9921	0.9611	0.9921
TOMM40 (10 SNPs)
0	0.0488	0.0483	0.0482	0.0495	0.0505	0.0323	0.0532
0.2	0.1051	0.1719	0.1347	0.1369	0.1110	0.0903	0.1116
0.3	0.2177	0.3643	0.2763	0.2889	0.2262	0.2053	0.2169
0.4	0.4429	0.6121	0.5018	0.5330	0.4605	0.4246	0.4256
0.5	0.5800	0.7304	0.6231	0.6673	0.5958	0.5593	0.5664
0.6	0.7196	0.8271	0.7369	0.7904	0.7346	0.6885	0.7036
0.7	0.8405	0.8983	0.8293	0.8856	0.8489	0.8015	0.8231

In setup 2 (Table 6), the aSPUset and aSPUset-Score yielded higher power than other tests as the proportion of the null SNPs in the SNP set increased. Throughout the simulations, the GEE-Score test performed similarly to MANOVA, confirming their equivalence.

Table 6. Simulation setup 2: power under varying sparsity levels of association pattern.

AMOTL1$+$ null SNPs
			GEE
No. total SNPs	No. causal SNPs	No. null SNPs	Score	aSPUset	aSPUset-Score	MANOVA	MDMR	MFLM
6	6	0	0.7436	0.7156	0.7967	0.7528	0.6607	0.7528
12	6	6	0.5332	0.6495	0.6923	0.5427	0.4904	0.5228
18	6	12	0.4160	0.6149	0.6336	0.4291	0.3884	0.3882
30	6	24	0.2950	0.4495	0.4617	0.3055	0.2819	0.2872
60	6	54	0.1813	0.3120	0.3150	0.1981	0.1756	0.2124
80	6	74	0.1442	0.2912	0.2912	0.1661	0.1434	0.1697

Computational time:

We reported the computational requirement of each method in Table 7 by taking the average computation time for simulation setup 2. MANOVA was computationally most efficient, followed by MFLM. As the number of SNPs increased, the GEE-Score test and the aSPUset-Score test became computationally more demanding, but still feasible.

Table 7. Mean computing times (in seconds) for simulation setup 2.

	GEE
No. total SNPs	Score	aSPUset	aSPUset-Score	MANOVA	MDMR	MFLM
12	1.1597	1.2472	1.6261	0.0149	24.2924	0.0354
18	1.3398	1.5062	2.2552	0.0156	22.2903	0.0385
30	2.2541	1.8766	3.7482	0.0172	21.5940	0.0449
60	6.5183	2.8785	11.1315	0.0211	19.3995	0.0612
80	11.8868	3.5546	20.4237	0.0243	18.4600	0.0722

Conclusions

We have presented a highly adaptive association test for multiple traits and multiple genetic variants. From the GWAS analyses of the ADNI-1 data (File S1), we observed its potential power gains in identifying cumulative weak effects of multiple associated SNPs in gene AMOTL1 with multiple traits, which were undetectable by several other gene-based tests and single SNP-based tests. Given that most common variants have only weak effects for complex diseases and traits, developing testing strategies to improve power in identifying multiple SNPs with weak effects is very important. Our proposed method is developed along this direction. Furthermore, due to its adaptiveness, it also retains power in the presence of only one or a few associated SNPs (or traits), as shown for the APOE gene with the ADNI-1 data (while several existing gene-based tests failed to capture this). Our proposed adaptive test is in contrast to most of the existing tests, which may be powerful in one or more situations, but not across a wide range of situations. In practice, since the true association pattern for a given gene and traits is unknown, it is unclear which nonadaptive test should be used; it will be convenient and promising to apply an adaptive test such as our proposed one.

We emphasize the potential power gain with the use of multiple traits, especially of intermediate phenotypes for a complex disease such as AD (Mukherjee et al. 2014; Chen et al. 2015). However, since it is unknown how many of, and in what association patterns, the multiple traits are associated with a gene (or a set of SNPs), a straightforward use of any multivariate test may lose, not gain, power. Again, the availability of a powerful and adaptive test such as our proposed one will largely facilitate its easy and effective use in practice.

Finally, we summarize the use of our proposed tests and make some recommendations. To assess an overall association between a set of SNPs and a set of traits, we recommend the use of the P-value of the aSPUset test. If it is significant, one can check the individual P-values of the SPU$\left({\gamma }_1,{\gamma }_2\right)$ tests to shed some light on the underlying association pattern. If a larger ${\gamma }_1$ (or ${\gamma }_2$) leads to a more significant P-value of the SPU test, it suggests a more sparse association pattern; that is, perhaps one or a fewer number of the SNPs (or traits) is or are associated. Furthermore, one can examine the P-value from the univariate test for each SNP–trait pair to identify which SNP–trait pairs contribute most to the overall association. For choosing candidate values of ${\gamma }_1$ and ${\gamma }_2,$ based on our limited experience, we suggest using ${\mathrm{\Gamma }}_1={\mathrm{\Gamma }}_2=\left\{1,2,\dots ,8,\mathrm{\infty }\right\}$ by default, although an optimal choice depends on the situation; using a too large or too small set ${\mathrm{\Gamma }}_1$ or ${\mathrm{\Gamma }}_2$ will lead to loss of power. A general guidance, taking ${\mathrm{\Gamma }}_1$ as an example (and similarly for ${\mathrm{\Gamma }}_2$), is to use ${\mathrm{\Gamma }}_1=\left\{1,2,\dots ,C_1,\mathrm{\infty }\right\}$ such that the SPU$\left(C_1,{\gamma }_2\right)$ test gives a P-value almost equal to that of SPU$\left(\mathrm{\infty },{\gamma }_2\right);$ a larger number of SNPs may require a larger value of $C_1.$ In addition, if some large univariate associations between various SNP–trait pairs are likely to be in opposite directions, only even integers are needed in ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2;$ if it is known a priori that large univariate associations are mainly in one direction, then using only odd integers may be most powerful; otherwise, both even and odd integers should be used. Given the relationships among the tests, we recommend the use of our proposed aSPUset and aSPUset-Score tests, although MFLM may also perform well for large genes; further evaluations are needed.

Appendix

Without loss of generality we center both $Y_i={\left(y_{i1},y_{i2},\dots ,y_{ik}\right)}^{\prime }$ and $x_i={\left(x_{i1},x_{i2},\dots ,x_{ip}\right)}^{\prime }$ to have their sample means ${\displaystyle {\sum }_{i=1}^n{Y}_i/n=0}$ and ${\displaystyle {\sum }_{i=1}^n{x}_i/n=0}.$ We consider the case without covariates, since several methods are applicable only to the case without covariates.

We rewrite the data format as a design matrix. Denote Λ as an $n\times p$ matrix, each row of which contains subject i’s genotype $x_i={\left(x_{i1},\dots ,x_{ip}\right)}^{\prime },$ and Θ as an $n\times k$ matrix, each row of which consists of multiple traits $Y_i={\left(y_{i1},\dots ,y_{ik}\right)}^{\prime }.$ Multivariate analysis can be derived from partitioning of the total sum of squares and cross-products (SSCP) matrix, the inner product ${\mathbf{\Theta }}^{\prime }\mathbf{\Theta }.$ According to the multivariate linear model, $\mathbf{\Theta }=\mathbf{\Lambda }B+E\text{,}$ where B is the matrix of model parameters, E is the matrix of errors, the fitted value matrix is defined as $\widehat{\mathbf{\Theta }}=\mathbf{\Lambda }\widehat{B}=\mathbf{\Lambda }{\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }\right)}^{-1}{\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }=H\mathbf{\Theta },$ and the matrix of residuals is R $=\mathbf{\Theta }-\widehat{\mathbf{\Theta }}=\left(\mathbf{I}-\mathbf{H}\right)\mathbf{\Theta },$ where H is a hat matrix.

We define each covariance estimate as follows. ${\mathit{S}}_x=\left(1/n\right){\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }$ is a $p\times p$ covariance estimate for genotype scores $x_i={\left(x_{i1},\dots ,x_{ip}\right)}^{\prime },$ and ${\mathit{S}}_y=\left(1/n\right){\mathbf{\Theta }}^{\prime }\mathbf{\Theta }$ is a $k\times k$ covariance estimate among k multiple traits $Y_i={\left(y_{i1},\dots ,y_{ik}\right)}^{\prime }.$ ${\mathit{S}}_{yx}=\left(1/n\right){\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }$ and ${\mathit{S}}_{xy}=\left(1/n\right){\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }$ are covariance estimates between two sets of variables $x_i$ and $Y_i.$

tr(A) stands for sum of diagonal elements of a matrix A. vec(A) represents a linear transformation that converts the matrix (A) into a column vector.

Appendix A: SPUw(2,2) and M-MeanStat; SPUw(∞,1) and M-Max

For each trait t and SNP j, their pairwise association is quantified by ${\tau }_{jt}={\displaystyle {\sum }_{i=1}^n{x}_{ij}\left(y_{it}-{\overline{y}}_t\right)={\displaystyle {\sum }_1^n{x}_{ij}{y}_{it}}},$ which follows a normal distribution asymptotically with mean zero and variance $\mathrm{var}\left({\tau }_{jt}|y_t\right)={\displaystyle {\sum }_{i=1}^n\mathrm{var}\left(x_{ij}\right)y_{it}^2}$ under the null hypothesis. Guo et al. (2013) defined the generalized Kendall’s τ statistic, $T_{jt}={\tau }_{jt}^2\mathrm{var}{\left({\tau }_{jt}|y_t\right)}^{-1}\sim {\chi }_1^2.$ Based on this, Guo et al. (2013) proposed M-MeanStat and M-MaxStat:

$$\begin{array}{c}\text{M-MeanStat}=\frac{1}{p}{\displaystyle \sum _{t=1}^k{\displaystyle \sum _{j=1}^p{T}_{jt}\mathrm{\propto }{\displaystyle \sum _{t=1}^k{\displaystyle \sum _{j=1}^p\frac{{\left({\displaystyle {\sum }_{i=1}^n{x}_{ij}{y}_{it}}\right)}^2}{{\displaystyle {\sum }_{i=1}^n\mathrm{var}\left(x_{ij}\right)y_{it}^2}}\approx {\displaystyle \sum _{t=1}^k{\displaystyle \sum _{j=1}^p{\left(\frac{{\displaystyle {\sum }_{i=1}^n{x}_{ij}{y}_{it}}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{x}_{ij}^2{y}_{it}^2}}}\right)}^2}}}}}},\\ \text{M-MaxStat}={\displaystyle \sum _{t=1}^k\stackrel{p}{\underset{j=1}{\max }}{T}_{jt}={\displaystyle \sum _{t=1}^k\stackrel{p}{\underset{j=1}{\max }}\frac{{\left({\displaystyle {\sum }_{i=1}^n{x}_{ij}{y}_{it}}\right)}^2}{{\displaystyle {\sum }_{i=1}^n\mathrm{var}\left(x_{ij}\right)y_{it}^2}}\approx {\displaystyle \sum _{t=1}^k\stackrel{p}{\underset{j=1}{\max }}{\left(\frac{{\displaystyle {\sum }_{i=1}^n{x}_{ij}{y}_{it}}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{x}_{ij}^2{y}_{it}^2}}}\right)}^2}}}.\end{array}$$ (A1)

If a canonical link function and a working independence model are used in GEE, the test statistics of $\text{SPUw}\left(2,2\right)$ and $\text{SPUw}\left(\mathrm{\infty },1\right)$ are defined by

$$\begin{array}{c}\text{SPUw}\left(2,2\right)\mathrm{\propto }{\displaystyle \sum _{t=1}^k{\displaystyle \sum _{j=1}^p{\left(\frac{{\displaystyle {\sum }_{i=1}^n{x}_{ij}{y}_{it}}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{x}_{ij}^2\mathrm{var}\left(y_{it}\right)}}}\right)}^2\approx {\displaystyle \sum _{t=1}^k{\displaystyle \sum _{j=1}^p{\left(\frac{{\displaystyle {\sum }_{i=1}^n{x}_{ij}{y}_{it}}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{x}_{ij}^2{y}_{it}^2}}}\right)}^2}}}},\\ \text{SPUw}\left(\mathrm{\infty },1\right)\mathrm{\propto }{\displaystyle \sum _{t=1}^k\stackrel{p}{\underset{j=1}{\max }}\left|\frac{{\displaystyle {\sum }_{i=1}^n{x}_{ij}{y}_{it}}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{x}_{ij}^2\mathrm{var}\left(y_{it}\right)}}}\right|\approx {\displaystyle \sum _{t=1}^k\stackrel{p}{\underset{j=1}{\max }}{\left(\frac{{\displaystyle {\sum }_{i=1}^n{x}_{ij}{y}_{it}}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{x}_{ij}^2{y}_{it}^2}}}\right)}^2}}.\end{array}$$ (A2)

Comparing the two sets of statistics in (A1) and (A2), we see that M-MeanStat and $\text{SPUw}\left(2,2\right)$ and M-Max and $\text{SPUw}\left(\mathrm{\infty },1\right)$ are approximately equivalent, respectively.

Appendix B: SPU(2,2) and MDMR

Under the working independence model, the test statistic of SPU(2,2) is stated as

$$\text{SPU}\left(2,2\right)={\displaystyle \sum _{t=1}^k{\displaystyle \sum _{j=1}^p{\left({\displaystyle \sum _{i=1}^n{x}_{ij}{y}_{it}}\right)}^2=\text{tr}\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }\right)}}.$$ (B1)

MDMR is a nonparametric modification of traditional Fisher’s MANOVA (McArdle and Anderson 2001). Wessel and Schork (2006) and Zapala and Schork (2012) introduced the method to applications in genetics and genomics. For a single trait, it is closely related to kernel methods (Schaid et al. 2005; Pan 2011).

Suppose $d_{ij}$ represents the distance between subjects i and j; let $A=\left(a_{ij}\right)=\left(-1/2\hspace{0.17em}{d}_{ij}^2\right)$ and G be its centered version. An F statistic can be constructed to test the hypothesis that the p regressor variables have no relationship to variation in the distance or dissimilarity of the n subjects reflected in the $n\times n$ distance/dissimilarity matrix. The pseudo-F statistic of MDMR is defined by

$$F=\frac{\text{tr}\left(\mathbf{H}\mathbf{G}\mathbf{H}\right)}{\text{tr}\left(\mathbf{I}-\mathbf{H}\right)\mathbf{G}\left(\mathbf{I}-\mathbf{H}\right)}.$$

If the Euclidean distance (i.e., $L_2$ norm) is used to construct the distance matrix G $=\mathbf{\Theta }{\mathbf{\Theta }}^{\prime },$ the MDMR test statistic is defined as

$$\text{MDMR}\propto \frac{\text{tr}\left(\mathbf{H}\mathbf{\Theta }{\mathbf{\Theta }}^{\prime }\mathbf{H}\right)}{\text{tr}\left(\mathbf{I}-\mathbf{H}\right)\mathbf{\Theta }{\mathbf{\Theta }}^{\prime }\left(\mathbf{I}-\mathbf{H}\right)}\propto \frac{1}{\text{tr}\left({\mathbf{R}}^{\prime }\mathbf{R}\right)/\text{tr}\left({\widehat{\mathbf{\Theta }}}^{\prime }\widehat{\mathbf{\Theta }}\right)}\propto \frac{1}{\left[\text{tr}\left({\widehat{\mathbf{\Theta }}}^{\prime }\widehat{\mathbf{\Theta }}\right)+\text{tr}\left({\mathbf{R}}^{\prime }\mathbf{R}\right)\right]/\text{tr}\left({\widehat{\mathbf{\Theta }}}^{\prime }\widehat{\mathbf{\Theta }}\right)}=\frac{\text{tr}\left({\widehat{\mathbf{\Theta }}}^{\prime }\widehat{\mathbf{\Theta }}\right)}{\text{tr}\left({\mathbf{\Theta }}^{\prime }\mathbf{\Theta }\right)}.$$

As usual, permutations are used to calculate P-values. Then $\text{tr}\left({\mathrm{\Theta }}^{\prime }\mathrm{\Theta }\right)$ is invariant across all permutations and can be ignored (Pan 2011). The test statistic arrives at

$$\text{MDMR}\propto \text{tr}\left({\widehat{\mathbf{\Theta }}}^{\prime }\widehat{\mathbf{\Theta }}\right)=\text{tr}\left({\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }{\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }\right)}^{-1}{\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }\right)=\text{tr}\left({\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }\right)}^{-1}{\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }\right).$$ (B2)

If we have a single SNP to be tested, i.e., Λ is an $n\times 1$ matrix, the test statistic (B2) reduces to $\text{MDMR}\propto m^{-1}\text{tr}\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }\right)\propto \text{tr}\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }\right)$ with ${\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }=m.$ Hence, SPU(2,2) and MDMR are equivalent for a single SNP and multiple traits, as established by Zhang et al. (2014). However, for multiple SNPs and multiple traits, by comparing (B1) and (B2), we see that in general they are not equivalent.

Appendix C: SPU(2,2) and KMR

With a working correlation matrix ${\mathit{R}}_{\text{w}}$ in GEE, the SPU(2,2) test can be rewritten as

$$\text{SPU}\left(2,2\right)=\text{tr}\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\mathit{R}}_{\mathbf{w}}^{\mathbf{-}\mathbf{1}}{\mathit{R}}_{\mathbf{w}}^{\mathbf{-}\mathbf{1}}{\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }\right)=\text{tr}\left({\mathit{R}}_{\mathbf{w}}^{\mathbf{-}\mathbf{1}}{\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\mathit{R}}_{\mathbf{w}}^{\mathbf{-}\mathbf{1}}\right).$$ (C1)

Maity et al. (2012) introduced multivariate phenotype association analysis by SNP set- or gene-based KMR. The authors assumed that the phenotypes are correlated while the individuals are independent. Suppose $\mathbf{\Psi }=\left({\mathit{\psi }}_{pq}\right)$ is the true correlation matrix for k traits with $p=1,\dots ,k,$ and $q=1,\dots ,k.$ Define ${\mathit{V}}_0=\mathbf{\Psi \otimes }{\mathit{I}}_{n\times n}$ and a kernel matrix ${\mathcal{K}}_{nk\times nk}.$ The score test under the null for KMR (Maity et al. 2012) is defined by

$$\text{KMR}=\text{vec}{\left(\mathbf{\Theta }\right)}^{\prime }{\mathit{V}}_{\mathbf{0}}^{\mathbf{-}\mathbf{1}}\hspace{0.17em}\mathcal{K}\hspace{0.17em}{\mathit{V}}_{\mathbf{0}}^{\mathbf{-}\mathbf{1}}\text{vec}\left(\mathbf{\Theta }\right)=\text{vec}{\left(\mathbf{\Theta }\right)}^{\prime }{\mathit{V}}_0^{-1}\hspace{0.17em}\text{diag}\left({\mathit{K}}_{\mathbf{1}},\dots ,{\mathit{K}}_{\mathit{k}}\right)\hspace{0.17em}{\mathit{V}}_{\mathbf{0}}^{\mathbf{-}\mathbf{1}}\text{vec}\left(\mathbf{\Theta }\right),$$

where each ${\mathit{K}}_1,\dots ,{\mathit{K}}_k$ is an $n\times n$ kernel matrix for each trait. Applying a linear kernel ${\mathit{K}}_1=,\dots ,={\mathit{K}}_k=\mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }$ yields

$$\begin{array}{c}\text{KMR}=\text{vec}{\left(\mathbf{\Theta }\right)}^{\prime }{\mathit{V}}_0^{-1}\left({\mathit{I}}_{k\times k}\otimes \mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }\right){\mathit{V}}_0^{-1}\text{vec}\left(\mathbf{\Theta }\right)=\text{vec}{\left(\mathbf{\Theta }{\mathbf{\Psi }}^{-1}\right)}^{\prime }\left(\mathit{I}\otimes \mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }\right)\text{vec}\left(\mathbf{\Theta }{\mathbf{\Psi }}^{-1}\right)\\ =\text{vec}{\left(\mathbf{\Theta }{\mathbf{\Psi }}^{-1}\right)}^{\prime }\text{vec}\left(\mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\mathbf{\Psi }}^{-1}\right)=\text{tr}\left({\mathbf{\Psi }}^{-1}{\mathbf{\Theta }}^{\prime }\mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\mathbf{\Psi }}^{-1}\right).\end{array}$$ (C2)

KMR (Equation C2) has the same test statistic as the GEE-SPU(2) test (Equation C1) if the working correlation ${\mathit{R}}_{\text{w}}$ is the true correlation structure of $Y_i$ [i.e., $\mathbf{\Psi }={\mathit{R}}_{\text{w}}=\text{Corr}\left(Y_i|H_0\right)$].

Appendix D: GEE-Score test and MANOVA

The GEE-Score test statistic with a working independence model in GEE is

$$\begin{array}{c}\text{GEE-Score}=\text{vec}{\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }\right)}^{\prime }{\left({\mathit{S}}_y\mathrm{\otimes }n{\mathit{S}}_x\right)}^{-1}\text{vec}\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }\right)=n\hspace{0.17em}\text{vec}{\left({\mathit{S}}_{xy}\right)}^{\prime }\left({\mathit{S}}_y^{-1}\mathrm{\otimes }{\mathit{S}}_x^{-1}\right)\text{vec}\left({\mathit{S}}_{xy}\right)\\ =n\hspace{0.17em}\text{tr}\left({\mathit{S}}_y^{-1}{\mathit{S}}_{yx}{\mathit{S}}_x^{-1}{\mathit{S}}_{xy}\right).\end{array}$$

In MANOVA, a measure of the strength of association between Θ (multiple traits) and Λ (genotype scores) for the multivariate model $\mathbf{\Theta }=\mathbf{\Lambda }B+E$ depends on a partition of matrix of total SSCP; i.e., ${\mathbf{\Theta }}^{\prime }\mathbf{\Theta }={\widehat{\mathbf{\Theta }}}^{\prime }\widehat{\mathbf{\Theta }}+{\mathbf{R}}^{\prime }\mathbf{R}$ (Haase 2011). Considering the Pillai–Bartlett (PB) trace, the MANOVA test statistic is stated as tr$\left({\widehat{\mathbf{\Theta }}}^{\prime }\widehat{\mathbf{\Theta }}{\left({\mathbf{\Theta }}^{\prime }\mathbf{\Theta }\right)}^{-1}\right)=\text{tr}\left({\mathbf{\Theta }}^{\prime }{\left({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }\right)}^{-1}{\mathbf{\Lambda }}^{\prime }\mathbf{\Theta }{\left({\mathbf{\Theta }}^{\prime }\mathbf{\Theta }\right)}^{-1}\right),$ which can be written in an alternate form $\text{tr}\left({\mathit{S}}_{yx}{\mathit{S}}_x^{-1}{\mathit{S}}_{xy}{\mathit{S}}_y^{-1}\right)=\text{tr}\left({\mathit{S}}_y^{-1}{\mathit{S}}_{yx}{\mathit{S}}_x^{-1}{\mathit{S}}_{xy}\right).$ Hence, the GEE-Score test and MANOVA using the PB trace are equivalent.