An Evolving Genetic Architecture Interacts with Hill–Robertson Interference to Determine the Benefit of Sex

Abstract

Sex is ubiquitous in the natural world, but the nature of its benefits remains controversial. Previous studies have suggested that a major advantage of sex is its ability to eliminate interference between selection on linked mutations, a phenomenon known as Hill–Robertson interference. However, those studies may have missed both important advantages and important disadvantages of sexual reproduction because they did not allow the distributions of mutational effects and interactions (i.e., the genetic architecture) to evolve. Here we investigate how Hill–Robertson interference interacts with an evolving genetic architecture to affect the evolutionary origin and maintenance of sex by simulating evolution in populations of artificial gene networks. We observed a long-term advantage of sex—equilibrium mean fitness of sexual populations exceeded that of asexual populations—that did not depend on population size. We also observed a short-term advantage of sex—sexual modifier mutations readily invaded asexual populations—that increased with population size, as was observed in previous studies. We show that the long- and short-term advantages of sex were both determined by differences between sexual and asexual populations in the evolutionary dynamics of two properties of the genetic architecture: the deleterious mutation rate ($U_{\mathrm{d}}$) and recombination load ($L_{\mathrm{R}}$). These differences resulted from a combination of selection to minimize $L_{\mathrm{R}},$ which is experienced only by sexuals, and Hill–Robertson interference experienced primarily by asexuals. In contrast to the previous studies, in which Hill–Robertson interference had only a direct impact on the fitness advantages of sex, the impact of Hill–Robertson interference in our simulations was mediated additionally by an indirect impact on the efficiency with which selection acted to reduce $U_{\mathrm{d}}.$

THE vast majority of organisms alive today have experienced some form of genetic exchange, or sex, in their recent evolutionary history, despite substantial costs (Weismann 1887; Maynard Smith 1978; Bell 1982; Otto and Lenormand 2002). Sex breaks up favorable genetic combinations and increases the risk of transmission of pathogens and selfish genetic elements. Sexual reproduction is often slower than asexual reproduction. In many sexually reproducing eukaryotes, sex involves costs of finding and attracting a mate and of mating in itself; in anisogamous species, if one sex contributes little to progeny production, sexual reproduction carries a twofold cost of producing that sex. The ubiquity of sex implies that it must confer considerable benefits to overcome these costs. However, the nature of these benefits is not well understood. In fact, >20 hypotheses have been proposed to explain the benefits of sex (Bell 1982; Kondrashov 1993; Hurst and Peck 1996; Otto and Lenormand 2002). While hypotheses predicting direct benefits exist [e.g., improved DNA repair (Bernstein et al. 1985)], the main benefits of sex are believed to be indirect, such as increased evolvability (Weismann 1887; Maynard Smith 1978; Bell 1982; Kondrashov 1993; Burt 2000; Otto and Lenormand 2002).

Indirect benefits of sex result from the ability of recombination to break down the linkage disequilibrium (LD) generated by mutation, genetic drift, and natural selection. If LD is predominantly negative, that is, if genotypes with the highest and lowest fitness are underrepresented in the population, then recombination can generate these extreme genotypes and increase the efficiency of natural selection (Otto and Lenormand 2002). In the absence of recombination, negative LD can accumulate in a population either through the action of natural selection alone [red queen hypothesis (Hamilton 1980) or mutational deterministic hypothesis (Kimura and Maruyama 1966; Kondrashov 1982, 1988; Charlesworth 1990; Barton 1995; Otto and Feldman 1997)] or through the combined actions of selection and genetic drift [Hill–Robertson interference (Hill and Robertson 1966; Felsenstein 1974; Comeron et al. 2008)]. Although there is evidence supporting the existence of red queen and mutational deterministic benefits of sex in specific populations, the conditions required to generate these benefits are thought to be too restrictive to provide a general explanation for the ubiquity of sex (Charlesworth 1993; Barton 1995; Otto and Feldman 1997; Otto and Nuismer 2004). In contrast, Hill–Robertson interference is thought to operate broadly (Comeron et al. 2008) and to provide strong benefits of sex (Otto and Barton 2001; Iles et al. 2003; Barton and Otto 2005; Keightley and Otto 2006; Gordo and Campos 2008; Hartfield et al. 2010).

Hill–Robertson interference is a phenomenon whereby, in a finite population, selection acting at one locus reduces the efficiency of selection at linked loci (Hill and Robertson 1966; Felsenstein 1974; Comeron et al. 2008). It takes at least four forms. First, deleterious alleles fix stochastically—a process known as Muller’s ratchet (Muller 1964; Haigh 1978; Gordo and Charlesworth 2000). Second, selection against deleterious alleles removes linked beneficial alleles from the population as a side effect—a process known as background selection (Charlesworth et al. 1993; Charlesworth 1994; Peck 1994). Third, competition between individuals carrying independent beneficial alleles slows down the spread of these beneficial alleles—a process known as the Fisher–Muller effect (Fisher 1930; Muller 1932; Gerrish and Lenski 1998). Fourth, selection for beneficial alleles causes linked deleterious alleles to rise in frequency in the population as a side effect—a process known as hitchhiking (Maynard Smith and Haigh 1974; Peck 1994). All forms of Hill–Robertson interference are strongest in asexuals, whose entire genomes are completely linked, and are weakened by sex.

The relative strengths of the benefits of sex arising from these different forms of Hill–Robertson interference are known to depend critically on population size and on the distribution of mutational effects on fitness. For example, Muller’s ratchet is strongest in small populations that often experience deleterious mutations, whereas the Fisher–Muller effect is strongest in large populations that often experience beneficial mutations. The increase in the strength of the Fisher–Muller effect between beneficial mutations with population size is intuitive because population size (N) affects the beneficial mutation supply rate ($N{U}_{\mathrm{b}},$ where $U_{\mathrm{b}}$ is the beneficial mutation rate).

More surprising is the recent finding from evolutionary simulations that interference between deleterious mutations can, on its own, also generate a large benefit of sex that increases with population size (Otto and Barton 2001; Iles et al. 2003; Barton and Otto 2005; Keightley and Otto 2006; Gordo and Campos 2008; Hartfield et al. 2010). This finding is surprising because neither Muller’s ratchet (Muller 1964; Haigh 1978; Gordo and Charlesworth 2000) nor background selection (Hudson and Kaplan 1994, 1995) is expected to increase in strength with population size. The mechanism underlying the dependency of the benefit of sex on population size was little explored in this previous body of work and is our focus here.

Box 1: Genetic architecture.

The genetic architecture refers to the patterns of gene action and interaction that specify a given phenotype and its variational properties. The distribution of allelic and mutational effects and the patterns of pleiotropy, dominance, and epistasis are all determined by the underlying genetic architecture (Hansen 2006; Rice 2008).

In our study, we focus on two components of the genetic architecture.

Deleterious mutation rate $\left(U_{\mathrm{d}}\right)$

The deleterious mutation rate is determined by the mutation rate $\left(U\right)$ and by the distribution of the effects of mutations on fitness. The latter, in turn, is influenced by epistatic interactions between new mutations and the genetic background of an individual. Thus, $U_{\mathrm{d}}$ is a property of individual organisms. The mean fitness of large populations at mutation–selection balance is expected to be

$$\widehat{W}\approx e^{-{\overline{U}}_{\mathrm{d}}}$$

(Haldane 1937; Kimura and Maruyama 1966).

Recombination load $\left(L_{\mathrm{R}}\right)$

Recombination load is reduction in the mean fitness of a population resulting from recombination (Charlesworth and Barton 1996). It is a measure of the cost of sex caused by breaking up beneficial combinations of alleles, and is influenced by epistatic interactions between alleles. $L_{\mathrm{R}}$ is a property of a population, but is influenced by the genotypes of individual organisms.

Our intuition is that assumptions made in previous work on the evolution of sex—that one or more of the deleterious mutation rate, distribution of mutation effects, and the epistatic interactions between mutations do not evolve—affected the magnitude and nature of the advantages of sex generated by Hill–Robertson interference in that work (e.g., Fisher 1930; Muller 1932, 1964; Hill and Robertson 1966; Felsenstein 1974; Haigh 1978; Peck 1994; Charlesworth 1994; Barton 1995; Otto and Feldman 1997; Gordo and Charlesworth 2000; Otto and Barton 2001; Iles et al. 2003; Barton and Otto 2005; Keightley and Otto 2006; Gordo and Campos 2008; Hartfield et al. 2010). The deleterious mutation rate, the distribution of mutational effects, and the epistatic interactions between mutations are all properties of the genetic architecture (Box 1) that are known to play an important role in the indirect benefits of sex (Kondrashov 1982, 1988; Charlesworth 1990; Otto and Feldman 1997). These properties can evolve in just a few generations (Burch and Chao 2004; Montville et al. 2005; Sanjuán et al. 2007; Silander et al. 2007). We know, from both theoretical (Poon and Otto 2000) and empirical (Silander et al. 2007) studies, that an evolving genetic architecture affects the benefits of sex in populations that are sufficiently small to be subject to Muller’s ratchet. As the fitness of asexual populations declines through operation of the ratchet, the rate of compensatory mutations increases, eventually halting the ratchet and limiting this cost of asexuality. We know less about how an evolving genetic architecture affects the benefit of sex in large populations.

In previous work, we studied a gene network model that explicitly incorporates an evolving genetic architecture (Wagner 1996; Siegal and Bergman 2002) and found that sex selects for a lower deleterious mutation rate, lower recombination load, and negative epistasis (Azevedo et al. 2006; Lohaus et al. 2010), three changes in the genetic architecture predicted to favor the maintenance of sex. We noted that population size affected the extent to which sexual reproduction led to an increase in mean fitness at equilibrium (the long-term advantage) and successfully invaded asexual populations (the short-term advantage), but we did not systematically explore these effects (Lohaus et al. 2010).

Here we build on our earlier work on the gene network model to investigate the extent to which Hill–Robertson interference interacts with the evolving genetic architecture to determine the advantage of sex. We compare sexual and asexual reproduction, manipulating the contribution of Hill–Robertson interference by altering population size. We look for a long-term advantage of sex by monitoring the evolution of fitness and the genetic architecture as sexual and asexual populations approach equilibrium. We also look for a short-term advantage of sex by monitoring the invasion of equilibrium sexual populations by asexual mutants and vice versa. We show that both genetic architecture evolution and Hill–Robertson interference contribute to the advantages of sex in the gene network model and that the magnitudes of their relative contributions depend on population size, as expected. As population size increased, the contribution of Hill–Robertson interference to both the short- and long-term advantages of sex increased.

Materials and Methods

Our gene network model is based on a model introduced by Wagner (1994, 1996).

Genotype

A haploid genotype is modeled as a network of n genes, each encoding a transcription factor that can, potentially, regulate its own expression or the expression of other genes. The gene network is represented by an $n\times n$ matrix, $R,$ where $r_{ij}\in R$ is the regulatory effect of the product of gene j on gene i.

Thus, row i of R represents gene i, including its cis-regulatory elements. Genes are evenly distributed on a linear chromosome in the same order as the rows in the R matrix $\left(i=1,2,\dots ,n\right).$ Genes 1 and n are at a map distance λ from each other. Adjacent pairs of genes are at a map distance $\mathrm{\lambda }/\left(n-1\right)$ from each other.

Phenotype

The expression pattern of an individual is represented by the vector $S,$ where $s_i\in S$ is the expression state of gene $i=1,2,\dots ,n.$ Expression states are discrete: a gene is either on $\left(s_i=+1\right)$ or off $\left(s_i=-1\right).$

The expression pattern of an individual at time t is given by the system of difference equations

$$s_i\left(t+1\right)=f\left[{\displaystyle \sum _{j=1}^n{r}_{ij}{s}_j\left(t\right)}\right],$$ (1)

where f is a step function that determines how the input from the gene network controls the expression of the target gene:

$$f\left(x\right)=\{\begin{array}{cc}+1& \text{if }x\ge 0\\ -1& \text{if }x<0.\end{array}$$

Starting from an initial gene expression pattern $S\left(0\right)$ at time $t=0,$ gene expression changes according to Equation 1 and is judged to reach a steady state if the following criterion is met: $S\left(t\right)=S\left(t-1\right).$ If a genotype does not achieve a gene expression steady state within $t\le 100$ time steps, it is considered inviable ($W=0,$ see next section). If a genotype achieves a gene expression steady state within $t\le 100$ time steps, it is considered viable $\left(W>0\right),$ and the steady-state gene expression pattern $\widehat{S}$ is its phenotype. Most random genotypes (see below) fail to produce a gene expression steady state (Pinho et al. 2014).

Fitness

The fitness of a viable genotype is given by

$$W=\exp \left[-\frac{D\left(\widehat{S},\dot{S}\right)}{\sigma }\right],$$ (2)

where $D\left(S,S^{\prime }\right)={\displaystyle {\sum }_{i=1}^n{\left(s_i-{s^{\prime }}_i\right)}^2}/\left(4n\right)$ measures the difference between expression patterns S and $S^{\prime },$ $\widehat{S}$ is the phenotype corresponding to the genotype, $\dot{S}$ is the optimal phenotype, and $\sigma >0$ is inversely related to the strength of stabilizing selection.

Random genotype

A random genotype is created by generating a random gene network, R, and a random initial gene expression pattern, $S\left(0\right).$ A random gene network is generated by randomly assigning to its $r_{ij}$ regulatory elements $\left(1-c\right)n^2$ zeros and $c{n}^2$ nonzero random variates drawn from a standard normal distribution (i.e., with zero mean and unit variance), where c is the connectivity density of the network. Networks with more than one weakly connected component (Newman 2010) are discarded. A random initial gene expression pattern is generated by filling the n entries of $S\left(0\right)$ with either $-1$ or $+1$ with equal probability.

Evolution

Evolution is simulated using an individual-based, Wright–Fisher model with constant population size, N, and nonoverlapping generations. Individuals undergo a selection–reproduction–mutation life cycle. At the beginning of a simulation, a viable random genotype is cloned N times to found a population. The optimal phenotype is defined as the phenotype of the founder. This aspect of the environment remains constant throughout the simulation.

Reproduction:

Parents for the next generation are chosen at random, with replacement, with probability proportional to their fitness (Equation 2). If the parent reproduces asexually, it generates a clone of itself. If two parents reproduce sexually, they form a transient diploid and produce one haploid recombinant offspring. The recombinant R matrix is generated by choosing one parent at random and copying the first row of its R matrix; the next row of R is copied from the same parent except if a crossover occurs, in which case the corresponding row of the R matrix of the other parent is copied instead. The process repeats for each row, switching between parents each time a crossover location is encountered. For each offspring, the number of crossovers is drawn randomly from a Poisson distribution with mean $2\lambda ,$ where λ is the genetic map length in morgans. Crossover locations are chosen randomly and occur between genes. No crossovers occur within the regulatory regions of a gene, maintaining each row as a completely linked locus. Unless otherwise stated, sexual reproduction occurs with free recombination [i.e., $\lambda /\left(n-1\right)=0.5$ morgans].

Both asexually and sexually produced offspring inherit the initial pattern of gene expression, $S\left(0\right),$ of the parents. This aspect of the environment also remains constant throughout the simulation.

Mutation:

Each individual offspring acquires a random number of mutations drawn from a Poisson distribution with mean U, the genomic mutation rate. A mutation is represented by a change to the value of one of the $c{n}^2$ nonzero regulatory elements $r_{ij},$ chosen at random; the mutated value is drawn randomly from a standard normal distribution. Mutation cannot create new regulatory interactions (i.e., a zero entry cannot become nonzero), but can transiently remove regulatory interactions (i.e., a nonzero entry may become approximately zero).

Reproductive mode

The reproductive mode of an individual is determined by its genotype at a modifier locus M. Unless otherwise stated, the M locus is unlinked to the genes involved in the gene network. There are two alleles at the modifier locus: m and M. We have implemented three different genetic bases for these reproductive modes, described below. Under all implementations, if a population is fixed for the m allele every individual reproduces asexually, and if it is fixed for the M allele every individual reproduces sexually. Thus, we refer to the m and M alleles as being for asexual and sexual reproduction, respectively. In all simulations where the M locus modifies reproductive mode, the m allele specifies no recombination (i.e., $\lambda =0$ morgans), and the M allele specifies free recombination [i.e., $\lambda /\left(n-1\right)=0.5$ morgans].

Separate sex:

The sexual and asexual subpopulations are reproductively isolated from each other. Sexuals do not experience a cost of finding mates. One individual is chosen for every reproductive event with probability proportional to its fitness. If it carries the m allele, it reproduces asexually. If it carries the M allele, a second individual carrying an M allele is chosen with probability proportional to its fitness, and the two individuals reproduce sexually and produce one recombinant offspring.

Recessive sex:

Asexual individuals always reproduce asexually; sexual individuals sometimes reproduce asexually. Two individuals are chosen for every reproductive event with probability proportional to their fitness. If one or both of the individuals carries the m allele, one of them reproduces asexually, regardless of its genotype at the M locus. If both individuals carry the M allele, they reproduce sexually and produce one recombinant offspring.

Dominant sex:

Sexual individuals always reproduce sexually, but they may recombine with asexual individuals. Two individuals are chosen for every reproductive event with probability proportional to their fitness. If both individuals carry the m allele, one of them reproduces asexually. If one or both of the individuals carry the M allele, they reproduce sexually and produce one recombinant offspring. The offspring inherits one of the parental alleles at the M locus, chosen randomly.

Population metrics

Mean fitness and log fitness:

$\overline{W}$ is the mean fitness and $\overline{\ln W}$ is the mean log fitness of all individuals present in the population at a given time (see Equation 2).

Genetic variance in log fitness:

$\mathrm{var(ln}W$) is the total variance among all individuals present in the population at a given time.

Mean and variance in log fitness under linkage equilibrium:

We estimated mean and variance in $\ln W$ for a population with the same allele frequencies but no LD (Barton 1995). We estimated these parameters from a sample of 100 “chimeras.” A chimeric R matrix was constructed by picking each row from the R matrices of any individual in the population with equal probability.

Effective population size:

To estimate effective population size, $N_{\mathrm{e}},$ a neutral locus was incorporated into the simulation. In sexuals, the neutral locus was not linked to the gene network loci. In each generation, the neutral locus acquired a random number of mutations drawn from a Poisson distribution with mean 1. Each mutation added to the neutral locus value a random draw from the standard normal distribution. The equilibrium variance $\left(\widehat{V}\right)$ at an unlinked neutral locus is expected to be N, the census population size. We calculated $N_{\mathrm{e}}$ as $\widehat{V}$ at the neutral locus. $N_{\mathrm{e}}$ estimates were obtained at generation ${10}^4,$ at which time all but the largest populations ($N={10}^4$) had achieved equilibrium variance at the neutral locus.

Genetic architecture

Deleterious mutation rate:

The deleterious mutation rate is defined as $U_{\mathrm{d}}=U\left(p_{\mathrm{d}}+p_{\mathrm{l}}\right),$ where U is the genomic mutation rate, and $p_{\mathrm{d}}$ and $p_{\mathrm{l}}$ are the proportions of nonlethal deleterious and lethal mutations, respectively (see Box 1). U is constant throughout the course of a simulation but $p_{\mathrm{d}}$ and $p_{\mathrm{l}}$ can evolve. We estimate the quantity $p_{\mathrm{d}}+p_{\mathrm{l}}$ for a genotype by generating 100 copies of the genotype carrying a single mutation and evaluating the proportion of them that have lower fitness than the original genotype.

Recombination load:

The recombination load is defined as $L_{\mathrm{R}}=\overline{\omega -\rho },$ where ω is the mean fitness of a pair of parental genotypes and ρ is the fitness of a single recombinant offspring from them, without mutation (see Box 1). $L_{\mathrm{R}}$ was calculated by averaging this measure across N independently chosen pairs of individuals, where each parent was chosen with probability proportional to their fitness (i.e., in the same way the population reproduced in the evolutionary simulations).

Epistasis:

We define multiplicative epistasis between two mutations, i and j, as $\epsilon =W_{i,j}/W-W_i{W}_j/W^2,$ where W is the fitness of the unmutated (test) genotype, $W_i$ and $W_j$ are the fitnesses of the single mutants, and $W_{i,j}$ is the fitness of the double mutant. Otto and Feldman (1997) introduced the standardized epistasis coefficient $\epsilon \ast =\epsilon /{\overline{s}}^2,$ where $\overline{s}=\left(W_i+W_j\right)/\left(2W\right)-1$ is the mean effect of a single mutation. We calculated means and variances of $\epsilon \ast$ across pairs of random nonlethal deleterious mutations, introduced individually and in combination into a random sample of 100 viable individuals without replacement (for $N<100,$ we sampled 100 viable individuals with replacement).

Invasion analysis

Populations were evolved for ${10}^4$ generations under either asexual or sexual reproduction (i.e., the population was fixed for either the m or the M allele, respectively), to allow sufficient time for the population to approach mutation–recombination–selection–drift equilibrium. We then mutated the allele at the modifier locus M (see Reproductive mode, above) in a single randomly chosen individual. In most population size $\times$ reproductive mode treatments, we measured the fixation probability of the novel modifier allele, u, relative to that of a neutral mutation ($u\ast =1/N$) in N replicate invasion trials per independently evolved population, for a total of $50N$ replicates. For the largest $N={10}^4$ populations, computational time limited us to $5N$ replicate asexual invasion trials and $10N$ replicate sexual invasion trials.

Evolution of recombination rate

Populations were evolved for ${10}^4$ generations with a modifier locus that was linked to a randomly chosen row of the R matrix and fixed for an allele that specified a map length of $\lambda =0$ morgans. After generation ${10}^4,$ the modifier locus experienced mutations at a rate of ${10}^{-3}$ per generation. Mutational effects on λ were $\pm 0.05$ morgans, with equal probability. Alleles conferring $\lambda <0$ were discarded. When two individuals with map lengths ${\lambda }_1$ and ${\lambda }_2$ reproduced, the expected number of crossovers in the offspring was ${\lambda }_1+{\lambda }_2.$

Parameter values

The parameter values used here differed from those used in previous work on the evolution of genetic architecture (Siegal and Bergman 2002; Azevedo et al. 2006; MacCarthy and Bergman 2007; Lohaus et al. 2010): the random gene networks were larger ($n=100$ genes) and sparser $\left(c=0.05\right),$ and the genomic mutation rate was higher $\left(U=1\right).$ These modifications have three advantages. First, the greater number of genes allows mutations to have a broad range of potential fitness effects, including beneficial, neutral, slightly deleterious, and lethal. Second, the higher U allows populations to show considerable mutation load at equilibrium (see Box 1) (Martin and Wagner 2009). Third, real gene networks are relatively sparse (Leclerc 2008).

Statistical analysis

All statistics were conducted using the R statistical package, version 3.2.1 (Ihaka and Gentleman 1996). Comparisons of evolutionary trajectories were conducted using the function lme of the nlme package to generate linear mixed-effects models (Pinheiro and Bates 2000). In these models, ln(time) in generations, sex (i.e., reproductive mode: sexual or asexual), and $\ln \left(N\right)$ were modeled as fixed effects. Statistical tests using linear models with only one fixed effect or with multiple fixed effects are described in text or in a detailed table, respectively. In all linear models, population founder was modeled as a random effect.

Data availability

Programs used to run all simulations were written in Python 2.7 and are available at https://bitbucket.org/cburch/whitlock-et-al-2016. The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Results

Sex has a long-term advantage

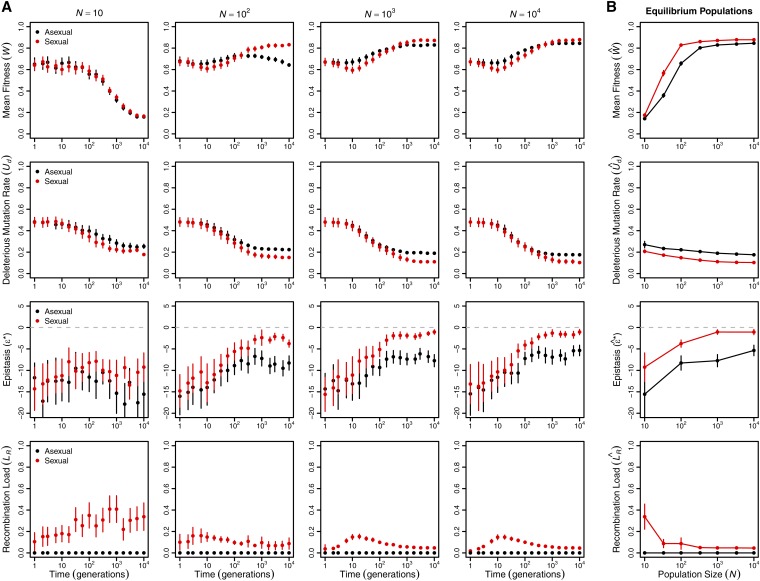
We simulated the evolution of haploid gene networks in populations ranging in size from $N=10$ to ${10}^4$ individuals. We set the genomic mutation rate to be high $\left(U=1\right)$ and stabilizing selection to be moderate ($\sigma =0.2$) to ensure the operation of all components of Hill–Robertson interference: Muller’s ratchet in smaller populations, the Fisher–Muller effect in larger populations, and hitchhiking and background selection at all population sizes. Mutants differing from the target expression state at i and $i+1$ genes differed in fitness by no more than 5% (i.e., $W_i-W_{i+1}<0.05,$ for all i). Populations were evolved for ${10}^4$ generations, allowing sufficient time for populations of all sizes to approach mutation–recombination–selection–drift equilibrium. To examine the evolutionary contributions of changes in the genetic architecture in these populations, we monitored mean fitness $\left(\overline{W}\right),$ deleterious mutation rate $\left(U_{\mathrm{d}}\right),$ epistasis $\left(\epsilon \ast \right),$ and recombination load $\left(L_{\mathrm{R}}\right)$ over the course of the simulations (Figure 1; note that time is plotted on a log scale).

Figure 1.

Sex has a long-term advantage. (A) Changes in mean fitness $\left(W\right),$ deleterious mutation rate $\left(U_{\mathrm{d}}\right),$ epistasis $\left(\epsilon \ast \right),$ and recombination load $\left(L_{\mathrm{R}}\right)$ over time in asexual (black) and sexual (red) populations of various sizes $\left(N\right).$ (B) Means at generation ${10}^4,$ after populations of all sizes achieved equilibrium in all properties. Values are means and 95% confidence intervals based on 50 replicate populations initiated from different randomly chosen founders.

Over the short term (generations 1–10), the most striking difference between sexual and asexual populations is that mean fitness declines significantly more quickly in large sexual populations than in large asexual populations (statistical analysis in Supplemental Material, Table S1). This pattern characterizes populations of at least 100 individuals [ln(time) × sex interaction estimated separately for each $N\ge 100:$ $\left|t\right|\ge 3.989,$ $\text{d}.\text{f}.=447,$ $P<0.0001,$ all tests] and appears to be largely the result of the recombination load increasing in sexual populations through generation 10 [effect of ln(time) on $L_{\mathrm{R}}:$ $\left|t\right|=3.975,$ $\text{d}.\text{f}.=1699,$ $P<0.0001$]. Smaller populations did not show a significant change in mean fitness in the first 10 generations [main effect of ln(time) and ln(time) × sex interaction estimated separately for each $N<100:$ $\left|t\right|\ge 1.946,$ $\text{d}.\text{f}.=447,$ $P>0.05,$ all tests].

Over the longer term (at ${10}^4$ generations; Figure 1B), sexual populations evolved significantly higher mean fitness at equilibrium than asexual populations $\left({\widehat{W}}_{\mathrm{sex}}>{\widehat{W}}_{\mathrm{asex}}\right),$ and the magnitude of the difference depended on population size (Table S2). In populations of ≤100 individuals, the difference appears primarily attributable to Muller’s ratchet, as all asexual populations in this size range exhibited a fitness decline between generations 100 and ${10}^4$ [Figure 1A; effect of ln(time) on mean fitness estimated separately for each $N\le 100:$ $\left|t\right|\ge 8.469,$ $\text{d}.\text{f}.=399,$ $P<0.0001,$ all tests]. Only the smallest sexual and asexual populations ($N=10$) evolved to indistinguishable equilibrium mean fitnesses, suggesting that the costs of recombination load in sexual populations and of Muller’s ratchet in asexual populations were of similar magnitude at this population size.

In populations of >100 individuals, the equilibrium mean fitness was determined by the evolving genetic architecture (Figure 1B). Both the deleterious mutation rate, $U_{\mathrm{d}}$ (Table S3; $P<0.0001$), and the recombination load, $L_{\mathrm{R}}$ (in sexuals: $\left|t\right|=7.251,$ $\text{d}.\text{f}.=299,$ $P<0.0001$), decreased significantly with population size. The proportions of all types of mutations—beneficial, neutral, deleterious, and lethal—evolved, but reductions in the proportion of lethal mutations ($p_{\mathrm{l}}$) and parallel increases in the proportion of neutral mutations ($p_{\mathrm{n}}$) made the strongest contributions to the decreases in $U_{\mathrm{d}}$ (Figure S1). The equilibrium mean fitness of large populations was well predicted by the mutation–selection balance equation in Box 1 (Figure 2), with large asexual populations closely matching the prediction (all $N\ge 333$ differing by $<1\%$) and sexual populations falling slightly below the prediction due to recombination load (all $N\ge 100$ differing by $>2.5\%$).

Figure 2.

Equilibrium mean fitness shows the effects of Muller’s ratchet, mutation load, and recombination load. The equilibrium mean fitness of large populations differed only slightly from the expectation at mutation–selection balance (Box 1). Values are means and 95% confidence intervals of the observed fitness in asexual (black) and sexual (red) populations after ${10}^4$ generations of evolution (replotted from Figure 1B). Solid lines show the expectation under the mutation load equation in Box 1 and dashed lines show 95% confidence intervals calculated from the observed $U_{\mathrm{d}}$ in each population. A and B show data from all populations (A) or from only the largest populations (B).

Sexual populations evolved negative epistasis between deleterious mutations (Figure 1), consistent with earlier results using a similar model with fewer genes (n = 10) (Azevedo et al. 2006; MacCarthy and Bergman 2007; Lohaus et al. 2010). However, the negative epistasis cannot account for the long-term advantage of sex in our model. If the negative epistasis we observed had produced a long-term advantage of sex, as expected (Kimura and Maruyama 1966; Kondrashov 1988; Charlesworth 1990), then sexual populations would have evolved a higher fitness at equilibrium than that predicted by the equation in Box 1. We found the opposite pattern (Figure 2).

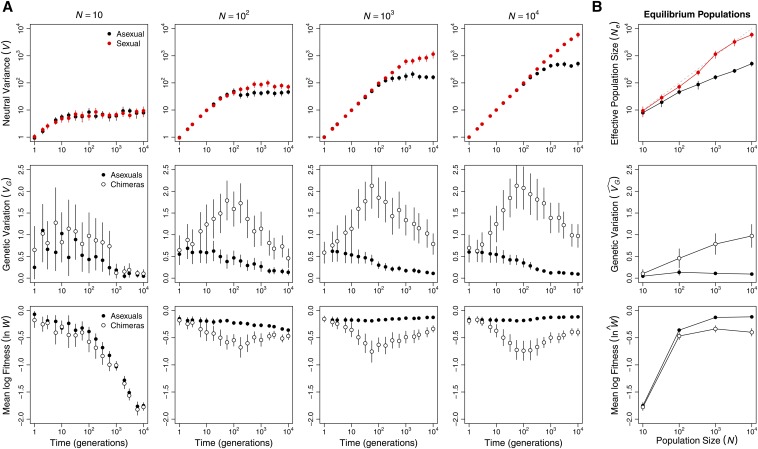
Although the operation of Muller’s ratchet (Kimura et al. 1963) was apparent only in populations of ≤100 individuals ($\widehat{W}\ll e^{-{\overline{U}}_{\mathrm{d}}};$ Figure 2), Hill–Robertson interference was also operating in larger asexual populations. Background selection reduced neutral genetic variation, a metric of $N_{\mathrm{e}},$ significantly more in large asexual populations than in small asexual populations (Figure 3B and Table S4). Thus, Hill–Robertson interference had an indirect effect on the mean fitness of larger populations via its effect on the efficiency with which selection acted to reduce $U_{\mathrm{d}}$ (Figure 1B). In further support of this conclusion, when sexual and asexual populations were subjected to a mutation rate $\left(U=0.1\right)$ that was too low for changes in $U_{\mathrm{d}}$ to have an appreciable effect on mean fitness, but sufficiently high to drive background selection, we observed no difference in mean fitness between sexual and asexual populations even at $N={10}^4$ (Figure S2). In addition, when network connectivity (c) was too low to drive differences among sexual and asexual populations in equilibrium $U_{\mathrm{d}},$ we again observed no difference in mean fitness between sexual and asexual populations (Figure S3).

Figure 3.

Hill–Robertson interference affected asexual populations of all sizes. (A) Hill–Robertson interference depressed variance at a neutral locus $\left(V\right)$ in asexual (black) compared to sexual (red) populations (top row). The LD that accumulated in asexual populations also decreased genetic variance in log fitness, V_G = $\mathrm{var}\left(\ln W\right),$ and increased mean log fitness, $\overline{\ln W}.$ Data in the middle and bottom rows compare these metrics in the real asexual populations (solid circles) and populations of chimeras with the same allele frequencies but no LD (open circles). (B) Means of each metric at generation ${10}^4.$ Effective population size $\left(N_{\mathrm{e}}\right)$ was estimated as $\widehat{V}$ (see Materials and Methods, Population metrics). Values are means and 95% confidence intervals based on 50 replicate populations initiated from different randomly chosen founders.

Sex has a short-term advantage in large populations

The data in Figure 1 document a long-term advantage to sexual reproduction at all population sizes. As a result, equilibrium sexual populations are expected to outcompete equilibrium asexual populations in head-to-head competition. However, the data in Figure 1 also indicate a short-term disadvantage associated with recombination load that is expected to impede both the origin and maintenance of sexual reproduction; a sexual mutant arising in an asexual population has an immediate disadvantage because it starts experiencing recombination load, whereas an asexual mutant arising in a sexual population has an immediate advantage because it stops experiencing recombination load.

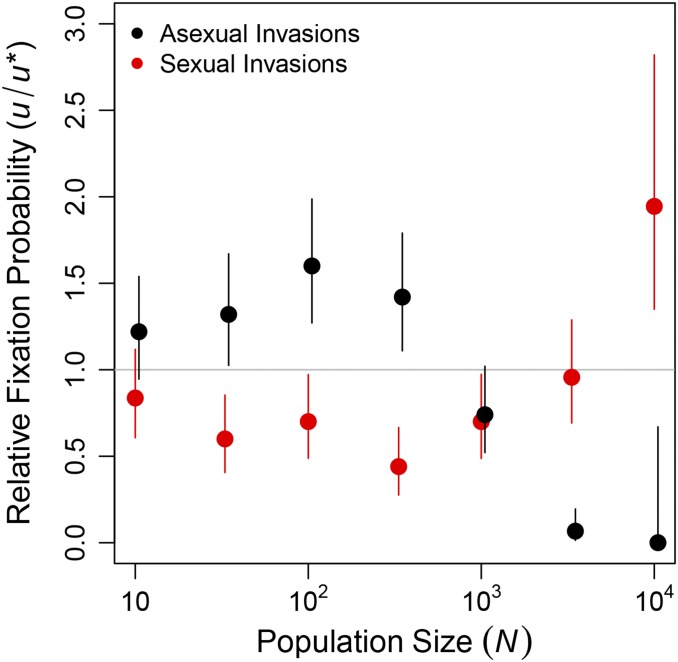
We next investigated whether the short-term advantages of sex were sufficient to enable sexual mutants to invade equilibrium asexual populations, despite this short-term disadvantage. Following the approach of Keightley and Otto (2006), we investigated the origin of sex by introducing a sexual mutant into equilibrium asexual populations. We similarly investigated the maintenance of sex by introducing an asexual mutant into equilibrium sexual populations. We then monitored the fate of the mutations until they were either fixed or lost from the population. We measured the fixation probability of the invading allele $\left(u\right)$ relative to that of a neutral mutation $\left(u\ast =1/N\right)$ in at least $5N$ replicate invasion trials at each population size.

In Figure 4, we show the effect of population size on these relative fixation probabilities, $u/u\ast .$ At small population sizes, asexual modifiers invaded successfully more often than sexual modifiers, and this difference increased with population size until it achieved a maximum near $N=100.$ As population size increased further, the trend reversed so that sexual modifiers invaded successfully more often than asexual modifiers in large populations ($N>{10}^3;$ Figure 4). In the largest populations we tested ($N={10}^4$), sexual mutants invaded asexual populations significantly more often than the neutral expectation ($u/u\ast =1.987,$ $n=1.56\times {10}^5,$ $P=0.0005$ by an exact binomial test). Although we report only the results of our separate sex implementation of sexual reproduction (see Materials and Methods, Reproductive mode) in Figure 4, we obtained qualitatively identical results using recessive sex (Figure S4A). Dominant sex was neither able to invade nor able to resist invasion by asexual modifiers (Figure S4B) for reasons we discuss in File S1.

Figure 4.

Sex has a short-term advantage in large populations. Asexual (black) or sexual (red) mutants were introduced into equilibrium sexual or asexual populations, respectively, at an initial frequency of $1/N.$ Frequencies of the modifier mutations were monitored until the modifiers were either fixed or lost. Values are the proportion of fixations $\left(u\right)$ divided by the neutral expectation ($u\ast =1/N$) and 95% confidence intervals based on $\ge 5N$ replicate invasion trials for each population size N. The data shown here are from the separate sex implementation of the reproductive mode (see Materials and Methods, Reproductive mode). Analogous data for recessive sex and dominant sex are shown in Figure S4.

Examining only the largest populations $\left(N={10}^4\right),$ we explored the sensitivity of the modifier fixation probabilities to the genome-wide mutation rate (U). Like the long-term advantage described above, this short-term advantage of sex disappeared when we reduced the mutation rate to $U=0.1$ (Figure S2). Although this mutation rate was sufficiently high to cause evolution of genetic architecture in the form of a decreased $U_d,$ it did not translate to a fitness advantage because mutations, deleterious or otherwise, are rare. Despite the substantial background selection at this mutation rate (Keightley and Otto 2006), asexual modifiers readily invaded equilibrium sexual populations and sexual modifiers were unable to invade equilibrium asexual populations (Figure S2).

The short-term advantage of sex is caused by Hill–Robertson interference, not epistasis

In our invasion simulations, the immediate population genetic consequence of introducing sex into an asexual population is the breakup of LD. Breaking up LD is expected to have two consequences. First, mean fitness will decline as beneficial combinations of alleles (positive LD) built up by selection are broken up; this selects against sex. Second, additive genetic variance in fitness will rise as negative LD built up by a combination of selection and genetic drift is broken up; this selects for sex. Figure 3 shows that both of these predictions are met for log fitness $\left(\ln W\right)$ for populations of ≥100 individuals.

If these immediate consequences of sex determined the invasion success of sexual modifiers, then we expect the increase in additive genetic variance to outweigh the decrease in mean fitness only in the largest populations ($N={10}^4;$ Figure 4 and Figure S4A). More precisely, higher recombination is expected to evolve if the net advantage of eliminating LD is positive, i.e., if $\mathrm{\Delta }\overline{\ln W}+\mathrm{\Delta }\mathrm{var}\left(\ln W\right)>0,$ where Δ indicates the difference between a statistic in the real population and that in a hypothetical population with the same allele frequencies but in linkage equilibrium (Barton 1995). Figure 3B shows that at generation ${10}^4$ the net advantage of eliminating LD increases with population size and that $\mathrm{\Delta }\overline{\ln W}+\mathrm{\Delta }\mathrm{var}\left(\ln W\right)>0$ for all asexual populations of ≥100 individuals (paired t-test: $t\ge 3.417,$ $\mathrm{d}\mathrm{.f}\mathrm{.}=49,$ $P\le 0.0013$).

These results agree qualitatively, but not quantitatively, with the data in Figure 4 and Figure S4A, where sex invades successfully only in much larger populations. One possible reason for the discrepancy is that the Barton (1995) prediction is for weak modifiers of recombination, whereas our results are for a maximal increase in the rate of recombination (increasing the genetic map length from $\lambda =0$ to 49.5 morgans). To test this possibility, we ran additional invasion simulations where we introduced into equilibrium asexual populations a weaker modifier of recombination that increased map length from $\lambda =0$ to only 0.05 morgans. The weaker modifier mutations exhibited higher fixation probabilities, exceeding the neutral expectation in populations of at least ${10}^3$ individuals (Figure S5).

In our model, the determinant of the short-term advantage of sex, negative LD, appears to have arisen from Hill–Robertson interference rather than from the negative epistasis that evolved in our simulations (Figure 1). Otto and Feldman (1997) predict the evolution of higher recombination rate only if the epistatic effects of mutations satisfy the condition

$$3\overline{\epsilon \ast }+{\left(\overline{\epsilon \ast }\right)}^2+\mathrm{var}\left(\overline{\epsilon \ast }\right)<0,$$

where $\epsilon \ast$ is a standardized epistasis coefficient (see Materials and Methods, Genetic architecture). None of the 50 populations summarized in Figure 1 (sexual or asexual) satisfied that condition at generation ${10}^4.$ Thus, epistasis cannot explain the accumulation of negative LD in large asexual populations. Instead, it must have been caused by Hill–Robertson interference.

Changes in the genetic architecture influence both the origin and maintenance of sex

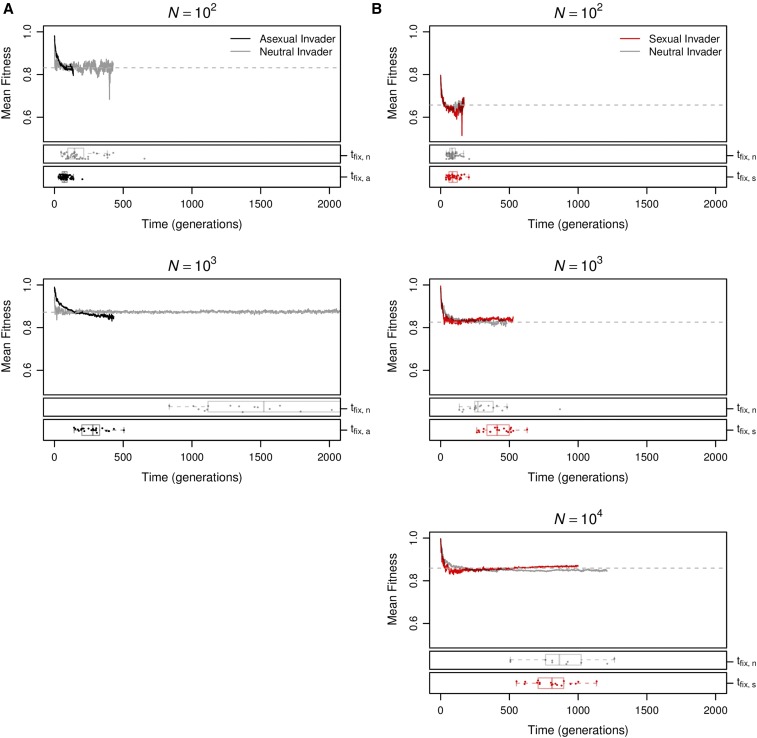
Changes in the genetic architecture played a decisive role in generating a long-term advantage of sex (Figure 1). Here we investigate the role of changes in the genetic architecture in the short-term advantage of sex. To understand why the origin and maintenance of sex were favored only when population size was large, we investigated the mean fitness dynamics and fixation times of the sexual and asexual genotypes that successfully invaded (Figure 5). The immediate and short-term fitness consequences of mutations that alter reproductive mode were predictable from the dynamics of genetic architecture evolution. Asexual modifiers arising in sexual populations experienced an immediate fitness benefit due to the disappearance of recombination load and the advantageous genetic architecture (low $U_{\mathrm{d}}$) they inherit from their sexual predecessors. The latter advantage decayed over time as asexual invaders evolved toward the asexual equilibrium. Most successful asexual invasions occurred quickly (Figure 5A, black points and boxplots), before the mean fitness of the invaders (Figure 5A, black lines) decayed below that of the resident sexual population (Figure 5A, dashed gray lines).

Figure 5.

Changes in the genetic architecture influence both the origin and maintenance of sex. We monitored the fixation and loss of asexual mutants introduced into equilibrium sexual populations (black lines, A), of sexual mutants introduced into equilibrium asexual populations (red lines, B), and of neutral mutants introduced into both sexual and asexual populations (solid gray lines, A and B, respectively). Lines show the evolution of mean fitness among invading mutants, averaged over at least 10 successful invasions. The equilibrium mean fitness of the populations being invaded is represented by a gray dashed line across each plot. Points and corresponding boxplots shown at the bottom of each plot indicate the time of fixation for individual neutral $\left(t_{\mathrm{fix},\mathrm{n}}\right),$ sexual $\left(t_{\mathrm{fix},\mathrm{s}}\right),$ or asexual $\left(t_{\mathrm{fix},\mathrm{a}}\right)$ mutations.

In contrast, sexual modifiers that successfully invaded asexual populations experienced a short-term fitness decline during the time when recombination load was accumulating, but evolved back toward the sexual equilibrium after sufficient time had passed to evolve an advantageous genetic architecture (compare fitness trajectories in Figure 5B to $U_{\mathrm{d}}$ and $L_{\mathrm{R}}$ trajectories in Figure 1A). Successful sexual modifiers arose by chance in high-fitness genomes, retained a higher fitness than the asexual mean for ∼100 generations (Figure 5B, red lines), and hitchhiked to a relatively high frequency as a result (Figure S6). In populations of size $N\le 100,$ the only sexual modifiers that fix appear to do so by hitchhiking quickly to fixation. In larger populations ($N\ge {10}^3$), the initial hitchhiking of sexual modifier mutations was critical to their invasion success because it enabled their persistence over the long timescale needed for the sexual invaders to evolve a higher mean fitness (Figure 5B, red lines) than that of the resident asexual population (Figure 5B, dashed gray lines). Similarly, population size (N) critically affected invasion probabilities because increasing N increased the transit time $\left(t_{\text{fix}}\right)$ of new mutations to fixation (Figure 5, red and black points and boxplots). Because the evolution of asexual disadvantages and sexual advantages is time dependent, sexual resident populations and sexual invaders can be successful only if they persist long enough for these differences to evolve. Thus, our data reveal that the evolutionary success of sex at only the largest population sizes resulted from an interaction between the increase in $t_{\text{fix}}$ and the differences in fitness dynamics between sexual and asexual invaders (Figure 5).

Selection favors moderate recombination rates

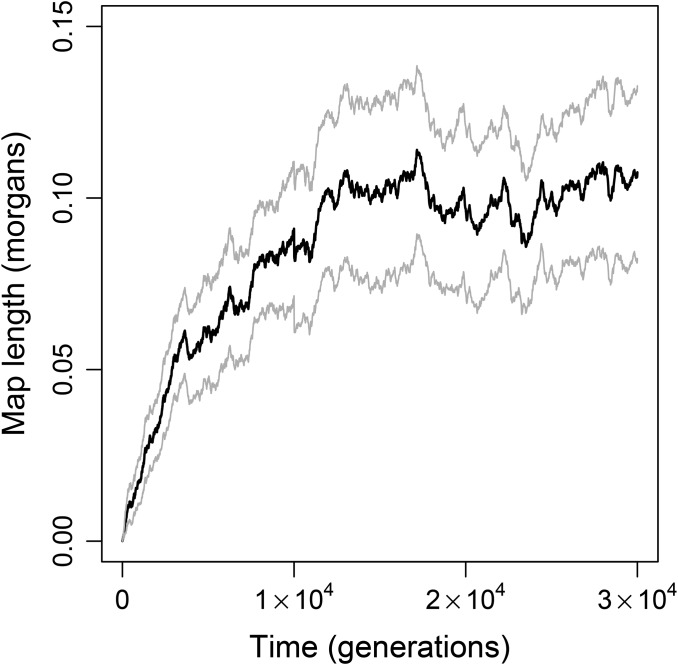
Thus far, we have compared asexual reproduction to sexual reproduction with free recombination. However, we found that a small increase in recombination rate is favored even when sex is not ($N={10}^3,$ compare Figure 4 and Figure S4A with Figure S5), suggesting that “a little sex may go a long way” (Hurst and Peck 1996) in our model. To investigate this phenomenon further, we allowed recombination rate to evolve in populations of $N={10}^3$ individuals. Like our investigations of the evolution of sexual reproduction, we began these simulations with populations that had evolved to a mutation–selection–drift equilibrium in the absence of recombination. Unlike the earlier simulations, mutations at the modifier locus were recurrent and had only small effects on the length of the genetic map $\lambda \left(\pm 0.05\hspace{0.17em}\mathrm{morgans}\right)$ and, therefore, on the recombination rate. Mean map length among 50 replicate simulations increased to $\overline{\lambda }\approx 0.1\hspace{0.17em}\mathrm{morgans}$ within $1.5\times {10}^4$ generations (Figure 6). Thus, selection in the gene network model readily promoted the evolution of moderate, but not high, recombination rates in populations of $N={10}^3$ individuals.

Figure 6.

Evolution of the recombination rate under recurrent mutation at the recombination modifier locus. Solid and shaded lines show the change in mean and $95\text{\%}$ confidence interval, respectively, of the genome map length (i.e., mean crossover probability) over time. Data are from 50 replicates initiated with the equilibrium asexual populations of size $N={10}^3$ shown in Figure 1.

Discussion

We simulated evolution in a computational model of gene networks to determine how Hill–Robertson interference interacts with an evolving genetic architecture to affect the evolutionary origin and maintenance of sex. We found that the benefit of sex increased with population size, in agreement with earlier studies (Iles et al. 2003; Keightley and Otto 2006; Gordo and Campos 2008; Hartfield et al. 2010). Those studies identified Hill–Robertson interference as the principal cause of this pattern. We found that Hill–Robertson interference also played a role in our model in creating both a long-term and a short-term advantage of sex. But we also showed that the long- and short-term advantages of sex were determined by differences between sexual and asexual populations in the evolutionary dynamics of two properties of the genetic architecture, $U_{\mathrm{d}}$ and $L_{\mathrm{R}}.$ We next sought to quantify the contribution of Hill–Robertson interference to these dynamics.

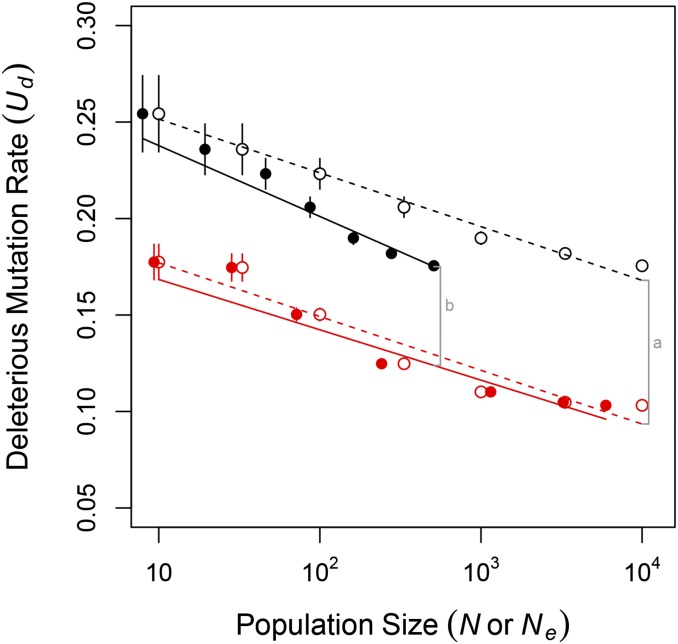
We documented two differences between sexual and asexual populations that likely affected the evolution of $U_{\mathrm{d}}.$ First, sexual populations uniquely experienced recombination load, $L_{\mathrm{R}}.$ We know from previous work that selection to minimize $L_{\mathrm{R}},$ alone, results in increasing robustness to both recombination and mutation, lowering $U_{\mathrm{d}}$ (Azevedo et al. 2006; Gardner and Kalinka 2006; Misevic et al. 2006; Martin and Wagner 2009; Lohaus et al. 2010). Second, asexual populations uniquely experienced Hill–Robertson interference that reduced $N_{\mathrm{e}}$ (Figure 3B). As in Keightley and Otto (2006), the reduction in $N_{\mathrm{e}}$ increased with population size, N. At $N=100,$ $N_{\mathrm{e}}$ was reduced by 36% (from 72 to 46 individuals); at $N={10}^4,$ $N_{\mathrm{e}}$ was reduced by 91% (from 5957 to 510 individuals). The reduced $N_{\mathrm{e}}$ in asexuals is expected to reduce the efficiency with which selection lowers $U_{\mathrm{d}}.$ In sum, sexuals may have evolved lower $U_{\mathrm{d}}$ than asexuals both because sexuals experienced stronger selection to do so and because Hill–Robertson interference reduced the efficiency of selection on $U_{\mathrm{d}}$ in asexuals.

We quantified how these differences in the strength and efficiency of selection contributed to the equilibrium $U_{\mathrm{d}}$ in sexual and asexual populations in Figure 7. In Figure 7, we compare the equilibrium $U_{\mathrm{d}}$ between sexual and asexual populations of the same census size, N, and of the same effective size, $N_{\mathrm{e}}.$ Differences in $U_{\mathrm{d}}$ between populations of the same census size resulted from differences in both the strength and efficiency of selection, whereas differences in $U_{\mathrm{d}}$ between populations of the same effective size resulted from differences only in the strength of selection. In Figure 7 we see that the effect on $U_{\mathrm{d}}$ of differences in the strength of selection (line b) decreased as population size increased, whereas the combined effect of differences in the strength and efficiency of selection (line a) was constant across the population sizes we examined. Thus, although differences in the strength of selection played a larger role than differences in the efficiency of selection at all the population sizes we examined, the relative contribution of selection efficiency grew with population size. In populations $>{10}^4$ individuals, the reduced selection efficiency caused by Hill–Robertson interference may have eventually come to play the dominant role in determining $U_{\mathrm{d}}$ and, consequently, mean fitness in asexual populations.

Figure 7.

Hill–Robertson interference explains part of the difference in equilibrium $U_{\mathrm{d}}$ between sexual (red) and asexual (black) populations. Shown are equilibrium values of the genome-wide deleterious mutation rate $U_{\mathrm{d}}$ vs. census population size N (open circles, replotted from Figure 1) and vs. effective population size $N_{\mathrm{e}}$ (solid circles). Lines are best fit linear models obtained separately using N (dashed lines) or $N_{\mathrm{e}}$ (solid lines) as a dependent variable together with reproductive mode. The total difference in $U_{\mathrm{d}}$ exhibited by sexual and asexual populations of census size $N={10}^4$ (gray line a) is attributable to differences in both the strength and the efficiency of selection acting on genetic architecture. The difference in $U_{\mathrm{d}}$ exhibited by sexual and asexual populations of effective size $N_{\mathrm{e}}=510$ (gray line b) is the proportion of the total difference that remained after controlling for differences in the efficiency of selection that arise through Hill–Robertson interference.

Our finding that Hill–Robertson interference contributed to the advantages of sex in part through its indirect effect on the evolution of genetic architecture differs from the findings of previous models in which the genetic architecture was static and Hill–Robertson interference directly determined the advantages of sex (Iles et al. 2003; Keightley and Otto 2006; Gordo and Campos 2008; Hartfield et al. 2010). The evolvable genetic architecture in the gene network model likely affected the contribution of Hill–Robertson interference in a number of ways. We focused on the evolving $U_{\mathrm{d}}$ because it was the primary determinant of equilibrium mean fitness in large populations, but we think that the evolving compensatory mutation rate (Figure S1) also played an important role. Compensatory mutations increased in frequency as fitness declined, ensuring that our populations achieved a fitness equilibrium. The fitness equilibrium was an important aspect of our model. The absence of compensatory mutations in the previous models (Muller 1964; Haigh 1978; Keightley and Otto 2006; Gordo and Campos 2008) ensured a perpetual decline in population mean fitness via Muller’s ratchet, regardless of population size, that would have been accelerated by Hill–Robertson interference in asexual populations. In our gene network model, Muller’s ratchet was eventually halted by an increasing frequency of compensatory mutations even at the smallest population sizes (Figure 1). As a result, direct effects of Hill–Robertson interference on advantages of sex in the gene network model were limited to populations that were small enough for Muller’s ratchet to operate over a wide fitness range.

One major difference between our results and those of earlier studies of Hill–Robertson interference is that we observed only moderate advantages of sex. The long-term advantage of sex observed here (${\widehat{W}}_{\mathrm{sex}}/{\widehat{W}}_{\mathrm{asex}}=1.04$ for $N={10}^4$) was substantial but may be considered weak compared to the twofold cost experienced by many sexual species in nature. The short-term advantage was even weaker: it disappeared when we imposed as little as a 1% cost of sex (Figure S7). We note, however, that modifiers of sex generated smaller short-term advantages than modifiers of recombination (compare the $N={10}^3$ populations in Figure 4, Figure S5, and Figure 6), as has been observed in other models (Keightley and Otto 2006).

We identified two additional factors that contribute to the advantages of sex in our model. First, a higher mutation rate U increases the advantage of sex. This has been found in other models (Keightley and Otto 2006; Gordo and Campos 2008). Note that the deleterious mutation rate evolved in our simulations $\left(U_{\mathrm{d}}\approx 0.2\right)$ is high, but not unrealistically so. For example, Drosophila melanogaster shows $U_{\mathrm{d}}\approx 1$ (Haag-Liautard et al. 2007). Second, a higher gene network connectivity increases the advantage of sex. We improved biological realism (Leclerc 2008) by using much sparser networks $\left(c=0.05\right)$ than earlier studies of this model (typically, $c=0.75$) (Siegal and Bergman 2002; Azevedo et al. 2006; MacCarthy and Bergman 2007; Lohaus et al. 2010). A connected transcriptional regulatory network of 75 transcription factors in yeast estimated $c=0.024$ (MacIsaac et al. 2006). Networks with similar connectivity in our model were not able to generate an advantage of sex ($c=0.02,$ Figure S3). However, the yeast estimate increases as new data become available (compare Harbison et al. 2004; MacIsaac et al. 2006). In addition, we do not know the extent to which this yeast network is representative of other networks in nature. A strict comparison of connectivities between our networks and real biological networks is likely misleading because we considered only random gene networks, a pattern of connectivity that is probably unrealistic (Milo et al. 2002; Shen-Orr et al. 2002).

The magnitudes of both the long- and short-term advantages of sex are likely to be affected additionally by many factors we have not considered here, such as deviations from random mating (Shields 1982; Jaffe 2000; Agrawal 2001; Siller 2001; Blachford and Agrawal 2006), population structure (Peck et al. 1999; Agrawal and Chasnov 2001; Salathé et al. 2006; Roze 2009; Hartfield et al. 2012), ploidy (Kirkpatrick and Jenkins 1989; Kondrashov and Crow 1991; Agrawal and Chasnov 2001; Otto 2003; Haag and Roze 2007; Roze 2009), number of loci (Iles et al. 2003), and environmental change (Charlesworth 1993; Barton 1995; Otto and Nuismer 2004; Carja et al. 2014; Nowak et al. 2014), leaving many questions yet to be answered.