Background Selection in Partially Selfing Populations

Abstract

Self-fertilizing species often present lower levels of neutral polymorphism than their outcrossing relatives. Indeed, selfing automatically increases the rate of coalescence per generation, but also enhances the effects of background selection and genetic hitchhiking by reducing the efficiency of recombination. Approximations for the effect of background selection in partially selfing populations have been derived previously, assuming tight linkage between deleterious alleles and neutral loci. However, loosely linked deleterious mutations may have important effects on neutral diversity in highly selfing populations. In this article, I use a general method based on multilocus population genetics theory to express the effect of a deleterious allele on diversity at a linked neutral locus in terms of moments of genetic associations between loci. Expressions for these genetic moments at equilibrium are then computed for arbitrary rates of selfing and recombination. An extrapolation of the results to the case where deleterious alleles segregate at multiple loci is checked using individual-based simulations. At high selfing rates, the tight linkage approximation underestimates the effect of background selection in genomes with moderate to high map length; however, another simple approximation can be obtained for this situation and provides accurate predictions as long as the deleterious mutation rate is not too high.

UNDERSTANDING the evolutionary consequences of transitions between reproductive systems has been the focus of an important number of theoretical and empirical studies. In particular, the shift from biparental sexual reproduction to self-fertilization has occurred frequently in plants and animals (Goodwillie et al. 2005; Jarne and Auld 2006), but the phylogenetic distribution of selfing lineages suggests that these are often relatively short-lived and may thus correspond to an “evolutionary dead end” or “blind alley” (e.g., Stebbins 1957; Williams 1992; Takebayashi and Morrell 2001; Goldberg et al. 2010; Igic and Busch 2013). A possible reason for the lack of macroevolutionary success of selfing species may be their reduced capacity to produce novel genotypes (in particular, genotypes adapted to new environmental conditions), due to a reduced efficiency of recombination. Furthermore, self-fertilization lowers the effective size of populations and should thereby decrease the efficiency of natural selection against deleterious alleles, which may lead to mutation accumulation and population extinction (Lynch et al. 1995; Schultz and Lynch 1997). Analyses based on molecular data show little evidence for increased ratios of nonsynonymous to synonymous substitutions ($d_{\mathrm{N}}/d_{\mathrm{S}}$) in selfing lineages that would indicate a reduced efficiency of purifying selection (Glémin and Muyle 2014; Hartfield 2015 and references therein): this may be due to the recent origin of those lineages or to the low rates of outcrossing maintained by most predominantly selfing species (Wright et al. 2013). However, several recent studies showed elevated ratios of nonsynonymous to synonymous polymorphism (${\pi }_{\mathrm{N}}/{\pi }_{\mathrm{S}}$) in various selfing species (compared with their outcrossing relatives), suggesting that deleterious alleles may reach higher frequencies in selfers (e.g., Brandvain et al. 2013; Burgarella et al. 2015; and other references listed in table 1 of Hartfield 2015).

The lower effective size of selfing populations has been demonstrated empirically using neutral diversity data from a variety of species (e.g., Charlesworth 2003; Glémin et al. 2006) and is thought to result from two types of effects. The first type is an automatic increase in the rate of coalescence per generation, since the ancestral lineages of the two homologous copies of a gene in an individual may coalesce in a single generation (with probability $1/2$) if this individual has been produced by selfing. Due to this effect, the effective population size is given by $N_{\mathrm{e}}=N/\left(1+F\right)$ (Pollak 1987; Nordborg 2000), where N is the census size and where the inbreeding coefficient F equals $\alpha /\left(2-\alpha \right)$ in a population in which a proportion α of individuals are produced by selfing. Therefore, $N_{\mathrm{e}}$ is expected to decline linearly from N to $N/2$ as α increases from 0 to 1. However, $N_{\mathrm{e}}$ may be further decreased (second effect) by selective sweeps or by selection against deleterious alleles (background selection) (Charlesworth et al. 1993; Charlesworth 2012), whose effects are amplified by the lower effective recombination rates of selfing populations.

Several models have computed the effect of background selection on neutral diversity in randomly mating populations, using different approaches (Hudson and Kaplan 1995; Nordborg et al. 1996; Santiago and Caballero 1998; Charlesworth 2012). These showed in particular that a deleterious allele at mutation–selection balance reduces the expected diversity at a linked neutral locus by a factor $\approx 1-\left(ush\right)/{\left(r+sh\right)}^2,$ where u is the mutation rate toward the deleterious allele, $sh$ the heterozygous fitness effect of this allele (assumed different from zero), and r the recombination rate between the two loci. The case of partially selfing populations has been addressed by Nordborg (1997), using a structured coalescent model and a separation of timescales argument. Indeed, assuming that recombination and coalescence of lineages present in different individuals occur at a much lower rate than the coalescence of lineages present in the same individual due to selfing, the population can be described in terms of haplotypes instead of diploid genotypes, which considerably simplifies the analysis. Under this assumption, the effect of a deleterious allele on linked neutral diversity is given by a similar expression as in the panmictic case, replacing $sh$ by $s\left[h\left(1-F\right)+F\right]$ (measuring the strength of selection against the deleterious allele in a partially selfing population) and r by the effective recombination rate $r\left(1-F\right)$ (see also Nordborg 2000). Extrapolating this result to the case of deleterious alleles segregating at many loci, Glémin (2007) and Glémin and Ronfort (2012) showed that the effective size of highly selfing populations may be strongly reduced by background selection effects.

Strictly, Nordborg’s (1997) result holds for tightly linked loci, since the separation of timescales argument supposes a low recombination rate. While the effective population size at a given locus should be little affected by loosely linked loci as long as the selfing rate remains moderate, this may be less so when the selfing rate is high, so that linkage disequilibria may extend over relatively large genetic distances (e.g., Nordborg et al. 2002). Using multilocus individual-based simulations of partially selfing populations, Kamran-Disfani and Agrawal (2014) observed discrepancies between the estimated $N_{\mathrm{e}}$ and predictions obtained by extrapolating Nordborg’s (1997) result over a whole genetic map. These may be caused by the fact that the effects of loosely linked loci are not sufficiently well predicted by the separation of timescales approximation and become important at high selfing rates.

In this article, I construct a model of background selection in partially selfing populations by extending the multilocus population genetics framework previously developed by Barton and Turelli (1991) and Kirkpatrick et al. (2002). As we will see, a strength of this approach is that it allows one to decompose evolutionary processes (here the background selection effect) into different terms involving linkage disequilibria and other forms of genetic associations, for which intuitive interpretation can be given. Expressions valid for any value of the recombination rate are derived and shown to converge to Nordborg’s (1997) result when linkage is tight. However, this tight linkage approximation may significantly underestimate the strength of background selection when the selfing rate is high (but <1); we will see that another approximation yielding better predictions at high selfing rates can be obtained from the general model. A good match between the analytical predictions and multilocus simulation results is observed as long as the genomic deleterious mutation rate U is not too high (0.1 per haploid genome), while discrepancies appear at higher values of U: those are likely due to genetic associations between deleterious alleles at different loci, which are neglected in the analysis.

Model

General method

As in previous models of background selection (e.g., Hudson and Kaplan 1995; Nordborg et al. 1996), I first consider the effect of a single deleterious allele maintained at mutation–selection balance at a given locus on the dynamics of genetic diversity at a linked neutral locus. This effect can be quantified by computing the expected change in neutral diversity over one generation, which is affected by various moments of genetic associations between the two loci (e.g., the variance in linkage disequilibrium and other moments of associations between genes present either on the same haplotype or on different haplotypes of a diploid individual). Assuming recurrent mutation at the neutral locus, the effective population size $N_{\mathrm{e}}$ at the neutral locus can be deduced from the expected neutral diversity at equilibrium (Nordborg et al. 1996). Alternatively, we may ignore mutation at the neutral locus and calculate $N_{\mathrm{e}}$ by equating the expected rate of loss in diversity per generation to $-1/\left(2N_{\mathrm{e}}\right),$ since diversity is eroded at a rate $-1/\left(2N\right)$ per generation in a Wright–Fisher population. This is the approach that is used here. Strictly, it relies on a quasi-equilibrium approximation, since moments of genetic associations (for example, the variance in linkage disequilibrium) are expressed in terms of diversity at the neutral locus and of the frequency of the deleterious allele, implying that these moments of genetic associations equilibrate fast relative to changes in allele frequencies. However, this approximation is justified when population size is sufficiently large (so that changes in allele frequencies due to drift remain small) and yields the same expression for $N_{\mathrm{e}}$ as what would be obtained by calculating the equilibrium neutral diversity under recurrent mutation.

I consider the following life cycle: N individuals are present at the start of each generation and produce a very large (effectively infinite) number of juveniles in proportion to their fitness. A proportion α of offspring is produced by selfing, while the remaining $1-\alpha$ is produced by random fusion of gametes. Finally, N individuals are sampled randomly among all juveniles produced, to form the next generation (drift). Fitness depends on genotype at the selected locus, where two alleles (denoted 0 and 1) are segregating: allele 1 is deleterious, reducing fitness by a factor $1-sh$ in the heterozygous state and $1-s$ in the homozygous state. The deleterious mutation rate (from allele 0 to allele 1) is denoted u. As in previous treatments (Hudson and Kaplan 1995; Nordborg et al. 1996) I assume that $sN\mathrm{\gg }1$ and $u\ll s,$ so that the frequency of the deleterious allele remains small and can be approximated by the deterministic mutation–selection balance frequency (strictly, this also assumes $N{p}_{\mathrm{del}}\gg 1,$ where $p_{\mathrm{del}}$ is the frequency of the deleterious allele). Finally, r measures the recombination rate between the two loci.

In the following I use a general method to compute the effects of selection, reproduction, and drift on moments of genetic associations. This method is based on a previous formalism for the analysis of multilocus models (Barton and Turelli 1991; Kirkpatrick et al. 2002), extended to include genetic drift. It was used previously to study selection for sex in finite diploid populations undergoing both sexual and asexual reproduction (Roze and Michod 2010) and is described in Appendix A for the case of a partially selfing population. To simplify the notation, the examples shown in Appendix A concern the case of a biallelic neutral locus; however, the method extends to multiple alleles, yielding the same expression for the decay of neutral diversity per generation. The analysis of the two-locus model then proceeds in three steps. First, I express the expected decay of genetic diversity per generation in terms of various genetic moments involving both loci. Then, recurrence equations describing the dynamics of these two-locus moments are derived (to the first order in $1/N$ and assuming that the deleterious allele stays at low frequency). Finally, these equations are solved to obtain expressions for two-locus moments at (quasi-)equilibrium, in terms of diversity at the neutral locus and of the different parameters of the model. Injecting these solutions into the equation describing the decay of neutral diversity yields an expression for the effect of the deleterious allele on $N_{\mathrm{e}}$ at the neutral locus.

The results of this two-locus model are then extrapolated to a situation where deleterious alleles segregate at a large number of loci, located at various genetic distances from the neutral locus. For this, I assume that the effects of the different selected loci on diversity at the neutral locus are multiplicative, thereby neglecting genetic associations between selected loci. In the absence of epistasis between deleterious alleles, this approximation is expected to yield correct results under random mating in the regime considered here (where selection against deleterious alleles is stronger than drift, e.g., Hudson and Kaplan 1995) but may be less accurate under partial selfing, as inbreeding generates different forms of associations between loci (correlations in homozygosity in particular, e.g., Roze 2015). Nonetheless, we will see that this assumption of multiplicative effects often generates accurate predictions, as long as the genomic deleterious mutation rate is not too high.

Defining genetic associations

The parameters and variables of the model are summarized in Table 1. Throughout the following, the neutral locus is denoted A, while the selected locus is denoted B. Two alleles denoted 0 and 1 segregate at each locus (we will see below how the notation can be extended to deal with multiple neutral alleles), allele 1 at locus B being the deleterious allele. Indicator variables $X_i^{\mathrm{M}}$ and $X_i^{\mathrm{P}}$ describe the genotype of an individual at locus i: these variables equal 1 if allele 1 is present on the maternally or paternally (respectively) inherited chromosome of this individual at locus i and 0 otherwise. The frequency of allele 1 at locus i (denoted $p_i$) is thus

$$p_i=\mathrm{E}\left[\frac{X_i^{\mathrm{M}}+X_i^{\mathrm{P}}}{2}\right],$$ (1)

where $\mathrm{E}$ stands for the average over all individuals in the population. Neglecting drift, the frequency of the deleterious allele at mutation–selection balance (denoted ${\tilde{p}}_B$) is given by

$${\tilde{p}}_B\approx \frac{u}{s\left[h\left(1-F\right)+F\right]}$$ (2)

with $F=\alpha /\left(2-\alpha \right)$ (e.g., Glémin 2003).

Table 1. Parameters and variables.

Symbol	Definition
N	Population size
α	Selfing rate
s	Strength of selection against the deleterious allele
h	Dominance coefficient of the deleterious allele
u	Mutation rate toward the deleterious allele
r	Recombination rate between the neutral locus and the selected locus
U	Genomic deleterious mutation rate (per haploid genome)
R	Genome map length
$p_A$	Frequency of allele 1 at locus A (neutral locus)
$p_B$	Frequency of allele 1 (deleterious allele) at locus B
${\tilde{p}}_B$	Deleterious allele frequency at mutation–selection balance
$D_{\mathbb{S},\mathbb{T}}$	Genetic association between the sets $\mathbb{S}$ and $\mathbb{T}$ of loci present on different haplotypes of an individual (see Equation 4)
$D_{AA}$	Genetic diversity at the neutral locus
F	Inbreeding coefficient (probability of identity-by-descent between the maternal and paternal copies of a gene, due to selfing)
${\phi }_{AB}$	Joint probability of identity-by-descent at loci A and B
$G_{AB}={\phi }_{AB}-F^2$	Identity disequilibrium between loci A and B
$\mathrm{E}\left[X\right]$	Average of the quantity X over all individuals
$\langle \mathrm{ℳ}\rangle$	Expected value of the moment $\mathrm{ℳ}$ over the stochastic process

For each locus i, centered variables ${\mathit{\zeta }}_i^{\mathrm{M}}$ and ${\mathit{\zeta }}_i^{\mathrm{P}}$ are defined as

$${\zeta }_i^{\mathrm{M}}=X_i^{\mathrm{M}}-p_i,{\zeta }_i^{\mathrm{P}}=X_i^{\mathrm{P}}-p_i.$$ (3)

Following Kirkpatrick et al. (2002), the association between the sets $\mathbb{S}$ and $\mathbb{T}$ of loci present on the two haplotypes of the same individual is given by

$$D_{\mathbb{S},\mathbb{T}}=\mathrm{E}\left[{\zeta }_{\mathbb{S},\mathbb{T}}\right],$$ (4)

where

$$\begin{array}{c}{\zeta }_{\mathbb{S},\mathbb{T}}=\frac{{\zeta }_{\mathbb{S}}^{\mathrm{M}}{\zeta }_{\mathbb{T}}^{\mathrm{P}}+{\zeta }_{\mathbb{S}}^{\mathrm{P}}{\zeta }_{\mathbb{T}}^{\mathrm{M}}}{2},\\ {\zeta }_{\mathbb{S}}^{\mathrm{M}}={\displaystyle \prod _{i\in \mathbb{S}}{\zeta }_i^{\mathrm{M}}},{\zeta }_{\mathbb{T}}^{\mathrm{P}}={\displaystyle \prod _{i\in \mathbb{T}}{\zeta }_i^{\mathrm{P}}}\end{array}$$ (5)

(note that $D_{\mathbb{S},\mathbb{T}}=D_{\mathbb{T},\mathbb{S}}$), and where sets $\mathbb{S}$ and $\mathbb{T}$ may be the empty set $\mathrm{Ø},$ A, B, or $AB.$ Associations between genes present on the same haplotype of an individual ($D_{\mathbb{S},\mathrm{Ø}}$) are simply denoted $D_{\mathbb{S}}.$ For example, $D_{A,A}=\mathrm{E}\left[\left(X_A^{\mathrm{M}}-p_A\right)\left(X_A^{\mathrm{P}}-p_A\right)\right]$ is a measure of the departure from Hardy–Weinberg equilibrium at locus A, while $D_{AB}=\left(1/2\right)\mathrm{E}\left[\left(X_A^{\mathrm{M}}-p_A\right)\left(X_B^{\mathrm{M}}-p_B\right)+\left(X_A^{\mathrm{P}}-p_A\right)\left(X_B^{\mathrm{P}}-p_B\right)\right]$ represents the linkage disequilibrium between loci A and B (genetic association between alleles present on the same haplotype, maternal or paternal). Similarly, $D_{A,B}=\left(1/2\right)\mathrm{E}\left[\left(X_A^{\mathrm{M}}-p_A\right)\left(X_B^{\mathrm{P}}-p_B\right)+\left(X_A^{\mathrm{P}}-p_A\right)\left(X_B^{\mathrm{M}}-p_B\right)\right]$ measures the association between alleles at loci A and B present on different haplotypes of the same individual.

Because population size is finite, allele frequencies and genetic associations are random variables. Throughout this article, I use the notation $\langle \mathrm{ℳ}\rangle$ for the expected value of the genetic moment $\mathrm{ℳ}$ (a product of allele frequencies, genetic associations, or both) at a given generation: for example, $\langle D_{AB}{}^2\rangle$ is the expected squared linkage disequilibrium between the two loci. In the following, the moment $\langle D_{AA}\rangle =\langle \left(1/2\right)\mathrm{E}\left[{\left(X_A^{\mathrm{M}}-p_A\right)}^2+{\left(X_A^{\mathrm{P}}-p_A\right)}^2\right]\rangle$ will be of particular importance: indeed, using the fact that ${\left(X_A^{\mathrm{M}}\right)}^2=X_A^{\mathrm{M}}$ and ${\left(X_A^{\mathrm{P}}\right)}^2=X_A^{\mathrm{P}}$ (since these variables equal 0 or 1), we obtain that $\langle D_{AA}\rangle =\langle p_A{q}_A\rangle$ (where $q_i=1-p_i$), thus representing the expected genetic diversity at locus A. Therefore, the effective population size at the neutral locus can be quantified by computing the rate of decay of $\langle D_{AA}\rangle$ per generation.

As mentioned above, the model can be extended to an arbitrary number n of alleles segregating at the neutral locus. In this case, we can define indicator variables $X_{A,k}^{\mathrm{M}}$ and $X_{A,k}^{\mathrm{P}}$ that equal 1 if the maternally (respectively, paternally) inherited chromosome of a given individual carries allele k at locus A (and 0 otherwise), with $k=1,\dots ,n.$ Vectors $X_A^{\mathrm{M}}$ and $X_A^{\mathrm{P}}$ are defined as $X_A^{\mathrm{M}}=\left(X_{A,1}^{\mathrm{M}},X_{A,2}^{\mathrm{M}},\dots ,X_{A,n}^{\mathrm{M}}\right)$ and $X_A^{\mathrm{P}}=\left(X_{A,1}^{\mathrm{P}},X_{A,2}^{\mathrm{P}},\dots ,X_{A,n}^{\mathrm{P}}\right);$ in each of these vectors (and for a given individual) a single element equals 1 while all other elements equal zero. Finally, the vector $p_A=\mathrm{E}\left[\left(X_A^{\mathrm{M}}+X_A^{\mathrm{P}}\right)/2\right]$ holds the frequencies of the different alleles at locus A in the population. Defining ${\zeta }_A^{\mathrm{M}}=X_A^{\mathrm{M}}-p_A$ and ${\zeta }_A^{\mathrm{P}}=X_A^{\mathrm{P}}-p_A,$ genetic associations may be defined in the same way as above, associations with two “A” subscripts involving a dot product between the corresponding ${\zeta }_A$ vectors. In particular,

$$D_{AA}=\frac{1}{2}\mathrm{E}\left[{\zeta }_A^{\mathrm{M}}.{\zeta }_A^{\mathrm{M}}+{\zeta }_A^{\mathrm{P}}.{\zeta }_A^{\mathrm{P}}\right]=1-{\displaystyle \sum _{k=1}^n{p}_{A,k}^2},$$ (6)

where $p_{A,k}$ is the frequency of allele k at locus A in the population. Similarly, $D_{A,A}=\mathrm{E}\left[{\zeta }_A^{\mathrm{M}}.{\zeta }_A^{\mathrm{P}}\right],$ while $D_{AB,A}=\left(1/2\right)\mathrm{E}\left[\left({\zeta }_A^{\mathrm{M}}.{\zeta }_A^{\mathrm{P}}\right)\left({\mathit{\zeta }}_B^{\mathrm{M}}+{\zeta }_B^{\mathrm{P}}\right)\right]$. Equation 6 shows that, as in the biallelic case, $\langle D_{AA}\rangle$ represents the expected genetic diversity at the neutral locus. As mentioned earlier, the method for computing multilocus moments is explained in Appendix A for the case of a biallelic neutral locus, but the results shown below are valid for any number of alleles segregating at this locus.

Multilocus simulations

Analytical predictions are tested using individual-based, multilocus simulations. The simulation program (written in C++ and available from Dryad) is very similar to the program used in Roze (2015), representing a population of N diploid individuals whose genome consists of a linear chromosome with total map length R. Relatively large values of R (usually 10 M) are used in most simulations to mimic a whole genome with multiple chromosomes. Each generation, deleterious alleles occur at rate U per haploid genome; all deleterious alleles have the same selection and dominance coefficient and have multiplicative effects on fitness (no epistasis). As we will see, variable selection coefficients have been implemented in a different version of the program. Offspring are formed by selfing with probability α and by random fusion of gametes with probability $1-\mathit{\alpha }\mathit{.}$ A neutral locus with an infinite number of possible alleles is located at the midpoint of the chromosome, mutating at a rate $\mu ={10}^{-3}$ per generation. The program runs for $2\times {10}^6$ generations, genetic diversity at the neutral locus being recorded every 50 generations and measured as $D=1-{\displaystyle {\sum }_i{p}_i{}^2}$ (where $p_i$ is the frequency of neutral allele i). The effective population size at the neutral locus is then estimated from $\overline{D}=4N_{\mathrm{e}}\mu /\left(1+4N_{\mathrm{e}}\mu \right),$ where $\overline{D}$ is the average neutral diversity at equilibrium, yielding

$$N_{\mathrm{e}}=\frac{\overline{D}}{4\mu \left(1-\overline{D}\right)}$$ (7)

(the exact expression including terms in ${\mathit{\mu }}^2$ yields undistinguishable results for the parameter values used here). In the simulations, $\overline{D}$ is obtained by averaging after a burn-in period of 15,000 generations, which was sufficient for diversity to reach equilibrium with $\mu =\mathrm{1}{\mathrm{0}}^{\mathrm{-}3}.$ As we will see, a different version of the program including a neutral sequence with an infinite number of sites was also used, in which case diversity takes longer to equilibrate.

Data availability

The author states that all data necessary for confirming the conclusions presented in the article are represented fully within the article. The Dryad DOI is doi:10.5061/dryad.p3r01.

Results

All results are obtained using the method presented in Appendix A for computing recursions for multilocus moments, implemented in a Mathematica notebook (Supplemental Material, File S1). All terms are derived to the first order in $1/N$ and to the first order in ${\tilde{p}}_B$ (the frequency of the deleterious allele at mutation–selection balance, given by Equation 2).

General results

The expected change in genetic diversity at locus A per generation can be written as

$$\langle \mathrm{\Delta }{D}_{AA}\rangle =\langle {\mathrm{\Delta }}_{\mathrm{s}}{D}_{AA}\rangle +\langle {\mathrm{\Delta }}_{\mathrm{d}}{D}_{AA}\rangle ,$$ (8)

where $\langle {\mathrm{\Delta }}_{\mathrm{s}}{D}_{AA}\rangle$ is the change in diversity due to selection and $\langle {\mathrm{\Delta }}_{\mathrm{d}}{D}_{AA}\rangle$ the change in diversity due to drift, given by

$$\langle {\mathrm{\Delta }}_{\mathrm{d}}{D}_{AA}\rangle =-\frac{1}{2N}\left(\langle D_{AA}\rangle +\langle D_{A,A}\rangle \right)$$ (9)

to leading order. In the absence of selection, $\langle {\mathrm{\Delta }}_{\mathrm{s}}{D}_{AA}\rangle$ = 0 while $\langle D_{A,A}\rangle$ at quasi-equilibrium is given by (from Equation A10)

$$\langle D_{A,A}\rangle =F\langle D_{AA}\rangle$$ (10)

with $F=\alpha /\left(2-\alpha \right),$ and the expected change in neutral diversity per generation thus becomes

$$\langle \mathrm{\Delta }{D}_{AA}\rangle =\langle {\mathrm{\Delta }}_{\mathrm{d}}{D}_{AA}\rangle =-\frac{1}{2N}\left(1+F\right)\langle D_{AA}\rangle .$$ (11)

This corresponds to the classical result that $N_{\mathrm{e}}$ = $N/\left(1+F\right)$ under partial selfing (Pollak 1987): the increased homozygosity caused by selfing amplifies the effect of drift, since the same allele is sampled twice every time a homozygote is sampled. When selection acts at locus B, we obtain the following expression for $\langle {\mathrm{\Delta }}_{\mathrm{s}}{D}_{AA}\rangle$ to the first order in s:

$$\begin{array}{c}\langle {\mathrm{\Delta }}_{\mathrm{s}}{D}_{AA}\rangle =-sh\left(\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle \right)\\ -s\left(1-2h\right)\left(\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle \right).\end{array}$$ (12)

An expression to the second order in s is provided in Appendix B; however, both expressions generally yield very similar quantitative results, although adding the terms in $s^2$ may slightly improve the predictions under loose linkage. The different terms that appear in Equation 12 may be interpreted as follows. From the definitions given in the previous section, the term $\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle$ may also be written as $\mathrm{E}\left[\left(1/2\right)\left({\zeta }_{AA}^{\mathrm{M}}+{\zeta }_{AA}^{\mathrm{P}}\right)\left({\zeta }_B^{\mathrm{M}}+{\zeta }_B^{\mathrm{P}}\right)\right]$ (where again $\mathrm{E}$ stands for the average over all individuals), thus measuring a covariance between $\left(1/2\right)\left({\zeta }_{AA}^{\mathrm{M}}+{\zeta }_{AA}^{\mathrm{P}}\right)$ and ${\zeta }_B^{\mathrm{M}}+{\zeta }_B^{\mathrm{P}}$ (note that $\mathrm{E}\left[{\zeta }_B^{\mathrm{M}}+{\zeta }_B^{\mathrm{P}}\right]=0$). The quantity $\left(1/2\right)\left({\zeta }_{AA}^{\mathrm{M}}+{\zeta }_{AA}^{\mathrm{P}}\right)$ is higher in individuals carrying rarer alleles at the neutral locus: for example, in the case of a biallelic neutral locus, it equals $p_A^2,$ $\left(p_A^2+q_A^2\right)/2,$ and $q_A^2$ in 00, 01, and 11 individuals, where $p_A$ is the frequency of allele 1. Furthermore, the quantity ${\mathit{\zeta }}_B^{\mathrm{M}}+{\zeta }_B^{\mathrm{P}}$ is higher in individuals carrying more deleterious alleles at the selected locus (it is nearly 0, 1, and 2 in individuals carrying 0, 1, and 2 deleterious alleles at locus B, assuming $p_B$ is small). Therefore, a positive value of $\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle$ indicates that rarer alleles at the neutral locus tend to be found in individuals carrying higher numbers of deleterious alleles at the selected locus, while a negative value of $\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle$ indicates the opposite. Recursions for the moments $\langle D_{AAB}\rangle$ and $\langle D_{AA,B}\rangle$ over one generation are given in Appendix B, to the first order in s, ${\tilde{p}}_B,$ and $1/N.$ In the absence of selfing ($\alpha =0$), we obtain that $\langle D_{AA,B}\rangle =0$ at quasi-equilibrium, while $\langle D_{AAB}\rangle$ is generated by the variance in linkage disequilibrium $\langle D_{AB}{}^2\rangle$ and by the effect of selection and is positive when $sh>0.$ Indeed, when a given neutral allele becomes associated (by chance) to the deleterious allele at locus B, this neutral allele tends to decrease in frequency, generating a positive $\langle D_{AAB}\rangle$ (the deleterious allele at locus B tends to become associated with rarer alleles at locus A). This in turns reduces genetic diversity at the neutral locus (as shown by Equation 12), since these rarer alleles will further decrease in frequency due to their association with the deleterious allele. Because partial selfing generates cross-haplotype associations (between genes present on different haplotypes of a diploid), $\langle D_{AAB}\rangle$ and $\langle D_{AA,B}\rangle$ are given by more complicated expressions when $\alpha >0,$ involving moments such as $\langle D_{AB}{D}_{A,B}\rangle ,$ $\langle D_{AB}{D}_{AB,B}\rangle ,$ or $\langle D_{AB,B}{}^2\rangle$ (see Appendix B).

Similarly, the quantity $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ that appears on the second line of Equation 12 measures a covariance between $\left(1/2\right)\left({\zeta }_{AA}^{\mathrm{M}}+{\zeta }_{AA}^{\mathrm{P}}\right)$ and ${\mathit{\zeta }}_{B,B},$ the quantity ${\zeta }_{B,B}$ being higher in homozygotes at locus B than in heterozygotes. A positive value of $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ thus indicates that rarer alleles at locus A tend to be found more often in homozygotes at locus B than in heterozygotes. As shown by Equation 12, this would reduce neutral diversity when the deleterious allele is partially recessive ($h<0.5$), since in this case homozygotes at the selected locus have a lower fitness than heterozygotes. A recursion for $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ is given in Appendix B (Equation B14); remarkably, it shows that identity disequilibrium (covariance in homozygosity) between the two loci generates negative $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ (that is, rarer alleles at locus A tend to be found more often in heterozygotes at locus B) even in the absence of selection. Indeed, setting $s=0$ in Equation B14 yields at quasi-equilibrium

$$\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle =-\frac{2}{N\left(2-\mathit{\alpha }\right)}{G}_{AB}{\tilde{p}}_B\langle D_{AA}\rangle ,$$ (13)

where $G_{AB}$ is the identity disequilibrium between loci A and B (Weir and Cockerham 1969). It is given by $G_{AB}={\phi }_{AB}-F^2,$ where

$${\phi }_{AB}=\frac{\alpha }{2-\alpha }\frac{2-\alpha -2\left(2-3\alpha \right)r\left(1-r\right)}{2-\alpha \left[1-2r\left(1-r\right)\right]}$$ (14)

is the probability of joint identity-by-descent at the two loci. This result may be interpreted as follows. Due to identity disequilibrium, the frequency of heterozygotes at locus A is higher among heterozygotes at locus B than among homozygotes. Furthermore, the frequency of rarer neutral alleles is higher among heterozygotes than among homozygotes at locus A (this is easily seen in the case of a biallelic locus): therefore, the frequency of rarer alleles at locus A should be higher among heterozygotes at locus B. As shown by Equation 12, this effect tends to increase neutral diversity, as long as the deleterious allele is partially recessive ($\mathit{h}\mathrm{<}0.5$), so that heterozygotes at locus B have a higher fitness than homozygotes. As shown in the next subsection (high effective recombination), the effect of identity disequilibrium dominates over all other effects when the effective recombination rate $r\left(1-F\right)$ is sufficiently high [more precisely, $r\left(1-F\right)\gg s$], in which case partially recessive deleterious alleles tend to increase neutral diversity (this effect usually stays rather small). However, weaker effective recombination increases the relative importance of the terms on the first line of Equation 12 that tend to decrease neutral diversity. Furthermore, weak effective recombination changes the sign of $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ (through the terms in s in Equation B14), due to the fact that the association between rarer alleles at locus A and the deleterious allele at locus B (represented by moments $\langle D_{AAB}\rangle$, $\langle D_{AA,B}\rangle$) generates an association between those rarer alleles and homozygosity for the deleterious allele at locus B.

As shown in Appendix B, calculating the different terms of Equation 12 at quasi-equilibrium requires computing six two-locus moments that are generated by finite population size: $\langle D_{AB}{}^2\rangle ,$ $\langle D_{AB}{D}_{A,B}\rangle ,$ $\langle D_{A,B}{}^2\rangle ,$ $\langle D_{AB}{D}_{AB,B}\rangle ,$ $\langle D_{A,B}{D}_{AB,B}\rangle ,$ and $\langle D_{AB,B}{}^2\rangle .$ Recursions for these moments are also given in Appendix B. Although the solutions obtained are rather complicated, they are readily computed numerically using Mathematica (see File S2); furthermore, we will see that they can be approximated by simpler expressions in several cases. Importantly, all expressions obtained are in $1/N$ and thus vanish when N tends to infinity.

Besides its effect on $\langle {\mathrm{\Delta }}_{\mathrm{s}}{D}_{AA}\rangle ,$ selection at locus B also affects the average excess homozygosity at locus A $\langle D_{A,A}\rangle$ and thus the term $\langle {\mathrm{\Delta }}_{\mathrm{d}}{D}_{AA}\rangle$ in Equation 8. Because $\langle D_{A,A}\rangle$ is multiplied by $1/N$ in Equation 9, it is sufficient to compute this moment in the limit as N tends to infinity, to obtain an expression for $\langle \mathrm{\Delta }{D}_{AA}\rangle$ to the first order in $1/N.$ Using the results in Roze (2015) (also derived in File S1), we have at quasi-equilibrium, to the first order in s and ${\tilde{p}}_B,$

$$\langle D_{A,A}\rangle =F\left[1-s\left(1-2h\right)G_{AB}{\tilde{p}}_B\right]\langle D_{AA}\rangle ,$$ (15)

where again $G_{AB}$ is the identity disequilibrium between loci A and B. Indeed, homozygosity at locus A is reduced when the deleterious allele at locus B is partially recessive ($h<1/2$), due to the fact that homozygotes at locus A tend to be also homozygous at locus B, while homozygotes at locus B have a lower fitness than heterozygotes.

Putting everything together, we obtain an expression for the change in diversity at locus A over one generation of the form

$$\mathrm{\Delta }\langle D_{AA}\rangle =-\frac{1}{2N}\left(1+F\right)\left(1+T{\tilde{p}}_B\right)\langle D_{AA}\rangle ,$$ (16)

where T is a function of s, h, r, and α. To the first order in ${\tilde{p}}_B,$ we thus have

$$N_{\mathrm{e}}=\frac{N}{1+F}{B}_{\mathrm{sel}},$$ (17)

where $B_{\mathrm{sel}}=1-T{\tilde{p}}_B$ represents the effect of background selection. Although the expression obtained for T from the equations given in Appendix B is complicated, we will now see that simple approximations can be obtained in several regimes (in particular, high effective recombination, tight linkage, and high selfing).

High effective recombination (with partial selfing)

Under partial selfing and when the effective recombination rate $r\left(1-F\right)$ is high (and assuming that the dominance coefficient h of the deleterious allele is significantly different from 0.5), Equation 12 is dominated by the term on the second line, since $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ is generated by drift even in the absence of selection and is thus proportional to $1/N$ (see Equation 13), while the terms $\langle D_{AAB}\rangle$ and $\langle D_{AA,B}\rangle$ on the first line are generated by selection and drift and are thus proportional to $s/N.$ Neglecting the term on the first line of Equation 12 and using Equations 9 and 15 yields the following expression for the change in neutral diversity, to the first order in s, ${\tilde{p}}_B,$ and $1/N:$

$$\mathrm{\Delta }\langle D_{AA}\rangle =-\frac{1}{2N}\left(1+F\right)\left[1-s\left(1-2h\right)\frac{4+\alpha }{2}{G}_{AB}{\tilde{p}}_B\right]\langle D_{AA}\rangle .$$ (18)

Using Equation 2, we obtain for the effective population size at the neutral locus

$$N_e\approx \frac{N}{1+F}\left[1+\frac{u\left(1-2h\right)}{h\left(1-F\right)+F}\frac{4+\alpha }{2}{G}_{AB}\right],$$ (19)

independent of s. Equation 19 shows that identity disequilibrium between the neutral and the selected locus ($G_{AB}$) increases the effective population size at the neutral locus when the deleterious allele is partially recessive. This is caused by two effects: (i) identity disequilibrium reduces the excess homozygosity at locus A caused by selfing (Equation 15), since homozygotes at locus A tend to be also homozygous at locus B, while homozygotes at locus B have a lower fitness than heterozygotes when the deleterious allele is partially recessive; and (ii) the higher fitness of heterozygotes at locus B increases diversity at locus A since heterozygotes at locus B tend to be also heterozygous at locus A (Equation 13).

This increase in effective population size caused by identity disequilibrium usually stays modest, however (since it is expected to occur only for high effective recombination), and is thus difficult to observe in simulations. Background selection has stronger effects when the effective recombination rate becomes low, in which case the term $\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle$ in the first line of Equation 12 becomes of the same order of magnitude as the term on the second line [indeed, we can show that the denominator of $\langle D_{AAB}\rangle$ and $\langle D_{AA,B}\rangle$ is proportional to ε when both $r\left(1-F\right)$ and s are of order ε], while the sign of $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ changes due to the effect of selection. Two approximations for this regime are given below (tight linkage, high selfing).

Random mating

In the absence of selfing ($\mathit{\alpha }=0$), Equations B4–B9 yield the following expressions for $\langle D_{AB}{}^2\rangle$ and $\langle D_{A,B}{}^2\rangle$ at quasi-equilibrium,

$$\langle D_{AB}{}^2\rangle =\frac{1+r^2\left(1-2sh\right)}{2N\left[1-{\left(1-r\right)}^2\left(1-2sh\right)\right]}{\tilde{p}}_B\langle D_{AA}\rangle$$ (20)

$$\langle D_{A,B}{}^2\rangle =\frac{1}{2N}{\tilde{p}}_B\langle D_{AA}\rangle ,$$ (21)

while $\langle D_{AB}{D}_{A,B}\rangle ,$ $\langle D_{AB}{D}_{AB,B}\rangle ,$ $\langle D_{A,B}{D}_{AB,B}\rangle ,$ and $\langle D_{AB,B}{}^2\rangle$ = 0. Furthermore, Equations B10–B14 yield

$$\langle D_{AAB}\rangle =\frac{2\mathit{sh}\left[\left(1-r\right)\langle D_{AB}{}^2\rangle +r\langle D_{A,B}{}^2\rangle \right]}{1-\left(1-r\right)\left(1-sh\right)},$$ (22)

while $\langle D_{AA,B}\rangle$ and $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ = 0. Finally, the rate of decay of neutral diversity is given by

$$\langle \mathrm{\Delta }{D}_{AA}\rangle =-sh\langle D_{AAB}\rangle -{\left(sh\right)}^2\left(\langle D_{AB}{}^2\rangle +\langle D_{A,B}{}^2\rangle \right)-\frac{1}{2N}\langle D_{AA}\rangle .$$ (23)

Under tight linkage (i.e., both r and s are of order ε, where ε is a small term), we obtain from Equations 20–22

$$\langle D_{AB}{}^2\rangle \approx \frac{{\tilde{p}}_B\langle D_{AA}\rangle }{4N\left(r+sh\right)}\gg \langle D_{A,B}{}^2\rangle ,$$ (24)

$$\langle D_{AAB}\rangle \approx \frac{sh{\tilde{p}}_B\langle D_{AA}\rangle }{2N{\left(r+sh\right)}^2},$$ (25)

giving

$$\langle \mathrm{\Delta }{D}_{AA}\rangle \approx -\frac{1}{2N}\left[1+{\left(\frac{sh}{r+sh}\right)}^2{\tilde{p}}_B\right]\langle D_{AA}\rangle$$ (26)

in agreement with the results obtained by Hudson and Kaplan (1995) and Nordborg et al. (1996). Under loose linkage ($r\gg s$), Equations 20–23 yield

$$\langle \mathrm{\Delta }{D}_{AA}\rangle \mathrm{\approx }-\frac{1}{2N}\left[1+\frac{{\left(sh\right)}^2\left(1+4r^2\right)}{r^2}{\tilde{p}}_B\right]\langle D_{AA}\rangle .$$ (27)

Setting $r=1/2$ in Equation 27 and replacing ${\tilde{p}}_B$ by $u/\left(sh\right)$ yields $N_{\mathrm{e}}\approx N\left(1-8shu\right),$ which is equivalent to Robertson’s (1961) heuristic result that selection at unlinked loci decreases the effective population size by four times the additive variance in fitness—indeed, the variance in fitness caused by selection against the deleterious allele is $\sim 2shu$ (see also Charlesworth 2012).

Tight linkage

When r is small, Nordborg’s (1997) separation of timescales argument can be used to express associations between genes present on different haplotypes of a diploid in terms of associations between genes present on the same haplotype (see also Nordborg 2000; Padhukasahasram et al. 2008). Consider for example the association $D_{A,B}$ between two genes sampled at loci A and B from different haplotypes of an individual. Going backward in time, two different events may happen to the ancestral lineages of these genes: they may find themselves on the same haplotype (which may take only a few generations if both lineages stay in the same individual due to selfing) or move to different individuals due to an outcrossing event, in which case it will take a long time before they find themselves again in the same individual (assuming N is large). To leading order, the probability that these lineages join on the same haplotype before moving to different individuals is F. Considering now all possible pairs of genes at loci A and B on different haplotypes of the same individual (in all individuals of the population) and going backward in time, we may assume that a proportion F of such pairs find themselves on the same haplotype after a small number of generations, while the remaining $1-F$ have moved to different individual lineages (and thus become independent): therefore, $D_{A,B}\approx F{D}_{AB}$—note that this approximation assumes tight linkage, as it neglects recombination events separating genes that have joined on the same haplotype, over the small number of generations considered. Using this approximation, we have

$$\langle D_{AB}{D}_{A,B}\rangle \approx F\langle D_{AB}{}^2\rangle ,\langle D_{A,B}{}^2\rangle \approx F^2\langle D_{AB}{}^2\rangle .$$ (28)

Similarly, $D_{AB,B}\approx F{D}_{ABB}=F\left(1-2p_B\right)D_{AB}$ (from Equation A9), which yields (assuming that $p_B$ is small)

$$\langle D_{AB}{D}_{AB,B}\rangle \approx F\langle D_{AB}{}^2\rangle ,\langle D_{A,B}{D}_{AB,B}\rangle \approx \langle D_{AB,B}{}^2\rangle \approx F^2\langle D_{AB}{}^2\rangle .$$ (29)

Finally, $D_{AAB,B}\approx F{D}_{AABB}=F\left(D_{AA}{D}_{BB}+\left(1-2p_B\right)D_{AAB}\right),$ from which we obtain (using the fact that the moment $\langle p_B{D}_{AAB}\rangle$ is negligible, as shown in File S1)

$$\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle \approx \langle D_{AA,B}\rangle \approx F\langle D_{AAB}\rangle .$$ (30)

Equations 28–30 can also be obtained from Equations B4–B14, under the assumption that r is small (see File S1). Plugging Equations 28–30 into Equation 12 yields

$$\langle {\mathrm{\Delta }}_{\mathrm{s}}{D}_{AA}\rangle \approx -s\left[h\left(1-F\right)+F\right]\langle D_{AAB}\rangle .$$ (31)

Furthermore, plugging Equations 29 and 30 into Equations B4 and B10 and assuming that r is small yields the same expressions as Equations 24 and 25 (obtained for random mating) for $\langle D_{AB}{}^2\rangle$ and $\langle D_{AAB}\rangle ,$ replacing h by $h\left(1-F\right)+F,$ r by $r\left(1-F\right),$ and N by $N/\left(1+F\right).$ Therefore, the present model converges to Nordborg’s (1997) result when loci are tightly linked.

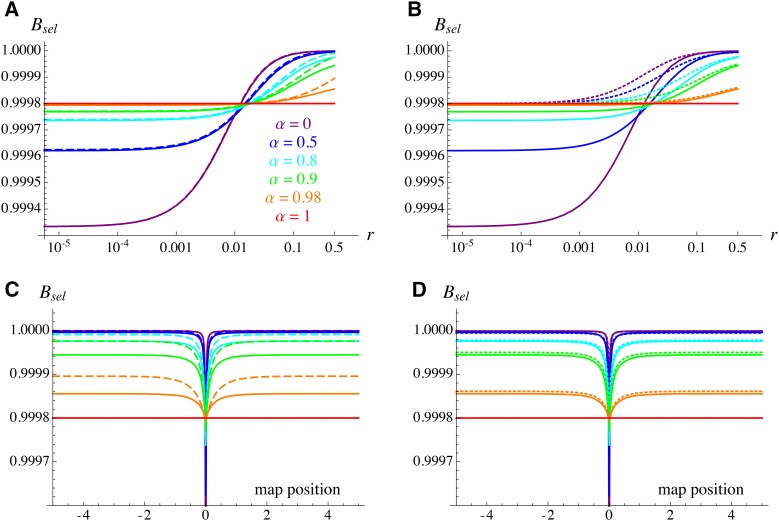
Figure 1A shows the decrease in effective population size at the neutral locus caused by the deleterious allele ($B_{\mathrm{sel}},$ see Equation 17), as a function of the recombination rate between the two loci (on a log scale). When r tends to zero, $B_{\mathrm{sel}}$ tends to $1-{\tilde{p}}_B,$ and selfing increases $N_{\mathrm{e}}$ (as it decreases the frequency of the deleterious allele). When r is sufficiently high, however (∼ >0.01 for the parameter values used in Figure 1), increased selfing causes stronger background selection. Under complete selfing ($\alpha =1$), $B_{\mathrm{sel}}$ becomes independent of r and is $\sim 1-u/s.$ As can be seen in Figure 1A, the tight linkage approximation accurately predicts the solution obtained from Equations B4–B14, except when r and α are high (in which case it underestimates the strength of background selection). As we will see, this discrepancy for high values of r may lead to substantial differences when integrating over a large genetic map, as the majority of deleterious alleles are only loosely linked to the neutral locus, yet significantly affect $N_{\mathrm{e}}$ at this locus when selfing is high (this is more visible in Figure 1C, showing the strength of background selection as a function of the position of the deleterious allele along the genetic map). Note, however, that the tight linkage approximation yields the same prediction as the more general model when $\alpha =1$ ($B_{\mathrm{sel}}\approx 1-u/s$).

Figure 1.

Background selection effect generated by a single deleterious allele ($B_{\mathrm{sel}},$ see Equation 17) on $N_{\mathrm{e}}$ at the neutral locus, as a function of the recombination rate r between the two loci (A and B) and of the position of the deleterious allele along a linear chromosome of total map length 10 M (C and D) (the neutral locus is located at position 0). Different colors correspond to different values of the selfing rate as indicated in A. Solid curves correspond to the results obtained from the equations in Appendix B, dashed curves in A and C correspond to the tight linkage approximation [Equation 26, replacing h by $h\left(1-F\right)+F$ and r by $r\left(1-F\right)$], and dotted curves in B and D correspond to the high selfing approximation (Equation 34). Parameter values: $s=0.05,$ $h=0.3,$ $u={10}^{-5}.$

High selfing

Simple approximations can also be obtained when the selfing rate is high, for any value of the recombination rate r. From Equations B4–B9 and assuming that α is close to 1, we obtain

$$\begin{array}{c}\langle D_{AB}{}^2\rangle \approx \langle D_{AB}{D}_{A,B}\rangle \approx \langle D_{A,B}{}^2\rangle \approx \langle D_{AB}{D}_{AB,B}\rangle \\ \approx \langle D_{A,B}{D}_{AB,B}\rangle \approx \langle D_{AB,B}{}^2\rangle \approx \frac{1+2r}{2N\left[s+2r\left(1-\alpha +s\right)\right]}{\tilde{p}}_B\langle D_{AA}\rangle .\end{array}$$ (32)

Furthermore, Equations B10–B14 yield

$$\begin{array}{c}\langle D_{AAB}\rangle \approx \langle D_{AA,B}\rangle \approx \langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle \\ \approx \frac{{\left(1+2r\right)}^{2}s}{N{\left[s+2r\left(1-\alpha +s\right)\right]}^2}{\tilde{p}}_B\langle D_{AA}\rangle ,\end{array}$$ (33)

which, using ${\tilde{p}}_B\approx u/s,$ generates the following approximation for the rate of decay of neutral diversity:

$$\langle \mathrm{\Delta }{D}_{AA}\rangle \approx -\frac{1}{2N}\left(1+F\right)\left[1+{\left(\frac{\left(1+2r\right)s}{s+2r\left(1-\alpha +s\right)}\right)}^2{\tilde{p}}_B\right]\langle D_{AA}\rangle .$$ (34)

Note that Equation 34 again yields $B_{\mathrm{sel}}\approx 1-u/s$ when $\alpha =1.$ As shown in Figure 1D, this approximation better matches the general model than the tight linkage approximation when the selfing rate is high (but <1) and when linkage is loose. However, Figure 1B shows that it differs substantially from the general model under tight linkage and is thus expected to perform poorly when the selfing rate is not high (since in this case background selection is mainly caused by deleterious alleles that are tightly linked to the neutral locus).

Multilocus extrapolation and simulations

Following previous work (e.g., Hudson and Kaplan 1995; Nordborg 1997; Glémin 2007; Kamran-Disfani and Agrawal 2014), results from the two-locus model may be extrapolated to the case of deleterious alleles segregating at multiple loci by assuming multiplicative effects of the different deleterious alleles on neutral diversity. When the neutral locus is located at the midpoint of a linear genome with total map length R, and when all deleterious alleles have the same selection and dominance coefficients (as in the simulation program), this yields (using Equation 2)

$$N_{\mathrm{e}}\approx \frac{N}{1+F}\exp \left[-\frac{U}{s\left[h\left(1-F\right)+F\right]}\times \frac{2}{R}{\displaystyle {\int }_0^{R/2}T\left(x\right)dx}\right],$$ (35)

where U is the deleterious mutation rate per haploid genome and $T\left(x\right)$ corresponds to the term T in Equation 16, in which the recombination rate r is expressed in terms of the genetic distance x (in morgans) between the neutral locus and the deleterious allele, using Haldane’s mapping function $r=\left(1/2\right)\left[1-e^{-2x}\right]$ (Haldane 1919). This integral can be computed numerically as shown in File S2.

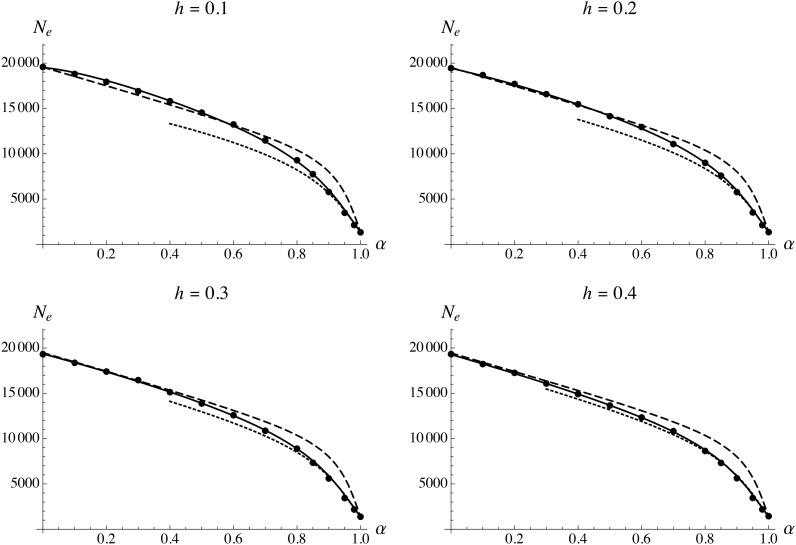
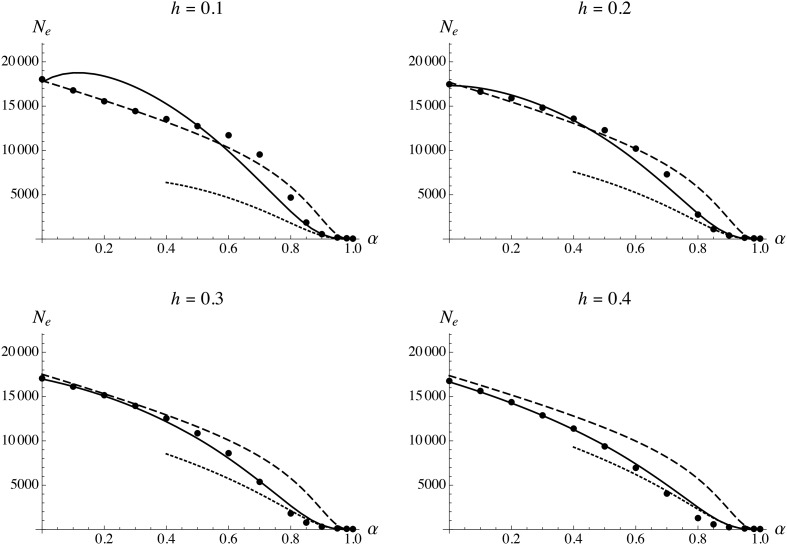
Figure 2 shows the effective size of a population of census size 20,000 as a function of the selfing rate, for a haploid genomic deleterious mutation rate $U=0.1$ and genome map length $R=10$ M. As can be seen in Figure 2, the analytical model (solid curves) fits well with the simulation results for all values of α. Note that in Figure 2, Figure 3, Figure 4, and Figure 5, solid curves have been obtained by calculating numerically the integral in Equation 35, using a system of recursions expressed to the second order in s for the different moments shown in Appendix B (see File S1 and File S2); however, the results obtained using the recursions given in Appendix B (expressed to the first order in s) are undistinguishable in most cases (results not shown). Explicit forms can be obtained for the integral in Equation 35 (as a function of R and the different parameters of the model), when using either the tight linkage approximation or the high selfing approximation, and are given in File S2. The results shown in Figure 2 confirm that the tight linkage approximation underestimates the effect of background selection when the selfing rate is high, as loosely linked deleterious alleles significantly affect neutral diversity. In this case, the high selfing approximation is more accurate, closely matching the simulation results when $\alpha >\mathrm{0.85.}$

Figure 2.

Effective population size $N_{\mathrm{e}}$ as a function of the selfing rate α, for different values of the dominance coefficient of deleterious alleles h. Solid circles show simulation results (in this and subsequent figures, error bars are smaller than the size of the solid circles), solid curves show analytical predictions from the complete model (see File S2), dashed curves show the tight linkage approximation [Equation 26, replacing h by $h\left(1-F\right)+F$ and r by $r\left(1-F\right)$], and dotted curves show the high selfing approximation (Equation 34). Parameter values: $N=20,000,$ $s=0.05,$ $U=0.1,$ $R=10.$

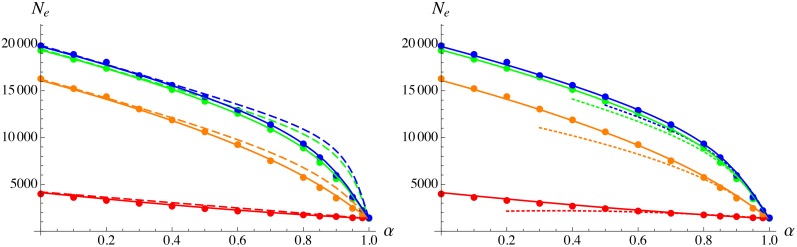
Figure 3.

Effective population size $N_{\mathrm{e}}$ as a function of the selfing rate α, for different values of genome map length R: 0.1 (red), 1 (orange), 10 (green), and 100 (blue). Solid circles show simulation results, solid curves show analytical predictions from the complete model, dashed curves (left) show the tight linkage approximation, and dotted curves (right) show the high selfing approximation. Parameter values: $N=20,000,$ $s=0.05,$ $h=0.3,$ $U=\mathrm{0.1.}$

Figure 4.

Effective population size $N_{\mathrm{e}}$ as a function of the selfing rate α, for different values of the strength of selection against deleterious alleles s: 0.005 (blue), 0.05 (green), and 0.5 (red). Solid circles show simulation results, solid curves show analytical predictions from the complete model, dashed curves (left) show the tight linkage approximation, and dotted curves (right) show the high selfing approximation. Parameter values: $N=20,000,$ $h=0.3,$ $U=0.1,$ $R=10.$

Figure 5.

Effective population size $N_{\mathrm{e}}$ as a function of the selfing rate α, for different values of the dominance coefficient of deleterious alleles h. Circles and curves are the same as in Figure 2 with $U=\mathrm{0.5.}$

Figure 3 and Figure 4 show that the full model provides accurate predictions for $N_{\mathrm{e}}$ for different values of map length R (from 0.1 to 100) and strength of selection against deleterious alleles s (from 0.005 to 0.5). As expected, the tight linkage approximation works better at lower values of R. When the selfing rate is low, increasing s magnifies the strength of background selection, while it has the opposite effect under high selfing (due to the fact that mutation-free individuals are more abundant when selection against deleterious alleles is stronger). Finally, Figure 5 shows that increasing the deleterious mutation rate U (to 0.5 per haploid genome) increases the strength of background selection, leading to very low values of $N_{\mathrm{e}}$ at high selfing rates ($N_{\mathrm{e}}$ estimated from the simulations is close to 45 when $\alpha =1$). When $U=0.5,$ discrepancies between the full model and the simulations appear at low values of h ($h=0.1$ in particular) and intermediate values of α: these are probably caused by genetic associations between selected loci (identity disequilibrium in particular), which are neglected in the analysis. Using an expression for the frequency of deleterious allele ${\tilde{p}}_B$ that takes into account the effect of identity disequilibria (Roze 2015) does not significantly improve the results (not shown). Discrepancies also appear at higher values of h and high selfing rate ($\alpha \approx$ 0.8–0.9), the analytical model underestimating the strength of background selection. Finally, the model overestimates the effect of background selection when the selfing rate is very high ($\alpha >0.95$), for all values of h: although this is not visible in Figure 5 (as $N_{\mathrm{e}}$ is very small when α is high), it becomes apparent when $N_{\mathrm{e}}$ is plotted on a log scale, as shown in Figure S1. For these parameter values ($\alpha =0.98,1$), selection against deleterious alleles is no longer efficient and these accumulate over time in the population (results not shown).

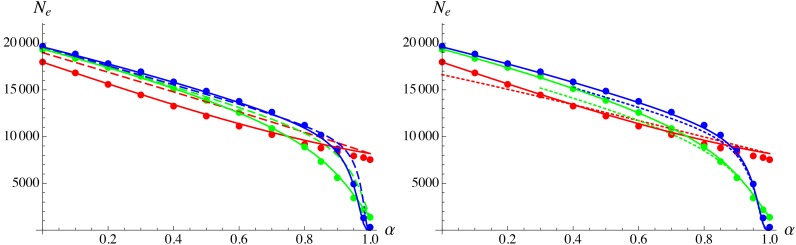
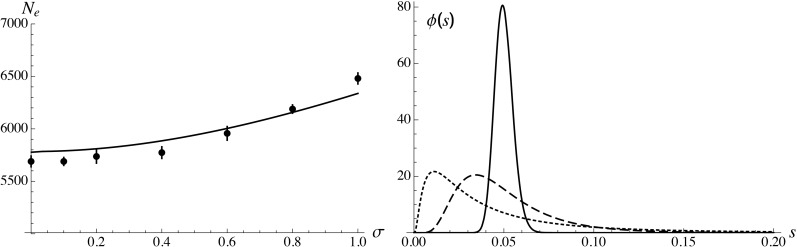
Equation 35 can be extended to the more realistic case where deleterious alleles at different loci have different fitness effects (assuming that selection remains sufficiently strong at most loci so that deleterious alleles stay near mutation–selection balance), by replacing s and h by functions of map position x (e.g., Charlesworth 2012). If the number of deleterious loci is large and if the distribution of fitness effects of mutations does not depend on genomic location, the integral in Equation 35 can be replaced by a double integral, over map position x and over the joint distribution of s and h. To test this, the simulation program was modified to include a log-normal distribution of selection coefficients s across loci, assuming a constant heterozygous effect of mutations ($sh$), generating a negative covariance between s and h (see figure 5 in Roze 2015). Figure 6 shows results for $\alpha =0.9$ and for different values of the variance of deleterious effects of mutations across loci, setting the average of the log-normal distribution and the heterozygous effect of mutations so that $\overline{s}=0.05$ and $\overline{h}=0.25$ in all cases. As can be seen in Figure 6, increasing the variance of s slightly increases $N_{\mathrm{e}},$ and this effect is captured by integrating Equation 34 (high selfing approximation) over the distribution of s.

Figure 6.

Left: effective population size $N_{\mathrm{e}}$ as a function of the standard deviation σ of $\ln s$ across loci, assuming a log-normal distribution of s and setting the average of $\ln s$ so that $\overline{s}=0.05$ for all values of σ. Solid curve shows prediction obtained by integrating Equation 34 over the distribution of s and over the genetic map; solid circles show simulation results. Parameter values: $N=20,000,$ $\alpha =0.9,$ $U=0.1,$ $R=10.$ In the simulations the heterozygous fitness effect $hs$ is the same for all mutations and adjusted so that $\overline{h}=0.25$ for all values of σ. Right: the distribution of s for $\sigma =0.1$ (solid curve), 0.5 (dashed curve), and 1 (dotted curve).

Temporal change in population size

It is worth emphasizing that the moment-based method presented in this article yields an expression for the “inbreeding effective size” (as it is based on the rate of decay of neutral diversity or the instantaneous rate of coalescence), while coalescent-based methods (e.g., Hudson and Kaplan 1995; Nordborg 1997) yield an expression for the “coalescence effective size,” corresponding to half the average coalescence time between two sequences randomly sampled from the population. After a single change in population size, and if selection and recombination rate are sufficiently large relative to $1/N_{\mathrm{e}},$ the different moments computed in Appendix B should equilibrate quickly relative to the change in neutral diversity, and the inbreeding effective population size should thus rapidly converge to its equilibrium value for the new census population size. By contrast, expected coalescence times will take longer to equilibrate. Assuming that the inbreeding effective size instantaneously reaches its new equilibrium value, the expected coalescence time t generations after the change is given by

$$\mathrm{E}{\left[T\right]}_t=2N_{\mathrm{e}}+{\left(1-\frac{1}{2N_{\mathrm{e}}}\right)}^t\left(\mathrm{E}{\left[T\right]}_0-2N_{\mathrm{e}}\right),$$ (36)

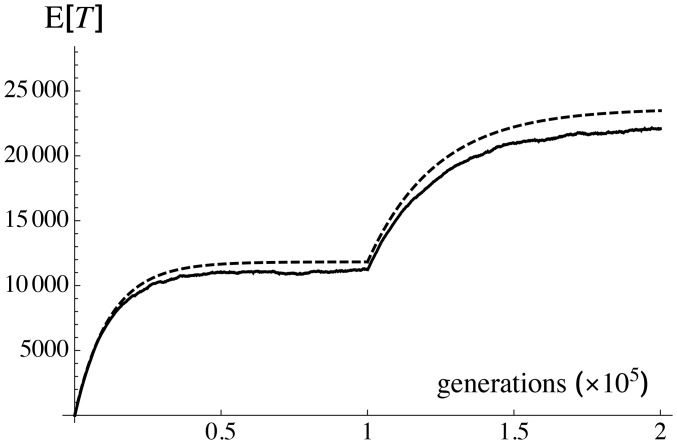
where $N_{\mathrm{e}}$ is the new inbreeding effective size and $\mathrm{E}{\left[T\right]}_0$ the average coalescence time at the time of the change in population size. To test this prediction, the simulation program was modified to include a neutral sequence with an infinite number of sites at the midpoint of the chromosome. Indeed, the expected coalescence time between two sequences is simply given by $D/\left(2\mu \right),$ where μ is the mutation rate within the sequence and D the average number of differences between two sequences, given by $D=2{\displaystyle {\sum }_i{p}_i{q}_i}$ (where the sum is over all segregating neutral sites within the sequence). Figure 7 shows an example in which $N=20,000$ during the first ${10}^5$ generations (starting from a monomorphic population, which is equivalent to the coalescence of all lineages at generation zero), while $N=40,000$ during the last ${10}^5$ generations. As can be seen in Figure 7, the quasi-equilibrium argument leading to Equation 36 correctly predicts the dynamics of $\mathrm{E}\left[T\right]$ both during the initial phase and after the change in population size. The quasi-equilibrium argument could also possibly be used in situations where population size changes continuously over time (i.e., exponential population growth), although this was not explored here.

Figure 7.

Average coalescence time between two randomly sampled sequences at a neutral locus located at the midpoint of the chromosome, as a function of time. The population is monomorphic at time zero (all lineages coalesce), $N=20,000$ during the first ${10}^5$ generations, and $N=40,000$ during the last ${10}^5$ generations. Parameter values: $\alpha =0.9,$ $s=0.05,$ $h=0.3,$ $U=0.1,$ $R=10.$ Dashed curve shows prediction from Equation 36, where the inbreeding effective size is obtained from Equation 35 and assumed to reach instantaneously its equilibrium value for a given N. Solid curve shows simulation results (average over 4000 replicate simulations), where $\mathrm{E}\left[T\right]$ is estimated from the diversity of a neutral sequence with an infinite number of sites (see text) and mutation rate $\mu ={10}^{-4}$ per generation.

Discussion

We have seen how multilocus population genetics theory can be used to express the effect of a deleterious allele at mutation–selection balance on the dynamics of diversity at a linked neutral locus in terms of moments of linkage disequilibrium and other genetic associations between these two loci. This provides an alternative to methods based on computing expected coalescence times of pairs of genes present on different types of genetic backgrounds (e.g., Nordborg 1997; Agrawal and Hartfield 2016) and allows one to decompose the background selection effect into different terms for which intuitive interpretation may be given. In a panmictic population, background selection is driven by the variance in linkage disequilibrium $\langle D_{AB}{}^2\rangle$ between the two loci: neutral alleles that become associated to the deleterious allele tend to decrease in frequency, eventually causing their loss from the population. Under partial selfing, background selection is reinforced by random associations between a given neutral allele and selected alleles present on the other haplotype of the same individual ($D_{A,B}$) and associations between neutral alleles and homozygosity at the selected locus ($D_{AB,B}$). Furthermore, we have seen that identity disequilibrium (correlation in heterozygosity between loci) has the opposite effect and enhances neutral diversity when the deleterious allele is partially recessive, but this effect usually stays modest.

Under tight linkage, the results converge to the approximation derived by Nordborg (1997), using a separation of timescales argument. In that case, the population behaves approximately as a panmictic population of size $N/\left(1+F\right),$ in which the dominance coefficient of the deleterious allele and the recombination rate are replaced by the effective parameters $h\left(1-F\right)+F$ and $r\left(1-F\right).$ Similarly, Agrawal and Hartfield (2016) showed that in a population reproducing sexually at rate σ and asexually (by mitosis) at rate $1-\mathit{\sigma },$ the effect of a deleterious allele located at a small recombination distance r from the neutral locus takes the same form as in a panmictic (fully sexual) population, replacing r by the effective recombination rate $r\sigma$ (as shown in Appendix C, the effect of partial asexuality can also be derived using the methods of the present article). However, Agrawal and Hartfield (2016) also showed that this tight linkage approximation underestimates the strength of background selection caused by loosely linked loci, which becomes important when sex is rare. We have seen that a similar result holds under partial selfing: at high selfing rates, neutral diversity may be significantly affected by loosely linked deleterious alleles, whose effect is underestimated by the tight linkage approximation. In that case, a more precise approximation is provided by Equation 34 above.

As mentioned previously (Nordborg 1997), assuming multiplicative effects of deleterious alleles at different loci on neutral diversity (Equation 35) should be less accurate under partial selfing than under random mating, since inbreeding generates different forms of genetic associations between those loci (e.g., Kamran-Disfani and Agrawal 2014; Roze 2015). Nevertheless, we have seen that Equation 35 yields accurate predictions as long as the genomic deleterious mutation rate stays moderate ($U=0.1,$ Figure 2, Figure 3, and Figure 4), so that the average number of deleterious alleles per genome is not too large. Another important assumption of the model is that selection against deleterious alleles is sufficiently strong relative to drift, so that these alleles are maintained near their deterministic mutation–selection equilibrium frequency. In the regime where $N_{\mathrm{e}}s\approx 1$ or lower, sometimes called “interference selection” or a “weak Hill–Robertson interference” regime (e.g., McVean and Charlesworth 2000; Comeron and Kreitman 2002; Good et al. 2014), background selection models assuming $N_{\mathrm{e}}s\gg 1$ may overestimate the effect of deleterious alleles on neutral diversity by several orders of magnitude (Kaiser and Charlesworth 2008; Good et al. 2014). This may possibly be due to negative linkage disequilibria between deleterious alleles generated by the Hill–Robertson effect (Hill and Robertson 1966), reducing the variance in fitness in the population and thus increasing coalescence times. As illustrated in Figure S1, this regime may be particularly important in highly selfing populations and when the deleterious mutation rate U is high, since $N_{\mathrm{e}}$ may be sufficiently reduced to affect the efficiency of selection at an important proportion of selected sites. This is confirmed by empirical observations of higher ratios of nonsynonymous to synonymous polymorphism (${\pi }_{\mathrm{N}}/{\pi }_{\mathrm{S}}$) in selfing lineages than in their outcrossing relatives (Glémin and Muyle 2014; Hartfield 2015 and references therein), indicating that a significant fraction of deleterious alleles may increase in frequency due to drift (in which case the assumption that $N_{\mathrm{e}}s\gg 1$ at most loci is not valid). It is thus important to keep in mind that background selection models such as the one presented here overestimate the reduction in $N_{\mathrm{e}}$ in such situations, and it would be interesting (although probably challenging) to obtain analytical predictions for neutral diversity in populations undergoing low rates of sex or high selfing rates and in which selection against a high proportion of deleterious mutations is rendered ineffective.

More generally, the strong reduction in effective population size of highly selfing (or asexual) populations caused by background selection may have an important influence on stochastic processes that would play a more marginal role in populations with larger $N_{\mathrm{e}}.$ For example, identity disequilibrium between selected loci in a partially selfing population generates positive linkage disequilibrium between these loci, but as shown by Kamran-Disfani and Agrawal (2014), stochastic forces generating negative linkage disequilibrium become stronger than this deterministic effect when the selfing rate is high. In a similar way, deterministic forces acting on the evolution of recombination rates (e.g., Roze and Lenormand 2005) or mutation rates (e.g., Lynch 2010) may be overwhelmed by stochastic forces under strong inbreeding. Developing analytical models that could scale these different types of effects may thus help us to better understand how mating systems affect the evolution of genetic architecture. The methods presented in this article could possibly be used to explore such questions.

Appendices

Appendix A: Deriving Recursions for Multilocus Moments

In the following, I use the notation ${D^{\prime }}_{\mathbb{S},\mathbb{T}}^{}$ for genetic associations measured at the next generation, while $D_{\mathbb{S},\mathbb{T}}^{\mathrm{juv}}$ and $D_{\mathbb{S},\mathbb{T}}^{\mathrm{par}}$ represent associations measured among juveniles (after reproduction, before drift) and among parents after selection (that is, weighting each parent by its relative fitness). Therefore, selection changes associations $D_{\mathbb{S},\mathbb{T}}$ to $D_{\mathbb{S},\mathbb{T}}^{\mathrm{par}},$ recombination and fertilization (with partial selfing) change associations $D_{\mathbb{S},\mathbb{T}}^{\mathrm{par}}$ to $D_{\mathbb{S},\mathbb{T}}^{\mathrm{juv}},$ and drift changes associations $D_{\mathbb{S},\mathbb{T}}^{\mathrm{juv}}$ to ${D^{\prime }}_{\mathbb{S},\mathbb{T}}^{}.$ Similarly, ${p^{\prime }}_i$ denotes allele frequencies at the next generation, while $p_i^{\mathrm{juv}}$ represents allele frequencies among juveniles (which are the same as among selected parents, as recombination and fertilization do not change allele frequencies). In the following I show how to derive equations representing these different steps. For this, I focus on examples rather than presenting general (and necessarily cumbersome) equations; however, general expressions are implemented in a Mathematica notebook (File S1). Throughout this article, I assume that selection is weak (s small) and that population size is sufficiently large so that $1/N\ll s,r;$ however, no assumption is done on the relative orders of magnitude of r and s. Finally, I assume that $u\ll s$ so that the frequency of the deleterious allele at mutation–selection balance (${\tilde{p}}_B,$ given by Equation 2) is small.

Drift

To illustrate the effect of drift on genetic moments, consider the expected diversity at the neutral locus, $\langle D_{AA}\rangle .$ By definition, $\langle {D^{\prime }}_{AA}^{}\rangle =\langle \left(1/2\right){\mathrm{E}}^{\prime }\left[{\left(X_A^M-{p^{\prime }}_A\right)}^2+{\left(X_A^P-{p^{\prime }}_A\right)}^2\right]\rangle ,$ where ${\mathrm{E}}^{\prime }$ is the average over all individuals of the next generation, while ${p^{\prime }}_A$ is the frequency of allele 1 at locus A among these individuals. Writing ${\mathrm{\Delta }}_d{p}_A={p^{\prime }}_A-p_A^{juv}$ the change in allele frequency due to drift, we have

$$\langle {D^{\prime }}_{AA}^{}\rangle =\langle \frac{1}{2}{\mathrm{E}}^{\prime }\left[{\left(X_A^M-p_A^{juv}-{\Delta }_d{p}_A\right)}^2+{\left(X_A^P-p_A^{juv}-{\Delta }_d{p}_A\right)}^2\right]\rangle .$$ (A1)

Expanding and grouping terms in ${\mathrm{\Delta }}_d{p}_A,$ this is

$$\begin{array}{c}\langle {D^{\prime }}_{AA}^{}\rangle =\langle \frac{1}{2}{\mathrm{E}}^{\prime }\left[{\left(X_A^M-p_A^{juv}\right)}^2+{\left(X_A^P-p_A^{juv}\right)}^2\right]\rangle \\ -2\langle {\mathrm{\Delta }}_d{p}_A\frac{1}{2}{\mathrm{E}}^{\prime }\left[\left(X_A^M-p_A^{juv}\right)+\left(X_A^P-p_A^{juv}\right)\right]\rangle +\langle {\left({\mathrm{\Delta }}_d{p}_A\right)}^2\rangle .\end{array}$$ (A2)

In the following, I use the notation $D_{\mathbb{S},\mathbb{T}}^{dft}$ for moments measured among individuals of the next generation (after drift), but using the values of allele frequencies (called “reference values” in Kirkpatrick et al. 2002) before drift (among juveniles): in particular, $D_{AA}^{dft}=\frac{1}{2}{\mathrm{E}}^{\prime }\left[{\left(X_A^M-p_A^{juv}\right)}^2+{\left(X_A^P-p_A^{juv}\right)}^2\right],$ while we have $D_A^{dft}=\frac{1}{2}{\mathrm{E}}^{\prime }\left[\left(X_A^M-p_A^{juv}\right)+\left(X_A^P-p_A^{juv}\right)\right].$ Noting that $D_A^{dft}={\mathrm{\Delta }}_d{p}_A,$ Equation A2 can be written as

$$\langle {D^{\prime }}_{AA}^{}\rangle =\langle D_{AA}^{dft}\rangle -\langle {\left(D_A^{dft}\right)}^2\rangle .$$ (A3)

Next, we can note that products of genetic associations may also be viewed as associations between genes present in two individuals, sampled with replacement from the whole population: for example, ${\left(D_A^{dft}\right)}^2$ is the association between one gene at locus A from a first individual and one gene at locus A from a second individual sampled with replacement from the population at the next generation (and using allele frequencies among juveniles as reference values). Following previous works (Roze and Rousset 2008; Roze 2009; Roze and Michod 2010), I thus write such products as single associations, using the symbol $\stackrel{⌢}{/}$ to separate sets of genes present in different individuals sampled with replacement from the population. Using this notation, ${\left(D_A^{dft}\right)}^2$ is written as $D_{A\stackrel{⌢}{/}A}^{dft},$ and Equation A3 becomes

$$\langle {D^{\prime }}_{AA}^{}\rangle =\langle D_{AA}^{dft}\rangle -\langle D_{A\stackrel{⌢}{/}A}^{dft}\rangle .$$ (A4)

Equation A4 corresponds to the first step of the computation of the effect of drift on genetic moments (i.e., taking into account changes in allele frequencies due to drift). The second (and last) step consists of expressing associations between genes present in different individuals sampled with replacement from the population (at the next generation) in terms of associations between genes in individuals sampled without replacement. For example, we have

$$\langle D_{A\stackrel{⌢}{/}A}^{dft}\rangle =\frac{1}{2N}\left(\langle D_{AA}^{dft}\rangle +\langle D_{A,A}^{dft}\rangle \right)+\left(1-\frac{1}{N}\right)\langle D_{A/A}^{dft}\rangle ,$$ (A5)

where $D_{A/A}^{dft}$ is the association between two genes at locus A from two individuals sampled without replacement, at the next generation (and using allele frequencies before drift as reference values). Indeed, two genes sampled with replacement from the population may be the same gene with probability $1/\left(2N\right),$ be the two homologous copies of the same individual with probability $1/\left(2N\right),$ or come from two different individuals with probability $1-1/N.$ Finally, because the different individuals of the next generation have been sampled independently from an infinite population of juveniles, associations between genes present in different individuals (and using as reference values allele frequencies among juveniles) are the same as associations measured among juveniles: in particular, $\langle D_{AA}^{dft}\rangle =\langle D_{AA}^{juv}\rangle ,$ $\langle D_{A,A}^{dft}\rangle =\langle D_{A,A}^{juv}\rangle ,$ and $\langle D_{A/A}^{dft}\rangle =\langle D_{A/A}^{juv}\rangle .$ Noting that $\langle D_{A/A}^{juv}\rangle =0$ [indeed, because the population of juveniles is infinite, we have $D_{A/A}^{juv}=D_{A\stackrel{⌢}{/}A}^{juv}={\left(D_A^{juv}\right)}^2,$ while $D_A^{juv}=0$ from the definition of genetic associations], we finally obtain

$$\langle {D^{\prime }}_{AA}^{}\rangle =\langle D_{AA}^{juv}\rangle -\frac{1}{2N}\left(\langle D_{AA}^{juv}\rangle +\langle D_{A,A}^{juv}\rangle \right),$$ (A6)

representing the effect of drift on the moment $\langle D_{AA}\rangle .$ Because all results are computed to the first order in $1/N,$ it is sufficient to express the moments that are multiplied by $1/\left(2N\right)$ in Equation A6 in the limit as N tends to infinity.

The same method can be used to compute the effect of drift on other genetic moments. For example, using the same reasoning as for deriving Equation A4 above, we obtain for the expected squared linkage disequilibrium

$$\langle {D^{\prime }}_{AB}^{}{}^2\rangle =\langle D_{AB\stackrel{⌢}{/}AB}^{dft}\rangle -2\langle D_{AB\stackrel{⌢}{/}A\stackrel{⌢}{/}B}^{dft}\rangle +\langle D_{A\stackrel{⌢}{/}A\stackrel{⌢}{/}B\stackrel{⌢}{/}B}^{dft}\rangle ,$$ (A7)

while computing these moments in terms of associations among juveniles yields

$$\langle {D^{\prime }}_{AB}^{}{}^2\rangle =\langle D_{AB}^{juv2}\rangle +\frac{1}{2N}\left(\langle D_{AABB}^{juv}\rangle +\langle D_{AB,AB}^{juv}\rangle -2\langle D_{AB}^{juv}{D}_{A,B}^{juv}\rangle -4\langle D_{AB}^{juv2}\rangle \right)+o\left(\frac{1}{N}\right).$$ (A8)

Again, because all results are computed to the first order in $1/N,$ it is sufficient to compute the four moments within parentheses in Equation A8 in the limit as population size tends to infinity [we will see below that the moments $\langle D_{AB}^{juv}{D}_{A,B}^{juv}\rangle$ and $\langle D_{AB}^{juv2}\rangle$ become negligible in this limit, while the moment $\langle D_{AB,AB}^{juv}\rangle$ is generated by selfing].

Equation A8 shows that genetic associations with repeated “B” indices (such as $D_{AABB}$) may appear within recursions (see also Equation A12). Because locus B is biallelic, these repeated indices can be eliminated using the relation (e.g., equation 5 in Kirkpatrick et al. 2002)

$$D_{\mathbb{S}ii}=p_i{q}_i{D}_{\mathbb{S}}+\left(1-2p_i\right)D_{\mathbb{S}i},$$ (A9)

where $\mathbb{S}$ is any set of loci, and i is a biallelic locus. However, repeated “A” indices will not be eliminated when computing recursions, so that the equations obtained still hold for the case where more than two alleles segregate at the neutral locus.

Recombination and fertilization

Computing moments measured among juveniles in terms of moments measured among selected parents is somewhat simpler, as recombination and fertilization do not change allele frequencies: therefore, we only have to consider the different possible modes of transmission of genes between generations. In particular, $\langle D_{AA}^{juv}\rangle =\langle D_{AA}^{par}\rangle ,$ while

$$\langle D_{A,A}^{juv}\rangle =\frac{\alpha }{2}\left(\langle D_{AA}^{par}\rangle +\langle D_{A,A}^{par}\rangle \right).$$ (A10)

Indeed, the two homologous genes of a juvenile at locus A come from the same parent if this juvenile has been produced by selfing (probability α), in which case they are copies of the same parental gene with probability 1/2, while they come from the two homologous genes of the parent with probability $1/2.$ With probability $1-\mathit{\alpha }$ the juvenile has been produced by outcrossing, in which case its two homologous genes are sampled with replacement from the parental population: the association thus becomes $D_{A\stackrel{⌢}{/}A}^{par}={\left(D_A^{par}\right)}^2,$ which equals zero (since $D_A^{par}=0$). Similarly, we have

$$\begin{array}{c}\langle D_{AB}^{juv}{}^2\rangle =\langle D_{AB\stackrel{⌢}{/}AB}^{juv}\rangle ={\left(1-r\right)}^2\langle D_{AB\stackrel{⌢}{/}AB}^{par}\rangle +2r\left(1-r\right)\langle D_{AB\stackrel{⌢}{/}A,B}^{par}\rangle \\ +r^2\langle D_{A,B\stackrel{⌢}{/}A,B}^{par}\rangle ,\end{array}$$ (A11)

while

$$\begin{array}{c}\langle D_{AB,AB}^{juv}\rangle =\frac{\alpha }{2}[{\left(1-r\right)}^2\left(\langle D_{AABB}^{par}\rangle +\langle D_{AB,AB}^{par}\rangle \right)\\ +2r\left(1-r\right)\left(\langle D_{AAB,B}^{par}\rangle +\langle D_{ABB,A}^{par}\rangle \right)\\ +r^2\left(\langle D_{AABB}^{par}\rangle +\langle D_{AB,AB}^{par}\rangle \right)]+\left(1-\alpha \right)\langle D_{AB\stackrel{⌢}{/}AB}^{juv}\rangle ,\end{array}$$ (A12)

where $\langle D_{AB\stackrel{⌢}{/}AB}^{juv}\rangle$ is given by Equation A11.

Selection

As for the effect of drift, computing the effect of selection on genetic moments can be decomposed into two steps (see also Barton and Turelli 1991; Kirkpatrick et al. 2002). The first step consists in taking into account the change in reference values (i.e., allele frequencies that appear within associations) due to selection: denoting $D_{\mathbb{S},\mathbb{T}}^{sel}$ moments measured among selected parents, but using allele frequencies before selection ($p_i$) as reference values (instead of allele frequencies after selection $p_i^{\mathrm{juv}}$), we have (following the same reasoning as for the derivation of Equations A4 and A7)

$$\langle D_{AA}^{par}\rangle =\langle D_{AA}^{sel}\rangle -\langle D_{A\stackrel{⌢}{/}A}^{sel}\rangle ,$$ (A13)

while

$$\langle D_{AB\stackrel{⌢}{/}AB}^{par}\rangle =\langle D_{AB\stackrel{⌢}{/}AB}^{sel}\rangle -2\langle D_{AB\stackrel{⌢}{/}A\stackrel{⌢}{/}B}^{sel}\rangle +\langle D_{A\stackrel{⌢}{/}A\stackrel{⌢}{/}B\stackrel{⌢}{/}B}^{sel}\rangle .$$ (A14)

Finally, computing associations measured after selection (using as reference values allele frequencies before selection) $D_{\mathbb{S},\mathbb{T}}^{sel},$ in terms of associations measured before selection $D_{\mathbb{S},\mathbb{T}},$ is done by weighting each individual by its relative fitness

$$D_{\mathbb{S},\mathbb{T}}^{sel}=\mathrm{E}\left[\frac{W}{\overline{W}}{\zeta }_{\mathbb{S},\mathbb{T}}\right],$$ (A15)

where E is the average over all individuals before selection, W is the fitness of the individual, and $\overline{W}=\mathrm{E}\left[W\right]$ is the mean fitness of the population. To express the right-hand side of Equation A15 in terms of genetic associations, it is useful to write $W/\overline{W}$ in terms of ${\mathit{\zeta }}_{\mathbb{S},\mathbb{T}}$ variables (e.g., Barton and Turelli 1991; Kirkpatrick et al. 2002). The fitness of an individual can be written as

$$W=1-sh\left(X_B^M+X_B^P\right)-s\left(1-2h\right)X_B^M{X}_B^P,$$ (A16)

which, after rearranging and averaging over all individuals, yields

$$\frac{W}{\overline{W}}=\frac{1-C-sh\left({\zeta }_B^M+{\zeta }_B^P\right)-s\left(1-2h\right)\left[{\zeta }_{B,B}+p_B\left({\zeta }_B^M+{\zeta }_B^P\right)\right]}{1-C-s\left(1-2h\right)D_{B,B}}$$ (A17)

with $C=2sh{p}_B+s\left(1-2h\right)p_B{}^2.$ Equation A17 thus takes the form of a polynomial of ${\zeta }_{\mathbb{S},\mathbb{T}}$ variables. However, because terms in $p_B$ and $D_{B,B}$ appear in the denominator, obtaining expressions in terms of moments of genetic associations and allele frequencies requires developing $W/\overline{W}$ as a Taylor series in s. To the first order in s, we have

$$\frac{W}{\overline{W}}=1-sh\left({\zeta }_B^M+{\zeta }_B^P\right)-s\left(1-2h\right)\left[{\zeta }_{B,B}-D_{B,B}+p_B\left({\zeta }_B^M+{\zeta }_B^P\right)\right].$$ (A18)

From this, we obtain, to the first order in s,

$$\begin{array}{c}\langle D_{AA}^{sel}\rangle =\langle \mathrm{E}\left[\frac{W}{\overline{W}}{\zeta }_{AA}\right]\rangle \\ =\langle D_{AA}\rangle -sh\left(\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle \right)\\ -s\left(1-2h\right)\left(\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle +\langle p_B{D}_{AAB}\rangle +\langle p_B{D}_{AA,B}\rangle \right).\end{array}$$ (A19)

Given that moments $\langle p_B{D}_{AAB}\rangle$ and $\langle p_B{D}_{AA,B}\rangle$ equal zero at quasi-equilibrium to the first order in $1/N$ and ${\tilde{p}}_B$ (see File S1), Equation A19 yields Equation 12 in the main text. Associations between genes present in different individuals are obtained similarly. For example, $\langle D_{A\stackrel{⌢}{/}A}^{sel}\rangle$ equals zero to the first order in s (because $D_A=0$), while Equation A18 yields the following expression to the second order in s:

$$\begin{array}{c}\langle D_{A\stackrel{⌢}{/}A}^{sel}\rangle =\langle E\left[\frac{W}{\overline{W}}{\zeta }_A\right]E\left[\frac{W}{\overline{W}}{\zeta }_A\right]\rangle \\ ={\left(sh\right)}^2\left(\langle D_{AB\stackrel{⌢}{/}AB}\rangle +2\langle D_{AB\stackrel{⌢}{/}A,B}\rangle +\langle D_{A,B\stackrel{⌢}{/}A,B}\rangle \right)\\ +2s^{2}h\left(1-2h\right)(\langle D_{AB\stackrel{⌢}{/}AB,B}\rangle +\langle D_{A,B\stackrel{⌢}{/}AB,B}\rangle \\ +\langle p_B{D}_{AB\stackrel{⌢}{/}AB}\rangle +2\langle p_B{D}_{AB\stackrel{⌢}{/}A,B}\rangle +\langle p_B{D}_{A,B\stackrel{⌢}{/}A,B}\rangle )\\ +s^2{\left(1-2h\right)}^2(\langle D_{AB,B\stackrel{⌢}{/}AB,B}\rangle +2\langle p_B{D}_{AB\stackrel{⌢}{/}AB,B}\rangle +2\langle p_B{D}_{A,B\stackrel{⌢}{/}AB,B}\rangle \\ +\langle p_B{}^2{D}_{AB\stackrel{⌢}{/}AB}\rangle +2\langle p_B{}^2{D}_{AB\stackrel{⌢}{/}A,B}\rangle +\langle p_B{}^2{D}_{A,B\stackrel{⌢}{/}A,B}\rangle ).\end{array}$$ (A20)

Equations A19 and A20 illustrate the fact that computing the effect of selection on a given genetic moment introduces more complicated moments, with a higher number of B indices. This may lead to an infinite system of recursions, as the effect of selection on these moments will introduce yet other moments with even more B indices. However, assuming $Ns\gg 1$ and $s\gg u$ (so that the frequency of the deleterious allele at mutation–selection balance, ${\tilde{p}}_B,$ remains small), we may neglect moments that are proportional to ${\tilde{p}}_B{}^2$—more precisely, moments that are $o\left({\tilde{p}}_B\right)$—to obtain expressions to the first order in ${\tilde{p}}_B.$ As we will see, using this “rare allele approximation” yields closed systems of recursions for genetic moments.

Rare allele approximation

Deriving expressions to the first order in ${\tilde{p}}_B$ can be done using the following general rule. Because all genetic associations involving at least one B index are proportional to $p_B,$ moments involving two elements with a B index (where an element is either an allele frequency $p_i$ or an association $D_{\mathbb{S},\mathbb{T}}$ among genes present in the same individual) are of order ${\tilde{p}}_B{}^2$ in the limit as population size tends to infinity. For example, $\langle p_B{D}_{AB}\rangle ,$ $\langle D_{AB}{}^2\rangle ,$ and $\langle D_{AB}{D}_{AB,B}\rangle$ are all of order ${\tilde{p}}_B{}^2$ as N tends to infinity, while $\langle D_{B,B}\rangle$ and $\langle D_{AB,AB}\rangle$ are of order ${\tilde{p}}_B$ in the same limit. Now, taking the effect of drift into account when computing recursions for genetic moments generally introduces moments with one less element carrying a B index, multiplied by $1/N.$ This is illustrated by Equation A8 showing the effect of drift on the moment $\langle D_{AB}{}^2\rangle$ (two elements with a B index): drift introduces two terms involving moments carrying a single element with a B index ($\langle D_{AABB}\rangle$ and $\langle D_{AB,AB}\rangle$). Because these moments are multiplied by $1/N$ in Equation A8, it is sufficient to express them in the limit as N tends to infinity: in this limit, these terms are thus proportional to ${\tilde{p}}_B$ (by contrast, the terms in $\langle D_{AB}{}^2\rangle /N$ and $\langle D_{AB}{D}_{A,B}\rangle /N$ in Equation A8 are proportional to ${\tilde{p}}_B{}^2$ and may thus be neglected). More generally, moments carrying x elements with a B index are thus of order ${\tilde{p}}_B{}^x$ in the limit as N tends to infinity and of order ${\tilde{p}}_B{}^{x-1}$ to the first order in $1/N$ (for $x>1$). To compute expressions to the first order in ${\tilde{p}}_B,$ we may thus neglect all moments that must be expressed to the first order in $1/N$ and that carry more than two elements with a B index (such as $\langle p_B{D}_{AB}{D}_{AB,B}\rangle$) and all moments expressed in the limit as N tends to infinity carrying more than one element with a B index (such as $\langle D_{AB}{}^2\rangle$). Using this approximation, Equation A20 simplifies to

$$\begin{array}{c}\langle D_{A\stackrel{⌢}{/}A}^{\mathrm{sel}}\rangle ={\left(sh\right)}^2\left(\langle D_{AB}{}^2\rangle +2\langle D_{AB}{D}_{A,B}\rangle +\langle D_{A,B}{}^2\rangle \right)\\ +2s^{2}h\left(1-2h\right)\left(\langle D_{AB}{D}_{AB,B}\rangle +\langle D_{A,B}{D}_{AB,B}\rangle \right)\\ +s^2{\left(1-2h\right)}^2\langle D_{AB,B}{}^2\rangle .\end{array}$$ (A21)

Furthermore, we obtain for the moments $\langle D_{AB\stackrel{⌢}{/}AB}^{\mathrm{par}}\rangle ,$ $\langle D_{AB\stackrel{⌢}{/}A,B}^{\mathrm{par}}\rangle ,$ and $\langle D_{A,B\stackrel{⌢}{/}A,B}^{\mathrm{par}}\rangle$ (that are needed to compute a recursion for $\langle D_{AB}{}^2\rangle$, as shown by Equation A11), to the first order in s

$$\langle D_{AB\stackrel{⌢}{/}AB}^{\mathrm{par}}\rangle =\left(1-2sh\right)\langle D_{AB}{}^2\rangle -2s\left(1-h\right)\langle D_{AB}{D}_{AB,B}\rangle$$ (A22)

$$\langle D_{AB\stackrel{⌢}{/}A,B}^{\mathrm{par}}\rangle =\left(1-2sh\right)\langle D_{AB}{D}_{A,B}\rangle -s\left(1-h\right)\left(\langle D_{AB}{D}_{AB,B}\rangle +\langle D_{A,B}{D}_{AB,B}\rangle \right)$$ (A23)

$$\langle D_{A,B\stackrel{⌢}{/}A,B}^{\mathrm{par}}\rangle =\left(1-2sh\right)\langle D_{A,B}{}^2\rangle -2s\left(1-h\right)\langle D_{A,B}{D}_{AB,B}\rangle .$$ (A24)

Appendix B: Recursions for Two-Locus Moments

Using the method shown in Appendix A, we obtain for the change in neutral diversity during selection, to the second order in s,

$$\begin{array}{c}\langle {\Delta }_{\mathrm{s}}{D}_{AA}\rangle =-sh\left(\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle \right)\\ -s\left(1-2h\right)\left(\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle \right)\\ -{\left(sh\right)}^2\left(\langle D_{AB}{}^2\rangle +2\langle D_{AB}{D}_{A,B}\rangle +\langle D_{A,B}{}^2\rangle \right)\\ -2s^{2}h\left(1-2h\right)\left(\langle D_{AB}{D}_{AB,B}\rangle +\langle D_{A,B}{D}_{AB,B}\rangle \right)\\ -s^2{\left(1-2h\right)}^2\langle D_{AB,B}{}^2\rangle ,\end{array}$$ (B1)

while the change in neutral diversity during drift is given by Equation 9 in the main text. The same method can be used to compute recursions for the different moments that appear in Equation B1, from which solutions at quasi-equilibrium can be obtained. For example, Equations A8, A11, and A22–A24 yield the following recursion for $\langle D_{AB}{}^2\rangle :$

$$\langle {D^{\prime }}_{AB}^{}{}^2\rangle =\left(1-2sh\right)\left[{\left(1-r\right)}^2\langle D_{AB}{}^2\rangle +2r\left(1-r\right)\langle D_{AB}{D}_{A,B}\rangle +r^2\langle D_{A,B}{}^2\rangle \right]-2s\left(1-h\right)\left[\left(1-r\right)\langle D_{AB}{D}_{AB,B}\rangle +r\langle D_{A,B}{D}_{AB,B}\rangle \right]+\frac{1}{2N}\left(\langle D_{AABB}\rangle +\langle D_{AB,AB}\rangle \right).$$ (B2)

To obtain an expression to the first order in $1/N,$ it is sufficient to express $\langle D_{AABB}\rangle$ and $\langle D_{AB,AB}\rangle$ in Equation B2 in the limit when N tends to infinity. Using Equation A9, we have $D_{AABB}=p_B{q}_B{D}_{AA}+\left(1-2p_B\right)D_{AAB}.$ Furthermore, $D_{AAB}$ equals zero at quasi-equilibrium in an infinite population (indeed, the solution obtained for $\langle D_{AAB}\rangle$ from the equations below is in $1/N$): therefore, $\langle D_{AABB}\rangle \approx {\tilde{p}}_B\langle D_{AA}\rangle$ when population size tends to infinity. From Equation A12, a recursion for $\langle D_{AB,AB}\rangle$ when N tends to infinity and $s=0$ is given by

$$\begin{array}{c}\langle {D^{\prime }}_{AB,AB}^{}\rangle =\frac{\alpha }{2}[\left[1-2r\left(1-r\right)\right]\left(\langle D_{AABB}\rangle +\langle D_{AB,AB}\rangle \right)\\ +2r\left(1-r\right)\left(\langle D_{AAB,B}\rangle +\langle D_{ABB,A}\rangle \right)].\end{array}$$ (B3)

Using $\langle D_{AABB}\rangle \approx {\tilde{p}}_B\langle D_{AA}\rangle$ and $\langle D_{AAB,B}\rangle =\langle D_{ABB,A}\rangle \approx F{\tilde{p}}_B\langle D_{AA}\rangle$ yields $\langle D_{AB,AB}\rangle ={\phi }_{AB}{\tilde{p}}_B\langle D_{AA}\rangle ,$ where ${\phi }_{AB}$ is given by Equation 14, and corresponds to the probability of joint coalescence of two pairs of genes sampled at loci A and B due to selfing, in an infinite population. It is possible to compute ${\phi }_{AB}$ to the first order in s, but the term in s is always negligible when selection is weak and is thus ignored here. Using the expressions just derived for $\langle D_{AABB}\rangle$ and $\langle D_{AB,AB}\rangle ,$ Equation B2 becomes

$$\begin{array}{c}\langle {D^{\prime }}_{AB}^{}{}^2\rangle =\left(1-2sh\right)\left[{\left(1-r\right)}^2\langle D_{AB}{}^2\rangle +2r\left(1-r\right)\langle D_{AB}{D}_{A,B}\rangle +r^2\langle D_{A,B}{}^2\rangle \right]\\ -2s\left(1-h\right)\left[\left(1-r\right)\langle D_{AB}{D}_{AB,B}\rangle +r\langle D_{A,B}{D}_{AB,B}\rangle \right]\\ +\frac{1}{2N}\left(1+{\phi }_{AB}\right){\tilde{p}}_B\langle D_{AA}\rangle .\end{array}$$ (B4)

Similarly, we obtain the following recursions for moments $\langle D_{AB}{D}_{A,B}\rangle ,$ $\langle D_{A,B}{}^2\rangle ,$ $\langle D_{AB}{D}_{AB,B}\rangle ,$ $\langle D_{A,B}{D}_{AB,B}\rangle ,$ and $\langle D_{AB,B}{}^2\rangle$ (which are also generated by finite population size), to the first order in s, ${\tilde{p}}_B,$ and $1/N$ (recursions to the second order in s are derived in File S1, but yield very similar quantitative results in most cases):

$$\begin{array}{c}\langle {D^{\prime }}_{AB}^{}{D^{\prime }}_{A,B}^{}\rangle =\frac{\alpha }{2}[\left(1-2sh\right)\left[\left(1-r\right)\langle D_{AB}{}^2\rangle +\langle D_{AB}{D}_{A,B}\rangle +r\langle D_{A,B}{}^2\rangle \right]\\ -s\left(1-h\right)[\left(2\left(1-r\right)+1\right)\langle D_{AB}{D}_{AB,B}\rangle \\ +\left(2r+1\right)\langle D_{A,B}{D}_{AB,B}\rangle ]]+\frac{1}{N}F{\tilde{p}}_B\langle D_{AA}\rangle \end{array}$$ (B5)

$$\begin{array}{c}\langle {D^{\prime }}_{A,B}^{}{}^2\rangle ={\left(\frac{\alpha }{2}\right)}^2[\left(1-2sh\right)\left(\langle D_{AB}{}^2\rangle +2\langle D_{AB}{D}_{A,B}\rangle +\langle D_{A,B}{}^2\rangle \right)\\ -4s\left(1-h\right)\left(\langle D_{AB}{D}_{AB,B}\rangle +\langle D_{A,B}{D}_{AB,B}\rangle \right)]\\ +\frac{1}{2N}\left(1+{\phi }_{AB}\right){\tilde{p}}_B\langle D_{AA}\rangle \end{array}$$ (B6)

$$\begin{array}{c}\langle {D^{\prime }}_{AB}^{}{D^{\prime }}_{AB,B}^{}\rangle =\frac{\alpha }{2}\left[\left(1-2sh\right)[{\left(1-r\right)}^2\langle D_{AB}{}^2\rangle +2r\left(1-r\right)\langle D_{AB}{D}_{A,B}\rangle +r^2\langle D_{A,B}{}^2\rangle \right]\\ +\left[1-s\left(3-h\right)\right]\left[\left(1-r\right)\langle D_{AB}{D}_{AB,B}\rangle +r\langle D_{A,B}{D}_{AB,B}\rangle \right]\\ -s\left(1-h\right)\langle D_{AB,B}{}^2\rangle ]+\frac{1}{2N}\left(F+{\phi }_{AB}\right){\tilde{p}}_B\langle D_{AA}\rangle \end{array}$$ (B7)

$$\begin{array}{c}\langle {D^{\prime }}_{A,B}^{}{D^{\prime }}_{AB,B}^{}\rangle ={\left(\frac{\alpha }{2}\right)}^2\left[\left(1-2sh\right)[\left(1-r\right)\langle D_{AB}{}^2\rangle +\langle D_{AB}{D}_{A,B}\rangle +r\langle D_{A,B}{}^2\rangle \right]\\ +\left(1-2s\right)\left(\langle D_{AB}{D}_{AB,B}\rangle +\langle D_{A,B}{D}_{AB,B}\rangle \right)\\ -2s\left(1-h\right)\left[\left(1-r\right)\langle D_{AB}{D}_{AB,B}\rangle +r\langle D_{A,B}{D}_{AB,B}\rangle \right]\\ -2s\left(1-h\right)\langle D_{AB,B}{}^2\rangle ]+\frac{1}{2N}\left(F+{\phi }_{AB}\right){\tilde{p}}_B\langle D_{AA}\rangle \end{array}$$ (B8)

$$\begin{array}{c}\langle {D^{\prime }}_{AB,B}^{}{}^2\rangle ={\left(\frac{\alpha }{2}\right)}^2[\left(1-2sh\right)\left[{\left(1-r\right)}^2\langle D_{AB}{}^2\rangle +2r\left(1-r\right)\langle D_{AB}{D}_{A,B}\rangle +r^2\langle D_{A,B}{}^2\rangle \right]\\ +2\left(1-2s\right)\left[\left(1-r\right)\langle D_{AB}{D}_{AB,B}\rangle +r\langle D_{A,B}{D}_{AB,B}\rangle \right]\\ +\left[1-2s\left(2-h\right)\right]\langle D_{AB,B}{}^2\rangle ]+\frac{1}{2N}\left(F+{\phi }_{AB}\right){\tilde{p}}_B\langle D_{AA}\rangle .\end{array}$$ (B9)

Equations B4–B9 can be solved at quasi-equilibrium (setting $\langle {\mathrm{ℳ}}^{\prime }\rangle =\langle \mathrm{ℳ}\rangle$ for each moment) to obtain expressions for the six moments of the form $Z{\tilde{p}}_B\langle D_{AA}\rangle /N,$ where Z is a function (that differs for each moment) of s, h, r, and α. Although these expressions are complicated, they are easily computed numerically using Mathematica (see File S2).

Recursions for the moments $\langle D_{AAB}\rangle$ and $\langle D_{AA,B}\rangle$ that appear on the first line of Equation 12 are given by (to the first order in s, ${\tilde{p}}_B,$ and $1/N$)

$$\begin{array}{c}\langle {D^{\prime }}_{AAB}^{}\rangle =\left(1-sh\right)\left[\left(1-r\right)\langle D_{AAB}\rangle +r\langle D_{AA,B}\rangle \right]\\ +2sh\left[\left(1-r\right)\langle D_{AB}{}^2\rangle +\langle D_{AB}{D}_{A,B}\rangle +r\langle D_{A,B}{}^2\rangle \right]\\ +2s\left(1-2h\right)\left[\left(1-r\right)\langle D_{AB}{D}_{AB,B}\rangle +r\langle D_{A,B}{D}_{AB,B}\rangle \right]\\ -s\left(1-h\right)\left(\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle \right)-\frac{1}{N}\langle D_{AB,A}\rangle \end{array}$$ (B10)

$$\begin{array}{c}\langle {D^{\prime }}_{AA,B}^{}\rangle =\frac{\alpha }{2}[\left(1-sh\right)\left(\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle \right)\\ +2sh\left(\langle D_{AB}{}^2\rangle +2\langle D_{AB}{D}_{A,B}\rangle +\langle D_{A,B}{}^2\rangle \right)\\ +2s\left(1-2h\right)\left(\langle D_{AB}{D}_{AB,B}\rangle +\langle D_{A,B}{D}_{AB,B}\rangle \right)\\ -2s\left(1-h\right)\left(\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle \right)]-\frac{1}{N}\langle D_{AB,A}\rangle .\end{array}$$ (B11)

It is sufficient to express the moment $\langle D_{AB,A}\rangle$ that appears in Equations B10 and B11 in the limit as N tends to infinity. To the first order in s, we have

$$\langle {D^{\prime }}_{AB,A}^{}\rangle =\frac{\alpha }{2}\left[\langle D_{AB,A}\rangle -s\left(1-h\right)\left(\langle D_{AB,AB}\rangle -\langle D_{A,A}{D}_{B,B}\rangle \right)\right],$$ (B12)

giving at quasi-equilibrium

$$\langle D_{AB,A}\rangle =-s\left(1-h\right)F{G}_{AB}{\tilde{p}}_B\langle D_{AA}\rangle$$ (B13)

(see also Roze 2015), where $G_{AB}={\phi }_{AB}-F^2$ is the identity disequilibrium between loci A and B. Finally, a recursion for $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ (second line of Equation 12) to the first order in s, ${\tilde{p}}_B,$ and $1/N$ is given by

$$\begin{array}{c}\langle {D^{\prime }}_{AAB,B}^{}\rangle -\langle {D^{\prime }}_{AA}^{}{D^{\prime }}_{B,B}^{}\rangle =\frac{\alpha }{2}[\left[1-s\left(2-h\right)\right]\left(\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle \right)\\ +\left(1-sh\right)\left[\left(1-r\right)\langle D_{AAB}\rangle +r\langle D_{AA,B}\rangle \right]\\ +2sh\left[\left(1-r\right)\langle D_{AB}{}^2\rangle +\langle D_{AB}{D}_{A,B}\rangle +r\langle D_{A,B}{}^2\rangle \right]\\ +2s\left(1-2h\right)\left[\left(1-r\right)\langle D_{AB}{D}_{AB,B}\rangle +r\langle D_{A,B}{D}_{AB,B}\rangle \right]\\ +2sh\left(\langle D_{AB}{D}_{AB,B}\rangle +\langle D_{A,B}{D}_{AB,B}\rangle \right)\\ +2s\left(1-2h\right)\langle D_{AB,B}{}^2\rangle ]-\frac{1}{2N}{G}_{AB}{\tilde{p}}_B\langle D_{AA}\rangle .\end{array}$$ (B14)

Equations B10, B11, and B14 can be solved to obtain expressions for $\langle D_{AAB}\rangle ,$ $\langle D_{AA,B}\rangle ,$ and $\langle D_{AAB,B}\rangle -\langle D_{AA}{D}_{B,B}\rangle$ at quasi-equilibrium (using the expressions for $\langle D_{AB}{}^2\rangle ,$ $\langle D_{AB}{D}_{A,B}\rangle ,$ $\langle D_{A,B}{}^2\rangle ,$ $\langle D_{AB}{D}_{AB,B}\rangle ,$ $\langle D_{A,B}{D}_{AB,B}\rangle ,$ and $\langle D_{AB,B}{}^2\rangle$ obtained from Equations B4–B9); again, Mathematica commands to obtain numerical solutions can be found in File S2. Approximations for high selfing are obtained by assuming that s and $o=1-\alpha$ are of order ε and expressing Equations B4–B14 to the first order in ε. Similarly, tight linkage approximations are obtained by assuming that s and r are of order ε (see File S1).

Appendix C: Partial Asexuality

Background selection under partial asexuality in diploids has been explored recently by Agrawal and Hartfield (2016), using coalescence models. The method presented in Appendix A can also be used for the case of a population in which a proportion σ of offspring are produced by sexual reproduction each generation (with random gamete fusion) and a proportion $1-\sigma$ by asexual reproduction (mitosis), as shown in Roze and Michod (2010). In particular, we obtain for the change in neutral diversity over one generation (to the second order in s and assuming that h is significantly different from zero)

$$\begin{array}{c}\langle \mathrm{\Delta }{D}_{AA}\rangle =-\frac{\langle D_{AA}\rangle }{2N}-sh\left(\langle D_{AAB}\rangle +\langle D_{AA,B}\rangle \right)\\ -{\left(sh\right)}^2\left(\langle D_{AB}{}^2\rangle +2\langle D_{AB}{D}_{A,B}\rangle +\langle D_{A,B}{}^2\rangle \right).\end{array}$$ (C1)

Recursions for the different moments that appear in Equation C1 are given by [to the first order in $1/N$ and ${\tilde{p}}_B\approx u/\left(sh\right)$]

$$\begin{array}{c}\langle {D^{\prime }}_{AB}^{}{}^2\rangle ={\left(1-sh\right)}^2[{\left(1-r\sigma \right)}^2\langle D_{AB}{}^2\rangle +2r\sigma \left(1-r\sigma \right)\langle D_{AB}{D}_{A,B}\rangle \\ +{\left(r\sigma \right)}^2\langle D_{A,B}{}^2\rangle ]+\frac{1}{2N}{\tilde{p}}_B\langle D_{AA}\rangle \end{array}$$ (C2)

$$\langle {D^{\prime }}_{AB}^{}{D^{\prime }}_{A,B}^{}\rangle ={\left(1-sh\right)}^2\left(1-\sigma \right)\left[\left(1-r\sigma \right)\langle D_{AB}{D}_{A,B}\rangle +r\sigma \langle D_{A,B}{}^2\rangle \right]$$ (C3)

$$\langle {D^{\prime }}_{A,B}^{}{}^2\rangle ={\left(1-sh\right)}^2{\left(1-\sigma \right)}^2\langle D_{A,B}{}^2\rangle +\frac{1}{2N}{\tilde{p}}_B\langle D_{AA}\rangle$$ (C4)

$$\begin{array}{c}\langle {D^{\prime }}_{AAB}^{}\rangle =\left(1-sh\right)\left[\left(1-r\sigma \right)\langle D_{AAB}\rangle +r\sigma \langle D_{AA,B}\rangle \right]\\ +2sh\left[\left(1-r\sigma \right)\langle D_{AB}{}^2\rangle +2\langle D_{AB}{D}_{A,B}\rangle +r\sigma \langle D_{A,B}{}^2\rangle \right]\end{array}$$ (C5)

$$\langle {D^{\prime }}_{AA,B}^{}\rangle =\left[\left(1-\sigma \right)\left(1-sh\right)\langle D_{AA,B}\rangle +2sh(\langle D_{AB}{D}_{A,B}\rangle +\langle D_{A,B}{}^2\rangle ]\right].$$ (C6)

Expressions for $\langle D_{AB}{}^2\rangle ,$ $\langle D_{AB}{D}_{A,B}\rangle ,$ $\langle D_{A,B}{}^2\rangle ,$ $\langle D_{AAB}\rangle ,$ and $\langle D_{AA,B}\rangle$ at quasi-equilibrium can be obtained from Equations C2–C6 and plugged into Equation C1. When the rate of sex σ is small, this yields equations 5 and 6 in Agrawal and Hartfield (2016).