Abstract
Many approaches for inferring adaptive molecular evolution analyze the unfolded site frequency spectrum (SFS), a vector of counts of sites with different numbers of copies of derived alleles in a sample of alleles from a population. Accurate inference of the high-copy-number elements of the SFS is difficult, however, because of misassignment of alleles as derived vs. ancestral. This is a known problem with parsimony using outgroup species. Here we show that the problem is particularly serious if there is variation in the substitution rate among sites brought about by variation in selective constraint levels. We present a new method for inferring the SFS using one or two outgroups that attempts to overcome the problem of misassignment. We show that two outgroups are required for accurate estimation of the SFS if there is substantial variation in selective constraints, which is expected to be the case for nonsynonymous sites in protein-coding genes. We apply the method to estimate unfolded SFSs for synonymous and nonsynonymous sites in a population of Drosophila melanogaster from phase 2 of the Drosophila Population Genomics Project. We use the unfolded spectra to estimate the frequency and strength of advantageous and deleterious mutations and estimate that ∼50% of amino acid substitutions are positively selected but that <0.5% of new amino acid mutations are beneficial, with a scaled selection strength of Nes ≈ 12.
Keywords: adaptation, distribution of fitness effects, Drosophila, site frequency spectrum (SFS)
MOST protein sequences are strongly conserved between closely related species, which suggests that most amino acid–changing mutations are selectively removed from populations (Graur and Li 2000). The nature of the selective forces acting on the mutations that become fixed between species is central to a variety of questions in population genetics. These include understanding the maintenance of variation within species, determining the causes of variation in nucleotide diversity across the genome, and discerning the nature of evolutionary adaptation. Evidence for pervasive selection in the genome comes from observations of positive correlations between nucleotide diversity at putatively neutrally evolving sites and the rate of recombination (Begun and Aquadro 1992) and negative correlations between local genomic diversity and the presence of functional elements (such as protein-coding exons or conserved noncoding elements) (Cai et al. 2009; Hernandez et al. 2011; Lohmueller et al. 2011; Halligan et al. 2013; Enard et al. 2014; Deinum et al. 2015). These correlations are likely to be caused by natural selection acting on functional sites in the genome reducing diversity at linked sites, but the precise nature of the selective forces involved is unresolved because both selective sweeps owing to positive selection and background selection caused by purifying selection can contribute to these patterns.
One approach to discriminating between the contributions of neutral, deleterious, and advantageous substitutions to molecular evolution is based on the McDonald-Kreitman (MK) test (McDonald and Kreitman 1991), which compares within-species polymorphism to between-species divergence. Initially conceived as a test of departure from neutrality in a specific gene, it was subsequently adapted to estimate the proportion of substitutions driven to fixation by positive selection between species for a class of sites in the genome (Fay et al. 2002; Smith and Eyre-Walker 2002). It does not, however, directly provide information on the rate of occurrence of advantageous mutations or on the magnitude of their selective effects. Furthermore, the approach is compromised if there has been a demographic change that alters the fixation probability of selected alleles (either advantageously or disadvantageously), the signature of which is not captured by analysis of the polymorphism data (Eyre-Walker 2002).
Other ways of combining polymorphism and divergence data or focusing on polymorphism data only to infer genome-wide selection may be more fruitful. Andolfatto (2007) and Macpherson et al. (2007) showed that there is a negative correlation between synonymous site polymorphisms and nonsynonymous divergence in Drosophila, and they used this information to estimate the strength of selection and frequency of adaptive protein evolution. Both studies concluded that there is widespread adaptive evolution, but estimates of the strength of selection and frequency of adaptive substitution depended on the size of the genomic window considered in the analyses. A related approach fits a population genetics model to mean reductions in diversity observed around nonsynonymous sites that have experienced a substitution between related species (Sattath et al. 2011). This does not depend on the use of a specific window size. The best-fitting model suggests that there is substantial variation in the fitness effects of adaptive amino acid substitutions in Drosophila, potentially shedding light on the different results of Andolfatto (2007) and Macpherson et al. (2007).
We have previously described an approach that attempts to simultaneously infer the rate and strength of deleterious and beneficial mutations occurring in a class of sites in the genome that exploits the shape of the unfolded site frequency spectrum (uSFS) (Schneider et al. 2011). The uSFS is a vector of counts of nucleotide sites with j copies of the derived allele, where 0 ≤ j ≤ n, and n is the number of gene copies in the sample (i.e., including sites fixed for ancestral or derived alleles). By using the uSFS, information for inferring the strength of selection can come mainly from current polymorphisms within a focal species rather than divergence from an outgroup species. The first step is to infer demographic parameters using the SFS for quasi-neutrally evolving sites, such as synonymous sites. Conditioning on the estimates of the demographic parameters, selection parameters are estimated for a selected site class SFS (e.g., for nonsynonymous sites). These parameters describe the distribution of fitness effects (DFE) for deleterious mutations and the frequency of occurrence and strength of selection for one or more classes of advantageous mutations. Inferring adaptive evolution parameters requires that there is an excess of high-frequency derived variants above and beyond that expected from demographic change and from negative selection acting on the bulk of mutations.
Applying the method of Schneider et al. (2011) or any method that uses the frequencies of high-frequency derived variants therefore depends on accurate inference of the uSFS. Inference of the uSFS is potentially compromised, however, by misassignment of the ancestral state, and this tends to affect high-frequency elements of the SFS disproportionately (Fay and Wu 2000; Baudry and Depaulis 2003; Hernandez et al. 2007; Glémin et al. 2015). Current methods for inferring the uSFS rely on a single outgroup (Hernandez et al. 2007). Schneider et al. (2011) also described a method for inferring the uSFS, but we have recently determined that this tends to overestimate the frequency of high-frequency derived variants (Halligan et al. 2013). Here we present a new method for inferring the uSFS using information from one or two outgroup species, which we thoroughly test by simulations. We apply this method to a recent whole-genome polymorphism data set for protein-coding genes from a sample of Drosophila melanogaster genomes originating from a Rwanda population close to their ancestral range. By use of the inferred uSFS, we estimate the frequencies and effects of deleterious and advantageous amino acid–changing mutations.
Materials and Methods
Inferring the uSFS: basic assumptions
A focal species is sequenced at multiple sites in a cohort of individuals sampled from a population. The possibility of more than two alleles segregating at a site in the focal species is disregarded. The consequences of this simplification are investigated in the simulations described later, which allow multiallelic sites. To infer the uSFS, we need to compute probabilities for the possible states of the alleles ancestral to the observed alleles in the focal species (Figure 1A). We compute these probabilities using information from a single gene copy, assumed to be randomly sampled at each site, from either one or two outgroup species. Polymorphisms in the common ancestor of the outgroup(s) and the focal species are disregarded; bias introduced by violating this assumption is investigated using the simulations. Initially, we assume that all types of base substitution are equally frequent. Distinct transition and transversion rates are subsequently incorporated. The consequences of violating the equal-mutation-rates assumption in the basic method are explored by the simulations.
Figure 1.
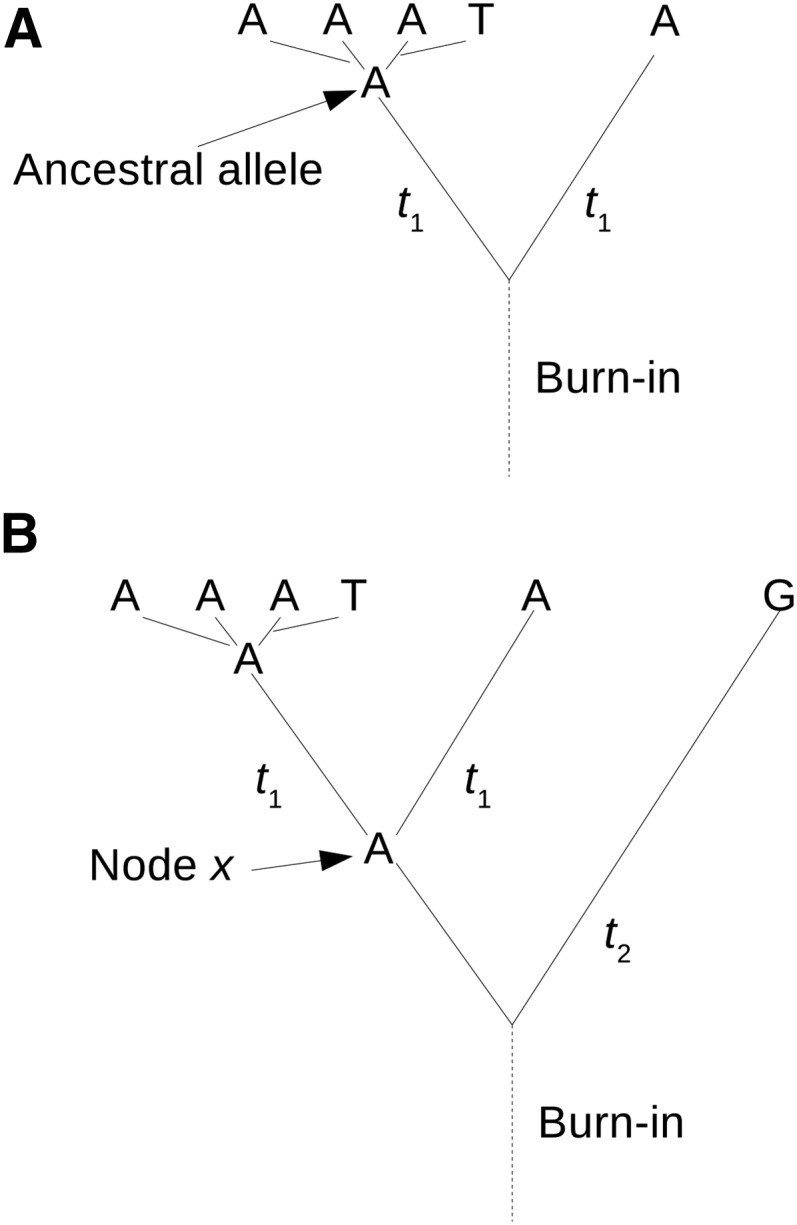
Example of a site at which four copies are sequenced in the focal species, where A is the major allele and the ancestral allele and T is the minor allele. (A) A single outgroup has the same state as the ancestral allele. (B) There are two outgroups and an internal node x. Time t2 is the total number of generations from x to outgroup 2.
Single-outgroup, single-mutation-rate parameter
Here we illustrate the approach for inferring the uSFS assuming a single outgroup and a single evolutionary divergence parameter K. This is the divergence between the allele ancestral to the observed allele(s) in the focal species and a single outgroup (Figure 1A). We do not need to consider mutations from the ancestral allele to the observed segregating alleles in the focal species. In this and the methods that follow (i.e., that allow different transition and transversion rates and two outgroups), a two-stage approach is implemented. First, the evolutionary divergence parameter(s) is estimated by maximum likelihood (ML). Second, assuming perfect knowledge of divergence parameter(s), the elements of the uSFS are estimated one by one by ML.
Single outgroup stage 1: ML estimation of K
Assume that the data consist of counts of numbers of different alleles observed in a sample of n copies in the focal species (n = 4 gene copies in Figure 1 and Table 1, for example) and a single copy from an outgroup species. Let K be the expected number of mutations distinguishing the allele ancestral to these four gene copies and the outgroup. Defining yi as the allelic configuration observed at site i in the focal species and the outgroup, and assuming independence among sites, the likelihood of the data for all sites combined is
| (1) |
If the focal species is monomorphic, there are two possible configurations of alleles (y1 and y2) (Table 1), and there are three configurations if the focal species is polymorphic (y3, y4, and y5) (Table 1). Noting the symmetry of configurations y3 and y4, Equation 1 therefore can be rewritten as
| (2) |
where zx,j is the number of sites showing the configuration with subscript x, given that there are j minor allele copies in the focal species.
Table 1. Five possible configurations (y1, …, y5) of numbers of copies of alleles at a site observed in the focal species and the outgroup for the case of four copies sampled in the focal species.
| Observed state | Conditional probability | |||||
|---|---|---|---|---|---|---|
| Configuration | Focal species | Outgroup | m = no. of mutations | |||
| y1 | AAAA | A | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | |||
| 2 | 1/3 | 0 | 1/3 | |||
| y2 | AAAA | T | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | |||
| 2 | 0 | 2/3 | 2/3 | |||
| y3 | AAAT | A | 0 | 1 | 0 | 1 |
| 1 | 0 | 1/3 | 1/3 | |||
| 2 | 1/3 | 2/9 | 5/9 | |||
| y4 | AAAT | T | 0 | 0 | 1 | 1 |
| 1 | 1/3 | 0 | 1/3 | |||
| 2 | 2/9 | 1/3 | 5/9 | |||
| y5 | AAAT | C | 0 | 0 | 0 | 0 |
| 1 | 2/3 | 2/3 | 4/3 | |||
| 2 | 4/9 | 4/9 | 8/9 | |||
There is either no copy or a single copy of a minor allele present in the focal species (T in this case). Assuming that there are from m = 0 to m = 2 mutations between the ancestral allele of the alleles present in the focal species and the outgroup (Figure 1), the conditional probabilitiesandof observing configuration x given that the ancestral allele is the major or minor allele, respectively, are shown.
Assuming that the number of mutations m is Poisson distributed with probability , the probability of configuration yx, given divergence K, is
| (3) |
where qx,m is the conditional probability for allelic configuration yx given that there are m mutations (Table 1). In practice, we considered only up to two mutations in the summation in Equation 3. Simulations with K up to 20% suggested that allowing more than two mutations had a negligible effect on estimates of K or the SFS elements.
To understand the table, note, for example, the probability q1,0 of observing configuration y1 = 1 if there have been no mutations; it is not possible to observe configuration y1 if there has been one mutation (i.e., q1,1 = 0); q1,2 = 1/3 because if there had been two mutations, nucleotide A could have mutated to any other nucleotide and then must have mutated back to A. The natural log likelihood with respect to K, i.e., log(Equation 2), was maximized by the Golden Search Algorithm (Press et al. 1992).
Single outgroup stage 2: ML estimation of the uSFS elements given K
The approach is to find the ML estimate of the proportion of probability density πj attributable to the major allele being ancestral vs. the minor allele being ancestral for each element of the SFS while assuming the fixed ML estimate of K from stage 1. There are therefore n/2 + 1 ML estimates to be made. To compute the likelihood of πj, we need to consider sites for which there are j copies of one allele and n − j copies of a different allele in the sample of n copies. For invariant sites (j = 0), there are z1,0 and z2,0 sites that have allelic configurations y1 and y2, respectively (Table 1). For variant sites (j ≠ 0), there are three possible allelic configurations (y3, y4, and y5) (Table 1), but sites where the outgroup allele is different from the copies observed in the focal species (configuration y5) provide no information about the uSFS and so can be disregarded. Note that these sites do contribute to the estimate of K. We therefore have z3,j and z4,j sites with the two informative configurations. The likelihood for variant sites that have j minor alleles in the focal species is
| (4) |
where the superscript maj (min) on q implies that the ancestral allele is the major (minor) allele (Table 1). The likelihood for invariant sites in the focal species is
| (5) |
We considered only up to two mutations in the summations in Equations 4 and 5. Log likelihood with respect to each πj was maximized by the Golden Search Algorithm.
This method can be adapted to infer uSFS elements where different transition and transversion rates have been estimated (Supplemental Material, File S1 and Table S1) and where there are two outgroups (File S1 and Table S2).
Simulations
We assessed the performance of the uSFS inference procedures using Monte Carlo simulations, which incorporate the possibility of polymorphisms in the population ancestral to the focal and outgroup species and unequal transition/transversion rates. We analyzed data sets containing large numbers of sites specifying the allelic states for n copies sampled from the population of a focal species and single copies sampled from populations of one or two outgroup species. The simulated populations were diploid and of constant population size N = 100. We generally assumed that the neutral diversity θ = 0.01 by setting the mutation rate per site per generation to μ = θ/4N. We simulated unlinked nucleotide sites that could be in one of four states (A, T, C, or G). An ancestral population was initiated with equal frequencies of the four nucleotides and allowed to evolve to mutation-drift equilibrium for 20N burn-in generations. A site of an individual was mutated with probability μ each generation by randomly altering its current nucleotide state. In general, the probability of a transition mutation was equal to 1/(1 + 2/β), where β > 1 implies that there is transition/transversion mutation bias. In the case of a single outgroup, two separate populations were each evolved for t1 generations after the burn-in to produce a focal population and the outgroup population (Figure 1A). When simulating two outgroups, an outgroup 2 population was evolved for (t1 + t2)/2 generations, and a second population was evolved for (t2 – t1)/2 generations up to node x (Figure 1B). Two populations then were each evolved from the node x population for t1 generations to produce a focal population and an outgroup 1 population.
In many simulations, we assumed that all sites evolve neutrally. We also simulated variation in the rate of substitution among sites caused by variation in the strength of purifying selection. A fraction C of sites was contributed by selectively constrained sites. Any allele that was different in state from the wild-type allele that arose at such sites was designated as mutant and had a selective disadvantage s/2. Effects on fitness were multiplicative. Fertility selection was carried out by sampling individuals for reproduction with replacement in proportion to their relative fitness.
We quantified bias (in percent) affecting estimates of elements of the SFS as the percentage deviation from the true value of that element. We also estimated the scaled root mean square error (RMSE in percent) for elements of the SFS. RMSE incorporates variance among estimates (because one method might produce less variable estimates of SFS elements about the true values than another) and is also influenced by bias:
| (6) |
where is the estimate for an SFS element from simulation replicate i, Yi is the corresponding true value of that element, and r is the number of simulation replicates.
D. melanogaster polymorphism data:
We obtained polymorphism data from an African population of D. melanogaster comprising 17 Rwandan haploid genomes (RG18N, RG19, RG2, RG22, RG24, RG25, RG28, RG3, RG32N, RG33, RG34, RG36, RG38N, RG4N, RG5, RG7, and RG9) that have been estimated to have the lowest levels of admixture with European populations (<3%) (see Pool et al. 2012, Figure 3b]. We downloaded FASTQ files from the Drosophila Population Genomics Project (DPGP; http://www.dpgp.org/dpgp2/candidate/). We further masked any regions of the African samples with evidence of admixture from European populations using the admixture coordinates reported by Pool et al. (2012). Following Pool et al. (2012), sites with a Burrows-Wheeler alignment (BWA) quality score below Q = 31 (equivalent to a Phred score of 48 and approximately equivalent to one error per 100 kb) also were masked. This produced the Q31 data set, which is the focus of most of the analysis. We also analyzed a more stringently filtered Q41 data set. From the FASTQ files, we extracted protein-coding regions using gene annotations from FlyBase v5.33 (www.flybase.org) and made FASTA files containing all samples (17 copies), and we excluded genes within non-crossing-over regions (see Campos et al. 2012). For each D. melanogaster gene with multiple transcripts, we chose one transcript at random. We included as outgroups the orthologous genes of D. simulans (r2.01) and D. yakuba (r1.3), obtained from the D. melanogaster–D. simulans–D. yakuba gene alignments of Hu et al. (2013), from which we selected the coding regions corresponding to our selected transcripts.
Estimating the DFE and rate and strength of adaptive mutations along with the frequency of adaptive substitutions
Assuming the inferred unfolded uSFSs for two outgroups and with no transition/transversion bias, we estimated parameters of the DFE and adaptive mutations by the ML method described by Schneider et al. (2011), which is incorporated into the software DFE-alpha (Keightley and Eyre-Walker 2007), with the following modifications: we first fitted a three-epoch demographic model to the neutral (i.e., synonymous) uSFS, allowing two changes of population size, first from N1 to N2 and then from N2 to N3 at times t2 and t3, respectively, while also fitting parameters specifying the fractions of unmutated sites (f0) and sites fixed by drift (f2N). By fitting this model to the DPGP synonymous uSFS, we found that high-frequency elements were underpredicted. The estimated uSFS for synonymous sites contains a small uplift in the last element, which cannot be explained under the demographic and mutational model fitted. This uplift could reflect hitchhiking with selected amino acid variants or positive selection on synonymous variants. Alternatively, it could be caused by residual misassignment of low-frequency variants. We assumed that such processes also affected the nonsynonymous uSFS and would lead to upwardly biased estimates of positive selection parameters if not corrected.
In a similar manner to that described by Glémin et al. (2015), which follows the approach of Eyre-Walker et al. (2006), we therefore corrected elements of the nonsynonymous uSFS Nj using the deviations of the observed elements Sj from the fitted elements Ej of the synonymous uSFS:
| (7) |
We assessed goodness of fit by comparing fitted uSFSs to observed uSFSs using a χ2 statistic, but because the numbers of sites in derived class j and ancestral class n − j are nonindependent, we did not perform formal significance tests.
Conditioning on the values of the parameters fitted to the synonymous SFS, parameters specifying the effects and relative frequencies of deleterious and advantageous mutations were fitted by ML to the corrected nonsynonymous uSFS. We either assumed that the fitness effects of deleterious mutations were drawn from a gamma distribution (which is specified by a shape and a scale parameter) or, following Kousathanas and Keightley (2013), that there were nd fixed classes of deleterious mutations, where the fitness effect and frequency of class i are sd,i and pd,i, respectively. We fitted na classes of advantageous mutations, where the fitness effect and frequency of class j are sa,j and pa,j, respectively, such that
| (8) |
The gamma DFE represents a single, continuously variable class of deleterious mutations.
To find maximum-likelihood estimates (MLEs), we carried out runs with large numbers of combinations of random starting values. We estimated 95% confidence limits for the proportion of adaptive mutations and their selective strength from profile likelihoods on the basis of drops in log likelihood of 2 units from their respective MLs (Cole et al. 2014). For each point in each profile likelihood, we used the highest likelihood obtained from 20 runs using different starting values sampled around the MLEs. Estimates of α, the proportion of adaptive substitutions, and ωa, the rate of adaptive substitution relative to the rate of neutral substitution, were obtained as described by Schneider et al. (2011).
Data availability
The authors state that all data necessary for confirming the conclusions presented in this article are represented fully within the article. The code for uSFS inference is available at www.homepages.ed.ac.uk/pkeightl/.
Results
Simulations: single outgroup
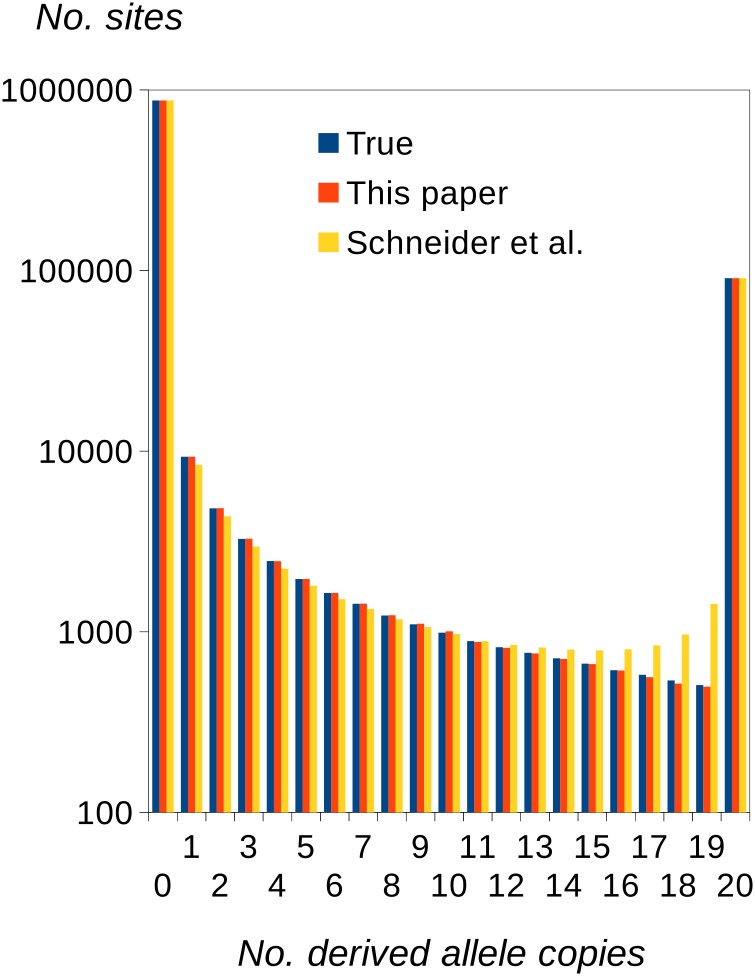
To investigate the performance of the uSFS inference procedure under circumstances where the data closely conform to the assumptions of the model, we simulated a focal population and a single outgroup with nucleotide divergence K = 0.1, no transition/transversion bias (β = 1), and no selection. We assumed that θ = 4Neμ = 0.01 so that θ << K and few polymorphic sites in the focal species are also polymorphic in the ancestral population prior to the split between the focal species and the outgroup. Figure 2 shows the true uSFS (calculated using knowledge of the ancestral state for each site) and the uSFSs inferred using the single-outgroup method described here and the method of Schneider et al. (2011). The new approach is therefore capable of estimating the uSFS with little bias on average, including high-frequency elements of the SFS. The method of Schneider et al. (2011) tends to overestimate high-frequency SFS elements, presumably because polymorphic sites having an outgroup allele inconsistent with either allele present in the focal species are misassigned. Our approach appears to give nearly unbiased estimates of the uSFS elements as long as the divergence to the outgroup is K < 0.3 (Figure S1).
Figure 2.
True uSFS (from simulation) and estimated uSFSs computed by the present method and by the method of Schneider et al. (2011), both using a single outgroup. Twenty copies were sampled at each site of the focal species. Diversity θ = 4Nμ = 0.01, and divergence between the focal species and the outgroup was K = 0.1. There were eight replicate simulations, each with 106 sites, resulting in a negligible sampling variance for elements of the estimated uSFSs.
We extended the method to include the estimation of separate transition and transversion rate parameters (File S1 and Table S1). This was tested by simulations of neutrally evolving sites and also produces nearly unbiased estimates of the uSFS in the presence of transition/transversion mutational bias (Figure S2A). The single-rate-parameter method also produces reasonably unbiased estimates of the uSFS as long as the transition/transversion mutation bias β < 2 (Figure S2B).
Simulations: two outgroups, neutrally evolving sites
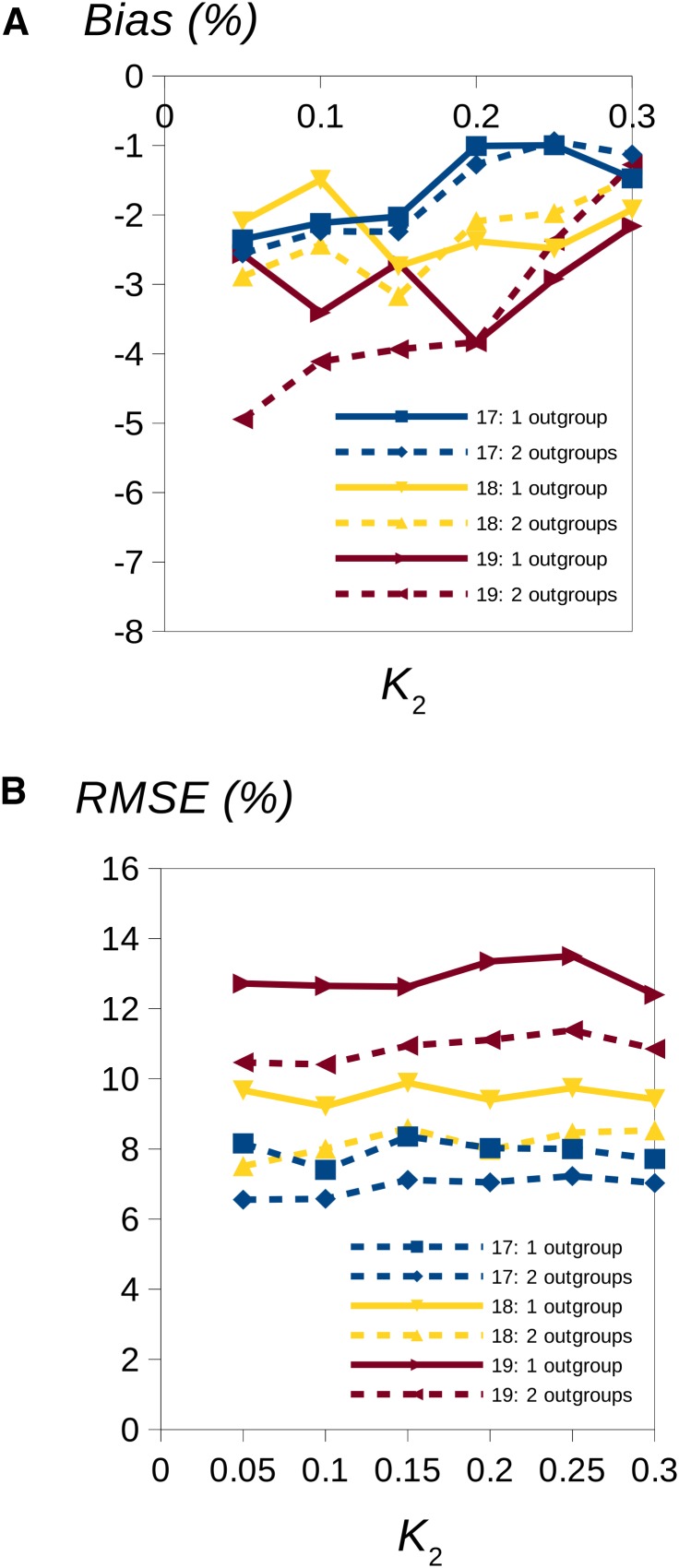
We then compared the performances of the uSFS inference procedures allowing one or two outgroups. The results suggest that there is a clear benefit from using a second outgroup in terms of lower variance among replicates (lower RMSE) (Figure 3) but potentially a cost in terms of higher bias (i.e., there is a tendency for underestimation of the high-frequency SFS elements), especially if the divergence from the second outgroup is small (Figure 3).
Figure 3.
Estimated bias (%) (A) and RMSE (B) for estimates of uSFS elements 17, 18, and 19 plotted against divergence K2 between node x and outgroup 2 (see Figure 1) for the case of 20 copies sampled at each site of the focal species. Positive and negative percent bias imply over- or underestimation of the SFS element, respectively. The solid and dotted lines show inferences using one or two outgroups, respectively. The divergence between the focal species and outgroup 1 was K1 = 0.1, and the diversity in the focal species was θ = 0.01. There was no transition/transversion bias. In each of 160 replicates, 105 sites were simulated.
Simulations: variable strength of purifying selection among sites
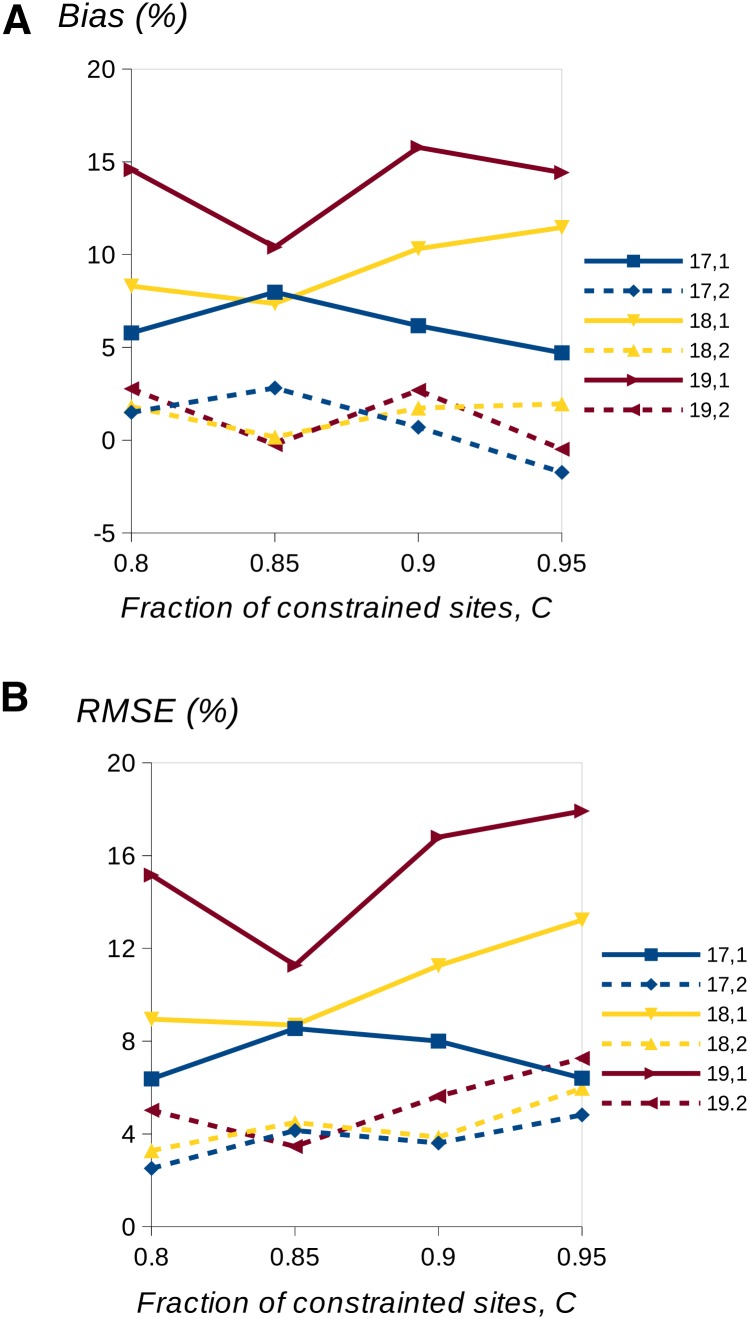
We then investigated the performance of the uSFS inference procedures in the presence of variation in the substitution rate and diversity among sites caused by purifying selection. We simulated this variation by assuming that a fraction C of sites is subject to negative selection (see Materials and Methods), the remainder evolving neutrally. We found that with C ≈ 0.85 and Ns = 10 (so that mutant alleles rarely become fixed), and divergence, diversity, and the shape of the SFS simulated are similar to what we observe in the D. melanogaster polymorphism data for nonsynonymous sites, although in this case we assume a constant population size.
We compared the accuracy of the inferred uSFS using one or two outgroups, focusing on the high-copy-number elements of the SFS, which are hardest to estimate accurately. We assumed a neutral divergence between the focal species and the first outgroup of K1 = 0.1 (which is similar to the D. melanogaster –D. simulans divergence) and a neutral divergence between the internal node and the second outgroup of K2 = 0.15. The results suggest that there is a clear benefit in terms of both reduced bias and reduced RMSE from using the information from a second outgroup (Figure 4 and Figure S3). Using information from a single outgroup, however, can lead to serious overestimation of the high-copy-number SFS elements (as much as 15% in the cases shown). Presumably, the benefit of using a second outgroup applies when there are other sources of variation in the substitution rate among sites, such as variation in the mutation rate.
Figure 4.
One- vs. two-outgroup comparison in the presence of variation among sites in selective constraints. The panels show bias (A) and RMSE (B) in the last three elements of the uSFS. For example, the label 17,1 refers to the bias/RMSE affecting element 17 with a single outgroup. A fraction C of sites was simulated with scaled selection coefficient Ns = −10, and the remainder evolve neutrally. A total of 105 sites were simulated per replication and 240 replicates. The divergence parameters for neutral alleles were K1 = 0.1 and K2 = 0.15.
Inference of uSFSs and frequency and strength of adaptive molecular evolution in the D. melanogaster proteome
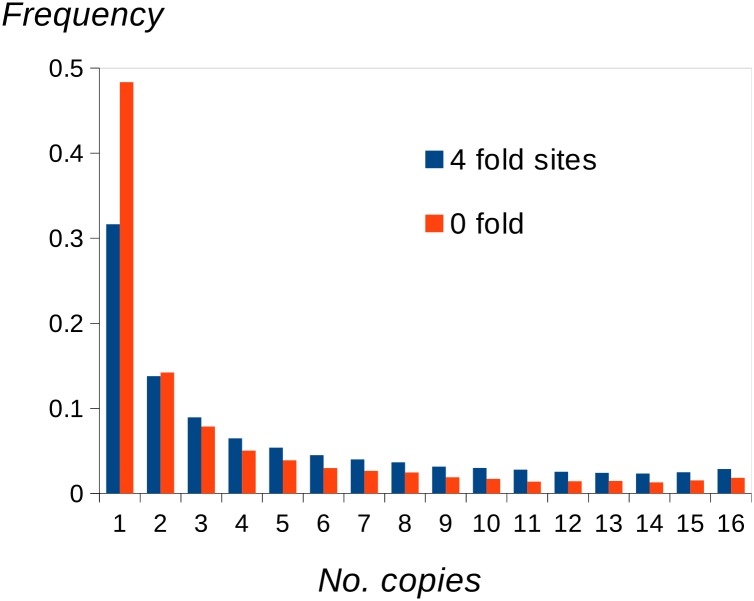
We applied the uSFS inference procedure to the polymorphism data set of protein-coding genes of the D. melanogaster DPGP phase 2. Using two outgroups (D. simulans and D. yakuba), we inferred uSFSs for four- and zerofold sites (Figure 5). As expected, nucleotide diversity at zerofold sites is substantially lower than that at fourfold sites, and there is an enrichment of zerofold singletons, consistent with negative selection acting on many nonsynonymous sites.
Figure 5.
Unfolded SFSs for zero- and fourfold sites of D. melanogaster protein-coding genes inferred using two outgroups (D. simulans and D. yakuba).
Given the inferred SFSs, we then applied the approach of Schneider et al. (2011) to estimate the rate of occurrence and selective strength of adaptive amino acid mutations. We fitted parameters of a three-epoch demographic model to the synonymous-site data (Table S3 and Figure S4); this model fit much better than a two-epoch model (log-likelihood difference = 221) and suggests that there was a population-size bottleneck followed by a population expansion. There is, however, an appreciable deviation between the observed and fitted synonymous uSFSs, particularly affecting the last element [Figure S4; χ2(16) = 138]. We assumed that misinference also would affect the nonsynonymous uSFSs, potentially leading to spurious estimates of adaptive molecular evolution. We therefore corrected the nonsynonymous uSFSs using the deviation between the observed and fitted synonymous uSFSs, as described in Materials and Methods. Uncorrected and corrected nonsynonymous uSFSs are shown in Figure S5.
Given the demographic parameter estimates from the synonymous site data, we then estimated parameters of the DFE for deleterious mutations and the proportion pa and scaled selection strength acting on one or more classes of adaptive mutations Nesa, assuming that the DFE is constant through time. Several models had similar levels of statistical support (Table 2). The best-fitting model gives an excellent fit to the data [Figure S5; χ2(16) = 16.9] and consisted of four classes of mutational effects: two classes of deleterious mutations, a class of neutral mutations, and a single class of advantageous mutations. There is substantial support for models with adaptive mutations (Δlog L = 93 between the best-fitting model and the same model excluding adaptive mutations). Assuming the four-class model, MLEs of the proportion of advantageous mutations and the scaled strength of selection acting on them are pa = 0.0045 [approximate upper 95% confidence interval (CI) = 0.012] and Nesa = 11.5 (approximate lower 95% CI = 5), respectively. Because we assume that the inferred SFSs are known with certainty, these 95% CIs are likely to be underestimates. Note that pa and sa are hard to estimate separately, but their product is well estimated. Other models that explain the data almost as well (gamma DFE, three classes of mutational effects) give somewhat different ML estimates of pa and Nesa, but the products of pa × Nesa are of similar magnitude (Table 2). Fitting additional classes of mutations (advantageous or deleterious) did not lead to a further increase in log likelihood. We then estimated the frequency of adaptive substitutions α and the rate of adaptive substitution relative to that of neutral substitution ωa from the proportions and fixation probabilities of the advantageous, neutral, and deleterious mutation classes. The estimates are α = 0.57 and ωa = 0.096 for the four-class model, but these are sensitive to the model assumed (Table 2).
Table 2. ML estimates of parameters from DFE-alpha for three different models.
| ML estimates | |||
|---|---|---|---|
| Parameter | Four classes | Three classes | Gamma |
| β | — | — | 0.35 |
| pd1 | 0.88 | 0.89 | 1 |
| Nesd1 | −177 | −167 | −2120 |
| pd2 | 0.076 | 0.10 | — |
| Nesd2 | −2.8 | −1.4 | — |
| pd3 | 0.039 | — | — |
| Nesd3 | 0 | — | — |
| pa | 0.0045 | 0.0093 | 0.0031 |
| Nesa | 11.5 | 6.7 | 17 |
| α | 0.57 | 0.89 | 0.68 |
| ωa | 0.096 | 0.14 | 0.091 |
| Δlog L | 0 | −0.6 | −2.1 |
The models assume that there are four or three classes of mutational effects or a gamma DFE. The difference in log likelihood (Δlog L) is the difference from the best-fitting model. The parameters of the model are as follows: β = shape of gamma distribution; pdi = proportion of deleterious mutations in category i; Nesdi = scaled selection coefficient for deleterious mutations in category i; pa = proportion of adaptive mutations; Nesa = scaled selection coefficient for adaptive mutations; α = proportion of amino acid substitutions fixed by positive selection; and ωa = rate of adaptive amino acid substitution relative to the neutral substitution rate.
Discussion
There were three main motivations for this study. First, we had determined that a previously described method to infer the uSFS (Schneider et al. 2011) tends to overestimate high-frequency SFS elements. Second, using parsimony for inferring ancestral states of high-frequency elements of the SFS is problematical because the corresponding low-frequency elements usually involve a far greater number of sites, and these tend to be misassigned as high-frequency elements, potentially leading to an overestimation of the frequency of alleles under positive selection. Third, large, genome-wide polymorphism data sets offer the opportunity to investigate the frequency and strength of ongoing adaptive molecular evolution using a method also described by Schneider et al. (2011), but this requires accurate inference of the uSFS. The development of this approach was motivated by inconsistent results emerging from the application of variants of the MK test, such as the methods of Welch (2006), DFE-alpha (Eyre-Walker and Keightley 2009), and DoFE (based on Eyre-Walker et al. 2006).
These methods all estimate the frequency of adaptive substitutions in a set of loci by contrasting polymorphism data in a focal species with divergence from an outgroup species. For example, many estimates of the proportion of adaptive amino acid substitutions α in plants are negative, some significantly, at face value, implying that there is little adaptive protein evolution (Gossmann et al. 2010). The true value of α cannot be negative, however, and this result may reflect the presence of widespread population structure in plant species, which distorts the SFS and could bias estimates of α downward. Some estimates of α in great apes are also negative (Good et al. 2013). A clear example of inconsistency comes from a reciprocal analysis of genome-wide polymorphism data in murid rodents, where an estimate of α in wild house mice using divergence from the rat is strongly and significantly positive, i.e., α ≈ 0.3 (Halligan et al. 2013), whereas an estimate using polymorphisms within wild brown rats and divergence from the mouse is strongly and significantly negative, i.e., α ≈ −0.3 (Deinum et al. 2015). The negative estimate presumably reflects a recent population bottleneck in the brown rat, leading to overprediction of the number of fixed, slightly deleterious mutations.
In contrast to MK-based methods, the method of Schneider et al. (2011) uses information on polymorphism data within a species to infer ongoing adaptive molecular evolution. It can be set up to use no information from sites fixed for the derived allele, but we did not do that here. By simulations, we investigated the circumstances under which accurate inference of the uSFS is possible. The most important potential source of misinference we identified is variation in the substitution rate, affecting the joint spectrum of polymorphisms in the focal species and divergence(s) from the outgroup(s). This could either be due to variation in the mutation rate between different kinds of sites or variation between sites in selective constraints or adaptive potential. In principle, it is possible to account for some components of variation in the mutation rate by explicit modeling (e.g., transition/transversion bias). Selection that varies among sites appears to be a more important issue, however, and is more difficult to model. Our simulations show that with a single outgroup only, high-copy-number uSFS elements are potentially seriously overestimated if there is variation in selective constraints among sites. This is so because the divergence between the ancestral allele and the outgroup is computed as an average across sites, but this will be lower than the divergence at the subset of unconstrained sites, so multiple hits are undercorrected at these sites. Our simulation results suggest that incorporating a second outgroup substantially corrects this problem, allowing accurate estimation of the uSFS. It should be feasible to extend our approach to include multiple outgroups, although there are presumably diminishing returns and potential biases from adding more distant outgroups. Incorporating data from multiple linked SNPs in a region also might add further information, although the rapid decay of linkage disequilibrium with distance between markers in Drosophila (Mackay et al. 2012) means that this would be of limited use.
We applied our new uSFS inference approach to the D. melanogaster DPGP phase 2 data for protein-coding genes, and several aspects of the results are noteworthy. The inferred uSFS for synonymous sites contains a small but appreciable uplift in the last element (Figure S4). With the demographic and mutational models fitted by DFE-alpha, however, it is not possible to obtain an uplift in the fitted uSFS. The apparent increase in the frequency of high-copy-number derived synonymous alleles could be genuine and explained, for example, by hitchhiking with linked selected amino acid variants or selection on synonymous variants (Zeng 2010; Clemente and Vogl 2012; Lawrie et al. 2013). If the uplift is an effect of selection on linked sites, we can assume that this also affects the nonsynonymous uSFS. This is the rationale for correcting the nonsynonymous uSFS based on the deviation from the fitted and observed synonymous uSFS. Alternatively, it could be caused by residual misassignment of low-frequency variants. We investigated whether this might be due to sequencing errors by analyzing a more stringent set of SNPs (Q41). The inferred uSFSs are extremely similar to the uSFSs analyzed (Q31) (Figure S6), suggesting that sequencing errors in DPGP are not an important source of misinference. We corrected the nonsynonymous uSFS based on the deviation from the fitted and observed synonymous uSFS.
Fitting the demographic parameters estimated from synonymous sites and then estimating selection parameters by ML resulted in a close fit to the corrected nonsynonymous uSFS (Figure S5), but several alternative models also give excellent fits (Table 2). Taking the best-fitting model at face value, the results therefore imply that there is a major contribution from adaptive amino acid substitutions to protein evolution in D. melanogaster, i.e., α ≈ 0.5. This figure is consistent with several studies employing variants of the MK test to estimate the frequency of adaptive protein evolution (Fay et al. 2002; Smith and Eyre-Walker 2002; Welch 2006; Andolfatto 2007; Eyre-Walker and Keightley 2009; Campos et al. 2014). The estimated selective effects of adaptive mutations are also consistent with estimates for the more common, weakly selected of the two classes inferred by Sattath et al. (2011) based on changes in diversity around substituted nonsynonymous sites. However, Sattath et al. (2011) estimated that only about 13% of amino acid substitutions cause selective sweeps, arguing that this low value could reflect a prevalence of partial sweeps. However, Schneider et al. (2011) used information from high-frequency polymorphisms, which is most relevant for inferring the ongoing strength of selection and the frequency of relatively weakly selected variants. This is so because strongly selected mutations are expected to be relatively rare and sweep rapidly to fixation, leaving little detectable footprint in the uSFS.
Acknowledgments
We are grateful to two anonymous referees for helpful comments. We also thank the UK Biotechnology and Biological Sciences Research Council for support.
Footnotes
Communicating editor: W. Stephan
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.188102/-/DC1.
Literature Cited
- Andolfatto P., 2007. Hitchhiking effects of recurrent beneficial amino acid substitutions in the Drosophila melanogaster genome. Genome Res. 17: 1755–1762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baudry E., Depaulis F., 2003. Effect of misoriented sites on neutrality tests with outgroup. Genetics 165: 1619–1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Begun D. J., Aquadro C. F., 1992. Levels of naturally occurring DNA polymorphism correlate with recombination rates in Drosophila melanogaster. Nature 356: 519–520. [DOI] [PubMed] [Google Scholar]
- Cai J. J., Macpherson M. J., Sella G., Petrov D. A., 2009. Pervasive hitchhiking at coding and regulatory sites in humans. PLoS Genet. 5: e1000336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campos J. L., Charlesworth B., Haddrill P. R., 2012. Molecular evolution in nonrecombining regions of the Drosophila melanogaster genome. Genome Biol. Evol. 4: 278–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campos J. L., Halligan D. L., Charlesworth B., Haddrill P. R., 2014. The relation between recombination rate and patterns of molecular evolution and variation in Drosophila melanogaster. Mol. Biol. Evol. 31: 1010–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemente F., Vogl C., 2012. Evidence for complex selection on fourfold degenerate sites in Drosophila melanogaster. J. Evol. Biol. 25: 2582–2595. [DOI] [PubMed] [Google Scholar]
- Cole S. R., Chu H., Greenland S., 2014. Maximum likelihood, profile likelihood, and penalized likelihood: a primer. Am. J. Epidemiol. 179: 252–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deinum E. E., Halligan D. L., Ness R. W., Zhang Y.-H., Cong L., et al. , 2015. Recent evolution in Rattus norvegicus is shaped by declining effective population size. Mol. Biol. Evol. 32: 2547–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enard D., Messer P. W., Petrov D. A., 2014. Genome-wide signals of positive selection in human evolution. Genome Res. 14: 885–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker A., 2002. Changing effective population size and the McDonald-Kreitman test. Genetics 162: 2017–2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker A., Keightley P. D., 2009. Estimating the rate of adaptive molecular evolution in the presence of slightly deleterious mutations and population size change. Mol. Biol. Evol. 26: 2097–2108. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A., Woolfit M., Phelps T., 2006. The distribution of fitness of new deleterious amino acid mutations in humans. Genetics 173: 891–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay J. C., Wu C.-I., 2000. Hitchhiking under positive Darwinian selection. Genetics 155: 1405–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay J. C., Wyckoff G. J., Wu C.-I., 2002. Testing the neutral theory of molecular evolution with genomic data from Drosophila. Nature 415: 1024–1026. [DOI] [PubMed] [Google Scholar]
- Glémin S., Arndt P. F., Messer P. W., Petrov D., Galtier N., et al. , 2015. Quantification of GC-biased gene conversion in the human genome. Genome Res. 25: 1215–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good J. M., Wiebe V., Albert F. W., Burbano H A., Kircher M., et al. , S 2013. Comparative population genomics of the ejaculate in humans and the great apes. Mol. Biol. Evol. 30: 964–976. [DOI] [PubMed] [Google Scholar]
- Gossmann T. I., Song B.-H., Windsor A. J., Mitchell-Olds T., Dixon C. J., et al. , 2010. Genome wide analyses reveal little evidence for adaptive evolution in many plant species. Mol. Biol. Evol. 27: 1822–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graur D., Li W.-H., 2000. Fundamentals of Molecular Evolution, Ed. 2 Sinauer Associates, Sunderland, MA. [Google Scholar]
- Halligan D. L., Kousathanas A., Ness R. W., Harr B., Eory L., et al. , 2013. Contributions of protein-coding and regulatory change to adaptive molecular evolution in murid rodents. PLoS Genet. 193: 1197–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez R. D., Williamson S. H., Zhu L., Bustamante C. D., 2007. Context-dependent mutation rates may cause spurious signatures of a fixation bias favoring higher GC-content in humans. Mol. Biol. Evol. 24: 2196–2202. [DOI] [PubMed] [Google Scholar]
- Hernandez R. D., Kelley J. L., Elyashiv E., Melton S. C., Auton A., et al. , 2011. Classic selective sweeps were rare in recent human evolution. Science 331: 920–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu T. T., Eisen M. B., Thornton K. R., Andolfatto P., 2013. A second-generation assembly of the Drosophila simulans genome provides new insights into patterns of lineage-specific divergence. Genome Res. 23: 89–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley P. D., Eyre-Walker A., 2007. Joint inference of the distribution of fitness effects of deleterious mutations and population demography based on nucleotide polymorphism frequencies. Genetics 177: 2251–2261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kousathanas A., Keightley P. D., 2013. A comparison of models to infer the distribution of fitness effects of new mutations. Genetics 193: 1197–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrie D. S., Messer P. W., Hershberg R., Petrov D. A., 2013. Strong purifying selection at synonymous sites in D. melanogaster. PLoS Genet. 9: e1003527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohmueller K. E., Albrechtsen A., Li Y., Kim S. Y., Korneliussen T., et al. , 2011. Natural selection affects multiple aspects of genetic variation at putatively neutral sites across the human genome. PLoS Genet. 7: e1002326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay T. F. C., Richards S., Stone E. A., Barbadilla A., Ayroles J. F., et al. , 2012. The Drosophila melanogaster genetic reference panel. Nature 482: 173–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macpherson J. M., Sella G., Davis J. C., Petrov D. A., 2007. Genomewide spatial correspondence between nonsynonymous divergence and neutral polymorphism reveals extensive adaptation in Drosophila. Genetics 177: 2083–2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald J. H., Kreitman M., 1991. Adaptive protein evolution at the Adh locus in Drosophila. Nature 351: 652–654. [DOI] [PubMed] [Google Scholar]
- Michaelson J. J., Shi Y., Gujral M., Zheng H., Malhotra D., et al. , 2012. Whole-genome sequencing in autism identifies hot spots for de novo germline mutation. Cell 151: 1431–1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pool J. E., Corbett-Detig R. B., Sugino R. P., Stevens K. A., Cardeno C. M., et al. , 2012. Population genomics of sub-Saharan Drosophila melanogaster: African diversity and non-African admixture. PLoS Genet. 8: e1003080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press W. H., Teukolsky S. A., Vetterling W. T., Flannery B. P., 1992. Numerical Recipes in C, Ed. 2 Cambridge University Press, New York. [Google Scholar]
- Sattath S., Elyashiv E., Kolodny O., Rinott Y., Sella G., 2011. Pervasive adaptive protein evolution apparent in diversity patterns around amino acid substitutions in Drosophila simulans. PLoS Genet. 7: e1001302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider A., Charlesworth B., Eyre-Walker A., Keightley P. D., 2011. A method for inferring the rate of occurrence and fitness effects of advantageous mutations. Genetics 189: 1427–1437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith N. G. C., Eyre-Walker A., 2002. Adaptive protein evolution in Drosophila. Nature 415: 1022–1024. [DOI] [PubMed] [Google Scholar]
- Welch J. J., 2006. Estimating the genome-wide rate of adaptive protein evolution in Drosophila. Genetics 173: 821–837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng K., 2010. A simple multiallele model and its application to identifying preferred–unpreferred codons using polymorphism data. Mol. Biol. Evol. 27: 1327–1337. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors state that all data necessary for confirming the conclusions presented in this article are represented fully within the article. The code for uSFS inference is available at www.homepages.ed.ac.uk/pkeightl/.