Automated Mapping of Phenotype Space with Single-Cell Data

Abstract

Accurate and rapid identification of cell populations is key to discovering novelty in multidimensional single cell experiments. We present a population finding algorithm X-shift that can process large datasets using fast KNN estimation of cell event density and automatically arranges populations by a marker-based classification system. X-shift analysis of mouse bone marrow data resolved the majority of known and several previously undescribed cell populations. Interestingly, previously known cell populations, as well as intermediate cell populations in early hematopoietic development, were described via novel marker combinations that were defined via routes to their locations in expressed marker space. X-shift provides a rapid, reliable approach to managed cell subset analysis that maximizes automation that not only best mimics human intuition, but as we show provides access to novel insights that “prior knowledge” might prevent the researcher from visualizing.

Recent years have seen rapid progress in multiparametric single cell proteomic and genomic research. One innovation is mass cytometry (CyTOF)—a single cell proteomics platform that combines elemental mass spectrometry with flow cytometry¹—enabling up to 50 parameters per single cell to be measured. High dimensional cytometry can be used to resolve discrete cell states such as the phenotypic continuums in hematopoietic cells² and B cells³. While, there are a surfeit of excellent clustering methods that have been developed to date for single cell analysis (see⁴ for a survey), few if any of those methods was tested for performance on high-dimensional CyTOF datasets (which represent unique computational complications as will be discussed below). A clustering system that could handle high parameter datasets and which performed robustly compared to published methods was required. Also, an algorithm was needed that can find the optimal number of clusters in a data-driven manner.

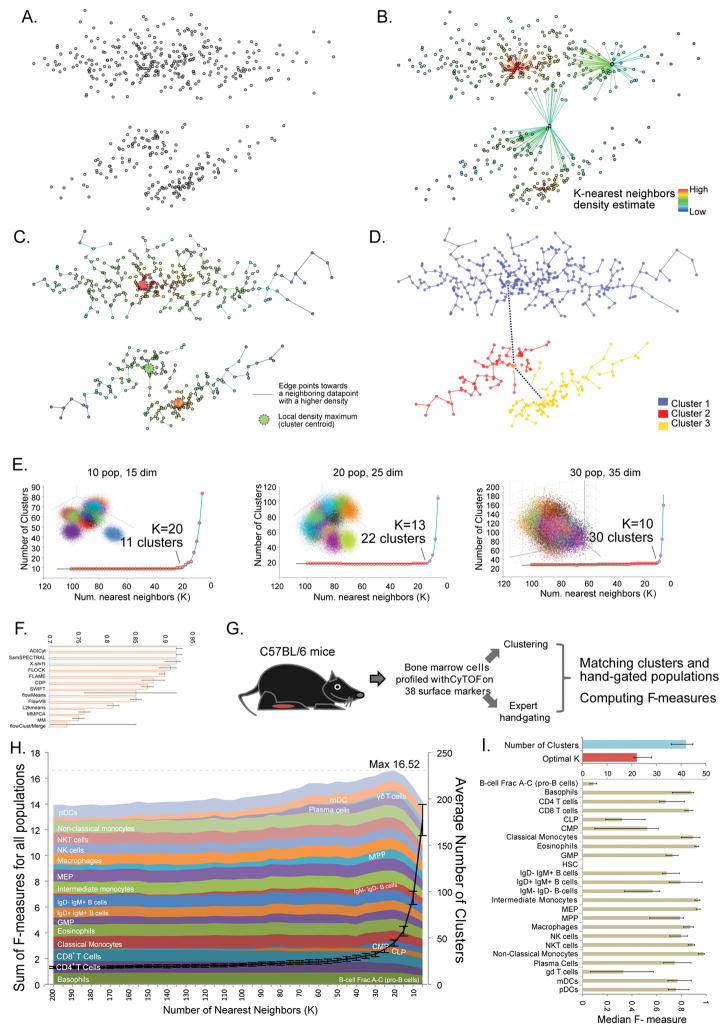
For this and reasons demonstrated below, X-Shift (so named by analogy with other mode-seeking algorithms) was developed to use a weighted K-nearest neighbor density estimation (KNN-DE)⁵. Given a dataset (Fig. 1a), X-shift computes the density estimate for each data point (Fig. 1b). It then searches for the local density maxima in a nearest-neighbor graph, which become cluster centroids. All the remaining data points are then connected to the centroids via density-ascending paths in the graph, thus forming clusters (Fig. 1c). The algorithm further checks for the presence of density minima on a straight line segment between the neighboring centroids and merges them as necessary (Fig. 1d). This is needed to ensure that the neighboring clusters, even if they have similar phenotypes, do in fact represent unique density-separated populations. Furthermore, clusters are merged based on a fixed Mahalanobis distance threshold.

Figure 1. X-shift algorithm design and validation.

(a–c) Workflow of X-shift algorithm (a) Synthetic 2-dimensional dataset with three ‘point clouds’. (b) K nearest neighbors density estimation. Example sets of 20 nearest neighbors are shown for 3 data points. (c) Connecting datapoints against the gradient of density estimate and finding local maxima (d) Testing neighboring populations for density-separation. (e) X-shift clustering of synthetic data. Randomly generated datasets with 10 populations in 15 dimensions, 20 populations in 25 dimensions and 30 populations in 35 dimensions were clustered with X-shift, varying the number of nearest neighbors (K) used for density estimate from 100 to 5. Blue line shows the fitting of the curve using line-plus-exponent regression. (f) Assessment of X-shift performance in automatic parameter-finding mode on 12-color FlowCAP I Normal Donor dataset, compared to FlowCAP I Challenge I submissions⁴. (g) The scheme of evaluation of X-shift performance against hand-gated CyTOF data. (h) X-shift clustering of mouse bone marrow data at various K settings were compared to hand-gates and the median F-measures over 10 biological replicates were plotted as stacked areas. Population labels are positioned to the point where each F-measure first reaches 90% of its maximum. (i) Results of X-shift analysis of bone marrow data when K was automatically selected for each of the 10 replicates. Bars show median values across replicates and error bars represent inter-quartile range.

KNN-DE has been established as an adaptive-bandwidth density estimator that overcomes certain sparseness issues associated with multidimensional spaces⁶. In simulated tests we found that KNN-DE faithfully captures the true probability density of sampled normal distribution mixtures even when the dimensionality of space reaches 100 dimensions (Supplementary Fig. 1). To further leverage the power of KNN-DE, we designed a fast KNN search algorithm that partitions the dataset into convex regions and uses distances to region centroids as a guide for neighbor search. In our tests X-shift employed with the improved search algorithm shows an estimated runtime of O(n^1.77) giving a 4 to 5-fold speedup over the exhaustive search which makes it possible to cluster datasets (several million cell events) on a standard multi-core workstation (Supplementary Fig. 1).

The resolution of X-shift clustering is defined by the number (K) of nearest neighbors that are used for the density estimate. Lower K values allow resolving small and closely-positioned populations, but the result becomes increasingly affected by stochastic variations. To study the X-shift dependence on K value, we generated a series of simulated cytometry datasets based on multivariate Gaussian mixture models with varying number of populations and dimensionality (see Methods). Clustering those datasets with K value within the [100, 5] interval resulted in a reproducible pattern (Fig. 1e). Initially, as K decreased the number of clusters grew very slowly, if at all. Towards the end of the range, the number of clusters matched the number of populations that was used to generate the dataset. At very low K the number of clusters exhibited exponential growth, suggesting over-fragmentation of populations. Manual inspection showed that the dataset tended to be under-clustered during the linear phase (not all populations separated) while at the exponential phase one population was often incorrectly split into multiple clusters. Similar results could be obtained in equal mixtures of normal and multivariate noncentral Student distributions, which are long-tailed and asymmetric. (Supplementary Fig. 2–4). We suspected that an optimal K value for each dataset might be selected automatically by finding the switching point in the cluster number plot, since this switch-point likely corresponds to the optimal balance between separating distinct populations while minimizing their over-fragmentation^7,8.

X-Shift was tested against top-performing algorithms from the FlowCAP I data analysis challenge⁴ using the 12-color normal donor dataset (NDD). Conforming to the rules of the FlowCAP challenge I, we ran X-shift in the automated mode, allowing optimal K to be selected by the switch-point-finding algorithm. The comparison of X-shift results to the hand-gating submissions using the original FlowCAP R scripts showed an average F-measure of 0.912, which closely matched the performance of the top algorithms in that challenge (Fig. 1f). Since X-shift was specifically developed to handle high-dimensional CyTOF data, we initiated a detailed validation of X-shift on a CyTOF dataset from mouse bone marrow. Replicate bone marrow samples were independently harvested from C57BL/6J mice (Fig. 1g), barcoded stained with a panel of 38 antibodies against surface markers based on an immune system reference map⁹, analyzed on CyTOF, and then independently hand-gated by 3 cytometry experts to identify 24 immune cell populations (Fig. 1g, Supplementary Fig. 5). Experts used the same gating strategy but placed the gate boundaries independently. The consensus assignment was used to establish the reference population list.

We computationally clustered each biological replicate over a range of K values using all surface markers. The clustering results were compared to the reference hand-gated cell populations (Methods) via F-measure to summarize the purity and yield of a given manually-gated population compared to its best-matched cluster. Fig. 1h shows the dependence of median F-measures for individual populations plotted as stacked areas as determined by the K value. The sum of all F-measures quantifies the overall similarity of clustering to the hand-gating. It commences at 13.92 ± 0.38 (K = 200) and increases slowly, reaching the maximum of 16.52 ± 0.24 when K = 20. This growth is accompanied to by a linear-like growth in the number of clusters. At lower K-values the cluster number curve switched into the exponential-like growth phase and F-measure decreased as down to 14.16 ± 0.19 at K = 5. When we next clustered each replicate separately and allowed the optimal K to be automatically determined we obtained the average F-measure sum was 16.72 ± 0.77, even slightly above the maximum seen earlier in the manual parameter adjustment run, and a median F-measure of 0.79 across populations (Fig. 1i). Therefore, a key attribute of X-shift is its ability to automatically estimate the optimal clustering parameter K by finding the switch-point in the plot of cluster number over various K. While the switchpoint-finding idea have been employed in various contexts^7,8, to our knowledge it remains an empirical rule not backed by a solid mathematical theory. In the case of X-shift, we speculate that the elbow point in the cluster number over K plot of X-shift is a result of a balance between bias and variance of the density estimate, which has been thoroughly investigated in the context of kernel density estimation¹⁰.

The same comparison was repeated for SPADE as well as top-performing flow data clustering methods that participated in FlowCAP competition on the same set of data⁴. Three methods failed to run on our dataset (AdiCYT⁴, FLOCK¹¹, FlowMerge⁸, Supplementary Fig. 6–7), while others showed a considerably lower (than 16.59 for X-shift) maximal F-measure sums: FlowPeaks¹²-14.79, SPADE¹³-14.86, PhenoGraph¹⁴-14.63, flowMeans⁴-14.38, SWIFT¹⁵-8.07 SamSPECTRAL¹⁶-7.34. Detailed results and comparisons are found in Supplementary Fig. 8. In comparison, X-Shift showed consistently more robust outcomes and was further evaluated for the biological relevance of the discovered subsets.

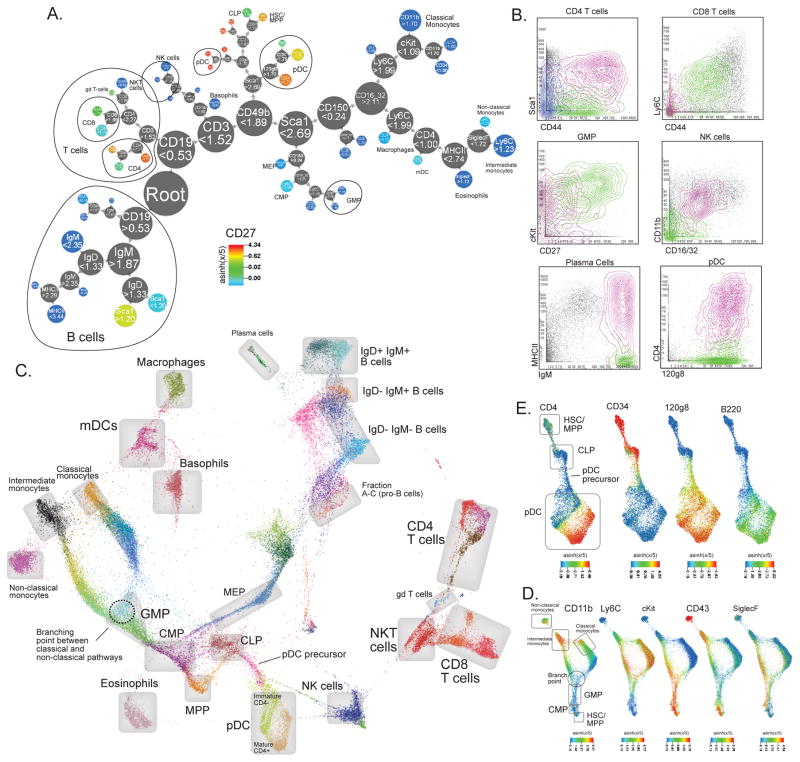
To represent X-shift derived populations we organized clusters into a hierarchical marker-based classification tree (which we term Divisive Marker Tree (DMT)). The iterative algorithm initiates DMT with a root node encompassing all clusters which then is subject to iterative binary division (see Methods for a detailed explanation). The resulting hierarchical binary classification (Fig. 2a) of cell types resembles manual gating hierarchies. By tracing the sequence of marker divisions from the root, the user can infer a concise marker-based signature for each cell population that uniquely differentiates it from other populations. The numerical values on each node specify the cutoff level for a given marker, here on asinh(x/5) scale. For instance, MPP population is CD19 < 0.53, CD3 < 1.52, CD49b < 1.89, Sca1 > 2.62, 120g8 < 1.70, CD27 > 1.62, CD34 > 1.72, cKit > 1.50.

Figure 2. X-shift clustering reveals novel features of mouse hematopoietic differentiation.

(a) Clustering of bone marrow replicate #7 with X-shift (K = 20 was auto-selected by the switch-point-finding algorithm) represented in a Divisive Marker Tree. Node radii are proportional to the cubic root of the number of cell events contained at each node. The tree is a nested representation, i.e. parent nodes contain the union of cell events of its children. Labels on nodes show marker cutoff values that define each sub-branch, expressed on the arsinh(x/5) scale. (b) X-shift finds biologically relevant subsets within the hand-gated cell populations (Bone marrow replicate #7, X-shift K = 20). (c) Single-cell Force-Directed Layout of Mouse Bone Marrow #7 (X-shift K = 20, color-coded for 48 clusters). Color code shows X-shift clusters and grey boxes show locations of hand-gated cell populations. (d) Force-directed layout of populations related to monocyte development. Color code represents expression levels of indicated markers. (e) Force-directed layout of populations related to pDC development. Color code represents expression levels of indicated markers.

X-shift and DMT allowed for identification of biologically relevant cell subsets within several hand-gated cell types (examples given in Fig. 2b and Supplementary Fig. 9a–b) that were not accounted for by the gating. For instance, CD4⁺ T cells were further split along CD44 and Sca1, which is in retrospect an expected result since those markers of activated and memory cells in mouse¹⁷. CD8⁺ T-cells were subdivided along CD44 and Ly6C, the latter one, being often used to call out myeloid cells, also is a marker of central memory cells¹⁸. Additional features of the dataset were highlighted by X-shift coupled to DMT: GMP cells were divided into 2 subsets by CD27 and cKit expression, supposedly representing discrete differentiation stages. X-shift also found a distinct MHCII+ subset in plasma cells, which is not widely known, but MHCII re-expression has been reported in the context of isotype-switching¹⁹. Plasmacytoid dendritic cells were split into CD4^hi and CD4^lo, which represent distinct maturation stages of pDCs²⁰. Similarly, NK cells are subdivided along CD11b and CD16/32 expression, representing distinct maturation stages. Further experimentation might be warranted to determine the biological importance of such results.

Several cell clusters could not be deduced from the surface marker expression profiles. To map these we sampled cells from clusters and arranged them in a force-directed graph layout (Fig. 2c). In this graph cell populations appear to form a hierarchical progression that corresponds to major hematopoietic lineages gradually developing from the progenitor MPP population: myeloid, erythroid, lymphoid. Mature peripheral populations, such as T-cells, visibly stand apart from the developmental continuum. Interestingly, the immature CD4- pDC population appears to be connected directly to the CLP through a distinct population of cells that appear to gradually lose CD34 and simultaneously upregulate 120g8, while other pDC markers, such as B220 and CD4, were found to be expressed only at the late stage of maturation (Fig. 2e and Supplementary Fig. 9a). Another intriguing point was the apparent branching of classical and intermediate/non-classical monocyte pathways, with a distinct GMP-like population situated at the branching point (Fig. 2d and Supplementary Fig. 9d). Such examples demonstrate that X-shift can find novel cell populations that could shed light on some of the intriguing questions that have not been decisively addressed to date, such as the origin of pDCs or the developmental order of monocyte subpopulations. Additional information about locations of hand-gated populations and marker expression in the force-directed layout map is available in Supplementary Fig. 10–15.

In summary X-shift, in combination with tailored visualization tools (Divisive Marker Trees and Single-cell Force-Directed Layouts) facilitates the exploration of single-cell analysis of complex systems. X-shift and associated visualization tools are freely available as a part of VorteX graphical environment: http://web.stanford.edu/~samusik/vortex/.

Online Methods

Weighted K-nearest neighbor density estimate

Identification of local density maxima has been addressed previously by a number of mode-seeking algorithms (e.g. mean-shift²¹, quick-shift²² and the recent algorithm by Rodriguez and Laio²³). Generally, those algorithms rely on kernel density estimation (KDE), the performance of which deteriorates in multidimensional data due to the sparseness of sample distribution⁶. The runtime of KDE is O(n²) in dataset size²¹.

We therefore approached the problem differently. Density estimation was computed as described in ⁵, setting nu=const and, p=1

$$\widehat{f}(x)=\frac{1}{{\text{nV}}_d}{\left(\frac{{\sum }_{j=0}^k{j}^d}{{\sum }_{j-0}^k\mid {\mathrm{X}}_j(\mathrm{x})-\mathrm{x}\mid }\right)}^d$$

Where n is the size of the dataset, V_d is the volume of a unit sphere in d dimensions, X_j(x) represents the j-th nearest neighbor of x, d is the number of dimensions and |x - y| is the distance between x and y. In the reason of numerical stability, X-shift computes a simplified version of density estimate that relates to the original density estimate by a monotonous transformation:

$${{\widehat{f}}^{\prime }}^{(x)}=-1/\frac{\sqrt[d]{{\text{nV}}_d\widehat{f}(x)}}{{\sum }_{j=0}^k{j}^d}=-\sum _{j-0}^k\mid {\mathrm{X}}_{(j)}(\mathrm{x})-\mathrm{x}\mid$$

Within X-shift algorithm all decisions about local maxima and data point assignment are being made solely based on inequality comparisons of density estimates, thus the monotonous transformation does not change the clustering output.

Distance metric

X-shift can work with any distance metric that satisfies the triangle inequality. All experiments in this work were carried out using angular distance, where |x - y| represents the angle between vectors x and y, computed via

$$\Vert x-y\Vert =arccos\left(\frac{x·y}{\sqrt{(x·x)(y·y)}}\right)$$

Fast search for K nearest neighbors

Large datasets present a challenge for KNN because the exhaustive search requires O(n²) steps. KD-trees have been successfully used to speed up the search, but their performance degrades in multidimensional space, typically above 10 dimensions²⁴. We designed a way to compute the exact KNN by partitioning the dataset into random convex regions and then using the distances to region centers and the triangle inequality to guide the KNN search. The algorithm is the following:

• Step 1. Split the dataset D into convex regions using K-means algorithm where K is set to be a square root of the dataset size. We found that running K-means for as little as 3 iterations produces sufficiently compact regions to yield a considerable speedup in the next step.

• Step 2. For each region A, find its centroid c. Create an ordered list B containing all data points in the dataset and sort it by |b_i - c| in ascending order using quicksort algorithm. Following the reverse triangle inequality, for each data point x in the region A it holds true that |x - b_i| ≥ |b_i, c| - |x, c|. Therefore for any point x in the region A, if data points in the list B are ordered by their the distance to c, they also appear to be ordered by the lower bound of their distance to x

  $$\mid b_i,-c\mid <\mid b_{i+1}-c\mid \Rightarrow inf(\mid x-b_i\mid )<inf(\mid x-b_{i+1}\mid ),$$

• Step 3. Initiate the list of k-nearest neighbors of a point x: neigh(x) by populating it with b₁…b_k data points from the ordered list B. Sort the list neigh(x) by the distance to x. Iterate through the rest of the list b_(k+1) … b_n, for each b_i finding the minimal index j such that the |x - b_i| < |x - neigh(x)_j|. If such j exists, insert the b_i into the neigh(x) at index j, shifting the anteceding members to the right and removing the last member off the list. Stop iterating through b_i in B when |b_i - c| - |x - c| > |x - neigh(x)_j|. At this point the lower bound estimate of distance to b_i: inf(|x, b_i|)= |b_i - c| - |x - c| is less than the distance to the k-th nearest neighbor in the current list. Since inf((|x - b_i+1|) > inf(|x - b_i|), it also means that none of the consecutive elements b_i+1…b_n can be closer to x than the neigh(x)_k. If this condition has been satisfied before i = n, it means that the k nearest neighbors of x have been found faster than it could have been done through an exhaustive search.

X-shift algorithm

• Step 1. For each data point in the dataset, compute density estimate using a method of choice. For the reason of speed, we prefer to use our fast KNN density estimate, but in principle any density estimation method, like kernel density estimate or multidimensional histogram, can be plugged into X-shift.

• Step 2. For each data point, find a nearest neighbor with a higher density estimate value and connect the two with a directed edge. If such neighbor does not occur within Z nearest neighbors, the point is added to a list of candidate cluster centroids. The number Z is chosen depending on the dataset size so that the Bonferroni-corrected p-value stays constant. Assuming that under null hypothesis the data point distribution is uniform (there are no clusters) and the density of neighbors of any point is equally probable to be higher or lower than of a point itself, the p-value for a data point to be pass a centroid test is equal to 2^Z, which is a probability of all of its Z neighbors to have a lower density by chance. After applying Bonferroni correction for multiple hypothesis testing, the number Z that would result in a centroid list with a given p_value can be estimated using the following formula:

  $$Z=-{\mathit{log}}_2(\raisebox{1ex}{$p_{\mathit{value}}$}\!\left/ \!\raisebox{-1ex}{$n$}\right.)$$

  where n is the dataset size. For all the experiments in this paper we fixed the default p-value at 0.01, which is expected to result in a reliable list of candidate centroids for each clustering run. Generally, there is no need to adjust the default value.

• Step 3: Determine which candidate centroids are Gabriel neighbors¹³ and test whether there is a minimum of density on the segment connecting the centroids. If there is not, then it means that the lower-density centroid is not a real local maximum and should get connected to the higher-density centroid. This merging step ensures the high quality of the output clusters. We found that changing the p-value and thus adjusting the number of tentative clusters has only a small effect on the number of clusters in the output, but increasing the p-value might notably increase the runtime, since the number of evaluations depends on the square of number of tentative centroids.

• Step 4: Put all the data points that are directly or indirectly connected to the centroid into a cluster.

• Step 5: Iteratively merge pairs of clusters with the lowest Mahalonobis distance, until all clusters have Mahalonobis distance of at least 2.0 between them, this cutoff corresponds to the theoretical density-separation cutoff of the normal distributions²⁶ and clusters that are closer than this threshold are likely to be spurious fragments.

Finding optimal K using line-plus-exponent regression

Given the numbers of clusters c₁…c_n obtained at different K values k₁…k_n in descending order, the algorithm iterates through k_i. First, linear regression coefficients c = b₁·k + a₁ are estimated based on (c_j, k_j), j = 1…i Next, exponential regression coefficients c = a₂e^b_2k are estimated based on (c′_j, k_j), j = 1…i and c′ = b₁·k + a₁. Finally, the sum of squares SS_i = Σ_t(c_t - (b₁·k_t + a₁ + a₂e^b_2k_t)) is computed and the switch-point k_i is selected by iterating through i = 2…n-1 such that SS_i is minimized.

Divisive marker tree

At each iteration the cluster set is partitioned into two subsets that have non-overlapping expression levels of a single marker. The dividing marker and the cut point are chosen to maximize the average correlation of expression profiles within the resulting groups. It is important in thinking about DMT to not interpret the binary division of cells as a “last use” of that marker—meaning the same marker can be used in the DMT trees as a divisive element multiple times—essentially a sliding scale for division of cell subsets that operates in an intuitive and natural manner.

The divisive maker tree is constructed via recursive binary partitioning of the set of marker expression vectors. On each iteration, the parent set of vectors P is divided into two subsets A and B, such that:

A and B have non-overlapping ranges of average expression values on at least one marker X, and vectors in A are always greater than vectors in B on this marker. In other words, there exists at least one marker x, for which it is true that a ∈ A ∧ b ∈ B ⇒ a_x > b_x

Out of all possible partitions that satisfy the previous condition, one is chosen that maximizes the average uncentered Pearson correlation r_ab =(a·b)/√((a·a)(b·b)) of the cluster expression profiles (computed on all markers) within the subsets. The two subbranches are labeled as “marker>cutoff” and “marker<cutoff”. Since for each given partition there can be several markers with non-overlapping expression values, the marker that has the largest variance-normalized difference between the two groups is chosen for labelling.

Force-directed layout

Cells events were selected randomly from each cluster (all cells from cluster smaller that 1,000 cells or 1,000 randomly sampled events from clusters larger than 1,000 cells). Cell events were put as nodes in a graph and connected with unweighted edges to 10 nearest neighbors in the phenotypic space (angular distance). The resulting graph was subject to force-directed layout using ForceAtlas2 algorithm²⁷. Layout and visualization were produced using Gephi-Toolkit v0.8.7 (http://gephi.org/toolkit/).

CyTOF methods

The CyTOF antibody panel was prepared and validated as described by Spitzer and co-workers⁹. Wild-type male C57BL/6 mice were purchased from The Jackson Laboratory at 11 weeks of age. Animals were rested in our animal facility for 1 week and sacrificed at 12 weeks of age. All mice were housed in an American Association for the Accreditation of Laboratory Animal Care–accredited animal facility and maintained in specific pathogen-free conditions. Animal experiments were approved and conducted in accordance with Stanford University Asia Pacific Laboratory Accreditation Cooperation #13605. After euthanasia by CO₂ inhalation, animals were perfused and femuri were isolated. Bone marrow was flushed and resuspended in PBS and 4°C. Cells were washed with PBS with 5 mM EDTA and resuspended 1:1 with PBS with 5 mM EDTA and 100 μM Cisplatin (Enzo Life Sciences, Farmingdale, NY) for 60s before quenching 1:1 with PBS with 0.5% BSA and 5 mM EDTA to determine viability. Cells were centrifuged at 500 g for 5 min at 4°C and resuspended in PBS with 0.5% BSA and 5 mM EDTA at a density between 2–5·10⁶ cells/ml. Suspensions were fixed for 10 min at RT using 1:1.4 Proteomic Stabilizer according to the manufacturer’s instructions (Smart Tube Inc., Palo Alto, CA) and frozen at −80°C. For the initial experiments, 10 total replicate mice were utilized. Mass-tag cellular barcoding was described as previously described. Cells were resuspended in PBS with 0.5% BSA and 0.02% NaN₃ and metal-labeled anti-CD16/32 antibody (Biolegend TruStain fcX, cat. No. 101320, Clone 93) was added at 20 μg/ml for 5 min at RT on a shaker to block Fc receptors and prevent non-specific staining. Surface marker antibodies were added, yielding 500 μL final reaction volumes, and stained at RT for 30min on a shaker. Cells were washed 2 times with PBS with 0.5% BSA and 0.02% NaN₃ then permeabilized with 4°C methanol for 10 min at 4°C. Cells were washed twice in PBS with 0.5% BSA and 0.02% NaN₃ and stained with intracellular antibodies in 500 μL for 30 min at RT on a shaker. Cells were washed twice in PBS with 0.5% BSA and 0.02% NaN₃ and then stained with 1 mL of 1:4000 191/193Ir DNA intercalator (Fluidigm) diluted in PBS with 1.6% PFA overnight. Cells were washed once with PBS with 0.5% BSA and 0.02% NaN₃ and then two times with double-deionized (dd)H₂O. Care was taken to ensure that buffers preceding analysis were not contaminated with metals in the mass range above 100 Da. Mass cytometry samples were diluted in ddH₂O containing bead standards (see below) to approximately 10⁶ cells per mL and then analyzed on a CyTOF2 mass cytometer (Fluidigm) equilibrated with ddH₂O. The final cell pellet was resuspended in ddH₂O containing a bead standard at a concentration ranging between 1 and 2*10⁴ beads/ml as previously described²⁸. The mixture of beads and cells were filtered through a 35-μm filter before analysis. Mass cytometry files from each experiment set were normalized together using the mass cytometry data normalization algorithm¹. Normalized data were gated to remove doublets, debris and neutrophils and the resulting FCS files were subject to further gating to identify specific populations and also processed by clustering algorithms.

Comparing clusters and hand-gated populations

Given the set of hand-gated populations, contingency matrix C was computed for each clustering, where C_ij is the number of cells in i-th cluster that belong to j-th population. Recall R and precision P matrices were computed: R_ij = C_ij/Σ_k(C_kj), P_ij = C_ij/Σ_k(C_ik). Both matrices were combined into F-measure matrix F_ij=2(R_ijP_ij)/(R_ij + P_ij). The F-measure matrix was used to find an optimal one-to-one assignment between clusters and hand-gated population using Hungarian algorithm, such that the sum of F-measures is maximized. Since the classical Hungarian algorithm solves an inverse problem, i.e. minimizes the sum of weights, the algorithm was actually run on the negative matrix F′= 1 - F. The Java implementation of Hungarian algorithm by Kevin Stern was obtained from http://software-and-algorithms.blogspot.com/

Data pre-processing and clustering

CyTOF experiment files were subject to de-barcoding and bead normalization¹. Then, data was pre-gated to remove doublets, dead cells, erythrocytes and neutrophils. Non-neutrophils population was subject to cluster analysis. Raw intensity values were subject to noise thresholding and asinh transformation y = asinh(max(x - 1, 0)/5. Transformed values were clustered with X-shift or other clustering methods.

Code and data availability

Source code is available from https://github.com/nolanlab/vortex. Source FCS files for clustering algorithm comparison and gating annotation file can be downloaded from https://web.stanford.edu/~samusik/Panorama%20BM%201-10.zip