Highlight
Roots in narrow-leafed lupin (Lupinus angustifolius) exhibit large phenotypic and genetic diversity. An association between root traits and DArT markers demonstrates potential for a marker-assisted selection programme for this species.
Key words: Diversity Arrays Technology (DArT), genetic diversity, molecular marker, narrow-leafed lupin, root trait, trait-marker association.
Abstract
Narrow-leafed lupin (Lupinus angustifolius L.) is the predominant grain legume crop in southern Australia, contributing half of the total grain legume production of Australia. Its yield in Australia is hampered by a range of subsoil constraints. The adaptation of lupin genotypes to subsoil constraints may be improved by selecting for optimal root traits from new and exotic germplasm sources. We assessed root trait diversity and genetic diversity of a core collection of narrow-leafed lupin (111 accessions) using 191 Diversity Arrays Technology (DArT) markers. The genetic relationship among accessions was determined using the admixture model in STRUCTURE. Thirty-eight root-associated traits were characterized, with 21 having coefficient of variation values >0.5. Principal coordinate analysis and cluster analysis of the DArT markers revealed broad diversity among the accessions. An ad hoc statistics calculation resulted in 10 distinct populations with significant differences among and within them (P < 0.001). The mixed linear model test in TASSEL showed a significant association between all root traits and some DArT markers, with the numbers of markers associated with an individual trait ranging from 2 to 13. The percentage of phenotypic variation explained by any one marker ranged from 6.4 to 21.8%, with 15 associations explaining >10% of phenotypic variation. The genetic variation values ranged from 0 to 7994, with 23 associations having values >240. Root traits such as deeper roots and lateral root proliferation at depth would be useful for this species for improved adaptation to drier soil conditions. This study offers opportunities for discovering useful root traits that can be used to increase the yield of Australian cultivars across variable environmental conditions.
Introduction
Narrow-leafed lupin (Lupinus angustifolius L.) has been a predominant grain legume crop and an important component of sustainable farming systems in southern Australia since its domestication was completed in Western Australia in the 1960s and 1970s (Gladstones et al., 1998; Buirchell, 2008; Berger et al., 2012a). It makes up about 50% of the total grain legume production in Australia, with approximately 80% produced in Western Australia (French and Buirchell, 2005; ABARES, 2014). As a legume species, narrow-leafed lupin provides substantial benefits to farming systems via the symbiotic fixation of nitrogen from the air and by acting as a disease break crop in cereal rotations. Although lupins grown in Australia are primarily used as animal feed, they also provide health benefits to humans, being gluten-free, high in protein, and low in fat and carbohydrates (Coffey, 1989; WADAF, 2007; Berger et al., 2013).
Despite their economic, agricultural, and dietary importance, grain yields and planting areas of narrow-leafed lupin have declined globally in the last decade (FAO, 2013) because of low productivity and poor market value. Unlike wheat (Triticum aestivum), barley (Hordeum vulgare), and other dominant crops in Mediterranean regions, current commercial cultivars of narrow-leafed lupin incorporate only a small fraction of their genetic diversity because of the short and fragmented domestication history (Zohary, 1999; Berger et al., 2013). However, the established germplasm pool of L. angustifolius at the Australian Lupin Collection, which comprises 2056 accessions (1327 wild, 214 cultivars, 431 advanced lines, 22 landraces, and 62 mutated lines) from diverse climatic and geographic locations, provides a broad genetic basis to improve crop breeding in this species (Clements and Cowling, 1991; Berger et al., 2013). In that respect, studies on phenotypic diversity and its relationship with genetic diversity in the wild germplasm offer opportunities for discovering unexploited traits that can be used to increase the yield of Australian cultivars across a range of environmental conditions.
Diversity in root system architecture (RSA) across a substantial subsample of the world collection of narrow-leafed lupin was characterized in a recent study (Chen et al., 2012). However, how the phenotypic diversity reflects the genetic diversity remains unknown. There is increasing interest in a genetic analysis of RSA and function, although the focus on the links between genes and root traits is primarily on the effects of genes that directly mediate small-scale phenomena (e.g. Little et al., 2005; Bengough et al., 2006, Cai et al., 2012; Canè et al., 2014; Mlodzinska et al., 2015). One of the most effective approaches to dissecting complicated quantitative traits is an analysis of quantitative trait loci (QTL), which helps to identify specific genes responsible for trait variation (Beebe et al., 2006; Weih et al., 2006; Acuna et al., 2014; Burton et al., 2014). Several types of molecular markers, such as Diversity Arrays Technology (DArT), simple sequence repeats, amplified fragment length polymorphisms, single nucleotide polymorphisms, and sequence-tagged sites, have been developed for analysing genetic diversity in various crop species (e.g. Kwon et al., 2012; El-basyoni et al., 2013; Aitken et al., 2014; Maccaferri et al., 2015; Moore et al., 2015; Uga et al., 2015; Zurek et al., 2015). The development of microarray hybridization-based technology, such as DArT, provides a useful tool to identify DNA variation at hundreds of genomic loci in parallel regardless of the sequence information (Jaccoud et al., 2001). Array-based marker technology permits the detection of population structure and relative kinship within collections (Wenzl et al., 2004; Maccaferri et al., 2015). In L. angustifolius, DArT marker analysis revealed the low genetic diversity present in the domesticated forms (Berger et al., 2012b), highlighting the need to identify and exploit useful diversity in the wild germplasm. The present study analysed genetic diversity in a core collection of wild narrow-leafed lupin using DArT markers and revealed correlations between root trait diversity (phenotype) and genetic diversity (molecular markers).
Materials and methods
Plant material and phenotyping
A set of 111 accessions of narrow-leafed lupin (L. angustifolius), consisting of 108 wild genotypes, one landrace, and two cultivars from 13 countries and four regions (Supplementary Table S1), was evaluated for phenotypic diversity in RSA traits (Table 1). They were studied under glasshouse conditions in Perth (31°58′S, 115°49′E) using a recently developed semi-hydroponic phenotyping system (Chen et al., 2011a, 2012). Detailed plant growth conditions, measurements, and calculations are described in Chen et al. (2012). Root parameters were measured 6 weeks after planting. Taproot lengths were measured 2, 4, and 6 weeks after planting and root growth rates (RGR) were calculated and classified according to incremental increases in taproot length within a given growth period. Root subsamples were scanned in greyscale using a desktop scanner (Epson Expression 1680; Epson, CA, USA) and root images were processed in WinRHIZO v2009 Pro (Regent Instruments, QC, Canada) for root length, root surface area, volume, average root diameter, and diameter class length (DCL, root length in a diameter class). The upper 0−20cm section (separated from the plant collar) of the root system was referred to in this study as ‘topsoil’ and the lower part as ‘subsoil’. There were 38 root traits included in this study, 17 of which had not been reported previously (Chen et al., 2012).
Table 1.
Description of 38 root traits obtained in a phenotyping experiment.
| Traits | Description | Unit | Mean | Median | CV | Correlated trait No. | PC |
|---|---|---|---|---|---|---|---|
| BD | Branch density (branch number/ taproot length) | m−1 taproot | 120 | 120.9 | 0.39 | 31 | 3 |
| BD_sub | Subsoil branch density | m−1 | 79.4 | 71.7 | 0.50 | 31 | 3 |
| BD_top | Topsoil branch density | m−1 | 218.9 | 208.3 | 0.35 | 32 | 9 |
| BI | Branch intensity (branch number/root length) | m−1 root | 22.1 | 20.8 | 0.34 | 34 | 7 |
| BL | Branch length | cm | 343 | 298.7 | 0.62 | 26 | 1 |
| BL/TRL | Branch length/taproot length | 4.83 | 4.31 | 0.53 | 32 | 1 | |
| BL_ind | Average individual branch length | cm | 4.16 | 3.77 | 0.44 | 28 | 2 |
| BL_sub | Subsoil branch length | cm | 129 | 100.7 | 0.81 | 20 | 1 |
| BL_top | Topsoil branch length | cm | 214 | 181.8 | 0.62 | 32 | 1 |
| BLR | Branch length topsoil/subsoil ratio | 2.25 | 1.72 | 0.78 | 14 | 7 | |
| BN | Branch number | root−1 | 84.8 | 78 | 0.47 | 23 | 1 |
| BN_2nd | Second-order branch number | root−1 | 14.7 | 106 | 1.20 | 23 | 5 |
| BN_sub | Subsoil branch number | 40.8 | 34.8 | 0.70 | 24 | 1 | |
| BN_top | Topsoil branch number | 43.8 | 41.7 | 0.35 | 23 | 9 | |
| BNR | Branch number topsoil/subsoil ratio | 1.41 | 1.17 | 0.65 | 32 | 9 | |
| DCL_med | Root length in diameter class 0.75−1.25 mm | cm | 156 | 134.3 | 0.51 | 33 | 1 |
| DCL_thick | Root length in diameter class ≥1.25 mm | cm | 102 | 89.5 | 0.72 | 32 | 1 |
| DCL_thin | Root length in diameter class <0.75mm | cm | 218 | 186.2 | 0.64 | 32 | 6 |
| LBL | Length of the longest branch | cm | 21.7 | 8 | 0.90 | 29 | 5 |
| RA | Root surface area | cm2 | 128 | 112.3 | 0.59 | 31 | 1 |
| RD | Average root diameter | mm | 0.97 | 0.98 | 0.16 | 29 | 6 |
| RGR_2−4wk | Root growth rate (2–4 weeks) | cm d−1 | 1.89 | 1.88 | 0.26 | 24 | 8 |
| RGR_2wk | Root growth rate (0- 2 weeks) | cm d−1 | 1.92 | 1.86 | 0.50 | 23 | 4 |
| RGR_4−6wk | Root growth rate (4–6 weeks) | cm d−1 | 1.61 | 1.51 | 0.24 | 21 | 6 |
| RGR_4wk | Root growth rate (0–4 weeks) | cm d−1 | 1.72 | 1.77 | 0.23 | 30 | 2 |
| RGR_6wk | Root growth rate (0–6 weeks) | cm d−1 | 1.32 | 1.29 | 0.44 | 28 | 3 |
| RL | Root length | cm | 416 | 376 | 0.53 | 17 | 1 |
| RL_sub | Subsoil root length | cm | 180 | 155 | 0.63 | 33 | 1 |
| RL_top | Topsoil root length | cm | 234 | 202 | 0.57 | 19 | 1 |
| RLR | Root length ratio topsoil/subsoil | cm cm−1 | 1.55 | 1.27 | 0.70 | 25 | 7 |
| RM | Root dry mass | mg | 249 | 219 | 0.61 | 32 | 1 |
| RMR | Root-to-shoot mass ratio | 0.65 | 0.63 | 0.24 | 18 | 8 | |
| RTD | Root tissue density (mass/volume) | mg cm−3 | 76.9 | 70.6 | 0.45 | 27 | 9 |
| RV | Root volume | cm3 | 3.27 | 2.83 | 0.69 | 33 | 1 |
| SRL | Specific root length (length/mass) | cm mg−1 | 23.2 | 20.8 | 0.35 | 34 | 7 |
| TRL_2wk | Taproot length after 2 weeks | cm | 45.1 | 42.3 | 0.24 | 24 | 8 |
| TRL_4wk | Taproot length after 4 weeks | cm | 70.9 | 69.7 | 0.23 | 12 | 2 |
| TRL_6wk | Taproot length | cm | 26.6 | 26.3 | 0.27 | 22 | 3 |
Mean, median, and CV values for each trait are given. CV values >0.5 are in bold. Number of significantly correlated traits at P < 0.05 is given for each trait according to Pearson correlation coefficient analysis. Branch length and number refer to first-order branches unless specified. Topsoil = 0−20cm depth; subsoil = 20−120cm depth.
DArT genotyping
A set of 191 DArT markers, including 37 mapped markers, was included in the assay (Berger et al., 2012b; Kroc et al., 2014). Genotyping was performed by Diversity Arrays Technology Pty Ltd (Canberra, Australia) using the protocols described by Kilian et al. (2012). Briefly, DNA samples of each genome were subjected to the PstI/BanII complexity reduction method (Jaccoud et al., 2001). Fluorescent nucleotides were used to label the resulting genomic representations that were hybridized on a microarray printed with the DArT clones. Following hybridization and washing, the microarrays were scanned for analyses. The DArT markers were scored either ‘1’ (if a fragment present) or ‘0’ (if absent).
Statistical analysis of trait data
IBM SPSS Statistics (Version 19, IBM Corp., Armonk, NY, USA) was used to analyse root trait data for genotype main effects with a general linear model (GLM) multivariate analysis after identifying non-significant differences between bins and harvesting times (Chen et al., 2012). Descriptive statistics were computed for each trait across all genotypes in IBM SPSS Statistics 19 (IBM Corp.). The coefficient of variation (CV) was calculated by dividing SD by the mean value. Pearson correlation coefficients (r) were used to determine the general relationship between root trait pairs (P ≤ 0.05) and to generate an agglomerative hierarchical clustering (AHC) dendrogram tree. Variability in root traits across genotypes was determined by principal component analysis (PCA; Jolliffe, 2002). Rotation converged in 30 iterations using Varimax with the Kaiser Normalization method; principal components (PCs) with eigenvalues >1.0 were considered significant (Tabachnik and Fidell, 1996).
Marker diversity analysis
The polymorphic information content (PIC) value indicates the informativeness of a marker locus or marker system. PIC was determined as follows:
where is the frequency of the i th allele in the examined genotypes (Weir, 1990). PIC values and the marker present frequency of each DArT marker were computed in PowerMarker 3.25 (Liu and Muse, 2005). The quality parameter Q for each marker was calculated by dividing the variance of the hybridization level for the marker between the two clusters (i.e. present and absent) by the total variance of the hybridization level of the marker.
Population structure analysis
The genetic diversity structure of the 111 genotypes was analysed using a distance-based method (Schlüter and Harris, 2006) and a model-based approach (Pritchard et al., 2000). Principal coordinate analysis (PCoA) was generated using Jaccard similarity matrices in FAMD 1.25 software (Schlüter and Harris, 2006). Two-dimensional scores were calculated and used to produce scatter plot matrices of scores. Jaccard’s similarity coefficient is defined as:
where denotes the number of markers for which the indicated combination of character states is found for a pair of samples i and j. Character states are band presence (1), band absence (0), and missing data (?). Jaccard’s coefficient was used for the clustering analysis with the neighbour-joining (NJ) method.
Members (accessions/genotypes) in subgroups were identified using a model-based approach for dominant DArT markers implemented in the STRUCTURE software (Pritchard et al., 2000). We used an admixture co-ancestry model with independent and correlated allele frequencies and a burn-in time of 50000. The number of Markov Chain Monte Carlo replications after burn-in was set at 100000 (Pritchard and Wen, 2004), with a K (number of populations) of up to 15 on the entire dataset (111 genotypes). The software provides the likelihood (the posterior probability) of the data for a given number of assumed populations K, and the value of K with the highest likelihood can be interpreted to correspond to an estimate for the underlying number of clusters. An ad hoc quantity (ΔK) based on the rate of the log probability of data between successive K values was used to determine the best K (Evanno et al., 2005):
where the log likelihood (estimated probability) for each K; and is the SD.
Marker-based relative kinship estimates have proven useful for quantitative inheritance studies in different populations (Loiselle et al., 1995; Ritland, 1996). This K estimate approximates identity by descent via adjusting the probability of identity by state between two individuals using the average probability of identity by state between random individuals (Yu et al., 2006). Using the best K, STRUCTURE computed a pairwise matrix, the allele-frequency divergence (i.e. the net nucleotide distance, δ), which was used to construct a phylogenetic tree topology according to an NJ method (Saitou and Nei, 1987) in MEGA 2.1 (Tamura et al., 2011). The analysis of molecular variance (AMOVA) was performed using standard Jaccard’s coefficients and a distance transformation ( to identify significant differences among populations and within populations (Excoffier et al., 1992).
Shannon’s index of diversity variance, and SD were calculated to measure the diversity of populations in the core collection (Shannon, 1948):
where s is the number of populations observed, is the number observed from the i th population, and N is the total number of individuals observed in the sample. P-values of t-tests based on and variances were computed using both Bowman’s and the bootstrap (10 000 times) method (Bowman et al., 1969). To further assess the existence of a genetic structure between identified clusters (populations), pairwise fixation index ( or Phi st) values were calculated as the proportion of population variance due to among-population variation [i.e.] (Weir and Cockerham, 1984). The total population that was used to calculate among Pop1 and Pop2 conformed to Pop1 + Pop2 using the software STRUCTURE and was tested by permutation. The values range from 0 to 1. A zero value implies complete panmixia (the two populations are interbreeding freely), whereas a value of 1 implies that all genetic variation is explained by the population structure (the two populations do not share any genetic diversity).
Trait-marker association analysis
A mixed linear model (MLM) association test of root traits incorporating population structure (Q) and relative kinship (K r) matrices was performed using the TASSEL (v. 2.1) software package (Yu et al., 2006; Bradbury et al., 2007). We also performed GLM (Bradbury et al., 2007) and structured association (SA) (Thornsberry et al., 2001) analyses with the same data, incorporating population structure information as a covariate and using 1000 permutations for the correction of multiple testing. Given that the MLM method performs better in controlling spurious associations (Yu et al., 2006; Aulchenko et al., 2007), we first ranked significant association from the MLM (P ≤ 0.05) and then compared the significance of these markers (P ≤ 0.05) in the permutation-based GLM and SA association tests.
Results
Root trait variation and correlations
A total of 38 root traits, including 17 previously not described, were obtained from the phenotyping experiment (Chen et al., 2012; Table 1). No serious departure from multivariate normality was found in a GLM analysis involving all trait data (the multivariate standard errors of skewness and kurtosis were 0.23 and 0.45, respectively). Values of the CV among the measured traits ranged from 0.16 (average root diameter [RD], branch density [BD]) to 1.2 (second-order branch number [BN_2nd]). Twenty-one traits had CV values >0.5 (Table 1).
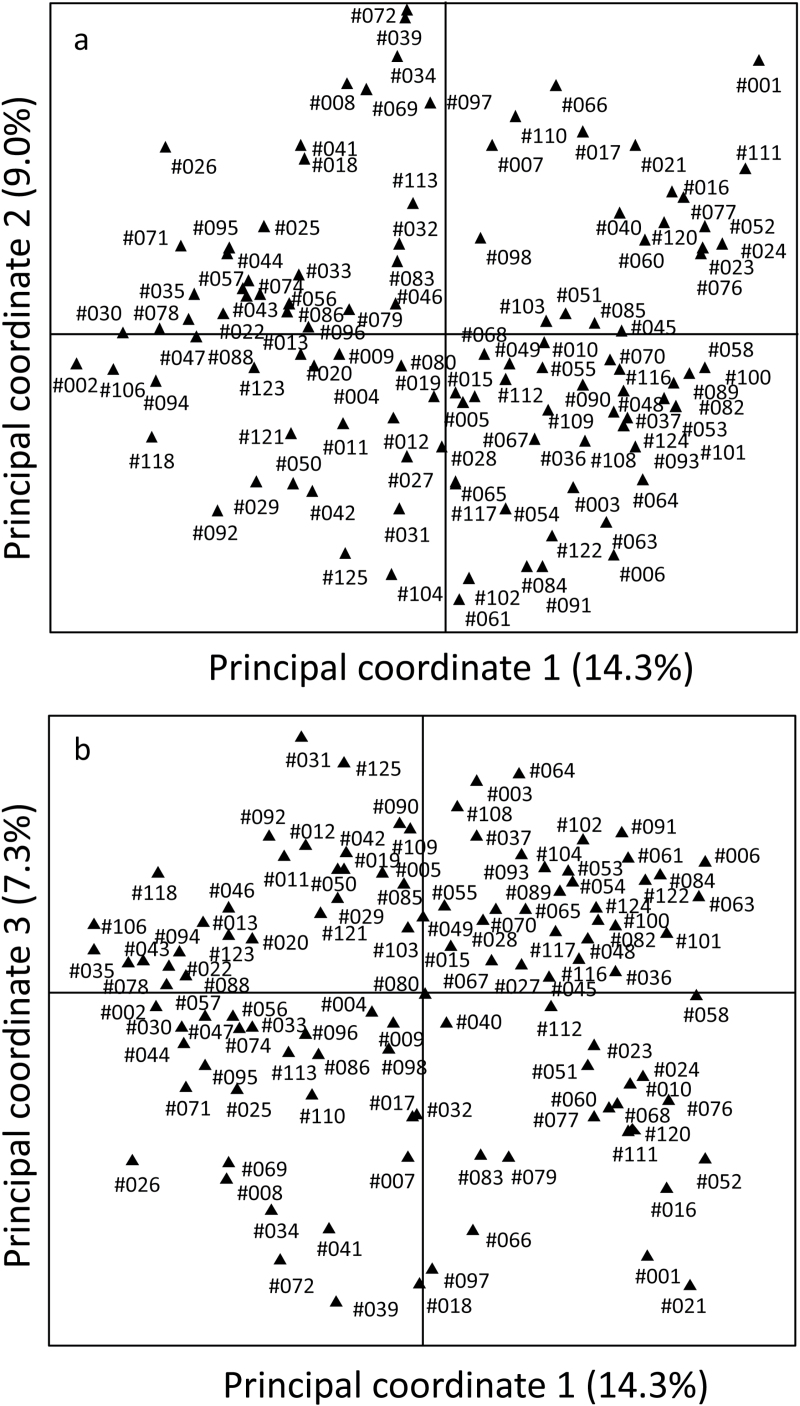
Pearson correlation coefficient analysis on the 38 root traits showed high correlations among individual traits. The number of traits significantly correlated to an individual trait ranged from 12 to 34 at P ≤ 0.05 (Table 1; correlation matrix not shown). To account for these correlations, multivariate traits were constructed using PCA, resulting in nine components (PCs) with eigenvalues >1 (Supplementary Fig. S1). The number of root traits allocated to an individual PC varied from 1 to 14, with PC4 containing only root growth rate at 0–2 weeks (RGR_2wk), and PC1 having 14 root traits including branch length (BL), branch number (BN), root length (RL), and root mass (RM) (Table 1). The scree plot of the PCA exhibited the total variance explained for each component. Nine components accounted for 90.7% of the variance (Supplementary Fig. S1). Among these, the first three components (PC1, PC2, and PC3; Fig. 1) represented 41.1%, 16.1%, and 12.5% of the variance, respectively, to explain a total of 69.7% of the variance.
Fig. 1.
Two-dimensional plot showing the variability of 38 root traits across 111 genotypes of L. angustifolius based on PCA. Components PC1 versus PC2 (a) and PC1 versus PC3 (b) represent 57.2% and 53.6% of the variability, respectively. For root trait notations see Table 1. This figure is available in colour at JXB online.
Phenotypic diversity among the collection
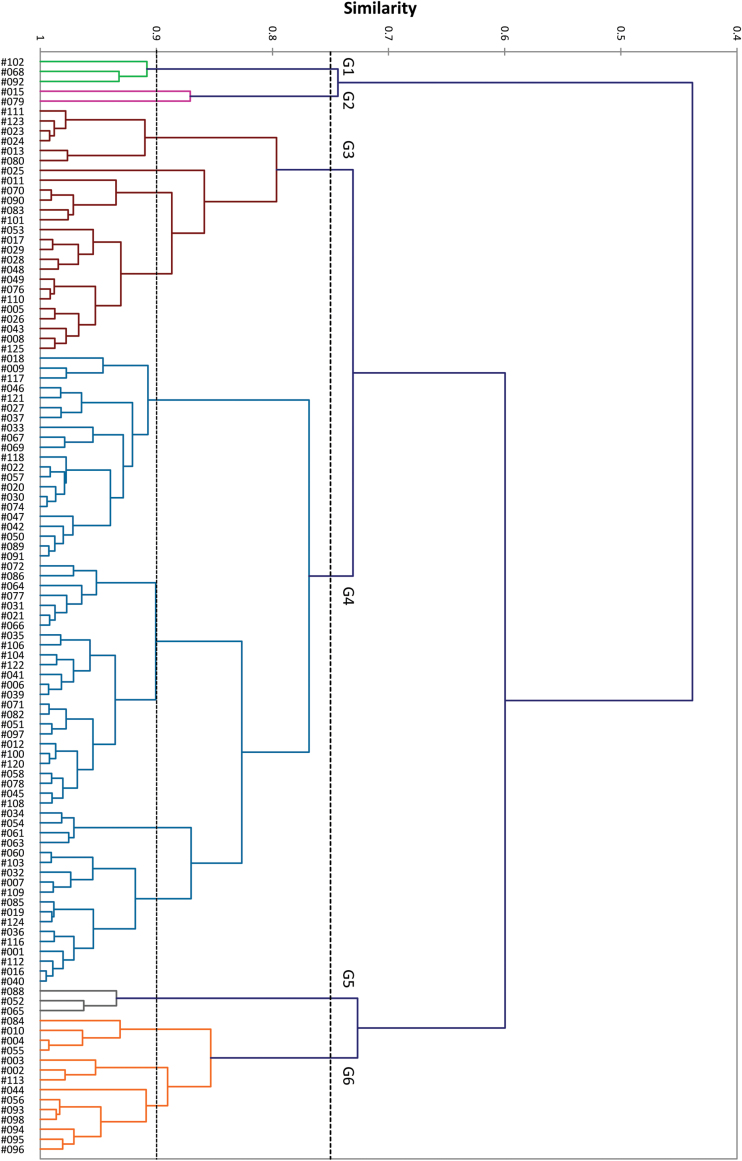
An AHC similarity dendrogram constructed with the Pearson correlation coefficients of root trait data showed a large diversity in root architecture traits among the core collection (Fig. 2). Six general groups of genotypes with relatively homogeneous root traits were identified at a similarity level of 0.75. The number of group members (genotypes) varied widely among groups. The smallest group (G2) contained two genotypes whereas the largest group (G4) consisted of 64 genotypes. At a similarity level of 0.9, groups G1, G3, G4, and G6 were further divided into two, four, five, and three subgroups, respectively. The grouping outcomes for genotypic variability and similarity in root traits did not reflect geographic origin (cf. Supplementary Table S1).
Fig. 2.
Dendrogram of AHC using the Pearson correlation coefficient on 38 root traits in XLSTAT (v2013.1). The 111 genotypes were assigned into one of six general groups (G1 to G6) at 0.75 similarity level (upper dashed line) containing 16 subgroups at 0.9 similarity level (lower dashed line). For more details on genotypes see Supplementary Table S1. This figure is available in colour at JXB online.
DArT marker variation
A total of 191 DArT markers were polymorphic among the 111 accessions. The present set of DArT markers contained between 0 and 28% missing observations. The PIC values of these markers varied from 0.086 to 0.375, with an average PIC value of 0.330 (Table 2). Marker present frequency of each marker ranged from 0.11 to 0.86 with an average of 0.41 (data not shown).
Table 2.
PIC values for 191 DArT markers used for L. angustifolius.
| PIC value a | Number of DArT markers | % total DArT markers |
|---|---|---|
| 0.4−0.3 | 150 | 78.5 |
| 0.3−0.2 | 33 | 17.3 |
| 0.2−0.1 | 6 | 3.1 |
| 0.1−0.0 | 2 | 1.1 |
a PIC values ranged from 0.086 to 0.36 with mean 0.33.
Genetic diversity in the collection
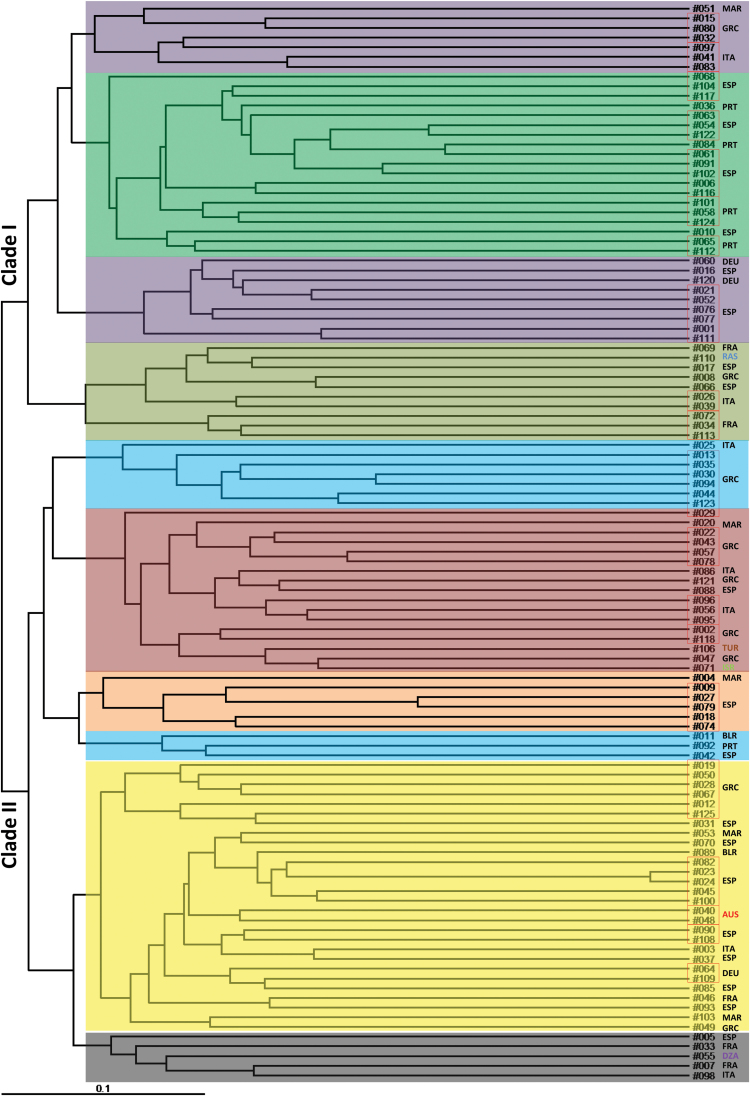
The genetic diversity of the 111 genotypes was assessed by PCoA using 191 DArT markers. PCoA identified 65 principal coordinates with positive eigenvalues, including 28 with values >1, indicating large diversity in the collection. The generated Jaccard similarity matrix was used to construct principal coordinate plots deciphering the genetic relationships among the genotypes. The first two principal coordinates derived from the scores jointly explained 23.3% of the total variance (Fig. 3). NJ tree topology constructed on the basis of the inter-individual genetic similarity (Jaccard’s coefficient) against 191 DArT markers showed a clear separation for most of the genotypes, suggesting significant diversity in this collection of accessions (Fig. 4).
Fig. 3.
PCoA of 111 L. angustifolius genotypes based on 191 DArT markers. The graphs show the position of each accession in the space spanned by coordinate 1 versus coordinate 2 (a), and coordinate 1 versus coordinate 3 (b) of a relative Jaccard similarity matrix with FAMD. For root trait notations see Table 1.
Fig. 4.
NJ tree of 111 L. angustifolius genotypes against 191 DArT markers with distance based on Jaccard’s coefficient. Country codes (on the right): AUS, Australia; BLR, Belarus; DEU, Germany; DZA, Algeria; ESP, Spain; FRA, France; GRC, Greece; ISR, Israel; ITA, Italy; MAR, Morocco; PRT, Portugal; RUS, Russia; TUR, Turkey. For more details on genotypes see Supplementary Table S1. This figure is available in colour at JXB online.
Population structure of the collection
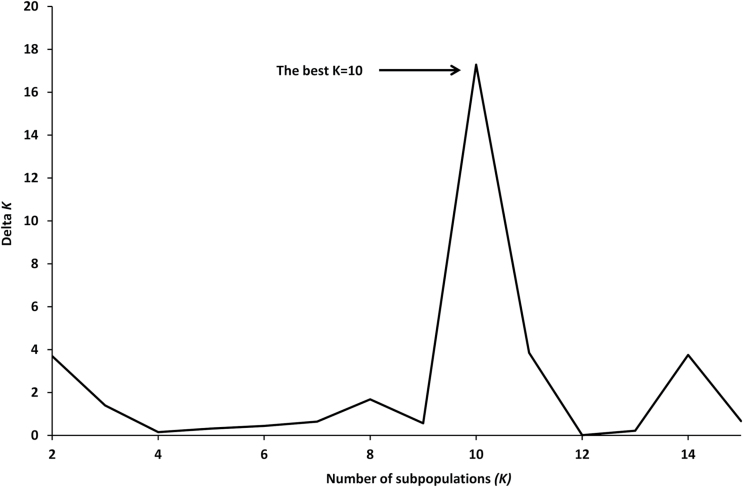
The genetic relationship among the 111 genotypes was analysed based on the DArT dataset. The true number of groups (populations) was determined using the admixture model in STRUCTURE and an ad hoc statistics (ΔK) calculation resulted in 10 distinct populations (Fig. 5). Differences among the 10 populations and within populations were significant based on AMOVA (P < 0.001) (Table 3). The genetic distances among populations were illustrated by an NJ tree using Jaccard’s coefficient (Fig. 4), and were consistent with the analysis using the allele-frequency divergence (net nucleotide distance, δ; data not shown). The average distance between individuals within each population ranged from 0.172 (Pop10) to 0.301 (Pop06) (Table 4). The composition of each population varied between 3 (Pop08) and 28 (Pop09) genotypes and consisted of collections from two to eight countries of origin. The two Australian cultivars in population 9 (Pop09) had a close genetic relationship with 26 other genotypes originating from Spain (12), Greece (7), Morocco (2), Germany (2), Belarus (1), France (1), and Italy (1). Forty-one genotypes from Spain were grouped into eight populations, indicating large diversity even within the same country of origin. There was no clear correlation between genetic relationship and geographic origin.
Fig. 5.
Determination of the true number of groups based on the second order rate of change of the likelihood (ΔK, see the calculation methods; Evanno et al., 2005) using DArT marker data. The true K(10) is shown as the uppermost level of structure.
Table 3.
AMOVA based on PCA-generated populations using standard Jaccard’s coefficients with distance transformation (d = 1− s).
| Source | d.f. | SD | Variance |
Variance,
% of total |
P |
|---|---|---|---|---|---|
| Among populations | 9 | 7.57 | 0.066 | 32.55 | <0.001 |
| Within populations | 101 | 13.9 | 0.138 | 67.45 | <0.001 |
| Total | 110 | 21.5 | 0.204 |
Table 4.
Composition of 10 populations obtained by the admixture model (Q matrix in STRUCTURE) in terms of entries belonging to particular countries of origin.
| Continent | Country | Pop01 | Pop02 | Pop03 | Pop04 | Pop05 | Pop06 | Pop07 | Pop08 | Pop09 | Pop10 | Subtotal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Africa | Algeria | 1 | 1 | |||||||||
| Morocco | 1 | 1 | 1 | 2 | 5 | |||||||
| Asia | Russia | 1 | 1 | |||||||||
| Turkey | 1 | 1 | ||||||||||
| Europe | Belarus | 1 | 1 | 2 | ||||||||
| France | 4 | 1 | 2 | 7 | ||||||||
| Germany | 2 | 2 | 4 | |||||||||
| Greece | 3 | 1 | 6 | 9 | 7 | 26 | ||||||
| Israel | 1 | 1 | ||||||||||
| Italy | 3 | 2 | 1 | 4 | 1 | 1 | 12 | |||||
| Portugal | 7 | 1 | 8 | |||||||||
| Spain | 12 | 7 | 2 | 1 | 5 | 1 | 12 | 1 | 41 | |||
| Oceania | Australia | 2 | 2 | |||||||||
| Subtotal | 7 | 19 | 9 | 10 | 7 | 17 | 6 | 3 | 28 | 5 | 111 | |
| Average distances | 0.213 | 0.207 | 0.236 | 0.193 | 0.301 | 0.310 | 0.204 | 0.194 | 0.215 | 0.172 | ||
Genetic variation among populations
Shannon’s index of diversity (H′) and the associated variance and SD (Table 5) were computed for 10 populations generated by PCA. Both Bowman’s and bootstrap methods generated similar H′ values for specific populations and geographic regions. However, Bowman’s method produced larger variances for each category than the bootstrap method (Table 5). Pop06 had the lowest H′ value with the largest variance among all populations in both analyses. In contrast, Pop02 had the highest H′ value with the smallest variance. Variations in Shannon’s index of diversity were related to the size of populations, reflecting variation in the geographic locations of each population (Tables 4 and 5).
Table 5.
Shannon’s index of diversity (H′), variance, and SD based on 10 populations and geographic regions computed using Bowman’s and bootstrap approaches in THE FAMD package.
| Group | Size | Bowman’s method | Bootstrapped (10 000 times) method | ||||
|---|---|---|---|---|---|---|---|
| Shannon’s index | Variance | SD | Shannon’s index | Variance | SD | ||
| Population | |||||||
| P01 | 7 | 6.91 | 2.74 | 1.66 | 6.92 | 0.005 | 0.068 |
| P02 | 19 | 7.33 | 0.13 | 0.36 | 7.33 | 0.001 | 0.023 |
| P03 | 9 | 7.21 | 0.54 | 0.74 | 7.23 | 0.002 | 0.040 |
| P04 | 10 | 7.25 | 0.58 | 0.76 | 7.23 | 0.001 | 0.034 |
| P05 | 7 | 7.26 | 0.77 | 0.88 | 7.25 | 0.001 | 0.037 |
| P06 | 17 | 6.19 | 9.00 | 3.00 | 6.17 | 0.019 | 0.137 |
| P07 | 6 | 7.13 | 1.31 | 1.15 | 7.14 | 0.002 | 0.048 |
| P08 | 3 | 7.23 | 0.52 | 0.73 | 7.22 | 0.002 | 0.042 |
| P09 | 28 | 7.25 | 0.64 | 0.80 | 7.26 | 0.001 | 0.036 |
| P10 | 5 | 7.05 | 3.07 | 1.75 | 7.05 | 0.003 | 0.056 |
| Region | |||||||
| Africa | 6 | 7.35 | 2.55 | 1.60 | 7.36 | 0.001 | 0.027 |
| Asia | 2 | 6.43 | 10.6 | 3.26 | 6.37 | 0.015 | 0.120 |
| Europe | 101 | 7.47 | 0.01 | 0.11 | 7.47 | 0.000 | 0.011 |
| Australia | 2 | 6.13 | 8.63 | 2.94 | 6.14 | 0.019 | 0.138 |
T-test analyses on population data exhibited significant differences between most population pairs (P ≤ 0.05; Table 6). For example, Pop01 significantly differed from all other populations (seven populations at P ≤ 0.01 level and one population at P ≤ 0.05) except for Pop10. Pop03 was significantly different from Pop01 and Pop06 (P < 0.01) and Pop10 (P ≤ 0 .05), but did not statistically differ from the other six populations. Population–population distances based on the Bayesian method ranged from 0.077 (Pop03 versus Pop05) to 0.146 (Pop02 versus Pop 03), indicating varied genetic relationships among populations (Supplementary Table S2). The genetic structure between identified populations was further assessed using pairwise F st analysis. The F st values estimated for population pairs ranged from 0.129 to 0.398, confirming pronounced genetic differentiation among populations (Supplementary Table S3).
Table 6.
P values of T-test for populations (upper part) and geographic regions (lower part) computed on Shannon’s index values and variances of the 10 populations that resulted from PCA analysis using bootstrapped method.
| Pop01 | Pop02 | Pop03 | Pop04 | Pop05 | Pop06 | Pop07 | Pop08 | Pop09 | |
|---|---|---|---|---|---|---|---|---|---|
| Pop02 | 0.001** | ||||||||
| Pop03 | 0.004** | 0.033 | |||||||
| Pop04 | 0.003** | 0.026* | 0.883 | ||||||
| Pop05 | 0.002** | 0.069 | 0.708 | 0.800 | |||||
| Pop06 | 0.008** | 0.004** | 0.005** | 0.005** | 0.005** | ||||
| Pop07 | 0.025* | 0.004** | 0.181 | 0.127 | 0.094* | 0.007** | |||
| Pop08 | 0.003** | 0.033* | 0.949 | 0.832 | 0.666 | 0.005** | 0.206 | ||
| Pop09 | 0.002** | 0.107 | 0.532 | 0.600 | 0.800 | 0.005** | 0.060 | 0.499 | |
| Pop10 | 0.162 | 0.003** | 0.029* | 0.022* | 0.016* | 0.010* | 0.271 | 0.034* | 0.011* |
| Africa | Asia | Europe | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Asia | 0.004** | ||||||||
| Europe | 0.003** | 0.003** | |||||||
| Australia | 0.003** | 0.268ns | 0.002** |
**P < 0.01; *P ≤ 0.05; ns = not significant. P-values obtained using Bowman’s method were all >0.05 (data not presented).
Trait-marker association
The MLM association test of root traits revealed associations between root traits and DArT markers. All 38 root traits showed significant (P ≤ 0.05) associations with DArT markers, while the number of markers associated with an individual trait ranged from 2 to 13 (Table 7). At a significance level of 0.01, 30 traits were associated with one to four marker(s) (Tables 7 and 8). Of these, the branch number topsoil to subsoil ratio (BNR) was associated with four markers (lPb−328947, lPb−329087, lPb−329141, and lPb−332488) (Table 8), and average root diameter (RD) was associated with four different markers (lPb−330348, lPb−333127, lPb−333527, and lPb−334753). Thirty of the 191 markers showed a significant association with root traits (α = 0.01). Among them, 16 were associated with multiple traits (two to eight), whereas each of the remaining 14 was associated with a single trait. Marker IPb–333104 had the highest association with root traits, including branch density (BD), branch number (BN), subsoil branch length (BL_sub), and root length in diameter class <0.75mm (DCL_thin) (Table 8). The percentage of phenotypic variation explained by a marker (Marker R 2) ranged from 6.4 (branch length topsoil to subsoil ratio, BLR) to 21.8 (root tissue density, RTD), with 15 associations having Marker R 2 values >10%. Genetic variation values ranged from 0 to 7994, with 23 associations having values >240. A wide range of values was observed for residual variation (0−17897).
Table 7.
Significant marker-trait associations analysis in narrow-leafed lupin.
| Traits | DArT marker number | |
|---|---|---|
| α = 0.05 | α = 0.01 | |
| BD | 7 | 2 |
| BD_sub | 7 | 1 |
| BD_top | 9 | 3 |
| BI | 6 | 1 |
| BL | 2 | 0 |
| BL/TRL | 2 | 0 |
| BL_ind | 2 | 0 |
| BL_sub | 13 | 2 |
| BL_top | 4 | 0 |
| BLR | 7 | 2 |
| BN | 11 | 2 |
| BN_2nd | 8 | 3 |
| BN_sub | 8 | 2 |
| BN_top | 9 | 3 |
| BNR | 11 | 4 |
| DCL_med | 11 | 1 |
| DCL_thick | 12 | 1 |
| DCL_thin | 5 | 3 |
| LBL | 9 | 1 |
| RA | 5 | 0 |
| RD | 12 | 4 |
| RGR_2−4wk | 9 | 1 |
| RGR_2wk | 9 | 3 |
| RGR_4−6wk | 9 | 3 |
| RGR_4wk | 10 | 1 |
| RGR_6wk | 12 | 3 |
| RL | 2 | 0 |
| RL_sub | 11 | 1 |
| RL_top | 4 | 0 |
| RLR | 6 | 0 |
| RM | 13 | 1 |
| RMR | 5 | 2 |
| RTD | 4 | 3 |
| RV | 7 | 1 |
| SRL | 5 | 2 |
| TRL_2wk | 9 | 3 |
| TRL_4wk | 8 | 1 |
| TRL_6wk | 9 | 2 |
Table 8.
Significant DArT markers associated with root traits of narrow-leafed lupin.
| Trait | Marker | Lineage groups |
Distance,
cM |
Site | F | P-value |
Error
DF |
Marker
R 2 |
Genetic
variance |
Residual
variance |
−2Ln
likelihood |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BD | lPb−333104 | 97/226 | 11.6 | 0.001 | 97 | 0.125 | 606 | 2101 | 1155 | ||
| BD | lPb−333527 | NLL−01 | 96.2 | 29 | 7.5 | 0.007 | 106 | 0.070 | 606 | 2101 | 1155 |
| BD_sub | lPb−333104 | 97/226 | 7.1 | 0.009 | 97 | 0.080 | 393 | 1535 | 1120 | ||
| BD_top | lPb−329031 | 42 | 7.0 | 0.010 | 94 | 0.068 | 1557 | 4090 | 1261 | ||
| BD_top | lPb−333104 | 97/226 | 18.0 | 0.000 | 97 | 0.194 | 1557 | 4090 | 1261 | ||
| BD_top | lPb−333527 | NLL−01 | 96.2 | 29 | 7.5 | 0.007 | 106 | 0.069 | 1557 | 4090 | 1261 |
| BI | lPb−333615 | 117/246 | 10.8 | 0.001 | 96 | 0.128 | 0 | 63 | 759 | ||
| BL_sub | lPb−332834 | 89/218 | 10.3 | 0.002 | 106 | 0.096 | 7482 | 4694 | 1318 | ||
| BL_sub | lPb−333104 | 97/226 | 7.1 | 0.009 | 97 | 0.069 | 7482 | 4694 | 1318 | ||
| BLR | 801605349012_H_24 | 178/307 | 6.9 | 0.010 | 106 | 0.064 | 0.9 | 1.9 | 427 | ||
| BLR | lPb−329428 | 52 | 9.1 | 0.003 | 95 | 0.087 | 0.9 | 1.9 | 427 | ||
| BN | lPb−329031 | 42 | 7.2 | 0.009 | 94 | 0.068 | 504 | 1010 | 1115 | ||
| BN | lPb−333104 | 97/216 | 15.5 | 0.000 | 97 | 0.153 | 504 | 1010 | 1115 | ||
| BN_2nd | 801605349014_O_17 | 186/315 | 9.1 | 0.003 | 89 | 0.096 | 24 | 268 | 898 | ||
| BN_2nd | lPb−333741 | 124/253 | 7.1 | 0.009 | 95 | 0.078 | 24 | 268 | 898 | ||
| BN_2nd | lPb−334500 | NLL−16 | 38.5 | 2 | 8.1 | 0.006 | 101 | 0.079 | 24 | 268 | 898 |
| BN_sub | 801605349003_F_3 | 171/300 | 7.4 | 0.008 | 88 | 0.076 | 278 | 528 | 1040 | ||
| BN_sub | lPb−333104 | 97/226 | 11.4 | 0.001 | 97 | 0.111 | 278 | 528 | 1040 | ||
| BN_top | lPb−329031 | 42 | 7.0 | 0.010 | 94 | 0.068 | 62 | 164 | 907 | ||
| BN_top | lPb−333104 | 97/226 | 18.2 | 0.000 | 97 | 0.194 | 62 | 164 | 907 | ||
| BN_top | lPb−333527 | NLL−01 | 96.2 | 29 | 7.5 | 0.007 | 106 | 0.069 | 62 | 164 | 907 |
| BNR | lPb−328947 | 40 | 7.6 | 0.007 | 107 | 0.070 | 0.5 | 0.7 | 283 | ||
| BNR | lPb−329087 | 43 | 13.4 | 0.000 | 99 | 0.132 | 0.5 | 0.7 | 283 | ||
| BNR | lPb−329141 | 45 | 11.1 | 0.001 | 93 | 0.116 | 0.5 | 0.7 | 283 | ||
| BNR | lPb−332488 | 86/215 | 11.5 | 0.001 | 102 | 0.106 | 0.5 | 0.7 | 283 | ||
| DCL_medium | lPb−334226 | 143/272 | 7.6 | 0.007 | 97 | 0.079 | 1267 | 5118 | 1268 | ||
| DCL_thick | lPb−329803 | 57 | 7.9 | 0.006 | 94 | 0.082 | 1724 | 3850 | 1246 | ||
| DCL_thin | lPb−333104 | 97/226 | 7.2 | 0.008 | 97 | 0.080 | 5615 | 17898 | 1392 | ||
| DCL_thin | lPb−333527 | NLL−01 | 96.2 | 29 | 7.9 | 0.006 | 106 | 0.074 | 5615 | 17898 | 1392 |
| DCL_thin | lPb−334226 | 143/272 | 8.7 | 0.004 | 97 | 0.084 | 5615 | 17898 | 1392 | ||
| LBL | 801605349007_M_5 | 175/304 | 8.1 | 0.005 | 96 | 0.083 | 247 | 261 | 914.1 | ||
| RD | lPb−330348 | 66/195 | 7.9 | 0.006 | 99 | 0.079 | 0 | 0 | −123 | ||
| RD | lPb−333127 | 21 | 10.7 | 0.002 | 89 | 0.126 | 0 | 0 | −123 | ||
| RD | lPb−333527 | NLL−01 | 96.2 | 29 | 11.7 | 0.001 | 106 | 0.110 | 0 | 0 | −123 |
| RD | lPb−334753 | 165/294 | 8.9 | 0.004 | 95 | 0.089 | 0 | 0 | −123 | ||
| RGR | lPb−331019 | 70/199 | 7.6 | 0.007 | 96 | 0.079 | 0.1 | 0.1 | 94 | ||
| RGR | lPb−334270 | 145/274 | 7.0 | 0.010 | 97 | 0.074 | 0.1 | 0.1 | 94 | ||
| RGR | lPb−334297 | 147/276 | 9.8 | 0.002 | 94 | 0.099 | 0.1 | 0.1 | 94 | ||
| RGR_2−4wk | lPb−329428 | 52 | 8.7 | 0.004 | 95 | 0.098 | 0.1 | 0.2 | 184 | ||
| RGR_2wk | lPb−333220 | 103/232 | 8.5 | 0.004 | 106 | 0.080 | 0.1 | 0.2 | 148 | ||
| RGR_2wk | lPb−333816 | 129/258 | 7.7 | 0.006 | 105 | 0.072 | 0.1 | 0.2 | 148 | ||
| RGR_2wk | lPb−333836 | NLL−07 | 29.1 | 14 | 7.5 | 0.008 | 83 | 0.097 | 0.1 | 0.2 | 148 |
| RGR_4−6wk | lPb−329031 | 42 | 7.0 | 0.010 | 94 | 0.074 | 0.3 | 0.6 | 294 | ||
| RGR_4−6wk | lPb−334226 | 143/272 | 8.9 | 0.004 | 97 | 0.095 | 0.3 | 0.6 | 294 | ||
| RGR_4wk | lPb−333228 | 102/231 | 7.2 | 0.009 | 96 | 0.075 | 0.0 | 0.1 | 93 | ||
| RL_sub | lPb−332834 | 89/218 | 10.6 | 0.002 | 106 | 0.098 | 7994 | 5529 | 1332 | ||
| RM | lPb−329803 | 57 | 7.9 | 0.006 | 94 | 0.080 | 5947 | 17706 | 1409 | ||
| RMR | lPb−334461 | 151/280 | 9.3 | 0.003 | 98 | 0.091 | 0 | 0 | −96 | ||
| RMR | lPb−334753 | 165/294 | 12.8 | 0.001 | 95 | 0.130 | 0 | 0 | −96 | ||
| RTD | lPb−329917 | 61 | 3.0 | 0.005 | 111 | 0.218 | 290 | 1030 | 1086 | ||
| RTD | lPb−333220 | 103/232 | 12.5 | 0.001 | 106 | 0.113 | 290 | 1030 | 1086 | ||
| RTD | lPb−333816 | 129/258 | 12.1 | 0.001 | 105 | 0.110 | 290 | 1030 | 1086 | ||
| RV | lPb−334500 | NLL−16 | 38.5 | 2 | 8.2 | 0.005 | 106 | 0.075 | 1.4 | 3.7 | 484 |
| SRL | lPb−330348 | 66/195 | 8.5 | 0.004 | 99 | 0.084 | 51 | 19.2 | 754 | ||
| SRL | lPb−334461 | 151/280 | 7.9 | 0.006 | 98 | 0.088 | 51 | 19.2 | 754 | ||
| TRL | lPb−333816 | 129/258 | 7.4 | 0.008 | 105 | 0.074 | 72 | 153 | 909 | ||
| TRL | lPb−334297 | 147/276 | 8.1 | 0.005 | 94 | 0.081 | 72 | 153 | 909 | ||
| TRL_2wk | lPb−333220 | 103/232 | 8.4 | 0.005 | 106 | 0.078 | 9.6 | 37.9 | 739 | ||
| TRL_2wk | lPb−333816 | 129/258 | 7.7 | 0.007 | 105 | 0.072 | 9.6 | 37.9 | 739 | ||
| TRL_2wk | lPb−333836 | NLL−07 | 29.1 | 14 | 7.7 | 0.007 | 83 | 0.096 | 9.6 | 37.9 | 739 |
| TRL_4wk | lPb−333228 | 102/231 | 7.1 | 0.009 | 96 | 0.077 | 26 | 87.4 | 836 |
Trait-marker association was performed with an MLM model incorporating population structure (Q-matrix) and kinship (Kr) in TASSEL 2.1. Marker R2 is the percentage of phenotypic variation explained by the marker. Only significant trait (α = 0.01)-trait-marker associations were included. Each trait is assigned to one of the nine PCs based on PCA with eigenvalues >1. The number of DArT markers found for each trait at α = 0.01 and 0.05 is presented.
Discussion
A wide genetic diversity in a range of root traits was identified in a collection of narrow-leafed lupin (L. angustifolius) comprising 108 wild types from around the world (Table 1; Fig. 4). Exploiting the diverse genetic and adaptive resources of this species is critical for its future (Berger et al., 2013) because the production of narrow-leafed lupin in Australia is hampered by terminal drought and a range of subsoil constraints (e.g. soil compaction, acidity, and aluminium toxicity; Turner and Asseng, 2005). These constraints limit root growth into deep horizons and thus restrict root access to water and nutrients (Adcock et al., 2007; Chen et al., 2014). Although the present study focused on characterizing genetic diversity in root traits, additional above-ground traits were measured in the phenotyping experiment. These included leaflet number, shoot height, shoot dry mass, total dry mass, the ratio of root dry mass to shoot dry mass, and the ratio of root dry mass to total dry mass (Chen et al., 2012). Pearson correlation analysis revealed a strong correlation (mostly at P < 0.01) between 15 root traits (e.g. root length, branch length, branch number, specific root length, and root tissue density) and a number of above-ground traits (e.g. leaflet number and shoot dry weight) (Chen et al., 2012).
RSA critically influences foraging and the capture of water and nutrients, and it thus determines crop productivity (Lynch, 1995). Studies have flagged root length, branching at depth, and seminal root angle as key traits likely to underpin further increases in the yield of crops such as wheat (e.g. Manschadi et al., 2010). An increased capacity to take up water from deep soil horizons has been linked to increased yield potential in sugar beet (Beta vulgaris) (Ober et al., 2005; Lynch and Wojciechowski, 2015); a similar connection was made for wheat in western and southern Australia (Wong and Asseng, 2006; Manschadi et al., 2010) and rice (Oryza sativa; Kondo et al., 1999; Kamoshita et al., 2000). Recently, we observed better performance in 2 of 10 selected wild L. angustifolius genotypes when compared with local cultivars at a Western Australian farm with subsoil compaction (Chen et al., 2014). Specifically selecting for improved root traits, such as root proliferation at depth, may result in yield increases, especially in drier soil conditions. This is particularly important because attempts to increase root density at depth using agronomic approaches (e.g. deep fertiliser placement and deep ripping) have been largely unsuccessful (e.g. Baddeley et al., 2007). Therefore, it may be possible to improve the ability of lupin genotypes to adapt to subsoil constraints by selecting for proxy root traits from new and exotic germplasm sources.
The subset of the world collection of L. angustifolius evaluated in this study exhibited large phenotypic and genetic diversity in a range of root traits (Table 1). Genetic material from a wide latitudinal range, involving 108 wild types, was used in our study to ensure the identification of genotypic variability in various RSA traits. Large morphological diversity in relation to geographical origins has been observed previously in narrow-leafed lupin accessions from the western Mediterranean (Gladstones and Crosbie, 1979) and Aegean (Clements and Cowling, 1994) regions. Crop cultivars with proxy RSA traits may have improved desirable agronomic traits such as yield, drought tolerance, and resistance to nutrient deficiencies (Tuberosa et al., 2002; Beebe et al., 2006; Steele et al., 2007). Developing high-throughput screening techniques for accurate and efficient phenotyping is critical for characterizing root-related traits in a wide-scale germplasm pool (De Dorlodot et al., 2007). We have recently established a novel semi-hydroponic phenotyping system to determine genetic variation in intrinsic RSA in the world collection of narrow-leafed lupin. Based on the results of a glasshouse phenotyping experiment (Chen et al., 2012), 10 genotypes with contrasting root characters were further examined in two different types of soils (Chen et al., 2011b) and in the field (Chen et al., 2014). There was relatively consistent ranking of genotypes between the two separate phenotyping experiments, and between phenotyping experiments and two different soil media in the glasshouse and the field (Chen et al., 2011b, 2012, 2014). Eco-geographical studies and field phenotyping on above-ground traits have previously been evaluated (Clements and Cowling, 1994). Because root phenotypic data reported here were obtained from the phenotyping experiment under carefully controlled environmental conditions, field phenotyping of the same set of the lupin collection for root traits is required to explore the potential gene-by-environment interactions. The genotypic variability in root traits and potential traits of interest identified in our glasshouse phenotyping experiment form a basis for field study.
This study used a set of DArT markers for genetic analysis and demonstrated a high level of polymorphism and high quality as assessed by the call rate, scoring reproducibility, and PIC values of these markers (Table 2). Genetic markers with high-level polymorphism are critical for use in fingerprinting and marker-assisted selection (MAS) programmes (Smith et al., 2000; Mace et al., 2008). Diversity arrays have been widely used for rapid and economical genotyping to any genome or complex genomic mixtures (Jaccoud et al., 2001; Akbari et al., 2006). The DArT markers used in this study comprised 37 markers mapped on the genome of narrow-leafed lupin (Table 8). Marker technology is developing rapidly and future research will be able to incorporate 50 000 DArTseq markers (Matthew Nelson, unpublished data).
Our study showed significant correlations between root traits and molecular markers using genome-wide association analysis (Tables 7 and 8). These results have a potential application in the selection of suitable root traits for targeted edaphic environmental adaptation. Short regions of conserved synteny between L. angustifolius and two model legume species (Medicago truncatula and Lotus japonicus) have been identified (Nelson et al., 2006, 2010; Kroc et al., 2014), and a low-density survey sequence of the L. angustifolius genome was described with a small proportion of scaffolds and large-insert library clones assigned to linkage groups (Lesniewska et al., 2011; Yang et al., 2013). An improved reference genetic map of L. angustifolius comprising 1475 primarily gene-based marker loci was recently reported (Kamphuis et al., 2015). The recent progress in genome mapping in narrow-leafed lupin provides useful tools for MAS and QTL cloning for RSA in wild L. angustifolius by exploiting genomic resources, candidate genes, and the knowledge gained from model species, particularly Arabidopsis (Sergeeva et al., 2006), M. truncatula and L. japonicus (Choi et al., 2004; Nelson et al., 2010), rice (Horii et al., 2005; Steele et al., 2007), and maize (Zea mays) (Giuliani et al., 2005). Combining phenotypic data of RSA features and genetic marker/QTL analysis will enable us to explore the inheritance of RSA traits in narrow-leafed lupin and to identify proxy traits, such as deeper roots and lateral root proliferation at depth, for enhancing adaptation to different edaphic environments, particularly drying soil conditions.
Supplementary data
Supplementary data are available at JXB online.
Table S1. Breeding status and country of origin of 111 L. angustifolius genotypes used in this study.
Table S2. Population–population distances: chord distance from allele-frequency estimates based on the Bayesian (non-uniform prior from among-population information) method (FAMD).
Table S3. Estimates of pairwise F st values for populations based on random allelic permutation testing of the DArT dataset (P < 0.01).
Figure S1. Scree plot of the PCA of all 38 root traits across 111 genotypes of L. angustifolius showing the total variance explained for each component (PC).
Acknowledgements
This study was supported by The Australian Research Council (DP0988193 and DP130104825), The Grains Research and Development Corporation, The National Natural Science Foundation of China (31471946), and The Chinese Academy of Sciences’ Hundred Talents Programme.
References
- ABARES 2014. Agricultural commodity statistics 2014 . Australian Bureau of Agricultural and Resource Economics and Sciences, Canberra, ACT. [Google Scholar]
- Acuna TB, Rebetzke GJ, He X, Maynol E, Wade LJ. 2014. Mapping quantitative trait loci associated with root penetration ability of wheat in contrasting environments. Molecular Breeding 34, 631–642. [Google Scholar]
- Adcock D, McNeill AM, McDonald GK, Armstrong RD. 2007. Subsoil constraints to crop production on neutral and alkaline soils in south-eastern Australia: a review of current knowledge and management strategies. Animal Production Science 47, 1245–1261. [Google Scholar]
- Aitken KS, McNeil MD, Hermann S, Bundock PC, Kilian A, Heller-Uszynska K, Henry RJ, Li J. 2014. A comprehensive genetic map of sugarcane that provides enhanced map coverage and integrates high-throughput Diversity Array Technology (DArT) markers. BMC Genomics 15, 152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akbari M, Wenzl P, Caig V, et al. 2006. Diversity arrays technology (DArT) for high-throughput profiling of the hexaploid wheat genome. Theoretical and Applied Genetics 113, 1409–1420. [DOI] [PubMed] [Google Scholar]
- Aulchenko YS, De Koning DJ, Haley C. 2007. Genomewide rapid association using mixed model and regression: a fast and simple method for genomewide pedigree-based quantitative trait loci association analysis. Genetics 177, 577–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baddeley JA, Bingham IJ, Hoad SP. 2007. Development of cereal root systems for sustainable agriculture. In: Østergård H, Backes G, Kovács G. (eds). Proceedings of the COST SUSVAR workshop on varietal characteristics of cereals in different growing systems with special emphasis on below ground traits. Danmarks Tekniske Universitet, Risø Nationallaboratoriet for Bæredygtig Energi, Roskilde, pp. 9–13. [Google Scholar]
- Beebe SE, Rojas-Pierce M, Yan X, Blair MW, Pedraza F, Munoz F, Tohme J, Lynch JP. 2006. Quantitative trait loci for root architecture traits correlated with phosphorus acquisition in common bean. Crop Science 46, 413–423. [Google Scholar]
- Bengough AG, Bransby MF, Hans J, McKenna SJ, Roberts TJ, Valentine TA. 2006. Root responses to soil physical conditions; growth dynamics from field to cell. Journal of Experimental Botany 57, 437–447. [DOI] [PubMed] [Google Scholar]
- Berger JD, Buirchell B, Luckett D, Nelson MN. 2012. b. Domestication bottlenecks limit genetic diversity and constrain adaptation in narrow-leafed lupin (Lupinus angustifolius L.). Theoretical and Applied Genetics 124, 637–652. [DOI] [PubMed] [Google Scholar]
- Berger JD, Buirchell BJ, Luchett DJ, Palta JA, Ludwig C, Liu DL. 2012. a. How has narrow-leafed lupin changed in its 1st 40 years as an industrial, broad-acre crop? A G x E-based characterization of yield–related traits in Australian cultivars. Field Crop Research 126, 152–164. [Google Scholar]
- Berger JD, Clements JC, Nelson MN, Kamphuis LG, Singh KB, Buirchell B. 2013. The essential role of genetic resources in narrow-leafed lupin improvement. Crop and Pasture Science 64, 361–373. [Google Scholar]
- Bowman KO, Hutcheson K, Odum EP, Shenton LR. 1969. Comments on the distribution of indices of diversity. Proceedings of International Symposium on Statistic Ecology 3, 315–359. [Google Scholar]
- Bradbury PJ, Zhang Z, Kroon DE, Casstevens TM, Ramdoss Y, Buckler ES. 2007. TASSEL: software for association mapping of complex traits in diverse samples. Bioinformatics 23, 2633–2635. [DOI] [PubMed] [Google Scholar]
- Buirchell BJ. 2008. Narrow-leafed lupin breeding in Australia – Where to from here? In: Palta JA, Berger JB. (eds). Lupins for health and wealth − Proceedings of the 12th International Lupin Conference . International Lupin Association, Canterbury, New Zealand, pp.226–230. [Google Scholar]
- Burton AL, Johnson JM, Foerster JM, Hirsch CN, Buell CR, Hanlon MT, Kaeppler SM, Brown KM, Lynch JP. 2014. QTL mapping and phenotypic variation for root architectural traits in maize (Zea mays L.). Theoretical and Applied Genetics 127, 2293–2311. [DOI] [PubMed] [Google Scholar]
- Cai H, Chen F, Mi G, Zhang F, Maurer HP, Liu W, Reif JC, Yuan L. 2012. Mapping QTLs for root system architecture of maize (Zea mays L.) in the field at different developmental stages. Theoretical and Applied Genetics 125, 1313–1324. [DOI] [PubMed] [Google Scholar]
- Canè MA, Maccaferri M, Nazemi G, Salvi S, Francia R, Colalongo C, Tuberosa R. 2014. Association mapping for root architectural traits in durum wheat seedlings as related to agronomic performance. Molecular Breeding 34, 1629–1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen YL, Dunbabin VM, Diggle AJ, Siddique KHM, Rengel Z. 2011. a. Development of a novel semi-hydroponic phenotyping system for studying root architecture. Functional Plant Biology 38, 355–363. [DOI] [PubMed] [Google Scholar]
- Chen YL, Dunbabin VM, Diggle AJ, Siddique KHM, Rengel Z. 2012. Assessing variability in root parameters of wild Lupinus angustifolius germplasm: basis for modelling root system structure. Plant and Soil 354, 141–155. [Google Scholar]
- Chen YL, Dunbabin VM, Postma J, Diggle AJ, Palta JA, Lynch JP, Siddique KHM, Rengel Z. 2011. b. Phenotypic variability and modelling of root structure of wild Lupinus angustifolius genotypes. Plant and Soil 348, 345–364. [Google Scholar]
- Chen YL, Palta J, Clements J, Buirchell B, Siddique KHM, Rengel Z. 2014. Root architecture alteration of narrow-leafed lupin and wheat in response to soil compaction. Field Crops Research 165, 61–70. [Google Scholar]
- Choi HK, Kim D, Uhm T, et al. 2004. A sequence-based genetic map of Medicago truncatula and comparison of marker collinearity with M. sativa . Genetics 166, 1463–1502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clements JC, Cowling WA. 1994. Patterns of morphological diversity in relation to geographical origins of wild Lupinus angustifolius from the Aegean region. Genetic Resources and Crop Evolution 41, 109–122. [Google Scholar]
- Clements JC, Cowling WA. 1991. Catalogue of the Australian lupin collection including field evaluation data for wild, semi-domesticated and fully domesticated accessions . Research Report 3/91. Department of Agriculture Western Australia, Perth, WA. [Google Scholar]
- Coffey R. 1989. Lupins as an energy-rich protein source for feed and food. In: Applewhite TH. (ed). Vegetable protein utilisation in human foods and animal feedstuffs . American Oil Chemists Society, Champaign, IL, pp 410–414. [Google Scholar]
- De Dorlodot S, Forster B, Pages L, Price A, Tuberosa R, Draye X. 2007. Root system architecture: opportunities and constraints for genetic improvement of crops. Trends in Plant Science 12, 474–481. [DOI] [PubMed] [Google Scholar]
- El-basyoni I, Baenziger PS, Dweikat I, Wang D, Eskridge K, Saadalla M. 2013. Using DArT markers to monitor genetic diversity throughout selection: a case study in Nebraska’s winter wheat breeding nurseries. Crop Science 53, 2363–2373. [Google Scholar]
- Evanno G, Regnaut S, Goudet J. 2005. Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Molecular Ecology 14, 2611–2620. [DOI] [PubMed] [Google Scholar]
- Excoffier L, Smouse PE, Quattro JM. 1992. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics 131, 479–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FAO 2013. FAOSAT. Vol. 2013 . Food and Agriculture Organization of the United Nations, Rome. [Google Scholar]
- French RJ, Buirchell BJ. 2005. Lupin: the largest grain legume crop in Western Australia, its adaptation and improvement through plant breeding. Crop & Pasture Science 56, 1169–1180. [Google Scholar]
- Giuliani S, Sanguineti MC, Tuberosa R, Bellotti M, Salvi S, Laudi P. 2005. Root-ABA1, a major constitutive QTL, affects maize root architecture and leaf ABA concentration at different water regimes. Journal of Experimental Botany 56, 3061–3070. [DOI] [PubMed] [Google Scholar]
- Gladstones JS, Atkins CA, Hamblin J. 1998. Lupins as crop plants: biology, production and utilization . CAB International, Wallingford, UK. [Google Scholar]
- Gladstones JS, Crosbie GB. 1979. Lupin wild types introduced into Western Australia to 1973 . Western Australian Department of Agriculture Technical Bulletin No 43. WA Department of Agriculture, Perth, WA. [Google Scholar]
- Horii H, Nemoto K, Miyamoto N, Harada J. 2005. Quantitative trait loci for adventitious and lateral roots in rice. Plant Breeding 125, 198–200. [Google Scholar]
- Jaccoud D, Peng K, Feinstein D, Kilian A. 2001. Diversity Arrays: a solid state technology for sequence information independent genotyping. Nucleic Acids Research 29(4), e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolliffe IT. 2002. Principal component analysis , second ed Springer, New York. [Google Scholar]
- Kamoshita A, Wade LJ, Yamauchi A. 2000. Genotypic variation in response of rainfed lowland rice to drought and rewatering. III. Water extraction during the drought period. Plant Production Science 3, 189–196. [Google Scholar]
- Kamphuis LG, Hane JK, Nelson MN, Gao L, Atkins CA, Singh KB. 2015. Transcriptome sequencing of different narrow-leafed lupin tissue types provides a comprehensive uni-gene assembly and extensive gene-based molecular markers. Plant Biotechnology Journal 13, 14–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilian A, Wenzl P, Huttner E, et al. 2012. Diversity arrays technology: a generic genome profiling technology on open platforms. In: Data production and analysis in population genomics . Humana Press, New York, pp. 67–89. [DOI] [PubMed] [Google Scholar]
- Kondo M, Murty MV, Aragones DV, Okada K, Winn T, Kwak KS. 1999. Characteristics of the root system and water uptake in upland rice. In: Ito O, O’Toole J, Hardy B. (eds). Genetic improvement of rice for water limited environments . International Rice Research Institute, Makati City, Philippines, pp 117–131. [Google Scholar]
- Kroc M, Koczyk G, Święcicki W, Kilian A, Nelson MN. 2014. New evidence of ancestral polyploidy in the Genistoid legume Lupinus angustifolius L.(narrow-leafed lupin). Theoretical and Applied Genetics 127, 1237–1249. [DOI] [PubMed] [Google Scholar]
- Kwon S, Brown A, Hu J, McGee R, Watt C, Kisha T, Timmerman-Vaughan G, Grusak M, McPhee KE, Coyne C. 2012. Genetic diversity, population structure and genome-wide marker-trait association analysis of the USDA pea (Pisum sativum L.) core collection. Genes and Genomics 34, 305–320. [Google Scholar]
- Lesniewska K, Książkiewicz M, Nelson MN, Mahé F, Aïnouche A, Wolko B, Naganowska B. 2011. Assignment of 3 genetic linkage groups to 3 chromosomes of narrow-leafed lupin. Journal of Heredity 102, 228–236. [DOI] [PubMed] [Google Scholar]
- Little DY, Rao HY, Oliva S, Daniel-Vedele F, Krapp A, Malamy JE. 2005. The putative high-affinity nitrate transporter NRT2.1 represses lateral root initiation in response to nutritional cues. Proceedings of the National Academy of Sciences of the United States of America 102, 13693–13698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu K, Muse SV. 2005. PowerMarker: integrated analysis environment for genetic marker data. Bioinformatics 21, 2128–2129. [DOI] [PubMed] [Google Scholar]
- Loiselle BA, Sork VL, Nason J, Graham C. 1995. Spatial genetic structure of a tropical understory shrunb, Psychotria officinalis (Rubiaceae). American Journal of Botany 82, 1420–1425. [Google Scholar]
- Lynch J. 1995. Root architecture and plant productivity. Plant Physiology 109, 7–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch JP, Wojciechowski T. 2015. Opportunities and challenges in the subsoil: pathways to deeper rooted crops. Journal of Experimental Botany 66, 2199–2210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maccaferri M, Ricci A, Salvi S, et al. 2015. A high‐density, SNP‐based consensus map of tetraploid wheat as a bridge to integrate durum and bread wheat genomics and breeding. Plant Biotechnology Journal 13, 648–663. [DOI] [PubMed] [Google Scholar]
- Mace ES, Xia L, Jordan DR, Halloran K, Parh DK, Huttner E, Wenzl P, Kilian A. 2008. DArT markers: diversity analyses and mapping in Sorghum bicolor . BMC Genomics 9, 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manschadi AM, Christopher JT, Hammer GL, Devoil P. 2010. Experimental and modelling studies of drought‐adaptive root architectural traits in wheat (Triticum aestivum L.). Plant Biosystems 144, 458–462. [Google Scholar]
- Młodzińska E, Kłobus G, Christensen MD, Fuglsang AT. 2015. The plasma membrane H(+)-ATPase AHA2 contributes to the root architecture in response to different nitrogen supply. Physiologia Plantarum 154, 270–282. [DOI] [PubMed] [Google Scholar]
- Moore CM, Richards RA, Rebetzke GJ. 2015. Phenotypic variation and QTL analysis for oil content and protein concentration in bread wheat (Triticum aestivum L.). Euphytica 204, 371–382 [Google Scholar]
- Nelson MN, Moolhuijzen PM, Boersma JG, et al. 2010. Aligning a new reference genetic map of Lupinus angustifolius with the genome sequence of the model legume, Lotus japonicus . DNA Research 17, 73–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson MN, Phan HT, Ellwood SR, et al. 2006. The first gene-based map of Lupinus angustifolius L. − location of domestication genes and conserved synteny with Medicago truncatula . Theoretical and Applied Genetics 113, 225–238. [DOI] [PubMed] [Google Scholar]
- Ober ES, Clark CJ, Bloa Ml, Smith CH. 2005. Root growth, soil water extraction and drought tolerance in sugar beet. Aspects of Applied Biology 73, 213–220. [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. 2000. Inference of population structure using multi-locus genotype data. Genetics 155, 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Wen W. 2004. Documentation for STRUCTURE software . The University of Chicago Press, Chicago, IL. [Google Scholar]
- Ritland K. 1996. Estimators for pairwise relatedness and individual inbreeding coefficients. Genetic Research 67, 175–186. [Google Scholar]
- Saitou N, Nei M. 1987. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Molecular Biology and Evolution 4, 406–425. [DOI] [PubMed] [Google Scholar]
- Schlüter PM., Harris SA. 2006. Analysis of multilocus fingerprinting data sets containing missing data. Molecular Ecology Notes 6, 569–572. [Google Scholar]
- Sergeeva LI, Keurentjes JJ, Bentsink L, Vonk J, van der Plas LH, Koornneef M, Vreugdenhil D. 2006. Vacuolar invertase regulates elongation of Arabidopsis thaliana roots as revealed by QTL and mutant analysis. Proceedings of the National Academy of Sciences of the United States of America 103, 2994–2999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon CE. 1948. A mathematical theory of communication. Bell System Technical Journal 27, 623–656. [Google Scholar]
- Smith JSC, Kresovich S, Hopkins MS, Mitchell SE, Dean RE, Woodman WL, Lee M, Porter K. 2000. Genetic diversity among elite sorghum inbred lines assessed with simple sequence repeats. Crop Science 40, 226–232. [Google Scholar]
- Steele KA, Virk DS, Kumar R, Prasad SC, Witcombe JR. 2007. Field evaluation of upland rice lines selected for QTLs controlling root traits. Field Crops Research 101, 180–186. [Google Scholar]
- Tabachnik BG, Fidell LS. 1996. Using multivariate statistics . Harper Collins, New York. [Google Scholar]
- Tamura K, Peterson D, Peterson N, Stecher G, Nei M, Kumar S. 2011. MEGA5: molecular evolutionary genetics analysis using maximum likelihood, evolutionary distance and maximum parsimony methods. Molecular Biology and Evolution 28, 2731–2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornsberry JM, Goodman MM, Doebley J, Kresovich S, Nielsen D, Buckler ES. 2001. Dwarf 8 polymorphisms associate with variation in flowering time. Nature Genetics 28, 286–289. [DOI] [PubMed] [Google Scholar]
- Tuberosa R, Salvi S, Sanguineti MC, Landi P, Maccaferri M, Conti S. 2002. Mapping QTLs regulating morpho‐physiological traits and yield: Case studies, shortcomings and perspectives in drought – stressed maize. Annals of Botany 89, 941–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner NC, Asseng S. 2005. Productivity, sustainability, and rainfall-use efficiency in Australian rainfed Mediterranean agricultural systems. Crop and Pasture Science 56, 1123–1136. [Google Scholar]
- Uga Y, Kitomi Y, Ishikawa S, Yano M. 2015. Genetic improvement for root growth angle to enhance crop production. Breeding Science 65, 111–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WADAF 2007. Australian sweet lupin: a very healthy asset . Department of Agriculture and Food of Western Australia, Perth, WA. [Google Scholar]
- Weih M, Rönnberg-Wästljung A, Glynn C. 2006. Genetic basis of phenotypic correlations among growth traits in hybrid willow (Salix dasyclados × S. viminalis) grown under two water regimes. New Phytologist 170, 467–477. [DOI] [PubMed] [Google Scholar]
- Weir BS, Cockerham CC. 1984. Estimating F-statistics for the analysis of population structure. Evolution 38, 1358–1370. [DOI] [PubMed] [Google Scholar]
- Weir BS. 1990. Genetic data analysis. Methods for discrete genetic data . Sinauer Associates Inc, Sunderland, MA. [Google Scholar]
- Wenzl P, Carling J, Kudrna D, Jaccoud D, Huttner E, Kleinhofs A, Kilian A. 2004. Diversity Arrays Technology (DArT) for whole-genome profiling of barley. Proceedings of the National Academy of Sciences of the United States of America 101, 9915–9920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong MTF, Asseng S. 2006. Determining the causes of spatial and temporal variability of wheat yields at sub-field scale using a new method of upscaling a crop model. Plant and Soil 283, 203–215. [Google Scholar]
- Yang H, Tao Y, Zheng Z, Zhang Q, Zhou G, Sweetingham MW, Howieson JG, Li C. 2013. Draft genome sequence, and a sequence-defined genetic linkage map of the legume crop species Lupinus angustifolius L. PLoS One 8(5), e64799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Pressoir G, Briggs WH, et al. 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nature Genetics 38, 203–208. [DOI] [PubMed] [Google Scholar]
- Zohary D. 1999. Monophyletic vs. polyphyletic origin of the crops on which agriculture was founded in the Near East. Genetic Resources and Crop Evolution 46, 133–142. [Google Scholar]
- Zurek PR, Topp CN, Benfey PN. 2015. Quantitative trait locus mapping reveals regions of the maize genome controlling root system architecture. Plant Physiology 167, 1487–1496. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.