In-drop capillary spooling of spider capture thread inspires hybrid fibers with mixed solid–liquid mechanical properties

Significance

The spiraling capture threads of spider orb webs are covered with thousands of tiny glue droplets whose primary function is to entrap insects. In this paper we demonstrate that the function of the drops goes beyond that of gluing prey for they also play a role in the mechanical properties of these fibers—usually ascribed solely to the complex molecular architecture of the silk. Indeed, each of the droplets can spool and pack the core silk filament, thus keeping the thread and the whole web under tension. We demonstrate that this effect is the result of the interplay between elasticity and capillarity by making a fully artificial drops-on-fiber compound as extensible as capture thread is.

Abstract

An essential element in the web-trap architecture, the capture silk spun by ecribellate orb spiders consists of glue droplets sitting astride a silk filament. Mechanically this thread presents a mixed solid–liquid behavior unknown to date. Under extension, capture silk behaves as a particularly stretchy solid, owing to its molecular nanosprings, but it totally switches behavior in compression to now become liquid-like: It shrinks with no apparent limit while exerting a constant tension. Here, we unravel the physics underpinning the unique behavior of this ”liquid wire” and demonstrate that its mechanical response originates in the shape-switching of the silk filament induced by buckling within the droplets. Learning from this natural example of geometry and mechanics, we manufactured programmable liquid wires that present previously unidentified pathways for the design of new hybrid solid–liquid materials.

Hybrids made of different materials often display effective properties far exceeding those of their components (1): zinc-coated steel is both strong and corrosion-resistant; metal foams (hybrids of metal and air) are stiff, light, and crushable at the same time, making them perfect candidates to absorb energy in a car crash (2, 3). Nature also provides many exquisite examples of hybrid design such as the seashell nacre, both stiff and tough thanks to its inner “brick-and-mortar” structure composed of rigid, though brittle, inclusions surrounded by a crack-arresting soft organic matrix (4), or the bamboo stem with its hollow core and honeycomb-shaped cells that maximize the ratio of bending rigidity over weight (5). A most interesting natural hybrid material is the spider’s capture thread, which consists of a core filament that supports glue droplets. Here we report the arresting mechanical behavior of this capture thread, which changes from solid-like in extension to liquid-like in compression. We trace this behavior back to the core filament’s buckling inside the droplets. A synthetic version of this natural system then allows us to copy the remarkable properties of spider’s capture thread and to manufacture a novel type of hybrid material.

Spiders use different kinds of silk to build their webs, and a typical ecribellate orb web combines dry and smooth radial threads with wet and droplet-covered spiral threads (6–10). The adhesive nature of these droplets enables the spiral capture thread to perform its primary function of catching insect prey (6). Apart from being sticky, these capture threads also prove to be particularly resilient to tensile tests: Extensive studies on their mechanical behavior (6, 11) revealed that, when stretched, the thread elongates to three times its web length without breaking and recoils back with no noticeable hysteresis or sagging when relaxed (12). This stretchiness confers spider silk a strength 10-fold that of natural or synthetic rubber (13, 14). These remarkable extensional properties rely on the macromolecular architecture of capture silk (15, 16). The ability to cope with stretch is crucial for spider capture threads for it provides their unusually large toughness (energy required for rupture), which in turn allows them to absorb the kinetic energy of incident prey without breaking. Far less understood is the behavior of the thread when compressed: unlike any solid fiber that sags or buckles, it stays taut and self-adapts to compression. Fig. 1 and Movie S1 illustrate this singular behavior, reminiscent of the response of liquid films to compression events: Liquid films do not buckle upon squeezing, but rather self-adapt (17). And, as for liquid films, self-adaptation for the capture thread is an indication for fiber self-tension. This liquid-like behavior in compression suggests that more than merely endowing the web with adhesion, capture silk might well have the additional mechanical function of preserving the web structural integrity. Indeed, without self-adaptation, single sticky strands would touch during relaxation events and thereby irremediably damage the web. With sagging suppressed, the sticky strands are secured apart.

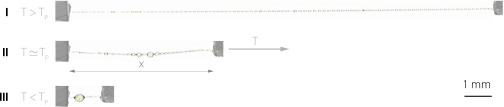
Fig. 1.

A liquid wire. Whether stretched or relaxed, the typical capture silk thread of an araneid orb spider (here N. edulis) remains taut. Force monitoring reveals that when subjected to large tension T, the fiber behaves like a spring (I). As T is decreased, a force plateau $T\simeq T_{\text{P}}$ is reached, along which the thread adopts a wide range of lengths, just as soap films do (II). At lower tensions, $T<T_{\text{P}}$, the thread is totally contracted (III). See Movie S1 for full cycle.

In the present paper, we investigate and disentangle the mechanism underpinning the unique behavior of spider capture silk. Based on these insights we design a mechanical hybrid that behaves as a solid when stretched, but as a liquid when compressed.

The spectacular macroscopic properties of hybrids often originate in a physical effect that occurs at the microstructural level [which needs not be molecular; see, e.g., the buckling of the walls of a unit cell in a cellular solid (2, 18)]. To investigate the physics of the mechanical hybrid character of spider capture thread, we performed mechanical tests on a single thread alongside microscopic observations of its microstructure. Fig. 2 shows the relaxation of a freshly harvested biological sample. Starting from a stretched state (region I), the force–elongation curve shows that the thread behaves as a regular elastic solid undergoing relaxation: The monitored tension decreases almost linearly with the imposed displacement. In this regime, the capture thread adopts a classic drop-on-straight filament conformation, evocative of unduloidal-shaped drops sitting astride textile fibers (19), glass filaments (20), mammalian hairs (21), or feathers (22). But, as relaxation proceeds further, the mechanical behavior of the capture thread switches from solid to liquid. This sudden change can be read directly from the mechanical testing: In region II, the recorded tension becomes virtually independent of the imposed displacement. This plateau tension is the typical signature of the response of liquid or soap films to tensile or compressive solicitations. Strikingly, this behavioral change coincides with a sharp modification of the microstructure: Whereas the overall composite remains taut, the core filament now buckles within each glue droplet (see Movie S2 for a close-up of this mechanism in action, and Movie S3 for combined microscopic observations and mechanical response measurements). At even higher compressions, spools of slack filament form within the drops and keep on accumulating until eventually the overall tension falls (region III). Such spools have previously been observed in samples of postmortem capture threads, but the physics underlying their formation, and in particular the potential roles of the filament molecular structure or of the glue viscoelasticity in this formation, has remained unclear so far (6).

Fig. 2.

Shape-induced functionalization. Quasi-static force measurements on spider capture threads combined with microscopic observations reveal that the core filament coils into the droplets ($\sim$ 250–300-μm wide) along a force plateau $T\sim T_{\text{P}}$ (liquid-like response). For larger forces, $T>T_{\text{P}}$, the fiber straightens and a solid-like behavior is recovered. The particular shape of this force–extension curve can be attributed to a shape-induced functionalization of the fiber by the glue droplets. See also Movies S2 and S3.

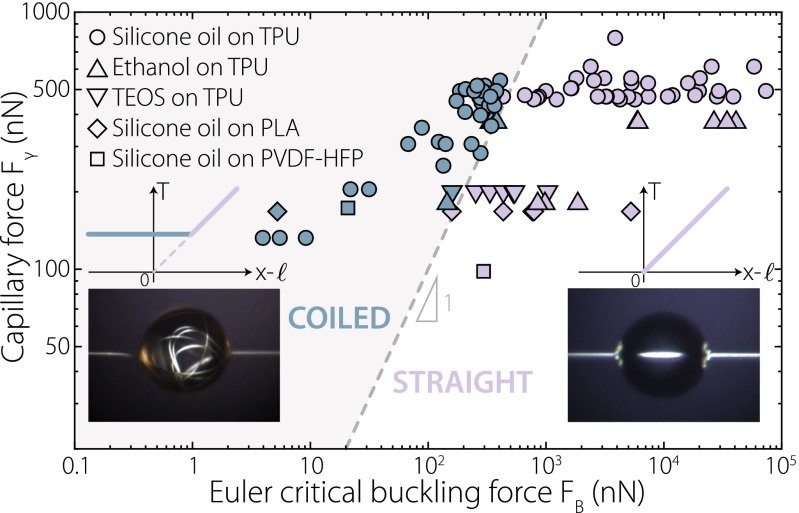
The coincidence between the change in the mechanical responses of the capture thread at the global scale and the change in the conformations of the core filament at the drop scale is intriguing and requires further investigation. Let us consider a composite system consisting of a synthetic core filament and of a liquid droplet, and examine the link between the global mechanical response of the system and the local filament geometry. Specifically we investigate the possibility of a buckling-induced activation of the composite. Surface tension is known to promote buckling (23, 24), snapping (25), or wrinkling (26) of thin lamellar structures. In the drop–filament composite, and in the absence of any external load, local buckling is initiated when the capillary force developed near each meniscus of a single drop $F_{\gamma }=2\pi h\gamma \cos \theta$ exceeds the Euler buckling load $F_B=kEI/D^2$, where h, γ, θ, $EI$, D, and k denote, respectively, the filament radius, the liquid–air surface tension, the contact angle of the liquid on the filament, the bending stiffness of the core filament, the wet length, and the Euler buckling factor. The $h^4$ scaling of the filament’s bending stiffness constitutes however a strong restriction for capillarity-induced buckling, typically limiting the manifestation of this phenomenon in filaments in the nanometer to micrometer range––thereby supporting the observed in-drop buckling of micronic spider capture threads, and explaining why hairs of 80-μm diameter do not buckle when wet, but rather simply clump (27). This fully mechanical scenario, involving capillarity and elasticity as the only ingredients, suggests that any drop sitting astride any filament could make it buckle, provided the force condition $F_{\gamma }>F_B$ is satisfied. To test this hypothesis, we conducted extensive experiments with various Newtonian liquid drops surrounding synthetic (i.e., nonbiological) filaments of different diameters and made of diverse materials. Upon release of external tension, we found in-drop elastocapillary buckling to be indeed activated as soon as the capillary force overcomes the Euler buckling load, irrespective of the materials involved; see Fig. 3 and Movie S4 for a demonstration of how to turn a common fiber into a liquid–solid hybrid. Note that we have here used the value $k={\pi }^2$ for the Euler buckling factor, expressing the fact that the fiber can freely rotate at the meniscii (simply supported buckling); see ref. 28. Contrary to conventional buckling, past the elastic instability threshold the core filament is not gently deformed but literally spooled and packed within the droplets, although the applied capillary force is constant. These behaviors, along with the localization of the bending deformation, are typical signatures of a subcritical instability. Furthermore, the global mechanical response of the composite changes instantly as soon as buckling is initiated at the drop scale: under large stretching, the composite behavior is that of the core filament, but switches to that of a liquid film when compressed past the threshold (see also Movie S5). Thus, the droplets have the double role of storing the excess thread and putting the whole composite in a state of tension. This behavior is all the more arresting because real liquid cylinders instantaneously disintegrate due to Rayleigh-plateau instability, making the liquid-like response of the composite truly unusual.

Fig. 3.

Spooling activation. In-drop spooling can also be achieved by synthetic fibers wet by droplets of various Newtonian liquids. The phase diagram summarizes experiments performed with different materials and liquids in a quasi-static displacement-controlled setting. Each experiment consists of releasing the external tension on an initially taut system. Spooled or straight filament conformations are then observed within the droplets (blue or purple points, respectively). These data demonstrate that the spooling threshold corresponds to a capillarity-induced buckling condition: Spooling spontaneously occurs as soon as the capillary force exerted by the drop $F_{\gamma }$ exceeds the Euler buckling load of the filament $F_B$. Note that, contrary to classic buckling, this spooling continues to proceed as long as the previous force condition is fulfilled, which suggests a subcritical nature for this elastocapillary instability. The composite overall mechanical response (sketched in insets) also sharply changes past the threshold to exhibit a liquid-like plateau force.

The geometry of slender elastic objects is known to control their mechanical response (29, 30). The composite under study here is no exception and we now explain how the in-drop filament geometry leads the thread to inherit the solid core filament mechanical properties when stretched, but the liquid drop properties when compressed. To shed light on this connection between the microstructure and the global mechanical response, we consider a simple model where a bendable and stretchable elastic filament of total length ℓ supports a liquid drop, the overall system now being subjected to an external tension T. Elastocapillary spooling activation can be described as a phase transition between a wet and coiled phase––where the filament is entirely packed within the liquid drop––and a dry and extended phase––where the filament runs straight outside the drop. The extended phase is characterized by a stretching modulus $EA$ and a rest length ${\ell }_{\text{e}}$. Under an applied tension, its extension is $x_{\text{e}}=\left(1+{\mathit{ϵ}}_{\text{e}}\right){\ell }_{\text{e}}$, where ${\mathit{ϵ}}_{\text{e}}$ is the extensional strain. The strain energy of the phase is then $\left(1/2\right){\ell }_{\text{e}}\hspace{0.17em}EA{\mathit{ϵ}}_{\text{e}}^2$, to which we add the solid–air interface energy $2\pi h{\gamma }_{\text{sv}}{\ell }_{\text{e}}$. The coiled phase is made up of the drop and the spooled filament inside the drop. The spools certainly adopt a complicated shape and the bending energy of the filament is $\left(1/2\right)EI{\displaystyle {\int }_0^{{\ell }_{\text{c}}}\kappa {\left(s\right)}^2\hspace{0.17em}\text{d}s}$, where κ is the curvature of the filament and $I=\pi h^4/4$. Approximating the drop as spherical and the spools as arcs of circle, we write $\kappa =2/D$, where D is the diameter of the drop. The bending energy is then $2\hspace{0.17em}{\ell }_{\text{c}}\hspace{0.17em}EI/D^2$. We note that in this approximation the extension of the phase $x_{\text{c}}=D$ is constant. We add the solid–liquid interface energy $2\pi h{\gamma }_{\text{sl}}{\ell }_{\text{c}}$ (the liquid–air interface energy, a constant, is not included) to obtain the total energy of the system $V=\left(\left(1/2\right)\hspace{0.17em}EA{\mathit{ϵ}}_{\text{e}}^2+2\pi h{\gamma }_{\text{sv}}\right){\ell }_{\text{e}}+\left(2\hspace{0.17em}EI/D^2+2\pi h{\gamma }_{\text{sl}}\right){\ell }_{\text{c}}$. We replace ${\ell }_{\text{c}}=\ell -{\ell }_{\text{e}}$ and, discarding constant terms, rewrite the total energy as $V=\left(\left(1/2\right)EA{\mathit{ϵ}}_{\text{e}}^2-2EI/D^2+2\pi h\gamma \cos \theta \right){\ell }_{\text{e}}$. Note that we have used the Young–Dupré wetting relation ${\gamma }_{\text{sv}}-{\gamma }_{\text{sl}}=\gamma \cos \theta$, where θ is the liquid contact angle on the filament and γ the liquid–air interface energy per area. We note that the latent energy cost per unit length ${\mathit{ϵ}}_0=2\pi h\gamma \cos \theta -\pi E{h}^4/2D^2$ involved in the transformation from the coiled to the extended phase is a typical signature of a first-order phase transition problem. From this expression we readily obtain a condition for spooling to be sustained. Indeed, for the coiled phase to be stable at small forces, ${\mathit{ϵ}}_0$ has to be positive. This condition can be recast into a condition for the radius, where we recover the fact that only thin filaments exhibit in-drop spooling:

$$h<{\left(4\gamma \cos \theta \right)}^{1/3}\hspace{0.17em}{E}^{-1/3}\hspace{0.17em}{D}^{2/3}.$$ [1]

Introducing the ratio $\rho ={\ell }_{\text{e}}/\ell$, we minimize V under the constraints of fixed extension $x=x_{\text{c}}+x_{\text{e}}$, and bounded ratio $0\le \rho \le 1$. In the limit where $D\ll \ell$ and ${\mathit{ϵ}}_0\ll EA$, we find that the system can be entirely in the coiled phase ($\rho =0$; filament fully packed in the drop) with tension $0<T<{\mathit{ϵ}}_0$, or entirely in the extended phase ($\rho =1$) with tension $T=EA\left(x/\ell -1\right)>{\mathit{ϵ}}_0$. A third interesting possibility consists of a mixture of phases $0<\rho <1$. In this latter case, part of the filament is packed in the drop whereas the outer part is taut, consistent with our observations. As ρ is changed, the tension remains constant to a plateau value $T=T_{\text{P}}={\mathit{ϵ}}_0$, with

$$T_{\text{P}}=2\pi h\gamma \cos \theta -\pi E\hspace{0.17em}{h}^4/2D^2.$$ [2]

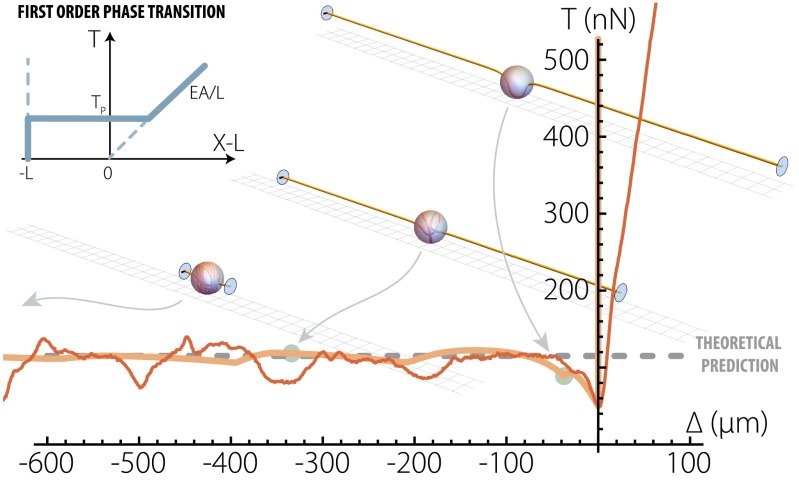
To further explore the mechanical response of the composite system, we also performed detailed numerical computations of equilibrium of an inextensible and flexible elastic filament (28, 29, 31). The filament, held at both extremities with imposed distance x, is subjected to attracting meniscus forces $F_{\gamma }$ at entrance and exit of a confining sphere. The loading $\left(x,T\right)$ diagram, shown in Fig. 4, reveals inhomogeneities in the Maxwell line (32). These inhomogeneities are due to fine details in the micromechanical response of the system. Setting $F_{\gamma }=2\pi h\gamma \cos \theta$, we plot in Fig. 4 the phase transition prediction given by Eq. 2, and we observe a nice agreement not only with the numerical computations, but also with nano-Newton–resolved mechanical testing of synthetic composites (here made of polyurethane filament and silicone oil droplet). We also note that both experiments and numerical simulations exhibit a kink between the two regimes that reveals a difference between the buckling threshold and the plateau tension, as already anticipated by our simple models and by the subcritical nature of the spooling (Fig. 3).

Fig. 4.

Structural phase transition and detailed mechanical response. Comparison between nano-Newton–resolved measurements on a composite polyurethane filament/silicone oil thread (red line), detailed simulations of an Elastica interacting with a droplet (orange line), and the first-order phase transition model (dashed gray line, full behavior also sketched in inset). Experiments were performed with a drop of wet length $D=62\pm 2\hspace{0.5em}\mathrm{\mu }\text{m}$ and a filament of radius $h=1\pm 0.2\hspace{0.5em}\mathrm{\mu }\text{m}$ and Young modulus $E=17\pm 3$ MPa. Numerical equilibria are here followed with a continuation procedure, with $F_{\gamma }=35EI/D^2$ and $L=20D$. The plateau tension $T_{\text{P}}$ given by the phase transition model 2 is here 115 nN. Beyond the nice overall agreement, the results reveal a difference between the buckling threshold and the plateau tension. This difference points to the subcritical nature of elastocapillary buckling, also evidenced by the sudden localization of the filament visible in the insets. The numerical simulations allow capture of the fine details in the micromechanical response observed in the experiments, resulting in inhomogeneities in the Maxwell plateau. Sensor drift forced us to adjust the reference level for the experimental measurements, but the level difference between buckling threshold and plateau tension is well recovered. See also Movies S4 and S5.

Unraveling the mechanics of spider capture silk allowed us to design a new type of fully self-assembling hybrid material with unprecedented mechanical function, switching from solid-like in extension to liquid-like in compression. This bioinspired hybrid can be manufactured with virtually any material, and provides novel functionalities such as fiber spooling or unspooling at the micronic level, or constant force application for a wide range of extension while preserving tautness and reversibility. Strikingly, rather than being a failure threshold, buckling in this case proves to be a necessary condition for material activation.

Materials and Methods

Capture Silk Samples.

Our Nephila edulis spider was kept in an $80\times 80\times 30$-cm vivarium, consisting of wood panels, PMMA windows, and artificial plants. The spider was kept at high humidity (above 70%) and comfortable temperature (above 22 °C) with a 12-h-day/12-h-night schedule. The spider was fed crickets and flies three times a week. Sections of web were carefully excised using a soldering iron for transfer within a rigid frame. To visualize the filament running through each droplet, the humidity was set to 100% relative humidity (rH) for 15 min before observation. The humidity was then stepped down to 50% (observation) rH.

Artificial Samples.

Polyurethane (TPU, Elastollan 1185A from BASF, Young’s modulus E = 17 MPa) granules were deposited on a hot plate at $230\hspace{0.5em}°$ C. After melting, we used a tweezers to pick up a small droplet which was then stretched quickly while at the same time being released into ambient room temperature. This resulted in the creation of micrometer-sized, meter-long, soft filaments. The filament was then deposited on the measuring setup as outlined below. A droplet of silicone oil (Rhodorsil 47V1000, surface tension $\gamma =21.1$ mN⋅m⁻¹) was then deposited by gently touching and brushing the filament with a drop hanging from a pipette. PLA (polylactic acid, Young’s modulus $E\sim$ 4 GPa in the glassy and $\sim$ 4 MPa in the rubbery state) filaments were processed the same way. Poly(vinylidene fluoride-co-hexafluoropropylene) (PVDF-HFP) samples were obtained by electrospinning. A droplet of PVDF-HFP (Young’s modulus $E\sim$ 10 MPa) in THF was electrospun at 12 kV using a charged syringe tip, at room temperature and rH. We thus obtain polymer cables made of many microfibers. The distribution of fibers radii and corresponding cable bending rigidity is inferred optically using a Leica macroscope. We measured contact angles by superimposing optical images of drops on fibers to corresponding calculated profiles, and found ${\theta }_Y=23°\pm 2°$ for TPU/silicone oil, ${\theta }_Y=19°\pm 2°$ for TPU/ethanol, ${\theta }_Y=31°\pm 2°$ for TPU/tetraethyl orthosilicate (TEOS), ${\theta }_Y=35°\pm 2°$ for PLA/silicone oil, and ${\theta }_Y=29°\pm 2°$ for PVDF-HFP/silicone oil. The surface tension of the liquid–air interface was measured to be $\gamma =22.1$ mN⋅m⁻¹ for ethanol, and $\gamma =23.5$ mN⋅m⁻¹ for TEOS.

Measurement Methods.

Filament samples were transferred to the measuring setup by coiling one end around the tip of a FemtoTools FT-FS1000 (FT-FS100) capacitive deflection force sensor with range 50 nN–1 mN (5 nN–100 μN) and gluing the other end to a glass slide as a base. The force sensor was mounted on a linear micropositioner SmarAct SLC-1730 (repeatability 0.5 μm) and measurements are performed through a work station by Universal Serial Bus (USB) connection. All of the tests were performed in stretching at a speed of $25\hspace{0.5em}\mathrm{\mu }\text{m/s}$, and considering the centimeter size in length of the sample, they can be considered to be quasi-static. The optical setup consisted of a Leica macroscope (VZ85RC) mounted on a microstep motor and a 3-megapixel Leica DFC-295 camera ($400\times$ zoom, 334-nm/pixel picture resolution) or a D800E Nikon camera with three 10-mm C-mount extension rings (937-nm/pixel video resolution and 374-nm/pixel photo resolution) alternatively. We used a Phlox 50- × 50-mm backlight, at 60,000 lx or alternatively an optical fiber with light-emitting diode lamp (Moritex MHF-M1002) with circular polarizer. Side views were acquired with a second D800E camera, with a 70-mm extension tube and a 100-mm macro Zeiss lens (7.27-μm/pixel video resolution). The force sensor was tared to zero with the fiber compressed slightly more than its slack length, so that it sags, but only minutely, be it for fibers with or without droplet. The measurement of the slack length was performed by pulling on the filament at one end by a few micrometers to straighten the fiber.

The TPU fiber diameter measurement was performed using Fiji software. A high-resolution picture of the fiber is analyzed using the following steps: The contrast is enhanced up to the point that 0.4% of the pixels are saturated, then the gray value of the pixels on a line perpendicular to the fiber axis is plotted. The typical curve obtained this way resembles a downward-pointing Gaussian; thus the diameter of the fiber is extracted as the full width at half minimum of the peak.

Numerical Computations.

The drop-on-fiber compound is modeled as an elastic filament, obeying Kirchhoff equilibrium equations, in interaction with a sphere. Except at the two “meniscus” points, the filament is prevented from touching or crossing the sphere through a soft-wall barrier potential. The equilibrium of the system is solved using two-points boundary-value problem techniques (shooting method in Mathematica, and collocation method using the Fortran - AUTO code).