Significance
The growing demand for customized electronic devices underpins the need for 3D fabrication methods that enable form factors well beyond those that are flat and rigid. A printing method is introduced for one-step fabrication of conductive and ductile metal features in planar and complex 3D shapes that combines direct ink writing with “on-the-fly” laser annealing.
Keywords: 3D printing, flexible electronics, conductive interconnects, silver ink, laser annealing
Abstract
The ability to pattern planar and freestanding 3D metallic architectures at the microscale would enable myriad applications, including flexible electronics, displays, sensors, and electrically small antennas. A 3D printing method is introduced that combines direct ink writing with a focused laser that locally anneals printed metallic features “on-the-fly.” To optimize the nozzle-to-laser separation distance, the heat transfer along the printed silver wire is modeled as a function of printing speed, laser intensity, and pulse duration. Laser-assisted direct ink writing is used to pattern highly conductive, ductile metallic interconnects, springs, and freestanding spiral architectures on flexible and rigid substrates.
The ability to create planar and freestanding 3D metal structures on demand at the microscale would enable myriad applications, including electronics (1–8), microelectromechanical systems (MEMS) (9, 10), metamaterials (11–13), and biomedical devices (14–16). For example, many electronic devices, such as inductors and antennas (4, 7), operate more efficiently in 3D form. However, that format is not well suited to standard photolithographic techniques. A one-step process for directly writing conductive, ductile metal wires and complex 3D architectures, such as freestanding spiral motifs, onto low-cost plastic and rigid substrates would enable high-performance, customizable electronic and other devices to be manufactured in a cost-effective and space-efficient manner. To date, several printing approaches have been developed to directly deposit conductive features, including roll-to-roll (17–19), inkjet printing (20, 21), meniscus printing (8), and direct ink writing (DIW) (1, 22). Although DIW has demonstrated spanning linear traces or short arcs printed out-of-plane, only meniscus-based electrodeposition printing has been used to generate freestanding 3D solid metal structures in arbitrary geometries. However, its ultralow print speed (<1 µm/s) coupled with the need for a conductive substrate have limited its widespread adoption (8).
Here, we introduce laser-assisted direct ink writing (laser-DIW), which combines printing of concentrated silver nanoparticle inks with focused infrared laser annealing to rapidly create high conductivity, ductile metallic wires and 3D architectures “on-the-fly” in a one-step, additive process. Laser-DIW offers three key advantages over other 3D printing techniques. First, by combining patterning and annealing in a single step, the printed metallic features exhibit the requisite mechanical properties needed to precisely fabricate arbitrary objects in midair, enabling complex curvilinear structures to be generated without the need for support material. Due to localized annealing, such features can be printed on low-cost plastic substrates, such as poly(ethylene terphthalate) (PET). Finally, the patterned features exhibit high electrical conductivity approaching that of bulk silver.
Results and Discussion
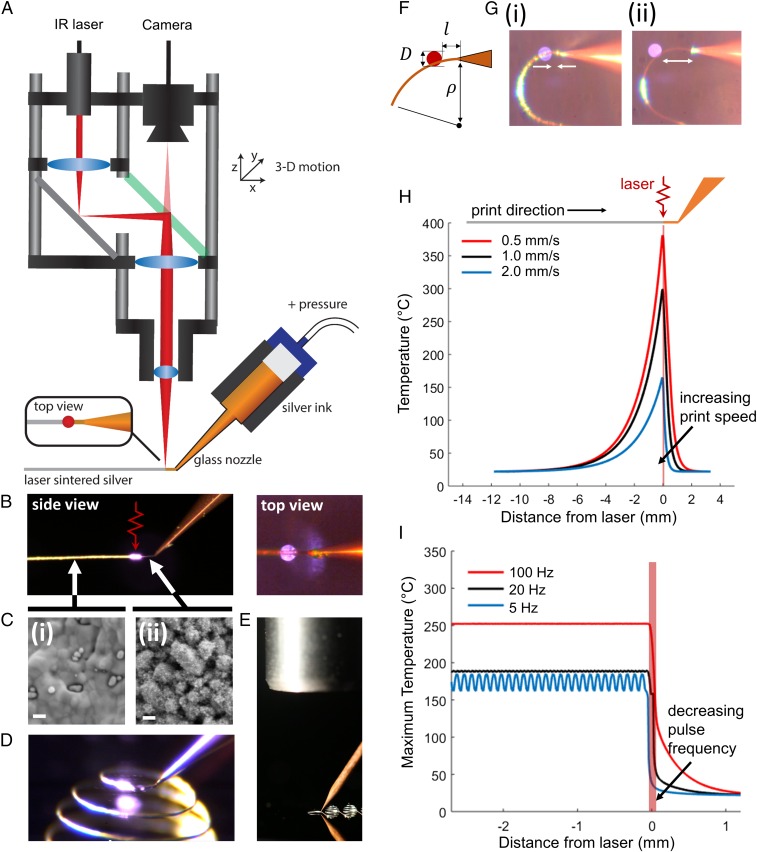
During laser-DIW, an 808-nm IR laser is focused to a 100-µm spot adjacent to the aperture of the glass nozzle through which a concentrated silver nanoparticle ink (85 wt % solids) is deposited (Fig. 1A and Fig. S1). Upon exiting the nozzle, the patterned features are rapidly heated by the focused laser to form a mechanically robust, electrically conductive wire. The printed silver wires vary in diameter from <1 µm to 20 µm depending on the nozzle diameter, extrusion pressure, and printing speeds used. The in-line laser annealing process induces a visible change of emissivity (dull to shiny) of the printed wires at the macroscale (Fig. 1B), as well as the densification of individual silver nanoparticles into larger grains at the microscale (Fig. 1C).
Fig. 1.
Laser-DIW. (A) Schematic of the laser-DIW printhead, which consists of the laser microscope, silver ink syringe, and nozzle. (B) Side and top views showing the IR laser (red arrow) focused immediately downstream of the nozzle. Note the change in emissivity of the silver ink upstream and downstream of the laser. (C) Nanostructure of (C, i) downstream laser-annealed silver and (C, ii) upstream as-printed silver features. (Scale bar, 100 nm.) (D) A side view showing freeform 3D printing of a metal hemispherical spiral. (E) A photograph showing the objective lens positioned directly above the nozzle with the 3D metallic structures printed below. (F) A schematic showing key parameters involved in printing curvilinear structures. (G) Examples of printing curvilinear shapes when the laser focus spot is placed (G, i) at an appropriate distance, or (G, ii) too far from the nozzle, wherein the silver ink does not impinge on the laser focus spot. Predicted silver ink temperature distribution at (H) various print speeds annealed via a 6-kW/cm2 CW illumination and using (I) various laser pulse repetition rates with a pulse duration of 1 ms and a peak laser intensity of 30 kW/cm2.
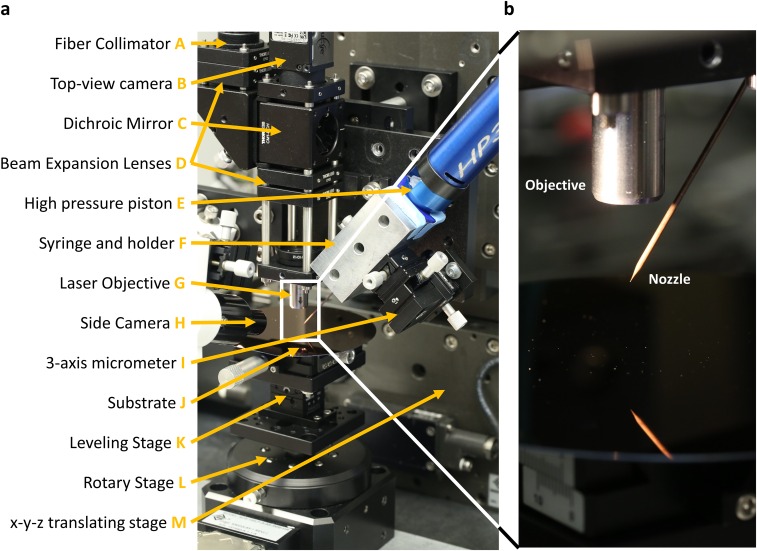
Fig. S1.
Laser-DIW apparatus. (A) A photograph showing the laser-DIW printhead that combines a laser microscope and silver ink extrusion system, both mounted on a three-axis printer, and the substrate on top of a rotating stage. (B) A photograph of the housing of the objective lens and nozzle above a silicon wafer substrate.
To print curvilinear features via laser-DIW, the sample must be rotated relative to the laser–nozzle axis using a rotary stage, such that the curvilinear wire is always patterned in a direction parallel to the laser–nozzle axis (Fig. 1 D and E, Fig. S2, and Supporting Information). As the rotary stage moves, there exists a minimum radius of curvature of the metal trace such that the wire passes through the laser spot, which depends upon the separation distance between the nozzle and the perimeter of the laser spot of diameter (Fig. 1F and Fig. S3):
| [1] |
To create sharp turns, the laser must be placed as close to the ink deposition nozzle as possible (Fig. 1G, Eq. 1). However, when the laser is positioned too close, heat is conducted upstream through the silver ink and into the nozzle, resulting in cessation of ink flow due to densification.
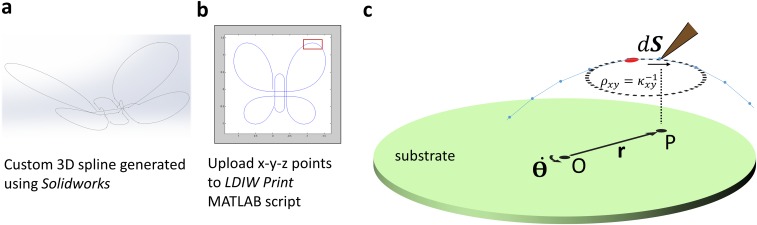
Fig. S2.
Printing curvilinear structures using a rotating stage. (A) A 3D spline created in SOLIDWORKS and (B) uploaded to a custom MATLAB script. (C) A diagram showing the rotating stage and a curvilinear wire being printed above.
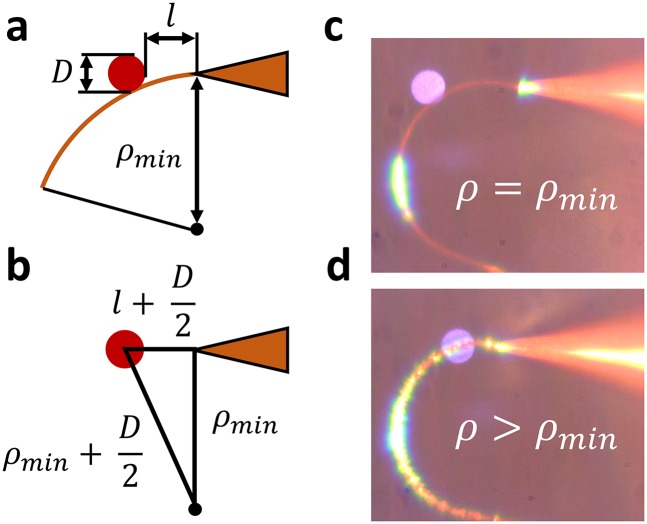
Fig. S3.
Deriving the minimum radius of curvature. (A and B) Schematic of a curved wire being printed, with radius of curvature, , such that the wire lies tangent to the laser spot. Examples of a laser spot set (C) too far, and (D) at an appropriate distance from the nozzle outlet.
To optimize the nozzle-to-laser separation distance, we use a simplified one-dimensional heat transfer model to study the temperature distribution along the silver wire during printing at a speed , which accounts for the input laser energy as well as convective and radiative heat loss. The temperature distribution is modeled by the following convection–diffusion equation:
| [2] |
where the density , the specific heat capacity , and the thermal conductivity of printed wire are a function of its thermal history. We numerically solve this partial differential equation using a finite-difference method (Supporting Information). The upstream heat transfer is reduced by three key mechanisms. First, using laser flash thermal analysis, we find that the heat-annealed silver features have a 50-fold higher thermal diffusivity compared with the as-printed silver ink (20 mm2 s−1 and 0.4 mm2 s−1, respectively). Hence, the laser-annealed regions of the printed silver wires serve as a downstream heat sink, limiting upstream heat transfer to the ink reservoir within the nozzle. Second, the printing speed limits upstream heat flow due to downstream heat advection, as shown by steady-state temperature curves generated by the simulation during printing at various speeds under continuous-wave (CW) laser illumination (Fig. 1H). As an approximation, a characteristic upstream heating distance, , is the length at which upstream conductive heat flux is balanced by downstream heat advection resulting from the printing velocity, i.e., the length for which the Péclet number is equal to unity:
| [3] |
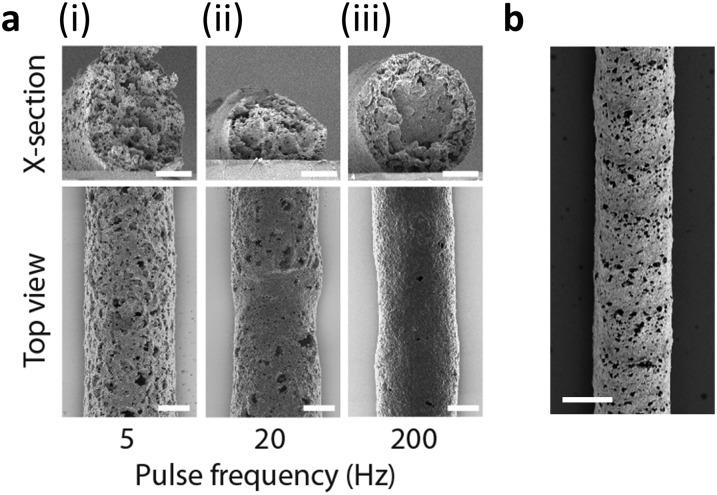
For example, using the thermal diffusivity for unannealed silver ink (as-printed), the characteristic upstream heating distance at a print speed of 1 mm s−1 is 400 µm. Notably, this printing speed is more than 1,000× higher than meniscus printing. Finally, operating the laser in a pulsed mode instead of CW allows one to achieve high maximum annealing temperatures while limiting the total heat transfer to the wire, with low pulse repetition rates (PRR) resulting in very limited upstream heat conduction (Fig. 1I). To achieve a uniform densification through the thickness of the printed wires, the laser pulse duration should be sufficiently long such that the characteristic thermal diffusion distance is large compared with the wire diameter:
| [4] |
For a pulse duration of 1 ms, this characteristic length is 40 µm, which is significantly larger than the thickest (∼20 µm) wires being printed. The simulation further predicts that for low PRR, the maximum temperature reached along the wire becomes nonuniform, even when all segments of the wire receive an equal laser exposure. This manifests in low PRR producing macroscopically heterogeneous wires with a nonuniform nanostructure (Fig. S4). Conversely, heating the wire at a 1-ms pulse duration at 100 Hz generates a silver wire with a uniform nano- and microstructure, as predicted by the more uniform thermal history (Fig. 1I). Importantly, the convection–diffusion equation (Eq. 2) used to generate the curves in Fig. 1 H and I assumes that the wire is being printed in midair, and therefore does not incorporate a substrate conduction-loss term. This assumption represents a worst-case scenario for thermal management, as a substrate would serve as a heat sink that limits upstream heat transfer. Printing directly onto a substrate would also significantly reduce the maximum annealing temperature, particularly when the wire is annealed by CW laser exposure, as a more uniform through-thickness heating would result in more heat loss to the substrate.
Fig. S4.
Effect of PRR on annealed silver microstructure. (A) Wire porosity decreases with increasing PRR. (B) Wires annealed at low PRR exhibit periodic heterogeneity. (Scale bar, 10 µm.)
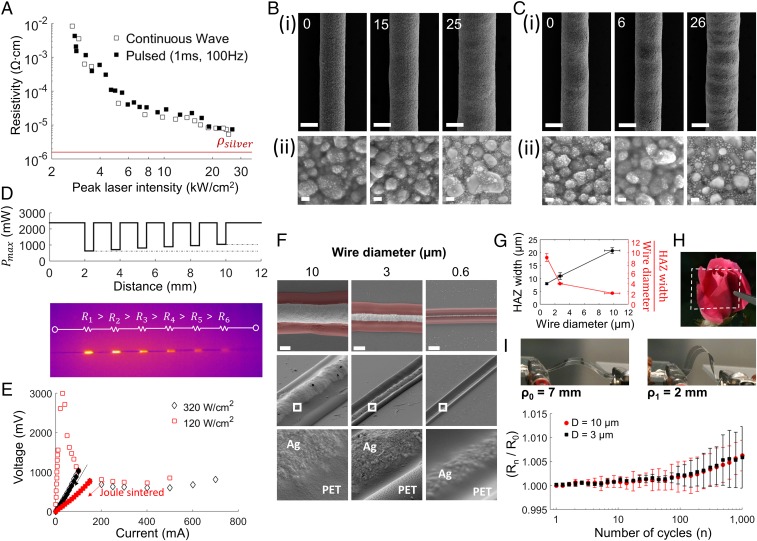
Next, we studied the effect of laser intensity, both CW and high-frequency pulses (100-Hz, 1-ms pulse duration), on the electrical conductivity of laser-DIW silver wires printed on a glass substrate (Fig. 2A). By modulating the incident laser intensity over an order of magnitude, the silver resistivity can be varied by more than 3 orders of magnitude. Annealing via a CW laser achieved slightly lower electrical resistivity than that of a pulsed laser of the same peak intensity, reaching a minimum resistivity of 5.4 × 10−6 Ω⋅cm, compared with that of bulk silver at 1.6 × 10−6 Ω⋅cm. The microstructure of printed wires produced by CW and pulsed laser operation show a similar progression with increasing laser intensity, i.e., they undergo both densification and grain growth as expected during thermal annealing (Fig. 2 B and C).
Fig. 2.
Electrical conductivity and nanostructure of laser-annealed silver wires. (A) Silver resistivity decreases with increasing laser intensity. The red line represents the resistivity of bulk silver metal. Microstructure of silver wires annealed by (B) CW and (C) pulsed (1-ms, 100-Hz) laser illumination. Numbers indicate peak illumination intensity in kW/cm2. [Scale bars, 10 µm (C, i), 100 nm (C, ii).] (D) A varying laser intensity profile (Top) results in corresponding IR emissions from resistive elements as current is passed through the wire. Each resistor is ∼500 µm in length. (E) I-V characteristics of two resistors formed at different laser intensities. Current is stepped up (unfilled) to a certain level, and then stepped down (filled). (F) SEM images of various diameter wires laser annealed onto PET films. (Top Row) Top view, false colored to reveal the HAZ extending from the printed silver wires. (Scale bar, 5 µm.) (Middle Row) Oblique views of printed silver wires. (Bottom Row) Magnified images of the interface between the printed silver (Ag) wire and PET substrate. (G) The width of the HAZ (black line) and the ratio of the HAZ width and the silver wire width (red line) vary with the diameter of the printed and annealed wires. Five wires are tested for each diameter. (H) An array of silver wires, with submicrometer widths, is printed onto a transparent PET film across a 1-cm2 area, using a wire spacing distance of 500 µm. The resulting film, indicated by the white dashed line, remains transparent. (I) Cyclic testing of the electrical resistance of 3- and 10-µm silver wires printed onto a 20-µm-thick PET film. The radius of curvature alternates between 2 and 7 mm. The graph shows the variation of resistance after n cycles (Rn) normalized to the initial resistance before cyclic testing (R0). Three wires are tested for each condition.
Unlike bulk thermal annealing methods, laser-DIW enables one to create patterned regions of low-to-high resistance simply by modulating the local laser intensity during silver ink printing. For example, when the laser power is modulated to varying degrees during printing, a series of 500-µm silver segments with graded resistivity is created in-line within the same conductive silver wire, as visualized by gradations in the infrared signatures upon passing a constant current along the printed wire (Fig. 2D). The I-V characteristics of resistors created in this manner are initially linear until a critical current is reached, beyond which Joule heating from resistive losses results in autoannealing of the resistors causing a large deviation from ohmic behavior (Fig. 2E). If, after the onset of autoannealing, the current is stepped back down, a new linear characteristic is observed with a lower value of resistance, representing the increased conductivity from autoannealing. This behavior is characteristic of a write-once read-many memory element (23, 24), or “antifuse” (25). We note that the critical current or potential difference at which the antifuse anneals can be programmed via careful choice of laser power.
Importantly, laser-DIW enables conductive silver wires to be patterned on flexible, low-cost plastic substrates, such as PET (Fig. 2F). PET is of particular interest for flexible electronic and photovoltaic applications owing to its high transparency and chemical stability (26). PET exhibits low absorptivity at the laser wavelength of 808 nm, and is therefore only heated indirectly by laser-annealed silver ink, which generates a localized heat-affected zone (HAZ) in the underlying plastic substrate. This HAZ effectively welds the silver to the PET (Fig. 2F, Bottom Row), yielding mechanical robust electrodes that can withstand a tape peel test. For printing on different polymeric substrates, the laser wavelength could be selected to ensure maximal optical transparency. As the laser energy is predominantly absorbed by the silver wire, and not by PET itself, the HAZ width increases with the diameter of the wire (Fig. 2G). Conversely, the ratio of the HAZ width to the wire diameter decreases with increasing wire diameter. Despite the formation of an HAZ, PET films with printed submicrometer silver wires with a center-to-center separation distance of 500 µm exhibit exceptional optical transparency (Fig. 2H). Next, cyclic tests were performed on wires printed onto a 20-µm PET film by varying the radius of curvature between 7 and 2 mm while monitoring changes in resistance. The resulting change in resistance (Fig. 2I) and per-cycle variation in resistance (Fig. S5) was minimal (<1%) throughout the 1,000-cycle test. However, our thick wires, due to the presence of microscopic defects and porosity, are not able to withstand the same degree of extension compared with defect-free thin-film approaches, which can reach a 50% strain (27).
Fig. S5.
Cyclic testing of the electrical resistance of 3- and 10-um wires printed onto a 20-um-thick PET film. (A) Photographs showing the film at the two extreme positions of the bend test and their radii of curvatures. (B) Per-cycle resistance variation of wires at around 10 and 1,000 cycles.
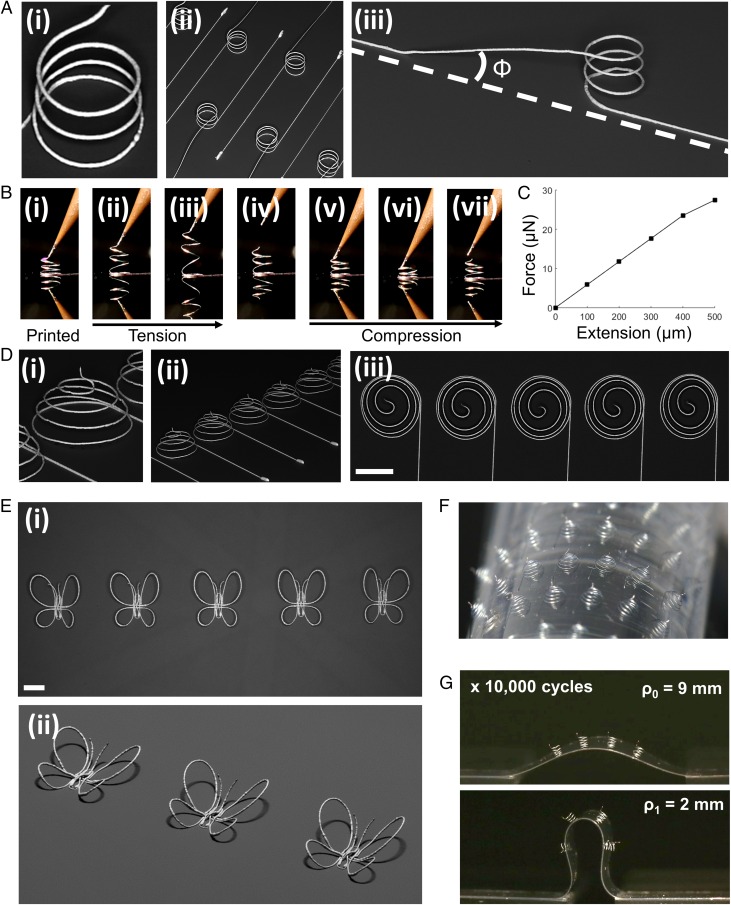
As a final demonstration of laser-DIW, we highlight the ability to print complex 3D metal architectures in midair without support materials. Specifically, we first created arrays of conductive coils, resembling electrical inductors, on a silicon substrate (Fig. 3A and Movie S1). In each coil, the helix is oriented vertically, and the wire begins and ends on the substrate to facilitate component connectivity. When mechanically tested, the printed helical springs exhibit elastic and plastic behavior in both tension and compression (Fig. 3B). The force–displacement curve for an 800-µm-tall helix, with a wire diameter of 20 µm, exhibits a linear response up to a 50% macroscopic strain (Fig. 3C). Such helical coils could not be printed solely by DIW, i.e., in the absence of laser annealing, because the as-printed ink is unable to retain the geometrical shape in midair. Next, we created 3D spiral arrays inspired by electrically small hemispherical spiral antenna designs (7). Using laser-DIW, we printed high-fidelity spiral features in midair, in the absence of an underlying hemispherical substrate (Fig. 3D and Movie S1). The construction of these shapes is highly repeatable leading to uniform spiral arrays (Fig. 3 D, ii and iii). As a final example, we show the construction of arbitrary 3D shapes, such as a butterfly, formed by printing multiple woven curvilinear wires that depart from the underlying substrate (Fig. 3E and Movie S1). Interestingly, these curvilinear structures can be printed on flexible PET substrates, and by virtue of the strong adhesion at the silver wire–substrate interface resulting from HAZ formation, these structures can readily withstand cyclic bending of the substrate (Fig. 3 F and G).
Fig. 3.
Freeform 3D metallic architectures. (A) Printed freestanding helical silver coils. Coil diameter = 500 µm. Dashed line indicates the plane of the substrate. (B) Mechanical testing of a printed helix. (B, i–iii) The helix reaches a strain of 150% in tension, (B, iv) then breaks at the point of contact and returns to a strain of 50%. (B, v and vi) The helix is then compressed to a strain of −50% with respect to the new equilibrium length at (B, iv), and upon release (B, vii) rebounds to a final strain of −20%. (C) A force–extension curve for an 800-µm-tall helix exhibits a linear-elastic behavior up to 50% strain. (D) Printed hemispherical spiral array. (E) Printed butterflies. (Scale bar, 1 mm.) (F) Hemispherical spiral array printed on a PET film, bent around a cylinder. (G) Printed helical coils on a PET substrate undergo 10,000 cycles between a radius of curvature between 2 and 9 mm.
In summary, we have demonstrated a method of printing planar and 3D metal architectures that combines laser-assisted annealing with direct writing of concentrated viscoelastic inks. Our approach is uniquely capable of printing elastic, complex curvilinear metal wires in free space on low-cost plastic substrates. Furthermore, we have patterned silver wires with tunable electrical resistivity, enabling the programmable patterning of conductive, resistive, and hybrid elements. The ability to print high-resolution, functional metal electrodes and complex structures on demand may open up new avenues for creating customized electronics, MEMs, and biomedical devices.
Methods
Silver Ink Synthesis.
The silver nanoparticle ink is synthesized using a protocol similar to that previously described (1). Briefly, 0.9 g of a 25% (wt/v) solution of 50 kDa poly(acrylic acid) (Polysciences Inc.) in water and 1.8 g of a 50% (wt/v) solution of 5 kDa poly(acrylic acid) (Polysciences Inc.) are dissolved into 50 g of distilled water in a clean 500-mL Erlenmeyer flask. Forty grams of diethanolamine (Sigma-Aldrich) is then added, and the solution is allowed to return to room temperature while stirring at 300 rpm using a 1-inch stir bar. In a second clean flask, 20 g of silver nitrate (Sigma-Aldrich) is dissolved in 20 g of distilled water and the solution is allowed to return to room temperature, before adding the solution to the contents of the first flask while stirring. The solution is covered and stirred for 24 h. During this time, the solution turns from colorless to a clear, pale brown color as silver nanoparticles precipitate out under the reducing conditions. After 24 h, the nanoparticles are ripened by increasing the temperature to 75 °C for 2 h. The solution is then cooled to room temperature. Next, we rapidly add 300 mL of ethanol to the solution, while stirring, to precipitate the nanoparticles. After 5 min of additional stirring, the nanoparticles are allowed to settle under quiescent conditions. The supernatant is decanted away, and the silver nanoparticle sediment is transferred quickly via a spatula into a separate 50-mL conical tube, ensuring that the suspension does not dry. The nanoparticles are then centrifuged at ∼13,000 g for 20 min into a dense pellet, and the supernatant is discarded. The nanoparticles are then suspended again by adding 15 mL of water followed by vigorous vortexing. The suspension is filtered through a 5-μm syringe filter, then split into two 50-mL conical tubes before adding 35 mL of ethanol into each tube. The nanoparticles are allowed to settle for 20 min before decanting the supernatant. The nanoparticle suspension in one conical tube is transferred to the other by use of a spatula before compacting the silver nanoparticles by centrifugation at 13,000 g for 20 min. The nanoparticle pellet is then transferred out of the conical tube using a spatula, and placed in a jar to be mixed in a planetary mixer (Thinky Corp.). The ink is then transferred via spatula into a 3-mL syringe (Nordson EFD) and centrifuged for 10 min at 4,000 g to remove trapped air. The syringe is then placed into an HP3 high-pressure dispensing adaptor (Nordson EFD), connected to a variable pressure supply (Nordson EFD), and a 2-inch-long glass nozzle with either a 10- or 1-µm inner diameter is added to the syringe (World Precision Instruments). The syringe and high-pressure adaptor are mounted onto the laser microscope and aligned with the focused laser spot.
Focused Laser and Ink Printhead Design.
A 5-W, 808-nm CW diode laser (Shanghai Laser & Optics Century Co. Ltd.) is connected to the laser microscope by means of a 200-µm multimode optical fiber (Thorlabs Inc.), and collimated via a 0.26-N.A., 11.07-mm collimating lens. The collimated beam is magnified 2× by a telescope consisting of a pair of IR antireflective achromatic doublet lenses (Thorlabs Inc.), and focused to a 100-µm spot using a 0.16-N.A., 12.43-mm working distance aspheric objective lens. The laser focus spot possesses a uniform, top-hat intensity distribution. The laser path includes a short-pass 750-nm dichroic mirror (Edmund Optics) that reflects the IR laser light, and transmits visible light collected by the objective to a camera (Imaging Development Systems, IDS) that serves as an alignment microscope. Importantly, to facilitate laser–nozzle alignment, the dichroic mirror is selected to enable a small amount of IR light to be transmitted (<1%) to enable visualization of the substrate-reflected laser light with the top alignment camera. The entire optical setup is mounted on an optical breadboard, which itself is mounted onto an x–y–z translating 3D printing gantry (Aerotech Inc.). The laser diode driver is modulated by a square-wave signal derived from either a waveform generator (Keysight) or a National Instruments NI-6211, to enable the precise variation of the laser pulse power, frequency, and duration.
To align the laser and ink deposition nozzle for printing, the laser is first focused onto the substrate by observing the laser spot on the alignment camera. Next, x, y, and z micrometers are used to move the silver ink syringe and nozzle relative to the focused laser spot. A separate side camera (IDS) is used to aid this process. For omnidirectional printing, the nozzle is typically placed ∼100 µm away from the laser spot. To begin printing, the silver ink is extruded through the nozzle by applying pressure (typically 150–200 psi), and the printer is translated in x, y, and z.
Rotary Stage Alignment.
For freeform 3D printing, a rotary stage is used for mounting the sample to enable the construction of curved lines. The rotary stage is positioned directly underneath the laser microscope. To identify the center of rotation, the laser is focused on the top surface of a glass slide colored with a permanent marker. As the stage is rotated through 360°, the laser spot ablates the permanent marker, tracing a circle whose center lies at the center of rotation. The center of rotation is then supplied to a custom MATLAB script that converts a series of x–y–z Gcode commands into a new set of commands in x–y–z, and θ.
Conductivity Measurements.
Four 75-mm electrodes, consisting of gold stripes, are patterned onto a 75-mm × 25-mm glass slide by sputter coating. Next, linear wires are printed perpendicular to the stripes and a four-point probe is used to measure resistance between the center two stripes, separated by 6.35 mm. To calculate electrical resistivity, their cross-sectional areas are measured by image analysis of scanning electron micrographs of cut wires.
Cyclic Mechanical Testing.
Three-centimeter-long silver wires were printed using laser-DIW onto a 20-µm-thick PET substrate. After printing, one end of the film is affixed to a stationary point and the other end is affixed to a point on an x–y–z translating gantry. Alligator clips and a resistance meter are used to monitor changes in resistance. Before cyclic testing, the gantry is moved toward the stationary point, imparting a small initial curvature on the wire, and the initial resistance R0 is recorded. Next, the gantry is translated toward and away from the stationary point to flex the film to a radius of curvature of 2 mm, while continuously monitoring the resistance.
Laser-DIW Apparatus
The apparatus is shown in Fig. S1. An 808-nm diode laser (Shanghai-Laser & Optics Century Co. Ltd.) is coupled via a Sub Miniature A connector to a 200-µm multimode optical fiber. The laser is collimated at the outlet of the multimode fiber by a collimating lens (A), and reflected by a 750-nm short-pass dichroic mirror (Edmund Optics Inc.) (C). The dichroic mirror was selected to transmit a small amount (<1%) of the laser light to enable visualization of the reflected laser spot by the microscope camera (Imaging Developing Systems, GmbH) for alignment purposes (B). The laser power, pulse duration, and pulse frequency are modulated by a square wave from a waveform generator (Keysight). The laser beam is expanded 2× via a pair of achromatic doublet lenses (D) before being focused by a 0.16-N.A., 15.29-mm focal distance aspheric objective lens (Thorlabs Inc.) (G). The silver ink is loaded into a syringe (F), which is extruded via a high-pressure piston (Nordson EFD) (E), pressurized via a pressure controller (Nordson EFD). For the purpose of alignment, the nozzle may be moved relative to the laser focus by means of a three-axis micrometer (I). The alignment and printing is aided by a side-view camera and lens system (Imaging Developing Systems, GmbH) (H). All of the systems described above are mounted onto a three-axis printing stage (Aerotech Inc.). The substrate (J) is mounted on a rotary stage (Aerotech Inc.) (L). An x–y leveling stage (K) lies in between the rotary stage and the substrate to ensure that the substrate x–y plane is aligned parallel to the x–y plane of the three-axis printer.
Equations of Motion for the 3D Printer and Rotary Stage
To generate a wire of arbitrary geometry in 3D space, a path is first drawn up using Bézier curves (Fig. S2A) and split up into piecewise linear segments (Fig. S2B). Studying an arbitrary curve to be printed (Fig. S2C), let represent a short segment that lies instantaneously tangent to the wire being printed at a velocity relative to the motion of a point on the substrate that lies immediately below the segment. In this case, as the wire is being printed, is related to by the equation
| [S1] |
The instantaneous x–y curvature of the wire being printed, , is defined by
| [S2] |
where represents the instantaneous x–y bearing of the wire segment, or equivalently, the current angle of the rotary stage. Thus, to print a wire with local curvature at a constant speed of , the rotary stage must be rotated at a rate equal to
| [S3] |
In addition to rotating the stage, the printer must be translated in x, y, and z to map both the translation of the point on the substrate as the stage rotates, and generate the net print velocity relative to the motion of . If represents the vector connecting the center of rotation of the rotary stage, , with point , then the printer must be translated with velocity governed by the following equation of motion:
| [S4] |
where denotes the unit vector along the rotation axis of the rotary stage. Using Eqs. S3 and S4, any arbitrarily shaped piecewise linear wire with G-code commands [xn, yn, zn] can be converted into new four-dimensional commands [xn, yn, zn, θn]. A custom script that implements the mathematical conversion necessary for laser-DIW has been made available at MATLAB Central (28).
Deriving the Minimum Radius of Curvature
When curvilinear features are written, the ink curves away from the laser–nozzle axis (Fig. S3A). The critical minimum radius of curvature, , is reached when the curved metal wire lies tangent to the laser spot (Fig. S3 A and B). In this scenario, a right-angled triangle defines the minimum radius of curvature:
| [S5] |
Heat-Flow Simulation
Eq. 2 in the main text was numerically solved using a finite-difference method. In solving this equation, the electrical and thermal conductivity, as well as the density and emissivity of the wire, is dependent on the time and temperature history of the silver during annealing. In contrast to long-duration thermal annealing in a furnace, the time and temperature history of laser annealed silver is highly dynamic. Thus, an approximation is made whereby the annealed state of a silver segment is dependent on its temperature history, and if the temperature of the segment has previously risen above a certain cutoff temperature, it is considered to be “annealed;” otherwise, it is “unannealed.” For these simulations, a cutoff temperature of 150 °C was selected as this is the temperature at which the silver wires become rapidly electrically conductive. Varying the cutoff temperature changes the simulated peak temperature reached by the silver, but does not otherwise significantly alter the thermal trends and patterns shown in Fig. 1.
In the model, the temperature is simulated across a stationary 15-mm window, through which a silver filament, simulated as a train of 10-µm discrete segments, flows in and out. The heat advection term is incorporated by introducing room-temperature segments from the right, and discarding annealed segments from the left at a rate that simulates the print speed. The simulation window length was chosen to be long relative to the heat diffusion distance to minimize edge effects associated with finite-difference methods. Each segment can exist in one of two states, annealed or unannealed, depending on whether the temperature history has exceeded the temperature cutoff for annealing, with simulation parameters used matching that for the ink and silver, respectively.
For computing the convective heat loss term
| [S6] |
we use a model of a horizontally oriented heated cylinder in air (29):
| [S7] |
where the Nusselt number, , is defined as
| [S8] |
and the Rayleigh number, , is given by
| [S9] |
where and are the Grashof and Prandtl numbers, respectively.
The radiative heat loss is calculated using the Stefan–Boltzmann equation:
| [S10] |
In its unsintered state, an emissivity value of unity is used, whereas in its annealed state, a value of 0.03 was used, matching that of bulk silver. The simplified thermal model does not incorporate enthalpy of vaporization, as differential scanning calorimetry analysis of the ink only exhibited a small endotherm compared with the specific heat capacity of the ink. Furthermore, the model does not account for enthalpic effects of polymer decomposition, as the very short heating time from the focused laser results in an incomplete burnout.
Varying Laser Pulse Frequency
The laser PRR affects the microstructure of the printed filaments (Fig. S4). At low PRR, the microstructure is highly porous throughout the thickness of the filament, whereas operating at a high PRR produces filaments that are uniform (Fig. S4A). Filaments that are annealed using low PRR exhibit a periodic, heterogeneous microstructure at a spatial frequency that is related to the print velocity and the PRR (Fig. S4B).
Cyclic Testing of Silver Wires Printed onto PET Substrates
The variation of the resistance of 10- and 3-µm-diameter wires printed onto a 20-µm-thick PET was measured during cyclic bending of the substrate between a radius of curvature of 7 mm and a radius of curvature of 2 mm. The cyclical variation in resistance Rn was normalized to the pretest resistance R0 measured at a radius of curvature of 7 mm. Representative cyclical resistance changes for 10-µm-diameter and 3-µm-diameter wires are shown in Fig. S5.
Supplementary Material
Acknowledgments
The authors thank James Weaver and Lori Sanders for their assistance with imaging and photography, and Dr. Bok Y. Ahn and Kundan Chaudhary for helpful discussions. This work is part of the “Light-Material Interactions in Energy Conversion” Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under Award DE-SC0001293.
Footnotes
Conflict of interest statement: J.A.L. has cofounded a startup company, Voxel8 Inc, that may seek to license the intellectual property related to laser direct ink writing.
This article is a PNAS Direct Submission. Y.-L.L. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1525131113/-/DCSupplemental.
References
- 1.Ahn BY, et al. Omnidirectional printing of flexible, stretchable, and spanning silver microelectrodes. Science. 2009;323(5921):1590–1593. doi: 10.1126/science.1168375. [DOI] [PubMed] [Google Scholar]
- 2.Xu S, et al. Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science. 2015;347(6218):154–159. doi: 10.1126/science.1260960. [DOI] [PubMed] [Google Scholar]
- 3.Kim D-H, et al. Materials and noncoplanar mesh designs for integrated circuits with linear elastic responses to extreme mechanical deformations. Proc Natl Acad Sci USA. 2008;105(48):18675–18680. doi: 10.1073/pnas.0807476105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pfeiffer C, Xu X, Forrest SR, Grbic A. Direct transfer patterning of electrically small antennas onto three-dimensionally contoured substrates. Adv Mater. 2012;24(9):1166–1170. doi: 10.1002/adma.201104290. [DOI] [PubMed] [Google Scholar]
- 5.Chang S, Sivoththaman S. A tunable rf MEMS inductor on silicon incorporating an amorphous silicon bimorph in a low-temperature process. IEEE Electron Device Lett. 2006;27(11):905–907. [Google Scholar]
- 6.Huang W, et al. On-chip inductors with self-rolled-up SiNx nanomembrane tubes: A novel design platform for extreme miniaturization. Nano Lett. 2012;12(12):6283–6288. doi: 10.1021/nl303395d. [DOI] [PubMed] [Google Scholar]
- 7.Adams JJ, Slimmer SC, Lewis JA, Bernhard JT. 3D-printed spherical dipole antenna integrated on small RF node. Electron Lett. 2015;51(9):661–662. [Google Scholar]
- 8.Hu J, Yu M-F. Meniscus-confined three-dimensional electrodeposition for direct writing of wire bonds. Science. 2010;329(5989):313–316. doi: 10.1126/science.1190496. [DOI] [PubMed] [Google Scholar]
- 9.Ching NNH, Wong HY, Li WJ, Leong PHW, Wen Z. A laser-micromachined multi-modal resonating power transducer for wireless sensing systems. Sens Actuators A Phys. 2002;97-98:685–690. [Google Scholar]
- 10.Felton S, Tolley M, Demaine E, Rus D, Wood R. A method for building self-folding machines. Science. 2014;345(6197):644–646. doi: 10.1126/science.1252610. [DOI] [PubMed] [Google Scholar]
- 11.Gansel JK, et al. Gold helix photonic metamaterial as broadband circular polarizer. Science. 2009;325(5947):1513–1515. doi: 10.1126/science.1177031. [DOI] [PubMed] [Google Scholar]
- 12.Soukoulis CM, Wegener M. Optical metamaterials--more bulky and less lossy. Science. 2010;330(6011):1633–1634. doi: 10.1126/science.1198858. [DOI] [PubMed] [Google Scholar]
- 13.Soukoulis CM, Wegener M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat Photonics. 2011;5(9):523–530. [Google Scholar]
- 14.Xu L, et al. 3D multifunctional integumentary membranes for spatiotemporal cardiac measurements and stimulation across the entire epicardium. Nat Commun. 2014;5:3329. doi: 10.1038/ncomms4329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ko HC, et al. A hemispherical electronic eye camera based on compressible silicon optoelectronics. Nature. 2008;454(7205):748–753. doi: 10.1038/nature07113. [DOI] [PubMed] [Google Scholar]
- 16.Çetin B, Kang Y, Wu Z, Li D. Continuous particle separation by size via AC-dielectrophoresis using a lab-on-a-chip device with 3-D electrodes. Electrophoresis. 2009;30(5):766–772. doi: 10.1002/elps.200800464. [DOI] [PubMed] [Google Scholar]
- 17.Bae S, et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nat Nanotechnol. 2010;5(8):574–578. doi: 10.1038/nnano.2010.132. [DOI] [PubMed] [Google Scholar]
- 18.Park S-C, et al. Millimeter thin and rubber-like solid-state lighting modules fabricated using roll-to-roll fluidic self-assembly and lamination. Adv Mater. 2015;27(24):3661–3668. doi: 10.1002/adma.201500839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Deng B, et al. Roll-to-roll encapsulation of metal nanowires between graphene and plastic substrate for high-performance flexible transparent electrodes. Nano Lett. 2015;15(6):4206–4213. doi: 10.1021/acs.nanolett.5b01531. [DOI] [PubMed] [Google Scholar]
- 20.Perelaer J, Hendriks CE, de Laat AWM, Schubert US. One-step inkjet printing of conductive silver tracks on polymer substrates. Nanotechnology. 2009;20(16):165303. doi: 10.1088/0957-4484/20/16/165303. [DOI] [PubMed] [Google Scholar]
- 21.Lessing J, et al. Inkjet printing of conductive inks with high lateral resolution on omniphobic “R(F) paper” for paper-based electronics and MEMS. Adv Mater. 2014;26(27):4677–4682. doi: 10.1002/adma.201401053. [DOI] [PubMed] [Google Scholar]
- 22.Ladd C, So J-H, Muth J, Dickey MD. 3D printing of free standing liquid metal microstructures. Adv Mater. 2013;25(36):5081–5085. doi: 10.1002/adma.201301400. [DOI] [PubMed] [Google Scholar]
- 23.Möller S, Perlov C, Jackson W, Taussig C, Forrest SR. A polymer/semiconductor write-once read-many-times memory. Nature. 2003;426(6963):166–169. doi: 10.1038/nature02070. [DOI] [PubMed] [Google Scholar]
- 24.Nilsson H-E, et al. Printed write once and read many sensor memories in smart packaging applications. IEEE Sens J. 2011;11(9):1759–1767. [Google Scholar]
- 25.Allen ML, et al. Electrical sintering of nanoparticle structures. Nanotechnology. 2008;19(17):175201. doi: 10.1088/0957-4484/19/17/175201. [DOI] [PubMed] [Google Scholar]
- 26.Kaltenbrunner M, et al. Ultrathin and lightweight organic solar cells with high flexibility. Nat Commun. 2012;3:770. doi: 10.1038/ncomms1772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lu N, Wang X, Suo Z, Vlassak J. Metal films on polymer substrates stretched beyond 50% Appl Phys Lett. 2007;91(22):221909. [Google Scholar]
- 28.Skylar-Scott MA, Gunasekaran S. 2015 Laser-DIW GCode Conversion. Available at www.mathworks.com/matlabcentral/fileexchange/54425-laser-diw-gcode-conversion, MATLAB Central File Exchange. Accessed December 10, 2015.
- 29.Churchill SW, Chu HHS. Correlating equations for laminar and turbulent free convection from a horizontal cylinder. Int J Heat Mass Transfer. 1975;18(9):1049–1053. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.