A novel method for integrating MEG and BOLD fMRI signals with the linear convolution model in human primary somatosensory cortex

INTRODUCTION

Developing in parallel with the wide variety of fMRI applications in neuroscience research are the more fundamental investigations into the complex neural, metabolic, and hemodynamic origins of the BOLD fMRI signal. Ideally, the definitive study would require comprehensive investigation of a large number of physiological variables associated with the signaling process by which neural activity leads to hyperemic hemodynamic responses. However, this is impractical and efforts have recently focused on developing techniques for integrating data from a limited number of modalities (e.g., fMRI and microelectrode recordings, fMRI and PET, etc).

For human studies, the range of available imaging techniques is further restricted by the requirement of noninvasiveness. Electrophysiology (EEG) and magnetoencephalography (MEG), which measure electrophysiological aspects of neural activity, are noninvasive options to study the effects of neurovascular coupling in humans and are complementary to BOLD fMRI measurements.

One way to examine the link between EEG/MEG and BOLD fMRI signals is in terms of the energy associated with metabolic demand required for the neural and hemodynamic response. For example, Babajani et al. [ 2005] developed a set of equations to relate MEG signals to BOLD fMRI signal changes using the energy consumed by the postsynaptic potential (PSP). The energy requirement for PSP production directly or indirectly results in a vascular response [c.f. Rossi, 2006] which, through the mechanisms of increased cerebral blood flow (CBF), volume (CBV), and cerebral metabolic rate of oxygen consumption (CMRO₂), give rise to measurable BOLD signal changes [Ogawa et al., 1990]. The equations of Babajani et al. [ 2005] involve many assumptions and have only been validated using simulations; nevertheless, it is worthwhile investigating whether the information preserved in MEG signals is sufficient to characterize and predict fMRI signals.

A simpler approach that has been widely used to predict hemodynamic signals in primary sensory cortices is based on the linear convolution model [Bandettini et al., 1993]. This model uses an empirical hemodynamic response function (HRF) to characterize the net effect of all physiological variables involved in neurovascular coupling. The input to the model approximates the neural activity associated with the sensory stimulus. The input, via mathematical convolution with the HRF, predicts the BOLD signal time‐course, but the accuracy of this prediction depends on how well the input to the model reflects neural activity. Hence, it is desirable to obtain measurements of neural activity to inform the convolution model input functions.

Such measurements have been obtained in several animals studies using, for example, local field potentials (LFPs) and action potentials [Logothetis et al., 2001, monkey visual cortex], and somatosensory‐evoked potentials (SEPs) [Ances et al., 2000, and Martindale et al., 2005, rat SI]. In humans, auditory evoked potentials [Eichele et al., 2005], and spontaneous power fluctuations in the EEG α‐rhythm [Goldman et al., 2002; Laufs et al., 2003] have been integrated into the convolution model.

Many human fMRI studies using the convolution model, however, have not obtained measurements of neural activity, such as studies investigating the linearity of the BOLD signal with respect to stimulus duration. These studies have found that brief stimuli (<4 s) elicit hemodynamic signals that cannot be well‐characterized using the simplest version of the convolution model based on using the stimulus envelope as an input waveform [e.g., Boynton et al., 1996; Pfeuffer et al., 2003; Vazquez and Noll, 1998]. However, animal studies that incorporate electrophysiological measurements of neural activity have found that responses to brief stimuli (<4 s) do not deviate from linearity [e.g., Ances et al., 2000; Martindale et al., 2003, 2005]. Several authors have suggested that nonlinearities in the signaling process between stimulus input to neural response may account for this discrepancy, such as adaptation of the neural signal [Boynton et al., 1996; Miller et al., 2001; Nangini et al., 2005; Pfeuffer et al., 2003; Soltysik et al., 2004]. This is plausible based on independent measurements of several aspects of neural activity (e.g., firing rates, evoked potentials, LFPs) in many sensory cortices that show transient signal increase followed by a steady‐state component in response to sensory stimuli [Albrecht et al., 1984; Ances et al., 2000; Logothetis et al., 2001; McLaughlin and Kelly, 1993; Nangini et al., 2006; Whitsel et al., 2003].

Because BOLD fMRI signal linearity studies in humans have not been conducted with a complementary neural measurement, it is unknown whether the failure of the convolution model is based on poor representation of the neural activity input to the convolution model [Martindale et al., 2005], or deviation from the convolution model itself. The natural next step is to investigate whether replacing the stimulus boxcar waveform with an appropriate waveform derived directly from MEG measurements can provide better characterization of BOLD signal behavior under the convolution model for different duration stimuli. This is plausible, given that under appropriate experimental conditions, the strength of the equivalent current dipole (ECD) obtained in MEG in response to sensory stimulation approximates the number of activated neurons and indirectly quantifies the area of cortical activation [Pantev et al., 1998].

A novel method of integrating MEG and BOLD fMRI data with the convolution model is presented based on a metabolic argument underlying neurovascular coupling. It is hypothesized that the energy density of the MEG waveform provides a good representation for the neural input function. To test this idea, the relationship between MEG energy density and BOLD signals in SI cortex is examined using the convolution model, based on MEG results in the literature obtained using 1 s trains of 22 Hz vibrotactile stimuli [Nangini et al., 2006]. The model results are compared with the typical formulation of the convolution model which uses the envelope of the stimulus profile as input.

MATERIALS AND METHODS

Theory

MEG signals are a consequence of postsynaptic potentials (PSPs) [e.g. Hamalainen et al., 1993], and PSPs have also been implicated in the generation of fMRI signals [Hamalainen et al., 1993; Lauritzen and Gold, 2003; Logothetis et al., 2001]. Thus, the metabolic energy required in PSP generation is likely to relate to both MEG and fMRI signals. The associated hemodynamic response is driven by the neural metabolic demand, although deviations in this relationship have been reported in patients with neurological abnormalities. For example, neuromagnetically active brain areas in the vicinity of high‐grade gliomas have been associated with reduced BOLD signal in the same area in some patients [Grummich et al., 2006]. Under conditions of healthy neurovascular coupling, the metabolic energy driving PSP generation, and consequently fMRI signals, could serve as an input to the convolution model. However, when only MEG and fMRI data are available, this metabolic demand can only be indirectly inferred.

In the postsynaptic cell, sodium–potassium pumps must hydrolyze ATP energy molecules in order to maintain ionic concentration gradients that allow current flow across the cell membrane [Laughlin et al., 1998]. These pumps consume ATP at a rate proportional to the current I [Attwell and Laughlin, 2001]:

(1)

where F is Faraday's constant (amount of electric charge in one mole of electrons). The molecular energy consumption thus gives rise to an ionic current, which in turn generates an electric and magnetic field measurable with EEG and MEG, respectively.

The energy contained in a magnetic field B is given by the energy density u (J/m³).

(2)

where μ₀ is the permeability of free space. This expression is valid for any volume of space in which a magnetic field exists. In the case of MEG, B is linearly related to the equivalent current dipole (ECD) source [Hamalainen et al., 1993], and the energy density can easily be obtained by squaring the ECD waveform. Thus, ECD² is proportional to u and proportional to metabolic energy demand.

The notion that the MEG energy density input to the convolution model can accurately predict SI BOLD signal data forms the basis of our hypothesis. The modeling and experimental details are given below.

Mathematical Modeling

An fMRI experiment was designed to assess the ability of MEG density waveforms, in comparison with stimulus‐derived waveforms, to characterize the fMRI signals from SI using the linear convolution model:

(3)

where r(t) is the predicted BOLD signal in units of percent (%), c is an amplitude scaling factor, HRF(t) is the hemodynamic response function, ⊗ denotes the convolution operator, and n(t) refers to the neural input function. The HRF represents the hemodynamic response to a brief stimulus; it has been measured across various primary sensory cortices and has been found to have a characteristic shape like the one shown in Figure 1. For the modeling, the HRF was assigned fixed parameter values (delay = 2 s, peak = 4 s, full‐width at half‐maximum ≈4 s, return to baseline ≈11 s) consistent with the literature [Friston et al., 1998; Kwong et al., 1992], and was normalized to 1.

Figure 1.

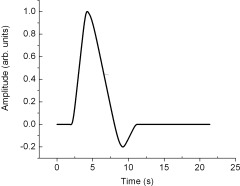
The HRF used in least‐squares fitting. The parameters of the HRF were obtained from the scientific literature (see text for details).

Model 1 represented the “simple” formulation, in which n was proportional to the envelope of the stimulus waveform. In Model 2, n was proportional to the energy density of the MEG source waveforms. The neural input function for each model was normalized to 1. Dimensional analysis of Eq. (3) shows that the scaling factor c must be in (%) units, identical to those of r(t).

Experimental Overview

Results from a previous MEG study were used to provide applicable ECD waveforms for predicting BOLD signals according to Eq. (3) using Model 2. The MEG study utilized 1 s trains of vibrotactile stimulation provided by a pneumatically controlled stimulus device configured to produce trains of 22 Hz oscillations in a circular membrane applied to the right index finger [Nangini et al., 2006]. The stimulus delivery is shown in Figure 2A, illustrating the stimulus profile waveform used as the input for Model 1.

Figure 2.

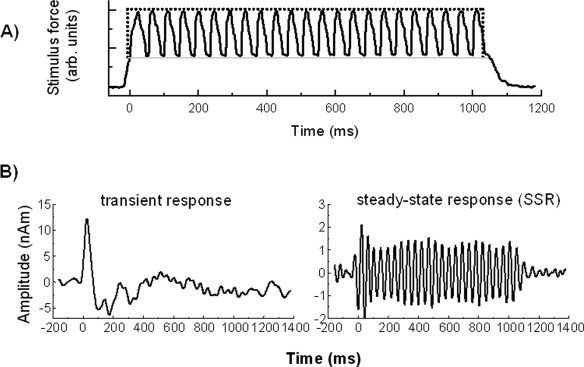
(A) The stimulus train used in MEG and fMRI experiments consisted of 22 Hz oscillations as recorded by force‐sensitive resistor (FSR) voltage, shown here for a 1,000 ms stimulus. The time axis has been adjusted so that zero coincides with the time at which the membrane first contacts the finger. Membrane contact with the finger is shown by a light gray line; the stimulus envelope is marked by a dotted line. (B) Group average transient response (left) and SSR (right) obtained from previous MEG experiments for ISI = 7,000 ms. (Adapted from Nangini et al., [ 2006]: Neuroimage 33:252–262, ©Academic Publishers).

MEG Study

As described in detail [Nangini et al., 2006], ECD source waveforms were fit to low (<20 Hz) and bandpass (18–30 Hz) filtered MEG data to isolate the transient responses and steady‐state responses (SSRs), respectively, to the vibrotactile stimulus train. These responses, averaged over a group of eleven healthy young adult participants, are shown in Figure 2B for an interstimulus interval (ISI) of 7,000 ms.

The MEG study showed that the SSR amplitude remained constant as a function of ISI, while the transient amplitude increased asymptotically to a maximum value by ISI = 7,000 ms. Consequently, a “composite” waveform consisting of the lowpass‐filtered transient response added to the envelope of the bandpass‐filtered SSR was created to represent the total MEG source waveform for a 1,000 ms stimulus duration. Because the transient response peaked near 50 ms and returned to baseline well before 200 ms, the shortest stimulus duration in the fMRI experiment, the MEG response waveforms for the subsecond stimulus durations were constructed by simply truncating the SSR envelope to terminate ∼100 ms after stimulus offset, as seen in the original 1,000 ms SSR waveform. The energy density, defined as the square of the ECD waveform (see above), was then computed for all three stimulus durations.

f MRI

Eleven healthy right‐handed young adults (7 males, 4 females, aged 23–36 years) participated in the fMRI experiment, performed at Sunnybrook Health Sciences Centre. Five had participated in the previous MEG study. FMRI was performed using a 3.0 T MRI system (Signa EXCITE 3.0T, release 11.0; GE Healthcare, Waukesha, WI) with spiral‐in/out k‐space acquisitions [Glover and Law, 2001] (FOV = 19 cm, matrix = 64 × 64, 4‐mm slice thickness, TE/TR/θ = 30/1,000/50). Voxel size was 3 × 3 × 4 mm³. Anatomical axial MRI with high spatial resolution was performed using conventional spoiled‐gradient (SPGR) imaging (24 cm FOV, 1.4 mm thickness, matrix = 256 × 128, TE/TR/θ = 6/35/35).

In the fMRI experiment, the stimulus apparatus and delivery were very similar to that reported in the MEG study described above, given that the pneumatic system was intrinsically fMRI‐compatible. The sole difference was that to test the ability to model BOLD responses, stimulus train duration was varied (200, 500, and 1,000 ms) and ISI was large (60 s for 4 participants, 50 s for 2, and 25 s for the other 5) to enable BOLD signals to return to baseline between stimulus trains. The fMRI stimulus paradigm consisted of three runs, one for each stimulus duration. In each run, four durations of 22 Hz vibrotactile stimulation were presented. There were at least 25 imaging measurements per stimulus duration to follow the time‐course of the resulting BOLD response. Each run was presented in random order with respect to stimulus duration. Based on previous experience in our lab, two inflatable membranes were placed on the palmar surface of the distal phalanges of the right index finger to increase signal‐to‐noise ratio of the fMRI responses. Cardiac and respiratory data were collected for each run using a photoplethysmograph and bellows, respectively.

fMRI Data Analysis

fMRI data were processed for each stimulus duration to obtain the BOLD signals from a region of interest (ROI) located in SI, and subsequently used as input data for both mathematical models. Using analysis of functional neuroimages (AFNI) software [Cox, 1996], the fMRI time series data were motion‐corrected, spatially smoothed with a Gaussian filter (FWHM = 6 mm), and corrected for cardiac and respiratory motion [Glover et al., 2000]. Each time point was normalized by the voxel‐wise time series mean to convert BOLD signals into units of percent signal change. Individual activation maps were created for each stimulus duration by linear regression using the AFNI program 3dDeconvolve. The regression model included a baseline second‐order polynomial and a reference waveform generated by convolving the envelope of the stimulus waveform with an hemodynamic response function (HRF) obtained using the AFNI waver program, with parameter values consistent with those reported in the literature (peak = 4–5 s, fall = 4–5 s) [Friston et al., 1998; Kwong et al., 1992]. The resulting activation maps were restricted to the SI hand region in the postcentral gyrus and corrected for multiple comparisons using the false‐discovery rate algorithm in AFNI (3dFDR) with q = 0.05 [Genovese et al., 2002].

The threshold activation maps for each stimulus duration were then used to localize SI functionally for inclusion in the mathematical modeling. The slice containing the SI hand region was identified for each participant based on the high‐resolution anatomical images, and only voxels activated in this slice were extracted. The “single trial average” was then calculated for each voxel time series, consisting of the average stimulus‐locked BOLD response for the four repetitions of each stimulus duration. These time‐averaged responses were then spatially averaged over all voxels in the ROI, producing a single time series representing the SI response. For each stimulus duration, individual ROI‐averaged time series were averaged across the group, and the mean and variance at each time point were used in the mathematical modeling.

All time series data for individuals were observed to lie within ±2.0 standard deviations from the mean at each time point. The notable exception was the data for the 500 ms stimulus duration for one participant, which fell substantially outside these boundaries. There are multiple sources of spurious signals that potentially could confound the BOLD responses of interest, such as cardiac or respiratory fluctuations, or a perturbation in the attention level of the participant. Consequently, these data were characterized as outliers and were excluded from subsequent reporting of the results. Including or excluding these data did not affect the main outcome of comparing Model 1 and Model 2, although model estimates were slightly affected (and parameter uncertainties increased) when the data were included.

Least‐Squares Fitting

The parameter value c [Eq. (3)] was obtained by calculating a least‐squares fit to minimize χ² (Matlab function “constr”; The Mathworks, Natick, MA) using the sum of the square of the residuals between each linear convolution model and the group average BOLD data, taking account of the variance calculated at each datum (see above). Data for all three stimulus durations were considered simultaneously. Uncertainty in the parameter estimate was determined from the Hessian matrix [Press et al., 1987]. Reduced χ² values, defined as χ_r ² = χ²/(DOF − 1), were computed to evaluate goodness‐of‐fit, where DOF was the number of degrees of freedom. For a good fit, the square of the residuals at each time point approaches the variance, such that χ${}_{\text{r}}^{\text{2}}$ ≈1 [McClave and Dietrich, 1982]. To determine whether using Model 2 versus Model 1 significantly improved model fits to the group data, an F‐test was conducted on the ratio s ${}_{\text{Model1}}^{\text{2}}$/s ${}_{\text{Model2}}^{\text{2}}$, where s ² was defined as the sum of the square of the residuals divided by N − 1, where N is the number of time points in the dataset.

RESULTS

Table I shows the number of participants who activated under each condition and the number of significantly activated voxels, broken down by stimulus duration and ISI. Three participants activated for the 200 ms stimulus, followed by six for the 500 ms stimulus, and four for the 1,000 ms stimulus. Among the participants who activated, the number of significantly activated voxels ranged from 9 to 287 (median = 98).

Table I.

Results of fMRI processing

	200 ms		500 ms		1000 ms
ISI (s)	Np	N	Np	N	Np	N
25 s	0	–	3	39, 48, 144	3	179, 94, 101
60 s	3	117, 13, 98	3	43, 106, 9	1	287

N_p = number of participants who activated; N = number of significantly active voxels.

Composite waveforms consisting of the lowpass‐filtered transient response added to the envelope of the bandpass‐filtered SSR are shown in Figure 3A for all stimulus durations. The shortest stimulus duration (200 ms) is too brief for the SSR to initiate; hence, this waveform consists of the transient response only. The corresponding energy density waveforms, given by the square of amplitude, are shown in Figure 3B. The energy density is clearly dominated by the transient response, which is much larger than that associated with the SSR for the 500 ms and 1,000 ms stimulus durations. These energy density waveforms were used in Model 2 for the neural input function n in Eq. (3). Note that the negative amplitudes in the transient waveforms of Figure 3A are now a positive contribution to the convolution integral in Model 2.

Figure 3.

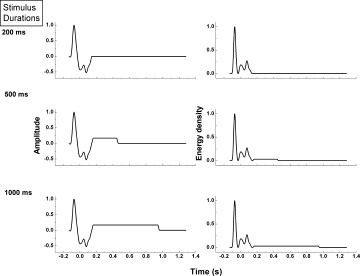
Left column: composite waveforms consisting of the transient response added to the envelope of the SSR for all three stimulus durations. The MEG response waveforms for the subsecond stimulus durations were constructed by simply truncating the SSR envelope. Edges in waveforms were not smoothed since this is intrinsically done by the low‐pass filter nature of the HRF. Right column: corresponding energy density functions for each composite waveform.

Figure 4 shows the BOLD fMRI experimental data and the two least‐squares model fits for the group average, for all stimulus durations. Qualitatively, both models fit the BOLD response at 500 ms stimulus duration. However, Model 1 predictions clearly underestimate and overestimate the peak BOLD signal amplitude at stimulus durations of 200 ms and 1,000 ms, respectively. In contrast, Model 2 predictions fit the peak amplitudes substantially better in both the short and long stimulus regime. Both model fits were similar in terms of their estimates of the BOLD signal before the peak response, i.e. in the rise time; however, because of the amplitude misfit of Model 1, the full‐width‐at‐half‐maximum (FWHM) for the 1,000 ms stimulus was overestimated compared to Model 2. Fit parameters (c, χ², reduced χ², s ²) are given in Table II for both models. The reduced χ² was improved by a factor of ∼20% in Model 2. F‐test results comparing Model 1 to Model 2 (F(74,74) = 1.37, P < 0.05) indicate that the improved fit to the data was statistically significant.

Figure 4.

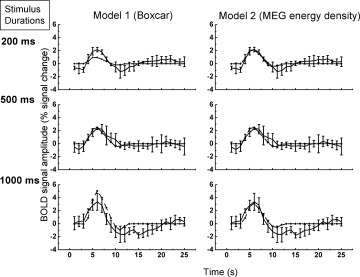
Least‐squares fitting results for Model 1 based on the Boxcar stimulus input waveform (left column) and for Model 2 based on the MEG energy density (right column). Solid line: BOLD data; Dash‐dot line: Model results. Model 2 provides a better fit to the experimental data.

Table II.

Least‐squares model fit parameters

Model	c (% ΔS)	χ2 (102)	Reduced χ2	s 2 (10−1)
1	(4.0 ± 0.2) × 10−3	1.6	2.1	4.8
2	(2.3 ± 0.1) × 10−4	1.2	1.6	3.2

DISCUSSION

The present study provides a simple, theoretical argument for using MEG‐derived energy density waveforms to improve prediction of the BOLD signal in the convolution model for short duration vibrotactile stimuli. The observed data experimentally support the theory: least‐squares fitting of the convolution models [Eq. (3)] to the BOLD data showed that Model 2 adequately represented the data within error (Fig. 4) substantially better than Model 1. The reduced χ² value for Model 2 improved by ∼20%, but was still higher than the expected value of 1.0 due to the variability of the BOLD data itself‐for example, in the initial amplitude (at time = 0) and the rise time at the 1,000 ms stimulus. These variations, however, are only minor considerations in the overall goodness‐of‐fit evaluation.

Physiological Neural Input Functions

As outlined in the introduction, numerous studies motivated the use of experimentally‐derived neural input functions in the convolution model. For example, Ances et al. [ 2000] and Eichele et al. [ 2005] used the amplitude change of the early latency evoked potential, as a function of time, in response to successive brief stimulus events in rat somatosensory and human auditory cortex, respectively. Such changes in neural activity were not observable in the present work due to differences in stimulus conditions; therefore, an alternative measure was required.

The present work derived a neural activity waveform based on the biophysics and neurophysiology of the MEG response. Magnetic fields due to neurons with elongated dendrites, such as the pyramidal cells, which constitute the majority of the neural population in the cerebral cortex [Creutzfeldt, 1995], sum to produce measurable magnetic fields outside the head. Owing to the cortical folding in SI, the magnetic fields generated by pyramidal cells in Area 3b will have a substantial tangential component, to which MEG is sensitive (see Hamalainen et al., 1993]. The MEG signal in SI is a consequence of the intracellular currents triggered by thalamic inputs from the periphery, and represents, at least in part, the time course of synchronously active neural populations.

It is thought that the main contribution to extracellular current comes from excitatory postsynaptic potentials (EPSPs) [Attwell and Iadecola, 2002; Mitzdorf, 1985], which likely reflect hemodynamic activity. The intracellular current (equal to the extracellular current due to current continuity) is the basis of the MEG signal. The energy contained in the MEG signal (proportional to the square of the current) can be thought of as the physical energy correlate of metabolic energy‐demanding processes. It is this energy function that, when input into the convolution model, ties the physics of MEG to the neurobiology of the BOLD signal. Although recent work has suggested that hemodynamic responses are triggered by neurotransmitter‐related signaling rather than direct local energy needs of the brain [Attwell and Iadecola, 2002], these signaling events themselves are correlated to energy demand. The present work does not need to consider whether the mechanisms underlying vasodilation to increase CBF are driven by neurotransmitters or by oxygen depletion in order for the energy argument to be valid, because either way neural activity is colocalized with oxygen usage [Attwell and Iadecola, 2002], in the absence of disease.

The amplitudes of evoked MEG or EEG signal components are not plausible candidates for the neural input function in the present formulation of the convolution model. The negative amplitude in these waveforms do not have a physical meaning when considering that it is the energy demand associated with neural activity that leads to BOLD signals. This is in contrast to a recent theoretical study [Robinson et al., 2006] in which simulated ERP waveforms were input into the hemodynamic state equations of Friston et al. [ 2003]. As a result, the signed area under the ERP waveform influenced the amplitude of the estimated BOLD signal. This alternate approach requires confirmation with experimental data, and it will be interesting to compare both these models in future.

Power Measures as Neural Correlates to BOLD Signal

The concept of an amplitude‐squared measure (i.e. energy density or power) has been used in several studies investigating the neural correlates of fMRI signals. For example, spectral power changes of microelectrode recordings as a function of time have been correlated with BOLD signals in monkey visual cortex [Logothetis et al., 2001]. An EEG‐fMRI study in human visual cortex found a linear relationship between mean powers of EEG current sources and neuronal efficacies derived from BOLD signals for a range of stimulus frequencies, and considered neurovascular coupling as a power transducer that transfers the power of neural activity across all frequencies into the vascular input [Wan et al., 2006]. Others have used power changes of ongoing EEG rhythms in the convolution model to predict BOLD signal changes [e.g. Goldman et al., 2002; Laufs et al., 2006; Moosmann et al., 2003, Parkes et al., 2006]. The current study is novel in that it uses the power of the stimulus‐locked evoked MEG activity to account for BOLD signal changes.

Critique of Convolution Model

The convolution model approach has been critiqued by some authors because it is unable to predict both neural and BOLD signals [Kilner et al., 2005]. They proposed a heuristic model that generates EEG spectral changes and resulting BOLD signal changes, showing that the rate of energy dissipation induced by transmembrane currents shifts the EEG spectral profile to higher frequencies, producing α‐band desynchronization that correlates with the BOLD signal [c.f. Goldman et al., 2002; Laufs et al., 2006; Moosmann et al., 2003]. The present study is similar in that, although it does not predict MEG signals, it attempts to unify MEG and fMRI signals based on a common energy argument. Theoretical studies have calculated the correlation between MEG signal amplitude and energy used by active neurons in units of [Na⁺] concentration [Aubert et al., 2001; Babajani et al., 2005]. Many assumptions are involved in these calculations, and the data in the current study are insufficient to model the numerous mathematical variables involved. Nevertheless, the argument for MEG energy density is simple and compelling.

Additional Limitations

The theoretical basis of the present study is a simplification of the processes underlying the generation of the BOLD signal. MEG signals are only surrogate measures of the neural activity and do not encompass other energy‐demanding processes that also contribute. For example, inhibition has been implicated at different stages of sensory processing [e.g. McLaughlin and Kelly, 1993] and is known to increase synaptic glucose uptake [Jueptner and Weiller, 1995]. However, the role of inhibition in BOLD signal generation is unclear. Waldvogel et al. [ 2000] did not see BOLD changes during an inhibition task and argued that inhibitory processes are more energy‐efficient on account of the low ratio of inhibitory to excitatory synapses (1:6) [see Salek‐Haddadi et al., 2003, for a review]. The relative contribution of power changes in stimulus‐locked brain activity versus ongoing brain rhythms is also unknown, since a study comparing them is currently lacking. In addition, although many studies suggest that a measure of synaptic input (such as the LFP) is a better correlate to hemodynamic activity than spiking output [e.g. Logothetis et al., 2001; Thomsen et al., 2004], action potentials have been found to demand the largest fraction of total energy (47%) in the rodent brain [Attwell and Laughlin, 2001]. However, in primates, action potentials were predicted to consume only 10% of the signaling energy [Attwell and Iadecola, 2002], consistent with the high density of mitochondria in dendrites [Wong‐Riley, 1989]. The postsynaptic/action potential origins of the BOLD signal remain intensely debated; nevertheless, the results reported here suggest that the EPSP current/MEG energy density provide a major contribution to BOLD fMRI signals.

An additional potential criticism involves the decision to use a standardized HRF based on published values. The effect of varying the HRF parameters on the fit results of Models 1 and 2 was investigated to determine if Model 2 improvements could be attributed to different HRF specifications. It was found that the goodness‐of‐fit for each model was influenced by different parameter combinations; however, Model 2 always accounted for more of the variance than Model 1. It is likely that refining the exact parameters of the HRF by, for example, using nonparametric equations, would not change the overall conclusion. This is plausible given that, for short stimulus durations (e.g. ≤4 s), it can be shown that the convolution of HRFs, having parameter values specified within a plausible range, with boxcar functions of increasing duration will always result in output amplitudes that scale with boxcar duration [c.f. Glover, 1999]. However, the peak amplitudes of the measured BOLD data did not increase proportionally to the stimulus duration; in fact, the amplitudes were very similar, within error. This is consistent with the information provided by MEG, which showed that the transient response was the dominant influence on the MEG waveform, so that small increases duration of the SSR, as in the current work, should not significantly alter the BOLD signal.

fMRI signals in SI cortex, however, were difficult to observe, as indicated by Table I. Others have also reported low success rates in response to vibrotactile stimuli [e.g. Tuunanen et al., 2003], but no systematic study has been conducted to determine the underlying cause. Passive vibrotactile stimulation requiring no attention and no response produces smaller fMRI signals in SI compared to vibrotactile stimulation requiring selected attention, such as discrimination of small frequency changes in the stimulus, consistent with electrophysiological observations [Staines et al., 2002]. In addition, it is possible that “resting state” fMRI signals could lead to substantial noise contamination [Kiviniemi et al., 2003]. Encouragingly, it was still possible to obtain statistically significant results across a small group of individuals in the present work.

To conclude, this study presents a novel way of integrating MEG and fMRI data within the context of the convolution model. Incorporating the energy density of neuromagnetic source waveforms was found to be an effective approach to modeling BOLD signals generated by constant‐amplitude vibrotactile stimulus trains in the subsecond stimulus regime. The modeling results provide insight into previous human studies which have not taken the temporal characteristics of the neural activity into account. Future work to evaluate the applicability of this approach across a wide range of stimulus delivery parameters will be very informative.